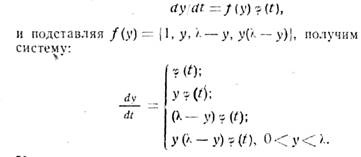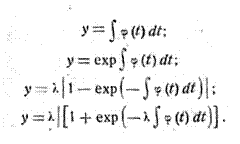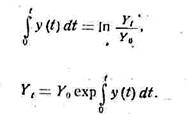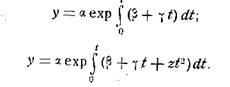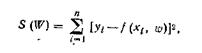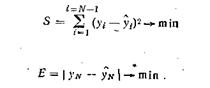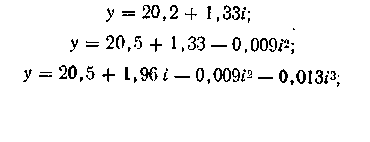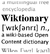Ошибка экстраполяции собственного опыта

Прогнозирование путём прямой экстраполяции. Ошибки прогнозирования

Министерство образования и науки РФ
ГОУ ВПО

Саратовский государственный технический
университет

Кафедра: организация перевозок и
управления на транспорте

Реферат

по дисциплине на тему

«Прогнозирование путём прямой
экстраполяции

Выполнил:                                      
                           студент АМФ гр.ОПТ41

Никитин Р.В.

Саратов 2006

Содержание

Введение                                                                                        
3

Прогнозирование путём прямой экстраполяции          
             4

Ошибки
прогнозирования                                                            16

Заключение                                                                         
          18

Список  используемых
источников                                             19

Введение

Процесс прогнозирования
достаточно актуален в настоящее время. Широка сфера его применения.
Прогнозирование широко используется в экономике, а именно в управлении. В
менеджменте понятие «планирование» и «прогнозирование» тесно переплетены. Они
не идентичны и не подменяют друг друга. Планы и прогнозы различаются между
собой временными границами, степенью детализации содержащихся в них
показателей, степенью точности и вероятности их достижения, адресностью и,
наконец, правовой основой. Прогнозы, как правило, носят индикативный характер,
а планы обладают силой директивного характера. Не подмена и противопоставление
плана и прогноза, а их правильное сочетание – таков путь планомерного регулирования
экономики в условиях рыночной экономики и перехода к ней.

Для того чтобы управлять
будущим, человечество создало определенные механизмы, которые в экономической
науке называются прогнозирование, макроэкономическое планирование и
экономическое программирование.[2]

Прогнозирование – это
предвидение, получение информации о будущем, которое базируется на специальном
научном исследовании.

Прогнозирование имеет два конкретных
аспекта: предсказывать и предвидеть. В зависимости от того, какой результат
необходимо получить или, что необходимо спрогнозировать, преимущество
предоставляется то одному, то другому аспекту.

Прогнозирование
необходимо, потому что будущее необычно и эффект многих решений, принимаемых
сегодня, на протяжении определённого времени не ощущаются. Поэтому точное
предвидение будущего повышает эффективность процесса принятия решения.

Прогнозирование путём прямой
экстраполяции.

Многие социальные
процессы, теоретически поддающиеся управлению, на практике развиваются
стихийно, что дает основание применять к ним методы естествоведческих
прогнозов. При этом следует иметь в виду, что стихийность протекания анали­зируемого
процесса может смениться строго контролируемым це­ленаправленным развитием
(например, давно назрела необходи­мость таких перемен в сферах расселения,
градостроительства, демографии и многих других). Такие изменения могут
осуществляться как волевым порядком, так и с учетом научного анализа, диагноза
и прогноза исследуемого явления. Из этого следует, что в отличие от
естественнонаучных социальный прогноз должен быть ориентирован не на
безусловное предсказание, а на содействие оптимизации принимаемых решений.

Реализуется эта задача
путем использования исследовательской техники поискового и нормативного
прогнозирования, дающего достаточно обоснованные материалы при выработке
рекоменда­ций для целеполагания, планирования, проектирования и управле­ния в
целом.

Основная задача
поискового прогноза при этом — выявление перспективных проблем, подлежащих
решению средствами управ­ления. Предсказание в данном случае носит сугубо
условный харак­тер, базирующийся на абстрагировании от возможного и даже не­обходимого
вмешательства со стороны сферы управления. Мето­дологически недопустимо сводить
социальный прогноз к поиску, но столь же недопустимо переходить сразу к
нормативной разра­ботке данной модели, не имея представления о проблемной
ситуации, в условиях которой и для преодоления которой будет функцио­нировать
предложенный оптимум.

В наиболее общем виде поисковый
(изыскательский, исследовательский, трендовый, генетический, эксплоративный)
прогноз выг­лядит как условное продолжение в будущее тенденций развития
изучаемых явлений, закономерности развития которых в прошлом и настоящем
достаточно хорошо известны. При этом заведомо абстрагируются от возможных и
даже необходимых, неизбежных плано­вых, программных проектных и организационных
решений, способ­ных существенно изменить наметившиеся тенденции. Суть и цель
прогнозного поиска не в адекватном предвосхищении будущего ре­ального состояния
прогнозируемого объекта, а в выяснении того, что реально произойдет при
сохранении существующих тенденций развития, т.е. при условии, что сфера влияния
не выработает поиско­вых решений, способных изменить неблагоприятные тенденции.

Исследовательская техника
разработки поискового прогноза базируется на принципе экстраполяции в будущее
(или интерполяции отсутствующих значений) динамических и на данных, закономерно­сти
развития которых в прошлом известны. Собственно экстраполя­ция (интерполяция)
может быть довольно сложной, учитывающей разнообразные факторы и делающей
прогноз более информатив­ным. При этом на практике поисковый прогноз дает не
одно, а це­лый ряд возможных значений, позволяющих точнее ориентироваться в
складывающейся ситуации.

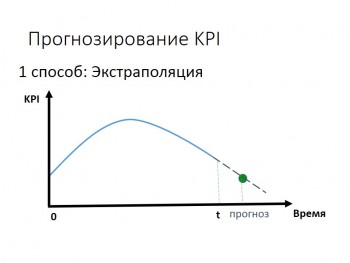
Наиболее простой является
так называемая прямая (механичес­кая, наивная) экстраполяция, которая
продолжает начатый динами­ческий ряд со времени основания до времени упреждения
прогно­за, реализуясь по принципу: если имеется 1, 2, 3, 4 (период основа­ния),
то при условии невмешательства извне и сохранения наметив­шейся тенденции
динамический ряд будет выглядеть как 5, 6, 7, 8 и т.д. по периоду упреждения
(или в случае интерполяции: если 1, 2, 3, 6, 7, 8, то в середине окажется 4, 5)
Не следует недооценивать эффек­тивность такой логики: во многих случаях жизни
важные социальные процессы развиваются именно подобным образом и прогноз на
этой основе оказывается в высокой степени достоверным.

Правда, на практике
социальные прогнозы часто развертывают­ся гораздо более сложным образом — не обязательно
линейно, а, допустим, в геометрической прогрессии, экспоненциально, гипер­болически,
логистически и т.д. Однако на каждый такой случай существует или может быть
введена соответствующая математичес­кая формула, позволяющая усложнять
экстраполяцию до любой требуемой степени. Поэтому 1, 2, 3, 4 не обязательно
должны озна­чать в экстраполяции 5, 6, 7, 8. Экстраполяция может выглядеть и
как 6, 9, 15, 24, и как 16, 32, 64, 128, и даже как 5, 4, 3, 2, 1 (в
зависимости от используемой формулы). Она может быть не только количествен­ной
(статистической), но и качественной (логической), например при экстраполяции
какого-нибудь явления на более широкий круг дру­гих явлений во времени или
пространстве (либо в том и другом сразу) с использованием метода аналогии.

Такая техника широко
используется в естествоведческих прогно­зах в тех случаях, когда исследуемые
процессы развиваются сооб­разно выявленным закономерностям устойчиво, без
отклонений и колебаний. В социальной сфере такие процессы встречаются редко.
Как правило, в своем развитии они претерпевают изменения, мате­матическая
формализация которых требует использования дополни­тельных приемов минимизации
недочетов прямой экстраполяции.

Один из них — вычленение
крайних возможных значений экстраполируемого динамического ряда по заранее
заданным критери­ям, т.е. определение верхней и нижней экстрем. Причем предпола­гается,
что за верхней экстремой простирается область абсолютно нереального,
фантастического, а за нижней — абсолютной невоз­можности функционирования прогнозируемого
объекта, область катастрофического. Сложность в использовании этого приема —
определение и основание критериев построения экстрем.

Другой прием (дополняющий
первый) — определение наибо­лее вероятного значения с учетом данных прогнозного
фона (науч­но-технического, демографического, экономического, социологи­ческого,
социокультурного, политического и международного). Не­обходимо выявить по
каждой группе наиболее информативные в каждом конкретном случае показатели и
соотнести их со значения­ми прямой экстраполяции, а если понадобится, — и со
значениями верхней и нижней экстрем. В результате операции будет определе­но
значение наиболее вероятного тренда — экстраполированной в будущее тенденции.

Таким образом, поисковый
прогноз содержит четыре основные компоненты:

1) данные прямой экстраполяции
динамических рядов исходной модели, служащие первоначальным ориентиром
дальнейших про­гнозных построений;

2) верхняя экстрема прогнозного
поиска: результат сопоставле­ния данных первой поисковой модели с данными
прогнозного фона. Позволяет определить максимальное отклонение тренда в сторону
области нереального;

3) нижняя экстрема прогнозного
поиска: вычисляется теми же способами, что и верхняя. Определяют максимально
возможное отклонение тренда до предела, за которым начинается область ката­строфического;

4) наиболее вероятный тренд
(экстраполированная в будущее тенденция) между верхней и нижней экстремами с
учетом данных прогнозного фона.[3]

В процессе
прогностического исследования недопустимо при­нижение значения ни одного из
перечисленных компонентов. Пер­вые три (прямая экстраполяция, верхняя и нижняя
экстремы) слу­жат как бы ограничителями наиболее вероятного тренда, очерчива­ющими
границы реального в возможных его изменениях. Прямая экстраполяция здесь играет
роль исходного момента, сдерживаю­щего фактора при чрезмерном разбросе оценок
противоречащих данных прогнозного фона.

Вместе же взятые, все
четыре компоненты расширяют познава­тельные возможности лиц, принимающих
решения, показывают недопустимость решений, выводящих объект на уровень утопии
или катастрофы, стимулируют эвристичность мышления, дают возмож­ность более
основательно взвешивать возможные последствия при­нимаемых решений, а все это
вместе обеспечивает высокую сте­пень объективности и, следовательно,
эффективность этих решений.[6]

Необходимо также
отметить, что при разработке целевых, пла­новых, программных, проектных,
организационных прогнозов спе­цифические особенности поискового прогноза будут
проявляться сообразно особенностям процессов разработки целей, планов, про­грамм,
проектов, организационных решений. Результатом прогноз­ного поиска будет не
реально ожидаемое состояние, к которому следует приспособиться, а комплекс
проблем, которые необходи­мо решить. Сама по себе цель поискового прогноза —
выявление ожидаемого проблемного состояния, перспективных проблем, каждая из
которых является составляющим звеном своеобразной ситуации — проблемной.

Прогнозирование размеров перевозок
основывается на ана­лизе развития экономики за прошедший период,    причем этот
анализ должен давать точную количественную    формулировку исследуемому
процессу перевозки грузов путем использования математико-статистических методов.
Предвидение будущего со­стояния размеров перевозок базируется на результатах
анализа прошлого и, следовательно, описывает перспективу в той мере, в какой
она определяется объективно сложившимися явлениями и процессами. При этом
используются главным образом мето­ды и модели экстраполяционного характера.
Методы экстраполирования опираются на принцип детерми­низма, согласно которому
будущее вытекает из настоящего, т. е. на преемственность связи между прошлым,
настоящим и Экстраполяция является  научным методом прогнозирования, так как ее
применение основано на учете объективно существу­ющей инерционности больших
систем, что подтверждается всем опытом социалистического строительства. Для
экономиче­ской системы этот закон выражается в невозможности ограниченными
средствами в короткие сроки изменить поведе­ние системы.

Существует много способов, приемов прогнозирования, осно­ванных
на экстраполяции тенденций. Однако большинство из них не учитывает специфику
объекта прогнозирования. Поэто­му рассмотрим методы и способы, повышающие
надежность  и точность экстраполяционных прогнозов размеров перевозок гру­зов
на уровне АТП, объединений и управлении.

Под точностью прогнозирования
размеров перевозок грузов (ошибкой прогноза) будем понимать величину отклонения
фак­тического значения прогнозируемого показателя от ее истинного значения.
Прогнозу присуща та или иная степень неопределен­ности, поэтому прогнозируемая
величина определяется с допуски разной вероятностью. Поэтому оценка   только
точности показателя является недостаточной. Эту оценку надо дополнить

показателем,  определяющим  надежность  самой  оценки 
точности. Под надежностью  прогнозирования    размеров    перевозок дует
понимать вероятность наступления предсказываемого бытия при заданном комплексе условий
и в пределах установленных допусков. Оценки точность и надежность
взаимосвязаны.

Чем шире установлен предел точности,
тем с. большей вероятностью он будет соблюдаться. Чем жестче допуск на величи­ну
показателя, тем меньше шансов на его такое соблюдение.

Поставленная задача решается в трех
направлениях: иссле­дование новых форм связи, разработка новых критериев оценки
моделей и разработка новых методов прогноза.[6]

Объектом прогнозирования служили
показатели размеров перевозок  Владимирского транспортного управ­ления за
1967—1975 гг.

Развитие транспорта характеризуется ростом объемов пере­возок
грузов, который зависит от уровня развития- экономики региона, сложившейся
системы внутренних и внешних связей. Высокие темпы развития общественного
производства обуслов­ливают быстрый рост перевозочной работы «транспорта.
Пропор­циональное развитие транспорта и всего народного хозяйства :в целом
достигается тогда, когда транспорт полностью удовлет­воряет потребности
экономики и населения в перевозках.

Анализируя содержание таблице  можно видеть, что рост объемов
перевозок грузов полностью определяется ростом вало­вой продукции
промышленности и сельского хозяйства Влади­мирской области, т. е. объем
перевозок грузов автомобильным транспортом общего пользования как бы ‘
синтезирует в себе размеры производства промышленной и сельскохозяйственной
продукции, развитие непроизводственной сферы и т. д. Таким образом, объем 
перевозок грузов  автомобильным  транспортом

общего
пользования, являясь важнейшим отраслевым показателем, в то же время отражает и
динамику развития экономики региона.
Следовательно, прогнозирование  размера перевозок грузов на основании данных за
прошлые периоды приобретает исключительно важное значение, так как от точности
прогнозирования размеров перевозок зависят реальность планов и их
согласованность с планами развития других отраслей.

Полная и систематизированная информация об объекте про­гнозирования
необходима для повышения достоверности и на­дежности прогноза. Ведь
практическая деятельность по состав­лению прогноза в том и состоит, что
обработанная определен­ным образом информация о состоянии объекта на текущий мо­мент,
о его тенденциях превращается в информацию о будущем состоянии объекта.

Наиболее ответственная часть работы по составлению крат­косрочного
прогноза заключается в выборе математической функции, которая отражает общую
тенденцию. Здесь очень важным становится правильный выбор вида кривой, потому
что если уравнение хорошо подобрано к исходным данным, то оно точнее выражает
общую тенденцию, что в конечном счете ска­зывается на результатах прогноза. Выбор
кривой, которая наи­лучшим образом описывает закономерности изменения данного
эмпирического ряда, одна из важнейших проблем экстраполяционного прогноза.

Вид моделей тенденций развития определяется внутренними свойствами
исследуемого процесса. Анализируя динамику раз­меров перевозок для обоснования
формы моделей, воспользу­емся методами теории экономического роста.

Процесс роста размеров перевозок на автомобильном транс­порте можно
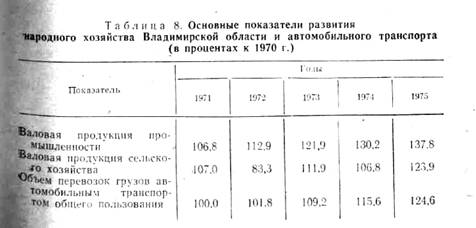
описать дифференциальным уравнением вида:

которое показывает, что изменение зависимой переменной (в на­шем
случае размер перевозок) зависит как от времени, так и от величины самих
размеров перевозок.

Рассматривая частный случай уравнения

                                                                                                   Эти уравнения показывают различные
варианты изменения размеров перевозок. Если ввести логарифмическую
производную(относительную скорость роста, пропорциональное увеличение в единицу
времени) то уравнение примет вид:

Эти уравнения содержат постоянную интегрирования, кото­рую
можно определить по заданному значению I, у

Каждая из перечисленных функций есть простая модель ди­намики
размеров перевозок, описывающая траекторию экономи­ческого роста. Эти функции
могут применяться и применяются для прогнозирования размеров перевозок на
макроуровне, где присутствует большая инерционность и темпы прироста пример­но
одинаковы. Это показано в работе, а также подтверж­дается нашими расчетами.

Инерционность развития в наибольшей мере присуща тем
параметрам, которые характеризуют макроструктуру народного хозяйства и в
меньшей мере проявляются на уровне отраслей, предприятий, отдельных участков
производства. В свою очередь, инерционность параметров, принадлежащих одному
уровню, но различным   отраслям,   предприятиям   тоже   различна.

В соответствии с вышесказанным инерционность элементов
транспортной системы — министерство, автоуправление, авто­транспортное
предприятие (объединение)- различна. Модели по­линомиального вида, полученные
методом прямой экстраполя­ции, достаточно хорошо работающие на высшем уровне,
могут быть не применимы для прогнозирования показателей низшего уровня.

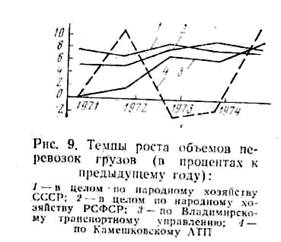
Анализ   
рис.    9    показывает, что на уровне автотранспортного предприятия
инерционность нам­ного меньше, а основная тенденция   часто искажена    
случайной составляющей, поэтому для прог­нозирования    на      уровне    АТП
(объединения)   необходимо   при­менять функции специального ви-1а,   
учитывающие    неравномер­ность темпа прироста в каждый момент времени, т. е.

Таким образом, рекомендуемый нами набор функций для
краткосрочного прогнозирования на уровне АТП и управлений включает не только
широко распространенные в практике эко­номического прогнозирования полиномы до
третьей степени включительно и экспоненциальную функцию, но и две еще не
применявшиеся формы связи (обобщенно-экспоненциальные функции). Параметры
прогнозирующих функций рассчитывают­ся методом наименьших квадратов.

Согласно 
методу наименьших  квадратов    находится    разность  y—f, а сумма квадратов этих разностей  S=будет
функцией неизвестных «параметров. Так,

Определяют такую оценку параметров №, которая минимизирует
5(1Г), для чего определяется й81с!№ и приравнивается нулю, что дает си­стему
т нормальных уравнений, которая должна быть решена относительно W

После нахождения неизвестных  параметров 
прогнозных  кривых  необходимо  оценить  их   близость  к  эмпирическим 
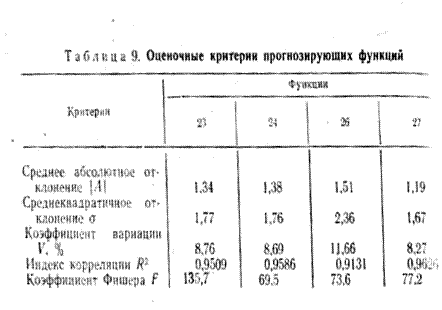
данным   и   выбрать  наилучшую функцию.   Критериями  выбора    являются:  
среднее  абсолютное     отклонение (|Л|);    среднеквадратичное   отклонение —
о; коэффициент вариации — V; индекc корреляции Я.²;  коэффициент
Фишера  Р. Все эти критерии предназна­чены для оценки качества
аппроксимации, поэтому использование их выбора наилучшей прогнозирующей
функции  может привести к большим погрешно­стям. В работе применяется новый
критерий — критерий  минимума  отклоне­ния  в  последней точке   (МОПТ). 
Рассмотрим    этот  метод  более  подробно. Применение этого критерия
основывается на  следующем:  качество прогнозов путем прямой экстраполяции
тенденций улучшается, если за прогнозирующую  функцию  выбирается  та, 
которая  дает  наименьшее   отклонение  в последней точке исследуемого
временного ряда, т. е. задача определения не­известных параметров принимает вид

Для отыскания наилучшей функции применялась следующая
процедура. Исходный временной ряд уменьшался на единицу, т. е. отбрасывалось по­следнее
значение ряда, которое служило для проверки условия минимально­сти. По
укороченному временному ряду находились параметры прогнозиру­ющих функций и
выбиралась та, которая обеспечивала минимальное откло­нение в последней точке.
Полученная форма связи применялась для экстра­поляции уже по полному временному
ряду.

С целью проверки изложенного метода прогнозирования на
конкретном цифровом материале были проведены экспериментальные расчеты по
опреде­лению перспективных величин размеров перевозок для предприятий Влади­мирского
транспортного управления.

Методику выбора лучшей функции проследим на примере
определения перспективной величины
выработки в тонно-километрах на одну списочную автомобиле-тонну по АТП
г. Суздаля (предпрогнозный период 9 лет). Для определения неизвестных
параметров и оценочных критериев функций использовалась   специально  
разработанная   авторами   программа   РРОС—1.

После расчета на  ЭВМ  были получены
следующие зависимости:

Поочерёдно все критерии, при
этом получены следующие средние ошибки прогноза

Критерий
выбора                                /А/                    F                МОПТ

Ошибка прогноза                              7,9                     7,8           5,3           4,8

Анализируя результаты,  приходим к
выводу о том, что критерий  мини­мума отклонения в последней точке является
наиболее целесообразным при    краткосрочном прогнозе на  уровне
автотранспортных  предприятий   (объединений).[1]

Основными источниками могут быть
названы:
1. Простое перенесение (экстраполяция) данных из прошлого в будущие (например, отсутствие
у фирмы иных вариантов прогноза, кроме 10% роста продаж).
2. Невозможность точно определить вероятность события и его воздействия на исследуемый
объект.
3. Непредвиденные трудности (разрушительные события), влияющие на
осуществление плана, например внезапное увольнение начальника отдела сбыта, ошибки
первой категории могут быть сужены путем применения методов регрессионного
анализа, криволинейного сглаживания и других техник.

Ошибки второй категории
частично могут быть преодолены при помощи метода Дельфи, сценариев, моделей, анализа
модели жизненного цикла. 

В целом точность
прогнозирования повышается по мере накопления опыта прогнозирования и отработки
его методов.[4]

ПУТИ ПОВЫШЕНИЯ
ЭФФЕКТИВНОСТИ И ОБОСНОВАННОСТИ ПРОГНОЗОВ

В наибольшей степени,
эффективность прогноза зависит от того, на сколько они  полезны для
планирования и осуществления деловых операций. Прогнозы полезны в тех  случаях,
когда его компоненты тщательно продуманы и ограничения, содержащиеся в  прогнозе
откровенно названы. Существует несколько способов сделать это.  Спросите себя,
для чего нужен прогноз, какие решения будут на нем основаны.
Этим определяется потребная точность прогноза. Некоторые решения принимать
опасно,  даже если возможная погрешность прогноза—менее 10%. Другие решения
можно  принимать безбоязненно даже при значительно более высокой допустимой
ошибке. Определите изменения, которые должны произойти, чтобы прогноз оказался 
достоверным. Затем с осмотрительностью оцените вероятность соответствующих
событий. Определите компоненты прогноза. Подумайте об источниках данных, определите,
насколько ценен опыт прошлого в составлении прогноза. Не настолько ли  быстры
изменения, что основанный на опыте прогноз будет бесполезным? Дают ли  данные
по подобным продуктам (или вариантам развития) основания для составления  прогноза
о судьбе вашего продукта? Насколько просто или недорого можно будет
получить надежную информацию об опыте прошлого? Определите, насколько структурированным
должен быть прогноз. При прогнозировании сбыта может быть  целесообразно
выделить отдельные части рынка (развивающиеся потребители,  стабильные потребители,
крупные и мелкие потребители, вероятность появления новых  потребителей и
т.п.).
Также путем повышения эффективности прогнозов является применение анализа  безубыточности.
Этот анализ определяет точку, в которой общий доход уравнивается с  суммарными
издержками, то есть точку, в которой предприятие становится прибыльным.  Точка
безубыточности обозначает ситуацию, при которой общий доход становится
равным суммарным издержкам. Для определения точки безубыточности необходимо учесть
три основных фактора: продажную цену единицы продукции, переменные  издержки на
единицу продукции и общие постоянные издержки на единицу продукции.[5]

Из всего вышесказанного
можно сделать вывод, что при современных условиях  функционирования рыночной
экономики, невозможно успешно управлять коммерческой  фирмой, без эффективного
прогнозирования её деятельности. От того, на сколько  прогнозирование будет
точным и своевременным, а также соответствовать поставленным
проблемам, будут зависеть, в конечном счете, прибыли, получаемые предприятием. 
Для того, чтобы эффект прогноза был максимально полезен, необходимо создание  на
средних и крупных предприятиях так называемых прогнозных отделов (для малых  предприятий
создание этих отделов будет нерентабельным). Но даже без таких отделов  обойтись
без прогнозирования невозможно. В этом случае прогноз должен быть получен
силами менеджеров и задействованными в этом процессе специалистами.
Что касается самих прогнозов, то они должны быть реалистичными, то есть их вероятность
должна быть достаточно высока и соответствовать ресурсам предприятия. Для
улучшения качества прогноза необходимо улучшить качество информации, необходимой
при его разработке. Эта информация, в первую очередь, должна обладать  такими
свойствами, как достоверность, полнота, своевременность и точность.  Так как
прогнозирование является отдельной наукой, то целесообразно (по мере  возможности)
использование нескольких методов прогнозирования при решении какой-
либо проблемы. Это повысит качество прогноза и позволит определить «подводные камни»,
которые могут быть незамечены при использовании только одного метода.  Также
необходимо соотносить полученный прогноз с прецедентами в решении данной  проблемы,
если такие имели место при похожих условиях функционирования  аналогичной
организации (конкурента). И при определенной корректировке, в
соответствии с этим прецедентом, принимать решения.

Список используемых источников

4. Поисковое социальное прогнозирование. М.: Наука, 1994.

5. Нормативное социальное прогнозирование. М.: Наука, 1997

6. Основы экономического и социального прогнозирова­ния / Под
ред. В.Н. Мосина, Д.М. Крука. М.: Высшая школа, 1985.

Изучение всех влияющих на исследуемый объект факторов одновременно
провести невозможно, поэтому в эксперименте рассматривается их ограниченное
число. Остальные активные факторы стабилизируются, т.е. устанавливаются на
каких-то одинаковых для всех опытов уровнях.

Некоторые факторы не могут быть обеспечены системами стабилизации
(например, погодные условия, самочувствие оператора и т.д.), другие же
стабилизируются с какой-то погрешностью (например, содержание какого-либо
компонента в среде зависит от ошибки при взятии навески и приготовления
раствора). Учитывая также, что измерение параметра у осуществляется
прибором, обладающим какой-то погрешностью, зависящей от класса точности
прибора, можно прийти к выводу, что результаты повторностей одного и того же
опыта у_к будут приближенными и должны
отличаться один от другого и от истинного значения выхода процесса.
Неконтролируемое, случайное изменение и множества других влияющих на процесс
факторов вызывает случайные отклонения измеряемой величины у_к
от ее истинного значения – ошибку опыта.

Каждый эксперимент содержит элемент неопределенности вследствие
ограниченности экспериментального материала. Постановка повторных (или
параллельных) опытов не дает полностью совпадающих результатов, потому что
всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно
оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в
одинаковых условиях несколько раз и затем берется среднее арифметическое всех
результатов. Среднее арифметическое у равно сумме всех n отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение результата любого опыта от среднего арифметического
можно представить как разность y₂–
, где y₂ – результат отдельного
опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений
повторных опытов. Для измерения этой изменчивости чаще всего используют
дисперсию.

Дисперсией называется среднее значение квадрата отклонений
величины от ее среднего значения. Дисперсия обозначается s² и
выражается формулой:

где (n-1)
– число степеней свободы, равное количеству опытов минус единица. Одна степень
свободы использована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положительным знаком,
называется средним квадратическим отклонением, стандартом или квадратичной
ошибкой:

Ошибка опыта является суммарной величиной, результатом многих
ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др.
Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.

Все ошибки принято разделять на два класса: систематические и
случайные (рисунок 1).

Систематические ошибки порождаются причинами, действующими
регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая ошибка – это ошибка,
которая остаётся постоянно или закономерно изменяется при повторных измерениях
одной и той же величины. Эти ошибки появляются вследствие неисправности
приборов, неточности метода измерения, какого либо упущения экспериментатора,
либо использования для вычисления неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка всех измерительных приборов и
безусловное выполнение выработанных практикой правил экспериментальных работ.
Если систематические ошибки вызваны известными причинами, то их можно
определить. Подобные погрешности можно устранить введением поправок.

Систематические ошибки находят, калибруя измерительные приборы и
сопоставляя опытные данные с изменяющимися внешними условиями (например, при
градуировке термопары по реперным точкам, при сравнении с эталонным прибором).
Если систематические ошибки вызываются внешними условиями (переменной
температуры, сырья и т.д.), следует компенсировать их влияние.

Случайными ошибками называются
те, которые появляются нерегулярно, причины, возникновения которых неизвестны и
которые невозможно учесть заранее. Случайные ошибки вызываются и объективными
причинами и субъективными. Например, несовершенством приборов, их освещением,
расположением, изменением температуры в процессе измерений, загрязнением
реактивов, изменением электрического тока в цепи. Когда случайная ошибка больше
величины погрешности прибора, необходимо многократно повторить одно и тоже
измерение. Это позволяет сделать случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше погрешности прибора, то уменьшать её нет
смысла. Такие ошибки имеют значение, которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми для измерений сделанных даже в
одинаковых условиях. Поскольку причины, приводящие к случайным ошибкам
неодинаковы в каждом эксперименте, и не могут быть учтены, поэтому исключить
случайные ошибки нельзя, можно лишь оценить их значения. При многократном
определении какого-либо показателя могут встречаться результаты, которые
значительно отличаются от других результатов той же серии. Они могут быть
следствием грубой ошибки, которая вызвана невнимательностью экспериментатора.

Систематические и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы исключать инструментальные ошибки, следует
проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта.
Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева
реакционной среды, разного способа перемешивания и т.п.

При повторении опытов такие ошибки могут вызвать большой разброс
экспериментальных результатов.

Очень важно исключить из экспериментальных данных грубые ошибки,
так называемый брак при повторных опытах. Грубые ошибки легко
обнаружить. Для выявления ошибок необходимо произвести измерения в других
условиях или повторить измерения через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность в записях, тщательность в работе и
записи результатов эксперимента. Грубая ошибка должна быть исключена из
экспериментальных данных. Для отброса ошибочных данных существуют определённые
правила.

Например, используют критерий Стьюдента t (Р;
f):
Опыт считается бракованным, если экспериментальное значение критерия t по
модулю больше табличного значения t (Р; f).

Если в распоряжении исследователя имеется экспериментальная оценка
дисперсии S²(y_k)
с небольшим конечным числом степеней свободы, то доверительные ошибки
рассчитываются с помощью критерий Стьюдента t (Р;
f):

ε()
= t (Р; f)* S(y_k)/= t (Р; f)* S()

ε(y_k) = t (Р; f)* S(y_k)

За последние несколько недель в различных СМИ появилось много статей с такими заголовками, как «Биотопливо против природы», «Биовредитель» и т.п. Все эти статьи – перепечатка новостей, базирующихся на одном исследовании Института европейской экологической политики (IEEP). Авторы исследования считают, что использование биотоплива является для природы более опасным явлением, нежели бензиновые выбросы из-за увеличения эмиссии углекислого газа, которое  произойдет из-за вырубки лесов, чтобы освободить  посевные площади под культуры для переработки на биотопливо.

Хотелось бы отметить принципиальные ошибки в таком подходе вообще и неприменимость выводов к России в частности.

В первую очередь, прогноз авторов исследования похож на прогнозы, которые делали достаточно умные люди в конце  XIX века по поводу тамошних проблем. Сто лет назад лучшие умы Лондона думали: что же больше всего грозит этому городу, от чего он может погибнуть? И все сошлись на том мнении, что Лондон через пятьдесят лет погибнет от конского навоза: он завалит Лондон до вторых этажей, так как рост количества транспортных средств – лошадей – будет таков, что не будет возможности убирать отходы.

Если бы в то время существовал этот институт, то он бы предоставил прогноз об экологической катастрофе из-за развития гужевого транспорта и предлагал бы соответствующие меры с общемировым контролем по использованию конной тяги.

Почему же умные и даже учёные мужи так ошиблись с прогнозом экологической катастрофы? Если кратко, то ответ будет состоять в двух словах: «ошибка экстраполяции». Если чуть подробнее, то это был прогноз методом непрерывной экстраполяции на время, превышающее время действия закона, отвечающего за линейное развитие системы. В данном случае тенденции развития гужевого транспорта экстраполировались на время, в течение которого сами эти тенденции могли подвергнуться значительному изменению.

Одна из таких ошибок авторов – использование текущих урожайностей культур и непринятие во внимание роста урожайности, связанного с развитием технологий.

На графике показана динамика сбора зерновых в мире, изменения посевных площадей и производства биотоплива с 1976 по 2005 годы. Хорошо видно, что за 30 лет сбор зерновых (пшеница, ячмень, кукуруза, рис) вырос на 1 млрд. тонн (на 53%), при этом посевные площади уменьшились на 54 млн. га (6%) – это примерно Франция или 15 Бельгий. На фоне таких изменений производство биотоплива в мире выросло с нуля до 30 млн. тонн (столько же потребляется бензина в России).

Такой рост производства зерновых обусловлен развитием технологий, обеспечивших 60%-ый рост урожайности за 30 лет – 2% в год! Как говорит современная наука, пока предела этому росту не видно. При этом доклад даже не учитывал новые поколения биотоплива из непищевого сырья, так же, как британские умы не могли представить скорость и масштабы развития автомобильных технологий.

Второе замечание, которое я хочу сделать, связано уже не столько с этим злополучным докладом, а с российским реалиями. Несмотря на засуху 2010 года, Россия собрала 65 млн. тонн зерна. При этом в округах, которых не сильно пострадали от засухи, увеличилось и производство зерна, и его урожайность. Это говорит о том, что системные инвестиции в производство зерна дали свои плоды, и даже в текущем, крайне неблагоприятном по погоде году, производство зерна превышает урожаи 1998-2000 годов. Какой из этого следует вывод? Несмотря на отдельные неблагоприятные годы, производство зерна в России будет расти из-за интенсификации сельского хозяйства и потепления климата, а объемы производства зерна будут серьезно превышать объемы внутреннего потребления и экспорта, так, как это произошло в 2008-2009 годах.

Для снятия переизбытка зерна с рынка и требуется производство биотоплива, которое может потребляться как в России, так и экспортироваться в ту же Европу. Нам не надо вырубать леса для производства биотоплива – чего так боятся европейцы, и воды у нас пока хватает.

Россия хорошо позиционирована, чтобы стать крупным поставщиком биотоплива в мире, как Бразилия. Дело только за принятием правильных решений, и умением анализировать исследования так, чтобы не быть похожими на те лучшие умы Лондона, которые боялись утонуть в навозе.

Алексей Аблаев,

президент Российской биотопливной ассоциации

Assessment |
Biopsychology |
Comparative |
Cognitive |
Developmental |
Language |
Individual differences |
Personality |
Philosophy |
Social |
Methods |
Statistics |
Clinical |
Educational |
Industrial |
Professional items |
World psychology |

Statistics:
Scientific method ·
Research methods ·
Experimental design ·
Undergraduate statistics courses ·
Statistical tests ·
Game theory ·
Decision theory

---

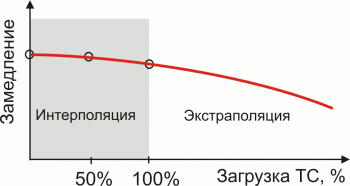
In statistics, extrapolation is the process of constructing new data points outside a discrete set of known data points. It is similar to the process of interpolation, which constructs new points between known points, but its results are often less meaningful, and are subject to greater uncertainty.

[]

[]

This means creating a tangent line at the end of the known data and extending it beyond that limit. A linear extrapolation will only provide good results when used to extend the graph of an approximately linear function. A linear extrapolation can be done easily with a ruler on a written graph or with a computer. An example is a trend line.

[]

A conic section can be created using five points near the end of the known data. If the conic section created is an ellipse or circle, it will curve back on itself. A parabolic or hyperbolic curve will not, but may curve back relative to the X-axis. This type of extrapolation could be done with a conic sections template on a written graph or with a computer.

[]

A polynomial curve can be created through the entire known data or just near the end. The resulting curve can then be extended beyond the end of the known data. Polynomial extrapolation is typically done by means of Lagrange interpolation or using Newton’s method of finite differences to create a Newton series that fits the data. The resulting polynomial may be used to extrapolate the data.

[]

Typically, the quality of a particular method of extrapolation is limited by the assumptions about the function made by the method. If the method assumes the data is smooth, then a non-smooth function will be poorly extrapolated.

Even for proper assumptions about the function, the extrapolation can diverge exponentially from the function. The classic example is truncated power series representations of sin(x) and related trigonometric functions. For instance, taking only data from near the x = 0, we may estimate that the function behaves as sin(x) ~ x. In the neighborhood of x = 0, this is an excellent estimate. Away from x = 0 however, the extrapolation moves arbitrarily away from the x-axis while sin(x) remains in the interval [−1,1]. I.e., the error increases without bound.

Taking more terms in the power series of sin(x) around x = 0 will produce better agreement over a larger interval near x = 0, but will still produce extrapolations that diverge away from the x-axis.

This divergence is a specific property of extrapolation methods and is only circumvented when the functional forms assumed by the extrapolation method (inadvertently or intentionally due to additional information) accurately represent the nature of the function being extrapolated. For particular problems, this additional information may be available, but in the general case, it is impossible to satisfy all possible function behaviors with a workably small set of potential behaviors.

The extent to which an extrapolation is accurate is known as the «prediction confidence interval,» and is usually expressed as an upper and lower boundary within which the prediction is expected to be accurate 19 times out of 20 (a 95% confidence interval).

[]

An extrapolation’s reliability is indicated by its prediction confidence interval, which often diverges to impossible values. Extrapolating beyond that range can lead to misleading results.

For example, the death rate from a new disease may increase dramatically early on. If the graph of the death rate is then extrapolated linearly, it might appear that the entire human population will be dead from the disease in a short number of years. In reality, the death rate from a newly discovered disease may fall as the susceptible die off and the remainder alter their behavior to avoid contracting the disease. Those who remain may also have a natural immunity to the disease or an acquired immunity due to exposure. Medical treatments affecting the spread and death rate of the disease may be developed, as well. A simple linear extrapolation assumes that there is an infinite population, and if the trend is growing faster than the population it will predict that more will have died than have ever been alive.

Similarly, if the amount of water in a lake is decreasing over time, a linear extrapolation will predict that there will be a negative amount of water shortly after the water is gone. This is an absurd result which indicates that the extrapolation is being performed in the wrong domain.

Selection of an improper domain, such as an infinite domain when all possible values are finite, or a negative domain for nonnegative values, is the second most common extrapolation error after failure to include a prediction confidence interval. See also: logistic curve.

[]

In complex analysis, a problem of extrapolation may be converted into an interpolation problem by the change of variable z ’ 1/z. This transform exchanges the part of the complex plane inside the unit circle with the part of the complex plane outside of the unit circle. In particular, the compactification point at infinity is mapped to the origin and vice versa. Care must be taken with this transform however, since the original function may have had «features», for example poles and other singularities, at infinity that were not evident from the sampled data.

Another problem of extrapolation is loosely related to the problem of analytic continuation, where (typically) a power series representation of a function is expanded at one of its points of convergence to produce a power series with a larger radius of convergence. In effect, a set of data from a small region is used to extrapolate a function onto a larger region.

Again, analytic continuation can be thwarted by function features that were not evident from the initial data.

Also, one may use sequence transformations like Padé approximants and Levin-type sequence transformations as extrapolation methods that lead to a summation of power series that are divergent outside the original radius of convergence. In this case, one often obtains
rational approximants.

References[]

• Extrapolation Methods. Theory and Practice by C. Brezinski and M. Redivo Zaglia, North-Holland, 1991.

See also[]

• Forecasting
• Multigrid method
• Prediction interval
• Regression analysis
• Richardson extrapolation
• Trend estimation

Template:Enwp

Добавлено в закладки: 0

Что такое метод экстраполяции? Описание и определение понятия.

Метод экстраполяции – это один из главных способов прогноза, который основывается на прогнозировании событий, учитывая анализ показателей, которые имели место в прошлые годы (при этом, не меньше чем за 5 – 8 лет). В данный момент есть приблизительно триста уравнений, которые дают возможность определить тенденции процессов и позволяют оценить  линейную простую зависимость явления и квадратичную зависимость.

Экстраполи́рование, экстраполя́ция, (от лат. extrā — снаружи, вне, кроме, за и лат. polire — выправляю, приглаживаю, меняю, изменяю) — это особенный вид аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не меж фиксированными значениями.

Другими словами, экстраполяция — это приближённое определение значений функции в точках, которые лежат вне отрезка, по её значениям в точках.

Методы

Во многих случаях методы экстраполяции похожи с методами интерполяции.

Самый распространённый способ экстраполяции — это параболическая экстраполяция, при которой в точке берётся значение многочлена степени, которая принимает в точке заданные значения. Для параболической экстраполяции применяют интерполяционные формулы.

Применение

Общее значение — это распространение выводов, которые получены из наблюдения над одной частью явления, на его другую часть.

В маркетинге — это распространение выявленных закономерностей развития изучаемого предмета на будущее.

В статистике — это распространение тенденций, установленных в прошлом, на будущий период (экстраполяция во времени используется для перспективных расчетов населения); распространение выборочных данных на прочую часть совокупности, которая не подвергнута наблюдению (экстраполяция в пространстве).

Одним из более распространенных способов краткосрочного прогнозирования экономических явлений — это экстраполяция

Термин “экстраполяция” имеет немного толкований в широком смысле экстраполяция – это способ научного исследования, который заключается в распространении выводов, которые получены из наблюдений за одной частью явления, на а другую его часть В узком смысле – это определение по нескольким данным функции прочих ее значений вне данного ряда за этим рядом.

Прогноз экстраполяции

Экстраполяция заключена в изучении сложившихся в настоящем и прошлом устойчивых тенденций экономического развития и их перенос на будущее

Цель данного прогноза — это показать, к каким итогам можно сделать в будущем, когда передвигаться к нему с аналогичной ускорением или скоростью, что и в прошлом

Прогноз определяет ожидаемые варианты данного экономического развития исходя из гипотезы, что главные факторы и тенденции прошлого периода сберегается на период прогноза или что возможно обосновать и учесть направление их изменений в рассматриваемой перспективе. Такую гипотезу выдвигают, учитывая инертность экономических процессов и явлений.

В прогнозировании экстраполяция используется при изучении временных рядов экстраполяции в общем типе можно представить, как определенное значение функции зависимо от особенностей изменения уровней в рядах динамики способы экстраполяции могут быть сложными и простыми.

Простые способы экстраполяции базируются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего абсолютного прироста, среднего уровня ряда, среднего темпа роста.

Различные способы экстраполяции

Рассмотрим детальнее названные способы экстраполяции.

При экстраполяции на основании среднего уровня ряда применяется принцип, при котором прогнозируемый уровень равняется среднему значению в прошлом уровней ряда.

В данной ситуации экстраполяция дает точечную прогностическую оценку. Точное совпадение данных оценок с фактическими данными — маловероятное явление. Таким образом, прогноз обязан быть в виде интервала значений.

Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его использование для прогнозирования увеличивает степень надежности прогноза. Однако недостаток рассматриваемого подходов периода — это то, что доверительный интервал не связывается с периодом предупреждения.

Экстраполяцию по среднему абсолютному приросту можно провести тогда, когда линейной считать общую тенденцию развития явления.

Чтобы рассчитать прогнозное значение, уровень необходимо определить абсолютный средний прирост. Затем, зная уровень ряда динамики, который принимают за основу экстраполяции.

Экстраполяцию по среднему темпу роста можно осуществить, когда есть основания полагать, что суммарная тенденция ряда динамики характеризуется показательной кривой.

Доверительный интервал прогноза по средним темпом роста можно определить лишь в том случае, когда средний темп роста рассчитывают при помощи статистического оценивания параметров экспоненциальной кривой.

Все три рассмотренные способа экстраполяции тренда простейшие, но вместе и самые приближенные.

Сложные способы экстраполяции предусматривают выявление главной тенденции, то есть использование статистических формул, которые описывают тренд.

Способы данной группы возможно разделить на два главных вида: адаптивные и аналитические (кривые роста).

Аналитические способы прогнозирования

В основание аналитических способов прогнозирования (кривых роста) лежит принцип получения при помощи метода самых малых квадратов оценки детерминированной компоненты, которая характеризует главную тенденцию

Адаптивные способы прогнозирования основываются на том, что процесс реализации их заключен в вычислении последовательных во времени значений прогнозируемого показателя, учитывая степень влияния прошлых уровней. К ним относят способы экспоненциальной и текучей средних, способ гармонических весов, способ авторегрессииї.

Способ аналитического выравнивания тренда (способ наименьших квадратов) может быть использован лишь тогда, когда развитие явления довольно хорошо описывают построенную модель и условия, которые определяют тенденцию развития в прошлом, не изменятся существенно в будущем. При выполнении данных требований прогнозирование производится при помощи подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждения.

Процедура создания прогноза по применению аналитического выравнивания тренда включает в себя такие этапы:

1) выбор формы кривой, которая отображает тенденцию;

2) определение показателей, характеризующие количественно тенденции изменений;

3) оценка вероятности прогнозных расчетов

Подбор формы кривой возможно осуществлять на основании построения графика, суммарный тип которого обычно дает возможность установить:

а) имеет динамический ряд показателя выраженную четко тенденцию;

б) если так, то данная тенденция плавная;

в) каков характер тенденции

Отвечая на данные вопросы, нужно помнить, что наружная простота графика ложная. Каждая динамическая задача намного сложнее от статического и каждая точка кривой — это результат изменения явления во времени и пространстве.

Ввиду этого для увеличения достоверности и обоснованности выравнивания для более точного выявления тенденции, которая есть, нужно провести вариантный расчет по некоторым аналитическими функциями и на основании статистических и экспертных оценок определить лучшую форму связей.

На втором этапе нужно определить параметры уравнения связи. Для того, чтобы их найти, применяют способ малых квадратов. В данной ситуации выравнивающая функция будет занимать данное положение среди факт политических значений показателей, при котором общее отклонение точек от функции будет наименьшим.

Обоснованную и достоверную оценку имеющимся результатам можно дать, применяя статистические показатели: средний коэффициент увеличения, коэффициент корреляции, остаточная и общая дисперсия, другой индекс корреляции, коэффициент корреляции ряда отклонений и исходного ряда, определенного по разнице выровненных и фактических по любой аналитической функции.

Для того, чтобы проверить гипотезу об отсутствии или наличии автокорреляции применяют таблицы с критическими значениями коэффициента автокорреляции при разных уровнях значимости. Когда табличное значение коефициэнта автокорреляции больше фактического, то возможно утверждать, что автокорреляция устраняется или отсутствует, а означает, возможно применять формулы для возиожностной оценки значений, которые прогнозируются по этому и точками.

Для прогноза были выбраны такие функции, как логарифмическая, линейная, ступенчатая, полиномиальная и экспоненциальная.

Не все выбранные аналитические функции выравнивают хорошо динамический выходной ряд. Об этом говорит значение индекса (коэффициента) корреляции Для того, чтобы прогнозировать, то есть продолжать сформированные тенденции на ближайшую перспективу, можно использовать лишь те функции, для которых индекс (коэффициент) корреляции больше 0,7 К таковым относят линейную, экспоненциальную и полиномиальную функцию. Последняя имеет самый большой коэффициент корреляции, равен 0,847, и самую малую величину остаточной дисперсией.

Порой, само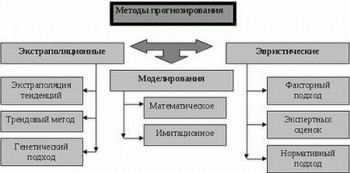й приемлемой формой аналитической функции для прогнозирования является полиномиальная функция, которая представлена уравнением:

Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на такие три месяца: у25 = 654,83; у = 655,93; у ”- 657,07 тыс грн 26 27

Возможность того, что экономический прогнозируемый показатель в заданный момент времени будет равняться значению, которое отвечает точечной прогноза, почти равняться нулю. Потому к точечному прогнозу границы вероятного изменения прогнозируемого значения показателя.

Заметим, что в полученных при прогнозировании оценок доверительных интервалов необходимо отнестись с осторожностью Это связывается со спецификой динамических рядов Их специфичность заключена в том, что увеличение количества наблюдений в статической совокупности дает возможность получить точные характеристики данной совокупности, в то время как аналогичное удлинение ряда динамики приводит не всегда к похожим результатам, особенно в тех ситуациях, когда ряды динамик применяются для прогнозирования. Данное обстоятельство связывается с тем, что информационная ценность уровней потеряется по мере их удаления от периода предубеждение, то есть означает уровни ряда динамики при прогнозировании неравноценно. Потому параметры уравнений аппроксимирующих кривых роста могут обладать погрешности и изменять собственные оценки при исключении части членов ряда или Анне добавил новых членов ряда динамики, что отображается на точности расчетных значений уровней ряда динамики. Помимо этого, параметры моделей тренда, которые получены способом самых малых квадратов, остаются неизменным и в течение рассматриваемого периода. На практике зачастую встречаются случаи, когда параметры моделей изменяются, а процедуры, которые сглаживают при помощи способа самых малых квадратов не могут определить такие изменения.

Поэтому наиболее эффективными являются адаптивные способы, в которых значимость уровней ряда динамики снижается по мере их удаления от прогнозируемого периода. К ним относят: способ текучих средних, способ экспоненциального сглаживания, способ гармонических весов и прочие, включаются в класс адаптивных способов.

Зачастую несколько динамики характеризуются резкими колебаниями показателей по годам. Данные ряды обычно, имеют слабую связь со временем и не проявляют четкой тенденции к изменению. В данной ситуации способы аналитического выравнивания малоэффективен, потому что возможность расчетов резко уменьшается. Доверительные границы прогноза порой оказываются шире, чем колебания показателя в некоторых динамиках.

При прогнозировании на основании временных рядов, которые весьма колеблются, можно применять способ текучих средних, при помощи которого возможно исключить случайные колебания временного ряда.

Интервал, величина которого все еще постоянная, постепенно помещается на одно наблюдение. Когда наблюдается определенная цикличность изменений показателей, интервал текучести равняется длительности циклу. В ситуации отсутствия цикличности в изменении показателей советуется исполнять различный расчет при параметре сглаживания. Лучший вариант определяется на основании дальнейшей оценки и выровненных рядов.

По данным выровненных значений ряда динамики производится подбор формы кривой, которая отражает тенденции развития явления. Полученное уравнение регрессии применяется для определения прогнозного значения исследуемого показатель.

На основании выровненных значений товарных запасов предприятия имеются такие значения коэффициента корреляции. Приведенные данные говорят, что наилучшие итоги должны по данным, которые выровнены на основании уровней исследуемого ряда динамики

Метод экспоненциального сглаживания

Экспоненциальное сглаживание – это выравнивание динамических рядов, весьма колеблются, цели стабильного прогнозирования По данному способу возможно дать обоснованные прогнозы на основе рядов динамики, имеют умеренный связь во времени, и обеспечить больше учета показателей, которые достигнуты за последние годы. Сущность метода оформляется в сглаживании временного ряда при помощи взвешенной текучей средней, в которые и веса подчиняются экспоненциальному закону.

Всякое сглажено значение рассчитано при помощи объединения прошлого текущего значения сглаженного значения и временного ряда. В данной ситуации текущие значения временного ряда разрешаются, учитывая константы, сглаживает.

Мы коротко рассмотрели метод экстраполяции: методы, применение. Оставляйте свои комментарии или дополнения к материалу.

Существует две в некотором смысле сходные логические ошибки, совершаемые при обсуждении политических проектов.
Сторонники национализации всего и вся нередко рассуждают следующим образом: сейчас товар X продается за деньги и его хватает не всем; если национализировать производство товара X и раздавать его гражданам бесплатно, вопрос денег исчезнет и товара X будет хватать всем. Ошибкой этого рассуждения является то грустное обстоятельство что производство товара X требует ресурсов и, следовательно, ограничено; цена товара X лишь отражает это обстоятельство, фундаментально присущее этому миру. Поэтому устранение денег из процесса потребления товара X не приводит к изобилию, но лишь смене критериев при производстве и распределении товара на политические и социальные.
Анархисты разных расцветок исходят из верного в некотором смысле определения государства как аппарата легитимного насилия, отчего нередко утверждают что устранение государства устранит и насилие в пользу мирного и благостного сотрудничества. Однако упорядоченное государство является не столько аппаратом легитимного насилия, сколько механизмом сотрудничества в деле упорядочивания и минимизации насилия, поэтому упадок государства неизбежно приводит не к устранению насилия в отношениях между людьми, а к практике этого насилия в более архаических формах.