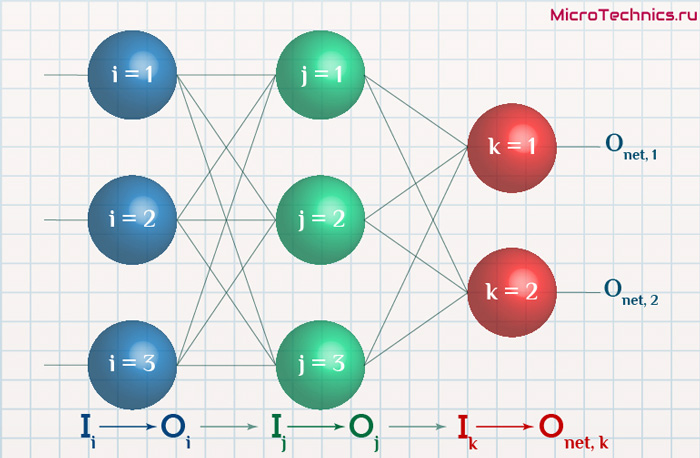
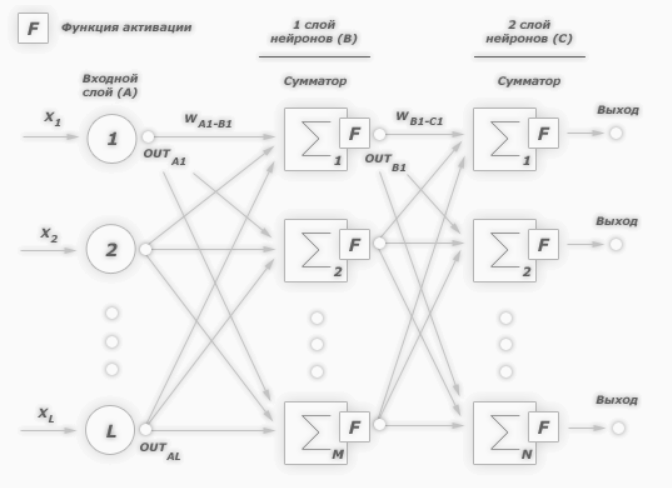
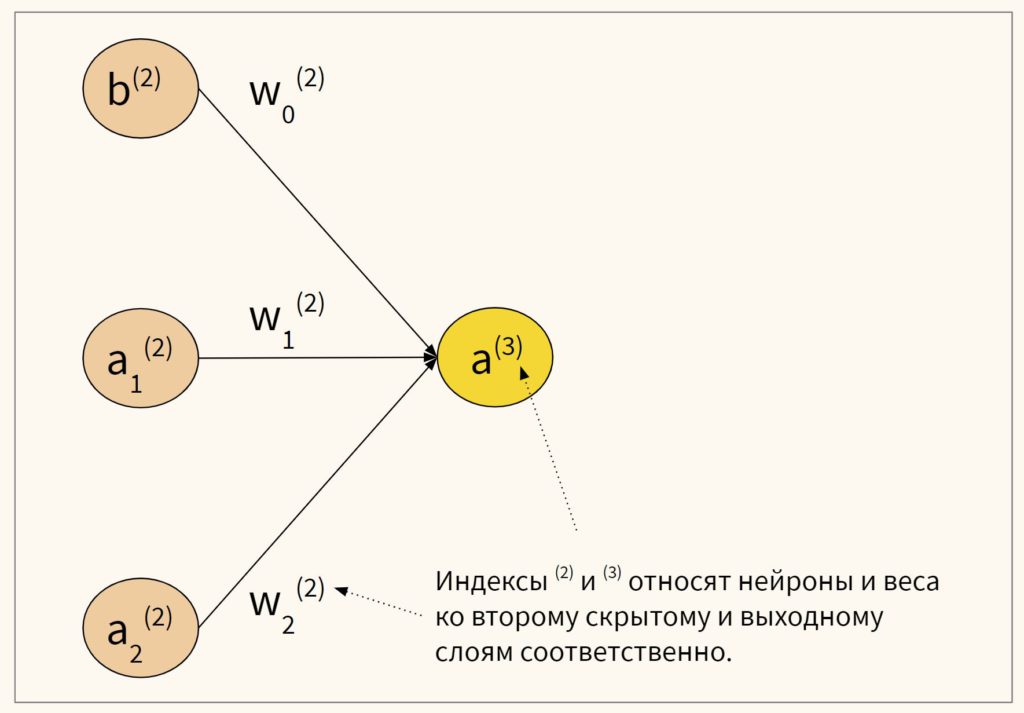
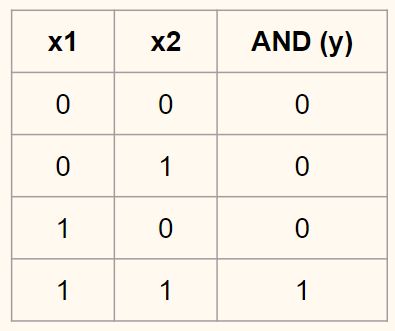
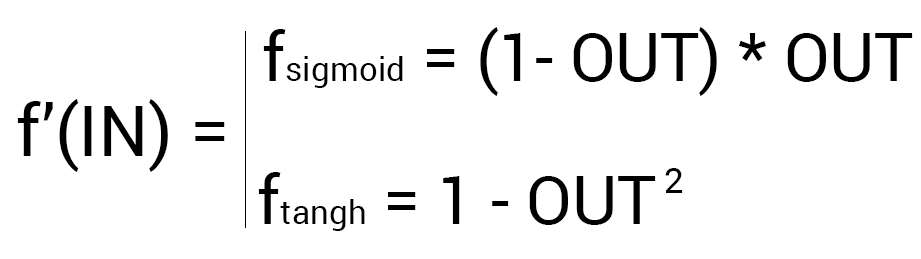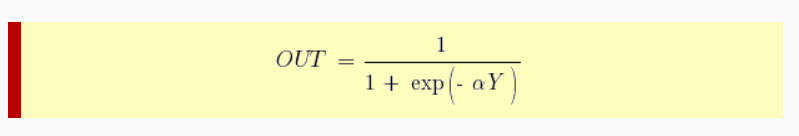Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
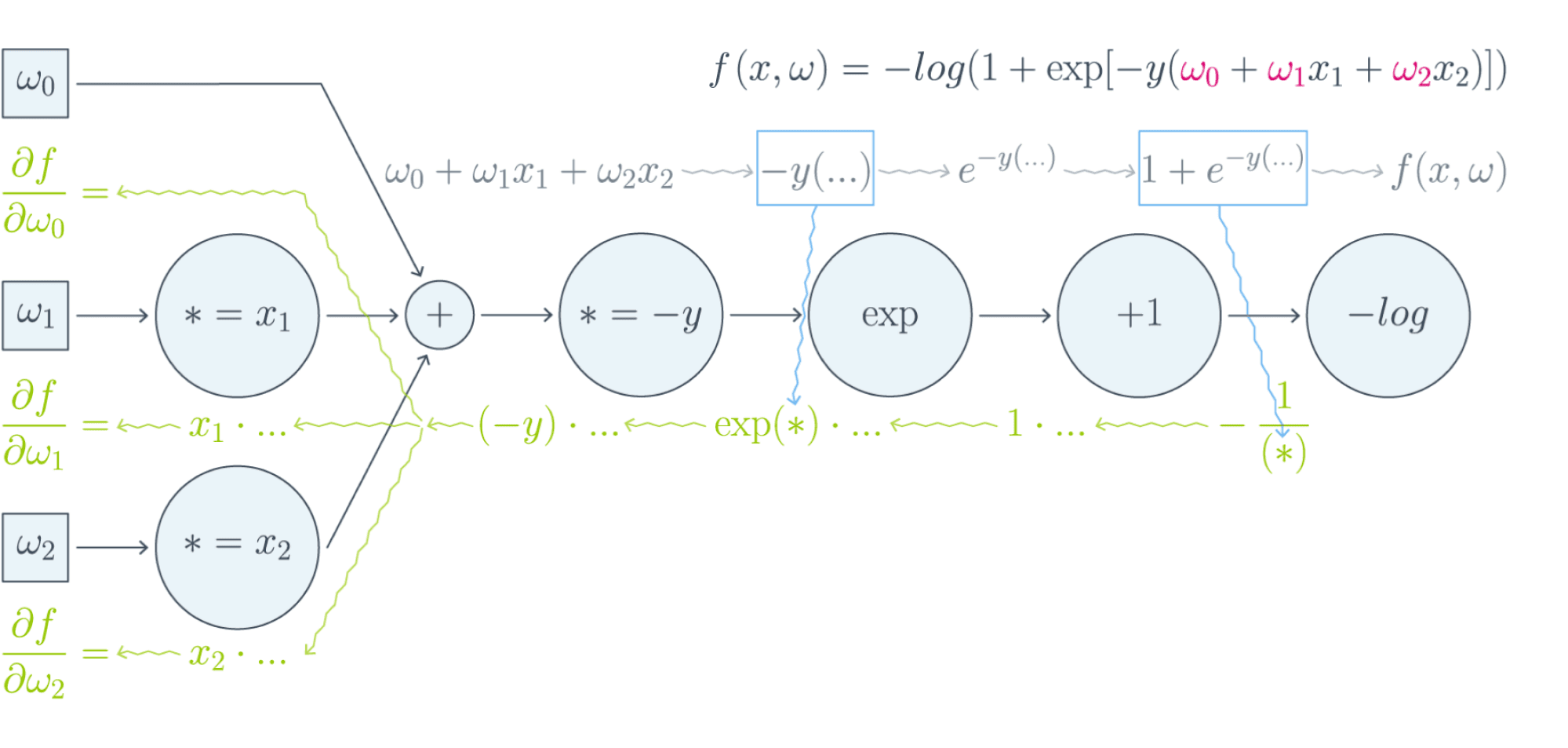
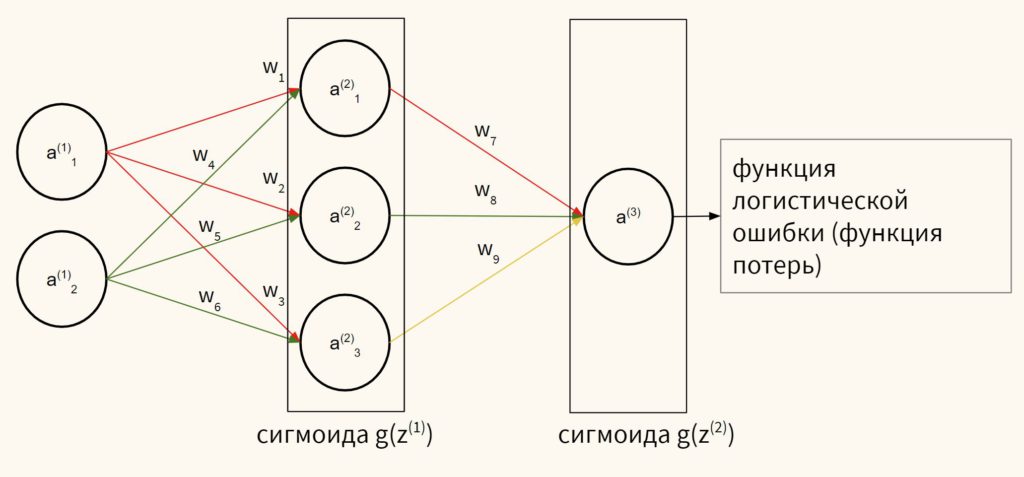
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
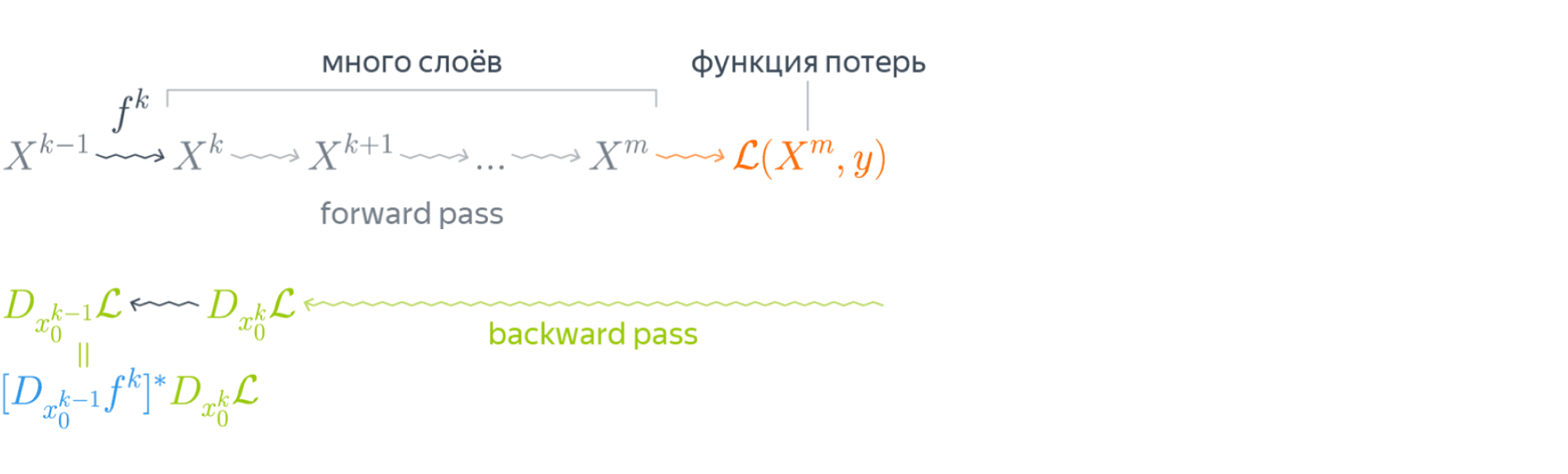
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
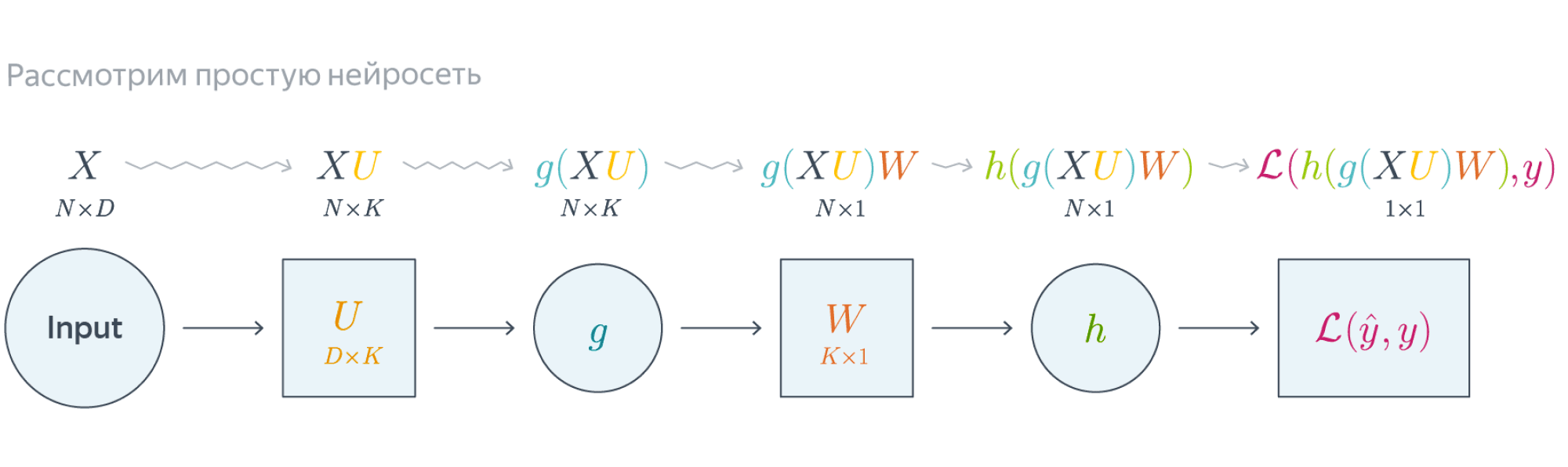
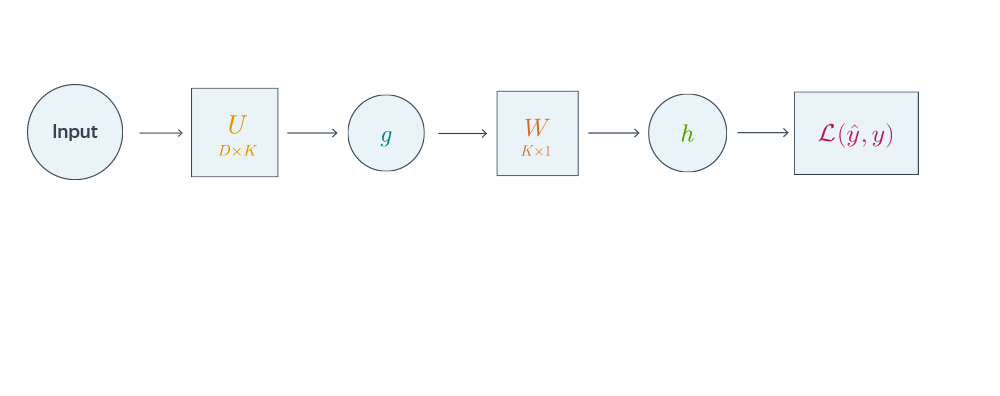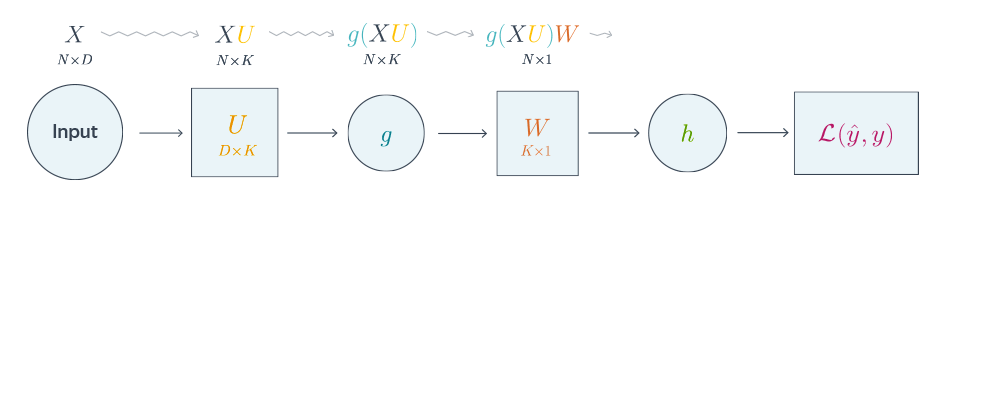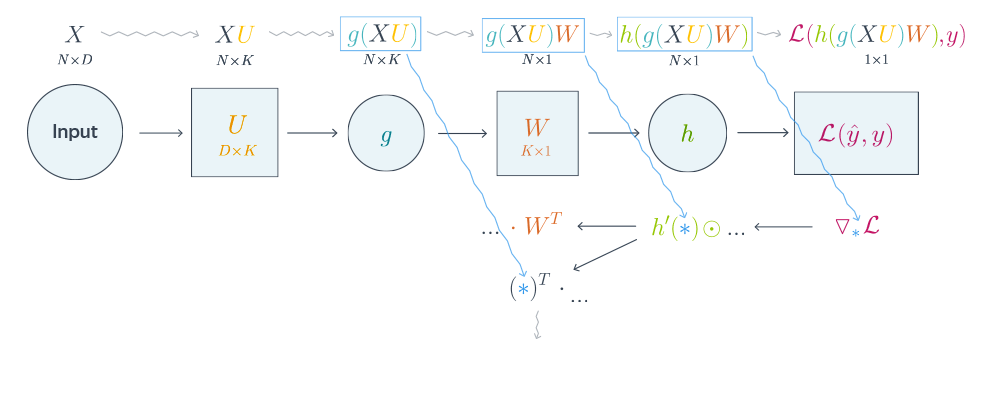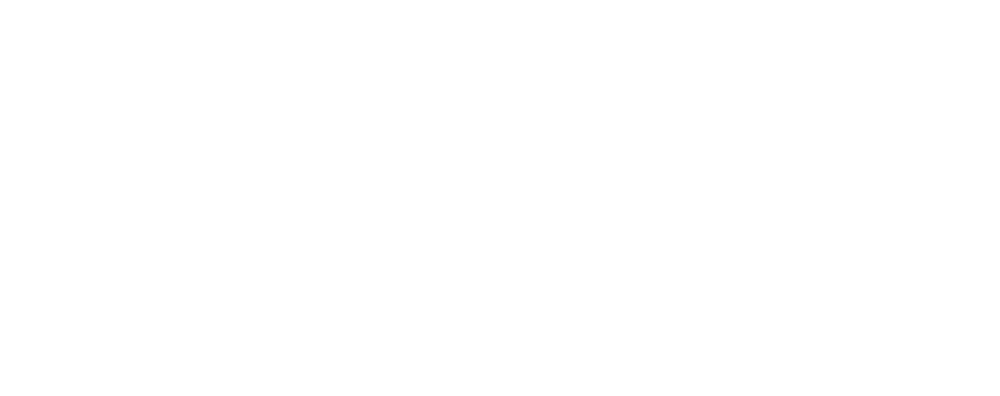
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Анализ ошибок в нейронных сетях
Перевод
Ссылка на автора
Анализ ошибок — это анализ ошибок. Хе хе! Ты не должен говорить мне это. На самом деле весь анализ ошибок столь же интуитивен. Но люди склонны упускать некоторые моменты в реальных проектах. Мы можем рассматривать это как своего рода переподготовку, которую можно проверить — когда разочарование заставляет нас забыть основы.
С такими богатыми библиотеками, как Pytorch и Tensorflow, большинство алгоритмов машинного обучения теперь доступны прямо из коробки — просто создайте экземпляр объекта и обучите его имеющимся данным. Вы готовы к работе!
Это может работать для тривиальных задач учебника, таких как Чтение цифр MNIST, Мы можем просто поиграть с несколькими конфигурациями и вскоре получить почти 100% точность. Но жизнь не так проста. Все становится все сложнее, когда мы пытаемся работать над «реальными» проблемами.
Разработка модели нейронной сети — это гораздо больше, чем просто создание экземпляра объекта Python. Что мне делать, если я понимаю, что моя модель не так точна, как хотелось бы? Должен ли я добавить слои? Должен ли я обрезать модель? Должен ли я изменить некоторые гиперпараметры? Это где анализ ошибок приходит.
Что такое анализ ошибок
Формально, анализ ошибок относится к процессу изучения примеров наборов разработчика, которые ваш алгоритм неверно классифицировал, чтобы мы могли понять основные причины ошибок. Это может помочь нам определить, какая проблема заслуживает внимания и насколько. Это дает нам направление для обработки ошибок.
Анализ ошибок — это не просто окончательная операция по спасению. Это должно быть частью основного развития. Как правило, мы начинаем с небольшой модели, которая должна иметь низкую точность (высокую погрешность). Затем мы можем приступить к оценке этой модели и проанализировать ошибки. Анализируя и исправляя такие ошибки, мы можем расти вместе с моделью.
Распространенные источники ошибок
Мы можем столкнуться с несколькими источниками ошибок. У каждой модели будут свои уникальные ошибки. И нам нужно смотреть на них индивидуально. Но типичные причины:
Неправильно маркированные данные
Большая часть маркировки данных восходит к людям. Мы можем извлекать данные из сети или опросов или из других источников. Основные материалы поступили от людей. И люди подвержены ошибкам. Таким образом, мы должны признать тот факт, что все наши данные по train / dev / test имеют ошибочные записи. Если наша модель хорошо построена и обучена должным образом, то она должна быть в состоянии преодолеть такие ошибки.
Размытая линия разграничения
Алгоритмы классификации работают хорошо, когда положительное и отрицательное четко разделены. Например, если мы пытаемся классифицировать изображения муравья и человека; демаркация довольно хорошая, и это должно помочь ускорить процесс обучения.
Но если мы хотим провести различие между мужской и женской фотографиями, это не так просто. Мы очень хорошо знаем крайности. Но демаркация не так ясна. Такая классификация естественно подвержена ошибкам. В таком случае мы должны работать над лучшим обучением вблизи этой туманной линии разграничения — возможно, предоставляя больше данных, которые находятся рядом с этой линией.
Переоснащение или занижение размера
Давайте рассмотрим тривиальный пример, чтобы понять концепцию. Предположим, мы работаем над классификатором изображений, чтобы различать ворону и попугая. Помимо размера, клюва, хвоста, крыльев … очевидным отличием является цвет. Но возможно как-то модель не узнает эту разницу. Таким образом, классифицирует маленькую ворону как попугая.
Это означает, что модели не удалось узнать измерение на основе доступных данных. Когда мы замечаем это, мы должны попытаться собрать больше данных, которые могут научить сеть классифицировать по цвету больше, чем другие параметры.
Точно так же возможно, что модель соответствует определенному измерению. Предположим, что в классификаторе Cat / Dog мы отмечаем в записях ошибок, что многие темные собаки были классифицированы как кошки, а светлые кошки были классифицированы как собаки. Это означает, что данные обучения не имели достаточного количества записей, которые могли бы обучить модель против такой неправильной классификации.
Многие другие
Это всего лишь несколько видов источников ошибок. Их может быть гораздо больше, которые можно обнаружить, проанализировав набор ошибок. Давайте не будем «переусердствовать» в нашем понимании, чтобы ограничить наш анализ этими типами ошибок.
Каждый анализ ошибок покажет нам новый набор источников проблем. Но правильный подход состоит в том, чтобы выявить любую склонность к недостаточному или избыточному подгонке — в целом или к определенной функции или набору функций или вокруг определенных значений некоторых входных функций.
Набор для глазных яблок
Теперь мы знаем, что в нашей модели есть ошибки и может быть несколько источников ошибок. Но как определить, какой? У нас есть миллионы записей в обучающем наборе и, по крайней мере, несколько тысяч в наборе разработчиков. Тестового набора пока не видно.
Мы не можем оценить каждую запись в тренировочном наборе. Мы также не можем оценить каждую запись в наборе разработчиков Чтобы определить тип ошибок, которые генерирует наша модель, мы разделили набор dev на две части — набор eyeball и blackbox set.
Набор глазного яблока — это набор образцов, который мы на самом деле оцениваем. Мы можем проверить эти записи вручную, чтобы угадать источник ошибок. Поэтому набор глазных яблок должен быть достаточно маленьким, чтобы мы могли работать вручную, и достаточно большим, чтобы получить статистическое представление всего набора разработчиков.
Анализируя ошибки в наборе глазного яблока, мы можем определить различные источники ошибок и вклад каждого из них. Получив эту информацию, мы можем начать работать с основными источниками ошибок. Как только мы сделаем соответствующие исправления, мы сможем продолжить поиск источников ошибок.
Обратите внимание, что анализ должен быть основан только на наборе глазного яблока. Если мы используем весь набор dev для этого анализа, мы в конечном итоге перегоним набор dev. Но если набор разработчиков недостаточно велик, мы должны использовать его целиком. В таком случае, мы просто должны отметить, что у нас есть высокий риск переоснащения набора разработчиков — и планировать остальное соответственно. (Возможно, мы можем использовать вращающийся набор разработчиков — где мы выбираем новый набор разработчиков из тренировочного набора при каждой попытке.)
Предвзятость и дисперсия
Работая над анализом ошибок, мы определяем определенный параметр или область проблем; или мы замечаем, что ошибка довольно равномерная. Как мы пойдем отсюда? Я получу больше данных? Это может звучать логично. Но не всегда так. Дополнительные данные не всегда могут помочь — после определенного момента любые другие данные могут быть просто избыточными. Нужна ли мне более богатая модель? Простое обогащение модели может значительно улучшить цифры — путем переоснащения. Это тоже не правильно! Итак, как мы решаем направление?
Предвзятость и дисперсия дают нам хорошее представление об этом. Проще говоря, если ошибка высока в обучающем наборе, а также в наборе разработчиков, то мы имеем высокий уклон. Хотя, если тренировочный набор хороший, а набор плохой, у нас высокая дисперсия. Смещение по существу подразумевает, что вывод плох для всех данных. Дисперсия подразумевает, что вывод хорош для некоторых данных и плох для остальных.
Если у нас есть модель с точностью 60% на тренировочном наборе. Естественно, мы называем это большим уклоном. С такой точностью мы можем даже не захотеть проверять набор разработчиков. Но, если ошибка обучающего набора намного лучше, чем наша цель, оставляя разработчик позади, мы можем назвать это высокой дисперсией. Это связано с тем, что поведение модели сильно зависит от доступных данных.
Можно интуитивно сказать, что если у нас высокий уклон, это означает, что мы недостаточно приспособлены. Это может быть связано с тем, что конкретная функция не обрабатывается должным образом или сама модель недостаточно богата. Исходя из этого, мы можем обновить решение для повышения производительности — путем улучшения конкретной функции или самой модели.
С другой стороны, высокая дисперсия означает, что мы недостаточно тренируемся. Нам нужно больше данных или нам нужно намного лучше обрабатывать имеющиеся данные. С этим мы могли бы тренировать лучшую модель.
Уменьшение смещения
Модель машинного обучения может учиться только на основе имеющихся данных. Некоторые ошибки неизбежны во входных данных. Это не человеческие ошибки, а истинные ограничения людей, которые классифицируют или тестируют модель. Например, если я не могу различить пару идентичных близнецов, я никак не могу сгенерировать помеченные данные и научить машину это делать!
Такое ограничение называется неизбежным смещением. Остальное можно избежать, и мы должны сосредоточиться на этом. Таким образом, когда мы выполняем анализ ошибок, когда мы пытаемся определить основную причину ошибки, мы должны учитывать смещение, которого можно избежать, а не смещение в целом.
Если наш анализ ошибок говорит нам, что смещение, которое можно избежать, является основным источником ошибок, мы можем попробовать некоторые из следующих шагов
Увеличить размер модели
Высокий уклон означает, что модель не может выучить все, что она может извлечь из доступных ей данных. Это происходит, когда модель недостаточно способна к обучению. Если модель имеет только два параметра, она не может узнать больше, чем могут содержать эти два параметра. Кроме того, любые новые данные обучения будут перезаписывать то, что они узнали из предыдущих записей. Модель должна иметь достаточно параметров для изучения — только тогда она может содержать информацию, необходимую для выполнения требуемой работы.
Следовательно, первичное решение высокого уклона состоит в создании более богатой модели.
Разрешить больше возможностей
Одним из основных шагов в нашей очистке данных является сокращение всех избыточных функций. На самом деле, ни одна функция не является избыточной. Но некоторые менее значимы, чем другие. А сокращение возможностей по существу отбрасывает такие функции с меньшей ценностью — таким образом, отбрасывая некоторую информацию с низким значением.
Это хорошо для начала. Но когда мы замечаем, что функции, которыми мы располагаем, не способны передавать требуемую информацию, мы должны переделать этап сокращения функций и позволить пройти еще некоторым функциям. Это может сделать модель богаче и дать ей больше информации для изучения
Уменьшить регуляризацию модели
Все методы регуляризации по существу держат параметры модели ближе к нулю. То есть он не позволяет каждому параметру «учиться слишком много». Это хорошая техника для обеспечения сбалансированности модели. Но когда мы понимаем, что модель не в состоянии учиться достаточно, мы должны уменьшить уровни регуляризации, чтобы каждый узел в сети мог учиться на основе данных, доступных для обучения.
Избегайте локального минимума
Локальный минимум является еще одним распространенным источником высокого уклона. У нас может быть богатая модель и хороший объем данных. Но если градиентный спуск застрянет на локальном минимуме, смещение не уменьшится. Существуют различные способы избежать локального минимума — случайные запуски (обучайте его снова и снова с разными начальными значениями. Поскольку каждый выбирает разностный путь, локальный минимум избегается). Или мы можем добавить импульс к градиентному спуску — это может снова предотвратить неглубокий минимум вдоль спуска.
Лучшая сетевая архитектура
Простое увеличение нейронов и слоев не обязательно улучшает модель. Использование соответствующей сетевой архитектуры может гарантировать, что новые слои действительно добавят ценность.
Исследователи сталкивались и работали над этими проблемами в прошлом и предоставили нам хорошие модели архитектуры, которые могут быть использованы для лучшего компромисса между смещением и дисперсией — например, AlexNet, RESNET, GoogleNet а также многое другое, Приспособление к такой архитектуре может помочь нам избежать многих наших проблем.
Уменьшение дисперсии
Если анализ ошибок указывает на то, что основной причиной ошибки является высокая дисперсия, мы можем использовать один из этих методов, чтобы уменьшить это.
Добавить больше данных обучения
Это основное решение. Дисперсия возникает, когда у нас недостаточно данных, чтобы обучить сеть наилучшей производительности. Таким образом, основной целью действий должно быть поиск дополнительных данных. Но это имеет свои пределы, так как данные не всегда доступны.
Добавить регуляризацию
Регуляризация L1 или L2 — это проверенные методы, позволяющие уменьшить проблему переоснащения и, таким образом, избежать высокой дисперсии По сути, они держат каждый параметр ближе к 0. Это означает, что ни один параметр не может учиться слишком много. Если один параметр содержит много информации, модель становится несбалансированной и приводит к переобучению и высокой дисперсии.
Методы регуляризации L1 и L2 помогают предотвратить такие проблемы. Регуляризация L1 быстрее и вычислительно проще. Он генерирует разреженные модели. Естественно, L2 намного точнее, поскольку имеет дело с более мелкими деталями.
Ранняя остановка
По мере того, как мы обучаем модель с использованием доступных данных обучения, каждая итерация делает модель немного лучше для доступных данных. Но чрезмерное количество итераций этого может привести к переобучению. Для этого нужно найти золотую середину. Лучший способ — это остановиться рано, а не осознавать, что мы уже перешли границы.
Уменьшить Особенности
Чем меньше функций, тем легче модель и, следовательно, меньше возможностей для переоснащения. У нас есть несколько алгоритмов выбора функций, таких как PCA, которые могут помочь нам определить минимальный и ортогональный набор функций, который может обеспечить более простой способ обучения моделей.
Знание предметной области также может помочь нам сократить количество функций. Мы также можем использовать результаты анализа ошибок, чтобы определить, как следует изменить набор функций, чтобы повысить производительность.
Уменьшить размер модели
Высокая дисперсия или переоснащение обычно означает, что у нас слишком много параметров для обучения. Если у нас недостаточно данных для обучения каждого из этих параметров, случайность значений инициализации остается в параметрах, что приводит к неверным результатам.
Уменьшение размера модели напрямую влияет на это.
Используйте разреженную модель
Иногда мы знаем, что размер модели является обязательным, и уменьшение размера приведет только к снижению функциональности. В таком случае мы можем рассмотреть возможность обучения разреженной модели. Это дает хорошее сочетание лучшей модели с меньшей дисперсией.
Модельная архитектура
Подобно уменьшению смещения, дисперсия также определяется архитектурой модели. Исследователи предоставили нам хорошие модели архитектуры, которые могут быть использованы для лучшего компромисса между смещением и дисперсией. Приспособление к такой архитектуре может помочь нам избежать многих наших проблем.
Резюме
Мы видели, что может быть много причин для ошибки в модели, которую мы обучаем. Каждая модель будет иметь уникальный набор ошибок и источников ошибок. Но, если мы будем придерживаться формального подхода к этому анализу, мы сможем не изобретать велосипед каждый раз.
Функция потерь (Loss Function, Cost Function, Error Function; J) – фрагмент программного кода, который используется для оптимизации Алгоритма (Algorithm) Машинного обучения (ML). Значение, вычисленное такой функцией, называется «потерей».
Функция (Function) потерь может дать бо́льшую практическую гибкость вашим Нейронным сетям (Neural Network) и будет определять, как именно выходные данные связаны с исходными.
Нейронные сети могут выполнять несколько задач: от прогнозирования непрерывных значений, таких как ежемесячные расходы, до Бинарной классификации (Binary Classification) на кошек и собак. Для каждой отдельной задачи потребуются разные типы функций, поскольку выходной формат индивидуален.
С очень упрощенной точки зрения Loss Function может быть определена как функция, которая принимает два параметра:
- Прогнозируемые выходные данные
- Истинные выходные данные
Эта функция, по сути, вычислит, насколько хорошо работает наша модель, сравнив то, что модель прогнозирует, с фактическим значением, которое она должна выдает. Если Ypred очень далеко от Yi, значение потерь будет очень высоким. Однако, если оба значения почти одинаковы, значение потерь будет очень низким. Следовательно, нам нужно сохранить функцию потерь, которая может эффективно наказывать модель, пока та обучается на Тренировочных данных (Train Data).
Этот сценарий в чем-то аналогичен подготовке к экзаменам. Если кто-то плохо сдает экзамен, мы можем сказать, что потеря очень высока, и этому человеку придется многое изменить внутри себя, чтобы в следующий раз получить лучшую оценку. Однако, если экзамен пройдет хорошо, студент может вести себя подобным образом и в следующий раз.
Теперь давайте рассмотрим классификацию как задачу и поймем, как в этом случае работает функция потерь.
Классификационные потери
Когда нейронная сеть пытается предсказать дискретное значение, мы рассматриваем это как модель классификации. Это может быть сеть, пытающаяся предсказать, какое животное присутствует на изображении, или является ли электронное письмо спамом. Сначала давайте посмотрим, как представлены выходные данные классификационной нейронной сети.
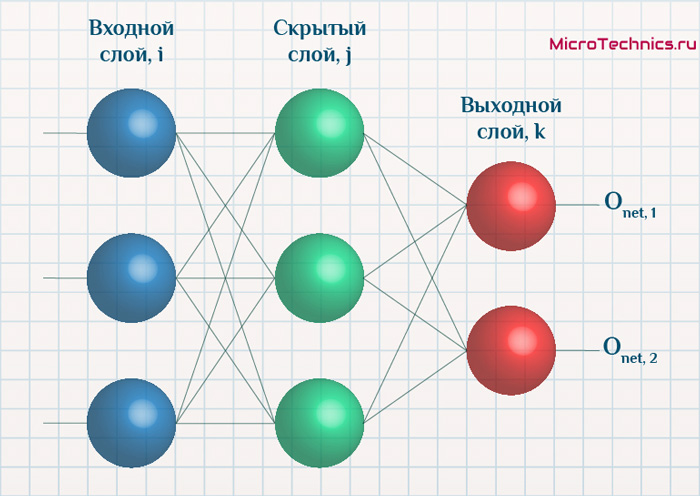
Количество узлов выходного слоя будет зависеть от количества классов, присутствующих в данных. Каждый узел будет представлять один класс. Значение каждого выходного узла по существу представляет вероятность того, что этот класс является правильным.
Как только мы получим вероятности всех различных классов, рассмотрим тот, что имеет наибольшую вероятность. Посмотрим, как выполняется двоичная классификация.
Бинарная классификация
В двоичной классификации на выходном слое будет только один узел. Чтобы получить результат в формате вероятности, нам нужно применить Функцию активации (Activation Function). Поскольку для вероятности требуется значение от 0 до 1, мы будем использовать Сигмоид (Sigmoid), которая приведет любое реальное значение к диапазону значений от 0 до 1.
По мере того, как входные реальные данные становятся больше и стремятся к плюс бесконечности, выходные данные сигмоида будут стремиться к единице. А когда на входе значения становятся меньше и стремятся к отрицательной бесконечности, на выходе числа будут стремиться к нулю. Теперь мы гарантированно получаем значение от 0 до 1, и это именно то, что нам нужно, поскольку нам нужны вероятности.
Если выход выше 0,5 (вероятность 50%), мы будем считать, что он попадает в положительный класс, а если он ниже 0,5, мы будем считать, что он попадает в отрицательный класс. Например, если мы обучаем нейросеть для классификации кошек и собак, мы можем назначить собакам положительный класс, и выходное значение в наборе данных для собак будет равно 1, аналогично кошкам будет назначен отрицательный класс, а выходное значение для кошек будет быть 0.
Функция потерь, которую мы используем для двоичной классификации, называется Двоичной перекрестной энтропией (BCE). Эта функция эффективно наказывает нейронную сеть за Ошибки (Error) двоичной классификации. Давайте посмотрим, как она выглядит.
Как видите, есть две отдельные функции, по одной для каждого значения Y. Когда нам нужно предсказать положительный класс (Y = 1), мы будем использовать следующую формулу:
$$Потеря = -log(Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$
И когда нам нужно предсказать отрицательный класс (Y = 0), мы будем использовать немного трансформированный аналог:
$$Потеря = -log(1 — Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$
Для первой функции, когда Ypred равно 1, потеря равна 0, что имеет смысл, потому что Ypred точно такое же, как Y. Когда значение Ypred становится ближе к 0, мы можем наблюдать, как значение потери сильно увеличивается. Когда же Ypred становится равным 0, потеря стремится к бесконечности. Это происходит, потому что с точки зрения классификации, 0 и 1 – полярные противоположности: каждый из них представляет совершенно разные классы. Поэтому, когда Ypred равно 0, а Y равно 1, потери должны быть очень высокими, чтобы сеть могла более эффективно распознавать свои ошибки.
Полиномиальная классификация
Полиномиальная классификация (Multiclass Classification) подходит, когда нам нужно, чтобы наша модель каждый раз предсказывала один возможный класс. Теперь, поскольку мы все еще имеем дело с вероятностями, имеет смысл просто применить сигмоид ко всем выходным узлам, чтобы мы получали значения от 0 до 1 для всех выходных значений, но здесь кроется проблема. Когда мы рассматриваем вероятности для нескольких классов, нам необходимо убедиться, что сумма всех индивидуальных вероятностей равна единице, поскольку именно так определяется вероятность. Применение сигмоида не гарантирует, что сумма всегда равна единице, поэтому нам нужно использовать другую функцию активации.
В данном случае мы используем функцию активации Softmax. Эта функция гарантирует, что все выходные узлы имеют значения от 0 до 1, а сумма всех значений выходных узлов всегда равна 1. Вычисляется с помощью формулы:
$$Softmax(y_i) = frac{e^{y_i}}{sum_{i = 0}^n e^{y_i}}space{,}space{где}$$
$$y_ispace{}{–}space{i-e}space{наблюдение}$$
Пример:
Как видите, мы просто передаем все значения в экспоненциальную функцию. После этого, чтобы убедиться, что все они находятся в диапазоне от 0 до 1 и сумма всех выходных значений равна 1, мы просто делим каждую экспоненту на сумму экспонент.
Итак, почему мы должны передавать каждое значение через экспоненту перед их нормализацией? Почему мы не можем просто нормализовать сами значения? Это связано с тем, что цель Softmax – убедиться, что одно значение очень высокое (близко к 1), а все остальные значения очень низкие (близко к 0). Softmax использует экспоненту, чтобы убедиться, что это произойдет. А затем мы нормализуем результат, потому что нам нужны вероятности.
Теперь, когда наши выходные данные имеют правильный формат, давайте посмотрим, как мы настраиваем для этого функцию потерь. Хорошо то, что функция потерь по сути такая же, как у двоичной классификации. Мы просто применим Логарифмическую потерю (Log Loss) к каждому выходному узлу по отношению к его соответствующему целевому значению, а затем найдем сумму этих значений по всем выходным узлам.
Эта потеря называется категориальной Кросс-энтропией (Cross Entropy). Теперь перейдем к частному случаю классификации, называемому многозначной классификацией.
Классификация по нескольким меткам
Классификация по нескольким меткам (MLC) выполняется, когда нашей модели необходимо предсказать несколько классов в качестве выходных данных. Например, мы тренируем нейронную сеть, чтобы предсказывать ингредиенты, присутствующие на изображении какой-то еды. Нам нужно будет предсказать несколько ингредиентов, поэтому в Y будет несколько единиц.
Для этого мы не можем использовать Softmax, потому что он всегда заставляет только один класс «становиться единицей», а другие классы приводит к нулю. Вместо этого мы можем просто сохранить сигмоид на всех значениях выходных узлов, поскольку пытаемся предсказать индивидуальную вероятность каждого класса.
Что касается потерь, мы можем напрямую использовать логарифмические потери на каждом узле и суммировать их, аналогично тому, что мы делали в мультиклассовой классификации.
Теперь, когда мы рассмотрели классификацию, перейдем к регрессии.
Потеря регрессии
В Регрессии (Regression) наша модель пытается предсказать непрерывное значение, например, цены на жилье или возраст человека. Наша нейронная сеть будет иметь один выходной узел для каждого непрерывного значения, которое мы пытаемся предсказать. Потери регрессии рассчитываются путем прямого сравнения выходного и истинного значения.
Самая популярная функция потерь, которую мы используем для регрессионных моделей, – это Среднеквадратическая ошибка (MSE). Здесь мы просто вычисляем квадрат разницы между Y и YPred и усредняем полученное значение.
Автор оригинальной статьи: deeplearningdemystified.com
Фото: @leni_eleni
Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
Что такое нейрон смещения?
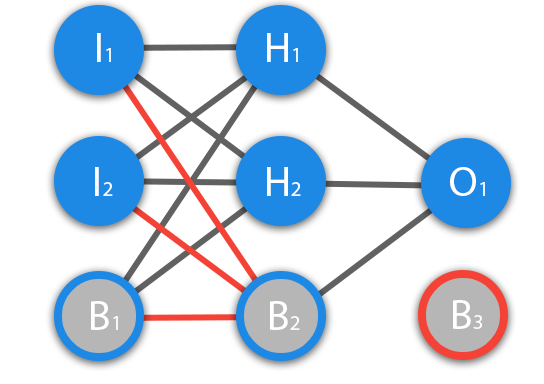
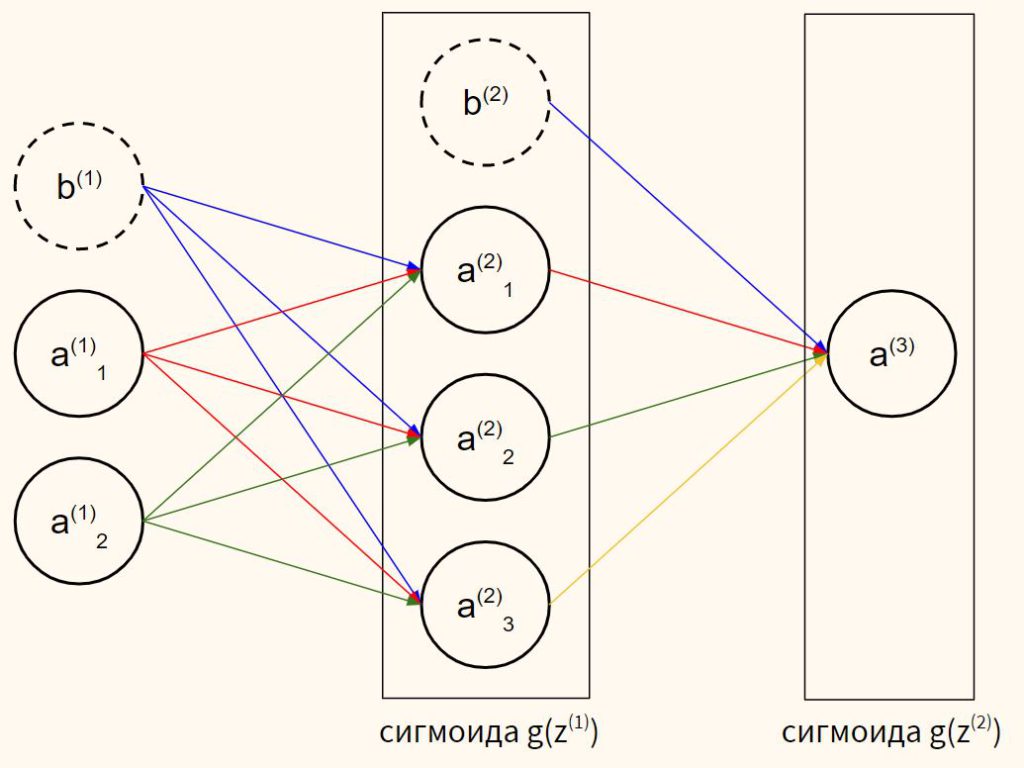
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
Для чего нужен нейрон смещения?
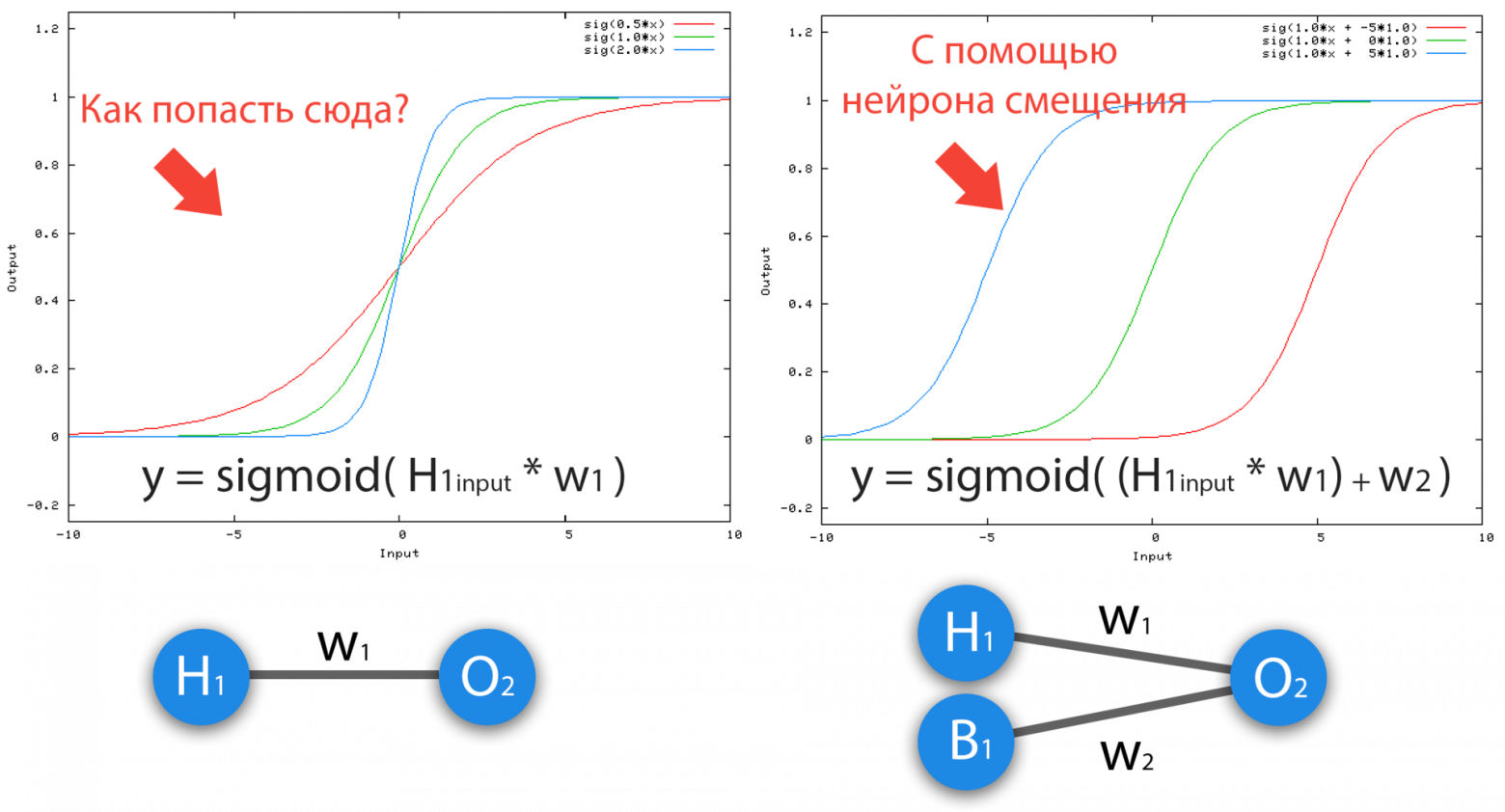
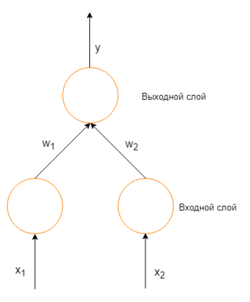
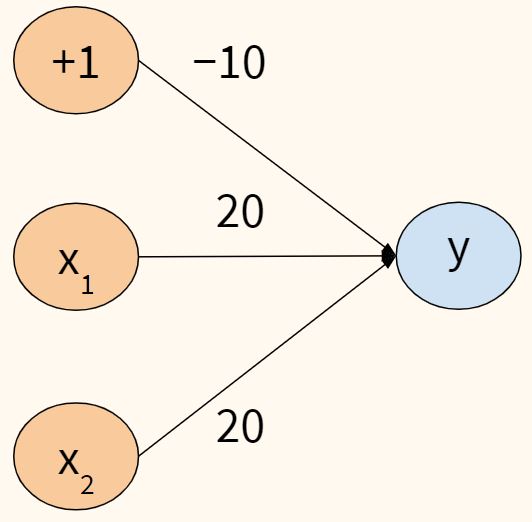
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
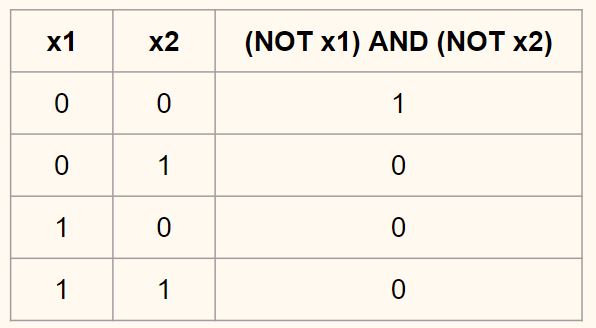
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = H1*w1+H2*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Как сделать чтобы НС давала правильные ответы?
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
- Метод обратного распространения (Backpropagation)
- Метод упругого распространения (Resilient propagation или Rprop)
- Генетический Алгоритм (Genetic Algorithm)
Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска.
Что такое градиентный спуск?
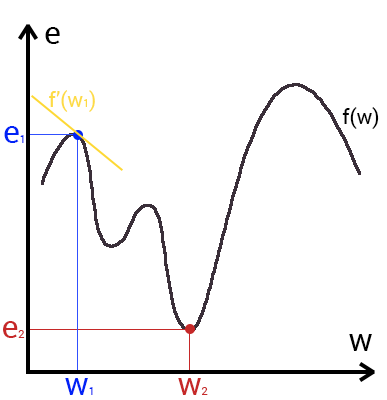
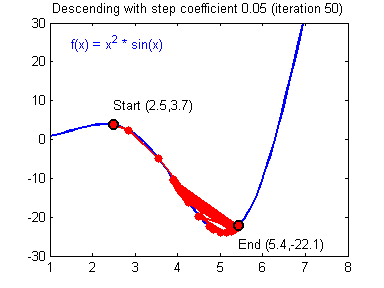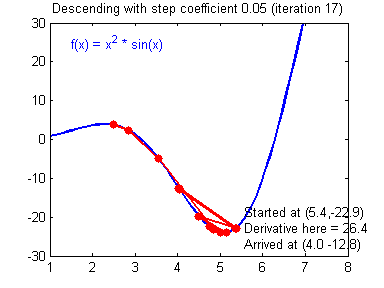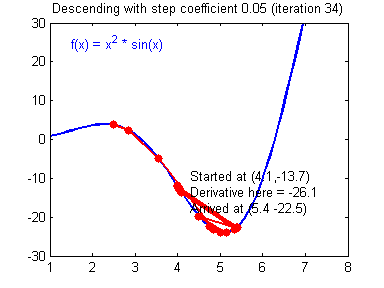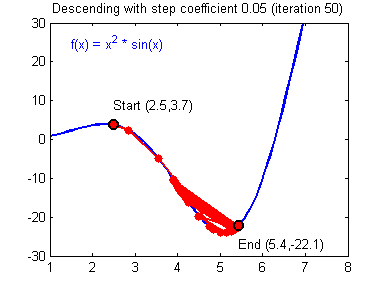
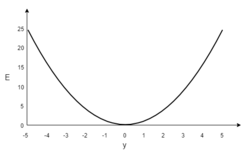
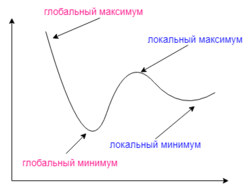
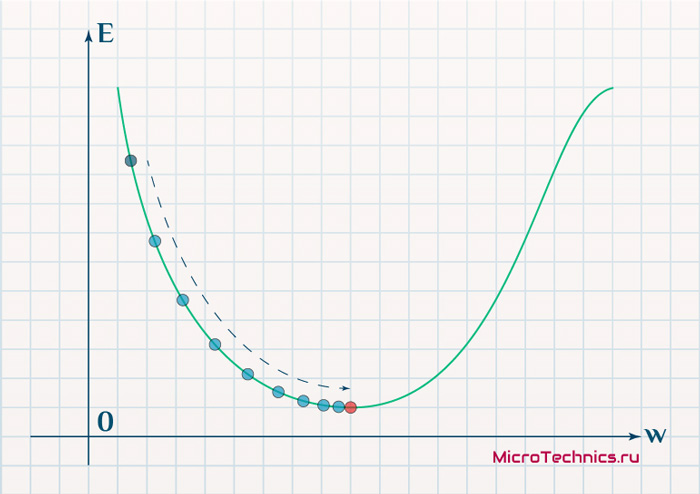
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
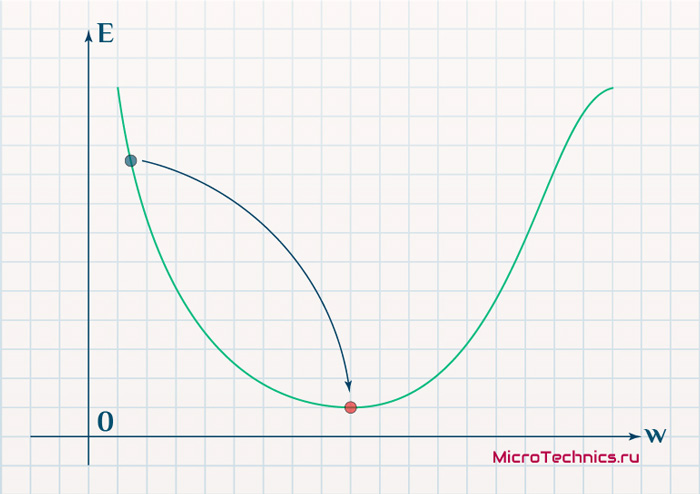
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
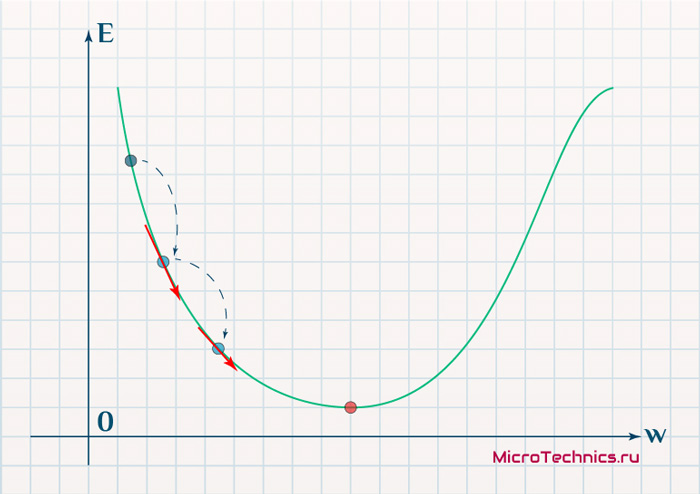
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
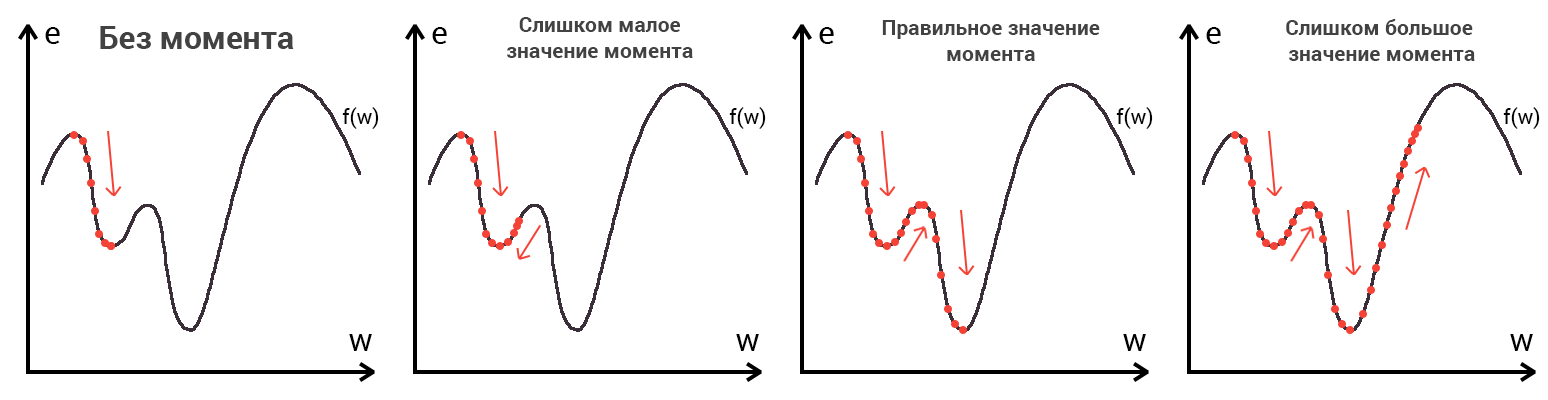
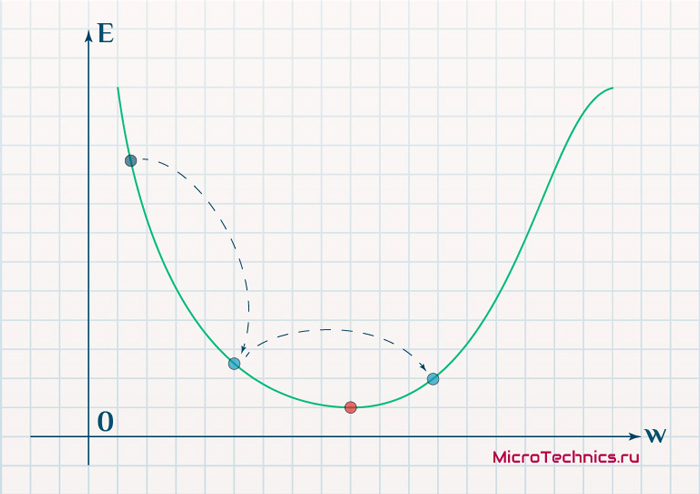
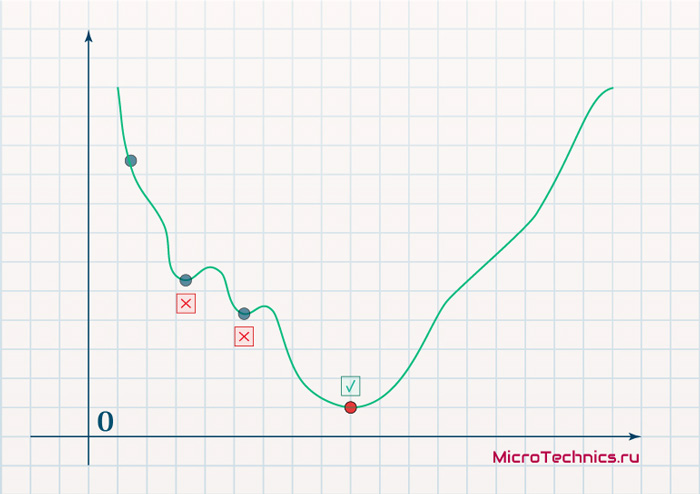
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
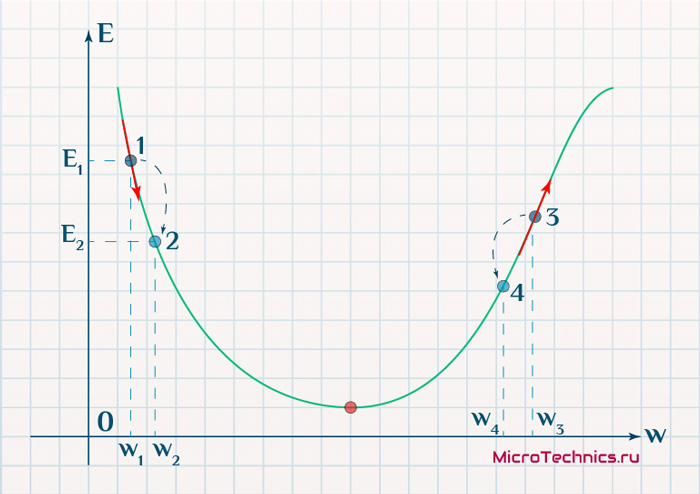
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Что такое Метод Обратного Распространения (МОР)?
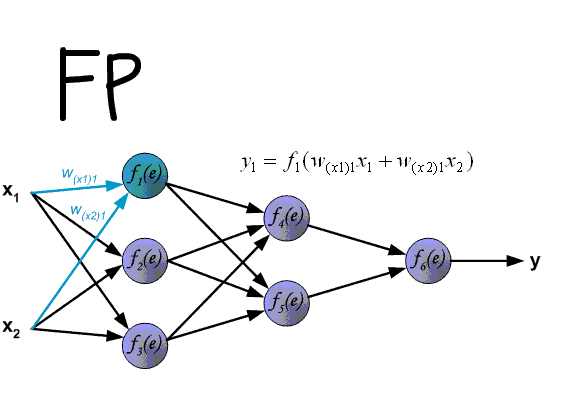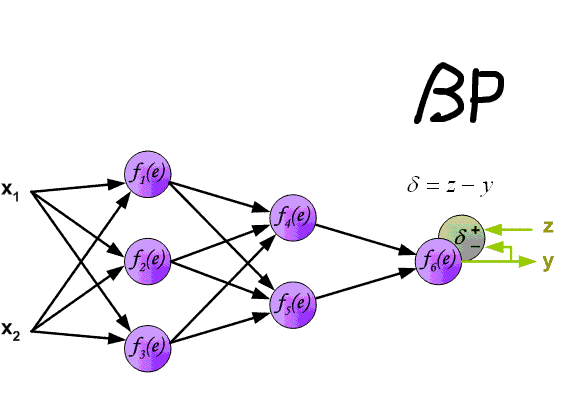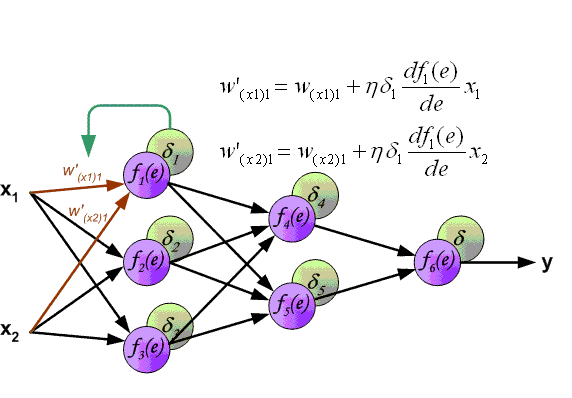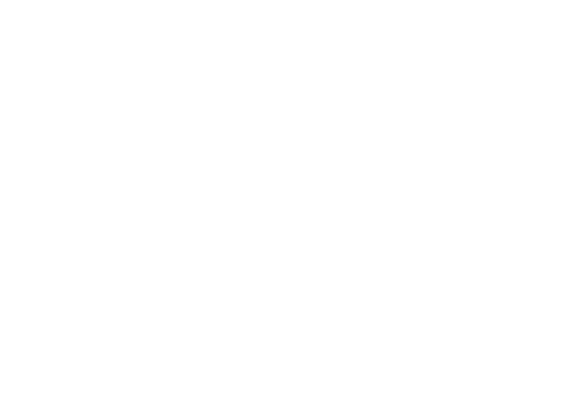
Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке:
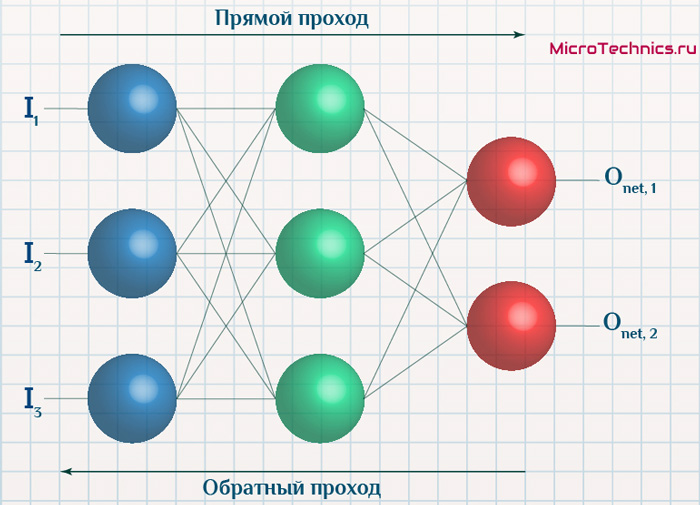
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
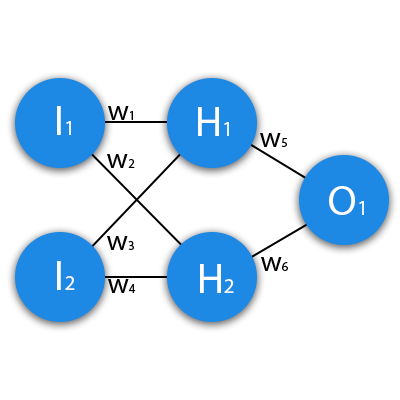
Данные задачи из предыдущей статьи
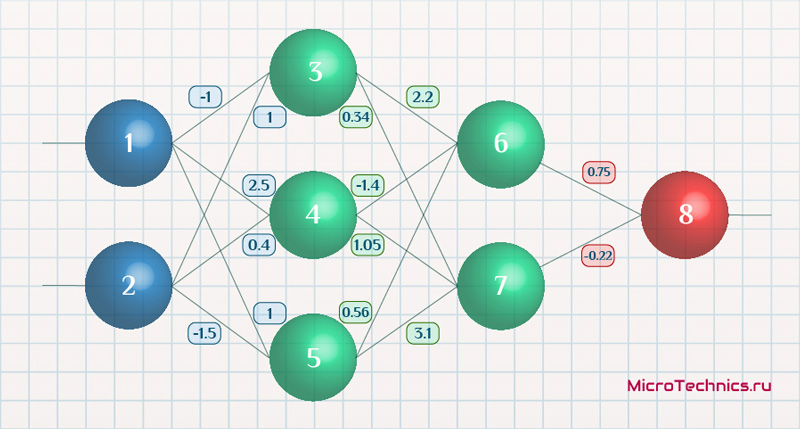
Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
O1ideal = 1 (0xor1=1)
Error = ((1-0.33)^2)/1=0.45
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.
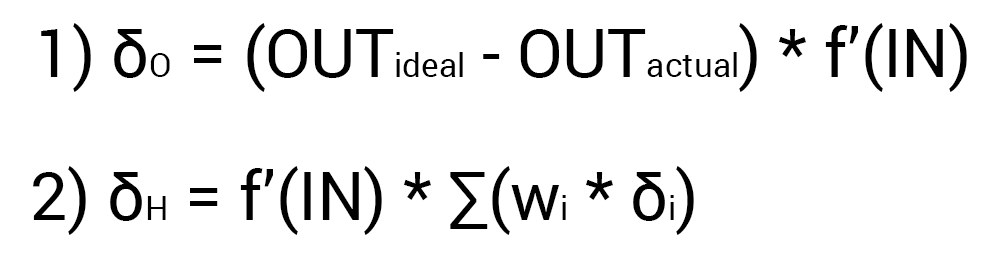
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.
Решение
O1output = 0.33
O1ideal = 1
Error = 0.45
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:
Решение
H1output = 0.61
w5 = 1.5
δO1 = 0.148
δH1 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:
Решение
H1output = 0.61
δO1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
Решение
E = 0.7
Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0
Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.
Решение
H2output = 0.69
w6 = -2.3
δO1 = 0.148
E = 0.7
Α = 0.3
Δw6(i-1) = 0
δH2 = ( (1 — 0.69) * 0.69 ) * ( -2.3 * 0.148 ) = -0.07
GRADw6 = 0.69 * 0.148 = 0.1
Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
w6 = w6 + Δw6 = -2.2
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.
Решение
w1 = 0.45, Δw1(i-1) = 0
w2 = 0.78, Δw2(i-1) = 0
w3 = -0.12, Δw3(i-1) = 0
w4 = 0.13, Δw4(i-1) = 0
δH1 = 0.053
δH2 = -0.07
E = 0.7
Α = 0.3
GRADw1 = 1 * 0.053 = 0.053
GRADw2 = 1 * -0.07 = -0.07
GRADw3 = 0 * 0.053 = 0
GRADw4 = 0 * -0.07 = 0
Δw1 = 0.7 * 0.053 + 0 * 0.3 = 0.04
Δw2 = 0.7 * -0.07 + 0 * 0.3 = -0.05
Δw3 = 0.7 * 0 + 0 * 0.3 = 0
Δw4 = 0.7 * 0 + 0 * 0.3 = 0
w1 = w1 + Δw1 = 0.5
w2 = w2 + Δw2 = 0.73
w3 = w3 + Δw3 = -0.12
w4 = w4 + Δw4 = 0.13
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.
Решение
I1 = 1
I2 = 0
w1 = 0.5
w2 = 0.73
w3 = -0.12
w4 = 0.13
w5 = 1.563
w6 = -2.2
H1input = 1 * 0.5 + 0 * -0.12 = 0.5
H1output = sigmoid(0.5) = 0.62
H2input = 1 * 0.73 + 0 * 0.124 = 0.73
H2output = sigmoid(0.73) = 0.675
O1input = 0.62* 1.563 + 0.675 * -2.2 = -0.51
O1output = sigmoid(-0.51) = 0.37
O1ideal = 1 (0xor1=1)
Error = ((1-0.37)^2)/1=0.39
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Что еще нужно знать о процессе обучения?
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Что такое гиперпараметры?
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
- Момент и скорость обучения
- Количество скрытых слоев
- Количество нейронов в каждом слое
- Наличие или отсутствие нейронов смещения
В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети.
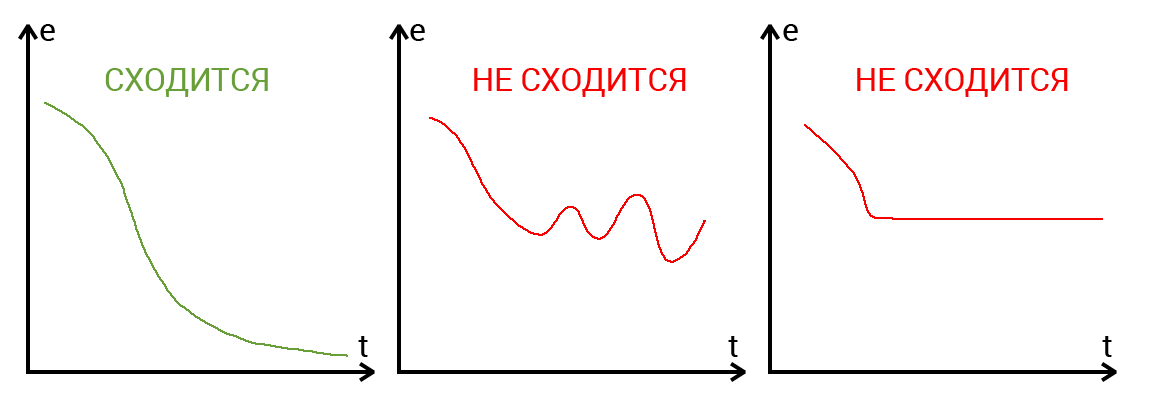
Что такое сходимость?
Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
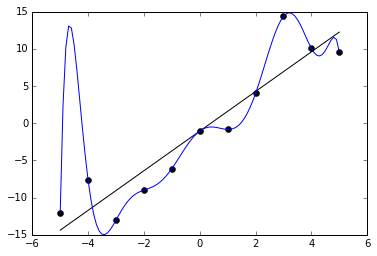
Что такое переобучение?
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.
Заключение
Надеюсь эта статья смогла прояснить ключевые моменты такого нелегко предмета, как Нейронные сети. Однако я считаю, что сколько бы ты статей не прочел, без практики такую сложную тему освоить невозможно. Поэтому, если вы только в начале пути и хотите изучить эту перспективную и развивающуюся отрасль, то советую начать практиковаться с написания своей НС, а уже после прибегать к помощи различных фреймворков и библиотек. Также, если вам интересен мой метод изложения информации и вы хотите, чтобы я написал статьи на другие темы связанные с Машинным обучением, то проголосуйте в опросе ниже за ту тему которую вам интересна. До встречи в будущих статьях
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Какая тема вам интересна больше всего?
13.56%
Обзор НС библиотеки для Android, написанной мной на Java c 0
214
53.68%
Другие виды нейросетей: Рекуррентные, Сверточные, LSTM
847
24.9%
Генетический алгоритм
393
7.86%
Методы регуляризации выходных данных
124
Проголосовали 1578 пользователей.
Воздержались 185 пользователей.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
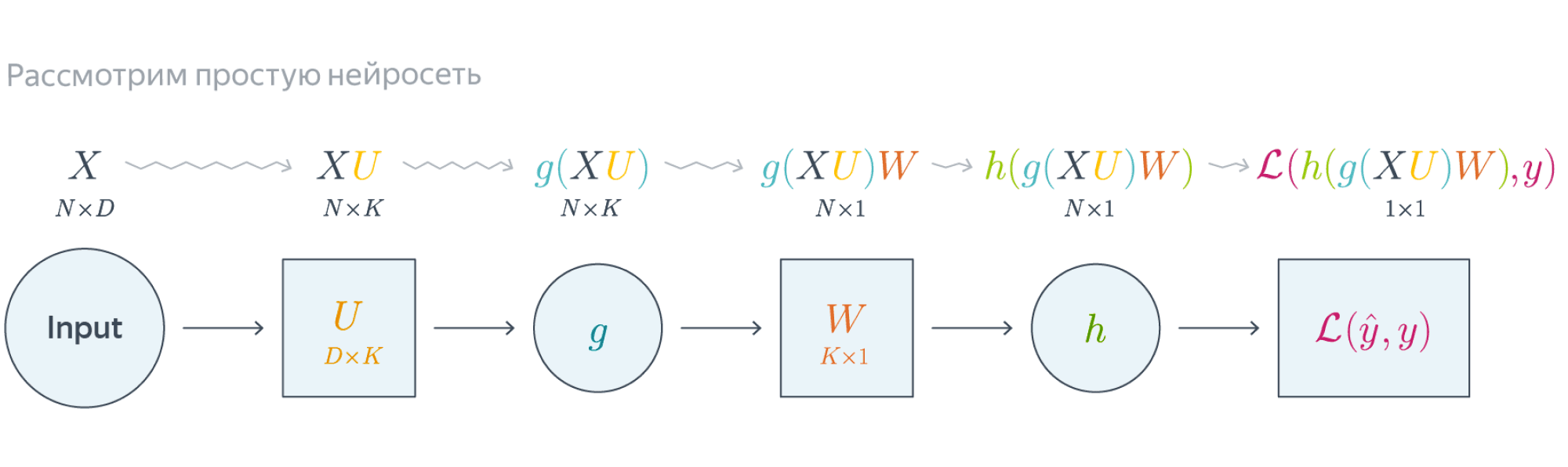
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):
То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:
Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:
В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 O_4 = 0.86 O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288
O_6 = f(I_6) = 0.54
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965
w_{68 medspace new} = 0.75+ 0.014 = 0.764
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998
w_{15 medspace new} = 1 + 0.00018 = 1.00018
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Все курсы > Оптимизация > Занятие 6
В рамках вводного курса мы начали изучать нейросети. Кроме того, нам знаком важный элемент алгоритма нейронной сети — умножение матриц.
На сегодняшнем занятии мы более подробно поговорим про то, почему нейросеть может оказаться более эффективным алгоритмом, чем рассмотренные ранее линейная и логистическая регрессия.
Кроме того, обладая знаниями о производной и градиенте, мы разберем до сих пор неизученный компонент, а именно процесс оптимизации, который в терминологии нейросетей называется обратным распространением, и построим несколько алгоритмов с нуля.
Зачем нужна нейронная сеть
Нелинейная гипотеза
Мы уже знаем, что некоторые гипотезы нелинейны. В случае задачи классификации и алгоритма логистической регрессии это означает, что, как видно на графике ниже, два класса нельзя разделить прямой линией (еще говорят, что они линейно неразделимы).
Можно обучить полиномиальную логистическую регрессию, однако с ростом количества признаков и степени полинома итоговое количество признаков, а значит и «затратность» алгоритма с точки зрения вычислительных ресурсов будет расти.
Для полинома n-ой степени (с одним признаком!) формула выглядит следующим образом.
$$ y = sum{}^n_{j=0} theta_j x^j $$
Например, полином второй степени будет иметь три коэффициента.
$$ y = theta_0 + theta_{1}x + theta_{2}x^2 $$
Полином второй степени с двумя признаками уже будет иметь шесть коэффициентов.
$$ y = theta_{0} + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
В целом, количество полиномиальных коэффициентов (N) можно рассчитать по формуле.
$$ N(n, d) = C(n+d, d), text{где} $$
- n — количество линейных признаков
- d — степень полинома
- C — количество возможных сочетаний
Используя пример выше, получим
$$ N(2, 2) = C(4, 2) = 6 $$
Полином третьей степени на основе десяти линейных признаков уже потребует создать 286 коэффициентов.
$$ N(10, 3) = C(13, 10) = 286 $$
Если речь идет о картинках 28 х 28 пикселей, то после «вытягивания» каждой картинки у нас появится датасет с 784 признаками. Значит, количество членов полинома второй степени составит
$$ N(784, 2) = C(786, 2) = 308 505 $$
Замечу, что примерное количество признаков полинома второй степени также можно посчитать по формуле $ frac{(n)^2}{2} $, то есть $ frac{(784)^2}{2} = 307 328 $
Такое количество признаков потребует очень больших вычислительных ресурсов. Посмотрим, как нейросеть может помочь справиться с этой сложностью.
Работа нейронной сети
Рассмотрим работу нейронных сетей с трех различных углов зрения.
Нейрон как дополнительный признак
Возьмем упрощенную модель нейронной сети с двумя скрытыми слоями.
Каждый нейрон каждого из скрытых слоев можно рассматривать как новый, дополнительный признак, зачастую нелинейный, способный уловить то, что не могут уловить линейные признаки. При этом умножение матриц, лежащее в основе работы нейронной сети, и векторизация операций позволяют сделать этот алгоритм достаточно быстрым.
Слой как модель логистической регрессии
Одновременно, если считать, что каждый скрытый слой проходит через функцию активации (activation function), зачастую сигмоиду, то каждый слой, кроме выходного, можно представить как, например, модель логистический регрессии.
Для модели представленной выше рассмотрим как из второго скрытого слоя получается значение выходного слоя.
- На основе первого скрытого слоя мы получили некоторые значения нейронов второго скрытого слоя ($a_1^{(2)}$ и $a_2^{(2)}$)
- У нас есть вектор весов ($w_1^{(2)}$ и $w_2^{(2)}$)
- Кроме того, мы добавим смещение (b^{(2))
Замечу, что для удобства матричных операций мы можем добавить еще один нейрон скрытого слоя ($w_0^{(2)}$) со значением 1 так, как мы это делали, например, в модели линейной регрессии.
Результат умножения двух векторов мы пропустим через сигмодиду или функцию активации (отсюда выбор буквы a для обозначения этих нейронов) и таким образом получим значение выходного слоя ($a^{(3)}$). Уверен, вы распознали уравнение логистической регрессии.
$$ a^{(3)} = g(w_0^{(2)} cdot b^{(2)} + w_1^{(2)} cdot a_1^{(2)} + w_2^{(2)} cdot a_2^{(2)}) $$
Соответственно, имея два скрытых слоя, мы строим две связанные между собой логистические регрессии. И вдвоем они могут запомнить более сложные зависимости, чем смогла бы одна такая модель, одновременно преодолевая проблему роста количества признаков полиномиальной модели.
Нейросеть и таблица истинности
Продемонстрируем, как нейросеть обучается на нелинейной гипотезе с помощью таблиц истинности.
Этот пример взят из курса по машинному обучению Эндрю Ына⧉ (Andrew Ng).
Рассмотрим линейно неразделимые данные двух классов (на рисунке слева) и упростим их до четырех наблюдений, которые могут принимать только значения 0 и 1 (на рисунке справа).
Логически такая схема соответствует условию $x_1 XNOR x_2$ или $ NOT x_1 XNOR x_2 $. В таблице истинности это условие выглядит так.
Другими словами, когда наблюдение по обоим признакам $x_1$ и $x_2$ имеет значение 0, то результатом будет класс 1, когда хотя бы один из признаков равен единице, то класс 0.
Построим нейросеть, которая будет предсказывать именно такую зависимость. Начнем с более простого компонента, а именно нейросети, которая делает прогноз в соответствии с логическим И (AND).
Итак, $x_1. x_2 in {0, 1} $ и $y = x_1 AND x_2 $. В нейросети будет два нейрона для признаков + смещение. Одновременно сразу пропишем веса модели.
Тогда выражение будет иметь вид, $y_{AND} = sigmoid(-30 + 20x_1 + 20x_2)$. Вспомним, как выглядит график сигмоиды.
Рассмотрим четыре варианта значений $x_1, x_2$ применительно к такой гипотезе.
- Если оба признака будут равны нулю, то результат линейного выражения будет равен $-30$. Если «пропустить» это значение через сигмоиду, то результат будет близок к нулю.
- Если один из них будет равен нулю, а второй единице, то результат будет равен $-10$. Сигмоида опять выдаст близкое к нулю значение.
- И только если оба признака равны единице, то результат будет равен 10 и сигмоида выдаст значение близкое к единице.
Это и есть условие логического И. Аналогичным образом можно подобрать веса для логического ИЛИ (OR).
Соответственно $y_{OR} = sigmoid(-10 + 20x_1 + 20x_2)$. Создадим еще более простую сеть для логического НЕ (NOT).
Как следствие, $y_{NOT} = sigmoid(10-20x_1)$. Создадим нейросеть, которая будет предсказывать NOT($x1$) AND NOT($x2$).
Объединим эти сети в одну.
Рассчитаем таблицу истинности.
Таким образом, мы видим, что на каждом последующем слое нейросеть строит все более сложную зависимость. Первый скрытый слой обучился достаточно простым зависимостям ($x_1$ AND $x_2$ и NOT($x_1$) AND NOT($x_2$)), второй слой дополнил это знание новым ($x1$ OR $x2$), и вместе они обучились выдавать достаточно сложный результат ($x_1$ XNOR $x_2$).
Подготовка данных
Давайте вновь возьмем данные о вине, построим вначале бинарный, а затем мультиклассовый классификатор и посмотрим, сможет ли нейросеть улучшить показатели логистической регрессии.
Откроем ноутбук к этому занятию⧉
Импортируем датасет о вине, удалим класс 2, из признаков оставим спирт и пролин, масштабируем данные.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# импортируем датасет from sklearn import datasets data = datasets.load_wine() # сформируем датафрейм и добавим целевую переменную df = pd.DataFrame(data.data, columns = data.feature_names) df[‘target’] = data.target # удалим класс 2 df = df[df.target != 2] # оставим только спирт и пролин X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # масштабируем признаки X = (X — X.mean()) / X.std() # посмотрим на размерность и оставшиеся классы df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Дополнительно преобразуем датафрейм признаков X в массив Numpy с размерность 2 x 130 и сделаем целевую переменную y двумерным массивом.
|
# каждый столбец — это одно наблюдение X = X.to_numpy().T X.shape |
|
y = y.to_numpy().reshape(1, —1) y.shape |
Нейросеть без смещения
Архитектура сети
Предлагаю идти от простого к сложному и на первом этапе создать алгоритм для бинарной классификации без смещения (bias) с приведенной ниже архитектурой.
Итак, сеть будет состоять из следующих слоев:
- входной слой $A^{(1)}$ из двух нейронов $a^{(1)}_1$ и $a^{(1)}_2$ т.е. двух признаков, на основе которых мы будем предсказывать класс вина;
- один скрытый слой $A^{(2)}$, состоящий из трех нейронов: $a^{(2)}_1$, $a^{(2)}_2$ и $a^{(2)}_3$; и
- выходной слой из одного нейрона $a^{(3)}$, т.е. вероятности принадлежности к одному из двух классов
Заглавной буквой, например, $A^{(1)}$ обозначаются сразу все нейроны, в данном случае, входного слоя, строчной с соответствющим индексом $a^{(1)}_1$ — отдельный нейрон этого слоя.
Также напомню, что у нас последовательная (sequential) архитектура сети, при которой каждый слой получает один тензор на вход и выдает также только один тензор. Кроме этого, мы используем полносвязные (дословно, «плотно связанные», dense, densely connected) слои, где каждый нейрон одного слоя связан с каждым нейроном последующего (обратите внимание на красные и зеленые стрелки между входным и скрытым слоями).
Размерность матриц
Алгоритм нейронной сети, в конечном счете, не более чем умножение матриц или, в общем случае, тензоров (отсюда, в частности, название библиотеки Tensorflow⧉, которой мы пользовались, изучая основы нейронных сетей) и после выбора архитектуры модели нам важно определиться с размерностью используемых нами матриц.
Первая матрица весов
Начнем со входного слоя, в который мы одновременно (за счет умножения матриц и векторизации кода) подадим матрицу из 130 наблюдений и двух признаков (после транспонирования размерность напомню была 2 x 130).
На нее мы будем умножать матрицу весов ($W^{(1)} cdot X$ или в терминологии слоев $W^{(1)} cdot A^{(1)}$). Как определить размерность матрицы весов? Очень просто, нужно взглянуть на количество нейронов скрытого слоя. Их три. Значит размерность первой матрицы весов составит 3 х 2.
Практический совет. Для того чтобы быстро найти размерность матрицы весов вспомним про две особенности умножения матриц:
- внутренние размеры, т.е. количество столбцов первой и строк второй, должны совпадать, в нашем случае 2 = 2.
- размерность результирующей матрицы будет равна внешним размерам умножаемых матриц, 3 и 130.
Итак, в скрытом слое у нас будет матрица 3 х 130, где каждый столбец — это три (активационных) нейрона для каждого из наблюдений.
Полносвязный слой
Убедимся, что такое умножение матриц обеспечивает умножение каждого нейрона входного слоя на каждый нейрон скрытого слоя (т.е. полносвязность, density, слоев). Для простоты, предположим, что у нас только четыре наблюдения, я не 130.
Рассмотрим первую операцию. Здесь веса $w_1$ и $w_4$ умножаются на нейроны входного слоя $a_1$ и $a_2$ и, таким образом, обеспечивают их «участие» в значении нейрона $a_1$ скрытого слоя. Аналогично, при второй операции за это отвечают $w_2$ и $w_5$. Наконец третий нейрон скрытого слоя рассчитывается благодаря весам $w_3$ и $w_6$ и опять же обоим нейронам входного слоя.
Эти же операции можно посмотреть на стрелках на схеме архитектуры сети.
Вторая матрица весов
Теперь, чтобы получить один единственный нейрон выходного слоя (вернее вектор-строку из 130 таких нейронов, 1 х 130), нам нужно новую матрицу весов умножить на результат скрытого слоя на $W^{(2)} cdot A^{(2)}$.
Очевидно, это должна быть матрица 1 х 3, потому что только она даст нам нужную итоговую размерность 1 x 130.
Важная деталь. Как нейроны скрытого слоя, так и нейрон выходного слоя проходят через функцию активации (activation function), в нашем случае сигмоиду (на схемах выше не показана).
В целом мы только что рассмотрели прямое распространение. Давайте напишем соответствующий код.
Код прямого распространения
Вначале объявим знакомые нам функции сигмоиды (функция активации) и логистической ошибки (функция потерь). Их место в архитектуре сети можно увидеть на схеме ниже.
Дополнительно замечу, что в нашей терминологии $z^(1)$ и $z^(2)$ — это результат умножения матрицы весов на матрицу нейронов соответствующего слоя, который мы «пропускаем» через сигмоиду (g). Т.е., например, для скрытого слоя
$$ Z^{(1)} = W^{(1)} cdot A^{(1)} $$
$$ A^{(2)} = g(Z^{(1)}) $$
|
# функция активации def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s # функция потерь def objective(y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) |
Теперь объявим веса и поместим признаки в нейроны скрытого слоя (исключительно ради единнобразия терминологии).
|
# зададим точку отсчета np.random.seed(33) # инициализируем случайные веса, # взятые из стандартного нормального распределения W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) # найдем количество наблюдений n = X.shape[1] # поместим признаки в нейроны входного слоя A1 = X |
Последовательно выполним операции умножения весов на нейроны и пропустим результаты через две сигмоиды.
|
# выполним умножение матриц W1 и A1 и «пропустим» результат через сигмоиду # в скобках указана итоговая размерность операции Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) # поступим аналогично с матрицами W2 и A2 Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # посмотрим, какую вероятность модель выдала для первого наблюдения A3[:,0] |
Найдем ошибку при текущих весах.
|
loss = objective(A3, y) loss |
Обратное распространение
Теперь главный вопрос. Как обновить веса так, чтобы уменьшить ошибку?
По большому счету нам нужно рассчитать частную производную функции логистической ошибки ($L$) относительно каждого веса ($w_1, w_2, w_3, …, w_9$), ведь именно их мы и будем обновлять. Начнем с весов второго слоя, а именно, $w_7, w_8, w_9$ (все вместе мы будем обозначать их как $W^{(2)}$).
Частные производные весов $W^{(2)}$
Согласно chain rule градиент (т.е. совокупность частных производных) весов второго слоя будет иметь вид
$$ frac{partial L}{partial w^{(2)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial w^{(2)} } $$
Что нам нужно сделать?
- Вначале найти производную функции логистической ошибки $ frac{partial L}{partial a^{(3)}} $
- После этого производную сигмоиды $frac{partial a^{(3)} }{partial z^{(2)}}$
- И наконец линейной функции $frac{ partial z^{(2)} }{partial w^{(2)} }$
- Перемножить эти производные
Возможно вы заметили, что выше использовались индексы (3) и (2), индекс (3) относит активационную функцию $a^{(3)}$ к третьему выходному слою, а линейную функцию $z^{(2)}$ и веса линейной функции $ w^{(2)} $ ко второму. В такой нотации нам будет удобнее в дальнейшем рассчитывать градиенты и писать код.
На всякий случай также уточню, что это будет поэлементное умножение или произведение Адамара (Hadamard product), которое мы будем обозначать через оператор $circ$.
Далее, уверен, вы обратили внимание на то, что мы выполняем операции в обратном от прямого распространения порядке: сначала производная ошибки, потом сигмоиды третьего слоя, затем линейной функции второго. Именно поэтому процесс называется обратным распространением ошибки (error back propagation).
Производная функции логистической ошибки
$$ frac{partial L}{partial a^{(3)}} = frac{partial}{partial a^{(3)}} left( -y log(a^{(3)})-(1-y) log(1-a^{(3)}) right) $$
Применим правило производной разности и вынесем константы.
$$ -y frac{partial}{partial a^{(3)}} log(a^{(3)})-(1-y) frac{partial}{partial a^{(3)}} log(1-a^{(3)}) $$
Найдем производную натурального логарифма, вынесем минус за скобку и вычтем одну дробь из другой.
$$ -left( frac{y}{a^{(3)}}-frac{(1-y) }{1-a^{(3)}} right) = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} $$
Производная сигмоиды
Производную сигмоиды мы уже находили.
$$ frac{partial a^{(3)} }{partial z^{(2)}} = g(z^{(2)}) (1-g(z^{(2)})) $$
При этом так как результат сигмоиды $ g(z^{(2)}) $ — это нейрон выходного слоя $ a^{(3)} $, то
$$ frac{partial a^{(3)} }{partial z^{(2)}} = a^{(3)} (1-a^{(3)}) $$
Производная линейной функции
Найдем производную линейной функции, расписав умножение для каждого веса и для каждого нейрона.
$$ frac{ partial }{partial w^{(2)} } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
Для того чтобы найти производную относительно, например, веса $w_7$, мы «замораживаем» (считаем константами, производная которых равна нулю) все веса кроме первого и тогда
$$ w_7^{1-1} times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = $$
$$ 1 times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = a^{(2)}_1 $$
Аналогичный результат мы получим, продифференцировав относительно других весов. Тогда,
$$ frac{ partial z^{(2)} }{partial w^{(2)}} = a^{(2)} $$
Наконец перемножим найденные производные и упростим выражение.
$$ frac{partial L}{partial w^{(2)}} = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} circ a^{(3)} (1-a^{(3)}) circ a^{(2)} = $$
$$ (a^{(3)}-y) circ a^{(2)} $$
В векторной нотации (и матричном умножении) получим
$$ frac{partial L}{partial W^{(2)}} = (A^{(3)}-y) cdot A^{(2)}.T times frac{1}{n} $$
Множитель $ frac{1}{n} $ усредняет градиент на количество наблюдений.
Дельта-правило ($ delta_2 $)
Замечу, что $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ также обозначают через греческую букву «дельта» (в нашем случае $delta_2$), и тогда градиент для обновления весов $W^{(2)}$, с учетом векторизованного кода, приобретет вид (опять же в векторной нотации)
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
В дальнейшем использование так называемого «дельта-правила» (delta rule) упростит наш код.
Обновление весов $W^{(2)}$
Остается только обновить веса $W^{(2)}$ в направлении антиградиента, умноженного на коэффициент скорости обучения.
$$ W^{(2)} := W^{(2)}-alpha times frac{partial L}{partial W^{(2)}}$$
Частные производные весов $W^{(1)}$
Теперь нужно найти производные относительно весов ($w_1, …, w_6$) или $W^{(1)}$. И мы снова должны «раскручивать» chain rule от функции логистической ошибки. На этот раз цепь будет более длинной.
$$ frac{partial L}{partial w^{(1)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } circ frac{ partial z^{(1)} }{partial w^{(1)} } $$
Нахождение производных
Вспомним, что первые два множителя $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ мы обозначили через $delta_2$.
Обратим внимание на третий множитель $ frac{ partial z^{(2)} }{partial a^{(2)} } $. В отличие от градиента весов $W^{(2)}$, где мы, напомню, искали производную линейной функции относительно весов $frac{ partial z^{(2)} }{partial w^{(2)} }$, здесь нас интересует частная производная относительно нейронов активационного слоя $a^{(2)}$.
Тогда в данном случае мы «замораживаем» (считаем константами) не веса, а нейроны $ a^{(2)} $ (считая веса просто числами) и, например, частная производная относительно $a^{(2)}_1$ будет равна
$$ frac{ partial }{partial a^{(2)}_1 } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
$$ w_7 times 1 + w_8 times 0 + w_9 times 0 = w_7 $$
Аналогично находим производные относительно других нейронов. В векторной нотации,
$$ frac{ partial z^{(2)} }{partial a^{(2)} } = W^{(2)}$$
Интересно, что ошибкой скрытого слоя $E_2$ (ошибкой $E_1$ была бы общая ошибка, которую мы рассчитали с помощью функции логистической ошибки) называют произведение
$$ E_2 = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } $$
Это утверждение более понятно, если переписать (в векторной нотации) выражение выше как,
$$ E_2 = W^{(2)}.T cdot delta_2 $$
То есть, мы по сути распространяем «ошибку» $ delta_2 $ (число, скаляр) на каждый из трех весов $W^{(2)}$.
Перейдем к четвертому множителю $ frac{ partial a^{(2)} }{partial z^{(1)} }$. Это снова производная сигмоиды, только уже «на слой раньше»,
$$ frac{ partial a^{(2)} }{partial z^{(1)} } = g(z^{(1)}) (1-g(z^{(1)})) = a^{(2)} (1-a^{(2)}) $$
И наконец пятый компонент,
$$ frac{ partial z^{(1)} }{partial w^{(1)} } = a^{(1)} $$
Дельта-правило ($ delta_1 $)
Аналогично предыдущему слою мы можем обозначить $ frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } $ как $ delta_1 $ (то есть мы опять взяли все множители, кроме последнего).
Градиент относительно $W^{(1)}$
В итоге градиент относительно весов $W^{(1)}$ имел бы вид,
$$ frac{partial L}{partial W^{(1)}} = left( E_2 circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или, раскрыв $E_2$,
$$ frac{partial L}{partial W^{(1)}} = left( ( W^{(2)}.T cdot delta_2) circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или через $ delta_1 $
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Обратите внимание на паттерн, градиент каждого слоя представляет собой произведение дельты на соответствующие нейроны активационного слоя, усредненное на количество наблюдений.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Разумеется, это правило справедливо и для большего количества скрытых слоев.
Обновление весов $W^{(1)}$
Обновление весов $W^{(1)}$ аналогично предыдущему слою.
$$ W^{(1)} := W^{(1)}-alpha times frac{partial L}{partial W^{(1)}}$$
Перейдем к коду.
Код обратного распространения
Продолжим писать код, которые мы начали, изучая прямое распространение.
|
# найдем дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) |
|
# обратите внимание, это одно число, как и результат # третьего слоя A3 (мы выводим первый столбец из 130) W2_delta[:, 0] |
|
# найдем дельту весов между слоями 1 и 2 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) |
|
# дельта 1 состоит уже из трех чисел, как и скрытый слой нейросети W1_delta[:, 0] |
|
array([-0.0099838 , 0.06300821, -0.01243332]) |
|
# напомню, что умножение дельты 2 на веса скрытого слоя W2 можно # считать «промежуточной ошибкой» сети или ошибкой скрытого слоя E2 = np.dot(W2.T, W2_delta) # то есть одно число W2_delta мы «распространили» на весь скрытый слой, # поэтому ошибка состоит из трех чисел E2[:, 0] |
|
array([-0.07704936, 1.03666489, -0.04989736]) |
|
# наконец найдем частную производную относительно весов W2 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) W2_derivative |
|
array([[-0.16738339, -0.23720379, 2.99973404]]) |
|
# и весов W1 # (размерность опять же должна совпадать с размерностью матриц весов) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 3) W1_derivative |
|
array([[-0.14145948, -0.12624909], [ 1.41742921, 1.87529043], [-0.19429558, -0.21266884]]) |
|
# обновим веса (скорость обучения возьмем равной единице) W2 = W2 — 1 * W2_derivative W1 = W1 — 1 * W1_derivative |
Обучение модели
Теперь соединим прямое и обратное распространение и с помощью цикла произведем обучение нейронной сети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
np.random.seed(33) W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) epochs = 100000 learning_rate = 1 n = X.shape[1] A1 = X for i in range(epochs): # рассчитываем прямое распространение Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # рассчитываем ошибку loss = objective(A3, y) # находим дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) # находим дельту весов между слоями 2 и 1 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # находим частные производные W2_derivative = np.dot(W2_delta, A2.T)/n # (1 x 3) W1_derivative = np.dot(W1_delta, A1.T)/n # (3 x 3) # обновляем веса W2 = W2 — learning_rate * W2_derivative W1 = W1 — learning_rate * W1_derivative # периодически выводим количество итераций и текущую ошибку if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) # можем добавить паузу для более аккуратного вывода time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 7.522291935047792 ———————— Эпоха: 20000 Ошибка: 0.7636370744482613 ———————— Эпоха: 40000 Ошибка: 0.7137144818217118 ———————— Эпоха: 60000 Ошибка: 0.6981278394758277 ———————— Эпоха: 80000 Ошибка: 0.6901729606032463 ———————— Итоговая ошибка 0.6847941294287265 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество.
|
A1 = X Z1 = np.matmul(W1, A1) A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) A3 = sigmoid(Z2) # A3.flatten() делает массив одномерным, # условие выводит True или False (1 или 0) y_pred, y_true = A3.flatten() >= 0.5, y.flatten() |
|
(array([[ 1.59357193e-03, -1.11510787e+00], [-2.70942468e+01, 1.10767378e+01], [-1.78982169e-03, 1.11459111e+00]]), array([[ 14.76831281, 8.70860599, -21.63309402]])) |
|
from sklearn.metrics import accuracy_score accuracy_score(y_true, y_pred) |
Инициализация весов
В моделях линейной и логистической регрессии в качестве начальных значений коэффициентов мы использовали нули, в алгоритме нейронной сети — случайные значения, почему так?
Если веса изначально равны нулю, то произойдет несколько нежелательных событий:
- значения активационных слоев $a_1^(2) = a_2^(2) = a_3^(2) $ будут одинаковыми, то есть запоминать одну и ту же зависимость
- более того, так как веса между вторым и третьим (выходным) слоем будут одинаковыми, то и значения матрицы $ delta_2 $ будут одинаковыми,
- а значит и частные производные, относящиеся к весам одного входного нейрона (например, $w_1, w_2, w_3$) будут одинаковыми
Таким образом, после, например, одного обновления весов, хотя значения весов $w_1, w_2, w_3$ не будут нулевыми, они будут одинаковыми. То же можно сказать про веса $w_4, w_5, w_6$. И снова $a_1^(2) = a_2^(2) = a_3^(2) $.
Как следствие, мы существенно ограничиваем возможности (гибкость) нейронной сети запоминать сложные зависимости.
Масштабирование целевой переменной
Как мы только что убедились, градиент нейронной сети зависит от целевой переменной. Если эта переменная имеет большой диапазон, то это может создать большую ошибку при вычислении градиента, что, в свою очередь, вызовет существенное изменение весов и дестабилизирует процесс обучения.
Очевидно после обучения и прогноза целевую переменную нужно вернуть к прежнему масштабу.
Модель в Tensorflow и Keras
Библиотека Keras представляет собой «надстройку«⧉ (интерфейс, API), через которую удобно создавать нейросети в библиотеке Tensorflow. Реализуем созданную выше несложную нейросеть в библиотеке Keras.
|
# в Google Colab уже установлена вторая версия библиотеки Tensorflow, # которая существенно отличается от первой версии import tensorflow as tf tf.__version__ |
В нейросеть мы будем подавать признаки и целевую переменную таким образом, чтобы объекты были строками.
Перейдем к созданию и обучению нейросети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# зададим две точки отсчета, одну в библиотеке Numpy np.random.seed(42) # вторую непосредственно в Tensorflow tf.random.set_seed(42) # зададим архитектуру: последовательная модель model = tf.keras.models.Sequential([ # с полносвязными слоями # также укажем нейроны скрытого и выходного слоев # откажемся от смещения tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = False), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = False) ]) # зададим особенности стохастического градиентного спуска (SGD) # в частности, откажемся от импульса # (подробнее об этом на последующих занятиях) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) # соберем все вместе, дополнительно укажем тип функции потерь и метрику качества model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) # зададим количество эпох, # размер batch, после которой мы обновляем веса, равен объему данных (fullbatch) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) |
|
<keras.callbacks.History at 0x7f5f49c0aa90> |
|
Model: «sequential_3» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_6 (Dense) (130, 3) 6 dense_7 (Dense) (130, 1) 3 ================================================================= Total params: 9 Trainable params: 9 Non—trainable params: 0 _________________________________________________________________ |
Оценим качество.
|
model.history.history[‘accuracy’][—1] |
Нейросеть со смещением
Добавим смещение, это должно сделать нашу модель более гибкой.
В отличие от линейных моделей, мы не будем использовать одну и ту же производную и для $b$, и для $W$ (с добавлением столбца из единиц в X). Это связано с тем, что в нейросетях при обратном распространении ошибку на смещение мы не распространяем.
Найдем производные смещения относительно сигмоиды (последний компонент в цепи производных).
$$ frac{ partial z^{(2)} }{partial b^{(2)}} = 1 $$
$$ frac{ partial z^{(2)} }{partial b^{(1)}} = 1 $$
Тогда в целом, используя дельта-правило, частные производные относительно $b^{(2)}$ и $b^{(1)}$ будут равны
$$ frac{partial L}{partial b^{(2)}} = sum delta_2 times frac{1}{n} $$
$$ frac{partial L}{partial b^{(1)}} = sum delta_1 times frac{1}{n} $$
Перейдем к коду.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
np.random.seed(33) # инициализируем веса W1 = np.random.randn(3, 2) # b1 будет иметь размерность 3 х 1, # потому что распространяется на три нейрона скрытого слоя b1 = np.random.randn(3, 1) W2 = np.random.randn(1, 3) b2 = np.random.randn(1, 1) n = X.shape[1] epochs = 100000 learning_rate = 1 A1 = X for i in range(epochs): # 3 х 2 на 2 х 130 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # (3 x 130) # 1 х 3 на 3 х 130 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # (1 x 130) loss = objective(A3, y) W2_delta = A3 — y # (1 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # keepdims сохраняет исходную размерность # 1 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 2 W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 10.080172158274355 ———————————— Эпоха: 20000 Ошибка: 0.5460931772435075 ———————————— Эпоха: 40000 Ошибка: 0.5235933834724054 ———————————— Эпоха: 60000 Ошибка: 0.5153108060799304 ———————————— Эпоха: 80000 Ошибка: 0.5104559107317911 ———————————— Итоговая ошибка 0.5070018571750416 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) y_pred, y_true = A3.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
TF / Keras. Добавим смещение в нашу модель в библиотеке Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_6» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_12 (Dense) (130, 3) 9 dense_13 (Dense) (130, 1) 4 ================================================================= Total params: 13 Trainable params: 13 Non-trainable params: 0 _________________________________________________________________ |
|
model.history.history[‘accuracy’][—1] |
|
(array([[ 6.12093182, -12.02342998], [-22.00510547, -9.19535995], [ 14.35718419, 9.69417827]]), array([[ 12.32118926, 15.26008905, -10.91093576]])) |
Два скрытых слоя
Добавим второй скрытый слой.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
np.random.seed(33) W1 = np.random.randn(3, 2) b1 = np.random.randn(3, 1) W2 = np.random.randn(3, 3) b2 = np.random.randn(3, 1) W3 = np.random.randn(1, 3) b3 = np.random.randn(1, 1) n = X.shape[1] epochs = 10000 learning_rate = 1 A1 = X for i in range(epochs): Z1 = np.dot(W1, A1) + b1 # (3 x 130) A2 = sigmoid(Z1) Z2 = np.dot(W2, A2) + b2 # (3 x 130) A3 = sigmoid(Z2) Z3 = np.dot(W3, A3) + b3 # (1 x 130) A4 = sigmoid(Z3) loss = objective(A4, y) W3_delta = A4 — y # (1 x 130) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (3 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # 3 х 130 на 130 х 3 W3_derivative = np.dot(W3_delta, A3.T) / n # (3 x 3) b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (3 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(1) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 11.483275165239569 ———————— Эпоха: 2000 Ошибка: 0.7137240298878413 ———————— Эпоха: 4000 Ошибка: 0.683999037922229 ———————— Эпоха: 6000 Ошибка: 0.6718618481850791 ———————— Эпоха: 8000 Ошибка: 0.6640320570961954 ———————— Итоговая ошибка 0.6583025695728971 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = sigmoid(Z3) y_pred, y_true = A4.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
Сравним с моделью в Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_2» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_4 (Dense) (130, 3) 9 dense_5 (Dense) (130, 3) 12 dense_6 (Dense) (130, 1) 4 ================================================================= Total params: 25 Trainable params: 25 Non-trainable params: 0 |
|
model.history.history[‘accuracy’][—1] |
Многоклассовая классификация
Создадим нейросеть, которая будет предсказывать вероятности нескольких классов. Во многом, идея алгоритма совпадает с softmax логистической регрессией.
Постановка задачи и архитектура
Возьмемся за ту же задачу, которую мы решили в рамках вводного курса с помощью библиотеки Keras, а именно создадим нейросеть, которая будет распознавать рукописные цифры из датасета MNIST.
Архитектуру модели сохраним прежней.

Функции активации
Как видно на графике, мы будем использовать сигмоиду для промежуточных слоев и softmax для выходного слоя.
|
def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s |
|
def softmax(z): # на выходном слое тензор будет иметь размерность 10 х 60000, # поэтому складывать мы будем по столбцам z = z — np.max(z, axis = 0, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = 0, keepdims = True) softmax = numerator / denominator return softmax |
Функция потерь
Функцией потерь будет категориальная кросс-энтропия.
|
def cross_entropy(probs, y_enc, epsilon = 1e—9): # опять же, так как softmax выдаст тензор 10 х 60000 # количество наблюдений содержится в атрибуте shape[1] n = probs.shape[1] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Обратное распространение
Очевидно, так как изменилась функция потерь и функция активации выходного слоя (softmax) необходимо заново рассчитать производные. Напомню, для весов $W^{(3)}$ цепное правило будет работать следующим образом.
$$ frac{partial L}{partial w^{(3)}} = frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}} circ frac{ partial z^{(3)} }{partial w^{(3)} } $$
При этом, оказывается, что производная первых двух компонентов $frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}}$ (т.е. кросс-энтропии и softmax) сводится к $a^{(4)}-y$ (она аналогична бинарной кросс-энтропии и сигмоиде, но находится⧉, разумеется, иначе).
Одновременно этот компонент производной представляет собой $delta_3$, которую для нахождения градиента необходимо умножить на $A^{(3)}.T$.
$$ frac{partial L}{partial W^{(3)}} = delta_3 cdot A^{(3)}.T times frac{1}{n} $$
Остальные производные находятся аналогично предыдущим моделям.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Подготовка данных
|
import mnist from tensorflow import keras |
|
def ohe(y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
X_train = mnist.train_images() y_train = mnist.train_labels() X_test = mnist.test_images() y_test = mnist.test_labels() X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 X_train = X_train.reshape((—1, 784)).T X_test = X_test.reshape((—1, 784)).T y_train_enc, y_test_enc = ohe(y_train).T, ohe(y_test).T X_train.shape, y_train_enc.shape |
|
((784, 60000), (10, 60000)) |
Обучение модели
Код ниже исполняется в Google Colab около 10 минут.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
np.random.seed(33) W1 = np.random.randn(64, 784) b1 = np.random.randn(64, 1) W2 = np.random.randn(64, 64) b2 = np.random.randn(64, 1) W3 = np.random.randn(10, 64) b3 = np.random.randn(10, 1) n = X_train.shape[1] epochs = 500 learning_rate = 1 A1 = X_train for i in range(epochs): # 64 x 784 на 784 x 60000 —> 64 x 60000 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # 64 x 64 на 64 x 60000 —> 64 x 60000 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # 10 x 64 на 64 x 60000 —> 10 x 60000 Z3 = np.dot(W3, A3) + b3 A4 = softmax(Z3) loss = cross_entropy(A4, y_train_enc) W3_delta = A4 — y_train_enc # (10 x 60000) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (64 x 60000) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (64 x 60000) # 10 x 60000 на 60000 x 64 —> 10 x 64 W3_derivative = np.dot(W3_delta, A3.T) / n b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 64 —> 64 x 64 W2_derivative = np.dot(W2_delta, A2.T) / n b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 784 —> 64 x 784 W1_derivative = np.dot(W1_delta, A1.T) / n b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 6.215969648082527 ———————— Эпоха: 100 Ошибка: 0.9316990279468341 ———————— Эпоха: 200 Ошибка: 0.7055264357349225 ———————— Эпоха: 300 Ошибка: 0.5950572560699322 ———————— Эпоха: 400 Ошибка: 0.5276765625306427 ———————— Итоговая ошибка 0.4813698685793663 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество на обучающей выборке.
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) |
|
y_pred = np.argmax(A4, axis = 0) y_pred[:4] |
|
from sklearn.metrics import accuracy_score accuracy_score(y_train, y_pred) |
Теперь на тестовых данных.
|
A1 = X_test Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) y_pred = np.argmax(A4, axis = 0) accuracy_score(y_test, y_pred) |
Алгоритм показал достаточно высокую точность и при увеличении количества эпох и настройке скорости обучения мог бы показать более высокий результат.
При этом очевидно, что модель, которую мы создали в рамках вводного курса в библиотеке Keras обучилась гораздо быстрее. На занятии по градиентному спуску мы посмотрим, как можно ускорить работу нашего алгоритма.
Подведем итог
На сегодняшнем занятии мы в деталях посмотрели на математику обратного распространения, а также с нуля построили несколько алгоритмов нейронных сетей.
На следующем занятии мы вернемся к теме качества алгоритмов, а также рассмотрим один из инструментов повышения этого качества, который называется регуляризацией.
Ответы на вопросы
Вопрос. Чем отличается умножение матриц от векторизации?
Ответ. Принцип умножения матриц относится к математике и описывает правила, по которым мы умножаем два двумерных тензора. Векторизация кода — термин из программирования, который позволяет избежать использования циклов в процессе выполнения кода.