Аннотация: Цель работы: Изучить и практически освоить метод Монте-Карло на примерах расчета площадей плоских фигур, объемов пространственных тел, а также вычисления кратных интегралов. Среда программирования — MATLAB.
Теоретическая часть
Сущность метода Монте-Карло состоит в следующем: требуется найти значение 


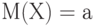
Практически же поступают следующим образом: производят 


и принимают 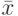
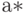

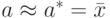
Поскольку метод Монте-Карло требует произведения большого числа испытаний, его часто называют методом статистических испытаний.
1. Оценка погрешности метода Монте-Карло
Как отмечалось, для получения оценки математического ожидания случайной величины 



При этом возможны следующие случаи оценки числа испытаний:
-
Случайная величина
распределена нормально и ее среднее квадратическое отклонение (стандартное отклонение)
известно. В этом случае с заданной вероятностью
верхняя граница ошибки определяется по формуле
(
4.1)где:
— число испытаний (разыгранных значений случайной величины
);
— значение аргумента функции Лапласа
или интеграла вероятности, при котором она равна половине заданной вероятности;
— известное среднее квадратическое отклонение.
Из формулы (4.1) может быть найдено число испытаний. Один из вариантов интеграла вероятностей (функции Лапласа) имеет вид [6]
(
4.2)Значения
табулированы и приведены в большинстве учебников по теории вероятностей и математической статистике.
В зарубежной литературе большое распространение получила так называемая функция ошибок (
)
:
(
4.3)Связь между функцией ошибок (4.3) и интегралом вероятностей (4.2) выражается в виде
(
4.4) -
Случайная величина
распределена нормально, причем ее среднее квадратическое отклонение неизвестно. В этом случае с заданной вероятностью
верхняя граница ошибки вычисляется по формуле
(
4.5)где:
— число испытаний;
— «исправленное» среднее квадратическое отклонение;
находят по специальным таблицам, например, приведенной в [6].
Из формулы (4.5) может быть найдено число испытаний для определения верхней границы ошибки.
- Случайная величина
распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (
), с вероятностью, приближенно равной
(заданной вероятностью), верхняя граница ошибки может быть вычислена по формуле (4.1), если среднее квадратическое отклонение случайной величины известно; если же оно неизвестно, то можно подставить в формулу (4.1) его оценку — «исправленное» среднее квадратическое отклонение — либо воспользоваться формулой (4.5). При этом чем больше число испытаний, тем меньше различие между результатами, которые дают обе формулы.
2. Вычисление кратных интегралов методом Монте-Карло
В случае когда, например, определенный интеграл не может быть вычислен в квадратурах, либо прибегают к численным методам интегрирования, либо расчет ведется с помощью метода Монте-Карло. Применение метода Монте-Карло становится оправданным при кратности интеграла больше трех. В данной лабораторной работе мы используем метод Монте-Карло для расчета интегралов с кратностью не более трех. Это позволит более ясно представить технику применения метода.
Сначала рассмотрим вычисление простого определенного интеграла
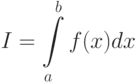 |
( 4.6) |
где 
Введем под знак интеграла постоянный множитель (равный единице):
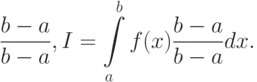 |
( 4.7) |
Вынесем из-под интеграла числитель дроби, получим
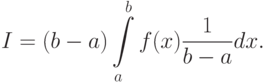 |
( 4.8) |
Как известно, если случайная величина 

Кроме того, если известно распределение случайной величины 

![M[x]](https://intuit.ru/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png)
Соответственно, математическое ожидание от функции случайной величины будет определяться следующим образом:
![M[f(x)]=intlimits_{a}^{b}f(x)frac{1}{b-a}dx.](https://intuit.ru/sites/default/files/tex_cache/42149a4cde11c98da0e505e2279d7980.png) |
( 4.9) |
Сопоставляя (4.8) и (4.9), приходим к выводу, что определенный интеграл может быть рассчитан по формуле
![I=(b-a)M[f(x)].](https://intuit.ru/sites/default/files/tex_cache/6a755a2e5019e4067dd39dccfab13a63.png) |
( 4.10) |
Несмещенной оценкой математического ожидания случайной величины, как известно, является ее среднее арифметическое. Поэтому математическое ожидание можем приближенно найти по формуле
![M[f(x)]approx frac{1}{n}sumlimits_{i=1}^{n}f(x_i).](https://intuit.ru/sites/default/files/tex_cache/1e2f3c404db3d6b0d0a520572ddefc3e.png) |
( 4.11) |
С учетом (4.11) получаем выражение для приближенного расчета определенного интеграла
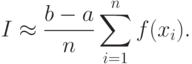 |
( 4.12) |
Чем больше число испытаний 
Рассмотрим общий подход вычисления 
Пусть задан 
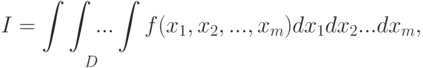 |
( 4.13) |
где подынтегральная функция 
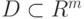
Погрузим область интегрирования 

![D^* = [a_1, b_1]times[a_2, b_2]times ... [a_m, b_m],](https://intuit.ru/sites/default/files/tex_cache/23a20b84ad54eb95a594f5c785f6284a.png) |
( 4.14) |
имеющий меру
 |
( 4.15) |
Определим в промежутке (4.15) функцию
 |
( 4.16) |
Тогда в соответствии с (4.13) и (4.16) получим
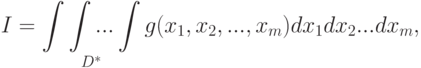 |
( 4.17) |
Введем в рассмотрение 

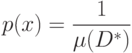 |
( 4.18) |
Функция плотности равномерного распределения есть величина постоянная, поэтому введем ее под знак интеграла (4.17) следующим образом:
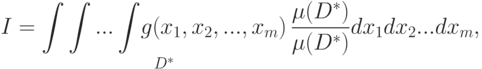 |
( 4.19) |
Вынесем числитель дроби за знак интеграла, т. е.
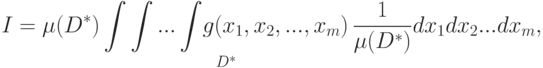 |
( 4.20) |
В (4.20) 


![I=mu (D^{*})M[g(x)],](https://intuit.ru/sites/default/files/tex_cache/cf20ace0be47f575d3035d97a4879769.png) |
( 4.21) |
где 
В свою очередь математическое ожидание может быть оценено с помощью арифметического среднего. Тогда приближенное значение 
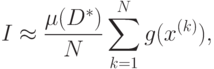 |
( 4.22) |
где 


Чтобы смоделировать выборку 


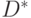



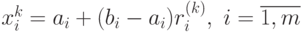
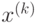
Таким образом, техника применения метода Монте-Карло здесь будет заключаться в определении области 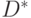

Расчет площадей и объемов можно рассматривать как частный случай вычисления кратных интегралов. Например, вычисление объема тел с помощью трехкратного интеграла сводится к взятию интеграла по области при подынтегральной функции, тождественно равной единице.
Asked
1 year, 2 months ago
Viewed
410 times
$begingroup$
I am new to Monte Carlo simulation and have a question. What is the connection between the standard errors of the estimates that we normally get from a regression and standard deviation of sampling distribution for the same parameter that we get from MC simulation. I notice that the mean of these two over several repetitions are very close. Conceptually I can understand that they should be close but still I am not quite clear about it! and what do we understand if these two values are not close? Is there any theoretical proof to show the connection between these two? Any clarification is much appreciated.
asked Nov 24, 2021 at 20:23
$endgroup$
1
$begingroup$
This is a great question. If we conceptualize repeating the experiment an infinite number of times then there is a one true standard error that we will never know. The standard error estimate produced my most regression packages replaces unknown parameters with estimates of these parameters. When you perform a simulation you can capture the estimated standard error in each simulated run and then plot these using a histogram. This shows the sampling variability of the standard error estimator. You can compare these standard error estimates to the Monte Carlo standard error. The Monte Carlo standard error can be brought arbitrarily close to the one true standard error with enough simulated runs.
In non-normal models the Wald, score, and likelihood ratio tests treat the estimated standard error as known (as if it is the one true standard error). In a normal model the t- and F- tests are special in that they account for the sampling variability of the standard error estimator.
answered Nov 24, 2021 at 21:43
$endgroup$
2
Asked
1 year, 2 months ago
Viewed
410 times
$begingroup$
I am new to Monte Carlo simulation and have a question. What is the connection between the standard errors of the estimates that we normally get from a regression and standard deviation of sampling distribution for the same parameter that we get from MC simulation. I notice that the mean of these two over several repetitions are very close. Conceptually I can understand that they should be close but still I am not quite clear about it! and what do we understand if these two values are not close? Is there any theoretical proof to show the connection between these two? Any clarification is much appreciated.
asked Nov 24, 2021 at 20:23
$endgroup$
1
$begingroup$
This is a great question. If we conceptualize repeating the experiment an infinite number of times then there is a one true standard error that we will never know. The standard error estimate produced my most regression packages replaces unknown parameters with estimates of these parameters. When you perform a simulation you can capture the estimated standard error in each simulated run and then plot these using a histogram. This shows the sampling variability of the standard error estimator. You can compare these standard error estimates to the Monte Carlo standard error. The Monte Carlo standard error can be brought arbitrarily close to the one true standard error with enough simulated runs.
In non-normal models the Wald, score, and likelihood ratio tests treat the estimated standard error as known (as if it is the one true standard error). In a normal model the t- and F- tests are special in that they account for the sampling variability of the standard error estimator.
answered Nov 24, 2021 at 21:43
$endgroup$
2
ЧАСТЬ
ЧЕТВЕРТАЯ
МЕТОД
МОНТЕ-КАРЛО. ЦЕПИ МАРКОВА
Глава двадцать
первая
МОДЕЛИРОВАНИЕ
(РАЗЫГРЫВАНИЕ)
СЛУЧАЙНЫХ ВЕЛИЧИН МЕТОДОМ МОНТЕ-КАРЛО
Датой
рождения метода Монте – Карло принято
считать 1949 г.. когда американские ученые
Н. Метрополис и С. Улам опубликовали
статью «Метод Монте-Карло», в которой
систематически его изложили. Название
метода связано с названием города Монте
– Карло, где в игорных домах (казино)
играют в рулетку из простейших устройств
для получения случайных чисел на
использовании которых основан этот
метод.
ЭВМ
позволяют легко получать так называемые
псевдослучайные числа (при решении
задач их применяют вместо случайных
чисел); это привело к широкому внедрению
метода во многие области науки и техники
(статистическая физика, теория массового
обслуживания, теория игр и др.). Метод
Монте-Карло используют для вычисления
интегралов, в особенности многомерных
для решения систем алгебраических
уравнений высокого порядка для
исследования различного рода сложных
систем (автоматического управления,
экологических, биологических и т.д.).
Сущность
метода Монте-Карло
состоит в следующем: требуется найти
значение а
некоторой
изучаемой величины. Для этого выбирают
такую величину
X,
математическое ожидание которой равно
а:
Практически
же поступают так: производят п
испытаний, в результате которых получают
n
возможных значении X,
вычисляют их среднее арифметическое
и принимают х
в качестве оценки (приближенного
значения) а*
искомого числа а:
Поскольку метод
Монте—Карло требует проведения большого
числа испытаний, его часто называют
методом
статистических испытаний.
Теория этого метода указывает, как
наиболее целесообразно выбрать случайную
величину X, как найти ее возможные
значения. В частности, разрабатываются
способы уменьшения дисперсии используемых
случайных величин, в результате чего
уменьшается ошибка, допускаемая при
замене искомого математического ожидания
а
его оценкой а*.
Отыскание возможных
значений случайной величины X
(моделирование)
называют «разыгрыванием случайной
величины». Изложим лишь некоторые
способы разыгрывания случайных величин
и укажем, как оценить допускаемую при
этом ошибку.
§ 2. Оценка погрешности метода Монте—Карло
Пусть для получения
оценки а*
математического ожидания а
случайной величины Х
было произведено п
независимых
испытаний (разыграно п
возможных значений X)
и по ним была найдена выборочная средняя
,
которая принята в качестве искомой
оценки: а*=х.
Ясно, что
если повторить опыт, то будут получены
другие возможные значения X,
следовательно, другая средняя, а
значит, и другая оценка а*.
Уже отсюда следует, что получить точную
оценку математического ожидания
невозможно. Естественно, возникает
вопрос о величине допускаемой ошибки.
Ограничимся отысканием лишь верхней
границы δ
допускаемой ошибки с заданной вероятностью
(надежностью) γ:
Интересующая нас
верхняя граница ошибки δ
есть не что иное, как «точность оценки»
математического ожидания по выборочной
средней при помощи доверительных
интервалов, о которой уже шла речь в
гл. XVI. Поэтому воспользуемся результатами,
полученными ранее, и рассмотрим
следующие три случая.
1. Случайная
величина Х
распределена нормально и ее среднее
квадратическое отклонение σ
известно.
В этом случае с надежностью γ
верхняя граница ошибки (см. гл. XVI, § 15)
(*)
где п—число
испытаний (разыгранных значений X);
t—
значение
аргумента функции Лапласа, при котором
Ф(t)=γ/2,
а—известное среднее квадратическое
отклонение X.
Пример 1.
С надежностью γ
=0,95 найти верхнюю границу ошибки σ,
если для оценки математического ожидания
нормальной величины Х
с известным средним квадратическим
отклонением, равным 0,5, было разыграно
100 возможных значений X.
Решение. По условию,
n=100,
σ=0,5,
Ф(t)=
0,95/2 =0,475. По таблице функции Лапласа (см.
приложение 2) находим t=1,96.
Искомая верхняя граница ошибки δ=
1,96·0,5/==0,098.
2. Случайная
величина Х
распределена нормально, причем ее
среднее квадратическое отклонение
σ
неизвестно.
В этом случае с надежностью γ
верхняя граница ошибки (см. гл. XVI, § 16)
(**)
где п—число
испытаний; s—«исправленное»
среднее квадратическое отклонение,
tγ
находят по таблице приложения 3.
Пример 2.
С надежностью γ
=0,95 найти верхнюю границу ошибки δ,
если для оценки математического ожидания
нормальной величины Х
было разыграно 100 ее возможных значений
и по ним найдено «исправленное» среднее
квадратическое отклонение s
==0,5. Решение. По условию, n=100,
s=0,5.
Используя таблицу приложения 3, по γ
=0,95, n=100
находим tγ,=1,984.
Искомая верхняя граница ошибки δ
= 1,984·0,5/
=0,099.
3. Случайная
величина Х
распределена по закону, отличному от
нормального.
В этом случае при достаточно большом
числе испытаний (n>30)
с надежностью, приближенно равной γ,
верхняя граница ошибки может быть
вычислена по формуле (*), если среднее
квадратическое отклонение σ
случайной величины Х
известно; если же σ
неизвестно, то можно подставить в формулу
(*) его оценку s—«исправленное»
среднее квадратическое отклонение либо
воспользоваться формулой (**). Заметим,
что чем больше п,
тем меньше различие между результатами,
которые дают обе формулы. Это объясняется
тем, что при п
—
распределение Стьюдента стремится к
нормальному (см. гл. XVI, § 16, замечание).
В частности (примеры 1 и 2), при n
=100, γ=0,95
верхняя граница ошибки равна 0,098 по
формуле (*) и 0,099 по формуле (**). Как видим,
результаты различаются незначительно.
Замечание. Для
того чтобы найти наименьшее число
испытаний, которые обеспечат наперед
заданную верхнюю границу ошибки δ,
надо выразить n
из формул (*) и (**):
Например, если
δ==0,098,
t=1,96,
=0,5, то минимальное число испытаний, при
которых ошибка не превысит 0,098, равно
п=1,9б2·0,52/0,0982=100.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Баранов В.А.
1
Данилов А.А.
2
Шумарова С.А.
1
1 ФГБОУ ВПО «Пензенский государственный университет Минобразования России»
2 ФБУ «Пензенский ЦСМ»
Метод Монте — Карло является эффективным инструментом оценивания характеристик случайных по-грешностей косвенных, совокупных и совместных измерений при любых законах распределения плотно-сти вероятностей погрешности результатов прямых измерений, в частности, среднего квадратического отклонения результатов измерений параметров комплексного сопротивления, определяющих качество высоковольтных электроизоляторов: электрическая емкость или обратная ей величина, активное элек-трическое сопротивление или проводимость, тангенс угла диэлектрических потерь или тангенс угла фа-зового сдвига. Распределение вероятностей погрешности результатов измерений этих параметров по значениям составляющих комплексного сопротивления, полученным прямым измерением с относитель-ной погрешностью менее ±1% с равномерным распределением вероятностей погрешности, является тре-угольным (тангенс угла диэлектрических потерь, тангенс угла фазового сдвига), равномерным (активное электрическое сопротивление или проводимость) или нормальным (электрическая емкость и обратная ей величина). При относительной погрешности результатов измерений составляющих комплексного сопротивления, превышающей ±1%, распределения вероятностей погрешности результатов измерений параметров комплексного сопротивления становятся заметно асимметричными. В таких случаях при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения вероятностей погрешности.
случайная погрешность.
метод Монте — Карло
комплексное сопротивление
измерения
1. Баранов В. А. Измерения параметров композиционных диэлектрических материалов. – Пенза : ИИЦ ПГУ, 2008. – 124 с.
2. Данилов А. А., Шумарова С. А. Об асимметрии функции плотности распределения ве-роятностей погрешности результатов измерений, полученных с помощью сложных измери-тельных каналов измерительных систем // Измерительная техника, . — 2012, . — № 11, . — С. 60 — 61.
3. ГОСТ 30421 — 96 Измерители электрической емкости, активного сопротивления и тан-генса угла потерь высоковольтные. Общие технические условия.
4. ПМГ 96 — 2009 Результаты и характеристики качества измерений. Формы представ-ления.
5. Сви П. М. Методы и средства диагностики оборудования высокого напряжения. — М. : Энергоатомиздат, 1992. — 240 с.
6. Соболь И. М. Метод Монте-Карло. – Москва., « : Наука», 1968. – 64 с.
Введение
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных величин, предложенный в 1949 году американскими математиками Дж. Нейманом и С. Уламом. Хотя метод был известен и ранее, но широкое применение он получил после появления ЭВМ [6]. В настоящее время метод Монте-Карло широко применяется при решении разнообразных задач многих отраслей науки и техники. Область его использования постоянно расширяется в условиях информатизации научной и производственной деятельности в связи с простым алгоритмом решения многих задач по сравнению с аналитическим решением, простотой оценок методической погрешности, слабой зависимостью точности от размерности пространства (числа независимых переменных).
В простейшем случае метод Монте-Карло состоит в синтезе математической модели объекта исследования в виде случайной величины, генерации ряда независимых испытаний (реализаций) этой случайной величины и определении статистических характеристик полученной выборки. Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. При этом метод Монте-Карло может быть использован не только для симметричных, но и для асимметричных распределений [2].
Ограничением применимости метода Монте-Карло в ходе научных исследований является то, что он не может заменить аналитические методы при исследовании малоизученных явлений и процессов, где на первом этапе необходимо выявление качественных закономерностей, описывающих объект исследования.
При проектировании измерительных устройств невозможность синтеза аналитической модели измерения не имеет значения, поскольку объект проектирования качественно определен на этапе составления уравнения измерения (функции преобразования). Последующий метрологический анализ позволяет получить оценку характеристик погрешности измерений, количественную характеристику точности, по известным характеристикам погрешности элементарных измерительных операций. Типичная методическая ошибка метода Монте-Карло 5-10% [6] полностью удовлетворяет требованиям к точности оценивания погрешности измерения.
Применение метода Монте-Карло дает наибольший эффект по сравнению с аналитическими методами при оценивании характеристик погрешности результатов косвенных, совместных и совокупных измерений, когда обрабатываются результаты прямых измерений двух и более величин.
Так, в работе [2] методом Монте-Карло получена оценка случайной погрешности произведения результатов измерений, полученных с помощью каналов измерительных систем с номинальной линейной функцией преобразования.
Аналогичные задачи возникают при разработке измерителей параметров электроизоляционных конструкций под рабочим напряжением для технического обслуживании систем электроснабжения по состоянию [5].
Материал и методы исследования
В ГОСТ 30421-96 установлены пары нормируемых электрических параметров электроизолятора, представленные в таблице 1 [3]. Пары составляют электрическая емкость или обратная ей величина
, активное электрическое сопротивление
или проводимость
, тангенс угла диэлектрических потерь
или тангенс угла фазового сдвига
.
Значения всех нормируемых параметров электроизоляторов могут быть определены по результатам измерений активной и реактивной
составляющих комплексного сопротивления (СКС) объекта измерений и частоты ω гармонического напряжения питания измерительной схемы при использовании схемы замещения объекта в виде параллельно соединенных резистора сопротивлением
и конденсатора емкостью
, если оценены соответствующие характеристики погрешности. Это позволяет разработать универсальный измеритель электрических параметров электроизоляторов [1].
Таблица 1 – Предпочтительные пары измеряемых величин
|
Предпочтительные пары |
|
|
Главная величина |
Дополнительный параметр |
|
С или 1/С С или 1/С С или 1/С R или G R или G tgδ |
tgδ R G С или 1/С tgφ С или 1/С |
Взаимосвязь нормируемых параметров электроизоляторов с СКС отражается с помощью формул:
,
,
,
,
,
.
В соответствии с ПМГ 96-2009 в случаях, когда результаты измерений используются совместно с другими результатами измерений, за характеристики качества измерений принимают точечные характеристики — среднеквадратичное отклонение погрешности или стандартную неопределенность [4]. Точечная характеристика должна сопровождаться указанием принятой аппроксимации закона распределения плотности вероятностей погрешности. ПМГ 96-2009 распространяются на случайные погрешности прямых измерений, функции плотности распределения вероятностей которых относятся к классу симметричных, одномодальных, усеченных функций. Оценки основаны на предположениях о распределении погрешностей прямых измерений по закону равномерной плотности как наихудшему (дающему для СКО оценку сверху) из законов распределения, относящихся к указанному классу, и отсутствует корреляция между величинами, измеряемыми прямым методом и, соответственно, погрешностями их измерений.
Для оценки характеристик случайной погрешности результатов измерений параметров электроизоляторов проведено моделирование в среде MathCAD методом Монте-Карло с построением по результатам статистических испытаний гистограммы распределения плотности вероятностей случайной погрешности. Входные переменные программы: число реализаций ; число интервалов ряда наблюдений (число столбцов гистограммы)
; номинальные значения СКС
и
, пределы допускаемой относительной случайной погрешности СКС; математическая модель, описывающая зависимость искомой величины от СКС. Выходные переменные программы: СКО СКС, СКО искомой величины. Число реализаций определяется в зависимости от требований к точности и заранее неизвестно, оно не должно быть менее 106 .
Для построения гистограммы использовалась встроенная функция: «hist(intvis,x)», которая определяет вектор частоты попадания данных в интервалы гистограммы; где «intvis» – вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания, «a<intvisi<b;х» – вектор случайных данных. Равномерный закон распределения плотности вероятности составляющих комплексного сопротивления задавался посредством встроенной функции «runif(x1,x2,x3)». Для вычисления среднеквадратического отклонения использовалась встроенная функция «stdev(x)».
В ходе исследований было принято: ,
МОм,
МОм,
,
Гц, пределы допускаемой относительной случайной погрешности результатов измерений СКС εRX и εXX, тангенса угла диэлектрических потерь εtgδ, тангенса угла фазового сдвига εtgφ, частоты напряжения питания измерительной схемы εω составляют ±1% номинальных значений и имеют равномерное распределение.
Результаты исследования и их обсуждение
Гистограмма распределения погрешности результата измерения тангенса угла потерь
и погрешности результата измерения тангенса угла фазового сдвига
имеет форму равнобедренного треугольника. При принятых номинальных значениях величин СКО = 0,008.
Гистограмма распределения погрешности результата измерения сопротивления
резистора эквивалентной схемы имеет форму прямоугольника, т.е. распределение равномерно, СКО = 0,012 МОм.
Распределение погрешности результата измерения проводимости
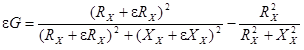
, близко к равномерному, СКО = 2,9 мСм.
Распределение погрешности результата измерения емкости эквивалентной схемы замещения
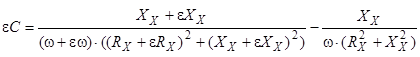
Плотность распределения вероятностей погрешности 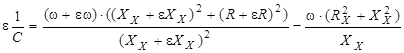
При погрешностях результатов измерений СКС более ±1% гистограммы распределения погрешностей результатов измерений величин, представленных в таблице, становятся заметно асимметричными. В этом случае при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения.
На рис. 1 представлена гистограмма распределения вероятности погрешности результатов измерений при εRx = 5%, εXx= ±10%, СКО
= 0,065, коэффициент асимметрии = 0,163.
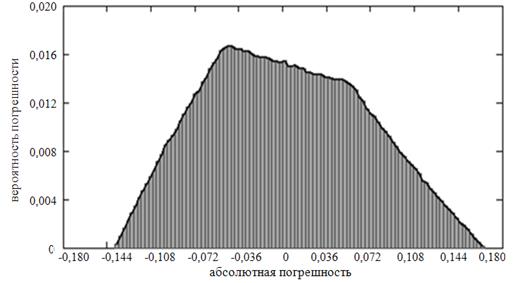
Рисунок 1. Гистограмма плотности распределения вероятностей результатов измерений tgε при εRx = 5%, εXx= ±10%.
На рис. 2 представлена гистограмма плотности распределения вероятностей результатов измерений емкости С при εRx = εXx= ±7%, СКО С=3,7 10-5 мкФ, коэффициент асимметрии = 0,152.
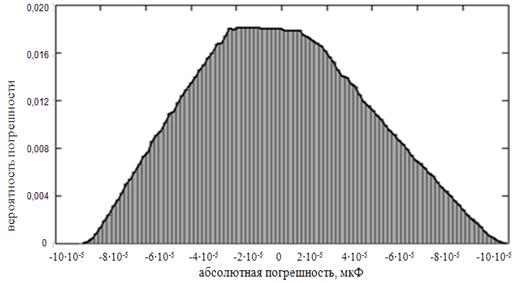
Рисунок 2. Гистограмма плотности распределения вероятностей результатов измерений емкости эквивалентной схемы замещения при εRx = εXx = ±7%.
На рис. 3 представлена гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx= ±7%, СКО Rx = 0,081, коэффициент асимметрии = 0,048.
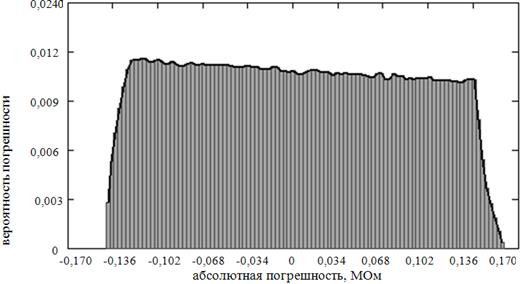
Рисунок 3. Гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx = ±7%.
Выводы
Метод Монте-Карло является эффективным инструментом оценивания характеристик случайных погрешностей косвенных, совокупных и совместных измерений при любых законах распределения вероятностей погрешности результатов прямых измерений, в частности среднего квадратического отклонения результатов измерений параметров комплексного сопротивления, определяющих качество высоковольтных электроизоляторов по ГОСТ 30421 — 96: электрическая емкость или обратная ей величина, активное электрическое сопротивление или проводимость, тангенс угла диэлектрических потерь или тангенс угла фазового сдвига.
Распределение плотности вероятностей погрешности результатов измерений этих параметров по значениям составляющих комплексного сопротивления, полученным прямым измерением с относительной погрешностью менее ±1% с равномерным распределением плотности вероятностей погрешности результатов измерений, является треугольным (тангенс угла диэлектрических потерь, тангенс угла фазового сдвига), равномерным (активное электрическое сопротивление или проводимость) или нормальным (электрическая емкость и обратная ей величина).
При относительной погрешности результатов измерений составляющих комплексного сопротивления, превышающей ±1%, распределения плотности вероятностей погрешности результатов измерений параметров комплексного сопротивления становятся заметно асимметричными. В таких случаях при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения вероятностей погрешности.
Рецензенты:
Цыпин Б.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника»,г. Пенза.
Громков Н.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника», г. Пенза.
Библиографическая ссылка
Баранов В.А., Данилов А.А., Шумарова С.А. ОЦЕНИВАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
ПАРАМЕТРОВ КОМПЛЕКСНОГО СОПРОТИВЛЕНИЯ МЕТОДОМ
МОНТЕ-КАРЛО // Современные проблемы науки и образования. – 2013. – № 5.
;
URL: https://science-education.ru/ru/article/view?id=10205 (дата обращения: 30.01.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Баранов В.А.
1
Данилов А.А.
2
Шумарова С.А.
1
1 ФГБОУ ВПО «Пензенский государственный университет Минобразования России»
2 ФБУ «Пензенский ЦСМ»
Метод Монте — Карло является эффективным инструментом оценивания характеристик случайных по-грешностей косвенных, совокупных и совместных измерений при любых законах распределения плотно-сти вероятностей погрешности результатов прямых измерений, в частности, среднего квадратического отклонения результатов измерений параметров комплексного сопротивления, определяющих качество высоковольтных электроизоляторов: электрическая емкость или обратная ей величина, активное элек-трическое сопротивление или проводимость, тангенс угла диэлектрических потерь или тангенс угла фа-зового сдвига. Распределение вероятностей погрешности результатов измерений этих параметров по значениям составляющих комплексного сопротивления, полученным прямым измерением с относитель-ной погрешностью менее ±1% с равномерным распределением вероятностей погрешности, является тре-угольным (тангенс угла диэлектрических потерь, тангенс угла фазового сдвига), равномерным (активное электрическое сопротивление или проводимость) или нормальным (электрическая емкость и обратная ей величина). При относительной погрешности результатов измерений составляющих комплексного сопротивления, превышающей ±1%, распределения вероятностей погрешности результатов измерений параметров комплексного сопротивления становятся заметно асимметричными. В таких случаях при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения вероятностей погрешности.
случайная погрешность.
метод Монте — Карло
комплексное сопротивление
измерения
1. Баранов В. А. Измерения параметров композиционных диэлектрических материалов. – Пенза : ИИЦ ПГУ, 2008. – 124 с.
2. Данилов А. А., Шумарова С. А. Об асимметрии функции плотности распределения ве-роятностей погрешности результатов измерений, полученных с помощью сложных измери-тельных каналов измерительных систем // Измерительная техника, . — 2012, . — № 11, . — С. 60 — 61.
3. ГОСТ 30421 — 96 Измерители электрической емкости, активного сопротивления и тан-генса угла потерь высоковольтные. Общие технические условия.
4. ПМГ 96 — 2009 Результаты и характеристики качества измерений. Формы представ-ления.
5. Сви П. М. Методы и средства диагностики оборудования высокого напряжения. — М. : Энергоатомиздат, 1992. — 240 с.
6. Соболь И. М. Метод Монте-Карло. – Москва., « : Наука», 1968. – 64 с.
Введение
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных величин, предложенный в 1949 году американскими математиками Дж. Нейманом и С. Уламом. Хотя метод был известен и ранее, но широкое применение он получил после появления ЭВМ [6]. В настоящее время метод Монте-Карло широко применяется при решении разнообразных задач многих отраслей науки и техники. Область его использования постоянно расширяется в условиях информатизации научной и производственной деятельности в связи с простым алгоритмом решения многих задач по сравнению с аналитическим решением, простотой оценок методической погрешности, слабой зависимостью точности от размерности пространства (числа независимых переменных).
В простейшем случае метод Монте-Карло состоит в синтезе математической модели объекта исследования в виде случайной величины, генерации ряда независимых испытаний (реализаций) этой случайной величины и определении статистических характеристик полученной выборки. Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. При этом метод Монте-Карло может быть использован не только для симметричных, но и для асимметричных распределений [2].
Ограничением применимости метода Монте-Карло в ходе научных исследований является то, что он не может заменить аналитические методы при исследовании малоизученных явлений и процессов, где на первом этапе необходимо выявление качественных закономерностей, описывающих объект исследования.
При проектировании измерительных устройств невозможность синтеза аналитической модели измерения не имеет значения, поскольку объект проектирования качественно определен на этапе составления уравнения измерения (функции преобразования). Последующий метрологический анализ позволяет получить оценку характеристик погрешности измерений, количественную характеристику точности, по известным характеристикам погрешности элементарных измерительных операций. Типичная методическая ошибка метода Монте-Карло 5-10% [6] полностью удовлетворяет требованиям к точности оценивания погрешности измерения.
Применение метода Монте-Карло дает наибольший эффект по сравнению с аналитическими методами при оценивании характеристик погрешности результатов косвенных, совместных и совокупных измерений, когда обрабатываются результаты прямых измерений двух и более величин.
Так, в работе [2] методом Монте-Карло получена оценка случайной погрешности произведения результатов измерений, полученных с помощью каналов измерительных систем с номинальной линейной функцией преобразования.
Аналогичные задачи возникают при разработке измерителей параметров электроизоляционных конструкций под рабочим напряжением для технического обслуживании систем электроснабжения по состоянию [5].
Материал и методы исследования
В ГОСТ 30421-96 установлены пары нормируемых электрических параметров электроизолятора, представленные в таблице 1 [3]. Пары составляют электрическая емкость или обратная ей величина
, активное электрическое сопротивление
или проводимость
, тангенс угла диэлектрических потерь
или тангенс угла фазового сдвига
.
Значения всех нормируемых параметров электроизоляторов могут быть определены по результатам измерений активной и реактивной
составляющих комплексного сопротивления (СКС) объекта измерений и частоты ω гармонического напряжения питания измерительной схемы при использовании схемы замещения объекта в виде параллельно соединенных резистора сопротивлением
и конденсатора емкостью
, если оценены соответствующие характеристики погрешности. Это позволяет разработать универсальный измеритель электрических параметров электроизоляторов [1].
Таблица 1 – Предпочтительные пары измеряемых величин
|
Предпочтительные пары |
|
|
Главная величина |
Дополнительный параметр |
|
С или 1/С С или 1/С С или 1/С R или G R или G tgδ |
tgδ R G С или 1/С tgφ С или 1/С |
Взаимосвязь нормируемых параметров электроизоляторов с СКС отражается с помощью формул:
,
,
,
,
,
.
В соответствии с ПМГ 96-2009 в случаях, когда результаты измерений используются совместно с другими результатами измерений, за характеристики качества измерений принимают точечные характеристики — среднеквадратичное отклонение погрешности или стандартную неопределенность [4]. Точечная характеристика должна сопровождаться указанием принятой аппроксимации закона распределения плотности вероятностей погрешности. ПМГ 96-2009 распространяются на случайные погрешности прямых измерений, функции плотности распределения вероятностей которых относятся к классу симметричных, одномодальных, усеченных функций. Оценки основаны на предположениях о распределении погрешностей прямых измерений по закону равномерной плотности как наихудшему (дающему для СКО оценку сверху) из законов распределения, относящихся к указанному классу, и отсутствует корреляция между величинами, измеряемыми прямым методом и, соответственно, погрешностями их измерений.
Для оценки характеристик случайной погрешности результатов измерений параметров электроизоляторов проведено моделирование в среде MathCAD методом Монте-Карло с построением по результатам статистических испытаний гистограммы распределения плотности вероятностей случайной погрешности. Входные переменные программы: число реализаций ; число интервалов ряда наблюдений (число столбцов гистограммы)
; номинальные значения СКС
и
, пределы допускаемой относительной случайной погрешности СКС; математическая модель, описывающая зависимость искомой величины от СКС. Выходные переменные программы: СКО СКС, СКО искомой величины. Число реализаций определяется в зависимости от требований к точности и заранее неизвестно, оно не должно быть менее 106 .
Для построения гистограммы использовалась встроенная функция: «hist(intvis,x)», которая определяет вектор частоты попадания данных в интервалы гистограммы; где «intvis» – вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания, «a<intvisi<b;х» – вектор случайных данных. Равномерный закон распределения плотности вероятности составляющих комплексного сопротивления задавался посредством встроенной функции «runif(x1,x2,x3)». Для вычисления среднеквадратического отклонения использовалась встроенная функция «stdev(x)».
В ходе исследований было принято: ,
МОм,
МОм,
,
Гц, пределы допускаемой относительной случайной погрешности результатов измерений СКС εRX и εXX, тангенса угла диэлектрических потерь εtgδ, тангенса угла фазового сдвига εtgφ, частоты напряжения питания измерительной схемы εω составляют ±1% номинальных значений и имеют равномерное распределение.
Результаты исследования и их обсуждение
Гистограмма распределения погрешности результата измерения тангенса угла потерь
и погрешности результата измерения тангенса угла фазового сдвига
имеет форму равнобедренного треугольника. При принятых номинальных значениях величин СКО = 0,008.
Гистограмма распределения погрешности результата измерения сопротивления
резистора эквивалентной схемы имеет форму прямоугольника, т.е. распределение равномерно, СКО = 0,012 МОм.
Распределение погрешности результата измерения проводимости
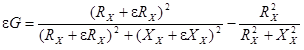
, близко к равномерному, СКО = 2,9 мСм.
Распределение погрешности результата измерения емкости эквивалентной схемы замещения
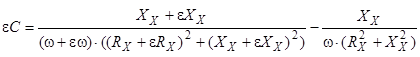
Плотность распределения вероятностей погрешности 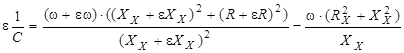
При погрешностях результатов измерений СКС более ±1% гистограммы распределения погрешностей результатов измерений величин, представленных в таблице, становятся заметно асимметричными. В этом случае при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения.
На рис. 1 представлена гистограмма распределения вероятности погрешности результатов измерений при εRx = 5%, εXx= ±10%, СКО
= 0,065, коэффициент асимметрии = 0,163.

Рисунок 1. Гистограмма плотности распределения вероятностей результатов измерений tgε при εRx = 5%, εXx= ±10%.
На рис. 2 представлена гистограмма плотности распределения вероятностей результатов измерений емкости С при εRx = εXx= ±7%, СКО С=3,7 10-5 мкФ, коэффициент асимметрии = 0,152.

Рисунок 2. Гистограмма плотности распределения вероятностей результатов измерений емкости эквивалентной схемы замещения при εRx = εXx = ±7%.
На рис. 3 представлена гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx= ±7%, СКО Rx = 0,081, коэффициент асимметрии = 0,048.

Рисунок 3. Гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx = ±7%.
Выводы
Метод Монте-Карло является эффективным инструментом оценивания характеристик случайных погрешностей косвенных, совокупных и совместных измерений при любых законах распределения вероятностей погрешности результатов прямых измерений, в частности среднего квадратического отклонения результатов измерений параметров комплексного сопротивления, определяющих качество высоковольтных электроизоляторов по ГОСТ 30421 — 96: электрическая емкость или обратная ей величина, активное электрическое сопротивление или проводимость, тангенс угла диэлектрических потерь или тангенс угла фазового сдвига.
Распределение плотности вероятностей погрешности результатов измерений этих параметров по значениям составляющих комплексного сопротивления, полученным прямым измерением с относительной погрешностью менее ±1% с равномерным распределением плотности вероятностей погрешности результатов измерений, является треугольным (тангенс угла диэлектрических потерь, тангенс угла фазового сдвига), равномерным (активное электрическое сопротивление или проводимость) или нормальным (электрическая емкость и обратная ей величина).
При относительной погрешности результатов измерений составляющих комплексного сопротивления, превышающей ±1%, распределения плотности вероятностей погрешности результатов измерений параметров комплексного сопротивления становятся заметно асимметричными. В таких случаях при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения вероятностей погрешности.
Рецензенты:
Цыпин Б.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника»,г. Пенза.
Громков Н.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника», г. Пенза.
Библиографическая ссылка
Баранов В.А., Данилов А.А., Шумарова С.А. ОЦЕНИВАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
ПАРАМЕТРОВ КОМПЛЕКСНОГО СОПРОТИВЛЕНИЯ МЕТОДОМ
МОНТЕ-КАРЛО // Современные проблемы науки и образования. – 2013. – № 5.
;
URL: https://science-education.ru/ru/article/view?id=10205 (дата обращения: 06.06.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
ЧАСТЬ
ЧЕТВЕРТАЯ
МЕТОД
МОНТЕ-КАРЛО. ЦЕПИ МАРКОВА
Глава двадцать
первая
МОДЕЛИРОВАНИЕ
(РАЗЫГРЫВАНИЕ)
СЛУЧАЙНЫХ ВЕЛИЧИН МЕТОДОМ МОНТЕ-КАРЛО
Датой
рождения метода Монте – Карло принято
считать 1949 г.. когда американские ученые
Н. Метрополис и С. Улам опубликовали
статью «Метод Монте-Карло», в которой
систематически его изложили. Название
метода связано с названием города Монте
– Карло, где в игорных домах (казино)
играют в рулетку из простейших устройств
для получения случайных чисел на
использовании которых основан этот
метод.
ЭВМ
позволяют легко получать так называемые
псевдослучайные числа (при решении
задач их применяют вместо случайных
чисел); это привело к широкому внедрению
метода во многие области науки и техники
(статистическая физика, теория массового
обслуживания, теория игр и др.). Метод
Монте-Карло используют для вычисления
интегралов, в особенности многомерных
для решения систем алгебраических
уравнений высокого порядка для
исследования различного рода сложных
систем (автоматического управления,
экологических, биологических и т.д.).
Сущность
метода Монте-Карло
состоит в следующем: требуется найти
значение а
некоторой
изучаемой величины. Для этого выбирают
такую величину
X,
математическое ожидание которой равно
а:
Практически
же поступают так: производят п
испытаний, в результате которых получают
n
возможных значении X,
вычисляют их среднее арифметическое
и принимают х
в качестве оценки (приближенного
значения) а*
искомого числа а:
Поскольку метод
Монте—Карло требует проведения большого
числа испытаний, его часто называют
методом
статистических испытаний.
Теория этого метода указывает, как
наиболее целесообразно выбрать случайную
величину X, как найти ее возможные
значения. В частности, разрабатываются
способы уменьшения дисперсии используемых
случайных величин, в результате чего
уменьшается ошибка, допускаемая при
замене искомого математического ожидания
а
его оценкой а*.
Отыскание возможных
значений случайной величины X
(моделирование)
называют «разыгрыванием случайной
величины». Изложим лишь некоторые
способы разыгрывания случайных величин
и укажем, как оценить допускаемую при
этом ошибку.
§ 2. Оценка погрешности метода Монте—Карло
Пусть для получения
оценки а*
математического ожидания а
случайной величины Х
было произведено п
независимых
испытаний (разыграно п
возможных значений X)
и по ним была найдена выборочная средняя
,
которая принята в качестве искомой
оценки: а*=х.
Ясно, что
если повторить опыт, то будут получены
другие возможные значения X,
следовательно, другая средняя, а
значит, и другая оценка а*.
Уже отсюда следует, что получить точную
оценку математического ожидания
невозможно. Естественно, возникает
вопрос о величине допускаемой ошибки.
Ограничимся отысканием лишь верхней
границы δ
допускаемой ошибки с заданной вероятностью
(надежностью) γ:
Интересующая нас
верхняя граница ошибки δ
есть не что иное, как «точность оценки»
математического ожидания по выборочной
средней при помощи доверительных
интервалов, о которой уже шла речь в
гл. XVI. Поэтому воспользуемся результатами,
полученными ранее, и рассмотрим
следующие три случая.
1. Случайная
величина Х
распределена нормально и ее среднее
квадратическое отклонение σ
известно.
В этом случае с надежностью γ
верхняя граница ошибки (см. гл. XVI, § 15)
(*)
где п—число
испытаний (разыгранных значений X);
t—
значение
аргумента функции Лапласа, при котором
Ф(t)=γ/2,
а—известное среднее квадратическое
отклонение X.
Пример 1.
С надежностью γ
=0,95 найти верхнюю границу ошибки σ,
если для оценки математического ожидания
нормальной величины Х
с известным средним квадратическим
отклонением, равным 0,5, было разыграно
100 возможных значений X.
Решение. По условию,
n=100,
σ=0,5,
Ф(t)=
0,95/2 =0,475. По таблице функции Лапласа (см.
приложение 2) находим t=1,96.
Искомая верхняя граница ошибки δ=
1,96·0,5/==0,098.
2. Случайная
величина Х
распределена нормально, причем ее
среднее квадратическое отклонение
σ
неизвестно.
В этом случае с надежностью γ
верхняя граница ошибки (см. гл. XVI, § 16)
(**)
где п—число
испытаний; s—«исправленное»
среднее квадратическое отклонение,
tγ
находят по таблице приложения 3.
Пример 2.
С надежностью γ
=0,95 найти верхнюю границу ошибки δ,
если для оценки математического ожидания
нормальной величины Х
было разыграно 100 ее возможных значений
и по ним найдено «исправленное» среднее
квадратическое отклонение s
==0,5. Решение. По условию, n=100,
s=0,5.
Используя таблицу приложения 3, по γ
=0,95, n=100
находим tγ,=1,984.
Искомая верхняя граница ошибки δ
= 1,984·0,5/
=0,099.
3. Случайная
величина Х
распределена по закону, отличному от
нормального.
В этом случае при достаточно большом
числе испытаний (n>30)
с надежностью, приближенно равной γ,
верхняя граница ошибки может быть
вычислена по формуле (*), если среднее
квадратическое отклонение σ
случайной величины Х
известно; если же σ
неизвестно, то можно подставить в формулу
(*) его оценку s—«исправленное»
среднее квадратическое отклонение либо
воспользоваться формулой (**). Заметим,
что чем больше п,
тем меньше различие между результатами,
которые дают обе формулы. Это объясняется
тем, что при п
—
распределение Стьюдента стремится к
нормальному (см. гл. XVI, § 16, замечание).
В частности (примеры 1 и 2), при n
=100, γ=0,95
верхняя граница ошибки равна 0,098 по
формуле (*) и 0,099 по формуле (**). Как видим,
результаты различаются незначительно.
Замечание. Для
того чтобы найти наименьшее число
испытаний, которые обеспечат наперед
заданную верхнюю границу ошибки δ,
надо выразить n
из формул (*) и (**):
Например, если
δ==0,098,
t=1,96,
=0,5, то минимальное число испытаний, при
которых ошибка не превысит 0,098, равно
п=1,9б2·0,52/0,0982=100.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Цель работы: Изучить и практически освоить метод Монте-Карло на примерах расчета площадей плоских фигур, объемов пространственных тел, а также вычисления кратных интегралов. Среда программирования — MATLAB.
Теоретическая часть
Сущность метода Монте-Карло состоит в следующем: требуется найти значение 


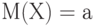
Практически же поступают следующим образом: производят 


и принимают 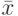
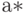

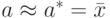
Поскольку метод Монте-Карло требует произведения большого числа испытаний, его часто называют методом статистических испытаний.
1. Оценка погрешности метода Монте-Карло
Как отмечалось, для получения оценки математического ожидания случайной величины 



При этом возможны следующие случаи оценки числа испытаний:
-
Случайная величина
распределена нормально и ее среднее квадратическое отклонение (стандартное отклонение)
известно. В этом случае с заданной вероятностью
верхняя граница ошибки определяется по формуле
(
4.1)где:
— число испытаний (разыгранных значений случайной величины
);
— значение аргумента функции Лапласа
или интеграла вероятности, при котором она равна половине заданной вероятности;
— известное среднее квадратическое отклонение.
Из формулы (4.1) может быть найдено число испытаний. Один из вариантов интеграла вероятностей (функции Лапласа) имеет вид [6]
(
4.2)Значения
табулированы и приведены в большинстве учебников по теории вероятностей и математической статистике.
В зарубежной литературе большое распространение получила так называемая функция ошибок (
)
:
(
4.3)Связь между функцией ошибок (4.3) и интегралом вероятностей (4.2) выражается в виде
(
4.4) -
Случайная величина
распределена нормально, причем ее среднее квадратическое отклонение неизвестно. В этом случае с заданной вероятностью
верхняя граница ошибки вычисляется по формуле
(
4.5)где:
— число испытаний;
— «исправленное» среднее квадратическое отклонение;
находят по специальным таблицам, например, приведенной в [6].
Из формулы (4.5) может быть найдено число испытаний для определения верхней границы ошибки.
-
Случайная величина
распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (
), с вероятностью, приближенно равной
(заданной вероятностью), верхняя граница ошибки может быть вычислена по формуле (4.1), если среднее квадратическое отклонение случайной величины известно; если же оно неизвестно, то можно подставить в формулу (4.1) его оценку — «исправленное» среднее квадратическое отклонение — либо воспользоваться формулой (4.5). При этом чем больше число испытаний, тем меньше различие между результатами, которые дают обе формулы.
2. Вычисление кратных интегралов методом Монте-Карло
В случае когда, например, определенный интеграл не может быть вычислен в квадратурах, либо прибегают к численным методам интегрирования, либо расчет ведется с помощью метода Монте-Карло. Применение метода Монте-Карло становится оправданным при кратности интеграла больше трех. В данной лабораторной работе мы используем метод Монте-Карло для расчета интегралов с кратностью не более трех. Это позволит более ясно представить технику применения метода.
Сначала рассмотрим вычисление простого определенного интеграла
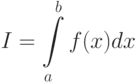 |
( 4.6) |
где 
Введем под знак интеграла постоянный множитель (равный единице):
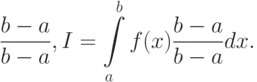 |
( 4.7) |
Вынесем из-под интеграла числитель дроби, получим
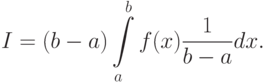 |
( 4.8) |
Как известно, если случайная величина 

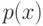
Кроме того, если известно распределение случайной величины 

![M[x]](https://intuit.ru/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png)
Соответственно, математическое ожидание от функции случайной величины будет определяться следующим образом:
![M[f(x)]=intlimits_{a}^{b}f(x)frac{1}{b-a}dx.](https://intuit.ru/sites/default/files/tex_cache/42149a4cde11c98da0e505e2279d7980.png) |
( 4.9) |
Сопоставляя (4.8) и (4.9), приходим к выводу, что определенный интеграл может быть рассчитан по формуле
![I=(b-a)M[f(x)].](https://intuit.ru/sites/default/files/tex_cache/6a755a2e5019e4067dd39dccfab13a63.png) |
( 4.10) |
Несмещенной оценкой математического ожидания случайной величины, как известно, является ее среднее арифметическое. Поэтому математическое ожидание можем приближенно найти по формуле
![M[f(x)]approx frac{1}{n}sumlimits_{i=1}^{n}f(x_i).](https://intuit.ru/sites/default/files/tex_cache/1e2f3c404db3d6b0d0a520572ddefc3e.png) |
( 4.11) |
С учетом (4.11) получаем выражение для приближенного расчета определенного интеграла
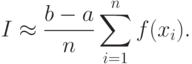 |
( 4.12) |
Чем больше число испытаний 
Рассмотрим общий подход вычисления 
Пусть задан 
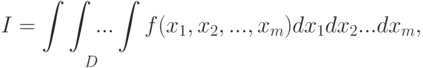 |
( 4.13) |
где подынтегральная функция 
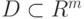
Погрузим область интегрирования 

![D^* = [a_1, b_1]times[a_2, b_2]times ... [a_m, b_m],](https://intuit.ru/sites/default/files/tex_cache/23a20b84ad54eb95a594f5c785f6284a.png) |
( 4.14) |
имеющий меру
 |
( 4.15) |
Определим в промежутке (4.15) функцию
 |
( 4.16) |
Тогда в соответствии с (4.13) и (4.16) получим
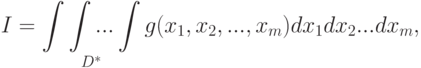 |
( 4.17) |
Введем в рассмотрение 

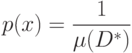 |
( 4.18) |
Функция плотности равномерного распределения есть величина постоянная, поэтому введем ее под знак интеграла (4.17) следующим образом:
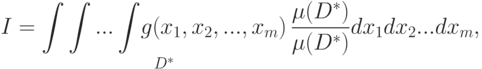 |
( 4.19) |
Вынесем числитель дроби за знак интеграла, т. е.
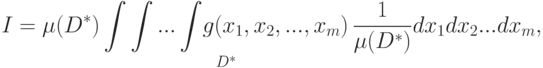 |
( 4.20) |
В (4.20) 


![I=mu (D^{*})M[g(x)],](https://intuit.ru/sites/default/files/tex_cache/cf20ace0be47f575d3035d97a4879769.png) |
( 4.21) |
где 
В свою очередь математическое ожидание может быть оценено с помощью арифметического среднего. Тогда приближенное значение 
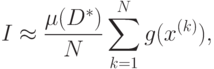 |
( 4.22) |
где 


Чтобы смоделировать выборку 


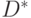



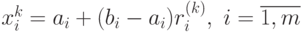
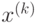
Таким образом, техника применения метода Монте-Карло здесь будет заключаться в определении области 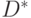

Расчет площадей и объемов можно рассматривать как частный случай вычисления кратных интегралов. Например, вычисление объема тел с помощью трехкратного интеграла сводится к взятию интеграла по области при подынтегральной функции, тождественно равной единице.
Сущность метода Монте-Карло состоит в следующем: требуется найти значение некоторой изучаемой величины. Для этого выбирают такую случайную величину , математическое ожидание которой равно : .
Практически же поступают так: производят испытаний, в результате которых получают возможных значений ; вычисляют их среднее арифметическое и принимают в качестве оценки (приближённого значения) искомого числа :
.
Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину , как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания его оценкой .
Оценка погрешности метода Монте-Карло
Пусть для получения оценки математического ожидания случайной величины было произведено независимых испытаний (разыграно возможных значений ) и по ним была найдена выборочная средняя , которая принята в качестве искомой оценки: . Ясно, что если повторить опыт, то будут получены другие возможные значения , следовательно, другая средняя, а значит, и другая оценка . Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы допускаемой ошибки с заданной вероятностью (надёжностью): .
Интересующая нас верхняя грань ошибки есть не что иное, как «точность оценки» математического ожидания по выборочной средней при помощи доверительных интервалов. Рассмотрим следующие три случая.
Случайная величина распределена нормально и её среднее
квадратичное отклонение известно. В этом случае с надёжностью верхняя граница ошибки
, (44)
где — число испытаний (разыгранных значений ); — значение аргумента функции Лапласа, при котором , — известное среднее квадратичное отклонение .
Случайная величина распределена нормально, причём её среднее квадратическое отклонение неизвестно. В этом случае с надёжностью верхняя граница ошибки
, (45)
где — число испытаний; — «исправленное» среднее квадратичное отклонение, .
Из изложенного следует, что метод Монте-Карло тесно связан с задачами теории вероятностей, математической статистики и вычислительной математики. В связи с задачей моделирования случайных величин (в особенности равномерно распределённых) существенную роль играют также методы теории чисел.
Среди других вычислительных методов, метод Монте-Карло выделяется своей простотой и общностью. Медленная сходимость является существенным недостатком метода, однако, могут быть указаны его модифификации, которые обеспечивают высокий порядок сходимости при определённых предположениях. Правда, вычислительная процедура при этом усложняется и приближается по своей сложности к другим процедурам вычислительной математики. Сходимость метода Монте-Карло является сходимостью по вероятности. Это обстоятельство вряд ли следует относить к числу его недостатков, ибо вероятностные методы в достаточной мере оправдывают себя в практических приложениях. Что же касается задач, имеющих вероятностное описание, то сходимостью по вероятности является даже в какой-то мере естественной при их исследовании
Многократное рассеяние
Пусть t — длина пути, пройденного электроном между двумя актами дискретных столкновений, Е — энергия, — скорость электрона. Азимутальный угол многократного рассеяния разыгрывается, с учетом трех членов разложения
(46)
(47)
где ф — приведенный угол
(48)
(49)
а B — является решением трансцендентного уравнения
(50)
с точностью
(51)
где
(52)
среднее число упругих столкновений на пути t. Для приближенного учета потерь энергии вместо Е и 2 мы используем и , где 1 и 2 относятся к началу и концу пути t.
Для выборки значений из распределения Мольер выражение можно представить в виде следующего разложения с последующим применением метода Батлера:
(53)


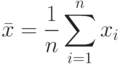
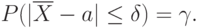
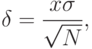
 — число испытаний (разыгранных значений случайной величины
— число испытаний (разыгранных значений случайной величины  — значение аргумента функции Лапласа
— значение аргумента функции Лапласа 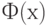 или интеграла вероятности, при котором она равна половине заданной вероятности;
или интеграла вероятности, при котором она равна половине заданной вероятности; — известное среднее квадратическое отклонение.
— известное среднее квадратическое отклонение.
 )
) 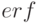 :
: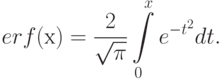

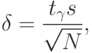
 — «исправленное» среднее квадратическое отклонение;
— «исправленное» среднее квадратическое отклонение;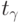 находят по специальным таблицам, например, приведенной в [6].
находят по специальным таблицам, например, приведенной в [6]. ), с вероятностью, приближенно равной
), с вероятностью, приближенно равной 
![M[x]=intlimits_{a}^{b}xfrac{1}{b-a}dx.](https://intuit.ru/sites/default/files/tex_cache/ab07d5a2a1952a4ee11260438dcb63e6.png)











