
Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования h. Применим так называемый принцип Рунге.
Пусть yn(T ) есть точное решение дифференциального уравнения y/ = f (x, y) при x = x0 + nh. Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
|
h |
|||||||
|
h |
(h) |
||||||
|
2 |
|||||||
|
ε 2 |
= |
yn |
− yn |
, |
|||
|
2 p −1 |
|||||||
где yn(h ) — приближение к точному решению yn(T ), вычисленное с шагом
|
h |
h |
h |
||||
|
приближение с шагом |
, ε |
2 |
= yn(T ) − yn |
2 |
. |
|
|
2 |
||||||
(7.5.1)
h
h , yn 2 — такое же
Так как для метода, описываемого формулами (7.4.13), p = 4, то
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= |
yn |
2 |
− yn(h) . |
(7.5.2) |
|||||
|
15 |
|||||||||||
Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная h p+1 , то есть yn(T ) = yn(h ) + Kh5 , что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что y(5)(x) практически постоянна, равна:
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= Kh5 |
= |
y |
2 |
− y(h) . |
|||||
|
15 |
|||||||||||
|
n |
n |
||||||||||
Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, использу-
kn(2) − kn(3)
ется такое оценочное правило: если ( ) ( ) достаточно велико (обычно больше несколь- kn1 − kn2
ких сотых), то шаг интегрирования необходимо уменьшить.
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части f (x, y).
7.6. Методы прогноза и коррекции
Отличительной чертой методов Рунге — Кутты является то, что при вычислении следующей точки (xn+1 , yn+1 ) используется информация только о предыдущей (xn , yn ). Зато при-
ходится вычислять значение правой части в нескольких промежуточных точках. Это нерационально, поскольку при налаженном процессе интегрирования имеется дополнительная информация — предыдущие точки решения.
169
Рассмотрим общую идею группы методов, известных в литературе под названием «методов прогноза и коррекции». Как ясно из названия, вначале «предсказывается» значение yn+1 , а затем используется тот или иной метод для «корректировки» этого значения. Эту же
формулу можно использовать сколько угодно раз для повторной корректировки уже скорректированного значения yn+1 .
Для демонстрации основных идей метода можно использовать для прогноза формулу
|
любого метода численного интегрирования. Воспользуемся формулой второго порядка |
|
|
yn(0+)1 = yn−1 + 2hf (xn , yn ), |
(7.6.1) |
где индекс (0) означает исходное приближение к yn+1 . Непосредственно из написанной формулы следует, что с ее помощью нельзя вычислить, например, y1 , ибо для этого потребовалась бы точка, расположенная перед начальной точкой y0 . Чтобы начать решение по методу
прогноза и коррекции, часто используется метод Рунге — Кутты.
Геометрически предсказание сводится к тому, что находится угол наклона касательной в точке (xn , yn ) (см. левый рисунок). После этого через точку (xn−1 , yn−1 ) проводится
|
L |
L |
L |
L |
||||
|
1 |
2 |
1 |
L3 |
||||
|
(xn+1 , yn(0+)1 ) |
(xn+1 , yn(1+)1 ) |
||||||
|
L |
|||||||
|
y = f (x) |
y = f (x) |
||||||
|
h |
h |
h |
h |
||||
|
xn−1 |
xn |
xn+1 |
xn−1 |
xn |
xn+1 |
||
|
прямая L , параллельная |
L |
. Предсказанное значение y(0) |
будет расположено там, где пря- |
||||
|
1 |
n+1 |
||||||
|
мая L |
пересечется с абсциссой x = xn+1. |
Скорректируем теперь предсказанное значение. |
Вычислим наклон касательной в точке (xn+1 , yn(0+)1 ). Эта касательная изображена на правом ри-
|
сунке и обозначена L2 . Усредним тангенсы углов наклона прямых L1 и L2 |
и получим пря- |
|||||
|
мую L . Наконец, проведем через точку (x |
n |
, y |
n |
) прямую L , параллельную L , и точка пере- |
||
|
3 |
||||||
|
сечения этой прямой с абсциссой x = xn+1 даст новое приближение (xn+1 , yn(1+)1 ). |
||||||
|
Это значение вычисляется по формуле |
||||||
|
yn(1+)1 = yn + |
h |
[f (xn , yn )+ f (xn+1 , yn(0+)1 )]. |
(7.6.2) |
|||
|
2 |
В общем случае i -е приближение, очевидно, будет находиться таким образом:
|
yn(i+)1 |
= yn + h [f (xn , yn )+ f (xn+1 , yn(i+−11))]. |
(7.6.3) |
|||
|
2 |
|||||
|
Итерационный процесс можно прекратить, когда |
|||||
|
yn(i++11) − yn(i+)1 |
< ε. |
(7.6.4) |
|||
К настоящему времени разработано много методов прогноза и коррекции разных порядков, обеспечивающих очень большую точность решения. В некоторых из них по заданной точностипредусмотренавтоматическийвыбор шага и автоматический выбор порядка метода.
170

7.7. Сравнение методов
а). Методы Рунге — Кутты.
1.В этих методах используется информация только об очередной точке решения, поэтому с их помощью можно начинать решение.
2.По той же самой причине приходится многократно вычислять функцию f (x, y).
3.Методы этой группы позволяют очень легко менять величину шага h.
4.При использовании этих методов трудно получить оценку ошибки интегрирования. б). Методы прогноза и коррекции.
1. Так как в этих методах используется информация о ранее вычисленных точках решения, то с их помощью нельзя начать решение.
2. Из-за использования информации о ранее вычисленных точках методы этой группы более экономичны по затратам машинного времени.
3. При любом изменении величины шага h приходится временно возвращаться к методам Рунге — Кутты.
4. В качестве побочного продукта вычислений получается хорошая оценка ошибки интегрирования.
Как всегда, наиболее целесообразным является использование при решении практи-
|
ческих задач комбинации этих двух методов. |
|
|
Пример. Методом Рунге — Кутты с шагом h = 0.1 найти на отрезке [0, 0.3] решение |
|
|
следующего дифференциального уравнения: y/ = cos bx |
с начальным условием |
|
a + y2 |
y(0)= 0, a =1.4, b = 2.6.
|
Обозначим через yi |
приближенное значение решения в точке xi . Формулы метода: |
|||||||||||||||||||||||||||||||||||||
|
y |
i+1 |
= y |
i |
+ hk |
, |
k |
i |
= |
1 (k (1) + |
2k (2) + |
2k (3) + k (4)), |
|||||||||||||||||||||||||||
|
i |
6 |
i |
i |
i |
i |
|||||||||||||||||||||||||||||||||
|
k (1) |
), |
|||||||||||||||||||||||||||||||||||||
|
= f (x |
, |
y |
||||||||||||||||||||||||||||||||||||
|
i |
i |
i |
||||||||||||||||||||||||||||||||||||
|
k (2) |
= f |
x |
i |
+ h |
, y |
i |
+ h k (1) , |
(7.7.1) |
||||||||||||||||||||||||||||||
|
i |
2 |
2 |
i |
|||||||||||||||||||||||||||||||||||
|
h |
h |
(2) |
||||||||||||||||||||||||||||||||||||
|
(3) |
= f |
, yi |
+ |
|||||||||||||||||||||||||||||||||||
|
ki |
xi + |
2 |
2 |
ki |
, |
|||||||||||||||||||||||||||||||||
|
(4) |
(3) |
|||||||||||||||||||||||||||||||||||||
|
ki |
= f (xi + h, yi + hki |
). |
||||||||||||||||||||||||||||||||||||
|
Все вычисления удобно располагать по схеме, указанной в таблице. |
||||||||||||||||||||||||||||||||||||||
|
i |
x |
y |
k |
y |
||||||||||||||||||||||||||||||||||
|
0 |
x0 |
y0 |
k0(1) |
k0(1) |
||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(1) |
k0(2) |
2k0(2) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(2) |
k0(3) |
2k0(3) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 + h |
y0 + hk0(3) |
k0(4) |
k0(4) |
|||||||||||||||||||||||||||||||||||
Она заполняется следующим образом.
1. Записываем в первой строке x0 , y0 , вычисляем f (x0 , y0 ) и заносим в таблицу в качестве k0(1).
171
|
2. |
Для |
второй |
строки |
вычисляем |
x |
0 |
+ |
h |
и |
y |
+ |
h |
k (1) , |
затем |
находим |
|||||||||||||
|
h |
h |
2 |
0 |
2 |
0 |
|||||||||||||||||||||||
|
(1) |
(2) |
|||||||||||||||||||||||||||
|
f x0 |
+ |
, y0 + |
k0 |
и записываем в качестве k0 |
. |
|||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
3. |
Находим |
y0 |
+ h k0(2) , вычисляем |
f x0 |
+ |
h |
, y0 + |
h |
k0(2) |
и записываем в таблицу на |
||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
место k0(3) . |
2 |
|||||||||||||||||||||||||||
|
+ hk0(3) , |
||||||||||||||||||||||||||||
|
4. |
Записываем |
в четвертой строке |
x0 + h |
и |
y0 |
затем |
находим |
|||||||||||||||||||||
|
k0(4 ) = f (x0 + h, y0 + hk0(3)). |
||||||||||||||||||||||||||||
|
5. |
Суммируем числа, стоящие в столбце y , делим на шесть и заносим в таблицу в |
|||||||||||||||||||||||||||
|
качестве |
y0 . |
|||||||||||||||||||||||||||
|
6. |
Вычисляем x1 |
= x0 + h , |
y1 = y0 + |
y0 . Затем все вычисления необходимо повторить |
||||||||||||||||||||||||
|
с пункта 1, принимая за начальную точку (x1, y1 ). |
Для контроля правильности выбора ша- |
|||||||||||||||||||||||||||
|
га h рекомендуется вычислять дробь θ = |
ki(2) − ki(3) |
. Величина θ не должна превышать двух |
||||||||||||||||||||||||||
|
ki(1) − ki(2) |
||||||||||||||||||||||||||||
— трех сотых. В противном случае шаг h следует уменьшить.
|
i |
x |
y |
k |
y |
θ |
|||||||||||
|
0 |
0.00 |
0.000000 |
0.714286 |
0.14286 |
||||||||||||
|
0.05 |
0.035714 |
0.707614 |
1.415228 |
|||||||||||||
|
0.05 |
0.035381 |
0.707626 |
1.415252 |
|||||||||||||
|
0.10 |
0.070763 |
0.687818 |
0.687818 |
0.0018 |
||||||||||||
|
0.705431 |
||||||||||||||||
|
1 |
0.10 |
0.705431 |
0.509261 |
0.509262 |
||||||||||||
|
0.15 |
0.730894 |
0.478185 |
0.956370 |
|||||||||||||
|
0.15 |
0.729340 |
0.478747 |
0.957494 |
|||||||||||||
|
0.20 |
0.753306 |
0.441084 |
0.441084 |
0.0018 |
||||||||||||
|
0.477368 |
||||||||||||||||
|
2 |
0.20 |
1.182799 |
0.310045 |
0.310045 |
||||||||||||
|
0.25 |
1.198301 |
0.280714 |
0.561428 |
|||||||||||||
|
0.25 |
1.196835 |
0.281062 |
0.562124 |
|||||||||||||
|
0.30 |
1.210905 |
0.248026 |
0.248026 |
0.0012 |
||||||||||||
|
0.280270 |
||||||||||||||||
|
3 |
0.30 |
1.463069 |
7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
Существует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение y(x) в виде таблицы значений y1 , y2 ,…, yn в точках x1 , x2 ,…, xn .
Простейшим методом численного интегрирования дифференциального уравнения первого порядка y/ = f (x, y), удовлетворяющего начальному условию y(x0 )= y0 , является метод Эйлера. В нем величины yi вычисляются по формуле
xi = x0 + ih, i = 0,1,2,…
yi+1 = yi + hf (xi , yi ).
172
Метод Эйлера относится к группе одношаговых, в которых для расчета точки (xi+1 , yi+1 ) требуется информация только о последней вычисленной точке (xi , yi ). Геометри-
ческая интерпретация метода изложена в подразд. 7.4.
В среде Mathcad имеется тринадцать встроенных функций решения дифференциальных уравнений и систем ( задача Коши, краевая задача, уравнения в частных производных). Самая употребительная из них — rkfixed, в которую заложен метод Рунге – Кутты четвертого порядка с постоянным шагом. Подпрограммы для метода Эйлера нет из-за его низкой точности. Формулы метода Эйлера настолько просты, что вычисления по ним можно организовать
|
с помощью дискретной переменной. |
|||||||||||||||||||||||||||||||||||
|
Рассмотрим пример. |
Решим |
задачу |
Коши |
для дифференциального |
уравнения |
||||||||||||||||||||||||||||||
|
y/ = cos(x − y)+ |
1.25y |
при y(0)= 0. |
|||||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
Введем начало программы |
y |
||||||||||||||||||||||||||||||||||
|
ORIGIN := 1 |
f (x, y):= cos(x − y)+1.25 |
a := 0 |
b := 1 |
h := 0.1 |
y0 := 0 |
||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
i := 1…11 |
xi := a |
+ h (i −1) |
|||||||||||||||||||||||||||||||||
|
i := 2…11 |
yi |
:= yi−1 + h f (xi−1 , yi−1 ) |
|||||||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||||
|
xT |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
||||||||||||||||||||||||
|
yT |
0.000 |
0.100 |
0.208 |
0.323 |
0.445 |
0.575 |
0.710 |
0.852 |
0.999 |
1.152 |
1.308 |
||||||||||||||||||||||||
Аналогичного результата можно достигнуть, введя подпрограмму, реализующую формулы (7.4.1) метода Эйлера:
z1:= Eiler(y0,0,1,0.1, f )
173
Минимальная переделка подпрограммы позволяет запрограммировать исправленный и модифицированный метод Эйлера по формулам (7.4.4) и (7.4.6).
z2 := Ieiler(y0,0,1,0.1, f ) z3 := Meiler(y0,0,1,0.1, f )
Обратимся теперь к средствам пакета Mathcad. Для решения обыкновенных «неособенных» дифференциальных уравнений здесь используются две функции rkfixed и Rkadapt,
|
реализующие метод Рунге – Кутты четвертого порядка с постоянным и переменным шагом. |
|
|
Набор параметров у этих подпрограмм одинаков: |
rkfixed(y, a,b, n, f ), где y = y(x0 ), |
|
a и b — начало и конец интервала интегрирования, n — |
число точек и, следовательно, шаг |
h = b −n a , f (x, y)— правая часть дифференциального уравнения. Несмотря на то что при ре-
шении дифференциального уравнения функция Rkadapt использует переменный шаг, она
|
тем не менее представляет ответ для n точек, находящихся на одинаковом расстоянии друг |
|||||||||||
|
от друга, равном h = |
b − a |
. |
|||||||||
|
n |
|||||||||||
|
Вводим следующую часть программы: |
yy1 |
||||||||||
|
yy1 := 0 fun(x, yy) |
:= cos(x − yy1 )+1.25 |
||||||||||
|
1.5 |
+ x |
||||||||||
|
z4 := rkfixed(yy,0,1,10,fun) |
|||||||||||
|
z5 := rkfixed(yy,0,1,20,fun) |
|||||||||||
|
z4 := Rkadapt(yy,0,1,10,fun) |
|||||||||||
|
i :=1…10 Er1 := |
(z4 2 ) −(z5 2 ) |
2 i |
|||||||||
|
i |
i |
||||||||||
|
174 |

errRGK = 5.291 10−3
|
errRKF := |
max(Er1) |
errRKF = 5.291 10−3 |
|
15 |
||
Обращение к rkfixed с h1 = 0.1 и h2 = 0.05 сделано для оценки погрешности интег-
рирования по правилу Рунге (7.5.2). errRKF — оценка погрешности.
На данном учебном примере, конечно, невозможно оценить выгоды использования функции Rkadapt вместо rkfixed. В более сложных случаях Rkadapt решает уравнение более точно и быстро. Даже в этом примере точность решения по Rkadapt выше, чем по rkfixed. Это видно из следующей таблицы:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|||||
|
z4 |
0.1040989 |
0.2161356 |
0.3357322 |
0.4625076 |
0.5960572 |
|||||
|
z5 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960578 |
|||||
|
z44 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960571 |
|||||
|
x |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|||||
|
z4 |
0.7359363 |
0.8816484 |
1.0326377 |
1.1882891 |
1.3479326 |
|||||
|
z5 |
0.7359370 |
0.8816491 |
1.0326386 |
1.1882900 |
1.3479335 |
|||||
|
z44 |
0.7359371 |
0.8816492 |
1.0326386 |
1.1882901 |
1.3479336 |
В заключение приведем подпрограмму RGK, реализующую формулы (7.4.13) метода Рунге – Кутты четвертого порядка. Далее, как и в предыдущем случае, произведена оценка погрешности по правилу Рунге и даны графики полученных решений. Программа метода Рунге – Кутты четвертого порядка (RGK) приведена после графиков проинтегрированных функций.
z6 := RGK (y0,0,1,0.1, f ) z7 := RGK (y0,0,1,0.05, f ) i := 1…10 Er2i := (z6 2 )i − (z7 2 )2 i
errRGK := max(Er2)
15

Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке x [0,1] с шагом h = 0.1 и оце-
|
нить погрешность интегрирования по правилу Рунге. |
|||||||||||||||||
|
1. |
y/ =1 + 0.2 y sin x − y2 , y |
(0) |
= 0.1. |
||||||||||||||
|
2. |
y/ = cos(x + y)+ 0.5(x − y), |
y(0)= 0. |
|||||||||||||||
|
3. |
y/ = |
cos x |
− 0.5y2 , |
y(0)= 0.2. |
|||||||||||||
|
x +1 |
|||||||||||||||||
|
4. |
y/ = (1 − y2 )cos x + 0.6 y, |
y(0)= 0. |
|||||||||||||||
|
5. |
y/ =1+0.4 ysin x −1.5y2 , |
y(0)=1. |
|||||||||||||||
|
6. |
y/ = |
cos y |
+ 0.3y2 , |
y(0)= 0. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
7. |
y/ = cos(1.5x + y)+ |
(x − y), |
y(0)= 0.5. |
||||||||||||||
|
8. |
y/ = 1 − sin(x + y)+ |
0.5y |
, y(0)= 0.3. |
||||||||||||||
|
x + 2 |
|||||||||||||||||
|
cos y |
|||||||||||||||||
|
9. |
y/ = |
+ 0.1y2 |
, y(0)= 0. |
||||||||||||||
|
1.5 + x |
|||||||||||||||||
|
10. |
y/ = 0.6 sin x −1.25y2 +1, y(0)=1. |
||||||||||||||||
|
11. |
y/ = cos(2x + y)+1.5(x − y), y(0)= 0.1. |
||||||||||||||||
|
12. |
y/ =1 − |
0.1y |
− sin(2x + y), |
y(0)= 0.5. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
13. |
y/ = |
cos y |
− 0.1y2 , y(0) |
= 0.2. |
|||||||||||||
|
1.25 + x |
|||||||||||||||||
|
y(0)= 0.5. |
|||||||||||||||||
|
14. |
y/ =1 + 0.8y sin x − 2 y2 , |
||||||||||||||||
|
176 |
Соседние файлы в предмете Вычислительная математика
- #
- #

Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования h. Применим так называемый принцип Рунге.
Пусть yn(T ) есть точное решение дифференциального уравнения y/ = f (x, y) при x = x0 + nh. Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
|
h |
|||||||
|
h |
(h) |
||||||
|
2 |
|||||||
|
ε 2 |
= |
yn |
− yn |
, |
|||
|
2 p −1 |
|||||||
где yn(h ) — приближение к точному решению yn(T ), вычисленное с шагом
|
h |
h |
h |
||||
|
приближение с шагом |
, ε |
2 |
= yn(T ) − yn |
2 |
. |
|
|
2 |
||||||
(7.5.1)
h
h , yn 2 — такое же
Так как для метода, описываемого формулами (7.4.13), p = 4, то
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= |
yn |
2 |
− yn(h) . |
(7.5.2) |
|||||
|
15 |
|||||||||||
Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная h p+1 , то есть yn(T ) = yn(h ) + Kh5 , что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что y(5)(x) практически постоянна, равна:
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= Kh5 |
= |
y |
2 |
− y(h) . |
|||||
|
15 |
|||||||||||
|
n |
n |
||||||||||
Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, использу-
kn(2) − kn(3)
ется такое оценочное правило: если ( ) ( ) достаточно велико (обычно больше несколь- kn1 − kn2
ких сотых), то шаг интегрирования необходимо уменьшить.
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части f (x, y).
7.6. Методы прогноза и коррекции
Отличительной чертой методов Рунге — Кутты является то, что при вычислении следующей точки (xn+1 , yn+1 ) используется информация только о предыдущей (xn , yn ). Зато при-
ходится вычислять значение правой части в нескольких промежуточных точках. Это нерационально, поскольку при налаженном процессе интегрирования имеется дополнительная информация — предыдущие точки решения.
169

Рассмотрим общую идею группы методов, известных в литературе под названием «методов прогноза и коррекции». Как ясно из названия, вначале «предсказывается» значение yn+1 , а затем используется тот или иной метод для «корректировки» этого значения. Эту же
формулу можно использовать сколько угодно раз для повторной корректировки уже скорректированного значения yn+1 .
Для демонстрации основных идей метода можно использовать для прогноза формулу
|
любого метода численного интегрирования. Воспользуемся формулой второго порядка |
|
|
yn(0+)1 = yn−1 + 2hf (xn , yn ), |
(7.6.1) |
где индекс (0) означает исходное приближение к yn+1 . Непосредственно из написанной формулы следует, что с ее помощью нельзя вычислить, например, y1 , ибо для этого потребовалась бы точка, расположенная перед начальной точкой y0 . Чтобы начать решение по методу
прогноза и коррекции, часто используется метод Рунге — Кутты.
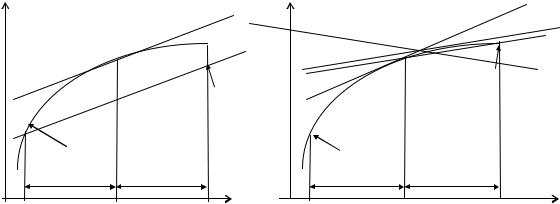
Геометрически предсказание сводится к тому, что находится угол наклона касательной в точке (xn , yn ) (см. левый рисунок). После этого через точку (xn−1 , yn−1 ) проводится
|
L |
L |
L |
L |
||||
|
1 |
2 |
1 |
L3 |
||||
|
(xn+1 , yn(0+)1 ) |
(xn+1 , yn(1+)1 ) |
||||||
|
L |
|||||||
|
y = f (x) |
y = f (x) |
||||||
|
h |
h |
h |
h |
||||
|
xn−1 |
xn |
xn+1 |
xn−1 |
xn |
xn+1 |
||
|
прямая L , параллельная |
L |
. Предсказанное значение y(0) |
будет расположено там, где пря- |
||||
|
1 |
n+1 |
||||||
|
мая L |
пересечется с абсциссой x = xn+1. |
Скорректируем теперь предсказанное значение. |
Вычислим наклон касательной в точке (xn+1 , yn(0+)1 ). Эта касательная изображена на правом ри-
|
сунке и обозначена L2 . Усредним тангенсы углов наклона прямых L1 и L2 |
и получим пря- |
|||||
|
мую L . Наконец, проведем через точку (x |
n |
, y |
n |
) прямую L , параллельную L , и точка пере- |
||
|
3 |
||||||
|
сечения этой прямой с абсциссой x = xn+1 даст новое приближение (xn+1 , yn(1+)1 ). |
||||||
|
Это значение вычисляется по формуле |
||||||
|
yn(1+)1 = yn + |
h |
[f (xn , yn )+ f (xn+1 , yn(0+)1 )]. |
(7.6.2) |
|||
|
2 |
В общем случае i -е приближение, очевидно, будет находиться таким образом:
|
yn(i+)1 |
= yn + h [f (xn , yn )+ f (xn+1 , yn(i+−11))]. |
(7.6.3) |
|||
|
2 |
|||||
|
Итерационный процесс можно прекратить, когда |
|||||
|
yn(i++11) − yn(i+)1 |
< ε. |
(7.6.4) |
|||
К настоящему времени разработано много методов прогноза и коррекции разных порядков, обеспечивающих очень большую точность решения. В некоторых из них по заданной точностипредусмотренавтоматическийвыбор шага и автоматический выбор порядка метода.
170

7.7. Сравнение методов
а). Методы Рунге — Кутты.
1.В этих методах используется информация только об очередной точке решения, поэтому с их помощью можно начинать решение.
2.По той же самой причине приходится многократно вычислять функцию f (x, y).
3.Методы этой группы позволяют очень легко менять величину шага h.
4.При использовании этих методов трудно получить оценку ошибки интегрирования. б). Методы прогноза и коррекции.
1. Так как в этих методах используется информация о ранее вычисленных точках решения, то с их помощью нельзя начать решение.
2. Из-за использования информации о ранее вычисленных точках методы этой группы более экономичны по затратам машинного времени.
3. При любом изменении величины шага h приходится временно возвращаться к методам Рунге — Кутты.
4. В качестве побочного продукта вычислений получается хорошая оценка ошибки интегрирования.
Как всегда, наиболее целесообразным является использование при решении практи-
|
ческих задач комбинации этих двух методов. |
|
|
Пример. Методом Рунге — Кутты с шагом h = 0.1 найти на отрезке [0, 0.3] решение |
|
|
следующего дифференциального уравнения: y/ = cos bx |
с начальным условием |
|
a + y2 |
y(0)= 0, a =1.4, b = 2.6.
|
Обозначим через yi |
приближенное значение решения в точке xi . Формулы метода: |
|||||||||||||||||||||||||||||||||||||
|
y |
i+1 |
= y |
i |
+ hk |
, |
k |
i |
= |
1 (k (1) + |
2k (2) + |
2k (3) + k (4)), |
|||||||||||||||||||||||||||
|
i |
6 |
i |
i |
i |
i |
|||||||||||||||||||||||||||||||||
|
k (1) |
), |
|||||||||||||||||||||||||||||||||||||
|
= f (x |
, |
y |
||||||||||||||||||||||||||||||||||||
|
i |
i |
i |
||||||||||||||||||||||||||||||||||||
|
k (2) |
= f |
x |
i |
+ h |
, y |
i |
+ h k (1) , |
(7.7.1) |
||||||||||||||||||||||||||||||
|
i |
2 |
2 |
i |
|||||||||||||||||||||||||||||||||||
|
h |
h |
(2) |
||||||||||||||||||||||||||||||||||||
|
(3) |
= f |
, yi |
+ |
|||||||||||||||||||||||||||||||||||
|
ki |
xi + |
2 |
2 |
ki |
, |
|||||||||||||||||||||||||||||||||
|
(4) |
(3) |
|||||||||||||||||||||||||||||||||||||
|
ki |
= f (xi + h, yi + hki |
). |
||||||||||||||||||||||||||||||||||||
|
Все вычисления удобно располагать по схеме, указанной в таблице. |
||||||||||||||||||||||||||||||||||||||
|
i |
x |
y |
k |
y |
||||||||||||||||||||||||||||||||||
|
0 |
x0 |
y0 |
k0(1) |
k0(1) |
||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(1) |
k0(2) |
2k0(2) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(2) |
k0(3) |
2k0(3) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 + h |
y0 + hk0(3) |
k0(4) |
k0(4) |
|||||||||||||||||||||||||||||||||||
Она заполняется следующим образом.
1. Записываем в первой строке x0 , y0 , вычисляем f (x0 , y0 ) и заносим в таблицу в качестве k0(1).
171

|
2. |
Для |
второй |
строки |
вычисляем |
x |
0 |
+ |
h |
и |
y |
+ |
h |
k (1) , |
затем |
находим |
|||||||||||||
|
h |
h |
2 |
0 |
2 |
0 |
|||||||||||||||||||||||
|
(1) |
(2) |
|||||||||||||||||||||||||||
|
f x0 |
+ |
, y0 + |
k0 |
и записываем в качестве k0 |
. |
|||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
3. |
Находим |
y0 |
+ h k0(2) , вычисляем |
f x0 |
+ |
h |
, y0 + |
h |
k0(2) |
и записываем в таблицу на |
||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
место k0(3) . |
2 |
|||||||||||||||||||||||||||
|
+ hk0(3) , |
||||||||||||||||||||||||||||
|
4. |
Записываем |
в четвертой строке |
x0 + h |
и |
y0 |
затем |
находим |
|||||||||||||||||||||
|
k0(4 ) = f (x0 + h, y0 + hk0(3)). |
||||||||||||||||||||||||||||
|
5. |
Суммируем числа, стоящие в столбце y , делим на шесть и заносим в таблицу в |
|||||||||||||||||||||||||||
|
качестве |
y0 . |
|||||||||||||||||||||||||||
|
6. |
Вычисляем x1 |
= x0 + h , |
y1 = y0 + |
y0 . Затем все вычисления необходимо повторить |
||||||||||||||||||||||||
|
с пункта 1, принимая за начальную точку (x1, y1 ). |
Для контроля правильности выбора ша- |
|||||||||||||||||||||||||||
|
га h рекомендуется вычислять дробь θ = |
ki(2) − ki(3) |
. Величина θ не должна превышать двух |
||||||||||||||||||||||||||
|
ki(1) − ki(2) |
||||||||||||||||||||||||||||
— трех сотых. В противном случае шаг h следует уменьшить.
|
i |
x |
y |
k |
y |
θ |
|||||||||||
|
0 |
0.00 |
0.000000 |
0.714286 |
0.14286 |
||||||||||||
|
0.05 |
0.035714 |
0.707614 |
1.415228 |
|||||||||||||
|
0.05 |
0.035381 |
0.707626 |
1.415252 |
|||||||||||||
|
0.10 |
0.070763 |
0.687818 |
0.687818 |
0.0018 |
||||||||||||
|
0.705431 |
||||||||||||||||
|
1 |
0.10 |
0.705431 |
0.509261 |
0.509262 |
||||||||||||
|
0.15 |
0.730894 |
0.478185 |
0.956370 |
|||||||||||||
|
0.15 |
0.729340 |
0.478747 |
0.957494 |
|||||||||||||
|
0.20 |
0.753306 |
0.441084 |
0.441084 |
0.0018 |
||||||||||||
|
0.477368 |
||||||||||||||||
|
2 |
0.20 |
1.182799 |
0.310045 |
0.310045 |
||||||||||||
|
0.25 |
1.198301 |
0.280714 |
0.561428 |
|||||||||||||
|
0.25 |
1.196835 |
0.281062 |
0.562124 |
|||||||||||||
|
0.30 |
1.210905 |
0.248026 |
0.248026 |
0.0012 |
||||||||||||
|
0.280270 |
||||||||||||||||
|
3 |
0.30 |
1.463069 |
7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
Существует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение y(x) в виде таблицы значений y1 , y2 ,…, yn в точках x1 , x2 ,…, xn .
Простейшим методом численного интегрирования дифференциального уравнения первого порядка y/ = f (x, y), удовлетворяющего начальному условию y(x0 )= y0 , является метод Эйлера. В нем величины yi вычисляются по формуле
xi = x0 + ih, i = 0,1,2,…
yi+1 = yi + hf (xi , yi ).
172

Метод Эйлера относится к группе одношаговых, в которых для расчета точки (xi+1 , yi+1 ) требуется информация только о последней вычисленной точке (xi , yi ). Геометри-
ческая интерпретация метода изложена в подразд. 7.4.
В среде Mathcad имеется тринадцать встроенных функций решения дифференциальных уравнений и систем ( задача Коши, краевая задача, уравнения в частных производных). Самая употребительная из них — rkfixed, в которую заложен метод Рунге – Кутты четвертого порядка с постоянным шагом. Подпрограммы для метода Эйлера нет из-за его низкой точности. Формулы метода Эйлера настолько просты, что вычисления по ним можно организовать
|
с помощью дискретной переменной. |
|||||||||||||||||||||||||||||||||||
|
Рассмотрим пример. |
Решим |
задачу |
Коши |
для дифференциального |
уравнения |
||||||||||||||||||||||||||||||
|
y/ = cos(x − y)+ |
1.25y |
при y(0)= 0. |
|||||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
Введем начало программы |
y |
||||||||||||||||||||||||||||||||||
|
ORIGIN := 1 |
f (x, y):= cos(x − y)+1.25 |
a := 0 |
b := 1 |
h := 0.1 |
y0 := 0 |
||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
i := 1…11 |
xi := a |
+ h (i −1) |
|||||||||||||||||||||||||||||||||
|
i := 2…11 |
yi |
:= yi−1 + h f (xi−1 , yi−1 ) |
|||||||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||||
|
xT |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
||||||||||||||||||||||||
|
yT |
0.000 |
0.100 |
0.208 |
0.323 |
0.445 |
0.575 |
0.710 |
0.852 |
0.999 |
1.152 |
1.308 |
||||||||||||||||||||||||
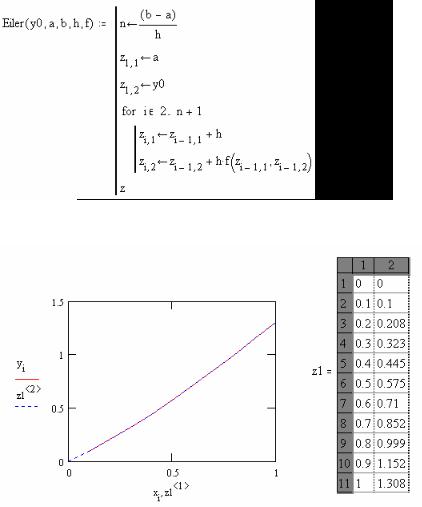
Аналогичного результата можно достигнуть, введя подпрограмму, реализующую формулы (7.4.1) метода Эйлера:
z1:= Eiler(y0,0,1,0.1, f )
173

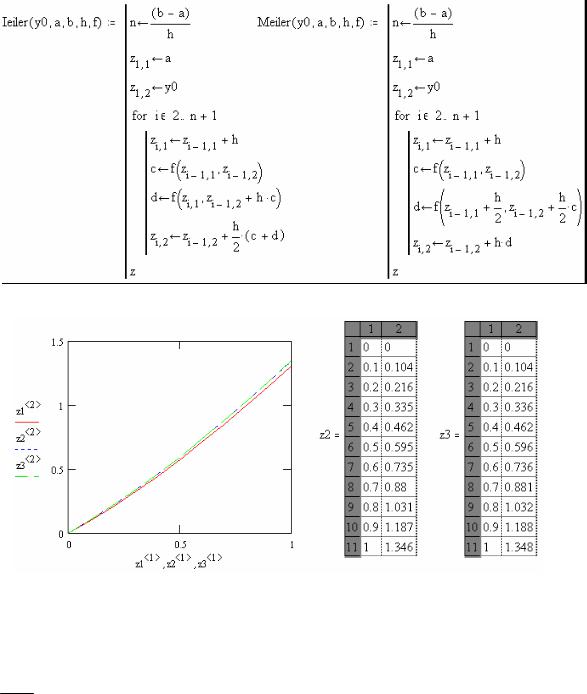
Минимальная переделка подпрограммы позволяет запрограммировать исправленный и модифицированный метод Эйлера по формулам (7.4.4) и (7.4.6).
z2 := Ieiler(y0,0,1,0.1, f ) z3 := Meiler(y0,0,1,0.1, f )
Обратимся теперь к средствам пакета Mathcad. Для решения обыкновенных «неособенных» дифференциальных уравнений здесь используются две функции rkfixed и Rkadapt,
|
реализующие метод Рунге – Кутты четвертого порядка с постоянным и переменным шагом. |
|
|
Набор параметров у этих подпрограмм одинаков: |
rkfixed(y, a,b, n, f ), где y = y(x0 ), |
|
a и b — начало и конец интервала интегрирования, n — |
число точек и, следовательно, шаг |
h = b −n a , f (x, y)— правая часть дифференциального уравнения. Несмотря на то что при ре-
шении дифференциального уравнения функция Rkadapt использует переменный шаг, она
|
тем не менее представляет ответ для n точек, находящихся на одинаковом расстоянии друг |
|||||||||||
|
от друга, равном h = |
b − a |
. |
|||||||||
|
n |
|||||||||||
|
Вводим следующую часть программы: |
yy1 |
||||||||||
|
yy1 := 0 fun(x, yy) |
:= cos(x − yy1 )+1.25 |
||||||||||
|
1.5 |
+ x |
||||||||||
|
z4 := rkfixed(yy,0,1,10,fun) |
|||||||||||
|
z5 := rkfixed(yy,0,1,20,fun) |
|||||||||||
|
z4 := Rkadapt(yy,0,1,10,fun) |
|||||||||||
|
i :=1…10 Er1 := |
(z4 2 ) −(z5 2 ) |
2 i |
|||||||||
|
i |
i |
||||||||||
|
174 |

errRGK = 5.291 10−3
|
errRKF := |
max(Er1) |
errRKF = 5.291 10−3 |
|
15 |
||
Обращение к rkfixed с h1 = 0.1 и h2 = 0.05 сделано для оценки погрешности интег-
рирования по правилу Рунге (7.5.2). errRKF — оценка погрешности.
На данном учебном примере, конечно, невозможно оценить выгоды использования функции Rkadapt вместо rkfixed. В более сложных случаях Rkadapt решает уравнение более точно и быстро. Даже в этом примере точность решения по Rkadapt выше, чем по rkfixed. Это видно из следующей таблицы:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|||||
|
z4 |
0.1040989 |
0.2161356 |
0.3357322 |
0.4625076 |
0.5960572 |
|||||
|
z5 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960578 |
|||||
|
z44 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960571 |
|||||
|
x |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|||||
|
z4 |
0.7359363 |
0.8816484 |
1.0326377 |
1.1882891 |
1.3479326 |
|||||
|
z5 |
0.7359370 |
0.8816491 |
1.0326386 |
1.1882900 |
1.3479335 |
|||||
|
z44 |
0.7359371 |
0.8816492 |
1.0326386 |
1.1882901 |
1.3479336 |
В заключение приведем подпрограмму RGK, реализующую формулы (7.4.13) метода Рунге – Кутты четвертого порядка. Далее, как и в предыдущем случае, произведена оценка погрешности по правилу Рунге и даны графики полученных решений. Программа метода Рунге – Кутты четвертого порядка (RGK) приведена после графиков проинтегрированных функций.
z6 := RGK (y0,0,1,0.1, f ) z7 := RGK (y0,0,1,0.05, f ) i := 1…10 Er2i := (z6 2 )i − (z7 2 )2 i
errRGK := max(Er2)
15

Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке x [0,1] с шагом h = 0.1 и оце-
|
нить погрешность интегрирования по правилу Рунге. |
|||||||||||||||||
|
1. |
y/ =1 + 0.2 y sin x − y2 , y |
(0) |
= 0.1. |
||||||||||||||
|
2. |
y/ = cos(x + y)+ 0.5(x − y), |
y(0)= 0. |
|||||||||||||||
|
3. |
y/ = |
cos x |
− 0.5y2 , |
y(0)= 0.2. |
|||||||||||||
|
x +1 |
|||||||||||||||||
|
4. |
y/ = (1 − y2 )cos x + 0.6 y, |
y(0)= 0. |
|||||||||||||||
|
5. |
y/ =1+0.4 ysin x −1.5y2 , |
y(0)=1. |
|||||||||||||||
|
6. |
y/ = |
cos y |
+ 0.3y2 , |
y(0)= 0. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
7. |
y/ = cos(1.5x + y)+ |
(x − y), |
y(0)= 0.5. |
||||||||||||||
|
8. |
y/ = 1 − sin(x + y)+ |
0.5y |
, y(0)= 0.3. |
||||||||||||||
|
x + 2 |
|||||||||||||||||
|
cos y |
|||||||||||||||||
|
9. |
y/ = |
+ 0.1y2 |
, y(0)= 0. |
||||||||||||||
|
1.5 + x |
|||||||||||||||||
|
10. |
y/ = 0.6 sin x −1.25y2 +1, y(0)=1. |
||||||||||||||||
|
11. |
y/ = cos(2x + y)+1.5(x − y), y(0)= 0.1. |
||||||||||||||||
|
12. |
y/ =1 − |
0.1y |
− sin(2x + y), |
y(0)= 0.5. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
13. |
y/ = |
cos y |
− 0.1y2 , y(0) |
= 0.2. |
|||||||||||||
|
1.25 + x |
|||||||||||||||||
|
y(0)= 0.5. |
|||||||||||||||||
|
14. |
y/ =1 + 0.8y sin x − 2 y2 , |
||||||||||||||||
|
176 |
Соседние файлы в предмете Вычислительная математика
- #
- #
Библиографическое описание:
Анализ влияния вычислительной погрешности в явных методах Рунге — Кутты / А. С. Пак, О. А. Кащеева, Н. А. Мелков [и др.]. — Текст : непосредственный // Молодой ученый. — 2020. — № 27 (317). — С. 18-23. — URL: https://moluch.ru/archive/317/72323/ (дата обращения: 30.01.2023).
Статья посвящена нахождению приемов и способов улучшения и оптимизации известных методов интегрирования систем обыкновенных дифференциальных уравнений (СОДУ). Задача уменьшения вычислительной погрешности при меньших затратах является наиболее актуальной для всех численных методов. В статье подробно рассматривается применение метода компенсированного суммирования для явного метода Рунге — Кутты четвертого порядка.
Ключевые слова:
система обыкновенных дифференциальных уравнений, компенсированное суммирование, алгоритм Гилла — Мёллера, методы Рунге — Кутты.
Двадцать первый век можно охарактеризовать как период, в течение которого классические методы решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты, разработанные для ручного счета, развивались исходя из требований и цифровых возможностей. Однако в практических вычислениях природа компьютерной арифметики может играть значительную и, возможно, подавляющую роль.
Алгоритм Гилла
— Мёллера
В книге Бутчера [1] представлен анализ влияния ошибки округления в явном методе Эйлера, а также приведен алгоритм Гилла — Мёллера (Гилл [2], Мёллер [4], [5]), который называют «компенсированным суммированием». В данном разделе будет проведен аналогичный численный эксперимент для преодоления последствий накопления ошибок округления в явном методе Рунге —Кутты 4-го порядка.
Пусть
— общая погрешность, вычисленная на шаге
,
— соответствующая погрешность вычисления производной на этом же шаге, тогда
последовательности точных и приближённых значений связаны между собой следующим образом
где
— ошибка округления, совершенная на этом шаге, а
— методическая погрешность. Данная операция приводит к следующему разностному уравнению
,
Так как, детальный анализ ошибки округления в расчетах данной задачи представлен в работе Хенричи [3], то вместо того, чтобы пытаться провести анализ
и
, а также, поскольку шаги вычисляются последовательно, заметим, что можно преодолеть наихудшие последствия накопления ошибок округления. Это делается путем оценки значения
на любом конкретном шаге, а затем добавление его к значению
, прежде чем оно будет добавлено на следующем шаге.
Этот усовершенствованный метод, который может быть использован для многих ситуаций, связанных с суммированием большого количества малых величин, и называют алгоритмом Гилла — Мёллера или «компенсированным суммированием».
«
Компенсированное суммирование
»
в
явном методе Рунге
— Кутты 4-го порядка
Общая схема явного метода Рунге — Кутты (ЯМРК) численного интегрирования СОДУ
выглядит следующим образом:
где функции
вычисляются по схеме
Здесь
— точное и приближенное значение s-й компоненты в точке
соответственно,
— точное значение s-й компоненты в точке
,
— шаг метода.
Традиционным считается символически представлять данный метод посредством таблиц Бутчера. Приведем пример таблицы Бутчера для ЯМРК 4-го порядка.
|
0 |
||||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Далее будет показано как применить «компенсированное суммирование» для уменьшения ошибки округления в ЯМРК четвертого порядка на примере системы дифференциальных уравнений
,
с начальным приближением
которое имеет аналитическое решение
Реализация данного метода была выполнена в системе научных вычислений MATLAB.
(ЯМРК4)
ЯМРК4 с компенсированным суммированием)
В данном примере была взята последовательность шагов
Результаты
Нанесем глобальные погрешности этих двух алгоритмов на один график в логарифмическом масштабе.
Видно, что явная форма дает результаты, которые сильнее ухудшаются при определенном шаге, в то время как компенсированная версия значительно улучшает результат.
Выводы
Как видно из проведенного исследования, метод «компенсированного суммирования» значительно улучшает ЯМРК четвертого порядка, а также его можно распространить и на другие численные методы интегрирования СОДУ.
Литература:
- Butcher J. C. «Numerical Methods for ordinary Differential Equations, Second Edition». The University of Auckland, New Zealand 2008, 463 p.
- Gill S. «A process for the step-by step integration of differential equations in an automatic computing machine». Proc. Cambridge Philos. Soc 1951.
- Henrici P. «Discrete Variable Methods in Ordinary Differential Equations». John Wiley & Sons Inc, New York 1962.
- Møller O. «Quasi double-precision in floating point addition». BIT 1965.
- Møller O. «Note on quasi double-precision». BIT 1965.
Основные термины (генерируются автоматически): явный метод, компенсированное суммирование, MATLAB, алгоритм, шаг.
The local error is typically estimated using something like an embedded pair of Runge-Kutta methods. The classic example would be the 4(5) pair (for instance, Dormand-Prince), where the error over a single step would be estimated by comparing the fourth- and fifth-order solutions. Other methods include approaches like halving the time step, or Richardson extrapolation.
The global estimate you’re referring to is one by Dahlquist, using the logarithmic norm, which is a bound on the growth of the norm of the solution to an ODE. (See reference 3 of this review paper on the logarithmic norm by Soderlind. A similar, weaker result was proven by Gronwall using Lipschitz constants; see Gronwall’s inequality.)
There are a variety of methods for bounding and estimating the global error in solutions of ODEs, and I’m sure I’ll fail to list all of them.
For estimates, the most recent paper I’m aware of is by Constantinescu, which has a large number of references worth looking at; other notable papers include the now-dated review by Skeel, the adjoint approach by Estep (he has a whole series of adjoint-based a posteriori error estimation papers), and the adjoint approach by Cao & Petzold.
Bounds could also be computed using interval arithmetic and Taylor methods. The thesis by Joseph Scott should have a number of references discussing this topic.
The local error is typically estimated using something like an embedded pair of Runge-Kutta methods. The classic example would be the 4(5) pair (for instance, Dormand-Prince), where the error over a single step would be estimated by comparing the fourth- and fifth-order solutions. Other methods include approaches like halving the time step, or Richardson extrapolation.
The global estimate you’re referring to is one by Dahlquist, using the logarithmic norm, which is a bound on the growth of the norm of the solution to an ODE. (See reference 3 of this review paper on the logarithmic norm by Soderlind. A similar, weaker result was proven by Gronwall using Lipschitz constants; see Gronwall’s inequality.)
There are a variety of methods for bounding and estimating the global error in solutions of ODEs, and I’m sure I’ll fail to list all of them.
For estimates, the most recent paper I’m aware of is by Constantinescu, which has a large number of references worth looking at; other notable papers include the now-dated review by Skeel, the adjoint approach by Estep (he has a whole series of adjoint-based a posteriori error estimation papers), and the adjoint approach by Cao & Petzold.
Bounds could also be computed using interval arithmetic and Taylor methods. The thesis by Joseph Scott should have a number of references discussing this topic.
Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования Применим так называемый принцип Рунге.
Пусть есть точное решение дифференциального уравнения
при
Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:

Где — приближение к точному решению
, вычисленное с шагом
,
— такое же приближение с шагом
,
.
Так как для метода, описываемого формулами (7.4.13), то

Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная , то есть
что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что
практически постоянна, равна:
Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, используется такое оценочное правило: если 
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части
| < Предыдущая |
|---|
Библиографическое описание:
Анализ влияния вычислительной погрешности в явных методах Рунге — Кутты / А. С. Пак, О. А. Кащеева, Н. А. Мелков [и др.]. — Текст : непосредственный // Молодой ученый. — 2020. — № 27 (317). — С. 18-23. — URL: https://moluch.ru/archive/317/72323/ (дата обращения: 06.06.2023).
Статья посвящена нахождению приемов и способов улучшения и оптимизации известных методов интегрирования систем обыкновенных дифференциальных уравнений (СОДУ). Задача уменьшения вычислительной погрешности при меньших затратах является наиболее актуальной для всех численных методов. В статье подробно рассматривается применение метода компенсированного суммирования для явного метода Рунге — Кутты четвертого порядка.
Ключевые слова:
система обыкновенных дифференциальных уравнений, компенсированное суммирование, алгоритм Гилла — Мёллера, методы Рунге — Кутты.
Двадцать первый век можно охарактеризовать как период, в течение которого классические методы решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты, разработанные для ручного счета, развивались исходя из требований и цифровых возможностей. Однако в практических вычислениях природа компьютерной арифметики может играть значительную и, возможно, подавляющую роль.
Алгоритм Гилла
— Мёллера
В книге Бутчера [1] представлен анализ влияния ошибки округления в явном методе Эйлера, а также приведен алгоритм Гилла — Мёллера (Гилл [2], Мёллер [4], [5]), который называют «компенсированным суммированием». В данном разделе будет проведен аналогичный численный эксперимент для преодоления последствий накопления ошибок округления в явном методе Рунге —Кутты 4-го порядка.
Пусть
— общая погрешность, вычисленная на шаге
,
— соответствующая погрешность вычисления производной на этом же шаге, тогда
последовательности точных и приближённых значений связаны между собой следующим образом
где
— ошибка округления, совершенная на этом шаге, а
— методическая погрешность. Данная операция приводит к следующему разностному уравнению
,
Так как, детальный анализ ошибки округления в расчетах данной задачи представлен в работе Хенричи [3], то вместо того, чтобы пытаться провести анализ
и
, а также, поскольку шаги вычисляются последовательно, заметим, что можно преодолеть наихудшие последствия накопления ошибок округления. Это делается путем оценки значения
на любом конкретном шаге, а затем добавление его к значению
, прежде чем оно будет добавлено на следующем шаге.
Этот усовершенствованный метод, который может быть использован для многих ситуаций, связанных с суммированием большого количества малых величин, и называют алгоритмом Гилла — Мёллера или «компенсированным суммированием».
«
Компенсированное суммирование
»
в
явном методе Рунге
— Кутты 4-го порядка
Общая схема явного метода Рунге — Кутты (ЯМРК) численного интегрирования СОДУ
выглядит следующим образом:
где функции
вычисляются по схеме
Здесь
— точное и приближенное значение s-й компоненты в точке
соответственно,
— точное значение s-й компоненты в точке
,
— шаг метода.
Традиционным считается символически представлять данный метод посредством таблиц Бутчера. Приведем пример таблицы Бутчера для ЯМРК 4-го порядка.
|
0 |
||||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Далее будет показано как применить «компенсированное суммирование» для уменьшения ошибки округления в ЯМРК четвертого порядка на примере системы дифференциальных уравнений
,
с начальным приближением
которое имеет аналитическое решение
Реализация данного метода была выполнена в системе научных вычислений MATLAB.
(ЯМРК4)
ЯМРК4 с компенсированным суммированием)
В данном примере была взята последовательность шагов
Результаты
Нанесем глобальные погрешности этих двух алгоритмов на один график в логарифмическом масштабе.
Видно, что явная форма дает результаты, которые сильнее ухудшаются при определенном шаге, в то время как компенсированная версия значительно улучшает результат.
Выводы
Как видно из проведенного исследования, метод «компенсированного суммирования» значительно улучшает ЯМРК четвертого порядка, а также его можно распространить и на другие численные методы интегрирования СОДУ.
Литература:
- Butcher J. C. «Numerical Methods for ordinary Differential Equations, Second Edition». The University of Auckland, New Zealand 2008, 463 p.
- Gill S. «A process for the step-by step integration of differential equations in an automatic computing machine». Proc. Cambridge Philos. Soc 1951.
- Henrici P. «Discrete Variable Methods in Ordinary Differential Equations». John Wiley & Sons Inc, New York 1962.
- Møller O. «Quasi double-precision in floating point addition». BIT 1965.
- Møller O. «Note on quasi double-precision». BIT 1965.
Основные термины (генерируются автоматически): явный метод, компенсированное суммирование, MATLAB, алгоритм, шаг.
В числовой анализ, то Методы Рунге – Кутты семья неявный и явный итерационные методы, которые включают хорошо известную процедуру, называемую Метод Эйлера, используется в временная дискретизация для приближенных решений обыкновенные дифференциальные уравнения.[1] Эти методы были разработаны около 1900 года немецкими математиками. Карл Рунге и Вильгельм Кутта.
Сравнение методов Рунге-Кутты для дифференциального уравнения y ‘= sin (t) ^ 2 * y (оранжевый — точное решение)
Метод Рунге – Кутты.
Склоны по классическому методу Рунге-Кутта
Наиболее широко известный член семейства Рунге-Кутта обычно упоминается как «RK4», «классический метод Рунге-Кутта» или просто как «метод Рунге-Кутта».
Пусть проблема начального значения указать следующее:
Здесь 











Теперь выберите размер шага час > 0 и определим
за п = 0, 1, 2, 3, …, используя[2]
- (Примечание: приведенные выше уравнения имеют разные, но эквивалентные определения в разных текстах).[3]
Здесь 



При усреднении четырех уклонов больший вес придается уклонам в средней точке. Если 

Метод RK4 — это метод четвертого порядка, а это означает, что локальная ошибка усечения является в порядке 

Во многих практических приложениях функция 



Явные методы Рунге – Кутты
Семья явный Методы Рунге – Кутты являются обобщением упомянутого выше метода RK4. Это дается
куда[5]
- (Примечание: приведенные выше уравнения могут иметь разные, но эквивалентные определения в некоторых текстах).[3]
Чтобы указать конкретный метод, необходимо указать целое число s (количество ступеней), а коэффициенты аij (для 1 ≤ j < я ≤ s), бя (за я = 1, 2, …, s) и cя (за я = 2, 3, …, s). Матрица [аij] называется Матрица Рунге – Кутты, в то время как бя и cя известны как веса и узлы.[6] Эти данные обычно хранятся в мнемоническом устройстве, известном как Таблица мясника (после Джон С. Батчер ):
А Серия Тейлор показывает, что метод Рунге – Кутты непротиворечив тогда и только тогда, когда
Также существуют сопутствующие требования, если требуется, чтобы метод имел определенный порядок. п, что означает, что локальная ошибка усечения равна O (часп+1). Их можно получить из определения самой ошибки усечения. Например, двухэтапный метод имеет порядок 2, если б1 + б2 = 1, б2c2 = 1/2, и б2а21 = 1/2.[7] Обратите внимание, что популярным условием определения коэффициентов является [8]
Однако одно это условие не является ни достаточным, ни необходимым для согласованности.[9]
В общем, если явный 






Доказуемые оценки выше означают, что мы не можем найти методы заказов 

Примеры
Метод RK4 подпадает под эти рамки. Его таблица[12]
-
0 1/2 1/2 1/2 0 1/2 1 0 0 1 1/6 1/3 1/3 1/6
Небольшая вариация «метода» Рунге – Кутты также принадлежит Кутте в 1901 году и называется правилом 3/8.[13] Основное преимущество этого метода заключается в том, что почти все коэффициенты ошибок меньше, чем в популярном методе, но для этого требуется немного больше FLOP (операций с плавающей запятой) на временной шаг. Его таблица Мясника
-
0 1/3 1/3 2/3 -1/3 1 1 1 −1 1 1/8 3/8 3/8 1/8
Однако самый простой метод Рунге – Кутты — это (вперед) Метод Эйлера, задаваемый формулой 
Методы второго порядка с двумя этапами
Пример метода второго порядка с двумя стадиями представлен метод средней точки:
Соответствующая таблица
Метод средней точки — не единственный метод Рунге – Кутты второго порядка, состоящий из двух этапов; существует семейство таких методов, параметризованных параметром α и задаваемых формулой[14]
Его таблица Мясника
В этой семье 

Использовать
В качестве примера рассмотрим двухэтапный метод Рунге – Кутты второго порядка с α = 2/3, также известный как Метод Ральстона. Это дано таблицей
| 0 | |||
| 2/3 | 2/3 | ||
| 1/4 | 3/4 |
с соответствующими уравнениями
Этот метод используется для решения задачи начального значения
с размером шага час = 0,025, поэтому метод должен состоять из четырех шагов.
Метод работает следующим образом:
 |
|||
 |
|||
 |
|||
 |
 |
 |
|
 |
|||
 |
|||
 |
 |
 |
|
 |
|||
 |
|||
 |
 |
 |
|
 |
|||
 |
|||
 |
 |
 |
|
 |
Численные решения соответствуют подчеркнутым значениям.
Адаптивные методы Рунге – Кутты.
Адаптивные методы предназначены для оценки локальной ошибки усечения одного шага Рунге – Кутты. Это делается двумя способами, один с порядком 

Во время интегрирования размер шага адаптируется так, что оцененная ошибка остается ниже определенного пользователем порога: если ошибка слишком велика, шаг повторяется с меньшим размером шага; если ошибка намного меньше, размер шага увеличивается для экономии времени. Это приводит к (почти) оптимальному размеру шага, что экономит время вычислений. Более того, пользователю не нужно тратить время на поиск подходящего размера шага.
Шаг младшего порядка определяется выражением
куда 
который 

| 0 | ||||||
 |
 |
|||||
 |
 |
 |
||||
 |
 |
 |
||||
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
 |
В Метод Рунге – Кутты – Фельберга. имеет два метода порядков 5 и 4. Его расширенная таблица Мясника:
| 0 | |||||||
| 1/4 | 1/4 | ||||||
| 3/8 | 3/32 | 9/32 | |||||
| 12/13 | 1932/2197 | −7200/2197 | 7296/2197 | ||||
| 1 | 439/216 | −8 | 3680/513 | -845/4104 | |||
| 1/2 | −8/27 | 2 | −3544/2565 | 1859/4104 | −11/40 | ||
| 16/135 | 0 | 6656/12825 | 28561/56430 | −9/50 | 2/55 | ||
| 25/216 | 0 | 1408/2565 | 2197/4104 | −1/5 | 0 |
Однако простейший адаптивный метод Рунге – Кутты предполагает комбинирование Метод Хойна, который имеет порядок 2, с Метод Эйлера, который является порядком 1. Его расширенная таблица Мясника:
| 0 | |||
| 1 | 1 | ||
| 1/2 | 1/2 | ||
| 1 | 0 |
Другими адаптивными методами Рунге – Кутты являются Богацкий – Шампиновый метод (порядки 3 и 2), Кэш – метод Карпа и Метод Дорманда – Принса (оба с порядком 5 и 4).
Неконфлюэнтные методы Рунге – Кутты
Метод Рунге-Кутты называется несговорчивый [15] если все 
Методы Рунге – Кутта-Нистрома.
Методы Рунге-Кутта-Нюстрёма — это специализированные методы Рунге-Кутты, которые оптимизированы для дифференциальных уравнений второго порядка вида:[16]
С другой стороны, общий метод Рунге-Кутта-Нюстрёма оптимизирован для дифференциальных уравнений второго порядка вида:[17]
Неявные методы Рунге – Кутты
Все методы Рунге-Кутты, упомянутые до сих пор, являются явные методы. Явные методы Рунге – Кутты, как правило, не подходят для решения жесткие уравнения потому что их область абсолютной стабильности мала; в частности, он ограничен.[18]Этот вопрос особенно важен при решении уравнения в частных производных.
Неустойчивость явных методов Рунге – Кутты мотивирует развитие неявных методов. Неявный метод Рунге – Кутты имеет вид
куда
[19]
Разница с явным методом заключается в том, что в явном методе сумма более j только подходит к я — 1. Это также отображается в таблице Бутчера: матрица коэффициентов 
Видеть Адаптивные методы Рунге-Кутты выше для объяснения 
Следствием этого различия является то, что на каждом шаге необходимо решать систему алгебраических уравнений. Это значительно увеличивает вычислительные затраты. Если метод с s этапов используется для решения дифференциального уравнения с м компонентов, то система алгебраических уравнений имеет РС составные части. Это можно противопоставить неявному линейные многоступенчатые методы (другое большое семейство методов для ODE): неявный s-шаговый линейный многоступенчатый метод требует решения системы алгебраических уравнений с м компоненты, поэтому размер системы не увеличивается с увеличением количества шагов.[20]
Примеры
Простейшим примером неявного метода Рунге – Кутты является метод обратный метод Эйлера:
Таблица Мясника для этого проста:
Эта таблица Бутчера соответствует формулам
который можно перестроить, чтобы получить формулу обратного метода Эйлера, указанную выше.
Другой пример неявного метода Рунге – Кутты — это трапеция. Его таблица Мясника:
Правило трапеции — это метод коллокации (как описано в этой статье). Все методы коллокации являются неявными методами Рунге-Кутты, но не все неявные методы Рунге-Кутты являются методами коллокации.[21]
В Методы Гаусса – Лежандра сформировать семейство методов коллокации на основе Квадратура Гаусса. Метод Гаусса – Лежандра с s этапов имеет порядок 2s (таким образом, могут быть построены методы сколь угодно высокого порядка).[22] Метод с двумя этапами (и, следовательно, порядок четыре) имеет таблицу Мясника:
[20]
Стабильность
Преимущество неявных методов Рунге – Кутты перед явными заключается в их большей устойчивости, особенно в применении к жесткие уравнения. Рассмотрим линейное тестовое уравнение y ‘ = λу. Примененный к этому уравнению метод Рунге – Кутты сводится к итерации 
[23]
куда е обозначает вектор единиц. Функция р называется функция устойчивости.[24] Из формулы следует, что р является фактором двух многочленов степени s если метод имеет s этапы.Явные методы имеют строго нижнетреугольную матрицу А, откуда следует, что det (я − zA) = 1 и что функция устойчивости является полиномом.[25]
Численное решение линейного тестового уравнения обращается в ноль, если | р(z) | <1 с z = часλ. Набор таких z называется область абсолютной стабильности. В частности, метод называется абсолютная стабильность я упал z с Re (z) <0 находятся в области абсолютной устойчивости. Функция устойчивости явного метода Рунге – Кутты является полиномом, поэтому явные методы Рунге – Кутты никогда не могут быть A-стабильными.[25]
Если метод имеет порядок п, то функция устойчивости удовлетворяет 

Метод Гаусса – Лежандра с s этапов имеет порядок 2s, поэтому его функция устойчивости является аппроксимацией Паде с м = п = s. Отсюда следует, что метод A-устойчив.[27] Это показывает, что A-стабильный Рунге – Кутта может иметь сколь угодно высокий порядок. Напротив, порядок A-стабильной линейные многоступенчатые методы не может превышать двух.[28]
B-стабильность
В А-стабильность Концепция решения дифференциальных уравнений связана с линейным автономным уравнением 



Позволять 



Метод Рунге-Кутты называется алгебраически устойчивый [29] если матрицы 



Вывод метода четвертого порядка Рунге – Кутты.
В общем, метод порядка Рунге – Кутты 
куда:
— приращения, полученные при оценке производных от 

Разрабатываем вывод[31] для метода Рунге – Кутты четвертого порядка по общей формуле с 

и 
куда 

и для предыдущих соотношений мы можем показать, что следующие равенства справедливы до 
куда:
полная производная от 
Если теперь выразить общую формулу, используя то, что мы только что вывели, мы получим:
и сравнивая это с Серия Тейлор из 

получаем систему ограничений на коэффициенты:
который при решении дает 
Смотрите также
- Метод Эйлера
- Список методов Рунге – Кутты
- Численные методы решения обыкновенных дифференциальных уравнений
- Метод Рунге – Кутта (SDE)
- Общие линейные методы
- Интегратор групп Ли
Примечания
- ^ ДЕВРИС, Пол Л.; ХАСБУН, Хавьер Э. Первый курс вычислительной физики. Второе издание. Jones and Bartlett Publishers: 2011. стр. 215.
- ^ Press et al. 2007 г., п. 908; Сюли и Майерс 2003, п. 328
- ^ а б Аткинсон (1989, п. 423), Хайрер, Норсетт и Ваннер (1993, п. 134), Кав и Калу (2008), §8.4) и Stoer & Bulirsch (2002)., п. 476) не учитывай час в определении этапов. Ашер и Петцольд (1998), п. 81), Мясник (2008), п. 93) и Изерлес (1996 г., п. 38) используйте у ценности как этапы.
- ^ а б Сюли и Майерс 2003, п. 328
- ^ Press et al. 2007 г., п. 907
- ^ Изерлес 1996, п. 38
- ^ Изерлес 1996, п. 39
- ^ Изерлес 1996, п. 39
- ^ В качестве контрпримера рассмотрим любую явную двухэтапную схему Рунге-Кутты с
и
и
выбрано случайно. Этот метод является непротиворечивым и (в общем) сходящимся первого порядка. С другой стороны, одноэтапный метод с
непоследовательно и не может сходиться, хотя тривиально
.
- ^ Мясник 2008, п. 187
- ^ Мясник 2008, стр. 187–196
- ^ а б Сюли и Майерс 2003, п. 352
- ^ Хайрер, Норсетт и Ваннер (1993, п. 138) относятся к Кутта (1901).
- ^ Сюли и Майерс 2003, п. 327
- ^ Ламберт 1991, п. 278
- ^ Dormand, J. R .; Принс, П. Дж. (Октябрь 1978 г.). «Новые алгоритмы Рунге-Кутты для численного моделирования в динамической астрономии». Небесная механика. 18 (3): 223–232. Дои:10.1007 / BF01230162.
- ^ Фельберг, Э. (октябрь 1974 г.). Классические формулы Рунге-Кутта-Нюстрёма седьмого, шестого и пятого порядков с пошаговым управлением для общих дифференциальных уравнений второго порядка (Отчет) (НАСА TR R-432 ред.). Центр космических полетов Маршалла, штат Алабама: Национальное управление по аэронавтике и исследованию космического пространства.
- ^ Сюли и Майерс 2003, стр. 349–351
- ^ Изерлес 1996, п. 41; Сюли и Майерс 2003, стр. 351–352
- ^ а б Сюли и Майерс 2003, п. 353
- ^ Изерлес 1996, стр. 43–44
- ^ Изерлес 1996, п. 47
- ^ Hairer & Wanner 1996 г., стр. 40–41
- ^ Hairer & Wanner 1996 г., п. 40
- ^ а б Изерлес 1996, п. 60
- ^ Изерлес 1996, стр. 62–63
- ^ Изерлес 1996, п. 63
- ^ Этот результат обусловлен Дальквист (1963).
- ^ Ламберт 1991, п. 275
- ^ Ламберт 1991, п. 274
- ^ PDF отчет об этом выводе
Рекомендации
- Рунге, Карл Давид Толме (1895), «Über die numerische Auflösung von Differentialgleichungen», Mathematische Annalen, Springer, 46 (2): 167–178, Дои:10.1007 / BF01446807.
- Кутта, Мартин (1901), Beitrag zur näherungweisen Integration totaler Differentialgleichungen.
- Ascher, Uri M .; Петцольд, Линда Р. (1998), Компьютерные методы решения обыкновенных дифференциальных и дифференциально-алгебраических уравнений, Филадельфия: Общество промышленной и прикладной математики, ISBN 978-0-89871-412-8.
- Аткинсон, Кендалл А. (1989), Введение в численный анализ (2-е изд.), Нью-Йорк: Джон Уайли и сыновья, ISBN 978-0-471-50023-0.
- Мясник, Джон С. (Май 1963 г.), «Коэффициенты для изучения интеграционных процессов Рунге-Кутта», Журнал Австралийского математического общества, 3 (2): 185–201, Дои:10.1017 / S1446788700027932.
- Мясник, Джон С. (1975), «Свойство устойчивости неявных методов Рунге-Кутта», КУСОЧЕК, 15 (4): 358–361, Дои:10.1007 / bf01931672.
- Мясник, Джон С. (2008), Численные методы решения обыкновенных дифференциальных уравнений., Нью-Йорк: Джон Уайли и сыновья, ISBN 978-0-470-72335-7.
- Cellier, F .; Кофман, Э. (2006), Непрерывное моделирование системы, Springer Verlag, ISBN 0-387-26102-8.
- Дальквист, Гермунд (1963), «Специальная задача устойчивости для линейных многоступенчатых методов», КУСОЧЕК, 3: 27–43, Дои:10.1007 / BF01963532, HDL:10338.dmlcz / 103497, ISSN 0006-3835.
- Форсайт, Джордж Э .; Малькольм, Майкл А .; Молер, Клив Б. (1977), Компьютерные методы математических вычислений, Prentice-Hall (см. главу 6).
- Хайрер, Эрнст; Норсетт, Сиверт Пол; Ваннер, Герхард (1993), Решение обыкновенных дифференциальных уравнений I: нежесткие задачи, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-56670-0.
- Хайрер, Эрнст; Ваннер, Герхард (1996), Решение обыкновенных дифференциальных уравнений II: жесткие и дифференциально-алгебраические задачи (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-60452-5.
- Изерлес, Арье (1996), Первый курс численного анализа дифференциальных уравнений, Издательство Кембриджского университета, ISBN 978-0-521-55655-2.
- Ламберт, JD (1991), Численные методы для обыкновенных дифференциальных систем. Проблема начальной стоимости, Джон Уайли и сыновья, ISBN 0-471-92990-5
- Кау, Аутар; Калу, Эгву (2008), Численные методы с приложениями (1-е изд.), Autarkaw.com.
- Кутта, Мартин (1901), «Beitrag zur näherungsweisen Integration Totaler Differentialgleichungen», Zeitschrift für Mathematik und Physik, 46: 435–453.
- Press, William H .; Флэннери, Брайан П .; Теукольский, Саул А.; Веттерлинг, Уильям Т. (2007), «Раздел 17.1 Метод Рунге-Кутты», Числовые рецепты: искусство научных вычислений (3-е изд.), Издательство Кембриджского университета, ISBN 978-0-521-88068-8. Также, Раздел 17.2. Адаптивный контроль размера шага для Рунге-Кутты.
- Стоер, Йозеф; Булирш, Роланд (2002), Введение в численный анализ (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-95452-3.
- Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ, Издательство Кембриджского университета, ISBN 0-521-00794-1.
- Тан, Делин; Чен, Чжэн (2012), «Об общей формуле метода Рунге-Кутты четвертого порядка» (PDF), Журнал математических наук и математического образования, 7 (2): 1–10.
- справочник по продвинутой дискретной математике игнорируется (код — mcs033)
внешняя ссылка
- «Метод Рунге-Кутта», Энциклопедия математики, EMS Press, 2001 [1994]
- Метод Рунге – Кутты 4-го порядка
- Реализация библиотеки компонентов трекера в Matlab — Реализует 32 встроенных алгоритма Рунге Кутта в
РунгеКстеп, 24 встроенных алгоритма Рунге-Кутта-Нистрома вРунгеKNystroemSStepи 4 общих алгоритма Рунге-Кутта-Нистрома вРунгеKNystroemGStep.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Методы Рунге-Кутта, а далее РК, являются важнейшими для решения задач Коши обыкновенного дифференциального уравнения y’ = f(x, y). Классическими являются 4-стадийные методы 4-го порядка. На данный момент известно большое количество методов более высокого порядка, дающих либо лучшую, либо такую же точность, но за меньший промежуток времени. Однако, классические методы остаются наиболее популярными при решении. Поэтому в этой статье мы сделаем обзор развития существующих методов РК [1-7], которые обходят некоторые недостатки классических методов.
Важнейшая составляющая современных методов – это автоматическая оценка локальной погрешности, получаемая благодаря вложенным методам РК. Вложенный метод РК позволяет достаточно точно найти локальную погрешность в вычислениях, при этом не требуя дополнительных вычислений функции f(x, y).
Без этой оценки приходится брать большой запас точности, т.е. устанавливать величину шага гораздо меньше, чем необходимо на самом деле. Из этого следует повышенный объем вычислений. При использовании автоматической оценки погрешности величину шага можно не только выбрать без ненужного запаса, но и вносить коррективы участках расчетов.
С точки зрения практики, наиболее значимыми в работе оказываются оценки погрешности, выдаваемые формулами по одному, двум и трем шагам соответственно. Первая предоставляет оценку погрешности с точностью до порядка, вторая – с точностью до умножения на константу, третья же оценка уже является в меру точной. Первые две оценки из-за малой точности могут использоваться только в вспомогательных целях. Оценка погрешности по трем этапам уже может применяться для автоматического выбора величины шага. Но для использования этой оценки нужны три шага одинаковых по величине.
1. КЛАССИЧЕСКИЕ МЕТОДЫ
Пусть дано y’ = f(t, y), t ∈ ℝ, y ∈ ℝ, и начальное условие y(t0) = y0. Выбираем некоторый малый шаг h и находим вектор y1 = y(t1) = y(t0 + h) по 4-стадийным формулам:
Все коэффициенты метода чаще всего записываются в виде таблицы Бутчера
при этом должны быть выполнены следующие соотношения
Коэффициенты метода не произвольны, они должны удовлетворять некоторой системе полиномиальных уравнений (условия порядка). Для классических методов – это система из 8 уравнений от 10 переменных. Значительное разнообразие ее решений может быть отображено параметрически. Пусть c2, c3 – свободные параметры, причем
, , , , , . (2)
Тогда остальные коэффициенты выражаются через них по формулам (см. (1), (2)):
Например, при , таблица Бутчера приобретает вид
Наиболее распространённым является метод с таблицей Бутчера4)
Однако, он не входит в семейство (3). Существуют другие подобные решения, но все они образуют одномерное многообразие.
2. ОДНОШАГОВАЯ ОЦЕНКА ПОГРЕШНОСТИ
Отсутствие вложенных формул пятого порядка для классических методов не свидетельствует о том, что погрешность нельзя оценить, но итог оценки получается очень грубым. Можно построить вложенный метод третьего порядка (см. [1], [7]). Для определения такой оценки добавим к формулам (1) еще одну:
. (5)
Заметим, что для нахождения k5 по формуле (5) не нужно дополнительное вычисление функции f (при c5 = 1), так как следующий шаг метода РК начинается с вычисления вектора , т.е. k5 все равно придется вычислять.
Для грубой оценки вектора погрешности можно использовать выражение
для некоторой константы C, зависящей от решаемой системы, и
В случае , (правило «3/8») процесс расчёта выглядит так:
и для грубой оценки вектора погрешности можно использовать выражение (6)
Для метода (4) аналогичная формула принимает вид
. (7)
Таким способом можно оценить локальную погрешность. Однако, получить более точные оценки не представляется возможным, но даже такая оценка позволяет избежать грубых ошибок при выборе шага интегрирования.
3. ОЦЕНКА ПОГРЕШНОСТИ ПО ДВУМ ШАГАМ
В случае, когда не получается построить вложенную формулу, то это не означает, что для данного метода не существует простых и достаточно точных методов оценки погрешности. К примеру, формула численного дифференцирования
дает возможность получить неплохой способ оценки погрешности, но для более-менее точной оценки придется использовать много последовательных значений yi.
Попробуем уменьшить необходимое количество шагов, используя не только yi, но и промежуточные величины ki с каждого шага метода РК.
Выполняя несколько шагов метода РК, мы последовательно вычисляем
Пусть таблица Бутчера 4-стадийного метода имеет вид (8)
и ее коэффициенты рассчитаны по формулам (3) для некоторых c2, c3.
Два шага этого метода в совокупности с вспомогательным “вложенным” шагом можно считать одним девяти стадийным методом с таблицей Бутчера.
Для того, чтобы получить истинный “вложенный” метод необходимо выбрать коэффициенты так, чтобы эта таблица давала метод пятого порядка, т.е. ее коэффициенты должны подходить семнадцати уравнениям Бутчера. Однако, если перейти к расчётам, то это не представляется возможным ни при каком выборе исходного метода (aij, bi, ci). Однако, выполнимо подобрать коэффициенты так, чтобы получился метод 4-го порядка, но отличный от исходного, дающегося коэффициентами bi.
Как в [7], будем искать в виде . Условия порядка оказываются однородными относительно βi. Получающаяся система уравнений имеет два линейно независимых решения.
Второе решение:
Для случая c2 = 1/3, c3 = 2/3 (“правило 3/8”) два решения можно взять в виде
(11)
Для схемы (4) коэффициенты имеют вид
(12)
Выпишем по этим данным общий алгоритм вычислений. Рассмотрим два шага метода РК с таблицей Бутчера (8):
Для оценки погрешности мы имеем формулу
, (14)
где для вектора (β1,…,β9) мы имеем два значения, указанные выше, (9), (10) – для общего случая, (11) – для “правила 3/8” и (12) – для метода (8).
Эти две формулы предоставляют два вектора погрешности err1 и err2, при этом величина каждой погрешности обладает тем же порядком, что и искомая погрешности метода — O(h5). Поэтому для увеличения надежности стоит брать сразу две величины. Численные эксперименты показывают, что для общей оценки локальной погрешности позволительно использовать величину
.
Такая оценка получается существенно более точной, чем (6), (7).
4. ОЦЕНКА ПОГРЕШНОСТИ ПО ТРЕМ ШАГАМ
Полученную оценку возможно сделать еще более точной, если взять три шага. В этом случае мы имеем 13 векторов:
Взяв их линейную комбинацию с подходящими коэффициентами, мы можем получить оценку погрешности с точностью до O(h6). Формулы расчета схожи с формулами (13), т.е. для оценки погрешности используется формулу вида
,
где коэффициенты βi являются решением системы из семнадцати уравнений Бутчера. Эти уравнения линейны относительно переменных βi, и система обладает двумерным пространством решений. В качестве свободных переменных можно выбрать β12, β13, остальные будут линейно выражатся через них. Следовательно, в общем случае βi будут линейно выражаться через β12, β13, причем коэффициенты будут достаточно сложными рациональными функциями от c2, c3, общая степень – до 7. Приведем поэтому решение для «правила 3/8»:
(15)
И для таблицы Бутчера (7):
. (16)
Такое решение обладает двумя преимуществами. Во-первых, коэффициенты βi невелики по абсолютной величине, а во-вторых, для получения оценки не нужно вычислять , т.е. ошибочно выбранный шаг можно будет исправить чуть раньше, чем при отличном выборе коэффициентов.
Погрешность для классических методов РК имеет порядок O(h5), а предложенная выше формула находит ее с точностью до O(h6). Таким образом, формула (15) дает практически точное значение погрешности.
ЗАКЛЮЧЕНИЕ
Во время разработки современных методов Рунге-Кутте, особое внимание уделяется вложенным методам (см., например, [1], [3], [4] и многие другие). Однако таких методов заметно меньше, а их нахождение гораздо труднее обычных. На сегодняшний день известно мало вложенных методов, да и те не всегда предоставляют достаточную эффективность.
Данная работа и приведённые в ней примеры показывают, что необходимость в поиске вложенных методов для автоматического управления длинной шага — отсутствует. Для каждого метода РК можно предложить довольно точный способ нахождения погрешности, который не будет требовать дополнительных вычислений в правой части уравнений. В данной статье это сделано для наиболее употребляемых классических методов Рунге-Кутте, однако нет никаких сомнений, что это можно сделать и со всеми остальными. С другой стороны, есть основания считать, что аналогичную оценку можно сделать и для случая трех последовательных шагов метода с различным шагом.
В целом, если удастся продвинуться в указанных направлениях, то для вычислений с автоматическим выбором шага оказывается возможным применять наиболее эффективные методы РК, не ограничиваясь лишь теми, для которых имеются вложенные.
СПИСОКЛИТЕРАТУРЫ
Butcher J.С. Numerical methods for ordinary differential equations (2nd ed.). New York: John Wiley, 2008.
Chan T.M.H., Butcher J.C. Multi-step zero approximations for stepsize control // Appl. Numer. Math. 2000. V. 34. P. 167–177.
Jackiewicz Z. General Linear Methods for Ordinary Differential Equations. New York: Wiley, 2009.
Jackiewicz Z., Verner J.H. Derivation and implementation of two-step Runge–Kutta pairs // Appl. Math. 2002.V. 19. P. 227–248.
Shampine L.F., Watts H.A. Comparing Error Estimators for Runge–Kutta methods // Math. Comp. 1971. V. 25. P. 445–455.
Verner J.H. Numerically optimal Runge–Kutta pairs with interpolants // Numerical Algorith. 2010. V. 53. P. 383–396.
Wanner G., Hairer E., Nørsett S.P. Solving ordinary differential equations I. Nonstiff Problems. 2Ed. Berlin: Springer, 2000.

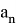
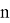
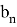
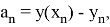
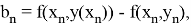
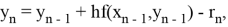
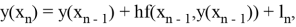
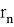
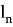
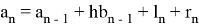
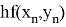
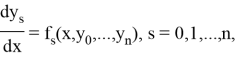
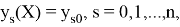
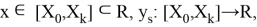
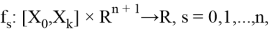
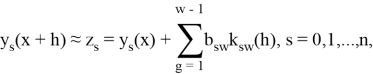
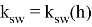
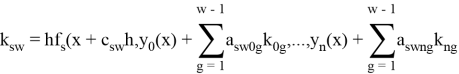
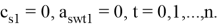
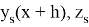
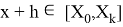
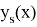
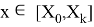
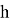
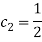
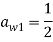
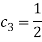
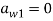
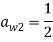
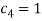
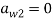
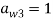
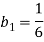
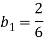
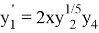
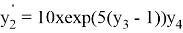
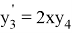
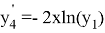
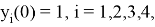
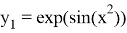
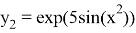
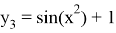
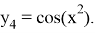


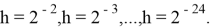
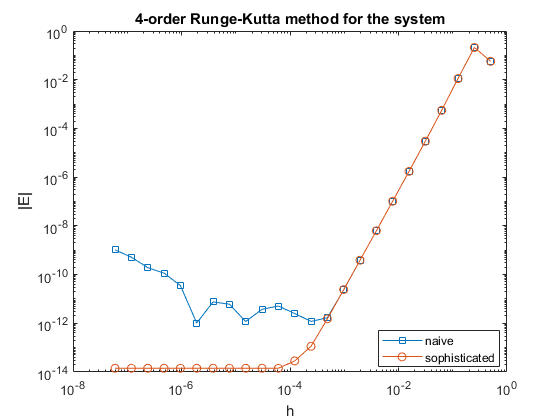















![{ displaystyle { frac {dy} {dt}} = tan (y) +1, quad y_ {0} = 1, t in [1,1.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a9f561fa8e63f2b86d6226df93dd25d29f76fc0)


















![{ displaystyle { begin {align} k_ {2} & = f left (y_ {t + h / 2} ^ {1}, t + { frac {h} {2}} right) = f left (y_ {t} + { frac {h} {2}} k_ {1}, t + { frac {h} {2}} right) & = f left (y_ {t}, t right) + { frac {h} {2}} { frac {d} {dt}} f left (y_ {t}, t right) k_ {3} & = f left (y_ {t + h / 2} ^ {2}, t + { frac {h} {2}} right) = f left (y_ {t} + { frac {h} {2}} f left (y_ {t} + { frac {h} {2}} k_ {1}, t + { frac {h} {2}} right), t + { frac {h} {2 }} right) & = f left (y_ {t}, t right) + { frac {h} {2}} { frac {d} {dt}} left [f left (y_ {t}, t right) + { frac {h} {2}} { frac {d} {dt}} f left (y_ {t}, t right) right] k_ {4} & = f left (y_ {t + h} ^ {3}, t + h right) = f left (y_ {t} + hf left (y_ {t} + { frac {h} {2}} k_ {2}, t + { frac {h} {2}} right), t + h right) & = f left (y_ {t} + hf left (y_ {t} + { frac {h} {2}} f left (y_ {t} + { frac {h} {2}} f left (y_ {t}, t right) ), t + { frac {h} {2}} right), t + { frac {h} {2}} right), t + h right) & = f left (y_ {t}, t right) + h { frac {d} {dt}} left [f left (y_ {t}, t right) + { frac {h} {2}} { frac {d} {dt}} left [f left (y_ {t}, t right) + { frac {h} {2}} { frac {d} {dt}} f left (y_ {t}, t right) right] right] end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7fab64b114fcd6b0ff7ccc1bb7d9754e3eace2d)

![{ displaystyle { begin {align} y_ {t + h} = {} & y_ {t} + h left lbrace a cdot f (y_ {t}, t) + b cdot left [f ( y_ {t}, t) + { frac {h} {2}} { frac {d} {dt}} f (y_ {t}, t) right] right. + & { } + c cdot left [f (y_ {t}, t) + { frac {h} {2}} { frac {d} {dt}} left [f left (y_ {t} , t right) + { frac {h} {2}} { frac {d} {dt}} f (y_ {t}, t) right] right] + & {} + d cdot left [f (y_ {t}, t) + h { frac {d} {dt}} left [f (y_ {t}, t) + { frac {h} {2 }} { frac {d} {dt}} left [f (y_ {t}, t) + left. { frac {h} {2}} { frac {d} {dt}} f (y_ {t}, t) right] right] right] right rbrace + { mathcal {O}} (h ^ {5}) = {} & y_ {t} + a cdot hf_ {t} + b cdot hf_ {t} + b cdot { frac {h ^ {2}} {2}} { frac {df_ {t}} {dt}} + c cdot hf_ {t } + c cdot { frac {h ^ {2}} {2}} { frac {df_ {t}} {dt}} + & {} + c cdot { frac {h ^ {3 }} {4}} { frac {d ^ {2} f_ {t}} {dt ^ {2}}} + d cdot hf_ {t} + d cdot h ^ {2} { frac {df_ {t}} {dt}} + d cdot { frac {h ^ {3}} {2}} { frac {d ^ {2} f_ {t}} {dt ^ {2}}} + d cdot { frac {h ^ {4}} {4}} { frac {d ^ {3} f_ {t}} {dt ^ {3}}} + { mathcal {O}} (h ^ { 5}) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d443e3cc50f9e0636ccb9094ff5c4c304b455d)

![{ displaystyle { begin {cases} & a + b + c + d = 1 [6pt] & { frac {1} {2}} b + { frac {1} {2}} c + d = { frac {1} {2}} [6pt] & { frac {1} {4}} c + { frac {1} {2}} d = { frac {1} {6}} [6pt] & { frac {1} {4}} d = { frac {1} {24}} end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5fde6d4547411755a49dbe4fb9078743a9f1a08)


