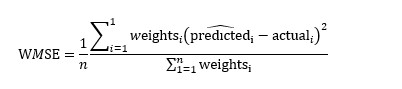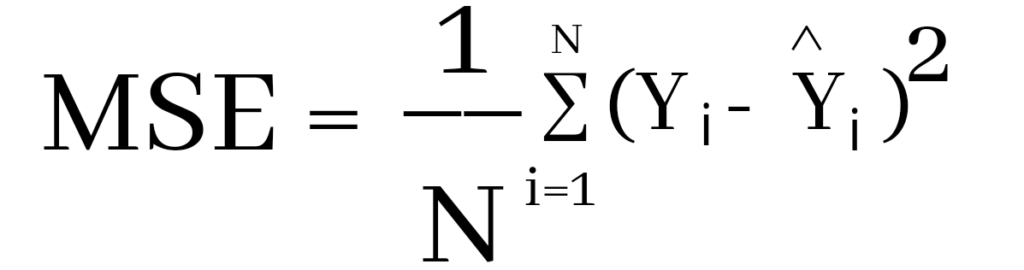Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
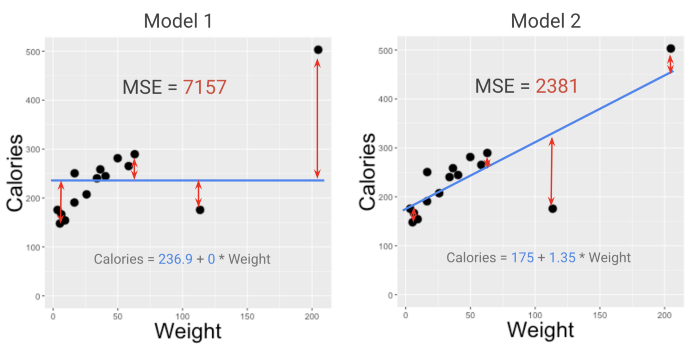
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
17 авг. 2022 г.
читать 1 мин
Среднеквадратическая ошибка (MSE) — это распространенный способ измерения точности предсказания модели. Он рассчитывается как:
MSE = (1/n) * Σ(фактическое – прогноз) 2
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
Чем ниже значение MSE, тем лучше модель способна точно предсказывать значения.
Как рассчитать MSE в Python
Мы можем создать простую функцию для вычисления MSE в Python:
import numpy as np
def mse(actual, pred):
actual, pred = np.array(actual), np.array(pred)
return np.square(np.subtract(actual,pred)).mean()
Затем мы можем использовать эту функцию для вычисления MSE для двух массивов: одного, содержащего фактические значения данных, и другого, содержащего прогнозируемые значения данных.
actual = [12, 13, 14, 15, 15, 22, 27]
pred = [11, 13, 14, 14, 15, 16, 18]
mse(actual, pred)
17.0
Среднеквадратическая ошибка (MSE) для этой модели оказывается равной 17,0 .
На практике среднеквадратическая ошибка (RMSE) чаще используется для оценки точности модели. Как следует из названия, это просто квадратный корень из среднеквадратичной ошибки.
Мы можем определить аналогичную функцию для вычисления RMSE:
import numpy as np
def rmse(actual, pred):
actual, pred = np.array(actual), np.array(pred)
return np.sqrt(np.square(np.subtract(actual,pred)).mean())
Затем мы можем использовать эту функцию для вычисления RMSE для двух массивов: одного, содержащего фактические значения данных, и другого, содержащего прогнозируемые значения данных.
actual = [12, 13, 14, 15, 15, 22, 27]
pred = [11, 13, 14, 14, 15, 16, 18]
rmse(actual, pred)
4.1231
Среднеквадратическая ошибка (RMSE) для этой модели оказывается равной 4,1231 .
Дополнительные ресурсы
Калькулятор среднеквадратичной ошибки (MSE)
Как рассчитать среднеквадратичную ошибку (MSE) в Excel
The mean squared error is a common way to measure the prediction accuracy of a model. In this tutorial, you’ll learn how to calculate the mean squared error in Python. You’ll start off by learning what the mean squared error represents. Then you’ll learn how to do this using Scikit-Learn (sklean), Numpy, as well as from scratch.
What is the Mean Squared Error
The mean squared error measures the average of the squares of the errors. What this means, is that it returns the average of the sums of the square of each difference between the estimated value and the true value.
The MSE is always positive, though it can be 0 if the predictions are completely accurate. It incorporates the variance of the estimator (how widely spread the estimates are) and its bias (how different the estimated values are from their true values).
The formula looks like below:
Now that you have an understanding of how to calculate the MSE, let’s take a look at how it can be calculated using Python.
Interpreting the Mean Squared Error
The mean squared error is always 0 or positive. When a MSE is larger, this is an indication that the linear regression model doesn’t accurately predict the model.
An important piece to note is that the MSE is sensitive to outliers. This is because it calculates the average of every data point’s error. Because of this, a larger error on outliers will amplify the MSE.
There is no “target” value for the MSE. The MSE can, however, be a good indicator of how well a model fits your data. It can also give you an indicator of choosing one model over another.
Loading a Sample Pandas DataFrame
Let’s start off by loading a sample Pandas DataFrame. If you want to follow along with this tutorial line-by-line, simply copy the code below and paste it into your favorite code editor.
# Importing a sample Pandas DataFrame
import pandas as pd
df = pd.DataFrame.from_dict({
'x': [1,2,3,4,5,6,7,8,9,10],
'y': [1,2,2,4,4,5,6,7,9,10]})
print(df.head())
# x y
# 0 1 1
# 1 2 2
# 2 3 2
# 3 4 4
# 4 5 4You can see that the editor has loaded a DataFrame containing values for variables x and y. We can plot this data out, including the line of best fit using Seaborn’s .regplot() function:
# Plotting a line of best fit
import seaborn as sns
import matplotlib.pyplot as plt
sns.regplot(data=df, x='x', y='y', ci=None)
plt.ylim(bottom=0)
plt.xlim(left=0)
plt.show()This returns the following visualization:
The mean squared error calculates the average of the sum of the squared differences between a data point and the line of best fit. By virtue of this, the lower a mean sqared error, the more better the line represents the relationship.
We can calculate this line of best using Scikit-Learn. You can learn about this in this in-depth tutorial on linear regression in sklearn. The code below predicts values for each x value using the linear model:
# Calculating prediction y values in sklearn
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(df[['x']], df['y'])
y_2 = model.predict(df[['x']])
df['y_predicted'] = y_2
print(df.head())
# Returns:
# x y y_predicted
# 0 1 1 0.581818
# 1 2 2 1.563636
# 2 3 2 2.545455
# 3 4 4 3.527273
# 4 5 4 4.509091Calculating the Mean Squared Error with Scikit-Learn
The simplest way to calculate a mean squared error is to use Scikit-Learn (sklearn). The metrics module comes with a function, mean_squared_error() which allows you to pass in true and predicted values.
Let’s see how to calculate the MSE with sklearn:
# Calculating the MSE with sklearn
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(df['y'], df['y_predicted'])
print(mse)
# Returns: 0.24727272727272714This approach works very well when you’re already importing Scikit-Learn. That said, the function works easily on a Pandas DataFrame, as shown above.
In the next section, you’ll learn how to calculate the MSE with Numpy using a custom function.
Calculating the Mean Squared Error from Scratch using Numpy
Numpy itself doesn’t come with a function to calculate the mean squared error, but you can easily define a custom function to do this. We can make use of the subtract() function to subtract arrays element-wise.
# Definiting a custom function to calculate the MSE
import numpy as np
def mse(actual, predicted):
actual = np.array(actual)
predicted = np.array(predicted)
differences = np.subtract(actual, predicted)
squared_differences = np.square(differences)
return squared_differences.mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714The code above is a bit verbose, but it shows how the function operates. We can cut down the code significantly, as shown below:
# A shorter version of the code above
import numpy as np
def mse(actual, predicted):
return np.square(np.subtract(np.array(actual), np.array(predicted))).mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714Conclusion
In this tutorial, you learned what the mean squared error is and how it can be calculated using Python. First, you learned how to use Scikit-Learn’s mean_squared_error() function and then you built a custom function using Numpy.
The MSE is an important metric to use in evaluating the performance of your machine learning models. While Scikit-Learn abstracts the way in which the metric is calculated, understanding how it can be implemented from scratch can be a helpful tool.
Additional Resources
To learn more about related topics, check out the tutorials below:
- Pandas Variance: Calculating Variance of a Pandas Dataframe Column
- Calculate the Pearson Correlation Coefficient in Python
- How to Calculate a Z-Score in Python (4 Ways)
- Official Documentation from Scikit-Learn
Improve Article
Save Article
Improve Article
Save Article
The Mean Squared Error (MSE) or Mean Squared Deviation (MSD) of an estimator measures the average of error squares i.e. the average squared difference between the estimated values and true value. It is a risk function, corresponding to the expected value of the squared error loss. It is always non – negative and values close to zero are better. The MSE is the second moment of the error (about the origin) and thus incorporates both the variance of the estimator and its bias.
Steps to find the MSE
- Find the equation for the regression line.
(1)
- Insert X values in the equation found in step 1 in order to get the respective Y values i.e.
(2)
- Now subtract the new Y values (i.e.
) from the original Y values. Thus, found values are the error terms. It is also known as the vertical distance of the given point from the regression line.
(3)
- Square the errors found in step 3.
(4)
- Sum up all the squares.
(5)
- Divide the value found in step 5 by the total number of observations.
(6)
Example:
Consider the given data points: (1,1), (2,1), (3,2), (4,2), (5,4)
You can use this online calculator to find the regression equation / line.
Regression line equation: Y = 0.7X – 0.1
| X | Y | |
|---|---|---|
| 1 | 1 | 0.6 |
| 2 | 1 | 1.29 |
| 3 | 2 | 1.99 |
| 4 | 2 | 2.69 |
| 5 | 4 | 3.4 |
Now, using formula found for MSE in step 6 above, we can get MSE = 0.21606
MSE using scikit – learn:
from sklearn.metrics import mean_squared_error
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
mean_squared_error(Y_true,Y_pred)
Output: 0.21606
MSE using Numpy module:
import numpy as np
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
MSE = np.square(np.subtract(Y_true,Y_pred)).mean()
Output: 0.21606
29.12.2019Python, Программы Python, Продвинутые компьютерные предметы
Среднее квадратичное отклонение (MSE) или Среднее квадратичное отклонение (MSD) оценщика измеряет среднее квадратов ошибок, то есть среднее квадратическое различие между оценочными значениями и истинным значением. Это функция риска, соответствующая ожидаемому значению квадрата потери ошибок. Это всегда неотрицательно, и значения, близкие к нулю, лучше. MSE является вторым моментом ошибки (относительно источника) и, таким образом, включает в себя как дисперсию оценки, так и ее смещение.
Шаги, чтобы найти MSE
- Найти уравнение для линии регрессии.
(1)
- Вставьте значения X в уравнение, найденное на шаге 1, чтобы получить соответствующие значения Y, т.е.
(2)
- Теперь вычтите новые значения Y (т.е.
) из исходных значений Y. Таким образом, найденные значения являются ошибочными терминами. Это также известно как вертикальное расстояние данной точки от линии регрессии.
(3)
- Возведите в квадрат ошибки, найденные в шаге 3.
(4)
- Подведите итог всех квадратов.
(5)
- Разделите значение, найденное на шаге 5, на общее количество наблюдений.
(6)
Пример:
Рассмотрим данные точки: (1,1), (2,1), (3,2), (4,2), (5,4)
Вы можете использовать этот онлайн калькулятор, чтобы найти уравнение / линию регрессии.
Уравнение линии регрессии: Y = 0,7X — 0,1
| X | Y | |
|---|---|---|
| 1 | 1 | 0.6 |
| 2 | 1 | 1.29 |
| 3 | 2 | 1.99 |
| 4 | 2 | 2.69 |
| 5 | 4 | 3.4 |
Теперь, используя формулу, найденную для MSE на шаге 6 выше, мы можем получить MSE = 0.21606
MSE, используя scikit — учиться:
from sklearn.metrics import mean_squared_error
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
mean_squared_error(Y_true,Y_pred)
Output: 0.21606
MSE с использованием модуля Numpy:
import numpy as np
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
MSE = np.square(np.subtract(Y_true,Y_pred)).mean()
Output: 0.21606
Рекомендуемые посты:
- ML | Потеря журнала и средняя квадратическая ошибка
- ML | Математическое объяснение СКО и R-квадрата ошибки
- Ошибка NZEC в Python
- Python | Ошибка подтверждения
- Ошибка с плавающей точкой в Python
- Python | 404 Обработка ошибок во Flask
- Python | Запрос пароля во время выполнения и завершение с сообщением об ошибке
- Python | Индекс ненулевых элементов в списке Python
- Python | Конвертировать список в массив Python
- Важные различия между Python 2.x и Python 3.x с примерами
- Чтение файловоподобных объектов Python из C | питон
- Python | Объединить значения ключа Python в список
- Python | Сортировать словари Python по ключу или значению
- Python | Набор 4 (словарь, ключевые слова в Python)
- Python | Добавить запись в библиотеки Python
Python | Средняя квадратическая ошибка
0.00 (0%) 0 votes
- sklearn.metrics.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput=‘uniform_average’, squared=True)[source]¶
-
Mean squared error regression loss.
Read more in the User Guide.
- Parameters:
-
- y_truearray-like of shape (n_samples,) or (n_samples, n_outputs)
-
Ground truth (correct) target values.
- y_predarray-like of shape (n_samples,) or (n_samples, n_outputs)
-
Estimated target values.
- sample_weightarray-like of shape (n_samples,), default=None
-
Sample weights.
- multioutput{‘raw_values’, ‘uniform_average’} or array-like of shape (n_outputs,), default=’uniform_average’
-
Defines aggregating of multiple output values.
Array-like value defines weights used to average errors.- ‘raw_values’ :
-
Returns a full set of errors in case of multioutput input.
- ‘uniform_average’ :
-
Errors of all outputs are averaged with uniform weight.
- squaredbool, default=True
-
If True returns MSE value, if False returns RMSE value.
- Returns:
-
- lossfloat or ndarray of floats
-
A non-negative floating point value (the best value is 0.0), or an
array of floating point values, one for each individual target.
Examples
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred, squared=False) 0.612... >>> y_true = [[0.5, 1],[-1, 1],[7, -6]] >>> y_pred = [[0, 2],[-1, 2],[8, -5]] >>> mean_squared_error(y_true, y_pred) 0.708... >>> mean_squared_error(y_true, y_pred, squared=False) 0.822... >>> mean_squared_error(y_true, y_pred, multioutput='raw_values') array([0.41666667, 1. ]) >>> mean_squared_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.825...
Examples using sklearn.metrics.mean_squared_error¶
Improve Article
Save Article
Improve Article
Save Article
In this article, we discussed the implementation of weighted mean square error using python.
Mean squared error is a vital statistical concept, that is nowadays widely used in Machine learning and Deep learning algorithm. Mean squared error is basically a measure of the average squared difference between the estimated values and the actual value. It is also called a mean squared deviation and is most of the time used to calibrate the accuracy of the predicted output. In this article, let us discuss a variety of mean squared errors called weighted mean square errors.
Weighted mean square error enables to provide more importance or additional weightage for a particular set of points (points of interest) when compared to others. When handling imbalanced data, a weighted mean square error can be a vital performance metric. Python provides a wide variety of packages to implement mean squared and weighted mean square at one go, here we can make use of simple functions to implement weighted mean squared error.
Formula to calculate the weighted mean square error:
Implementation of Weighted Mean Square Error
- For demonstration purposes let us create a sample data frame, with augmented actual and predicted values, as shown.
- Calculate the squared difference between actual and predicted values.
- Define the weights for each data point based on the importance
- Now, use the weights to calculate the weighted mean square error as shown
Code Implementation:
Python3
import pandas as pd
import numpy as np
import random
d = {'Actual': np.arange(0, 20, 2)*np.sin(2),
'Predicted': np.arange(0, 20, 2)*np.cos(2)}
data = pd.DataFrame(data=d)
y_weights = np.arange(2, 4, 0.2)
diff = (data['Actual']-data['Predicted'])**2
weighted_mean_sq_error = np.sum(diff * y_weights) / np.sum(y_weights)
Output:
Weighted Mean Square Error
Let us cross verify the result with the result of the scikit-learn package. to verify the correctness,
Code:
Python3
weighted_mean_sq_error_sklearn = np.average(
(data['Actual']-data['Predicted'])**2, axis=0, weights=y_weights)
weighted_mean_sq_error_sklearn
Output:
verify the result
Improve Article
Save Article
Improve Article
Save Article
In this article, we discussed the implementation of weighted mean square error using python.
Mean squared error is a vital statistical concept, that is nowadays widely used in Machine learning and Deep learning algorithm. Mean squared error is basically a measure of the average squared difference between the estimated values and the actual value. It is also called a mean squared deviation and is most of the time used to calibrate the accuracy of the predicted output. In this article, let us discuss a variety of mean squared errors called weighted mean square errors.
Weighted mean square error enables to provide more importance or additional weightage for a particular set of points (points of interest) when compared to others. When handling imbalanced data, a weighted mean square error can be a vital performance metric. Python provides a wide variety of packages to implement mean squared and weighted mean square at one go, here we can make use of simple functions to implement weighted mean squared error.
Formula to calculate the weighted mean square error:
Implementation of Weighted Mean Square Error
- For demonstration purposes let us create a sample data frame, with augmented actual and predicted values, as shown.
- Calculate the squared difference between actual and predicted values.
- Define the weights for each data point based on the importance
- Now, use the weights to calculate the weighted mean square error as shown
Code Implementation:
Python3
import pandas as pd
import numpy as np
import random
d = {'Actual': np.arange(0, 20, 2)*np.sin(2),
'Predicted': np.arange(0, 20, 2)*np.cos(2)}
data = pd.DataFrame(data=d)
y_weights = np.arange(2, 4, 0.2)
diff = (data['Actual']-data['Predicted'])**2
weighted_mean_sq_error = np.sum(diff * y_weights) / np.sum(y_weights)
Output:
Weighted Mean Square Error
Let us cross verify the result with the result of the scikit-learn package. to verify the correctness,
Code:
Python3
weighted_mean_sq_error_sklearn = np.average(
(data['Actual']-data['Predicted'])**2, axis=0, weights=y_weights)
weighted_mean_sq_error_sklearn
Output:
verify the result
Перевод
Ссылка на автора
Показатели эффективности прогнозирования по временным рядам дают сводку об умениях и возможностях модели прогноза, которая сделала прогнозы.
Есть много разных показателей производительности на выбор. Может быть непонятно, какую меру использовать и как интерпретировать результаты.
В этом руководстве вы узнаете показатели производительности для оценки прогнозов временных рядов с помощью Python.
Временные ряды, как правило, фокусируются на прогнозировании реальных значений, называемых проблемами регрессии. Поэтому показатели эффективности в этом руководстве будут сосредоточены на методах оценки реальных прогнозов.
После завершения этого урока вы узнаете:
- Основные показатели выполнения прогноза, включая остаточную ошибку прогноза и смещение прогноза.
- Вычисления ошибок прогноза временного ряда, которые имеют те же единицы, что и ожидаемые результаты, такие как средняя абсолютная ошибка.
- Широко используются вычисления ошибок, которые наказывают большие ошибки, такие как среднеквадратическая ошибка и среднеквадратичная ошибка.
Давайте начнем.
Ошибка прогноза (или остаточная ошибка прогноза)
ошибка прогноза рассчитывается как ожидаемое значение минус прогнозируемое значение.
Это называется остаточной ошибкой прогноза.
forecast_error = expected_value - predicted_valueОшибка прогноза может быть рассчитана для каждого прогноза, предоставляя временной ряд ошибок прогноза.
В приведенном ниже примере показано, как можно рассчитать ошибку прогноза для серии из 5 прогнозов по сравнению с 5 ожидаемыми значениями. Пример был придуман для демонстрационных целей.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
print('Forecast Errors: %s' % forecast_errors)При выполнении примера вычисляется ошибка прогноза для каждого из 5 прогнозов. Список ошибок прогноза затем печатается.
Forecast Errors: [-0.2, 0.09999999999999998, -0.1, -0.09999999999999998, -0.2]Единицы ошибки прогноза совпадают с единицами прогноза. Ошибка прогноза, равная нулю, означает отсутствие ошибки или совершенный навык для этого прогноза.
Средняя ошибка прогноза (или ошибка прогноза)
Средняя ошибка прогноза рассчитывается как среднее значение ошибки прогноза.
mean_forecast_error = mean(forecast_error)Ошибки прогноза могут быть положительными и отрицательными. Это означает, что при вычислении среднего из этих значений идеальная средняя ошибка прогноза будет равна нулю.
Среднее значение ошибки прогноза, отличное от нуля, указывает на склонность модели к превышению прогноза (положительная ошибка) или занижению прогноза (отрицательная ошибка). Таким образом, средняя ошибка прогноза также называется прогноз смещения,
Ошибка прогноза может быть рассчитана непосредственно как среднее значение прогноза. В приведенном ниже примере показано, как среднее значение ошибок прогноза может быть рассчитано вручную.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
bias = sum(forecast_errors) * 1.0/len(expected)
print('Bias: %f' % bias)При выполнении примера выводится средняя ошибка прогноза, также известная как смещение прогноза.
Bias: -0.100000Единицы смещения прогноза совпадают с единицами прогнозов. Прогнозируемое смещение нуля или очень маленькое число около нуля показывает несмещенную модель.
Средняя абсолютная ошибка
средняя абсолютная ошибка или MAE, рассчитывается как среднее значение ошибок прогноза, где все значения прогноза вынуждены быть положительными.
Заставить ценности быть положительными называется сделать их абсолютными. Это обозначено абсолютной функциейабс ()или математически показано как два символа канала вокруг значения:| Значение |,
mean_absolute_error = mean( abs(forecast_error) )кудаабс ()делает ценности позитивными,forecast_errorодна или последовательность ошибок прогноза, иимею в виду()рассчитывает среднее значение.
Мы можем использовать mean_absolute_error () функция из библиотеки scikit-learn для вычисления средней абсолютной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_absolute_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mae = mean_absolute_error(expected, predictions)
print('MAE: %f' % mae)При выполнении примера вычисляется и выводится средняя абсолютная ошибка для списка из 5 ожидаемых и прогнозируемых значений.
MAE: 0.140000Эти значения ошибок приведены в исходных единицах прогнозируемых значений. Средняя абсолютная ошибка, равная нулю, означает отсутствие ошибки.
Средняя квадратическая ошибка
средняя квадратическая ошибка или MSE, рассчитывается как среднее значение квадратов ошибок прогноза. Возведение в квадрат значений ошибки прогноза заставляет их быть положительными; это также приводит к большему количеству ошибок.
Квадратные ошибки прогноза с очень большими или выбросами возводятся в квадрат, что, в свою очередь, приводит к вытягиванию среднего значения квадратов ошибок прогноза, что приводит к увеличению среднего квадрата ошибки. По сути, оценка дает худшую производительность тем моделям, которые делают большие неверные прогнозы.
mean_squared_error = mean(forecast_error^2)Мы можем использовать mean_squared_error () функция из scikit-learn для вычисления среднеквадратичной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_squared_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
print('MSE: %f' % mse)При выполнении примера вычисляется и выводится среднеквадратическая ошибка для списка ожидаемых и прогнозируемых значений.
MSE: 0.022000Значения ошибок приведены в квадратах от предсказанных значений. Среднеквадратичная ошибка, равная нулю, указывает на совершенное умение или на отсутствие ошибки.
Среднеквадратическая ошибка
Средняя квадратичная ошибка, описанная выше, выражается в квадратах единиц прогнозов.
Его можно преобразовать обратно в исходные единицы прогнозов, взяв квадратный корень из среднего квадрата ошибки Это называется среднеквадратичная ошибка или RMSE.
rmse = sqrt(mean_squared_error)Это можно рассчитать с помощьюSQRT ()математическая функция среднего квадрата ошибки, рассчитанная с использованиемmean_squared_error ()функция scikit-learn.
from sklearn.metrics import mean_squared_error
from math import sqrt
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)При выполнении примера вычисляется среднеквадратичная ошибка.
RMSE: 0.148324Значения ошибок RMES приведены в тех же единицах, что и прогнозы. Как и в случае среднеквадратичной ошибки, среднеквадратическое отклонение, равное нулю, означает отсутствие ошибки.
Дальнейшее чтение
Ниже приведены некоторые ссылки для дальнейшего изучения показателей ошибки прогноза временных рядов.
- Раздел 3.3 Измерение прогнозирующей точности, Практическое прогнозирование временных рядов с помощью R: практическое руководство,
- Раздел 2.5 Оценка точности прогноза, Прогнозирование: принципы и практика
- scikit-Learn Metrics API
- Раздел 3.3.4. Метрики регрессии, scikit-learn API Guide
Резюме
В этом руководстве вы обнаружили набор из 5 стандартных показателей производительности временных рядов в Python.
В частности, вы узнали:
- Как рассчитать остаточную ошибку прогноза и как оценить смещение в списке прогнозов.
- Как рассчитать среднюю абсолютную ошибку прогноза, чтобы описать ошибку в тех же единицах, что и прогнозы.
- Как рассчитать широко используемые среднеквадратические ошибки и среднеквадратичные ошибки для прогнозов.
Есть ли у вас какие-либо вопросы о показателях эффективности прогнозирования временных рядов или об этом руководстве?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
In this article, we are going to learn how to calculate the mean squared error in python? We are using two python libraries to calculate the mean squared error. NumPy and sklearn are the libraries we are going to use here. Also, we will learn how to calculate without using any module.
MSE is also useful for regression problems that are normally distributed. It is the mean squared error. So the squared error between the predicted values and the actual values. The summation of all the data points of the square difference between the predicted and actual values is divided by the no. of data points.
Where Yi and Ŷi represent the actual values and the predicted values, the difference between them is squared.
Derivation of Mean Squared Error
First to find the regression line for the values (1,3), (2,2), (3,6), (4,1), (5,5). The regression value for the value is y=1.6+0.4x. Next to find the new Y values. The new values for y are tabulated below.
| Given x value | Calculating y value | New y value |
|---|---|---|
| 1 | 1.6+0.4(1) | 2 |
| 2 | 1.6+0.4(2) | 2.4 |
| 3 | 1.6+0.4(3) | 2.8 |
| 4 | 1.6+0.4(4) | 3.2 |
| 5 | 1.6+0.4(5) | 3.6 |
Now to find the error ( Yi – Ŷi )
We have to square all the errors
By adding all the errors we will get the MSE
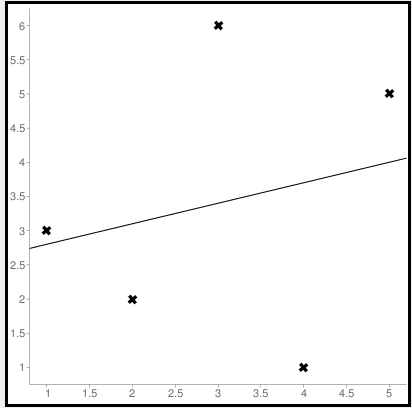
Line regression graph
Let us consider the values (1,3), (2,2), (3,6), (4,1), (5,5) to plot the graph.
The straight line represents the predicted value in this graph, and the points represent the actual data. The difference between this line and the points is squared, known as mean squared error.
Also, Read | How to Calculate Square Root in Python
To get the Mean Squared Error in Python using NumPy
import numpy as np true_value_of_y= [3,2,6,1,5] predicted_value_of_y= [2.0,2.4,2.8,3.2,3.6] MSE = np.square(np.subtract(true_value_of_y,predicted_value_of_y)).mean() print(MSE)
Importing numpy library as np. Creating two variables. true_value_of_y holds an original value. predicted_value_of_y holds a calculated value. Next, giving the formula to calculate the mean squared error.
Output
3.6400000000000006
To get the MSE using sklearn
sklearn is a library that is used for many mathematical calculations in python. Here we are going to use this library to calculate the MSE
Syntax
sklearn.metrices.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared=True)
Parameters
- y_true – true value of y
- y_pred – predicted value of y
- sample_weight
- multioutput
- raw_values
- uniform_average
- squared
Returns
Mean squared error.
Code
from sklearn.metrics import mean_squared_error true_value_of_y= [3,2,6,1,5] predicted_value_of_y= [2.0,2.4,2.8,3.2,3.6] mean_squared_error(true_value_of_y,predicted_value_of_y) print(mean_squared_error(true_value_of_y,predicted_value_of_y))
From sklearn.metrices library importing mean_squared_error. Creating two variables. true_value_of_y holds an original value. predicted_value_of_y holds a calculated value. Next, giving the formula to calculate the mean squared error.
Output
3.6400000000000006
Calculating Mean Squared Error Without Using any Modules
true_value_of_y = [3,2,6,1,5]
predicted_value_of_y = [2.0,2.4,2.8,3.2,3.6]
summation_of_value = 0
n = len(true_value_of_y)
for i in range (0,n):
difference_of_value = true_value_of_y[i] - predicted_value_of_y[i]
squared_difference = difference_of_value**2
summation_of_value = summation_of_value + squared_difference
MSE = summation_of_value/n
print ("The Mean Squared Error is: " , MSE)
Declaring the true values and the predicted values to two different variables. Initializing the variable summation_of_value is zero to store the values. len() function is useful to check the number of values in true_value_of_y. Creating for loop to iterate. Calculating the difference between true_value and the predicted_value. Next getting the square of the difference. Adding all the squared differences, we will get the MSE.
Output
The Mean Squared Error is: 3.6400000000000006
Calculate Mean Squared Error Using Negative Values
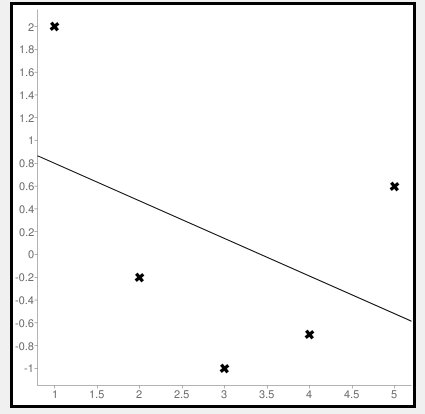
Now let us consider some negative values to calculate MSE. The values are (1,2), (3,-1), (5,0.6), (4,-0.7), (2,-0.2). The regression line equation is y=1.13-0.33x
The line regression graph for this value is:
New y values for this will be:
| Given x value | Calculating y value | New y value |
|---|---|---|
| 1 | 1.13-033(1) | 0.9 |
| 3 | 1.13-033(3) | 0.1 |
| 5 | 1.13-033(5) | -0.4 |
| 4 | 1.13-033(4) | -0.1 |
| 2 | 1.13-033(2) | 0.6 |
Code
>>> from sklearn.metrics import mean_squared_error >>> y_true = [2,-1,0.6,-0.7,-0.2] >>> y_pred = [0.9,0.1,-0.4,-0.1,0.6] >>> mean_squared_error(y_true, y_pred)
First, importing a module. Declaring values to the variables. Here we are using negative value to calculate. Using the mean_squared_error module, we are calculating the MSE.
Output
0.884
Bonus: Gradient Descent
Gradient Descent is used to find the local minimum of the functions. In this case, the functions need to be differentiable. The basic idea is to move in the direction opposite from the derivate at any point.
The following code works on a set of values that are available on the Github repository.
Code:
#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
def compute_error(b, m, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (m * x + b)) ** 2
return totalError / float(len(points))
def gradient_step(
b_current,
m_current,
points,
learningRate,
):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2 / N) * (y - (m_current * x + b_current))
m_gradient += -(2 / N) * x * (y - (m_current * x + b_current))
new_b = b_current - learningRate * b_gradient
new_m = m_current - learningRate * m_gradient
return [new_b, new_m]
def gradient_descent_runner(
points,
starting_b,
starting_m,
learning_rate,
iterations,
):
b = starting_b
m = starting_m
for i in range(iterations):
(b, m) = gradient_step(b, m, array(points), learning_rate)
return [b, m]
def main():
points = genfromtxt('data.csv', delimiter=',')
learning_rate = 0.00001
initial_b = 0
initial_m = 0
iterations = 10000
print('Starting gradient descent at b = {0}, m = {1}, error = {2}'.format(initial_b,
initial_m, compute_error(initial_b, initial_m, points)))
print('Running...')
[b, m] = gradient_descent_runner(points, initial_b, initial_m,
learning_rate, iterations)
print('After {0} iterations b = {1}, m = {2}, error = {3}'.format(iterations,
b, m, compute_error(b, m, points)))
if __name__ == '__main__':
main()
Output:
Starting gradient descent at b = 0, m = 0, error = 5671.844671124282
Running...
After 10000 iterations b = 0.11558415090685024, m = 1.3769012288001614, error = 212.262203123587941. What is the pip command to install numpy?
pip install numpy
2. What is the pip command to install sklearn.metrices library?
pip install sklearn
3. What is the expansion of MSE?
The expansion of MSE is Mean Squared Error.
Conclusion
In this article, we have learned about the mean squared error. It is effortless to calculate. This is useful for loss function for least squares regression. The formula for the MSE is easy to memorize. We hope this article is handy and easy to understand.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Время на прочтение
4 мин
Количество просмотров 3.7K

Функции потерь Python являются важной частью моделей машинного обучения. Эти функции показывают, насколько сильно предсказанный моделью результат отличается от фактического.
Существует несколько способов вычислить эту разницу. В этом материале мы рассмотрим некоторые из наиболее распространенных функций потерь.
Ниже будут рассмотрены следующие четыре функции потерь.
-
Среднеквадратическая ошибка
-
Среднеквадратическая ошибка
-
Средняя абсолютная ошибка
-
Кросс-энтропийные потери
Из этих четырех функций потерь первые три применяются к модели классификации.
1. Среднеквадратическая ошибка (MSE)
Среднеквадратичная ошибка (MSE) рассчитывается как среднее значение квадратов разностей между прогнозируемыми и фактически наблюдаемыми значениями. Математически это можно выразить следующим образом:
Реализация MSE на языке Python выглядит следующим образом:
import numpy as np # импортируем библиотеку numpy
def mean_squared_error(act, pred): # функция
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
differences_squared = diff ** 2 # возводим в квадрат (чтобы избавиться от отрицательных значений)
mean_diff = differences_squared.mean() # находим среднее значение
return mean_diff
act = np.array([1.1,2,1.7]) # создаем список актуальных значений
pred = np.array([1,1.7,1.5]) # список прогнозируемых значений
print(mean_squared_error(act,pred))
Выход :
0.04666666666666667Вы также можете использовать mean_squared_error из sklearn для расчета MSE. Вот как работает функция:
from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred)
Выход :
0.04666666666666667
2. Корень среднеквадратической ошибки (RMSE)
Итак, ранее, для того, чтобы найти действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями (там могли быть положительные и отрицательные значения), мы возводили их в квадрат (для того чтобы отрицательные значения участвовали в расчетах в полной мере). Это была среднеквадратичная ошибка (MSE).
Корень среднеквадратической ошибки (RMSE) мы используем для того чтобы избавиться от квадратной степени, в которую мы ранее возвели действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями. Математически мы можем представить это следующим образом:
Реализация Python для RMSE выглядит следующим образом:
import numpy as np
def root_mean_squared_error(act, pred):
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
differences_squared = diff ** 2 # возводим в квадрат
mean_diff = differences_squared.mean() # находим среднее значение
rmse_val = np.sqrt(mean_diff) # извлекаем квадратный корень
return rmse_val
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
print(root_mean_squared_error(act,pred))
Выход :
0.21602468994692867
Вы также можете использовать mean_squared_error из sklearn для расчета RMSE. Давайте посмотрим, как реализовать RMSE, используя ту же функцию:
from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred, squared = False) #Если установлено значение False, функция возвращает значение RMSE.
Выход :
0.21602468994692867
Если для параметра squared установлено значение True, функция возвращает значение MSE. Если установлено значение False, функция возвращает значение RMSE.
3. Средняя абсолютная ошибка (MAE)
Средняя абсолютная ошибка (MAE) рассчитывается как среднее значение абсолютной разницы между прогнозами и фактическими наблюдениями. Математически мы можем представить это следующим образом:
Реализация Python для MAE выглядит следующим образом:
import numpy as np
def mean_absolute_error(act, pred): #
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
abs_diff = np.absolute(diff) # находим абсолютную разность между прогнозами и фактическими наблюдениями.
mean_diff = abs_diff.mean() # находим среднее значение
return mean_diff
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act,pred)
Выход :
0.20000000000000004
Вы также можете использовать mean_absolute_error из sklearn для расчета MAE.
from sklearn.metrics import mean_absolute_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act, pred)
Выход :
0.20000000000000004
4. Функция потерь перекрестной энтропии в Python
Функция потерь перекрестной энтропии также известна как отрицательная логарифмическая вероятность. Это чаще всего используется для задач классификации. Проблема классификации — это проблема, в которой вы классифицируете пример как принадлежащий к одному из более чем двух классов.
Давайте посмотрим, как вычислить ошибку в случае проблемы бинарной классификации.
Давайте рассмотрим проблему классификации, когда модель пытается провести классификацию между собакой и кошкой.
Код Python для поиска ошибки приведен ниже.
from sklearn.metrics import log_loss
log_loss(["Dog", "Cat", "Cat", "Dog"],[[.1, .9], [.9, .1], [.8, .2], [.35, .65]])
Выход :
0.21616187468057912
Мы используем метод log_loss из sklearn.
Первый аргумент в вызове функции — это список правильных меток классов для каждого входа. Второй аргумент — это список вероятностей, предсказанных моделью.
Вероятности представлены в следующем формате:
[P(dog), P(cat)]
Заключение
Это руководство было посвящено функциям потерь в Python. Мы рассмотрели различные функции потерь как для задач регрессии, так и для задач классификации. Надеюсь, вам понравился материал, ведь все было достаточно легко и понятно!
Кстати, для тех, кто хотел бы пойти дальше в изучении функций потерь, мы предлагаем разобрать одну вот такую — это очень интересная функция потерь Triplet Loss в Python (функцию тройных потерь), которую для вас любезно подготовил автор.
17 авг. 2022 г.
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогноза модели, является MSE , что означает среднеквадратичную ошибку.Он рассчитывается как:
MSE = (1/n) * Σ(факт – прогноз) 2
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
Чем ниже значение MSE, тем лучше модель способна точно прогнозировать значения.
Как рассчитать MSE в Excel
Чтобы рассчитать MSE в Excel, мы можем выполнить следующие шаги:
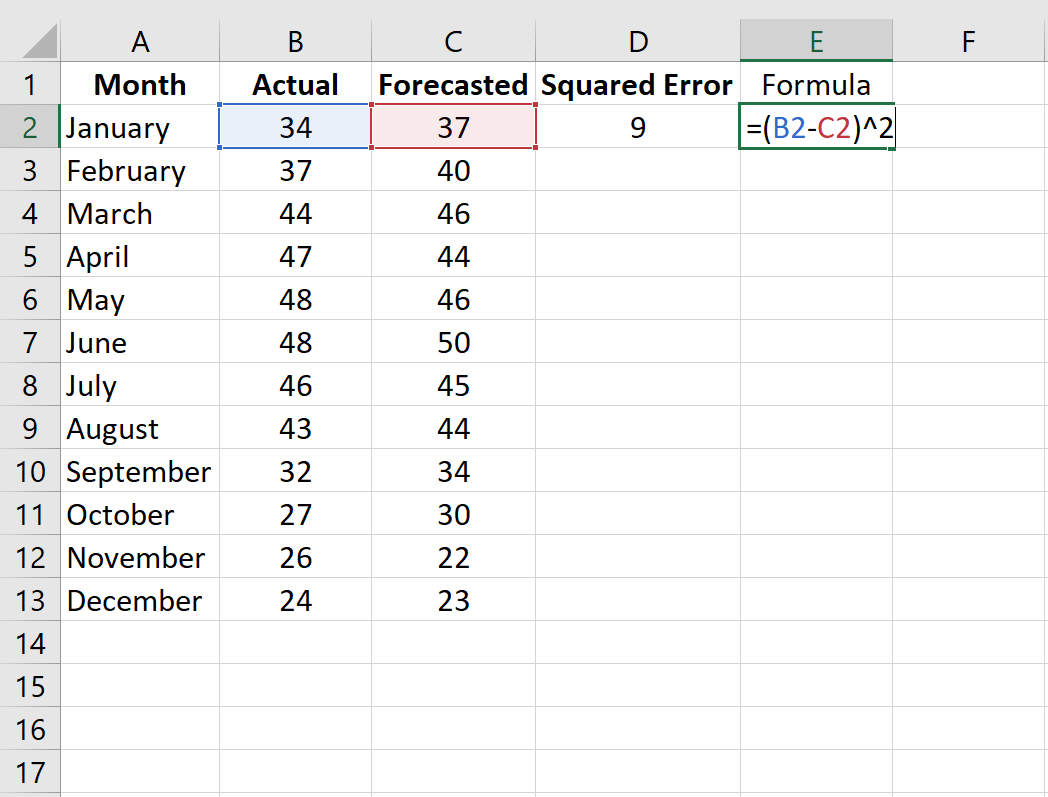
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
Шаг 2: Рассчитайте квадрат ошибки для каждой строки.
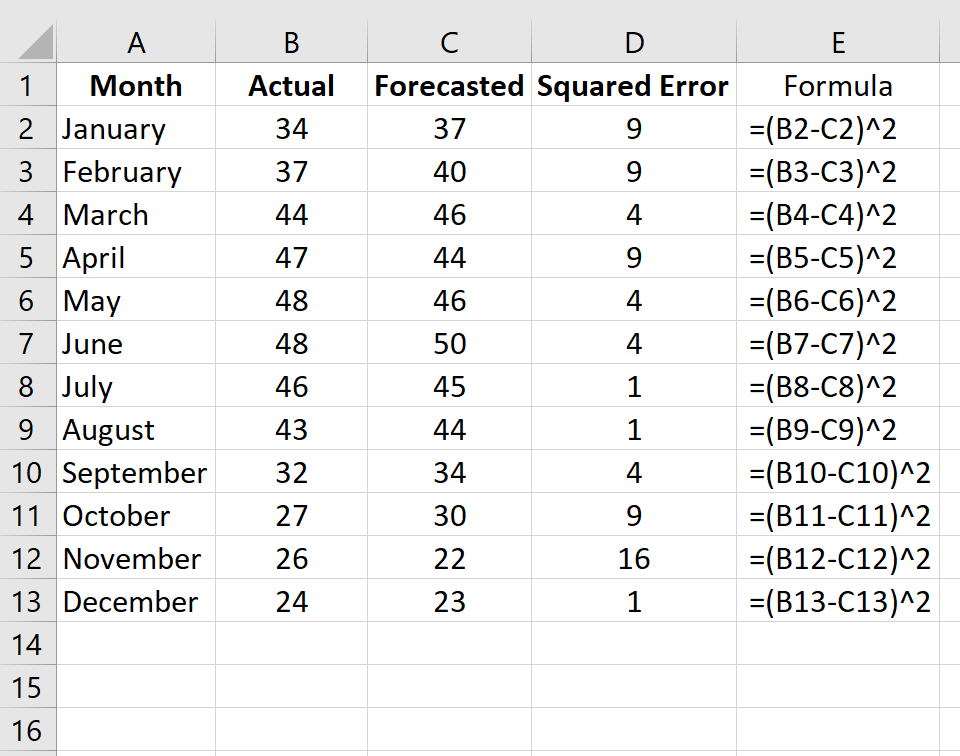
Напомним, что квадрат ошибки рассчитывается как: (факт – прогноз) 2.Мы будем использовать эту формулу для расчета квадрата ошибки для каждой строки.
Столбец D отображает квадрат ошибки, а столбец E показывает формулу, которую мы использовали:
Повторите эту формулу для каждой строки:
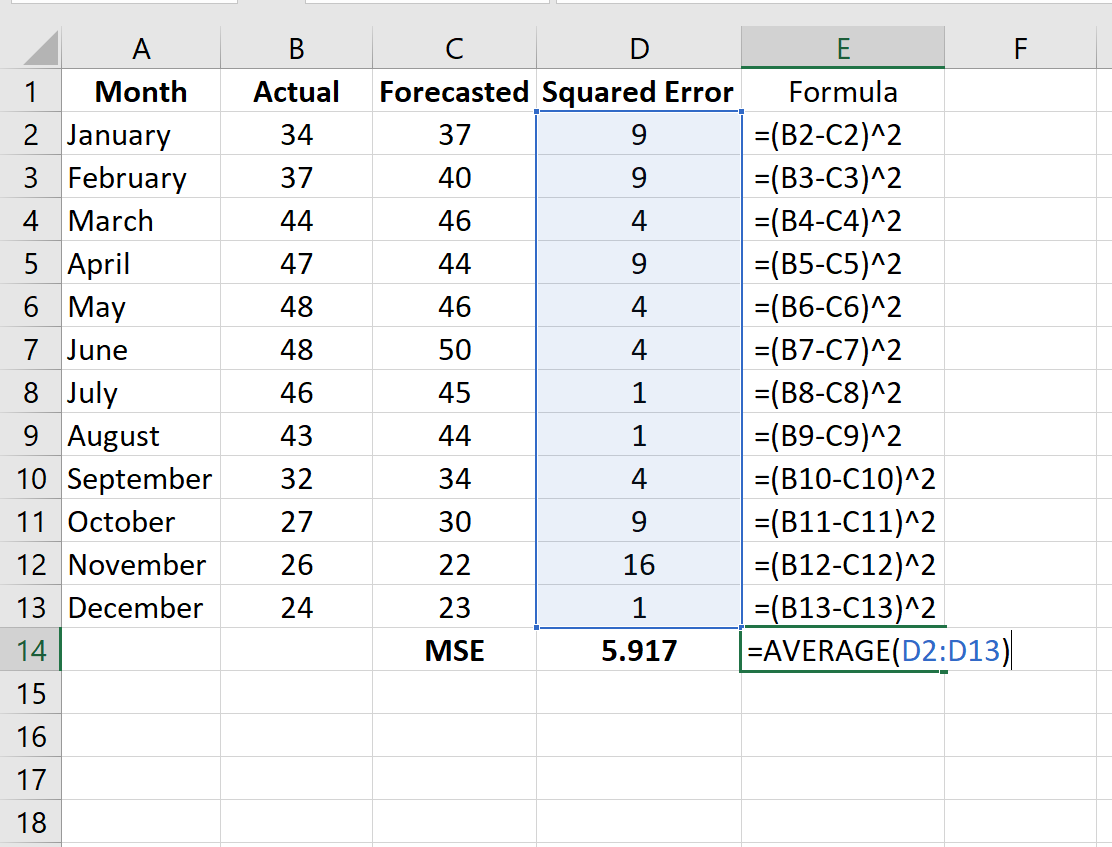
Шаг 3: Рассчитайте среднеквадратичную ошибку.
Рассчитайте MSE, просто найдя среднее значение в столбце D:
MSE этой модели оказывается равным 5,917 .
Дополнительные ресурсы
Двумя другими популярными показателями, используемыми для оценки точности модели, являются MAD — среднее абсолютное отклонение и MAPE — средняя абсолютная процентная ошибка. В следующих руководствах объясняется, как рассчитать эти показатели в Excel:
Как рассчитать среднее абсолютное отклонение (MAD) в Excel
Как рассчитать среднюю абсолютную ошибку в процентах (MAPE) в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
В большинстве описаний среднеквадратичной ошибки (mean square errore, MSE) упускается один важнейший нюанс: метрики и функции потерь — это не совсем одно и то же. Для оценки и оптимизации производительности модели в машинном обучении нужны две отдельные функции потерь. MSE может быть либо тем, либо другим, либо третьим — выбор за исследователем.
Чтобы было понятнее, что имеется в виду под оценкой производительности и оптимизацией, вместо отвлеченных рассуждений обратимся к конкретным примерам. Для демонстрации будем использовать среднеквадратичную ошибку (MSE), но имейте в виду: MSE — это полезная метрика, но не панацея. Итак, погрузимся в тему!
https://t.me/python_job_interview
Что такое MSE?
Среднеквадратичная ошибка (MSE) — одна из множества метрик, которые используются для оценки эффективности модели. Для расчета MSE необходимо возвести в квадрат количество обнаруженных ошибок и найти среднее значение.
Зачем вычислять MSE?
Это можно сделать для 2 целей.
- Оценка производительности — визуальное определение того, насколько хорошо работает модель. Другими словами, это возможность быстро понять, с чем предстоит работать.
- Оптимизация модели позволяет выяснить, достигнуто ли наилучшее из возможных соответствий или же требуются улучшения. Другими словами, определить, какая модель максимально подходит для работы с выбранными точками данных.
Если вы предпочитаете учиться на видео, переходите по этой ссылке (англ. язык):
https://youtube.com/watch?v=j8VjRnaHRBM%3Ffeature%3Doembed
Оценка производительности (метрика)
Цель оценки производительности заключается в том, чтобы человек мог составить представление об эффективности модели.
Метрика производительности показывает, насколько хорошо работает модель. К слову, “модель” — это просто популярное слово для “инструкции”, а инструкция “хороша”, если при введении исходных данных обеспечивает результат, близкий к ожидаемому. Метрика позволяет оценить, насколько близки результаты модели к ожидаемым (причем исследователь сам должен определить, что значит “близки”). MSE — это всего лишь одна из многих возможных метрик.
ЕСЛИ МОДЕЛЬ СОВЕРШЕННА, MSE = 0.
Откуда берется MSE? Мы вычисляем эту метрику, находя ошибки, которые допустила модель. Поэтому она является функцией ошибочности. Чем ниже MSE, тем лучше работает модель. Когда ошибок совсем нет, MSE = 0. Беглый взгляд на MSE дает представление о том, насколько хорошо модель соответствует или не соответствует данным.
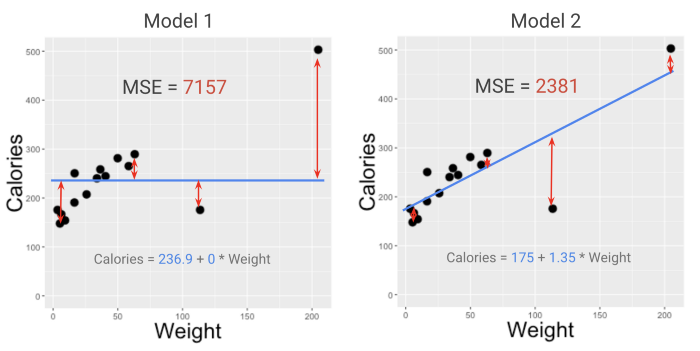
Взглянув на MSE двух моделей из примера со смузи в моем курсе (смотрите видео здесь), можно легко определить фаворита. Модель с меньшим MSE (2381, а не 7157) лучше подходит к данным. Но что означают эти цифры?
МЕТРИКИ ДОЛЖНЫ БЫТЬ РАССЧИТАНЫ ТАК, ЧТОБЫ ИМЕТЬ СМЫСЛ ДЛЯ ЛЮДЕЙ И ЭФФЕКТИВНО ПЕРЕДАВАТЬ ИНФОРМАЦИЮ.
Приведенные выше значения MSE не очень удобны для осмысления. Это проблема, если нужна достаточно информативная метрика. Метрики должны быть рассчитаны так, чтобы иметь смысл для людей и эффективно передавать информацию. Можно ли улучшить значение MSE?
Да, конечно. Вот вам RMSE!
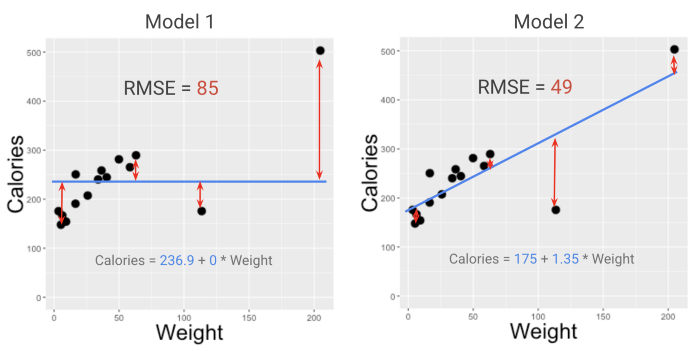
Для оценки производительности модели (на глаз) RMSE часто является лучшим выбором, чем MSE. RMSE — это просто корень квадратный из MSE (R означает root, “корень”).
При поиске более подходящей метрики, исследователи предпочитают RMSE, потому что она переводит MSE в более понятную для человека шкалу. Это не совсем то, что покажет, “насколько велики наши ошибки в среднем”, но достаточно близко к тому, что можно принять во внимание, чтобы предотвратить риски.
ИССЛЕДОВАТЕЛИ ПРЕДПОЧИТАЮТ RMSE, ПОТОМУ ЧТО ЭТА МЕТРИКА ПЕРЕВОДИТ MSE В БОЛЕЕ УДОБНУЮ ДЛЯ ВОСПРИЯТИЯ ШКАЛУ.
Но что если вы настаиваете на еще более точной метрике — той, что даст корректное представление о среднем размере ошибок? В таком случае можно воспользоваться метрикой, называемой средним абсолютным отклонением или MAD (mean absolute deviation). Иногда ее также называют MAE (mean absolute error).
Чтобы вычислить MAD, нужно просто игнорировать знаки (“+” и “-”) перед значениями всех ошибок и найти среднее значение. В отличие от RMSE, MAD является абсолютным выражением среднего размера ошибок.
MAD ПОКАЗЫВАЕТ, НАСКОЛЬКО ОШИБОЧНА МОДЕЛЬ В СРЕДНЕМ.
MAD — лучшая метрика производительности по сравнению с RMSE, потому что ее легче понять и связать с процессом оптимизации. Она более значима для исследователя и понятнее для человека. Но подходит ли она для машин?
Оптимизация модели (функция потерь)
Вторая цель использования MSE — это оптимизация модели. Здесь в дело вступают функции потерь.
Функция потерь — это формула, которую алгоритм машинного обучения пытается минимизировать на этапе оптимизации/подгонки модели. Разложим это понятие по полочкам.
https://youtube.com/watch?v=I2Ek0icqMXE%3Ffeature%3Doembed
Фрагмент из курса MFML для тех, кому нужно освежить в памяти понятие оптимизации модели
Предположим, планируется использование одного из самых простых алгоритмов МО — OLS (ordinary least squares, метод простых наименьших квадратов). Это означает, что модель, с которой предстоит работать, обладает простейшей формой — прямой линией.
Линия, проведенная через данные, имеет наклон и точку пересечения с координатной осью. Установка этих двух параметров зависит от вас!
Y = ТОЧКА ПЕРЕСЕЧЕНИЯ + НАКЛОН * X
Рациональный подход требует выбора модели, которая лучше всего подходит для работы с исходными данными. Другими словами, оптимальным выбором будет модель, которая максимально адаптирована к исходным данным. Следовательно, нужна функция оценки, которая становится больше, когда модель подходит хуже, и меньше — в обратном случае.
Эта функция позволит изменять параметры точки пересечения и наклона, наблюдая за изменением оценки. Такую функцию оценки называют “функцией потерь” — чем больше потери, тем хуже модель.
Ошибочность? Заядлые перфекционисты уверены: ошибки — это плохо. Поэтому выразим ошибочность в терминах наших ошибок. Любая функция потерь, которая становится больше, когда больше ошибок, подойдет? Технически — да. Практически — нет.
Вот как это работает, если выбрать MSE в качестве функции потерь: цель оптимизации — найти точку пересечения и наклон, которые дают как можно более низкое значение MSE. Как это происходит, показано в видео ниже.
https://youtube.com/watch?v=j8VjRnaHRBM%3Ffeature%3Doembed
Не стоит искать оптимальное значение MSE методом проб и ошибок (перебирание различных комбинаций наклона и точки пересечения вручную — медленный и скучный процесс).
Получить мгновенный результат позволят вычисления или алгоритм оптимизации, которые подскажут, какими должны быть необходимые параметры. Что касается алгоритмов оптимизации, то вам, скорей всего, не придется разрабатывать их с нуля. Наверняка будет возможность импортировать те, которые кто-то другой уже создал. Чаще всего с MSE очень удобно работать.
Что же происходит “за кулисами”? Есть формула, которая указывает, где именно должна располагаться линия, чтобы значение MSE было минимальным. Запускаемому коду даже не нужно постепенно приближаться к решению — он просто использует эту формулу, чтобы точно указать наклон и точку пересечения, наилучшие из возможных для работы линейной модели с данными.
источник
Просмотры: 1 277
Гораздо легче что-то измерить, чем понять, что именно вы измеряете
Джон Уильям Салливан
Задачи машинного обучения с учителем как правило состоят в восстановлении зависимости между парами (признаковое описание, целевая переменная) по данным, доступным нам для анализа. Алгоритмы машинного обучения (learning algorithm), со многими из которых вы уже успели познакомиться, позволяют построить модель, аппроксимирующую эту зависимость. Но как понять, насколько качественной получилась аппроксимация?
Почти наверняка наша модель будет ошибаться на некоторых объектах: будь она даже идеальной, шум или выбросы в тестовых данных всё испортят. При этом разные модели будут ошибаться на разных объектах и в разной степени. Задача специалиста по машинному обучению – подобрать подходящий критерий, который позволит сравнивать различные модели.
Перед чтением этой главы мы хотели бы ещё раз напомнить, что качество модели нельзя оценивать на обучающей выборке. Как минимум, это стоит делать на отложенной (тестовой) выборке, но, если вам это позволяют время и вычислительные ресурсы, стоит прибегнуть и к более надёжным способам проверки – например, кросс-валидации (о ней вы узнаете в отдельной главе).
Выбор метрик в реальных задачах
Возможно, вы уже участвовали в соревнованиях по анализу данных. На таких соревнованиях метрику (критерий качества модели) организатор выбирает за вас, и она, как правило, довольно понятным образом связана с результатами предсказаний. Но на практике всё бывает намного сложнее.
Например, мы хотим:
- решить, сколько коробок с бананами нужно завтра привезти в конкретный магазин, чтобы минимизировать количество товара, который не будет выкуплен и минимизировать ситуацию, когда покупатель к концу дня не находит желаемый продукт на полке;
- увеличить счастье пользователя от работы с нашим сервисом, чтобы он стал лояльным и обеспечивал тем самым стабильный прогнозируемый доход;
- решить, нужно ли направить человека на дополнительное обследование.
В каждом конкретном случае может возникать целая иерархия метрик. Представим, например, что речь идёт о стриминговом музыкальном сервисе, пользователей которого мы решили порадовать сгенерированными самодельной нейросетью треками – не защищёнными авторским правом, а потому совершенно бесплатными. Иерархия метрик могла бы иметь такой вид:
- Самый верхний уровень: будущий доход сервиса – невозможно измерить в моменте, сложным образом зависит от совокупности всех наших усилий;
- Медианная длина сессии, возможно, служащая оценкой радости пользователей, которая, как мы надеемся, повлияет на их желание продолжать платить за подписку – её нам придётся измерять в продакшене, ведь нас интересует реакция настоящих пользователей на новшество;
- Доля удовлетворённых качеством сгенерированной музыки асессоров, на которых мы потестируем её до того, как выставить на суд пользователей;
- Функция потерь, на которую мы будем обучать генеративную сеть.
На этом примере мы можем заметить сразу несколько общих закономерностей. Во-первых, метрики бывают offline и online (оффлайновыми и онлайновыми). Online метрики вычисляются по данным, собираемым с работающей системы (например, медианная длина сессии). Offline метрики могут быть измерены до введения модели в эксплуатацию, например, по историческим данным или с привлечением специальных людей, асессоров. Последнее часто применяется, когда метрикой является реакция живого человека: скажем, так поступают поисковые компании, которые предлагают людям оценить качество ранжирования экспериментальной системы еще до того, как рядовые пользователи увидят эти результаты в обычном порядке. На самом же нижнем этаже иерархии лежат оптимизируемые в ходе обучения функции потерь.
В данном разделе нас будут интересовать offline метрики, которые могут быть измерены без привлечения людей.
Функция потерь $neq$ метрика качества
Как мы узнали ранее, методы обучения реализуют разные подходы к обучению:
- обучение на основе прироста информации (как в деревьях решений)
- обучение на основе сходства (как в методах ближайших соседей)
- обучение на основе вероятностной модели данных (например, максимизацией правдоподобия)
- обучение на основе ошибок (минимизация эмпирического риска)
И в рамках обучения на основе минимизации ошибок мы уже отвечали на вопрос: как можно штрафовать модель за предсказание на обучающем объекте.
Во время сведения задачи о построении решающего правила к задаче численной оптимизации, мы вводили понятие функции потерь и, обычно, объявляли целевой функцией сумму потерь от предсказаний на всех объектах обучающей выборке.
Важно понимать разницу между функцией потерь и метрикой качества. Её можно сформулировать следующим образом:
-
Функция потерь возникает в тот момент, когда мы сводим задачу построения модели к задаче оптимизации. Обычно требуется, чтобы она обладала хорошими свойствами (например, дифференцируемостью).
-
Метрика – внешний, объективный критерий качества, обычно зависящий не от параметров модели, а только от предсказанных меток.
В некоторых случаях метрика может совпадать с функцией потерь. Например, в задаче регрессии MSE играет роль как функции потерь, так и метрики. Но, скажем, в задаче бинарной классификации они почти всегда различаются: в качестве функции потерь может выступать кросс-энтропия, а в качестве метрики – число верно угаданных меток (accuracy). Отметим, что в последнем примере у них различные аргументы: на вход кросс-энтропии нужно подавать логиты, а на вход accuracy – предсказанные метки (то есть по сути argmax логитов).
Бинарная классификация: метки классов
Перейдём к обзору метрик и начнём с самой простой разновидности классификации – бинарной, а затем постепенно будем наращивать сложность.
Напомним постановку задачи бинарной классификации: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_iin{0, 1}$ построить модель, которая по объекту $x$ предсказывает метку класса $f(x)in{0, 1}$.
Первым критерием качества, который приходит в голову, является accuracy – доля объектов, для которых мы правильно предсказали класс:
$$ color{#348FEA}{text{Accuracy}(y, y^{pred}) = frac{1}{N} sum_{i=1}^N mathbb{I}[y_i = f(x_i)]} $$
Или же сопряженная ей метрика – доля ошибочных классификаций (error rate):
$$text{Error rate} = 1 — text{Accuracy}$$
Познакомившись чуть внимательнее с этой метрикой, можно заметить, что у неё есть несколько недостатков:
- она не учитывает дисбаланс классов. Например, в задаче диагностики редких заболеваний классификатор, предсказывающий всем пациентам отсутствие болезни будет иметь достаточно высокую accuracy просто потому, что больных людей в выборке намного меньше;
- она также не учитывает цену ошибки на объектах разных классов. Для примера снова можно привести задачу медицинской диагностики: если ошибочный положительный диагноз для здорового больного обернётся лишь ещё одним обследованием, то ошибочно отрицательный вердикт может повлечь роковые последствия.
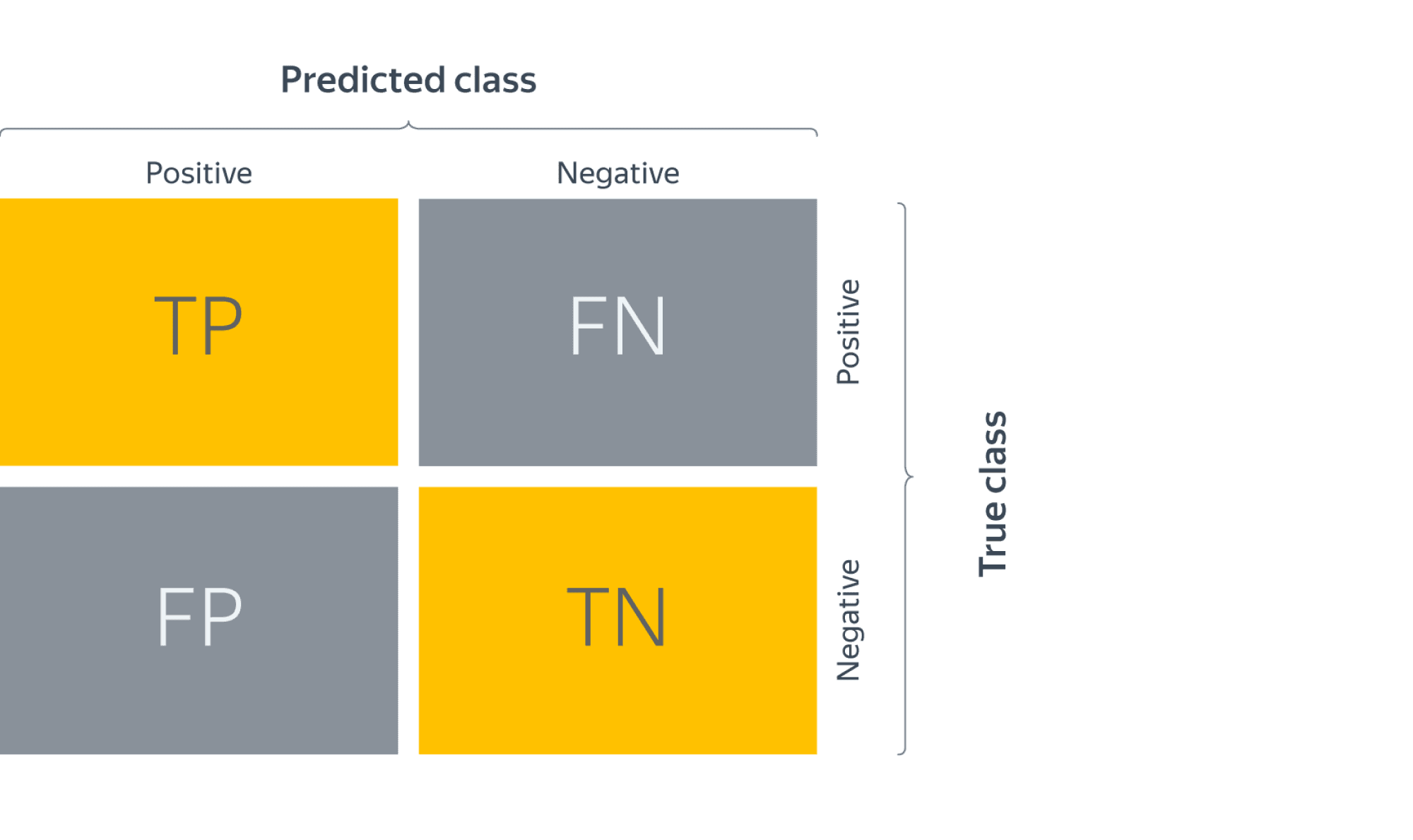
Confusion matrix (матрица ошибок)
Исторически задача бинарной классификации – это задача об обнаружении чего-то редкого в большом потоке объектов, например, поиск человека, больного туберкулёзом, по флюорографии. Или задача признания пятна на экране приёмника радиолокационной станции бомбардировщиком, представляющем угрозу охраняемому объекту (в противовес стае гусей).
Поэтому класс, который представляет для нас интерес, называется «положительным», а оставшийся – «отрицательным».
Заметим, что для каждого объекта в выборке возможно 4 ситуации:
- мы предсказали положительную метку и угадали. Будет относить такие объекты к true positive (TP) группе (true – потому что предсказали мы правильно, а positive – потому что предсказали положительную метку);
- мы предсказали положительную метку, но ошиблись в своём предсказании – false positive (FP) (false, потому что предсказание было неправильным);
- мы предсказали отрицательную метку и угадали – true negative (TN);
- и наконец, мы предсказали отрицательную метку, но ошиблись – false negative (FN). Для удобства все эти 4 числа изображают в виде таблицы, которую называют confusion matrix (матрицей ошибок):
Не волнуйтесь, если первое время эти обозначения будут сводить вас с ума (будем откровенны, даже профи со стажем в них порой путаются), однако логика за ними достаточно простая: первая часть названия группы показывает угадали ли мы с классом, а вторая – какой класс мы предсказали.
Пример
Попробуем воспользоваться введёнными метриками в боевом примере: сравним работу нескольких моделей классификации на Breast cancer wisconsin (diagnostic) dataset.
Объектами выборки являются фотографии биопсии грудных опухолей. С их помощью было сформировано признаковое описание, которое заключается в характеристиках ядер клеток (таких как радиус ядра, его текстура, симметричность). Положительным классом в такой постановке будут злокачественные опухоли, а отрицательным – доброкачественные.
Модель 1. Константное предсказание.
Решение задачи начнём с самого простого классификатора, который выдаёт на каждом объекте константное предсказание – самый часто встречающийся класс.
Зачем вообще замерять качество на такой модели?При разработке модели машинного обучения для проекта всегда желательно иметь некоторую baseline модель. Так нам будет легче проконтролировать, что наша более сложная модель действительно дает нам прирост качества.
from sklearn.datasets
import load_breast_cancer
the_data = load_breast_cancer()
# 0 – "доброкачественный"
# 1 – "злокачественный"
relabeled_target = 1 - the_data["target"]
from sklearn.model_selection import train_test_split
X = the_data["data"]
y = relabeled_target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.dummy import DummyClassifier
dc_mf = DummyClassifier(strategy="most_frequent")
dc_mf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
y_true = y_test y_pred = dc_mf.predict(X_test)
dc_mf_tn, dc_mf_fp, dc_mf_fn, dc_mf_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 0 | FN = 53 |
| Истинный класс — | FP = 0 | TN = 90 |
Обучающие данные таковы, что наш dummy-классификатор все объекты записывает в отрицательный класс, то есть признаёт все опухоли доброкачественными. Такой наивный подход позволяет нам получить минимальный штраф за FP (действительно, нельзя ошибиться в предсказании, если положительный класс вообще не предсказывается), но и максимальный штраф за FN (в эту группу попадут все злокачественные опухоли).
Модель 2. Случайный лес.
Настало время воспользоваться всем арсеналом моделей машинного обучения, и начнём мы со случайного леса.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)
y_true = y_test
y_pred = rfc.predict(X_test)
rfc_tn, rfc_fp, rfc_fn, rfc_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 52 | FN = 1 |
| Истинный класс — | FP = 4 | TN = 86 |
Можно сказать, что этот классификатор чему-то научился, т.к. главная диагональ матрицы стала содержать все объекты из отложенной выборки, за исключением 4 + 1 = 5 объектов (сравните с 0 + 53 объектами dummy-классификатора, все опухоли объявляющего доброкачественными).
Отметим, что вычисляя долю недиагональных элементов, мы приходим к метрике error rate, о которой мы говорили в самом начале:
$$text{Error rate} = frac{FP + FN}{ TP + TN + FP + FN}$$
тогда как доля объектов, попавших на главную диагональ – это как раз таки accuracy:
$$text{Accuracy} = frac{TP + TN}{ TP + TN + FP + FN}$$
Модель 3. Метод опорных векторов.
Давайте построим еще один классификатор на основе линейного метода опорных векторов.
Не забудьте привести признаки к единому масштабу, иначе численный алгоритм не сойдется к решению и мы получим гораздо более плохо работающее решающее правило. Попробуйте проделать это упражнение.
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() ss.fit(X_train)
scaled_linsvc = LinearSVC(C=0.01,random_state=42)
scaled_linsvc.fit(ss.transform(X_train), y_train)
y_true = y_test
y_pred = scaled_linsvc.predict(ss.transform(X_test))
tn, fp, fn, tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 50 | FN = 3 |
| Истинный класс — | FP = 1 | TN = 89 |
Сравним результаты
Легко заметить, что каждая из двух моделей лучше классификатора-пустышки, однако давайте попробуем сравнить их между собой. С точки зрения error rate модели практически одинаковы: 5/143 для леса против 4/143 для SVM.
Посмотрим на структуру ошибок чуть более внимательно: лес – (FP = 4, FN = 1), SVM – (FP = 1, FN = 3). Какая из моделей предпочтительнее?
Замечание: Мы сравниваем несколько классификаторов на основании их предсказаний на отложенной выборке. Насколько ошибки данных классификаторов зависят от разбиения исходного набора данных? Иногда в процессе оценки качества мы будем получать модели, чьи показатели эффективности будут статистически неразличимыми.
Пусть мы учли предыдущее замечание и эти модели действительно статистически значимо ошибаются в разную сторону. Мы встретились с очевидной вещью: на матрицах нет отношения порядка. Когда мы сравнивали dummy-классификатор и случайный лес с помощью Accuracy, мы всю сложную структуру ошибок свели к одному числу, т.к. на вещественных числах отношение порядка есть. Сводить оценку модели к одному числу очень удобно, однако не стоит забывать, что у вашей модели есть много аспектов качества.
Что же всё-таки важнее уменьшить: FP или FN? Вернёмся к задаче: FP – доля доброкачественных опухолей, которым ошибочно присваивается метка злокачественной, а FN – доля злокачественных опухолей, которые классификатор пропускает. В такой постановке становится понятно, что при сравнении выиграет модель с меньшим FN (то есть лес в нашем примере), ведь каждая не обнаруженная опухоль может стоить человеческой жизни.
Рассмотрим теперь другую задачу: по данным о погоде предсказать, будет ли успешным запуск спутника. FN в такой постановке – это ошибочное предсказание неуспеха, то есть не более, чем упущенный шанс (если вас, конечно не уволят за срыв сроков). С FP всё серьёзней: если вы предскажете удачный запуск спутника, а на деле он потерпит крушение из-за погодных условий, то ваши потери будут в разы существеннее.
Итак, из примеров мы видим, что в текущем виде введенная нами доля ошибочных классификаций не даст нам возможности учесть неравную важность FP и FN. Поэтому введем две новые метрики: точность и полноту.
Точность и полнота
Accuracy — это метрика, которая характеризует качество модели, агрегированное по всем классам. Это полезно, когда классы для нас имеют одинаковое значение. В случае, если это не так, accuracy может быть обманчивой.
Рассмотрим ситуацию, когда положительный класс это событие редкое. Возьмем в качестве примера поисковую систему — в нашем хранилище хранятся миллиарды документов, а релевантных к конкретному поисковому запросу на несколько порядков меньше.
Пусть мы хотим решить задачу бинарной классификации «документ d релевантен по запросу q». Благодаря большому дисбалансу, Accuracy dummy-классификатора, объявляющего все документы нерелевантными, будет близка к единице. Напомним, что $text{Accuracy} = frac{TP + TN}{TP + TN + FP + FN}$, и в нашем случае высокое значение метрики будет обеспечено членом TN, в то время для пользователей более важен высокий TP.
Поэтому в случае ассиметрии классов, можно использовать метрики, которые не учитывают TN и ориентируются на TP.
Если мы рассмотрим долю правильно предсказанных положительных объектов среди всех объектов, предсказанных положительным классом, то мы получим метрику, которая называется точностью (precision)
$$color{#348FEA}{text{Precision} = frac{TP}{TP + FP}}$$
Интуитивно метрика показывает долю релевантных документов среди всех найденных классификатором. Чем меньше ложноположительных срабатываний будет допускать модель, тем больше будет её Precision.
Если же мы рассмотрим долю правильно найденных положительных объектов среди всех объектов положительного класса, то мы получим метрику, которая называется полнотой (recall)
$$color{#348FEA}{text{Recall} = frac{TP}{TP + FN}}$$
Интуитивно метрика показывает долю найденных документов из всех релевантных. Чем меньше ложно отрицательных срабатываний, тем выше recall модели.
Например, в задаче предсказания злокачественности опухоли точность показывает, сколько из определённых нами как злокачественные опухолей действительно являются злокачественными, а полнота – какую долю злокачественных опухолей нам удалось выявить.
Хорошее понимание происходящего даёт следующая картинка: 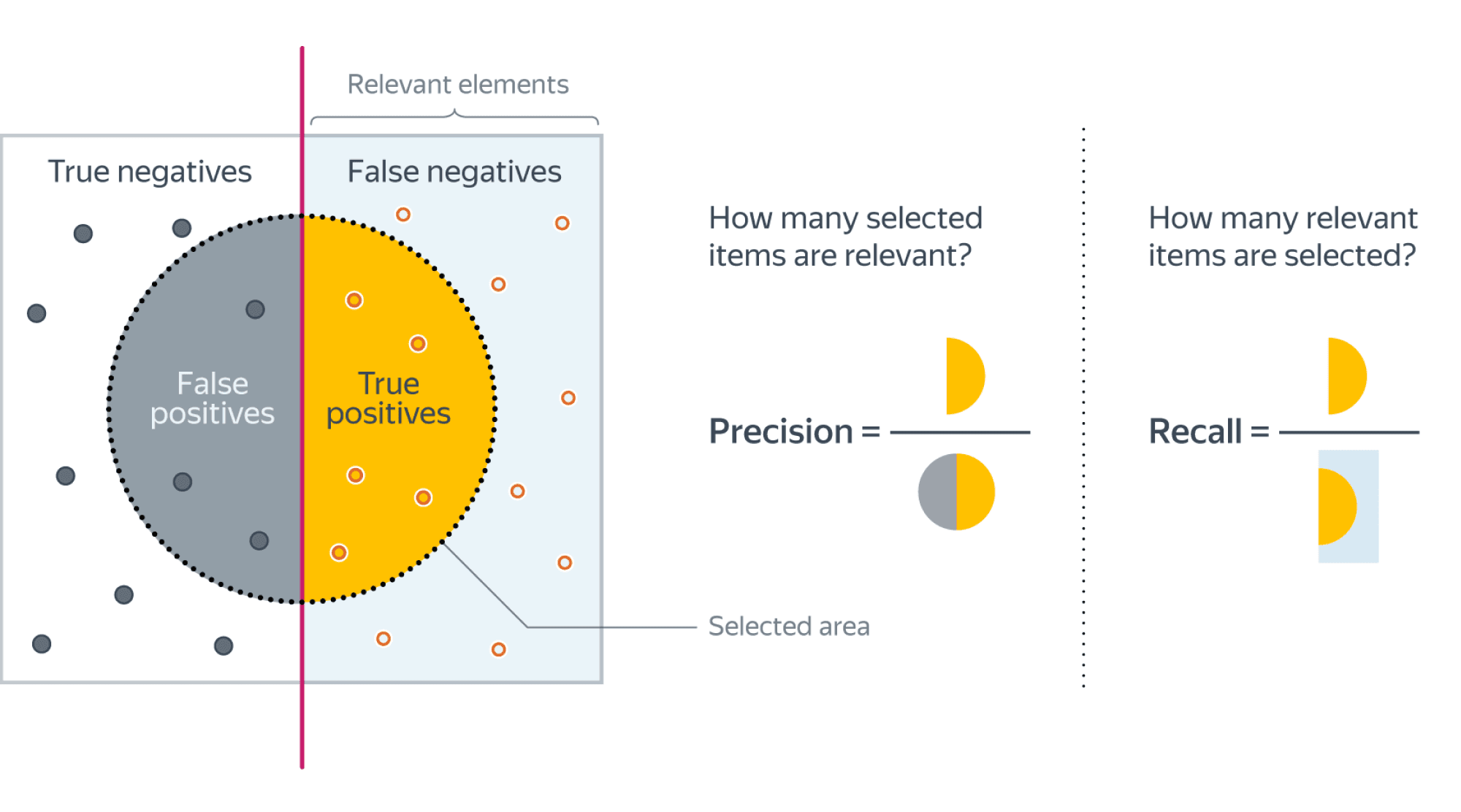
Recall@k, Precision@k
Метрики Recall и Precision хорошо подходят для задачи поиска «документ d релевантен запросу q», когда из списка рекомендованных алгоритмом документов нас интересует только первый. Но не всегда алгоритм машинного обучения вынужден работать в таких жестких условиях. Может быть такое, что вполне достаточно, что релевантный документ попал в первые k рекомендованных. Например, в интерфейсе выдачи первые три подсказки видны всегда одновременно и вообще не очень понятно, какой у них порядок. Тогда более честной оценкой качества алгоритма будет «в выдаче D размера k по запросу q нашлись релевантные документы». Для расчёта метрики по всей выборке объединим все выдачи и рассчитаем precision, recall как обычно подокументно.
F1-мера
Как мы уже отмечали ранее, модели очень удобно сравнивать, когда их качество выражено одним числом. В случае пары Precision-Recall существует популярный способ скомпоновать их в одну метрику — взять их среднее гармоническое. Данный показатель эффективности исторически носит название F1-меры (F1-measure).
$$
color{#348FEA}{F_1 = frac{2}{frac{1}{Recall} + frac{1}{Precision}}} = $$
$$ = 2 frac{Recall cdot Precision }{Recall + Precision} = frac
{TP} {TP + frac{FP + FN}{2}}
$$
Стоит иметь в виду, что F1-мера предполагает одинаковую важность Precision и Recall, если одна из этих метрик для вас приоритетнее, то можно воспользоваться $F_{beta}$ мерой:
$$
F_{beta} = (beta^2 + 1) frac{Recall cdot Precision }{Recall + beta^2Precision}
$$
Бинарная классификация: вероятности классов
Многие модели бинарной классификации устроены так, что класс объекта получается бинаризацией выхода классификатора по некоторому фиксированному порогу:
$$fleft(x ; w, w_{0}right)=mathbb{I}left[g(x, w) > w_{0}right].$$
Например, модель логистической регрессии возвращает оценку вероятности принадлежности примера к положительному классу. Другие модели бинарной классификации обычно возвращают произвольные вещественные значения, но существуют техники, называемые калибровкой классификатора, которые позволяют преобразовать предсказания в более или менее корректную оценку вероятности принадлежности к положительному классу.
Как оценить качество предсказываемых вероятностей, если именно они являются нашей конечной целью? Общепринятой мерой является логистическая функция потерь, которую мы изучали раньше, когда говорили об устройстве некоторых методов классификации (например уже упоминавшейся логистической регрессии).
Если же нашей целью является построение прогноза в терминах метки класса, то нам нужно учесть, что в зависимости от порога мы будем получать разные предсказания и разное качество на отложенной выборке. Так, чем ниже порог отсечения, тем больше объектов модель будет относить к положительному классу. Как в этом случае оценить качество модели?
AUC
Пусть мы хотим учитывать ошибки на объектах обоих классов. При уменьшении порога отсечения мы будем находить (правильно предсказывать) всё большее число положительных объектов, но также и неправильно предсказывать положительную метку на всё большем числе отрицательных объектов. Естественным кажется ввести две метрики TPR и FPR:
TPR (true positive rate) – это полнота, доля положительных объектов, правильно предсказанных положительными:
$$ TPR = frac{TP}{P} = frac{TP}{TP + FN} $$
FPR (false positive rate) – это доля отрицательных объектов, неправильно предсказанных положительными:
$$FPR = frac{FP}{N} = frac{FP}{FP + TN}$$
Обе эти величины растут при уменьшении порога. Кривая в осях TPR/FPR, которая получается при варьировании порога, исторически называется ROC-кривой (receiver operating characteristics curve, сокращённо ROC curve). Следующий график поможет вам понять поведение ROC-кривой.
Желтая и синяя кривые показывают распределение предсказаний классификатора на объектах положительного и отрицательного классов соответственно. То есть значения на оси X (на графике с двумя гауссианами) мы получаем из классификатора. Если классификатор идеальный (две кривые разделимы по оси X), то на правом графике мы получаем ROC-кривую (0,0)->(0,1)->(1,1) (убедитесь сами!), площадь под которой равна 1. Если классификатор случайный (предсказывает одинаковые метки положительным и отрицательным объектам), то мы получаем ROC-кривую (0,0)->(1,1), площадь под которой равна 0.5. Поэкспериментируйте с разными вариантами распределения предсказаний по классам и посмотрите, как меняется ROC-кривая.
Чем лучше классификатор разделяет два класса, тем больше площадь (area under curve) под ROC-кривой – и мы можем использовать её в качестве метрики. Эта метрика называется AUC и она работает благодаря следующему свойству ROC-кривой:
AUC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. предсказание классификатора на первом объекте больше:
$$
color{#348FEA}{operatorname{AUC} = frac{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j] I^{prime}[f(x_{i}) < f(x_{j})]}{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j]}}
$$
$$
I^{prime}left[f(x_{i}) < f(x_{j})right]=
left{
begin{array}{ll}
0, & f(x_{i}) > f(x_{j}) \
0.5 & f(x_{i}) = f(x_{j}) \
1, & f(x_{i}) < f(x_{j})
end{array}
right.
$$
$$
Ileft[y_{i}< y_{j}right]=
left{
begin{array}{ll}
0, & y_{i} geq y_{j} \
1, & y_{i} < y_{j}
end{array}
right.
$$
Чтобы детальнее разобраться, почему это так, советуем вам обратиться к материалам А.Г.Дьяконова.
В каких случаях лучше отдать предпочтение этой метрике? Рассмотрим следующую задачу: некоторый сотовый оператор хочет научиться предсказывать, будет ли клиент пользоваться его услугами через месяц. На первый взгляд кажется, что задача сводится к бинарной классификации с метками 1, если клиент останется с компанией и $0$ – иначе.
Однако если копнуть глубже в процессы компании, то окажется, что такие метки практически бесполезны. Компании скорее интересно упорядочить клиентов по вероятности прекращения обслуживания и в зависимости от этого применять разные варианты удержания: кому-то прислать скидочный купон от партнёра, кому-то предложить скидку на следующий месяц, а кому-то и новый тариф на особых условиях.
Таким образом, в любой задаче, где нам важна не метка сама по себе, а правильный порядок на объектах, имеет смысл применять AUC.
Утверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.
ПодробнееУтверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.» details=»Продемонстрируем это на следующем примере: пусть наша выборка состоит из $9100$ объектов класса $0$ и $10$ объектов класса $1$, и модель расположила их следующим образом:
$$underbrace{0 dots 0}_{9000} ~ underbrace{1 dots 1}_{10} ~ underbrace{0 dots 0}_{100}$$
Тогда AUC будет близка к единице: количество пар правильно расположенных объектов будет порядка $90000$, в то время как общее количество пар порядка $91000$.
Однако самыми высокими по вероятности положительного класса будут совсем не те объекты, которые мы ожидаем.
Average Precision
Будем постепенно уменьшать порог бинаризации. При этом полнота будет расти от $0$ до $1$, так как будет увеличиваться количество объектов, которым мы приписываем положительный класс (а количество объектов, на самом деле относящихся к положительному классу, очевидно, меняться не будет). Про точность же нельзя сказать ничего определённого, но мы понимаем, что скорее всего она будет выше при более высоком пороге отсечения (мы оставим только объекты, в которых модель «уверена» больше всего). Варьируя порог и пересчитывая значения Precision и Recall на каждом пороге, мы получим некоторую кривую примерно следующего вида:
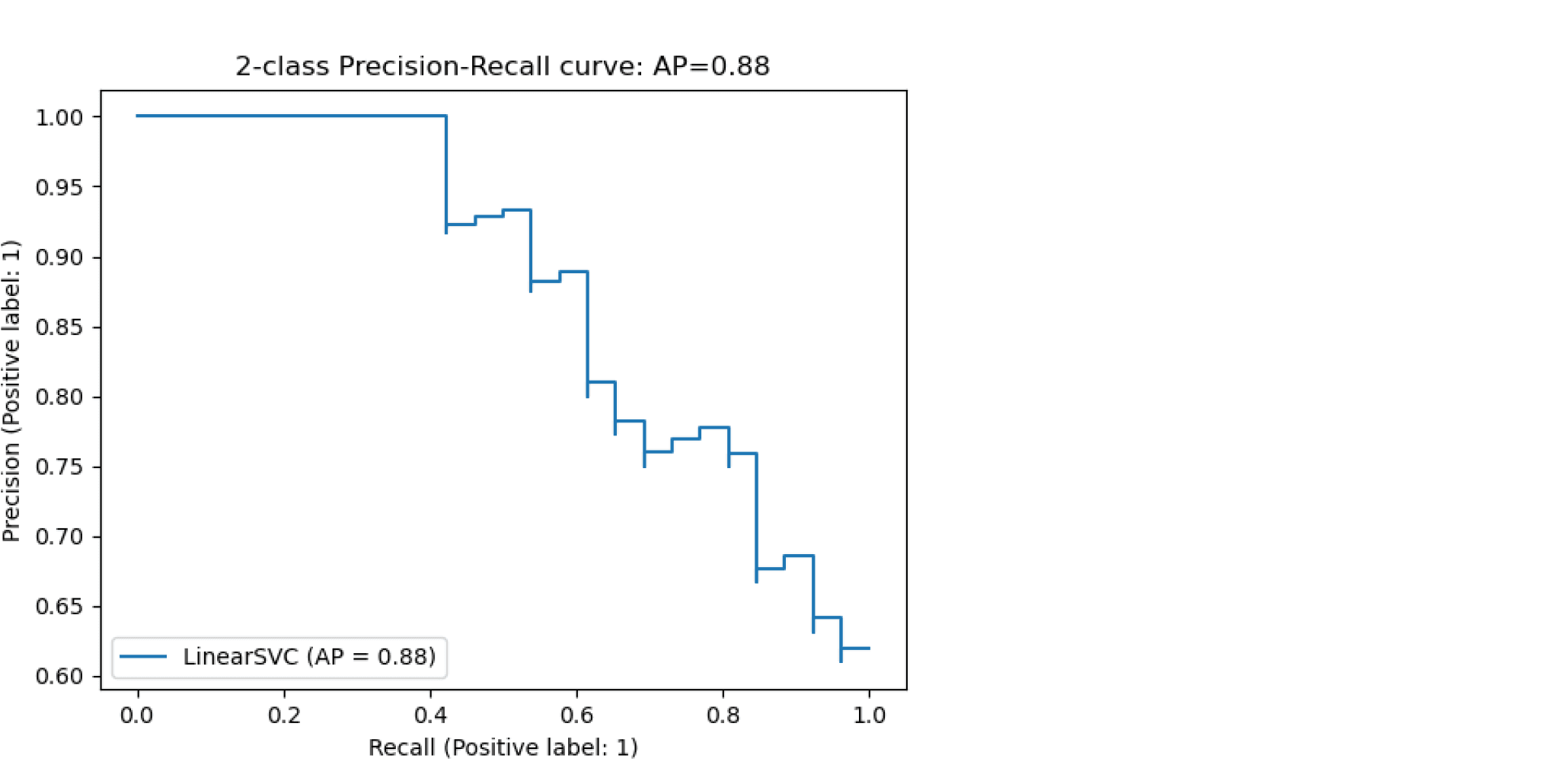
Рассмотрим среднее значение точности (оно равно площади под кривой точность-полнота):
$$ text { AP }=int_{0}^{1} p(r) d r$$
Получим показатель эффективности, который называется average precision. Как в случае матрицы ошибок мы переходили к скалярным показателям эффективности, так и в случае с кривой точность-полнота мы охарактеризовали ее в виде числа.
Многоклассовая классификация
Если классов становится больше двух, расчёт метрик усложняется. Если задача классификации на $K$ классов ставится как $K$ задач об отделении класса $i$ от остальных ($i=1,ldots,K$), то для каждой из них можно посчитать свою матрицу ошибок. Затем есть два варианта получения итогового значения метрики из $K$ матриц ошибок:
- Усредняем элементы матрицы ошибок (TP, FP, TN, FN) между бинарными классификаторами, например $TP = frac{1}{K}sum_{i=1}^{K}TP_i$. Затем по одной усреднённой матрице ошибок считаем Precision, Recall, F-меру. Это называют микроусреднением.
- Считаем Precision, Recall для каждого классификатора отдельно, а потом усредняем. Это называют макроусреднением.
Порядок усреднения влияет на результат в случае дисбаланса классов. Показатели TP, FP, FN — это счётчики объектов. Пусть некоторый класс обладает маленькой мощностью (обозначим её $M$). Тогда значения TP и FN при классификации этого класса против остальных будут не больше $M$, то есть тоже маленькие. Про FP мы ничего уверенно сказать не можем, но скорее всего при дисбалансе классов классификатор не будет предсказывать редкий класс слишком часто, потому что есть большая вероятность ошибиться. Так что FP тоже мало. Поэтому усреднение первым способом сделает вклад маленького класса в общую метрику незаметным. А при усреднении вторым способом среднее считается уже для нормированных величин, так что вклад каждого класса будет одинаковым.
Рассмотрим пример. Пусть есть датасет из объектов трёх цветов: желтого, зелёного и синего. Желтого и зелёного цветов почти поровну — 21 и 20 объектов соответственно, а синих объектов всего 4.
Модель по очереди для каждого цвета пытается отделить объекты этого цвета от объектов оставшихся двух цветов. Результаты классификации проиллюстрированы матрицей ошибок. Модель «покрасила» в жёлтый 25 объектов, 20 из которых были действительно жёлтыми (левый столбец матрицы). В синий был «покрашен» только один объект, который на самом деле жёлтый (средний столбец матрицы). В зелёный — 19 объектов, все на самом деле зелёные (правый столбец матрицы).
Посчитаем Precision классификации двумя способами:
- С помощью микроусреднения получаем $$
text{Precision} = frac{dfrac{1}{3}left(20 + 0 + 19right)}{dfrac{1}{3}left(20 + 0 + 19right) + dfrac{1}{3}left(5 + 1 + 0right)} = 0.87
$$ - С помощью макроусреднения получаем $$
text{Precision} = dfrac{1}{3}left( frac{20}{20 + 5} + frac{0}{0 + 1} + frac{19}{19 + 0}right) = 0.6
$$
Видим, что макроусреднение лучше отражает тот факт, что синий цвет, которого в датасете было совсем мало, модель практически игнорирует.
Как оптимизировать метрики классификации?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы $F$ на валидационной выборке была минимальная/максимальная. Лучший способ добиться минимизации метрики $F$ — оптимизировать её напрямую, то есть выбрать в качестве функции потерь ту же $F(a(X), Y)$. К сожалению, это не всегда возможно. Рассмотрим, как оптимизировать метрики иначе.
Метрики precision и recall невозможно оптимизировать напрямую, потому что эти метрики нельзя рассчитать на одном объекте, а затем усреднить. Они зависят от того, какими были правильная метка класса и ответ алгоритма на всех объектах. Чтобы понять, как оптимизировать precision, recall, рассмотрим, как расчитать эти метрики на отложенной выборке. Пусть модель обучена на стандартную для классификации функцию потерь (LogLoss). Для получения меток класса специалист по машинному обучению сначала применяет на объектах модель и получает вещественные предсказания модели ($p_i in left(0, 1right)$). Затем предсказания бинаризуются по порогу, выбранному специалистом: если предсказание на объекте больше порога, то метка класса 1 (или «положительная»), если меньше — 0 (или «отрицательная»). Рассмотрим, что будет с метриками precision, recall в крайних положениях порога.
- Пусть порог равен нулю. Тогда всем объектам будет присвоена положительная метка. Следовательно, все объекты будут либо TP, либо FP, потому что отрицательных предсказаний нет, $TP + FP = N$, где $N$ — размер выборки. Также все объекты, у которых метка на самом деле 1, попадут в TP. По формуле точность $text{Precision} = frac{TP}{TP + FP} = frac1N sum_{i = 1}^N mathbb{I} left[ y_i = 1 right]$ равна среднему таргету в выборке. А полнота $text{Recall} = frac{TP}{TP + FN} = frac{TP}{TP + 0} = 1$ равна единице.
- Пусть теперь порог равен единице. Тогда ни один объект не будет назван положительным, $TP = FP = 0$. Все объекты с меткой класса 1 попадут в FN. Если есть хотя бы один такой объект, то есть $FN ne 0$, будет верна формула $text{Recall} = frac{TP}{TP + FN} = frac{0}{0+ FN} = 0$. То есть при пороге единица, полнота равна нулю. Теперь посмотрим на точность. Формула для Precision состоит только из счётчиков положительных ответов модели (TP, FP). При единичном пороге они оба равны нулю, $text{Precision} = frac{TP}{TP + FP} = frac{0}{0 + 0}$то есть при единичном пороге точность неопределена. Пусть мы отступили чуть-чуть назад по порогу, чтобы хотя бы несколько объектов были названы моделью положительными. Скорее всего это будут самые «простые» объекты, которые модель распознает хорошо, потому что её предсказание близко к единице. В этом предположении $FP approx 0$. Тогда точность $text{Precision} = frac{TP}{TP + FP} approx frac{TP}{TP + 0} approx 1$ будет близка к единице.
Изменяя порог, между крайними положениями, получим графики Precision и Recall, которые выглядят как-то так:
Recall меняется от единицы до нуля, а Precision от среднего тагрета до какого-то другого значения (нет гарантий, что график монотонный).
Итого оптимизация precision и recall происходит так:
- Модель обучается на стандартную функцию потерь (например, LogLoss).
- Используя вещественные предсказания на валидационной выборке, перебирая разные пороги от 0 до 1, получаем графики метрик в зависимости от порога.
- Выбираем нужное сочетание точности и полноты.
Пусть теперь мы хотим максимизировать метрику AUC. Стандартный метод оптимизации, градиентный спуск, предполагает, что функция потерь дифференцируема. AUC этим качеством не обладает, то есть мы не можем оптимизировать её напрямую. Поэтому для метрики AUC приходится изменять оптимизационную задачу. Метрика AUC считает долю верно упорядоченных пар. Значит от исходной выборки можно перейти к выборке упорядоченных пар объектов. На этой выборке ставится задача классификации: метка класса 1 соответствует правильно упорядоченной паре, 0 — неправильно. Новой метрикой становится accuracy — доля правильно классифицированных объектов, то есть доля правильно упорядоченных пар. Оптимизировать accuracy можно по той же схеме, что и precision, recall: обучаем модель на LogLoss и предсказываем вероятности положительной метки у объекта выборки, считаем accuracy для разных порогов по вероятности и выбираем понравившийся.
Регрессия
В задачах регрессии целевая метка у нас имеет потенциально бесконечное число значений. И природа этих значений, обычно, связана с каким-то процессом измерений:
- величина температуры в определенный момент времени на метеостанции
- количество прочтений статьи на сайте
- количество проданных бананов в конкретном магазине, сети магазинов или стране
- дебит добывающей скважины на нефтегазовом месторождении за месяц и т.п.
Мы видим, что иногда метка это целое число, а иногда произвольное вещественное число. Обычно случаи целочисленных меток моделируют так, словно это просто обычное вещественное число. При таком подходе может оказаться так, что модель A лучше модели B по некоторой метрике, но при этом предсказания у модели A могут быть не целыми. Если в бизнес-задаче ожидается именно целочисленный ответ, то и оценивать нужно огрубление.
Общая рекомендация такова: оценивайте весь каскад решающих правил: и те «внутренние», которые вы получаете в результате обучения, и те «итоговые», которые вы отдаёте бизнес-заказчику.
Например, вы можете быть удовлетворены, что стали ошибаться не во втором, а только в третьем знаке после запятой при предсказании погоды. Но сами погодные данные измеряются с точностью до десятых долей градуса, а пользователь и вовсе может интересоваться лишь целым числом градусов.
Итак, напомним постановку задачи регрессии: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_i in mathbb{R}$ построить модель f(x).
Величину $ e_i = f(x_i) — y_i $ называют ошибкой на объекте i или регрессионным остатком.
Весь набор ошибок на отложенной выборке может служить аналогом матрицы ошибок из задачи классификации. А именно, когда мы рассматриваем две разные модели, то, глядя на то, как и на каких объектах они ошиблись, мы можем прийти к выводу, что для решения бизнес-задачи нам выгоднее взять ту или иную модель. И, аналогично со случаем бинарной классификации, мы можем начать строить агрегаты от вектора ошибок, получая тем самым разные метрики.
MSE, RMSE, $R^2$
MSE – одна из самых популярных метрик в задаче регрессии. Она уже знакома вам, т.к. применяется в качестве функции потерь (или входит в ее состав) во многих ранее рассмотренных методах.
$$ MSE(y^{true}, y^{pred}) = frac1Nsum_{i=1}^{N} (y_i — f(x_i))^2 $$
Иногда для того, чтобы показатель эффективности MSE имел размерность исходных данных, из него извлекают квадратный корень и получают показатель эффективности RMSE.
MSE неограничен сверху, и может быть нелегко понять, насколько «хорошим» или «плохим» является то или иное его значение. Чтобы появились какие-то ориентиры, делают следующее:
-
Берут наилучшее константное предсказание с точки зрения MSE — среднее арифметическое меток $bar{y}$. При этом чтобы не было подглядывания в test, среднее нужно вычислять по обучающей выборке
-
Рассматривают в качестве показателя ошибки:
$$ R^2 = 1 — frac{sum_{i=1}^{N} (y_i — f(x_i))^2}{sum_{i=1}^{N} (y_i — bar{y})^2}.$$
У идеального решающего правила $R^2$ равен $1$, у наилучшего константного предсказания он равен $0$ на обучающей выборке. Можно заметить, что $R^2$ показывает, какая доля дисперсии таргетов (знаменатель) объяснена моделью.
MSE квадратично штрафует за большие ошибки на объектах. Мы уже видели проявление этого при обучении моделей методом минимизации квадратичных ошибок – там это проявлялось в том, что модель старалась хорошо подстроиться под выбросы.
Пусть теперь мы хотим использовать MSE для оценки наших регрессионных моделей. Если большие ошибки для нас действительно неприемлемы, то квадратичный штраф за них — очень полезное свойство (и его даже можно усиливать, повышая степень, в которую мы возводим ошибку на объекте). Однако если в наших тестовых данных присутствуют выбросы, то нам будет сложно объективно сравнить модели между собой: ошибки на выбросах будет маскировать различия в ошибках на основном множестве объектов.
Таким образом, если мы будем сравнивать две модели при помощи MSE, у нас будет выигрывать та модель, у которой меньше ошибка на объектах-выбросах, а это, скорее всего, не то, чего требует от нас наша бизнес-задача.
История из жизни про бананы и квадратичный штраф за ошибкуИз-за неверно введенных данных метка одного из объектов оказалась в 100 раз больше реального значения. Моделировалась величина при помощи градиентного бустинга над деревьями решений. Функция потерь была MSE.
Однажды уже во время эксплуатации случилось ч.п.: у нас появились предсказания, в 100 раз превышающие допустимые из соображений физического смысла значения. Представьте себе, например, что вместо обычных 4 ящиков бананов система предлагала поставить в магазин 400. Были распечатаны все деревья из ансамбля, и мы увидели, что постепенно число ящиков действительно увеличивалось до прогнозных 400.
Было решено проверить гипотезу, что был выброс в данных для обучения. Так оно и оказалось: всего одна точка давала такую потерю на объекте, что алгоритм обучения решил, что лучше переобучиться под этот выброс, чем смириться с большим штрафом на этом объекте. А в эксплуатации у нас возникли точки, которые плюс-минус попадали в такие же листья ансамбля, что и объект-выброс.
Избежать такого рода проблем можно двумя способами: внимательнее контролируя качество данных или адаптировав функцию потерь.
Аналогично, можно поступать и в случае, когда мы разрабатываем метрику качества: менее жёстко штрафовать за большие отклонения от истинного таргета.
MAE
Использовать RMSE для сравнения моделей на выборках с большим количеством выбросов может быть неудобно. В таких случаях прибегают к также знакомой вам в качестве функции потери метрике MAE (mean absolute error):
$$ MAE(y^{true}, y^{pred}) = frac{1}{N}sum_{i=1}^{N} left|y_i — f(x_i)right| $$
Метрики, учитывающие относительные ошибки
И MSE и MAE считаются как сумма абсолютных ошибок на объектах.
Рассмотрим следующую задачу: мы хотим спрогнозировать спрос товаров на следующий месяц. Пусть у нас есть два продукта: продукт A продаётся в количестве 100 штук, а продукт В в количестве 10 штук. И пусть базовая модель предсказывает количество продаж продукта A как 98 штук, а продукта B как 8 штук. Ошибки на этих объектах добавляют 4 штрафных единицы в MAE.
И есть 2 модели-кандидата на улучшение. Первая предсказывает товар А 99 штук, а товар B 8 штук. Вторая предсказывает товар А 98 штук, а товар B 9 штук.
Обе модели улучшают MAE базовой модели на 1 единицу. Однако, с точки зрения бизнес-заказчика вторая модель может оказаться предпочтительнее, т.к. предсказание продажи редких товаров может быть приоритетнее. Один из способов учесть такое требование – рассматривать не абсолютную, а относительную ошибку на объектах.
MAPE, SMAPE
Когда речь заходит об относительных ошибках, сразу возникает вопрос: что мы будем ставить в знаменатель?
В метрике MAPE (mean absolute percentage error) в знаменатель помещают целевое значение:
$$ MAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ left|y_i — f(x_i)right|}{left|y_iright|} $$
С особым случаем, когда в знаменателе оказывается $0$, обычно поступают «инженерным» способом: или выдают за непредсказание $0$ на таком объекте большой, но фиксированный штраф, или пытаются застраховаться от подобного на уровне формулы и переходят к метрике SMAPE (symmetric mean absolute percentage error):
$$ SMAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ 2 left|y_i — f(x_i)right|}{y_i + f(x_i)} $$
Если же предсказывается ноль, штраф считаем нулевым.
Таким переходом от абсолютных ошибок на объекте к относительным мы сделали объекты в тестовой выборке равнозначными: даже если мы делаем абсурдно большое предсказание, на фоне которого истинная метка теряется, мы получаем штраф за этот объект порядка 1 в случае MAPE и 2 в случае SMAPE.
WAPE
Как и любая другая метрика, MAPE имеет свои границы применимости: например, она плохо справляется с прогнозом спроса на товары с прерывистыми продажами. Рассмотрим такой пример:
| Понедельник | Вторник | Среда | |
|---|---|---|---|
| Прогноз | 55 | 2 | 50 |
| Продажи | 50 | 1 | 50 |
| MAPE | 10% | 100% | 0% |
Среднее MAPE – 36.7%, что не очень отражает реальную ситуацию, ведь два дня мы предсказывали с хорошей точностью. В таких ситуациях помогает WAPE (weighted average percentage error):
$$ WAPE(y^{true}, y^{pred}) = frac{sum_{i=1}^{N} left|y_i — f(x_i)right|}{sum_{i=1}^{N} left|y_iright|} $$
Если мы предсказываем идеально, то WAPE = 0, если все предсказания отдаём нулевыми, то WAPE = 1.
В нашем примере получим WAPE = 5.9%
RMSLE
Альтернативный способ уйти от абсолютных ошибок к относительным предлагает метрика RMSLE (root mean squared logarithmic error):
$$ RMSLE(y^{true}, y^{pred}| c) = sqrt{ frac{1}{N} sum_{i=1}^N left(vphantom{frac12}log{left(y_i + c right)} — log{left(f(x_i) + c right)}right)^2 } $$
где нормировочная константа $c$ вводится искусственно, чтобы не брать логарифм от нуля. Также по построению видно, что метрика пригодна лишь для неотрицательных меток.
Веса в метриках
Все вышеописанные метрики легко допускают введение весов для объектов. Если мы из каких-то соображений можем определить стоимость ошибки на объекте, можно брать эту величину в качестве веса. Например, в задаче предсказания спроса в качестве веса можно использовать стоимость объекта.
Доля предсказаний с абсолютными ошибками больше, чем d
Еще одним способом охарактеризовать качество модели в задаче регрессии является доля предсказаний с абсолютными ошибками больше заданного порога $d$:
$$frac{1}{N} sum_{i=1}^{N} mathbb{I}left[ left| y_i — f(x_i) right| > d right] $$
Например, можно считать, что прогноз погоды сбылся, если ошибка предсказания составила меньше 1/2/3 градусов. Тогда рассматриваемая метрика покажет, в какой доле случаев прогноз не сбылся.
Как оптимизировать метрики регрессии?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы F на валидационной выборке была минимальная/максимальная. Аналогично задачам классификации лучший способ добиться минимизации метрики $F$ — выбрать в качестве функции потерь ту же $F(a(X), Y)$. К счастью, основные метрики для регрессии: MSE, RMSE, MAE можно оптимизировать напрямую. С формальной точки зрения MAE не дифференцируема, так как там присутствует модуль, чья производная не определена в нуле. На практике для этого выколотого случая в коде можно возвращать ноль.
Для оптимизации MAPE придётся изменять оптимизационную задачу. Оптимизацию MAPE можно представить как оптимизацию MAE, где объектам выборки присвоен вес $frac{1}{vert y_ivert}$.








![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)


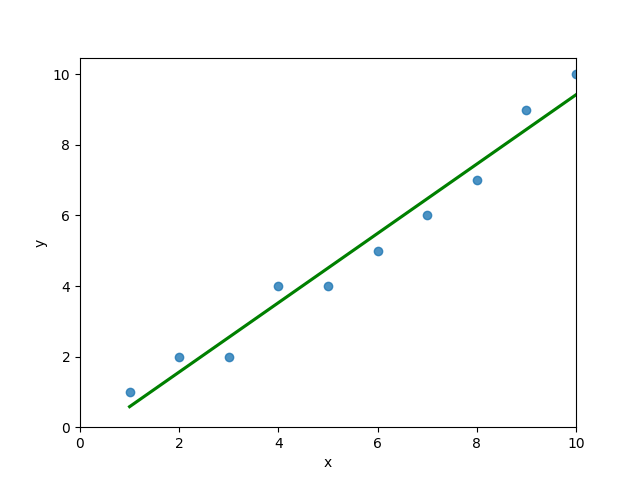
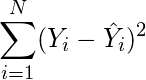
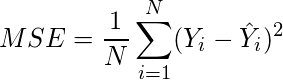
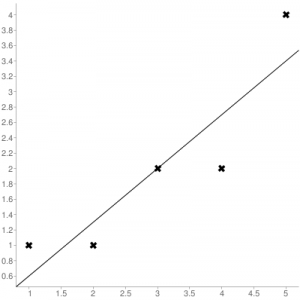


 ) из исходных значений Y. Таким образом, найденные значения являются ошибочными терминами. Это также известно как вертикальное расстояние данной точки от линии регрессии.
) из исходных значений Y. Таким образом, найденные значения являются ошибочными терминами. Это также известно как вертикальное расстояние данной точки от линии регрессии.