Чтобы
деление было правильным, необходимо
соблюдать следующие правила.
1.
Соразмерность деления: объем делимого
понятия должен быть равен сумме объемов
членов деления. Например, высшие растения
делятся на травы, кустарники и деревья.
Электрический ток делится на постоянный
и переменный.
Нарушение
этого правила ведет к ошибкам двух
видов:
а)
неполное деление, когда перечисляются
не все виды данного родового понятия.
Ошибочными будут такие деления: «Энергия
делится на механическую и химическую»
(здесь нет, например, указания на
электрическую энергию, атомную энергию).
«Арифметические действия делятся на
сложение, вычитание, умножение, деление,
возведение в степень» (не указано
«извлечение корня»);
б)
деление с лишними членами. Пример этого
ошибочного деления: «Химические элементы
делятся на металлы, неметаллы и сплавы».
Здесь .лишний член («сплавы»), а сумма
объемов понятий «металл» и «неметалл»
исчерпывает объем понятия «химический
элемент».
2.
Деление должно проводиться только по
одному основанию. Это означает, что
нельзя брать два или большее число
признаков, по которым бы производилось
деление.
Если
будет нарушено это правило, то произойдет
перекрещивание объемов понятий, которые
появились в результате деления. Правильные
«деления: «Волны делятся на продольные
и поперечные». «В промышленности
получение стали осуществляется тремя
способами: кислородно-конверторным,
мартеновским и в электропечах».
Неправильным является такое деление:
«Транспорт делится на наземный, водный,
воздушный, транспорт общего пользования,
транспорт личного пользования», — ибо
допущена ошибка «подмена основания»,
т. е. деление произведено не по одному
основанию. Сначала в качестве основания
деления берется вид среды, в которой
осуществляются перевозки, а затем за
основание деления берется назначение
транспорта.
3.
Члены деления должны исключать друг
друга, т. е. не иметь общих элементов,
быть соподчиненными понятиями, объемы
которых не пересекаются.
Это
правило тесно связано с предыдущим, так
как если деление осуществляется не по
одному основанию, то члены деления не
будут исключать друг друга. Примеры
ошибочных делений: «Дроби бывают
десятичными, правильными, неправильными,
периодическими, непериодическими»;
«Войны бывают справедливыми,
несправедливыми, освободительными,
захватническими, мировыми»; «Треугольники
бывают прямоугольными, тупоугольными,
остроугольными, равнобедренными,
подобными». В этих примерах члены деления
не исключают друг друга. Это следствие
допущенной ошибки смешения различных
оснований деления.
4.
Деление должно быть непрерывным, т. е.
нельзя делать скачки в делении. Будет
допущена ошибка, если мы скажем: «Сказуемые
делятся на простые, на составные
глагольные и составные именные».
Правильным будет сначала разделить
сказуемые на простые и составные, а
затем уже составные сказуемые разделить
на составные глагольные и составные
именные.
Будет
допущена ошибка, если мы разделим
удобрения на органические, азотные,
фосфорные и калийные. Правильным будет
сначала разделить удобрения на
органические и минеральные, а затем уже
минеральные удобрения разделить на
азотные, фосфорные и калийные.
Упражнение
1 . Проведите
операцию деления следующих понятий:
Задание:
Проведите операцию деления следующих
понятий: государство, звезда, занятие,
система, болезнь, экзамен, логический
союз, население земного шара, одежда,
часы, язык, акция, клетка, устройство,
закон, город, лекарство, экономика,
наука, искусство, религия, литература.
1)
В доктринах национальной безопасности
многих стран по критерию взаимопонимания
и взаимосотрудничества государства
мира разделяются на группы: друзья,
союзники, потенциальные союзники,
партнеры, потенциальные партнеры,
недружественные государства, потенциальные
противники, противники, потенциальные
агрессоры, агрессоры.
Пояснение:
Деление по видоизменению признака, а
именно по критерию взаимопонимания.
2)
3везды бывают новорожденными, молодыми,
среднего возраста и старыми.
Пояснение:
Деление по видоизменению признака, а
именно по возрасту звёзд.
3)
По своей природе занятия бывают полезными
и бесполезными, последние иногда могут
длиться часами, а иногда не занимают и
пары минут.
Пояснение:
Дихотомическое деление.
4)
По природному происхождению можно
выделить естественные, искусственные
и смешанные системы.
Пояснение:
Деление по видоизменению признака.
5)
В медицине существуют болезни зрительной
системы, дыхательной системы,
сердечнососудистой системы, системы
пищеварения, мочеполовой системы,
болезни костного скелета, нервной
системы и др.
Пояснение:
Деление по видоизменению признака, а
именно по областям поражения.
6)
На сессии вас ждут письменные, устные,
а также экзамены в виде тестов.
Пояснение:
Деление по видоизменению признака.
7)
Сложные суждения образуются из простых
суждений с помощью логических союзов:
конъюнкции, дизъюнкции, импликации,
эквиваленции и отрицания.
Пояснение:
Деление по видоизменению признака.

Как правило, население земного шара,
разделяют на три большие расы, или расы
первого порядка: экваториальная, или
австрало-негроидная; евразийская, или
европеоидная; азиатско-американская,
или монголоидная.
Пояснение:
Деление по видоизменению признака, а
именно по расе.
9)
В нашем магазине вы сможете купить
летнюю, зимнюю и демисезонную одежду.
Пояснение:
Деление по видоизменению признака.
10)
Часы можно разделить по размерам и
портативности на карманные, наручные,
каретные, настольные, настенные,
напольные, башенные.
Пояснение:
Деление по видоизменению признака, а
именно по размеру.
11)
Человеческие языки разделяют на
естественные человеческие языки,
искусственные языки, жестовые языки.
Пояснение:
Деление по видоизменению признака.
12)
Существуют именные, предъявительские,
простые, привилегированные, учредительские
и другие акции.
Пояснение:
Деление по видоизменению признака.
13)
Клетки растений, грибов, бактерий и
животных различны по своему строению.
Пояснение:
Деление по видоизменению признака.
14)
По воздействию на объект различают
следующие устройства: режущие, давящие,
шлифующие, ударные, крепёжно-зажимные
и др.
Пояснение:
Деление по видоизменению признака.
15)
Выделяют три категории законов:
конституционные, органические и
ординарные.
Пояснение:
Деление по видоизменению признака.
16)
Современные города делятся на малые
(до 50 тысяч жителей), средние (50—100 тысяч),
большие (100—250 тысяч), крупные (250—500
тысяч), крупнейшие (500 тысяч — 1 миллион)
и города-миллионеры (свыше 1 миллиона
жителей).
Пояснение:
Деление по видоизменению признака, а
именно по количеству населения.
17)
В аптеке вы можете приобрести лекарства
по рецепту и без рецепта врача, без
рецепта отпускаются косметические и
не косметические средства.
Пояснение:
Дихотомическое деление.
18)
По предмету изучения научная экономика
делится на общую, микроэкономику,
макроэкономику, мезоэкономику и мировую
экономику.
Пояснение:
Деление по видоизменению признака.
19)
Все науки обычно делятся на три группы:
естественные науки, социальные и
гуманитарные науки, формальные науки.
Пояснение:
Деление по видоизменению признака.
20)
Классифицировать искусство довольно
сложно, однако выделяют четыре вида
основных образующих искусств:
изобразительное, музыкальное, танцевальное,
литературное.
Пояснение:
Деление по видоизменению признака.
21)
Под мировыми религиями принято понимать
буддизм, христианство и ислам.
Пояснение:
Деление по видоизменению признака,
деление произведено в порядке древности
религии.
22)
В современной литературе можно выделить
такие основные виды как художественная
литература, учебная литература, научная
и научно-популярная литература, и
техническая литература.
Пояснение:
Деление по видоизменению признака.
Упражнение
2
Проверьте
правильность операции деления и назовите
ошибку, если она есть:
Юлия Валерьевна Шульгина
Эксперт по предмету «Логика»
преподавательский стаж — 10 лет
Задать вопрос автору статьи
Сущность деления понятия
Определение 1
Деление понятия – это логическая операция, позволяющая выявить все существующие виды некоторого рода на основании какого-либо общего признака.
В обыденной жизни люди постоянно сталкиваются с необходимостью распределить множество предметов на группы тем или иным образом. Например, человек хочет расставить книги в своей домашней библиотеке:
- можно расставить их по тематике: на одну полку поставить справочники и учебники, на другую – поэзию, на третью – детективы и т. д.;
- можно распределить их по фамилиям авторов в алфавитном порядке;
- можно группировать по цвету переплета и т. д.
В каждом описанном варианте все предметы одной группы будут обладать специфическим признаком, отличающим их от предметов другой группы (ни один из предметов другой группы таким признаком обладать не будет). Так, среди сборников стихов не окажется ни одного справочника.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 4 500 ₽
Нередко условия требуют мысленного распределения, а не физической расстановки предметов.
Например, треугольники можно разделить на тупоугольные, прямоугольные и остроугольные.
Описанная мыслительная операция является делением понятия. Ее отличительная черта – разбиение объема некоторого класса (понятия) на подклассы (группы) в зависимости от обладания некоторым специфическим признаком. Логическое деление предназначено для того, чтобы установить все разновидности предметов, которым присуще содержание понятия, подвергающегося делению.
К операции логического деления прибегают и в том случае, когда нужно провести обзор материала или упорядочить его, составить план работы, как-либо систематизировать множество предметов. Особенно важна эта операция для научного познания, поскольку она помогает раскрыть объем понятия путем выделения в нем всех возможных подгрупп.
Определение 2
Признак, по наличию которого выполняют деление, называется основанием деления.
«Деление понятия: правила и возможные ошибки» 👇
Например, государства бывают республиками и монархиями. Основание деления – форма правления.
Определение 3
Группы, которые получены в ходе деления, называют видами или членами деления.
Выбор основания деления определяется целью, конкретной решаемой задачей. Задачи бывают разными, поэтому одно и то же понятие может делиться по разным признакам.
Например, согласные звуки делятся на глухие и звонкие; на твердые и мягкие.
Выбирая основание деления, желательно останавливаться на существенных признаках. Такое деление имеет эвристическую ценность, т.к. способствует более глубокому пониманию природы входящих в понятие объектов.
Деление бывает двух видов:
- дихотомическое деление, при котором объем понятия распределяют на два класса, противоречащих друг другу: предметы одного класса обладают признаком, а предметы второго класса не обладают им;
- деление по видоизменению признака, при котором объем понятия распределяют на подмножества, в каждом из которых признак, служащий основанием деления, проявляется со своими особенностями.
Правила деления понятия
При делении понятия необходимо соблюдать ряд правил.
Правило соразмерности заключается в том, что объединение (сумма) объемов членов деления должно совпадать с объемом исходного понятия. Это значит, что ни один предмет, принадлежащий исходному понятию, не должен быть пропущен, и ни один лишний предмет не должен быть добавлен. При нарушении этого правила возникают ошибки неполного или избыточного деления. Ошибка неполного деления часто возникает при попытке провести дихотомическое деление, если выделяют два противоположных (но не противоречащих) класса; а также при делении по видоизменению признака, если перечисляют не все получаемые члены деления.
Пример неполного деления: «Посуда бывает металлической, керамической и стеклянной». Здесь пропущена пластиковая посуда.
Пример избыточного деления: «Предложения бывают вопросительными, побудительными, повествовательными и такими, от которых нельзя отказаться». Здесь предложения как грамматическая категория поделены на виды в зависимости от цели высказывания (вопросительные, побудительные, повествовательные), а затем добавлен лишний член – «такие, от которых нельзя отказаться».
Правило несовместимости заключается в том, что члены деления должны быть несовместимыми понятиями, т. е. исключать друг друга. Иными словами, каждый элемент должен входить только в одно подмножество. Если это правило нарушено, возникает ошибка перекрещивания (пересечения) понятия;
Например: «Фильмы бывают смешными и грустными». Существуют трагикомедии, сочетающие в себе грустные и веселые элементы, – при таком делении их пришлось бы относить к обеим категориям.
Иллюстрацией перекрещивания понятий может служить анекдот про обезьяну, которая не могла определиться, к какой группе зверей ей нужно примкнуть – к умным или к красивым.
Правило единственного основания заключается в том, что деление должно быть выполнено по одному основанию. Это правило касается деления по видоизменению признака. Его суть состоит в том, что нельзя делить понятие с использованием одновременно нескольких признаков. При нарушении этого правила часто одновременно возникает и ошибка пересечения.
Пример деления по разным основаниями: «Тексты бывают художественными, научными, официально-деловыми, рукописными, печатными, безграмотными».
Правило непрерывности заключающееся в том, что при делении нельзя сразу переходить к подвиду от рода, минуя вид. Другими словами, нельзя допускать «скачки»: деление нужно выполнять последовательно. Это требование касается поэтапного, многоступенчатого деления. Если нарушить его, деление будет непонятным и громоздким, стройность мышления нарушится.
Пример «скачка» в делении понятия: «Членами предложения являются подлежащее, сказуемое и второстепенные члены». Правильное деление – это деление на главные и второстепенные члены. Далее главные члены делятся на подлежащее и сказуемое, а второстепенные – на определение, дополнение, обстоятельство, т. е. сначала выделяются виды, а затем в каждом виде – подвиды.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
1.12. Правила деления
Существует несколько логических правил деления понятия. Нарушение хотя бы одного из них приводит к тому, что объем понятия не раскрывается, и деление не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении.
1. Деление должно проводиться по одному основанию, т. е. при делении понятия следует придерживаться только одного выбранного признака. Например, в делении: Люди бывают мужчинами, женщинами и учителями используются два разных основания – пол и профессия, что недопустимо. Ошибка, возникающая при нарушении этого правила, называется подменой основания. В делении с подменой основания может использоваться не только два разных основания, как в приведенном выше примере, но и больше. Например, в делении: Люди бывают мужчинами, женщинами, китайцами и блондинами, как видим, используются три различных основания – пол, национальность и цвет волос, что, конечно же, тоже является ошибкой.
2. Деление должно быть полным, т. е. надо перечислить все возможные результаты деления (суммарный объем всех результатов деления должен быть равен объему исходного делимого понятия). Например, деление: Учебные заведения бывают начальными и средними является неполным, т. к. не указан еще один результат деления – высшие учебные заведения. Но как быть, если надо перечислять не два или три, а десятки или сотни результатов деления. В этом случае можно употреблять понятия: и другие, и прочие, и так далее, и тому подобное, которые будут включать в себя не перечисленные результаты деления. Например: Люди бывают русскими, немцами, китайцами, японцами и представителями других национальностей.
3. Результаты деления не должны пересекаться, т. е. понятиям, представляющим собой результаты деления, следует быть несовместимыми, их объемы не должны иметь общих элементов (на схеме Эйлера круги, обозначающие результаты деления, не должны соприкасаться, располагаясь отдельно друг от друга). Например, в делении: Страны мира делятся на северные, южные, восточные и западные допущена ошибка – пересечение результатов деления. На первый взгляд приведенное в качестве примера деление кажется безошибочным: оно проведено по одному основанию (сторона света) и является полным (все стороны света перечислены). Чтобы увидеть ошибку в данном делении надо рассуждать так. Возьмем какую-нибудь страну, например, Канаду и ответим на вопрос – является ли она северной? Конечно, является, т. к. расположена в северном полушарии Земли. Теперь ответим на вопрос, является ли Канада западной страной? Да, потому что она расположена в западном полушарии Земли. Таким образом, получается, что Канада – одновременно и северная, и западная страна, т. е. она является общим элементом объемов понятий северные страны и западные страны, а значит, эти понятия, а вернее их объемы, пересекаются. То же самое можно сказать и относительно понятий южные страны и восточные страны. На схеме Эйлера результаты деления из нашего примера будут располагаться так:
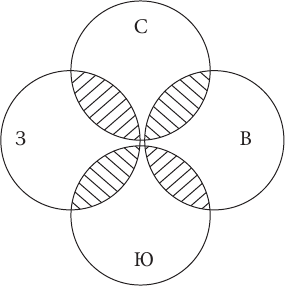
Вспомним, каждая классификация построена таким образом, что любой элемент, попадающий в одну ее группу (часть, вид), ни в коем случае не попадает в другие. Это и есть следствие непересечения результатов деления или их взаимоисключения при составлении какой угодно классификации.
4. Деление должно быть последовательным, т. е. не допускающим пропусков и скачков. Рассмотрим следующее деление: Леса бывают хвойными, лиственными, смешанными и сосновыми. Явно лишним здесь выглядит понятие сосновые леса, в силу чего допущенная в делении ошибка напоминает подмену основания (см. первое правило). Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Подмена основания присутствует в таком, например, делении: Леса бывают хвойными, лиственными, смешанными, подмосковными и таежными. (Деление проведено по двум разным основаниям – тип древесных листьев и географическое местонахождение леса). Вернемся к нашему первому примеру. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведенном примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Еще раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении: Учебные заведения бывают начальными, средними, высшими и университетами присутствует скачок, а в делении: Учебные заведения бывают начальными, средними, высшими и коммерческими допущена подмена основания.
Приведем еще несколько примеров правильного деления, а также – деления, в котором нарушены рассмотренные правила и допущены различные ошибки.
а) Транспорт бывает наземным, подземным, водным, воздушным, общественным и личным (подмена основания).
б) По темпераменту люди делятся на сангвиников, меланхоликов, флегматиков и холериков (пересечение результатов деления).
в) Геометрические фигуры делятся на плоские, объемные, треугольники и квадраты (скачок в делении).
г) Отбор в живой природе бывает искусственным или естественным (правильное деление).
д) Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими (пересечение результатов деления).
е) Запоминания бывают произвольными и непроизвольными (правильное деление – дихотомическое).
ж) Математические действия делятся на сложение, вычитание, умножение, деление, возведение в степень, извлечение корня и нахождение логарифма (правильное деление).
з) Животные делятся на хищников, травоядных, всеядных и млекопитающих (подмена основания).
и) Энергия бывает механической и химической (неполное деление).
Данный текст является ознакомительным фрагментом.
Читайте также
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
Обычно в учебниках логики формулируются лишь правила таксономического деления. Мы попытаемся распространить эти правила и на мереологическое деление.Правило 1. Деление должно быть соразмерным, т.е. в случае
[Лекция 8], часы 23, 24 Обстояние. Сущность деления на планы. Феноменологический анализ смысла
[Лекция 8], часы 23, 24
Обстояние. Сущность деления на планы. Феноменологический анализ смысла
1) Я пытался наметить Вам ту общую сферу, в которой помещаются третий и четвертый план философского содержания.Эта сфера есть объективное обстояние: это тот предмет, на который
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
Обычно в учебниках логики формулируются лишь правила таксономического деления. Мы попытаемся распространить эти правила и на мереологическое деление.Правило 1. Деление должно быть соразмерным, т.е. в случае
1. Правила доказательства
1. Правила доказательства
Классификация правил доказательства обусловлена его структурой — наличием в нем тезиса, оснований и способа доказательства.Правила тезиса. Тезис — центральный пункт доказательства. Поэтому требования предъявляются прежде всего к нему.1.
II. Разрешение космологической идеи о целокупности деления данного целого в созерцании
II. Разрешение космологической идеи о целокупности деления данного целого в созерцании
Если я делю целое, данное в созерцании, то я иду от обусловленного к условиям его возможности. Деление частей (subdivisio или decompositio) есть регресс в ряду этих условий. Абсолютная целокупность
ПРАВИЛА ПРИЛИЧИЯ
ПРАВИЛА ПРИЛИЧИЯ
Одна школьница как-то спросила моего приятеля: целуясь, нужно закрывать глаза или можно оставлять их открытыми? Я вместе с этой школьницей очень сожалею, что в школе не преподают правил приличия в
§ 4. Правила для определений
§ 4. Правила для определений
Правила образования определений удобно обсуждать, не ограничиваясь аристотелевским анализом. Ниже приведены основные аспекты этих правил:1. Определение должно представлять сущность того, что в нем определяется. Определяющее выражение
Правила для руководства ума*
Правила для руководства ума*
Правило I
Целью научных занятий должно быть направление ума таким образом, чтобы он мог выносить твердые и истинные суждения обо всех тех вещах, которые ему встречаются.Таково обыкновение людей, что всякий раз, когда они замечают какое-либо
19. Правила определения
19. Правила определения
Истинность определения зависит не только от правильности подачи его содержания, но и от того, насколько стройно и последовательно будет выстроена его форма. Если истинность определения зависит от того, точно ли отражает его содержание все
20. Правила деления понятий
20. Правила деления понятий
Деление – это логическая операция, с помощью которой объем понятия, именуемый множеством, расчленяется на ряд подмножеств. С помощью этой операции раскрывается объем понятия, тогда как определение раскрывает его содержание.Непрерывность
22. Классификация деления
22. Классификация деления
Одним из особых видов деления является классификация. Это планомерное, последовательное деление понятий с распределением видов во взаимообусловленную систему, в рамках которой последние делятся на подвиды, подвиды также разбиваются на члены
43. Правила индукции
43. Правила индукции
Чтобы избегать ошибок, неточностей и неправильностей в своем мышлении, не допускать курьезов, нужно соблюдать требования, которые определяют правильность и объективную обоснованность индуктивного вывода. Ниже подробнее рассмотрены эти
2. Правила деления понятий
2. Правила деления понятий
Деление представляет собой процесс важный и зачастую непростой. В результате далеко не всегда этот процесс приводит к верному результату. Бывает, что последний содержит ошибочно добавленный не в свой класс элемент. Все это может приводить к
Основание деления
Основание деления
Когда мы делим понятие на виды, мы делим не просто так, а на основании чего-нибудь. Если мы делим женщин на блондинок, брюнеток и рыжих основанием будет являться их цвет волос. Если мы делим женщин на русских, цыганок и негритянок, основанием будет
Правила деления
Правила деления
1. Деление должно быть соразмерноДругими словами, мы должны никого не забыть. Если мы разделим холодное оружие на сабли и кастеты — это будет несоразмерное деление. Так как есть ещё и, например, топоры. Деление должно быть полным.Обратная ошибка —
II Разрешение космологической идеи о целокупности деления данного целого в созерцании
II
Разрешение космологической идеи о целокупности деления данного целого в созерцании
Если я делю целое, данное в созерцании, то я иду от обусловленного к условиям его возможности. Деление частей (subdivisio или decompositio) есть регресс в ряду этих условий. Абсолютная целокупность
В настоящей статье рассматриваются причины и
пути предупреждения у учащихся ошибок,
заключающихся в пропуске цифр частного (потеря
нулей в частном) и в по лучении лишних цифр в
частном.
Основными причинами указанных выше ошибок
являются следующие:
- неумение учащихся осознанно определять
количество цифр в частном; - имеющееся у большинства учащихся представление
о том, что меньшее число не делится даже с
остатком на большее число, а значит, и частного в
этом случае не будет; - формальное усвоение способа образования
неполных делимых; - отсутствие значения о том, что каждое неполное
делимое обязательно дает цифру частного в
соответствующем разряде.
Остановимся на каждой из указанных причин и
путях их устранения.
Обычно определение количества цифр в частном
проводится в результате таких рассуждений:
“Первое неполное делимое 8 сотен, значит, в
частном будет три цифры…”
Однако абсолютное большинство опрошенных
учащихся не смогли объяснить, почему из того, что
если первое неполное делимое 8 сотен, то в частном
будет три цифры. Отсутствие логического перехода
от разряда первого неполного делимого к
количеству цифр частного — основная причина
непонимания учащимися этого шага, а потому и его
невыполнения.
Подробнее объяснение определения количества
цифр частного дано в пособии для учителя при
выполнении деления 936 на 4: “9 сотен — это первое
неполное делимое. Когда разделим сотни, то в
частном получим сотни, а сотни в записи числа
стоят на третьем месте, значит, в частном будет 3
цифры”.
Приведенные рассуждения конкретизируют важное
общее положение: разряд первого неполного
делимого является и высшим разрядом частного.
Указанное общее положение необходимо довести и
до учащихся. Это может быть сделано в результате
обобщения способа определения количества цифр
частного для конкретных случаев деления уже на
уроке ознакомления с алгоритмом деления.
Ниже описан возможный вариант соответствующей
части урока.
После объяснения и выполнения деления
одним-двумя учащимися у доски учитель просит
детей назвать первый шаг алгоритма. Они называют
выделение первого неполного делимого,
определение количества цифр частного. Затем
детям дается задание: для каждого случая деления
(785:5, 434:7, 12360:6, 1736:8) выделить первое неполное
делимое и определить количество цифр частного,
проведя необходимые рассуждения.
Учитель направляет ответы учащихся так, чтобы
количество цифр частного определялось, в
результате примерно таких рассуждений: “Первое
неполное делимое в примере 785:5 будет 7 сотен,
значит, первая цифра частного будет обозначать
сотни. Тогда в частном будут сотни, десятки и
единицы, т. е. три цифры”. “Во втором примере (434:7)
первое неполное делимое 43 десятка, значит, первая
цифра частного будет обозначать десятки (высший
разряд частного – десятки). Значит, частное будет
состоять из десятков и единиц. Частное —
двузначное число”. “В третьем примере (12 360:6)
первое неполное делимое 12 тысяч, значит, высший
разряд частного — тысячи. Тогда частное будет
состоять из тысяч, сотен, десятков и единиц,
значит, в частном — четыре цифры”. “В четвертом
примере (1 736:8) первое неполное делимое 17 сотен,
значит, высший разряд частного — сотни. Поэтому
частное будет содержать сотни, десятки и единицы,
т. е. три цифры”.
При выполнении этого задания полезно на доске
выделить первое неполное делимое, ниже записать
название разряда этого неполного делимого и
название высшего разряда частного, отметить
точками количество цифр частного. Общий вывод —
разряд первого неполного делимого является
высшим разрядом частного — может быть сделан
самим учителем. Требовать запоминания учащимися
определения этого, вывода не нужно.
Далее дети продолжают выполнение
тренировочных упражнений в делении на
однозначное число, комментируя каждый шаг
алгоритма и объясняя способ определения
количества цифр частного.
В дальнейшем полезно в устные упражнения
включать специальные задания на определение
количества цифр частного, например, такие:
1. Сколько цифр будет содержать частное и
почему, если первое неполное делимое 12 десятков? 4
сотни? 57 тысяч? 19 десятков тысяч?
2. Выполняя деление в следующих случаях:
1) 9870:35
2) 136576:64
3) 95345:485
4) 76171:19
5) 720036:36
ученик в частном получил соответственно:
1) трехзначное число; 2) четырехзначное число; 3)
двухзначное число; 4) четырехзначное число; 5)
трехзначное число.
В каких случаях частное найдено неверно?
Почему?
3. Не выполняя действий деления и умножения,
укажите, какие из равенств неверны:
116174:58=203
44172:9 =4908
21476:7 =368
Верно ли, что меньшее число не делится на
большее? Верно, но лишь для деления нацело.
Действительно, разделить нацело одно число на
другое — это значит найти такое третье целое
неотрицательное число, умножив на которое
делитель получим делимое. Если делимое меньше
делителя (но не равно нулю), то такого целого
неотрицательного числа найти нельзя, т. е. для
случая деления, например, 2:7 частного при делении
нацело не существует.
Другое дело, если рассматривается деление с
остатком. В этом случае разделить, например, 3 на 11
означает найти таких два целых неотрицательных
числа — частное и остаток, чтобы сумма
произведения частного на делитель и остатка была
равна делимому. Указанному условию для чисел 3 и 11
удовлетворяют частное и остаток 3. Действительно:
0.11+3=3, т. е. 3:11=0 (ост. 3), где 3<11. Причем это
частное и остаток легко найти, используя
известный прием деления с остатком: “З не
делится нацело на 11. Самое большое число, которое
делится нацело на 11 и меньше 3, есть число 0.
Разделим 0 на 11, получим частное 0. Из делимого 3
вычтем 0, получим 3. Это остаток. Причем 3 меньше 11.
Итак, частное при делении 3 на 11 равно 0, остаток
равен З”.
В каждом шаге алгоритма письменного деления
выполняется именно деление с остатком, так как
при делении неполного делимого на делитель
всегда требуется найти два числа: частное и
остаток. А поэтому и случай, когда неполное
делимое меньше делителя, следует рассматривать
как деление с остатком.
Покажем теперь, как рассуждает ученик, если он
считает, что меньшее число не делится на большее,
т. е. рассматривает это деление как деление
нацело.
Пусть, например, нужно разделить 642 на 6. Найдя
первую цифру частного — 1, учащиеся часто
рассуждают так: “4 на 6 не делится, значит, буду
делить на б число 42. 42 разделить на 6, получится 7.
Частное равно 17”. В этих рассуждениях ошибочным
является утверждение 4 на 6не делится, из которого
уже логически следует оставшаяся часть
рассуждений. Действительно, слова не делится
означают частного не существует, а раз не
существует, то никакой цифры в частном от деления
4 на 6 появиться не должно! Постановка нуля в
частном в этом случае есть нарушение логики.
Появление этой цифры в частном логически
оправдано, если объяснение дается такое: “4
десятка не делится на 6 так, чтобы в частном
получился хотя бы один десяток, поэтому десятков
в частном будет 0”. Однако это объяснение для
слабых учащихся не всегда может быть оправдано,
так как после слов не делится мысль о том, что
частного в этом случае нет, может возникнуть у
них раньше, чем дальнейшие рассуждения. Ведь весь
жизненный опыт учащихся формирует у них (может
быть, неявно) абсолютно верное утверждение:
“Если какое-то действие (в широком смысле) нельзя
выполнить, то и никакого результата у такого
действия не будет!”
Предотвратить возникновение ошибок поможет
рассмотрение деления в случае, когда делимое
меньше делителя, как деления с остатком. Для
этого перед ознакомлением с алгоритмом
письменного деления следует повторить прием
деления с остатком, предлагая учащимся найти
частное и остаток и для выражений вида: 7:23, 2:5, 9:15 и
т. п.
При выполнении письменного деления в
рассмотренном выше случае (642:6 рассуждения
учащихся могут быть такими: “Второе неполное
делимое 4 десятка. 4 десятка разделим на 6. Получим
частное 0 десятков и остаток 4 десятка. 4 меньше,
чем 6, значит, цифра частного найдена верно.
Образуем следующее неполное делимое…”
Формальное усвоение учащимися способа
образования неполных делимых проявляется в том,
что, во-первых, учащиеся не определяют разряд
неполного делимого, а лишь формально
приписывают, сносят цифру полного делимого;
во-вторых, неполными делимыми считают только
числа, большие делителя, а потому при письменном
делении, например, 780 702 указывают только два
неполных делимых: 78 дес. тыс. и 702 ед., хотя в
действительности неполных делимых здесь пять: 78
дес. тыс., ,0 тыс., 7 сот., 70 дес., 702 ед.
Покажем возможные пути устранения
рассматриваемой причины ошибок.
Способ образования неполных делимых состоит из
двух операций: перевода единиц высшего разряда
(перевода остатка) в единицы следующего низшего
разряда и сложение полученного круглого числа с
единицами этого же разряда, имеющимися в полном
делимом.
При ознакомлении с алгоритмом письменного
деления необходимо выделить этот способ для
осознания и запоминания учащимися. Важно при
этом подчеркнуть, что следующее неполное делимое
единицы разряда непосредственно следующего
(низшего) за разрядом предыдущего неполного
делимого, что никаких пропусков и повторений
разрядов не должно быть.
Для закрепления полезно предложить учащимся,
например, такое задание: “При письменном делении
некоторых чисел первое неполное делимое
оказалось равным 28 тысячам. Единицы какого
разряда содержат второе неполное делимое,
третье, четвертое?”
Для осознанного овладения учащимися способом
образования неполных делимых полезно постепенно
осуществлять переход от полных рассуждений при
выполнении письменного деления к кратким,
предлагая учащимся некоторое время проводить
при делении примерно такие рассуждения:
Рисунок 1
“Первое неполное делимое 10 тыс., значит, в
частном будут тысячи, сотни, десятки и единицы, т.
е. четыре цифры. Разделю 10 на 6. Получу в разряде
тысяч в частном I. Умножу 1 на 6. Вычту из 10 число 6.
Второе неполное делимое 43 сотни. 43 разделю на 6.
Получу в частном разряде сотен 7. Умножу 7 на 6 и
вычту 42 из 43. Следующее неполное делимое 15
десятков. 15 делю на 6. В разряде десятков частного
получу 2. Умножу 2 на 6 и вычту 12 из 15. И т. д.”
При рассмотрении первого примера деления с
нулем в частном полезно использовать такую же
запись, как и для случаев без нуля в частном, и
проводить рассуждения так, как это показано ниже:
Рисунок 2
“Первое неполное делимое 4 сотни, значит в
частном будут сотни, десятки и единицы т. е. три
цифры. 4 разделю на 4, в раз ряде сотен получу 1. 1
умножу на 4. Все сотни разделили. Следующее
неполное дели мое 3 десятка. Разделю 3 на 4, получу
в разряде десятков частного 0. 0 умножу на 3, получу
0. Вычту 0 из 3. Остаток 3.
Следующее неполное делимое 32 единицы Разделю 32
на 4, получу 8 в разряде единиц частного. Частное
чисел 432 и 4 равно 108”.
Затем учитель говорит, что умножение нуля на 3 и
вычитание нуля из трех можно выполнить устно, не
записывая результате и показывает сокращенную
запись алгоритма деления для случая деления с
нулем в частном:
Рисунок 3
Рассуждения же проводятся точно так как и при
использовании первой записи.
При рассмотрении случаев деления на двузначное
число с нулем в частном также полезно в записи
иметь каждое из неполных делимых, даже если это
делимое равно нулю. Важно приучить детей к
соблюдению такой последовательности выполнения
деления: после получения неполного делимого
нужно обязательно найти соответствующую цифру
частного, записать ее в частном лишь после этого
образовывать следую неполное делимое. Выработка
у учащихся привычки всегда при выполнении
письменного деления придерживаться указанной
последовательности и есть основной путь
устранения причины ошибок, отмеченной нами выше.
Покажем на примере 480024: 24, как может быть
оформлена запись алгоритма письменного деления
и какими рассуждениями целесообразно ее
сопровождать:
Рисунок 4
“Первое неполное делимое 48 десятков тысяч,
значит, в частном будут десятки тысяч, единицы
тысяч, сотни, десятки и единицы, т. е. пять цифр.
Разделю 48 на 24, получится 2 в разряде десятков
тысяч в частном. Все десятки тысяч разделились,
остаток 0. Образую второе неполное делимое: 0
тысяч. 0 разделю на 24, получится 0 в разряде единиц
тысяч в частном. Следующее неполное делимое 0
сотен. 0 разделю на 24, получится 0 в разряде сотен в
частном. Следующее неполное делимое 2 десятка. 2
разделю на 24, в частном в разряде десятков получу
0, в остатке 2. Следующее неполное делимое 24
единицы. 24 разделю на 24, получится 1 в разряде
единиц частного. Частное чисел 480024 и 24 равно 20001”.
В дальнейшем применяется обычная запись, но в
случае затруднений, ошибок можно прибегать и к
приведенной выше записи или же к такой, как
показано ниже:
Рисунки 5 и 6
В заключение отметим, что формирование любого
навыка идет успешнее, если этот навык осознанный.
Именно поэтому усиление внимания учителей ко
всем отмеченным выше моментам в обучении
алгоритму письменного деления будет
способствовать выработке более прочных
вычислительных навыков.
Георгий Челпанов
Задача деления. От процесса определения отличается процесс деления (divisio). Различие между ними заключается в том, что определение раскрывает содержание понятия, а деление раскрывает его объём. Задача деления заключается в том, чтобы указать все виды, совокупность которых составляет объём данного понятия. Так, например, понятие «треугольник» мы могли делить следующим образом:
Треугольник (A):
• Прямоугольный (B)
• Остроугольный (C)
• Тупоугольный (D)
У нас было понятие «треугольник» (A), и мы перечислили все частные понятия: B, C и D, входящие в объём этого более общего понятия, которое относится к ним, как род к своим видам.
То понятие, объём которого мы раскрываем, называется делимым (totum dividendum), а те виды, которые получаются от деления, называются членами деления (membra divisionis).
Основание деления. Когда мы производим деление рода на виды, то мы обращаем внимание на те признаки, которыми обладают одни виды и не обладают другие. Тот признак, который даёт нам возможность разделить род на виды, называется основанием деления (fundamentum divisionis). Основанием вышеприведённого деления понятия «треугольник» была величина углов в треугольнике. Но можно, это же самое понятие делить по какому-нибудь другому основанию, например положить в основание деления отношение сторон треугольника по величине. Тогда деление представится в следующем виде:
Треугольник (A):
• Равносторонний (B)
• Равнобедренный (C)
• Разносторонний (D)
Процесс несколько усложняется, если полученные от деления виды в свою очередь делить на подвиды (этот процесс называется подразделением ). Так, например, вид понятия «треугольник», именно тупоугольный треугольник (или какой-нибудь другой), можно в свою очередь подразделить на подвиды: равнобедренный и разносторонний; разумеется, деление и подразделение будут относиться к одному понятию: дихотомия. В процессе деления иногда употребляется приём, который называется дихотомией и который заключается в деления данного понятия A на противоречащие понятия B и не-B. Берём какое-нибудь понятие, которое нам надо разделить, например понятие «человек»; выделяем в одну группу какой-нибудь из видов, заключающихся в этом понятии, например вид «славянин», а в другую группу – «не-славянин» – относим все прочие виды. Затем с этим вторым отрицательным понятием поступаем точно таким же образом: подразделяем понятие «не-славянин» на две группы; в одну из них относим, например, подвид «германец», а в другую – все прочие остающиеся подвиды, соединяя их в одно понятие «не-германец»; затем с этим понятием поступаем точно так же, как и с предыдущим, и продолжаем наше деление до тех пор, пока оно не окажется исчерпанным.
Человек:
• Славянин
• Не-славянин:
• Германец
• Не-германец
И т.д.
Этот приём имеет тот недостаток, что оставляет каждый раз крайне неопределённой часть объёма делимого понятия, именно ту часть, которая обозначается частицей не, но, с другой стороны, значительно облегчает самый процесс деления, потому что придаёт ему исчерпывающий характер, почему его иногда называют исчерпывающим делением. Что оно имеет исчерпывающий характер, можно объяснить при помощи следующего примера. Если мы разделим всех обитателей Европы и Азии на расы – белую и жёлтую, то может оказаться, что некоторые племена не подойдут ни под одну из этих рас и мы не будем в состоянии поместить их в нашем делении, но этого не будет в том случае, если мы будем делить дихотомически.
Обитатели земного шара:
• Белые
• Не-белые:
• Жёлтые
• Не-жёлтые
При таком делении всякое новое племя должно будет войти в последнюю группу, которая не будет ни белой, ни жёлтой. В этом заключаются преимущества дихотомического деления.
Правила деления. Деление должно подчиняться следующим правилам:
1. Деление должно быть адекватно, или соразмерно. Это значит, что если мы перечисляем по какому-нибудь основанию или принципу виды данного родового понятия, то мы должны точно перечислить все виды, не уменьшая и не увеличивая их количества, т.е. сумма видов должна равняться делимому роду.
Если при делении мы не перечислим всех видов, т.е. если эта сумма будет меньше, то у нас получится деление неполное; если же мы в объём делимого понятия введём виды, которые в нём на самом деле не содержатся, то у нас получится деление слишком обширное, т.е. указанная сумма будет больше. Например, положив в основание деления понятия «треугольник» величину его углов, мы могли бы получить такое деление:
Треугольник:
• Остроугольный
• Тупоугольный
Ясно, что это деление неполное, ибо здесь не хватает одного члена деления, потому что в объёме понятия «треугольник» находится ещё один вид, который при делении нами пропущен, именно прямоугольный треугольник.
Неполным было бы деление людей на порочных и добродетельных, деление научных теорий на истинные и ложные, потому что в этих делениях упускаются промежуточные ступени. Кроме людей порочных и добродетельных есть люди, о которых нельзя сказать, что они порочны, но нельзя также сказать, что они добродетельны; кроме истинных и ложных теорий существуют ещё теории частью истинные и частью ложные.
Обратная ошибка будет получаться в том случае, если мы, деля какое-либо понятие, вводим в его объём такой вид, который не входит в действительности в его объём. Если бы мы, например, разделили понятие «дерево» на «дуб», «ель», «фиалка», то очевидно, что вид «фиалка» относится к объёму совсем другого понятия и что при делении понятия «дерево» он попал в число членов его неправильно.
2. Члены деления должны исключать друг друга. Это требование станет ясным, если мы возьмём для примера, следующее деление:
Книги:
• Французские
• Немецкие
• Словари и т.д.
Это деление неправильно, ибо понятие, например, «французские книги» и понятие «словари» не исключают друг друга: книга может быть и французской и словарём в одно и то же время. Или возьмём в пример также другое деление понятия «книги»:
Книги:
• Полезные
• Понятные
• Интересные и т.д.
Здесь один вид книг не исключает из своего объёма других видов: полезная книга может быть в одно и то же время и понятной и интересной. Ошибки, как в первом, так и во втором из приведённых примеров деления произошли потому, что не было выдержано третье требование правильного деления, а именно:
3. Деление должно иметь одно основание. При делении понятий чаще всего повторяется ошибка, заключающаяся в том, что в процессе деления меняется основание деления.
Произведём деление народов Европы:
Народы Европы:
• Магометане
• Христиане
• Французы
• Немцы и т.д.
Это деление неправильно, ибо мы, взяв сначала основанием деления понятие «религия», затем меняем это основание на другое, именно на понятие «национальность».
Или другой пример:
Прямолинейные фигуры:
• Треугольники
• Параллелограммы
• Прямоугольники
• Многоугольники
Это деление также неправильно, так как у нас здесь скрещиваются такие различные основания деления, как число сторон, направление сторон, величина углов. Такое деление называется перекрёстным.
Итак, третье условие правильности деления заключается в том, чтобы при последовательном перечислении видов делимого понятия было выдержано одно основание деления. Но следует заметить, что одно основание деления должно быть выдержано только при первом делении понятия; уже при вторичном делении, т.е. при подразделении, основание деления должно измениться. Так, например, если мы разделили понятие «треугольник», взяв основанием деления величину углов, на такие виды, как остроугольный, прямоугольный и тупоугольный, то, желая далее продолжать деление какого-нибудь из этих членов деления, мы уже должны основание деления изменить. Так, понятие «остроугольный треугольник» мы можем делить ещё далее, если возьмём основанием деления уже не величину углов, а отношение сторон по величине.
Треугольник:
1) Тупоугольный
2) Прямоугольный
3) Остроугольный:
а) равносторонний
б) равнобедренный
в) разносторонний
4. Деление должно быть непрерывным, т.е. при делении какого-либо понятия нужно переходить к ближайшему низшему роду, в противном случае будет получаться то, что называется скачком в делении. Если бы мы понятие «природа» разделили на 1) «животные», 2) «растения», 3) «минералы», то в этом делении был бы слишком внезапный переход от понятия «природа» к понятиям «минералы», «животные». Чтобы исправить ошибку, следует вставить между понятием «природа» и членами вышеприведённого деления ещё два посредствующих звена.
Именно: понятия «мир неорганический» и «мир органический». Тогда деление приняло бы следующий вид:
Природа:
Мир органический:
• животные
• растения
Мир неорганический:
• минералы и проч.
Вопросы для повторения
Какова задача деления? Что называется делимым понятием? Что называется членами деления? Что такое основание деления? Что такое подразделение? Что такое дихотомия? Его преимущества и недостатки. Перечислите правила деления. Приведите примеры ни каждое правило и укажите применение каждого правила.
Источник: Учебник логики (для гимназий и самообразования). — 2-е изд. — Киев ; Одесса: И.А. Розов, 1906 (Киев). — [2], IV, II, 177 с.
Комментарии для сайта Cackle
Юлия Валерьевна Шульгина
Эксперт по предмету «Логика»
преподавательский стаж — 10 лет
Задать вопрос автору статьи
Сущность деления понятия
Определение 1
Деление понятия – это логическая операция, позволяющая выявить все существующие виды некоторого рода на основании какого-либо общего признака.
В обыденной жизни люди постоянно сталкиваются с необходимостью распределить множество предметов на группы тем или иным образом. Например, человек хочет расставить книги в своей домашней библиотеке:
- можно расставить их по тематике: на одну полку поставить справочники и учебники, на другую – поэзию, на третью – детективы и т. д.;
- можно распределить их по фамилиям авторов в алфавитном порядке;
- можно группировать по цвету переплета и т. д.
В каждом описанном варианте все предметы одной группы будут обладать специфическим признаком, отличающим их от предметов другой группы (ни один из предметов другой группы таким признаком обладать не будет). Так, среди сборников стихов не окажется ни одного справочника.

Английский язык для начинающих
Не откладывай мечты — начни говорить под руководством опытного преподавателя
Узнать подробнее
Нередко условия требуют мысленного распределения, а не физической расстановки предметов.
Например, треугольники можно разделить на тупоугольные, прямоугольные и остроугольные.
Описанная мыслительная операция является делением понятия. Ее отличительная черта – разбиение объема некоторого класса (понятия) на подклассы (группы) в зависимости от обладания некоторым специфическим признаком. Логическое деление предназначено для того, чтобы установить все разновидности предметов, которым присуще содержание понятия, подвергающегося делению.
К операции логического деления прибегают и в том случае, когда нужно провести обзор материала или упорядочить его, составить план работы, как-либо систематизировать множество предметов. Особенно важна эта операция для научного познания, поскольку она помогает раскрыть объем понятия путем выделения в нем всех возможных подгрупп.
Определение 2
Признак, по наличию которого выполняют деление, называется основанием деления.
«Деление понятия: правила и возможные ошибки» 👇
Например, государства бывают республиками и монархиями. Основание деления – форма правления.
Определение 3
Группы, которые получены в ходе деления, называют видами или членами деления.
Выбор основания деления определяется целью, конкретной решаемой задачей. Задачи бывают разными, поэтому одно и то же понятие может делиться по разным признакам.
Например, согласные звуки делятся на глухие и звонкие; на твердые и мягкие.
Выбирая основание деления, желательно останавливаться на существенных признаках. Такое деление имеет эвристическую ценность, т.к. способствует более глубокому пониманию природы входящих в понятие объектов.
Деление бывает двух видов:
- дихотомическое деление, при котором объем понятия распределяют на два класса, противоречащих друг другу: предметы одного класса обладают признаком, а предметы второго класса не обладают им;
- деление по видоизменению признака, при котором объем понятия распределяют на подмножества, в каждом из которых признак, служащий основанием деления, проявляется со своими особенностями.
Правила деления понятия
При делении понятия необходимо соблюдать ряд правил.
Правило соразмерности заключается в том, что объединение (сумма) объемов членов деления должно совпадать с объемом исходного понятия. Это значит, что ни один предмет, принадлежащий исходному понятию, не должен быть пропущен, и ни один лишний предмет не должен быть добавлен. При нарушении этого правила возникают ошибки неполного или избыточного деления. Ошибка неполного деления часто возникает при попытке провести дихотомическое деление, если выделяют два противоположных (но не противоречащих) класса; а также при делении по видоизменению признака, если перечисляют не все получаемые члены деления.
Пример неполного деления: «Посуда бывает металлической, керамической и стеклянной». Здесь пропущена пластиковая посуда.
Пример избыточного деления: «Предложения бывают вопросительными, побудительными, повествовательными и такими, от которых нельзя отказаться». Здесь предложения как грамматическая категория поделены на виды в зависимости от цели высказывания (вопросительные, побудительные, повествовательные), а затем добавлен лишний член – «такие, от которых нельзя отказаться».
Правило несовместимости заключается в том, что члены деления должны быть несовместимыми понятиями, т. е. исключать друг друга. Иными словами, каждый элемент должен входить только в одно подмножество. Если это правило нарушено, возникает ошибка перекрещивания (пересечения) понятия;
Например: «Фильмы бывают смешными и грустными». Существуют трагикомедии, сочетающие в себе грустные и веселые элементы, – при таком делении их пришлось бы относить к обеим категориям.
Иллюстрацией перекрещивания понятий может служить анекдот про обезьяну, которая не могла определиться, к какой группе зверей ей нужно примкнуть – к умным или к красивым.
Правило единственного основания заключается в том, что деление должно быть выполнено по одному основанию. Это правило касается деления по видоизменению признака. Его суть состоит в том, что нельзя делить понятие с использованием одновременно нескольких признаков. При нарушении этого правила часто одновременно возникает и ошибка пересечения.
Пример деления по разным основаниями: «Тексты бывают художественными, научными, официально-деловыми, рукописными, печатными, безграмотными».
Правило непрерывности заключающееся в том, что при делении нельзя сразу переходить к подвиду от рода, минуя вид. Другими словами, нельзя допускать «скачки»: деление нужно выполнять последовательно. Это требование касается поэтапного, многоступенчатого деления. Если нарушить его, деление будет непонятным и громоздким, стройность мышления нарушится.
Пример «скачка» в делении понятия: «Членами предложения являются подлежащее, сказуемое и второстепенные члены». Правильное деление – это деление на главные и второстепенные члены. Далее главные члены делятся на подлежащее и сказуемое, а второстепенные – на определение, дополнение, обстоятельство, т. е. сначала выделяются виды, а затем в каждом виде – подвиды.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
1.12. Правила деления
Существует несколько логических правил деления понятия. Нарушение хотя бы одного из них приводит к тому, что объем понятия не раскрывается, и деление не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении.
1. Деление должно проводиться по одному основанию, т. е. при делении понятия следует придерживаться только одного выбранного признака. Например, в делении: Люди бывают мужчинами, женщинами и учителями используются два разных основания – пол и профессия, что недопустимо. Ошибка, возникающая при нарушении этого правила, называется подменой основания. В делении с подменой основания может использоваться не только два разных основания, как в приведенном выше примере, но и больше. Например, в делении: Люди бывают мужчинами, женщинами, китайцами и блондинами, как видим, используются три различных основания – пол, национальность и цвет волос, что, конечно же, тоже является ошибкой.
2. Деление должно быть полным, т. е. надо перечислить все возможные результаты деления (суммарный объем всех результатов деления должен быть равен объему исходного делимого понятия). Например, деление: Учебные заведения бывают начальными и средними является неполным, т. к. не указан еще один результат деления – высшие учебные заведения. Но как быть, если надо перечислять не два или три, а десятки или сотни результатов деления. В этом случае можно употреблять понятия: и другие, и прочие, и так далее, и тому подобное, которые будут включать в себя не перечисленные результаты деления. Например: Люди бывают русскими, немцами, китайцами, японцами и представителями других национальностей.
3. Результаты деления не должны пересекаться, т. е. понятиям, представляющим собой результаты деления, следует быть несовместимыми, их объемы не должны иметь общих элементов (на схеме Эйлера круги, обозначающие результаты деления, не должны соприкасаться, располагаясь отдельно друг от друга). Например, в делении: Страны мира делятся на северные, южные, восточные и западные допущена ошибка – пересечение результатов деления. На первый взгляд приведенное в качестве примера деление кажется безошибочным: оно проведено по одному основанию (сторона света) и является полным (все стороны света перечислены). Чтобы увидеть ошибку в данном делении надо рассуждать так. Возьмем какую-нибудь страну, например, Канаду и ответим на вопрос – является ли она северной? Конечно, является, т. к. расположена в северном полушарии Земли. Теперь ответим на вопрос, является ли Канада западной страной? Да, потому что она расположена в западном полушарии Земли. Таким образом, получается, что Канада – одновременно и северная, и западная страна, т. е. она является общим элементом объемов понятий северные страны и западные страны, а значит, эти понятия, а вернее их объемы, пересекаются. То же самое можно сказать и относительно понятий южные страны и восточные страны. На схеме Эйлера результаты деления из нашего примера будут располагаться так:

Вспомним, каждая классификация построена таким образом, что любой элемент, попадающий в одну ее группу (часть, вид), ни в коем случае не попадает в другие. Это и есть следствие непересечения результатов деления или их взаимоисключения при составлении какой угодно классификации.
4. Деление должно быть последовательным, т. е. не допускающим пропусков и скачков. Рассмотрим следующее деление: Леса бывают хвойными, лиственными, смешанными и сосновыми. Явно лишним здесь выглядит понятие сосновые леса, в силу чего допущенная в делении ошибка напоминает подмену основания (см. первое правило). Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Подмена основания присутствует в таком, например, делении: Леса бывают хвойными, лиственными, смешанными, подмосковными и таежными. (Деление проведено по двум разным основаниям – тип древесных листьев и географическое местонахождение леса). Вернемся к нашему первому примеру. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведенном примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Еще раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении: Учебные заведения бывают начальными, средними, высшими и университетами присутствует скачок, а в делении: Учебные заведения бывают начальными, средними, высшими и коммерческими допущена подмена основания.
Приведем еще несколько примеров правильного деления, а также – деления, в котором нарушены рассмотренные правила и допущены различные ошибки.
а) Транспорт бывает наземным, подземным, водным, воздушным, общественным и личным (подмена основания).
б) По темпераменту люди делятся на сангвиников, меланхоликов, флегматиков и холериков (пересечение результатов деления).
в) Геометрические фигуры делятся на плоские, объемные, треугольники и квадраты (скачок в делении).
г) Отбор в живой природе бывает искусственным или естественным (правильное деление).
д) Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими (пересечение результатов деления).
е) Запоминания бывают произвольными и непроизвольными (правильное деление – дихотомическое).
ж) Математические действия делятся на сложение, вычитание, умножение, деление, возведение в степень, извлечение корня и нахождение логарифма (правильное деление).
з) Животные делятся на хищников, травоядных, всеядных и млекопитающих (подмена основания).
и) Энергия бывает механической и химической (неполное деление).
Данный текст является ознакомительным фрагментом.
Читайте также
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
Обычно в учебниках логики формулируются лишь правила таксономического деления. Мы попытаемся распространить эти правила и на мереологическое деление.Правило 1. Деление должно быть соразмерным, т.е. в случае
[Лекция 8], часы 23, 24 Обстояние. Сущность деления на планы. Феноменологический анализ смысла
[Лекция 8], часы 23, 24
Обстояние. Сущность деления на планы. Феноменологический анализ смысла
1) Я пытался наметить Вам ту общую сферу, в которой помещаются третий и четвертый план философского содержания.Эта сфера есть объективное обстояние: это тот предмет, на который
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
§ 6. ПРАВИЛА ДЕЛЕНИЯ. ОШИБКИ, ВОЗМОЖНЫЕ ПРИ ДЕЛЕНИИ
Обычно в учебниках логики формулируются лишь правила таксономического деления. Мы попытаемся распространить эти правила и на мереологическое деление.Правило 1. Деление должно быть соразмерным, т.е. в случае
1. Правила доказательства
1. Правила доказательства
Классификация правил доказательства обусловлена его структурой — наличием в нем тезиса, оснований и способа доказательства.Правила тезиса. Тезис — центральный пункт доказательства. Поэтому требования предъявляются прежде всего к нему.1.
II. Разрешение космологической идеи о целокупности деления данного целого в созерцании
II. Разрешение космологической идеи о целокупности деления данного целого в созерцании
Если я делю целое, данное в созерцании, то я иду от обусловленного к условиям его возможности. Деление частей (subdivisio или decompositio) есть регресс в ряду этих условий. Абсолютная целокупность
ПРАВИЛА ПРИЛИЧИЯ
ПРАВИЛА ПРИЛИЧИЯ
Одна школьница как-то спросила моего приятеля: целуясь, нужно закрывать глаза или можно оставлять их открытыми? Я вместе с этой школьницей очень сожалею, что в школе не преподают правил приличия в
§ 4. Правила для определений
§ 4. Правила для определений
Правила образования определений удобно обсуждать, не ограничиваясь аристотелевским анализом. Ниже приведены основные аспекты этих правил:1. Определение должно представлять сущность того, что в нем определяется. Определяющее выражение
Правила для руководства ума*
Правила для руководства ума*
Правило I
Целью научных занятий должно быть направление ума таким образом, чтобы он мог выносить твердые и истинные суждения обо всех тех вещах, которые ему встречаются.Таково обыкновение людей, что всякий раз, когда они замечают какое-либо
19. Правила определения
19. Правила определения
Истинность определения зависит не только от правильности подачи его содержания, но и от того, насколько стройно и последовательно будет выстроена его форма. Если истинность определения зависит от того, точно ли отражает его содержание все
20. Правила деления понятий
20. Правила деления понятий
Деление – это логическая операция, с помощью которой объем понятия, именуемый множеством, расчленяется на ряд подмножеств. С помощью этой операции раскрывается объем понятия, тогда как определение раскрывает его содержание.Непрерывность
22. Классификация деления
22. Классификация деления
Одним из особых видов деления является классификация. Это планомерное, последовательное деление понятий с распределением видов во взаимообусловленную систему, в рамках которой последние делятся на подвиды, подвиды также разбиваются на члены
43. Правила индукции
43. Правила индукции
Чтобы избегать ошибок, неточностей и неправильностей в своем мышлении, не допускать курьезов, нужно соблюдать требования, которые определяют правильность и объективную обоснованность индуктивного вывода. Ниже подробнее рассмотрены эти
2. Правила деления понятий
2. Правила деления понятий
Деление представляет собой процесс важный и зачастую непростой. В результате далеко не всегда этот процесс приводит к верному результату. Бывает, что последний содержит ошибочно добавленный не в свой класс элемент. Все это может приводить к
Основание деления
Основание деления
Когда мы делим понятие на виды, мы делим не просто так, а на основании чего-нибудь. Если мы делим женщин на блондинок, брюнеток и рыжих основанием будет являться их цвет волос. Если мы делим женщин на русских, цыганок и негритянок, основанием будет
Правила деления
Правила деления
1. Деление должно быть соразмерноДругими словами, мы должны никого не забыть. Если мы разделим холодное оружие на сабли и кастеты — это будет несоразмерное деление. Так как есть ещё и, например, топоры. Деление должно быть полным.Обратная ошибка —
II Разрешение космологической идеи о целокупности деления данного целого в созерцании
II
Разрешение космологической идеи о целокупности деления данного целого в созерцании
Если я делю целое, данное в созерцании, то я иду от обусловленного к условиям его возможности. Деление частей (subdivisio или decompositio) есть регресс в ряду этих условий. Абсолютная целокупность

