Ошибка округления формула - Не ошибается лишь тот, кто ничего не делает!

Ошибки округления

Даже
если предположить, что исходная информация
не содержит никаких ошибок и все
вычислительные процессы конечны и не
приводят к ошибкам ограничения, то все
равно в этом случае присутствует третий
тип ошибок – ошибки округления.
Предположим, что вычисления производятся
на машине, в которой каждое число
представляется 5-ю значащими цифрами,
и что необходимо сложить два числа
9.2654 и 7.1625, причем эти два числа являются
точными. Сумма их равна 16.4279, она содержит
6 значащих цифр и не помещается в разрядной
сетке нашей гипотетической машины.
Поэтому 6-значный результат будет
округлен
до 16.428, и при этом возникает ошибка
округления.
Так как компьютеры всегда работают с
конечным числом значащих цифр, то
потребность в округлении возникает
довольно часто.

Вопросы
округления относятся только к
действительным числам. При выполнении
операций с целыми числами потребность
в округлении не возникает. Сумма, разность
и произведение целых чисел сами являются
целыми числами; если результат слишком
велик, то это свидетельствует об ошибке
в программе. Частное от деления двух
целых чисел не всегда является целым
числом, но при делении целых чисел
дробная часть отбрасывается.

Абсолютная и относительная погрешности

Допустим,
что точная ширина стола – А=384 мм, а мы,
измерив ее, получили а=381 мм. Модуль
разности между точным значением
измеряемой величины и ее приближенным
значением называется абсолютной
погрешностью
.
В данном примере абсолютная погрешность
3 мм. Но на практике мы никогда не знаем
точного значения измеряемой величины,
поэтому не можем точно знать абсолютную
погрешность.

Но
обычно мы знаем точность измерительных
приборов, опыт наблюдателя, производящего
измерения и т.д. Это дает возможность
составить представление об абсолютной
погрешности измерения. Если, например,
мы рулеткой измеряем длину комнаты, то
нам нетрудно учесть метры и сантиметры,
но вряд ли мы сможем учесть миллиметры.
Да в этом и нет надобности. Поэтому мы
сознательно допускаем ошибку в пределах
1 см. абсолютная погрешность длины
комнаты меньше 1 см. Измеряя длину
какого-либо отрезка миллиметровой
линейкой, мы имеем право утверждать,
что погрешность измерения не превышает
1 мм.

Абсолютная
погрешность _а
приближенного числа а дает возможность
установить границы, в которых лежит
точное число А:

Абсолютная
погрешность не является достаточным
показателем качества измерения и не
характеризует точность вычислений или
измерений. Если известно, что, измерив
некоторую длину, мы получили абсолютную
погрешность в 1 см, то никаких заключений
о том, хорошо или плохо мы измеряли,
сделать нельзя. Если мы измеряли длину
карандаша в 15 см и ошиблись на 1 см, наше
измерение никуда не годится. Если же мы
измеряли 20-метровый коридор и ошиблись
всего на 1 см, то наше измерение – образец
точности. Важна
не только сама абсолютная погрешность,
но и та доля, которую она составляет от
измеренной величины.
В первом примере абс. погрешность 1 см
составляет 1/15 долю измеряемой величины
или 7%, во втором – 1/2000 или 0.05%. Второе
измерение значительно лучше.

Относительной
погрешностью называют отношение
абсолютной погрешности к абсолютному
значению приближенной величины:

В
отличие от абсолютной погрешности,
которая обычно есть величина размерная,
относительная погрешность всегда есть
величина безразмерная. Обычно ее выражают
в %.

Пример

При измерении
длины в 5 см допущена абсолютная
погрешность в 0.1 см. Какова относительная
погрешность? (Ответ 2%)

При
подсчете числа жителей города, которое
оказалось равным 2000000,
допущена
погрешность 100 человек. Какова относительная
погрешность? (Ответ
0.005%)

Результат
всякого измерения выражается числом,
лишь приблизительно характеризующим
измеряемую величину. Поэтому при
вычислениях мы имеем дело с приближенными
числами. При записи приближенных чисел
принимается, что последняя цифра справа
характеризует величину абсолютной
погрешности.

Например,
если записано 12.45, то это не значит, что
величина, характеризуемая этим числом,
не содержит тысячных долей. Можно
утверждать, что тысячные доли при
измерении не учитывались, следовательно,
абсолютная погрешность меньше половины
единицы последнего разряда:
.
Аналогично, относительно приближенного
числа 1.283, можно сказать, что абсолютная
погрешность меньше 0.0005:.

Приближенные
числа принято записывать так, чтобы
абсолютная погрешность не превышала
единицы последнего десятичного разряда.
Или, иначе говоря, абсолютная
погрешность приближенного числа
характеризуется числом десятичных
знаков после запятой.

Как же
быть, если при тщательном измерении
какой-нибудь величины получится, что
она содержит целую единицу, 2 десятых,
5 сотых, не содержит тысячных, а
десятитысячные не поддаются учету? Если
записать 1.25, то в этой записи тысячные
не учтены, тогда как на самом деле мы
уверены, что их нет. В таком случае
принято ставить на их месте 0, – надо
писать 1.250. Таким образом, числа 1.25 и
1.250 обозначают не одно и то же. Первое –
содержит тысячные; мы только не знаем,
сколько именно. Второе – тысячных не
содержит, о десятитысячных ничего
сказать нельзя.

Сложнее
приходится при записи больших приближенных
чисел. Пусть число жителей деревни равно
2000 человек, а в городе приблизительно
457000
жителей. Причем относительно города в
тысячах мы уверены, но допускаем
погрешность в сотнях и десятках. В первом
случае нули в конце числа указывают на
отсутствие сотен, десятков и единиц,
такие нули мы назовем значащими;
во втором случае нули указывают на наше
незнание числа сотен, десятков и единиц.
Такие нули мы назовем незначащими.
При записи приближенного числа,
содержащего нули надо дополнительно
оговаривать их значимость. Обычно нули
– незначащие. Иногда на незначимость
нулей можно указывать, записывая число
в экспоненциальном виде (457*10³).

Сравним
точность двух приближенных чисел 1362.3
и 2.37. В первом абсолютная погрешность
не превосходит 0.1, во втором – 0.01. Поэтому
второе число выглядит более точным, чем
первое.

Подсчитаем
относительную погрешность. Для первого
числа
;
для второго.
Второе число значительно (почти в 100
раз) менее точно, чем первое. Получается
это потому, что в первом числе дано 5
верных (значащих) цифр, тогда как во
втором – только 3.

Все
цифры приближенного числа, в которых
мы уверены, будем называть верными
(значащими) цифрами. Нули сразу справа
после запятой не бывают значащими, они
лишь указывают на порядок стоящих правее
значащих цифр. Нули в крайних правых
позициях числа могут быть как значащими,
так и не значащими. Например, каждое из
следующих чисел имеет 3 значащие цифры:
283*10⁵,
200*10²,
22.5, 0.0811, 2.10, 0.0000458.

Пример

Сколько
значащих (верных) цифр в следующих
числах:

0.75
(2), 12.050 (5), 1875*10⁵
(4), 0.06*10⁹
(1)

Оценить
относительную погрешность следующих
приближенных чисел:

0.989
(0.1%),

нули
значащие: 21000 (0.005%),

0.000
024
(4%),

0.05 (20%)

Нетрудно
заметить, что для примерной оценки
относительной погрешности числа
достаточно подсчитать количество
значащих цифр. Для числа, имеющего только
одну значащую цифру относительная
погрешность около 10%;

с
2-мя значащими цифрами – 1%;

с
3-мя значащими цифрами – 0.1%;

с
4-мя значащими цифрами – 0.01% и т.д.

При
вычислениях с приближенными числами
нас будет интересовать вопрос: как,
исходя из данных приближенных чисел,
получить ответ с нужной относительной
погрешностью.

Часто
при этом все исходные данные приходится
брать с одной и той же погрешностью,
именно с погрешностью наименее точного
из данных чисел. Поэтому часто приходится
более точное число заменять менее точным
– округлять.

округление
до десятых 27.136 
27.1,

округление
до целых 32.8 
33.

Правило
округления: Если крайняя левая из
отбрасываемых при округлении цифр
меньше 5, то последнюю сохраняемую цифру
не изменяют; если крайняя левая из
отбрасываемых цифр больше 5 или если
она равна 5, то последнюю сохраняемую
цифру увеличивают на 1.

Пример

округлить
до десятых 17.96 (18.0)

округлить
до сотых 14.127 (14.13)

округлить,
сохранив 3 верные цифры: 83.501 (83.5), 728.21
(728), 0.0168835 (0.01688).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

For the acrobatic movement, roundoff, see Roundoff.

In computing, a roundoff error,^[1] also called rounding error,^[2] is the difference between the result produced by a given algorithm using exact arithmetic and the result produced by the same algorithm using finite-precision, rounded arithmetic.^[3] Rounding errors are due to inexactness in the representation of real numbers and the arithmetic operations done with them. This is a form of quantization error.^[4] When using approximation equations or algorithms, especially when using finitely many digits to represent real numbers (which in theory have infinitely many digits), one of the goals of numerical analysis is to estimate computation errors.^[5] Computation errors, also called numerical errors, include both truncation errors and roundoff errors.

When a sequence of calculations with an input involving any roundoff error are made, errors may accumulate, sometimes dominating the calculation. In ill-conditioned problems, significant error may accumulate.^[6]

In short, there are two major facets of roundoff errors involved in numerical calculations:^[7]

The ability of computers to represent both magnitude and precision of numbers is inherently limited.
Certain numerical manipulations are highly sensitive to roundoff errors. This can result from both mathematical considerations as well as from the way in which computers perform arithmetic operations.

Representation error[edit]

The error introduced by attempting to represent a number using a finite string of digits is a form of roundoff error called representation error.^[8] Here are some examples of representation error in decimal representations:

Notation	Representation	Approximation	Error
1/7	0.142 857	0.142 857	0.000 000 142 857
ln 2	0.693 147 180 559 945 309 41…	0.693 147	0.000 000 180 559 945 309 41…
log₁₀ 2	0.301 029 995 663 981 195 21…	0.3010	0.000 029 995 663 981 195 21…
³√2	1.259 921 049 894 873 164 76…	1.25992	0.000 001 049 894 873 164 76…
√2	1.414 213 562 373 095 048 80…	1.41421	0.000 003 562 373 095 048 80…
e	2.718 281 828 459 045 235 36…	2.718 281 828 459 045	0.000 000 000 000 000 235 36…
π	3.141 592 653 589 793 238 46…	3.141 592 653 589 793	0.000 000 000 000 000 238 46…

Increasing the number of digits allowed in a representation reduces the magnitude of possible roundoff errors, but any representation limited to finitely many digits will still cause some degree of roundoff error for uncountably many real numbers. Additional digits used for intermediary steps of a calculation are known as guard digits.^[9]

Rounding multiple times can cause error to accumulate.^[10] For example, if 9.945309 is rounded to two decimal places (9.95), then rounded again to one decimal place (10.0), the total error is 0.054691. Rounding 9.945309 to one decimal place (9.9) in a single step introduces less error (0.045309). This can occur, for example, when software performs arithmetic in x86 80-bit floating-point and then rounds the result to IEEE 754 binary64 floating-point.

Floating-point number system[edit]

Compared with the fixed-point number system, the floating-point number system is more efficient in representing real numbers so it is widely used in modern computers. While the real numbers are infinite and continuous, a floating-point number system is finite and discrete. Thus, representation error, which leads to roundoff error, occurs under the floating-point number system.

Notation of floating-point number system[edit]

A floating-point number system is characterized by integers:

Any has the following form:

${displaystyle x=pm (underbrace {d_{0}.d_{1}d_{2}ldots d_{p-1}} _{text{mantissa}})_{beta }times beta ^{overbrace {E} ^{text{exponent}}}=pm d_{0}times beta ^{E}+d_{1}times beta ^{E-1}+ldots +d_{p-1}times beta ^{E-(p-1)}}$

where $d_{i}$ is an integer such that ${displaystyle 0leq d_{i}leq beta -1}$ for , and is an integer such that .

Normalized floating-number system[edit]

IEEE standard[edit]

In the IEEE standard the base is binary, i.e. , and normalization is used. The IEEE standard stores the sign, exponent, and mantissa in separate fields of a floating point word, each of which has a fixed width (number of bits). The two most commonly used levels of precision for floating-point numbers are single precision and double precision.

Precision	Sign (bits)	Exponent (bits)	Mantissa (bits)
Single	1	8	23
Double	1	11	52

Machine epsilon[edit]

Machine epsilon can be used to measure the level of roundoff error in the floating-point number system. Here are two different definitions.^[3]

Roundoff error under different rounding rules[edit]

There are two common rounding rules, round-by-chop and round-to-nearest. The IEEE standard uses round-to-nearest.

x	Round-by-chop	Roundoff Error	Round-to-nearest	Roundoff Error
1.649	1.6	0.049	1.6	0.049
1.650	1.6	0.050	1.6	0.050
1.651	1.6	0.051	1.7	-0.049
1.699	1.6	0.099	1.7	-0.001
1.749	1.7	0.049	1.7	0.049
1.750	1.7	0.050	1.8	-0.050

Calculating roundoff error in IEEE standard[edit]

Suppose the usage of round-to-nearest and IEEE double precision.

Example: the decimal number ${displaystyle (9.4)_{10}=(1001.{overline {0110}})_{2}}$ can be rearranged into

${displaystyle +1.underbrace {0010110011001100110011001100110011001100110011001100} _{text{52 bits}}110ldots times 2^{3}}$

Since the 53-rd bit to the right of the binary point is a 1 and is followed by other nonzero bits, the round-to-nearest rule requires rounding up, that is, add 1 bit to the 52-nd bit. Thus, the normalized floating-point representation in IEEE standard of 9.4 is

${displaystyle fl(9.4)=1.0010110011001100110011001100110011001100110011001101times 2^{3}.}$

This representation is derived by discarding the infinite tail

${displaystyle 0.{overline {1100}}times 2^{-52}times 2^{3}=0.{overline {0110}}times 2^{-51}times 2^{3}=0.4times 2^{-48}}$

from the right tail and then added ${displaystyle 1times 2^{-52}times 2^{3}=2^{-49}}$ in the rounding step.

Then ${displaystyle fl(9.4)=9.4-0.4times 2^{-48}+2^{-49}=9.4+(0.2)_{10}times 2^{-49}}$

Thus, the roundoff error is ${displaystyle (0.2times 2^{-49})_{10}}$ .

Measuring roundoff error by using machine epsilon[edit]

The machine epsilon ${displaystyle epsilon _{text{mach}}}$ can be used to measure the level of roundoff error when using the two rounding rules above. Below are the formulas and corresponding proof.^[3] The first definition of machine epsilon is used here.

Theorem[edit]

Round-by-chop: ${displaystyle epsilon _{text{mach}}=beta ^{1-p}}$
Round-to-nearest: ${displaystyle epsilon _{text{mach}}={frac {1}{2}}beta ^{1-p}}$

Proof[edit]

Let ${displaystyle x=d_{0}.d_{1}d_{2}ldots d_{p-1}d_{p}ldots times beta ^{n}in mathbb {R} }$ where , and let be the floating-point representation of .
Since round-by-chop is being used, it is

${displaystyle {begin{aligned}{frac {|x-fl(x)|}{|x|}}&={frac {|d_{0}.d_{1}d_{2}ldots d_{p-1}d_{p}d_{p+1}ldots times beta ^{n}-d_{0}.d_{1}d_{2}ldots d_{p-1}times beta ^{n}|}{|d_{0}.d_{1}d_{2}ldots times beta ^{n}|}}\&={frac {|d_{p}.d_{p+1}ldots times beta ^{n-p}|}{|d_{0}.d_{1}d_{2}ldots times beta ^{n}|}}\&={frac {|d_{p}.d_{p+1}d_{p+2}ldots |}{|d_{0}.d_{1}d_{2}ldots |}}times beta ^{-p}end{aligned}}}$

In order to determine the maximum of this quantity, the is a need to find the maximum of the numerator and the minimum of the denominator. Since ${displaystyle d_{0}neq 0}$ (normalized system), the minimum value of the denominator is . The numerator is bounded above by . Thus, ${displaystyle {frac {|x-fl(x)|}{|x|}}leq {frac {beta }{1}}times beta ^{-p}=beta ^{1-p}}$ . Therefore, ${displaystyle epsilon =beta ^{1-p}}$ for round-by-chop.
The proof for round-to-nearest is similar.

Note that the first definition of machine epsilon is not quite equivalent to the second definition when using the round-to-nearest rule but it is equivalent for round-by-chop.

Roundoff error caused by floating-point arithmetic[edit]

Even if some numbers can be represented exactly by floating-point numbers and such numbers are called machine numbers, performing floating-point arithmetic may lead to roundoff error in the final result.

Addition[edit]

Machine addition consists of lining up the decimal points of the two numbers to be added, adding them, and then storing the result again as a floating-point number. The addition itself can be done in higher precision but the result must be rounded back to the specified precision, which may lead to roundoff error.^[3]

This example shows that roundoff error can be introduced when adding a large number and a small number. The shifting of the decimal points in the mantissas to make the exponents match causes the loss of some of the less significant digits. The loss of precision may be described as absorption.^[11]

Note that the addition of two floating-point numbers will result in a roundoff error when their sum is an order of magnitude greater than that of the larger of the two.

This kind of error can occur alongside an absorption error in a single operation.

Multiplication[edit]

In general, the product of 2p-digit mantissas contains up to 2p digits, so the result might not fit in the mantissa.^[3] Thus roundoff error will be involved in the result.

Division[edit]

In general, the quotient of 2p-digit mantissas may contain more than p-digits.Thus roundoff error will be involved in the result.

Subtraction[edit]

Absorption also applies to subtraction.

The subtracting of two nearly equal numbers is called subtractive cancellation.^[3]
When the leading digits are cancelled, the result may be too small to be represented exactly and it will just be represented as .

Even with a somewhat larger epsilon , the result is still significantly unreliable in typical cases. There is not much faith in the accuracy of the value because the most uncertainty in any floating-point number is the digits on the far right.

This is closely related to the phenomenon of catastrophic cancellation, in which the two numbers are known to be approximations.

Accumulation of roundoff error[edit]

Errors can be magnified or accumulated when a sequence of calculations is applied on an initial input with roundoff error due to inexact representation.

Unstable algorithms[edit]

An algorithm or numerical process is called stable if small changes in the input only produce small changes in the output, and unstable if large changes in the output are produced.^[12] For example, the computation of using the «obvious» method is unstable near x=0 due to the large error introduced in subtracting two similar quantities, whereas the equivalent expression ${displaystyle textstyle {f(x)={frac {x}{{sqrt {1+x}}+1}}}}$ is stable.^[12]

Ill-conditioned problems[edit]

Even if a stable algorithm is used, the solution to a problem may still be inaccurate due to the accumulation of roundoff error when the problem itself is ill-conditioned.

The condition number of a problem is the ratio of the relative change in the solution to the relative change in the input.^[3] A problem is well-conditioned if small relative changes in input result in small relative changes in the solution. Otherwise, the problem is ill-conditioned.^[3] In other words, a problem is ill-conditioned if its condition number is «much larger» than 1.

The condition number is introduced as a measure of the roundoff errors that can result when solving ill-conditioned problems.^[7]

References[edit]

^ Butt, Rizwan (2009), Introduction to Numerical Analysis Using MATLAB, Jones & Bartlett Learning, pp. 11–18, ISBN 978-0-76377376-2
^ Ueberhuber, Christoph W. (1997), Numerical Computation 1: Methods, Software, and Analysis, Springer, pp. 139–146, ISBN 978-3-54062058-7
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Forrester, Dick (2018). Math/Comp241 Numerical Methods (lecture notes). Dickinson College.
^ Aksoy, Pelin; DeNardis, Laura (2007), Information Technology in Theory, Cengage Learning, p. 134, ISBN 978-1-42390140-2
^ Ralston, Anthony; Rabinowitz, Philip (2012), A First Course in Numerical Analysis, Dover Books on Mathematics (2nd ed.), Courier Dover Publications, pp. 2–4, ISBN 978-0-48614029-2
^ Chapman, Stephen (2012), MATLAB Programming with Applications for Engineers, Cengage Learning, p. 454, ISBN 978-1-28540279-6
^ ^a ^b Chapra, Steven (2012). Applied Numerical Methods with MATLAB for Engineers and Scientists (3rd ed.). McGraw-Hill. ISBN 9780073401102.
^ Laplante, Philip A. (2000). Dictionary of Computer Science, Engineering and Technology. CRC Press. p. 420. ISBN 978-0-84932691-2.
^ Higham, Nicholas John (2002). Accuracy and Stability of Numerical Algorithms (2 ed.). Society for Industrial and Applied Mathematics (SIAM). pp. 43–44. ISBN 978-0-89871521-7.
^ Volkov, E. A. (1990). Numerical Methods. Taylor & Francis. p. 24. ISBN 978-1-56032011-1.
^ Biran, Adrian B.; Breiner, Moshe (2010). «5». What Every Engineer Should Know About MATLAB and Simulink. Boca Raton, Florida: CRC Press. pp. 193–194. ISBN 978-1-4398-1023-1.
^ ^a ^b Collins, Charles (2005). «Condition and Stability» (PDF). Department of Mathematics in University of Tennessee. Retrieved 2018-10-28.

External links[edit]

Roundoff Error at MathWorld.
Goldberg, David (March 1991). «What Every Computer Scientist Should Know About Floating-Point Arithmetic» (PDF). ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. S2CID 222008826. Retrieved 2016-01-20. ([1], [2])
20 Famous Software Disasters

Источник

Для акробатических движений, округления см. Округлять.

А ошибка округления,^[1] также называемый ошибка округления,^[2] разница между результатом, полученным данным алгоритм с использованием точной арифметики и результата, полученного с помощью того же алгоритма с использованием округленной арифметики конечной точности.^[3] Ошибки округления возникают из-за неточности в представлении действительных чисел и выполняемых с ними арифметических операций. Это форма ошибка квантования.^[4] При использовании приближения уравнения или алгоритмов, особенно при использовании конечного числа цифр для представления действительных чисел (которые теоретически имеют бесконечно много цифр), одна из целей числовой анализ должен оценивать ошибки вычислений.^[5] Ошибки вычислений, также называемые числовые ошибки, включить оба ошибки усечения и ошибки округления.

Когда выполняется последовательность вычислений с вводом, содержащим ошибку округления, ошибки могут накапливаться, иногда доминируя при вычислении. В плохо воспитанный проблемы, может накапливаться значительная ошибка.^[6]

Короче говоря, в численных расчетах есть два основных аспекта ошибок округления:^[7]

Цифровые компьютеры имеют ограничения по величине и точности их способности представлять числа.
Некоторые числовые операции очень чувствительны к ошибкам округления. Это может быть связано как с математическими соображениями, так и с тем, как компьютеры выполняют арифметические операции.

Ошибка представления

Ошибка, возникающая при попытке представить число с помощью конечной строки цифр, является формой ошибки округления, называемой ошибка представления.^[8] Вот несколько примеров ошибок представления в десятичных представлениях:

Обозначение	Представление	Приближение	Ошибка
1/7	0.142 857	0.142 857	0.000 000 142 857
пер. 2	0.693 147 180 559 945 309 41…	0.693 147	0.000 000 180 559 945 309 41…
бревно₁₀ 2	0.301 029 995 663 981 195 21…	0.3010	0.000 029 995 663 981 195 21…
³√2	1.259 921 049 894 873 164 76…	1.25992	0.000 001 049 894 873 164 76…
√2	1.414 213 562 373 095 048 80…	1.41421	0.000 003 562 373 095 048 80…
е	2.718 281 828 459 045 235 36…	2.718 281 828 459 045	0.000 000 000 000 000 235 36…
π	3.141 592 653 589 793 238 46…	3.141 592 653 589 793	0.000 000 000 000 000 238 46…

Увеличение числа цифр, разрешенных в представлении, уменьшает величину возможных ошибок округления, но любое представление, ограниченное конечным числом цифр, все равно вызовет некоторую степень ошибки округления для бесчисленное множество действительные числа. Дополнительные цифры, используемые для промежуточных этапов расчета, известны как охранные цифры.^[9]

Многократное округление может привести к накоплению ошибок.^[10] Например, если 9,945309 округляется до двух десятичных знаков (9,95), а затем снова округляется до одного десятичного знака (10,0), общая ошибка составляет 0,054691. Округление 9,945309 до одного десятичного знака (9,9) за один шаг приводит к меньшей ошибке (0,045309). Обычно это происходит при выполнении арифметических операций (см. Потеря значимости ).

Система счисления с плавающей запятой

По сравнению с система счисления с фиксированной точкой, то система счисления с плавающей запятой более эффективен при представлении действительных чисел, поэтому широко используется в современных компьютерах. Пока реальные цифры бесконечны и непрерывны, система счисления с плавающей запятой конечно и дискретно. Таким образом, в системе счисления с плавающей точкой возникает ошибка представления, которая приводит к ошибке округления.

Обозначение системы счисления с плавающей запятой

Система счисления с плавающей запятой характеризуется целые числа:

: основание или основание

: точность

: диапазон экспоненты, где

это нижняя граница и

это верхняя граница

Любой имеет следующий вид:

${ displaystyle x = pm ( underbrace {d_ {0} .d_ {1} d_ {2} ldots d_ {p-1}} _ { text {mantissa}}) _ { beta} times beta ^ { overbrace {E} ^ { text {exponent}}} = pm d_ {0} times beta ^ {E} + d_ {1} times beta ^ {E-1} + ldots + d_ {p-1} times beta ^ {E- (p-1)}}$

куда $d_ {i}$ такое целое число, что ${ displaystyle 0 leq d_ {i} leq beta -1}$ за

, и

такое целое число, что

Нормализованная система с плавающей запятой

${ Displaystyle 2 ( бета -1) бета ^ {р-1} (U-L + 1) +1}$ , куда

считает выбор знака, положительный или отрицательный

считает выбор первой цифры

${ displaystyle beta ^ {p-1}}$ считает оставшуюся мантиссу

считает выбор показателей

считает тот случай, когда число

Стандарт IEEE

в IEEE стандартная база двоичная, т.е. , и используется нормализация. Стандарт IEEE хранит знак, показатель степени и мантиссу в отдельных полях слова с плавающей запятой, каждое из которых имеет фиксированную ширину (количество бит). Два наиболее часто используемых уровня точности для чисел с плавающей запятой — это одинарная точность и двойная точность.

Точность	Знак (биты)	Экспонента (биты)	Мантисса (биты)
Одинокий	1	8	23
Двойной	1	11	52

Машина эпсилон

Машина эпсилон может использоваться для измерения уровня ошибки округления в системе счисления с плавающей запятой. Вот два разных определения.^[3]

${ displaystyle epsilon _ {mach} = max _ {x} { frac {| x-fl (x) |} {| x |}}}$

Ошибка округления при разных правилах округления

Существует два общих правила округления: округление за отрезком и округление до ближайшего. Стандарт IEEE использует округление до ближайшего.

Округление до ближайшего: устанавливается равным ближайшему числу с плавающей запятой к . Когда есть ничья, используется число с плавающей запятой, последняя сохраненная цифра которого четная.
- Для стандарта IEEE, где базовый является , это означает, что когда есть ничья, она округляется так, чтобы последняя цифра была равна .
- Это правило округления более точное, но более затратное с точки зрения вычислений.
- Округление таким образом, чтобы последняя сохраненная цифра была даже при равенстве, гарантирует, что она не округляется систематически в большую или меньшую сторону. Это сделано для того, чтобы избежать возможности нежелательного медленного дрейфа в длинных вычислениях просто из-за смещения округления.

В следующем примере показан уровень ошибки округления в соответствии с двумя правилами округления.^[3] Правило округления (округление до ближайшего) в целом приводит к меньшей ошибке округления.

Икс	По очереди	Ошибка округления	Округление до ближайшего	Ошибка округления
1.649	1.6	0.049	1.6	0.049
1.650	1.6	0.050	1.6	0.050
1.651	1.6	0.051	1.7	-0.049
1.699	1.6	0.099	1.7	-0.001
1.749	1.7	0.049	1.7	0.049
1.750	1.7	0.050	1.8	-0.050

Расчет ошибки округления в стандарте IEEE

Предположим, что используется округление до ближайшего и двойная точность IEEE.

Пример: десятичное число ${ displaystyle (9.4) _ {10} = (1001. { overline {0110}}) _ {2}}$ может быть преобразован в

${ displaystyle +1. underbrace {0010110011001100110011001100110011001100110011001100} _ { text {52 бит}} 110 ldots times 2 ^ {3}}$

Поскольку ${ displaystyle 53 ^ {rd}}$ бит справа от двоичной точки — это и за ним следуют другие ненулевые биты, правило округления до ближайшего требует округления, то есть добавления немного к ${ displaystyle 52 ^ {nd}}$ кусочек. Таким образом, нормализованное представление с плавающей запятой в стандарте IEEE является

${ displaystyle fl (9.4) = 1,0010110011001100110011001100110011001100110011001101 times 2 ^ {3}}$

Это представление получается отбрасыванием бесконечного хвоста

${ displaystyle 0. { overline {1100}} times 2 ^ {- 52} times 2 ^ {3} = 0. { overline {0110}} times 2 ^ {- 51} times 2 ^ { 3} = 0,4 times 2 ^ {- 48}}$

из правого хвоста, а затем добавил ${ displaystyle 1 times 2 ^ {- 52} times 2 ^ {3} = 2 ^ {- 49}}$ на этапе округления.

потом ${ displaystyle fl (9,4) = 9,4–0,4 times 2 ^ {- 48} +2 ^ {- 49} = 9,4 + (0,2) _ {10} times 2 ^ {- 49}}$

Таким образом, ошибка округления равна ${ displaystyle (0,2 times 2 ^ {- 49}) _ {10}}$ .

Измерение ошибки округления с помощью машины эпсилон

Машина эпсилон ${ displaystyle epsilon _ {mach}}$ может использоваться для измерения уровня ошибки округления при использовании двух вышеупомянутых правил округления. Ниже приведены формулы и соответствующие доказательства.^[3] Здесь используется первое определение машинного эпсилона.

Теорема

По очереди: ${ displaystyle epsilon _ {mach} = beta ^ {1-p}}$
Округление до ближайшего: ${ displaystyle epsilon _ {mach} = { frac {1} {2}} beta ^ {1-p}}$

Доказательство

Позволять ${ displaystyle x = d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} d_ {p} ldots times beta ^ {n} in mathbb {R}}$ куда , и разреши быть представлением с плавающей запятой Икс . Поскольку используется последовательное нарезание, ${ displaystyle { begin {align} { frac {| x-fl (x) |} {| x |}} & = { frac {| d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} d_ {p} d_ {p + 1} ldots times beta ^ {n} -d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} times beta ^ {n} |} {| d_ {0} .d_ {1} d_ {2} ldots times beta ^ {n} |}} & = { frac {| d_ {p}. d_ {p + 1} ldots times beta ^ {np} |} {| d_ {0} .d_ {1} d_ {2} ldots times beta ^ {n} |}} & = { frac {| d_ {p} .d_ {p + 1} d_ {p + 2} ldots |} {| d_ {0} .d_ {1} d_ {2} ldots |}} times beta ^ {- p} end {выровнено}}}$ * Чтобы определить максимум этой величины, необходимо найти максимум числителя и минимум знаменателя. С ${ displaystyle d_ {0} neq 0}$ (нормализованная система), минимальное значение знаменателя равно . Числитель ограничен сверху величиной . Таким образом, ${ displaystyle { frac {| x-fl (x) |} {| x |}} leq { frac { beta} {1}} times beta ^ {- p} = beta ^ {1 -п}}$ . Следовательно, ${ displaystyle epsilon = beta ^ {1-p}}$ для округления до ближайшего. Доказательство для округления до ближайшего аналогично.

Обратите внимание, что первое определение машинного эпсилон не совсем эквивалентно второму определению при использовании правила округления до ближайшего, но оно эквивалентно для последовательного перехода.

Ошибка округления, вызванная арифметикой с плавающей запятой

Даже если некоторые числа могут быть представлены в точности числами с плавающей запятой и такие числа называются номера машин, выполнение арифметики с плавающей запятой может привести к ошибке округления в окончательном результате.

Добавление

Машинное сложение состоит из выстраивания десятичных знаков двух добавляемых чисел, их сложения и последующего сохранения результата как числа с плавающей запятой. Само сложение может быть выполнено с более высокой точностью, но результат должен быть округлен до указанной точности, что может привести к ошибке округления.^[3]

Например, добавив к ${ displaystyle 2 ^ {- 53}}$ в IEEE двойной точности следующим образом:

${ displaystyle { begin {align} 1,00 ldots 0 times 2 ^ {0} +1,00 ldots 0 times 2 ^ {- 53} & = 1. underbrace {00 ldots 0} _ { text { 52 бита}} times 2 ^ {0} +0. Underbrace {00 ldots 0} _ { text {52 бит}} 1 times 2 ^ {0} & = 1. underbrace {00 ldots 0} _ { text {52 бита}} 1 times 2 ^ {0} end {выровнено}}}$

Из этого примера видно, что при сложении большого числа и малого числа может возникнуть ошибка округления, поскольку сдвиг десятичных знаков в мантиссах для согласования показателей степени может вызвать потерю некоторых цифр.

Умножение

В общем, продукт -цифровые мантиссы содержат до цифр, поэтому результат может не соответствовать мантиссе.^[3] Таким образом, в результат будет включена ошибка округления.

Разделение

В общем, частное -цифровые мантиссы могут содержать более -цифры.^[3] Таким образом, в результат будет включена ошибка округления.

Вычитающая отмена

Вычитание двух почти равных чисел называется вычитающее аннулирование.^[3]

Накопление ошибки округления

Ошибки могут увеличиваться или накапливаться, когда последовательность вычислений применяется к начальному входу с ошибкой округления из-за неточного представления.

Нестабильные алгоритмы

Алгоритм или численный процесс называется стабильный если небольшие изменения на входе вызывают только небольшие изменения на выходе, и это называется неустойчивый если производятся большие изменения на выходе.^[11]

Последовательность вычислений обычно происходит при запуске какого-либо алгоритма. Количество ошибок в результате зависит от стабильность алгоритма. Ошибка округления будет увеличиваться из-за нестабильных алгоритмов.

Например, ${ displaystyle y_ {n} = int _ {0} ^ {1} , { frac {x ^ {n}} {x + 5}} dx}$ за с ${ displaystyle y_ {0}}$ данный. Легко показать, что ${ displaystyle y_ {n} = { frac {1} {n}} - 5лет_ {n-1}}$ . Предполагать ${ displaystyle y_ {0}}$ это наше начальное значение и имеет небольшую ошибку представления epsilon , что означает, что начальный вход в этот алгоритм ${ displaystyle y_ {0} + epsilon}$ вместо ${ displaystyle y_ {0}}$ . Затем алгоритм выполняет следующую последовательность вычислений.

${ displaystyle { begin {align} y_ {1} & = 1-5 (y_ {0} + epsilon) = 1-5y_ {0} -5 epsilon y_ {2} & = { frac { 1} {2}} - 5 (1-5y_ {0} -5 epsilon) = { frac {1} {2}} - 5 + 25y_ {0} + 5 ^ {2} epsilon vdots y_ {n} & = ldots + 5 ^ {n} epsilon end {выровнено}}}$

Ошибка округления увеличивается в последующих вычислениях, поэтому этот алгоритм нестабилен.

Плохо обусловленные проблемы

Сравнение1

Сравнение 2

Даже если используется стабильный алгоритм, решение проблемы все равно может быть неточным из-за накопления ошибки округления, когда сама проблема плохо воспитанный.

В номер условия Задачи — это отношение относительного изменения решения к относительному изменению на входе.^[3] Проблема в том хорошо кондиционированный если небольшие относительные изменения входных данных приводят к небольшим относительным изменениям в решении. В противном случае проблема в плохо воспитанный.^[3] Другими словами, проблема в том, плохо воспитанный если его число условия «намного больше», чем .

Число обусловленности вводится как мера ошибок округления, которые могут возникнуть при решении плохо обусловленных задач.^[7]

Например, многочлены высшего порядка имеют тенденцию быть очень плохо воспитанный, то есть они очень чувствительны к ошибке округления.^[7]

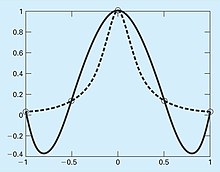
В 1901 г. Карл Рунге опубликовал исследование об опасностях полиномиальной интерполяции высокого порядка. Он посмотрел на следующую простую на вид функцию:

${ displaystyle f (x) = { frac {1} {1 + 25x ^ {2}}}}$

который сейчас называется Функция Рунге. Он взял равноудаленные точки данных из этой функции на интервале [-1, 1] . Затем он использовал интерполяционные полиномы возрастающего порядка и обнаружил, что по мере того, как он брал больше точек, полиномы и исходная кривая значительно отличались, как показано на Рисунке «Сравнение1» и Рисунке «Сравнение 2». Дальше ситуация сильно ухудшилась с увеличением заказа. Как показано на Рисунке «Сравнение 2», посадка стала еще хуже, особенно в конце интервала.

Нажмите на рисунки, чтобы увидеть полное описание.

Пример из реального мира: отказ ракеты Patriot из-за увеличения ошибки округления

Американская ракета Patriot

25 февраля 1991 года, во время войны в Персидском заливе, американская ракетная батарея «Пэтриот» в Дхаране, Саудовская Аравия, не смогла перехватить приближающуюся иракскую ракету «Скад». Скад врезался в казармы американской армии и убил 28 солдат. Отчет о Счетная палата правительства озаглавленный «Противоракетная оборона Patriot: проблема программного обеспечения, приведшая к отказу системы в Дахране, Саудовская Аравия», сообщает о причине сбоя: неточный расчет времени с момента загрузки из-за компьютерных арифметических ошибок. В частности, время в десятых долях секунды, измеренное внутренними часами системы, было умножено на 10, чтобы получить время в секундах. Этот расчет был выполнен с использованием 24-битного регистра с фиксированной точкой. В частности, значение 1/10, которое имеет неограниченное двоичное расширение, было прервано на 24 бита после точки счисления. Маленькая ошибка прерывания, умноженная на большое число, дающее время в десятых долях секунды, привела к значительной ошибке. Действительно, батарея Patriot проработала около 100 часов, и простой расчет показывает, что результирующая временная погрешность из-за увеличенной ошибки прерывания составила около 0,34 секунды. (Число 1/10 равно ${ displaystyle 1/2 ^ {4} + 1/2 ^ {5} + 1/2 ^ {8} + 1/2 ^ {9} + 1/2 ^ {12} + 1/2 ^ {13} + ldots}$ . Другими словами, двоичное разложение 1/10 равно . Теперь 24-битный регистр в Патриоте хранится вместо вводя ошибку двоичный, или около десятичный. Умножая на количество десятых долей секунды в 100 часов дает ). Скад едет примерно 1676 метров в секунду, и поэтому за это время проходит более полукилометра. Этого было достаточно, чтобы приближающийся Скад находился за пределами «ворот дальности», которые отслеживал Патриот. По иронии судьбы, тот факт, что вычисление плохого времени было улучшено в некоторых частях кода, но не во всех, способствовал возникновению проблемы, поскольку это означало, что неточности не отменялись.^[12]

Смотрите также

Точность (арифметика)
Усечение
Округление
Потеря значимости
Плавающая точка
Алгоритм суммирования Кахана
Машина эпсилон
Полином Уилкинсона

внешняя ссылка

Ошибка округления в MathWorld.
Гольдберг, Дэвид (Март 1991 г.). «Что должен знать каждый компьютерный ученый об арифметике с плавающей точкой» (PDF). Опросы ACM Computing. 23 (1): 5–48. Дои:10.1145/103162.103163. Получено 2016-01-20. ([1], [2] )
20 известных программных катастроф

Источник

Округление результатов

Обработка
результатов измерений в лабораториях
проводятся на калькуляторах и ПК. Иногда
можно увидеть, как магически действует
на многих студентов после вычислений
длинный ряд цифр после запятой. Однако
легко видеть, например, что запись
бессмысленна. При ошибке 0.076 последние
пять цифр числа не означает ровно ничего.

Если
допустить ошибку в сотых долях, то
тысячным, тем более десятитысячным
долям веры нет. Грамотная запись
результата была бы 2.87 ± 0.08. Всегда нужно
производить необходимые округления,
чтобы не было ложного впечатления о
большей, чем это есть на самом деле,
точности результатов.

Правила
округления:

1. Погрешность
измерения округляют до первой значащей
цифры, всегда увеличивая ее на единицу.

Примеры:
8.27 ≈ 9; 0.237 ≈ 0.3;

0.0862
≈ 0.09; 0.00035 ≈ 0.0004;

857.3
≈ 900; 43.5 ≈ 50.

2. Результаты
измерения округляют с точностью «до
погрешности», т.е. последняя значащая
цифра в результате должна находиться
в том же разряде, что и в погрешности.

Примеры:
243.871 ± 0.026 ≈ 243.87 ± 0.03;

243.871 ± 2.6 ≈ 244 ± 3;

1053 ± 47 ≈ 1050 ± 50.

3. Округление
результата измерения достигается
простым отбрасыванием цифр, если первая
из отбрасываемых цифр меньше 5.

Примеры:
8.337 (округлить до десятых) ≈ 8.3;

833.438
(округлить до целых) ≈ 833;

0.27375
(округлить до сотых) ≈ 0.27.

4. Если
первая из отбрасываемых цифр больше
или равна 5, (а за ней одна или несколько
цифр отличны от нуля), то последняя из
остающихся цифр увеличивается на
единицу.

Примеры:
8.3351 (округлить дл сотых) ≈ 8.34;

0.2510
(округлить до десятых) ≈ 0.3;

271.515
(округлить до целых) ≈ 272.

5. Если
отбрасываемая цифра равна 5, а за ней
нет значащих цифр (или стоят одни нули),
то последнюю оставляемую цифру увеличивают
на единицу, когда она нечетная, и оставляют
неизменной, когда она четная.

Примеры:
0.875 (округлить до сотых) ≈ 0.88;

0.5450 (округлить до
сотых) ≈ 0.54;

275.500
(округлить до целых) ≈ 276;

276.500
(округлить до целых) ≈ 276.

Обработка результатов косвенного измерения

К
косвенным измерениям прибегают, когда
физическую величину нельзя измерить
непосредственно или ее непосредственное
измерение затруднительно. В табл. 30
приведены формулы вычисления погрешностей
для различных видов математических
операций между измеряемыми величинами.

В
лабораторной практике большинство
измерений – косвенные и интересующая
величина является функцией одной или
нескольких непосредственно измеряемых
величин:

(10)

Как
следует из теории вероятностей, среднее
значение величины определяется
подстановкой в формулу (10) средних
значений непосредственно измеряемых
величин, т.е.

(11)

Требуется
найти абсолютную и относительную ошибки
этой функции, если известны ошибки
независимых переменных.

Рассмотрим
два крайних случая, когда ошибки являются
либо систематическими, либо случайными.
Единого мнения относительно вычисления
систематической ошибки косвенных
измерений нет. Однако если исходить из
определения систематической ошибки
как максимально возможной ошибки, то
целесообразно находить систематическую
ошибку
по
формулам

(12)

или

(13)

где
– частные производные функции (10) по
аргументу
найденные
в предположении, что все остальные
аргументы, кроме того, по которому
находится производная, постоянные;

– систематические ошибки аргументов.

Формулой
(12) удобно пользоваться в случае, если
функция имеет вид суммы или разности
аргументов. Выражение (13) применять
целесообразно, если функция имеет вид
произведения или частного аргументов.

Для
нахождения случайной ошибки
косвенных
измерений следует пользоваться формулами:

(14)

или

(15)

где
– доверительные интервалы при заданных
доверительных вероятностях (надежностях)
для аргументов
.
Следует иметь в виду, что доверительные
интервалы
должны быть взяты при одинаковой
доверительной вероятности.

В
этом случае надежность для доверительного
интервала
будет тоже P.

Часто
наблюдается случай, когда систематическая
ошибка и случайная ошибка близки друг
к другу, и они обе в одинаковой степени
определяют точность результата. В этом
случае общая ошибка ∑ находится как
квадратичная сумма случайной Δ и
систематической δ ошибок с вероятностью
не менее чем P, где P – доверительная
вероятность случайной ошибки:

При
проведении косвенных измерений в
невоспроизводимых условиях функцию
находят для каждого отдельного измерения,
а доверительный интервал вычисляют для
получения значений искомой величины
по тому же методу, что и для прямых
измерений.

Следует
отметить, что в случае функциональной
зависимости, выраженной формулой,
удобной для логарифмирования, проще
сначала определить относительную
погрешность, а затем из выражения
найти абсолютную погрешность.

Прежде
чем приступать к измерениям, всегда
нужно подумать о последующих расчетах
и выписать формулы, по которым будут
рассчитываться погрешности. Эти формулы
позволят понять, какие измерения следует
производить особенно тщательно, а на
какие не нужно тратить больших усилий.

При
обработке результатов косвенных
измерений предлагается следующий
порядок операций:

1. Все
величины, находимые прямыми измерениями,
обработать в соответствии с правилами
обработки результатов прямых измерений.
При этом для всех измеряемых величин
задать одно и то же значение надежности
P.

2. Оценить
точность результата косвенных измерений
по формулам (12) – (13), где производные
вычислить при средних значениях величин.
Если ошибка отдельных измерений входит
в результат дифференцирования несколько
раз, то надо сгруппировать все члены,
содержащие одинаковый дифференциал, и
выражения в скобках, стоящие перед
дифференциалом
взять
по модулю; знак d
заменить
на Δ.

3. Случайную
и систематическую ошибки необходимо
сложить по правилу сложения ошибок.

4. Определите
относительную погрешность результата
серии косвенных измерений

5. Результат
измерения записать в виде:

Пример.
Находится объем цилиндра по формуле

где
d
– диаметр цилиндра, h
– высота цилиндра.

Обе
эти величины определяются непосредственно.
Пусть измерение этих величин дало
следующие результаты:

при
одинаковой надежности
.

Среднее
значение объема, согласно (11) равно

Воспользовавшись
выражением (15) имеем:

;

,
;

;

Так
как измерения производились микрометром,
цена деления которого 0.01 мм, то
систематические ошибки
.
На основании (13) систематическая ошибкабудет

Абсолютная
погрешность измерения равна

Таким
образом, результат измерения равен

или
после округления имеет вид

Относительная
погрешность

Окончательно можно
записать

при
,.

Соседние файлы в папке 07-02-2013_14-00-36

Содержание

- - 0.0.0.1 Правила округления

1 Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!
2 Физика — рефераты, конспекты, шпаргалки, лекции, семинары
3 Правила округления значений погрешностей и результатов измерения

Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.

Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.

Правила округления

Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.
Примеры:

8.27 ≈ 9 0.237 ≈ 0.3

0.0862 ≈ 0.09 0.00035 ≈ 0.0004

857.3 ≈ 900 43.5 ≈ 50
Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности.
Примеры:

243.871 ± 0.026 ≈ 243.87 ± 0.03;
243.871 ± 2.6 ≈ 244 ± 3;
1053 ± 47 ≈ 1050 ± 50.

Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5.
Примеры:

8.337 (округлить до десятых) ≈ 8.3;
833.438 (округлить до целых) ≈ 833;
0.27375 (округлить до сотых) ≈ 0.27.

Если первая из отбрасываемых цифр больше или равна 5 , (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу.
Примеры:

8.3351 (округлить дл сотых) ≈ 8.34;
0.2510 (округлитьь до десятых) ≈ 0.3;
271.515 (округлить до целых) ≈ 272.

Если отбрасываемая цифра равна 5 , а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная.
Примеры:

0.875 (округлить до сотых) ≈ 0.88;
0.5450 (округлить до сотых) ≈ 0.54;
275.500 (округлить до целых) ≈ 276;
276.500 (округлить до целых) ≈ 276.

Примечание.

Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например, 0,00807 в этом числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7 ; первые три нуля незначащие.
8.12 · 10 3 в этом числе 3 значащих цифры.
Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 верны целые и десятые доли.
Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35&middot10 -3 и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для логарифмирования.

Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!

Физика — рефераты, конспекты, шпаргалки, лекции, семинары

Правила округления значений погрешностей и результатов измерения

Погрешности измерений показывают также, какие цифры в полученном результате измерения сомнительны, поэтому нет смысла в записи погрешности с большим числом знаков.

По обычаю ограничиваются одной значащей цифрой и только при особо точных измерениях погрешность записывается двумя или тремя цифрами.

Используют 3 правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:

1. Погрешность результата измерения показывается двумя значащими цифрами, если первая из них 1 или 2, и одной — если первая цифра 3 и более.

2. Результат измерения округляется до того же десятичного разряда, которым заканчивается округления значение абсолютной погрешности.

3. Округление производится только в конечной ответы, а все предварительные расчеты проводят с одним — двумя лишними знаками.

В соответствии с правилом 1 установлены и нормированные значения погрешностей 3В: в числах 1,5% или 2,5% показываются два знака, но в числах 0,5%, 4%, 6%; показывается только один знак.

При округлении результатов измерения используют еще такие правила:

1) лишние цифры в целых чисел заменяют нулями, а в дробных десятичных отвергают; н., 732 «700.

2) если первая из заменяемых нулями или откидываемых цифр 5, то последняя из оставшихся цифр увеличивается на 1;

3) если отвергаем цифра = 5 со следующими нулями, то округление производится до ближнего четного числа.

Результаты измерения можно записать некоторыми значимыми цифрами и рядом нулей, но в этом случае и нули должны полностью определенное значение и характеризуют погрешность измерения. Н., пусть результат измерения их = 9,5 B, который можно записать цифрами: 9,5; 9,50; 9,500. В этих случаях нули после последней значащей цифры определяют показатель достоверности результатов измерения. С этой точки зрения эти записи необходимо читать так: 9,45

Правила записи чисел по СТ СЭВ 543 — 77

1. Значащие цифры данного числа — все цифры от первой слева, не равной нулю, до последней справа. При этом нули, следующие из множителя 10, не учитывают.

а) Число 12,0 имеет три значащие цифры.

б) Число 30 имеет две значащие цифры.

в) Число 120 . 10 имеет три значащие цифры.

г) 0,514 . 10 имеет три значащие цифры.

д) 0,0056 имеет две значащие цифры.

2. Если необходимо указать, что число является точным, после числа указывают слово «точно» или последнюю значащую цифру печатают жирным шрифтом. Например, в печатном тексте: 1 кВт . ч = 3600 Дж (точно).

3. Различают записи приближенных чисел по количеству значащих цифр.

а) Различают числа 2,4 и 2,40. Запись 2,4 означает, что верны только целые и десятые доли, истинное значение числа может быть, например, 2,43 и 2,38. Запись 2,40 означает, что верны и сотые доли: истинное значение числа может быть 2,403 и 2,398, но не 2,41 и не 2,382.

б) Запись 382 означает, что все цифры верны: если за последнюю цифру ручаться нельзя, то число должно быть записано 3,8 . 10 .

в) Если в числе 4720 верны лишь две первые цифры, оно должно быть быть записано 47 * 10 или 4,7 * 10 .

4. Число, для которого указывают допустимое отклонение, должно иметь последнюю значащую цифру того же разряда, как и последняя значащая цифра отклонения.

а) Правильно: 17,0 + 0,2. Неправильно: 17 + 0,2 или 17,00 + 0,2.

б) Правильно: 12,13 + 0,17. Неправильно: 12,13 + 0,2.

в) Правильно: 46,40 + 0,15. Неправильно: 46,4 + 0,15 или 46,402 + 0,15.

5. Числовые значения величины и её погрешности (отклонения) целесообразно записывать с указанием одной и той же единицы величины.

6. Интервалы между числовыми значениями величин целесообразно записывать:

от 60 до 100, свыше 120 до 150.

Правила округления чисел по СТ СЭВ 543 — 77

1. Округление числа представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.

2. В случае, если первая из отбрасываемых цифр (считая слева направо) менее 5, то последнюю сохраняемую цифру не меняют.

Пример: Округление числа 12,23 до трех значащих цифр дает 12,2.

3. В случае, если первая из отбрасываемых цифр (считая слева направо) равна 5, то последнюю сохраняемую цифру увеличивают на единицу.

Пример: Округление числа 0,145 до двух цифр дает 0,15.

Примечание. В тех случаях, когда следует учитывать результаты предыдущих округлений, поступают следующим образом.

Если отбрасываемая цифра получена в результате округления в меньшую сторону, то последнюю оставшуюся цифру увеличивают на единицу (с переходом при необходимости в следующие разряды).

Пример: Округление числа 0,25 (полученного в результате предыдущего округления числа 0,252) дает 0,3 .

4. В случае, если первая из отбрасываемых цифр (считая слева направо) более 5, то последнюю сохраняемую цифру увеличивают на единицу.

Пример: Округление числа 0,156 до двух значащих цифр дает 0,16.

Округление выполняют сразу до желаемого количества значащих цифр, а не по этапам.

Пример: Округление числа 565,46 до трех значащих цифр дает 565.

6. Целые числа округляют по тем же правилам , что и дробные.

Пример: Округление числа 23456 до двух значащих цифр дает 23* 10 .

Из книги Л.И. Любимов, И.Д. Форсилова, Е.З. Шапиро

«Поверка средств электрических измерений. Справочная книга».

Ленинград, Энергоатомиздат, Ленинградское отделение, 1987 год

стр. 47 . 2.7. Правила округления и записи результатов измерений

Погрешность результата измерений позволяет определить те цифры результата, которые являются достоверными. Нецелесообразно удерживать в выражении для измеренного значения физической величины большое число цифр, т.к. цифры младших разрядов могут оказаться недостоверными.

Существуют определенные правила округления.

1. В выражении погрешности удерживается не более двух значащих цифр, причем последняя цифра обычно округляется до нуля или пяти. Две цифры следует обязательно удерживать в том случае, когда цифра старшего разряда менее 3.

2 . Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.

Пример. 235,732 + 0,15 округляется до 235,73 + 0,15, но не до 235,7 + 0,15.

При промежуточных вычислениях целесообразно, чтобы используемые числа содержали на одну значащую цифру больше, чем будет в окончательном результате. Это позволяет уменьшить погрешность от округления.

3. Если первая из отбрасываемых цифр (считая слева направо) меньше пяти, то остающиеся цифры не меняются.

Пример. 442,749 + 0,4 округляется до 442,7 + 0,4.

4. Если первая из отбрасываемых цифр больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.

Пример. 37,268 + 0,5 округляется до 37,3 + 0,5; 37,253 + 0,5 округляется до 37,3 + 0,5.

5. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.

Пример. Поэтапное округление результата измерения 220,46 + 4 дает на первом этапе 220,5 + 4 и на втором 221 + 4, в то время как правильный результат округления 220 + 4.

Особенно внимательно нужно относиться к записи результата измерения без указания погрешности (что в общем случае крайне нежелательно). В этом случае в записываемом числе оставляются только те цифры, за достоверность которых можно ручаться, т.е. все значащие цифры записанного числа должны быть достоверными. Значащими цифрами числа считаются все цифры от первой слева, не равной нулю, до последней записанной справа цифры, при этом нули, записанные в виде множителя 10 в степени п, не учитываются. Поэтому записи 2,4 х 10 В в степени 3 и 2400 В не являются тождественными. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может быть, например, 2,42 или 2,38 кВ. Запись 2400 В означает, что верны и единицы вольт, истинное значение может быть 2400,2 или 2390,8 В, но не 2420 или 2380 В.

Из книги П.В. Новицкий и И.А. Зограф

«Оценка погрешностей результатов измерений»

Ленинград, Энергоатомиздат, Ленинградское отделение, 1991 год

стр. 25 1 — 4. ПРАВИЛА ОКРУГЛЕНИЯ ЗНАЧЕНИЙ ПОГРЕШНОСТИ И РЕЗУЛЬТАТА ИЗМЕРЕНИЙ

Рассчитывая значения погрешности, особенно при пользовании электронным калькулятором, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормируемые значения погрешности средств измерения, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна — две значащие цифры. При этом приходится учитывать следующее. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 — 50 %), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т. е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.

Исходя из этого на практике установилось такое правило: если полученное число начинается с цифры, равной или большей 3, то в нем сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нем сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5 % указываются два знака, но в числах 0,5; 4; 6 % указывается

В итоге можно сформулировать три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

1 . Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, — если первая есть 3 и более.

2 . Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

3 . Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним — двумя лишними знаками.

Пример . На вольтметре класса точности 2,5 с пределом измерений 300 В был получен отсчет измеряемого напряжения Х = 267,5 В.

Расчет погрешности удобнее вести в следующем порядке: сперва необходимо найти абсолютную погрешность, а затем — относительную. Абсолютная погрешность / (Х) = jo X к /100; при jo = 2,5 % и Х к = 300 В это даёт / (Х) = 2,5 х 300 / 100 = 7,5 В

8 В; относительная

jo = / o x 100 / X = 7,5 x 100 / 267,5 = 2,81 %

Так как первая значащая цифра значения абсолютной погрешности (7,5 В) больше трех, то это значение должно быть округлено по обычным правилам округления до 8 В, но в значении относительной погрешности (2,81 %) первая значащая цифра меньше 3, поэтому здесь должны быть сохранены в ответе два десятичных разряда и указано j ( x ) = 2,8 %. Полученное значение Х = 267,5 В должно быть округлено до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности , т. е. до целых единиц вольт.

Таким образом, в окончательном ответе должно быть сообщено: «Измерение произведено с относительной погрешностью j ( x ) = 2,8 % . Измеренное напряжение Х = (268 + В или Х = 268 В + 8 В.

При этом более наглядно указать пределы интервала неопределенности измеренной величины в виде Х = (260 — 276) В или 260 В X

Наряду с изложенными правилами округления значений погрешностей результатов измерения иногда предлагаются более обоснованные, но и более сложные правила. Недостаток изложенных правил состоит в том, что относительная погрешность от округления изменяется скачком при переходе, например, от числа 0,29, когда она составляет (0,30 — 0,29) / 0,30 = 3 %, к числу 0,3, когда она будет (0,4 — 0,3) / 0,3 = 30 %. Для устранения столь резкого скачка относительной погрешности округления предлагается каждую декаду возможных значений округляемой погрешности делить на три части: от 0,1 до 0,2, от 0,2 до

0,5 и от 0,5 до 1,0, и в каждой из этих частей использовать свой шаг округления, соответственно равный 0,02, 0,05 и 0,1. Тогда ряд разрешенных к употреблению округленных значений погрешностей получает вид: 0,10 — 0,12 — 0,14 — 0,16 — 0,18 — 0,20 — 0,25 — 0,30 — 0,35 — 0,40 — 0,45 — 0,5 — 0,6 — 0,7 — 0,8 — 0,9 — 1,0. Бесспорное преимущество такого ряда состоит в том, что погрешность от округления на границах участков изменяется лишь от 5 до 10 % . Однако при использовании такого правила округления погрешности последние цифры результата, оставляемые после округления, также должны соответствовать приведенному ряду.

Из книги В.А.Кузнецова и Г.В.Ялунина » МЕТРОЛОГИЯ

теоретические, прикладные и законодательные основы «

Москва, Изд — во стандартов, 1998 г.

стр. 215 7.6 Рекомендуемые правила по округлению результатов измерений

Результаты измерений следует округлять по сложившимся правилам. В основе этих правил лежит следующее положение: числовое значение результата измерений представляется так, чтобы оно оканчивалось десятичным знаком того же разряда, какой имеет погрешность этого результата.

Правила округления результата измерений для случаев обычных измерений, не связанных с необходимостью получения высокоточных результатов:

1) погрешность результата измерений представляется с одной или двумя значащими цифрами. Две значащие цифры приводятся в случае выполнения точных измерений;

2) результат измерений округляется так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности. Если числовое значение результата измерения представляется десятичной дробью, оканчивающейся нулями, то нули отбрасываются только до того разряда, который соответствует разряду числового значения погрешности;

3) если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры в

числе не изменяют. Если эта цифра равна или больше 5, то последнюю оставляемую цифру увеличивают на единицу. Лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают. Например, числовое значение результата измерения составляет 25,458 при погрешности результата, выраженной пределами + 0 ,02; округление результата будет 25,46. Если пределы погрешности имеют + 0,002, то числовое значение результата сохраняется полностью. Числовое значение результата измерений 105553 получено с погрешностью + 0,0005. В нем сохраняются четыре значащие цифры и округление даст число 105600; если числовое значение результата 105,553, то при тех же условиях округление дает число 105,6;

4) если отбрасываемая цифра равна пяти, а следующие за ней цифры неизвестны (отсутствуют) или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Число 105,5 при сохранении трех значащих цифр округляют до 106;

5) правила, изложенные в п.1. 4, применяются только при округлении окончательных результатов. Все промежуточные результаты целесообразно представлять тем числом разрядов, которые удается получить

Ошибки округления , ^[1] также называется ошибка округления , ^[2] представляют собой разность между результатом полученного по заданному алгоритму с использованием точного арифметическим и результат получает тем же самый алгоритм с использованием конечной точности, округленная арифметики. ^[3] Ошибки округления возникают из-за неточности в представлении действительных чисел и выполняемых с ними арифметических операций. Это форма ошибки квантования . ^[4] При использовании приближенных уравнений или алгоритмов, особенно при использовании конечного числа цифр для представления действительных чисел (которые теоретически имеют бесконечное количество цифр), одна из целейчисленный анализ предназначен для оценки ошибок вычислений. ^[5] Ошибки вычислений, также называемые числовыми ошибками , включают как ошибки усечения, так и ошибки округления.

Когда выполняется последовательность вычислений с вводом, включающим любую ошибку округления, ошибки могут накапливаться, иногда доминируя в вычислении. В плохо обусловленных проблемах может накапливаться значительная ошибка. ^[6]

Короче говоря, есть два основных аспекта ошибок округления, связанных с численными расчетами: ^[7]

Цифровые компьютеры имеют ограничения по величине и точности их способности представлять числа.
Некоторые численные операции очень чувствительны к ошибкам округления. Это может быть связано как с математическими соображениями, так и с тем, как компьютеры выполняют арифметические операции.

Ошибка представления

Ошибка, возникающая при попытке представить число с помощью конечной строки цифр, является формой ошибки округления, называемой ошибкой представления . ^[8] Вот несколько примеров ошибок представления в десятичных представлениях:

Обозначение	Представление	Приближение	Ошибка
1/7	0. 142 857	0,142 857	0,000 000 142 857
пер 2	0,693 147 180 559 945 309 41 …	0,693 147	0,000 000 180 559 945 309 41 …
журнал ₁₀ 2	0,301 029 995 663 981 195 21 …	0,3010	0,000 029 995 663 981 195 21 …
³ √ 2	1,259 921 049 894 873 164 76 …	1,25992	0,000 001 049 894 873 164 76 …
√ 2	1,414 213 562 373 095 048 80 …	1,41421	0,000 003 562 373 095 048 80 …
е	2,718 281 828 459 045 235 36 …	2,718 281 828 459 045	0,000 000 000 000 000 235 36 …
π	3,141 592 653 589 793 238 46 …	3,141 592 653 589 793	0,000 000 000 000 000 238 46 …

Увеличение числа цифр, разрешенных в представлении, снижает величину возможных ошибок округления, но любое представление, ограниченное конечным числом цифр, все равно вызовет некоторую степень ошибки округления для несчетного количества действительных чисел. Дополнительные цифры, используемые на промежуточных этапах вычислений, называются защитными цифрами . ^[9]

Многократное округление может привести к накоплению ошибок. ^[10] Например, если 9,945309 округляется до двух десятичных знаков (9,95), а затем снова округляется до одного десятичного знака (10,0), общая ошибка составляет 0,054691. Округление 9,945309 до одного десятичного знака (9,9) за один шаг приводит к меньшей ошибке (0,045309). Обычно это происходит при выполнении арифметических операций (см. « Потеря значимости» ).

Система счисления с плавающей точкой

По сравнению с системой счисления с фиксированной запятой, система счисления с плавающей запятой более эффективна при представлении действительных чисел, поэтому она широко используется в современных компьютерах. Пока реальные цифры бесконечны и непрерывны, система счисления с плавающей запятой конечно и дискретно. Таким образом, ошибка представления, которая приводит к ошибке округления, возникает в системе счисления с плавающей запятой.

Обозначение системы счисления с плавающей запятой

Система счисления с плавающей запятой характеризуется целые числа:

: основание или основание

: точность

: диапазон экспоненты, где это нижняя граница и это верхняя граница

Любой имеет следующий вид:

куда целое число такое, что для , а также целое число такое, что .

Нормализованная система с плавающей запятой

Система счисления с плавающей запятой нормализуется, если первая цифра всегда отличен от нуля, если только число не равно нулю. ^[3] Поскольку мантиссамантисса ненулевого числа в нормированной системе удовлетворяет . Таким образом, нормализованная форма ненулевого числа с плавающей запятой IEEE : куда . В двоичном формате первая цифра всегдапоэтому он не записывается и называется неявным битом. Это дает дополнительный бит точности, так что ошибка округления, вызванная ошибкой представления, уменьшается.
Поскольку система счисления с плавающей запятой является конечным и дискретным, он не может представлять все действительные числа, что означает, что бесконечные действительные числа могут быть аппроксимированы только некоторыми конечными числами с помощью правил округления . Приближение заданного действительного числа с плавающей запятой к можно обозначить.
- Общее количество нормализованных чисел с плавающей запятой равно

, куда

считает выбор знака, положительный или отрицательный

считает выбор первой цифры

считает оставшуюся мантиссу

считает выбор показателей

считает тот случай, когда число .

Стандарт IEEE

В стандарте IEEE база двоичная, т.е., и используется нормализация. Стандарт IEEE хранит знак, показатель степени и мантиссу в отдельных полях слова с плавающей запятой, каждое из которых имеет фиксированную ширину (количество бит). Два наиболее часто используемых уровня точности для чисел с плавающей запятой — это одинарная точность и двойная точность.

Точность	Знак (биты)	Экспонента (биты)	Мантисса (биты)
Одинокий	1	8	23
Двойной	1	11	52

Машинный эпсилон

Машинный эпсилон может использоваться для измерения уровня ошибки округления в системе счисления с плавающей запятой. Вот два разных определения. ^[3]

Машинный эпсилон, обозначаемый , — максимально возможная абсолютная относительная ошибка представления ненулевого действительного числа в системе счисления с плавающей запятой.

Машинный эпсилон, обозначаемый , это наименьшее число такой, что . Таким образом, в любое время .

Ошибка округления при разных правилах округления

Существует два распространенных правила округления: округление за отрезком и округление до ближайшего. Стандарт IEEE использует округление до ближайшего.

По очереди : Основание- расширение усекается после цифра.
- Это правило округления смещено, потому что оно всегда приближает результат к нулю.
Округление до ближайшего : устанавливается равным ближайшему числу с плавающей запятой к . При равенстве используется число с плавающей запятой, последняя сохраненная цифра которого четная.
- Для стандарта IEEE, где базовый является , это означает, что когда есть ничья, она округляется так, чтобы последняя цифра была равна .
- Это правило округления более точное, но более затратное с точки зрения вычислений.
- Округление таким образом, чтобы последняя сохраненная цифра была даже при равенстве, гарантирует, что она не округляется систематически в большую или меньшую сторону. Это сделано для того, чтобы избежать возможности нежелательного медленного отклонения в длинных вычислениях просто из-за смещения округления.
В следующем примере показан уровень ошибки округления в соответствии с двумя правилами округления. ^[3] Правило округления, округление до ближайшего, в целом приводит к меньшей ошибке округления.

Икс	По очереди	Ошибка округления	Округление до ближайшего	Ошибка округления
1,649	1.6	0,049	1.6	0,049
1,650	1.6	0,050	1,7	0,050
1,651	1.6	0,051	1,7	-0,049
1,699	1.6	0,099	1,7	-0,001
1,749	1,7	0,049	1,7	0,049
1,750	1,7	0,050	1,8	-0,050

Расчет ошибки округления в стандарте IEEE

Предположим, что используется округление до ближайшего и двойная точность IEEE.

Пример: десятичное число может быть преобразован в

Поскольку бит справа от двоичной точки — это и за ним следуют другие ненулевые биты, правило округления до ближайшего требует округления, то есть добавления немного к немного. Таким образом, нормализованное представление с плавающей запятой в стандарте IEEE является

Теперь ошибку округления можно вычислить при представлении с участием .

Это представление получается путем отбрасывания бесконечного хвоста

из правого хвоста, а затем добавил на этапе округления.

потом .

Таким образом, ошибка округления равна .

Измерение ошибки округления с помощью машинного эпсилона

Машина эпсилон может использоваться для измерения уровня ошибки округления при использовании двух вышеупомянутых правил округления. Ниже приведены формулы и соответствующие доказательства. ^[3] Здесь используется первое определение машинного эпсилон.

Теорема

По очереди:
Округление до ближайшего:

Доказательство

Позволять куда , и разреши быть представлением с плавающей запятой . Поскольку используется последовательное нарезание,
* Чтобы определить максимум этой величины, необходимо найти максимум числителя и минимум знаменателя. С (нормализованная система), минимальное значение знаменателя равно . Числитель ограничен сверху. Таким образом,. Следовательно,для порезки. Доказательство для округления до ближайшего аналогично.

Обратите внимание, что первое определение машинного эпсилон не совсем эквивалентно второму определению при использовании правила округления до ближайшего, но оно эквивалентно для последовательного перехода.

Ошибка округления, вызванная арифметикой с плавающей запятой

Даже если некоторые числа могут быть представлены точно числами с плавающей запятой и такие числа называются машинными числами , выполнение арифметических операций с плавающей запятой может привести к ошибке округления в окончательном результате.

Дополнение

Машинное сложение состоит из выравнивания десятичных знаков двух добавляемых чисел, их сложения и последующего сохранения результата как числа с плавающей запятой. Само сложение может быть выполнено с более высокой точностью, но результат должен быть округлен до указанной точности, что может привести к ошибке округления. ^[3]

Например, добавив к в IEEE двойной точности следующим образом:

Это сохранено как поскольку в стандарте IEEE используется округление до ближайшего. Следовательно, равно в IEEE двойной точности и ошибка округления .

Умножение

В общем, продукт -цифровые мантиссы содержат до цифр, поэтому результат может не соответствовать мантиссе. ^[3] Таким образом, в результат будет включена ошибка округления.

Например, рассмотрим нормализованную систему счисления с плавающей запятой с основанием и цифры мантиссы не более . потом а также . Обратите внимание, что но так как там самое большее цифры мантиссы. Ошибка округления будет.

Подразделение

В общем, частное -цифровые мантиссы могут содержать более -цифры. ^[3] Таким образом, в результат будет включена ошибка округления.

Например, если приведенная выше нормализованная система счисления с плавающей запятой все еще используется, то но . Итак, хвост отрезан.

Вычитающая отмена

Вычитание двух почти равных чисел называется вычитанием . ^[3]

Когда начальные цифры отменяются, результат может быть слишком маленьким для точного представления, и он будет представлен просто как .
- Например, пусть и здесь используется второе определение машинного эпсилон. Какое решение?
  Известно, что а также почти равные числа, и . Однако в системе счисления с плавающей запятой. Несмотря на то что достаточно большой, чтобы быть представленным, оба экземпляра были округлены, давая .
Даже с несколько большим , в типичных случаях результат по-прежнему существенно ненадежен. Нет особой веры в точность значения, потому что наибольшая неопределенность в любом числе с плавающей запятой — это цифры в крайнем правом углу.
- Например, . Результат ясно представима, но в это мало веры.

Накопление ошибки округления

Нестабильные алгоритмы

Алгоритм или численный процесс называется стабильным, если небольшие изменения на входе вызывают только небольшие изменения на выходе, и называется нестабильным, если производятся большие изменения на выходе. ^[11]

Последовательность вычислений обычно происходит при запуске какого-либо алгоритма. Количество ошибок в результате зависит от стабильности алгоритма . Ошибка округления будет увеличиваться нестабильными алгоритмами.

Например, для с участием данный. Легко показать, что. Предполагать это наше начальное значение и имеет небольшую ошибку представления , что означает, что начальный вход в этот алгоритм вместо того . Затем алгоритм выполняет следующую последовательность вычислений.

Ошибка округления увеличивается в последующих вычислениях, поэтому этот алгоритм нестабилен.

Плохо обусловленные проблемы

Даже если используется стабильный алгоритм, решение проблемы может быть неточным из-за накопления ошибок округления, когда сама проблема плохо обусловлена .

Число обусловленности проблемы — это отношение относительного изменения решения к относительному изменению входных данных. ^[3] Проблема хорошо обусловлена, если небольшие относительные изменения входных данных приводят к небольшим относительным изменениям в решении. В противном случае проблема плохо обусловлена . ^[3] Другими словами, проблема является плохо обусловленной, если ее число условий «намного больше», чем.

Пример из реального мира: отказ ракеты «Патриот» из-за увеличения ошибки округления

Американская ракета Пэтриот

25 февраля 1991 года, во время войны в Персидском заливе, американская ракетная батарея «Пэтриот» в Дхаране, Саудовская Аравия, не смогла перехватить приближающуюся иракскую ракету «Скад». Скад врезался в казармы американской армии и убил 28 солдат. Отчет тогдашней Главной бухгалтерииозаглавленный «Противоракетная оборона Patriot: проблема программного обеспечения, приведшая к отказу системы в Дахране, Саудовская Аравия», сообщает о причине сбоя: неточный расчет времени с момента загрузки из-за компьютерных арифметических ошибок. В частности, время в десятых долях секунды, измеренное внутренними часами системы, было умножено на 10, чтобы получить время в секундах. Этот расчет был выполнен с использованием 24-битного регистра с фиксированной запятой. В частности, значение 1/10, которое имеет неограниченное двоичное расширение, было прервано на 24 бита после точки счисления. Небольшая ошибка прерывания, умноженная на большое число, дающее время в десятых долях секунды, привела к значительной ошибке. Действительно, батарея Patriot проработала около 100 часов,и простой расчет показывает, что результирующая временная ошибка из-за увеличенной ошибки прерывания составила около 0,34 секунды. (Число 1/10 равно. Другими словами, двоичное разложение 1/10 равно. Теперь 24-битный регистр в Патриоте хранится вместо вводя ошибку двоичный, или около десятичный. Умножая на количество десятых долей секунды в часов дает ). Скад едет примерно1676 метров в секунду, то есть за это время проходит более полукилометра. Этого было достаточно, чтобы приближающийся Скад находился за пределами «ворот дальности», которые отслеживал Патриот. По иронии судьбы, тот факт, что вычисление плохого времени было улучшено в некоторых частях кода, но не во всех, способствовал возникновению проблемы, поскольку это означало, что неточности не отменялись. ^[12]

См. Также

Точность (арифметика)
Усечение
Округление
Потеря значимости
Плавающая запятая
Алгоритм суммирования Кахана
Машина эпсилон
Полином Уилкинсона

Ссылки

↑ Butt, Rizwan (2009), Введение в численный анализ с использованием MATLAB , Jones & Bartlett Learning, стр. 11–18, ISBN 978-0-76377376-2
^ Ueberhuber, Christoph W. (1997), Численный 1: Методы, программное обеспечение и анализ ., М., С. 139-146, ISBN 978-3-54062058-7
^ ^Б^с^д^е^е^г^ч^я^J^K Форрестер, Дик (2018). Math / Comp241 Численные методы (конспекты лекций) . Колледж Дикинсона .
^ Аксой, Пелин; ДеНардис, Лаура (2007), Информационные технологии в теории , Cengage Learning, стр. 134, ISBN 978-1-42390140-2
^ Ральстон, Энтони; Рабиновиц, Филип (2012), Первый курс численного анализа , Dover Books on Mathematics (2-е изд.), Courier Dover Publications, стр. 2–4, ISBN 978-0-48614029-2
^ Чапман, Стивен (2012), Программирование MATLAB с приложениями для инженеров , Cengage Learning, стр. 454, ISBN 978-1-28540279-6
^ ^a ^b Чапра, Стивен (2012). Прикладные численные методы с MATLAB для инженеров и ученых (3-е изд.). ISBN компании McGraw-Hill Companies, Inc. 9780073401102.
^ Laplante, Филип А. (2000). Словарь компьютерных наук, инженерии и технологий . CRC Press . п. 420. ISBN 978-0-84932691-2.
^ Хайэм, Николас Джон (2002). Точность и устойчивость численных алгоритмов (2-е изд.). Общество промышленной и прикладной математики (SIAM). С. 43–44. ISBN 978-0-89871521-7.
Перейти ↑ Volkov, EA (1990). Численные методы . Тейлор и Фрэнсис . п. 24. ISBN 978-1-56032011-1.
^ Коллинз, Чарльз (2005). «Состояние и стабильность» (PDF) . Департамент математики Университета Теннесси . Проверено 28 октября 2018 .
^ Арнольд, Дуглас. «Неудача ракеты» Патриот » . Проверено 29 октября 2018 .

Дальнейшее чтение

Мэтт Паркер (2021). Humble Pi: Когда математика идет не так в реальном мире . Книги Риверхеда. ISBN 978-0593084694.

Внешние ссылки

Ошибка округления в MathWorld.
Гольдберг, Дэвид (март 1991). «Что должен знать каждый компьютерный ученый об арифметике с плавающей запятой» (PDF) . ACM Computing Surveys . 23 (1): 5–48. DOI : 10.1145 / 103162.103163 . Проверено 20 января 2016 .( [1] , [2] )
20 известных программных катастроф

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

где tilde a – приближение к точному значению .
Относительная погрешность определяется формулой

$delta(tilde a)=frac{|tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, , абсолютная погрешность . Записывая число в виде

имеем , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$Delta(tilde a)<0,5cdot10^{m-n+1} ,$

где — порядок (вес) старшей цифры, — количество верных значащих цифр.
В рассматриваемом примере $Delta(tilde a)le0,5cdot10^{3-2+1}le0,5cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$delta(tilde a)lefrac{Delta(tilde a)}{alpha_m}10^mlefrac{10^{m-n+1}}{alpha_m10^m}lefrac{1}{alpha_m10^{n-1}},$

где alpha_m — старшая значащая цифра числа.

Для двоичного представления чисел имеем $delta(tilde a)le2^{-n}$ .

Тот факт, что число tilde a является приближенным значением числа с абсолютной погрешностью , записывают в виде

причем числа tilde a и записываются с одинаковым количеством знаков после запятой, например, или $a=2,347pm2cdot10^{-3}$ .

Запись вида

означает, что число tilde a является приближенным значение числа с относительной погрешностью .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

AX=F

характеризуется невязкой

где tilde X — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина является функцией параметров — приближенное значение . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = suplimits_{(t_1, ldots ,t_n) in Omega } left|{a(t_1, ldots ,t_n) - a^*}right| ,$

Предельной относительной погрешностью называется величина .

Пусть $left|{t_j - t_j^*}right| le Delta (t_j^* ), qquad j = 1 div n$ — приближенное значение . Предполагаем, что — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, ldots ,t_n) - a^* = sumlimits_{j = 1}^n gamma_j (alpha )(t_j - t_j^*),$

где $gamma_j (alpha ) = a^{prime}_{t_j}(t_1^* + alpha (t_1 - t_1^*), ldots ,t_n^* + alpha (t_n - t_n^*)), qquad 0 le alpha le 1$ .

Отсюда

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_1 (a^*) = sumlimits_{j = 1}^n b_j Delta (t_j^*),$

где $b_j = suplimits_Omega left|{a^{prime}_{t_j}(t_1, ldots ,t_n)}right|$ .

Можно показать, что при малых $rho = sqrt{{(Delta (t_1^* ))}^2 + ldots + {(Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_2 (a^*),$

где $D_2 (a^*) = sumlimits_{j = 1} left|{gamma_j (0)}right| Delta (t^*)$ .

Несложно показать, что:

— предельная погрешность суммы или разности равна сумме предельных погрешностей.
$delta (t_1^* cdots t_m^* cdot d_1^{* - 1} cdots d_m^{* - 1} ) = delta (t_1^* ) + ldots + delta (t_m^*) + delta (d_1^*) + ldots + delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом tilde a , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=underbrace{pm2^p}_{order}underbrace{left(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}+frac{a_{t+1}}{2^{t+1}}+dotsright)}_{mantissa},$

где $a_j={0\1$ , — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$tilde a=pm2^pleft(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}right).$

Абсолютная погрешность округления в этом случае равна

$a-tilde a=pm2^pleft(frac{a_{t+1}}{2^{t+1}}+frac{a_{t+2}}{2^{t+2}}+dotsright).$

Наибольшая погрешность будет в случае $a_{t+1}=1, qquad a_{t+2}=1,$ , тогда

$|a-tilde a|lepm2^pfrac{1}{2^{t+1}}underbrace{left(1+frac{1}{2}+frac{1}{2^2}+dotsright)}_{=2}=2^{p-t}.$

Т.к. , где — мантисса числа , то всегда a_1=1 . Тогда $|a|ge2^pcdot2^{-1}=2^{p-1}$ и относительная погрешность равна $frac{|a-tilde a|}{|a|}le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$frac{|a-tilde a|}{|a|}le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде , где $|epsilon|le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через fl(x) (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

где box — любая из арифметических операций, $|epsilon|le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

сумма приближенных чисел равна

где — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

Относительная погрешность суммы нескольких чисел равна

( 2 )

$delta(S)=frac{Delta(S)}{S}=frac{a_1}{S}left(frac{Delta(a_1)}{a_1}right)+frac{a_2}{S}left(frac{Delta(a_2)}{a_2}right)+dots=frac{a_1delta(a_1)+a_2delta(a_2)+dots}{S},$

где — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

( 3 )

tilde S=(tilde S_1+x_3)(1+delta_2)=(x_1+x_2)(1+delta_1)(1+delta_2)+x_3(1+delta_2).

При другой последовательности действий погрешность будет другой:

tilde S=(x_3+x_2)(1+delta_1)(1+delta_2)+x_1(1+delta_2).

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

где

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

tilde S=a_1cdot a_2(1+delta(a_1))(1+delta(a_2))

≅

с точностью величин второго порядка малости относительно delta .

Тогда .

Если $S=frac{a_1}{a_2}$ , то $Delta(S)=frac{a_1(1+delta_1)}{a_2(1+delta_2)}-frac{a_1}{a_2}=frac{a_1(delta_1-delta_2)}{a_2(1+delta_2)}approx frac{a_1}{a_2}(delta_1-delta_2), qquad delta(S)$ ≅

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$delta_Sigma approx delta_{fl} quad sqrt{n},$

где – суммарная погрешность, $|delta_{fl}|leepsilon$ – погрешность выполнения операций с плавающей точкой, epsilon – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции y=f(x) , вызываемая достаточно малой погрешностью аргумента , оценивается величиной .

Если f(x)>0 , то $delta(y)=frac{|f'(x)|}{f(x)}Delta(x)=left|(ln(f(x)))'right|cdotDelta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями аргументов оценивается величиной:

$Delta(y)=sumlimits_{i=1}^nleft|frac{partial f}{partial x_i}right|Delta(x_i)$

Если , то $delta(y)=sumlimits_{i=1}^nfrac{1}{f}cdotleft|frac{partial f}{partial x_i}right|cdotDelta(x_i)=sumlimits_{i=1}^{n}left|frac{partial l_n(f)}{partial x_i}right|Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной y=f(x) , если f(x) дифференцируема и :

$Delta(x)=frac{1}{|f'(x)|}Delta(y)$ .

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности , то:

$Delta(x_i)=frac{Delta(y)}{left|frac{partial f}{partial x_i}right|}qquad$

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$Delta(x_i)=frac{Delta(y)}{nleft|frac{partial f}{partial x_i}right|},qquad i=overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 pm 0,01i.$

Если компьютер работает при $delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

u''(t) = u(t), qquad u(0) = 1, qquad u'(0) = - 1.

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность delta в их задании приведет к появлению члена , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$stackrel{cdot}{u} = 10u,qquad u = u(t),\ u(t_0) = u_0,qquad t in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение u(t_0) известно лишь приближенно: , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность u* - u будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| le varepsilon.$

Очевидно, что:

$maxlimits_{t in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $delta: qquad|u_0^* - u_0| < delta, qquad delta le varepsilon e^{ - 10}$ при t_0= 0 .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

$left{ begin{array}{l} u + 10v = 11, \ 100u + 1001v = 1101; \ end{array} right.$

является пара чисел .

Изменив правую часть системы на 0,01 , получим возмущенную систему:

$left{ begin{array}{l} u + 10v = 11.01, \ 100u + 1001v = 1101; \ end{array} right.$

с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки , разность которых составляет .

В памяти машины эти же числа представляются в виде:

u_M = u(1 + delta_M^u), quad v_M = v(1 + delta_M^v)

, причем

Тогда:

u_M - u approx udelta_M^u, quad v_M - v approx vdelta_M^v.

Относительная ошибка при вычислении разности будет равна:

$delta = frac{(u_M - v_M) - (u - v)}{(u - v)} = frac{(u_M - u) - (v_M - v)}{(u - v)} = frac{delta_M^u - delta_M^v}{(u - v)}.$

Очевидно, что $delta = left|{frac{delta_M^u - delta_M^v}{Delta }} right| le frac{2delta_M}{0,001} approx 2000delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, quad i ge 0, quad u_0 = a,quad q > 0, quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + delta_i) = u_{i + 1} + qdelta_i$ , т.е. $delta_{i + 1} = qdelta_i,quad i = 0,1,ldots$ .

Следовательно, если |q| > 1 , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

8.27 ≈ 9	0.237 ≈ 0.3
0.0862 ≈ 0.09	0.00035 ≈ 0.0004
857.3 ≈ 900	43.5 ≈ 50

Ошибки округления

Абсолютная и относительная погрешности

Representation error[edit]

Floating-point number system[edit]

Notation of floating-point number system[edit]

Normalized floating-number system[edit]

IEEE standard[edit]

Machine epsilon[edit]

Roundoff error under different rounding rules[edit]

Calculating roundoff error in IEEE standard[edit]

Measuring roundoff error by using machine epsilon[edit]

Theorem[edit]

Proof[edit]

Roundoff error caused by floating-point arithmetic[edit]

Addition[edit]

Multiplication[edit]

Division[edit]

Subtraction[edit]

Accumulation of roundoff error[edit]

Unstable algorithms[edit]

Ill-conditioned problems[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Ошибка представления

Система счисления с плавающей запятой

Обозначение системы счисления с плавающей запятой

Нормализованная система с плавающей запятой

Стандарт IEEE

Машина эпсилон

Ошибка округления при разных правилах округления

Расчет ошибки округления в стандарте IEEE

Измерение ошибки округления с помощью машины эпсилон

Теорема

Доказательство

Ошибка округления, вызванная арифметикой с плавающей запятой

Добавление

Умножение

Разделение

Вычитающая отмена

Накопление ошибки округления

Нестабильные алгоритмы

Плохо обусловленные проблемы

Пример из реального мира: отказ ракеты Patriot из-за увеличения ошибки округления

Смотрите также

Рекомендации

внешняя ссылка

Округление результатов

Обработка результатов косвенного измерения

Правила округления

Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!

Физика — рефераты, конспекты, шпаргалки, лекции, семинары

Правила округления значений погрешностей и результатов измерения

Ошибка представления

Система счисления с плавающей точкой

Обозначение системы счисления с плавающей запятой

Нормализованная система с плавающей запятой

Стандарт IEEE

Машинный эпсилон

Ошибка округления при разных правилах округления

Расчет ошибки округления в стандарте IEEE

Измерение ошибки округления с помощью машинного эпсилона

Теорема

Доказательство

Ошибка округления, вызванная арифметикой с плавающей запятой

Дополнение

Умножение

Подразделение

Вычитающая отмена

Накопление ошибки округления

Нестабильные алгоритмы

Плохо обусловленные проблемы

Пример из реального мира: отказ ракеты «Патриот» из-за увеличения ошибки округления

См. Также

Ссылки

Дальнейшее чтение

Внешние ссылки

Материал из MachineLearning.

Содержание