Ошибка определения дальности

Содержание раздела «Точность радиолокационных измерений»

1. Точность определения дальности
   • Случайная ошибка измерения
   • Математические соотношения
   • Систематические ошибки измерения
2. Точность измерения угловых координат
3. Как выполняется измерение для оценки точности радиолокатора?
4. Примеры

Точность радиолокационных измерений

Точность это степень соответствия между оцениваемыми или измеряемыми значениями параметров
(координаты и/или скорость движения) лоцируемого объекта в определенный момент времени и их истинными значениями.
В радиолокации точность измерения обычно представляется как статистическая мера систематической ошибки,
которая характеризуется следующими свойствами:

1. Предсказуемость: Точность позиционирования определяется при использовании географических или геодезических систем координат Земли.
2. Повторяемость: Означает то, что результаты измерения одной и той же системой в сходных условиях,
   будут характеризоваться близкими значениями точности в пределах некоторого интервала времени.
3. Относительность: Точность измерений относительно одной позиции может быть пересчитана для другой позиции (пренебрегая всевозможными ошибками).

Заявленное значение требуемой точности показывает,
что определяемое системой измерения значение того или иного параметра может отклоняться от его истинного значения,
и указывает интервал значений, в котором находится истинное значение с заданной вероятностью.
Рекомендуемое значение вероятности 95%, что соответствует интервалу,
равному удвоенному среднеквадратическому отклонению относительно среднего значения для нормального (Гауссового) распределения случайной величины.
Предположение, что все известные поправки учтены, означает, что ошибки оценивания будут иметь средние значения (смещения), близкие к нулю.

Любое остаточное смещение должно быть небольшим по сравнению с заявленной точностью.
Истинное значение — это значение, которое в рабочих условиях наилучшим образом характеризует измеряемую величину,
наблюдаемую в пределах репрезентативного (достаточного) интервала времени, площади и / или объема с учетом расположения и влияющих факторов.

ошибка измерения

импульс+шум

порог

идеальный импульс

Рисунок 1. Искажение фронта импульса под воздействием шумов

ошибка измерения

импульс+шум

порог

идеальный импульс

Рисунок 1. Искажение фронта импульса под воздействием шумов

Точность определения дальности

Теоретическая максимально достижимая точность измерения дальности методом радиолокационной импульсной дальнометрии
зависит от точности измерения времени запаздывания отраженного сигнала.

Случайные ошибки измерения

Случайные ошибки измерения в
импульсных радиолокаторах
возникают когда передний фронт отраженного сигнала искажается под воздействием шумов.
На отраженный сигнал всегда накладываются шумы, в результате чего увеличивается амплитуда принятого сигнала.
Это вызывает смещение переднего фронта импульса и, следовательно, является причиной ошибки измерения времени запаздывания отраженного сигнала.

На Рисунке 1 показано влияние шумов на обнаруживаемый передний фронт эхо-сигнала.
Сплошной линией (фиолетовой) изображен идеальный трапецеидальный импульс с довольно крутыми фронтом и спадом.
Этот импульс не может быть слишком близким к прямоугольному, поскольку это потребовало бы бесконечно широкой полосы частот.
Время задержки импульса измеряется в момент времени, когда его амплитуда достигает порогового значения, обычно на уровне 0,707 от максимальной амплитуды.
Однако на отраженный импульс накладывается шум (зеленая линия).
Измеренным может быть только напряжение, являющееся суммой мгновенных значений амплитуды импульса и шума
(желтая синяя пунктирная линия).
Это напряжение достигнет порогового значения раньше, чем напряжение идеального (в отсутствии шумов) импульса.
Разница между ними — это случайная ошибка измерения времени задержки, вызванная влиянием
шумов[1].

Если длительность импульса известна (что невозможно для первичного радиолокатора, а только для
вторичного радиолокатора),
то эта случайная ошибка может быть уменьшена математически путем одновременной оценки переднего фронта и спада (заднего фронта) импульса.
В других случаях, какой-либо учет случайной ошибки не представляется возможным.

Математический контекст

Как следует из Рисунка 1, точность измерения дальности в основном зависит от
уровня шума
или, точнее, от соотношения между амплитудой импульса и уровнем шума.
Количественно это соотношение описывается отношением «сигнал-шум».
Уровень шума, в свою очередь, зависит от ширины полосы пропускания приемного тракта.
Крутизна фронта и спада прошедшего тракт отраженного импульса также зависит от этой ширины.
Для значений отношения «сигнал-шум», значительно больших единицы, между этими величинами существует следующее
соотношение:[2]

где δR — ошибка измерения;
c₀ — скорость света
B — ширина полосы пропускания;
SNR — отношение «сигнал-шум».
(1)

Однако ширина полосы пропускания является также существенным фактором,
влияющим на
разрешение радиолокатора по дальности
S_r = c₀ / 2B.
Таким образом, максимально достижимая точность измерения дальности (характеризуемая ошибкой измерения дальности)
может быть представлена как функция разрешения радиолокатора по дальности:

(2)

Отсюда следует, что максимально достижимая ошибка измерения дальности должна быть значительно лучше чем разрешающая способность по дальности.

Систематические ошибки измерения

Систематические ошибки измерения, в отличие от случайных ошибок, могут быть учтены или уменьшены, в случае, если удается определить причины их возникновения.

В импульсных радиолокаторах
время задержки обычно измеряется между передним фронтом излучаемого импульса и передним фронтом отраженного от цели импульса.
Точность измерения в таком случае будет зависеть от частоты следования тактовых (измерительных) импульсов,
по количеству которых между заданными моментами времени измеряется
длительность интервала.
Очевидно, что в промежутке между тактовыми импульсами измерение не может быть произведено,
что приводит к возникновению систематической ошибки измерения дальности.
На практике точность измерения дальности зависит от размера отдельной ячейки дальности, используемой при обработке сигнала.
В соответствии с рекомендациями
ИКАО[3]
для радиолокаторов систему управления воздушным движением размер ячейки должен быть 1/128 морской мили,
то есть около 14,5 м, что соответствует интервалу времени почти 10 нс.

В
радиолокаторах непрерывного излучения
измерение сдвига фазы принятого сигнала относительно текущей фазы передатчика может содержать (хотя и неоднозначную) информацию о дальности.

Точность измерения дальности в
радиолокаторах непрерывного излучения с частотной модуляцией
также определяется параметрами передатчика, особенно наклоном и линейностью закона изменения частоты.

Точность измерения углов

стандартные требования в
зависимости от дальности

точность измерения азимута:

методом скользящего окна

моноимпульсным методом

дальность от радара (в морских милях)

Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)

стандартные требования в
зависимости от дальности

точность измерения азимута:

методом скользящего окна

моноимпульсным методом

дальность от радара (в морских милях)

Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)

Точность измерения углов зависит как от внутренних методов обработки сигнала так и от внешних условий.
Аномальные условия распространения,
которые часто возникают из-за изменений давления воздуха,
влияют на измерение угла места и могут влиять на измерение горизонтального угла (азимута), вызывая возникновение случайной ошибки измерения.
Однако более частые источники возникновения систематических ошибок определяются внутренними факторами.

Например, измерение угла
методом скользящего окна
является довольно неточным.
На практике половина ширины диаграммы направленности антенны делится на число квантований, определяемое используемым методом
(например, 8 или 16 периодов следования импульсов) и таким образом приводит к систематической ошибке порядка одного градуса. В
корреляционных методах,
где выполняется интерполяция промежуточных значений, достигается более высокая точность измерения.
Наилучшая точность измерения угловых координат на данный момент достигается при использовании метода
конического сканирования и при
моноимпульсной пеленгации.

Как выполняются измерения для оценки точности радиолокатора?

Порядок проведения таких измерений определяется их целью, а именно: координаты, измеренные радиолокатором сравниваются с действительными координатами цели.
Для радиолокаторов наблюдения за воздушным движением для этой цели выполняется испытательный полет (облет), например, компанией
FCS Flight Calibration Services GmbH.
На борту самолета Learjet 35 располагается регистратор, который записывает текущие координаты самолета,
получаемые дифференциальной системой спутниковой навигации GPS
с ошибками менее одного метра.
В то же время траектория полета самолета регистрируется на радиолокаторе.
Оба регистратора синхронизируются при помощи сигналов единого времени, получаемых ими от системы GPS,
и результаты измерений сравниваются между собой.

При обработке результатов сравнения измеренных и действительных значений координат цели применяются методы математической статистики.
Явные ошибочные измерения исключаются из анализа, поскольку необходимо определить систематическую составляющую ошибки измерения радиолокатора.
Это не означает, однако, что требуется значительное количество зондирующих импульсов (возможно, для получения хорошего значения).
В радиолокаторах, использующих моноимпульсный метод пеленгации значение ошибки измерения определяется для каждого импульса.
Если используется метод скользящего окна, то соответствующее значение определяется для конкретного требуемого числа импульсов.

Для достижения хорошей точности измерения дальности требуется, чтобы зондирующие импульсы имели стабильный и крутой фронт.
Такой фронт часто не наблюдается при использовании
внутриимпульсной модуляции.
Но тут необходимо учитывать, что измерение дальности выполняется после сжатия отраженного импульса.
В этой точке, уже после сжатия, импульс вновь имеет крутой фронт.

Единственным условием проведения подобных измерений является отсутствие помех.
Это означает, что эхо-сигнал не должен смешиваться с внешними помехами.
Однако внутренние шумы всегда будут присутствовать в тракте прохождения отраженного сигнала.
Поэтому результативные измерения возможны когда уровень отраженного от летательного аппарата сигнала будет существенно выше
уровня шума.
Наконец, калибровка полета должна выявлять возможные дополнительные систематические ошибки, а не случайные ошибки.

Примеры

В таблице 1 приведены характеристики точности для некоторых радиолокаторов.

Название радиолокатора	Ошибка измерения углов	Ошибка измерения дальности	Ошибка измерения высоты
BOR–A 550	< ±0.3°	< 20 м
LANZA	< ±0.14°	< 50 м	340 м ≈ 1150 футов (на дальности 100 морских миль)
GM 400	< ±0,3°	< 50 м	600 м ≈ 2000 футов (на дальности 100 морских миль)
RRP–117	< ±0,18°	< 463 м	1000 м ≈ 3000 футов (на дальности 100 морских миль)
MSSR-2000	< ±0.049°	< 44.4 м
STAR-2000	< ±0.16°	< 60 м
Variant	< ±0.25°	< 25 м

Таблица 1. Примеры

Примітки

1. Merrill I. Skolnik: »Introduction to Radar Systems» McGraw-Hill Europe, 2001, ISBN 007-118189-x, S. 317,
   Topic 6.3 Theoretical Accuracy of Radar Measurements
2. G. Richard Curry: »Radar System Performance Modeling» 2005, ISBN 978-1-58053-816-9, S.168
3. ICAO Annex 10 — Volume 4. Aeronautical Telecommunications — Surveillance and Collision Avoidance Systems, Topic 4.3.2.1.3 Range and Bearing Accuracy,
   (Bundesamt für Zivilluftfahrt, Schweiz)

Неправильное определение дальности до цели является самой распространенной причиной промахов при дальнейстрельбе. Более распространенной, чем плохая оценка ветра, более распространенной, чем дергание спускового крючка, чем неправильный вынос точки прицеливания или внесение упреждений. Более распространенной, чем неправильный расчет вертикальных поправок. 

Способы определения дальности до цели, ошибки в определении дальности, определение дальности сквозь прицельную сетку, с помощью большого пальца и глазомерные способы.

Если вы неправильно определили дальности до цели, скорее всего вы промахнетесь. На это есть несколько причин. Самая серьезная из них состоит в том, что траектория пули, которая является дугой, начинает все более и более понижаться на больших расстояниях, поэтому даже небольшая ошибка оказывает большое влияние. Ниже мы показали траекторию пули .308 Federal Match.

Обратите внимание, что на 100, 200, и 300 ярдах, она летит по пологой траектории. Даже если вы совершили большую ошибку в определении дальности — скажем, решили, что цель находится от вас в 300 ярдах, тогда как действительная дальность составила 200 ярдов — на близком расстоянии, вы вероятно поразите свою цель, целясь в центр груди.

Но, например, вы ошибочно решили, что цель находится на 600 ярдах, а на самом деле только на 500 ярдах — хорошо, сейчас разница в траектории составляет около 3 футов. Вы видите, на более дальнем расстоянии, пуля снижается по более крутой дуге, и даже незначительные ошибки становятся главными.

К сожалению, по мере увеличения дальности до цели, мы также чаще и понятнее всего делаем ошибки при ее определении. Но другой серьезной проблемой, связанной с определением дальности до цели, является то, что ошибки суммируются и усложняют все последующие вычисления поправок на ветер, упреждений, и так далее. И это может приводить к промахам даже на близких дистанциях.

Посмотрите на рисунки ниже, в которых мы рассматриваем суммарное влияние ошибок при стрельбе по цели, которая находится всего в 400 ярдах. Несмотря на то, что снайпер сделал каждое отдельное вычисление правильно, за исключением первоначального определения дальности до цели, он полностью промахнулся по относительно близкой цели.

Кумулятивный эффект ошибки в определении дальности до цели.

Поскольку ряд других факторов при прицеливании требуют увеличения поправок по мере увеличения расстояния, они очень чувствительны к любой ошибке при определении дальности до цели. Поэтому изначальные ошибки в определении дальности до цели становятся кумулятивными, и даже незначительная ошибка может приводить к полному промаху.

Для нашего примера давайте примем, что цель действительно находится на дальности 400 ярдов, но наш снайпер ошибочно решил, что дальность составляет 300 ярдов. Мы будем предполагать, что он стреляет 168 грановой пулей .308 Match и винтовка пристреляна на 300 ярдах. Обратите внимание, как накапливаются его ошибки :

Таким образом, мы показали на иллюстрации, как всего одна фундаментальная ошибка в определении дальности до цели накапливается и ведет к полному промаху.

Эти поправки отличаются только из-за разницы в измерении дальности. Этот промах вызван плохим определением дальности. В то время как правильно использованная поправка должна привести к поражению центра масс.

Мы собираемся рассмотреть несколько различных устройств и способов определения дальности до цели, но по мере их рассмотрения, имейте в виду, что вы должны практиковать их в положении лежа. Таким образом, вы будете учиться использовать их так, как вы будете фактически действовать.

Определение дальности до цели сквозь прицельную сетку оптического прицела или бинокля.

Любая прицельная сетка типа «дуплекс» имеет присущую ей способность к измерению дальностей. Все, что нужно — это точные размеры сетки. Рассмотрим прицельную сетку «дуплекс» фирмы Leupold, какая существует в прицеле 3,5-10x, при его установке на максимальную кратность.

Самая тонкая часть прицельных нитей составляет 10 МОА от края до края. Это соответствует 10 дюймам на 100 ярдах, затем 20 дюймам на 200 ярдах, и так далее. Мы показали, как эта сетка выглядит при наложении на человека. Обратите внимание, что мы всегда оставляем верхнюю толстую часть прицельной нити над верхней частью его головы, не в ногах, поскольку вероятность того, что мы будем видеть верхнюю часть цели, а не ее основание, гораздо выше, особенно на больших дальностях.

Когда она находится в 600 ярдах от нас, цель заполняет всю тонкую часть сетки. Но будьте осторожны: чтобы быть точным, вы всегда определяете дальности до цели с помощью своего прицела, установленного на ту же кратность.

Мы можем поблагодарить Специального Агента ФБР Мэтью Боуэн Джонсона (Matthew Bowen Johnson) за развитие этого способа во время своей службы на Курсах огневой подготовки ФБР в Куантико. Он прекрасный стрелок и истинный джентльмен-южанин. Его способ работает с любой сеткой типа «дуплекс». Все, что вам нужно, это точные размеры сетки.

Компания Leupold развила способ Специального Агента Джонсона далее и ввела кольцо измерения дальности, расположив его рядом с кольцом регулировки кратности на своих прицелах Vari-X III. Все, что нужно сделать стрелку — покрутить кольцо регулировки кратности вперед-назад, пока перекрестие прицельной сетки и края «дуплекса» не охватят отрезок в 16 дюймов, а затем считать значение дальности с кольца регулировки кратности.

Это не настолько точно, как измерение дальностей с помощью лазерного дальномера, но точнее, чем большинство глазомерных способов. Некоторые изготовители оптических прицелов, включая компанию Schmidt Bender, для быстрого определения дальностей помещают в прицельной сетке вертикальный «ступенчатый» дальномер.

Здесь, стрелок помещает вертикальную шкалу на человеческую цель, чтобы определить дальность, вводит поправку, и стреляет. Это также не очень точный способ, но он чрезвычайно быстр и предназначен только для относительно близких дистанций, до 400 метров.

Способ измерения дальности до цели с помощью большого пальца и глазомерные способы.

Я должен также поблагодарить Специального Агента ФБР Джонсона за обучение меня способу определения дальности до цели, который вероятно восходит ко временам длинной кентуккийской винтовки.

Как показано на иллюстрации, полностью вытяните одну руку и поднимите свойбольшой палец так, чтобы ноготь был сразу под вашей целью, и цель находилась на самом краю ногтя. А теперь представьте, что ваша цель повернулась налево, и сделала определенное количество обычных шагов, чтобы пройти всю ширину вашего ногтя. Это и есть дальность до нее в сотнях ярдов.

Если требуется только один шаг, она в 50 ярдах от вас. Два шага означает, что она в 100 ярдах, и так далее. Но только до 200 ярдов максимум, потому что вы вероятно не сможете точно разделить ширину вашего пальца точнее, чем на одну четверть.

Наша следующая иллюстрация показывает способ, давно используемый в войсках. Он называется способ «футбольного поля» или «100-ярдовых отрезков». Чтобы использовать его, мысленно разделите расстояние на 100-ярдовые отрезки, отчетливо представляя себе длину футбольного поля. Или представьте первые 100 ярдов. Затем мысленно добавляйте их снова и снова до полной дальности.

Когда расстояние становится больше, чем 500 ярдов, или если какой-либо элемент земной поверхности расположен ниже вашей линии наблюдения, способ футбольного поля становится менее и менее точным. Обычно, лучше разделить все расстояние пополам, а затем оценить только ближайшую половину и удвоить ее. Не удивительно, что такой способ назван способом «половины дистанции».

Используя любой способ определения расстояний — и особенно глазомерный — сравните ваши результаты с теми, которые получил ваш товарищ по команде, и возьмите среднюю величину. Обычно, эта средняя величина точнее, чем любая из ваших индивидуальных оценок.

При использовании этих глазомерных способов существует опасность, что в некоторых ситуациях наши глаза могут нас обманывать. Эти общие визуальные эффекты показаны на иллюстрации.

Цель кажется ближе, когда :

Она находится за понижением местности, большая часть которого скрыта от вашего взгляда.
Вы наблюдаете вниз с возвышенности.
Вы смотрите вдоль прямой линии, например, автомобильной или железной дороги.
Она находится на плоской, однообразной поверхности. Подобноснегу или песку, особенно при ярком солнечном свете.

Цель кажется дальше, если :

Она невелика по сравнению с окружающей ее местностью.
Она находится выше, чем вы.
Поле зрения очень узкое, как например, при наблюдении вдоль тропы.
Вы смотрите через понижение местности, и оно целиком видимо для вас.

Использование топографической карты для определения дальности до цели.

Когда я говорю курсантам, что один из самых легких и самых точных способов определения дальности является использованиекарты, они обычно говорят: «Почему, я даже не мог подумать об этом». Это настолько элементарно и так очевидно, но очень часто это последний способ, об использовании которого думает снайпер. А он вероятно должен быть первым.

Очевидно, что самый простой подход — это нанести на карту место вашего расположения иместоположение вашей цели и просто измерить расстояние. Хотя это не всегда работает. Потому что иногда вы не уверены в расположении вашей цели. В этой ситуации осмотритесь вокруг, пока вы не увидите какой-то заметный местный предмет, который вероятно расположен на том же расстоянии, и измерьте это расстояние на вашей карте.

Более точная оценка дальности может быть произведена путем использованияGPS совместно с вашей картой. Убедившись, что рядом есть отличительный местный предмет возле цели. Установите свое точное расположение по GPS. Нанесите это место и место расположения цели на карту. Затем измерьте расстояние и вы узнаете его.

Подсчет столбов и опор ЛЭП для определения дальности до цели.

Если вы тщательно посмотрите вокруг в районе ваших действий, вы возможно, обратите внимание на некоторые искусственные местные предметы, установленные на одинаковом расстоянии друг от друга, и которые вы можете использовать для определения дальности. Чаще всего встречаются столбы от заборов и опоры ЛЭП или телефонных линий. Подобные предметы могут быть очень полезны. Но убедитесь в том, что они действительно размещены через стандартные интервалы.

Поскольку опоры ЛЭП дороги в установке, и большинство землевладельцев их не любят, энергетические компании стремятся разместить их как можно дальше друг от друга, насколько позволяют требования безопасности. И обычно это точно определенное расстояние. Хотя дополнительные опоры могут быть добавлены для дополнительной поддержки на реке или на холме, расстояние должно быть относительно постоянным.

С другой стороны, столбы от забора изменяются от землевладельца к землевладельцу, и я бы колебался слишком довериться последовательному интервалу. Хотя, конечно, это стоит проверить.

Влияние ошибки в определении дальности до цели.

Поскольку траектория пули в начале имеет легкий наклон вверх, а затем понижается сильнее и сильнее по мере замедления пули, ошибки в определении большой дальности до цели прощаются намного меньше, чем ошибки на коротких дистанциях.

Чтобы помочь вам оценить это, мы приводим данные для 168 грановой пули .308 Match, чтобы показать, как небольшая ошибка в 10 ярдов при определении дальности до цели влияет на положение пули на различных дальностях.

Сейчас посмотрите, насколько легко подумать, что цель находится в 750 ярдах, когда она на самом деле в 800 ярдах. Но эта ошибка в 50 ярдов (менее 10 процентов) приведет к тому, что пуля попадет в 32 дюймах ниже, значительный промах. Помните об этом, когда определяете дальности до цели.

По материалам книги «Совершенный снайпер. Учебное пособие для армейских и полицейских снайперов».
Maj. John L. Plaster, USAR (Ret.)

Стрельба всегда сопровождается ошибками.

Сегодня поговорим об ошибках стрельбы — конкретно об ошибках подготовки исходных данных и влиянии на них баллистики патрона.

Основными ошибками подготовки данных являются:

1. Ошибка определения дальности до цели. Опытный стрелок определяет дальность (без приборов) со срединной ошибкой 10%, средний — 15%.
2. Ошибка определения скорости ветра. Срединная ошибка составляет 1,5 м/с.
3. Ошибка определения скорости цели — 20%.
4. Ошибка определения курсового угла цели — 10° или 0,17 радиана.

Ошибка определения дальности.

Итак, стрелок глядя на бегущую фигуру (мишень №8) определил, что дальность до цели 500 метров и выставил прицел 5. Это совершенно не означает, что до цели 500 метров, если стрелок опытный то срединная ошибка составит 10% или 50 метров. Таким образом цель будет находится в интервале 450-550 метров с вероятностью 0,5, т.е. в половине случаев. Естественно, что в другой половине случаев, т.е. с вероятностью 0,5, цель будет находится вне этого интервала. Как ближе (вероятность 0,25), так и дальше (вероятность 0,25) этого интервала.
Пока все сказанное никак не зависит от оружия в руках стрелка, но настала пора определить отклонение СТП из-за этой ошибки. Как ни странно, но пули летают по кривой и превышение траектории над линией прицеливания прямо зависит от баллистики оружия, точнее в очень большой степени определяется патроном. Численно вертикальное отклонение СТП равно ошибке дальности умноженной на тангенс угла падения пули на дистанции выставленного прицела (т.е. в данном случае 500 м). Сам угол можно взять из основной таблицы оружия или определить сразу тангенс из таблицы превышения траекторий. Рассмотрим АКМ и АК74:

1. Из таблицы превышений АКМ видно, что на 450 м (с прицелом 5) превышение 0,55 метра, а на 550 м понижение -0,83 метра. Таким образом за 100 м пути пуля падает на 1,38 метра, т.е. тангенс tg=(0,55-(-0,83))/100=0,0138. Умножим на ошибку в 50 метров и получим 50*0,0138=0,69 метра. С вероятностью 0,5 СТП отклонится по вертикали не более чем на 0,69 метра. С вероятностью 0,54 отклонение не выйдет за вертикальный габарит цели. (от центра до края цели 0,75 метра)
2. Из таблицы превышений АК74 видно, что на 450 м (с прицелом 5) превышение 0,31 метра, а на 550 м понижение -0,42 метра. Таким образом за 100 м пули пуля падает на 0,73 метра, т.е. тангенс tg=(0,31-(-0,42))/100=0,0073. Умножим на ошибку в 50 метров и получим 50*0,0073=0,365~0,37 метра. С вероятностью 0,5 СТП отклонится по вертикали не более чем на 0,37 метра. С вероятностью 0,83 отклонение не выйдет за вертикальный габарит цели.

​Как видно баллистика влияет на отклонение пули из-за ошибки определения дальности. На малых дистанциях отклонения пули малы сразу по двум причинам: а) малы ошибки, 10% от 200 метров и 10% от 500 это совершенно разные величины; б) на малых дальностях углы падения также малы.  Но с ростом дальности ошибки быстро растут и разница между АК74 и АКМ становится все больше. Тут можно вспомнить и стрельбу на большие дальности, важнейшим условием результативности которой является очень точное измерение дальности до цели и скорости ветра, что без приборов практически невозможно. Какой толк от винтовки с «субминутной» кучностью на дальности 1000 м если у Вас нет дальномера и ошибка в определении дальности, в лучшем случае, составляет ±100 метров?

Ошибка определения скорости ветра.

Зная срединную ошибку — 1,5 м/с можно определить боковое срединное вероятное отклонение пули на определенной дальности. Для этого нам понадобится таблица поправок на изменение метеоусловий из все того же НСД или таблиц стрельбы ГРАУ. Итак, все теже АКМ и АК74, дистанция 500 метров:

1. Из таблички для АКМ видно, что на 500 м снос ветром 10 м/с равен 3,4 метра, тогда снос ветром 1,5 м/с равен 3,4/10*1,5=0,51 метра. Т.е. с вероятностью 0,5 СТП отклонится в боковом направлении на расстояние не более 0,51 метра или с вероятностью 0,26 отклонение не выйдет за габарит цели (от центра до края цели 0,25 метра.).
2. Из таблички для АК74 видно, что на 500 м снос ветром 10 м/с равен 2,18 метра, тогда снос ветром 1,5 м/с равен 2,18/10*1,5=0,33 метра.  Т.е. с вероятностью 0,39 отклонение не выйдет за габарит цели.

Как и в случае с определением дальности на малых дистанциях отклонения достаточно малы, но с ростом дальности сильно увеличиваются.

Ошибка определения скорости цели Численно равна Еv=0,2Vц. В этот раз возьмем дистанцию поменьше, 300 метров думаю хватит. Бегущая фигура перемещается поперек линии стрельбы со скоростью

Vц=3 м/с на дистанции 300 метров. Ошибка определения скорости 20%, т.е.  0,2Vц=0,6 м/с. Боковое отклонение пули численно равно подлетному времени пули умноженному на ошибку 0,2tVц. И на величину этой ошибки также оказывает влияние баллистика, а конкретно подлетное время пули которе можно взять из основной таблицы в НСД.

1. Для АКМ табличка дает t=0,52 с, таким образом бовокое отклонение составит 0,2*0,52*3=0,31 метра. С вероятностью 0,41 отклонение не выйдет за габарит цели.
2. Для АК74 t=0,39 с. Бовокое отклонение составит 0,2*0,39*3=0,23 метра. С вероятностью 0,54 отклонение не выйдет за габарит цели.

Ошибка определения курсового угла цели. Eφ=0,17 радиан. Рассмотрим случай стрельбы по цели перемещающейся под углом к линии стрельбы. Дистанция 300 м, бегущая фигура перемещается со скоростью 3 м/с под углом  φ=45°. Тогда бокове отклонение пули будет складываться из ошибки определения скорости цели и ошибки определения курсового угла по следующей формуле , при угле φ=45° sinφ=cosφ=0,707. Как не трудно увидеть выражение под корнем не зависит от баллистики, зато подлетное время t зависит. Выражение под корнем будет равно 0,6^2*0,707^2+0,17^2*3^2*0,707^2=0,31, кв. корень 0,31=0,557 метра.

1. Для АКМ Evz=0,557t=0,557*0,52=0,29 метра. С вероятностью 0,44 отклонение не выйдет за габарит цели.
2. Для АК74 Evz=0,557t=0,557*0,39=0,22 метра. С вероятностью 0,56 отклонение не выйдет за габарит цели.

Основной вывод — баллистика оружия оказывает большое влияние на вероятность попадания в цель по причине меньшего отклонения пуль из-за ошибок подготовки исходных данных. 5,45-мм автоматная пуля обладает более настильной траекторией, меньшим ветровым сносом и меньшим подлетным временем чем 7,62-мм автоматная пуля, в значительной степени именно эти факторы позволяют АК74 стрелять эффективней АКМа. Меньший импульс отдачи и вес патрона не относится к ошибкам подготовки, но забывать о этих факторах не стоит.

Содержание раздела «Точность радиолокационных измерений»

1. Точность определения дальности
   • Случайная ошибка измерения
   • Математические соотношения
   • Систематические ошибки измерения
2. Точность измерения угловых координат
3. Как выполняется измерение для оценки точности радиолокатора?
4. Примеры

Точность радиолокационных измерений

Точность это степень соответствия между оцениваемыми или измеряемыми значениями параметров
(координаты и/или скорость движения) лоцируемого объекта в определенный момент времени и их истинными значениями.
В радиолокации точность измерения обычно представляется как статистическая мера систематической ошибки,
которая характеризуется следующими свойствами:

1. Предсказуемость: Точность позиционирования определяется при использовании географических или геодезических систем координат Земли.
2. Повторяемость: Означает то, что результаты измерения одной и той же системой в сходных условиях,
   будут характеризоваться близкими значениями точности в пределах некоторого интервала времени.
3. Относительность: Точность измерений относительно одной позиции может быть пересчитана для другой позиции (пренебрегая всевозможными ошибками).

Заявленное значение требуемой точности показывает,
что определяемое системой измерения значение того или иного параметра может отклоняться от его истинного значения,
и указывает интервал значений, в котором находится истинное значение с заданной вероятностью.
Рекомендуемое значение вероятности 95%, что соответствует интервалу,
равному удвоенному среднеквадратическому отклонению относительно среднего значения для нормального (Гауссового) распределения случайной величины.
Предположение, что все известные поправки учтены, означает, что ошибки оценивания будут иметь средние значения (смещения), близкие к нулю.

Любое остаточное смещение должно быть небольшим по сравнению с заявленной точностью.
Истинное значение — это значение, которое в рабочих условиях наилучшим образом характеризует измеряемую величину,
наблюдаемую в пределах репрезентативного (достаточного) интервала времени, площади и / или объема с учетом расположения и влияющих факторов.

ошибка измерения

импульс+шум

порог

идеальный импульс

Рисунок 1. Искажение фронта импульса под воздействием шумов

ошибка измерения

импульс+шум

порог

идеальный импульс

Рисунок 1. Искажение фронта импульса под воздействием шумов

Точность определения дальности

Теоретическая максимально достижимая точность измерения дальности методом радиолокационной импульсной дальнометрии
зависит от точности измерения времени запаздывания отраженного сигнала.

Случайные ошибки измерения

Случайные ошибки измерения в
импульсных радиолокаторах
возникают когда передний фронт отраженного сигнала искажается под воздействием шумов.
На отраженный сигнал всегда накладываются шумы, в результате чего увеличивается амплитуда принятого сигнала.
Это вызывает смещение переднего фронта импульса и, следовательно, является причиной ошибки измерения времени запаздывания отраженного сигнала.

На Рисунке 1 показано влияние шумов на обнаруживаемый передний фронт эхо-сигнала.
Сплошной линией (фиолетовой) изображен идеальный трапецеидальный импульс с довольно крутыми фронтом и спадом.
Этот импульс не может быть слишком близким к прямоугольному, поскольку это потребовало бы бесконечно широкой полосы частот.
Время задержки импульса измеряется в момент времени, когда его амплитуда достигает порогового значения, обычно на уровне 0,707 от максимальной амплитуды.
Однако на отраженный импульс накладывается шум (зеленая линия).
Измеренным может быть только напряжение, являющееся суммой мгновенных значений амплитуды импульса и шума
(желтая синяя пунктирная линия).
Это напряжение достигнет порогового значения раньше, чем напряжение идеального (в отсутствии шумов) импульса.
Разница между ними — это случайная ошибка измерения времени задержки, вызванная влиянием
шумов[1].

Если длительность импульса известна (что невозможно для первичного радиолокатора, а только для
вторичного радиолокатора),
то эта случайная ошибка может быть уменьшена математически путем одновременной оценки переднего фронта и спада (заднего фронта) импульса.
В других случаях, какой-либо учет случайной ошибки не представляется возможным.

Математический контекст

Как следует из Рисунка 1, точность измерения дальности в основном зависит от
уровня шума
или, точнее, от соотношения между амплитудой импульса и уровнем шума.
Количественно это соотношение описывается отношением «сигнал-шум».
Уровень шума, в свою очередь, зависит от ширины полосы пропускания приемного тракта.
Крутизна фронта и спада прошедшего тракт отраженного импульса также зависит от этой ширины.
Для значений отношения «сигнал-шум», значительно больших единицы, между этими величинами существует следующее
соотношение:[2]

где δR — ошибка измерения;
c₀ — скорость света
B — ширина полосы пропускания;
SNR — отношение «сигнал-шум».
(1)

Однако ширина полосы пропускания является также существенным фактором,
влияющим на
разрешение радиолокатора по дальности
S_r = c₀ / 2B.
Таким образом, максимально достижимая точность измерения дальности (характеризуемая ошибкой измерения дальности)
может быть представлена как функция разрешения радиолокатора по дальности:

(2)

Отсюда следует, что максимально достижимая ошибка измерения дальности должна быть значительно лучше чем разрешающая способность по дальности.

Систематические ошибки измерения

Систематические ошибки измерения, в отличие от случайных ошибок, могут быть учтены или уменьшены, в случае, если удается определить причины их возникновения.

В импульсных радиолокаторах
время задержки обычно измеряется между передним фронтом излучаемого импульса и передним фронтом отраженного от цели импульса.
Точность измерения в таком случае будет зависеть от частоты следования тактовых (измерительных) импульсов,
по количеству которых между заданными моментами времени измеряется
длительность интервала.
Очевидно, что в промежутке между тактовыми импульсами измерение не может быть произведено,
что приводит к возникновению систематической ошибки измерения дальности.
На практике точность измерения дальности зависит от размера отдельной ячейки дальности, используемой при обработке сигнала.
В соответствии с рекомендациями
ИКАО[3]
для радиолокаторов систему управления воздушным движением размер ячейки должен быть 1/128 морской мили,
то есть около 14,5 м, что соответствует интервалу времени почти 10 нс.

В
радиолокаторах непрерывного излучения
измерение сдвига фазы принятого сигнала относительно текущей фазы передатчика может содержать (хотя и неоднозначную) информацию о дальности.

Точность измерения дальности в
радиолокаторах непрерывного излучения с частотной модуляцией
также определяется параметрами передатчика, особенно наклоном и линейностью закона изменения частоты.

Точность измерения углов

стандартные требования в
зависимости от дальности

точность измерения азимута:

методом скользящего окна

моноимпульсным методом

дальность от радара (в морских милях)

Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)

стандартные требования в
зависимости от дальности

точность измерения азимута:

методом скользящего окна

моноимпульсным методом

дальность от радара (в морских милях)

Рисунок 2: Зависимость точности измерения угловых координат от дальности
(Источник: Лаборатория Линкольна)

Точность измерения углов зависит как от внутренних методов обработки сигнала так и от внешних условий.
Аномальные условия распространения,
которые часто возникают из-за изменений давления воздуха,
влияют на измерение угла места и могут влиять на измерение горизонтального угла (азимута), вызывая возникновение случайной ошибки измерения.
Однако более частые источники возникновения систематических ошибок определяются внутренними факторами.

Например, измерение угла
методом скользящего окна
является довольно неточным.
На практике половина ширины диаграммы направленности антенны делится на число квантований, определяемое используемым методом
(например, 8 или 16 периодов следования импульсов) и таким образом приводит к систематической ошибке порядка одного градуса. В
корреляционных методах,
где выполняется интерполяция промежуточных значений, достигается более высокая точность измерения.
Наилучшая точность измерения угловых координат на данный момент достигается при использовании метода
конического сканирования и при
моноимпульсной пеленгации.

Как выполняются измерения для оценки точности радиолокатора?

Порядок проведения таких измерений определяется их целью, а именно: координаты, измеренные радиолокатором сравниваются с действительными координатами цели.
Для радиолокаторов наблюдения за воздушным движением для этой цели выполняется испытательный полет (облет), например, компанией
FCS Flight Calibration Services GmbH.
На борту самолета Learjet 35 располагается регистратор, который записывает текущие координаты самолета,
получаемые дифференциальной системой спутниковой навигации GPS
с ошибками менее одного метра.
В то же время траектория полета самолета регистрируется на радиолокаторе.
Оба регистратора синхронизируются при помощи сигналов единого времени, получаемых ими от системы GPS,
и результаты измерений сравниваются между собой.

При обработке результатов сравнения измеренных и действительных значений координат цели применяются методы математической статистики.
Явные ошибочные измерения исключаются из анализа, поскольку необходимо определить систематическую составляющую ошибки измерения радиолокатора.
Это не означает, однако, что требуется значительное количество зондирующих импульсов (возможно, для получения хорошего значения).
В радиолокаторах, использующих моноимпульсный метод пеленгации значение ошибки измерения определяется для каждого импульса.
Если используется метод скользящего окна, то соответствующее значение определяется для конкретного требуемого числа импульсов.

Для достижения хорошей точности измерения дальности требуется, чтобы зондирующие импульсы имели стабильный и крутой фронт.
Такой фронт часто не наблюдается при использовании
внутриимпульсной модуляции.
Но тут необходимо учитывать, что измерение дальности выполняется после сжатия отраженного импульса.
В этой точке, уже после сжатия, импульс вновь имеет крутой фронт.

Единственным условием проведения подобных измерений является отсутствие помех.
Это означает, что эхо-сигнал не должен смешиваться с внешними помехами.
Однако внутренние шумы всегда будут присутствовать в тракте прохождения отраженного сигнала.
Поэтому результативные измерения возможны когда уровень отраженного от летательного аппарата сигнала будет существенно выше
уровня шума.
Наконец, калибровка полета должна выявлять возможные дополнительные систематические ошибки, а не случайные ошибки.

Примеры

В таблице 1 приведены характеристики точности для некоторых радиолокаторов.

Название радиолокатора	Ошибка измерения углов	Ошибка измерения дальности	Ошибка измерения высоты
BOR–A 550	< ±0.3°	< 20 м
LANZA	< ±0.14°	< 50 м	340 м ≈ 1150 футов (на дальности 100 морских миль)
GM 400	< ±0,3°	< 50 м	600 м ≈ 2000 футов (на дальности 100 морских миль)
RRP–117	< ±0,18°	< 463 м	1000 м ≈ 3000 футов (на дальности 100 морских миль)
MSSR-2000	< ±0.049°	< 44.4 м
STAR-2000	< ±0.16°	< 60 м
Variant	< ±0.25°	< 25 м

Таблица 1. Примеры

Примітки

1. Merrill I. Skolnik: »Introduction to Radar Systems» McGraw-Hill Europe, 2001, ISBN 007-118189-x, S. 317,
   Topic 6.3 Theoretical Accuracy of Radar Measurements
2. G. Richard Curry: »Radar System Performance Modeling» 2005, ISBN 978-1-58053-816-9, S.168
3. ICAO Annex 10 — Volume 4. Aeronautical Telecommunications — Surveillance and Collision Avoidance Systems, Topic 4.3.2.1.3 Range and Bearing Accuracy,
   (Bundesamt für Zivilluftfahrt, Schweiz)

Рассматриваемая оптико-электронная стереоскопическая система измерения дальности (рисунок 1) содержит захватное устройство, состоящее из левой и правой цифровых камер, каждая из которых размещены на жестком стержне, и ЭВМ, выполняющую функцию вычислительного блока с измерительным приложением [3], совместно обеспечивающих возможность захвата стереоизображений и автоматическое измерение дальности до указанных пользователем объектов.

Рисунок 1. Внешний вид оптико-электронной

стереоскопической системы

Дальность D (рисунок 2) до объекта Ц в определялась по величинам параллакса γ₂, базы прибора В и фокусного расстояния объективов f по следующему выражению [1, с. 273, 2 с. 43]

Испытание оптико-электронной стереоскопической системы измерения дальности показало, что в целом ошибка определения дальности лежит в пределах расчетных значений [1, с. 273], но вместе с тем и выявило рад недостатков, а именно:

— для обеспечения точных измерений необходима предварительная настройка (калибровка) захватного устройства, заключающаяся в приведении оптических осей левой и правой камер к параллельному состоянию в пространстве, что было связано с достаточно большими временными затратами, кроме того, незначительные воздействия на захватное устройство приводили к необходимости проведения повторной калибровки;

— малейшее отклонение оптических осей камер от параллельного состояния в пространстве приводило к значительным ошибкам в измерении дальности, иногда вплоть до получения отрицательных значений;

— неоднократно при настроенном захватном устройстве наблюдались ошибки измерения, когда до явно расположенных на разном удалении объектов измеренная макетом дальность составляла одну и туже величину.

Помимо этого, на взгляд авторов, недостатком рассматриваемой оптико-электронной стереоскопической системы измерения дальности являлась необходимость постоянного наведения оптической оси левой камеры на объект интереса, что при проведении достаточно большого количества измерений до объектов расположенных в разных частях поле зрения значительно увеличивало время работы и способствовало «растройке» захватного устройства, а так же то, что для использования подобных систем в различных системах технического зрения для обеспечения высокоточных измерений необходимо осуществлять подбор по техническим данным двух идентичные камер, что накладывает определенные ограничения на практическую реализацию.

Для устранения причин возникновения выявленных недостатков был проведен анализ практического применения рассматриваемой оптико-электронной системы измерения дальности и выражений (1) и (2) положенных в основу её работы.

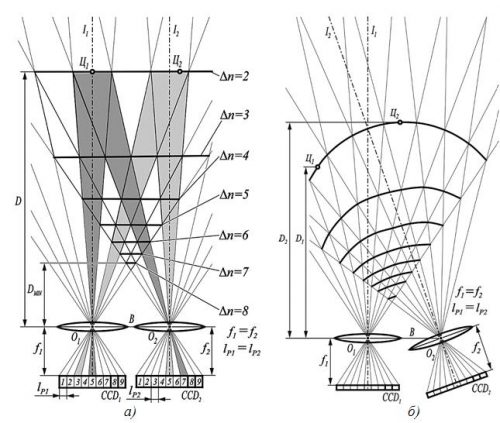
Если обеспечена строгая параллельность оптических осей камер, входящих в состав захватного устройства, то рабочую зону, т.е. зону пересечения полей зрений используемых камер, как показано на геометрической модели, представленной на рисунке 3,а, условно можно представить в виде совокупности четырёхугольников образованных при пересечении полей зрения отдельных элементов фоточувствительного приемника высокого разрешения, например пикселей ПЗС-матриц.

На рисунке 3,а ПЗС-матрицы CCD₁ и CCD₂ для наглядности представлены состоящими из девяти пикселей. Размеры четырехугольников определяют величину ошибки определения дальности. В месте с тем, как следует из выражений (1) и (2), в пределах рабочей зоны можно отобразить линии равных смещений, т.е. линий при нахождении в любой из точек которых объекта, до которого определяется дальность, смещение ∆l_Г будет неизменно. Так, например, как показано на рисунке 3,а, при нахождении объекта интереса в любой из точек, принадлежащих линии ∆n=2, например, в точках Ц₁ и Ц₂, смещение изображений всегда будет равно двум линейным размерам пикселя. Из этого следует, что дальность до объекта определяется как расстояние по перпендикуляру от базовой линии О₁О₂. Это условие всегда необходимо учитывать, особенно в тех случаях, когда измерение дальности проводится до различных объектов относительно одной точки на местности, в которой установлена измерительная система.

При невыполнении условия параллельности оптических осей объективов используемых камер линии с одинаковыми смещениями принимают вид близкий к дуге (рисунок 3,б), что приводит к неоднозначности в определении дальности относительно базовой линии О₁О₂. Так из геометрической модели, представленной на рисунке 3,б видно, что до объекта Ц₁, как и до объекта Ц₂ дальности относительно базовой линии О₁О₂ составят D₁, D₂, при этом D₁ ≠ D₂, хотя из выражений (1) и (2) следует что дальности D₁ и D₂ должны быть равны, так как объекты Ц₁ и Ц₂ находятся на линии с одинаковыми смещениями изображений во всех её точках.

Рисунок 3. Геометрия линий равных смещений при:

 а – идеально откалиброванном захватном устройстве;

б – при отклонении правой камеры от параллельного состояния

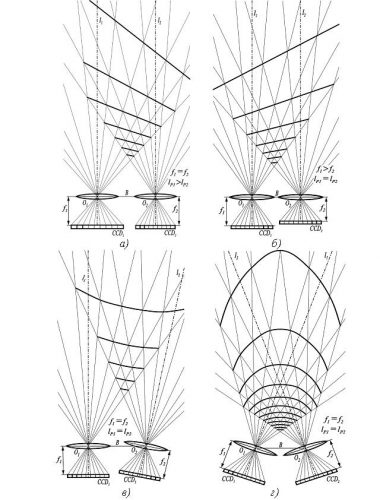
На рисунке 4,а—г иллюстрируются геометрия линий равных смещений в различных условиях: когда обе камеры имеют одинаковые параметры (фокусные расстояния объективов f и размеры пикселей l_P), но их оптические оси I₁, I₂ или сходятся (рисунок 4,а) в плоскости измерений или расходятся (рисунок 4,б); когда оптические оси I₁, I₂ обеих камер параллельны, но сами камеры имеют объективы с различными фокусными расстояниями f₁ ≠ f₂ (рисунок 4,в); или когда уже размеры пикселей ПЗС-матриц CCD₁ и ССD₂ неодинаковы, то есть l_P1 ≠ l_P2 (рисунок 4,г).

Рисунок 4. Геометрия линий равных смещений в различных условиях

Понятно, что в действительности с учетом разброса технических данных при изготовлении камер, точности проведенной калибровки захватного устройства будет наблюдаться ситуация объединяющая в себе в той или иной мере все приведенные на рисунке 4,а—г случаи.

Кроме этого, необеспечение параллельности оптических осей камер захватного устройства приводят к возникновению ошибок измерения дальности.

Рассмотрим этот случай.

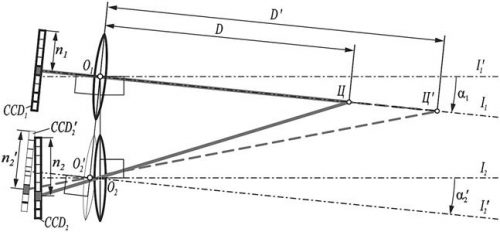
Пусть в захватном устройстве используются две идентичных цифровых видеокамеры, подобранные таким образом, что разбросом их характеристик можно пренебречь, а оптические оси I₁, I₂, объективы оптическими центрами О₁, О₂, ПЗС-матрицы CCD₁ и CCD₂ определяют действительное положение камер захватного устройства в пространстве, тогда I₁′, I₂′, О₂′, CCD₂′ будут отражать положение элементов камер принимаемое в расчетах согласно выражения (1). Дальность D соответствует действительной дальности до объекта интереса, D′ – расчетной дальности.

Как показано на рисунке 5, оптическая ось левой (верхней) камеры I₂′ отклонена от оси I₁′, которую бы она занимала в случае абсолютной параллельности оптических осей, на некоторый угол α₁. Изображение от объекта Ц, пройдя через оптический центр О₂ объектива второй камеры, спроецируется на ПЗС CCD₂ в точке, соответствующей номеру пикселя n₂.

В месте с тем, формула расчета дальности (1) не имеет переменной, характеризующей отклонение оптической оси второй камеры, а это приведет к тому, что в вычислениях будет принято положение камеры соответствующее I₂′, О₂′ и CCD₂′ не совпадающее с действительными I₂, О₂, CCD₂, и характеризующая положение правой камеры отклонённой от действительного положение по часовой стрелке на угол α₂′, когда оптические оси I₁ и I₂′ будут параллельны.

Рисунок 5. Возникновение ошибки измерения дальности

Проведя из пикселя матрицы CCD′₂ с номером соответствующим действительно измеренному n₂′=n₂ через расчетный оптический центр объектива О₂′ до пересечения с действительной оптической осью I₁, на которой по условиям находится объект интереса Ц, получим точку расчетного положения объекта Ц′. Из представленной геометрической модели видно, что рассчитанная дальность D′ не будет соответствовать действительной дальности D, а значит будет допущена ошибка в определении дальности. При этом ошибка определения дальности, как видно из рисунка 5, будет тем значительнее, тем больше угол α₁.

Работа по устранению выявленных источников возникновения ошибок и неоднозначности измерения дальности позволила ряд задач, заключающихся в обеспечении:

— безошибочного измерения дальности до объектов в условиях непараллельности оптических осей левой и правой камер, а также, когда левая и правая камеры имеют как одинаковые, так и различные технические данные, а именно фокусные расстояния объективов и параметры фоточувствительных приемников высокого разрешения;

— однозначности измерений дальностей до всех объектов независимо от их расположения в рабочей зоне.

Раскрытие решения указанных задач на взгляд авторов заслуживает отдельных публикаций, поэтому в данной статье не приведено.

Список литературы:

1. Зубарь А.В., Программно-аппаратная реализация оптико-электронной стереосистемы определения дальности // Зубарь А.В., Кайков К.В., Майстренко В.А. // Омский научный вестник № 3 (123) – Омск: ОмГТУ, 2013. – с. 273-278.
2. Коротаев, В. В. Телевизионные измерительные системы // В. В. Коротаев, А. В. Краснящих // Учеб. пособие. – СПб.: СПбГУ ИТМО, 2008. – с. 43–47.
3. Программа вычисления дальности до объектов интереса по изображениям с двух цифровых видеокамер // Свидетельство о государственной регистрации ПрЭВМ № 2013661916 от 18 декабря 2013 г.[schema type=»book» name=»Источники возникновения ошибок и неоднозначности измерений дальности оптико-электронной стереоскопической системой » author=»Зубарь Алексей Владимирович, Кайков Кирилл Владимирович, Аппинг Гарри Анатольевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-20″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

Составляющими
инструментальной ошибки измерения
дальнос­ти являются:

ошибка
за счет изменения времени запаздывания
сигнала при прохождении через приемный
тракт;

ошибка
съема координат.

Ошибка
за счёт изменения времени запаздывания
в приёмном тракте имеет систематическую
и случайную составляющие. Систематическая
составляющая обусловлена конечным
значением полосы пропускания усилительных
каскадов (главным образом УПЧ), что
приводит к растягиванию фронтов и
задержке сигналов. Время запаздывания
в приёмном тракте РЛС обычно составляет
величину tзап
пр = = (0,3…3)τи.
Оно может быть скомпенсировано путём
соответствующей расстановки импульсов
запуска оконечного устройства.

Случайная
составляющая времени задержки обусловлена
из­менением полосы пропускания
каскадов из-за изменения их режи­мов
работы вследствие нестабильностей
источников питания, ухо­да параметров
элементов под действием дестабилизирующих
фак­торов, старения деталей и т. д.
Среднее квадратическое значение
нестабильности времени запаздывания
составляет σt
зап = 0,1 …0,2
мкс, что соответствует ошибке измерения
дальности 15…30 м.

Ошибка, возникающая
при съёме координат, зависит от вида
съёма.

При
визуальном съёме она обусловлена:

неточностью
формирования масштабных отметок
дальности (МОД);

неточностью
определения центра отметки;

интерполяцией
положения центра отметки относительно
МОД.

Для исключения
ошибок измерения дальности, связанных
с не­линейностью развертки индикатора,
осуществляют электрическую калибровку
шкалы дальности путём формирования МОД
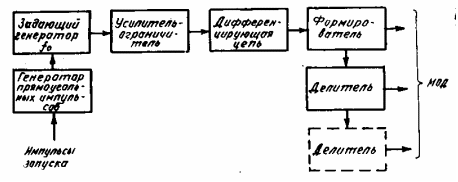
различ­ных градаций. Обычно устройство
формирования МОД выполня­ется по
структурной схеме (рис. 12.1). С приходом
импульса запускa генератор
прямоугольных импульсов формирует
импульс с дли­тельностью, равной
времени прямого хода развертки индикатора.
В течение этого времени задающий
генератор генерирует непре­рывные
колебания с частотой f₀,
которые затем ограничиваются,
дифференцируются и используются для
запуска формирователя.

Рис. 12.1. Устройство
формирования масштабных отметок
дальности

Последний формирует
МОД, представляющие собой видеоимпульсы
с длительностью 1…2 мкс и периодом
повторения Т₀,
определяющим минимальную градацию МОД
(расстояние в километрах между масштабными
отметками): Δr_шк
= сТ₀/2
= с/2f₀.
Для удобства отсчёта путём последующего
деления формируются МОД больших градаций.
Нестабильность частоты задающего
генерато­ра приводит к смещению МОД
на развертке индикатора и, следо­вательно,
к ошибке измерения дальности,
обусловленной неточнос­тью формирования
МОД. Эта ошибка σ_RМОД
= rσ_j
/f₀
, где σ_j
—полуширина спектра флюктуации
колебании задающего генератора.

При переходе от
σ_j
к долговременной относительной
нестабиль­ности частоты δf
= Δf_max/f₀
= 3σ_f
/f₀,

σ_RМОД
= rδf
/3

(12.13)

Расчеты
по формуле (12.13) показывают, что требования
к стабильности частоты задающего
генератора, при которых влиянием ошибки
формирования МОД можно пренебречь,
достаточно жест­кие и диктуют
необходимость использования специальных
схем генераторов: с контуром ударного
возбуждения или с кварцевой стабилизацией.

Максимальное
значение ошибки за счет неточного
определения центра отметки составляет
половину отметки

(12.14)

где m_R
= ΔR/Lpr
— масштаб по дальности;

ΔR
— диапазон дальностей, выносимых
на индикатор;

Lpr
— длина развертки дальности;

dл
— диаметр луча ЭЛТ.

Среднее
квадратическое значение ошибки
определения центра отметки

(12.15)

Эта ошибка в РЛС
с ИКО составляет 200 … 300 м. Для её уменьшения
необходимо использовать ЭЛТ с высоким
качеством Qтр
= Dтр/dл
(здесь Dтр
— диаметр экрана трубки), а также
специальные индикаторы типа азимут—дальность
(НАД) или специальные режимы ИКО: кольцевой
(с задержкой начала развертки) или
секторный (со смещением центра на край
экрана).

Ошибка интерполяции
при использовании электрической шкалы

Она
может быть довольно значительной для
её снижения необходимо предусматривать
более мелкие градации МОД (Δrшк
= 1 …2 км).

Суммарная ошибка
измерения дальности, обусловленная
визуальным съёмом:

(12.16)

При автоматическом
съёме дальность измеряется по номеру
канала дальности N,
в котором находится сигнал цели

r*
= NΔr,

где
Δr
— диапазон дальностей, перекрываемых
одним дальностным каналом.

Причинами
возникновения ошибки съёма дальности
в этом случае являются дискретизация
по дальности и нестабильность частоты
повторения импульсов дискретизации
Fд.

Ошибка дискретизации
определяется соотношением

(12.17)

а ошибка,
обусловленная нестабильностью Fд,
по аналогии с (12.13)

(12.18)

С
учетом (12.17), (12.18)

(12.19)

Для
уменьшения этой ошибки необходимо
увеличивать частоту дискретизации и
повышать её стабильность, используя
генераторы импульсов с кварцевой
стабилизацией. Однако следует помнить,
что увеличение Fд
связано с увеличением числа каналов
дальнос­ти и, следовательно, аппаратурных
затрат.

При полуавтоматическом
съёме оператор совмещает электронный
маркер с центром отметки, после чего
нажимает кнопку съёма и координаты цели
в кодированном виде поступа­ют в канал
связи с потребителем радиолокационной
информации.

Ошибка
измерения дальности при этом обусловлена:

неточностью
определения центра отметки (см. (12.15));

неточностью
совмещения маркера с центром отметки;

дискретностью
представления дальности (см. (12.17)).

Ошибка, обусловленная
неточностью совмещения маркера,
оп­ределяется соотношением

σ_R
МАРК = m_R
d_МАРК
/3, где
d_МАРК
— диаметр маркера (обычно d_МАРК
= dл).

Суммарная ошибка
съёма

(12.20)

Для уменьшения
этой ошибки необходимо принимать такие
же меры, как при визуальном и автоматическом
съёме.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ВКР.766.02.РТС2022.ПЗ
61 Лист Дата Подп.
№ докум. Лис.
Вим Рисунок 4.9 График распределения ошибок определения дальности для усреднения по семи обзора
4.4. Оценка ошибок определения дальности протяженной надводного
обьекта по девяти обзорам.
0 0,02 0,04 0,06 0,08 0,1 0,12
-15
-10
-5 0
5 10 15 20 25 ц

ВКР.766.02.РТС2022.ПЗ
62 Лист Дата Подп.
№ докум. Лис.
Вим Из приложения Таблица 3 Построим график зависимости среднеквадратичного отклонения потрем об- зорам.(Рис.4.10) Рис График зависимости СКО по семи обзорам Построим график шумовой состовляющей дальности цели , вычисленного согласно разработанного алгоритма от числа обзоров РЛС на интервале наблюдения н, где число обзоров РЛС Рис)
Рис График шумовой состовляющей дальности цели
В результате расчетов было получено значение СКО=2,82 м y = -13,32x + 2617,7
R² = 0,9997 0
500 1000 1500 2000 2500 3000 1
3 5
7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 ц = -0,0003x + 0,0498
R² = 2E-06
-6
-4
-2 0
2 4
6 0
10 20 30 40 ц- шума 9

ВКР.766.02.РТС2022.ПЗ
63 Лист Дата Подп.
№ докум. Лис.
Вим
Рис. 4.12
График распределения ошибок определения дальности для усреднения поде- вяти обзорам Из полученных графиков можно сделать вывод, что наиболее оптимальным является усреднение по девяти обзорам, так как дальнейшее усреднение не приводит к значительному уменьшению ошибки.
4.5 Сравнительный анализ ошибок определения координатных параметров протяженого надводного обьекта. Построим график зависимости среднеквадратичного отклонения от времени
Рис график зависимости среднеквадратичного отклонения от времени
0 0,02 0,04 0,06 0,08 0,1 0,12
-15
-10
-5 0
5 10 15 20 25
P(Пц-9)f(σ9)
0,00 1,00 2,00 3,00 4,00 5,00 6,00 2
3 4
5 6
7 8
9 10
CКО-Dц=F(L)

ВКР.766.02.РТС2022.ПЗ
64 Лист Дата Подп.
№ докум. Лис.
Вим С помощью полученных данных построим таблицу оценки ошибок при различных значениях времени tуср
P КО
∆D3
СКО ∆D5
СКО ∆D7
СКОΔD9 68% мм мм мм мм мм Рис. 4.14– График зависимости СКО от времени
ВЫВОД ПО ГЛАВЕ Ошибки определения координат протяженного надводного объекта, для разработанного алгоритма при усреднении по девяти обзорам, составила 2,9 метров для дальности .

ВКР.766.02.РТС2022.ПЗ
65 Лист Дата Подп.
№ докум. Лис.
Вим
ВЫВОД ПО РАБОТЕ
1. По проведенным исследованиям был выбран способ нахождения дальности протяженного надводного объекта
2. На основе выбранного способа был разработан алгоритм нахождения дальности и пеленга протяжённого надводного объекта заданного класса
3. Проведенная оценка эффективности определения дальности цели , что при увеличении времени наблюдения вероятность правильного нахождения данных возросло.
4. По проведенным исследованиям были выполнены расчеты по определению ошибки нахождения дальности по усреднению числа обзоров.
5. На основе проведенных расчетов и исследований вычислили, что при усреднении по девяти обзорам, ошибка нахождения дальности цели будет минимальной.

ВКР.766.02.РТС2022.ПЗ
66 Лист Дата Подп.
№ докум. Лис.
Вим
Приложения 1 Таблица №1
N
L
Пц
D1 э ш
1 2
62,93 2666,25 2666,356
-0,1064 2
3 63,19 2651,25 2653,212
-1,9624 3
4 62,84 2640 2640,054
-0,0536 4
5 62,75 2625 2626,88
-1,88 5
6 62,49 2613,75 2613,692 0,0584 6
7 62,31 2598,75 2600,488
-1,7384 7
8 61,88 2587,5 2587,27 0,2296 8
9 62,14 2572,5 2574,038
-1,5376 9
10 61,61 2561,25 2560,79 0,46 10 11 61,61 2550 2547,528 2,4724 11 12 61,61 2531,25 2534,25
-3,0004 12 13 61,17 2520 2520,958
-0,9584 13 14 61,00 2512,5 2507,652 4,8484 14 15 61,00 2493,75 2494,33
-0,58 15 16 60,82 2482,5 2480,994 1,5064 16 17 60,29 2467,5 2467,642
-0,1424 17 18 60,38 2456,25 2454,276 1,9736 18 19 60,29 2445 2440,896 4,1044 19 20 59,85 2426,25 2427,5
-1,25 20 21 59,68 2411,25 2414,09
-2,8396 21 22 59,50 2400 2400,664
-0,6644 22 23 59,33 2390 2387,224 2,7756 23 24 59,59 2381,25 2373,77 7,4804 24 25 59,06 2358,75 2360,3
-1,55 25 26 59,15 2351,25 2346,816 4,4344 26 27 58,80 2336,25 2333,316 2,9336 27 28 58,45 2317,5 2319,802
-2,3024 28 29 58,45 2310 2306,274 3,7264 29 30 58,36 2291,25 2292,73
-1,48 30 31 58,10 2276,25 2279,172
-2,9216 31 32 57,92 2265 2265,598
-0,5984 32 33 57,66 2248 2252,01
-4,0104 33 34 57,57 2235 2238,408
-3,4076 34 35 57,04 2223,75 2224,79
-1,04 35 36 57,13 2208,75 2211,158
-2,4076 36 37 56,87 2201,25 2197,51 3,7396 37 38 56,95 2178,75 2183,848
-5,0984 38 39 56,78 2167,5 2170,172
-2,6716

ВКР.766.02.РТС2022.ПЗ
67 Лист Дата Подп.
№ докум. Лис.
Вим
39 40 56,34 2152,5 2156,48
-3,98 40 41 56,25 2141,25 2142,774
-1,5236 41 42 56,25 2130 2129,052 0,9476 42 43 55,63 2115 2115,316
-0,3164 43 44 55,55 2100 2101,566
-1,5656 44 45 55,28 2088,75 2087,8 0,95 45 46 55,11 2073,75 2074,02
-0,2696 46 47 54,76 2062,5 2060,224 2,2756 47 48 54,32 2047,5 2046,414 1,0856 48 49 54,40 2036,25 2032,59 3,6604 49 50 54,23 2021,25 2018,75 2,5 Таблица № 2
Dmax
Dtr
ΔD
Dmax3
Dtr3
ΔD-3 2647,5 2658,572
-11,072 2655 2645,208 9,792 2628,75 2631,844
-3,094 2643,75 2645,208
-1,458 2617,5 2618,48
-0,98 2633,75 2631,844 1,906

ВКР.766.02.РТС2022.ПЗ
68 Лист Дата Подп.
№ докум. Лис.
Вим
2617,5 2605,116 12,384 2621,25 2618,48 2,77 2595 2591,752 3,248 2610 2605,116 4,884 2568,75 2578,388
-9,638 2593,75 2591,752 1,998 2576,25 2565,024 11,226 2580 2578,388 1,612 2542,5 2551,66
-9,16 2562,5 2565,024
-2,524 2535 2538,296
-3,296 2551,25 2551,66
-0,41 2523,75 2524,932
-1,182 2533,75 2538,296
-4,546 2505 2511,568
-6,568 2521,25 2524,932
-3,682 2501,25 2498,204 3,046 2510 2511,568
-1,568 2501,25 2484,84 16,41 2502,5 2498,204 4,296 2482,5 2471,476 11,024 2495 2484,84 10,16 2452,5 2458,112
-5,612 2478,75 2471,476 7,274 2452,5 2444,748 7,752 2462,5 2458,112 4,388 2441,25 2431,384 9,866 2448,75 2444,748 4,002 2415 2418,02
-3,02 2436,25 2431,384 4,866 2396,25 2404,656
-8,406 2417,5 2418,02
-0,52 2381,25 2391,292
-10,042 2397,5 2404,656
-7,156 2354 2377,928
-23,928 2377,167 2391,292
-14,1253 2381,25 2364,564 16,686 2372,167 2377,928
-5,76133 2340 2351,2
-11,2 2358,417 2364,564
-6,14733 2343,75 2337,836 5,914 2355 2351,2 3,8 2332,5 2324,472 8,028 2338,75 2337,836 0,914 2295 2311,108
-16,108 2323,75 2324,472
-0,722 2291,25 2297,744
-6,494 2306,25 2311,108
-4,858 2283,75 2284,38
-0,63 2290 2297,744
-7,744 2268,75 2271,016
-2,266 2281,25 2284,38
-3,13 2250 2257,652
-7,652 2267,5 2271,016
-3,516 2248,7 2244,288 4,412 2255,817 2257,652
-1,83533 2227,5 2230,924
-3,424 2242,067 2244,288
-2,22133 2201,25 2217,56
-16,31 2225,817 2230,924
-5,10733 2208,75 2204,196 4,554 2212,5 2217,56
-5,06 2197,5 2190,832 6,668 2202,5 2204,196
-1,696 2186,25 2177,468 8,782 2197,5 2190,832 6,668 2171,25 2164,104 7,146 2185 2177,468 7,532 2156,25 2150,74 5,51 2171,25 2164,104 7,146 2141,25 2137,376 3,874 2156,25 2150,74 5,51 2133,75 2124,012 9,738 2143,75 2137,376 6,374 2115 2110,648 4,352 2130 2124,012 5,988 2100 2097,284 2,716 2116,25 2110,648 5,602 2077,5 2083,92
-6,42 2097,5 2097,284 0,216 2070 2070,556
-0,556 2082,5 2083,92
-1,42

ВКР.766.02.РТС2022.ПЗ
69 Лист Дата Подп.
№ докум. Лис.
Вим
2062,5 2057,192 5,308 2070 2070,556
-0,556 2047,5 2043,828 3,672 2060 2057,192 2,808 2025 2030,464
-5,464 2045 2043,828 1,172 2006,25 2017,1
-10,85 2026,25 2030,464
-4,214
Dmax
5
Dtr5
ΔD-5 Dmax7 Dtr7
ΔD-7
Dmax
9
Dtr 9
ΔD-9 2633,
25 2631,8 44 1,40 6
2622,
75 2618,4 8
4,27 2605,
5 2605,1 16 0,38 4
2618,5 71 2618,4 8
0,0914 29 2595 2591,7 52 3,24 8
2608,3 93 2605,1 16 3,2768 57 2580 2578,3 88 1,61 2
2592,3 21 2591,7 52 0,5694 29 2605,4 17 2605,1 16 0,3006 67 2563,
5 2565,0 24
—
1,52 4
2578,9 29 2578,3 88 0,5405 71 2592,9 17 2591,7 52 1,1646 67 2549,
25 2551,6 6 -2,41 2565,5 36 2565,0 24 0,5117 14 2578,3 33 2578,3 88
—
0,0546 7
2536,
5 2538,2 96
—
1,79 6
2549,4 64 2551,6 6
—
2,1957 1
2564,5 83 2565,0 24
—
0,4406 7
2521,
5 2524,9 32
—
3,43 2
2536,0 71 2538,2 96
—
2,2245 7
2551,6 67 2551,6 6
0,0066 67 2513,
25 2511,5 68 1,68 2
2526,4 29 2524,9 32 1,4965 71 2538,7 5
2538,2 96 0,454 2502,
75 2498,2 04 4,54 6
2513,0 36 2511,5 68 1,4677 14 2526,2 5
2524,9 32 1,318 2488,
5 2484,8 4
3,66 2500,1 79 2498,2 04 1,9745 71 2513,3 33 2511,5 68 1,7653 33 2478 2471,4 76 6,52 4
2488,3 93 2484,8 4
3,5528 57 2499,5 83 2498,2 04 1,3793 33

ВКР.766.02.РТС2022.ПЗ
70 Лист Дата Подп.
№ докум. Лис.
Вим
2466 2458,1 12 7,88 8
2476,6 07 2471,4 76 5,1311 43 2488,3 33 2484,8 4
3,4933 33 2448,
75 2444,7 48 4,00 2
2463,7 5
2458,1 12 5,638 2475 2471,4 76 3,524 2431,
5 2431,3 84 0,11 6
2448,7 5
2444,7 48 4,002 2460,8 33 2458,1 12 2,7213 33 2417,
25 2418,0 2 -0,77 2431,6 07 2431,3 84 0,2231 43 2447,0 83 2444,7 48 2,3353 33 2397,
55 2404,6 56
—
7,10 6
2413,2 5
2418,0 2
-4,77 2430,7 22 2431,3 84
—
0,6617 8
2385,
55 2391,2 92
—
5,74 2
2403,0 71 2404,6 56
—
1,5845 7
2417,3 89 2418,0 2
—
0,6311 1
2370,
55 2377,9 28
—
7,37 8
2387 2391,2 92
-4,292 2401,5 56 2404,6 56
—
3,1004 4
2360,
05 2364,5 64
—
4,51 4
2373,0 71 2377,9 28
—
4,8565 7
2389,4 72 2391,2 92
—
1,8197 8
2350,
3 2351,2
-0,9 2361,2 86 2364,5 64
—
3,2782 9
2376,1 39 2377,9 28
—
1,7891 1
2338,
5 2337,8 36 0,66 4
2346,8 21 2351,2
—
4,3785 7
2359,8 89 2364,5 64
—
4,6751 1
2320,
5 2324,4 72
—
3,97 2
2333,9 64 2337,8 36
—
3,8717 1
2346,1 39 2351,2
—
5,0611 1
2309,
25 2311,1 08
—
1,85 8
2323,9 29 2324,4 72
—
0,5434 3
2333,6 39 2337,8 36
—
4,1971 1
2294,
25 2297,7 44
—
3,49 4
2307,8 57 2311,1 08
—
3,2508 6
2321,1 39 2324,4 72
—
3,3331 1
2277,
75 2284,3 8 -6,63 2295 2297,7 44
-2,744 2309,5 83 2311,1 08
—
1,5246 7
2268,
49 2271,0 16
—
2,52 6
2281,4 21 2284,3 8
—
2,9585 7
2294,8 56 2297,7 44
—
2,8884 4

ВКР.766.02.РТС2022.ПЗ
71 Лист Дата Подп.
№ докум. Лис.
Вим
2255,
74 2257,6 52
—
1,91 2
2266,4 21 2271,0 16
—
4,5945 7
2282,3 56 2284,3 8
—
2,0244 4
2239,
24 2244,2 88
—
5,04 8
2253,0 29 2257,6 52
—
4,6234 3
2266,5 22 2271,0 16
—
4,4937 8
2227,
24 2230,9 24
—
3,68 4
2241,2 43 2244,2 88
—
3,0451 4
2252,7 72 2257,6 52
—
4,8797 8
2216,
74 2217,5 6 -0,82 2228,9 21 2230,9 24
—
2,0025 7
2241,9 39 2244,2 88
—
2,3491 1
2204,
25 2204,1 96 0,05 4
2217,1 36 2217,5 6
—
0,4242 9
2230,2 72 2230,9 24
—
0,6517 8
2193 2190,8 32 2,16 8
2205,8 86 2204,1 96 1,6897 14 2217,7 72 2217,5 6
0,2122 22 2184 2177,4 68 6,53 2
2192,6 79 2190,8 32 1,8465 71 2205,2 72 2204,1 96 1,0762 22 2170,
5 2164,1 04 6,39 6
2180,3 57 2177,4 68 2,8891 43 2193,1 89 2190,8 32 2,3568 89 2157,
75 2150,7 4
7,01 2170,7 14 2164,1 04 6,6102 86 2180,4 17 2177,4 68 2,9486 67 2143,
5 2137,3 76 6,12 4
2157,3 21 2150,7 4
6,5814 29 2167,9 17 2164,1 04 3,8126 67 2129,
25 2124,0 12 5,23 8
2143,3 93 2137,3 76 6,0168 57 2156,6 67 2150,7 4
5,9266 67 2113,
5 2110,6 48 2,85 2
2127,8 57 2124,0 12 3,8451 43 2142,0 83 2137,3 76 4,7073 33 2099,
25 2097,2 84 1,96 6
2113,3 93 2110,6 48 2,7448 57 2127,9 17 2124,0 12 3,9046 67 2085 2083,9 2
1,08 2100 2097,2 84 2,716 2114,1 67 2110,6 48 3,5186 67 2071,
5 2070,5 56 0,94 4
2086,6 07 2083,9 2
2,6871 43 2100,4 17 2097,2 84 3,1326 67 2056,
5 2057,1 92
—
0,69 2
2071,0 71 2070,5 56 0,5154 29 2085,8 33 2083,9 2
1,9133 33 2042,
25 2043,8 28
—
1,57 8
2055,5 36 2057,1 92
—
1,6562 9
2070,8 33 2070,5 56 0,2773 33

ВКР.766.02.РТС2022.ПЗ
72 Лист Дата Подп.
№ докум. Лис.
Вим Таблица №3
-14,97
—
14,2215 -13,473
—
12,7245 -11,976
СКО
=
4,99 1,33
P(Пц
-3)
0,00088 8
0,00137 7
0,00208 8
0,00309 6
0,00448 8 х
—
14,97 1,00
P(Пц
-3)-Н
0,00066 6
0,00103 3
0,00156 6
0,00232 2
0,00336 6 х
14,97
∆x
0,748 5
—
11,2275
—
10,479
—
9,7305
-8,982
—
8,2335
-7,485
—
6,7365
-5,988
—
5,239 5
0,00636 1
0,0088 14 0,0119 43 0,0158 22 0,0204 94 0,0259 55 0,0321 41 0,0389 15 0,046 069 0,00477 1
0,0066 11 0,0089 58 0,0118 67 0,0153 72 0,0194 68 0,0241 08 0,0291 89 0,034 554
—
4,491
—
3,7425 -2,994
—
2,2455 -1,497
—
0,7485
-1,6E-
15 0,7485 1,497 0,053 324 0,0603 48 0,0667 78 0,0722 5
0,0764 3
0,0790 54 0,0799 48 0,0790 54 0,0764 3
0,039 996 0,0452 65 0,0500 88 0,0541 92 0,0573 28 0,0592 96 0,0599 66 0,0592 96 0,0573 28 2,2455 2,994 3,7425 4,491 5,2395 5,988 6,7365 7,485 8,2335 0,0722 5
0,0667 78 0,0603 48 0,0533 24 0,0460 69 0,0389 15 0,0321 41 0,0259 55 0,0204 94 0,0541 92 0,0500 88 0,0452 65 0,0399 96 0,0345 54 0,0291 89 0,0241 08 0,0194 68 0,0153 72

ВКР.766.02.РТС2022.ПЗ
73 Лист Дата Подп.
№ докум. Лис.
Вим
8,982 9,7305 10,479 11,227 5 11,976 12,724 5 13,473 14,221 5
14,97 0,0158 22 0,0119 43 0,0088 14 0,0063 61 0,0044 88 0,0030 96 0,0020 88 0,0013 77 0,0008 88 0,0118 67 0,0089 58 0,0066 11 0,0047 71 0,0033 66 0,0023 22 0,0015 66 0,0010 33 0,0006 66
СКО=
4,04
-20,2 -19,19 -18,18 -17,17 -16,16 х
-20,2 0,99
P(Пц-
5)
3,68E-
07 1,24E-
06 3,96E-
06 1,18E-
05 3,31E-
05 х
20,2 1,00
P(Пц-
5)-Н
3,72E-
07 1,26E-
06 4E-06 1,19E-
05 3,35E-
05
∆x
1,01
—
15,1 5
-14,14
-13,13
-12,12
-11,11
-10,1
-9,09
-8,08
-7,07 8,73
E-05 0,0002 16 0,0005 02 0,0010 97 0,0022 51 0,0043 39 0,0078 56 0,0133 64 0,0213 56 8,81
E-05 0,0002 18 0,0005 07 0,0011 08 0,0022 73 0,0043 82 0,0079 35 0,0134 98 0,0215 69
-6,06
-5,05
-4,04
-3,03
-2,02
-1,01 4E-15 1,01 2,02 0,0320 59 0,0452 1
0,0598 94 0,0745 39 0,0871 45 0,0957 1
0,0987 48 0,0957 1
0,0871 45 0,0323 79 0,0456 62 0,0604 93 0,0752 84 0,0880 16 0,0966 67 0,0997 36 0,0966 67 0,0880 16

ВКР.766.02.РТС2022.ПЗ
74 Лист Дата Подп.
№ докум. Лис.
Вим
3,03 4,04 5,05 6,06 7,07 8,08 9,09 10,1 11,11 0,0745 39 0,0598 94 0,0452 1
0,0320 59 0,0213 56 0,0133 64 0,0078 56 0,0043 39 0,0022 51 0,0752 84 0,0604 93 0,0456 62 0,0323 79 0,0215 69 0,0134 98 0,0079 35 0,0043 82 0,0022 73 12,12 13,13 14,14 15,15 16,16 17,17 18,18 19,19 20,2 0,00109 7
0,00050 2
0,00021 6
8,73E
-05 3,31E
-05 1,18E
-05 3,96E
-06 1,24E
-06 3,68E-07 0,00110 8
0,00050 7
0,00021 8
8,81E
-05 3,35E
-05 1,19E
-05 4E-06 1,26E
-06 3,72E-07
СКО
=
3,41
-10,23 -9,3775
-8,525 -7,6725
-6,82 х
—
23,87 1,17
P(Пц
-7)
0,0013 0,00266 7 0,00514 0,00930 8
0,01583 3 х
10,23 1,00
P(Пц
-7)-Н
0,00110 9
0,00227 5
0,00438 6
0,00794 2
0,01350 9
∆x
0,852 5
—
5,9675
-5,115
—
4,2625
-3,41
—
2,557 5
-1,705
—
0,8525
-1,8E-
15 0,8525 0,0253 01 0,0379 82 0,0535 63 0,0709 59 0,088 31 0,1032 45 0,1133 92 0,1169 92 0,1133 92 0,0215 88 0,0324 07 0,0457 02 0,0605 45 0,075 35 0,0880 93 0,0967 51 0,0998 22 0,0967 51 1,705 2,557 5
3,41 4,2625 5,115 5,9675 6,82 7,6725 8,525 0,1032 45 0,088 31 0,0709 59 0,0535 63 0,0379 82 0,0253 01 0,0158 33 0,0093 08 0,0051 4

ВКР.766.02.РТС2022.ПЗ
75 Лист Дата Подп.
№ докум. Лис.
Вим
0,0880 93 0,075 35 0,0605 45 0,0457 02 0,0324 07 0,0215 88 0,0135 09 0,0079 42 0,0043 86 9,3775 10,23 11,0825 11,935 12,7875 13,64 14,492 5
15,34 5
16,197 5
0,00266 7
0,0013 0,00059 5
0,00025 6
0,00010 3
3,92
E-05 1,4E-
05 4,69E
-06 1,47E-
06 0,00227 5
0,00110 9
0,00050 8
0,00021 8
8,82E-
05 3,35
E-05 1,19E-
05 4E-
06 1,26E-
06 17,05 17,902 5
18,75 5
19,607 5 20,46 21,312 5
22,16 5
23,017 5
23,87 4,36E
-07 1,21E-
07 3,16E
-08 7,74E-
09 1,78E
-09 3,85E-
10 7,83E
-11 1,49E-
11 2,68E-12 3,72E
-07 1,03E-
07 2,69E
-08 6,6E-
09 1,52E
-09 3,29E-
10 6,68E
-11 1,27E-
11 2,29E-12
СКО
=
2,88
-8,64
-7,92
-7,2
-6,48
-5,76 х
—
20,16 1,39
P(Пц
-9)
0,00153 9
0,00315 7
0,00608 6
0,01102 1
0,01874 7 х
8,64 1,00
P(Пц
-9)-Н
0,00110 9
0,00227 5
0,00438 6
0,00794 2
0,01350 9
∆x
0,72
-5,04
-4,32
-3,6
-2,88
-2,16
-1,44
-0,72
-2,9E-
15 0,72 0,0299 57 0,0449 71 0,0634 2
0,0840 18 0,1045 62 0,1222 45 0,1342 6
0,1385 22 0,1342 6
0,0215 88 0,0324 07 0,0457 02 0,0605 45 0,0753 5
0,0880 93 0,0967 51 0,0998 22 0,0967 51 1,44 2,16 2,88 3,6 4,32 5,04 5,76 6,48 7,2

ВКР.766.02.РТС2022.ПЗ
76 Лист Дата Подп.
№ докум. Лис.
Вим
0,1222 45 0,1045 62 0,0840 18 0,0634 2
0,0449 71 0,0299 57 0,0187 47 0,0110 21 0,0060 86 0,0880 93 0,0753 5
0,0605 45 0,0457 02 0,0324 07 0,0215 88 0,0135 09 0,0079 42 0,0043 86 7,92 8,64 9,36 10,08 10,8 11,52 12,24 12,96 13,68 0,00315 7
0,00153 9
0,00070 5
0,00030 3
0,00012 2
4,65E
-05 1,66E
-05 5,55E
-06 1,75E
-06 0,00227 5
0,00110 9
0,00050 8
0,00021 8
8,82E-
05 3,35E
-05 1,19E
-05 4E-
06 1,26E
-06 14,4 15,12 15,84 16,56 17,28 18 18,72 19,44 20,16 5,16E-
07 1,43E-
07 3,74E-
08 9,16E-
09 2,11E-
09 4,56E-
10 9,27E-
11 1,77E-
11 3,17E-
12 3,72E-
07 1,03E-
07 2,69E-
08 6,6E-
09 1,52E-
09 3,29E-
10 6,68E-
11 1,27E-
11 2,29E-
12