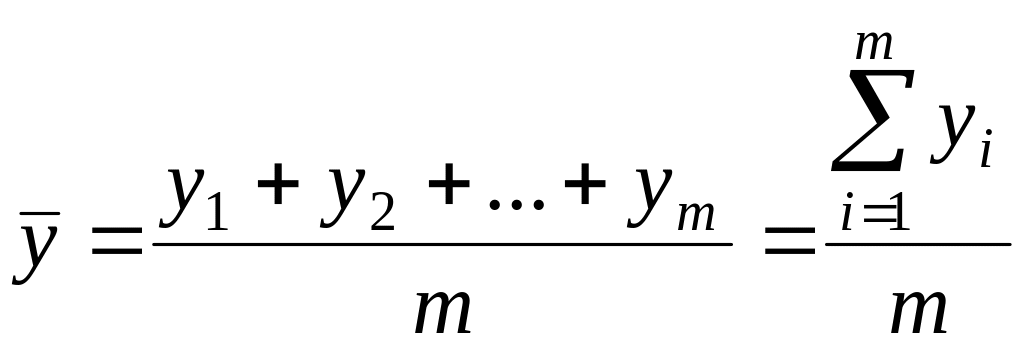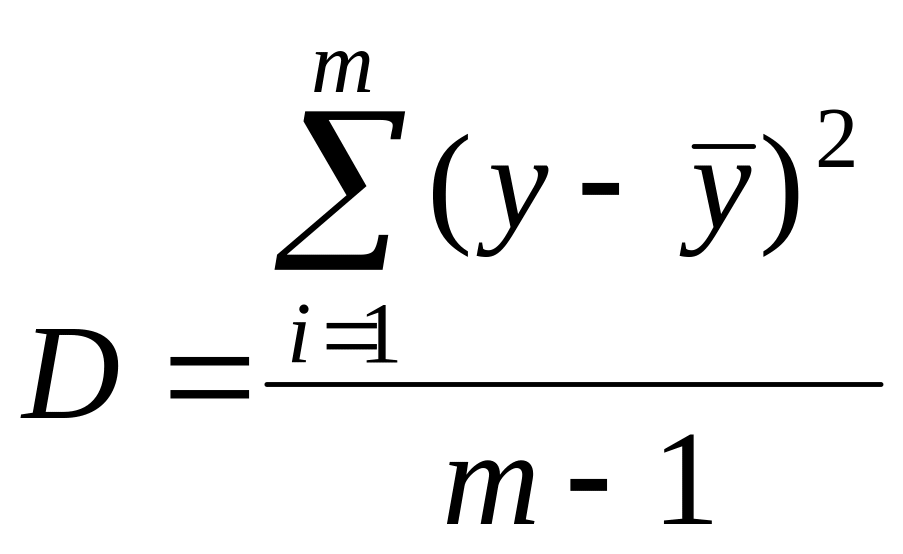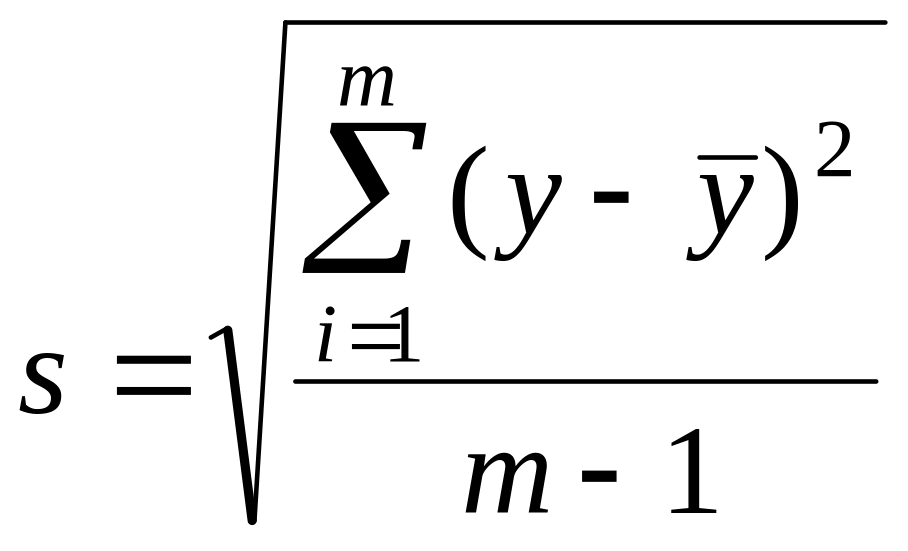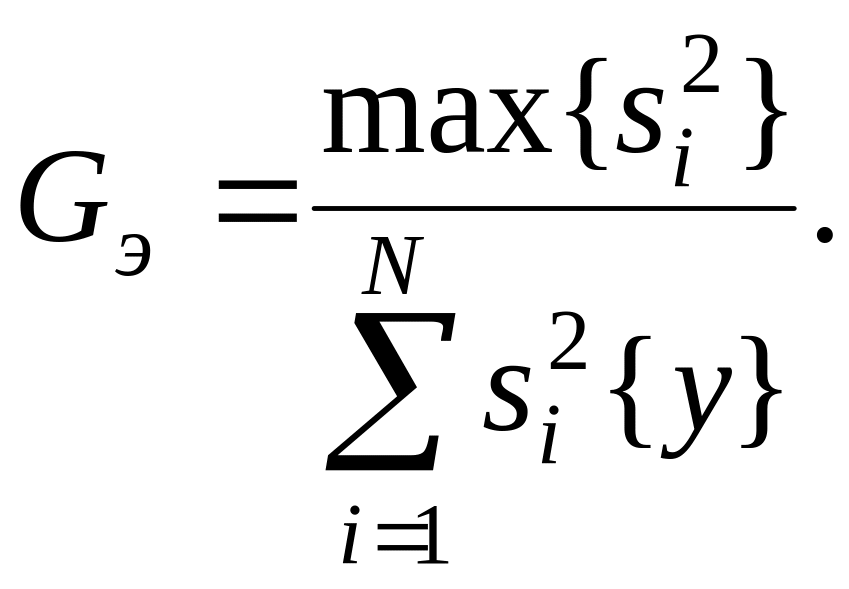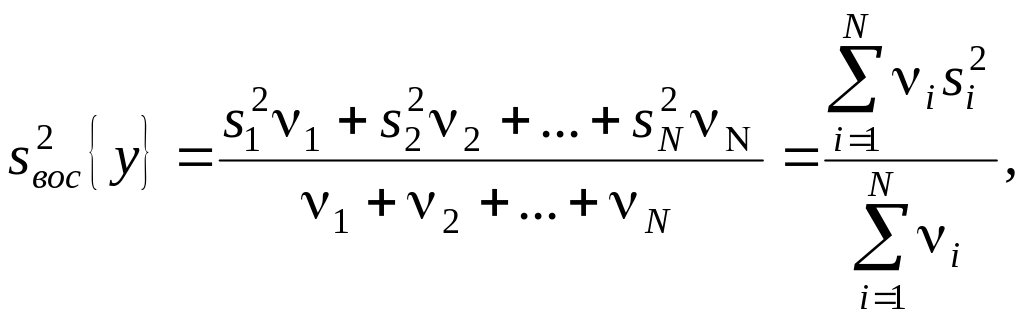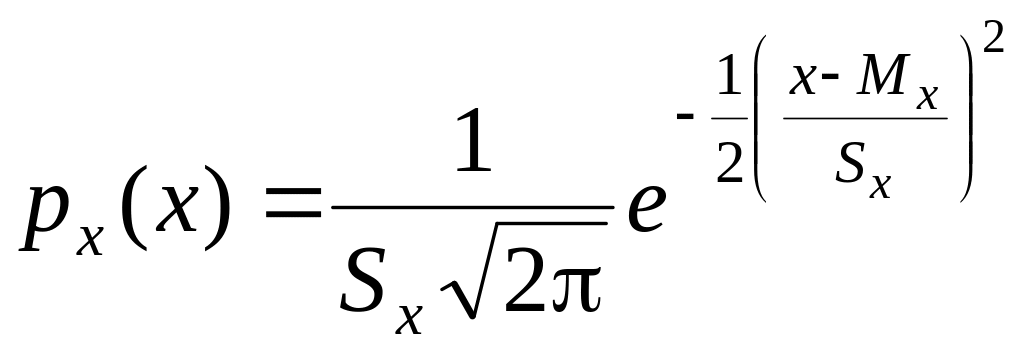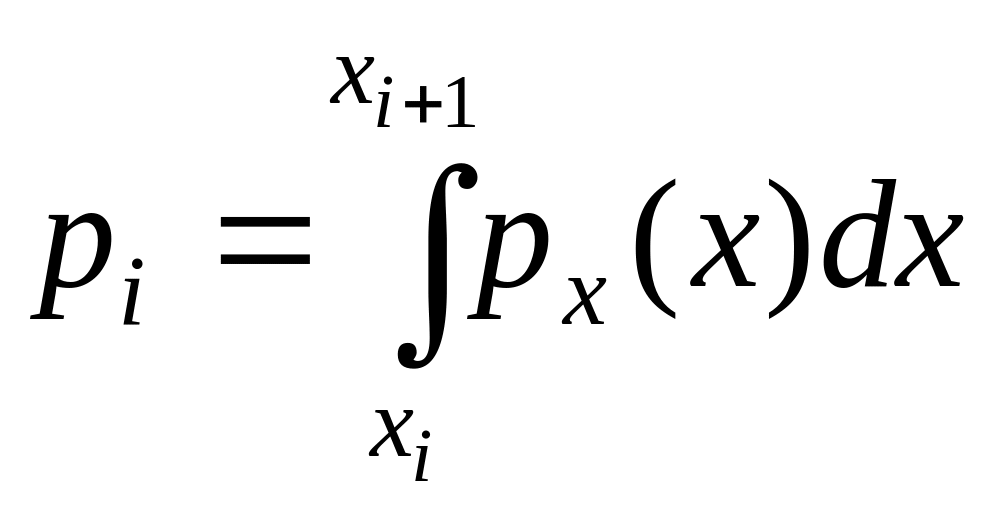Ошибка опыта рассчитать

Интересный сюжет, отличная развязка, авторский стиль.

Нет.

    Ошибка опыта 5 / находится по формуле [c.147]

    По данным [561 ошибка опыта [у] = 3,24, = 3. [c.150]

    Si.fl [у] — соответственно дисперсия неадекватности и ошибка опыта эти величины находят по формулам (VII.26) и (VII.27) со значениями степеней свободы Д и /2, вычисленными из равенств (VI 1.51) и (VI 1.52). [c.157]

    При 800° С количество углерода, отложившегося в виде кокса примерно такое же, как для бензола (в пределах ошибки опыта). Но при 900 и 1000° С наблюдается заметно ббльшая скорость разложения. Последнее противоречит утверждению Тиличеева, однако возможно, что при таких высоких температурах скорость разложения уже не зависит от нафталина и бензола, как таковых, а скорее от высших продуктов конденсации. Разложение нафталина в этой области катализируется контактным веществом с примесью кокса или углерода. [c.98]

    Расчеты изобарных потенциалов и констант равновесия различных реакций легко выполняются путем комбинирования изобарных потенциалов реакций образования соединений из простых веществ. Стандартный изобарный потенциал любой химической реакции равен алгебраической сумме соответствующих величин для реакций образования всех участников реакции. Таблицы стандартных изобарных потенциалов образования химических соединений при 1 атм и 25 X являются важнейшей сводкой исходных данных для термодинамических расчетов. Эти табличные данные в большинстве случаен вычислены путем комбинации данных для других реакций. Поэтому онн связаны с ошибками опыта, которые суммируются при сочетании величин ЛС и могут составить большую относительную величину, если значение AG° образования невелико и получено путем вычитания больших величин. [c.300]

    Полученные данные сопоставить с рассчитанными величинами по уравнению Нернста, указав ошибки опыта в процентах. [c.303]

    Определение элементного состава нефтей проводится общепринятыми методами анализа органических соединений, в частности углерод и водород — сожжением, по Либиху, или в калориметрической бомбе, азот, — по Дюма, сера, — по Кариусу, а кислород, — по разности, причем на процент его содержания ложатся все ошибки опыта. [c.76]

    Изучение скоростей реакций при обычных концентрациях показало, что расход олефина подчиняется первому кинетическому порядку, концентрации О2 и NHg не влияют на кинетику процесса, а суммарная энергия активации равна 16—20 ккал/моль (66,9-10 —83,6- 10 Дж/моль). Найдено, что в пределах ошибки опыта скорости окисления и окислительного аммонолиза идентичны [87]. Формальная кинетическая схема [c.160]

    Оказалось, что растворимость 2 %-ного водного раствора ДЭГ в гексане не отличается от растворимости воды в гексане (в пределах ошибки опыта) и равна 0,008 % при 20°С, отсюда ориентировочные потери ДЭГ за счет [c.58]

    Остаточная сумма квадратов складывается из дисперсии, обусловленной ошибкой опыта, и дисперсии, обусловленной взаимодействиями факторов, если такие имеются  [c.103]

    Из этой схемы видно, что двумя способами было получено одно и то же значение теплового эффекта (в пределах ошибки опыта). Химическое уравнение вместе с теплотой процесса называется термохимическим уравнением. С ними можно производить любые четыре алгебраических действия. [c.67]

    Давление пара серного эфира при 293 К равно 0,589-10 Па, а давление пара раствора, содержащего 0,0061 кг бензойной кислоты в 0,05 кг эфира при той же температуре, равно 0,548-10 Па. Рассчитайте молекулярную массу бензойной кислоты в эфире и относительную ошибку опыта в процентах по сравнению с величиной, приведенной в справочных таблицах. [c.202]

    Различие в степени соответствия экспериментальным данным уравнений (111,85) и (1И,87) совершенно незначительно и может быть объяснено ошибками опыта. [c.93]

    Распределение исходного фиксированного радиоактивного углеродного атома в (1- С] фенилциклогексане протекает медленнее, чем межмолекулярный перенос циклогексильной группы между фенилциклогексаном и [1—6- С] бензолом в таких же условиях. Особенно быстро межмолекулярная миграция циклогексильной группы протекает в начальный период реакции диспропорционирования (г/= 0,73 ч- ), в то время как распределение радиоактивности между атомами углерода этой группы в первые 30 мин вообще не наблюдается или настолько мало, что составляет величину, меньшую ошибки опыта. [c.205]

    С учетом погрешности измерения температуры 0,5 К отклонения АТ укладывались в пределах ошибки опыта. [c.107]

    При невысоком содержании непредельных углеводородов (до 10%) метод йодных чисел довольно точен. При больших значениях йодных чисел ошибка опыта возрастает. Свет, повышение температуры уменьшают точность определения в связи с развитием побочных реакций (например, замещения). При анализе высокомолекулярных топлив (например, дизельных) для улучшения условий реакций навеску топлива растворяют в небольшом количестве ацетона. [c.138]

    Коэффициенты уравнений регрессии и ошибка опыта рассчитывались по известным формулам 14—5]. [c.140]

    Таким образом, введение второго заместителя в положение 6 привело к более заметному повышению стойкости углеводородного димера, чем введение в положение 3. То есть в рассмотренных случаях, в среде Д, УА и А, стойкость димеров и КПЗ была ниже, если оба -заместителя находились в одном кольце. Исключение составил Э, в котором КПЗ с 2,3-ДМН оказался несколько прочнее, но в этом случае разница была невелика и сопоставима с ошибкой опыта. Тот факт, что наибольшая разница стойкости димеров [c.134]

    Если УРгг значительно превосходит величину ошибки опыта, то это указывает на криволинейный характер поверхности отклика и требует введения в уравнение регрессии членов с квадратичными эффектами. [c.148]

    Однако, результаты расчетов термодинамических величин для предельных углеводородов, выполненных в предположении о свободном вращении групп атомов вокруг связи С—С, не согласуется с опытом. Например, вычисленная величина энтропии этана для 298° К отличается на 1,57 кал град моль от найденной экспериментально, полученной из. измерений зависимости теплоемкости этана от температуры п широком интервале температур. Это расхождение, превышающее ошибку опыта примерно в десять раз, было объяснено тем, что вращение метильных групп вокруг связи С—С происходит не свободно, а заторможено с потенциалом торможения порядка 3000 кал/молъ. Торможение вращения группы около С—С связи является следствием взаимных влияний атомов вращающихся групп. [c.190]

    В исследованиях Джоуля, Роуланда (1880), Микулеску (1892) и др. использовались методы трения в металлах, удара, прямого превращения работы электрического тока в теплоту, растяжения твердых тел и др. Коэффициент J всегда постоянен в пределах ошибки опыта. [c.30]

    Колебания величины Кх не закономерны и могут быть объяснены ошибками опыта. Если принять Кх= и вычислить У по уравнению (VIII, 38), то полученные величины оказываются близкими к опытным. Раствор четырех участников реакции оказывается близким к идеальному при любых концентрациях, что является, скорее, исключением. [c.285]

    Это расхождение уже нельзя объяснить ни ошибками опыта, ни неправильностью в выборе стэфф- В частности, для совпадения расчетных и опытных значений пришлось бы принять [c.127]

    По методу Раста ohjhj определено, что температура плавлении смеси, содержащей 0,0152 г нафталина и 0,2568 г камфоры, составляла 156,5°, а температура нлав ления чистой камфоры 180, О. Для кам( юры Кэ == 49,8°. Рассчитать молекуля.п-ный вес нафталина и относительную ошибку опыта в процентах. [c.195]

    Азот определяется по Дюма, а кислород по разности, поэтому все ошибки опытов ложатся на кислород. Опособ непосредственного определения т ислорода (в виде воды) Ван-Молена дает достаточно точные результаты. Определение элементарного анализа не входит в круг тех обычных исследований, которым подвергается нефть и про-ИЗВ0Д1ГГСЯ в случае научного анализа. В таблице 1 приведены результаты анализа нефтей главных месторождений. [c.20]

    Как вывод из этон таблицы, можно сгса зать, что результаты определения индукционных периодов б обоих приборах практически одинаичовы. Разница между ними не превосходит ошибки опыта при параллельных определениях в одном и том же приборе. [c.182]

    Как И В предыдуш ем случае, эти коэфициенты сохраняют силу для масел различных вязкостей, но только для вискозиметра Энглера. Таблицу Ганса можно еш,е дополнить данньши Оффер-мана (190), коюрЫй предложил коэфициент для 25 сл, причем наблюдается время истечения только 10 сл в вискозиметре Уббелоде. Для веретенных и машинных масел при 50° он равен 13,07, нри 20° — 13,03 для цилиндровых при 50° = 12,9. Необходимо заметить, что скорость вьггекания небольших объемов масла слишком велика, и при постоянной ошибке опыта она обусловливает более высокий процент погрешности. [c.259]

    Для всех- контрольных точек значения /-крнтерня для уровня значимости Я = 0 05 меньше табличное. На рис. 53 показаны линии равного значения актив-иогт I катализатора, (/[ и прочности уз, построенные но уравнениям (VI. 17) и (VI. 18). Наибольшая активность ката-лиза/ора соответствует области, где значения компонента Х >0,4. Прочность, равн и 65%. является вполне удовлетворительной. Наибольший интерес представ, .яют точки, лежащие па пересечении лини 1 равного выхода /2 = 65% с линией равного выхода (/1=100%, Опыт 10 (см. таблицу, рнс, 53). поставленный в указанной области, дал хорошее (в пределах ошибки опыта) совпадение расчет-Н1.1Х и экспериментальных результатов. [c.273]

    Можно показать, что в по очень широком температурном интервале при обычных ошибках опыта значения константы скорости, вычисляемые по простой формуле Аррепиуса (2.11) и формуле, в которой учитывается зависимость предэкспоненциального множителя от температуры, часто оказываются неразличимыми. [c.12]

    Значения начальных скоростей реакции превращения бензол-карбоксилатов калия представлены в табл. 2. Из таблицы следует, что начальная скорость превращения исходного вещества (в пределах ошибки опыта) может быть определена как сумма начальных скоростей отщепления карбоксилатной группы (декарбоксилиро-вание) и присоединения к другой молекуле исходного вещества (карбоксилирование). Так как скорости декарбоксилирования и карбоксилирования равны, то обмен карбоксилатными группами может быть выражен уравнением  [c.160]

    Результаты опытов по термическому превращению пиперилена при атмосферном давлении, температурах 650—750 °С и разбавлении водяным паром в мольном отношении 1 7,6 показали, что скорости распада пиперилена и образования дивинила и циклопентадиена формально описываются уравнениями второго порядка. Однако эти реакции не могут иметь второй порядок, так как изменение разбавления водяным паром от 1 до 16 моль на 1 моль пиперилена в пределах ошибки опыта на результаты термического превращения пиперилена не влияет. Хорошее совпадение расчетной кривой и экспериментальных точек (см. рис. 29.3) было получено, когда для описания изменения концентраций основных продуктов были использованы уравнения скорости первого порядка для самотормозящихся реакций [20], а распад дивинила и циклопентаднена описывался уравнениями скоростей второго порядка  [c.240]

Для
определения вероятностных характеристик
погрешностей используются исходные
данные, полученные предварительно
опытным путем, посредством физического
эксперимента. Результаты эксперимента
в виде выборки некоторого объема n
обрабатывают методами математической
статистики и таким образом получают
оценочные характеристики погрешностей.

Познакомимся с
вычислением ошибки опыта, или, как ее
часто называют, ошибки воспроизводимости.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое

равно сумме всех m
отдельных результатов, деленной на
количество параллельных опытов

(7.1)

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность

–
у,
где у
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
Дисперсией называется среднее значение
квадрата отклонений величины от ее
среднего значения. Дисперсия обозначается
D
и выражается формулой

(7.2)

где
(m
– 1) – число
степеней свободы, равное количеству
опытов минус единица. Одна степень
свободы использована для вычисления
среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой

. (7.3)

Стандарт
имеет размерность той величины, для
которой он вычислен. Дисперсия и стандарт
– это меры рассеяния, изменчивости. Чем
больше дисперсия и стандарт, тем больше
рассеяны значения параллельных опытов
около среднего значения.

Критерии
исключения грубых ошибок.
Ошибка опыта является суммарной
величиной, результатом многих ошибок:
ошибок измерений факторов, ошибок
измерения функции отклика и др. Каждую
из этих ошибок можно, в свою очередь,
разделить на составляющие.

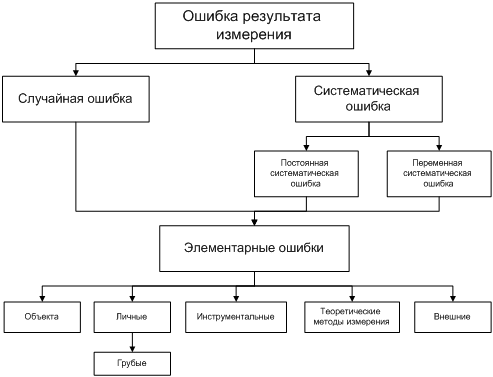
Все
ошибки принято разделять на случайные,
систематические и промахи. Систематические
ошибки
находят, калибруя измерительные приборы
и сопоставляя опытные данные с
изменяющимися внешними условиями, при
сравнении с эталонным прибором. Если
систематические ошибки вызываются
внешними условиями (переменной
температуры, и т. д.), следует компенсировать
их влияние. Случайными
ошибками
называются те, которые появляются
нерегулярно, причины возникновения
которых неизвестны и которые невозможно
учесть заранее. При повторении опытов
такие ошибки могут вызвать большой
разброс экспериментальных результатов.

Очень важно
исключить из экспериментальных данных
грубые ошибки. Грубая погрешность,
или промах, – это погрешность результата
отдельного измерения, входящего в ряд
измерений, которая для данных условий
резко отличается от остальных результатов
этого ряда. Источником грубых погрешностей
нередко бывают резкие изменения условий
измерения и ошибки, допущенные оператором.
К ним можно отнести:

• неправильный
  отсчет по шкале измерительного прибора,
  происходящий из-за неверного учета
  цены малых делений шкалы;

• неправильная
  запись результата наблюдений, значений
  отдельных мер использованного набора,
  например гирь;

• хаотические
  изменения параметров питающего средства
  измерений (СИ) напряжения, например его
  амплитуды или частоты.

Причинами
грубых погрешностей могут быть внезапные
и кратковременные изменения условий
измерения и оставшиеся незамеченными
неисправности в аппаратуре. Если промахи
обнаруживают в процессе измерений, то
результаты их содержащие отбрасывают.
Однако чаще всего промахи выявляют при
статистической обработке результатов
измерений с помощью специальных
критериев.

Корректная
статистическая обработка выборки
возможна только при ее однородности,
т.е. в том случае, когда все ее члены
принадлежат к одной и той же генеральной
совокупности. В противном случае
обработка данных бесмысленна. “Чужие”
отсчеты по своим значениям могут
существенно не отличаться от “своих”
отсчетов. Их можно обнаружить только
по виду гистограмм или дифференциальных
законов распределения. Наличие таких
аномальных отсчетов принято называть
загрязнениями
выборки, однако выделить члены выборки,
принадлежащие каждой из генеральных
совокупностей, практически невозможно.

Если
“свои” и “чужие” отсчеты различаются
по значениям, то их исключают из выборки.
Особую неприятность доставляют отсчеты,
которые хотя и не входят в компактную
группу основной массы отсчетов выборки,
но и не удалены от нее на значительное
расстояние, – так называемые предполагаемые
промахи. Отбрасывание “слишком”
удаленных от центра выборки отсчетов
называется “цензурированием” выборки.
Это осуществляется с помощью специальных
критериев.

При
однократных измерениях обнаружить
промах не представляется возможным.
Для уменьшения вероятности появления
промахов измерения проводят два-три
раза и за результат принимают среднее
арифметическое полученных отсчетов.
При многократных измерениях для
обнаружения промахов используют
статистические критерии, предварительно
определив, какому виду распределения
соответствует результат измерений.

Вопрос
о том, содержит ли результат наблюдений
грубую погрешность, решается общими
методами проверки статистических
гипотез. Проверяемая гипотеза состоит
в утверждении, что результат наблюдения
x_i
не содержит грубой погрешности, т.е.
является одним из значений измеряемой
величины. Пользуясь определенными
статистическими критериями, пытаются
опровергнуть выдвинутую гипотезу. Если
это удается, то результат наблюдений
рассматривают как содержащий грубую
погрешность и его исключают.

Для
выявления грубых погрешностей задаются
вероятностью q
(уровнем значимости) того, что сомнительный
результат действительно мог иметь место
в данной совокупности результатов
измерений.

Критерий
“трех сигм”
применяется для результатов измерений,
распределенных по нормальному закону.
По этому критерию считается, что
результат, возникающий с вероятностью
q

0,003, маловероятен и его можно считать
промахом, если

,
где S_y
– оценка СКО измерений. Величины

и S_y
вычисляют без учета экстремальных
значений y_i.
Данный критерий надежен при числе
измерений n

20… 50.

Это
правило обычно считается слишком
жестким, поэтому рекомендуется [5]
назначать границу цензурирования в
зависимости от объема выборки: при 6 <
n

100 она равна 4S_y;
при 100 < n

1000 – 4,5S_y;
при 1000 < n

10000 – 5S_y.
Данное правило применимо только для
нормального закона.

Вариационный
критерий Диксона.
Этот критерий очень удобен и достаточно
мощен (с малыми вероятностями ошибок).
При его применении полученные результаты
наблюдений записывают в вариационный
возрастающий ряд y₁,
y₂,
…, y_n
(y₁<
y₂
< …< y_n).
Критерий Диксона определяется как
K_D=(y_n–
y_n—1)/
(y_n–
y₁).
Критическая область для этого критерия
P(K_D>Z_q)
= q.
Значения Z_q
приведены в таблице 6.

Таблица 6. Значения критерия Диксона.

Существуют и другие
критерии исключения грубых ошибок [5],
например, критерии Граббса, Шовене,
Шарлье, Романовского.

Дисперсия
воспроизводимости параллельных опытов.
При планировании физического эксперимента
определяются точки xⁱ
(
)
в факторном пространстве, в которых
определяется экспериментальное значение
функции отклика. Так как функция отклика
y
имеет случайный характер, то в каждой
точке xⁱ
проводятся m
повторных опытов, и дисперсия всего
эксперимента получается в результате
усреднения дисперсий всех опытов. По
терминологии, принятой в планировании
эксперимента, речь идет о подсчете
дисперсии воспроизводимости эксперимента.

В
каждой точке результаты наблюдений

,


,
… ,


усредняются:

. (7.5)

С
целью оценки ошибки воспроизводимости
в каждом опыте, состоящем из m
повторных наблюдений, подсчитываются
дисперсия

и стандарт

по формулам:

; (7.6)

,
(7.7)

где
(m–1)
– число степеней свободы, равное
количеству повторных опытов, минус
единица;

–
среднее арифметическое, определяемое
по формуле (7.5).

Если дисперсии
D_i
(
),
вычисленные по формулам (7.6) однородны,
то можно вычислить средневзвешенную
дисперсию с суммарным числом степеней
свободы. Такая дисперсия является
значительно более надежной оценкой
дисперсии воспроизводимости, чем
отдельные выборочные дисперсии.
Однородность дисперсий означает, что
среди всех суммируемых дисперсий нет
таких, которые бы значительно превышали
все остальные.

Для проверки
однородности дисперсий

,
полученных по выборкам одинакового
объема m, используется
критерий Кохрэна, который определяется
отношением максимальной дисперсии к
сумме всех дисперсий

. (7.8)

С
критерием Кохрэна связаны числа степеней
свободы ₁=m
– 1 и ₂
= N.
Гипотеза об однородности дисперсией
подтверждается, если экспериментальное
значение критерия Кохрэна не превышает
табличного значения (Приложение 2).

В
случае однородности дисперсий можно
усреднять дисперсии и для подсчета
дисперсии воспроизводимости эксперимента
с числом степеней свободы _вос=N
(m
– 1) пользоваться формулой

(7.9)

Такой формулой можно
пользоваться в случаях, когда число
повторных опытов одинаково во всей
матрице.

На
практике часто приходится сталкиваться
со случаями, когда число повторных
опытов различно. Это происходит вследствие
отброса грубых наблюдений, неуверенности
экспериментатора в правильности
некоторых результатов (в таких случаях
возникает желание еще и еще раз повторить
опыт) и т. п.

Тогда
при усреднении дисперсий приходится
пользоваться средним взвешенным
значением дисперсий, взятым с учетом
числа степеней свободы

(7.10)

где



– дисперсия первого опыта,


– дисперсия второго опыта и т. д., ν₁
– число степеней свободы в первом опыте,
равное числу параллельных опытов m
минус 1, т. е. ν₁=
m₁–1;
ν₂
– число степеней свободы во втором
опыте и т. д. Число степеней свободы
средней дисперсии принимается равным
сумме чисел степеней свободы дисперсий,
из которых она вычислена.

После исключения
из повторных опытов грубых ошибок во
всех опытах необходимо снова проверить
однородность дисперсий

.

Отметим, что
повторные опыты нельзя путать с повторными
измерениями в одном опыте. Такие измерения
часто делаются и являются полезными,
но не могут заменить повторных опытов.

Определение
закона распределения результатов
измерений или случайных погрешностей
измерений.
При определении закона распределения
случайных погрешностей измерений
переходят от выборки результатов
измерений y₁,
y₂,
y₃,
…, y_n
к выборке отклонений от среднего
арифметического результатов измерений
Δy₁,
Δy₂,
Δy₃,
…, Δy_n,
где Δ y_i
= y_i
–

.

Первым
шагом при идентификации закона
распределения является построение по
результатам измерения y_i,
i=1,
2, …, n,
вариационного
ряда
(упорядоченной выборки). В вариационном
ряду результаты измерения располагают
в порядке возрастания. Далее этот ряд
разбивают на оптимальное число r,
как правило одинаковых интервалов
длиной

.

Далее
определяют число попаданий m_i
(частоты) результатов измерений в
интервалы группирования. В рассматриваемом
интервале отношение частоты m_i
к общему числу n
измерений определяет частность

(7.11)

или
оценочную вероятность появления
соответствующего результата измерения.
Частоту появления результата измерения
можно графически представить в виде
гистограммы, т.е. ступенчатой диаграммы
оценки p^*
плотности вероятности распределения
результатов измерения по размеру.
Частота p_i
соответствует площади i-го
прямоугольника, а оценку плотности
вероятности получают делением частости
(площади) на интервал h
(основание):

(7.12)

При
увеличении числа интервалов и
соответственно уменьшении их длины
гистограмма все более приближается к
гладкой кривой – графику плотности
распределения вероятности.

По
виду построенной гистограммы может
быть оценен закон распределения
результатов измерений.

Принято
считать, что в большинстве тщательно
поставленных экспериментов ошибки с
хорошим приближением подчинены
нормальному закону распределения

, (7.13)

где
е
– основание натурального логарифма,
p_x(x)
– плотность распределения вероятности.
Теоретически это утверждение обосновывается
исходя из центральной предельной теоремы
теории вероятностей, которая утверждает,
что сумма многих независимых источников
погрешностей с произвольными функциями
распределения асимптотически имеет
нормальное распределение, если только
ни одна из этих погрешностей не является
превалирующей.

В
результате получим следующий график:

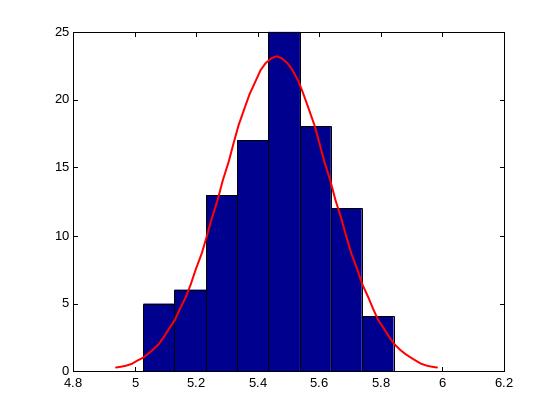
При
числе наблюдений n
> 50 для проверки гипотезы о нормальности
закона распределения случайной величины
часто используют критерий согласия ².
Идея этого метода состоит в контроле
отклонений гистограммы экспериментальных
данных от гистограммы с таким же числом
интервалов, построенных на основе
нормального закона распределения.

Для
этого критерия мерой отклонения
статистического распределения случайной
величины от нормального закона служит
величина

²
=

, (7.14)

где
m_i
– экспериментальные значения частот
в интервалах разбиения [x_i,
x_i+1];
n
– число интервалов разбиения;

– теоретические вероятности попадания
результатов наблюдения в интервалы
разбиения.

Величина
_k²
подчиняется ²
распределению с k
степенями свободы. Для нормального
распределения число степеней свободы
определяют по формуле k = m – 3.

Методика проверки
соответствия принятого и экспериментального
законов распределения заключается в
следующем:

• определяются
  среднее арифметическое значение

  измеряемой величины по формуле (7.1) и
  среднеквадратическое отклонение
  результата измерения s_y
  по формуле (7.3);

• группируются
  результаты наблюдений по интервалам
  длиной h,
  число которых определяется так же, как
  и при построении гистограммы;

• вычисляется
  число наблюдений для каждого из
  интервалов, теоретически соответствующее
  нормальному закону распределения. Для
  этого сначала от реальных середин
  интервалов y_i0
  переходят к нормированным серединам
  
  .
  Затем для каждого значения z_i
  с помощью аналитической модели находят
  функции плотности вероятности по
  формуле

По
найденному значению f(z_i)
определяют ту часть N_i
имеющихся наблюдений, которая теоретически
должна быть в каждом из интервалов

,
где n
– общее число наблюдений.

• если
  в какой-либо интервал теоретически
  попадает меньше пяти наблюдений, то в
  обеих гистограммах его соединяют с
  соседним интервалом. После этого
  определяют число степеней свободы ν
  = m
  – 3, где m
  – общее число интервалов. Если было
  произведено укрупнение интервалов, то
  m
  – общее число интервалов после
  укрупнения;

• по
  формуле (7.14) определяют эмпирическое
  значение величины χ²;

• выбирают
  уровень значимости критерия q.
  Он должен быть небольшим, чтобы была
  мала вероятность совершить ошибку
  первого рода. При заданном уровне
  значимости q
  и числу степеней свободы ν
  находят границу критической области
  
  ,
  такую что
  
  =
  q.
  Вероятность того, что полученное
  значение χ²
  превышает

  ,
  равна q
  и мала. Поэтому, если оказывается
  
  ,
  то гипотеза о нормальности закона
  распределения опытных данных принимается,
  т.е. она правдоподобна и не противоречит
  опытным данным с доверительной
  вероятностью p
  =1– q.
  В противном случае гипотеза отвергается,
  как противоречащая опытным данным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Статьи
Главная страница

Из графика
видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):

Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:

Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.

Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).

Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1).  Рассчитаем среднее значение и, чтобы  оценить
разброс данных найдем величины DХ = Х –
Х_ср

Ясно, что
величины DХ  как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:

и среднеквадратичное или стандартное отклонение выборки:

Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.

Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:

Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.

И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):

Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = s_ср*t_{f, P}

Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%

Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.

Окончательно
для измеряемой величины Х получаем значение Х_сред±s_ср*t_f,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6

Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30

Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:

Косвенные определения.

Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.

Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.

Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd²/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):

Окончательный
результат V=2510±20 (мм³) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).

План проведения измерений:

[1]

1.   Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.

2.   
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.

3.   
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.

4.   
Расчет
среднего значения Х_ср, и стандартного отклонение среднего
значения s_cp

5.   
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*s_cp

6.   
Сравнение случайной и приборной погрешности, при этом возможны варианты:

—    
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор

—    
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.

—    
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=

7.   
Записывается окончательный результат Х = Х_ср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Х_ср

Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)

Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать  измерение той величины, вклад ошибки которой в DХ наиболее существенен.

Изучение зависимостей.

Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.

При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.

Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:

Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.

Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.

Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:

Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s²
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
^[2].

Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:

Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул,  необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.

В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать –  в следующей
статье.

Литература:

[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.

[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.

Проведение
эксперимента

Познакомимся с
вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.

Ошибки параллельных
опытов

Каждый
эксперимент содержит элемент неопределен­ности вследствие ограниченности
экспериментального ма­териала. Постановка повторных (или параллельных) опытов
не дает полностью совпадающих результатов, потому что всегда существует ошибка
опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным
опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях
несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее
арифметическое  равно сумме всех п отдельных резуль­татов, деленной на количество
параллельных опытов п

.

Отклонение
результата любого опыта от среднего арифметического можно представить как
разность  где  – результат отдельного опыта. Наличие
откло­нения свидетельствует об изменчивости, вариации значе­ний повторных
опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию.
Диспер­сией называется среднее значение квадрата отклонений величины от ее
среднего значения. Дисперсия обозна­чается s² и
выражается формулой

.

где (n – 1) – число
степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы
исполь­зована для вычисления среднего.

Корень квадратный из
дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением,
стандартом или квадратичной ошибкой

Стандарт имеет
размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это
меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше
рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся
суммарной величиной, результатом многих ошибок: ошибок измерений факторов,
ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою
очередь, разделить на состав­ляющие.

Вопрос о классификации ошибок
довольно сложный и вызывает много дискуссий. В качестве примера одной из
возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория
ошибок измере­ний» (М., изд-во «Недра», 1967).

Все ошибки принято разделять
на два класса: система­тические и случайные.

Систематические ошибки
порождаются причинами, действующими регулярно, в определенном направлении. Чаще
всего эти ошибки можно изучить и определить количественно.

Систематические ошибки
находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися
внешними условиями (например, при градуи­ровке термопары по реперным точкам,
при сравнении с эта­лонным прибором).

Если систематические ошибки
вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет
компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются
те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и
которые невозможно учесть заранее.

Систематические и случайные
ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного
нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении
опытов такие ошибки могут вызвать большой разброс эксперимен­тальных
результатов.

Очень важно исключить из экспе­риментальных
данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных
опытов существуют правила. Для определения брака используют, например, кри­терий
Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается
бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра
оптимизации

Дисперсия всего эксперимента
получается в результате усреднения дисперсий всех опытов. По терми­нологии,
принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра
оптимизации  или, что то же самое, дисперсии воспроизводимости эксперимента

При подсчете дисперсии
параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в
матрице N, а затем разделить на N(n — 1):

,

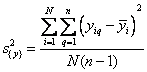
Где i = 1, 2, …, N;      q = 1, 2, …, n.

Такой формулой можно
пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости
проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов
во всех экспериментальных точках. На практике весь­ма часто приходится
сталкиваться со случаями, когда число повторных опытов различно. Это происходит
вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в
правильности некоторых результатов (в таких случаях возникает желание еще и еще
раз повторить опыт) и т.п.

Тогда при усреднении
дисперсий приходится пользо­ваться средним взвешенным значением дисперсий,
взятым с учетом числа степеней свободы

,

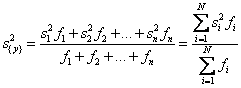
где

– дисперсия i-го опыта;

 – число степеней свободы i-м опыте, равное числу параллельных опытов
n_i минус 1.

Число степеней
свободы средней дисперсии принима­ется равным сумме чисел степеней свободы
дисперсий, из которых она вычислена.

Случай с неравным числом
наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности
матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов,
приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует
забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять
нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в
однородности суммируемых дисперсий.

Проверка
однородности дисперсий

Проверка однородности
дисперсий производится с помощью различных статистических критериев. Простей­шим
из них является критерий Фишера, предназначенный для сравнения двух дисперсий.
Критерий Фишера (F—критерий)
представляет собою отношение большей дисперсии к меньшей. Полученная величина
сравнивается с таблич­ной величиной F-критерия.

Если полученное значение
дисперсионного отно­шения больше приведенного в таблице для соответствую­щих
степеней свободы и выбранного уровня значимости, это означает, что дисперсии
значимо отличаются друг от друга, т. е. что они неоднородны.

Если сравниваемое количество
дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться
критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках
имеется одина­ковое число повторных опытов. При этом подсчитывается дисперсия в
каждой горизонтальной строке матрицы

,

а затем из
всех дисперсий находится наибольшая  ко­торая делится на сумму всех дисперсий. Критерий Кохрена – это
отношение максимальной дисперсии к сумме всех дисперсий

.

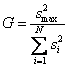
Гипотеза
об однородности дисперсий подтверждается, если экспериментальное значение
критерия Кохрена не превы­шает табличного значения. Тогда можно усреднять дис­персии
и пользоваться формулой

.

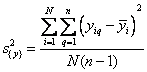
Если возникает предположение
о наличии неодно­родности дисперсий для случая, когда число повторных опытов неодина­ково
во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой
формуле подсчитывается дисперсия воспроизводимости

.

Далее
находится величина

,

где

.

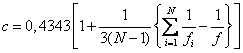
Здесь число
степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании экспе­римента типа
2^k это число равно числу опытов в матрице.

Бартлет показал, что величина
 приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия
Бартлета проверяется обычным способом.

Критерий Бартлета базируется
на нормальном распре­делении. Если имеются отклонения от нормального распре­деления,
то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить
использование F-критерия даже в тех случаях, когда число
дисперсий больше двух. Делается это следующим образом. Из всех дисперсий
выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между
собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо,
то диспер­сии, имеющие промежуточные значения, также не могут значимо
отличаться друг от друга. Тогда всю группу дис­персий можно считать
принадлежащей к единой совокуп­ности. В таких случаях нет надобности применять
кри­терий Бартлета.

Рандомизация

Чтобы исключить влияние
систематических ошибок, вызванных внешними условиями (переменой температуры,
сырья, лаборанта и т. д.), рекомендуется случайная пос­ледовательность при
постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать
во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Если экспериментатор
располагает сведениями о пред­стоящих изменениях внешней среды, сырья,
аппаратуры и т. п., то целесообразно планировать эксперимент таким образом,
чтобы эффект влияния внешних условий был сме­шан с определенным
взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья
матрицу 2³ можно разбить на два блока таким образом, чтобы эффект
сырья сказался на величине трехфакторного взаимодейст­вия. Тогда все линейные
коэффициенты и парные взаимо­действия будут освобождены от влияния
неоднородности сырья.

В этой матрице при
составлении блока 1 отобраны все строки, для которых , а при составления бло­ка 2 – все строки,
для которых . Различие в сырье можно рассматривать как
новый фактор . Тогда матрица 2³, разбитая на
два блока, представляет собой полуреплику 2^4-1 с определяющим
контрастом .

,                 ;

,                ;

,               ;

,                  ;

,                 ;

,              ;

,              ;

,                ;

Эффект сырья
отразился на подсчете свободного члена b₀ и
эффекта взаимодействия второго порядка b₁₂₃.

Аналогично можно разбить на
два блока любой экспе­римент типа 2³. Главное – правильно выбрать
взаимодей­ствие, которым можно безболезненно пожертвовать. При отсутствии
априорных сведений выбирают взаимодействие самого высокого порядка: x₁x₂x₃ для 2³, x₁x₂x₃х₄ для 2⁴, x₁x₂x₃x₄x₅ 2⁵ и т. д. Но если
экспериментатору известно, что одно из парных взаимодействий лишено, например,
физико-химического смысла, то можно пожертвовать парным взаимодействием.

Матрицу типа 2^k можно разбить на количество блоков 2ⁿ (n – степень
двойки) при . Так, матрица 2³
разбивается на два блока по четыре опыта в каждом и на четыре блока по
два опыта в каждом. Матрица 2⁴ – на два блока по 8 опытов в каждом,
на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.

Изучение всех влияющих на исследуемый объект факторов одновременно
провести невозможно, поэтому в эксперименте рассматривается их ограниченное
число. Остальные активные факторы стабилизируются, т.е. устанавливаются на
каких-то одинаковых для всех опытов уровнях.

Некоторые факторы не могут быть обеспечены системами стабилизации
(например, погодные условия, самочувствие оператора и т.д.), другие же
стабилизируются с какой-то погрешностью (например, содержание какого-либо
компонента в среде зависит от ошибки при взятии навески и приготовления
раствора). Учитывая также, что измерение параметра у осуществляется
прибором, обладающим какой-то погрешностью, зависящей от класса точности
прибора, можно прийти к выводу, что результаты повторностей одного и того же
опыта у_к будут приближенными и должны
отличаться один от другого и от истинного значения выхода процесса.
Неконтролируемое, случайное изменение и множества других влияющих на процесс
факторов вызывает случайные отклонения измеряемой величины у_к
от ее истинного значения – ошибку опыта.

Каждый эксперимент содержит элемент неопределенности вследствие
ограниченности экспериментального материала. Постановка повторных (или
параллельных) опытов не дает полностью совпадающих результатов, потому что
всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно
оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в
одинаковых условиях несколько раз и затем берется среднее арифметическое всех
результатов. Среднее арифметическое у равно сумме всех n отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение результата любого опыта от среднего арифметического
можно представить как разность y₂–
, где y₂ – результат отдельного
опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений
повторных опытов. Для измерения этой изменчивости чаще всего используют
дисперсию.

Дисперсией называется среднее значение квадрата отклонений
величины от ее среднего значения. Дисперсия обозначается s² и
выражается формулой:

где (n-1)
– число степеней свободы, равное количеству опытов минус единица. Одна степень
свободы использована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положительным знаком,
называется средним квадратическим отклонением, стандартом или квадратичной
ошибкой:

Ошибка опыта является суммарной величиной, результатом многих
ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др.
Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.

Все ошибки принято разделять на два класса: систематические и
случайные (рисунок 1).

Систематические ошибки порождаются причинами, действующими
регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая ошибка – это ошибка,
которая остаётся постоянно или закономерно изменяется при повторных измерениях
одной и той же величины. Эти ошибки появляются вследствие неисправности
приборов, неточности метода измерения, какого либо упущения экспериментатора,
либо использования для вычисления неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка всех измерительных приборов и
безусловное выполнение выработанных практикой правил экспериментальных работ.
Если систематические ошибки вызваны известными причинами, то их можно
определить. Подобные погрешности можно устранить введением поправок.

Систематические ошибки находят, калибруя измерительные приборы и
сопоставляя опытные данные с изменяющимися внешними условиями (например, при
градуировке термопары по реперным точкам, при сравнении с эталонным прибором).
Если систематические ошибки вызываются внешними условиями (переменной
температуры, сырья и т.д.), следует компенсировать их влияние.

Случайными ошибками называются
те, которые появляются нерегулярно, причины, возникновения которых неизвестны и
которые невозможно учесть заранее. Случайные ошибки вызываются и объективными
причинами и субъективными. Например, несовершенством приборов, их освещением,
расположением, изменением температуры в процессе измерений, загрязнением
реактивов, изменением электрического тока в цепи. Когда случайная ошибка больше
величины погрешности прибора, необходимо многократно повторить одно и тоже
измерение. Это позволяет сделать случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше погрешности прибора, то уменьшать её нет
смысла. Такие ошибки имеют значение, которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми для измерений сделанных даже в
одинаковых условиях. Поскольку причины, приводящие к случайным ошибкам
неодинаковы в каждом эксперименте, и не могут быть учтены, поэтому исключить
случайные ошибки нельзя, можно лишь оценить их значения. При многократном
определении какого-либо показателя могут встречаться результаты, которые
значительно отличаются от других результатов той же серии. Они могут быть
следствием грубой ошибки, которая вызвана невнимательностью экспериментатора.

Систематические и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы исключать инструментальные ошибки, следует
проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта.
Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева
реакционной среды, разного способа перемешивания и т.п.

При повторении опытов такие ошибки могут вызвать большой разброс
экспериментальных результатов.

Очень важно исключить из экспериментальных данных грубые ошибки,
так называемый брак при повторных опытах. Грубые ошибки легко
обнаружить. Для выявления ошибок необходимо произвести измерения в других
условиях или повторить измерения через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность в записях, тщательность в работе и
записи результатов эксперимента. Грубая ошибка должна быть исключена из
экспериментальных данных. Для отброса ошибочных данных существуют определённые
правила.

Например, используют критерий Стьюдента t (Р;
f):
Опыт считается бракованным, если экспериментальное значение критерия t по
модулю больше табличного значения t (Р; f).

Если в распоряжении исследователя имеется экспериментальная оценка
дисперсии S²(y_k)
с небольшим конечным числом степеней свободы, то доверительные ошибки
рассчитываются с помощью критерий Стьюдента t (Р;
f):

ε()
= t (Р; f)* S(y_k)/= t (Р; f)* S()

ε(y_k) = t (Р; f)* S(y_k)