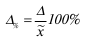Ошибка представительства также называется

ОГЛАВЛЕНИЕ
1. Аномалии силы тяжести
2
2. Виды аномалий силы тяжести
2
2.1 Аномалии в свободном воздухе
2
2.2 Влияние рельефа
3
2.3 Аномалии Буге
4
2.4 Поправка за рельеф. Аномалия Фая.
5
3. Статистические характеристики аномалий силы тяжести
7
4. Гравиметрические съемки
9
4.1 Виды гравиметрических съемок
9
4.2 Выполнение съемки
11
4.3 Топографо-геодезическое обеспечение съемки
14
5. Гравиметрические карты
16
5.1 Общие сведения о составлении гравиметрических карт
16
5.2 Точность гравиметрических карт
18
5.3 Косвенная интерполяция аномалий в свободном воздухе
20
5.4. Ошибка представительства
21
Литература
24
1. Аномалии силы тяжести
Если изучение внешнего гравитационного поля Земли сводится к определению — остаточной (аномальной) части полного (действительного) потенциала (Разд. 3)
где – нормальный потенциал,
то исходными данными для этого служат аномалии силы тяжести.
Аномалией силы тяжести называют разность между измеренным (действительным) значением силы тяжести и её нормальным (теоретическим) значением. В общем случае она обозначается, как .
Аномалии силы тяжести связаны с аномальном потенциалом через производную по вертикальному направлению:
Аномалии силы тяжести измеряются в миллигалах. Карты аномалий силы тяжести называются гравиметрическими картами, изолинии на них (линии равных аномалий) называются изоаномалами.
2. Виды аномалий силы тяжести
2.1 Аномалии в свободном воздухе
В самом общем случае для точки с координатами ( вычисляют нормальную силу тяжести на отсчётном эллипсоиде по формуле Сомильяны или по формуле Гельмерта (Разд. 3), а затем приводят её к высоте точки над эллипсоидом введением поправки, которая называется поправкой за высоту в нормальное значение или редукцией в свободном воздухе:
(1.0)
в линейном приближении или с точностью до членов второго порядка:
(1.1)
где высота точки M над отсчетным эллипсоидом. всегда отрицательна, поскольку нормальная сила тяжести убывает с высотой.
Аномалия силы тяжести
называется чистой аномалией в свободном воздухе.
Если подставить в (1.0) или в (1.1) вместо геодезической высоты высоту в поле силы тяжести (или над уровнем моря) , то такая аномалия в свободном воздухе называется смешанной.
Аномалии в свободном воздухе являются важнейшими для геодезии и используются для учета неоднородности поля силы тяжести в инженерных задачах, нахождения других элементов аномального поля, а также установления системы высот.
2.2 Влияние рельефа
В тех случаях, когда предметом изучения является не столько сама картина распределения аномалий, сколько информация о массах аномальной плотности, сосредоточенных под земной поверхностью (например, залежи полезных ископаемых или подземных карстовых пустотах), возникает задача отделения влияния этих масс от других источников вариации аномалий, и прежде всего — от влияния рельефа.
Для точки на земной поверхности, в которой производятся измерения , определяющую роль в её изменении, согласно закону обратного квадрата расстояния, играют близлежащие топографические массы.
Несложно показать, что зависимость аномалии в свободном воздухе от высоты (отметки точки) выражается, как
Отсюда следует, что карты аномалий в свободном воздухе и топографические карты сильно взаимно коррелированны, что мешает обнаруживать и изучать аномальные плотности. Поэтому в аномалии (точнее, в величину ) вносят различные поправки за притяжение рельефа.
2.3 Аномалии Буге
Простейший способ учета рельефа предложил П. Буге (1698-1758) : для каждой точки вводится поправка, эквивалентная притяжению бесконечного плоского слоя (Разд. 2) или пластины Буге. Толщина слоя равна высоте точки над уровнем моря, а плотность – средней плотности земной коры. Поправка называется поправка за притяжение промежуточного слоя или редукция Буге:
где – гравитационная постоянная, — плотность земной коры, для которой обычно берут одно из стандартных значений: 2,67, 2,60 или 2,30 г/.
Подставив численные значения и , получим: где высота должна быть выражена в метрах, а — в миллигалах.
Редукция Буге «убирает» все притягивающие массы между уровнем моря и данной точкой.
Аномалия силы тяжести в редукции Буге или просто аномалия Буге равна:
(1.2)
При удачно подобранной плотности промежуточного слоя аномалии Буге некоррелированы с рельефом, и карты аномалий Буге адекватно отображают картину недр на данной территории. Поэтому карты аномалий Буге при разных значениях стандартной плотности используются в гравиразведке.
2.4 Поправка за рельеф. Аномалия Фая.
Более сложная процедура учета притяжения топографических масс требует вычисления поправки за рельеф , которая должна отражать в окрестностях исследуемой точки отступления физической поверхности Земли от горизонтальной плоскости, проходящей через неё. Точка находится на поверхности земли, поэтому введение этой поправки интерпретируется как выравнивание окружающих холмов и впадин до уровенной поверхности, которую на локальном участке можно считать за плоскость. Удаляются соседние массы, расположенные выше уровня этой поверхности и потому уменьшающие силу тяжести (как бы «притягивающие вверх»), и заполняются впадины, которые, находясь ниже, также ослабляли силу тяжести. В итоге, поправка за рельеф всегда приводит к увеличению , то есть всегда положительна. После её введения полученное (увеличенное) значение силы тяжести соответствует такому, какое было бы, если бы реальная физическая поверхность совпадала бы с уровенной, проходящей через данную точку (рис. 2.1).
рис. 2.1 Поправка за рельеф
Опуская вывод, запишем, что для топографических масс в пределах круговой области σ поправка за рельеф вычисляется, как
где – отметка текущей точки интегрирования (притягивающего элемента топографических масс), — горизонтальное проложение до текущей точки интегрирования, – наклонное расстояние до неё. Интегрирование производится по топографической карте с помощью палетки или по цифровой модели рельефа. Учитывается притяжение рельефа в области радиусом до 50 км вокруг пункта, а в горных районах до 200 км. Поправка за рельеф в горных районах может превышать 100 мГал.
Если в аномалию в свободном воздухе ввести поправку за рельеф, то получим аномалию силы тяжести, которую называют аномалией Фая.
В равнинной местности, где поправки за рельеф становятся пренебрегаемо малыми, аномалии Фая совпадают с аномалиями в свободном воздухе. Там же, где влияние рельефа значительно, аномалии в свободном воздухе отличаются от аномалий Фая на величину поправки за рельеф.
Аномалии в свободном воздухе и аномалии Фая применяются для определения элементов аномального потенциала и для изучения фигуры Земли. Аномалии Буге используются в геодезии для косвенной интерполяции аномалий в свободном воздухе и аномалий Фая.
Применение обеих поправок (за промежуточный слой и за рельеф) даёт полную (уточнённую) аномалию Буге:
3. Статистические характеристики аномалий силы тяжести
Аномалии силы тяжести находят на пунктах гравиметрической съемки, которая часто не только не равномерна, но и содержит неизученные площади. Вместе с тем, в теории определения гравитационного поля Земли и при решении геофизических задач предполагается, что аномалии силы тяжести заданы непрерывно. Линейное интерполирование аномалий между пунктами съемки и, тем более, экстраполирование неизбежно связано с ошибками, особенно при редкой съемке и сложном аномальном поле. Поэтому в таких задачах, а также при точностных расчетах, используют статистические свойства аномалий силы тяжести, считая аномалии случайными величинами, а поле аномалий — изотропным, т.е. не зависящим от направления.
Одной из статистических характеристик является дисперсия аномалий – математическое ожидание квадрата отклонения аномалии от средней ее величины, которая после центрирования аномалий становится равной нулю. Такие аномалии называют центрированными. Среднее квадратическое отклонение будет равно .
Но одинаковую дисперсию могут иметь поля различной сложности. Поэтому второй характеристикой поля служит статистическая связь (корреляция, ковариация) аномалий при разных расстояниях между точками на гравиметрической карте.
Ковариацией называют математическое ожидание произведения аномалий во всех парах точек при постоянном расстоянии между ними, число пар равно :
При , очевидно, – т. е. при нулевом расстоянии между точками ковариация равна дисперсии.
По мере увеличения расстояния между точками величина уменьшается – медленней или быстрее, в зависимости от сложности поля. Поэтому второй характеристикой поля аномалий является расстояние корреляции . Это расстояние , на котором ковариация уменьшается вдвое, т.е. становится равной половине дисперсии:
При достаточно большом расстоянии ковариация стремится к нулю. Аналитическая зависимость ковариации от расстояния называется ковариационной (корреляционной) функцией .
Глобальное поле аномалий в свободном воздухе характеризуется величинами:
и .
Предложены разные модели ковариационной функции аномалий. Для местных исследований, при которых аномалии можно считать заданными на плоскости, часто пользуются моделью Джордана (1972 г.)
(3.1)
где .
График функции показан на рис. 3.1.
Рис. 3.1 Ковариационная функция Джордана
Параметры функции находят эмпирически по имеющейся гравиметрической съемке, предварительно исключив общий тренд аномалий, вызванный притяжением периферийных масс. Тренд аппроксимируют линейной или параболической функцией. Получив ковариации для нескольких расстояний , по графику эмпирической ковариационной функции находят расстояние корреляции.
4. Гравиметрические съемки
4.1 Виды гравиметрических съемок
Гравиметрические съемки выполняют для определения аномалий силы тяжести на пунктах с целью составления гравиметрических карт и каталогов. Гравиметрическая съемка предусматривает гравиметрические и топографо-геодезические работы.
Различают несколько видов гравиметрической съемки.
1. Мировая гравиметрическая съемка, образованная всеми доступными гравиметрическими данными, необходима для решения геодезических и навигационных задач.
2. Для изучения общих особенностей аномального поля силы тяжести на территориях протяженностью в сотни и тысячи километров выполняют региональную съемку. По ее результатам строят карты в масштабе 1:1000000 и 1:500000 с сечением изолиний (изоаномал) 5 мГал и намечают участки для более детальных съемок.
3. Для изучения районов, которые могут содержать месторождения полезных ископаемых, обнаружения перспективных геологических образований выполняют поисковую съемку и строят гравиметрические карты в масштабе 1:200000 и 1:100000 с сечением соответственно 2 и 1 мГал.
4. Для изучения залежей и пород, вмещающих полезные ископаемые, определения формы, размеров и глубины залегания геологических тел предназначена детальная гравиметрическая съемка. Ее выполняют для составления карт масштабов от 1:50000 до 1:5000 с сечением изоаномал соответственно от 0,5 до 0,05 мГал. Расстояние между пунктами разных съемок составляет соответственно от 5 км до 10-50 м.
5. При изучении малых территорий (участков распространения карста, возможного разуплотнения грунта при строительстве объектов, историко-архитектурных территорий и т.п.) применяют микрогравиметрическую съемку. Шаг съемки, в зависимости от изучаемого объекта, — 5 м, иногда 2 и даже 1 м, а сечение – 5 или 2 мкГал.
Пункты съемки часто располагают на прямолинейных параллельных профилях, особенно при детальных съемках. Расстояние между профилями обычно превышает расстояние между пунктами на профиле. При относительно равномерном распределении пунктов на местности съемка называется площадной, она позволяет построить гравиметрическую карту. Если расстояние между профилями в пять и более раз превышает шаг съемки по профилю, съемка будет профильной, по ее результату строят профили аномалий силы тяжести.
На гравиметрических картах чаще всего показаны аномалии Буге.
4.2. Выполнение съемки
Полевые работы при гравиметрической съемке обычно начинаются с создания местной опорной сети гравиметрических пунктов, которая служит обоснованием рядовой съемки. Точность пунктов опорной сети должна в 1,5-2 раза превышать точность рядовой съемки, а расстояние между опорными пунктами быть приемлемым для надежного контроля дрейфа гравиметров при рядовой съемке. Измерения в опорной сети выполняют группой гравиметров, по возможности короткими рейсами. Исходным служит пункт Государственной фундаментальной гравиметрической сети (ГФГС) или пункт Государственной гравиметрической сети 1 класса (ГГС-1), если речь не идёт о микрогравиметрической съемке.
В зависимости от внешних условий и состояния дорожной сети применяют разные схемы измерений: центральную систему, двухступенчатую систему, схему узловых точек.
Центральная система предусматривает связи пункта опорной сети с исходным пунктом многократными наблюдениями. Точность опорной сети находят по формуле для равноточных измерений
(4.1)
где
(4.2)
– ошибка единичного определения ,
— уклонение измеренного приращения силы тяжести от среднего,
— общее число измерений в сети на определяемых пунктах.
Если все пункты опорной сети не удается определить по схеме центральной системы, то применяют двухступенчатую систему, состоящую из каркасной и заполняющей опорных сетей. Каркасные пункты определяют по центральной системе, а заполняющие – в рейсах между каркасными пунктами. Уравнивание выполняют, считая каркасную сеть жесткой, либо каркасную и заполняющую сети уравнивают совместно, с учетом весов измерений.
Если центральную и двухступенчатую системы сложно осуществить, то создают полигональную систему измерений, по возможности, с небольшим числом сторон. Каждую связь в полигоне выполняют независимыми гравиметрическими рейсами в последовательности 1-2-1.
Если опорная сеть не была создана до начала рядовой съемки или в условиях плохих дорог, заболоченной местности и т.п., применяют методику узловых пунктов, строя сеть рейсами от одного или нескольких исходных пунктов. Узловые пункты образуются при пересечениях независимых рейсов. Сеть узловых пунктов уравнивают.
Рис. 4.1 Построение гравиметрических рейсов.
Измерения в рядовой сети проводят гравиметрическими рейсами между пунктами опорной сети. Рейс начинают и заканчивают на одном и том же опорном пункте (рис. 4.1а) либо на разных (рис. 4.1б), стараясь ограничить его продолжительность временем, за которое смещение нуль-пункта можно считать линейным. Внешние условия наблюдений в течение рейса должны быть по возможности неизменными. На каждом пункте фиксируют время наблюдений, и, если прибор не термостатирован, берут отсчет по термометру гравиметра.
Повторные наблюдения на определяемых пунктах в обратном ходе, как показывает опыт, неэффективны, поскольку увеличивают продолжительность рейса.
Обработку наблюдений начинают с вычисления показаний гравиметра в миллигалах. Затем по опорным отсчетам находят скорость смещения нуль-пункта (мГал/час):
— если рейс начинается и заканчивается на одном опорном пункте A (рис 4.1a)
или
— если начальный и конечный пункты разные (рис. 4.1б).
Поправка за смещение нуль-пункта вводится в показания гравиметра пропорциональные времени от начала рейса
.
В коротких рейсах эта поправка учитывает и влияние переменного лунно-солнечного притяжения.
Для оценки точности измерений силы тяжести в каждый рейс включают один или несколько пунктов из предыдущих рейсов, выполняют независимые контрольные рейсы. Оценку точности делают по формулам 4.1 и 4.2.
4.3 Топографо-геодезическое обеспечение съемки
Чтобы определить требования к планово-высотному обеспечению съемки, обратимся к формуле (1.2) для вычисления аномалии Буге:
(4.3)
Ошибку нормальной силы тяжести на отсчетной поверхности представим как:
где – ошибка определения координаты (где ось направлена на север)
горизонтальный градиент нормальной силы тяжести. Полагая получим . Такую точность с избытком обеспечивают автономные GPS-определения и крупномасштабные топографические карты.
Найдем величину ошибки определения высоты гравиметрического пункта, ограничив ее влияние на величину аномалии Буге величиной 0,01 мГал. Согласно (4.3)
При плотности горных пород приближенно имеем
и
GPS-определения позволяют получить высоту пункта с ошибкой 4 см за несколько минут при удалении от базовой станции до 30-50 км. В сильно залесенной местности или на застроенных территориях при необходимости прокладывают тахеометрические или нивелирные ходы. Применяют и крупномасштабные аэроснимки, позволяющие достигнуть точности 2-5 см
Требования к сечению изоаномал и точности геодезического обеспечения съемок разной детальности приведены в таблице 4.1
Таблица 4.1 Требования к планово-высотному обоснованию гравиметрических карт
5. Гравиметрические карты
5.1. Общие сведения о составлении гравиметрических карт
Гравиметрические карты составляют как для больших территорий, охватывающих обширные регионы, целые страны и континенты, так и для небольших участков детальных съемок. На мелкомасштабных картах чаще всего показаны на суше аномалии Буге, а на море аномалии в свободном воздухе. Крупномасштабные карты строят по аномалиям Буге. На картах аномалий Буге обязательно указывается плотность промежуточного слоя.
Часто карта объединяет съемки разных лет, выполненные по разным схемам и с разной точностью. Поэтому предварительно проводят критический анализ результатов измерений, приводят их к единому гравиметрическому уровню и единому нормальному полю и устраняют возможные расхождения на границах съемок. При этом стараются сохранить детальность более подробных съемок.
Для вычисления нормальной силы тяжести в отечественной практике пользуются формулой Гельмерта (Разд. 3) с поправкой −14 мГал в Потсдамскую систему (Разд. 4).
Рис. 5.1. Карта аномалий Буге сечением 0,5 мГал, гравиметрические профили и пункты детальной съемки при гравиметрической разведке.
При составлении детальных карт аномалий Буге важно уверенно выбирать плотность топографических масс для вычисления поправки за притяжение промежуточного слоя. Величина плотности может ощутимо меняться. В частности, для Москвы характерна величина 2,14 г/, а для Серпухова 2,39 г/. Плотность находят по образцам горных пород либо подбирают такую величину, при которой корреляция аномалий Буге с высотами гравиметрических пунктов становится минимальной.
Для составления карт масштабов 1:50000 и мельче пользуются стандартными значениями плотности 2,30 или 2,67 г/.
Поправку за рельеф вводят для составления карт масштаба 1:25000 и крупнее, причем в тех случаях, когда она превышает половину заданной ошибки определения аномалии на пункте.
5.2 Точность гравиметрических карт
При построении изоаномал на гравиметрической карте предполагается линейное изменение аномалий между смежными пунктами, из-за чего возникают неизбежные ошибки. Для оценки точности карты М.С. Молоденский ввел понятие ошибки интерполяции , т.е. среднего квадратического расхождения интерполированного и измеренного значения аномалии на том же пункте:
где — число пунктов.
Ошибка полностью характеризует точность гравиметрической карты. Для определения ошибки интерполяции разрежают имеющуюся съемку, строят карту заново и находят разности на исключенных пунктах и сравнивают с исходными. Затем процедуру повторяют. Имея в виду, что при сплошной съемке расстояние между пунктами равно нулю и величина тоже равнялась бы нулю, интерполируют полученный результат для шага съемки оцениваемой карты.
Ошибка интерполяции (таблица 4.2) аномалий силы тяжести зависит от сложности аномального поля, расстояния между пунктами и ошибки определения аномалии на гравиметрическом пункте. Ошибка , в свою очередь, складывается из ошибки измерений силы тяжести и влияния ошибок определения координат и высот гравиметрических пунктов (таблица 4.1). Ошибка носит название полной ошибки интерполяции.
Таблица 4.2 Полная ошибка интерполяции E
Таблица 4.2 показывает, что полная ошибка интерполяции должна быть меньше (в 22,5 раза) сечения карты аномалий Буге, а ошибка измерения должна быть в 24 раза меньше .
При детальной гравиметрической съемке пользуются приближенным линейным соотношением , где — коэффициент, зависящий от характера аномального поля. В равнинных районах для аномалий Буге принимают мГал/км, а в горных районах величина в 2-3 раза больше.
Величину
зависящую от плотности пунктов съемки и сложности аномального поля, называют чистой ошибкой интерполяции. Чтобы по возможности увеличить шаг съемки и уменьшить стоимость работ стараются уменьшить ошибку .
Чистую ошибку интерполяции можно оценить по формуле, полученной Ю.М. Нейманом, основанной на ковариационной функции Джордана (3.1):
где – дисперсия, – расстояние корреляции аномалий силы тяжести, — среднее расстояние между пунктами съемки.
По этой формуле можно найти расстояние между пунктами при планировании съемки, оценив величины и по изученному району со схожим рельефом и геологическим строением.
5.3 Косвенная интерполяция аномалий в свободном воздухе
Интерполирование аномалий в свободном воздухе между гравиметрическими пунктами может сопровождаться значительными ошибками из-за сильной зависимости аномалий от высоты. Ошибка легко может превышать 10 мГал даже при расстояниях в несколько километров. Поэтому часто применяют предложенный М.С. Молоденским метод косвенной интерполяции аномалий в свободном воздухе, основанный на различии характера поля аномалий в свободном воздухе и Буге.
Это различие иллюстрируют гравиметрические карты на рис. 5.2.
Рис. 5.2. Участок неравномерной гравиметрической съемки (Японские о-ва).
а – аномалии в свободном воздухе; сечение 10 мГал. б – аномалии Буге, плотность 2,60 г/см3; сечение 5 мГал.
Как видно, сечение карты аномалий Буге меньше, а изоаномалы более плавные и монотонные, чем на карте аномалий в свободном воздухе. Поэтому интерполирование аномалий Буге на определяемые пункты будет точнее интерполирования аномалий в свободном воздухе.
Переход к искомой аномалии в свободном воздухе осуществляется прибавлением поправки за притяжение промежуточного слоя
Поправка при плотности составит примерно 0,10·H мГал. Если высоту пункта определять по топографической карте, то даже считая ошибку определения высоты в 2 м при сечении рельефа 5 м на карте масштаба 1:25000, получим погрешность поправки 0,2 мГал, что не скажется на точности результата косвенной интерполяции.
5.4. Ошибка представительства
Современные схемы вычисления элементов аномального поля по гравиметрической съемке предусматривают применение средних значений аномалий силы тяжести по трапециям стандартных размеров. Точность этих средних значений называют ошибкой представительства, поскольку среднее значение аномалии характеризует аномальное поле всей трапеции.
Ошибка представительства – это среднее квадратическое уклонение аномалий силы тяжести на гравиметрических пунктах трапеции от средней аномалии :
Ошибки средних аномалий значительно меньше ошибки представительства. Ее величина зависит от размеров трапеции и сложности аномального поля. Если нанести на гравиметрическую карту прямоугольную сетку так, чтобы на каждую ячейку приходился один пункт, то зависимость ошибки представительства от размера ячейки описывается эмпирическими формулами
где – стороны ячейки, в которой находится один гравиметрический пункт, – коэффициенты, зависящие от сложности аномального поля. В равнинном районе с небольшими изменениями аномалии принимают .
Вторую формулу называют формулой де Грааф-Хантера (1935 г.).
Для оценки ошибки представительства Л.В. Огородовой (1987 г.) предложена эмпирическая формула
основанная на ковариационной функции Джордана (3.1),
где – дисперсия, — расстояние корреляции аномалий силы тяжести, — расстояние между гравиметрическими пунктами.
При увеличении расстояния между пунктами ошибка представительства растет быстрее ошибки интерполяции, а при они примерно одинаковы.
На рис. 5.3 показана гравиметрическая изученность и распределение по трапециям ошибки представительства.
Рис. 5.3. Изученность севера о. Мадагаскар и окружающих акваторий (а); число гравиметрических пунктов в одноградусных трапециях, средняя аномалия в свободном воздухе и ошибка представительства (б)
Литература
1. Огородова Л.В., Шимбирев Б.П., Юзефович А.П. Гравиметрия – М.:, Недра, 1978 г., –325с.
2. Юзефович А.П. Поле силы тяжести и его изучение. — М.: Изд-во. МИИГАиК, 2014. –194 с.
3. ГКИНП (ГНТА) — 04-122-03 Инструкция по развитию высокоточной государственной гравиметрической сети России, Москва, ЦНИИГАиК, 2004

Ошибка — репрезентативность

Cтраница 1

Ошибки репрезентативности делятся на случайные и систематические. Случайные ошибки возникают вследствие того, что выборочная совокупность недостаточно точно воспроизводит всю совокупность вследствие несплошного характера наблюдения. Случайные ошибки могут быть доведены до незначительных размеров, как это показано далее, а главное, размеры и пределы их можно определить с достаточной точностью на основании закона больших чисел. На этом законе базируется теория выборочного метода.
 [1]

Ошибки репрезентативности, т.е. расхождения между данными выборочного наблюдения и данными всей совокупности, могут быть получены только при несплошном наблюдении, они про-изводны от самой сути выборочного наблюдения. При этом существуют и, соответственно, аудиторы должны различать две разные группы ошибок репрезентативности: случайные и систематические.
 [2]

Ошибки репрезентативности также бывают случайными и систематическими. Случайные ошибки репрезентативности возникают, если отобранная совокупность неполно воспроизводит совокупность в целом. Величина этих ошибок может быть оценена.
 [3]

Ошибка Д является ошибкой репрезентативности ( представительства) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть ее ( выборка), отобранная случайно. Эту ошибку часто называют случайной ошибкой репрезентативности. Ее не следует путать с систематической ошибкой репрезентативности, появляющейся в результате нарушения принципа случайности при отборе элементов в выборку.
 [4]

При прочих равных условиях ошибка репрезентативности возрастает по мере увеличения вариабельности объектов изучаемой совокупности и уменьшается при увеличении объема выборки.
 [5]

В отличие от ошибок регистрации ошибки репрезентативности характерны только для несплошного наблюдения. Они возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит генеральную совокупность в целом.
 [6]

Разность между результатами выборочного и сплошного наблюдения называется ошибками репрезентативности.
 [7]

После проведения выборки рассчитывают возможные ошибки выборочных показателей ( ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.
 [8]

Очень часто малоопытный социолог не улавливает разницы между проблемой ошибки репрезентативности выборки и ошибки вывода из данного конкретного распределения в рамках выборочной совокупности.
 [9]

Если разность между ошибками регистрации этих видов обследования превысит ошибку репрезентативности, то общая ошибка при несплошном наблюдении может оказаться меньше, чем ошибка регистрации сплошного наблюдения. Особенно вероятен такой результат при выборочном наблюдении.
 [10]

Ошибки наблюдения подразделяются на два вида: ошибки регистрации и ошибки репрезентативности.
 [11]

Ошибки статистического наблюдения могут быть разбиты на две группы: ошибки репрезентативности и ошибки регистрации.
 [12]

Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.
 [13]

Поэтому при несплошном обследовании общая ошибка наблюдения является суммой ошибки регистрации и ошибки репрезентативности. Однако это отнюдь не означает, что при любом несплошном наблюдении ошибка будет больше, чем при сплошном.
 [14]

Отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности называется ошибкой репрезентативности.
 [15]

Страницы:  

   1

   2

---

Подборка по базе: Слайды из лекции для семинара 6 (дискретные случайные величины, план-конспект лекции с поварами.docx, Презентация по лекции 1.pdf, Бухучет за 4 лекции.pptx, К лекции 1.pptx, вопросы к лекции 1.docx, Мини-тест к лекции №2 по дисциплине _Экономическая культура и фи, Мини-тест к лекции №3 по дисциплине _Экономическая культура и фи, Котлы лекции.docx, Гражданский процесс Практическое задание к лекции 4.doc

---

Здесь есть ответы на некоторые лекции по истории, а также на промежуточные тесты по ТПЭФМ

Можно воспользоваться поиском вопросов по ключевым словам.

• Срок засекречивания сведений, составляющих государственную тайну, не должен превышать 30 лет

Нельзя засекречивать информацию о:

+чрезвычайных происшествиях и катастрофах, угрожающих жизни граждан

выпуске и поставке вооружения

средствах и методах разведывательной деятельности

запасах и объемах добычи металлов платиновой группы

• Судебная система включает в себя:

  федеральные суды общей юрисдикции

  суды (мировые судьи и конституционные (уставные) суды) субъектов РФ

  все ответы неверны

  все ответы правильны

  Конституционный Суд РФ

  систему арбитражных судов

  Наверное все

• Какие существуют степени секретности сведений, составляющих государственную тайну?

  для служебного пользования

  секретно

  совершенно секретно

  особой важности

  чрезвычайно важно

• Секретно, совершенно секретно, особой важности — правильные ответы

Какие юридические последствия влечет допуск к государственной тайне?

право на дополнительный отпуск

право на досрочную пенсию

досрочное расторжение трудового договора
+процентная надбавка к заработной плат

Государственную тайну составляют сведения о:

чрезвычайных происшествиях и катастрофах, угрожающих безопасности и здоровью граждан, и их последствиях
+состоянии здоровья высших должностных лиц Российской Федерации

фактах нарушения прав и свобод человека и гражданина

фактах нарушения законности органами государственной власти и их должностными лицами
+лицах, сотрудничающих или сотрудничавших на конфиденциальной основе с органами, осуществляющими разведывательную, контрразведывательную и оперативно-розыскную деятельность

1) Да
2) 1240
3) Даниил Александрович
4) Тевтонский орден
5) Ярослав Вселодавич
6) Владимиро-суздальское княжество
7) представители полузависимого населения
разгром новгородцев и подписание мирного договора
9) от падения Западной Римской империи
10) Василий Шуйский
11) Богдан Хмельницкий

1) политические свободы
Расстрел
2) Кадеты и октябристы
3) Военный коммунизм
4) отруб и хутор
5) Япония
6) меньшевик
7) Искра
Юденич
9) Март 1918
10) Россия практически выиграла (изм.)

1) январь 1924
2) монополия
3) Монголия
4) 23 августа 39
5) Румыния, Финляндия, Венгрия
6) Тегенеран
7) Курильские острова
Чичерин
9) Освобождения Праги
10) 28 сентября 39 года
11) Прибалтика и Молдавия

1) Варшавский договор и Взаимопомощь
2) Вывод советских войск объедение Германии
3) Первый секретарь ЦК КПСС
4) 20
5) Либерман
6) Ельцин
7) Борьба с доходами и я — скорость социально-экономического развития страны
август 1991
9) Рейган
10) ликвидация аппарата массовых репрессий и отмена однопартийной системы
11) Андропов
12) пенсия колхозникам и бесплатное образование в вузах

1) Кочубей, Новосильцев, Чарторыйский
2) Суд присяжных и состязательность судебного процесса
3) Лейпцигская битва
4) Киселёв
5) Герцен
6) синдикаты
7) получала полную автономию
Северный Кавказ, Финляндия, Закавказье
9) Германия и Австро-Венгрия, и Российская империя (изм.)

1) 17 августа 1998

1) 17 августа 1998
2) 26 марта 2000
3) Гайдар
4) сентябрь 2001
5) развитая концепция социализма и первая чеченская война
6) август 2008 (изм.)

1) Исполнительной
2) всенародный референдум
3) 6 лет
4) нет
5) национально-территориальному
6) исполнительной

• Какие юридические последствия влечет допуск к государственной тайне?

  право на дополнительный отпуск

  право на досрочную пенсию

  досрочное расторжение трудового договора
  +процентная надбавка к заработной плат

20 апрѣля

Задача линейного программирования
1. всегда ставится на максимум
2. всегда ставится на минимум
+3. может ставиться как на максимум, так и на минимум

Задача линейного программирования неразрешима, если
1. у нее не ограничена ОДП
+2. у нее не ограничена целевая функция
3. у нее ограничена целевая функция
4. у нее нет допустимых планов
5. у нее ограничена ОДП

Сколько допустимых планов может иметь задача линейного программирования (не целочисленная)?
0 или 1
всегда 1
+0, 1 или бесконечное множество

Ограничения задачи линейного программирования могут быть
1. только неравенствами
+2. уравнениями и/или нестрогими неравенствами
3. только уравнениями
4. любыми уравнениями и неравенствами
5. только строгими неравенствами

План, удовлетворяющий системе ограничений, называется…(напишите прилагательное в творительном падеже)
Ответ: допустимым

Оптимальное значение целевой функции называется… (в именительном падеже)
Ответ: оптимум (изм.)

Что такое оптимальный план задачи линейного программирования?

любая вершина области допустимых планов

+допустимый план, при подстановке которого в целевую функцию она принимает свое максимальное или минимальное значение

план, с рассмотрения которого следует начать решение задачи (изм.)

Что такое область допустимых планов задачи линейного программирования?
1. произвольный набор допустимых планов
2. полуплоскость, в которой находятся допустимые планы
+3. вся совокупность допустимых планов

По какой причине задача линейного программирования может не иметь решения?
1. только если целевая функция не ограничена
2. только если область допустимых планов пуста
+3. если целевая функция не ограничена или если область допустимых планов пуста

8 мая

• Что такое производная функции?
  1. Отношение приращения функции к приращению аргумента
  2. Приращение функции при изменении аргумента
  +3. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю
  4. Отношение приращения аргумента к приращению функции

• Отметьте верные утверждения:
  1. степень аргумента функции можно выносить за знак производной
  +2. производная сложной функции равна производной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной
  3. производная частного двух функций равна частному производных этих функций, если знаменатель не равен нулю
  4. производная постоянной равна нулю
• Вычислить производную функции y=(x+2)/(x-3) при x=4
  Ответ 0
• у = 100х. y’ =
  Ответ 100

• Вычислить производную функции cosx2
  1. y=2cosx
  2. у=2sinx
  +3. y=-2cosx*2sinx=-sin2x

• В каких случаях можно в точке менять местами символы предела и функции?
  1. Для функции, имеющей предел в точке хо
  2. Для возрастающей функции
  3. Всегда
  +4. Для непрерывной в точке хо функции

• В каких случаях функция имеет в точке х0 устранимый разрыв I рода?
  1. Если не существует конечный предел функции в этой точке.
  2. Если не существует хотя бы один из конечных односторонних пределов функции слева или справа.
  3. Если существуют, но не совпадают конечные пределы функции слева и справа в точке х0.
  +4. Если пределы функции слева и справа в точке хо конечны и совпадают, но не равны значению функции в этой точке

9 мая

• Если точка является точкой локального максимума, то…(отметьте верные утверждения)
  1. в этой точке производная положительна
  2. при переходе через эту точку производная функции меняет знак с минуса на плюс
  +3. при переходе через эту точку производная функции меняет знак с плюса на минус
  4. это критическая точка
  5. в этой точке вторая производная положительна
• Градиент функции 7х1 — х2 имеет координаты:
  1. (7; 1)
  2. (7х1; х2)
  +3. (7; -1)

• Какая из перечисленных функций является линейной функцией трех переменных
  1) z=√(х1∙х2∙х3)
  2) z=5×1+3×2+7
  3) z=x1+2×2
  +4) z=5×1+3×2-x3+10
  5) z=4x+5y

• Отметьте верные утверждения:
  +1. плоскость – двумерное координатное пространство
  2. любое множество содержит свои граничные точки
  +3. если к открытому шару присоединить сферу того же радиуса с тем же центром, то будет получен замкнутый шар
  4. любое множество содержит свои внешние точки
  +5. для шара любая точка соответствующей сферы (с тем же центром и радиусом) является граничной

10 мая

• Отметьте правильные утверждения о градиенте и линиях уровня линейной функции двух переменных.
  +1. линии уровня параллельны друг другу
  2. градиент и линия уровня параллельны друг другу
  +3. градиент и линия уровня перпендикулярны друг другу

• Точка n-мерного пространства – это
  1. совокупность n вещественных чисел, расположенных в произвольном порядке вещественное число
  2. только упорядоченная совокупность n натуральных чисел
  +3. упорядоченная совокупность n вещественных чисел
  4. натуральное число

• Функция является z=√(х1∙х2∙х3)
  1. функцией двух переменных
  +2. функцией трех переменных
  3. линейной
  +4. нелинейной
  5. функцией четырех переменных (изм.)

• лекция 16
• Абсолютный прирост в рядах динамики исчисляется как ___ уровней ряда
  +разность
  сумма
  частное
  произведение (изм.)

• 10. В теории статистики при изучении рядов динамики выделяют …
  Укажите не менее двух вариантов ответа
  +A. сезонные колебания
  +B. тренд
  c. сглаженные колебания
  d. результаты интерполяции
• Моментным рядом динамики является ряд
  1)среднегодовой численности населения страны за последние десять лет
  +2)численность населения страны на 1 января каждого года
  3)урожайности зерновых культур за каждый год
  4)затрат средств на охрану труда за 2000-2007гг.

• Относительный показатель динамики – это __
  абсолютный прирост
  размах вариации
  удельный вес в %
  +темп роста в %
• Относительный показатель структуры — это ___
  разность между долями
  +удельный вес в %
  темп прироста в %
  темп роста в %

• Плавное и устойчивое изменение уровней явления во времени, свободное от случайных колебаний
  1. размахом (амплитудой)
  2. модой
  +3. трендом
• Ряд динамики это –
  +1. Числовые значения статистического показателя, представленные во временной последовательности
  2. Показатель, который характеризует, во сколько раз данный уровень ряда больше начального (базисного) или предшествующего (цепного) уровня или какую долю от них составляет
  3. Разделение множества единиц изучаемой совокупности на группы по отдельным существенным для них признакам

• По средней ___ определяется средний уровень интервального ряда динамики
  +1. арифметической
  2. геометрической
  3. квадратической
  4. хронологической

• 136. В статистической практике средние темпы роста уровней ряда динамики можно вычислить по следующим данным…
  +а) средние темпы роста +б) цепные темпы роста в) базисный абсолютный прирост
  г) цепные абсолютные приросты (изм.)

• ЛЕКЦИЯ 18
• Относительный показатель структуры – это ___
  1. абсолютный прирост
  2. относительный прирост
  +3. удельный вес в %
  4. темп роста в %

• Расчет коэффициента детерминации невозможен без значения коэффициента
  1. Ассоциации
  2. Эластичности
  +3. Корреляции
  4. Контингенции
• Форма организации системы, которая состоит из отдельных элементов и связей между ними это
  1. Методика +2. Структура
  3. Задача
• Назовите основное преимущество фасетной классификации:
  +1. недостаточно полное использование емкости
  2. слабая гибкость
  3. гибкость структуры ее построения
• Особая форма сопоставления структуры одной и той же величины признака, характеризуемой с двух разных сторон или в двух различных аспектах это
  +1. Баланс
  2. Ряд
  3. Рост

• Разграничение общей статистической совокупности на группы качественно однородных единиц, называется
  1. классификацией
  +2. группировкой
  3. группировочный признак
  4. сводкой
• Группировка, в которой качественно неоднородная совокупность делится на отдельные, качественно однородные группы и на этой основе выявляются типы социально-экономических явлений, называется
  +1. типологической
  2. комбинированной
  3. аналитической
  4. структурной
• Сумма относительных показателей структуры, рассчитанных по одной совокупности, должна быть _____
  +1. строго равной 100%
  2. меньше 100%
  3. меньше 100% или равной 100%
  4. больше 100%

• Если темп роста оплаты труда составил в 2007 г.- 107,5%, в 2008 г.- 108%, то в среднем заработная
  +16,1 %

• Статистическая совокупность – это
  в) реально существующее множество однородных элементов, обладающих общими признаками и внутренней связью;

• ПРОМЕЖУТОЧНЫЙ ТЕСТ
• Группировка, в которой качественно неоднородная совокупность делится на отдельные, качественно однородные группы и на этой основе выявляются типы социально-экономических явлений, называется
  1. аналитической
  2. комбинированной
  3. структурной
  +4. типологической
  Группировка, которая решает задачу выявления и характеристики социально-экономических типов, называется
  1. комбинированной
  2. структурной
  3. аналитической
  +4. типологической
  Если темп роста оплаты труда составил в 2007г. – 107,5%, в 2008г. – 108%, то заработная плата за два года увеличилась на…% 16.1 (изм.)

Индекс, который рассматривается в виде сравнения обобщенных величин (совокупности единиц в целом), называют
+1. сводным
2. индивидуальным
3. территориальным
4. средним

• В статистике используются … измерители
  1. Качественные и расчетные
  2. Количественные и неколичественные
  3. Количественные и качественные
  +4. Стоимостные и натуральные
• В теории статистики при изучении рядов динамики выделяют
  +1. сезонные колебания
  2. смешанные колебания
  3. результат интерполяции
  +4. тренд
• В ящике 2 синих и 3 красных шара. Последовательно, один за другим, берут 2 шара. Какова вероятность того, что второй шар синий, если первый оказался красным?
  Ответ 0.5
• Величина интервала в ряде распределения определяется______
  1. верхней границей интервала
  2. нижней границей интервала
  3. по формуле Стерджесса
  +4. разностью верхней и нижней границ интервала

• Из корзины, содержащей 2 красных и 3 зелёных яблока, переложили наугад одно яблоко в корзину, содержащую 3 красных и 6 зелёных. Найти вероятность вынуть после этого красное яблоко из второй корзины. 0.34
• Индекс цен по методу Пааше рассчитывается с использованием весов
  1. отчетного и базисного периода
  2. базисного периода
  +3. отчетного периода
  4. без использования весов
• Исследование взаимосвязей варьирующих признаков в пределах однородной совокупности называется ______ группировкой.
  1. множественной
  +2. аналитической
  3. структурной
  4. типологической

Какая из случайных величин не является дискретной?
1. объем продаж молока за день (в пакетах)
+2. объем продаж разливного молока за день
3. количество покупателей молока за день

• Какие из следующих утверждений относительно дискретной случайной вели-чины верны?
  +1. Множество её значений дискретное или счётное.
  2. Она не может принимать отрицательные значения.
  3. Её значения непрерывно меняются на некотором промежутке.
  +4. Её значения изолированы друг от друга.
  5. Её значения обязательно целые.

• Какова вероятность, что при подбрасывании игральной кости выпадет число очков, кратное трём? (ответ в десятичных дробях с точностью до сотых) 0.33

• Коэффициент вариации является … показателем вариации
  1. Натуральным
  2. Средним
  3. Абсолютным
  +4. Относительным
• Мода в ряде распределения — это ____
  1. среднее значение признака в совокупности
  +2. наиболее часто встречающееся значение признака в совокупности
  3. разность между максимальным и минимальным значениями
  4. наибольшее значение признака в совокупности
• Моментным рядом динамики является ряд
  1. урожайности зерновых культур за каждый год
  2. затраты средств на охрану труда за 2000-2007 гг.
  +3. численности населения страны на 1 января каждого года
  4. среднегодовой численности страны за последние 10 лет
• Может ли в схеме испытаний Бернулли факт наступления события А в одном из опытов влиять на возможность его появления в остальных опытах?
  1. Всегда влияет.
  2. Не влияет только при малой вероятности события А.
  3. Влияет только при большом числе опытов.
  +4. Не может влиять
• Отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности называется
  +1. Доля выборки
  2. Единица
  3. Отбор
• Ошибка представительства так же называется
  1. Ошибка совокупности
  +2. Ошибка репрезентативности
  3. Среднеквадратическая ошибка
• По количеству ступеней отбора выборка делится на
  1. Длинную и короткую
  +2. Одноступенчатая и многоступенчатую
  3. Моментную и постоянную

Сколько значений может принимать дискретная случайная величина?
1. всегда бесконечное число значений
+2. конечное или бесконечное число значений
3. только конечное число значений

• Стоимостные измерители позволяют
  1. используются в тех случаях, когда единицы измерения соответствуют потребительским свойствам изучаемых явлений.
  +2. дать денежную оценку изучаемым явлениям и процессам
  3. характеризуют изменение уровней сложных социально – экономических показателей во времени

• Что называется ошибкой первого рода?
  +1. Ошибка, в результате которой отвергается правильная основная гипотеза Н0 и принимается ложная Н1
  2. Ошибка в расчётах, приводящая к фатальным последствиям, например, взрыву АЭС
  3. Ошибка, в результате которой принимается ложная основная гипотеза Н0 и отвергается правильная конкурирующая гипотеза Н1

• Что такое условная вероятность?
  +1. Вероятность некоторого события, при условии, что другое событие произошло.
  2. Вероятность, оцененная экспертом при определенных условиях.
  3. Недостоверная оценка вероятности события.

• Ширина интервалов в рядах распределения может быть равной и неравной
  +1. да, верно
  2. нет, всегда равной

• Являются ли несовместными события «цена товара более 100 руб.» и «цена товара менее 50 руб.»?
  1. Нет
  2. Информации для ответа недостаточно
  +3. Да

• Какое событие является противоположным событию «все филиалы фирмы прошли аудиторскую проверку»?
  1. Не все филиалы фирмы прошли аудиторскую проверку.
  2. Один филиал фирмы прошел аудиторскую проверку.
  3. Несколько филиалов фирмы прошли аудиторскую проверку.
  +4. Все филиалы фирмы не прошли аудиторскую проверку.

• По трём районам города имеются следующие данные (на конец года):
  Район Число отделений
  сбербанка Среднее число вкладов в
  отделении Средний размер
  вклада в рублях
  1 4 1376 2780
  2 9 1559 3251
  3 5 1315 2565Чему будет равен средний размер вклада в Сбербанке (в рублях) в целом по городу? 2978.97

• Предприятие планировало увеличить выпуск продукции в 2013 г. по сравнению с 2012 г. на 17 %. Фактический же объем выпуска составил 113,4 % от прошлогоднего уровня. Относительный показатель реализации плана в % равен 96.9

вчера

• Чему равен среднегодовой объем реализации сахара населению России за 2014-2016 в тысячах тонн?
  Годы Продано сахара, тыс.тонн
  2014 2905
  2015 2585
  2016 2647 Ответ 2712

• ПРОМЕЖУТОЧНЫЙ ТЕСТ 1
• Градиент функции 7х1 — х2 имеет координаты:
  1. (7; 1)
  2. (7х1; х2)
  +3. (7; -1)
• Вычислить производную функции cosx2
  1. y=2cosx
  2. у=2sinx
  +3. y=-2cosx*2sinx=-sin2x
• Можно ли решить систему
  5×1+2×2=0
  -x1+5×2=2
  по формулам Крамера? ДА
• Определитель
  2 3
  1 -5
  равен
  Ответ -13
• Определитель
  2 4
  6 2
  равен
  Ответ -20

• Вычислить определитель
  1 -5 3 0
  2 4 6 2
  1 2 3 4
  1 2 3 1 0

• Чему равен определитель матрицы
  4 0 0
  A = -7 5 0
  3 10 2 40
• Чему равен определитель матрицы
  10 3
  1 5 47
• Какая из перечисленных функций является линейной функцией трех переменных
  1) z=√(х1∙х2∙х3)
  2) z=5×1+3×2+7
  3) z=x1+2×2
  +4) z=5×1+3×2-x3+10
  5) z=4x+5y

• Квадратная матрица, в которой все недиагональные элементы равны нулю, — … (напишите прилагательное в именительном падеже) диагональная
• у = 100. y’ =100

• Элементы матрицы, у которых номер строки равен номеру столбца, — … элементы (напишите прилагательное в именительном падеже множественного числа) диагональные
• Точка n-мерного пространства – это
  1. совокупность n вещественных чисел, расположенных в произвольном порядке вещественное число
  2. только упорядоченная совокупность n натуральных чисел
  +3. упорядоченная совокупность n вещественных чисел
  4. натуральное число

• Если (x0,y0) – решение системы уравнений
  3x-4y=-20
  x-2y=-9
  то x0+y0 равно
  +1. 1.5
  2. — 1.5
  3. 5.5
  4. -5.5

Что называется линией уровня функции z=f(x,y)
+1. Множество всех точек плоскости, для которых функция имеет одно и то же значение
2. Множество всех точек плоскости, для которых совпадают значения частных производных функции по х и по у.
3. Множество всех точек плоскости, для которых градиент функции имеет одно и то же значение
4. Множество всех точек плоскости, для которых функция положительна

• Сколько значений может принимать дискретная случайная величина? +1. конечное или бесконечное число значений
  2. всегда бесконечное число значений
  3. только конечное число значений (изм.)

• Определить тип функции f(x)=ln(1+x)/(1-x)
  1. нечетная
  2. четная
  +3. общего вида
• Определить тип функции f(x)=x4/cosx-√(1-x2) четная
• Определить тип функции f(x)=cosx+x2
  1. нечетная
  +2. четная
  3. общего вида

Может ли график непрерывной функции иметь вертикальные асимптоты? да

Обозначим (x0; y0) Решение системы
x1-x2=-4
2×1+x2=-5
Найти x0+y0 -4

• Можно ли решить систему
  x1+2×2+3×3=6
  4×1+5×2+6×3=15
  7×1+8×2+9×3=24
  методом обратной матрицы нет

• Если все элементы матрицы равны нулю, то эта матрица — … (напишите прилагательное в именительном падеже) нулевая

• Если все элементы квадратной матрицы ниже (или выше) главной диагонали равны нулю, то эта матрица – … (напишите прилагательное в именительном падеже) треугольная

Выберите правильное утверждение.
1. Производная отношения двух функций равна отношению их производных.
+2. Производная от суммы нескольких функций равна сумме их производных.
3. Производная от произведения нескольких функций равна сумме их производных.
4. Производная от произведения нескольких функций равна произведению их производных.

Матрица
1 2
A = 4λ-1 6
вырождена при λ равном 1

Даны матрицы
1 2 3 1 2
A = 4 5 6 , B = 3 4
5 6
Найти элемент С12 матрицы C=AB 28

Даны матрицы
2 -3 -4 1
A = 0 1 , B = 0 2
Тогда A+В равно -2 -2 0 3

Дана матрица
1 2 3
A = 4 1 2
3 4 1
Найти элемент b13 матрицы B=2AT-A 3
Выберите правильное утверждение.
1. Производная отношения двух функций равна отношению их производных.
+2. Производная от суммы нескольких функций равна сумме их производных.
3. Производная от произведения нескольких функций равна сумме их производных.
4. Производная от произведения нескольких функций равна произведению их производных. (изм.)

Корень уравнения
1 2
3 4 = 2x
равен 5

|А| = 8. Чему равно число |АТ|?
Ответ 8

|А| = 8. Матрица В получена из матрицы А перестановкой местами двух столбцов. Чему равно число |В|?
Ответ -8
Выбрать, какие значения не может принять ранг матрицы размера:
1. 4
+2. 1.5
+3. -2
4. 3
5. 6 (изм.)

сего дня

 Если точка является точкой локального экстремума, то…(отметьте верные утверждения)
+1. таких точек может быть несколько на одном и том же промежутке
+2. производная в этой точке равна нулю или не существует
3. такая точка всегда только одна на одном и том же промежутке
4. в этой точке всегда достигается наибольшее или наименьшее значение функции на всей области определения
+5. в некоторой ее окрестности значения функции всегда не больше (или всегда не меньше), чем значение функции в этой точке

Если функция дифференцируема в точке, то…(отметьте верные утверждения)
1. она не имеет производную в этой точке
+2. она имеет производную в этой точке
3. в этой точке производная равна нулю
+4. ее производная существует при любых значениях аргумента

Какое из утверждений о функции f(x)=2/(x+5) верно?
1. Функция имеет устранимый разрыв I рода в точке х=-5
2. Функция непрерывна на всей числовой оси
3. Функция имеет неустранимый разрыв I рода в точке х=-5
4. Функция имеет разрыв II рода в точке х=5
+5. Функция имеет разрыв II рода в точке х=-5

Может ли график непрерывной функции иметь вертикальные асимптоты
нет

Может ли горизонтальная асимптота графика функции иметь вид х=а
нет

Что называется линией уровня функции z=f(x,y)
+1. Множество всех точек плоскости, для которых функция имеет одно и то же значение
2. Множество всех точек плоскости, для которых совпадают значения частных производных функции по х и по у.
3. Множество всех точек плоскости, для которых градиент функции имеет одно и то же значение
4. Множество всех точек плоскости, для которых функция положительна

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

2. Ошибки выборочного наблюдения

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.

Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:

где µ_x– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µ_x зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:

В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.

Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:

Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности ^x и величину предельной ошибки этой средней ^?_x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.

Данный текст является ознакомительным фрагментом.