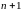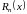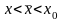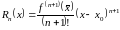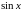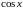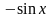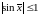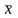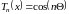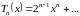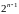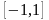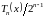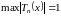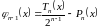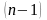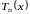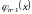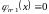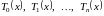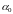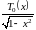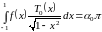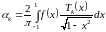Ошибка приближения ряда тейлора - Не ошибается лишь тот, кто ничего не делает!

Погрешность по формуле тейлора

Задача. Оценить с помощью формулы Тейлора абсолютную погрешность приближенной формулы:

Решение. Для получения оценки абсолютной погрешности нужно оценить остаточный член

Остаточный член в форме Лагранжа:

Где

Тогда по формуле Тейлора с остаточным членом в форме Лагранжа имеем:

Где

Найдем

Учитывая условие , из которого следует, что получаем:

Это и есть искомая оценка абсолютной погрешности приближенной формулы при

Ответ: .

< Предыдущая		Следующая >

Источник

По мере того, как степень полинома Тейлора увеличивается, он приближается к правильной функции. Это изображение показывает грех Икс и его тейлоровские приближения полиномами степени 1, 3, 5, 7, 9, 11, и 13 в Икс = 0.

Часть цикла статей о

Исчисление

Основная теорема
Интегральное правило Лейбница

Пределы функций
Непрерывность

Теорема о среднем значении
Теорема Ролля

Дифференциальный

Определения
Производная (обобщения ) Дифференциальный бесконечно малый функции общий
Концепции
Обозначение дифференциации Вторая производная Неявное дифференцирование Логарифмическое дифференцирование Связанные ставки Теорема Тейлора
Правила и личности
Сумма Товар Цепь Мощность Частное Правило L’Hôpital Обратный Генерал Лейбниц Формула Фаа ди Бруно

интеграл

Определения
Списки интегралов Интегральное преобразование
Первообразный интеграл (неподходящий ) Интеграл Римана Интеграция Лебега Контурная интеграция Интеграл от обратных функций
Интеграция
Запчасти Диски Цилиндрические оболочки Замена (тригонометрический, Weierstrass, Эйлер ) Формула Эйлера Неполные фракции Изменение порядка Формулы приведения Дифференцируя знаком интеграла

Серии

Тесты сходимости
Геометрический (арифметико-геометрический ) Гармонический Чередование Мощность Биномиальный Тейлор
Предел слагаемого (тест на срок) Соотношение Корень интеграл Прямое сравнение Сравнение пределов Чередование серий Конденсация Коши Дирихле Авель

Вектор

Теоремы
Градиент Расхождение Завиток Лапласиан Производная по направлению Идентичности
Градиент Зелень Стокса Расхождение обобщенный Стокса

Многовариантный

Формализмы
Матрица Тензор Внешний вид Геометрический
Определения
Частная производная Кратный интеграл Линейный интеграл Поверхностный интеграл Объемный интеграл Якобиан Гессен

Специализированный

Дробное
Маллявин
Стохастик
Вариации

Глоссарий исчисления

Глоссарий исчисления
Список тем по математике

В математика, то Серия Тейлор из функция является бесконечная сумма терминов, которые выражаются через функции производные в одной точке. Для большинства обычных функций функция и сумма ее ряда Тейлора в этой точке равны. Серии Тейлора названы в честь Брук Тейлор который ввел их в 1715 г.

Если ноль — это точка, в которой рассматриваются производные, ряд Тейлора также называется Серия Маклорена, после Колин Маклорен, который широко использовал этот особый случай из серии Тейлора в 18 веке.

В частичная сумма сформированный п первый член ряда Тейлора — это многочлен степени п это называется пth Полином Тейлора функции. Полиномы Тейлора — это приближения функции, которые обычно становятся лучше при п увеличивается. Теорема Тейлора дает количественные оценки ошибки, вносимой использованием таких приближений. Если ряд Тейлора функции равен сходящийся, его сумма равна предел из бесконечная последовательность полиномов Тейлора. Функция может отличаться от суммы ее ряда Тейлора, даже если ее ряд Тейлора сходится. Функция аналитический в какой-то момент Икс если он равен сумме своего ряда Тейлора по некоторой открытый интервал (или же открытый диск в комплексная плоскость ) содержащий Икс. Это означает, что функция аналитична в каждой точке интервала (или круга).

Определение

Серия Тейлора настоящий или же комплексная функция ж (Икс) то есть бесконечно дифференцируемый в настоящий или же комплексное число а это степенной ряд

${ displaystyle f (a) + { frac {f '(a)} {1!}} (xa) + { frac {f' '(a)} {2!}} (xa) ^ {2} + { frac {f '' '(a)} {3!}} (xa) ^ {3} + cdots,}$

куда п! обозначает факториал из п. В более компактном сигма-обозначение, это можно записать как

${ displaystyle sum _ {n = 0} ^ { infty} { frac {f ^ {(n)} (a)} {n!}} (x-a) ^ {n},}$

куда ж^(п)(а) обозначает пth производная из ж оценивается в момент а. (Производная нулевого порядка от ж определяется как ж сам и (Икс − а)⁰ и 0! оба определены как 1.)

Когда а = 0, серию также называют Серия Маклорена.^[1]

Примеры

Серия Тейлора для любого многочлен — это сам многочлен.

Серия Маклорена для 1/1 − Икс это геометрическая серия

${ Displaystyle 1 + х + х ^ {2} + х ^ {3} + cdots,}$

поэтому серия Тейлора для 1/Икс в а = 1 является

${ displaystyle 1- (x-1) + (x-1) ^ {2} - (x-1) ^ {3} + cdots.}$

Интегрируя приведенный выше ряд Маклорена, мы находим ряд Маклорена для ln (1 — Икс), куда пер обозначает натуральный логарифм:

${ displaystyle -x - { tfrac {1} {2}} x ^ {2} - { tfrac {1} {3}} x ^ {3} - { tfrac {1} {4}} x ^ {4} - cdots.}$

Соответствующий ряд Тейлора для пер Икс в а = 1 является

${ displaystyle (x-1) - { tfrac {1} {2}} (x-1) ^ {2} + { tfrac {1} {3}} (x-1) ^ {3} - { tfrac {1} {4}} (x-1) ^ {4} + cdots,}$

и, в более общем плане, соответствующий ряд Тейлора для пер Икс в произвольной ненулевой точке а является:

${ displaystyle ln a + { frac {1} {a}} (xa) - { frac {1} {a ^ {2}}} { frac { left (xa right) ^ {2}} {2}} + cdots.}$

Серия Маклорена для экспоненциальная функция е^Икс является

${ displaystyle { begin {align} sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} & = { frac {x ^ {0}} { 0!}} + { Frac {x ^ {1}} {1!}} + { Frac {x ^ {2}} {2!}} + { Frac {x ^ {3}} {3! }} + { frac {x ^ {4}} {4!}} + { frac {x ^ {5}} {5!}} + cdots & = 1 + x + { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {6}} + { frac {x ^ {4}} {24}} + { frac {x ^ {5}} { 120}} + cdots. End {align}}}$

Приведенное выше разложение справедливо, поскольку производная от е^Икс относительно Икс это также е^Икс, и е⁰ равно 1. Это оставляет условия (Икс − 0)^п в числителе и п! в знаменателе для каждого члена в бесконечной сумме.

История

Греческий философ Зенон рассмотрел проблему суммирования бесконечного ряда для достижения конечного результата, но отклонил это как невозможное;^[2] результат был Парадокс Зенона. Потом, Аристотель предложил философское разрешение парадокса, но математическое содержание, по-видимому, оставалось неразрешенным, пока не было рассмотрено Архимед, как это было до Аристотеля досократическим атомистом Демокрит. Это было через Архимеда метод истощения что бесконечное количество прогрессивных подразделений может быть выполнено для достижения конечного результата.^[3] Лю Хуэй несколько столетий спустя независимо использовал аналогичный метод.^[4]

В XIV веке самые ранние примеры использования рядов Тейлора и близких к ним методов были даны Мадхава Сангамаграмы.^[5]^[6] Хотя никаких записей о его работах не сохранилось, более поздние работы Индийские математики предполагают, что он обнаружил ряд частных случаев из серии Тейлора, в том числе для тригонометрические функции из синус, косинус, касательная, и арктангенс. В Керальская школа астрономии и математики далее расширил свои работы с помощью различных расширений серий и рациональных приближений до 16 века.

В 17 веке Джеймс Грегори также работал в этой области и опубликовал несколько серий Маклорена. Однако только в 1715 г. был наконец предоставлен общий метод построения этих рядов для всех функций, для которых они существуют. Брук Тейлор,^[7] в честь которого теперь назван сериал.

Серия Маклорен была названа в честь Колин Маклорен, профессор из Эдинбурга, опубликовавший частный случай результата Тейлора в 18 веке.

Аналитические функции

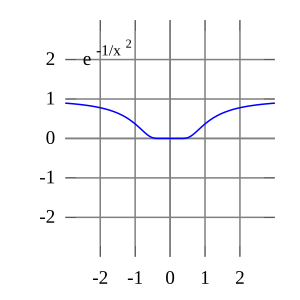
Функция е^{(−1/Икс²)} не аналитический в Икс = 0: ряд Тейлора идентично 0, хотя функция — нет.

Если ж (Икс) дается сходящимся степенным рядом в открытом диске (или интервале действительной прямой) с центром в б в комплексной плоскости это называется аналитический на этом диске. Таким образом, для Икс на этом диске, ж дается сходящимся степенным рядом

$f (x) = sum _ {n = 0} ^ { infty} a_ {n} (x-b) ^ {n}.$

Дифференциация по Икс формула выше п раз, затем установка Икс = б дает:

${ frac {f ^ {(n)} (b)} {n!}} = a_ {n}$

и поэтому разложение в степенной ряд согласуется с рядом Тейлора. Таким образом, функция аналитична в открытом круге с центром в б тогда и только тогда, когда его ряд Тейлора сходится к значению функции в каждой точке диска.

Если ж (Икс) равна сумме своего ряда Тейлора для всех Икс в комплексной плоскости это называется весь. Многочлены, экспоненциальная функция е^Икс, а тригонометрические функции синус и косинус являются примерами целых функций. Примеры неполных функций включают квадратный корень, то логарифм, то тригонометрическая функция касательная и обратная ей, арктан. Для этих функций ряды Тейлора не сходиться если Икс далеко от б. То есть серия Тейлора расходится в Икс если расстояние между Икс и б больше, чем радиус схождения. Ряд Тейлора можно использовать для вычисления значения всей функции в каждой точке, если значение функции и всех ее производных известно в одной точке.

Использование ряда Тейлора для аналитических функций включает:

Частичные суммы ( Полиномы Тейлора ) ряда можно использовать как приближение функции. Эти приближения хороши, если включено достаточно много членов.
Дифференцирование и интегрирование степенных рядов может выполняться последовательно по каждому члену, что делает его особенно простым.
An аналитическая функция однозначно продолжается до голоморфная функция на открытом диске в комплексная плоскость. Это делает машины комплексный анализ имеется в наличии.
(Усеченный) ряд может использоваться для численного вычисления значений функции (часто путем преобразования полинома в Чебышевская форма и оценивая его с помощью Алгоритм Кленшоу ).
Алгебраические операции можно легко проделать с представлением степенного ряда; например, Формула Эйлера следует из разложений в ряд Тейлора для тригонометрических и экспоненциальных функций. Этот результат имеет фундаментальное значение в таких областях, как гармонический анализ.
Аппроксимации с использованием первых нескольких членов ряда Тейлора могут сделать неразрешимые в противном случае проблемы возможными для ограниченной области; этот подход часто используется в физике.

Ошибка аппроксимации и сходимость

Синусоидальная функция (синий цвет) близко аппроксимируется своим полиномом Тейлора степени 7 (розовый) для полного периода с центром в начале координат.

Многочлены Тейлора для ln (1 + Икс) обеспечивают только точные приближения в диапазоне −1 < Икс ≤ 1. За Икс > 1, Многочлены Тейлора более высокой степени дают худшие приближения.

Приближения Тейлора для ln (1 + Икс) (чернить). За Икс > 1, приближения расходятся.

Изображение справа — точное приближение грех Икс вокруг точки Икс = 0. Розовая кривая — многочлен седьмой степени:

$sin left (x right) приблизительно x - { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} - { frac {x ^ {7}} {7!}}. !$

Погрешность этого приближения не более |Икс|⁹/9!. В частности, для −1 < Икс < 1, ошибка меньше 0,000003.

Напротив, также показано изображение функции натурального логарифма. ln (1 + Икс) и некоторые из его многочленов Тейлора вокруг а = 0. Эти приближения сходятся к функции только в области −1 < Икс ≤ 1; вне этой области полиномы Тейлора более высокой степени хуже приближения для функции.

В ошибка понесенные при приближении функции ее пМногочлен Тейлора -й степени называется остаток или же остаточный и обозначается функцией р_п(Икс). Теорема Тейлора может быть использована для оценки размер остатка.

В общем, ряды Тейлора не обязательно сходящийся вообще. И на самом деле набор функций со сходящимся рядом Тейлора представляет собой скудный набор в Fréchet space из гладкие функции. И даже если ряд Тейлора функции ж сходится, его предел не обязательно должен быть равен значению функции ж (Икс). Например, функция

${ displaystyle f (x) = { begin {cases} e ^ {- { frac {1} {x ^ {2}}}} & { text {if}} x neq 0 0 & { текст {if}} x = 0 end {case}}}$

является бесконечно дифференцируемый в Икс = 0, и там все производные равны нулю. Следовательно, ряд Тейлора ж (Икс) о Икс = 0 тождественно нулю. Тем не мение, ж (Икс) не является нулевой функцией, поэтому не равен ее ряду Тейлора вокруг начала координат. Таким образом, ж (Икс) является примером неаналитическая гладкая функция.

В реальный анализ, этот пример показывает, что есть бесконечно дифференцируемые функции ж (Икс) чьи серии Тейлора нет равно ж (Икс) даже если они сходятся. Напротив, голоморфные функции учился в комплексный анализ всегда имеют сходящийся ряд Тейлора, и даже ряд Тейлора мероморфные функции, которые могут иметь особенности, никогда не сходятся к значению, отличному от самой функции. Сложная функция е^−1/z², однако, не приближается к 0, когда z приближается к 0 по мнимой оси, так что это не непрерывный в комплексной плоскости и его ряд Тейлора не определен в 0.

В более общем плане каждая последовательность действительных или комплексных чисел может выглядеть как коэффициенты в ряд Тейлора бесконечно дифференцируемой функции, определенной на вещественной прямой, как следствие Лемма Бореля. В результате радиус схождения ряда Тейлора может быть нулевым. Существуют даже бесконечно дифференцируемые функции, определенные на вещественной прямой, ряды Тейлора которых всюду имеют радиус сходимости 0.^[8]

Функцию нельзя записать в виде ряда Тейлора с центром в необычность; в этих случаях часто все же можно добиться разложения в ряд, если допустить также отрицательные степени переменной Икс; видеть Серия Laurent. Например, ж (Икс) = е^{−1/Икс²} можно записать как серию Лорана.

Обобщение

Однако есть обобщение^[9]^[10] ряда Тейлора, который сходится к значению самой функции для любого ограниченный непрерывная функция на (0,∞), используя исчисление конечные разности. В частности, имеется следующая теорема в силу Эйнар Хилле, что для любого т > 0,

$lim _ {h to 0 ^ {+}} sum _ {n = 0} ^ { infty} { frac {t ^ {n}} {n!}} { frac { Delta _ {h } ^ {n} f (a)} {h ^ {n}}} = f (a + t).$

Здесь Δ^п
_час это п-й конечно-разностный оператор с размером шага час. Этот ряд в точности совпадает с рядом Тейлора, за исключением того, что вместо дифференцирования появляются разделенные различия: ряд формально подобен ряду Серия Ньютон. Когда функция ж аналитический в а, члены ряда сходятся к членам ряда Тейлора и в этом смысле обобщают обычный ряд Тейлора.

В общем, для любой бесконечной последовательности а_я, выполняется тождество степенного ряда:

$sum _ {n = 0} ^ { infty} { frac {u ^ {n}} {n!}} Delta ^ {n} a_ {i} = e ^ {- u} sum _ {j = 0} ^ { infty} { frac {u ^ {j}} {j!}} A_ {i + j}.$

Так, в частности,

${ displaystyle f (a + t) = lim _ {h to 0 ^ {+}} e ^ {- { frac {t} {h}}} sum _ {j = 0} ^ { infty } f (a + jh) { frac { left ({ frac {t} {h}} right) ^ {j}} {j!}}.}.}$

Серия справа — это ожидаемое значение из ж (а + Икс), куда Икс это Распределенный по Пуассону случайная переменная что принимает значение jh с вероятностью е^−т/час·(т/час)^j/j!. Следовательно,

${ displaystyle f (a + t) = lim _ {h to 0 ^ {+}} int _ {- infty} ^ { infty} f (a + x) dP _ {{ frac {t} {h}}, h} (x).}$

В закон больших чисел означает, что тождество выполнено.^[11]

Список некоторых общих функций серии Маклорена

Далее следуют несколько важных расширений серии Maclaurin.^[12] Все эти расширения действительны для сложных аргументов Икс.

Экспоненциальная функция

В экспоненциальная функция $e ^ {x}$ (с базой е ) имеет серию Маклорена

${ displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2} } {2!}} + { Frac {x ^ {3}} {3!}} + Cdots}$

Он сходится для всех Икс.

Натуральный логарифм

В натуральный логарифм (с базой е ) имеет серию Маклорена

${ displaystyle { begin {align} ln (1-x) & = - sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n}} = - x- { frac {x ^ {2}} {2}} - { frac {x ^ {3}} {3}} - cdots, ln (1 + x) & = sum _ {n = 1} ^ { infty} (- 1) ^ {n + 1} { frac {x ^ {n}} {n}} = x - { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {3}} - cdots. end {align}}}$

Они сходятся для . (Кроме того, серия для ln (1 — Икс) сходится для Икс = −1, а серия для ln (1 + Икс) сходится для Икс = 1.)

Геометрическая серия

В геометрическая серия и его производные имеют ряд Маклорена

${ displaystyle { begin {align} { frac {1} {1-x}} & = sum _ {n = 0} ^ { infty} x ^ {n} { frac {1} { (1-x) ^ {2}}} & = sum _ {n = 1} ^ { infty} nx ^ {n-1} { frac {1} {(1-x) ^ {3 }}} & = sum _ {n = 2} ^ { infty} { frac {(n-1) n} {2}} x ^ {n-2}. end {выравнивается}}}$

Все сходятся для . Это частные случаи биномиальный ряд приведено в следующем разделе.

Биномиальный ряд

В биномиальный ряд это степенной ряд

${ displaystyle (1 + x) ^ { alpha} = sum _ {n = 0} ^ { infty} { binom { alpha} {n}} x ^ {n}}$

коэффициенты которого являются обобщенными биномиальные коэффициенты

${ displaystyle { binom { alpha} {n}} = prod _ {k = 1} ^ {n} { frac { alpha -k + 1} {k}} = { frac { alpha ( alpha -1) cdots ( alpha -n + 1)} {n!}}.}$

(Если п = 0, этот продукт пустой продукт и имеет значение 1.) Он сходится при для любого действительного или комплексного числа α.

Когда α = −1, по сути, это бесконечный геометрический ряд, упомянутый в предыдущем разделе. Особые случаи α = 1/2 и α = −1/2 дай квадратный корень функция и ее обратный:

${ displaystyle { begin {align} (1 + x) ^ { frac {1} {2}} & = 1 + { tfrac {1} {2}} x - { tfrac {1} {8} } x ^ {2} + { tfrac {1} {16}} x ^ {3} - { tfrac {5} {128}} x ^ {4} + { tfrac {7} {256}} x ^ {5} - ldots, (1 + x) ^ {- { frac {1} {2}}} & = 1 - { tfrac {1} {2}} x + { tfrac {3} {8}} x ^ {2} - { tfrac {5} {16}} x ^ {3} + { tfrac {35} {128}} x ^ {4} - { tfrac {63} {256 }} x ^ {5} + ldots. end {align}}}$

Когда только линейный член сохраняется, это упрощает биномиальное приближение.

Тригонометрические функции

Обычный тригонометрические функции и их обратные имеют следующий ряд Маклорена:

${ displaystyle { begin {align} sin x & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} && = x - { frac {x ^ {3}} {3!}} + { Frac {x ^ {5}} {5!}} - cdots && { text {для всех }} x [6pt] cos x & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n)!}} x ^ {2n} && = 1 - { frac {x ^ {2}} {2!}} + { Frac {x ^ {4}} {4!}} - cdots && { text {для всех}} x [6pt] tan x & = sum _ {n = 1} ^ { infty} { frac {B_ {2n} (- 4) ^ {n} left (1-4 ^ {n} right)} {(2n)!}} X ^ {2n-1} && = x + { frac {x ^ {3}} {3}} + { frac {2x ^ {5}} {15}} + cdots && { text {for}} | x | <{ frac { pi} {2}} [6pt] sec x & = sum _ {n = 0} ^ { infty} { frac {(- 1) ^ {n} E_ {2n}} {(2n)!}} X ^ {2n} && = 1 + { frac {x ^ {2}} {2}} + { frac {5x ^ {4 }} {24}} + cdots && { text {for}} | x | <{ frac { pi} {2}} [6pt] arcsin x & = sum _ {n = 0} ^ { infty} { frac {(2n)!} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} && = x + { frac {x ^ {3}} {6}} + { frac {3x ^ {5}} {40}} + cdots && { text {for}} | x | leq 1 [6pt] arccos x & = { frac { pi} {2}} - arcsin x & = { frac { pi} {2}} - sum _ {n = 0} ^ { infty} { frac {(2n) !} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} && = { frac { pi} {2}} - x - { frac { x ^ {3}} {6}} - { frac {3x ^ {5}} {4 0}} - cdots && { text {for}} | x | leq 1 [6pt] arctan x & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {2n + 1}} x ^ {2n + 1} && = x - { frac {x ^ {3}} {3}} + { frac {x ^ {5}} {5} } - cdots && { text {for}} | x | leq 1, x neq pm i end {align}}}$

Все углы выражены в радианы. Цифры B_k появляясь в расширениях загар Икс являются Числа Бернулли. В E_k в расширении сек Икс находятся Числа Эйлера.

Гиперболические функции

В гиперболические функции имеют ряды Маклорена, тесно связанные с рядами для соответствующих тригонометрических функций:

${ displaystyle { begin {align} sinh x & = sum _ {n = 0} ^ { infty} { frac {x ^ {2n + 1}} {(2n + 1)!}} && = x + { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} + cdots && { text {для всех}} x [6pt] cosh x & = sum _ {n = 0} ^ { infty} { frac {x ^ {2n}} {(2n)!}} && = 1 + { frac {x ^ {2}} {2! }} + { frac {x ^ {4}} {4!}} + cdots && { text {для всех}} x [6pt] tanh x & = sum _ {n = 1} ^ { infty} { frac {B_ {2n} 4 ^ {n} left (4 ^ {n} -1 right)} {(2n)!}} x ^ {2n-1} && = x - { frac {x ^ {3}} {3}} + { frac {2x ^ {5}} {15}} - { frac {17x ^ {7}} {315}} + cdots && { text { for}} | x | <{ frac { pi} {2}} [6pt] operatorname {arsinh} x & = sum _ {n = 0} ^ { infty} { frac {(-1 ) ^ {n} (2n)!} {4 ^ {n} (n!) ^ {2} (2n + 1)}} x ^ {2n + 1} &&&& { text {for}} | x | leq 1 [6pt] operatorname {artanh} x & = sum _ {n = 0} ^ { infty} { frac {x ^ {2n + 1}} {2n + 1}} &&&& { text { for}} | x | leq 1, x neq pm 1 end {выровнено}}}$

Цифры B_k появляясь в сериале для танх Икс являются Числа Бернулли.

Расчет ряда Тейлора

Существует несколько методов вычисления ряда Тейлора большого числа функций. Можно попытаться использовать определение ряда Тейлора, хотя это часто требует обобщения формы коэффициентов в соответствии с очевидной закономерностью. В качестве альтернативы можно использовать такие манипуляции, как подстановка, умножение или деление, сложение или вычитание стандартных рядов Тейлора, чтобы построить ряд Тейлора функции, поскольку ряд Тейлора является степенным рядом. В некоторых случаях можно также получить ряд Тейлора, многократно применяя интеграция по частям. Особенно удобно использование системы компьютерной алгебры для расчета ряда Тейлора.

Первый пример

Чтобы вычислить полином Маклорена 7-й степени для функции

${ displaystyle f (x) = ln ( cos x), quad x in left (- { frac { pi} {2}}, { frac { pi} {2}} right )}$

сначала можно переписать функцию как

{ Displaystyle е (х) = пер { bigl (} 1 + ( соз х-1) { bigr)} !}

Ряд Тейлора для натурального логарифма (с использованием нотация большой O )

${ displaystyle ln (1 + x) = x - { frac {x ^ {2}} {2}} + { frac {x ^ {3}} {3}} + {O} left (x ^ {4} right) !}$

а для косинусной функции

${ displaystyle cos x-1 = - { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} - { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) !}$

Разложение последнего ряда имеет нулевой постоянный срок, что позволяет подставить вторую серию в первую и легко опустить члены более высокого порядка, чем 7-я степень, используя большой О обозначение:

${ Displaystyle { begin {align} е (х) & = ln { bigl (} 1 + ( соз х-1) { bigr)} & = ( соз х-1) - { tfrac {1} {2}} ( cos x-1) ^ {2} + { tfrac {1} {3}} ( cos x-1) ^ {3} + {O} left (( cos x-1) ^ {4} right) & = left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} - { frac {x ^ {6}} {720}} + {O} left (x ^ {8} right) right) - { frac {1} {2}} left (- { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} + {O} left (x ^ {6} right) right) ^ {2} + { frac {1} {3}} left (- { frac {x ^ {2}} {2}} + O left (x ^ {4} right) right) ^ {3} + {O } left (x ^ {8} right) & = - { frac {x ^ {2}} {2}} + { frac {x ^ {4}} {24}} - { frac {x ^ {6}} {720}} - { frac {x ^ {4}} {8}} + { frac {x ^ {6}} {48}} - { frac {x ^ {6 }} {24}} + O left (x ^ {8} right) & = - { frac {x ^ {2}} {2}} - { frac {x ^ {4}} { 12}} - { frac {x ^ {6}} {45}} + O left (x ^ {8} right). End {align}} !}$

Поскольку косинус — это даже функция, коэффициенты при всех нечетных степенях Икс, Икс³, Икс⁵, Икс⁷, … должно быть равно нулю.

Второй пример

Предположим, нам нужен ряд Тейлора в 0 функции

$g (x) = { frac {e ^ {x}} { cos x}}. !$

Для экспоненциальной функции

${ displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2} } {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots !}$

и, как в первом примере,

${ displaystyle cos x = 1 - { frac {x ^ {2}} {2!}} + { frac {x ^ {4}} {4!}} - cdots !}$

Предположим, что степенной ряд равен

${ displaystyle { frac {e ^ {x}} { cos x}} = c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots !}$

Тогда умножение на знаменатель и подстановка ряда косинуса дает

${ displaystyle { begin {align} e ^ {x} & = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + cdots right) cos x & = left (c_ {0} + c_ {1} x + c_ {2} x ^ {2} + c_ {3} x ^ {3} + c_ {4} x ^ {4} + cdots right) left (1 - { frac {x ^ {2}} {2!}} + { frac {x ^ {4}} {4!}} - cdots right) & = c_ {0} - { frac {c_ {0}} {2}} x ^ {2} + { frac {c_ {0}} {4!}} x ^ {4} + c_ {1} x - { frac {c_ {1}} {2}} x ^ {3} + { frac {c_ {1}} {4!}} x ^ {5} + c_ {2} x ^ {2} - { frac {c_ {2}} {2}} x ^ {4} + { frac {c_ {2}} {4!}} x ^ {6} + c_ {3} x ^ {3} - { frac {c_ {3}} {2}} x ^ {5} + { frac {c_ {3}} {4!}} X ^ {7} + c_ {4} x ^ {4} + cdots end {align}} !}$

Сбор условий до четвертого порядка доходности

${ displaystyle e ^ {x} = c_ {0} + c_ {1} x + left (c_ {2} - { frac {c_ {0}} {2}} right) x ^ {2} + слева (c_ {3} - { frac {c_ {1}} {2}} right) x ^ {3} + left (c_ {4} - { frac {c_ {2}} {2}} + { frac {c_ {0}} {4!}} right) x ^ {4} + cdots !}$

Ценности $c_ {i}$ можно найти путем сравнения коэффициентов с верхним выражением для $e ^ {x}$ , что дает:

${ displaystyle { frac {e ^ {x}} { cos x}} = 1 + x + x ^ {2} + { frac {2x ^ {3}} {3}} + { frac {x ^ {4}} {2}} + cdots. !}$

Третий пример

Здесь мы используем метод, называемый «косвенное расширение», чтобы расширить данную функцию. В этом методе используется известное разложение Тейлора экспоненциальной функции. Чтобы расширить (1 + Икс)е^Икс как серию Тейлора в Икс, воспользуемся известным рядом Тейлора функции е^Икс:

${ displaystyle e ^ {x} = sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {n!}} = 1 + x + { frac {x ^ {2} } {2!}} + { Frac {x ^ {3}} {3!}} + { Frac {x ^ {4}} {4!}} + Cdots.}$

Таким образом,

${ displaystyle { begin {align} (1 + x) e ^ {x} & = e ^ {x} + xe ^ {x} = sum _ {n = 0} ^ { infty} { frac { x ^ {n}} {n!}} + sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} {n!}} = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + Sum _ {n = 0} ^ { infty} { frac {x ^ {n + 1}} { n!}} & = 1+ sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {n!}} + sum _ {n = 1} ^ { infty} { frac {x ^ {n}} {(n-1)!}} = 1+ sum _ {n = 1} ^ { infty} left ({ frac {1} {n!} } + { frac {1} {(n-1)!}} right) x ^ {n} & = 1+ sum _ {n = 1} ^ { infty} { frac {n + 1} {n!}} X ^ {n} & = sum _ {n = 0} ^ { infty} { frac {n + 1} {n!}} X ^ {n}. End {выровнено}}}$

Ряд Тейлора как определения

Классически алгебраические функции определяются алгебраическим уравнением, а трансцендентные функции (включая те, что обсуждались выше) определяются некоторым свойством, которое выполняется для них, например дифференциальное уравнение. Например, экспоненциальная функция — функция, которая везде равна своей производной и принимает значение 1 в начале координат. Однако с равным успехом можно определить аналитическая функция своей серией Тейлора.

Ряды Тейлора используются для определения функций и «операторы «в различных областях математики. В частности, это верно в областях, где классические определения функций не работают. Например, используя ряды Тейлора, можно расширить аналитические функции на наборы матриц и операторов, такие как матричная экспонента или же матричный логарифм.

В других областях, таких как формальный анализ, удобнее работать напрямую с степенной ряд самих себя. Таким образом, можно определить решение дифференциального уравнения в качестве степенной ряд, который, как надеются доказать, является рядом Тейлора искомого решения.

Ряд Тейлора от нескольких переменных

Ряд Тейлора также может быть обобщен на функции более чем одной переменной с^[13]^[14]

${ displaystyle { begin {align} T (x_ {1}, ldots, x_ {d}) & = sum _ {n_ {1} = 0} ^ { infty} cdots sum _ {n_ { d} = 0} ^ { infty} { frac {(x_ {1} -a_ {1}) ^ {n_ {1}} cdots (x_ {d} -a_ {d}) ^ {n_ {d }}} {n_ {1}! cdots n_ {d}!}} , left ({ frac { partial ^ {n_ {1} + cdots + n_ {d}} f} { partial x_ {1} ^ {n_ {1}} cdots partial x_ {d} ^ {n_ {d}}}} right) (a_ {1}, ldots, a_ {d}) & = f ( a_ {1}, ldots, a_ {d}) + sum _ {j = 1} ^ {d} { frac { partial f (a_ {1}, ldots, a_ {d})} { частичный x_ {j}}} (x_ {j} -a_ {j}) + { frac {1} {2!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} { frac { partial ^ {2} f (a_ {1}, ldots, a_ {d})} { partial x_ {j} partial x_ {k}}} (x_ {j} -a_ {j}) (x_ {k} -a_ {k}) & qquad qquad + { frac {1} {3!}} sum _ {j = 1} ^ {d} sum _ {k = 1} ^ {d} sum _ {l = 1} ^ {d} { frac { partial ^ {3} f (a_ {1}, ldots, a_ {d})} { частичный x_ {j} partial x_ {k} partial x_ {l}}} (x_ {j} -a_ {j}) (x_ {k} -a_ {k}) (x_ {l} -a_ {l }) + cdots end {выровнены}}}$

Например, для функции это зависит от двух переменных, Икс и у, ряд Тейлора второго порядка о точке (а, б) является

${ Displaystyle f (a, b) + (xa) f_ {x} (a, b) + (yb) f_ {y} (a, b) + { frac {1} {2!}} { Big (} (xa) ^ {2} f_ {xx} (a, b) +2 (xa) (yb) f_ {xy} (a, b) + (yb) ^ {2} f_ {yy} (a, б) { Big)}}$

где нижние индексы обозначают соответствующие частные производные.

Разложение в ряд Тейлора второго порядка скалярнозначной функции более чем одной переменной можно компактно записать как

${ Displaystyle Т ( mathbf {x}) = е ( mathbf {a}) + ( mathbf {x} - mathbf {a}) ^ { mathsf {T}} Df ( mathbf {a}) + { frac {1} {2!}} ( mathbf {x} - mathbf {a}) ^ { mathsf {T}} left {D ^ {2} f ( mathbf {a}) right } ( mathbf {x} - mathbf {a}) + cdots,}$

куда D ж (а) это градиент из ж оценивается в Икс = а и D² ж (а) это Матрица Гессе. Применяя многоиндексная запись ряд Тейлора для нескольких переменных принимает вид

${ Displaystyle T ( mathbf {x}) = sum _ {| alpha | geq 0} { frac {( mathbf {x} - mathbf {a}) ^ { alpha}} { alpha !}} left ({ mathrm { partial} ^ { alpha}} f right) ( mathbf {a}),}$

что следует понимать как еще более сокращенный мультииндекс версия первого уравнения этого абзаца с полной аналогией для случая одной переменной.

Пример

Аппроксимация функции рядами Тейлора второго порядка (оранжевым цветом) ж (Икс,у) = е^Икс ln (1 + у) вокруг происхождения.

Чтобы вычислить разложение в ряд Тейлора второго порядка вокруг точки (а, б) = (0, 0) функции

${ Displaystyle е (х, у) = е ^ {х} пер (1 + у),}$

сначала вычисляются все необходимые частные производные:

${ displaystyle { begin {align} f_ {x} & = e ^ {x} ln (1 + y) [6pt] f_ {y} & = { frac {e ^ {x}} {1 + y}} [6pt] f_ {xx} & = e ^ {x} ln (1 + y) [6pt] f_ {yy} & = - { frac {e ^ {x}} { (1 + y) ^ {2}}} [6pt] f_ {xy} & = f_ {yx} = { frac {e ^ {x}} {1 + y}}. End {выровнено}} }$

Оценка этих производных в начале координат дает коэффициенты Тейлора

${ Displaystyle { begin {align} f_ {x} (0,0) & = 0 f_ {y} (0,0) & = 1 f_ {xx} (0,0) & = 0 f_ {yy} (0,0) & = - 1 f_ {xy} (0,0) & = f_ {yx} (0,0) = 1. end {выравнивается}}}$

Подставляя эти значения в общую формулу

${ Displaystyle { begin {align} T (x, y) = & f (a, b) + (xa) f_ {x} (a, b) + (yb) f_ {y} (a, b) & {} + { frac {1} {2!}} left ((xa) ^ {2} f_ {xx} (a, b) +2 (xa) (yb) f_ {xy} (a, b ) + (yb) ^ {2} f_ {yy} (a, b) right) + cdots end {align}}}$

производит

${ displaystyle { begin {align} T (x, y) & = 0 + 0 (x-0) +1 (y-0) + { frac {1} {2}} { Big (} 0 ( x-0) ^ {2} +2 (x-0) (y-0) + (- 1) (y-0) ^ {2} { Big)} + cdots & = y + xy- { frac {y ^ {2}} {2}} + cdots end {align}}}$

С ln (1 + у) аналитичен в |у| < 1, у нас есть

${ displaystyle e ^ {x} ln (1 + y) = y + xy - { frac {y ^ {2}} {2}} + cdots, qquad | y | <1.}$

Сравнение с рядом Фурье

Тригонометрический Ряд Фурье позволяет выразить периодическая функция (или функция, определенная на закрытом интервале [а,б]) как бесконечную сумму тригонометрические функции (синусы и косинусы ). В этом смысле ряд Фурье аналогичен ряду Тейлора, поскольку последний позволяет выразить функцию в виде бесконечной суммы полномочия. Тем не менее, две серии отличаются друг от друга в нескольких важных моментах:

Конечные усечения ряда Тейлора ж (Икс) о сути Икс = а все в точности равны ж в а. Напротив, ряд Фурье вычисляется путем интегрирования по всему интервалу, поэтому, как правило, нет такой точки, где все конечные усечения ряда являются точными.
Вычисление ряда Тейлора требует знания функции на произвольном малом район точки, тогда как вычисление ряда Фурье требует знания функции во всей ее области определения интервал. В определенном смысле можно сказать, что ряд Тейлора «локален», а ряд Фурье — «глобален».
Ряд Тейлора определен для функции, имеющей бесконечно много производных в одной точке, тогда как ряд Фурье определен для любой интегрируемая функция. В частности, функцию нельзя было нигде дифференцировать. (Например, ж (Икс) может быть Функция Вейерштрасса.)
Сходимость обоих рядов имеет очень разные свойства. Даже если ряд Тейлора имеет положительный радиус сходимости, полученный ряд может не совпадать с функцией; но если функция аналитическая, то ряд сходится точечно функции, и равномерно на каждом компактном подмножестве интервала сходимости. Что касается ряда Фурье, если функция интегрируемый с квадратом то ряд сходится в среднее квадратичное, но необходимы дополнительные требования для обеспечения поточечной или равномерной сходимости (например, если функция периодическая и класса C¹ тогда сходимость равномерная).
Наконец, на практике нужно аппроксимировать функцию конечным числом членов, скажем, многочленом Тейлора или частичной суммой тригонометрического ряда соответственно. В случае ряда Тейлора ошибка очень мала в окрестности точки, в которой она вычисляется, в то время как она может быть очень большой в удаленной точке. В случае ряда Фурье ошибка распределяется по области определения функции.

Смотрите также

Асимптотическое разложение
Производящая функция
Серия Мадхава
Интерполяция разделенной разности Ньютона
Аппроксимация Паде
Серия Puiseux
Оператор сдвига

Примечания

^ Томас и Финни 1996, §8.9
^ Линдберг, Дэвид (2007). Начало западной науки (2-е изд.). Издательство Чикагского университета. п. 33. ISBN 978-0-226-48205-7.
^ Клайн, М. (1990). Математическая мысль от древних до наших дней. Нью-Йорк: Издательство Оксфордского университета. стр.35 –37. ISBN 0-19-506135-7.
^ Boyer, C .; Мерцбах, У. (1991). История математики (Второе исправленное изд.). Джон Уайли и сыновья. стр.202–203. ISBN 0-471-09763-2.
^ «Ни Ньютон, ни Лейбниц — Предыстория исчисления и небесной механики в средневековой Керале» (PDF). MAT 314. Колледж Канисиуса. В архиве (PDF) из оригинала от 23.02.2015. Получено 2006-07-09.
^ С. Г. Дани (2012). «Древнеиндийская математика — конспект». Резонанс. 17 (3): 236–246. Дои:10.1007 / s12045-012-0022-у.
^ Тейлор, Брук (1715). Methodus Incrementorum Directa et Inversa [Прямые и обратные методы увеличения] (на латыни). Лондон. п. 21–23 (Предложение VII, Теория 3, Кор. 2). Переведено на английский язык Струик, Д. Дж. (1969). Справочник по математике 1200–1800 гг.. Кембридж, Массачусетс: Издательство Гарвардского университета. С. 329–332.
^ Рудин, Вальтер (1980), Реальный и комплексный анализ, Нью-Дели: Макгроу-Хилл, стр. 418, упражнение 13, ISBN 0-07-099557-5
^ Феллер, Уильям (1971), Введение в теорию вероятностей и ее приложения, Том 2 (3-е изд.), Wiley, стр. 230–232..
^ Хилле, Эйнар; Филлипс, Ральф С. (1957), Функциональный анализ и полугруппы, Публикации Коллоквиума AMS, 31, Американское математическое общество, стр. 300–327..
^ Феллер, Уильям (1970). Введение в теорию вероятностей и ее приложения. 2 (3-е изд.). п. 231.
^ Большинство из них можно найти в (Абрамовиц и Стегун 1970 ).
^ Ларс Хёрмандер (1990), Анализ дифференциальных операторов в частных производных, том 1, Springer, уравнение. 1.1.7 и 1.1.7 ′
^ Duistermaat; Колк (2010), Распространения: теория и приложения, Бирхаузер, гл. 6

внешняя ссылка

«Серия Тейлор», Энциклопедия математики, EMS Press, 2001 [1994]
Вайсштейн, Эрик В. «Серия Тейлор». MathWorld.
Полином Тейлора — практическое введение
Мадхава Сангамаграммы
«обсуждение метода Паркера-Сохацкого «
Еще одна визуализация Тейлора — где можно выбрать точку аппроксимации и количество производных
Возвращение к ряду Тейлора для численных методов в Численные методы для студентов STEM
Золушка 2: расширение Тейлора
Серия Тейлор
Обратные тригонометрические функции Ряд Тейлора
«Суть исчисления: серия Тейлора» — через YouTube.

Источник

Наиболее простым
и достаточно эффективным способом
приближения функций является использование
формулы Тейлора для их разложения в
степенной ряд. Пусть задана непрерывная
функция

,
имеющая непрерывные производные до
порядка

включительно. Такую функцию можно
разложить в некоторой окрестности точки

по степеням

по формуле Тейлора:

,
(3.1)

где

– остаточный член (ошибка, погрешность),
связанный с заменой при вычислении

бесконечного степенного ряда первыми
его

членами.

Ошибку ограничения
можно оценить по формуле,
где

:

Формула Тейлора
не только дает возможность организовать
численный метод вычисления значений
функции

,
но и позволяет оценить величину ошибки
приближения, возникающей в результате
ограничения количества рассматриваемых
членов ряда. При ее использовании
требуется определить точку

,
в окрестностях которой будет производиться
разложение функции, при этом следует
руководствоваться соображениями
точности представления коэффициентов
ряда (3.1) и величиной используемого
интервала области определения, внутри
которого будут производиться вычисления.

Рассмотрим
разложение в ряд Тейлора функции

.
Найдем соответствующие производные и
в результате получим последовательность
функций:

,

,
… . Если положить

,
то последовательность функций
преобразуется в ряд чисел 1, 0, –1, 0, 1, 0,
–1, 0, …, тогда по формуле (3.1) мы имеем:

Оценим величину
ошибки приближения при рассмотрении
первых четырех членов ряда

и

,

поскольку

для любых

.

Из полученной
оценки погрешности видно, что ошибка
приближения зависит от

и если не изменить число членов ряда в
представлении функции

,
то для достаточно больших

значение погрешности может превысить
1.

3.1.2. Полиномы Чебышева

Формула Тейлора
при разложении функции в степенной ряд
дает сходимость, зависящую от значения

.
Возникает идея поиска такого многочлена

,
чтобы максимальная ошибка приближения
функции

была бы наименьшей. Данная задача была
решена великим русским математиком
П.Л.Чебышевым и получила название задачи
о наилучшем приближении.

Пусть задана
некоторая функция

,
которую на отрезке

требуется приблизить многочленом

таким образом, чтобы

т.е. подобрать
такие коэффициенты

,
чтобы максимальная величина модуля
разности между

была наименьшей для любых

Определение.
Полиномом Чебышева называется многочлен
вида

,
где

.

Заметим, что
полиномы Чебышева не являются
тригонометрическими функциями, однако
доказательство данного утверждения
приводить не будем. Используя известные
формулы тригонометрии, найдем первые
три многочлена:

Для вычисления
многочленов Чебышева практичнее
использовать следующее рекуррентное
соотношение:

.
(3.2)

Свойства
многочленов Чебышева:

Учитывая формулу
(3.2), можно установить, что

,

,
то есть коэффициент
при старшей степени

многочлена Чебышева равен

.
Полиномы Чебышева

образуют ортогональный базис (с весом

)
на множестве функций, непрерывных на
отрезке

,
и удовлетворяют следующим равенствам:

(3.3)

3. Многочлены
Чебышева доставляют минимум максимальной
ошибки приближения, то есть являются
многочленами наилучшего приближения
для класса функции, непрерывных на
отрезке

.
Докажем данный факт.

Чебышев показал,
что точная верхняя грань (supremum,
супремум) многочлена

среди всех многочленов

с коэффициентом 1 при старшей степени

на отрезке

наименьшая. Действительно,

,
откуда

,
тогда

,
причем экстремумы принимают попеременно
положительные и отрицательные значения
на отрезке [–1,1], так как

– гармоническая функция. Количество
экстремумов равно

.
Рассмотрим разность:

,
которая является многочленом степени

(поскольку члены

уничтожаются). Если экстремальное
значение

меньше, чем у

,
то в

экстремальных точках полинома

функция

принимает по очереди положительные и
отрицательные значения. Следовательно,

имеет

действительных
корней, чего не тожет быть, так как
степень многочлена равна

.
Тогда выполняется тождество

или

Последнее свойство
полиномов Чебышева представляет большой
интерес для численного анализа. Если
какая-либо ошибка приближения может
быть выражена многочленом Чебышева
степени

,
то любое другое выражение для ошибки в
виде многочлена степени

,
имеющего тот же самый коэффициент при
старшей степени

,
будет иметь на отрезке [–1,1] большую
максимальную ошибку, чем чебышевское.

Практика
использования полиномов Чебышева для
решения задачи приближения функции

заключается в следующем. Поскольку
система функций

образует базис, то на отрезке [–1,1] любую
функцию можно представить как линейную
комбинацию

,

.
(3.4)

Коэффициенты
разложения можно определить, используя
свойство ортогональности (3.3) полиномов
Чебышева. Для определения

почленно умножим левую и правую часть
выражения (3.4) на

и проинтегрируем:

Учитывая
ортогональность, имеем:

или

.

Аналогично можно
вычислить остальные коэффициенты
разложения (3.4):

.
(3.5)

Единственной
проблемой разложения функции

по полиномам Чебышева является вычисление
достаточно сложных интегралов вида
(3.5).

Соседние файлы в папке 3-й семестр

Источник

Asked
6 years, 4 months ago

Viewed
108 times

$begingroup$

I know how to find the remainder or error of a taylor approximation at any given point, but what if:
f(x) = 2x³ — 4x + 7 is approximated to a quadratic polynomial function at x=c. What would be the maximum error of the approximation in the interval
|x-1|<1/4?

asked Feb 4, 2017 at 19:57

$endgroup$

You must log in to answer this question.

Browse other questions tagged

.

Источник

grizzly в сообщении #951685 писал(а):

(кстати, почему Вы пишете ?

Ну просто я по примеру в учебнике делаю, там так написано, хотя понятно, что $xi<3$ строго.

grizzly в сообщении #951685 писал(а):

Подумайте на досуге, при каких условиях ситуация становится ещё хуже, чем в Вашем примере, а при каких — лучше.

Я так понимаю , чем ближе точка $x$ к точке, в которой мы аппроксимировали функцию многочленом Тейлора (в моём примере,чем ближе к 0), тем оценка остаточного члена будет более адекватна, потому что для $xi$ будет меньший «разброс» значений.

Источник

Определение

Примеры

История

Аналитические функции

Ошибка аппроксимации и сходимость

Обобщение

Список некоторых общих функций серии Маклорена

Экспоненциальная функция

Натуральный логарифм

Геометрическая серия

Биномиальный ряд

Тригонометрические функции

Гиперболические функции

Расчет ряда Тейлора

Первый пример

Второй пример

Третий пример

Ряд Тейлора как определения

Ряд Тейлора от нескольких переменных

Пример

Сравнение с рядом Фурье

Смотрите также

Примечания

Рекомендации

внешняя ссылка

3.1.2. Полиномы Чебышева

You must log in to answer this question.

Browse other questions tagged .

Browse other questions tagged

.