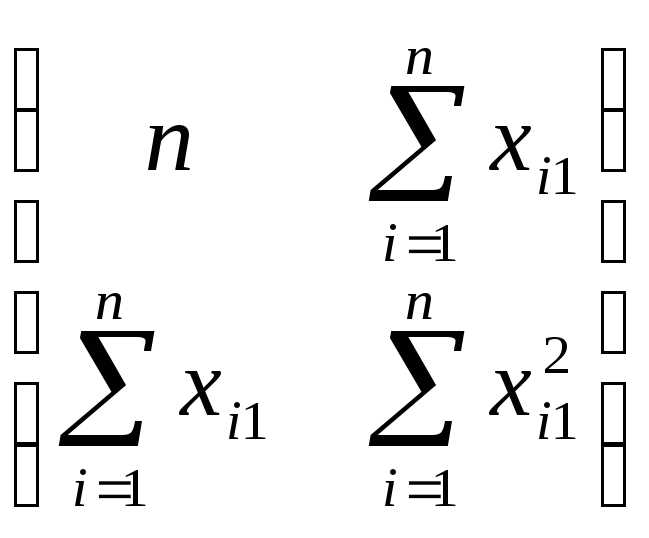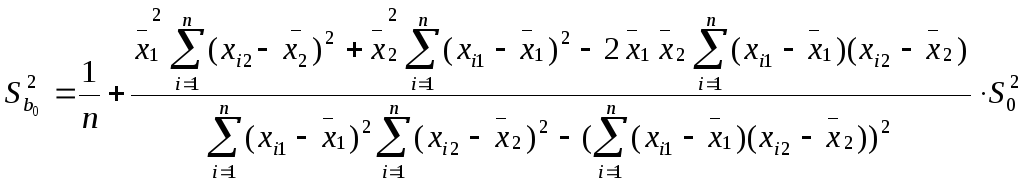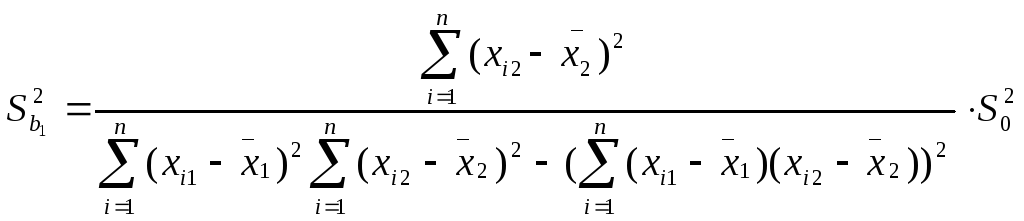Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
In statistics, regression is a technique that can be used to analyze the relationship between predictor variables and a response variable.
When you use software (like R, SAS, SPSS, etc.) to perform a regression analysis, you will receive a regression table as output that summarize the results of the regression. It’s important to know how to read this table so that you can understand the results of the regression analysis.
This tutorial walks through an example of a regression analysis and provides an in-depth explanation of how to read and interpret the output of a regression table.
A Regression Example
Suppose we have the following dataset that shows the total number of hours studied, total prep exams taken, and final exam score received for 12 different students:
To analyze the relationship between hours studied and prep exams taken with the final exam score that a student receives, we run a multiple linear regression using hours studied and prep exams taken as the predictor variables and final exam score as the response variable.
We receive the following output:
Examining the Fit of the Model
The first section shows several different numbers that measure the fit of the regression model, i.e. how well the regression model is able to “fit” the dataset.
Here is how to interpret each of the numbers in this section:
Multiple R
This is the correlation coefficient. It measures the strength of the linear relationship between the predictor variables and the response variable. A multiple R of 1 indicates a perfect linear relationship while a multiple R of 0 indicates no linear relationship whatsoever. Multiple R is the square root of R-squared (see below).
In this example, the multiple R is 0.72855, which indicates a fairly strong linear relationship between the predictors study hours and prep exams and the response variable final exam score.
R-Squared
This is often written as r2, and is also known as the coefficient of determination. It is the proportion of the variance in the response variable that can be explained by the predictor variable.
The value for R-squared can range from 0 to 1. A value of 0 indicates that the response variable cannot be explained by the predictor variable at all. A value of 1 indicates that the response variable can be perfectly explained without error by the predictor variable.
In this example, the R-squared is 0.5307, which indicates that 53.07% of the variance in the final exam scores can be explained by the number of hours studied and the number of prep exams taken.
Related: What is a Good R-squared Value?
Adjusted R-Squared
This is a modified version of R-squared that has been adjusted for the number of predictors in the model. It is always lower than the R-squared. The adjusted R-squared can be useful for comparing the fit of different regression models to one another.
In this example, the Adjusted R-squared is 0.4265.
Standard Error of the Regression
The standard error of the regression is the average distance that the observed values fall from the regression line. In this example, the observed values fall an average of 7.3267 units from the regression line.
Related: Understanding the Standard Error of the Regression
Observations
This is simply the number of observations our dataset. In this example, the total observations is 12.
Testing the Overall Significance of the Regression Model
The next section shows the degrees of freedom, the sum of squares, mean squares, F statistic, and overall significance of the regression model.
Here is how to interpret each of the numbers in this section:
Regression degrees of freedom
This number is equal to: the number of regression coefficients – 1. In this example, we have an intercept term and two predictor variables, so we have three regression coefficients total, which means the regression degrees of freedom is 3 – 1 = 2.
Total degrees of freedom
This number is equal to: the number of observations – 1. In this example, we have 12 observations, so the total degrees of freedom is 12 – 1 = 11.
Residual degrees of freedom
This number is equal to: total df – regression df. In this example, the residual degrees of freedom is 11 – 2 = 9.
Mean Squares
The regression mean squares is calculated by regression SS / regression df. In this example, regression MS = 546.53308 / 2 = 273.2665.
The residual mean squares is calculated by residual SS / residual df. In this example, residual MS = 483.1335 / 9 = 53.68151.
F Statistic
The f statistic is calculated as regression MS / residual MS. This statistic indicates whether the regression model provides a better fit to the data than a model that contains no independent variables.
In essence, it tests if the regression model as a whole is useful. Generally if none of the predictor variables in the model are statistically significant, the overall F statistic is also not statistically significant.
In this example, the F statistic is 273.2665 / 53.68151 = 5.09.
Significance of F (P-value)
The last value in the table is the p-value associated with the F statistic. To see if the overall regression model is significant, you can compare the p-value to a significance level; common choices are .01, .05, and .10.
If the p-value is less than the significance level, there is sufficient evidence to conclude that the regression model fits the data better than the model with no predictor variables. This finding is good because it means that the predictor variables in the model actually improve the fit of the model.
In this example, the p-value is 0.033, which is less than the common significance level of 0.05. This indicates that the regression model as a whole is statistically significant, i.e. the model fits the data better than the model with no predictor variables.
Testing the Overall Significance of the Regression Model
The last section shows the coefficient estimates, the standard error of the estimates, the t-stat, p-values, and confidence intervals for each term in the regression model.
Here is how to interpret each of the numbers in this section:
Coefficients
The coefficients give us the numbers necessary to write the estimated regression equation:
yhat = b0 + b1x1 + b2x2.
In this example, the estimated regression equation is:
final exam score = 66.99 + 1.299(Study Hours) + 1.117(Prep Exams)
Each individual coefficient is interpreted as the average increase in the response variable for each one unit increase in a given predictor variable, assuming that all other predictor variables are held constant. For example, for each additional hour studied, the average expected increase in final exam score is 1.299 points, assuming that the number of prep exams taken is held constant.
The intercept is interpreted as the expected average final exam score for a student who studies for zero hours and takes zero prep exams. In this example, a student is expected to score a 66.99 if they study for zero hours and take zero prep exams. Be careful when interpreting the intercept of a regression output, though, because it doesn’t always make sense to do so.
For example, in some cases, the intercept may turn out to be a negative number, which often doesn’t have an obvious interpretation. This doesn’t mean the model is wrong, it simply means that the intercept by itself should not be interpreted to mean anything.
Standard Error, t-stats, and p-values
The standard error is a measure of the uncertainty around the estimate of the coefficient for each variable.
The t-stat is simply the coefficient divided by the standard error. For example, the t-stat for Study Hours is 1.299 / 0.417 = 3.117.
The next column shows the p-value associated with the t-stat. This number tells us if a given response variable is significant in the model. In this example, we see that the p-value for Study Hours is 0.012 and the p-value for Prep Exams is 0.304. This indicates that Study Hours is a significant predictor of final exam score, while Prep Exams is not.
Confidence Interval for Coefficient Estimates
The last two columns in the table provide the lower and upper bounds for a 95% confidence interval for the coefficient estimates.
For example, the coefficient estimate for Study Hours is 1.299, but there is some uncertainty around this estimate. We can never know for sure if this is the exact coefficient. Thus, a 95% confidence interval gives us a range of likely values for the true coefficient.
In this case, the 95% confidence interval for Study Hours is (0.356, 2.24). Notice that this confidence interval does not contain the number “0”, which means we’re quite confident that the true value for the coefficient of Study Hours is non-zero, i.e. a positive number.
By contrast, the 95% confidence interval for Prep Exams is (-1.201, 3.436). Notice that this confidence interval does contain the number “0”, which means that the true value for the coefficient of Prep Exams could be zero, i.e. non-significant in predicting final exam scores.
Additional Resources
Understanding the Null Hypothesis for Linear Regression
Understanding the F-Test of Overall Significance in Regression
How to Report Regression Results
Значения стандартных
ошибок позволяет оценивать точность
эмпирических коэффициентов уравнений
регрессии и проверять выдвигаемые
относительно них гипотезы.
Выборочные дисперсии
эмпирических коэффициентов множественной
регрессии можно определить следующим
образом:
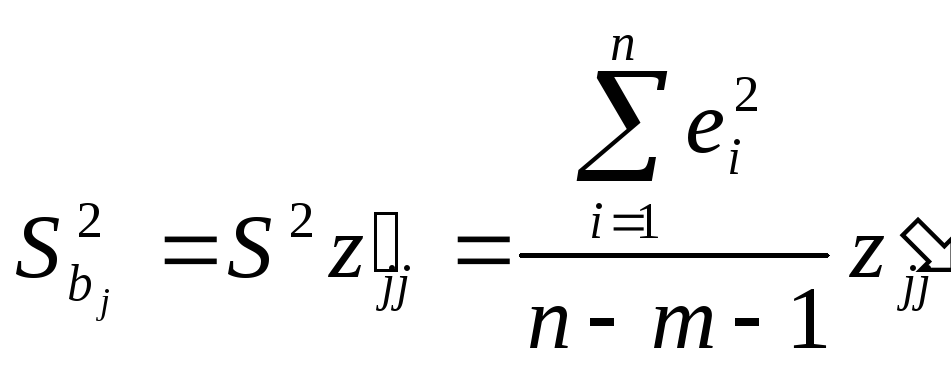
j
= 1,2,…,m (2.9)
Здесь z’jj — j-тый
диагональный элемент матрицы Z-1
= (XTX)-1.
Рассмотрим пример
с m=1,
где m — количество объясняющих переменных.
*
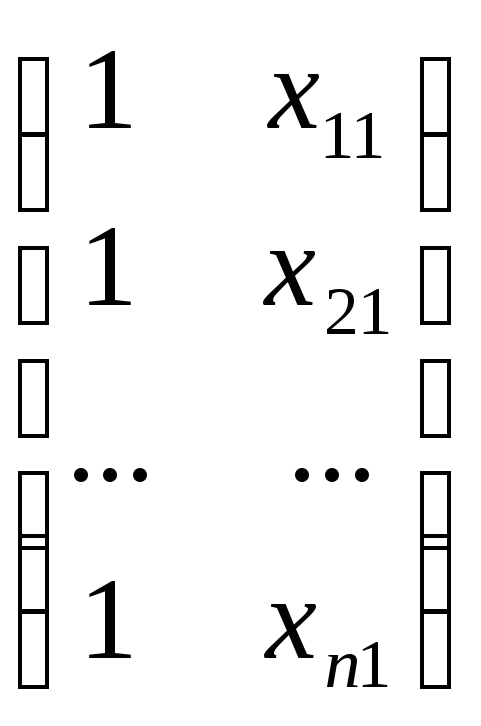
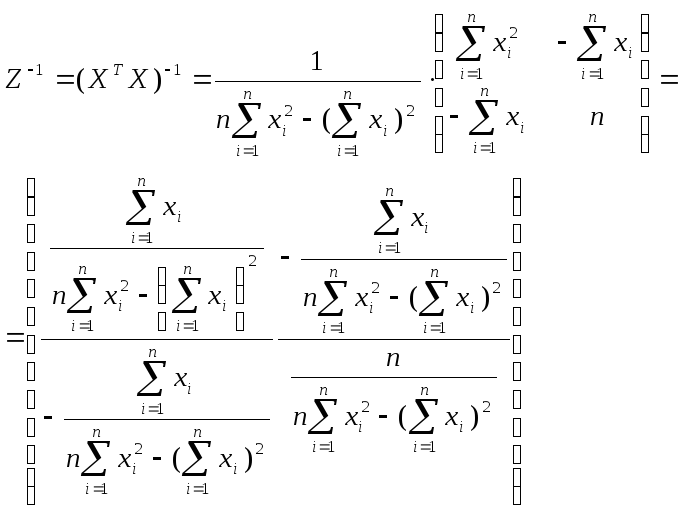
Найдем величину
обратной матрицы Z-1.
Она будет иметь следующий вид:
При этом:
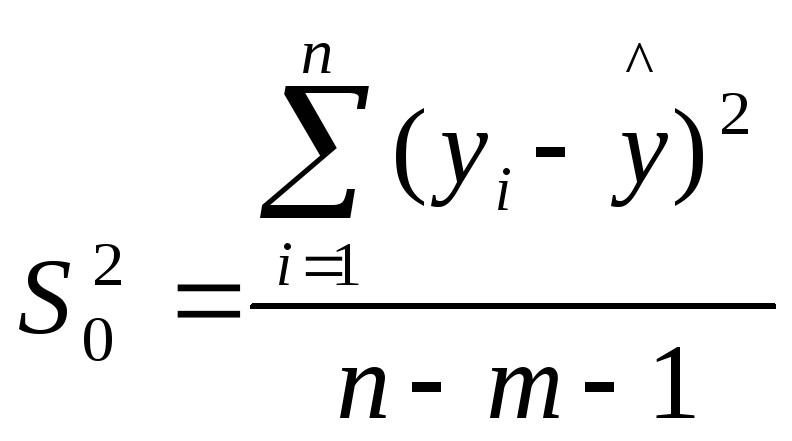
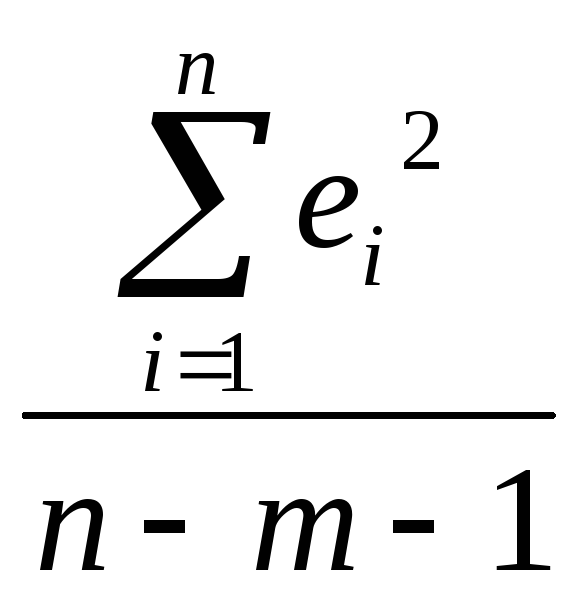
где m — количество
объясняющих переменных модели.
В частности, для
уравнения множественной регрессии:
Y = b0
+ b1X1
+ b2X2
с двумя объясняющими
переменными m=2
используются следующие формулы:
,
,
Здесь Sbj
— стандартная
ошибка коэффициента регрессии; S0
— стандартная
ошибка множественной регрессии
(несмещенная оценка).
По аналогии с
парной регрессией после определения
точечных оценок bj
коэффициентов
βj (j=1,2,…,m)
теоретического уравнения множественной
регрессии могут быть рассчитаны
интервальные оценки указанных
коэффициентов.
Доверительный
интервал, покрывающий с надежностью
(1-α)
неизвестное значение параметра βj,
определяется как:
(2.11)
Далее, как и в
случае парной регрессии, статистическая
значимость коэффициентов множественной
регрессии с m
объясняющими переменными проверяется
на основе t-статистики:
(2.12)
имеющей в данном
случае распределение Стьюдента с числом
степеней свободы
.
При требуемом уровне значимости
наблюдаемое значение t-статистики
сравнивается с критической точнойраспределения
Стьюдента.
В случае, если
,
то статистическая значимость
соответствующего коэффициента
множественной регрессии подтверждается.
Это означает, что факторXj
линейно связан с зависимой переменной
Y.
Если же установлен факт незначимости
коэффициента bj,
то рекомендуется исключить из уравнения
переменную Xj.
Это не приведет к существенной потере
качества модели, но сделает ее более
конкретной.
2.4. Проверка общего качества уравнения регрессии
После проверки
значимости каждого коэффициента
регрессии обычно проверяется общее
качество уравнения регрессии. Для этой
цели, как и в случае парной регрессии,
используется коэффициент детерминации
R2,
который в общем случае рассчитывается
по формуле:
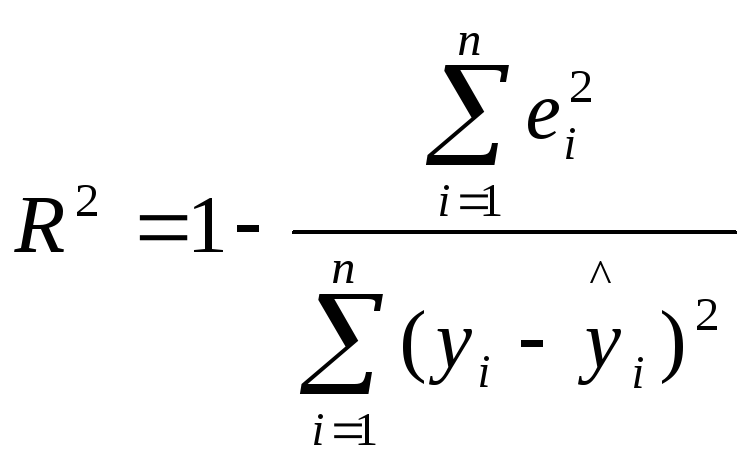
Коэффициент
детерминации характеризует тесноту
связи рассматриваемого набора факторов
с исследуемым признаком или, иначе,
оценивает тесноту совместного влияния
факторов на результат.
Для множественной
регрессии коэффициент детерминации
является неубывающей функцией от числа
объясняющих переменных. Добавление
новой объясняющей переменной никогда
не уменьшает значение R2.
Иногда при расчете
коэффициента детерминации для получения
несмещенных оценок в числителе и
знаменателе вычитаемой из единицы дроби
делается поправка на число степеней
свободы. Вводится так называемый
скорректированный (исправленный)
коэффициент детерминации:
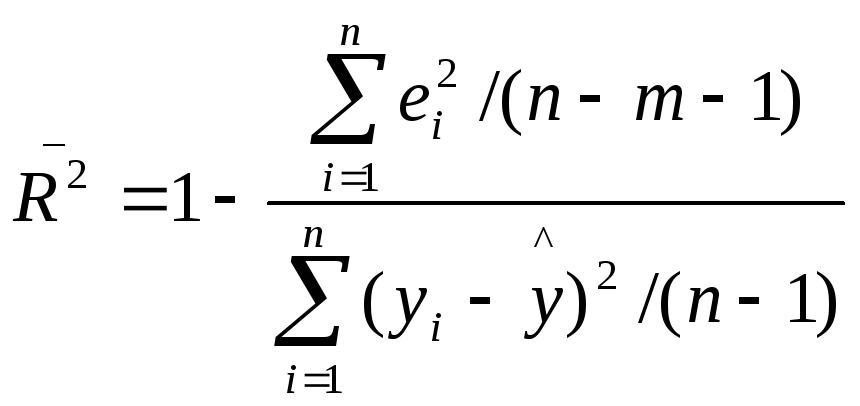
Соотношение может
быть представлено в следующем виде:
(2.15)
Из чего следует,
что
<
для
m
> 1. С ростом значения m
скорректированный коэффициент
детерминации
растет
медленнее, чем обычный коэффициент
детерминации
.
Другими словами, он корректируется в
сторону уменьшения с ростом числа
объясняющих переменных. Нетрудно
заметить, что
=
только при
.
может
принимать и отрицательные значения
(например, при
).
Доказано, что
увеличивается
при добавлении новой объясняющей
переменной тогда и только тогда, когдаt
– статистика
для этой переменной по модулю больше
единицы. Поэтому добавление в модель
новых объясняющих переменных осуществляется
до тех пор, пока растет скорректированный
коэффициент детерминации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
1.2.1. Стандартная ошибка оценки по регрессии
Обозначается как
Sy,xи вычисляется по формуле
Sy,x=.
Стандартная ошибка
оценки по регрессии показывает, на
сколько в среднем мы ошибаемся, оценивая
значение зависимой переменной по
найденному уравнению регрессии при
фиксированном значении независимой
переменной.
Квадрат стандартной
ошибки по регрессии является несмещенной
оценкой дисперсии 2,
т.е.
=
=
.
Дисперсия ошибок
характеризует воздействие в модели
(1.1) неучтенных факторов и ошибок.
1.2.2. Оценка
значимости уравнения регрессии
(дисперсионный анализ регрессии)
Для оценки
значимости уравнения регрессии
устанавливают, соответствует ли выбранная
модель анализируемым данным. Для этого
используется дисперсионный анализ
регрессии. Основная его посылка – это
разложение общей суммы квадратов
отклонений
на
составляющие. Известно, что такое
разложение имеет вид
=
+
.
Второе слагаемое
в правой части разложения – это часть
общей суммы квадратов отклонений,
объясняемая действием случайных и
неучтенных факторов. Первое слагаемое
этого разложения – это часть общей
суммы квадратов отклонений, объясняемая
регрессионной зависимостью. Следовательно,
если регрессионная зависимость между
уихотсутствует, то
общая сумма квадратов отклонений
объясняется действием только случайных
факторов или ошибок, т.е.=
.
В случае функциональной зависимости
между уихдействие
случайных факторов и ошибок отсутствует
и тогда=
.
Будучи отнесенными к соответствующему
числу степеней свободы, эти суммы
называются средними квадратами отклонений
и служат оценками дисперсиив
разных предположениях.
MSE= ()/(n–2)
– остаточная дисперсия, которая является
оценкойв
предположении отсутствия регрессионной
зависимости, аMSR= ()/1
– аналогичная оценка без этого
предположения. Следовательно, если
регрессионная зависимость отсутствует,
то эти оценки должны быть близкими.
Сравниваются они на основе критерия
Фишера:F=MSR/MSE.
Расчетное значение
этого критерия сравнивается с критическим
значением F(с числом степеней свободы числителя,
равным 1, числом степеней свободы
знаменателя, равнымn–2,
и фиксированным уровнем значимости).
ЕслиF<F, то гипотеза о не значимости
уравнения регрессии не отклоняется, т.
е. признается, что уравнение регрессии
незначимо. В этом случае надо либо
изменить вид зависимости, либо пересмотреть
набор исходных данных.
При компьютерных
расчетах оценка значимости уравнения
регрессии осуществляется на основе
дисперсионного анализа регрессии в
таблицах вида:
Таблица
1.1
Дисперсионный
анализ регрессии
|
Источник вариации |
Суммы квадратов |
Степени свободы |
Средние квадраты |
F-отношение |
p-value |
|
Модель |
SSR |
1 |
MSR |
MSR/MSE |
Уровень |
|
Ошибки |
SSE |
n–2 |
MSE |
значимости |
|
|
общая |
SST |
n–1 |
Здесь p-value– это вероятность выполнения неравенстваF<F,
т. е. того, что расчетное значениеF-статистики попало в
область принятия гипотезы. Если эта
вероятность мала (меньше),
то нулевая гипотеза отклоняется.
Для множественной регрессии формула несмещенной оценки дисперсии случайной ошибки имеет вид
begin{equation*} widehat {sigma ^2}=S^2=frac 1{n-k}{ast}sum _{i=1}^ne_i^2 end{equation*}
Она почти такая же, как для парной регрессии за тем исключением, что в знаменателе вместо выражения (left(n-2right)) стоит (left(n-kright)). Если извлечь корень из этой величины, то можно получить стандартную ошибку регрессии
begin{equation*} mathit{SEE}=sqrt{S^2}=sqrt{frac 1{n-k}{ast}sum _{i=1}^ne_i^2} end{equation*}
Расчет стандартной ошибки регрессии — это один из способов оценить точность вашей модели в целом. То есть оценить, насколько хорошо она соответствует данным. Чем меньше стандартная ошибка регрессии, тем лучше ваша модель соответствует доступным вам наблюдениям.
Следующая характеристика качества подгонки — это коэффициент детерминации (R^2).
Для множественной регрессии с константой так же, как и для парной, верно, что общая сумма квадратов может быть представлена как сумма квадратов остатков и объясненная сумма квадратов:
begin{equation*} sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2 end{equation*}
Поэтому и (R^2) может быть рассчитан в точности таким же образом, как и для модели парной регрессии:
begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{sum _{i=1}^nleft(widehat y_i-overline yright)^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{widehat {mathit{Var}}left(widehat yright)}{widehat {mathit{Var}}left(yright)} end{equation*}
И точно так же, как и в случае парной регрессии, он будет лежать между нулем и единицей. Если ваша модель хорошо соответствует данным, то (R^2) будет близок к единице, если нет, то к нулю. Ещё раз подчеркнем, что условие (sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2) выполняется только тогда, когда в модели есть константа. Если же ее нет, то указанное равенство, вообще говоря, неверно, и (R^2) не обязан лежать между нулем и единицей, и интерпретировать стандартным образом его нельзя.
Некоторые эконометристы старой школы придают важное значение величине коэффициента (R^2). Действительно, если он близок к единице, то это, как правило, приятная новость. Однако не стоит переоценивать эту характеристику качества модели потому, что у коэффициента (R^2) есть существенные ограничения:
- Высокий (R^2) характеризует наличие множественной корреляции между регрессорами и зависимой переменной, но ничего не говорит о наличии или отсутствии причинно-следственной связи между анализируемыми переменными. Вспомните примеры из первой главы, где мы обсуждали, что высокая корреляция не гарантирует причинно-следственной связи.
- (R^2) не может быть использован для принятия решения о том, стоит ли добавлять в модель новые переменные или нет. Дело в том, что, когда вы добавляете новые переменные в ваше уравнение, качество подгонки данных не может стать хуже, следовательно, и сумма квадратов остатков не может увеличиться. В теории она может остаться неизменной, но на практике она всегда будет уменьшаться. А в этом случае, как видно из расчетной формулы, (R^2) будет увеличиваться. Получается, что какие бы дурацкие новые переменные вы ни добавляли в модель, коэффициент (R^2) будет увеличиваться (или, в крайнем случае, оставаться неизменным).
Последний из указанных недостатков легко можно преодолеть. Для этого есть усовершенствованная версия (R^2), которую называют скорректированным (или нормированным) коэффициентом (R^2) ( (R^2) adjusted):
begin{equation*} R_{mathit{adj}}^2=R^2-frac{k-1}{n-k}{ast}left(1-R^2right) end{equation*}
(R_{mathit{adj}}^2) меньше, чем обычный (R^2), на величину (frac{k-1}{n-k}{ast}left(1-R^2right)), которая представляет собой штраф за добавление избыточных переменных. Обратите внимание, что при прочих равных этот штраф растет по мере увеличения параметра (k), характеризующего число коэффициентов в вашей модели. Если вы будете добавлять в модель много регрессоров, которые не вносят существенного вклада в объяснение зависимой переменной, то (R^2_{mathit{adj}}) будет снижаться.
Поэтому, если вы хотите сравнить межу собой модели с разным числом объясняющих переменных, то лучше использовать (R^2_{mathit{adj}}), чем обычный (R^2). А ещё лучше обращать внимание не только на этот коэффициент, но и на прочие характеристики адекватности вашей модели, которые мы обсудим в этой книге.
Чтобы понять, откуда берется формула для скорректированного R-квадрата, запишем обычный R-квадрат следующим образом:
begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{frac{sum _{i=1}^ne_i^2} n}{frac{sum _{i=1}^nleft(y_i-overline yright)^2} n}. end{equation*}
В числителе дроби стоит выборочная дисперсия остатков, а в знаменателе — выборочная дисперсия зависимой переменной. Если и ту, и другую дисперсии заменить их несмещенными аналогами, то получим следующее выражение:
begin{equation*} 1-frac{S^2}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}. end{equation*}
Легко проверить, что это и есть скорректированный R-квадрат:
begin{equation*} 1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{n-1}{n-k}frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{n-1}{n-k}left(1-R^2right)= end{equation*}
begin{equation*} R^2-frac{k-1}{n-k}{ast}left(1-R^2right)=R_{mathit{adj}}^2. end{equation*}