Слайд 1Лекция 4
Количественные характеристики случайной величины. Описательная
статистика

Слайд 2Вопросы:
1. Меры положения.
2. Меры рассеивания признака.
3. Асимметрия
и эксцесс.

Слайд 3 Меры положения
определяют положение центра эмпирического
распределения.
— мода;
— медиана;
— среднее арифметическое;
— среднее
гармоническое;
— среднее квадратическое;
— среднее кубическое;
— среднее геометрическое;

Слайд 4Средняя величина признака
– обобщающий показатель, характеризующий
типичный уровень варьирования изучаемого признака.
хi –
варианты значений признака, N – объем выборочной совокупности.

Слайд 5Среднее гармоническое
нескольких положительных чисел называется число, обратное
среднему арифметическому их обратных, т. е. число
В
статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

Слайд 6Медиана
– значение признака, которое лежит в середине
ранжируемого ряда и делит этот ряд на
две равные части.
n – выборочная совокупность.

Слайд 7Мода
– наиболее часто встречающееся значение признака.

Слайд 8Графическое представление мер положения
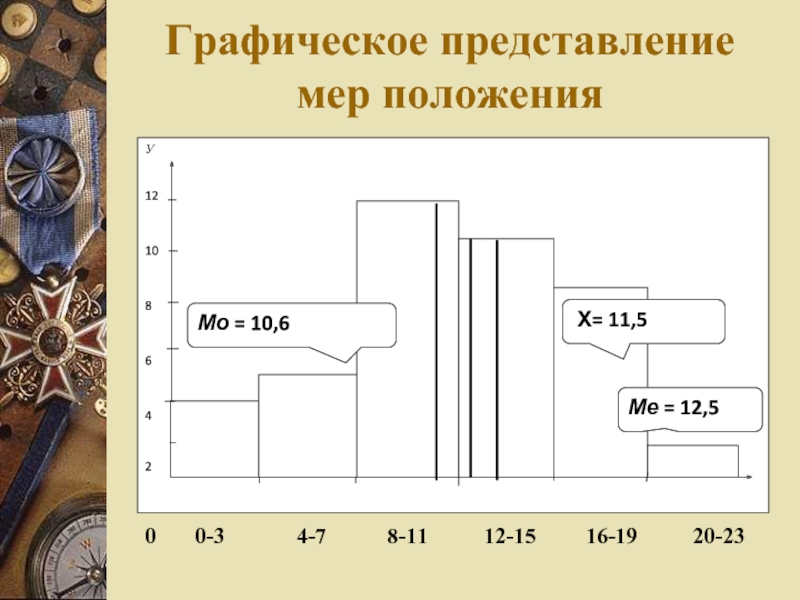
Слайд 9Меры рассеивания признака
различия индивидуальных значений признака у
единиц совокупности.
— размах колебаний,
— среднее линейное отклонение,
—
среднее квадратическое отклонение,
— дисперсия.

Слайд 10Причины варьирования признаков
1. Влияние неучтенных признаков (влияние
погодных условий, эмоциональное состояние испытуемых, мотивация, утомляемость
и т.п.)
2. Случайные факторы, обусловливающие случайное поведение изучаемого признака (эффект социальной фасилитации).
3. Ошибки измерения, которые складываются из систематических погрешностей измерительных приборов, личных ошибок исследователя (описки, пропуски, округления и т.п.) и случайных ошибок измерения.

Слайд 11Размах вариации
вычисляется как разность между максимальной и
минимальной вариантами выборки
Хmax – максимальное значение признака;
Хmin – минимальное значение признака.

Слайд 12Дисперсия
средний квадрат отклонения значений признака от среднего
арифметическогоS2.
Хi – значение признака; – среднее
значение признака; n — объем выборки.

Слайд 13Стандартное отклонение (или среднее квадратическое отклонение)
— положительный
корень квадратный из дисперсии (сгруппированных данных)
S =

Слайд 14Коэффициент вариации
это выражение в процентах отношения
стандартного отклонения к среднеарифметическому значению.
где —
среднее значение признака, — среднеквадратичное отклонение.

Слайд 15Коэффициент вариации
если коэффициент вариации не превышает
25 %, то выборку можно считать однородной.

Слайд 16Асимметрия
— статистический показатель для сравнительного анализа степени
смещения показателей распределения признака относительно среднего значения

Слайд 17Асимметрия
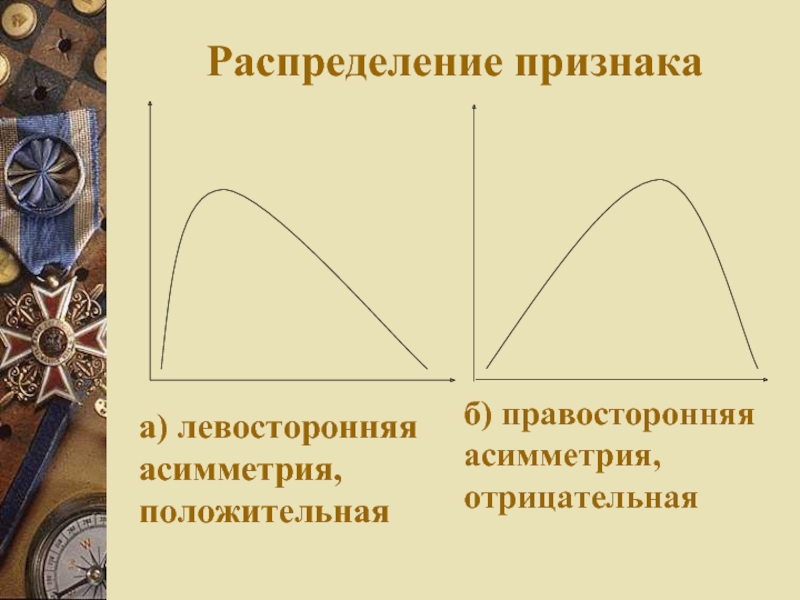
при левосторонней симметрии принимают положительные значения, а
при правосторонней – отрицательные. Правосторонняя асимметрия свидетельствует
о том, что большинство значений признаков смещено в область высоких значений и наоборот.

Слайд 18Распределение признака
а) левосторонняя асимметрия, положительная
б) правосторонняя асимметрия,
отрицательная
Слайд 19Коэффициент асимметрии можно рассчитать по формуле Линдберга

Слайд 20Эксцесс
– это количественная мера остро или высоковершинности
распределения.
Эксцесс может быть положительным и отрицательным.
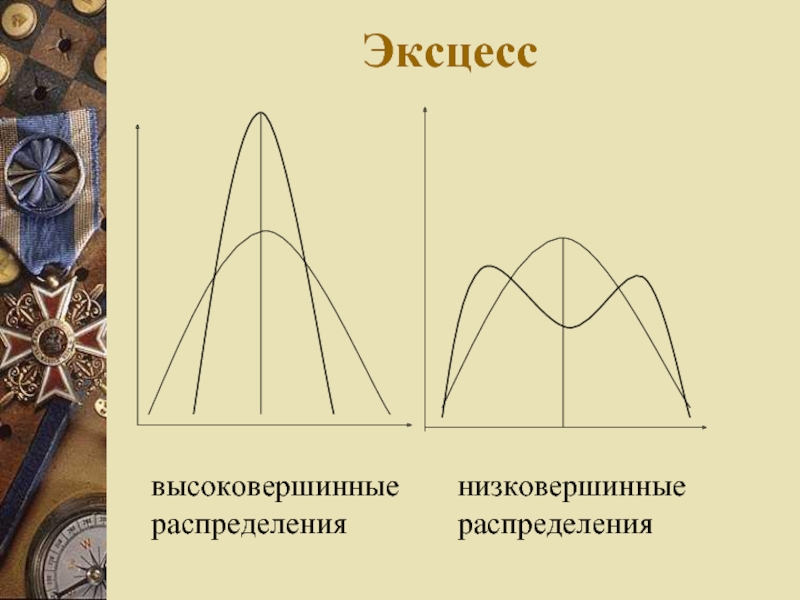
У высоковершинных распределений показатель эксцесса имеет положительный знак, а у низковершинных – отрицательный знак.

Слайд 21Эксцесс
высоковершинные распределения
низковершинные распределения
Слайд 23Ошибки репрезентативности
ошибка репрезентативности асимметрии
ошибка репрезентативности
эксцесса

Слайд 24Условия нормальности распределения
(по Пустыльнику Е.И. 1968)

Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi X )
N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8 16 20 24 32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
= 17
2) 16 20 24 32
= 23
3) 8
16 24 32
= 20
4) 8
16 20 32
= 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n 30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
= 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,
означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что будет находиться в пределах
доверительного интервала x — t SX + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX + t SX
9 — 1,96
3271
.
327
.
92+1,96
100
100
или 9+ 0.196 3,27 9 + 1..96 3,27 или 8. 36 9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр
находится в интервале 8.36 — 9.64.
95%
В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):
,
где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):
,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
;
.
Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
83. Определение доверительных границ средних и относительных величин.
Знание
величины ошибки недостаточно для того,
чтобы быть уверенным в результатах
выборочного исследования, так как
конкретная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
определения точности, с которой
исследователь желает получить результат,
в статистике используется такое понятие,
как вероятность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:
Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безошибочного прогноза 95% равен 2,6;
при вероятности безошибочного
прогноза 99% — 3,0; при вероятности
безошибочного прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы,
в которых с определенной вероятностью
безошибочного прогноза заключено
действительное значение статистической
величины,
характеризующей
всю генеральную совокупность (средней
или относительной).
Для
определения доверительных границ
используются следующие формулы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Справочник /
Лекторий Справочник /
Лекционные и методические материалы по статистике /
Ошибка репрезентативности и доверительный интервал для
генерального параметра
Конспект лекции по дисциплине «Ошибка репрезентативности и доверительный интервал для
генерального параметра»,
pdf
Файл загружается
Благодарим за ожидание, осталось немного.
Конспект лекции по дисциплине «Ошибка репрезентативности и доверительный интервал для
генерального параметра».
pdf
txt
Конспект лекции по дисциплине «Ошибка репрезентативности и доверительный интервал для
генерального параметра», текстовый формат
Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi X )
N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8 16 20 24 32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
= 17
2) 16 20 24 32
= 23
3) 8
16 24 32
= 20
4) 8
16 20 32
= 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n 30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
= 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,
означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что будет находиться в пределах
доверительного интервала x — t SX + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX + t SX
9 — 1,96
3271
.
327
.
92+1,96
100
100
или 9+ 0.196 3,27 9 + 1..96 3,27 или 8. 36 9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр
находится в интервале 8.36 — 9.64.
95%
Статистика
Статистика
Курс : Статистика
Статистика В.М. Гусаров Москва, Юнити , 2003г
Статистика В.С. Мхиторян , Москва, Экономист, 2005г.
Статистика И.И. Елисеева
Статисти…
Смотреть все
Поделись лекцией и получи скидку!
Заполни поля, отправь лекцию и мы вышлем тебе скидку-промокод на Автор24
Предмет
Название лекции
Авторы
Описание
Другие Экономические предметы
-
Экономика
-
Менеджмент
-
Бухгалтерский учет и аудит
-
Управление персоналом
-
Статистика
-
Маркетинг
-
Экономика предприятия
-
Государственное и муниципальное управление
-
Финансовый менеджмент
-
Эконометрика
-
Финансы
-
Менеджмент организации
-
Бизнес-планирование
-
Управление проектами
-
Экономический анализ
-
Экономическая теория
-
Микро-, макроэкономика
-
Инновационный менеджмент
-
Логистика
-
Анализ хозяйственной деятельности
Доверительный интервал за 15 минут
Добрый день, уважаемые читатели!
Меня зовут Кирилл Мильчаков. Сегодня мы продолжаем наш разговор о биостатистике. Тема сегодняшней нашей беседы будет «Доверительный интервал». Что такое доверительный интервал? Вы наверняка встречались с ним в научной литературе. Доверительный интервал 95 %, либо сочетание символов ДИ и CI (confidence interval) 95 %. Что же означают эти 95 %? Какие он еще может принимать значения? И как его рассчитывать самостоятельно? Об этом обо всем сегодня мы и поговорим в этой статье.
Видео-версия статьи о доверительном интервале
Генеральная совокупность и выборочная совокупность
Прежде чем углубляться в тайны доверительного интервала, хотел бы вспомнить с вами 2 основных понятия статистической совокупности, с которыми чаще всего работают – это генеральная совокупность или выборочная совокупность или выборка.
Генеральная совокупность – это тот массив данных, о которых вы хотите сделать выводы.
Выборка является частью генеральной совокупности, которая участвует непосредственно в вашем эксперименте. Есть такое понятие как репрезентативность, сегодня мы не будем его касаться, главное запомнить, что выборка должна быть репрезентативной.
Если привести небольшой пример относительно генеральной совокупности и выборки, то можно вспомнить о простом случае из вашей жизни. Когда вы хотите узнать, достаточно ли посолен суп, вы берете ложку супа и пробуете его. Вам необязательно есть весь суп, чтобы понять, насколько он посолен. Ложка в данном случае является выборкой, по которой вы делаете вывод обо всей кастрюле супа. В данном случае кастрюля супа является генеральной совокупностью, а ложка супа является выборкой.
Итак, мы вспомнили с вами о 2 ключевых статистических совокупностях – о генеральной совокупности и выборочной совокупности. Теперь нужно вспомнить, что типы исследования, которые проводятся над генеральной совокупностью и выборочной совокупностью, называют по-разному. Над генеральной совокупностью проводятся так называемые сплошные исследования, над выборочной совокупностью – выборочные.
Теперь вспомним небольшие отличия между параметрами этих 2 совокупностей. Сегодня для того, чтобы понять, что такое доверительный интервал, нам понадобятся следующие вещи: во-первых, отличие средней арифметической в генеральной совокупности и в выборочной совокупности. В генеральной совокупности она имеет значок µ (мю), в выборочной – это x̅ (х с чертой) — это средние арифметические по каждому виду совокупности.
Далее нужно знать, что стандартное отклонение имеет значок выборочной – либо S, либо SD (standard deviation), а в случае генеральной совокупности оно носит название среднеквадратичного отклонения и обозначается буквой σ (сигма).
Приведем пример расчета доврительного интервала
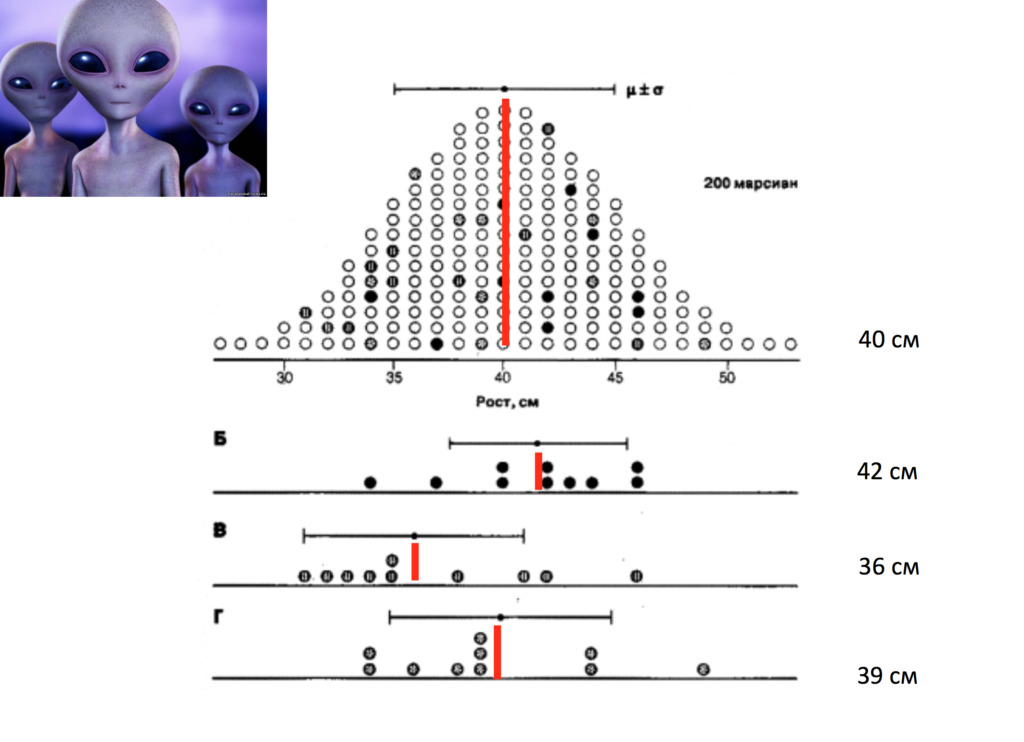
Представьте чисто гипотетическую ситуацию, когда перед нами стоит задача исследований среднего роста марсианина. Для того, чтобы его узнать, было отправлено 3 экспедиции. Первой из них повезло больше всего: они смогли поймать каждого из 200 марсианин и померить его рост.
Как мы помним, по закону нормального распределения по оси Х находится величина изучаемого признака, либо варианта (в данном случае это рост в сантиметрах), а по оси Y – частота встречаемости какого-то признака (мы его обозначаем буквой П.
Итак, оказалось, что у всех 200 марсиан средний рост составил 40 сантиметров. Таким образом, первая экспедиция смогла провести так называемое сплошное исследование, так как поработала со всеми единицами наблюдения генеральной совокупности. Поэтому мы имеем право назвать этот параметр µ.
Однако, второй и третьей экспедиции повезло гораздо меньше. Они попали в самые плохо населенные участки Марса и смогли отобрать только 10 марсиан. В данном случае оказалось, что средний рост по их выборке составил всего 38 сантиметров в первом случае и 41 сантиметр во втором случае.
Что же делать? Да, у нас есть данные из самого полного исследования, которое относится к первой экспедиции. Но представьте, что ни одна бы из них не смогла бы поработать со всей совокупностью полностью, и у нас были бы данные только от второй и третьей экспедиции. Что же в этой ситуации делать? Видно, что никто 40 сантиметров в действительности не достиг: во второй экспедиции Б она равна 38 сантиметрам, а в экспедиции В – 41 сантиметр. То есть в реальности никто не достиг 40 сантиметров. Что же делать в данном случае?
И вот здесь на помощь к нам приходит доверительный интервал, точнее оценка параметра. Доверительный интервал является вторым этапом оценки параметра. Прежде чем строить доверительный интервал, нам нужно понять, насколько в принципе этот параметр наша средняя (x̅б, x̅в) может отличаться, ошибаться от реального параметра в генеральной совокупности. Насколько?
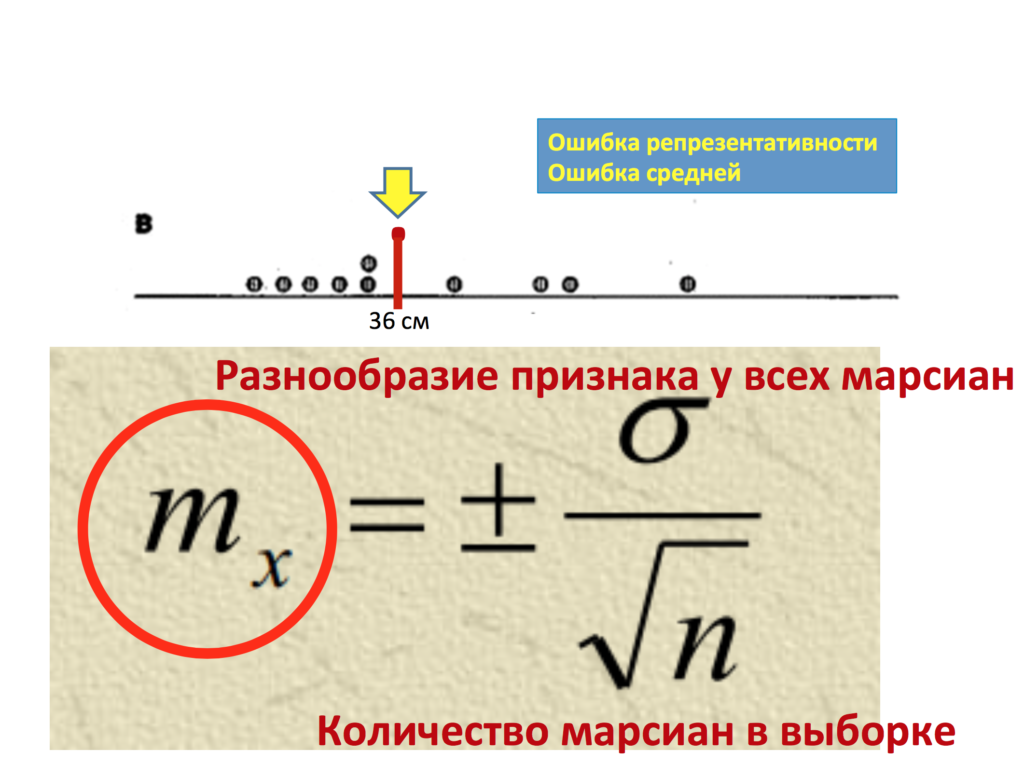
И тут нам помогает оценка параметра или нахождение ошибки репрезентативности. Ошибка репрезентативности обозначается mr или mx. Чаще я использую mr. Что же это значит? mr по-английски обозначается как standard error, по-русски она часто называется стандартная ошибка средней или ошибка репрезентативности. Как же она находится? А находится она следующим образом? Она учитывает стандартное квадратичное отклонение в генеральной совокупности и размер в выборке. От чего же зависит ошибка репрезентативности? А зависит она от 2 вещей: от среднеквадратичного отклонения в генеральной совокупности (я напоминаю, это насколько каждая варианта отличается от средней, о законе нормального распределения мы с вами поговорим в следующий раз) и от размера выборки или . То есть, таким образом, чем менее разбросан признак генеральной совокупности, и чем больше у нас размер выборки, тем меньше наша ошибка репрезентативности.
Итак, предположим, мы нашли нашу ошибку репрезентативности mr. В данном случае она составила 2,7 сантиметра. Но что же это нам дает? А дает нам это уже достаточно много. Теперь мы, зная, насколько в принципе наша выборка может ошибаться относительно генеральной совокупности, можем составить определенное предположение о том, где же находится реальный параметр – реальные 40 сантиметров генеральной совокупности на основании данных лишь нашей выборки.
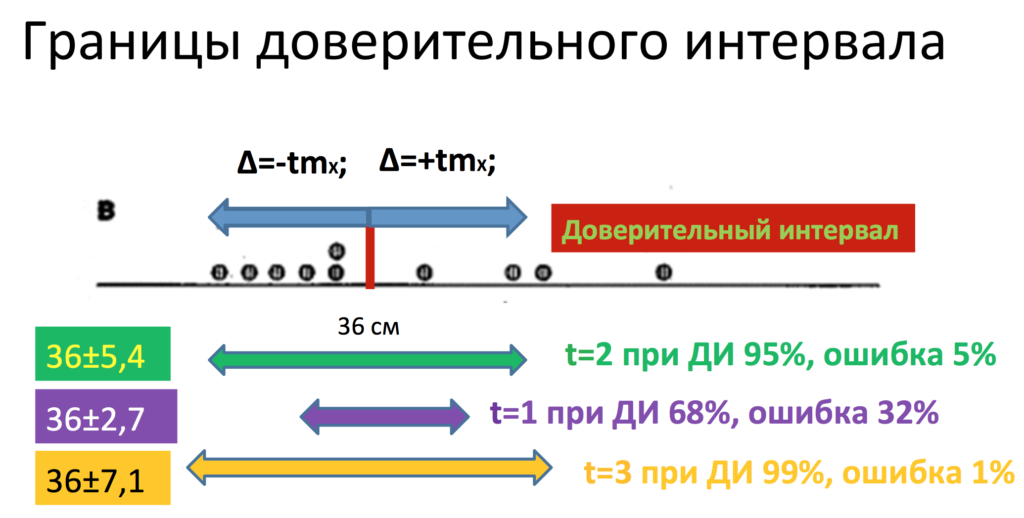
Каким же образом это происходит? Мы провели точечную оценку нашего параметра. Дальше происходит второй этап построения доверительного интервала – это интервальная оценка параметра. Каким же образом строится этот интервал? А складывается он из 2 вещей: так называемой предельной ошибки +∆ и -∆. Формула нахождения предельной ошибки достаточно проста и составляет:
±∆ = t*mr
Для того, чтобы не залезать в критерий Стьюдента сегодня, я скажу лишь, что:
для доверительного интервала 95 % используется t=2,
для доверительного интервала 99 % используется t=3
и для доверительного интервала 68 % используется t=1.
Итак, после того, как мы нашли нашу предельную ошибку, мы можем построить доверительный интервал. Но для этого нам нужно самим задать тот доверительный интервал, который для нас подходит больше всего. Чаще всего в медицине используется вероятность ошибки 5 %, то есть доверительный интервал 95 % или вероятность ошибки 5 % (р=0,05, р=5 %).
Что же значат эти 95 %? А значат они следующее, что с 95%-ной вероятностью в нашем интервале лежит реальное значение, и лишь в 5 % случаев мы ошибаемся. То есть в нашем конкретном случае наша ошибка репрезентативности составила 2,7 сантиметра. Предельная ошибка отсюда будет равна чему? Именно 5,4 сантиметра, то есть доверительный интервал, так как здесь и плюс, и минус, то есть нам нужно ошибку умножить на 2, составил 10,8 сантиметров. А именно наши 38 см±5,4 см. Ширина всего доверительного интервала составляет 10,8 см. Напомню, что он складывается из положительной и отрицательной предельных ошибок вокруг нашей выборочной средней.
Итак, говоря о доверительном интервале, нужно сделать ряд важных выводов.
- Во-первых, доверительный интервал относится к выборочной совокупности. Он показывает, насколько параметры из выборочной совокупности могут отличаться от реально существующих данных в генеральной совокупности. Насколько мы ошибаемся при формировании той или иной выборки, мы закладываем в так называемую ошибку репрезентативности, в ошибку средней и вокруг нее собственно и строим доверительный интервал.
- Ширину доверительного интервала задает собственно сам исследователь, варьируя тот критерий t, который он принимает в качестве необходимого. Чаще всего применяется t=2, которое и соответствует ширине доверительного интервала 95 %. 95 % означает, что с 95%-ной вероятностью действительно вокруг выборочной средней существует определенный доверительный интервал, в который и попадает реально существующая средняя из генеральной совокупности. Этот доверительный интервал может быть либо уже, если t=1; либо шире, если t=3.
- Доверительный интервал задается самостоятельно исследователем. Чаще всего он равен 95 %.
Если это видео оказалось Вам полезным, оно хотя бы немного раскрыло тайны доверительного интервала, ставьте лайки, подписывайтесь на наши рассылки и в комментариях пишите, какие темы по биостатистике вам бы были интересны для следующих выпусков. На этом я с вами прощаюсь. Меня зовут Кирилл. Пока!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях: