Ошибка репрезентативности эксель - Не ошибается лишь тот, кто ничего не делает!

Содержание

Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
Вопросы и ответы

Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.

Расчет ошибки средней арифметической

Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.

В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.

Способ 1: расчет с помощью комбинации функций

Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.

Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.

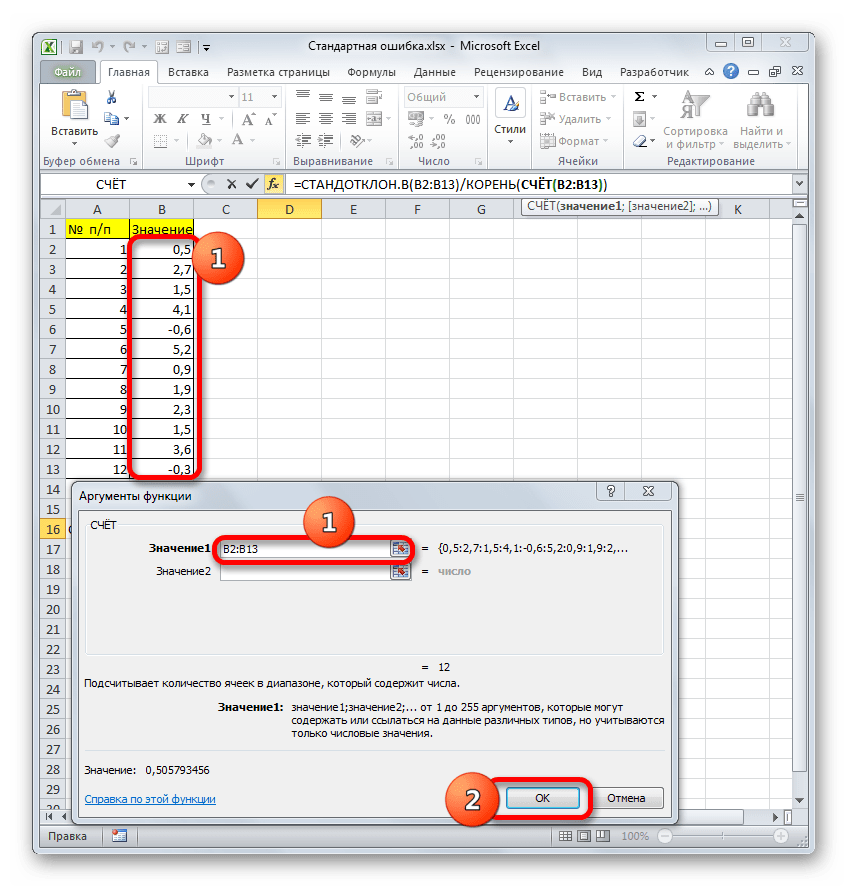
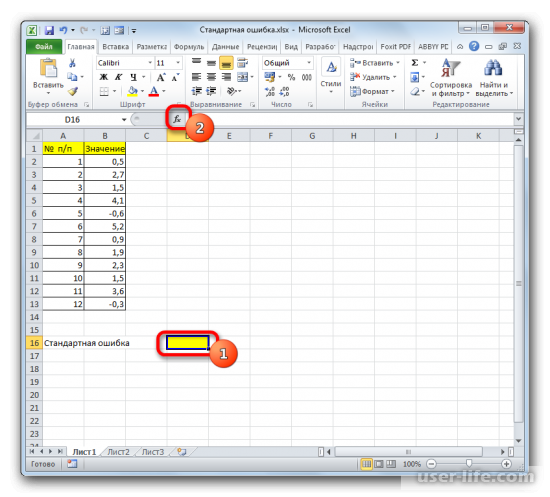
Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».

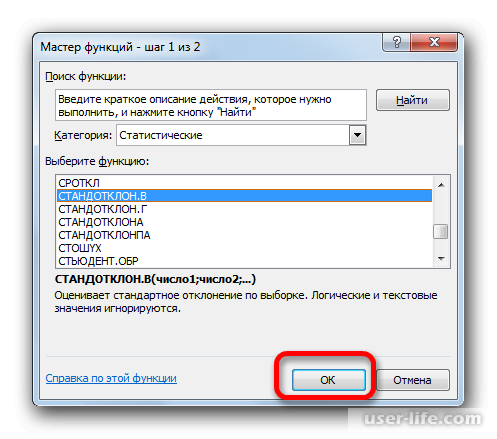
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».

Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)

«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.

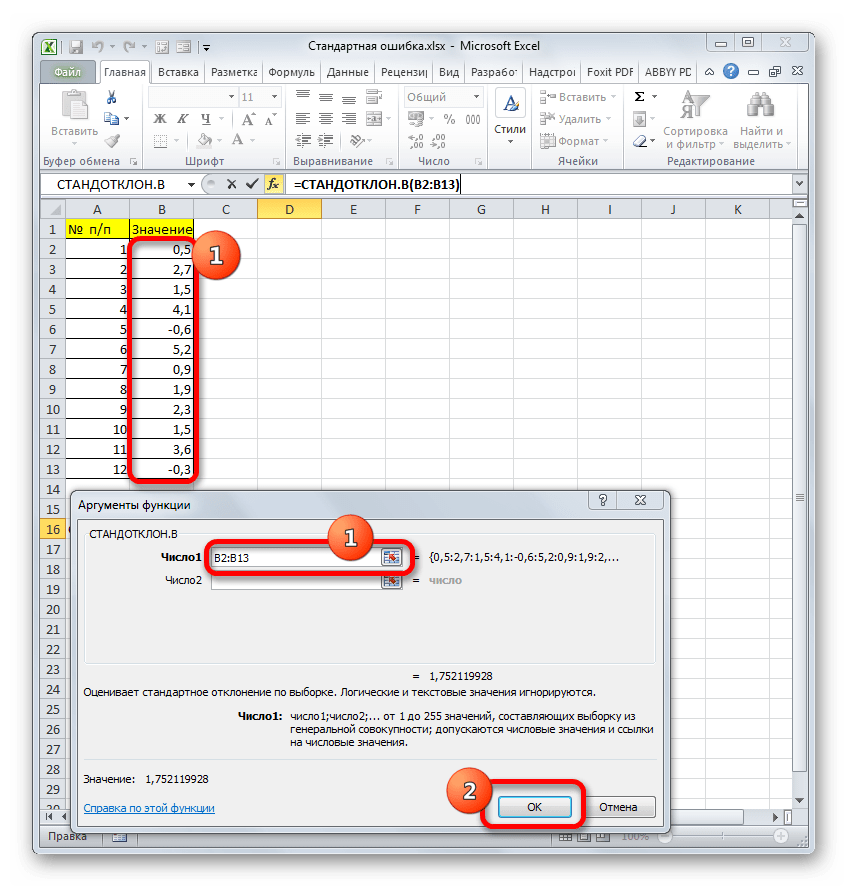
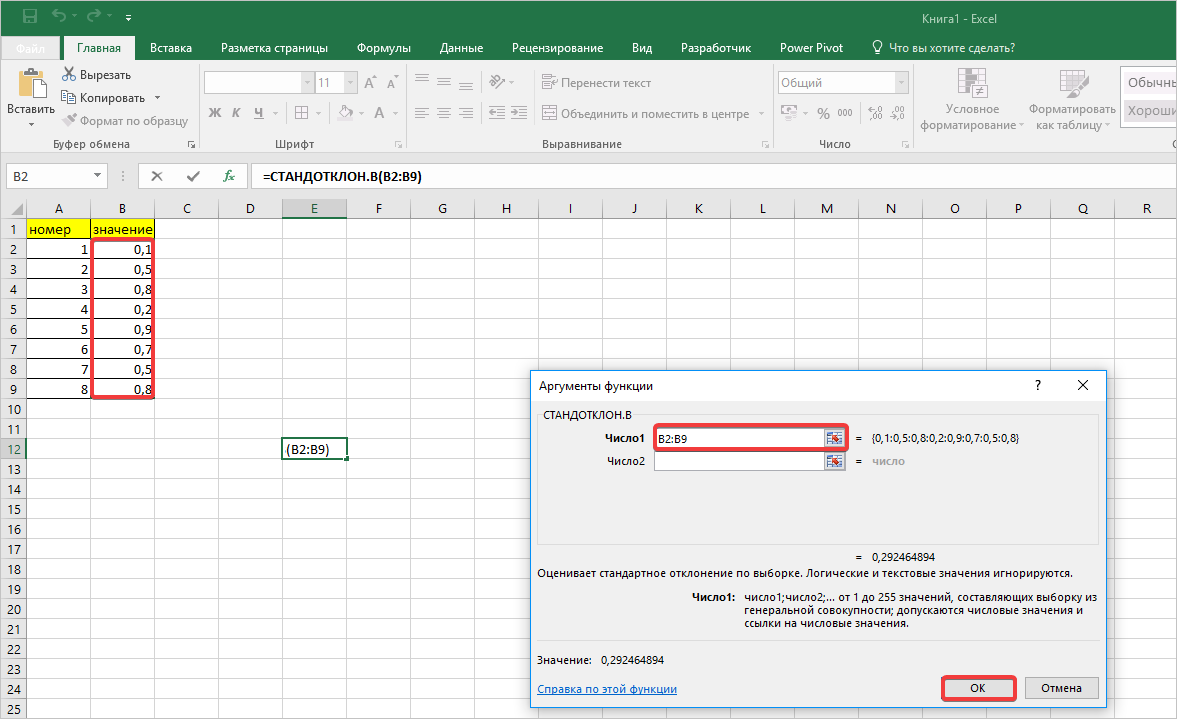
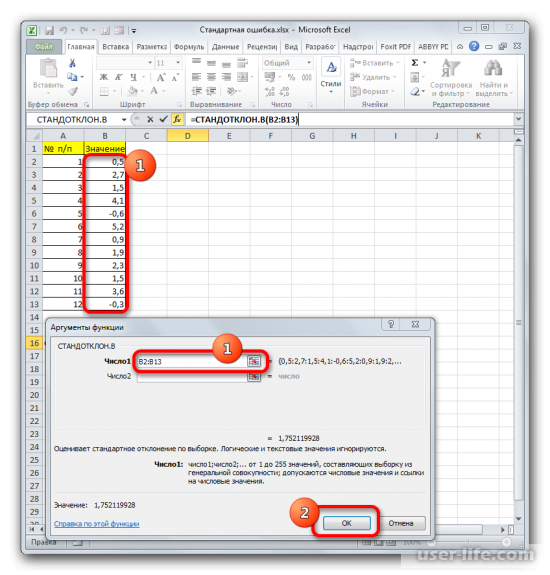
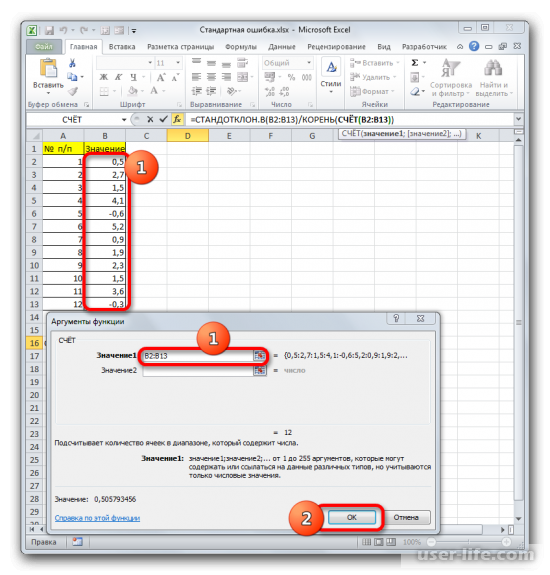
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».

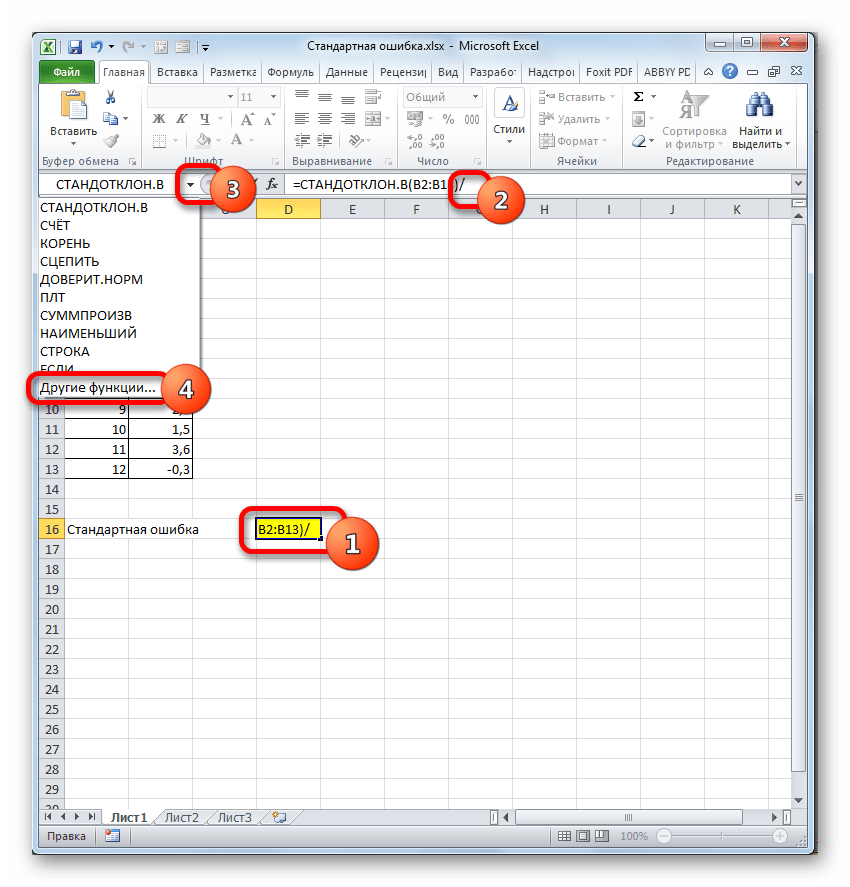
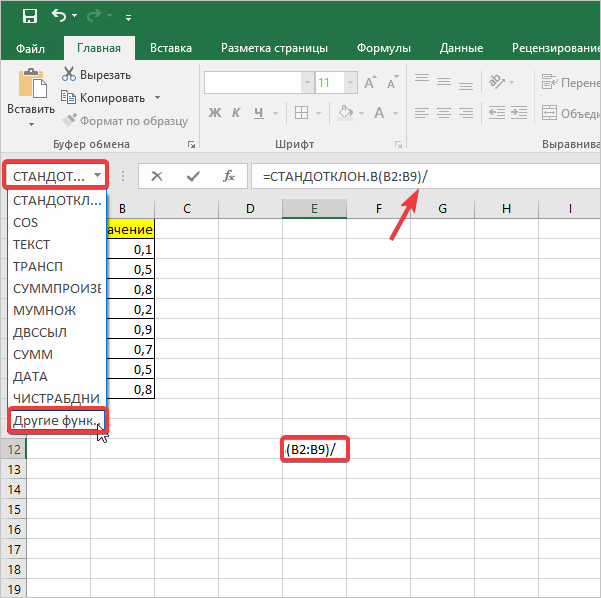
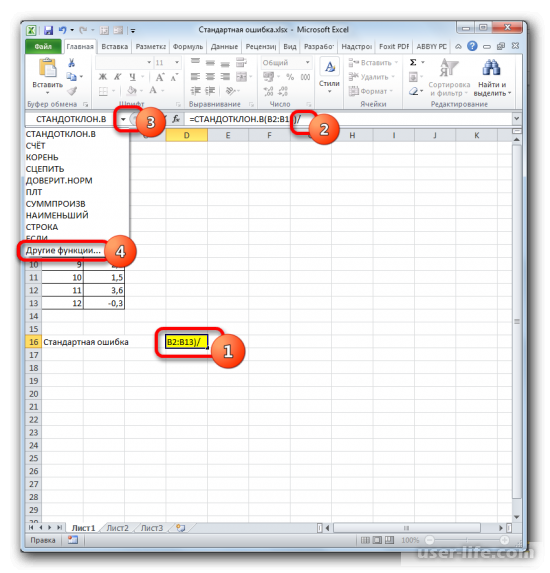
В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».

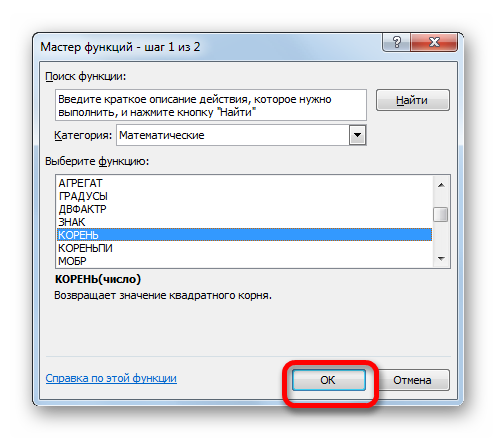
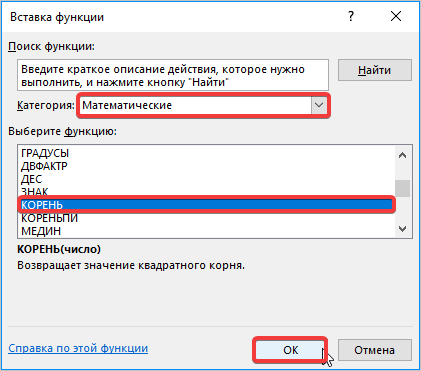
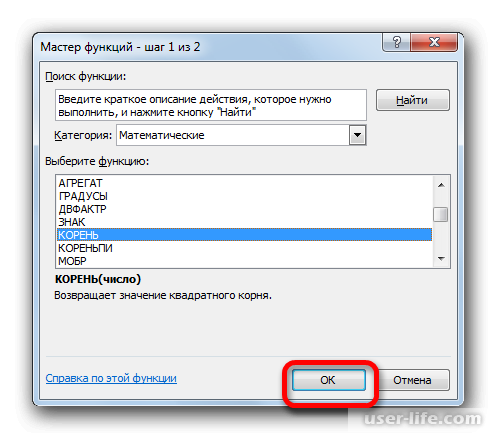
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».

Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)

Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.

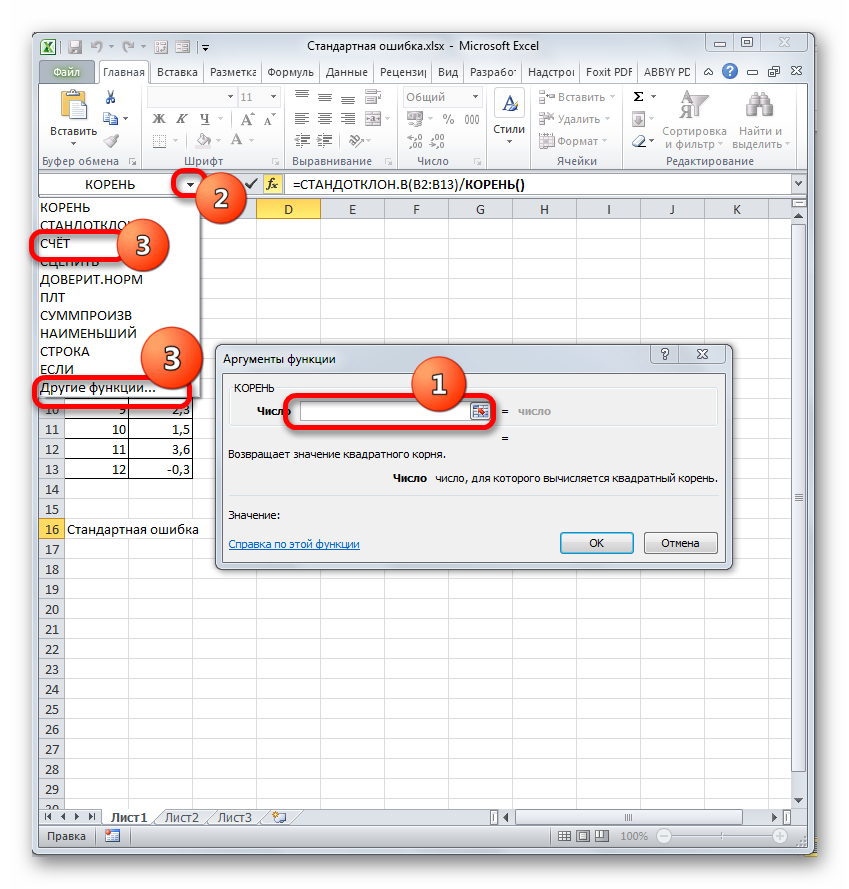
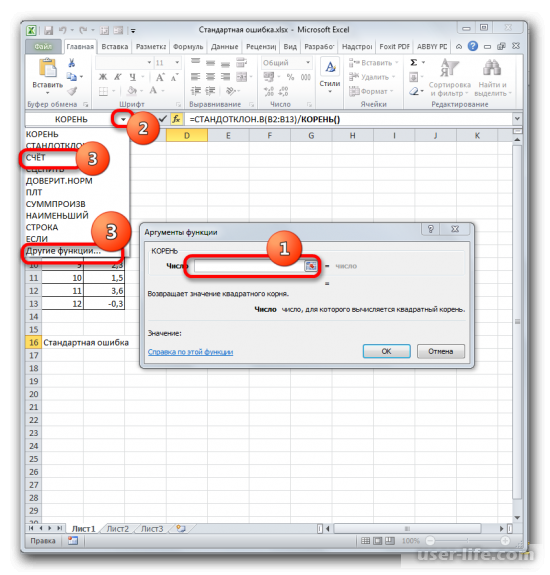
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».

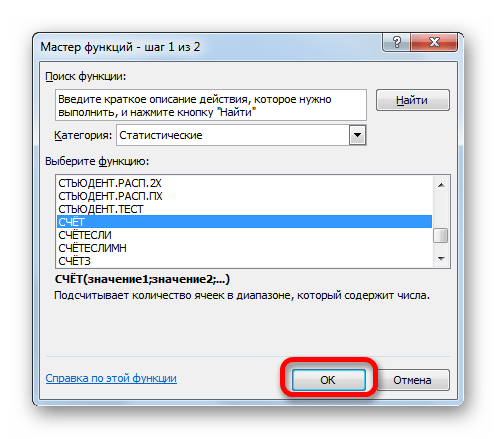
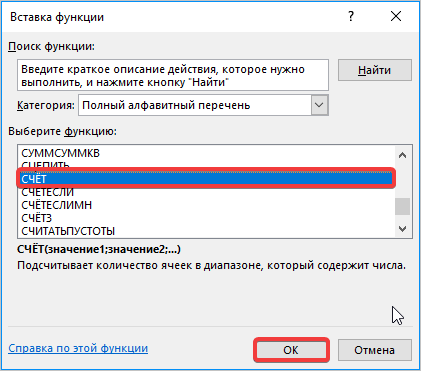
В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».

Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)

В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».

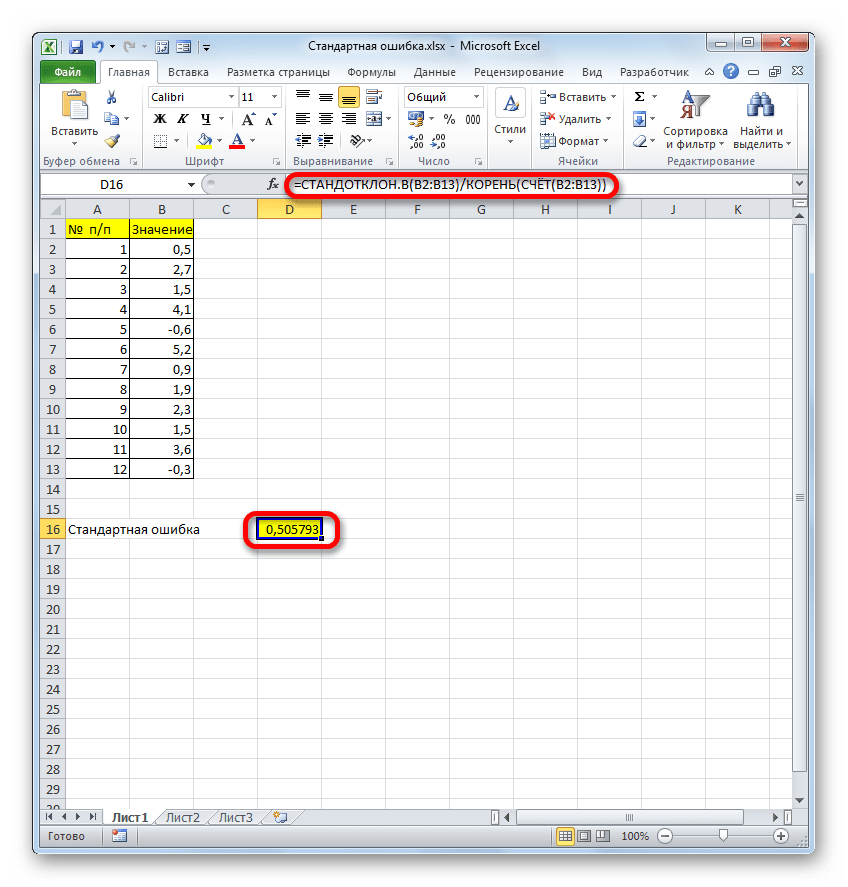
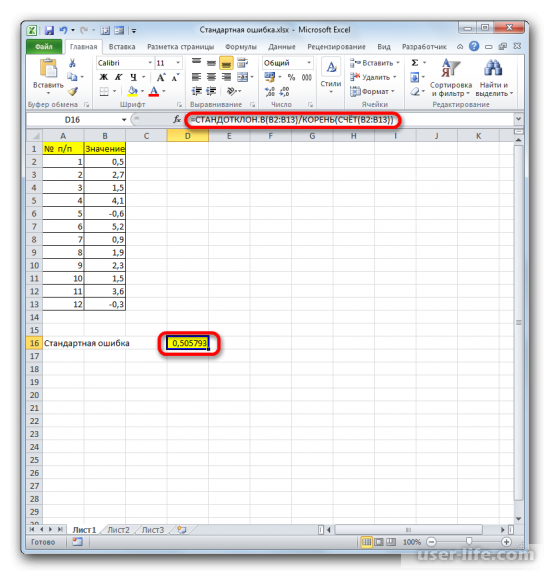
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))

Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.

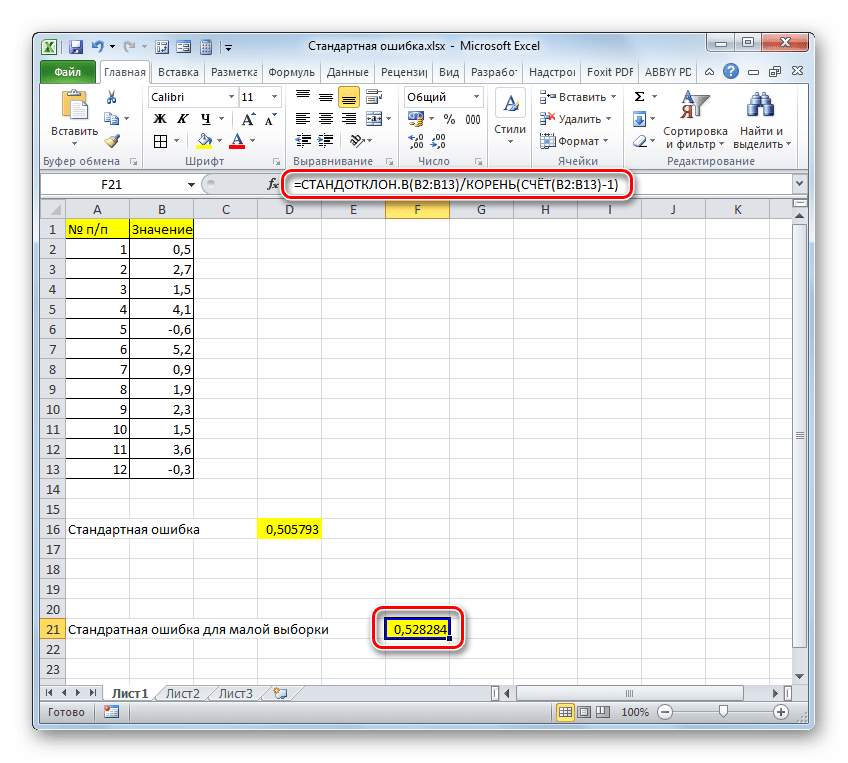
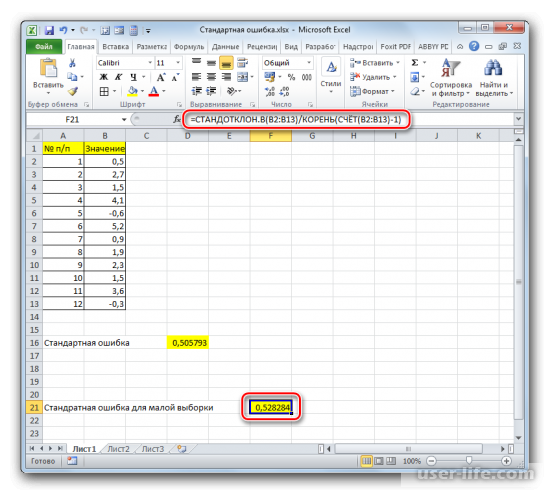
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:

=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)

Урок: Статистические функции в Экселе

Способ 2: применение инструмента «Описательная статистика»

Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.

Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.

После того, как открыт документ с выборкой, переходим во вкладку «Файл».

Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».

Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».

В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.

Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.

После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».

После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.

Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.

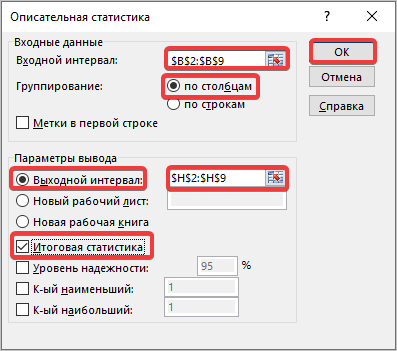
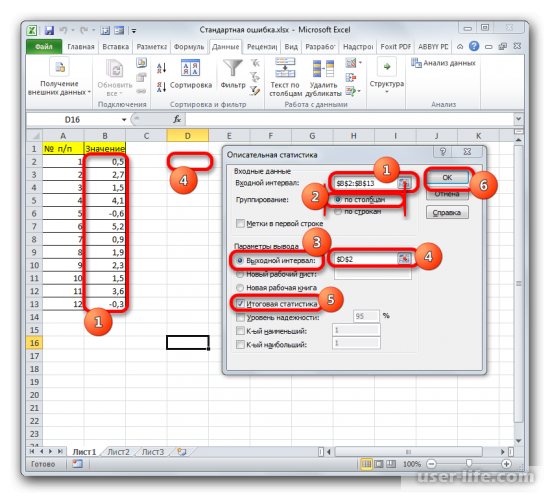
Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
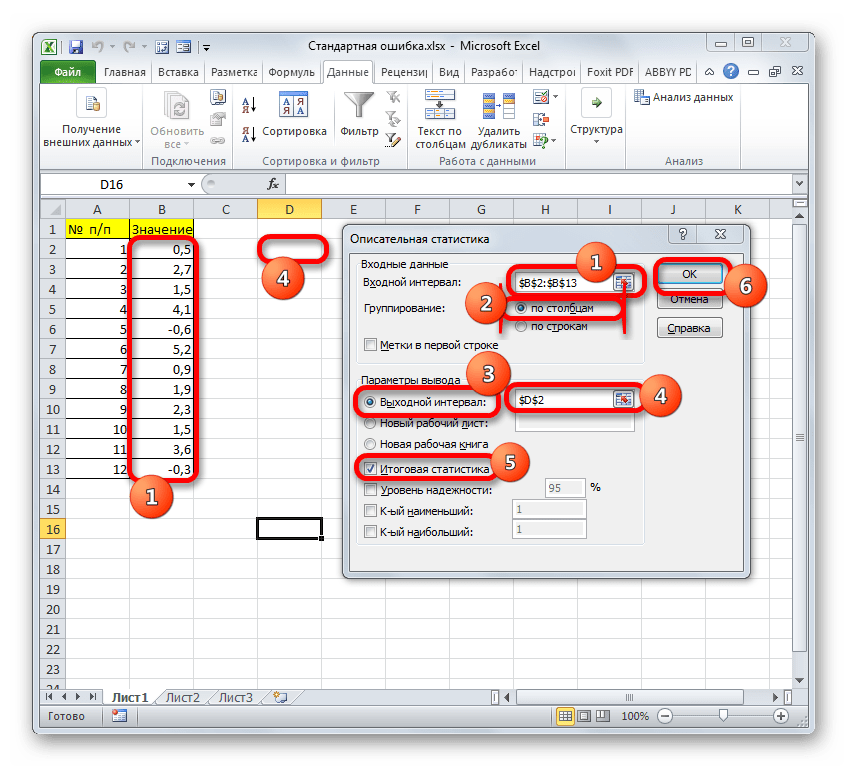
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.

В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.

Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.

Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.

Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.

После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.

После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.

Урок: Описательная статистика в Экселе

Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.

Источник

К
ПРОГРАММАМ, ВЫПОЛНЯЮЩИМ ФУНКЦИИ
АНАЛОГИЧНЫЕ ПРОГРАММЕ EXCEL, ОТНОСЯТСЯ:

а)
Super Calc

б)
Word

в)
Lotus-1-2-3

г)
Quattro Pro

д)
PowerPoint

е)
ACCESS

Решение:
электронные
таблицы, или табличные процессоры,
являются удобным средством проведения
расчетов и анализа результатов научных
исследований. Они предназначены для
работы с таблицами чисел и выполнения
относительно несложных расчетов с
большим количеством идентичных данных,
например, бухгалтерских. Наиболее
популярными электронными таблицами
являются: Super Calc, Quattro Pro, Lotus‑1‑2‑3
и Microsoft
Excel.

Правильный
ответ:
а, в, г.

Литература:
Сабанов В.И. Медицинская информатика и
автоматизированные системы управления
в здравоохранении. Учебно-методическое
пособие к практическим занятиям / В.И.
Сабанов, А.Н. Голубев, Е.Р. Комина. –
Волгоград: Изд-во ВолГМУ, 2006. – 144с. –
стр. 54.

ДЛЯ
ВЫЧИСЛЕНИЯ СРЕДНЕГО АРИФМЕТИЧЕСКОГО
ЗНАЧЕНИЯ ПРИМЕНЯЕТСЯ ФУНКЦИЯ …

а)
МЕДИАНА(…)

б)
СРГАРМ(…)

в)
СРЗНАЧ(…)

г)
СРГЕОМ(…)

Решение:
для
вычисления среднего арифметического
значения применяется функция
срзнач(диапазон
ячеек).

Правильный
ответ:
в.

Литература:
Симонович С.В. Информатика. Базовый
курс: Учебник для вузов.-3-е изд. Стандарт
третьего поколения. — СПб.: Питер, 2011. —
640с.: ил. – стр. 344.

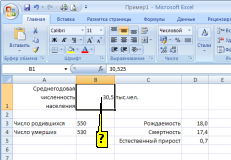
В
ЯЧЕЙКЕ В1 ОТОБРАЖЕНО ЧИСЛО 30,5
(СМ. РИСУНОК),
ПРИ ЭТОМ В ВЫЧИСЛЕНИЯХ ИСПОЛЬЗУЕТСЯ
ЗНАЧЕНИЕ …

а)
30,5

б)
30,525

в)
в зависимости от настройки
программы: 30,5 или 30,525

Решение:
в
ячейке B1
отображено число 30,5 (см.рисунок), при
этом в вычислениях используется значение
30,525.

Правильный
ответ:
б.

Литература:
Симонович С.В. Информатика. Базовый
курс: Учебник для вузов.-3-е изд. Стандарт
третьего поколения. — СПб.: Питер, 2011. —
640с.: ил. – стр. 337.

ДЛЯ
ПОДКЛЮЧЕНИЯ К ПРОГРАММЕ EXCEL ПАКЕТА
СТАТИСТИЧЕСКОГО АНАЛИЗА ДАННЫХ
ПОЛЬЗОВАТЕЛЮ ТРЕБУЕТСЯ ВЫПОЛНИТЬ
СЛЕДУЮЩЕЕ ДЕЙСТВИЕ …

а)
произвести установку модуля «Пакет
анализа» из режима «Надстройки» программы

б)
удалить программу Excel и произвести ее
повторную стандартную установку

в)
перезагрузить компьютер

Решение:
для подключения к программе Excel пакета
статистического анализа данных необходимо
подключить модуль «Пакет анализа» из
режима «Надстройки» основного меню
программы.

Правильный
ответ:
а.

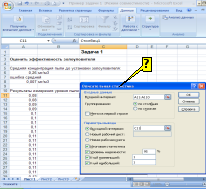
ВЫЗОВ
ПАКЕТА ВЫЧИСЛЕНИЯ СРЕДНИХ ВЕЛИЧИН И
ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯДА В
ПРОГРАММЕ EXCEL ПРОИЗВОДИТСЯ КОМАНДОЙ
…

а)
«Сервис (Данные)» → «Обработка данных»
→ «Поиск решения»

б)
«Сервис (Данные)» → «Анализ данных» →
«Описательная статистика»

в)
«Сервис (Данные)» → «Обработка данных»
→ «Основная статистика»

Решение:
вызов пакета вычисления средних величин
и характеристик вариационного ряда в
программе Excel производится командой
«Сервис (Данные)» → «Анализ данных» →
«Описательная статистика».

Правильный
ответ:
б.

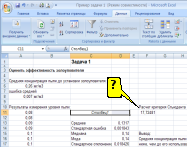
РЕЗУЛЬТАТ
ОБРАБОТКИ ВАРИАЦИОННОГО РЯДА, ВЫПОЛНЕННЫЙ
МОДУЛЕМ «ОПИСАТЕЛЬНАЯ СТАТИСТИКА»
ПРОГРАММЫ EXCEL (СМ. РИСУНОК), БУДЕТ
ПОМЕЩЕН В СЛЕДУЮЩИЕ ЯЧЕЙКИ …

а)
начиная с ячейки А11

б)
начиная с ячейки С11

в)
в диапазоне ячеек A11:A110

г)
в ячейку A110

Решение:
результат обработки вариационного
ряда, выполненный модулем «описательная
статистика» программы Excel размещается
в выходном интервале (см.рисунок) начиная
с ячейки С11 и ниже.

Правильный
ответ:
б.

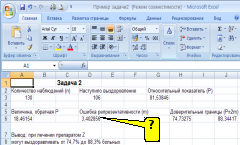
ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА СТЬЮДЕНТА В
ПРОГРАММЕ EXCEL (СМ. РИСУНОК) ЯВЛЯЕТСЯ …

а)
=(A6-D13)/корень(A8^2+D14^2)

б)
=(A6+D13)*корень(A8^2+D14^2)

в)
=(A6-D13)/корень(A8^2-D14^2)

Решение:
формулой вычисления коэффициента
Стьюдента в программе Excel (см.рисунок)
является «=(A6-D13)/корень(A8^2+D14^2)».

Правильный
ответ:
а.

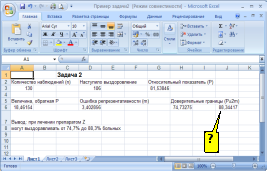
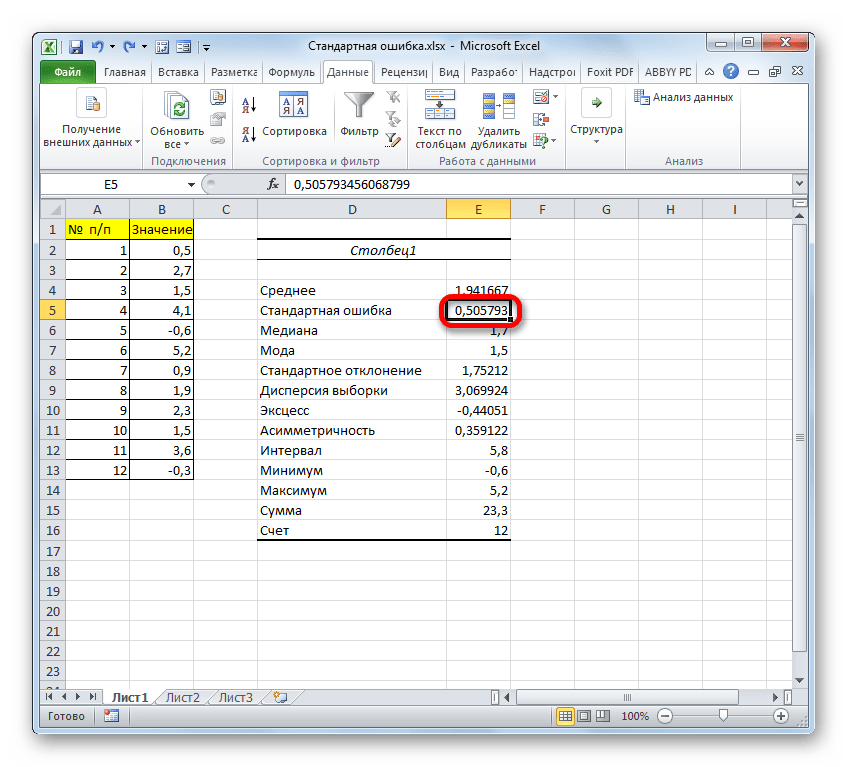
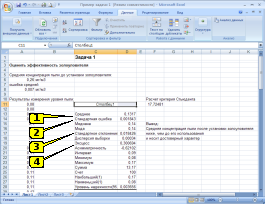
ОБОЗНАЧЕНИЕ
ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ В ТАБЛИЦЕ
РЕЗУЛЬТАТОВ ОБРАБОТКИ ВАРИАЦИОННОГО
РЯДА ПАКЕТОМ «ОПИСАТЕЛЬНАЯ СТАТИСТИКА»
ПРОГРАММЫ EXCEL (СМ. РИСУНОК) СООТВЕТСТВУЕТ
ПОЗИЦИИ …

а)
1

б)
2

в)
3

г)
4

Решение:
обозначение ошибки репрезентативности
в таблице результатов обработки
вариационного ряда пакетом «Описательная
статистика» программы Excel (см.рисунок)
соответствует позиция 2 (Стандартная
ошибка).

Правильный
ответ:
б.

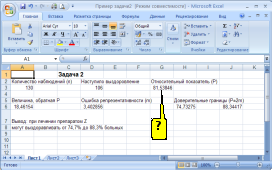
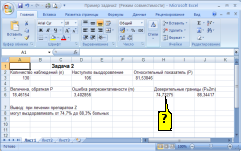
ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ ОТНОСИТЕЛЬНОГО ПОКАЗАТЕЛЯ
(P) В ПРОГРАММЕ EXCEL (СМ. РИСУНОК)
ЯВЛЯЕТСЯ …

а)
=A1*100/D3

б)
=D3*100/A3

в)
=A2*100/D2

г)
=Д3*100/А3

Решение:
формулой вычисления относительного
показателя (P)
в программе Excel (см.рисунок) является
«=D3*100/A3».

Правильный
ответ:
б.

ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ ВЕЛИЧИНЫ, ОБРАТНОЙ P, В
ПРОГРАММЕ EXCEL (СМ. РИСУНОК) ЯВЛЯЕТСЯ …

а)
= 100 — G2

б)
= 100 — А5

в)
= 100 — G3

г)
= 100 — Г3

Решение:
формулой вычисления величины, обратной
P, в программе Excel (см. рисунок) является
«= 100 — G3».

Правильный
ответ:
в.

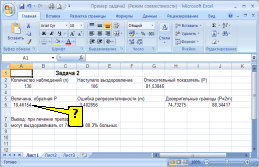
ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ
ОТНОСИТЕЛЬНОГО ПОКАЗАТЕЛЯ В ПРОГРАММЕ
EXCEL (СМ. РИСУНОК) ЯВЛЯЕТСЯ …

а)
=корень(G3*A6/A3)

б)
=корень(Г3*A6/A3)

в)
=корень(G3*A6*A3)

г)
=корень(Щ3*A6*A3)

Решение:
формулой вычисления ошибки репрезентативности
относительного показателя в программе
Excel (см. рисунок) является «=корень(G3*A6/A3)».

Правильный
ответ:
а.

ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ НИЖНЕЙ ДОВЕРИТЕЛЬНОЙ
ГРАНИЦЫ В ПРОГРАММЕ EXCEL (СМ. РИСУНОК)
ЯВЛЯЕТСЯ …

а)
=G2-2*D5

б)
=Г3-2*D6

в)
=G3-2*D6

г)
=G3+2*D6

Решение:
формулой вычисления нижней доверительной
границы в программе Excel (см. рисунок)
является «=G3-2*D6».

Правильный
ответ:
в.

ФОРМУЛОЙ
ВЫЧИСЛЕНИЯ ВЕРХНЕЙ ДОВЕРИТЕЛЬНОЙ
ГРАНИЦЫ В ПРОГРАММЕ EXCEL (СМ. РИСУНОК)
ЯВЛЯЕТСЯ …

а)
=G2+2*D5

б)
=Г3-2*D6

в)
=G3-2*D6

г)
=G3+2*D6

Решение:
формулой вычисления верхней доверительной
границы в программе Excel (см. рисунок)
является «=G3+2*D6».

Правильный
ответ:
г.

Источник

Загрузить PDF

В этой статье мы расскажем вам, как в Excel вычислить стандартную ошибку среднего. Для этого стандартное отклонение (σ) нужно разделить на квадратный корень (√) из размера выборки (N).

Шаги

1

Запустите Excel. Нажмите на значок в виде белой буквы «Х» на зеленом фоне.
2

Откройте или создайте таблицу Excel. Чтобы открыть готовую таблицу с данными, нажмите «Открыть» на левой панели. Чтобы создать таблицу, нажмите «Создать» и введите данные.
3
Вычислите стандартное отклонение. Чтобы сделать это, нужно выполнить несколько действий, но в Excel можно просто ввести следующую формулу: =СТАНДОТКЛОН.В(''диапазон ячеек'').
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите =СТАНДОТКЛОН.В(A1:A20), чтобы вычислить стандартное отклонение.
4
Введите формулу для вычисления стандартной ошибки среднего в пустой ячейке. Формула выглядит так:=СТАНДОТКЛОН.В(''диапазон ячеек'')/КОРЕНЬ(СЧЁТ("диапазон ячеек")).
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите формулу =СТАНДОТКЛОН.В(A1:A20)/КОРЕНЬ(СЧЁТ(A1:A20)). Так вы вычислите стандартную ошибку среднего.
Реклама

Об этой статье

Эту страницу просматривали 33 378 раз.

Была ли эта статья полезной?

Источник

Стандартная ошибка появляется при прогнозировании каких-либо данных или арифметических вычислениях, поэтому важно научиться находить этот параметр. В этой публикации разбираем, как найти и исправить стандартную ошибку путем использования инструментов Excel.

Расчет средней арифметической ошибки

В Microsoft Excel цельность и однородность выборки определяется при помощи стандартной ошибки. Стандартная ошибка — это квадратный корень из дисперсии. В приложении предусмотрено два варианта поиска стандартной ошибки: при помощи пакетного анализа и расширенных функций программы.
Чтобы найти значение средней арифметической, необходимо выполнить деление суммарной величины выборки на ее количество в электронной книге.

Расчет стандартной ошибки при помощи встроенных функций

Для того, чтобы правильно вычислять, необходимо изучить пошаговую инструкцию. В этом способе подбор результатов будет осуществляться с помощью комбинированных манипуляций.

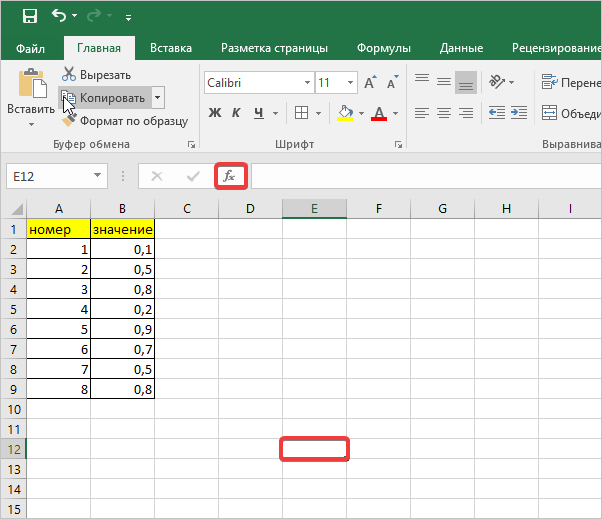
Для расчетов будем использовать таблицу с выборкой чисел. Кликаем на любой пустой ячейке на листе, где будет отображаться результат. Затем нажимаем кнопку «Вставить функцию.

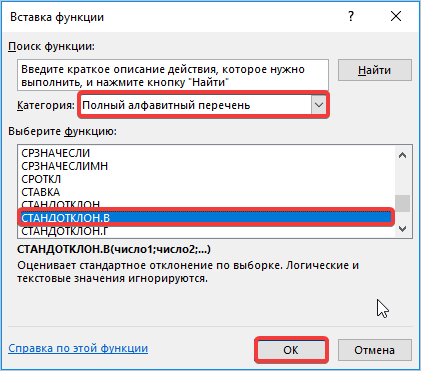
Далее перед вами открывается диалоговое окно, в котором необходимо использовать «СТАНДОТКЛ.В», для этого в поле «Категория» необходимо выбрать «Полный алфавитный перечень». Затем нажмите кнопку «ОК».

В окне «Аргументы функции» кликаем в первом поле «Число 1», затем выполняем выделение мышью диапазона ячеек со значениями таблицы и нажимаем кнопку «ОК».

Далее активируем ячейку с нашими значениями, переходим в строку формулы и ставим после значений наклонную линию. Переходим в поле наименования, кликаем на указывающий вниз флажок, где из списка выбираем «Другие функции».

Снова активируется окно с перечнем функций, в котором необходимо выбрать категорию «Математические», затем функцию «Корень». Далее нажмите кнопку «ОК».

Далее открывается окно, в котором необходимо заполнить поле с числом. Для этого переходим в поле «Имя», где спускаемся к пункту «Счет». Если его нет, ищите в дополнительных функциях.

После выполнения этих шагов, стандартная ошибка высчитывается автоматически, пользователю остается только сверить их и проверить значение на некорректное отображение.

Важно!

Для малых и стандартных выборок необходимо использовать разные формулы. В первом случае (если находится до 30 значений), ее необходимо видоизменить.

Решение задачи с помощью опции «Описательная статистика»

Благодаря опции «Описательная статистика» удается выполнить вычисление по различным критериям. По этим правилам удается найти среднюю арифметическую ошибку. Для использования данного метода предварительно нужно запустить «Пакет анализа».

Переходим во вкладку «Файл», где перемещаемся в пункт «Параметры». Далее нажимаем на запись «Надстройки».

Открывается окошко, в нем в графе «Управление» должно быть прописано «Надстройки Excel», затем рядом нажимаем кнопку «Параметры».

В появившемся окне находим «Пакет анализа» и нажимаем кнопку «ОК».

Далее выбираем любую свободную ячейку, переходим во вкладку «Данные» и нажимаем «Анализ данных» в блоке «Анализ».

Происходит запуск вспомогательного окошка, в котором необходимо выбрать из всех инструментов «Описательную статистику» и нажать кнопку «ОК».

Открывается новый мастер значений. Здесь нужно вводить данные предельно внимательно. В поле «Входной интервал» вносим адрес диапазона ячеек с выборкой. Затем указываем параметр «Группирование» «По столбцам». Затем выбираем место для «выходного интервала», его должно быть столько же, сколько и «входного». Ставим галочку напротив «Итоговая статистика» и нажимаем кнопку «ОК».

В результате вычислений вы получаете небольшую таблицу, в которой указаны все данные с определенной стандартной ошибкой.

Источник

Стандартная ошибка в Excel

Расчет с помощью комбинаций функций

На примере рассмотрим составленный алгоритм действий по расчету ошибки средней арифметической с использованием комбинаций функций. Для того чтобы выполнить задачу, нужно использовать операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ. Выборка будет использоваться из 12 чисел, которые представлены в таблице.

Выделите ячейку, в которой отобразится итоговое значение стандартной ошибки. Кликаете на иконку «Вставить функцию».

Появится Мастер функций, в котором нужно произвести перемещение в блок «Статистические». Появится список наименований, выбираете «СТАНДОТКЛОН.В».

Запустится окно аргументов выбранного оператора, предназначенного для оценивания стандартного отклонения при выборке. У него такой синтаксис – =СТАНДОТКЛОН.В(число1;число2;…). Устанавливаете курсор в полу «Число1». Далее, зажав левую кнопку мыши, выделяете курсором весь диапазон выборки, чтобы координаты этого массива отобразились там же в поле окна. Кликаете на ОК.

В ячейке появится проделанный результат, но это еще не то, что мы хотим получить в итоге. Теперь нужно стандартное отклонение разделить на квадратный корень от числа элементов выборки. Выделяете ячейку с нужной функцией и устанавливаете курсор мышки в строку формул. Дописываете выражение, которое там уже существует, знаком деления (/). Далее нажимаете на пиктограмму перевернутого вниз углом треугольника (находится слева от строки формул). Должен открыться список недавно использованных функций. Находите оператора «КОРЕНЬ» и нажимаете на него. Если его нет в списке, то кликайте на «Другие функции…».

Должен снова запуститься Мастер функций, в котором нужно перейти в категорию «Математические». Выделяете там «КОРЕНЬ» и кликаете ОК.

Далее должно открыться окно аргументов функции КОРЕНЬ. Его синтаксис простой – =КОРЕНЬ(число). Устанавливаете курсор в поле «Число» и нажимаете на уже знакомый треугольник, чтобы показался список последних использованных функций. Находите «СЧЕТ» и нажимаете на него. Если в списке его нет, тогда нажимаете на «Другие функции…».

Появится раскрывшееся окно Мастера функций, в котором нужно переместиться в группу «Статистические». В ней выделяете «СЧЕТ» и кликаете ОК.

Должно запуститься окно аргументов функции СЧЕТ. Синтаксис функции будет таким – =СЧЁТ(значение1;значение2;…). Ставите курсор в строку «Значение1» и зажимаете левую кнопку мыши, чтобы выделить весь диапазон выборки. Когда координаты отобразятся, жмите ОК.

Когда будет выполнено последнее действие, то не только произведется расчет количества ячеек, которые заполнены числами, но и вычисляется ошибка средней арифметической. Величина будет выведена в ячейку с размещенной сложной формулой, вид которой таков – =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)).

Если выборка до 30 единиц, тогда лучше применять немного другую формулу – =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1).

Применение инструмента «Описательная статистика»

Когда будет открыт документ с выборкой, нужно перейти во вкладку «Файл».

В левом вертикальном меню заходите в раздел «Параметры».

Должно запуститься окно параметров Excel, в левой части которого нужно перейти в «Надстройки».

В самом низу окна находите «Управление» в выставляете в нем параметр «Надстройки Excel». Кликаете на «Перейти…» справа от него.

В окне надстроек появится список скриптов, которые доступны и нужно отметить галочкой «Пакет анализа», а затем нажать ОК.

Теперь на странице должна появиться новая группа инструментов «Анализ». Для перехода к ней кликаете на вкладку «Данные».

Кликаете на «Анализ данных» в блоке инструментов «Анализ» в самом конце.

Запустится окно выбора инструмента анализа, в котором необходимо выделить «Описательная статистика» и нажать справа на ОК.

Далее запустится окно настроек инструмента комплексного статистического анализа «Описательная статистика». Здесь нужно установить все так, в зависимости от того, что именно вы хотите получить в итоге.

После всех совершенных манипуляций, инструмент «Описательная статистика» должен отобразить результаты обработки выборки на текущем листе. Разноплановых статистических показателей будет немало, но среди них находится и тот, который нам нужен – «Стандартная ошибка».

Microsoft Excel

трюки • приёмы • решения

Какие существуют ошибки в Excel и как их исправлять

Когда вы вводите или редактируете формулу, а также когда меняется одно из входных значений функции, Excel может показать одну из ошибок вместо значения формулы. В программе предусмотрено семь типов ошибок. Давайте рассмотрим их описание и способы устранения.

#ДЕЛ/О! — данная ошибка практически всегда означает, что формула в ячейке пытается разделить какое-то значение на ноль. Чаще всего это происходит из-за того, что в другой ячейке, ссылающейся на данную, находится нулевое значение или значение отсутствует. Вам необходимо проверить все связанные ячейки на предмет наличия таких значений. Также данная ошибка может возникать, когда вы вводите неправильные значения в некоторые функции, например в ОСТАТ() , когда второй аргумент равен 0. Также ошибка деления на ноль может возникать, если вы оставляете пустые ячейки для ввода данных, а какая-либо формула требует некоторые данные. При этом будет выведена ошибка #ДЕЛ/0!, что может смутить конечного пользователя. Для этих случаев вы можете использовать функцию ЕСЛИ() для проверки, например =ЕСЛИ(А1=0;0;В1/А1) . В этом примере функция вернет 0 вместо ошибки, если в ячейке А1 находится нулевое или пустое значение.
#Н/Д — данная ошибка расшифровывается как недоступно, и это означает, что значение недоступно функции или формуле. Вы можете увидеть такую ошибку, если введете неподходящее значение в функцию. Для исправления проверьте прежде всего входные ячейки на предмет ошибок, особенно если в них тоже появляется данная ошибка.
#ИМЯ? — данная ошибка возникает, когда вы неправильно указываете имя в формуле или ошибочно задаете имя самой формулы. Для исправления проверьте еще раз все имена и названия в формуле.
#ПУСТО! — данная ошибка связана с диапазонами в формуле. Чаще всего она возникает, когда в формуле указывается два непересекающихся диапазона, например =СУММ(С4:С6;А1:С1) .
#ЧИСЛО! — ошибка возникает, когда в формуле присутствуют некорректные числовые значения, выходящие за границы допустимого диапазона.
#ССЫЛКА! — ошибка возникает, когда были удалены ячейки, на которые ссылается данная формула.
#ЗНАЧ! — в данном случае речь идет об использовании неправильного типа аргумента для функции.

Если при вводе формулы вы случайно неправильно расставили скобки, Excel выведет на экран предупреждающее сообщение — см. рис. 1. В этом сообщении вы увидите предположение Excel о том, как их необходимо расставить. В случае если вы подтверждаете такую расстановку, нажмите Да. Но зачастую требуется собственное вмешательство. Для этот нажмите Нет и исправьте скобки самостоятельно.

Обработка ошибок с помощью функции ЕОШИБКА()

Перехватить любые ошибки и обработать их можно с помощью функции ЕОШИБКА() . Данная функция возвращает истину или ложь в зависимости от того, появляется ли ошибка при вычислении ее аргумента. Общая формула для перехвата выглядит так: =ЕСЛИ(ЕОШИБКА(выражение);ошибка; выражение) .

Рис. 1. Предупреждающее сообщение о неправильно расставленных скобках

Функция если вернет ошибку (например, сообщение), если при расчете появляется ошибка. Например, рассмотрим следующую формулу: =ЕСЛИ(ЕОШИБКА(А1/А2);””; А1/А2) . При возникновении ошибки (деление на 0) формула возвращает пустую строку. Если же ошибки не возникает, возвращается само выражение А1/А2 .

Существует другая, более удобная функция ЕСЛИОШИБКА() , которая совмещает две предыдущие функции ЕСЛИ() и ЕОШИБКА() : ЕСЛИОШИБКА(значение;значение при ошибке) , где: значение — выражение для расчета, значение при ошибке — возвращаемый результат в случае ошибки. Для нашего примера это будет выглядеть так: =ЕСЛИОШИБКА(А1/А2;””) .

How to dou

Когда вы создаете граф в Excel и ваши данные являются средствами, рекомендуется включить стандартную ошибку каждого значения на вашем графике. Это дает зрителю представление о распространении баллов вокруг каждого среднего.

Вот пример ситуации, когда это возникает. Данные являются (вымышленными) результатами тестов для четырех групп людей. Каждый заголовок столбца указывает количество времени подготовки для восьми человек в группе. Вы можете использовать графические возможности Excel для рисования графика. Поскольку независимая переменная является количественной, граф линии является подходящим.

Четыре группы, их средства, стандартные отклонения и стандартные ошибки. На графике показаны групповые средства.

Для каждой группы вы можете использовать AVERAGE для вычисления среднего и STDEV. S для вычисления стандартного отклонения. Вы можете рассчитать стандартную ошибку каждого среднего. Выберите ячейку B12, поэтому в поле формулы показано, что вы вычислили стандартную ошибку для столбца B по этой формуле:

= B11 / SQRT (COUNT (B2: B9))

Фокус в том, чтобы получить каждую стандартную ошибку в графике. В Excel 2016 это легко сделать, и оно отличается от предыдущих версий Excel. Начните с выбора графика. Это приведет к появлению вкладок Design and Format. Выберите

Дизайн | Добавить элемент диаграммы | Ошибка баров | Дополнительные параметры ошибок.

Путь к вставке баров ошибок.

В меню «Бары ошибок» вы должны быть осторожны. Один из вариантов – стандартная ошибка. Избегай это. Если вы считаете, что этот выбор указывает Excel на стандартную ошибку каждого значения на графике, будьте уверены, что Excel не имеет абсолютно никакого представления о том, о чем вы говорите. Для этого выбора Excel вычисляет стандартную ошибку набора из четырех средств – не стандартную ошибку в каждой группе.

Дополнительные параметры панели ошибок являются подходящим выбором. Откроется панель «Формат ошибок».

Панель «Ошибки формата».

В области «Направление» панели выберите переключатель рядом с «Оба», а в области «Стиль конца» выберите переключатель рядом с «Кап».

Один выбор в области «Сумма ошибки» – это стандартная ошибка. Избегайте этого. Это не означает, что Excel помещает стандартную ошибку каждого среднего на график.

Прокрутите вниз до области «Сумма ошибки» и выберите переключатель рядом с «Пользовательский». Это активирует кнопку «Укажите значение». Нажмите эту кнопку, чтобы открыть диалоговое окно «Пользовательские ошибки». С помощью курсора в поле «Положительное значение ошибки» выберите диапазон ячеек, который содержит стандартные ошибки ($ B $ 12: $ E $ 12). Вставьте вкладку «Отрицательная ошибка» и сделайте то же самое.

Диалоговое окно «Нестандартные ошибки».

Это поле Negative Error Value может дать вам небольшую проблему. Перед тем, как вводить диапазон ячеек, убедитесь, что он очищен от значений по умолчанию.

Нажмите «ОК» в диалоговом окне «Нестандартные ошибки» и закройте диалоговое окно «Формат ошибок», и график будет выглядеть следующим образом.

График группы означает, включая стандартную ошибку каждого среднего.

Стандартная ошибка средней арифметической

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ 2 – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Источник

Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi  X )

N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8  16  20  24  32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
 = 17
2) 16 20 24 32
 = 23
3) 8
16 24 32
 = 20
4) 8
16 20 32
 = 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что  , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n  30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда 
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
 = 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,

означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и  = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что  будет находиться в пределах
доверительного интервала x — t SX     + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX     + t SX
9 — 1,96
3271
.
327
.
   92+1,96
100
100
или 9+ 0.196  3,27    9 + 1..96  3,27 или 8. 36    9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр 
находится в интервале 8.36 — 9.64.
95%

Источник