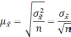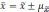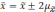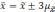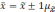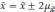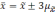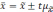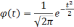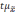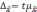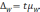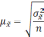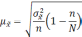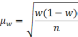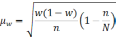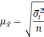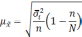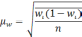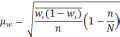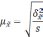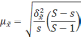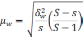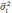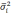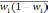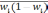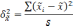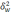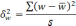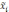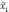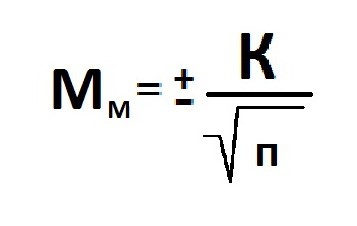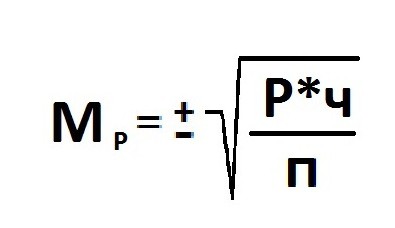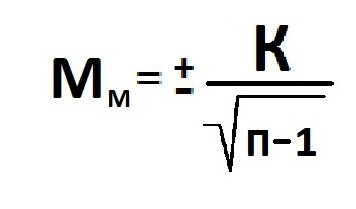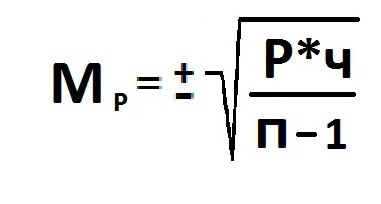а) Виды ошибок
В процессе исследования явлений может
возникать отклонение исчисленных
показателей от их действительной
величины, то есть могут возникать ошибки
статистического наблюдения.
По источникам происхождения ошибки
наблюдения можно подразделить на
следующие:
-
преднамеренные;
-
непреднамеренные,
которые в свою очередь делятся на:
-
случайные;
-
систематические;
-
репрезентативности
(представительности).
Преднамеренные(сознательные, злостные) получаются в
результате того, что сознательно
сообщаются неправильные данные. Например,
сокрытие фирмами прибыли от налогообложения,
искажение сведений об объеме выпускаемой
продукции, приписки и т. д.
Законом
предусматривается применение экономических
и административных мер к предприятиям
и лицам за злостные ошибки (иногда и
уголовная ответственность).
Непреднамеренные
случайныеошибки чаще связаны с
невнимательностью регистратора,
небрежностью в заполнении документов,
неточностью измерительных приборов,
ошибками в ответах опрашиваемых.
Непреднамеренные
систематическиеошибки возникают
при округлении признака в большую или
меньшую сторону, при использовании ЭВМ.
Ошибки
репрезентативности(представительности)
свойственны несплошному наблюдению,
они возникают вследствие неправильного
выбора единиц для обследования, нарушен
принцип случайного отбора, и выборочная
совокупность не полно характеризует
генеральную.
Б) Способы предотвращения ошибок статистического наблюдения
Чтобы
предупредить возникновение ошибок или
уменьшить их размеры необходимо:
-
обеспечивать
правильный подбор и подготовку кадров; -
вести широкую
разъяснительную работу, применять меры
взыскания за искажение фактов; -
проводить
систематический контроль.
Контроль может
быть: счетным и логическим.
Счетный контроль
заключается в проверке точности
арифметических расчетов.
Логический
контроль проводится путем сопоставления
полученных данных с известными признаками,
логическое осмысление, сопоставление
с данными за прошлый период.
Например, о
заработной плате работников предприятия
можно судить по отчету, по труду и по
отчету о себестоимости продукции.
Сведения о заработной плате должны быть
одинаковыми, сопоставимыми (приведите
примеры).
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибка
репрезентативности
— расхождение между выборочной
характеристикой и характеристикой
генеральной совокупности.
Ошибки
репрезентативности
-
Систематические
— возникают в результате нарушения
научных принципов отбора единиц
совокупности (преднамеренные и
непреднамеренные). -
Случайные
возникают в результате несплошного
характера наблюдения (средняя и
предельная ошибки выбора).
Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.
Средняя
ошибка выборки
— такое расхождение между средними
выборочной и генеральной совокупностями,
которое не превышает ±.
В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:
Формула
для определения величины средней ошибки
выборки для количественного признака:
Формула
для определения величины средней ошибки
выборки для альтернативного признака:
Полученное
значение средней ошибки необходимо для
установления возможного значения 
Которое определяется по формуле:
Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.
В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

вероятность достигает 0,954 (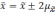
Если утроить значение то вероятность
увеличится до 0,997 (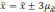
|
Возможное |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:
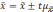
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:
На
практике пользуются готовыми таблицами
этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 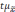
Полученную величину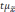
ошибкой выборки.
Предельная
ошибка выборки
—
максимально
возможное расхождение выборочной и
генеральной средних,
т.е.
максимум ошибки при заданной вероятности
ее появления.
Предельная
ошибка выборки для количественного
признака:
Предельная
ошибка выборки для альтернативного
признака:
В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:
|
Способ |
Оцениваемый |
Повторный |
Бесповторный |
|
Собственно случайный механический |
Средняя |
|
|
|
Доля |
|
|
|
|
Типический |
Средняя |
|
|
|
Доля |
|
|
|
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
— средняя из групповых дисперсий;
wi
— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;
— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S
– общее число серий;
s
– число отобранных серий;
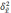
межгрупповая дисперсия средних,
определяемая по формуле:
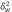
межгрупповая дисперсия доли, определяемая
по формуле:
— средняя
i-й
серии;
—
средняя по всей выборочной совокупности;
w
— доля признака i-й
серии;
— общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
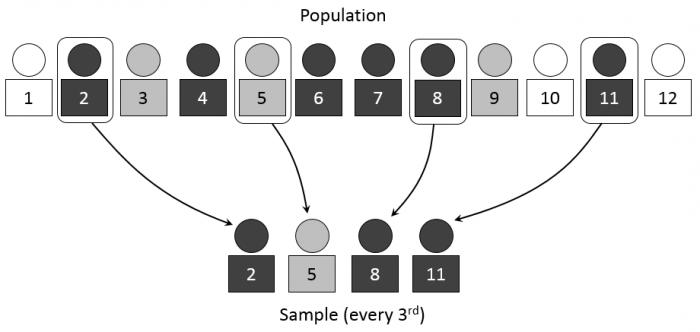
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Пример об ошибке репрезентативности
Лекция 4.1 Выборочный метод
К настоящему времени Вы заработали баллов: 0 из 0 возможных.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
Генеральная совокупность — вся подлежащая изучению совокупность объектов (наблюдений).
Генеральная совокупность носит гипотетический характер. Она представляет собой совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данных условиях. Даже если бы у нас была возможность провести сплошное исследование всей совокупности признака, все равно в нее не попали бы объекты, которое по какой то причине отсутствуют на текущий момент, но должны были существовать при данных условиях.
Та часть объектов, которая отобрана для непосредственного изучения, называется выборочной совокупностьюили выборкой
Сущность выборочного метода
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности выносить суждение о её свойствах в целом
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть репрезентативной(представительной).
Репрезентативная выборка сохраняет и повторяет структуру генеральной совокупности.
Если две выборки взяты из одной генеральной совокупности, то разница в получаемых оценках (например, средних) будет носить случайный характер, как следствие ошибки репрезентативности
Ошибка репрезентативности возникает по причине того, что мы исследуем не всю совокупность, а только её части (выборки). Мы получаем случайную комбинацию элементов из генеральной совокупности.
Для того, чтобы минимизировать различия однородных (взятых из одной генеральной совокупности) выборок необходимо правильным образом их формировать.
Наилучшим способом формирования репрезентативной выборки является случайный отбор элементов из генеральной совокупности без расчленения на части или группы (случайная выборка).
Пример об ошибке репрезентативности
Рассмотрим следующий пример.
Исследователь задался вопросом: «существуют ли различия в эмпатических способностях между психологами и педагогами?». Для того чтобы это прояснить он набрал две группы испытуемых в соответствии с их профессиональной деятельностью и предложил им заполнить опросник на эмпатические способности. Далее, он рассчитал среднее значение в каждой группе.
В группе психологов среднее составило 23,4 балла, а в группе педагогов 21,1. Таким образом, разница в средних между группами составила2,3 балла (23,4 — 21,1 = 2,3).
Если бы представители этих профессий не отличались по изучаемому признаку, тогда разница в средних равнялась бы нулю.
Однако, можно ли считать эту разницу в 2,3 балла достаточной, чтобы судить о реальных различиях между группами? Может сложится так, что психологи и педагоги по эмпатии в реальности не отличаются (выборки однородны), а разница в 2,3 балла, полученная исследователем носит случайный характер, как ошибка репрезентативности.
Таким образом, мы можем сформулировать две гипотезы:
Гипотезы являются альтернативами по отношению к друг другу. Принятие одной из них как верной влечет за собой исключение «истинности» другой.
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА
Статистическая гипотеза – это любое предположение о виде или параметрах неизвестного закона распределения (закона распределения генеральной совокупности)
В статистике принято формулировать пару гипотез. Первая гипотеза называется нулевой, а вторая – альтернативной.
| Нулевая гипотеза Н | Альтернативная гипотеза Н1 |
| 1. 1. Является проверяемой 2. Обычно гипотеза об отсутствии явления (например, различий или зависимости) | Является логическим отрицанием нулевой |
| Поскольку нулевая гипотеза является проверяемой, то её можно отвергать и принимать | Альтернативную гипотезу принимают как следствие отрицания нулевой гипотезы |
пример:
· Н (нулевая): Женщины не отличаются от мужчин по среднему уровню развития эмпатических способностей (средние значения равны)
· Н1 (альтернативная): Средний уровень эмпатических способностей выше у женщин по сравнению с мужчинами
пример:
· Н (нулевая): Линейная корреляция между самооценкой и тревожностью равна 0
· Н1 (альтернативная): Самооценка отрицательно связана с тревожностью (линейная корреляция меньше нуля / чем выше самооценка, тем ниже тревожность и наоборот)
Вопрос:Какая из двух формулировок соответствует нулевой гипотезе Н?
· А) между психологами и педагогами нет различий по среднему уровню выраженности эмпатии
· Б) между психологами и педагогами есть различия по среднему уровню выраженности эмпатии
Статистический критерий
Правило, по которому нулевая гипотеза отвергается или принимается, называется статистическим критерием.
Статистика – это специально составленная выборочная характеристика (распределение), у которой есть критическое значение такое, что если верна нулевая гипотеза, то вероятность (α) того, что случайная величина превысит это критическое значение, мала (Кремер Н.Ш., 2004).
Критическое значение делит распределение «нулевой гипотезы» на две области: область допустимых значений и область критических значений
Таким образом, критические значения позволяют исследователю либо принять, либо отвергнуть нулевую гипотезу.
В математической статистике можно подбирать критические значение для разных альфа-уровней (уровней значимости). Чаще всего:
1. Критическое значение, которое выделяет критическую область с вероятностью α
Источник
Ошибки статистического наблюдения и основные приёмы их устранения



Всякое статистическое наблюдение должно быть полным и достоверным. Однако по ряду причин степень точности данных может быть различной.
Все ошибки наблюдения подразделяются на два вида:
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи.
Ошибки регистрации могут возникать как при сплошном наблюдении, так и при несплошном и имеют следующие виды:
Случайные ошибки – это ошибки, которые возникают в результате небрежной описки или невнимательного отношения регистратора при заполнении формуляра (ошибки в подсчёте).
Систематические ошибки – это ошибки, которые искажают сведения по каждой отдельной единице наблюдения в одном и том же направлении.
Систематические ошибки делятся на:
Преднамеренные ошибки (сознательные, тенденциозные ошибки), возникающие в результате сознательного искажения статистической информации. К ним относятся: приписки, неправильные сведения об объёме выпущенной продукции, об остатках сырья и материалов и т. д.
Непреднамеренные ошибки – это ошибки, которые возникают в результате случайных причин, т.е. неумышленно (неисправность измерительных приборов, невнимательность регистратора и т.д.).
Ошибки репрезентативности свойственны несплошному наблюдению. Они возникают в результате выборочного наблюдения, когда отобранная часть единиц совокупности недостаточно полно отражает состав всей изучаемой совокупности.
Ошибки репрезентативности (так же, как и ошибки регистрации) могут быть случайными и систематическими.
Случайные ошибки оцениваются с помощью математических методов.
Систематические ошибки – это отклонения, которые возникают в результате случайного отбора единиц изучаемой совокупности. Их размеры не поддаются количественной оценке.
Для выявления и устранения допущенных при регистрации ошибок применяются следующие методы:
а) внешний контроль;
б) логический контроль;
в) счётный контроль.
При внешнем контроле проверяется: правильность оформления документов; наличие всех необходимых записей, которые предусмотрены инструкцией и т.д.
Логический контроль заключается в проверке ответов на вопросы программы наблюдения путём сопоставления полученных данных с другими источниками.
Сущность счётного (арифметического) контроля заключается в счётной проверке всех итоговых показателей, которые содержатся в отчётности или формуляре исследования. Задачей такого контроля является исправление итогов и отдельных числовых показателей.
В ряде случаев, при счётном контроле данных статистического наблюдения применяется метод балансовой увязки показателей (наличие на начало отчётного периода плюс поступления минус расход должно быть равно наличию на конец отчётного периода). Такой метод применяют: при проверках поголовья скота, при учёте поступления и расхода сырья и материалов и т.д.
Указанные методы проверки достоверности статистического наблюдения позволяют сократить до минимального значения допуск ошибок.
Источник
Репрезентативность — что это за процесс? Ошибка репрезентативности
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Источник
6. Достоверность статистических данных и
ошибки статистического наблюдения
Важнейшим требованием
предъявляемым к статистическим данным является их достоверность. Под достоверностью
данных наблюдения понимается степень приближения, соответствия
данных тому, что есть на самом деле. Расхождение межу фактическим значением и
результатом наблюдения называют погрешностью (ошибкой) наблюдения.
Ошибки наблюдения
разнообразны по происхождению и своему содержанию. В зависимости от
причин возникновения различают следующие виды ошибок:
• методические ошибки;
• ошибки регистрации;
• ошибки
репрезентативности (представительности).
Методические ошибки возникают
в результате использования несовершенных методик, неправильных теоретических
концепций, лежащих в основе исследования.
Ошибки регистрации возникают при
получении данных об отдельных единицах совокупности вследствие неправильного
установления фактов в процессе наблюдения или неправильной их записи. Они
подразделяются на:
-объективные (непреднамеренные)
причиной появления которых является неправильное восприятие наблюдаемых фактов,
неисправность измерительных приборов и неправильная регистрация. Такие ошибки
являются результатом добросовестного заблуждения регистратора;
— субъективные (преднамеренные)
ошибки, возникающие по причине сознательного искажения фактов. К ним относятся
всевозможные преднамеренные ошибки и приписки, при которых опрашиваемый
преднамеренно сообщает неправильные сведения; регистратор преднамеренно
воздействует на респондента с целью получения нужного ответа; регистратор
преднамеренно искажает в формулярах результаты наблюдения.
Ошибки репрезентативности
(представительности) характерны только для несплошного наблюдения.
Они возникают в результате того, что состав отобранной для обследования части
единиц совокупности (выборки) не полностью отражает состав и свойства всей
изучаемой совокупности, несмотря на то, что регистрация сведений по каждой
отобранной единице была проведена точно.
По форме проявления (по
влиянию на результат) ошибки делятся на:
• систематически;
• случайные.
Систематические ошибки возникают
по какой-то определенной причине и вызывают одностороннее искажение значений
признака у наблюдаемых единиц (увеличение или уменьшение). Они очень опасны,
так как величина показателя, рассчитанная в целом по всей совокупности будет
включать накопленную ошибку.
Случайные ошибки являются
результатом действия различных случайных факторов. Они не имеют какой-либо
направленности. В больших совокупностях в результате действия закона больших
чисел эти ошибки взаимно погашаются и не оказывают существенного влияния на
точность наблюдения.
Оба вида ошибок в любом
исследовании выступают совместно и составляют совокупную ошибку наблюдения Δ:
Δ=σ+ε;
где σ — систематическая
ошибка наблюдения,
ε — случайная ошибка
наблюдения.
Для выявления и
исправления ошибок, данные наблюдения необходимо тщательно контролировать.
Процедура контроля сводится к следующему:
• Проверка материалов
наблюдения на полноту и правильность оформления. Проверяется полнота охвата
статистических единиц наблюдения, правильность заполнения каждого формуляра.
• Арифметический
(счетный) контроль. Этот вид контроля основан на использовании
количественных связей между показателями, которые могут быть проверены
арифметическими действиями. Такие связи обычно отражаются в заголовках граф или
строк формуляров. Например, графа x = графа y — графа z и т.д. Арифметический
контроль используется для проверки итоговых данных, с его помощью устанавливается
наличие ошибки.
• Логический контроль основан
на использовании логической взаимосвязи показателей, установлении логического
соответствия между ними. Он не выявляет ошибки наблюдения, а лишь ставит под
сомнение правильность полученных данных. Логический контроль заключается в
проверке ответов на вопросы программы наблюдения путем их логического
осмысления или сравнения полученных данных с другими источниками по данному
вопросу. Классическим примером логического контроля является соответствие данных
при переписи населения о возрасте, образовании и семейном положении. Для
проверки данных наблюдения обычно составляется схема контроля, в которую
включаются различные виды контроля. При обнаружении ошибок нельзя
самостоятельно их исправлять. Для этого необходимо получить дополнительную
информацию путем повторного наблюдения. Данные наблюдения считаются принятыми,
если они прошли контроль, и в них внесены все необходимые исправления.
Проверкой собранных данных заканчивается начальная стадия статистического
исследования. После этого можно переходить ко второй стадии исследования
обработке данных наблюдения. Обработка заключается в классификации и
систематизации полученного статистического материала, осуществляемых через
сводку и группировку.
О сводке и группировке мы
поговорим с Вами в следующей лекции.
1. Статистика как наука изучает:
а) единичные явления;
б) массовые явления;
в) периодические события.
2. Термин «статистика» происходит от слова:
а) статика;
б) статный;
в) статус.
3. Статистика зародилась и оформилась как самостоятельная учебная дисциплина:
а) до новой эры, в Китае и Древнем Риме;
б) в 17-18 веках, в Европе;
в) в 20 веке, в России.
4. Статистика изучает явления и процессы посредством изучения:
а) определенной информации;
б) статистических показателей;
в) признаков различных явлений.
5. Статистическая совокупность – это:
а) множество изучаемых разнородных объектов;
б) множество единиц изучаемого явления;
в) группа зафиксированных случайных событий.
6. Основными задачами статистики на современном этапе являются:
а) исследование преобразований экономических и социальных процессов в обществе; б) анализ и прогнозирование тенденций развития экономики; в) регламентация и планирование хозяйственных процессов;
а) а, в
б) а, б
в) б, в
7. Статистический показатель дает оценку свойства изучаемого явления:
а) количественную;
б) качественную;
в) количественную и качественную.
8. Основные стадии экономико-статистического исследования включают: а) сбор первичных данных, б) статистическая сводка и группировка данных, в) контроль и управление объектами статистического изучения, г) анализ статистических данных
а) а, б, в
б) а, в, г
в) а ,б, г
г) б, в, г
9. Закон больших чисел утверждает, что:
а) чем больше единиц охвачено статистическим наблюдением,тем лучше проявляется общая закономерность;
б) чем больше единиц охвачено статистическим наблюдением, тем хуже проявляется общая закономерность;
в) чем меньше единиц охвачено статистическим наблюдением, тем лучше проявляется общая закономерность.
10. Современная организация статистики включает: а) в России — Росстат РФ и его территориальные органы, б) в СНГ — Статистический комитет СНГ, в) в ООН — Статистическая комиссия и статистическое бюро, г) научные исследования в области теории и методологии статистики
а) а, б, г
б) а, б, в
в) а, в, г
1. Статистическое наблюдение – это:
а) научная организация регистрации информации;
б) оценка и регистрация признаков изучаемой совокупности;
в) работа по сбору массовых первичных данных;
г) обширная программа статистических исследований.
2. Назовите основные организационные формы статистического наблюдения:
а) перепись и отчетность;
в) разовое наблюдение;
г) опрос.
3. Перечень показателей (вопросов) статистического наблюдения, цель, метод, вид, единица наблюдения, объект, период статистического наблюдения излагаются:
а) в инструкции по проведению статистического наблюдения;
б) в формуляре статистического наблюдения;
в) в программе статистического наблюдения.
4. Назовите виды статистического наблюдения по степени охвата единиц совокупности:
а) анкета;
б) непосредственное;
в) сплошное;
г) текущее.
5. Назовите виды статистического наблюдения по времени регистрации:
а) текущее, б) единовременное; в) выборочное; г) периодическое; д) сплошное
а) а, в, д
б) а, б, г
в) б, г, д
6. Назовите основные виды ошибок регистрации: а) случайные; б) систематические; в) ошибки репрезентативности; г) расчетные
а) а
б) а, б
в) а, б, в,
г) а, б, в, г
7. Несплошное статистическое наблюдение имеет виды: а) выборочное;
б) монографическое; в) метод основного массива; г) ведомственная отчетность
а) а, б, в
б) а, б, г
в) б, в, г
8. Организационный план статистического наблюдения регламентирует: а) время и сроки наблюдения; б) подготовительные мероприятия;
в) прием, сдачу и оформление результатов наблюдения; г) методы обработки данных
а) а, б, г
б) а, б, в
9. Является ли статистическим наблюдением наблюдения покупателя за качеством товаров или изменением цен на городских рынках?
а) да
б) нет
10. Ошибка репрезентативности относится к:
а) сплошному наблюдению;
б) не сплошному выборочному наблюдению.
1. Статистическая сводка — это:
а) систематизация и подсчет итогов зарегистрированных фактов и данных;
б) форма представления и развития изучаемых явлений;
в) анализ и прогноз зарегистрированных данных.
2. Статистическая группировка — это:
а) объединение данных в группы по времени регистрации;
б) расчленение изучаемой совокупности на группы по существенным признакам;
в) образование групп зарегистрированной информации по мере ее поступления.
3. Статистические группировки могут быть: а) типологическими; б) структурными; в) аналитическими; г) комбинированными
а) а
б) а, б
в) а, б, в
г) а, б, в, г
4. Группировочные признаки, которыми одни единицы совокупности обладают, а другие — нет, классифицируются как:
а) факторные;
б) атрибутивные;
в) альтернативные.
5. К каким группировочным признакам относятся: образование сотрудников, профессия бухгалтера, семейное положение:
а) к атрибутивным;
б) к количественны.
6. Ряд распределения — это:
а) упорядоченное расположение единиц изучаемой совокупности по группам;
б) ряд значений показателя, расположенных по каким-то правилам.
7. К каким группировочным признакам относятся: сумма издержек обращения, объем продаж, стоимость основных фондов
а) к дискретным;
б) к непрерывным.
8. Какие виды статистических таблиц встречаются:
а) простые и комбинационные;
б) линейные и нелинейные.
1. Статистический показатель — это
а) размер изучаемого явления в натуральных единицах измерения
б) количественная характеристика свойств в единстве с их качественной определенностью
в) результат измерения свойств изучаемого объекта
2. Статистические показатели могут характеризовать:
а) объемы изучаемых процессов
б) уровни развития изучаемых явлений
в) соотношение между элементами явлений
г) а, б, в
3. По способу выражения абсолютные статистические показатели подразделяются на: а) суммарные; б) индивидуальные; в) относительные; г) средние; д) структурные
а) а, д
б) б, в
в) в, г
г) а, б
4. В каких единицах выражаются абсолютные статистические показатели?
а) в коэффициентах
б) в натуральных
в) в трудовых
5. В каких единицах будет выражаться относительный показатель, если база сравнения принимается за единицу?
а) в процентах
б) в натуральных
в) в коэффициентах
6. Относительные показатели динамики с переменной базой сравнения подразделяются на:
а) цепные
б) базисные
7. Сумма всех удельных весов показателя структуры
а) строго равна 1
б) больше или равна 1
в) меньше или равна 1
8. Относительные показатели по своему познавательному значению подразделяются на показатели: а) выполнения и сравнения, б) структуры и динамики, в) интенсивности и координации, г) прогнозирования и экстраполяции
а) а, б, г
б) б, в, г
в) а, б, в
9. Статистические показатели по сущности изучаемых явлений могут быть:
а) качественными
б) объёмными
в) а, б
10. Статистические показатели в зависимости от характера изучаемых явлений могут быть:
а) интервальными
б) моментными
в) а, б
1. Исчисление средних величин — это
а) способ изучения структуры однородных элементов совокупности
б) прием обобщения индивидуальных значений показателя
в) метод анализа факторов
2. Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените?
а) средняя арифметическая
б) средняя арифметическая взвешенная
в) средняя гармоническая
3. Средняя геометрическая — это:
а) корень из произведения индивидуальных показателей
б) произведение корней из индивидуальных показателей
4. По какой формуле производится вычисление средней величины в интервальном ряду?
а) средняя арифметическая взвешенная
б) средняя гармоническая взвешенная
5. Могут ли взвешенные и невзвешенные средние, рассчитанные по одним и тем же данным, совпадать?
а) да
б) нет
6. Как изменяется средняя арифметическая, если все веса уменьшить в А раз?
а) уменьшатся
б) увеличится
в) не изменится
7. Как изменится средняя арифметическая, если все значения определенного признака увеличить на число А?
а) уменьшится
б) увеличится
в) не изменится
8. Значения признака, повторяющиеся с наибольшей частотой, называется
а) модой
б) медианой
9. Средняя хронологическая исчисляется
а) в моментных рядах динамики с равными интервалами
б) в интервальных рядах динамики с равными интервалами
в) в интервальных рядах динамики с неравными интервалами
10. Медиана в ряду распределения с четным числом членов ряда равна
а) полусумме двух крайних членов
б) полусумме двух срединных членов
1. Что понимается в статистике под термином «вариация показателя»?
а) изменение величины показателя
б) изменение названия показателя
в) изменение размерности показателя
2. Укажите показатели вариации
а) мода и медиана
б) сигма и дисперсия
в) темп роста и прироста
3. Показатель дисперсии — это:
а) квадрат среднего отклонения
б) средний квадрат отклонений
в) отклонение среднего квадрата
4. Коэффициент вариации измеряет колеблемость признака
а) в относительном выражении
б) в абсолютном выражении
5. Среднеквадратическое отклонение характеризует
а) взаимосвязь данных
б) разброс данных
в) динамику данных
6. Размах вариации исчисляется как
а) разность между максимальным и минимальным значением показателя
б) разность между первым и последним членом ряда распределения
7. Показатели вариации могут быть
а) простыми и взвешенными
б) абсолютными и относительными
в) а) и б)
8. Закон сложения дисперсий характеризует
а) разброс сгруппированных данных
б) разброс неупорядоченных данных
9. Средне квадратическое отклонение исчисляется как
а) корень квадратный из медианы
б) корень квадратный из коэффициента вариации
в) корень квадратный из дисперсии
10. Кривая закона распределения характеризует
а) разброс данных в зависимости от уровня показателя
б) разброс данных в зависимости от времени
1. Выборочный метод в статистических исследованиях используется для:
а) экономии времени и снижения затрат на проведение статистического исследования;
б) повышения точности прогноза;
в) анализа факторов взаимосвязи.
2. Выборочный метод в торговле используется:
а) при анализе ритмичности оптовых поставок;
б) при прогнозировании товарооборота;
в) при разрушающих методах контроля качества товаров.
3. Ошибка репрезентативности обусловлена:
а) самим методом выборочного исследования;
б) большой погрешностью зарегистрированных данных.
4. Коэффициент доверия в выборочном методе может принимать значения:
а) 1, 2, 3;
б) 4, 5, 6;
в) 7, 8, 9.
5. Выборка может быть: а) случайная, б) механическая, в) типическая, серийная, д) техническая
а) а, б, в, г,
б) а, б, в, д
в) б, в, г, д
6. Необходимая численность выборочной совокупности определяется:
а) колеблемостью признака;
б) условиями формирования выборочной совокупности;
7. Выборочная совокупность отличается от генеральной:
а) разными единицами измерения наблюдаемых объектов;
б) разным объемом единиц непосредственного наблюдения;
в) разным числом зарегистрированных наблюдений.
8. Средняя ошибка выборки:
а) прямо пропорциональна рассеяности данных;
б) обратно пропорциональна разбросу варьирующего признака;
в) никак не зависит от колеблемости данных;
9. Повторный отбор отличается от бесповторного тем, что:
а) отбор повторяется, если в процессе выборки произошел сбой;
б) отобранная однажды единица наблюдения возвращается в генеральную совокупность;
в) повторяется несколько раз расчет средней ошибки выборки.
10. Малая выборка — это выборка объемом:
а) 4-5 единиц изучаемой совокупности;
б) до 50 единиц изучаемой совокупности;
в) до 30 единиц изучаемой совокупности.
1. Ряд динамики характеризует: а) структуру совокупности по какому-то признаку; б) изменение характеристик совокупности во времени; в) определенное значение признака в совокупности; г) величину показателя на определенную дату или за определенный период
а) а, б
б) б, г
в) б, в
2. Ряд динамики может состоять: а) из абсолютных суммарных величин; б) из относительных и средних величин;
а) а
б) б
в) а, б
3. Ряд динамики, характеризующий уровень развития социально-экономического явления на определенные даты времени, называется:
а) интервальным;
б) моментным.
4. Средний уровень интервального ряда динамики определяется как:
а) средняя арифметическая;
б) средняя хронологическая.
5. Средний уровень моментного ряда динамики исчисляется как: а) средняя арифметическая взвешенная при равных интервалах между датами; б) при неравных интервалах между датами как средняя хронологическая, в) при равных интервалах между датами как средняя хронологическая;
а) а
б) б
в) б, в
6. Абсолютный прирост исчисляется как: а) отношение уровней ряда; б) разность уровней ряда. Темп роста исчисляется как: в) отношение уровней ряда; г) разность уровней ряда;
а) а, в
б) б, в
в) а, г
7. Для выявления основной тенденции развития используется: а) метод укрупнения интервалов; б) метод скользящей средней; в) метод аналитического выравнивания; г) метод наименьших квадратов;
а) а, г
б) б, г
в) а, б, г
г) а, б, в
8. Трендом ряда динамики называется:
а) основная тенденция;
б) устойчивый темп роста.
9. Прогнозирование в статистике ‑ это:
а) предсказание предполагаемого события в будущем;
б) оценка возможной меры изучаемого явления в будущем.
10. К наиболее простым методам прогнозирования относят:
а) индексный метод;
б) метод скользящей средней;
в) метод на основе среднего абсолютного прироста.
1. Статистический индекс — это:
а) критерий сравнения относительных величин;
б) сравнительная характеристика двух абсолютных величин;
в) относительная величина сравнения двух показателей.
2. Индексы позволяют соизмерить социально-экономические явления:
а) в пространстве;
б) во времени;
в) в пространстве и во времени.
3. В индексном методе анализа несуммарность цен на разнородные товары преодолевается:
а) переходом от абсолютных единиц измерения цен к относительной форме;
б) переходом к стоимостной форме измерения товарной массы.
4. Можно ли утверждать, что индивидуальные индексы по методологии исчисления адекватны темпам роста:
а) можно;
б) нельзя.
5. Сводные индексы позволяют получить обобщающую оценку изменения:
а) по товарной группе;
б) одного товара за несколько периодов.
6. Может ли в отдельных случаях средний гармонический индекс рассчитываться по средней гармонической невзвешенной:
а) может;
б) не может.
7. Индексы переменного состава рассчитываются:
а) по товарной группе;
б) по одному товару.
8. Может ли индекс переменного состава превышать индекс фиксированного состава:
а) может;
б) не может.
9. Первая индексная мультипликативная модель товарооборота – это:
а) произведение индекса цен на индекс физического объема товарооборота;
б) произведение индекса товарооборота в сопоставимых ценах на индекс средней цены постоянного состава;
в) а, б.
10. Вторая факторная индексная мультипликативная модель анализа – это:
а) произведение индекса постоянного состава на индекс структурных сдвигов;
б) частное от деления индекса переменного состава на индекс структурных сдвигов;
в) а, б.
1. Статистическая связь — это:
а) когда зависимость между факторным и результирующим
показателями неизвестна;
б) когда каждому факторному соответствует свой результирующий показатель;
в) когда каждому факторному соответствует несколько разных значений результирующего показателя.
2. Термин корреляция в статистике понимают как:
а) связь, зависимость;
б) отношение, соотношение;
в) функцию, уравнение.
3. По направлению связь классифицируется как:
а) линейная;
б) прямая;
в) обратная.
4. Анализ взаимосвязи в статистике исследует:
а) тесноту связи;
б) форму связи;
в) а, б
5. При каком значении коэффициента корреляции связь можно считать умеренной?
а) r = 0,43;
б) r = 0,71.
6. Термин регрессия в статистике понимают как: а) функцию связи, зависимости; б) направление развития явления вспять; в) функцию анализа случайных событий во времени; г) уравнение линии связи
а) а, б
б) в, г
в) а, г
7. Для определения тесноты связи двух альтернативных показателей применяют:
а) коэффициенты ассоциации и контингенции;
б) коэффициент Спирмена.
8. Дайте классификацию связей по аналитическому выражению:
а) обратная;
б) сильная;
в) прямая;
г) линейная.
9. Какой коэффициент корреляции характеризует связь между YиX:
а) линейный;
б) частный;
в) множественный.
10. При каком значении линейного коэффициента корреляции связь между YиXможно признать более существенной:
а) ryx = 0,25;
б) ryx = 0,14;
в) ryx = — 0,57.