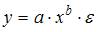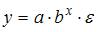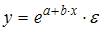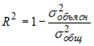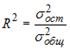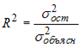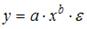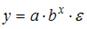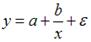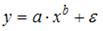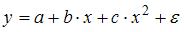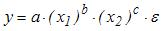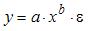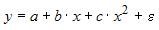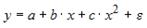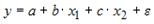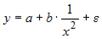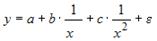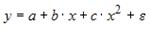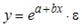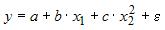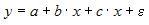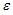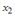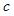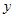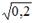Ошибкой спецификации эконометрической модели уравнения регрессии является …
- оценка параметров при помощи МНК
- учет случайных факторов
- расчет показателей качества модели
- использование парной регрессии вместо множественной
Тип вопроса: Вопрос с одним правильными вариантом
Ответ на этот вопрос уже получили: 288 раз(а)
Помогли ответы? Ставь лайк 👍
Вопрос задал(а): Анонимный пользователь, 09 Январь 2017 в 20:42
На вопрос ответил(а): Астафьева Любовь, 09 Январь 2017 в 20:42
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 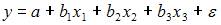
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 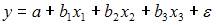
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 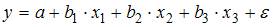






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 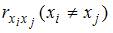

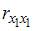
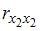
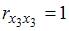
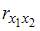
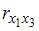
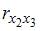
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
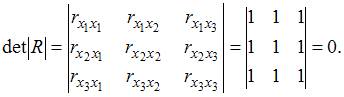
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

Ошибка спецификации эконометрической модели уравнения регрессии
Ошибка спецификации
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. [c.36]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]
Смотреть страницы где упоминается термин Ошибка спецификации
Экономико-математический словарь Изд.5 (2003) — [ c.338 ]
Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
| Название | Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие |
| Дата | 02.02.2019 |
| Размер | 1.2 Mb. |
| Формат файла | |
| Имя файла | Baza_po_ekonometrike.doc |
| Тип | Документы #66133 |
| страница | 1 из 4 |
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
4. В модели вида количество объясняющих переменных равно …
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
3. Дана матрица парных коэффициентов корреляции.
Коллинеарными являются факторы …
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
Фиктивными переменными не являются …
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный
для типа дома монолитный
для типа дома кирпичный
для типа дома монолитный
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.
4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет
5. В эконометрике фиктивной переменной принято считать …
переменную, принимающую значения 0 и 1
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
минимизации суммы квадратов
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
критерий Гольдфельда – Квандта
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников .После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений, . Тогда значение коэффициента детерминации равно …
3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …
остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
http://economy-ru.info/info/15273/
http://topuch.ru/tema-1-specifikaciya-ekonometricheskoj-modeli-oshibki-specifik-v2/index.html
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 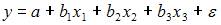
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 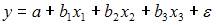
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 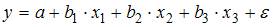






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 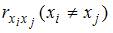

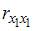
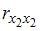
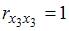
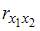
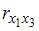
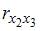
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
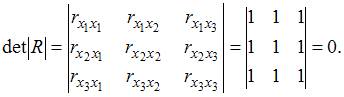
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

Проявления, последствия и методика устранения ошибки спецификации эконометрической модели, состоящей в неверном выборе типа функции, играющей роль уравнения регрессии
Читайте также:
- I. Последствия участия Японии в Первой мировой войне
- III. Последствия принятия наследства
- Абсолютная тупость сердца: понятие, методика определения. Границы абсолютной тупости сердца в норме. Изменения границ абсолютной тупости сердца в патологии.
- Абсолютные и относительные показатели силы связи в уравнениях парной регрессии.
- Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
- Автокорреляция случайного возмущения. Причины. Последствия
- Активная подвижность нижнего легочного края , методика проведения, нормативы. Диагностическое значение изменений активной подвижности нижнего легочного края.
- Алгоритм обратного распространения ошибки
- Безработ: определение, типы, естественный уровень, социально-экономические последствия.
- Безработица : определение, типы, измерение, последствия
- Безработица, ее причины и формы, последствия.
- Безработица: её сущность, виды и социально-экономические последствия.
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения регрессии: Пусть на первом этапе была сделана спецификация модели в виде: 
Иными словами, математические ожидания эндогенной переменной, полученные с помощью функций fT и fF не совпадают, т.е. первая предпосылка теоремы Гаусса-Маркова M(ulx)=0 не выполняется. Следовательно, в результате оценивания такой модели параметры а0 и а1 будут смещенными. В таком случае следует, используя диаграмму рассеивания, выбрать из арсенала моделей функций регрессии более подходящую кандидатуру и повторить процедуру построения регрессионной модели.
2. В уравнение регрессии включена лишняя (незначимая) переменная: Пусть на этапе спецификации в модель включена «лишняя» переменная, например, X2: «Правильная» спецификация должна иметь вид: Последствия: 1) Оценки параметров а0, а1, а2 останутся несмещенными, но потеряют свою эффективность (точность).2) Увеличивается ошибка прогноза по модели как за счет ошибок оценок коэффициентов и σu, так и за счет последнего слагаемого. Диагностика: В моделях множественной регрессии необходимо для каждого коэффициента уравнения проверять статистическую гипотезу H0: ai=0. Для этого достаточно оценить дробь Стьюдента и сравнить ее значение с критическим значением распределения Стьюдента, которое вычисляется по значению доверительной вероятности и значению степени свободы n2 = n – (k+1). Если неравенство справедливо, то переменная принимается незначимой и может быть удалена из спецификации модели.
3. В уравнении регрессии пропущена значимая переменная: . Последствия такие же, как и в первом случае: получаем смещенные оценки параметров модели. Для устранения необходимо вернуться к изучению особенностей поведения экономического объекта, выявить опущенные переменные и дополнить ими модель. Проблемы в использовании переменных: 1) Не возможно получение данных по переменной. 2) Не возможно измерить количественно переменную. Такие ситуации характерны для переменных социально-экономического характера. Выход из ситуации – подбор переменной заместителя. В качестве замещающей переменной часто используется время и лаговые переменные.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
V7: Система линейных одновременных уравнений
S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами
-: состоятельности, смещенности и эффективности
+: состоятельности, несмещенности и эффективности
-: состоятельности, смещенности и неэффективности
-: несостоятельности, смещенности и эффективности
S: Для регрессионной модели вида 
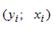
S: Для обнаружения автокорреляции в остатках используется
+: статистика Дарбина – Уотсона
-: критерий Гольдфельда – Квандта
S: Величина 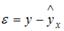
S: Строится эконометрическая модель линейного уравнения множественной регрессии вида
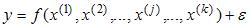

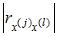
S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение
S: В эконометрической модели линейного уравнения регрессии
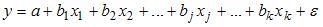
S: Система эконометрических уравнений включает совокупность _________ переменных.
S: Несмещенность оценок параметров регрессии означает, что …
-: дисперсия остатков минимальная
-: точность оценок выборки увеличивается с увеличением объема выборки
+: математическое ожидание остатков равно нулю
-: дисперсия остатков не зависит от величины
S: Дана автокорреляционная функция временного ряда
Верным будет утверждение, что ряд …
-: содержит только тенденцию, и не содержит сезонной компоненты
-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту
+: имеет выраженную сезонную компоненту с лагом 4
-: имеет выраженную сезонную компоненту с лагом 6
S: Если параметр эконометрической модели является статистически значимым, то его значение признается …
+: равным коэффициенту парной корреляции
S: Для регрессионной модели вида 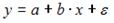
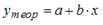

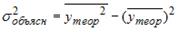

-:
+:
-:
-:
S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 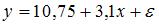
S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
-:
-:
-:
+:
S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …
-: принадлежность тому или иному региону
-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье
+: площадь жилья (м2)
S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
+:
-:
-:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
-:
-:
-:
+:
S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 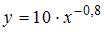
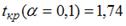
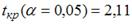
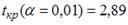
-: при уровне значимости 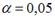
-: при уровне значимости 
-: эластичность спроса по цене составляет –0,8
+: при уровне значимости 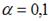
S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.
-: стохастические и вероятностные
-: линейные и парные
-: множественные и парные
+: линейные и нелинейные
S: Дана таблица исходных данных для построения эконометрической регрессионной модели:
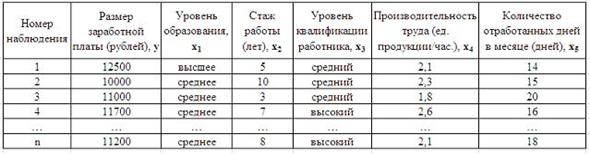
Фиктивными переменными не являются …
-: уровень квалификации работника
S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …
-: коэффициента множественной корреляции
-: показателей существенности параметров модели
+: матрицы парных коэффициентов линейной корреляции
-: системы нормальных уравнений МНК
S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 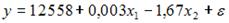
-: увеличится на 1,67
-: изменится на (-1,67)
-: изменится на 0,003
+: уменьшится на (-1,67)
S: В модели вида 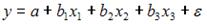
S: В модели множественной регрессии 
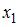
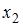
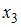
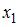
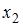
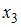
S: В уравнении линейной множественной регрессии: 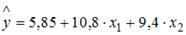
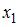
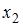
-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.
-: на 1% … увеличится на 10,8%
-: на 1 тыс. руб. … увеличится на 10,8%
+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
S: Переменная х является нелинейной в уравнении
-:
-:
+:
-:
S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является
-:
-:
+:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 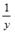
-:
-:
-:
+:
S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 
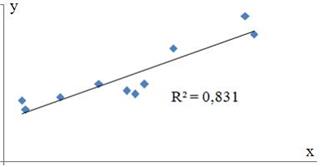
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.
S: Пусть 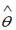




S: Степенной модельюне является регрессионная модель …
-:
+:
-:
-:
S: Нелинейным уравнением множественной регрессии является …
+:
-:
-:
-:
S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
+: бесконечно большого количества
S: В эконометрической модели линейного уравнения регрессии 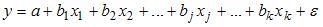
+:
S: Для эконометрической модели линейного уравнения множественной регрессии вида 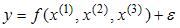
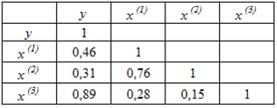
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
S: Регрессионная модель вида 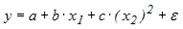
-: переменной
+: переменной
-: параметра
-: переменной
S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет
-:
-:
S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.
-: гомоскедастичными и некоррелированными
+: автокоррелированными и/или гетероскедастичными
S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
S: Автокорреляцией уровней ряда называется корреляционная зависимость между …
-: факторами, формирующими уровень ряда
-: уровнями двух рядов
+: последовательными уровнями ряда
-: компонентами, образующими уровни ряда
S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 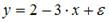
S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 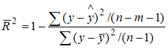
+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
-: n – число параметров при независимых переменных; m – число наблюдений
-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
S: Для эконометрической модели вида 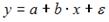


S: Ошибкой спецификации эконометрической модели уравнения регрессии является …
+: использование парной регрессии вместо множественной
-: расчет показателей качества модели
-: учет случайных факторов
-: оценка параметров при помощи МНК
S: В модели множественной регрессии 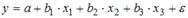
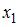
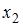
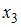
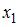
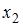
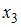
S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
-: между трендовой, сезонной и случайной компонентами
+: первого, второго, третьего и последующих порядков
-: факторов, формирующих уровень ряда
-: между несколькими временными рядами
S: Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …
-: yt = 7; T = 6,5; S = 0; E = 0,5
-: yt = 7; T = -3,5; S = -2; E = -1
+: yt = 7; T = 3,5; S = 2; E = 1
-: yt = 7; T = 3,5; S = -2; E = 1
источники:
http://studall.org/all4-3748.html
http://lektsia.com/2×1276.html
к ошибкам спецификации
относятся не неправильный выбор той
или иной математической функции для
,
но и недоучет в уравнении регрессии
какого-то существенного фактора, то
есть использование парной регрессии
вместо множественной.
2. Для регрессионной
модели вида
необходим
минимальный объем наблюдений, содержащий
_____ объектов наблюдения.
«15».
3. Нелинейным по
объясняющим переменным, но линейным по
параметрам уравнением регрессии
является …
4. В модели вида
количество
объясняющих переменных равно …3.
5. При идентификации
модели множественной регрессии
количество
оцениваемых параметров равно …Итого
5 параметров.
1. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,
и
близок
к единице. Это означает, что факторы,
и
…мультиколлинеарны
2. При моделировании
линейного уравнения множественной
регрессии вида
необходимо,
чтобы выполнялось требование отсутствия
взаимосвязи между …
между x1
и x2.
3. Дана матрица
парных коэффициентов корреляции.

являются факторы …
и
коллинеарны.
4. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,
и
близок
к нулю. Это означает, что факторы,
и
…мультиколлинеарность
факторов.
5. Для эконометрической
модели линейного уравнения множественной
регрессии вида
построена
матрица парных коэффициентов линейной
корреляции (y
– зависимая переменная; х(1),
х(2),
х(3),
x(4)–
независимые переменные):
Коллинеарными
(тесно связанными) независимыми
(объясняющими) переменными не
являются
…x(2)
и x(3)
1. Дана таблица
исходных данных для построения
эконометрической регрессионной модели:
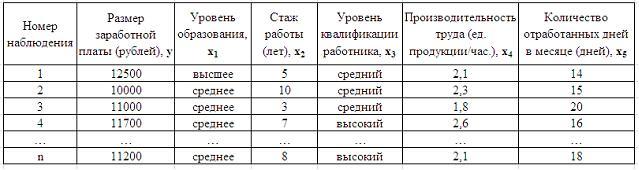
переменными не
являются …
стаж работы
производительность
труда
2. При исследовании
зависимости потребления мяса от уровня
дохода и пола потребителя можно
рекомендовать …
использовать
фиктивную переменную – пол потребителя
разделить
совокупность на две: для потребителей
женского пола и для потребителей мужского
пола
3. Изучается
зависимость цены квартиры (у)
от ее жилой площади (х)
и типа дома. В модель включены фиктивные
переменные, отражающие рассматриваемые
типы домов: монолитный, панельный,
кирпичный. Получено уравнение регрессии:
,
где

уравнениями регрессии для кирпичного
и монолитного являются …
для типа дома
кирпичный
для типа дома
монолитный
4. При анализе
промышленных предприятий в трех регионах
(Республика Марий Эл, Республика Чувашия,
Республика Татарстан) были построены
три частных уравнения регрессии:
для
Республики Марий Эл;
для
Республики Чувашия;
для
Республики Татарстан.
Укажите вид
фиктивных переменных и уравнение с
фиктивными переменными, обобщающее три
частных уравнения регрессии.
5. В эконометрике
фиктивной переменной принято считать
…
переменную,
принимающую значения 0 и 1
описывающую
количественным образом качественный
признак
1. Для регрессионной
модели зависимости среднедушевого
денежного дохода населения (руб., у)
от объема валового регионального
продукта (тыс. р., х1)
и уровня безработицы в субъекте (%, х2)
получено уравнение
.
Величина коэффициента регрессии при
переменнойх2
свидетельствует о том, что при изменении
уровня безработицы на 1% среднедушевой
денежный доход ______ рубля при неизменной
величине валового регионального
продукта.
изменится на
(-1,67)
2. В уравнении
линейной множественной регрессии:
,
где– стоимость основных фондов (тыс. руб.);
–
численность занятых (тыс. чел.);y
– объем промышленного производства
(тыс. руб.) параметр при переменной х1,
равный 10,8, означает, что при увеличении
объема основных фондов на _____ объем
промышленного производства _____ при
постоянной численности занятых.
на 1 тыс. руб. …
увеличится на 10,8 тыс. руб.
3. Известно, что
доля остаточной дисперсии зависимой
переменной в ее общей дисперсии равна
0,2. Тогда значение коэффициента
детерминации составляет …0,8
4. Построена
эконометрическая модель для зависимости
прибыли от
реализации единицы продукции (руб., у)
от величины оборотных средств предприятия
(тыс. р., х1):
.
Следовательно, средний размер прибыли
от реализации, не зависящий от объема
оборотных средств предприятия, составляет
_____ рубля. 10,75
5. F-статистика
рассчитывается как отношение ______
дисперсии к ________ дисперсии, рассчитанных
на одну степень свободы.факторной
… остаточной
1. Для эконометрической
модели уравнения регрессии ошибка
модели определяется как ______ между
фактическим значением зависимой
переменной и ее расчетным значением.Разность
2. Величина
называется
…случайной
составляющей
3. В эконометрической
модели уравнения регрессии величина
отклонения фактического значения
зависимой переменной от ее расчетного
значения характеризует …ошибку
модели
4. Известно, что
доля объясненной дисперсии в общей
дисперсии равна 0,2. Тогда значение
коэффициента детерминации составляет
… 0,2
5. При методе
наименьших квадратов параметры уравнения
парной линейной регрессии
определяются
из условия ______ остатков.минимизации
суммы квадратов
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
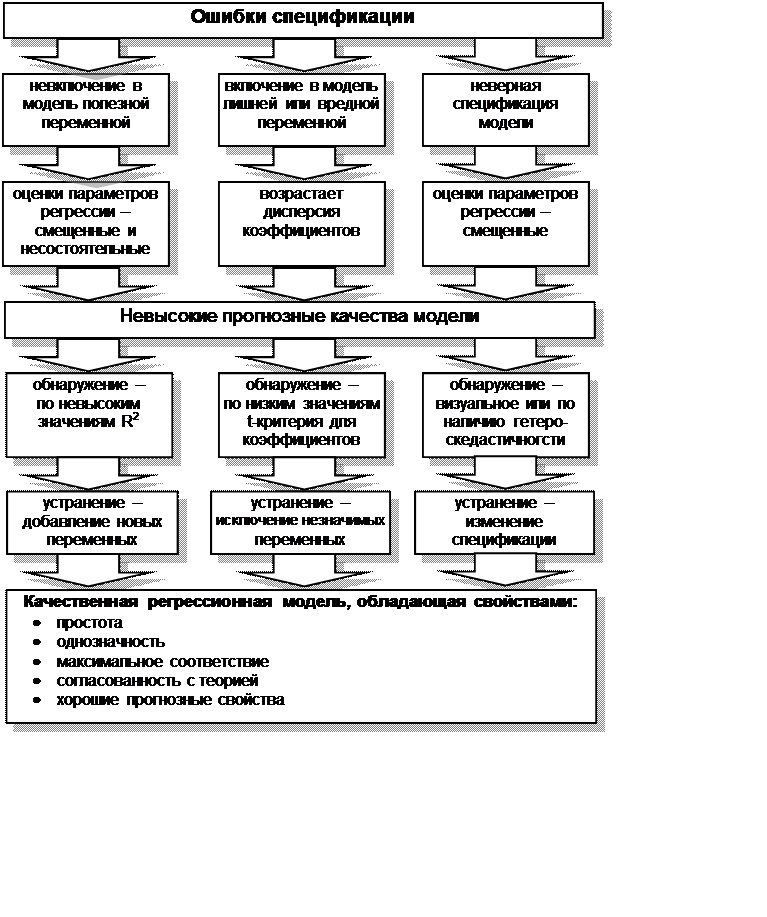
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели