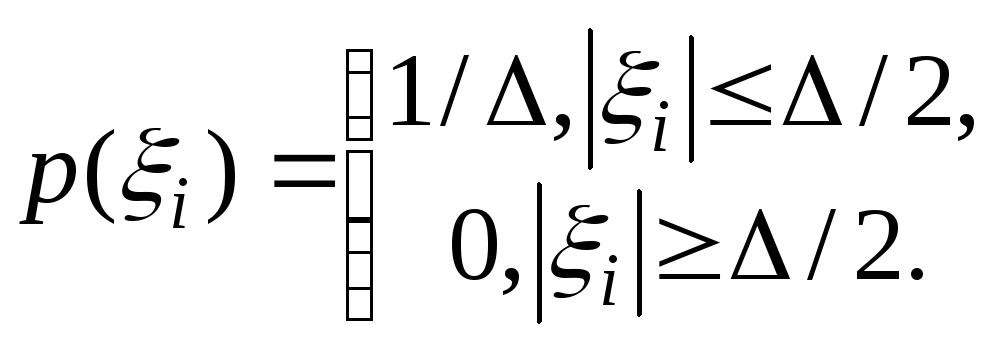Ошибка восстановления сигнала

Теорема
Котельникова точно справедлива только
для сигналов с финитным (конечным)
спектром. На рис. 4.15 показаны некоторые
варианты финитных спектров.

Однако
спектры реальных информационных сигналов
бесконечны (рис. 4.16). В этом случае теорема
Котельникова справедлива с погрешностью.

Погрешность
дискретизации определяется энергией
спектральных составляющих сигнала,
лежащих за пределами частоты
(рис. 4.16).

.

Вторая причина
возникновения погрешностей — неидеальность
восстанавливающего ФНЧ.

Таким
образом? погрешность дискретизации и
восстановления непрерывного сигнала
определяется следующими причинами:

1. Спектры реальных
   сигналов не финитны.

2. АЧХ реальных ФНЧ
   неидеальны.

Рис.4.17.
Структурная схема RC-фильтра

Например,
если в качестве ФНЧ использовать
RC-фильтр
(рис.4.17), то восстановленный сигнал на
его выходе будет иметь вид, представленный
на рис.4.18.

Импульсная
реакция RC-фильтра
равна:

.

Вывод:
чем выше
и чем ближе характеристики ФНЧ к
идеальным, тем ближе восстановленный
сигнал к исходному.

4.6. Квантование сообщений. Ошибки квантования

Итак
показано, что передачу практически
любых сообщений
можно свести к передаче их отсчетов,
или чисел,
следующих друг за другом с интервалом
дискретности.
Тем самым непрерывное (бесконечное)
множество возможных значений сообщения
заменяетсяконечным
числом его дискретных значений
.
Однако сами эти числа имеют непрерывную
шкалу уровней (значений), то есть
принадлежат опять же континуальному
множеству. Дляабсолютно
точного
представления таких чисел, к примеру,
в десятичной (или двоичной) форме,
необходимо теоретически бесконечное
число разрядов. Вместе с тем, на практике
нет необходимости в абсолютно точном
представлении значений
,
как и любых чисел вообще.

Во-первых,
сами источники сообщений обладают
ограниченным динамическим диапазоном
и вырабатывают исходные сообщения с
определенным уровнем искажений и ошибок.
Этот уровень может быть большим или
меньшим, но абсолютной точности
воспроизведения достичь невозможно.

Во-вторых,
передача сообщений по каналам связи
всегда производится в присутствии
различного рода помех. Поэтому, принятое
(воспроизведенное) сообщение (оценка
сообщения
)
всегда в определенной степени отличается
от переданного, то есть на практикеневозможна
абсолютно точная передача сообщений
при наличии помех в канале связи.

Наконец,
сообщения передаются для их восприятия
и использования получателем. Получатели
же информации — органы чувств человека,
исполнительные механизмы и т.д. — также
обладают конечной разрешающей
способностью, то есть не замечают
незначительной разницы между абсолютно
точным и
приближенным
значениями
воспроизводимого сообщения. Порог
чувствительности к искажениям также
может быть различным, но он всегда есть.

С
учетом этих замечаний процедуру
дискретизации сообщений можно продолжить,
а именно подвергнуть отсчеты

квантованию.

Процесс
квантования состоит в замене непрерывного
множества значений отсчетов
дискретным
множеством
.
Тем самым точные значения чиселзаменяются их приблизительными
(округленными до ближайшего разрешенного
уровня) значениями. Интервал между
соседними разрешенными уровнями,
или уровнями квантования,называетсяшагом
квантования.

Различают
равномерное и неравномерное квантование.
В большинстве случаев применяется и
далее подробно рассматривается
равномерное квантование (рис. 4.19), при
котором шаг квантования постоянный:
;
однако иногда определенное преимущество
дает неравномерное квантование, при
котором шаг квантования
разный
для различных
(рис. 4.20).

Квантование
приводит к искажению сообщений. Если
квантованное сообщение, полученное в
результате квантования отсчета
,
обозначить как
,
то

где

— разность между истинным значением
элементарного сообщения

и
квантованным
сообщением (ближайшим разрешенным
уровнем)
,
называемая ошибкой
квантования, или шумом
квантования.
Шум квантования оказывает на процесс
передачи информации по существу такое
же влияние, как и помехи в канале связи.
Помехи, так же как и квантование, приводят
к тому, что оценки
,
получаемые на приемной стороне системы
связи, отличаются на некоторую величину
от истинного значения.

Поскольку
квантование сообщений приводит к
появлению ошибок и потере некоторой
части информации, можно определить
цену таких потерь
и среднюю величину ошибки, обусловленной
квантованием:

Чаще
всего в качестве функции потерь (цены
потерь) используется квадратичная
функция вида

В
этом случае мерой ошибок квантования
служит дисперсия этих ошибок. Для
равномерного
-уровневого
квантования с шагом

дисперсия ошибок квантования определяется
следующим образом:

.
(4.9)

Абсолютное
значение ошибки квантования не превосходит
половины шага квантования
,
и
тогда при
достаточно большом числе уровней
квантования
и малой величине
плотность
распределения вероятностей ошибок
квантования

можно
считать равномерной на интервале +
… —:

В
результате величина ошибки квантования
определится соотношением

(4.10)

и
соответствующим выбором шага квантования

может быть сделана сколь угодно малой
или сведена к любой наперед заданной
величине.

Относительно
требуемой точности передачи отсчетов
сообщений можно высказать те же
соображения, что и для ошибок временной
дискретизации: шумы квантования или
искажения, обусловленные квантованием,
не имеют существенного значения, если
эти искажения меньше ошибок, обусловленных
помехами и допустимых техническими
условиями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Исследование погрешности восстановления сигнала по результатам его преобразования

Вадим Жмудь1, Вольфрам Хардт2 1НГТУ, Новосибирск, Россия, 2Университет Хемница, Хемниц, Германия

Аннотация: Традиционно считается, что при использовании аналого-цифрового преобразования следует соблюсти требования теоремы Котельникова (Шеннона и Найквиста по англоязычной литературе). Согласно этой теореме частота преобразования должна, как минимум, вдвое превышать верхнюю граничную частоту спектра преобразуемого сигнала. Также традиционно считается, что наличие высокочастотных шумов более одного кванта пребразования по уровню крайне неблагоприятно влияет на результат преобразования. Из этого следует необходимость предварительной фильтрации сигнала до начала преобразования по условиям этого соотношения. В данной статье путем моделирования в программе показано, что условия указанной теоремы недостаточны более чем на порядок. Вместе с тем показано, что влияние высокочастотных шумов намного меньше сказывается на погрешности

преобразования, нежели влияние

недостаточности частоты преобразования. Кроме того, это влияние шумов также достаточно сильно ослабляется за счет увеличения частоты преобразования. На этом основании обоснованы рекомендации увеличить требование указанной теоремы, как минимум, в 25 раз, то есть требовать 50-кратного превышения частоты

преобразования над верхней граничной частотой входного сигнала.

Ключевые слова: преобразование сигналов, АЦП, теорема Котельникова, теорема Шеннона, частота Найквиста, моделирование, погрешность

ВВЕДЕНИЕ

Известно, что при применении АЦП необходимо выполнение условий теоремы Котельникова (в иностранной литературе также встречается название «теорема Шеннона» или «теорема Котельникова-Шеннона», «теорема отсчетов»).

Ее суть состоит в том, что непрерывный сигнал с ограниченным спектром можно абсолютно точно представить набором его отдельных значений («отсчетов»), следующих с равными интервалами, при условии, что частота следования этих отсчетов, как минимум, вдвое

превышает верхнюю границу спектра указанного сигнала.

Введем термины. Верхняя (граничная) частота спектра сигнала /В — это та частота, выше которой никаких компонент в спектре сигнала не содержится. Само значение этой частоты может содержаться в спектре, но с пренебрежимо малой амплитудой.

Теорема Котельникова для АЦП: на один период Тв верхней частотной границы /в = 1 / Тв спектра преобразуемого сигнала должно приходиться не менее двух отсчетов АЦП. То есть частота квантования / должна, как минимум, вдвое превышать верхнюю частоту сигнала /в:

/ > /в ^ яя = 0 ^ /к > 2/в. (1)

В этой записи знаки неравенства должны быть одинаковыми, а именно, допустима и такая запись:

/ > /в ^ S(f) = 0 ^ /к > 2/в . (2)

Требования, сформулированного теоремой Котельникова лишь теоретически достаточно для восстановления сигнала по оптимальному правилу и лишь применительно к идеализированному сигналу (с ограниченным спектром), который в природе не встречается.

Во-первых, конечный (ограниченный) спектр может характеризовать лишь бесконечный во времени сигнал. Во-вторых, само значение отсчетов должно быть взято с наивысшей точностью (идеально). В-третьих, на практике невозможна ситуация, чтобы при некоторой частоте квантования сигнал можно восстановить идеально, а при частоте на любую сколь угодно малую величину больше эта задача была неразрешимой. Кроме того, процедура восстановления исходного сигнала по его отсчетам никогда не бывает оптимальной. Поэтому на практике рекомендуется использовать заведомо большую частоту квантования по времени (частоту взятия отсчетов).

В работе [2] рекомендуется увеличивать частоту квантования по сравнению с требованием теоремы Котельникова в к = 1,5-2 раза. Эта рекомендация не подкреплена экспериментально, поэтому может быть поставлена под сомнение.

В данной статье осуществляется исследование с целью отыскания обоснованного

значения коэффициента к, т. е. отыскивается обоснованное значение соотношения между верхней границей спектра преобразуемого сигнала и частотой его преобразования.

1. СУТЬ МОДЕЛЬНОГО ЭКСПЕРИМЕНТА

Требования теоремы Котельникова нельзя понимать буквально. Ошибкой было бы думать, что обеспечение условий соотношения (1) или (2) обеспечивает достаточно точное преобразование аналогового сигнала (т. е. его последующее восстановление в цифровом виде с достаточно малой погрешностью). На деле прагматический подход, состоящий в предположении, что частота квантования должна в десять и более раз превышать верхнюю границу частотного спектра входного сигнала дает лучшие результаты, поскольку преобразуемый сигнал не бесконечен во времени, метод фильтрации и метод восстановления не оптимален, и т. д.

Для наглядности осуществим моделирование преобразования сигнала в программе У1з8Ы.

Поскольку чисто гармонический сигнал преобразовывать не интересно, можно при этом упустить некоторые тонкости, будем преобразовывать сумму двух квазигармонических сигналов. Вид этих сигналов показан на Рис. 1 и 2.

1.2 1.0

Рис. 1. Квазигармонический сигнал с линейно нарастающей амплитудой, частота равна 1 рад/с

1.2

21-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

О 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эвс)

Рис. 2. Квазигармонический сигнал с линейно ниспадающей амплитудой, частота равна 2 рад/с

Период самой высокой частоты в этом сигнале примерно можно считать равным 3 с. Исходя из этих условий, преобразование с периодом 1,4 с отвечает требованиям теоремы.

Это в полной мере относится не только к

каждому сигналу в отдельности, но и к сумме этих сигналов, которая показана на Рис. 3.

При моделировании работы АЦП вначале используем период преобразования, равный 0,4 с, чтобы на интервале, равном периоду наивысшей частоты было существенно больше, чем два отсчета. На Рис. 4 показан результат преобразования этого сигнала, на Рис. 5 исходный сигнал и результат преобразования объединены в одних осях для наглядности, на Рис. 6 показана ошибка преобразования.

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эвс)

Рис. 3. Преобразуемый сигнал, являющийся суммой сигналов по Рис. 1 и 2

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эвс)

Рис. 4. Результат преобразования сигнала по Рис. 3 при периоде преобразования 0,4 с

Рис. 5. Исходный сигнал и результат его преобразования в одних осях для сравнения

Ошибка преобразования для графика на Рис. 6 получена простым вычитанием из исходного сигнала результата его преобразования. Эта ошибка слишком велика, т. к. в пиковом значении она достигает 70 % амплитуды входного сигнала. Это объясняется не достаточно корректным сравнением результатов, что легко исправить. Операция

преобразования получает исходный сигнал и поддерживает его неизменным на протяжении всего времени до следующего преобразования, тогда как на самом деле этот отсчет относится к моменту начала ступенчатого сигнала, формируемого преобразователем.

Рис. 6. Ошибка преобразования, получаемая вычитанием из исходного сигнала результата его преобразования

Следовательно, для восстановления истинной шкалы времени результат преобразования следует сдвинуть на половину периода преобразования влево, но поскольку сдвиг во времени вперед невозможен, осуществим задержку исходного сигнала на время, равное половине периода преобразования. Ошибка преобразования, вычисленная после такой коррекции, показана на Рис. 7, она явно меньше, чем ошибка, показанная ранее на Рис. 6, и все же еще слишком велика: в пиковом значении достигает 40 % амплитуды входного сигнала.

Рис. 7. Ошибка преобразования после уточнения вносимого запаздывания операцией преобразования, равного половине периода преобразования; данный результат получен путем вычитания из исходного сигнала, задержанного на 0,2 с, сигнала, полученного в результате преобразования

На Рис. 8 даны для сравнения исходный сигнал и результат преобразования после фильтрации, но без указанного сдвига.

При этом фильтр используется с передаточной функцией следующего вида:

Ъф(*)=

1

Рис. 8. Сравнение исходного сигнала и сигнала, полученного в результате преобразования и последующей фильтрации

Фильтр также вносит свое запаздывание, поэтому сравнение исходного сигнала и результата преобразования при условии, что оба эти сигнала пропущены через идентичные фильтры, все же не дает достаточного совпадения, как показано на Рис. 9. На Рис. 10 даны эти же сигналы с учетом сдвига, т. е. в исходный сигнал внесено дополнительное запаздывание на половину периода частоты преобразования. Видно, что полученные сигналы почти полностью совпадают. Ошибка преобразования — это разность этих сигналов. Она показана на Рис. 11, при этом масштаб увеличен в 20 раз. Видно, сколь мала ошибка преобразования в данном случае: в пиковом значении она достигает лишь 3% от амплитуды входного сигнала.

(1 + 0,1?)’

(3)

Рис. 9. Сравнение исходного сигнала и сигнала, полученного в результате преобразования после того, как оба сигнала подверглись идентичной последующей фильтрации

Хотя оставшиеся 3 % по-прежнему слишком велики, следует учесть, что примененный фильтр излишне широк для этого случая. Также далее будет показано, что свой вклад в остаточную ошибку вносит недостаточная точность моделирования, связанная с выбранным шагом интегрирования.

На Рис. 12 показан сигнал с добавлением гауссовых шумов, что применено для исследования вопроса о том, как высокочастотные шумы проявляются при преобразовании.

1.2 1.0 .6 .2 0 -.2 -.6 -1.0 : У Г № V У ь V

2.5 5 7.5 10 2.5 15 17.5 20 22.5 25 27.5 30 3 «Пте (зес) 2.5 35 37.5 40 2.5 46 47.5 50

Рис. 10. То же, что на Рис. 9, с введением дополнительного запаздывания в исходный сигнал на величину 0,2 с

.05 .04

.06′-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 11. Ошибка преобразования, полученная вычитанием двух графиков из Рис. 10, с последующим увеличением масштаба по оси ординат в 20 раз

Результат преобразования этого сигнала показан на Рис. 13. На Рис. 14 показана ошибка преобразования, определенная по простейшему алгоритму, то есть вычитанием преобразованного сигнала из исходного.

» о 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 12. Вид исходного сигнала при добавлении в него гауссовых шумов (стандартное отклонение 0,1)

На Рис. 15 даны в одних осях преобразованный сигнал, пропущенный через фильтр и исходный сигнал, пропущенный через идентичный фильтр и задержанный на половину периода преобразования. На Рис. 16 показана ошибка преобразования, вычисленная вычитанием двух сигналов из Рис. 15. После учета запаздываний, так же, как было сделано на Рис. 11, ошибка существенно уменьшается, как показано на Рис. 16.

«140 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50

Рис. 13. Результат преобразования сигнала по Рис. 12 при тех же условиях

Покажем, что увеличение частоты преобразования эффективно снижает ошибку преобразования. На Рис. 17 показана ошибка преобразования (без фильтрации и задержки) в результате того, что частота преобразования увеличена в 4 раза. На Рис. 18 — совмещенные исходный сигнал и результат преобразования. На Рис. 19 показана ошибка после применения всех мер компенсации задержек. В пиковом значении ошибка уменьшилась в 3 раза по сравнению с результатом, показанном на Рис. 16.

-1.2′-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 14. Ошибка преобразования (отличие сигнала на Рис. 13 от сигнала на Рис. 12)

1.2

-1.2′-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 15. В одних осях исходный сигнал, подверженный шумам, а затем пропущенный через фильтр и задержанный на 0,2 с, а также сигнал, полученный в результате преобразования, пропущенный через идентичный фильтр

О 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эес)

Рис. 16. Ошибка преобразования в условиях шумов, аналогично Рис. 11, масштаб увеличен только в 5 раз

:

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 17. Ошибка преобразования в тех же условиях по сигналу и шумам без фильтрации и задержки при увеличении частоты преобразования в 4 раза (период равен 0,1 с)

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 18. Исходный сигнал с фильтрацией и задержкой и результат преобразования с фильтрацией в тех же условиях, при увеличении частоты преобразования в 4 раза (как на Рис. 17)

~25] Г

.20 —

.15 —

.10 —

.10 .15 .20

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 19. Ошибка результата преобразования в тех же условиях, что на рис. 16, при увеличении частоты преобразования в 4 раза (как на Рис. 17)

Если и далее повышать частоту преобразования, ошибка также уменьшается,

что иллюстрируют аналогичные графики на Рис. 20-22.

1.2

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

«1-20 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 20. Исходный сигнал и результат преобразования при периоде преобразования, равном 1 с (в 2,5 раза выше, чем в первом эксперименте); шумы отсутствуют

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 21. Исходный сигнал после фильтрации и задержки и результат преобразования по Рис. 20 после фильтрации

1 2|

_121-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 22. Ошибка преобразования (разность сигналов на Рис. 21), масштаб тот же, что на Рис. 21

Если же частоту преобразования уменьшить, то ошибка увеличивается, что иллюстрируют аналогичные графики на Рис. 23-25. При добавлении гауссовых шумов ситуация еще больше ухудшается. На Рис. 26 показан сигнал с гауссовыми шумами и результат его преобразования. На Рис. 27 показаны оба этих сигнала после прохождения ими тех же идентичных фильтров. На Рис. 28 показана ошибка преобразования для этого случая, полученная вычитанием сигналов, показанных на Рис. 27, друг из друга. Как видно из этого результата, наличие высокочастотных шумов существенно увеличивает ошибку

преобразования. Применение более высокой

частоты преобразования, хотя и не столь высокой, чтобы высокочастотные гауссовы шумы стали удовлетворять условиям теоремы Котельникова, позволяет многократно снизить указанную ошибку, порождаемую гауссовыми шумами.

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (гес)

Рис. 23. Исходный сигнал и результат преобразования при изменении частоты преобразования (период равен 1,4 с)

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 24. Исходный сигнал после фильтрации и задержки и результат преобразования по Рис. 20 после фильтрации при изменении частоты преобразования как на Рис. 23

1 2|

«1-20 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 25. Ошибка преобразования (разность сигналов на рис. 24), масштаб тот же, что на рис. 24

Действительно, на Рис. 29 показаны тот же входной сигнал с теми же гауссовыми шумами и результат его преобразования при увеличении частоты преобразования в 75 раз, а именно: период преобразования стал 0,02 с. На рис. 30 показаны оба сигнала после фильтрации при внесении соответствующего запаздывания во входной сигнал, равного половине периода преобразования. Видно, что визуально эти сигналы совпадают. На Рис. 31 показана ошибка преобразования, вычисленная как разница

между двумя сигналами, показанными на Рис. 30. Для наглядности масштаб сохранен, так же, как и на Рис. 25. Видно, что ошибка резко уменьшилась.

Рис. 26. То же, что на рис. 23 при наличии гауссовых шумов

«1-20 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (зес)

Рис. 27. То же, что на рис. 24 при наличии гауссовых шумов

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (вес)

Рис. 28. То же, что на рис. 25 при наличии гауссовых шумов

Рис. 29. То же, что на рис. 26 при увеличении частоты преобразования в 75 раз (период преобразования равен 0,02 с)

1.2

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эвс)

Рис. 30. Разница входного сигнала (после фильтрации и сдвига) и результата преобразования при условиях по Рис. 29 (гауссов шум, период преобразования 0,02 с)

1.2

4

: О :

-1.2-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 «Пте (эвс)

Рис. 31. Ошибка преобразования (разница сигналов на рис. 30), масштаб тот же, что на рис. 30

Рассмотрим работу АЦП без гауссовых шумов при указанной высокой частоте преобразования. Вид ошибки преобразования в этом случае показан на Рис. 32. При этом масштаб по оси ординат увеличен в 100 раз. Пиковое значение погрешности составляет 0,8 %. В этом случае уже сказывается недостаточная точность моделирования, что проявляется в том, что при уменьшении шага квантования по времени (называемого шагом интегрирования) вдвое ошибка преобразования также падает вдвое, что показано на Рис. 33.

.012 .010

.010

°120 2.5 5 7.5 10 1 2.5 15 17.5 20 22.5 25 27.5 30 32.5 35 37.5 40 42.5 45 47.5 50 Пте (эвс)

Рис. 32. Ошибка преобразования для этого же случая при отсутствия шумов: масштаб по оси ординат увеличен в 100 раз

Покажем, что ошибка преобразования все же зависит не только и не столько от шага интегрирования, и что ранее выполненное моделирование дает корректные выводы. Для этого сохраняя указанное уменьшенное

значение шага интегрирования, начнем увеличивать период преобразования. Результат показан на Рис. 34.

Рис. 33. То же, что и на Рис. 32 при уменьшении вдвое шага интегрирования при моделировании: ошибка преобразования уменьшилась в 2 раза

При увеличении периода до значения 0,8 с ошибка увеличивается незначительно. При дальнейшем удвоении периода ошибка увеличилась примерно на 10 % от ее значения, и достигла 0,5 % от входного сигнала. При следующем удвоении периода преобразования ошибка возросла более чем втрое, в пиковом значении достигла 1,75 % от амплитуды входного сигнала. На Рис. 35 приведена схема для формирования тестового сигнала и моделирования работы АЦП, а на Рис. 36 приведена схема для моделирования фильтров.

Рис. 34. То же, что и на рис. 33 при увеличении периода преобразования: 1 — 0,08 с; 2 — 0,16 с; 3 -0,32 с

Рис. 35. Структура для моделирования источника преобразуемого сигнала, генератора шума и АЦП (имитируется устройством выборки-хранения «Б&Ы»)

Рис. 36. Структура для моделирования двух фильтров и звена запаздывания (к Рис. 31)

ОБСУЖДЕНИЕ И ВЫВОДЫ

Поскольку на практике после получения отсчетов входного сигнала с помощью АЦП для дальнейшей обработки никогда не применяется метод восстановления, который предполагается при доказательстве теоремы Котельникова, и поскольку всегда преобразуется конечный сигнал, а не бесконечный во времени, выполнение условий теоремы недостаточно для восстановления исходного сигнала по полученным его отсчетам. При моделировании в данной работе использовался именно такой способ обработки полученной последовательности отсчетов, который используется практически во всех реальных системах. В этих условиях выявлено, что для данного сигнала при отсутствии шумов период преобразования должен быть не более 0,08 с, что составляет около 40 отсчетов на период высшей частоты в преобразуемом сигнале. При наличии шумов даже этого может оказаться недостаточно. Можно рекомендовать 50-100 отсчетов на период. Тем самым можно утверждать, что желательное соотношение между верхней граничной частотой спектра преобразуемого сигала и частотой его преобразование задается следующим соотношением:

/ > /в ^ Б (/) = 0 ^ /к > 50/в. (4)

Дополнительные соображения состоят в том, что любой АЦП дает результат, квантованный не только по времени, но и по уровню. Проблемы, порождаемые квантованием по уровню, никак не рассматривается при выводе теоремы Котельникова. Уменьшение шага

квантования по времени способствует снижению проблем, порождаемых квантованием по уровню. Это также можно показать моделированием.

ЗАКЛЮЧЕНИЕ

Показано, что предположение о том, что требования теоремы Котельникова слишком слабы, подтвердились. Предположение, что увеличение частоты квантования в 1,5-2 раза достаточно [2], не подтвердилось. Рекомендуемый запас составляет 20 — 25 раз, т. е. рекомендуемая частота преобразования дложна в 40-50 раз превышать верхнюю границу спектра преобразуемого сигнала. Это требование не относится к преобразованию заведомо гармонического сигнала с целью получения сигнала разностной частоты, что используется для измерения разностей фаз [6, 7]. В дальнейшем целесообразно детально исследовать влияние дискретности преобразования по уровню на ошибку преобразования и снижение этого влияния за счет повышения частоты преобразования.

ЛИТЕРАТУРА

[1] Жмудь, В. А. Моделирование замкнутых систем автоматического управления: учебное пособие для академического бакалавриата / В. А. Жмудь. -2-е изд., испр. и доп. — М.: Издательство Юрайт, 2017. — 126 с. — (Бакалавр. Академический курс). -ISBN 978-5-534-03410-3. URL: http: //urait. ru/catalog/403 830

[2] В.А. Жмудь, В.А. Тайченачев. Системы автоматического управления высшей точности: учеб. пособие , В.А. Жмудь, А.В. Тайченачев; Новосиб. Гос. ун-т — Новосибирск: ИПЦ НГУ, 2016. — 178 с.

С.В. Каменский, Г.А. Французова, Г.П. Чикильдин, В.А. Жмудь, А.С. Востриков, Ю.Е.

[3]

Е.А. Басыня,

В.Г. Трубин.

управления, монография / редакцией Г.А. Изд-во НГТУ,

Воскобойников, Системы автоматического мехатроники и робототехники: коллектив авторов; под общей Французовой. — Новосибирск: 2017. — 210 с.

[4] V A Zhmud, L V Dimitrov. The influence of the type of the test signal on the result of numerical optimization of regulators. . IOP Conf. Series: Journal of Physics: Conf. Series 803 (2017) 012186 doi:10.1088/1742-6596/803/1/012186. http://iopscience.iop.org/article/10.1088/1742-6596/803/1/012186/pdf

[5] V A Zhmud, I L Reva, L V Dimitrov. Design of robust systems by means of the numerical optimization with harmonic changing of the model parameters. IOP Conf. Series: Journal of Physics: Conf. Series 803 (2017) 012185 doi:10.1088/1742-6596/803/1/012185.

http://iopscience.iop.org/article/10.1088/1742-6596/803/1/012185/pdf

[6] Precision frequency meter for basic metrology and displacement measurements / Zhmud, V., Goncharenko, A., Liapidevskiy, A.V. 2015. Testing and Measurement: Techniques and Applications -Proceedings of the 2015 International Conference on

Testing and Measurement: Techniques and Applications, TMTA 2015 pp. 125-130. [7] V. Zhmud, L. Dimitrov. Designing of the Precision Automatic Control Systems. Monography. -Novosibirsk, Publishing house «KANT», 2017. -126 p.

Investigation of the Error of Signal Recovery from the Results of its Sampling

V. A. ZHMUD, W. HARDT

Novosibirsk State Technical University. Novosibirsk. Russia; Department of Computer Science, Chemnitz University of Technology, Chemnitz, Germany

Abstract: Traditionally, when using an analog-to-digital conversion, it is necessary to observe the requirements of Kotel’nikov’s theorem (Shannon and Nyquist in the English-language literature). According to this theorem, the frequency of the transformation should, at least, twice exceed the upper boundary frequency of the spectrum of the signal being converted. It is also traditionally considered that the presence of high-frequency noises of more than one quantization of the level of the leveling has an extremely unfavorable effect on the result of the conversion. From this the need follows for pre-filtering of the signal before the transformation begins according to the conditions of this relationship. In this paper, by modeling in the VisSim program, it is shown that the conditions of this theorem are insufficient; the difference is more than an order of magnitude. At the same time, it is shown that the influence of high-frequency noises affects the conversion error much less than the effect of insufficient conversion frequency. In addition, this effect of noise is also greatly weakened by increasing the conversion frequency. The recommendations are based on thid are to increase the requirement of this theorem by at least 25 times, that is, requiring a 50 times excess of the conversion frequency over the upper boundary frequency of the input signal.

Key words: signal transformation, ADC, Kotel’nikov theorem, Nyquist theorem, Shannon theorem, Nyquist frequency, simulation, error

REFERENCES

[1] Zhmud, V. A. Modelirovanie zamknutyh sistem avtomaticheskogo upravlenija: uchebnoe posobie dlja akademicheskogo bakalavriata / V. A. Zhmud. — 2-e izd., ispr. i dop. — M.: Izdatel’stvo Jurajt, 2017. — 126 s. — (Bakalavr. Akademicheskij kurs). — ISBN 978-5534-03410-3. URL: http://urait.ru/catalog/403830

[2] V.A. Zhmud, V.A. Tajchenachev. Sistemy avtomaticheskogo upravlenija vysshej tochnosti: ucheb. posobie, V.A. Zhmud, A.V. Tajchenachev; Novosib. Gos. un-t — Novosibirsk: IPC NGU, 2016. -178 s.

[3] S.V. Kamenskij, G.A. Francuzova, G.P. Chikil’din, V.A. Zhmud, A.S. Vostrikov, Ju.E. Voskobojnikov, E.A. Basynja, V.G. Trubin. Sistemy avtomaticheskogo upravlenija, mehatroniki i robototehniki: monografija / kollektiv avtorov; pod obshhej redakciej G.A. Francuzovoj. — Novosibirsk: Izd-vo NGTU, 2017. — 210 s.

[4] V A Zhmud, L V Dimitrov. The influence of the type of the test signal on the result of numerical optimization of regulators. . IOP Conf. Series: Journal of Physics: Conf. Series 803 (2017) 012186 doi: 10.1088/1742-6596/803/1/012186. http://iopscience.iop.org/article/10.1088/1742-6596/803/1/012186/pdf

[5] V A Zhmud, I L Reva, L V Dimitrov. Design of robust systems by means of the numerical optimization with harmonic changing of the model parameters. IOP Conf. Series: Journal of Physics: Conf. Series 803 (2017) 012185 doi:10.1088/1742-6596/803/1/012185.

http://iopscience.iop.org/article/10.1088/1742-6596/803/1/012185/pdf

[6] Precision frequency meter for basic metrology and displacement measurements / Zhmud, V., Goncharenko, A., Liapidevskiy, A.V. 2015. Testing and Measurement: Techniques and Applications -Proceedings of the 2015 International Conference on Testing and Measurement: Techniques and Applications, TMTA 2015 pp. 125-130.

[7] V. Zhmud, L. Dimitrov. Designing of the Precision Automatic Control Systems. Monography. -Novosibirsk, Publishing house «KANT», 2017. -126 p.

Вадим Аркадьевич Жмудь —

заведующий кафедрой

Автоматики НГТУ, профессор, доктор технических наук. E-mail: oao nips@bk.ru

Wolfram Hardt —

Department of Computer Science, Chemnitz University of Technology, Chemnitz, Germany Prodekan für Internationales, Direktor Universitätsrechenzentrum, Professor für Techniche Informatik, Techniche Universitat Chemnitz, Germany

E-mail: hardt@cs.tu-chemnitz.de

Ошибка — восстановление

Cтраница 1

Ошибки восстановления вертикальных ирофижй Н20, обусловленные случайными ошибками затменного метода.
 [1]

Доказать, что ошибка восстановления e ( f) х ( /) — х ( /) наблюдателями полного порядка и Люинбергера асимптотически стремится к нулю.
 [2]

Таким образом, ошибка восстановления будет стремиться к нулю, если можно найти матрицу K ( t), при которой система (7.7) становится асимптотически устойчивой. Аналогично устанавливается возможность выбора матрицы F, которая делает систему (7.1) асимптотически устойчивой.
 [3]

Это означает, что асимптотическое поведение ошибки восстановления e ( i) определяется одновременно с асимптотическими свойствами любого возмущенного движения наблюдателя.
 [4]

Как видно из рис. 10.71 величина ошибки восстановления фазы S 2 практически не изменяется. При приближении S к единице значение ошибки резко возрастает. Был проведен эксперимент с набором из 10 интерферограмм, каждая из которых была получена в результате интерференции световой волны с фазой (10.166) и плоской световой волны, перпен дикулярно плоскости регистрации, с изменением геометрического размера области регистрации от 2 мм до 3 мм.
 [6]

При этом кривая 1 относится к ошибке восстановления максимального ( пикового) значения интенсивности в линии, а кривые 2, 3 и 4 — соответственно к ошибке при восстановлении спектральных интервалов между точками контура на высотах 0 2; 0 5 и 0 7 от максимума. Роль формы ядра К ( х) и поведение алгоритма с изменением числа итераций N нетрудно выяснить, переходя к фурье-образам соответствующих функций.
 [7]

Интервал дискретизации следует выбирать таким, чтобы ошибка восстановления непрерывного полезного сигнала не превышала заданного значения.
 [8]

Как нетрудно видеть, в области больших a Ts ошибка восстановления сигнала является весьма значительной ( что, в частности, свидетельствует о существенном отличии условий передачи непрерывного несингулярного сигнала от идеальных, — см. гл.
 [9]

При проектировании систем с требуемой точностью первоочередной задачей является определение интервала дискретизации, при котором ошибка восстановления исходного сигнала не будет превышать заданной. В основе решения этой задачи лежит обобщенная теорема отсчетов.
 [10]

Следует отметить, что присутствие в правой части (8.23) члена FI — FI приводит к появлению методической ошибки в векторе ошибки восстановления, порожденной реакцией на эти слагаемые.
 [11]

Как видно, при малых глубинах модуляции е вследствие резкого увеличения удельного веса дискретных компонент в спектре мощности импульсного 4 сигнала соответственно увеличиваются и ошибки восстановления.
 [12]

Температурные поля, полученные методом ES1 в трех сечениях плазменной струи, показаны на рис. 6.19. Как и следовало ожидать, поля температур струи, невозмущенной инжектирующим потоком газа, осесимметричны в пределах ошибки восстановления во всех трех исследуемых сечениях. При введении инжектирующего потока форма температурного поля меняется наиболее значительно вблизи сопла. Здесь изотермы расширяются в направлении, поперечном вектору скорости этого потока При малом расходе инжектирующего газа ( G 0 07 г / с) температура на оси струи в сечении, отстоящем на расстоянии 1 см от сопла, практически та же, что и без потока; в сечении, отстоящем от сопла на 2 см, она уже несколько меньше, что можно объяснить турбулентным перемешиванием основной и дополнительной струй. В сечении 3 см уменьшение более заметно.
 [13]

Применение этого принципа позволяет доказать, что матрица коэффициентов К оптимального регулятора, замкнутого по полному вектору состояния ж, остается неизменной и в том случае, когда замыкание система производится по оценкам вектора состояния х, восстановленным наблюдающим устройством, параметры которого определены из условия минимума среднего квадрата ошибки восстановления.
 [14]

Страницы:  

   1

   2