Предыдущий пост см. здесь.
Проверка статистических гипотез
Для статистиков и исследователей данных проверка статистической гипотезы представляет собой формальную процедуру. Стандартный подход к проверке статистической гипотезы подразумевает определение области исследования, принятие решения в отношении того, какие переменные необходимы для измерения предмета изучения, и затем выдвижение двух конкурирующих гипотез. Во избежание рассмотрения только тех данных, которые подтверждают наши субъективные оценки, исследователи четко констатируют свою гипотезу заранее. Затем, основываясь на данных, они применяют выборочные статистики с целью подтвердить либо отклонить эту гипотезу.
Проверка статистической гипотезы подразумевает использование тестовой статистики, т.е. выборочной величины, как функции от результатов наблюдений. Тестовая статистика (test statistic) — это вычисленная из выборочных данных величина, которая используется для оценивания прочности данных, подтверждающих нулевую статистическую гипотезу и служит для выявления меры расхождения между эмпирическими и гипотетическими значениями. Конкретные методы проверки называются тестами, например, z-тест, t-тест (соответственно z-тест Фишера, t-тест Студента) и т.д. в зависимости от применяемых в них тестовых статистик.
Примечание. В отечественной статистической науке используется «туманный» термин «статистика критерия». Туманный потому здесь мы снова наблюдаем мягкую подмену: вместо теста возникает критерий. Если уж на то пошло, то критерий — это принцип или правило. Например, выполняя z-тест, t-тест и т.д., мы соответственно используем z-статистику, t-статистику и т.д. в правиле отклонения гипотезы. Это хорошо резюмируется следующей ниже таблицей:
|
Тестирование гипотезы |
Тестовая статистика |
Правило отклонения гипотезы |
|
z-тесты |
z-статистика |
Если тестовая статистика ≥ z или ≤ -z, то отклонить нулевую гипотезу H0. |
|
t-тесты |
t-статистика |
Если тестовая статистика ≥ t или ≤ -t, то отклонить нулевую гипотезу H0. |
|
Анализ дисперсии (ANOVA) |
F-статистика |
Если тестовая статистика ≥ F, то отклонить нулевую гипотезу H0. |
|
Тесты хи-квадрат |
Статистика хи-квадрат |
Если тестовая статистика ≥ χ, то отклонить нулевую гипотезу H0. |
Для того, чтобы помочь сохранить поток посетителей веб-сайта, дизайнеры приступают к работе над вариантом веб-сайта с использованием всех новейших методов по поддержанию внимания аудитории. Мы хотели бы удостовериться, что наши усилия не напрасны, и поэтому стараемся увеличить время пребывания посетителей на обновленном веб-сайте.
Отсюда главный вопрос нашего исследования состоит в том, «приводит ли обновленный вид веб-сайта к увеличению времени пребывания на нем посетителей»? Мы принимаем решение проверить его относительно среднего значения времени пребывания. Теперь, мы должны изложить две наши гипотезы. По традиции считается, что изучаемые данные не содержат того, что исследователь ищет. Таким образом, консервативное мнение заключается в том, что данные не покажут ничего необычного. Все это называется нулевой гипотезой и обычно обозначается как H0.
При тестировании статистической гипотезы исходят из того, что нулевая гипотеза является истинной до тех пор, пока вес представленных данных, подтверждающих обратное, не сделает ее неправдоподобной. Этот подход к поиску доказательств «в обратную сторону» частично вытекает из простого психологического факта, что, когда люди пускаются на поиски чего-либо, они, как правило, это находят.
Затем исследователь формулирует альтернативную гипотезу, обозначаемую как H1. Она может попросту заключаться в том, что популяционное среднее отличается от базового уровня. Или же, что популяционное среднее больше или меньше базового уровня, либо больше или меньше на некоторую указанную величину. Мы хотели бы проверить, не увеличивает ли обновленный дизайн веб-сайта время пребывания, и поэтому нашей нулевой и альтернативной гипотезами будут следующие:
-
H0: Время пребывания для обновленного веб-сайта не отличается от времени пребывания для существующего веб-сайта
-
H1: Время пребывания для обновленного веб-сайта больше по сравнению с временем пребывания для существующего веб-сайта
Наше консервативное допущение состоит в том, что обновленный веб-сайт никак не влияет на время пребывания посетителей на веб-сайте. Нулевая гипотеза не обязательно должна быть «нулевой» (т.е. эффект отсутствует), но в данном случае, у нас нет никакого разумного оправдания, чтобы считать иначе. Если выборочные данные не поддержат нулевую гипотезу (т.е. если данные расходятся с ее допущением на слишком большую величину, чтобы носить случайный характер), то мы отклоним нулевую гипотезу и предложим альтернативную в качестве наилучшего альтернативного объяснения.
Указав нулевую и альтернативную гипотезы, мы должны установить уровень значимости, на котором мы ищем эффект.
Статистическая значимость
Проверка статистической значимости изначально разрабатывалась независимо от проверки статистических гипотез, однако сегодня оба подхода очень часто используются во взаимодействии друг с другом. Задача проверки статистической значимости состоит в том, чтобы установить порог, за пределами которого мы решаем, что наблюдаемые данные больше не поддерживают нулевую гипотезу.
Следовательно, существует два риска:
-
Мы можем принять расхождение как значимое, когда на самом деле оно возникло случайным образом
-
Мы можем приписать расхождение случайности, когда на самом деле оно показывает истинное расхождение с популяцией
Эти две возможности обозначаются соответственно, как ошибки 1-го и 2-го рода:
|
H0 ложная |
H0 истинная |
|
|
Отклонить H0 |
Истинноотрицательный исход |
Ошибка 1-го рода (ложноположительный исход) |
|
Принять H0 |
Ошибка 2-го рода (ложноотрицательный исход) |
Истинноположительный исход |
Чем больше мы уменьшаем риск совершения ошибок 1-го рода, тем больше мы увеличиваем риск совершения ошибок 2-го рода. Другими словами, с чем большей уверенностью мы хотим не заявлять о наличии расхождения, когда его нет, тем большее расхождение между выборками нам потребуется, чтобы заявить о статистической значимости. Эта ситуация увеличивает вероятность того, что мы проигнорируем подлинное расхождение, когда мы с ним столкнемся.
В статистической науке обычно используются два порога значимости. Это уровни в 5% и 1%. Расхождение в 5% обычно называют значимым, а расхождение в 1% — крайне значимым. В формулах этот порог часто обозначается греческой буквой α (альфа) и называется уровнем значимости. Поскольку, отсутствие эффекта по результатам эксперимента может рассматриваться как неуспех (эксперимента либо обновленного веб-сайта, как в нашем случае), то может возникнуть желание корректировать уровень значимости до тех пор, пока эффект не будет найден. По этой причине классический подход к проверке статистической значимости требует, чтобы мы устанавливали уровень значимости до того, как обратимся к нашим данным. Часто выбирается уровень в 5%, и поэтому мы на нем и остановимся.
Проверка обновленного дизайна веб-сайта
Веб-команда в AcmeContent была поглощена работой, конструируя обновленный веб-сайт, который будет стимулировать посетителей оставаться на нем в течение более длительного времени. Она употребила все новейшие методы и, в результате мы вполне уверены, что веб-сайт покажет заметное улучшение показателя времени пребывания.
Вместо того, чтобы запустить его для всех пользователей сразу, в AcmeContent хотели бы сначала проверить веб-сайт на небольшой выборке посетителей. Мы познакомили веб-команду с понятием искаженности выборки, и в результате там решили в течение одного дня перенаправлять случайные 5% трафика на обновленный веб-сайт. Результат с дневным трафиком был нам предоставлен одним текстовым файлом. Каждая строка показывает время пребывания посетителей. При этом, если посетитель пользовался исходным дизайном, ему присваивалось значение «0», и если он пользовался обновленным (и надеемся, улучшенным) дизайном, то ему присваивалось значение «1».
Выполнение z-теста
Ранее при тестировании с интервалами уверенности мы располагали лишь одним популяционным средним, с которым и выполнялось сравнение.
При тестировании нулевой гипотезы с помощью z-теста мы имеем возможность сравнивать две выборки. Посетители, которые видели обновленный веб-сайт, отбирались случайно, и данные для обеих групп были собраны в тот же день, чтобы исключить другие факторы с временной зависимостью.
Поскольку в нашем распоряжении имеется две выборки, то и стандартных ошибок у нас тоже две. Z-тест выполняется относительно объединенной стандартной ошибки, т.е. квадратного корня суммы дисперсий (вариансов), деленных на размеры выборок. Она будет такой же, что и результат, который мы получим, если взять стандартную ошибку обеих выборок вместе:
Здесь σ2a — это дисперсия выборки a, σ2b — дисперсия выборки b и соответственно na и nb — размеры выборок a и b. На Python объединенная стандартная ошибка вычисляется следующим образом:
def pooled_standard_error(a, b, unbias=False):
'''Объединенная стандартная ошибка'''
std1 = a.std(ddof=0) if unbias==False else a.std()
std2 = b.std(ddof=0) if unbias==False else b.std()
x = std1 ** 2 / a.count()
y = std2 ** 2 / b.count()
return sp.sqrt(x + y)С целью выявления того, является ли видимое нами расхождение неожиданно большим, можно взять наблюдавшиеся расхождения между средними значениями на объединенной стандартной ошибке. Эту статистическую величину принято обозначать переменной z:
Используя функции pooled_standard_error, которая вычисляет объединенную стандартную ошибку, z-статистику можно получить следующим образом:
def z_stat(a, b, unbias=False):
return (a.mean() - b.mean()) / pooled_standard_error(a, b, unbias)Соотношение z объясняет, насколько средние значения отличаются относительно величины, которую мы ожидаем при заданной стандартной ошибке. Следовательно, z-статистика сообщает нам о том, на какое количество стандартных ошибок расходятся средние значения. Поскольку стандартная ошибка имеет нормальное распределение вероятностей, мы можем связать это расхождение с вероятностью, отыскав z-статистику в нормальной ИФР:
def z_test(a, b):
return stats.norm.cdf([ z_stat(a, b) ])В следующем ниже примере z-тест используется для сравнения результативность двух веб-сайтов. Это делается путем группировки строк по номеру веб-сайта, в результате чего возвращается коллекция, в которой конкретному веб-сайту соответствует набор строк. Мы вызываем groupby('site')['dwell-time'] для конвертирования набора строк в набор значений времени пребывания. Затем вызываем функцию get_group с номером группы, соответствующей номеру веб-сайта:
def ex_2_14():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе z-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
print('a n: ', a.count())
print('b n: ', b.count())
print('z-статистика:', z_stat(a, b))
print('p-значение: ', z_test(a, b))a n: 284
b n: 16
z-статистика: -1.6467438180091214
p-значение: [0.04980536]Установление уровня значимости в размере 5% во многом аналогично установлению интервала уверенности шириной 95%. В сущности, мы надеемся убедиться, что наблюдавшееся расхождение попадает за пределы 95%-го интервала уверенности. Если это так, то мы можем утверждать, что нашли результат с 5%-ым уровнем значимости.
P-значение — это вероятность совершения ошибки 1-го рода в результате неправильного отклонения нулевой гипотезы, которая в действительности является истинной. Чем меньше p-значение, тем больше определенность в том, что нулевая гипотеза является ложной, и что мы нашли подлинный эффект.
Этот пример возвращает значение 0.0498, или 4.98%. Поскольку оно немногим меньше нашего 5% порога значимости, мы можем утверждать, что нашли нечто значимое.
Приведем еще раз нулевую и альтернативную гипотезы:
-
H0: Время пребывания на обновленном веб-сайте не отличается от времени пребывания на существующем веб-сайте
-
H1: Время пребывания на обновленном веб-сайте превышает время пребывания на существующем веб-сайте.
Наша альтернативная гипотеза состоит в том, что время пребывания на обновленном веб-сайте больше.
Мы готовы заявить о статистической значимости, и что время пребывания на обновленном веб-сайте больше по сравнению с существующим веб-сайтом, но тут есть одна трудность — чем меньше размер выборки, тем больше неопределенность в том, что выборочное стандартное отклонение совпадет с популяционным. Как показано в результатах предыдущего примера, наша выборка из обновленного веб-сайта содержит всего 16 посетителей. Столь малые выборки делают невалидным допущение о том, что стандартная ошибка нормально распределена.
К счастью, существует тест и связанное с ним распределение, которое моделирует увеличенную неопределенность стандартных ошибок для выборок меньших размеров.
t-распределение Студента
Популяризатором t-распределения был химик, работавший на пивоварню Гиннес в Ирландии, Уилльям Госсетт, который включил его в свой анализ темного пива Стаут.
В 1908 Уильям Госсет опубликовал статью об этой проверке в журнале Биометрика, но при этом по распоряжению своего работодателя, который рассматривал использованную Госсеттом статистику как коммерческую тайну, был вынужден использовать псевдоним. Госсет выбрал псевдоним «Студент».
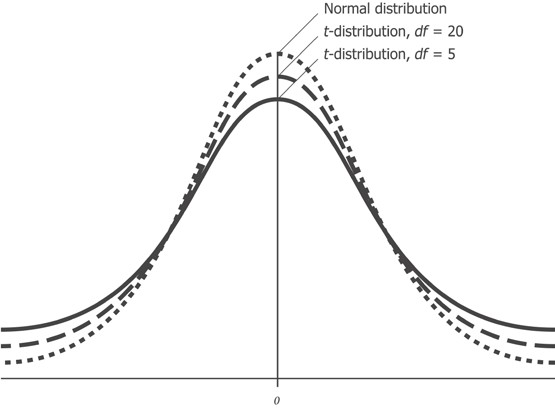
В то время как нормальное распределение полностью описывается двумя параметрами — средним значением и стандартным отклонением, t-распределение описывается лишь одним параметром, так называемыми степенями свободы. Чем больше степеней свободы, тем больше t-распределение похоже на нормальное распределение с нулевым средним и стандартным отклонением, равным 1. По мере уменьшения степеней свободы, это распределение становится более широким с более толстыми чем у нормального распределения, хвостами.
Приведенный выше рисунок показывает, как t-распределение изменяется относительно нормального распределения при наличии разных степеней свободы. Более толстые хвосты для выборок меньших размеров соответствуют увеличенной возможности наблюдать более крупные отклонения от среднего значения.
Степени свободы
Степени свободы, часто обозначаемые сокращенно df от англ. degrees of freedom, тесно связаны с размером выборки. Это полезная статистика и интуитивно понятное свойство числового ряда, которое можно легко продемонстрировать на примере.
Если бы вам сказали, что среднее, состоящее из двух значений, равно 10 и что одно из значений равно 8, то Вам бы не потребовалась никакая дополнительная информация для того, чтобы суметь заключить, что другое значение равно 12. Другими словами, для размера выборки, равного двум, и заданного среднего значения одно из значений ограничивается, если другое известно.
Если напротив вам говорят, что среднее, состоящее из трех значений, равно 10, и первое значение тоже равно 10, то Вы были бы не в состоянии вывести оставшиеся два значения. Поскольку число множеств из трех чисел, начинающихся с 10, и чье среднее равно 10, является бесконечным, то прежде чем вы сможете вывести значение третьего, второе тоже должно быть указано.
Для любого множества из трех чисел ограничение простое: вы можете свободно выбрать первые два числа, но заключительное число ограничено. Степени свободы могут таким образом быть обобщены следующим образом: количество степеней свободы любой отдельной выборки на единицу меньше размера выборки.
При сопоставлении двух выборок степени свободы на две единицы меньше суммы размеров этих выборок, что равно сумме их индивидуальных степеней свободы.
t-статистика
При использовании t-распределения мы обращаемся к t-статистике. Как и z-статистика, эта величина количественно выражает степень маловероятности отдельно взятого наблюдавшегося отклонения. Для двухвыборочного t-теста соответствующая t-статистика вычисляется следующим образом:
Здесь Sa̅b̅ — это объединенная стандартная ошибка. Объединенная стандартная ошибка вычисляется таким же образом, как и раньше:
Однако это уравнение допускает наличие информации о популяционных параметрах σa и σb, которые можно аппроксимировать только на основе крупных выборок. t-тест предназначен для малых выборок и не требует от нас принимать допущения о поплуляционной дисперсии (вариансе).
Как следствие, объединенная стандартная ошибка для t-теста записывается как квадратный корень суммы стандартных ошибок:
На практике оба приведенных выше уравнения для объединенной стандартной ошибки дают идентичные результаты при заданных одинаковых входных последовательностях. Разница в математической записи всего лишь служит для иллюстрации того, что в условиях t-теста мы на входе зависим только от выборочных статистик. Объединенная стандартная ошибка может быть вычислена следующим образом:
def pooled_standard_error_t(a, b):
'''Объединенная стандартная ошибка для t-теста'''
return sp.sqrt(standard_error(a) ** 2 +
standard_error(b) ** 2)Хотя в математическом плане t-статистика и z-статистика представлены по-разному, на практике процедура вычисления обоих идентичная:
t_stat = z_stat
def ex_2_15():
'''Вычисление t-статистики
двух вариантов дизайна веб-сайта'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_stat(a, b)-1.6467438180091214Различие между двумя выборочными показателями является не алгоритмическим, а концептуальным — z-статистика применима только тогда, когда выборки подчинены нормальному распределению.
t-тест
Разница в характере работы t-теста вытекает из распределения вероятностей, из которого вычисляется наше p-значение. Вычислив t-статистику, мы должны отыскать ее значение в t-распределении, параметризованном степенями свободы наших данных:
def t_test(a, b):
df = len(a) + len(b) - 2
return stats.t.sf([ abs(t_stat(a, b)) ], df)Значение степени свободы обеих выборок на две единицы меньше их размеров, и для наших выборок составляет 298.
Напомним, что мы выполняем проверку статистической гипотезы. Поэтому выдвинем нашу нулевую и альтернативную гипотезы:
-
H0: Эта выборка взята из популяции с предоставленным средним значением
-
H1: Эта выборка взята из популяции со средним значением большего размера
Выполним следующий ниже пример:
def ex_2_16():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе t-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test(a, b)array([ 0.05033241])Этот пример вернет p-значение, составляющее более 0.05. Поскольку оно больше α, равного 5%, который мы установили для проверки нулевой гипотезы, то мы не можем ее отклонить. Наша проверка с использованием t-теста значимого расхождения между средними значениями не обнаружила. Следовательно, наш едва значимый результат z-теста отчасти объясняется наличием слишком малой выборки.
Двухсторонние тесты
В нашей альтернативной гипотезе было принято неявное допущение, что обновленный веб-сайт будет работать лучше существующего. В процедуре проверки нулевой статистической гипотезы предпринимаются особые усилия для обеспечения того, чтобы при поиске статистической значимости мы не делали никаких скрытых допущений.
Проверки, при выполнении которых мы ищем только значимое количественное увеличение или уменьшение, называются односторонними и обычно не приветствуются, кроме случая, когда изменение в противоположном направлении было бы невозможным. Название термина «односторонний» обусловлено тем, что односторонняя проверка размещает всю α в одном хвосте распределения. Не делая проверок в другом направлении, проверка имеет больше мощности отклонить нулевую гипотезу в отдельно взятом направлении и, в сущности, понижает порог, по которому мы судим о результате как значимом.
Статистическая мощность — это вероятность правильного принятия альтернативной гипотезы. Она может рассматриваться как способность проверки обнаруживать эффект там, где имеется искомый эффект.
Хотя более высокая статистическая мощность выглядит желательной, она получается за счет наличия большей вероятности совершить ошибку 1-го рода. Правильнее было бы допустить возможность того, что обновленный веб-сайт может в действительности оказаться хуже существующего. Этот подход распределяет нашу α одинаково по обоим хвостам распределения и обеспечивает значимый результат, не искаженный под воздействием априорного допущения об улучшении работы обновленного веб-сайта.
В действительности в модуле stats библиотеки scipy уже предусмотрены функции для выполнения двухвыборочных t-проверок. Это функция stats.ttest_ind. В качестве первого аргумента мы предоставляем выборку данных и в качестве второго — выборку для сопоставления. Если именованный аргумент equal_var равен True, то выполняется стандартная независимая проверка двух выборок, которая предполагает равные популяционные дисперсии, в противном случае выполняется проверка Уэлша (обратите внимание на служебную функцию t_test_verbose, (которую можно найти среди примеров исходного кода в репо):
def ex_2_17():
'''Двухсторонний t-тест'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test_verbose(a, sample2=b, fn=stats.ttest_ind) #t-тест Уэлша{'p-значение': 0.12756432502462475,
'степени свободы ': 17.761382349686098,
'интервал уверенности': (76.00263198799597, 99.89877646270826),
'n1 ': 284,
'n2 ': 16,
'среднее x ': 87.95070422535211,
'среднее y ': 122.0,
'дисперсия x ': 10463.941024237296,
'дисперсия y ': 6669.866666666667,
't-статистика': -1.5985205593851322}По результатам t-теста служебная функция t_test_verbose возвращает много информации и в том числе p-значение. P-значение примерно в 2 раза больше того, которое мы вычислили для односторонней проверки. На деле, единственная причина, почему оно не совсем в два раза больше, состоит в том, что в модуле stats имплементирован легкий вариант t-теста, именуемый t-тестом Уэлша, который немного более робастен, когда две выборки имеют разные стандартные отклонения. Поскольку мы знаем, что для экспоненциальных распределений среднее значение и дисперсия тесно связаны, то этот тест немного более строг в применении и даже возвращает более низкую значимость.
Одновыборочный t-тест
Независимые выборки в рамках t-тестов являются наиболее распространенным видом статистического анализа, который обеспечивает очень гибкий и обобщенный способ установления, что две выборки представляют одинаковую либо разную популяцию. Однако в случаях, когда популяционное среднее уже известно, существует еще более простая проверка, представленная функцией библиотеки sciзy stats.ttest_1samp.
Мы передаем выборку и популяционное среднее относительно которого выполняется проверка. Так, если мы просто хотим узнать, не отличается ли обновленный веб-сайт значимо от существующего популяционного среднего времени пребывания, равного 90 сек., то подобную проверку можно выполнить следующим образом:
def ex_2_18():
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
return t_test_verbose(b, mean=90, fn=stats.ttest_1samp) {'p-значение ': 0.13789520958229415,
'степени свободы df ': 15.0,
'интервал уверенности': (78.4815276659039, 165.5184723340961),
'n1 ': 16,
'среднее x ': 122.0,
'дисперсия x ': 6669.866666666667,
't-статистика ': 1.5672973291495713}Служебная функция t_test_verbose не только возвращает p-значение для выполненной проверки, но и интервал уверенности для популяционного среднего. Интервал имеет широкий диапазон между 78.5 и 165.5 сек., и, разумеется, перекрывается 90 сек. нашего теста. Как раз он и объясняет, почему мы не смогли отклонить нулевую гипотезу.
Многократные выборки
В целях развития интуитивного понимания относительно того, каким образом t-тест способен подтвердить и вычислить эти статистики из столь малых данных, мы можем применить подход, который связан с многократными выборками, от англ. resampling. Извлечение многократных выборок основывается на допущении о том, что каждая выборка является лишь одной из бесконечного числа возможных выборок из популяции. Мы можем лучше понять природу того, какими могли бы быть эти другие выборки, и, следовательно, добиться лучшего понимания опорной популяции, путем извлечения большого числа новых выборок из нашей существующей выборки.
На самом деле существует несколько методов взятия многократных выборок, и мы обсудим один из самых простых — бутстрапирование. При бустрапировании мы генерируем новую выборку, неоднократно извлекая из исходной выборки случайное значение с возвратом до тех пор, пока не сгенерируем выборку, имеющую тот же размер, что и оригинал. Поскольку выбранные значения возвращаются назад после каждого случайного отбора, то в новой выборке то же самое исходное значение может появляться многократно. Это как если бы мы неоднократно вынимали случайную карту из колоды игральных карт и каждый раз возвращали вынутую карту назад в колоду. В результате время от времени мы будем иметь карту, которую мы уже вынимали.
Бутстраповская выборка, или бутстрап, — синтетический набор данных, полученный в результате генерирования повторных выборок (с возвратом) из исследуемой выборки, используемой в качестве «суррогатной популяции», в целях аппроксимации выборочного распределения статистики (такой как, среднее, медиана и др.).
В библиотеке pandas при помощи функции sample можно легко извлекать бутстраповские выборки и генерировать большое число многократных выборок. Эта функция принимает ряд опциональных аргументов, в т.ч. n (число элементов, которые нужно вернуть из числового ряда), axis (ось, из которой извлекать выборку) и replace (выборка с возвратом или без), по умолчанию равный False. После этой функции можно задать метод агрегирования, вычисляющий сводную статистику в отношении бутстраповских выборок:
def ex_2_19():
'''Построение графика синтетических времен пребывания
путем извлечения бутстраповских выборок'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
xs = [b.sample(len(b), replace=True).mean() for _ in range(1000)]
pd.Series(xs).hist(bins=20)
plt.xlabel('Бутстрапированные средние значения времени пребывания, сек.')
plt.ylabel('Частота')
plt.show()Приведенный выше пример наглядно показывает результаты на гистограмме:
Гистограмма демонстрирует то, как средние значения изменялись вместе с многократными выборками, взятыми из времени пребывания на обновленном веб-сайте. Хотя на входе имелась лишь одна выборка, состоящая из 16 посетителей, бутстрапированные выборки очень четко просимулировали стандартную ошибку изначальной выборки и позволили визуализировать интервал уверенности (между 78 и 165 сек.), вычисленный ранее в результате одновыборочного t-теста.
Благодаря бутстрапированию мы просимулировали взятие многократных выборок, при том, что у нас на входе имелась всего одна выборка. Этот метод обычно применяется для оценивания параметров, которые мы не способны или не знаем, как вычислить аналитически.
Проверка многочисленных вариантов дизайна
Было разочарованием обнаружить отсутствие статистической значимости на фоне увеличенного времени пребывания пользователей на обновленном веб-сайте. Хотя хорошо, что мы обнаружили это на малой выборке пользователей, прежде чем выкладывать его на всеобщее обозрение.
Не позволяя себя обескуражить, веб-команда AcmeContent берется за сверхурочную работу и создает комплект альтернативных вариантов дизайна веб-сайта. Беря лучшие элементы из других проектов, они разрабатывают 19 вариантов для проверки. Вместе с нашим изначальным веб-сайтом, который будет действовать в качестве контрольного, всего имеется 20 разных вариантов дизайна веб-сайта, куда посетители будут перенаправляться.
Вычисление выборочных средних
Веб-команда разворачивает 19 вариантов дизайна обновленного веб-сайта наряду с изначальным. Как отмечалось ранее, каждый вариант дизайна получает случайные 5% посетителей, и при этом наше испытание проводится в течение 24 часов.
На следующий день мы получаем файл, показывающий значения времени пребывания посетителей на каждом варианте веб-сайта. Все они были промаркированы числами, при этом число 0 соответствовало веб-сайту с исходным дизайном, а числа от 1 до 19 представляли другие варианты дизайна:
def ex_2_20():
df = load_data('multiple-sites.tsv')
return df.groupby('site').aggregate(sp.mean)Этот пример сгенерирует следующую ниже таблицу:
|
site |
dwell-time |
|
0 |
79.851064 |
|
1 |
106.000000 |
|
2 |
88.229167 |
|
3 |
97.479167 |
|
4 |
94.333333 |
|
5 |
102.333333 |
|
6 |
144.192982 |
|
7 |
123.367347 |
|
8 |
94.346939 |
|
9 |
89.820000 |
|
10 |
129.952381 |
|
11 |
96.982143 |
|
12 |
80.950820 |
|
13 |
90.737705 |
|
14 |
74.764706 |
|
15 |
119.347826 |
|
16 |
86.744186 |
|
17 |
77.891304 |
|
18 |
94.814815 |
|
19 |
89.280702 |
Мы хотели бы проверить каждый вариант дизайна веб-сайта, чтобы увидеть, не генерирует ли какой-либо из них статистически значимый результат. Для этого можно сравнить варианты дизайна веб-сайта друг с другом следующим образом, причем нам потребуется вспомогательный модуль Python itertools, который содержит набор функций, создающих итераторы для эффективной циклической обработки:
import itertools
def ex_2_21():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
по принципу "каждый с каждым"'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
pairs = [list(x) # найти сочетания из n по k
for x in itertools.combinations(range(len(groups)), 2)]
for pair in pairs:
gr, gr2 = groups.get_group( pair[0] ), groups.get_group( pair[1] )
site_a, site_b = pair[0], pair[1]
a, b = gr['dwell-time'], gr2['dwell-time']
p_val = stats.ttest_ind(a, b, equal_var = False).pvalue
if p_val < alpha:
print('Варианты веб-сайта %i и %i значимо различаются: %f'
% (site_a, site_b, p_val))Однако это было бы неправильно. Мы скорее всего увидим статистическое расхождение между вариантами дизайна, показавшими себя в особенности хорошо по сравнению с вариантами, показавшими себя в особенности плохо, даже если эти расхождения носили случайный характер. Если вы выполните приведенный выше пример, то увидите, что многие варианты дизайна веб-сайта статистически друг от друга отличаются.
С другой стороны, мы можем сравнить каждый вариант дизайна веб-сайта с нашим текущим изначальным значением — средним значением времени пребывания, равным 90 сек., измеренным на данный момент для существующего веб-сайта:
def ex_2_22():
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group( site_a )['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается: %f'
% (site_a, p_val))В результате этой проверки будут идентифицированы два варианта дизайна веб-сайта, которые существенно отличаются:
Вариант 6 веб-сайта значимо отличается: 0.005534
Вариант 10 веб-сайта 10 значимо отличается: 0.006881Малые p-значения (меньше 1%) указывают на то, что существует статистически очень значимые расхождения. Этот результат представляется весьма многообещающим, однако тут есть одна проблема. Мы выполнили t-тест по 20 выборкам данных с уровнем значимости α, равным 0.05. Уровень значимости α определяется, как вероятность неправильного отказа от нулевой гипотезы. На самом деле после 20-кратного выполнения t-теста становится вероятным, что мы неправильно отклоним нулевую гипотезу по крайней мере для одного варианта веб-сайта из 20.
Сравнивая таким одновременным образом многочисленные страницы, мы делаем результаты t-теста невалидными. Существует целый ряд альтернативных технических приемов решения проблемы выполнения многократных сравнений в статистических тестах. Эти методы будут рассмотрены в следующем разделе.
Поправка Бонферрони
Для проведения многократных проверок используется подход, который объясняет увеличенную вероятность обнаружить значимый эффект в силу многократных испытаний. Поправка Бонферрони — это очень простая корректировка, которая обеспечивает, чтобы мы вряд ли совершили ошибки 1-го рода. Она выполняется путем настройки значения уровня значимости для тестов.
Настройка очень простая — поправка Бонферрони попросту делит требуемое значение α на число тестов. Например, если для теста имелось k вариантов дизайна веб-сайта, и α эксперимента равно 0.05, то поправка Бонферрони выражается следующим образом:
Она представляет собой безопасный способ смягчить увеличение вероятности совершения ошибки 1-го рода при многократной проверке. Следующий пример идентичен примеру ex-2-22, за исключением того, что значение α разделено на число групп:
def ex_2_23():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
против исходного (0) с поправкой Бонферрони'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05 / len(groups)
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group(site_a)['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается от исходного: %f'
% (site_a, p_val))Если вы выполните приведенный выше пример, то увидите, что при использовании поправки Бонферрони ни один из веб-сайтов больше не считается статистически значимым.
Метод проверки статистической значимости связан с поддержанием равновесия — чем меньше шансы совершения ошибки 1-го рода, тем больше риск совершения ошибки 2-го рода. Поправка Бонферрони очень консервативна, и весьма возможно, что из-за излишней осторожности мы пропускаем подлинное расхождение.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В заключительном посте, посте №4, этой серии постов мы проведем исследование альтернативного подхода к проверке статистической значимости, который позволяет устанавливать равновесие между совершением ошибок 1-го и 2-го рода, давая нам возможность проверить все 20 вариантов веб-сайта одновременно.
С каждым днем количество данных становится больше и больше. И как говорится, чем больше ты знаешь, тем больше ты задаешь вопросов, и тем больше ты хочешь получить ответов. Получить ответы на основе данных можно с помощью статистики. А именно, если требуется что-то сравнить, поможет проверка статистических гипотез.
Что же такое статистическая гипотеза. Приведём определение из Википедии.
Статистическая гипотеза — предположение о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть применением статистических методов к данным выборки.
Случайная величина, например, среднее, берется из выборки, которая тоже должна быть взята случайно и в ней должно быть от 30 элементов. Если выборка берется не случайно, то и данные будут не достоверные. Значение в 30 элементов это научно доказанный факт, так как начиная от 30 выборочные среднее и дисперсия близки к реальному среднему и дисперсии генеральной совокупности.
В общем виде алгоритм проверки выглядит следующим образом:
1. Формулировка основной гипотезы Н₀ и альтернативной гипотезы Н₁;
2. Задание уровня значимости α;
Определение уровня значимости довольно большая тема, поэтому обозначим кратко основные моменты.
Есть стандартные уровни значимости 0,1; 0,05; 0,01; 0,001.
И условно их можно выбирать так. Если объем выборки небольшой до 100 единиц, то можно вполне отвергнуть нулевую гипотезу при уровне значимости 0,05 или даже 0,1. При объеме выборки, измеряемой сотнями – от 100 до 1000, следует понизить уровень значимости хотя бы до 0,01. А при больших выборках, измеряемых тысячами наблюдений, уверенно отвергать нулевую гипотезу можно только при значимости меньшей 0,001.
В целом же для каждой конкретной задачи нужно смотреть на данные и подбирать уровень значимости, который в лучшей мере подойдет для этих данных.
3. Выбор статистического критерия;
4. Определения правила принятия решения;
5. Принятие решения на основе данных.
Теперь проведем тест на Python используя библиотеку scipy.stats.
Гипотеза: средние показатели переменных различаются.
— Сформулируем нулевую гипотезу (Н₀). Среднее значение тарифов тариф_1 и тариф_2 одинаковое.
— Сформулируем альтернативную гипотезу (Н₁). Среднее значение тарифов тариф_1 и тариф_2 разное.
Для примера возьмем распределение для тарифа_1 в виде data_1, а для тарифа_2 в виде data_2
Будем использовать следующие данные для проверки гипотез.
data_1 = np.random.uniform(-1, 0, 1000) # равномерное распределение тариф1
data_2 = np.random.normal(-1, 2, 1000) # нормальное распределение тариф2
В нашем примере будем использовать α = 0.05
Первым тестом для проверки будет тест Шапиро-Уилка.
Тест оценивает набор данных и дает количественную оценку вероятности того, что данные были получены из Гауссовского (нормального) распределения.
Для теста используется формула:
Здесь S2 — сумма квадратов отклонений значений выборки от среднего арифметического:
Значение B2 находят по формуле:
data = pd.concat([data_1, data_2]).reset_index(drop=True)
# сделаем генеральное распределение для проведение теста
stat, p = stats.shapiro(data)
print(‘Statistics=%.3f, p-value=%.3f’ % (stat, p))
if p < alpha:
print(‘Отклонить гипотезу о нормальности’)
else:
print(‘Принять гипотезу о нормальности’)
Statistics=0.919, p-value=0.000
Отклонить гипотезу о нормальности
Тест показал, что нормальность не соблюдается.
Следующий тест, тест Левена.
Логическая статистика, используемая для оценки равенства дисперсий для переменной, рассчитанной для двух или более групп. Некоторые распространенные статистические процедуры предполагают, что дисперсии популяций, из которых взяты различные выборки, равны. Тест Левена оценивает это предположение. Он проверяет нулевую гипотезу о том, что дисперсии популяции равны. Если результирующее p-значение теста Левена меньше некоторого уровня значимости (обычно 0.05), полученные различия в выборочных дисперсиях вряд ли имели место на основе случайной выборки из популяции с равными дисперсиями. Таким образом, нулевая гипотеза равных дисперсий отвергается и делается вывод о наличии разницы между дисперсиями в популяции.
Для теста используется формула:
Где:
k — это число различных групп, к которым принадлежат отобранные случаи,
N_i — это количество случаев в i группе,
N — это общее количество случаев во всех группах,
Y_ij — это значение измеряемой переменной для j случая из i группы,
Первое среднее по группе j
Второе медиана по группе i
test_leven, p = stats.levene(data_1, data_2)
print(‘Statistics=%.3f, p-value=%.3f’ % (test_leven, p))
alpha = 0.05
if p < alpha:
print(‘Отклонить гипотезу о равенстве дисперсий’)
else:
print(‘Принять гипотезу о равенстве дисперсий’)
Statistics=1272.766, p-value=0.000
Отклонить гипотезу о равенстве дисперсий
Проверим гипотезу с помощью scipy.stats.ttest_ind, так как с его помощью можно сравнить средние двух совокупностей.
results = stats.ttest_ind(
data_1[0],
data_2[0],
equal_var=False) # Так как нормальность не соблюдается
print(‘p-значение:’, results.pvalue)
if (results.pvalue < alpha):
print(«Отвергаем нулевую гипотезу»)
else:
print(«Не получилось отвергнуть нулевую гипотезу»)
p-значение: 2.19278763437e-16
Отвергаем нулевую гипотезу
Тест показывает, что гипотеза Н₀ не подтверждена, следовательно, отвергаем нулевую гипотезу. Поэтому принимаем альтернативную гипотезу Н₁, cреднее значение тарифа_1 и тарифа_2 разное.
В статистике есть и другие тесты для проверки гипотезы, главное понять какой конкретный тест подходит для Ваших данных. И не допускать ошибок первого и второго рода. Так как вероятность принять неправильную гипотезу, Н₀, или отвергнуть правильную всегда есть. Поэтому тестов много, как и данных, найдите правильный тест для своих гипотез.
27 февраля 2017 г.
Метрики качества классификаторов
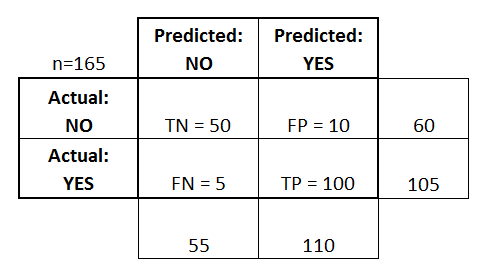
Матрица ошибок (Confusion matrix)
Матрица ошибок — это способ разбить объекты на четыре категории в зависимости от комбинации истинного ответа и ответа алгоритма.
Основные термины:
- TPTP — истино-положительное решение;
- TNTN — истино-отрицательное решение;
- FPFP — ложно-положительное решение (Ошибка первого рода);
- FNFN — ложно-отрицательное решение (Ошибка второго рода).
Интерактивная картинка с большим числом метрик
Accuracy — доля правильных ответов:
Accuracy=TP+TNP+N=TP+TNTP+TN+FP+FN{displaystyle mathrm {Accuracy} ={frac {mathrm {TP} +mathrm {TN} }{P+N}}={frac {mathrm {TP} +mathrm {TN} }{mathrm {TP} +mathrm {TN} +mathrm {FP} +mathrm {FN} }}}
Данная матрика имеет существенный недостаток — её значение необходимо оценивать в контексте баланса классов. Eсли в выборке 950 отрицательных и 50 положительных объектов, то при абсолютно случайной классификации мы получим долю правильных ответов 0.95. Это означает, что доля положительных ответов сама по себе не несет никакой информации о качестве работы алгоритма a(x), и вместе с ней следует анализировать соотношение классов в выборке.
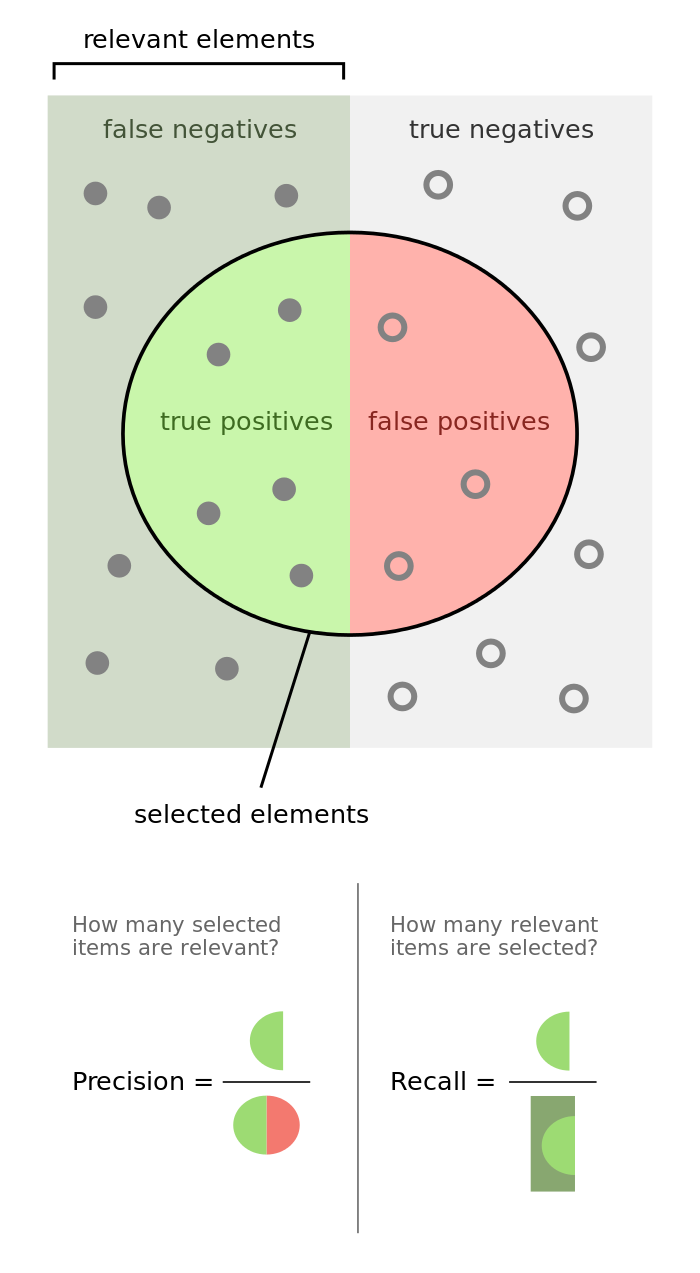
Гораздо более информативными критериями являются точность (precision) и полнота (recall).
Точность показывает, какая доля объектов, выделенных классификатором как положительные, действительно является положительными:
Precision=TPTP+FPPrecision = frac{TP}{TP+FP}
Полнота показывает, какая часть положительных объектов была выделена классификатором:
Recall=TPTP+FNRecall = frac{TP}{TP+FN}
Существует несколько способов получить один критерий качества на основе точности и полноты. Один из них — F-мера, гармоническое среднее точности и полноты:
F_beta = (1 + beta^2) cdot frac{mathrm{precision} cdot mathrm{recall}}{(beta^2 cdot mathrm{precision}) + mathrm{recall}} = frac {(1 + beta^2) cdot mathrm{true positive} }{(1 + beta^2) cdot mathrm{true positive} + beta^2 cdot mathrm{false negative} + mathrm{false positive}}
Среднее гармоническое обладает важным свойством — оно близко к нулю, если хотя бы один из аргументов близок к нулю. Именно поэтому оно является более предпочтительным, чем среднее арифметическое (если алгоритм будет относить все объекты к положительному классу, то он будет иметь recall = 1 и precision больше 0, а их среднее арифметическое будет больше 1/2, что недопустимо).
Чаще всего берут β=1beta=1, хотя иногда встречаются и другие модификации. F2F_2 острее реагирует на recall (т. е. на долю ложноположительных ответов), а F0.5F_{0.5} чувствительнее к точности (ослабляет влияние ложноположительных ответов).
В sklearn есть удобная функция sklearn.metrics.classification_report, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
import pandas as pd import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler, LabelEncoder from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn import datasets import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline %config InlineBackend.figure_format = 'svg'
from sklearn.metrics import classification_report y_true = [0, 1, 2, 2, 2] y_pred = [0, 0, 2, 2, 1] target_names = ['class 0', 'class 1', 'class 2'] print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
micro avg 0.60 0.60 0.60 5
macro avg 0.50 0.56 0.49 5
weighted avg 0.70 0.60 0.61 5
Линейная классификация
Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на две полуплоскости, в каждой из которых прогнозируется одно из двух значений целевого класса.
Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.
Указанная разделяющая плоскость называется линейным дискриминантом.
Логистическая регрессия
Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим «умением» – прогнозировать вероятность отнесения наблюдения к классу. Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].
iris = pd.read_csv("https://nagornyy.me/datasets/iris.csv")
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.057333 | 3.758000 | 1.199333 |
| std | 0.828066 | 0.435866 | 1.765298 | 0.762238 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
sns.pairplot(iris, hue="species")
/usr/local/lib/python3.7/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
sns.lmplot(x="petal_length", y="petal_width", data=iris)
X = iris.iloc[:, 2:4].values y = iris['species'].values
array([‘setosa’, ‘setosa’, ‘setosa’, ‘setosa’, ‘setosa’], dtype=object)
from sklearn.preprocessing import LabelEncoder le = LabelEncoder() le.fit(y) y = le.transform(y) y[:5]
iris_pred_names = le.classes_ iris_pred_names
array([‘setosa’, ‘versicolor’, ‘virginica’], dtype=object)
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import StandardScaler sc = StandardScaler() sc.fit(X_train) X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test)
X_train[:5], X_train_std[:5]
(array([[3.5, 1. ],
[5.5, 1.8],
[5.7, 2.5],
[5. , 1.5],
[5.8, 1.8]]), array([[-0.18295039, -0.29318114],
[ 0.93066067, 0.7372463 ],
[ 1.04202177, 1.63887031],
[ 0.6522579 , 0.35083601],
[ 1.09770233, 0.7372463 ]]))
from sklearn.linear_model import LogisticRegression lr = LogisticRegression(C=100.0, random_state=1) lr.fit(X_train_std, y_train)
/usr/local/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:433: FutureWarning: Default solver will be changed to ‘lbfgs’ in 0.22. Specify a solver to silence this warning.
FutureWarning)
/usr/local/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:460: FutureWarning: Default multi_class will be changed to ‘auto’ in 0.22. Specify the multi_class option to silence this warning.
«this warning.», FutureWarning)
LogisticRegression(C=100.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class=’warn’,
n_jobs=None, penalty=’l2′, random_state=1, solver=’warn’,
tol=0.0001, verbose=0, warm_start=False)
lr.predict_proba(X_test_std[:3, :])
array([[2.77475804e-08, 6.31730607e-02, 9.36826912e-01],
[7.87476628e-03, 9.91707489e-01, 4.17744834e-04],
[8.15542033e-01, 1.84457967e-01, 8.14812482e-12]])
lr.predict_proba(X_test_std[:3, :]).sum(axis=1)
lr.predict_proba(X_test_std[:3, :]).argmax(axis=1)
Предсказываем класс первого наблюдения
lr.predict(X_test_std[0, :].reshape(1, -1))
На основе его коэффициентов:
array([0.70793846, 1.51006688])
X_test_std[0, :].reshape(1, -1)
array([[0.70793846, 1.51006688]])
y_pred = lr.predict(X_test_std)
print(classification_report(y_test, y_pred, target_names=iris_pred_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 16
versicolor 1.00 0.94 0.97 18
virginica 0.92 1.00 0.96 11
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Машина опорных векторов
Основная идея метода — перевод исходных векторов в пространство более высокой размерности и поиск разделяющей гиперплоскости с максимальным зазором в этом пространстве. Две параллельных гиперплоскости строятся по обеим сторонам гиперплоскости, разделяющей классы. Разделяющей гиперплоскостью будет гиперплоскость, максимизирующая расстояние до двух параллельных гиперплоскостей. Алгоритм работает в предположении, что чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше будет средняя ошибка классификатора.
На практике случаи, когда данные можно разделить гиперплоскостью, довольно редки. В этом случае поступают так: все элементы обучающей выборки вкладываются в пространство X более высокой размерности, так, чтобы выборка была линейно разделима.
from sklearn.svm import SVC svm = SVC(kernel='linear', C=1.0, random_state=1) svm.fit(X_train_std, y_train)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=’auto_deprecated’,
kernel=’linear’, max_iter=-1, probability=False, random_state=1,
shrinking=True, tol=0.001, verbose=False)
Kernel (ядро) отвечается за гиперплоскость и может принимать значения linear (для линейной), rbf (для нелинейной) и другие.
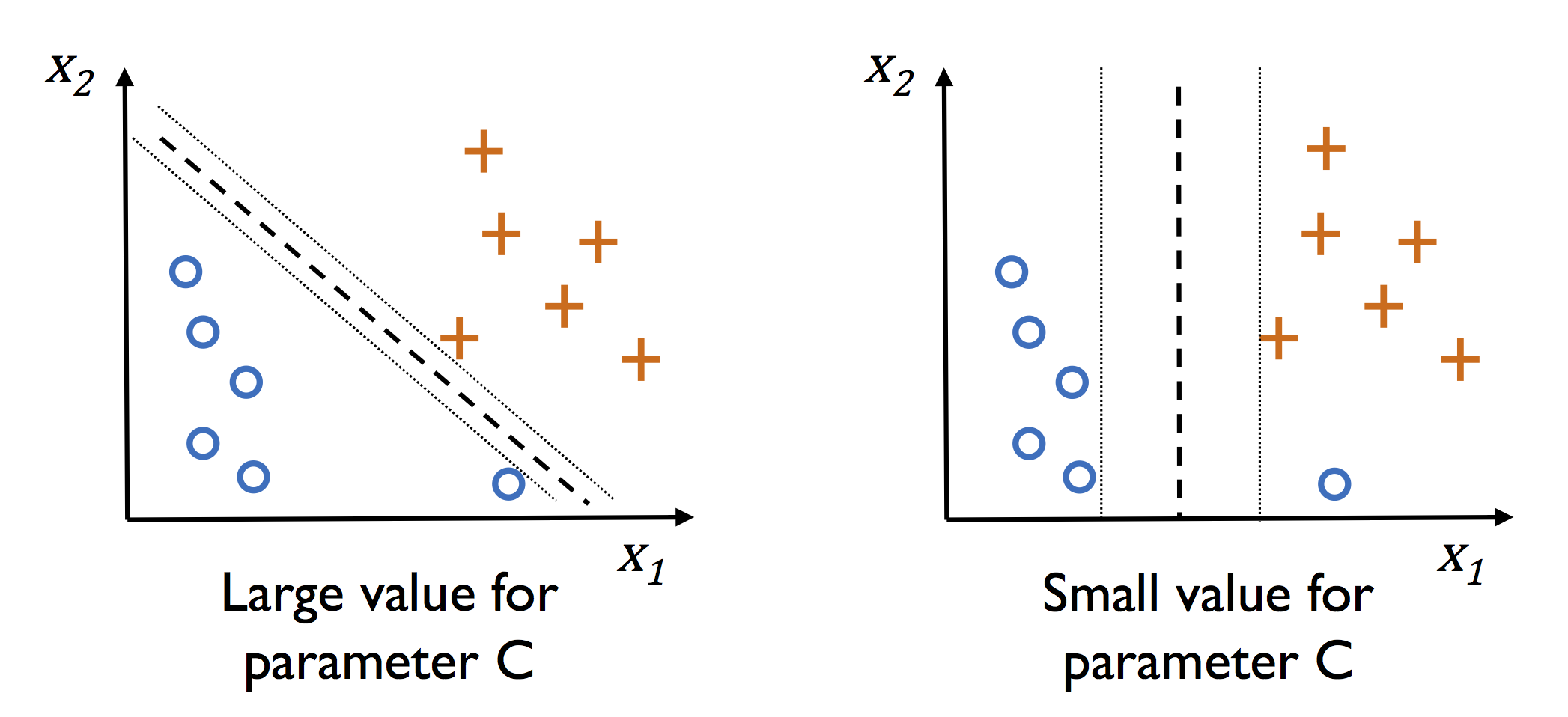
С — параметр регуляризации. Он в том числе контролирует соотношение между гладкой границей и корректной классификацией рассматриваемых точек.
gamma — это «ширина» rbf ядра (kernel). Она участвует в подгонке модели и может являться причиной переобучения.
y_pred_svm = svm.predict(X_test_std)
print(classification_report(y_test, y_pred_svm, target_names=iris_pred_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 16
versicolor 1.00 0.94 0.97 18
virginica 0.92 1.00 0.96 11
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Нелинейная классификация
svm_rbf = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0) svm_rbf.fit(X_train_std, y_train)
SVC(C=10.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=0.1, kernel=’rbf’,
max_iter=-1, probability=False, random_state=1, shrinking=True,
tol=0.001, verbose=False)
y_pred_svm_rbf = svm_rbf.predict(X_test_std) print(classification_report(y_test, y_pred_svm_rbf, target_names=iris_pred_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 16
versicolor 1.00 0.94 0.97 18
virginica 0.92 1.00 0.96 11
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Деревья решений
Деревья решений используются в повседневной жизни в самых разных областях человеческой деятельности.
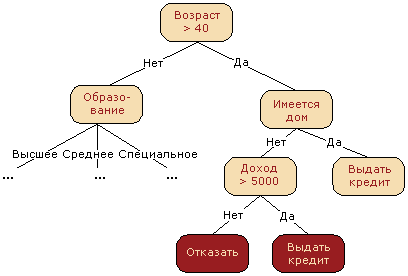
До внедрения масштабируемых алгоритмов машинного обучения в банковской сфере задача кредитного скоринга решалась экспертами. Решение о выдаче кредита заемщику принималось на основе некоторых интуитивно (или по опыту) выведенных правил, которые можно представить в виде дерева решений:
В этом случае можно сказать, что решается задача бинарной классификации (целевой класс имеет два значения: «Выдать кредит» и «Отказать») по признакам «Возраст», «Наличие дома», «Доход» и «Образование».
Дерево решений как алгоритм машинного обучения – по сути то же самое. Огромное преимущество деревьев решений в том, что они легко интерпретируемы, понятны человеку.
В основе популярных алгоритмов построения дерева решений лежит принцип жадной максимизации прироста информации – на каждом шаге выбирается тот признак, при разделении по которому прирост информации оказывается наибольшим. Дальше процедура повторяется рекурсивно, пока энтропия не окажется равной нулю или какой-то малой величине (если дерево не подгоняется идеально под обучающую выборку во избежание переобучения).
Плюсы:
- Порождение четких правил классификации, понятных человеку, например, «если возраст < 25 и интерес к мотоциклам, то отказать в кредите». Это свойство называют интерпретируемостью модели;
- Деревья решений могут легко визуализироваться, как сама модель (дерево), так и прогноз для отдельного взятого тестового объекта (путь в дереве);
- Быстрые процессы обучения и прогнозирования;
- Малое число параметров модели;
- Поддержка и числовых, и категориальных признаков.
Минусы:
- У порождения четких правил классификации есть и другая сторона: деревья очень чувствительны к шумам во входных данных, вся модель может кардинально измениться, если немного изменится обучающая выборка (например, если убрать один из признаков или добавить несколько объектов), поэтому и правила классификации могут сильно изменяться, что ухудшает интерпретируемость модели;
- Разделяющая граница, построенная деревом решений, имеет свои ограничения (состоит из гиперплоскостей, перпендикулярных какой-то из координатной оси), и на практике дерево решений по качеству классификации уступает некоторым другим методам;
from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(criterion='gini', max_depth=4, random_state=1) tree.fit(X_train_std, y_train)
DecisionTreeClassifier(class_weight=None, criterion=’gini’, max_depth=4,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=1,
splitter=’best’)
y_pred_tree = tree.predict(X_test_std) print(classification_report(y_test, y_pred_tree, target_names=iris_pred_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 16
versicolor 1.00 0.94 0.97 18
virginica 0.92 1.00 0.96 11
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Collecting pydotplus
[?25l Downloading https://files.pythonhosted.org/packages/60/bf/62567830b700d9f6930e9ab6831d6ba256f7b0b730acb37278b0ccdffacf/pydotplus-2.0.2.tar.gz (278kB)
[K 100% |████████████████████████████████| 286kB 1.5MB/s
[?25hRequirement already satisfied: pyparsing>=2.0.1 in /usr/local/lib/python3.7/site-packages (from pydotplus) (2.3.0)
Building wheels for collected packages: pydotplus
Running setup.py bdist_wheel for pydotplus … [?25ldone
[?25h Stored in directory: /Users/hun/Library/Caches/pip/wheels/35/7b/ab/66fb7b2ac1f6df87475b09dc48e707b6e0de80a6d8444e3628
Successfully built pydotplus
Installing collected packages: pydotplus
Successfully installed pydotplus-2.0.2
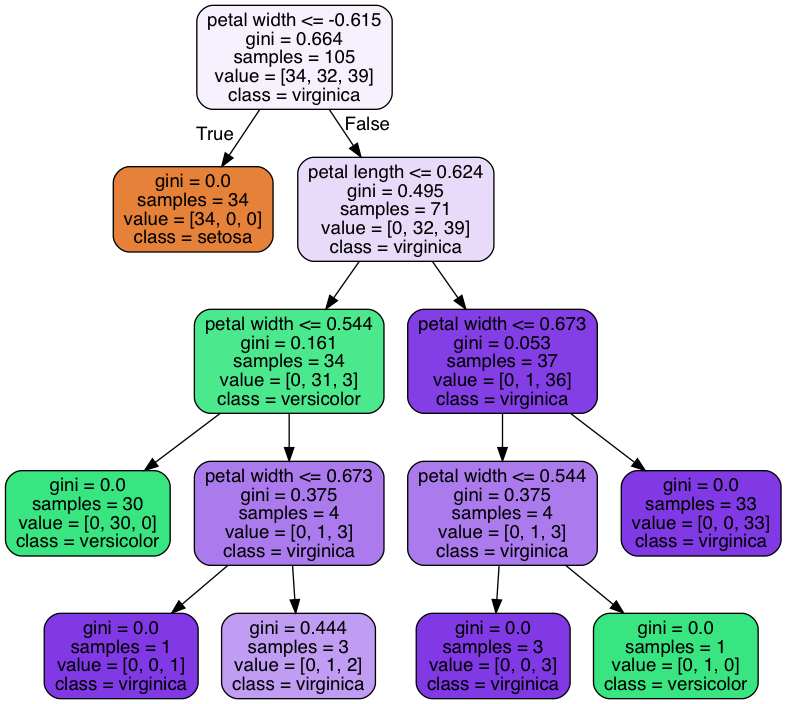
from pydotplus import graph_from_dot_data from sklearn.tree import export_graphviz dot_data = export_graphviz(tree, filled=True, rounded=True, class_names=iris_pred_names, feature_names=['petal length', 'petal width'], out_file=None) graph = graph_from_dot_data(dot_data)
Метод ближайших соседей
Метод ближайших соседей (k Nearest Neighbors, или kNN) — тоже очень популярный метод классификации, также иногда используемый в задачах регрессии. Это, наравне с деревом решений, один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей, какие преобладают, таков и ты. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
- Вычислить расстояние до каждого из объектов обучающей выборки
- Отобрать k объектов обучающей выборки, расстояние до которых минимально
- Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди k ближайших соседей
Под задачу регрессии метод адаптируется довольно легко – на 3 шаге возвращается не метка, а число – среднее (или медианное) значение целевого признака среди соседей.
Примечательное свойство такого подхода – его ленивость. Это значит, что вычисления начинаются только в момент классификации тестового примера, а заранее, только при наличии обучающих примеров, никакая модель не строится. В этом отличие, например, от ранее рассмотренного дерева решений, где сначала на основе обучающей выборки строится дерево, а потом относительно быстро происходит классификация тестовых примеров.
Качество классификации/регрессии методом ближайших соседей зависит от нескольких параметров:
- число соседей
- метрика расстояния между объектами (часто используются метрика Хэмминга, евклидово расстояние, косинусное расстояние и расстояние Минковского). Отметим, что при использовании большинства метрик значения признаков надо масштабировать. Условно говоря, чтобы признак «Зарплата» с диапазоном значений до 100 тысяч не вносил больший вклад в расстояние, чем «Возраст» со значениями до 100.
- веса соседей (соседи тестового примера могут входить с разными весами, например, чем дальше пример, тем с меньшим коэффициентом учитывается его «голос»)
Плюсы и минусы метода ближайших соседей
Плюсы:
- Простая реализация;
- Неплохо изучен теоретически;
- Как правило, метод хорош для первого решения задачи;
- Можно адаптировать под нужную задачу выбором метрики или ядра (ядро может задавать операцию сходства для сложных объектов типа графов, а сам подход kNN остается тем же);
- Неплохая интерпретация, можно объяснить, почему тестовый пример был классифицирован именно так.
Минусы:
- Метод считается быстрым в сравнении, например, с композициями алгоритмов, но в реальных задачах, как правило, число соседей, используемых для классификации, будет большим (100-150), и в таком случае алгоритм будет работать не так быстро, как дерево решений;
- Если в наборе данных много признаков, то трудно подобрать подходящие веса и определить, какие признаки не важны для классификации/регрессии;
- Зависимость от выбранной метрики расстояния между примерами. Выбор по умолчанию евклидового расстояния чаще всего ничем не обоснован. Можно отыскать хорошее решение перебором параметров, но для большого набора данных это отнимает много времени;
- Нет теоретических оснований выбора определенного числа соседей — только перебор (впрочем, чаще всего это верно для всех гиперпараметров всех моделей). В случае малого числа соседей метод чувствителен к выбросам, то есть склонен переобучаться;
- Как правило, плохо работает, когда признаков много, из-за «прояклятия размерности». Про это хорошо рассказывает известный в ML-сообществе профессор Pedro Domingos – тут в популярной статье «A Few Useful Things to Know about Machine Learning», также «the curse of dimensionality» описывается в книге Deep Learning в главе «Machine Learning basics».
Класс KNeighborsClassifier в Scikit-learn
Основные параметры класса sklearn.neighbors.KNeighborsClassifier:
- weights: «uniform» (все веса равны), «distance» (вес обратно пропорционален расстоянию до тестового примера) или другая определенная пользователем функция
- algorithm (опционально): «brute», «ball_tree», «KD_tree», или «auto». В первом случае ближайшие соседи для каждого тестового примера считаются перебором обучающей выборки. Во втором и третьем — расстояние между примерами хранятся в дереве, что ускоряет нахождение ближайших соседей. В случае указания параметра «auto» подходящий способ нахождения соседей будет выбран автоматически на основе обучающей выборки.
- leaf_size (опционально): порог переключения на полный перебор в случае выбора BallTree или KDTree для нахождения соседей
- metric: «minkowski», «manhattan», «euclidean», «chebyshev» и другие
from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski') knn.fit(X_train_std, y_train) y_pred_knn = knn.predict(X_test_std) print(classification_report(y_test, y_pred_knn, target_names=iris_pred_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 16
versicolor 1.00 1.00 1.00 18
virginica 1.00 1.00 1.00 11
micro avg 1.00 1.00 1.00 45
macro avg 1.00 1.00 1.00 45
weighted avg 1.00 1.00 1.00 45
Домашнаяя работа
Примените изученные классификаторы для предсказания выживаемости на Титанике и постойте наилучший классификатор. Каковы значения основных его метрик?
Опирайтесь на эти статьи:
- Kaggle и Titanic — еще одно решение задачи с помощью Python
- Основы анализа данных на python с использованием pandas+sklearn
- Титаник на Kaggle: вы не дочитаете этот пост до конца
Принимать решения без данных это как играть в русскую рулетку: повезет – не повезет. Поэтому данные нужно копить с первого дня жизни бизнеса. Данные это сырье для бизнеса, и по началу они будут помогать принимать решения без особых затрат. Но когда количество данных перевалит за 1 Tb, бизнесу станет сложнее быстро выжимать фичи по векторам на регулярной основе. Помочь может визуализация данных. Имея в багаже математическую базу и возможности Python при использовании библиотек matplotlib, seaborn и plotly, можно покрыть большинство потребностей по визуализации графиков для руководства и для принятия решений.
Существует множество инструментов для визуализации данных: R, Python, JS, Matlab, Scala и Java. R это больше язык для исследователей и студентов, поэтому у него на данный момент больше полезных библиотек для визуализации, чем у Python. Но Python лучше для дальнейшей интеграции разработки.
На больших проектах, где положительные изменения дают 1%<, аналитика необходима. Как минимум, нужно не только проверить результаты a/b теста, но и как эти две группы пользователей вели себя до эксперимента. И отсечь влияние других экспериментов, прошлых и нынешних.
Примерный пайплайн такой:
— проверяем данные на нормальность;
— проверяем отличия с помощью статистического теста;
— доверительным интервалом оцениваем масштаб (среднее при нормальности или медиана для ненормальности данных);
— сравниваем с прошлым поведением групп пользователей;
Данных для визуализации на Python должно быть много, иначе нет смысла в распределенном анализе. Если данных много, то вы почти всегда получите маленькое p-value, и вам останется только проработать нормальность данных, их независимость и т.п. Для расчёт размера выборки нужны тесты для анализа мощности (power tests). На маленьких выборках статистические тесты могут быть менее эффективны, чем экспертная оценка, а на больших данных будут видны даже минимальные отклонение от нормальности. Также, при малой выборке мы не можем использовать центральную предельную теорему.
Основная библиотека для визуализации это Matplotlib. Отмечу, что Matplotlib пусть и очень популярная, но достаточно старая и сложная библиотека, и для комфортной работы лучше использовать API поверх Matplotlib, такие как Seaborn, у которого много своих способов построения графиков. При том, достаточно эстетичных. Достаточно добавить sns.set(), посмотрим на примере:
import matplotlib matplotlib.use('TkAgg') import numpy as np from matplotlib import pyplot as plt import seaborn as sns; sns.set() norm_data = np.random.normal(size = 1000, loc = 0, scale = 1) plt.hist(norm_data) plt.show()
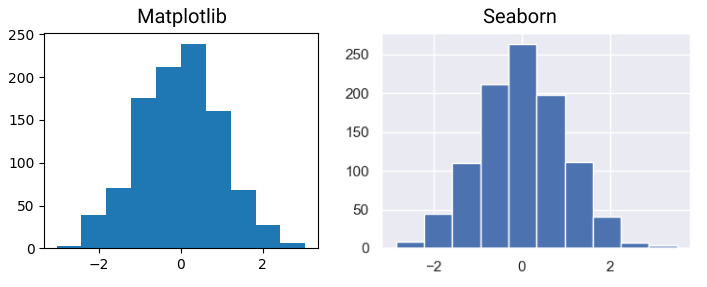
Мы построили наш первый график, используя Python. Конечно, хочется быстрее перейти от работы со списками к работе с массивами значений. Но для начала немного освежим теорию математической статистики:
Нулевая гипотеза всегда консервативна (проще проверяется), а альтернативная гипотеза это ненормальное распределение. В первую очередь проверяется нормальность данных, так как для среднего и стандартного отклонения нормальное распределение может быть лишь одно, ненормальных распределений возможно бесконечное количество. Проверка нормальности возможна тестом Shapiro-Wilk, который проверяет нулевую гипотезу о происхождении данных из нормального распределения. Есть понятие смеси распределений, в этом случае приходится обращаться к Марковской цепи Монте-Карло (MCMC).
Проверка результатов a/b-теста это частный случай проверки статистической гипотезы. Статистическая гипотеза это предположене о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть. По умолчанию требуется проверить гипотезу H0, это называется нулевая гипотеза. Она истинна, пока не доказано обратное. Если доказано обратное, то побеждает альтернативная H1 гипотеза .
Принято использовать следующие обозначения:
| Показатель | Генеральная совокупность | Выборка |
| Дисперсия | σ² | s² |
| Размер выборки | N | n |
| Коэффицент корреляции | p | r |
Генеральная совокупность и выборка. В чем разница? Выборка это набор данных, который у нас есть. Генеральная совокупность это вообще все данные, которые можно учесть при расчетах. Простой пример: у нас есть пирог, мы отрезаем кусочек и пробуем. Если торт вкусный, то на основании выборки (кусочка) мы делаем вывод про всю генеральную совокупность (торт).
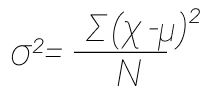
Например, у нас есть выборка из нормального распределения с неизвестным параметром α и известным параметром σ = 1. H0 = параметр α равен некому значению, при этом гипотеза создается еще до данных, а не является их следствием. Проверяя H0, мы по выборке считаем некое значение и сравниваем его с теоретическим. Когда мы рассматриваем выборку, допускаем отклонения от теоретических значений, так как среднее арифметическое никогда не бывает равно мат. ожиданию, оно будет отклоняться. И мы стараемся установить, какое отклонение полученного значения от теоретического мы готовы считать допустимым (незначимым), и какое отклонение нельзя списать на случайные факторы (значимое). Если отклонение значимо, тогда H0 отвергается. Отклонение не значимо, H0 подтверждается.
Коэффицент корреляции. Корреляция это взаимосвязь двух и более случайных величин. Корреляция бывает очень разной: сильной в разной степени, негативной. В интернете очень любят сравнивать две никак не связанные величины, например, количество zoom-митингов в Чите и проданных ножей в Алабаме. Причинно-следственной связи никакой, но может быть схожесть поведения показателей.
Для работы нам нужно:
- Определиться с H0 и H1.
- Мы предполагаем, что нулевая гипотеза верна, и задаем некую статистику (функция от выборки), обозначим ее как T. У нас есть нормально распределенная случайная величина с неизвестной дисперсией, тогда используется такая статистика:
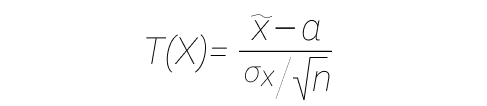
- В формуле выше статистика имеет распределение Стьюдента (t-распределение) с параметром df = n-1, где n — объем выборки. Если в формуле выше X имеет нормальное распределение, то такая статистика имеет распределение Стьюдента, мы берем это как доказанный факт. При нормальном распределении σ = 1, a = 0.
- Если известно мат. ожидание, а дисперсия не известна, и мы хотим проверить гипотезу о дисперсии, то берем квантили распределения хи-квадрат. Распределение хи-квадрат это другое распределение. Для большинства других распределений таких статистик нет. Например, выборочное среднее равномерного распределения довольно сложно считать, и мы считаем по ЦПД (число объектов в выборке = бесконечность, значит распределение близко к нормальному). Этим пользуются крупные компании, у них куча трафика. Если трафика мало, то можно заняться оптимизацией. Скорость a/b-тестов можно увеличить за счет управления чувствительностью тестов: оптимизация дисперсии, менять описательные статистики, трансформировать данные и изменять размерность данных (поубирали хвосты — дисперсия уменьшилась).
- Далее уровень значимости α — допустимая вероятность ошибки первого рода (те самые 0.05), значение варьируется в зависимости от задачи.
- Определяется критическая область. Ω = визуально это некий отрезок, который говорит нам о том, что значение T из пунктов выше попадает в критическую область.
- проводим статистический тест: для выборки считаем значение T (статистика, функция от выборки), и если оно принадлежит Ω, то считаем, что данные противоречат гипотезе H0 и мы принимаем H1.
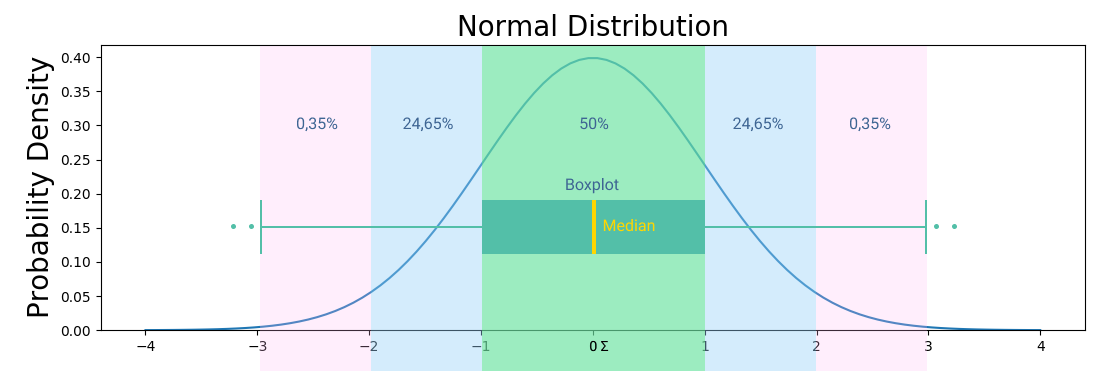
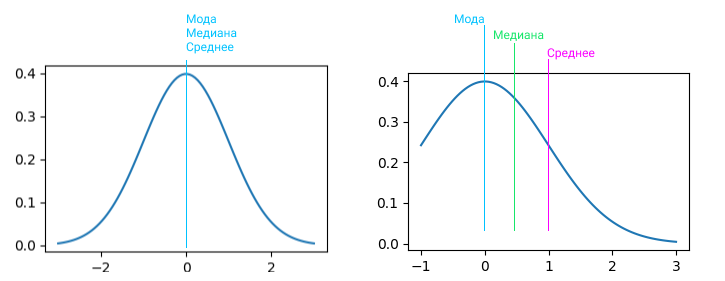
Стандартное отклонение это квадратный корень дисперсии. Другими словами, это среднее значение квадрата разности значений в наборе данных от среднего значения. Если данные нормально распределены, то нужны среднее и дисперсия. Для проверки гипотез о дисперсии нормального распределения используются квантили распределения хи-квадрат. Остальные распределения, по большей части, не имеют соответствующих статистик, поэтому принято использовать центральную предельную теорему с некой погрешностью. На графиках выше и ниже вы можете видеть примеры визуализации нормального распределения.
Среднее, медиана и мода это показатели центра распределения. А вариация распределения, изменчивость/волатильность выборки описывается параметром «Дисперсия». И тут в дело вступаем стандартное отклонение, это дочерний показатель от дисперсии. Показывает, на сколько в среднем отклоняются элементы выборки от среднего значения. Если средний китаец знает 3000 иероглифов, то стандартное отклонение 400 иероглифов. Если у нас среднее значение 100 заявок, а стандратное отклонение 300 заявок, то данные очень сильно колеблятся, это называется коэффциент вариации. просто делим стандартное отклонение на среднее и получаем на выходе %, так что это процентная величина отклонения.
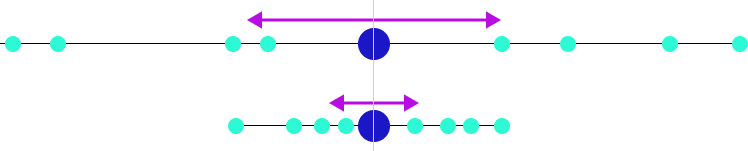
Дисперсия это не константа, с ней можно работать. Существует децильный метод. Мы берем все данные из теста и контроля и делим распределение на некое количество квартилей, децилей, перцентилей. Внутри каждого микро-набора данных будет своя размерность данных, по которому мы и будем оценивать эксперимент. 1-ая дециль будет содержать минимальные значения, 10-ая — самые большие. В таком подходе дисперсия уменьшается за счет уменьшения разброса данных. Необходимо использовать поправки на множественное сравнение: классический/консервативный Бонферони, метод Холма, Бенджамини-Иекутиели, Бенджамини-Хохберг. Или просто уменьшать p-value.
Если не хотим разбираться с нормальным распределением, то используем статистический метод бутстрэппинг.
На картинке вы можете видеть центральную линию, это медиана. Медиана это расстановка элементов выборки от меньшего к большему и берем самый центральный элемент выборки. Помимо удаления выбросов из данных, подсчета размера выборки, кластеризации группы пользователей, обычно всех интересует адекватная мера центральной тенденции, которая может быть представлена следующими понятиями:
- Среднее арифметическое значение в данных. Идея в том, что если взять любое типичное значение из набора данных, оно будет похоже на среднее значение. Не самый надежный способ, очень аффектится экстремально высокими или низкими значениями. 2+4+6+26 / 4 = 9,5, любимый подход недобросовестных СМИ.
- Медиана. В отличии от среднего арифметического, все значения сортируются в порядке возрастания и в качестве среднего значения берется то, что окажется в середине списка. Считается более надежным подходом, так как более робаста. Робастность = устойчивость к большим и малым значениям. Если в списке четное количество значений, то высчитывается среднее между двумя значениями из центра отсортированного набора данных.
- Мода. Значение, которое можно встретить в данных чаще остальных. Это менее среднее значение, чем два предыдущих. Скорее, это наиболее тяжеловесный фактор, который влияет на среднее значение в данных.
Разберем пример. Выбираем статистику, у нас гипотеза про математическое ожидание нормально распределенной случайной величины с известной дисперсией, вы берем чуть другую статистику (формулу), не такую как была в примере выше. Если H0 верна, то статистика (T) имеет нормальное стандартное распределение.

Нулевая гипотеза, что a = 6. Далее мы в рамках эксперимента нашли выборку, и хотим проверить гипотезу.
import numpy as np from scipy import stats data = np.random.normal(10,1,size = 200) data
Перейдем к проверке статистической значимости. Допустим, мы выгрузили данные по транзакциям за месяц и хотим понять, были ли отклонения от нормального поведения. α = 0,05. Внесем числа в формулу:
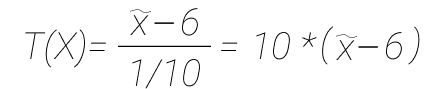
Далее работаем с критической областью. То, какую критическую область мы выберем, зависит от альтернативной гипотезы. Может быть двусторонней, левосторонней или правосторонней, в зависимости от задачи. В нашем случае значение может сместиться и на лево, и на право, поэтому выбираем двустороннюю критическую область. Выбрав двусторонний тест, мы задали условие для проверки гипотезы. Двусторонний тест не предполагает, что мы заранее знаем, какое значение будет больше, а какое меньше. Такой тест более консервативен и более общий, чем односторонний. Мы просто воспользуемся правилом двух сигм и получим интервал, или пользуемся таблицой квантилей. Квантили и квартили, тут все просто. Расставляем значения по порядку, например 100 элементов: 1,2,3….99, 100, и берем пятый квантиль — 5. Квартиль это частный случай квантиль, самые частотные квартили это 25%, 50% и 75%.
Найти квантили довольно просто: правило двух сигм дает интервал, в который с вероятностью 95% мы попадаем, и 5% что не попадаем. Квантиль будет 2 и -2. То есть, α/2 и 1-α/2, это квантили стандартного распределения. 2 и есть квантиль порядка 1-α/2, = 0.975. Теперь мы можем взять выборку, вычислить от нее значение статистики (T), и при попадании в критическую область отвергаем H0. Освежим в памяти сигмы: три сигмы это 99,73%, две сигмы это 95,45%, одна сигма это 68,27%.
Считаем мат. ожидание, mean = data.mean(). Результат 9.9296. И статистика: T = 10 * (mean - 6), результат 39.2962. Наша критическая область от бесконечности до 2 или от -2 до минус бесконечности, значение попало в область. Мы отвергаем гипотезу. Тут дело в том, что чем меньше α, тем шире критическая область, так мы можем управлять точностью теста и шансом отвергнуть гипотезу. И давайте пример посложнее:
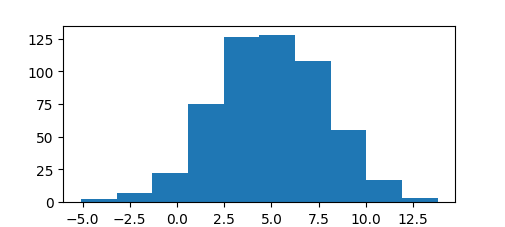
import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats from matplotlib import pyplot x = stats.norm.rvs(loc=5, scale=3, size=543) print (stats.shapiro(x)) pyplot.hist(x) pyplot.show()
Я осознанно не использую seed, так как чем больше вариативность полученных вами результатов, тем лучше. У меня возвращено 2 значения: значение статистики теста, и связанное с ним значение p-value, в моем случае получилось 0.011658577248454094. А так как 0.0116 < 0.05, и для отклонения нулевой гипотезы p-value должно быть не выше альфы 0,05, то у нас есть веские доказательства того, что мы отвергаем нулевую гипотезу на уровне значимости 0,05.
Но перед тем, как делать вывод об отсутствии различий, мы еще должны выяснить, была ли мощность использованного статистического критерия достаточной для их обнаружения. А мощность упирается в размер выборки. Нельзя сравнивать близкие законы при малых объёмах выборок.
Меняем Критерий Шапиро-Уилка на тест Андерсона, print (stats.anderson(x)), проверяем еще раз, что данные в выборке более менее нормально распределены. За тестом Андерсона Дарлинга часто используют w^2 Мизеса. Результат можно проверить даже визуально:
Давайте проведем F-тест, так как настало время проверки статистической значимости различий. Допустим, нужно сравнить работу продажников из двух городов.
Используем для этого ANOVA (дисперсионный анализ) из библиотеки Scipy, командой stats.f_oneway. Нулевая гипотеза ANOVA предполагает, что мат. ожидания совпадают. Если t-критерий Стьюдента используется для сравнения среднего значения в двух независимых или зависимых группах, то f-критерий проверяет, есть ли вообще разница. Можно использовать для большего количества выборок, чем 2. Разумеется, ANOVA не является f-тестом в полной мере, это модель регрессии и считается обобщенной линейной моделью (GLM). ANOVA используется для сравнения среднего значения какого-то признака в независимых группах.
import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats a = [2,3,1,4,3,4,2,4,-1,32,12,53,2,2,3,2.3,2,4.2,3,32,1] b = [3,4,-1,3,4,43,4,14,2.3,1,3,2.3,12,42,2.4,3,4,1,4,1,2] print (stats.f_oneway(a,b))
Получаем F-статистику F_onewayResult(statistic=0.0386380063725391, pvalue=0.8451628704190369), что говорит нам, больше ли дисперсия между группами, чем дисперсия внутри групп, и вычисляет вероятность наблюдения этого коэффициента дисперсии, используя F-распределение. Конечно, для научных публикаций данных недостаточно, нет степеней свободы. Но заветный P-value мы получили и теперь знаем, что раз 0.8451628704190369 > 0.05, то работа продажников явно завязана не только на тех данных, что у нас имеются. У нас отказ от нулевой гипотезы, так как данные не выглядят нормально. Нулевая гипотеза a = b, альтернативная a ≠ b. На самом деле, если нет желания разбираться с кучей критериев, достаточно освоить ANOVA и Bootstrap, так как все укладывается в общие линейные модели.
Сравним средние двух выборок с помощью T-test. Для T-test нам нужны среднее выборки, ее размер и отклонение. Мы хотим узнать, есть ли различия в двух группах данных, пусть это будут результаты A/B теста для туториалов в мобильном приложении. Для этого нужно интерпретировать статистическое значение в двустороннем тесте с примерно нормальным распределением, что означает, что нулевая гипотеза может быть отвергнута, когда средние значения двух выборок слишком отличаются. В R мы использовали функцию t.test() для простого t-теста Стьюдента, в Python мы пойдем более комплексным путем. Можно выполнить как односторонний, так и двусторонний T-test в Python. Если у вас много шума в данных, не забудьте сделать дисперсию. Стьюдента для независимых выборок считают с равными дисперсиями. Честно говоря, T-test самый консервативный из всех, ему нужна полная гомогенность выборок (50 на 50), и строго нормальное распределение. Для тестов бинарных или непрерывных метрик не подойдет.
У двустороннего теста и p-value получится в два раза больше, чем у одностороннего, поэтому двусторонний тест имеет более строгие критерии для отклонения нулевой гипотезы. Гипотетически, из двустороннего p-value можно получить одностороннее, но при правильно проведенном тесте не должно возникнуть такой необходимости. При двустороннем тесте мы делим p-value 0.05 на два, и отдаем по 0.025 на положительный и отрицательный концы распределения. При одностороннем тесте весь p-value 0.05 располагается в одном конце распределения. Так как второй конец распределения игнорируется, то есть вероятность ошибки: создав новый туториал, можно протестировать односторонним тестом, лучше ли новый туториал предыдущего. Но информация о том, хуже ли новый туториал предыдущего, будет проигнорирована. Но если новый туториал рассчитан на другую аудиторию и мы точно знаем, что он не может быть хуже, то односторонний тест вам подходит и даст бОльшую точность.
Вводные для следующего примера: нулевая гипотеза что мат. ожидания для двух групп равны, дисперсии равны. Данные представляют финансовые результаты двух разных интернет-магазинов схожей тематики.
import matplotlib matplotlib.use('TkAgg') from scipy import stats a = [742,148,423,424,122,432,-1,232,243,332,213] b = [-1,3,4,2,1,3,2,4,1,2] print (stats.ttest_ind(a,b))
Результаты завязаны на проблеме Беренса-Фишера, так как точного решения не существует, но вероятность позволяет нам сделать вывод. Если сделать поправку на то, что при маленькой выборке никак не сгруппированных данных у нас большая дисперсия (проверяем дисперсию командой print(np.var(a)) ), то качество данных можно поставить под сомнение. Если данные не распределены нормально, нужен критерий Манна-Уитни, также известный как Критерий Уилкоксона. Выборка у нас небольшая, поэтому Манна-Уитни вполне подойдет, ранги не будут сильно пересекаться. Запуская Манна-Уитни, мы преобразовываем данные в ранги, строим два распределения рангов и пытаемся узнать разность 50-х квартилей ранговых распределений.
Общее предположение Манна-Уитни что все наблюдения из обеих групп независимы и непрерывны. Про непрерывность есть нюанс: допускается небольшое повторение элементов в выборках. H0 = если мы возьмем по одному случайному элементу из первого и второго распределений, то элемент из первого распределения с вероятностью ≠ 1/2 больше, чем элемент из второго распределения. Для начала задаем некую U-статистику, чье распределение мы знаем при условии, что нулевая гипотеза верна:
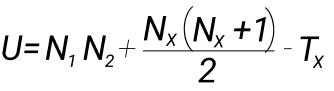
Например, у нас есть две выборки: 1,3,4,6 и 2,7,8. Создаем единый ряд от минимального значения к максимальному: 1,2,3,4,6,7,8. И прописывем ранги, чем ченьше значение, тем меньше ранг. Разбиваем полученный ряд значений по рангам:
| Значение в ряде | Ранг |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 6 | 5 |
| 7 | 6 |
| 8 | 7 |
Считаем сумму значений рангов: T1 = 1+3+4+5 и T2 = 2+6+7. Tx как максимальная это 15 (T2). Nx = это кол-во элементов в выбранной группе с максимальным рангом, то есть 3. Далее проставляем значения в формулу и считаем статистику: U = 4 * 3 + ((2 * (2+1)) / 2) — 15 = 12 + 3 — 15 = 0. Если выборка маленькая, то открываем справочник и смотрим критические значения.
import matplotlib matplotlib.use('TkAgg') from scipy import stats a = [742, 148, 423, 424, 122, 432, -1, 232, 243, 332, 213] b = [-1, 3, 4, 2, 1, 3, 2, 4, 1, 2] u, p_value = stats.mannwhitneyu(a, b) print("two-sample wilcoxon-test", p_value)
P-value стал 0.0007438622219910575. Сравнивать выборки можно и визуально:
import matplotlib matplotlib.use('TkAgg') import numpy as np from scipy.stats import ttest_ind import matplotlib.pyplot as plt a = np.random.normal(loc=0,scale=24,size=4454) b = np.random.normal(loc=-1,scale=1,size=7643) print(ttest_ind(a,b)) plt.hist(a, bins=24, color='g', alpha=0.75) plt.hist(b, bins=24, color='y', alpha=0.55) plt.show()
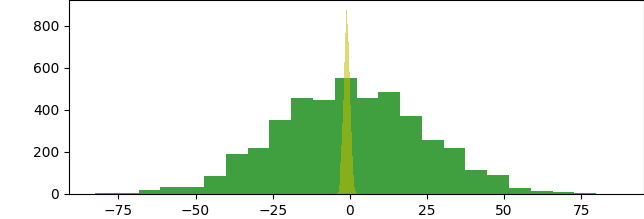
Что намного меньше 0.05, т.е. мы отклоняем нулевую гипотезу критерия Стьюдента про равенство средних. У интернет-магазинов слишком разные данные, нужна сегментация .
Теперь рассмотрим двусторонний тест для нулевой гипотезы о том, что ожидаемое среднее значение одной выборки независимых наблюдений равно среднему значению другой. Аспект «двусторонний» означает, что мы рассматриваем верхнюю и нижнюю границы распределения совокупности данных. Стандартные отклонения должны быть одинаковыми.
import matplotlib matplotlib.use('TkAgg') from scipy import stats from scipy import stats a = stats.norm.rvs(loc = 5,scale = 10,size = 23000) b = stats.norm.rvs(loc = 5,scale = 10,size = 23425) print stats.ttest_ind(a,b)
Получаем statistic=-0.7043486133916781, pvalue=0.4812192321148787, что намного больше 0,05. А так как р > 0.05 мы считаем маловероятной ошибкой, а р <= 0.05 высоковероятной, то две выборки можно считать равными. Также, для проверки равенства средних подходят Критерий Манна-Уитни, Уилкоксона, Краскера-Уолласа.
Визуализация
Данные важно визуализировать. Не только потому, что заказчики вашей работы — визуалы, есть и более технические особенности. Например, Квартет Энскомба. Это 4 набора точек, у каждой есть X и Y, и по цифрам они идентичны. Но если их визуализировать, то видно, что по показателям выборки из X и Y равны друг другу, а по форме на графике — нет. У всех данных ниже параметры mean=7.50, std=1.94, r=0.82.
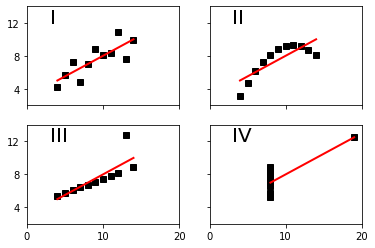
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np sns.set() data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) for col in 'xy': sns.kdeplot(data[col], bw=.2, shade=False, label="MAU"), plt.show()
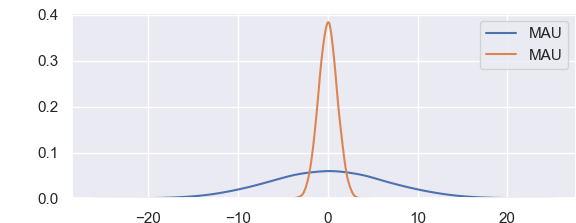
График выше прекрасно подходит для визуального сравнения двух выборок. Доверительный интервал находится между 5 и 95 процентым квантилем, 90% доверительный интервал это двусторонний критерий между 5 и 95.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[3.4, 1.87], [2.8, 1.44]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) sns.distplot(data['x']) sns.distplot(data['y']); plt.show()
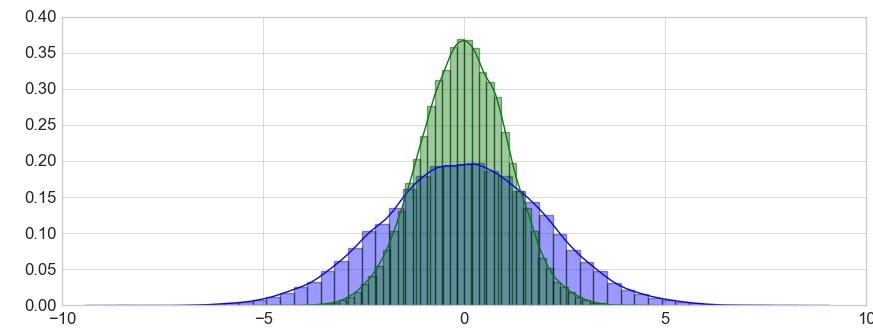
Представленные выше графики достаточно стандартны и вы неоднократно их строили или, по крайней мере, видели. А вот следующий график, Jointplot, уже куда интереснее. Он совмещает в себе гистограммы по x и y, и включает типичный график рассеяния. Получается своеобразный куб из гистограмм.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) with sns.axes_style('white'): sns.jointplot("x", "y", data, kind='kde'); plt.show()
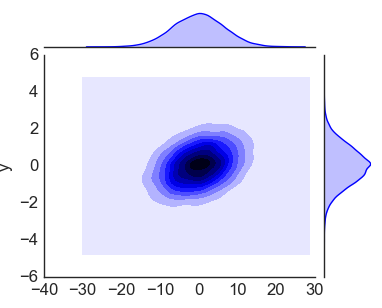
Получилось! Далее построим диаграмму рассеивания.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np a = np.random.rand(20) b = [3, 4, 3.4, 6, 7, 8, 9, 10, 4, 0.3, 4.2, 4, 23, 3, 33, 3, 1, 4, 0.1, 4.2] colors = np.random.rand(20) plt.scatter(a, b, c=colors, s=100, alpha=0.65, marker=(5, 0)) plt.show()
График интересен тем, что полученные рассеивающиеся паттерны позволяют увидеть разные типы корреляции. Стремится с правый верхний угол — хорошая тенденция, расположилось горизонтально — нейтральная тенденция, стремится в левый верхний угол — негативная тенденция.
И Box Plot, куда же без него. Работает с группой из минимум пяти чисел: минимум, первый квартиль, медиана, третий квартиль и максимум. Усы идут от каждого квартиля до минимума или максимума. Всегда можно получить подробную справку по параметрам boxplot, достаточно вбить команду ? sns.boxplot.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd b = [1, 2, 3, 4, 3.4, 6, 7, 8, 9, 8, 4, 0.3, 4.2, 14, 21, 1, -8] df = pd.DataFrame(b) sns.boxplot(data=df) plt.show()
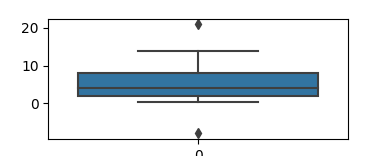
На картинке видно выше, что в наборе данных есть выбросы, в таком случае бывает полезно использовать интерквартильный размах. Это разница между третьим и первым квартилем. Я беру это значение как 1,5 квартиля в обе стороны, от 25-го и 75-го перцентиля. Давайте еще один пример, в котором посмотрим на квартили.
import seaborn as sns sns.boxplot(data["x"]) data["x"].describe()
count 23.000000 mean 0.112399 std 0.071212 min 0.007407 25% 0.055556 50% 0.103704 75% 0.166667 max 0.244444 Name: x, dtype: float64
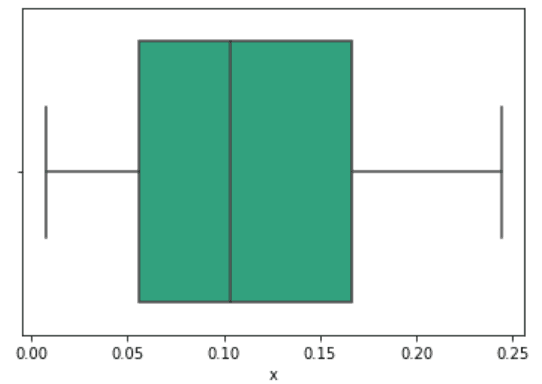
Медиана это 50-ый перцентиль, линия в центре. Данные выше это выгрузка хитов от поведения пользователя, поэтому 50-ый перцентиль это 0,10 кликов. Левая граница большого квадрата это 25-ый перцентиль, значение первого квартиля. И третий квартиль, 75-ый перцентиль. Вертикальные линии по краям показывают статистически значимую выборку.
92 перцентиль отходит от левого края середины графика нормального распределения. Перцентиль это процент, который меньше чем пороговое значение. Узнать вероятность можно и в Excel =NORM.S.INV(0.92), получим результат 1.40507156. Аналогично можно получить перцентиль для левой стороны графика, например, =NORM.S.INV(0.08) и получаем -1.4050716.
А теперь немного 3D, бизнес такое любит:
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D x = np.arange(-2, 5, 0.85) xlen = len(x) y = np.arange(-5, 2, 0.25) ylen = len(y) x, y = np.meshgrid(x, y) r = np.sqrt(x**2 + y**2) z = np.sin(r * 1.3) ax = plt.figure(figsize=(8,6)) ax = ax.add_subplot(1,1,1, projection='3d') ax.plot_surface(x, y, z, cmap=cm.coolwarm, edgecolor='black', linewidth=0.23, antialiased=True) plt.show()
Python Seaborn это лучшее решение для визуализации привлекательных статистических диаграмм. Если же ваша цель это интерактивные графики в вебе, то Python Bokeh, Pygal, Plotly это ваш выбор. Изучайте Python и мат. стат, и ваш продуктовый дизайн сильно вырастет.
C примерами на Python.
Всем привет, меня зовут Вячеслав Зотов, я аналитик в студии Whalekit. В этом тексте я расскажу про статистические тесты и сравнение воронок, а также мы попробуем разобраться, что объединяет χ²-тесты, какова область их применения и подробно исследуем применимость χ²-тестов к анализу воронок. И все это с примерами на Python.
Тест χ² — очень полезный аналитический инструмент, который тем не менее часто вызывает у аналитиков недопонимание и путаницу. Прежде всего это происходит из-за того, что существует целое семейство тестов χ², имеющих разные области применения. Дополнительную путаницу создает то, что тесты χ² часто рекомендуют применять для анализа продуктовых и маркетинговых воронок, а это обычно приводит к ошибочному использованию тестов.
1. χ²-распределение
Начнем с импорта библиотек:
import warnings
warnings.filterwarnings(‘ignore’)
import os
import math
import random
import re
import pandas as pd
import numpy as np
import scipy.stats as stats
from matplotlib import pyplot as plt
import matplotlib.ticker as mtick
import seaborn as sns
from matplotlib import cm
import matplotlib.colors
Распределение χ² возникает при возведении в квадрат нормально распределенной случайной величины:
np.random.seed(1234)
size = 10000 # размеры случайных переменных
loc = 0
scale = 1
result = pd.DataFrame([[0] * size], index = [‘chi2_1’]).T
plt.figure(figsize = (15, 5))
# перебираем значения степеней свободы k
for k in range(2, 22, 3):
# создаем фрейм результатов
current_result = pd.DataFrame([[0] * size], index = [1]).T
# генерируем нужное количество нормально распределенных переменных, находим сумму их квадратов
for i in range(1, k + 1): current_result[i] = pd.Series(np.random.normal(loc = loc, scale = scale, size = size))
# находим сумму квадратов
current_result[‘chi2’] = (current_result * current_result).sum(axis = 1)
sns.kdeplot(current_result[‘chi2’], label = ‘k = {}’.format(k))
plt.legend(title = ‘Степени свободы’), plt.ylabel(‘$f_k(x)$’), plt.xlabel(‘$x$’), plt.title(‘Распределения $chi_k^2$’)
plt.show()
2. χ²-тесты
Существует три χ²-теста.
- Тест на гомогенность (test of homogeneity, он же goodness of fit) — непараметрический, одновыборочный тест, который проверяет соответствие наблюдаемого распределения категориальной случайной величины некоторому эталонному распределению. В Python реализован функцией scipy.stats.chisquare.
- Тест на независимость (он же test of independence/association) — непараметрический, одновыборочный тест, который проверяет наличие связи между двумя категориальными переменными. В Python реализован функцией scipy.stats.chi2_contingency.
- Тест для дисперсии — параметрический (параметр — дисперсия), одновыборочный тест, который проверяет равенство дисперсии непрерывной случайной величины заданному порогу. В Python для него нет готовой функции.
Первые два теста используют критерий согласия Пирсона (КСП), который имеет распределение χ². Третий тест никак не относится к первым двум за исключением того, что статистика, которую он использует, также имеет распределение χ² (об этом ниже).
Критерий согласия Пирсона рассчитывается по формуле:
Здесь:
- O — наблюдаемое значение;
- E — ожидаемое значение.
Таким образом, КСП — это разница между наблюдаемым и ожидаемым значением, возведенная в квадрат (нам важно не направление отличий, а только факт их наличия) и нормированная с помощью деления на ожидаемое значение (чтобы слишком быстро не росла).
Если мы сравниваем набор наблюдаемых значений с набором эталонов, то формула КСП приобретает вид:
В том случае, когда O и E имеют нормальное распределение, КСП имеет распределение χ².
Получается, что мы можем провести статистический тест с гипотезами:
- H0: между наблюдаемым распределение и эталонным распределением нет различий;
- H1: между наблюдаемым распределение и эталонным распределением есть различия.
Если различий нет, то КСП будет стремиться к нулю. В противном случае она окажется за пределами интервала наиболее вероятных значений:
Тесты с КСП, таким образом, непараметрические (поскольку не оценивают никакие из параметров распределений) и односторонние (так как статистика всегда положительная за счет возведения в квадрат — вот некоторые рассуждения на этот счет). Поскольку тест непараметрический, мы можем напрямую сравнивать полученную статистику с эталонным распределением (без применения несмещенных оценок как в z— и t-тестах).
Остался маленький нюанс — O и E должны иметь нормальное распределение. При работе с категориальными переменными это достигается за счет нормальной аппроксимации биномиального распределения (вот обсуждение по теме).
2.1 χ²-тест на гомогенность (homogeneity, goodness of fit)
Предположим, что у нас есть таблица реально наблюдаемых вероятностей появления наблюдений в группах (Observed) и ожидаемых вероятностей появления (Expected):
Тогда гипотезы для теста goodness of fit можно представить таким образом:
- H0: O₁ = O₂ = O₃ = … = Oₙ (то есть наблюдение может относиться с равной вероятностью к каждой из групп);
- H1: Хотя бы одна из вероятностей Oᵢ не равна остальным.
или таким:
- H0: O₁ = E₁, O₂ = E₂, O₃ = E₃, …, Oₙ = Eₙ (то есть вероятности соответствуют ожидаемому распределению);
- H1: хотя бы в одном случае Oᵢ не равна Eᵢ (то есть вероятности не соответствуют ожидаемому распределению).
Пример расчета статистики (источник):
Для полученную статистики можно рассчитать p-value для распределения χ² при числе степеней свободы d = (n-1) = 4:
1 — stats.chi2.cdf(52.75, 4)
9.612521889579284e-11
Сравнив его с уровнем значимости α = 0.05, можно сделать вывод о том, что нулевая гипотеза отвергается и конфеты распределены по вкусам неравномерно.
Напишем функцию для проведения теста:
def diy_chisquare(observed, expected):
# рассчитываем статистику
k = len(observed) # число степеней свободы
statistic = (((observed — expected)**2)/expected).sum() # КСП
# рассчитываем p-value
p_value = 1 — stats.chi2.cdf(statistic, k — 1) # вероятность получить значение выше или равное статистике
return k — 1, statistic, p_value
Сравним ее результат со встроенным методом, используя предыдущий пример:
# задаем исходные данные
np.random.seed(1234)
data = np.array([180, 250, 120, 225, 225])
expected = np.array([200, 200, 200, 200, 200])
# результат самодельного теста
display(diy_chisquare(data, expected))
# результат встроенного теста
from scipy.stats import chisquare
chisquare(data, expected)
(4, 52.75, 9.612521889579284e-11)
Power_divergenceResult(statistic=52.75, pvalue=9.612518035368181e-11)
Результаты полностью совпадают.
Интереса ради исследуем вопрос о том, как размер выборки влияет на то, будет ли распределение КСП соответствовать распределению χ². Зададим функцию проведения эксперимента:
def generate_max_likelihood_distro(size, num_samples, sample_size, k_range, ax, ax2, ax3, title):
ks_results = []
for line_i, k in enumerate(k_range): # перебираем степени свободы (количество классов, на которые разбиваются наблюдения)
data = pd.Series(np.random.choice(k, size, p = [1 / k] * k)) # не генерируем равномерно распределенный массив групп наблюдений
max_likelihood = []
for i in range(num_samples):
observed = data.sample(sample_size, replace = True).value_counts() # считаем, сколько раз появилось каждое из значений
expected = sample_size/k # ожидаемое число значений
max_likelihood += [[i,
k — 1,
(((observed — expected)**2)/expected).sum() # максимальное правдоподобие
]]
max_likelihood = pd.DataFrame(max_likelihood, columns = [‘Sample #’, ‘Degrees of freedom’, ‘Max likelyhood distribution’])
# строим графики распределений
sns.kdeplot(max_likelihood[‘Max likelyhood distribution’], label = ‘k = {}’.format(k), ax = ax)
ax.legend(title = ‘Степени свободы’), ax.set_ylabel(‘$f_k(x)$’), ax.set_xlabel(‘$x$’), ax.set_title(title)
# строим qq-графики
stats.probplot(max_likelihood[‘Max likelyhood distribution’],
dist = stats.chi2, sparams = (k — 1), # chi2 с числом степеней свободы k-1
plot = ax2, fit = False)
line_index = (line_i + 1) * 2
(ax2.get_lines()[line_index — 2].set_color(ax.get_lines()[line_i].get_color()),
ax2.get_lines()[line_index — 2].set_label(‘k = {}’.format(k)),
ax2.get_lines()[line_index — 2].set_markersize(3),
ax2.get_lines()[line_index — 2].set_alpha(0.5)
)
ax2.get_lines()[line_index — 1].set_color(‘lightgrey’), ax2.get_lines()[line_index — 1].set_linestyle(‘:’)
ax2.set_title(‘Соответствие распределению $chi^2$’), ax2.legend(title = ‘Степени свободы’)
# проводим КС-тест
ks_stat, ks_p = stats.kstest(max_likelihood[‘Max likelyhood distribution’], ‘chi2’, args = (k — 1, ))
ks_results.append([k, ks_stat, ks_p])
ks_results = pd.DataFrame(ks_results, columns = [‘k’, ‘statistic’, ‘p’]).set_index(‘k’)
ks_results[[‘p’]].plot(ax = ax3, xticks = ks_results.index, label = ‘$p$-value’)
ax3.axhline(0.05 / len(k_range), color = ‘red’, linestyle = ‘:’, label = ‘alpha = {:.2f}’.format(0.05 / len(k_range))) # с коррекцией Бонферрони
ax3.set_ylabel(‘$p$-value’), ax3.set_xlabel(‘$k$ (степени свободы)’), ax3.set_title(‘Результаты КС-теста’), ax3.legend()
Исследуем влияние размера выборки на соответствие статистики распределению χ²:
np.random.seed(12345)
size = 100000 # размер «генеральной совокупности» — исходной большой выборки
num_samples = 1000
sample_size = 100
plt.figure(figsize = (25, 12))
sample_sizes = [10, 50, 100, 500, 1000, 2000]
for i, sample_size in enumerate(sample_sizes):
generate_max_likelihood_distro(size, num_samples, sample_size,
range(2, 22, 3),
title = ‘Размер выборки $n = {}$’.format(sample_size),
ax = plt.subplot(3, len(sample_sizes), i + 1),
ax2 = plt.subplot(3, len(sample_sizes), len(sample_sizes) + i + 1),
ax3 = plt.subplot(3, len(sample_sizes), len(sample_sizes) * 2 + i + 1),
)
plt.tight_layout()
Наблюдения и выводы:
- при увеличении размера выборки результат становится менее шумным;
- сами распределения весьма похожи на χ²;
- QQ-plot показывает, что распределение статистики становится близко к χ² даже для малых k, когда размер выборки превышает 100 наблюдений;
- тест Колмогорова-Смирнова также показывает, что с ростом размера выборок статистика уверенно приближается к χ².
Мы показали эмпирически, что КСП действительно имеет распределение χ².
2.2 χ²-тест на независимость
Тест χ²-тест на независимость (test of independence/association) отличается от предыдущего теста постановкой гипотез:
- H0: категориальные переменные A и B независимы;
- H1: категориальные переменные A и B связаны между собой.
Допустим, у нас есть таблица сопряженности (из примера). Таблица сопряженности описывает наблюдаемые (observed) результаты:
Согласно теореме умножения вероятностей, в том случае, когда две случайные величины A и B независимы, вероятность получить совместное событие равна P(AB) = P(A) ⋅ P(B). Таким образом, наши ожидаемые (expected) величины можно рассчитать по формуле умножения вероятностей и свести в таблицу:
Используя эту таблицу, мы можем рассчитать статистику по формуле:
Готовую статистику можно подставить в CDF для распределения χ² и получить p-value.
Напишем функцию для расчетов:
def diy_chi2_contingency(contingency_table):
# общее число наблюдений
total = contingency_table.sum().sum()
# суммы по строкам и столбцам
col_probs = contingency_table.sum(axis = 0).values
row_probs = contingency_table.sum(axis = 1).values
# превращаем их в вероятности
col_probs = col_probs / total
row_probs = row_probs / total
# рассчитываем ожидаемые значения
expected = np.array([col_probs]).T @ np.array([row_probs]) # перемножаем вектор-столбец вероятностей в рядах на вектор-стороку вероятностей в столбцах
expected = expected.T
expected = expected * total
# рассчитываем статистику
statistic = ((contingency_table.values — expected)**2)/expected
statistic = statistic.sum()
# определяем число степеней свободы
dof = (contingency_table.shape[0] — 1) * (contingency_table.shape[1] — 1)
# рассчитываем p-value
p_value = 1 — stats.chi2.cdf(statistic, dof) # вероятность получить значение выше или равное критерию МП
return dof, statistic, p_value
contingency_table = pd.DataFrame([[11, 3, 8], [2, 9, 14], [12, 13, 28]])
diy_chi2_contingency(contingency_table)
(4, 11.942092624356777, 0.01778711460986071)
Сравним результат со встроенной функцией:
from scipy.stats import chi2_contingency
chi2_contingency(contingency_table)[0:3]
(11.942092624356777, 0.0177871146098607, 4)
Результаты полностью идентичны.
2.3 χ²-тест для дисперсии
Третий вид χ²-теста не имеет никакой связи с предыдущими за исключением того, что его статистика, которая рассчитывается по формуле
также имеет распределение:
Вот доказательство. Здесь S — это наблюдаемое выборочное СКО, а σ — ожидаемое СКО.
Пример расчета статистики тут.
В Python нет встроенной функции, но можно ее написать: пример.
Тест χ² для дисперсии не используется для сравнения выборок. Для этого служит F-тест (очень чувствителен к требованию нормальности данных), а для ненормальных данных — тесты Левена или Бартлетта (оба есть в Python).
Нас, как практиков, конечно же, прежде всего интересует вопрос — можно ли использовать этот тест для ненормально распределенных данных (потому что на практике мы практически никогда не работаем с нормальными распределениями).
Для этого сравним распределение статистики для нормально распределенных и экспоненциально распределенных данных. Кроме того, оценим влияние размера выборки на результат:
np.random.seed(1234)
size = 100000 # размер «генеральной совокупности» — исходной большой выборки
num_samples = 1000
sample_size = 1000
std_threshold = 1.1
data_norm = pd.Series(np.random.normal(0, std_threshold, size))
data_exp = pd.Series(np.random.exponential(std_threshold, size))
plt.figure(figsize = (25, 5))
sample_sizes = [10, 30, 50, 100, 500, 1000]
for i, sample_size in enumerate(sample_sizes):
statistics = []
for j in range(num_samples):
statistics += [[j,
(sample_size — 1) * data_norm.sample(sample_size, replace = True).var() / (std_threshold ** 2), # статистика для нормально распределенных данных
(sample_size — 1) * data_exp.sample(sample_size, replace = True).var() / (std_threshold ** 2) # статистика для жкспоненциально распределенных данных
]]
statistics = pd.DataFrame(statistics, columns = [‘Sample #’, ‘Statistic (normal data)’, ‘Statistic (exponential data)’])
# строим графики распределений
ax = plt.subplot(1, len(sample_sizes), i + 1)
sns.kdeplot(statistics[‘Statistic (normal data)’], label = ‘Нормально распределенные данные’, color = ‘orange’, linestyle = ‘:’, ax = ax)
sns.kdeplot(statistics[‘Statistic (exponential data)’], label = ‘Экспоненциально распределенные данные’, color = ‘orange’, ax = ax)
sns.kdeplot(pd.Series(np.random.chisquare(sample_size — 1, size)), color = ‘blue’, label = ‘Эталонное распределение $chi^2$’, ax = ax)
plt.title(‘Размер выборки: {}’.format(sample_size)), plt.xlabel(‘Статистика’), plt.ylabel(‘Частота’)
if i == 0: plt.legend()
plt.tight_layout()
Наблюдения:
- распределение статистики для нормально распределенных данных повторяет ожидаемое распределение:
- распределение статистики для экспоненциально распределенных данных отличается от эталонного распределения. Более того, различие, похоже, растет с ростом размера выборки.
Вывод: промысловой ценности не имеет.
3. Связь между z-тестом и χ²-тестом (и тестом Фишера)
Довольно часто встречаются попытки использовать χ²-тест вместо z-теста для пропорций. Также можно встретить утверждения о том, что z-тест эквивалентен χ²-тесту для ситуации с двумя классами. Имеется в виду эквивалентность результатов между:
- двухвыборочным z-тестом для пропорций;
- тестом χ² на независимость данных (test of independence) в ситуации, когда таблица сопряженности имеет размерность 2 x 2.
Пример: допустим, у нас есть результаты бинарного эксперимента:
np.random.seed(1234)
size = 1000
p = 0.4
data = pd.Series(np.random.choice(2, size, p = [1 — p, p]))
Эти результаты можно представить в виде таблицы сопряженности, если добавить к ним ожидаемые значения:
contingency_table = pd.DataFrame([data.value_counts().values, [500, 500]], index = [‘Observed’, ‘Expected’])
contingency_table
Результат χ²-теста на независимость:
from scipy.stats import chi2_contingency
chi2_statistic, p_value, dof, exp = chi2_contingency(contingency_table, correction = False) # отключаем коррекцию (с ней результат чуть-чуть отличается)
chi2_statistic, p_value
(14.555161038503186, 0.00013611529553341273)
Результат двухвыборочного z-теста для пропорций:
from statsmodels.stats.proportion import proportions_ztest
z_statistic, p_value = proportions_ztest(contingency_table[0], contingency_table.sum(axis = 1), alternative = ‘two-sided’)
z_statistic, p_value
(3.815122676730484, 0.00013611529553341327)
p-value полностью совпадают. Более того, z-статистика равна квадратному корню из χ²-статистики:
z_statistic, math.sqrt(chi2_statistic)
(3.815122676730484, 3.8151226767304856)
Демонстрация математической эквивалентности: тут и тут.
Нужно отметить, что тест на гомогенность не эквивалентен z-тесту:
from scipy.stats import chisquare
chi2_statistic, p_value = chisquare(contingency_table.loc[‘Observed’], f_exp = contingency_table.loc[‘Expected’]) # тестируем наблюдаемые величины на равновероятность
chi2_statistic, p_value
(28.9, 7.62129129638297e-08)
Тест Фишера часто рекомендуют применять вместо χ²-теста для таблиц сопряженности размером 2 х 2 в тех случаях, когда частоты очень малы (ячейки таблицы сопряженности имеют значения <= 5). Если тест Фишера до какой-то степени эквивалентен χ²-тесту, то он должен быть эквивалентен и z-тесту для пропорций. Действительно, p-value довольно похожи:
from scipy.stats import fisher_exact
fisher_exact(contingency_table, alternative = ‘two-sided’)
(1.4096385542168675, 0.00016169735747221216)
4. Размер выборки для χ²-теста
Утверждается, что размер выборки должен быть такой, чтобы:
- каждая из ячеек таблицы сопряженности была больше 5 (если нет, то это легко исправляется умножением таблицы на нужный множитель);
- общий размер сэмпла был не более 500, так как увеличение размера сэмпла вызывает рост статистики и вероятности ложноположительных результатов.
Проверим это на практическом примере.
Возьмем таблицу сопряженности, при которой тест подтверждает нулевую гипотезу (это слегка модифицированная таблица ожидаемых значений из одного из предыдущих примеров) и будем последовательно увеличивать размер выборки:
# тестовые данные
test_table = pd.DataFrame([[6, 5.5, 11], [6.25, 7, 12.5], [13.25, 13.25, 26.5]])
# последовательно увеличиваем количество наблюдений
result = []
for mult in range(1, 100, 1):
current = test_table * mult
statistic_ind, p_ind, _, _ = chi2_contingency(current) # тест по увеличиваемой таблице
result += [[current.sum().sum(), p_ind, statistic_ind]]
result = pd.DataFrame(result, columns = [‘sample_size’, ‘p-value’, ‘statistic’]).set_index(‘sample_size’)
# график p-value
ax = result[‘p-value’].plot(figsize = (10, 5), color = ‘red’, grid = True)
plt.ylabel(‘p-value’), plt.xlabel(‘Размер выборки’)
# график статистики
ax2 = ax.twinx()
result[‘statistic’].plot(ax = ax2, color = ‘blue’, label = ‘Статистика’)
# собираем легенду
lines, labels = ax.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines + lines2, labels + labels2, loc = 1, title = ‘Параметры’)
plt.ylabel(‘Статистика’), plt.title(‘Влияние размера выборки на результаты теста $chi^2$’);
Видно, что с ростом размера выборки статистика растет линейно, при этом p-value стремится к 0 и рано или поздно тест покажет статистически значимые отличия при исходных пропорциях.
Таким образом, размер выборки желательно брать достаточно малый (видимо, 500 — хорошая практическая граница).
5. Применение χ²-тестов для анализа множественных пропорций
Довольно часто встречаются утверждения, что χ²-тест можно применять для сравнения множественных пропорций. Например, при сравнении нескольких воронок (скажем, в процессе A/B-тестирования) предлагается вместо серии последовательных z-тестов для пропорций применять тест χ². В этом разделе мы посмотрим, какие из χ²-тестов применимы для задачи анализа воронок.
Сразу можно сказать, что для анализа воронок неприменим тест χ² для дисперсии.
Чтобы разобраться с оставшимися двумя видами тестов χ², представим, что нам нужно проанализировать результаты А/B теста, в котором тестировались два вида воронок — воронка контрольной группы (A) и воронка тестовой группы (B).
Теоретически, χ²-тест на гомогенность можно применить, если рассматривать воронку контрольной группы как набор ожидаемых значений (expected), а воронку тестовой группы — как набор наблюдаемых значений (observed). Тогда тест покажет наличие статистически значимого отличия между observed и expected.
Аналогично χ²-тест на независимость можно применять для анализа любого числа воронок, если рассматривать все эти воронки как таблицу сопряженности. В этом случае тест покажет, зависит ли переменная «шаги воронки» от переменной «группа теста» или нет.
Но, кажется, здесь возникает нюанс. Дело в том, что логика обоих видов χ²-теста предполагает, что на их вход подаются таблицы сопряженности. Таблицу сопряженности, прежде всего, характеризует то, что в ней каждый объект наблюдений может попадать в одну единственную категорию. Это условия, очевидно, не выполняется для таблиц воронок, так как каждый объект наблюдений (в случае с воронками — это пользователь) может выполнить несколько шагов воронки и оказаться сразу в нескольких категориях.
Чтобы превратить таблицу воронок в таблицу сопряженности, нужно провести простую трансформацию — посчитать, сколько пользователей ушло из воронки на каждом из шагов. Таким образом, для каждого пользователя в таблице остается одно единственное наблюдение. Например, таблица сопряженности для таблицы из двух воронок из примера выше будет иметь вид:
В этом примере мы полагаем, что пользователь не может перепрыгивать через шаги воронок, поэтому число отвалившихся пользователей для каждого шага равно разности уникальных пользователей на двух соседних шагах.
Есть ли какое-либо отличие в результатах, получаемых при подстановке в χ²-тесты таблиц воронок и таблиц сопряженности? Действительно, довольно легко подобрать пример, для которого тест, проведенный на данных таблицы сопряженности, даст правильный результат, а тест проведенный на таблице воронок — неправильный. К примеру, возьмем воронки из примера выше.
У них есть явные отличия, но χ²-тест для гомогенности, выполненный на таблице воронок показывает отсутствие отличий, а тот же тест, выполненный по таблице сопряженности, показывает, что отличия есть:
Казалось бы, все просто — трансформируем таблицы воронок в таблицы сопряженности, подаем их в χ²-тесты и получаем правильный результат. Но где гарантия, что получившийся выше результат не случаен, и в особенности, что результаты тестов никак не зависят от формы воронок. Давайте это проверим.
5.1 Зависимость результатов χ²-тестов от формы воронок
Сначала протестируем, как от формы воронок зависит вероятность ошибки первого рода (вероятность обнаружить отличия там, где их нет). Для этого проведем серию экспериментов:
- создадим набор воронок, состоящих из трех шагов. Каждая воронка будет описываться парой чисел — вероятностью конвертироваться из первого во второй шаг и вероятностью конверсии из второго шага в третий. То есть воронка 100 -> 50 -> 25 будет описываться парой чисел [0.5, 0.5];
- для каждой из созданных воронок построим N пар выборок;
- для каждой из пар выборок проведем 5 тестов:
- χ²-тест на гомогенность по таблице воронок;
- χ²-тест на гомогенность по таблице сопряженности;
- χ²-тест на независимость по таблице воронок;
- χ²-тест на независимость по таблице сопряженности;
- z-тест, сравнивающий доли пользователей, достигших последнего шага воронок.
Начнем с функции построения воронок:
# строим воронки, из которых будем делать сэмплирование
# pop_size — количество пользователей, которые участвуют в каждой воронке
# coeffs — массив процентных значений отличий воронок для тестирования ошибок второго рода
# rel — параметр, управляющий тем, какая воронка будет получена — абсолютная (доля рассчитывается от первого шага воронки) или относительная (доля рассчитывается от предыдущего шага)
def generate_funnel_log(pop_size, coeffs, rel = False, random_state = 12345):
# задаем начальный шаг
result = pd.DataFrame([[0, 1]] * pop_size, columns = [‘step’, ‘user_id’])
result[‘user_id’] = result[‘user_id’].apply(lambda x: ».join(random.choice(‘abcdefghij1234567890’) for i in range(10)))
# на каждом шаге берем только нужный процент пользователей, достигших прошлого шага
for step, step_coeff in enumerate(coeffs):
current = result.query(‘step == @step’)
# если относительная воронка, то число уников на этом шаге считаем как % от предыдущего, если абсолютная, то от всей популяции
current_pop = pop_size
if rel: current_pop = current[‘user_id’].nunique()
current = current.sample(int(np.ceil(current_pop * step_coeff)), random_state = random_state)
current[‘step’] = step + 1
result = result.append(current)
return result
С помощью этой функции сконструируем воронки разной формы:
# конструируем разные формы воронок
# steps — на сколько шагов будут разбиты относительные шаги воронок
# pop_size — количество пользователей, которые участвуют в каждой воронке
# differences — массив процентных значений отличий воронок для тестирования ошибок второго рода
# file_name — файл, в который будут записаны результаты генерации лога (при определенных условиях его генерация может занимать существенное время)
def generate_funnel_set(steps, pop_size, differences = [], file_name = None):
result = pd.DataFrame()
funnel_num = 0
# проверяем ранее сгенерированный файл лога воронки
if file_name is not None:
try:
return pd.read_csv(file_name)
except:
print(f'{file_name} не существует.’)
# добавляем 1 к списку различий, чтобы сгенерировать исходную воронку
differences = [1] + differences
for first_step_prob in np.linspace(0, 1, num = steps):
for second_step_prob in np.linspace(0, 1, num = steps):
# отсекаем ситуации, когда воронка плоская
if first_step_prob == 0 or second_step_prob == 0: continue
funnel_coeffs = [first_step_prob, second_step_prob]
# генерируем набор воронок, имеющих отличия от исходной воронки
# здесь же генерируется и она сама с diff = 1
for i, diff in enumerate(differences):
current_funnel = generate_funnel_log(pop_size, [x * diff for x in funnel_coeffs], rel = True)
# номер воронки для быстрого к ней обращения
current_funnel[‘funnel_num’] = funnel_num
current_funnel[‘funnel_diff_num’] = i
# параметры воронки
current_funnel[‘first_step_prob’] = first_step_prob
current_funnel[‘second_step_prob’] = second_step_prob
current_funnel[‘diff’] = diff
result = result.append(current_funnel)
funnel_num += 1
# сохраняем воронку в файл
if file_name is not None:
result.to_csv(file_name)
return result
# набор воронок
log = generate_funnel_set(steps = 25, pop_size = 10000, differences = [], file_name = ‘sample_log.csv’)
display(log.query(‘funnel_num == 10’)[[‘first_step_prob’, ‘second_step_prob’]].drop_duplicates())
report = log.query(‘funnel_num == 10’).groupby(‘step’).agg({‘user_id’: ‘nunique’})
report[‘perc’] = report[‘user_id’] / report.loc[0, ‘user_id’]
display(report)
Построим некоторые из полученных воронок и посмотрим, на какие классы мы можем их разделить:
# выбираем 5 произвольных воронок
sample_funnels = log[‘funnel_num’].drop_duplicates().sample(5, random_state = 1234567)
# строим их
report = log.query(‘funnel_num in @sample_funnels’)
report[‘funnel_name’] = report.apply(lambda x: f»№{x[‘funnel_num’]}. Отн. конверсия {x[‘first_step_prob’]:.2%} -> {x[‘second_step_prob’]:.2%}», axis = 1)
report = report.pivot_table(index = ‘step’, columns = ‘funnel_name’, values = ‘user_id’, aggfunc = ‘nunique’)
report = report.div(report.loc[0], axis = 1)
# выводим графики
ax = report.plot(figsize = (15, 7), grid = True)
ax.yaxis.set_major_formatter(mtick.PercentFormatter(1))
ax.set_xticks(report.index)
plt.xlabel(‘Шаг воронки’), plt.ylabel(‘Абсолютная вероятность конверсии’), plt.legend(title = ‘Воронки’)
plt.title(‘Различные классы воронок’);
Видно, что воронки, в сущности, делятся на три класса:
- воронки с немедленным падением — те, у которых на первом шаге наблюдается падение на более, чем 50% от нулевого. В этом случае конверсия во второй шаг не важна. На графике к этой категории относятся воронки №211 и №214;
- воронки с умеренным угасанием — те, у которых падение на первом шаге составляет не более 50% от нулевого, а на втором шаге — не более, чем 50% от первого. Например, этим критериям соответствует воронка №377;
- воронки с быстрым угасанием на втором шаге. На картинке выше это воронки №491 и №532.
Если мы построим график, у которого по оси X отложена вероятность конверсии из шага 0 в шаг 1, а по оси Y — вероятность конверсии из шага 1 в шаг 2, то воронки расположатся на нем вот так:
report = log.query(‘funnel_num in @sample_funnels’)
plot_data = report[[‘funnel_num’, ‘first_step_prob’, ‘second_step_prob’]].drop_duplicates()
x, y, t = plot_data[‘first_step_prob’].values, plot_data[‘second_step_prob’].values, plot_data[‘funnel_num’].values
ax = plt.axes()
plt.scatter(x, y)
plt.xlim((0, 1)), plt.ylim((0, 1))
# границы типов воронок
ax.axvline(0.5, linestyle = ‘-.’, color = ‘red’)
ax.hlines(y = 0.5, xmin = 0.5, xmax = 1, linestyle = ‘-.’, color = ‘red’)
ax.text(0.07, 0.9, ‘Быстрое’, fontsize = 15, color = ‘red’)
ax.text(0.55, 0.9, ‘Умеренное’, fontsize = 15, color = ‘red’)
ax.text(0.55, 0.3, ‘Быстроеn2-й шаг’, fontsize = 15, color = ‘red’);
for i, txt in enumerate(t):
ax.annotate(txt, (x[i] + 0.03, y[i]))
plt.xlabel(‘Вероятность конверсии в первый шаг’), plt.ylabel(‘Вероятность конверсии во второй шаг’);
Если мы проведем для каждой воронки серию тестов, то мы сможем построить график вероятности, на котором будет показан шанс допустить ошибку первого рода. Он будет выглядеть примерно так:
Здесь зеленым цветом обозначены области с умеренной вероятностью допустить ошибку, а оттенки красного показывают области с высокими вероятностями ошибок.
Подготовим набор воронок, которые будут использоваться при тестировании:
# генерирует набор воронок, в котором будут не только исходные воронки, но и отличающиеся от них на 75%, 50% и 25%
funnel_log = generate_funnel_set(steps = 25, pop_size = 2000, differences = [0.9, 0.8, 0.7], file_name = ‘funnel_log.csv’)
display(funnel_log.query(‘funnel_num == 10’)[[‘diff’, ‘first_step_prob’, ‘second_step_prob’]].drop_duplicates())
Зададим функции для проведения экспериментов:
- run_experiment получает на вход данные воронок, получает из них выборки нужного размера, формирует таблицы воронок и сопряженности, а также проводит по ним статистические тесты;
- run_error_experiments перебирает наборы воронок для тестирования и для каждого набора вызывает функцию run_experiment. Помимо этого, run_error_experiments отображает графики результатов.
# для каждого сочетания воронок проводим серию экспериментов
# funnel_log — лог с данными воронок
# sample_size — размер выборок, формируемых в каждом из экспериментов
# number_of_experiments — число экспериментов для каждой из воронок
# alpha — уровень значимости
# test_func — функция, описывающая набор статистических тестов, которые проводятся в каждом из экспериментов
# result_column_names — словарь человеко-читаемых названий колонок с результатами экспериментов
# compare_func — функция, служащая для сравнения p-value в каждом из экспериментов с уровнем значимости
def run_experiment(funnel_log, sample_size, number_of_experiments, alpha, test_func, compare_func):
result = []
errors = 0
# проводим эксперименты
for i in range(number_of_experiments):
# составляем выборки из всех групп
funnel = pd.DataFrame()
for j, group in enumerate(funnel_log[‘group’].unique()):
test_users = funnel_log.query(‘group == @group’)[‘user_id’].drop_duplicates().sample(sample_size, random_state = i + j)
current_funnel = funnel_log.query(‘group == @group and user_id in @test_users’)
funnel = funnel.append(current_funnel)
# формируем таблицу воронок
funnel = funnel.pivot_table(index = ‘step’, columns = ‘group’, values = ‘user_id’, aggfunc = ‘nunique’).fillna(0)
# игнорируются ситуации, когда из-за малого размера выборки воронка состоит только из первого шага
if funnel.shape[0] == 1:
errors += 1
continue
# формируем таблицу сопряженности
for col in funnel.columns:
funnel[f’cont_{col}’] = funnel[col] — funnel[col].shift(-1)
# заполняем пропуски в последнем ряду оставшимися пользователями
funnel_cols = [x for x in funnel.columns if ‘cont’ not in str(x)]
cont_cols = [x for x in funnel.columns if ‘cont’ in str(x)]
funnel.loc[funnel.index.max(), cont_cols] = funnel.loc[funnel.index.max(), funnel_cols].values
# если в таблице сопряженности попадаются нули, то пропускаем такие ситуации
if (funnel[cont_cols] == 0).max().max():
errors += 1
continue
# проводим тесты
result += [test_func(funnel)]
result = pd.DataFrame(result)
result = result.apply(compare_func, args = [alpha], axis = 1)
return list(result.mean().values), errors
# функция отрисовки карты ошибок
def show_contour(data, x_col, y_col, z_col, levels, ax, title):
z = data.pivot_table(index = y_col, columns = x_col, values = z_col, aggfunc = ‘max’)
x, y = z.columns, z.index.values
# закраска областей
ax.contourf(x, y, z, levels = levels, cmap = color_map, alpha = 0.3, norm = matplotlib.colors.BoundaryNorm(levels,len(levels)))
line_colors = [‘black’ for l in levels]
# линии уровня
cp = ax.contour(x, y, z, levels = levels, colors = ‘black’)
ax.clabel(cp, fontsize = 8, colors = line_colors)
# границы типов воронок
ax.axvline(0.5, linestyle = ‘-.’, color = ‘red’)
ax.hlines(y = 0.5, xmin = 0.5, xmax = z.columns.values[-1], linestyle = ‘-.’, color = ‘red’)
ax.text(0.07, 0.9, ‘Быстрое’, fontsize = 15, color = ‘red’)
ax.text(0.55, 0.9, ‘Умеренное’, fontsize = 15, color = ‘red’)
ax.text(0.55, 0.41, ‘Быстроеn2-й шаг’, fontsize = 15, color = ‘red’)
# подписи осей и заголовки
plt.xlabel(‘Вероятность конверсии в первый шаг’), plt.ylabel(‘Вероятность конверсии во второй шаг’)
plt.title(title)
# funnel_log — лог с данными воронок
# diffs — набор воронок, которые сравниваются с эталонной. Например, если diff = [0.7], то c эталонной воронкой будет сравниваться воронка, имеющая 30% отличие от эталонной
# sample_size — размер выборок, формируемых в каждом из экспериментов
# number_of_experiments — число экспериментов для каждой из воронок
# alpha — уровень значимости
# test_func — функция, описывающая набор статистических тестов, которые проводятся в каждом из экспериментов
# result_column_names — словарь человеко-читаемых названий колонок с результатами экспериментов
# compare_func — функция, служащая для сравнения p-value в каждом из экспериментов с уровнем значимости
# levels — линии уровня на карте ошибок
# color_map — цвета для отображения уровней ошибок
# filename_template — шаблон имени файлов, в которые будут записаны результаты экспериментов
def run_error_experiments(funnel_log, diffs, sample_size, number_of_experiments, alpha, test_func, result_column_names, compare_func, levels, color_map, suptitle, filename_template):
# проверяем наличие более ранних рассчетов
existing_result_files = [f for f in os.listdir(‘.’) if re.match(filename_template, f)]
if len(existing_result_files) > 0:
# если результаты более ранниз рассчетов найдены, то просто читаем их
result = pd.read_csv(filename_template + ‘_result.csv’)
errors = pd.read_csv(filename_template + ‘_errors.csv’)
else:
# если нет — считаем все заново
result = []
errors = []
for funnel_num in funnel_log[‘funnel_num’].unique():
# A-воронка
current_funnel_log = funnel_log.query(‘funnel_num == @funnel_num and diff == 1’)
current_funnel_log[‘group’] = 0
# последовательно формируем B-воронки с разной степенью отличия от исходной
for i, diff in enumerate(diffs):
current_funnel_log_another = funnel_log.query(‘funnel_num == @funnel_num and diff == @diff’)
current_funnel_log_another[‘group’] = i + 1
current_funnel_log = current_funnel_log.append(current_funnel_log_another)
# для каждой пары проводим эксперимент
current_exp_results, current_exp_errors = run_experiment(current_funnel_log,
sample_size = sample_size,
number_of_experiments = number_of_experiments,
alpha = alpha,
test_func = test_func,
compare_func = compare_func
)
# собираем разультаты в единый массив
result += [[funnel_num, current_funnel_log[‘first_step_prob’].max(), current_funnel_log[‘second_step_prob’].max()] + current_exp_results]
errors += [[funnel_num, current_funnel_log[‘first_step_prob’].max(), current_funnel_log[‘second_step_prob’].max(), current_exp_errors]]
result = pd.DataFrame(result, columns = [‘funnel_num’, ‘first_step_prob’, ‘second_step_prob’] + list(result_column_names.keys()))
errors = pd.DataFrame(errors, columns = [‘funnel_num’, ‘first_step_prob’, ‘second_step_prob’, ‘errors’])
# сохраняем результаты рассчетов в файлы
result.to_csv(filename_template + ‘_result.csv’, index = False)
errors.to_csv(filename_template + ‘_errors.csv’, index = False)
# визуализация
plt.figure(figsize = (30, 7))
for i, col in enumerate(result_column_names.keys()):
show_contour(result, ‘first_step_prob’, ‘second_step_prob’, col, levels, ax = plt.subplot(1, len(result_column_names), i + 1), title = result_column_names[col])
plt.suptitle(suptitle)
plt.show()
return result, errors
Зададим начальные условия экспериментов и наборы тестовых функций:
# начальные условия
number_of_experiments = 100
alpha = 0.05
# тестировочная функция для двух воронок
two_funnel_test_function = lambda funnel: [chisquare(funnel[1], funnel[0]).pvalue, # тест на гомогенность по таблице воронок
chisquare(funnel[‘cont_1’], funnel[‘cont_0’]).pvalue, # тест на гомогенность по таблице сопряженности
chi2_contingency(funnel[[0, 1]])[1], # тест на независимость по таблице воронок
chi2_contingency(funnel[[‘cont_0’, ‘cont_1’]])[1], # тест на независимотьс по таблице сопряженности
proportions_ztest(funnel.loc[funnel.shape[0] — 1, [0, 1]].values, funnel.loc[0, [0, 1]].values)[1] # z-тест на последний шаг воронки
]
two_funnel_result_column_names = {‘chisquare_funnel’: ‘$chi^2$-тест на гомогенность, таблица воронок’,
‘chisquare_cont’: ‘$chi^2$-тест на гомогенность, таблица сопряженности’,
‘chi2_contingency_funnel’: ‘$chi^2$-тест на независимость, таблица воронок’,
‘cchi2_contingency_cont’: ‘$chi^2$-тест на независимость, таблица сопряженности’,
‘z_test’: ‘z-тест по последнему шагу воронок’}
# тестирововчная функция для 3 и более воронок
mult_funnel_test_function = lambda funnel: [chi2_contingency(funnel[[x for x in funnel.columns if ‘cont’ not in str(x)]])[1], # тест на независимость по таблице воронок
chi2_contingency(funnel[[x for x in funnel.columns if ‘cont’ in str(x)]])[1] # тест на независимость по таблице сопряженности
]
mult_funnel_result_column_names = {‘chi2_contingency_funnel’: ‘$chi^2$-тест на независимость, таблица воронок’,
‘cchi2_contingency_cont’: ‘$chi^2$-тест на независимость, таблица сопряженности’}
Зададим графические элементы для отображения карт ошибок:
# графические элементы
# уровни и цвета для тестирования ошибок первого рода
type_1_error_levels = [0, 0.01, 0.05, 0.1, 0.2, 0.3, 1]
type_1_error_color_map = matplotlib.colors.ListedColormap([‘forestgreen’,
‘palegreen’,
‘lightcoral’,
‘indianred’,
‘maroon’,
‘red’])
# уровни и цвета для тестирования ошибок второго рода
type_2_error_levels = [0, 0.1, 0.5, 0.7, 0.9, 0.95, 0.98, 1]
type_2_error_color_map = matplotlib.colors.ListedColormap([‘forestgreen’,
‘lightcoral’,
‘indianred’,
‘brown’,
‘firebrick’,
‘maroon’,
‘red’])
# уровни и цвета для анализа технических ошибок при тестировании
error_levels = [0, 0.1, 0.25, 0.5, 0.75, 0.9, 1]
error_color_map = matplotlib.colors.ListedColormap([‘palegreen’,
‘honeydew’,
‘floralwhite’,
‘bisque’,
‘navajowhite’ ,
‘red’])
5.1.1 Ошибки первого рода при сравнении двух воронок
Начнем с тестирования двух воронок и сравним, сколько ошибок первого рода (воронки одинаковые, но тест находит различие) возникает при применении разных тестов:
# ошибки первого рода для двух воронок
diffs = [1]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = two_funnel_test_function,
result_column_names = two_funnel_result_column_names,
compare_func = lambda x, alpha: x < alpha,
levels = type_1_error_levels,
color_map = type_1_error_color_map,
suptitle = f’Вероятность ошибки первого рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, $\alpha$ = {alpha}’,
filename_template = f’chi2_type1err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Выводы и наблюдения:
- лучше всего себя показал χ²-тест на независимость на таблице воронок — он продемонстрировал низкий процент ошибок первого рода для любых форм воронок вне зависимости от размера выборки;
- χ²-тест на гомогенность по таблице воронок показывает стабильно хорошие результаты для воронок с умеренным падением и стабильно плохие для воронок с быстрым падением;
- χ²-тест на гомогенность по таблице сопряженности стабильно находит отличия там, где их нет, для любых форм воронок и размеров выборок. Доля ошибок доходит до 30%;
- χ²-тест на независимость по таблице сопряженности и z-тест по последнему шагу воронок показывают приемлемые результаты только на больших выборках.
Удивительно, но, похоже, что тесты на сырых воронках дают более правильные результаты, если оценивать по ошибкам первого рода.
В процессе тестирования мы с вами получали ситуации, вызывающие ошибки. Например, таблицы сопряженности с нулевыми ячейками. Давайте посмотрим, как распределены ошибки, чтобы понять, насколько мы можем доверять полученным результатам.
# анализ ошибок
# data — фрейм с ошибками, полученными при тестировании
# num_exp — число экспериментов для каждой из воронок
# levels — линии уровня на карте ошибок
# color_map — цвета для отображения уровней ошибок
# title — заголовок графиков
def viz_errors(data, num_exp, levels, color_map, title = ‘Число ошибок формирования воронок и таблиц сопряженности в зависимости от размера выборки’):
plt.figure(figsize = (30, 5))
for i, ss in enumerate(data.keys()):
z = data[ss].pivot_table(index = ‘second_step_prob’, columns = ‘first_step_prob’, values = ‘errors’, aggfunc = ‘max’)
z = z / num_exp
x, y = z.index.values, z.columns
# закраска областей
ax = plt.subplot(1, len(errors.keys()), i + 1)
ax.contourf(x, y, z, levels = levels, cmap = color_map, alpha = 0.3, norm = matplotlib.colors.BoundaryNorm(levels,len(levels)))
line_colors = [‘black’ for l in levels]
# линии уровня
cp = ax.contour(x, y, z, levels = levels, colors = ‘black’)
ax.clabel(cp, fontsize = 8, colors = line_colors)
plt.xlabel(‘Вероятность конверсии в первый шаг’), plt.ylabel(‘Вероятность конверсии во второй шаг’)
plt.title(f’Размер выборки: {ss}’)
plt.suptitle(title)
# проверим число сгенерированных ошибок
viz_errors(errors, number_of_experiments, levels = error_levels, color_map = error_color_map)
Из графика выше видно, что в основном мы можем доверять результатам, полученным для размера выборок больше 100 элементов. Для меньших выборок нужно быть аккуратными с анализом результатов для воронок с быстрым падением — тут доля ошибок может доходить до 90%.
5.1.2 Ошибки второго рода при сравнении двух воронок
Проанализируем ошибки второго рода (ситуации, когда различия есть, но они не обнаруживаются тестом). Для начала взглянем на ситуацию, когда воронки отличаются на 10%:
# ошибки второго рода для двух воронок
diffs = [0.9]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = two_funnel_test_function,
result_column_names = two_funnel_result_column_names,
compare_func = lambda x, alpha: x > alpha,
levels = type_2_error_levels,
color_map = type_2_error_color_map,
suptitle = f’Вероятность ошибки второго рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, воронки отличаются на {1-diffs[0]:.0%}, $\alpha$ = {alpha}’,
filename_template = f’chi2_type2err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Выводы и наблюдения:
- хуже всего себя показал χ²-тест на независимость по таблице воронок — даже на выборках больших размеров этот тест не находит отличия там, где они есть;
- χ²-тест на гомогенность по таблице воронок и z-тест показывают сопоставимые результаты. В основном они хорошо работают на больших выборках и только в ситуациях умеренного падения;
- лучше всего себя показывают тесты на гомогенность и независимость, выполненные на таблицах сопряженности. С ростом размеров выборок они все лучше и лучше находят различия для воронок с резким падением на втором шаге и для воронок с умеренным падением.
Похоже, что тесты по таблицам сопряженности и z-тест обладают большей мощностью, чем тесты по таблицам воронок.
Теперь проанализируем ситуацию, когда воронки отличаются на 20%:
# ошибки второго рода для двух воронок
diffs = [0.8]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = two_funnel_test_function,
result_column_names = two_funnel_result_column_names,
compare_func = lambda x, alpha: x > alpha,
levels = type_2_error_levels,
color_map = type_2_error_color_map,
suptitle = f’Вероятность ошибки второго рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, воронки отличаются на {1-diffs[0]:.0%}, $\alpha$ = {alpha}’,
filename_template = f’chi2_type2err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Картина в целом аналогична предыдущему примеру:
- хуже всего тесты работают для воронок с быстрым падением;
- самые плохие результаты показывает χ²-тест на независимость на таблице воронок;
- лучше всего себя проявили тесты на гомогенность и независимость, выполненные по таблицам сопряженности;
- z-тест, похоже, лучше всего работает для воронок с умеренным падением.
Наконец, рассмотрим ситуацию, когда воронки отличаются на 30%:
# ошибки второго рода для двух воронок
diffs = [0.7]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = two_funnel_test_function,
result_column_names = two_funnel_result_column_names,
compare_func = lambda x, alpha: x > alpha,
levels = type_2_error_levels,
color_map = type_2_error_color_map,
suptitle = f’Вероятность ошибки второго рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, воронки отличаются на {1-diffs[0]:.0%}, $\alpha$ = {alpha}’,
filename_template = f’chi2_type2err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Видно, что с ростом размера выборок практически все χ²-тесты показывают сопоставимые результаты, а z-тест довольно плохо работает в ситуация быстро падающих воронок.
Общие выводы для ситуации с двумя воронками:
- χ²-тесты по таблицам сопряженности демонстрируют самую высокую мощность — они способны обнаружить разницу в воронках даже при небольших отличиях, если выборка достаточно велика;
- в то же время они демонстрируют самые высокие ошибки первого рода — чаще засекают разницу там, где ее на самом деле нет;
- χ²-тесты по таблицам воронок показывают обратные результаты. Они консервативны, реже допускают ошибки первого рода, но чаще — второго;
- z-тест не показывает существенно более хороших результатов по сравнению с χ²-тестами. Кроме того, z-тест хорошо работает преимущественно в регионе воронок с умеренным падением;
- при работе с любым χ²-тестом нужно быть внимательным при анализе воронок с быстрым падением — это регион высоких ошибок второго рода для любого χ²-теста;
- из всех χ²-тестов наиболее предпочтительным является χ²-тест на независимость — он демонстрирует оптимальное соотношение между вероятностью ошибок первого рода и мощностью;
- при росте размера выборки нет особенной разницы, проводите ли вы χ²-тест по таблице сопряженности или по таблице воронок.
5.2 Ситуация множественных воронок
В этом разделе мы посмотрим, как увеличение числа сравниваемых воронок повлияет на результаты тестирования. Для сравнения множества воронок будем использовать χ²-тесты на независимость. Сначала мы сравним ошибки первого рода для трех и четырех воронок, у которых нет отличий. Это, конечно, не даст исчерпывающего ответа на вопрос, как поведут себя тесты с ростом числа воронок, но поможет определить примерное направление развития результатов:
# ошибки первого рода для трех воронок
diffs = [1, 1]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = mult_funnel_test_function,
result_column_names = mult_funnel_result_column_names,
compare_func = lambda x, alpha: x < alpha,
levels = type_1_error_levels,
color_map = type_1_error_color_map,
suptitle = f’Вероятность ошибки первого рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, $\alpha$ = {alpha}’,
filename_template = f’chi2_contingency_multiple_type1err_ss{ss}_numexp{number_of_experiments}_diffs{len(diffs)}’)
errors[ss] = err
results[ss] = res
Проведем тесты для четырех воронок:
# ошибки первого рода для четырех воронок
diffs = [1, 1, 1]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = mult_funnel_test_function,
result_column_names = mult_funnel_result_column_names,
compare_func = lambda x, alpha: x < alpha,
levels = type_1_error_levels,
color_map = type_1_error_color_map,
suptitle = f’Вероятность ошибки первого рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, $\alpha$ = {alpha}’,
filename_template = f’chi2_contingency_multiple_type1err_ss{ss}_numexp{number_of_experiments}_diffs{len(diffs)}’)
errors[ss] = err
results[ss] = res
Оценим доли технических ошибок:
# проверим число сгенерированных ошибок
viz_errors(errors, number_of_experiments, levels = error_levels, color_map = error_color_map)
Выводы и наблюдения:
- как и в случае с двумя воронкам, тесты, проведенные по таблицам воронок, показывают меньшую вероятность ошибок первого рода;
- точность тестов, проведенных по таблицам сопряженности, увеличивается с ростом размера выборок. Интересно, что при размере выборки 100, вероятность ошибок первого рода резко возрастает для практически любых форм воронок, затем снова падает с увеличением размеров выборок. Природа этого эффекта не совсем ясна;
- нет существенной разницы между результатами, полученными для трех и четырех воронок;
- доля технических ошибок велика для воронок с граничными формами. Например, для воронок с резким падением. Но, начиная с выборок, имеющих размер от 100 наблюдений и более, результаты становятся достаточно консистентными.
Перейдем к анализу ошибок второго рода. Смоделируем ситуацию трех воронок, из которых одна имеет отличие в 10% от остальных двух:
# ошибки второго рода для трех воронок
diffs = [1, 0.9]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = mult_funnel_test_function,
result_column_names = mult_funnel_result_column_names,
compare_func = lambda x, alpha: x > alpha,
levels = type_2_error_levels,
color_map = type_2_error_color_map,
suptitle = f’Вероятность ошибки второго рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, одна из воронок отличается на {1-diffs[1]:.0%}, $\alpha$ = {alpha}’,
filename_template = f’chi2_contingency_type2err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Далее смоделируем ситуацию, когда одна из трех воронок имеет 10% отличие от эталона, а вторая — 30% отличие:
# ошибки второго рода для трех воронок
diffs = [0.9, 0.7]
results, errors = {}, {}
for ss in [25, 50, 100, 200, 500]:
res, err = run_error_experiments(funnel_log, diffs = diffs, sample_size = ss, number_of_experiments = number_of_experiments, alpha = alpha,
test_func = mult_funnel_test_function,
result_column_names = mult_funnel_result_column_names,
compare_func = lambda x, alpha: x > alpha,
levels = type_2_error_levels,
color_map = type_2_error_color_map,
suptitle = f’Вероятность ошибки второго рода для различных видов теста $chi^2$ и различных форм воронок, размер выборки {ss}, одна из воронок отличается на {1-diffs[1]:.0%}, $\alpha$ = {alpha}’,
filename_template = f’chi2_contingency_type2err_ss{ss}_diff{str(diffs[0]).replace(«.», «»)}_numexp{number_of_experiments}’)
errors[ss] = err
results[ss] = res
Выводы и наблюдения:
- в обоих экспериментах тесты по таблицам сопряженности показывают более высокую мощность;
- вероятность ошибки второго рода для тестов по таблице воронок падает с увеличением размеров выборок и ростом отличий воронок, но даже в самом лучшем случае тесты по таблице воронок показывают неплохие результаты только для воронок с умеренным падением.
Итак, проведя серию экспериментов, мы можем сделать следующие практические выводы:
- для анализа воронок z-тест менее предпочтителен, чем тест χ²;
- для анализа воронок из всех тестов χ² больше всего подходит тест на независимость;
- в ситуации сравнения двух воронок и большого размера выборок χ²-тест на независимость дает примерно одинаковые результаты при проведении теста на таблице воронок и на таблице сопряженности;
- в случае сравнения нескольких воронок выигрывает χ²-тест на независимость, проводимый по таблице сопряженности. Таким образом, можно рекомендовать всегда пользоваться тестом χ²-тест на независимость по таблице сопряженности для анализа воронок.
Выводы
- Для практических целей бизнес-аналитики применимы только тесты χ²-тест на независимость и гомогенность.
- В ситуации анализа двух пропорций z-тест полностью эквивалентен χ²-тесту на независимость с таблицей сопряженности 2 x 2.
- Для проведения χ²-тестов имеет смысл брать выборки размером порядка 500 наблюдений.
- При решении задач сравнения воронок с помощью χ²-теста предпочтительнее использовать χ²-тест на независимость, проводимый по таблице сопряженности, поскольку он обеспечивает оптимальные результаты с точки зрения ошибок первого и второго рода при сравнении двух и более воронок.
Вы можете скачать ноутбук для этой статьи тут (имейте в виду, что пересчет ошибок может занять значительное время).