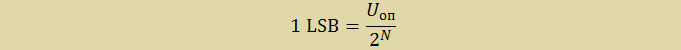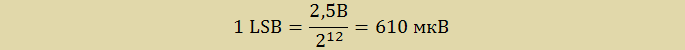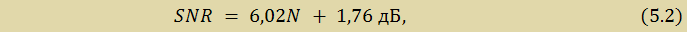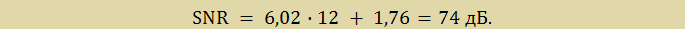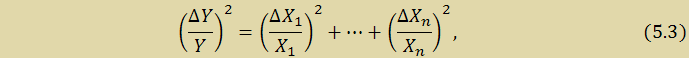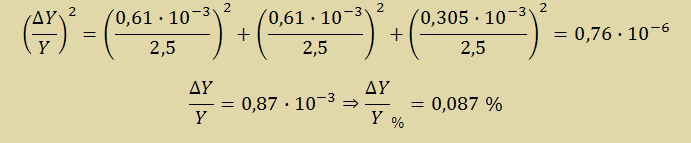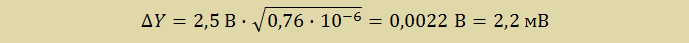
1.3.1 Преобразование аналог—цифра. Шумы квантования
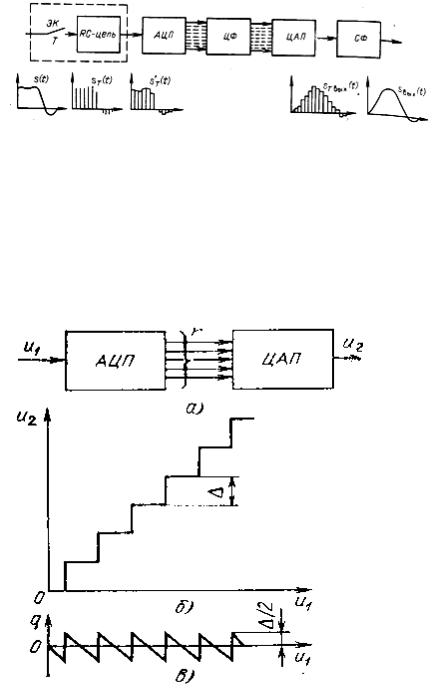
Погрешности преобразования входного сигнала из аналоговой формы в цифровую возникает при квантовании сигнала на конечное, ограниченное число уровней. Чтобы выявить характер этой погрешности приведем структурную схему (рис.1.10) и вы-елим из нее два устройства: аналоговоцифровой преобразователь (АЦП) и цифро-аналоговый преобразователь
(ЦАП).
Рис.1.10. Функциональная схема преобразования аналог-цифра и обратно – цифра-аналог Рассмотрим сначала совместную работу этих устройств без учета цифрового
фильтра при подаче на вход АЦП постоянного напряжения различного уровня u1 (рис. 1.11, а).
Рис. 1.11 Преобразование аналог-цифра и цифра-аналог (а), характеристика квантования (б) и ошибка квантования (в)
Основным параметром АЦП является число разрядов, использу-емых для кодирования входного напряжения. При двоичном ко-де число разрядов определяется числом триггеров регистра, каждый из которых может находиться в одном из двух состоя-ний: с нулевым или ненулевым напряжением на выходе. Одному из этих состояний условно приписывается нуль, а другому — единица. При числе двоичных элементов r на выходе АЦП по-лучается комбинация (кодовое число) из r символов, каждый из которых может принимать одно из двух значений (нуль или единица).
Число возможных различных комбинаций L= 2r и опре-деляет число дискретных уровней, на которое может быть раз-бит диапазон изменения входного напряжения.
В ЦАП осуществляется обратное преобразование. Каж-дой комбинации нулей и единиц, поступающих на вход ЦАП, соответствует определенный дискретный уровень выходного напряжения. В результате при равномерном шаге квантования А 30
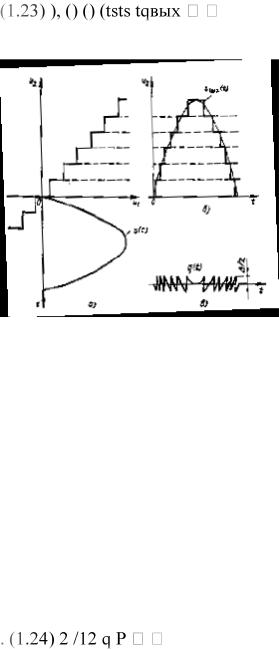
зависимость u2 от u1 приобретает вид ломаной линии, показанной на рис. 1.11, б.
Устройство, обладающее подобной характеристикой, должно рассматриваться как нелинейное, а разность u2-u1=q — как ошибка, погрешность квантования. Видно, что наибольшая ошибка, по абсолютной величине не превышающая Δ/2, с возрастанием u2 остается неизменной
(рис. 1.11, в).
Предположим, что входное колебание s(t) является гармоническим (рис. 1.12, а). Колебание sвыx (t) приобретает ступенчатую форму, отличающуюся от входного колебания s (t) (рис. 1.12, б, тонкая линия), а ошибка квантования принимает вид функции
представленной на рис. 1.12, в.
Рис 1.12. Сигнал на входе (а) и выходе (б) квантующего устройства; помеха квантования
При изменении в широких пределах амплитуды и частоты гармонического колебания s(t) изменяется только частота следования зубцов: форма их остается близкой к треугольной при неизменной амплитуде Δ/2. Функцию q
(t) можно назвать помехой или шумом квантования. Нетрудно вычислить среднюю мощность шума квантования. При допущении треугольной формы зубцов (рис. 1.11, в) с амплитудой Δ/2 средняя длительность одного зубца мощность равна (1/3) (Δ/2)2 = Δ2/12. Так как эта величина не зависит от длительности зубца, можно считать, что средняя мощность шума квантования
При грубой оценке превышения сигнала над шумом квантования исходят из соотношения или, в децибе-
2 ( / ) 10lg2 10 2 lg2 6 r дБ s q дБ D
В современных АЦП число разрядов достигает десяти и более. При этом величина , характеризующая динамический дапазон АЦП, равна примерно 60 дБ (6 дБ на один разряд). дБ D
Другой важной характеристикой шума квантования является его спектральная характеристика. При гармоническом колебании на входе АЦП помеха квантования является периодической функцией времени. Спектр ее является линейчатым, содержащим только частоты, кратные частоте входного колебания. Из-за зубчатой формы функции q (t) (см. рис. 1.12, в) спектр шума содержит высшие гармоники
Раскладываем по полочкам параметры АЦП
Время на прочтение
10 мин
Количество просмотров 54K
Привет, Хабр! Многие разработчики систем довольно часто сталкиваются с обработкой аналоговых сигналов. Не все манипуляции с сигналами можно осуществить в аналоговой форме, поэтому требуется переводить аналог в цифровой мир для дальнейшей постобработки. Возникает вопрос: на какие параметры стоит обратить внимание при выборе микроконтроллера или дискретного АЦП? Что все эти параметры означают? В этой статье постараемся детально рассмотреть основные характеристики АЦП и разобраться на что стоит обратить внимание при выборе преобразователя.
Введение
Начать бы хотелось с интересного философского вопроса: если аналоговый сигнал — это бесконечность, теряем ли мы при оцифровке сигнала бесконечное количество информации? Если это так, тогда какой смысл существования такого неэффективного преобразования?
Для того, чтобы ответить на этот вопрос, разберемся с тем, что такое аналого-цифровое преобразование сигнала. Основной график, который отражает работу АЦП – передаточная характеристика преобразования. В идеальном мире это была бы прямая линия, то есть у каждого аналогового уровня сигнала имелся бы единственный цифровой эквивалент.
Рис. 1: Идеальная характеристика АЦП
Однако из-за наличия различных видов шума, мы не можем увеличивать разрядность АЦП до бесконечности. То есть существует предел, который ограничивает минимальную цену деления шкалы. Другими словами, уменьшая деление шкалы мы рано или поздно «упремся» в шум. Да, конечно, можно сделать хоть 100-битный АЦП, однако большинство бит данного АЦП не будут нести полезную информацию. Именно поэтому характеристика АЦП имеет ступенчатую форму, что равносильно наличию конечной разрядности АЦП.
Проектируя систему необходимо выбирать АЦП, который бы обеспечил отсутствие потери информации при оцифровке. Для того, чтобы выбрать преобразователь, необходимо понять, какие параметры его характеризуют.
Параметры АЦП можно разделить на 2 группы:
- Статические — характеризуют АЦП при постоянном или очень медленно изменяющемся входном сигнале. К данным параметрам можно отнести: максимальное и минимальное допустимое значение входного сигнала, разрядность, интегральную и дифференциальную нелинейности, температурную нестабильность параметров преобразования и др.
- Динамические — определяют максимальную скорость преобразования, предельную частоту входного сигнала, шумы и нелинейности.
Статические параметры
- Максимальный (Vref) и минимальный (обычно 0) уровни входного сигнала — устанавливают диапазон шкалы преобразования, относительно которой будет оцениваться входной сигнал (рис. 1). Также этот параметр может обозначаться как FS — full scale. Для дифференциального АЦП шкала определяется от -Vref до +Vref, однако для упрощения далее будем рассматривать только single-ended шкалы.
- Разрядность (N) — разрядность выходного кода, характеризующая количество дискретных значений (
), которые преобразователь может выдать на выходе (рис. 1).
- Ток потребления (Idd) — сильно зависит от частоты преобразования, поэтому информацию об этом параметре лучше искать на соответствующем графике.
- МЗР (LSB) – младший значащий разряд (Least Significant Bit) — минимальное входное напряжение, разрешаемое АЦП (по сути единичный шаг в шкале преобразования). Определяется формулой:
(рис. 1).
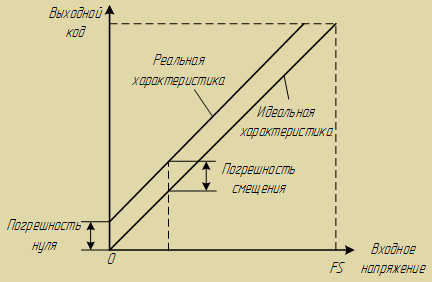
- Ошибка смещения (offset error) – определяется как отклонение фактической передаточной характеристики АЦП от передаточной характеристики идеального АЦП в начальной точке шкалы. Измеряется в долях LSB. При ошибке смещения переход выходного кода от 0 в 1 происходит при входном напряжении отличном от 0.5LSB (рис. 2).
Рис. 2: Ошибка смещения
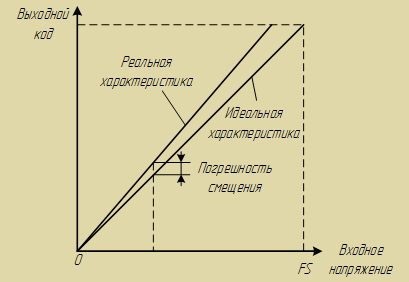
Существует и другой вариант квантователя, когда переход осуществляется при целых значения LSB (характеристика у него будет смещена относительно первого варианта, который представлен на рисунке 2). Оба этих квантователя равноправны, и для простоты далее будем рассматривать только первый вариант. - Ошибка усиления (gain error) – определяется как отклонение средней точки последнего шага преобразования (которому соответствует входное напряжение Vref) реального АЦП от средней точки последнего шага преобразования идеального АЦП после компенсации ошибки смещения (рис. 3).
Рис. 3: Ошибка усиления
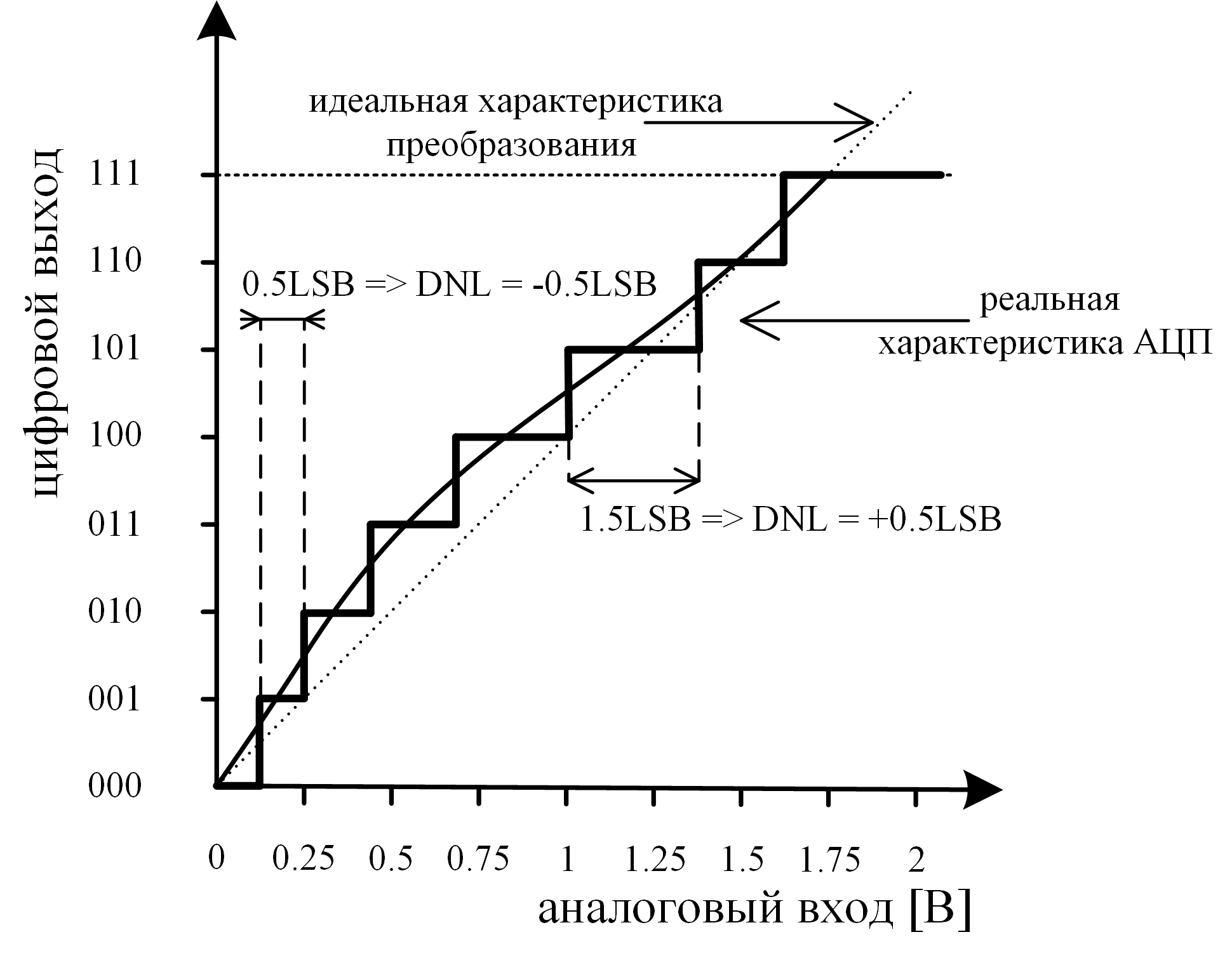
- Дифференциальная нелинейность (DNL — Differential nonlinearity) – отклонение ширины ступеньки на передаточной характеристике реального АЦП от номинальной ширины ступеньки у идеального преобразователя. Из-за дифференциальной нелинейности шаги квантования имеют различную ширину (рис. 4).
Рис. 4: Дифференциальная нелинейность
Для 3-х битного АЦП с рисунка 4:
- Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
Рис. 5: Интегральная нелинейность
- Общая нескорректированная ошибка ( TUE — Total Unadjusted Error) – абсолютная ошибка, включающая в себя следующие ошибки: квантования, смещения, усиления и нелинейности. Другими словами, это максимальное отклонение между реальной и идеальной характеристикой преобразования. Для идеального АЦП TUE = 0.5LSB, обусловлена ошибкой квантования (или шум квантования — возникает из-за округления значения аналогового сигнала, которое соответствует цифровому коду). Ошибки усиления и смещения обычно вносят наиболее весомый вклад в абсолютную ошибку. Однако с точки зрения динамических параметров (см. ниже) ошибки смещения и усиления ничтожны, так как они не порождают нелинейных искажений.
Динамические параметры
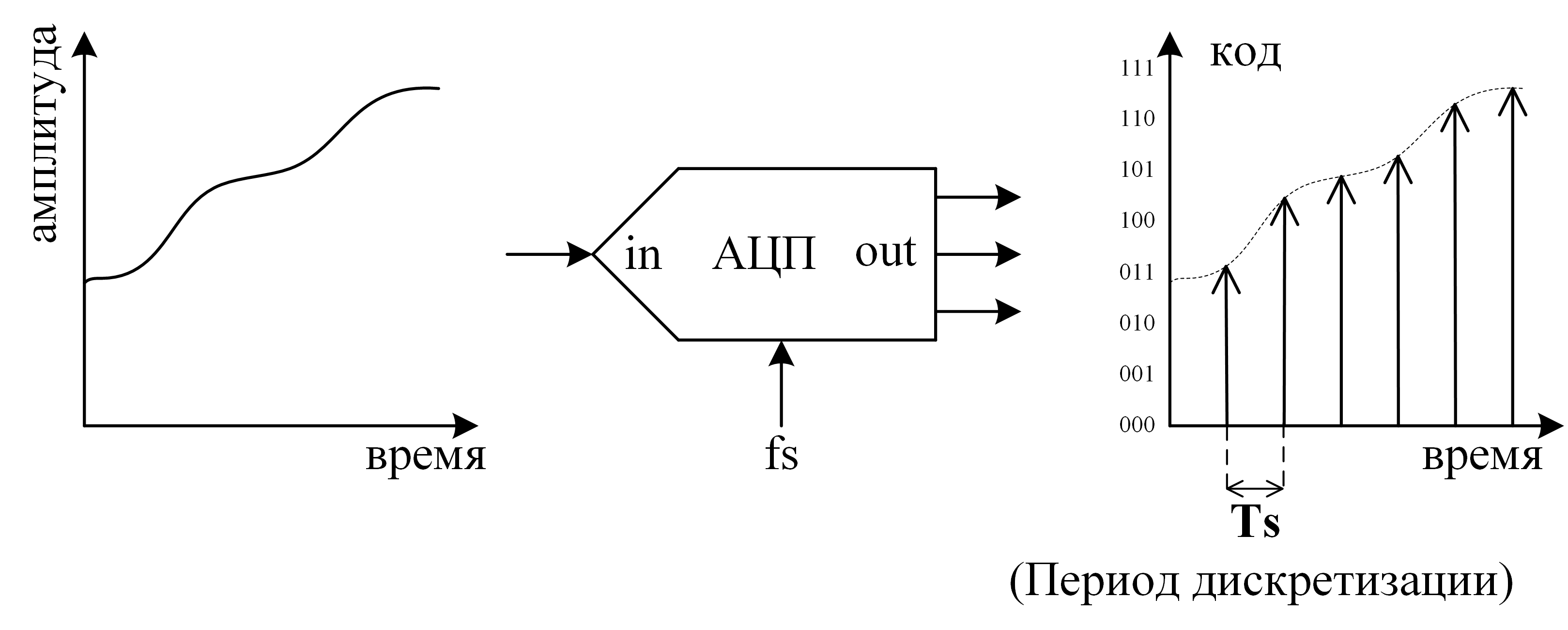
- Частота дискретизации (fs — sampling frequency) — частота, при которой происходит преобразование в АЦП (ну или 1/Ts, где Ts — период выборки). Измеряется числом выборок в секунду. Обычно под данным обозначением подразумевают максимальную частоту дискретизации, при которой специфицированы параметры преобразователя (рис. 6).
Рис. 6: Процесс преобразования АЦП
- Отношение сигнал/шум (SNR — Signal-to-Noise Ratio) — определяется как отношение мощности обрабатываемого сигнала к мощности шума, добавляемого в процессе преобразования. SNR обычно выражается в децибелах (дБ) и рассчитывается по следующей формуле:
Наглядно данное выражение продемонстрированно на рисунке 7.
Рис. 7: Отношение сигнал/шум
Для оценки SNR АЦП при разработке системы можно воспользоваться следующей формулой:
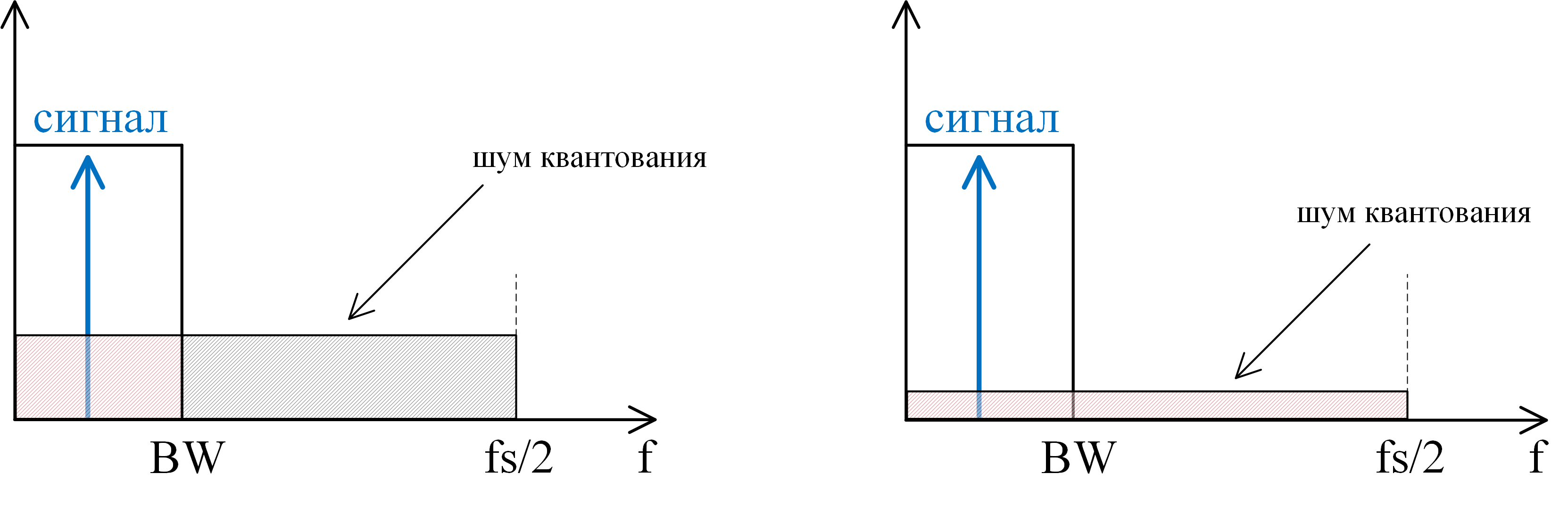
Первые 2 слагаемых учитывают уровень сигнала и ошибку квантования (нужно понимать, что формула верна для сигнала размаха полной шкалы). Третье слагаемое учитывает эффект передискретизации (выигрыш по обработке или processing gain): если полоса обрабатываемого сигнала (BW < fs/2), то, применив цифровой фильтр низких частот (либо полосовой, тут зависит все от полосы и несущей) к результату преобразования, можно вырезать часть шума АЦП, а оставшаяся часть будет распределена от 0 до BW (рис. 8). Если шум АЦП равномерно распределен по всем частотам (т.н. «белый» шум) интегральный шум после фильтрации уменьшится в fs/2 / BW раз, что и отражает третий член формулы.
Рис. 8: Увеличение SNR за счет передискретизации
- Общие нелинейные искажения (THD — total harmonic distortion). Прежде, чем сигнал преобразовывается в цифровой код, он проходит через нелинейные блоки, которые искажают сигнал. К примеру, пусть есть сигнал с частотой f. Пройдя через нелинейный блок к нему добавятся компоненты с частотами 2f, 3f, 4f … — 2-я, 3-я, 4-я и т.д. гармоники входного сигнала. Если дискретизированный сигнал разложить в спектр с помощью ДПФ (Дискретного Преобразования Фурье), мы увидим, что все эти гармоники «перенеслись» в первую зону Найквиста (от 0 до fs/2) (рис. 9).
Рис. 9: Нелинейные искажения
Побочные гармоники искажают обрабатываемый сигнал, что ухудшает производительность системы. Этот эффект можно измерить, используя характеристику общие нелинейные искажения. THD определяется как отношение суммарной мощности гармонических частотных составляющих к мощности основной (исходной) частотной составляющей (в некоторых документациях выражается в дБ):
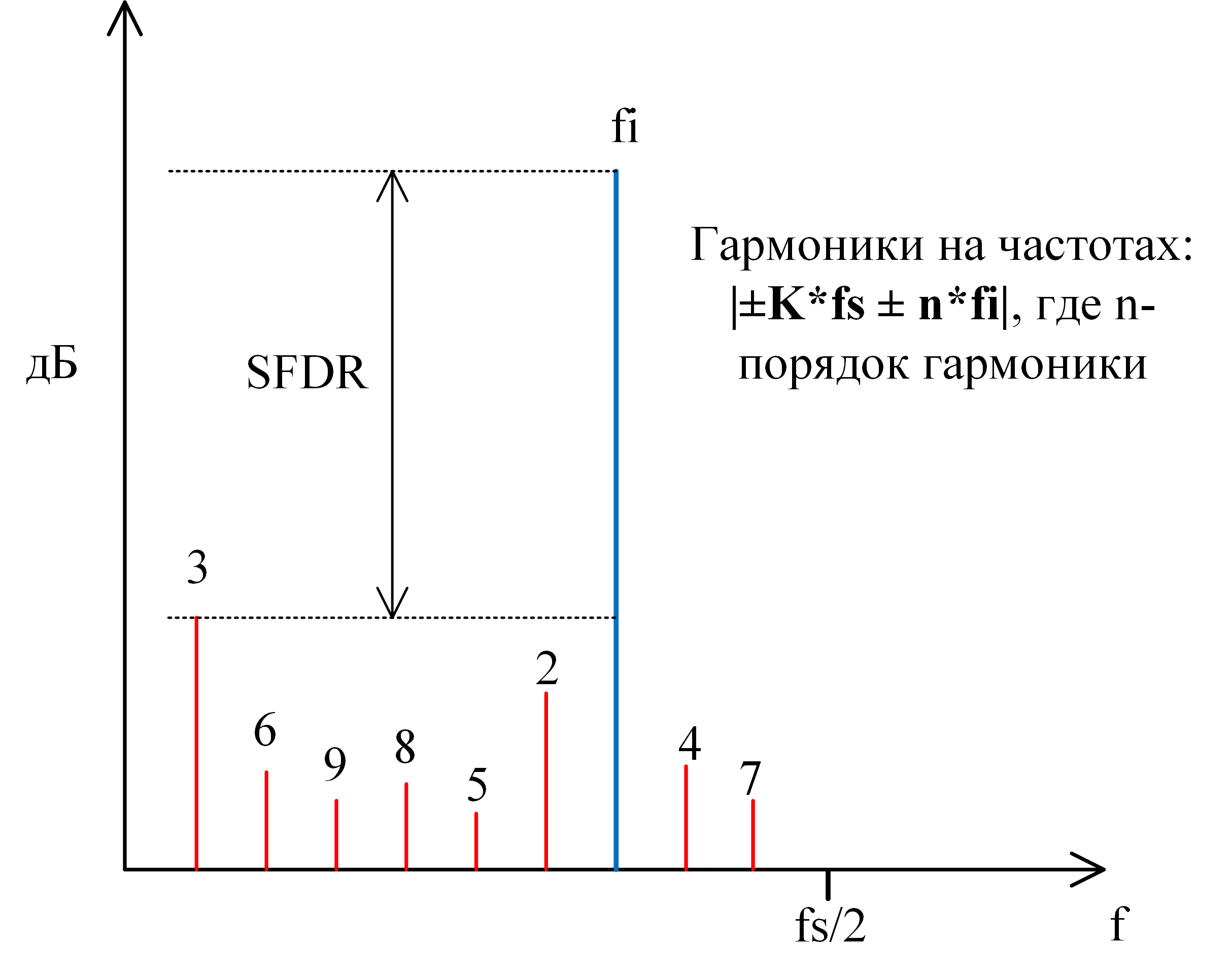
- Динамический диапазон, свободный от гармоник (SFDR — Spurious-Free Dynamic Range). Является отношением мощности полезного сигнала к мощности наибольшего «спура» (любая паразитная составляющая в спектре, не обязательно гармонического происхождения), присутствующего в спектре (рис. 9).
- Отношение сигнал / шум и нелинейные искажения (SINAD — signal-to-noise and distortion ratio). Аналогичен SNR, но помимо шума учитывает все виды помех и искажений, возникающих при аналого-цифровом преобразовании. SINAD является одним из ключевых параметром, характеризующим АЦП (в некоторых источниках обозначается как SNDR):
- Эффективное число бит (ENOB — effective number of bits) – некая абстрактная характеристика, показывающая сколько на самом деле бит в выходном коде АЦП несет в себе полезную информацию. Может принимать дробные значения.
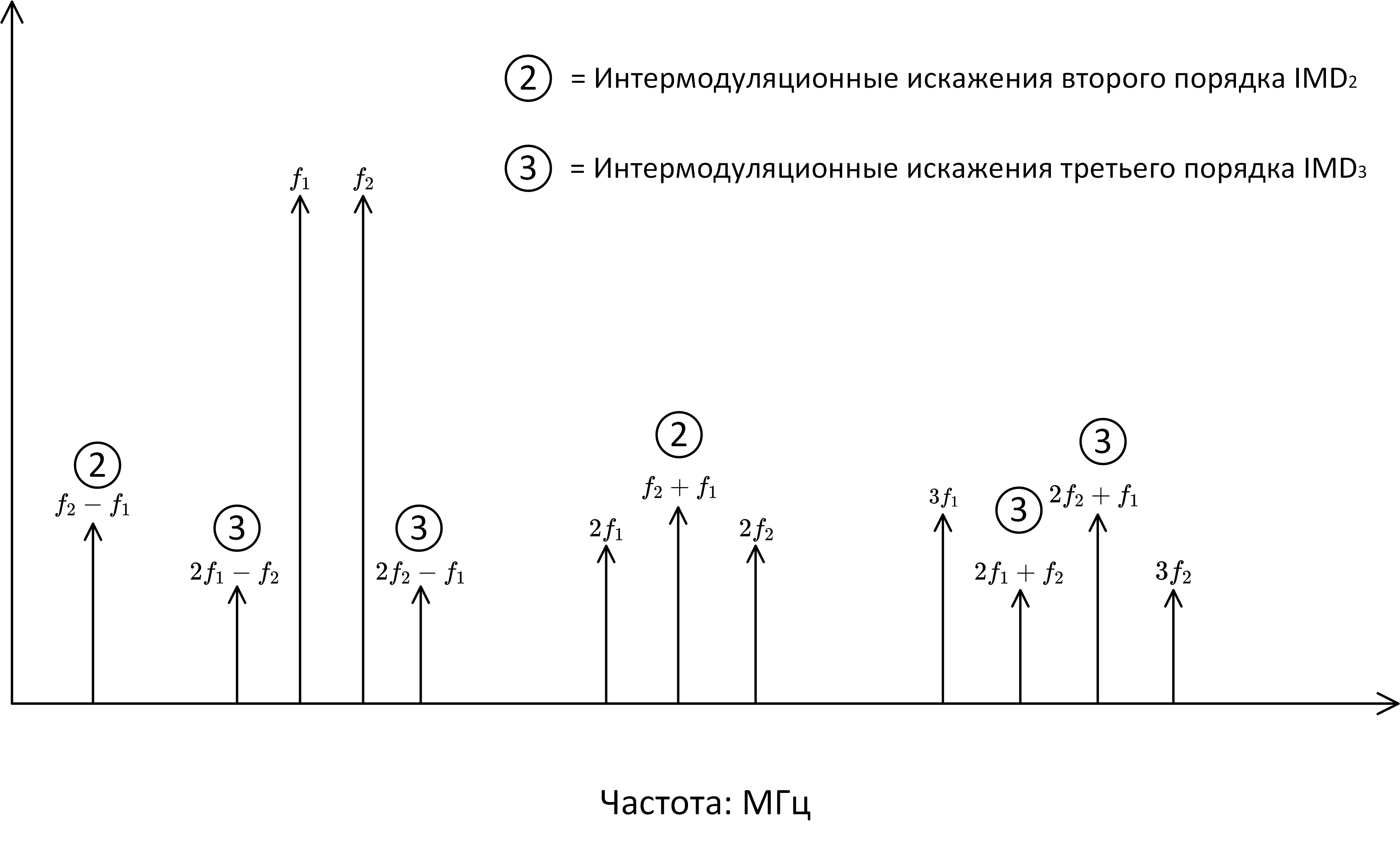
- Интермодуляционные искажения (IMD — intermodulation distortion). Рассмотренные прежде динамические параметры измеряются, когда на вход подается однотональный гармонический сигнал. Такие однотональные тесты хороши, когда АЦП обрабатывает широкополосные сигналы. В этом случае гармоники, располагающиеся выше fs/2 отражаются в первую зону Найквиста и, следовательно, всегда учитываются в расчете параметров. Однако, имея дело с узкополосными сигналами или АЦП с передискретизацией, даже гармоники низкого порядка (2-я, 3-я) могут иметь достаточно высокую частоту, чтобы выйти из рассматриваемого частотного диапазона (или не отразиться в этот диапазон в случае выхода за fs/2). В этом случае эти гармоники не будут учтены, что приведёт к ошибочному завышению динамических параметров.
Для решения этой проблемы используются бигармонические тесты. На вход подают две спектрально чистых синусоиды одинаковой мощности с частотамии
, которые находятся на близком расстоянии друг от друга. Нелинейность преобразователя порождает дополнительные тоны в спектре (их называют интермодуляционными искажениями) на частотах
, где
– произвольные целые числа.
Полезность бигармонического теста в том, что некоторые из интермодуляционных продуктов располагаются в спектре очень близко к исходному сигналу и, следовательно, дают полную информацию о нелинейности АЦП. В частности, интермодуляционные искажения 3-го порядка находятся на частотахи
(рис. 10).
Рис. 10: интермодуляционные искажения
При построении РЧ систем могут быть интересны так же продукты 2-го и более высокого порядка. Параметр АЦП, характеризующий его интермодуляционные искажения n-го порядка, определяется формулой:
[dBc], где
– мощность идентичных синусоид на входе,
– мощность одного из продуктов. Например
– отношение мощности на
к мощности на
Полоса пропускания АЦП и субдискретизация (undersamling/sub-sampling)
Полоса пропускания преобразователя (FPBW — Full Power (Analog) Bandwidth). Обычно ширина полосы преобразователя составляет несколько зон Найквиста. Этот параметр должен быть в спецификации, но, если его нет, можно попробовать самостоятельно оценить минимально возможное значение полосы пропускания для данного АЦП. За период выборки емкость УВХ должна зарядиться с точностью 1 LSB. Если период выборки равен
, то ошибка выборки сигнала полной шкалы равна:
Решив относительно t, получаем:
Положив, что
, определим минимальную полосу АЦП (для
):
Например, для 16 битного АЦП с частотой дискретизации 80 Мвыб/c и шкалой 2 В ограничение снизу для полосы пропускания, рассчитанное по этой формуле, составит FPBW = 282 МГц.
Analog Bandwidth является очень важным параметром при построении систем, которые работают в режиме субдискретизации (“undersampling”). Объясним это подробнее.
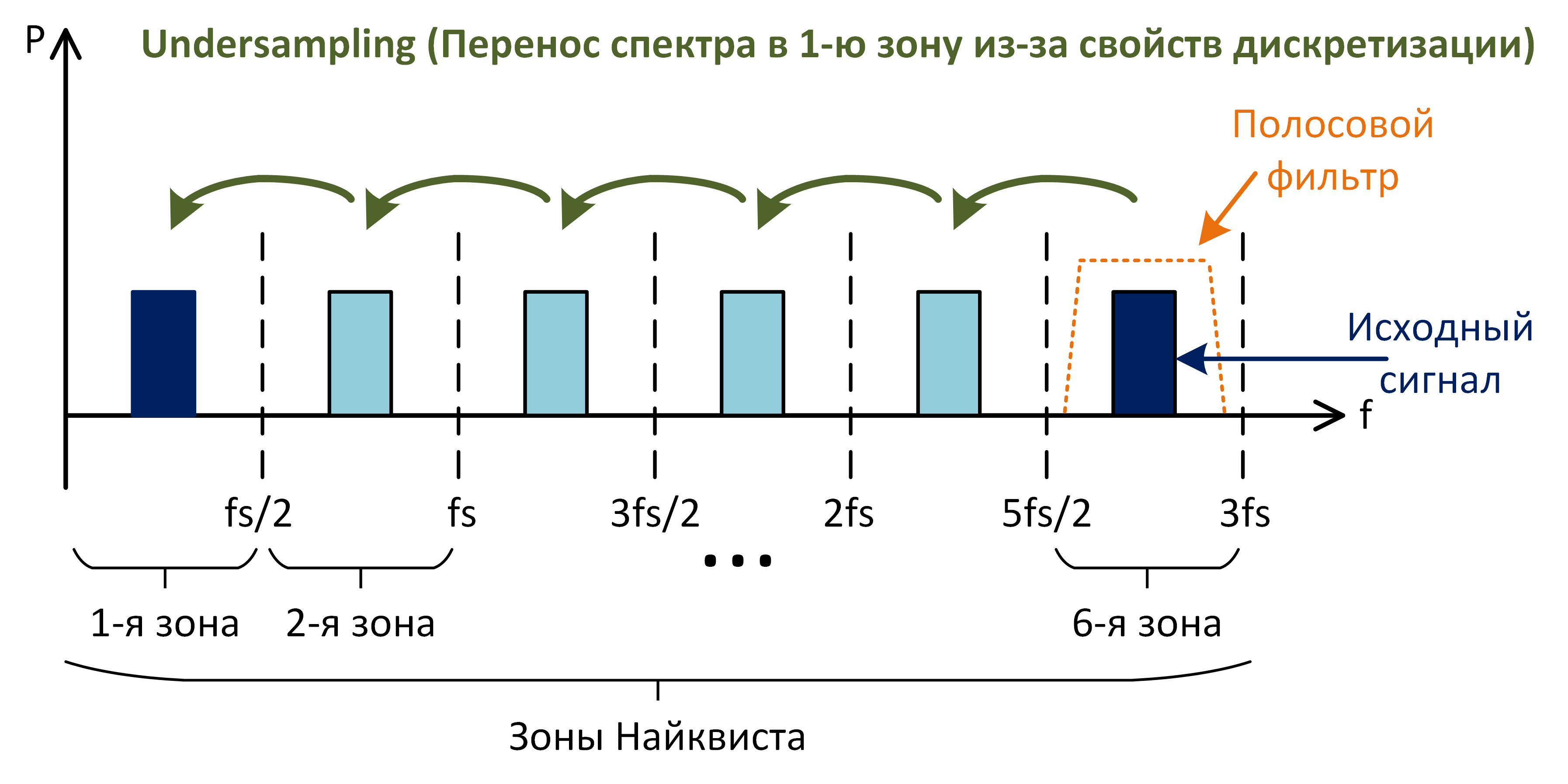
Согласно критерию Найквиста, ширина спектра обрабатываемого сигнала должна быть как минимум в 2 раза меньше частоты дискретизации, чтобы избежать элайзинга. Здесь важно, что именно ширина полосы, а не просто максимальная частота сигнала. Например, сигнал, спектр которого расположен целиком в 6-й зоне Найквиста может быть теоретически дискретизован без потери информации (рис. 11). Ограничив спектр этого сигнала антиэлайзинговым фильтром, его можно подавать на дискретизатор с частотой fs. В результате сигнал отразится в каждой зоне.
Рис. 11: undersampling
Свойство переноса спектра при дискретизации
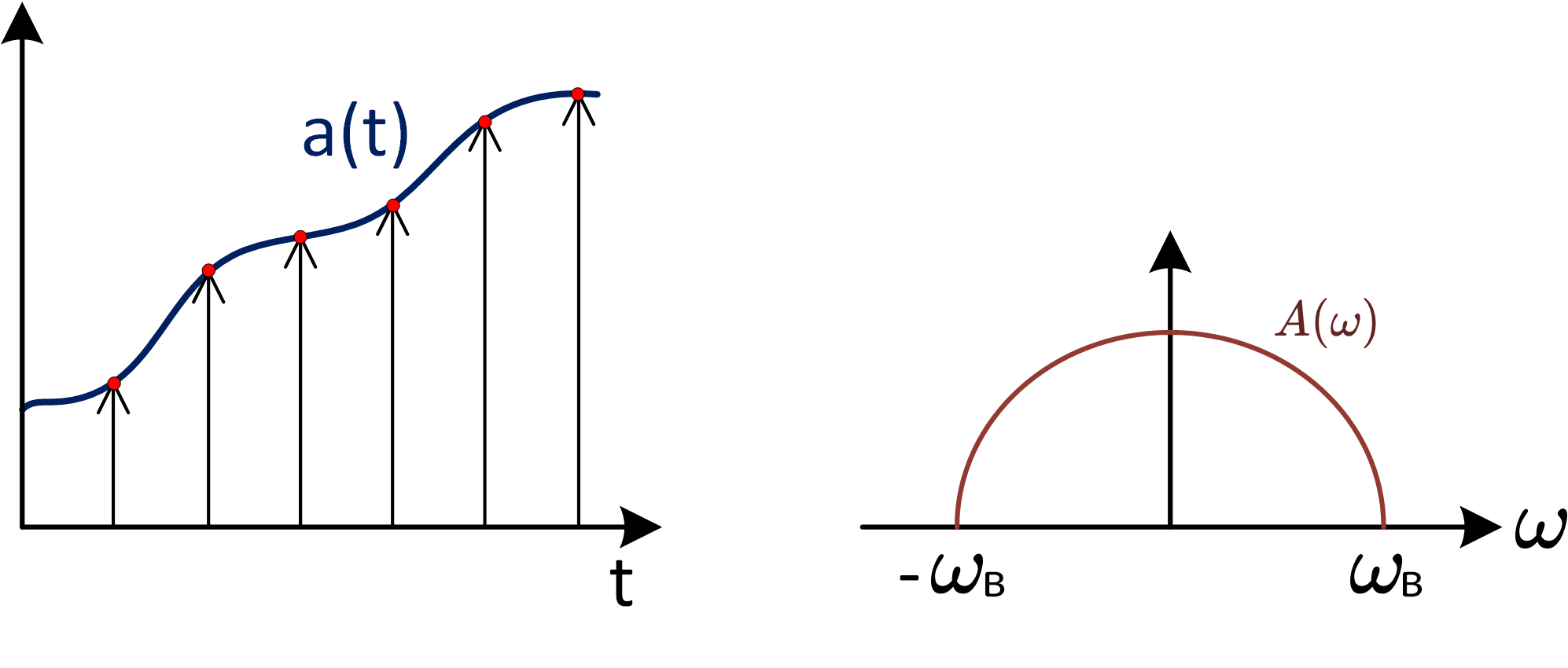
Undersampling или sub-sampling имеет место быть из-за свойств дискретизации. Рассмотрим на примере, пусть имеется сигнал a(t) и его спектральная плотность
(рис. 12). Необходимо найти спектральную плотность
сигнала после дискретизации сигнала
.
Рис 12: дискретизация непрерывного сигнала
По фильтрующему свойству дельта-функции:
После дискретизации
:
где
С помощью формулы Релея вычислим спектр:
Из этого выражения следует что спектр сигнала будет повторяться во всех зонах Найквиста.
Итак, если есть хороший антиэлайзинговый фильтр, то соблюдая критерий Найквиста, можно оцифровывать сигнал с частотой дискретизации намного ниже полосы АЦП. Но использовать субдискретизацию нужно осторожно. Следует учитывать, что динамические параметры АЦП деградируют (иногда очень сильно) с ростом частоты входного сигнала, поэтому оцифровать сигнал из 6-й зоны так же «чисто», как из 1-й не получится.
Несмотря на это субдискритезация активно используется. Например, для обработки узкополосных сигналов, когда не хочется тратиться на дорогой широкополосный быстродействующий АЦП, который вдобавок имеет высокое потребление. Другой пример – выборка ПЧ (IF-sampling) в РЧ системах. Там благодаря undersampling можно исключить из радиоприемного тракта лишнее аналоговое звено — смеситель (который переносит сигнал на более низкую несущую или на 0).
Сравним архитектуры
На данный момент в мире существует множество различных архитектур АЦП. У каждой из них есть свои преимущества и недостатки. Не существует архитектуры, которая бы достигала максимальных значений всех, описанных выше параметров. Проанализируем какие максимальные параметры скорости и разрешения смогли достичь компании, выпускающие АЦП. Также оценим достоинства и недостатки каждой архитектуры (более подробно о различных архитектурах можно прочитать в статье на хабр).
Таблица сравнения архитектур
Информацию для таблицы брал на сайте arrow, поэтому если что-то упустил поправляйте в комментариях.
Заключение
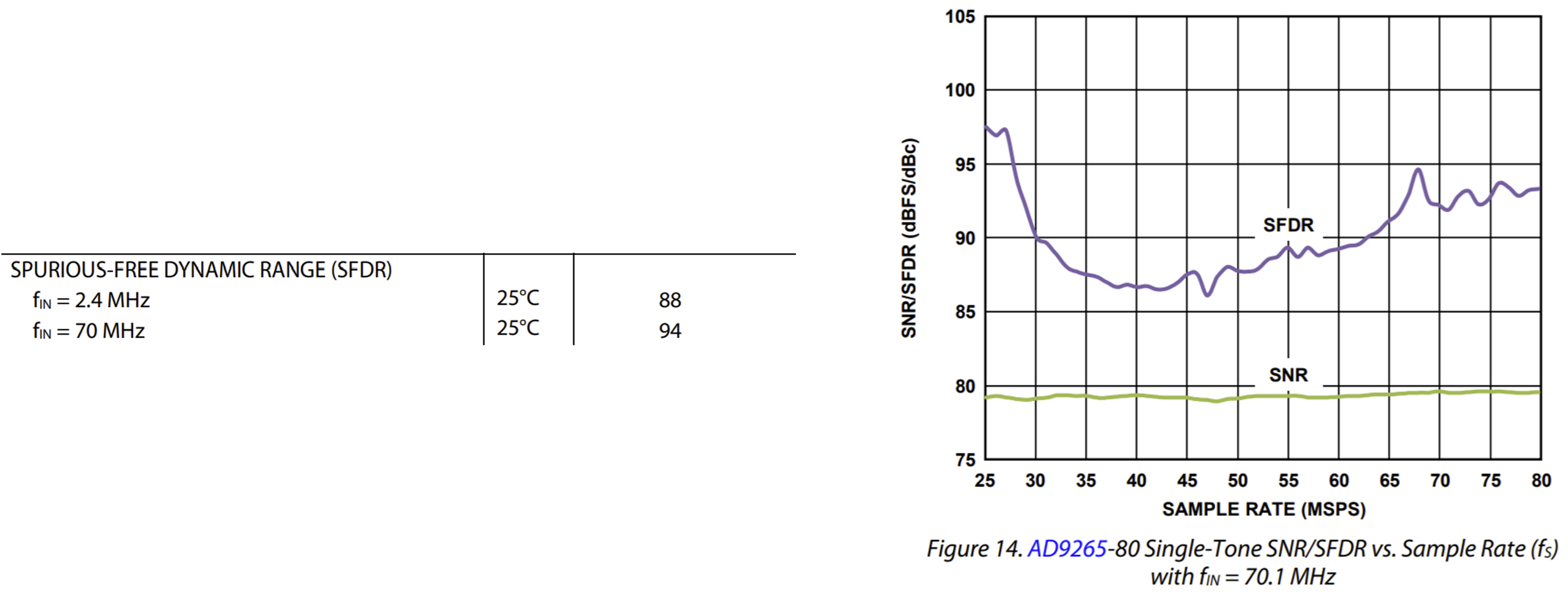
Описав параметры разрабатываемой вами системы, можно понять, какие характеристики АЦП для вас являются критичными. Однако не стоит забывать, что динамические параметры преобразователей сильно зависят от многих факторов (частота дискретизации, частота входного сигнала, амплитуда входного сигнала и тд.) Зачастую в таблицах параметров в документации указывают только «красивые» (с точки зрения маркетинга) цифры. Приведу пример, возьмем АЦП ad9265 и рассмотрим его параметр SFDR при частоте входного сигнала 70 МГц:
Таблица показывает значение SFDR при максимальных значениях частоты дискретизации, однако если вы будете использовать частоту ниже (к примеру 40 МГц), вы не получите этих «хороших» значений. Поэтому советую анализировать характеристики АЦП по графикам, чтобы примерно понимать, сможет ли данная микросхема обеспечить нужную вам точность преобразования.
Выпускная квалификационная работа. Часть 5.
5.1 Основные определения
5.2 Погрешности АЦП
5.3 Экспериментальные исследования
5.4 Выводы
5.1 Основные определения
Измерение – это операция, в результате которой мы узнаем, во сколько раз измеряемая величина больше или меньше соответствующей величины, принятой за эталон.
Интегральная нелинейность — представляет собой максимальное отклонение любого кода от прямой линии, проведенной через крайние точки передаточной функции АЦП. Крайними точками являются: нулевая, находящаяся на 0.5LSB ниже точки появления первого кода, и последняя — на 0.5LSB выше граничного кода шкалы.
Дифференциальная нелинейность DNL (differential non-linearity) — представляет собой разницу между измеренной и идеальной шириной 1 кванта (1 LSB) АЦП.
Ошибка смещения — представляет собой отклонение момента первичной смены кода с (000Н) на (001Н) от идеального значения, то есть +0.5LSB.
Ошибка усиления — представляет отклонение реального коэффициента усиления тот идеального.
LSB (least significant bit) или МЗБ (младший значащий бит) – это наименьшее значение напряжения, которое может быть измерено АЦП. Находиться по формуле:
где Uоп – значения источника опорного напряжения (ИОН), N разрядность АЦП. В данном случае:
Uоп = 2,5 В — значение напряжения внутреннего ИОН.
Систематические ошибки – ошибки, величина которых одинакова во всех измерениях, приводящих одним и тем же методом с помощью одних и тех же измерительных приборов. Ошибка смещения и ошибка усиления относятся к случайным ошибкам.
Случайные ошибки – ошибки, величина которых различна даже дл измерений, выполненных одинаковым образом. Интегральная и дифференциальная нелинейности относятся к систематические ошибкам.
5.2 Погрешности АЦП
В АЦП и ЦАП различают четыре типа погрешностей по постоянному току: погрешность смещения, погрешность усиления и два типа погрешностей, связанных с линейностью: интегральная и дифференциальная нелинейность. Погрешности смещения и усиления АЦП и ЦАП аналогичны погрешностям смещения и усиления в усилителях.
Рисунок 5.1 – Погрешность смещения нуля
Погрешность смещения равна погрешности нуля во всем диапазоне входного напряжения и постоянна.
Рисунок 5.2 – Погрешность усиления
Погрешность усиления вызывает погрешность смещения. Причем погрешность смещения не постоянна и не равна погрешность смещения нуля.
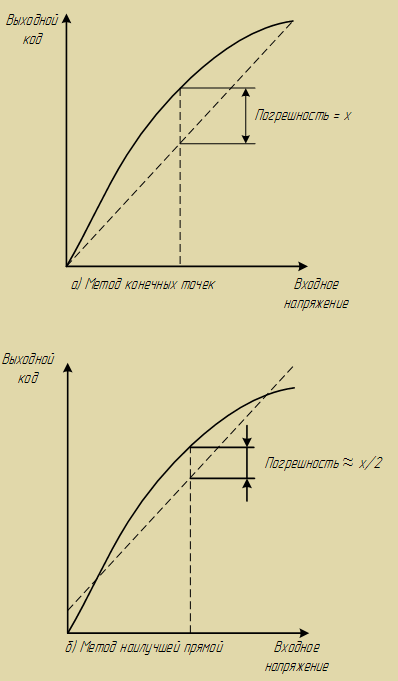
Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии. В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов). Существует два общих метода аппроксимации характеристики передачи: метод конечных точек и метод наилучшей прямой.
Рисунок 5.3 – Определение погрешности измерения по а) методу конечных точек и по б) методу наилучшей прямой
При использовании метода конечных точек измеряется отклонение произвольной точки характеристики от прямой, проведенной из начала координат. Таким образом, измеряют значения интегральной нелинейности преобразователей, используемых в задачах измерения и управления.
Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока. Он менее чувствителен к нелинейностям технических характеристик. По методу наилучшего приближения через характеристику передачи устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой. Как правило, интегральная нелинейность, измеренная таким образом, учитывает только 50% нелинейности, оцененной методом конечных точек.
Другой тип нелинейности преобразователей – дифференциальная нелинейность. Она связана с нелинейностью кодовых переходов преобразователя. В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В АЦП, при переходе с одного цифрового уровня на следующий, значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы. Наиболее распространенным проявлением DNL в АЦП являются пропущенные коды.
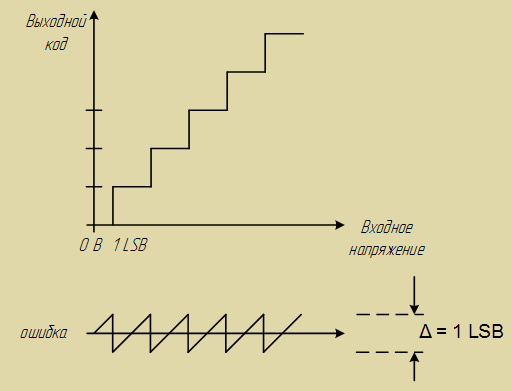
Переходы АЦП (идеальные) имеют место, начиная с 1/2 LSB выше нуля, и далее через каждый LSB, до 11/2 LSB ниже полной аналоговой шкалы. Так как входной аналоговый сигнал АЦП может иметь любое значение, а выходной цифровой сигнал квантуется, может существовать различие до 1/2 LSB между реальным входным аналоговым сигналом и точным значением выходного цифрового сигнала. Этот эффект известен как ошибка или неопределенность квантования. В приложениях, использующих сигналы переменного тока, эта ошибка квантования вызывает явление, называемое шумом квантования.
Рисунок 5.4 – Шум квантования АЦП
Среднеквадратичное значение шума. приблизительно равно весу наименьшего значащего разряда (LSB) Δ, деленному на √12. При этом предполагается, что амплитуда сигнала составляет, по крайней мере, несколько младших разрядов, так что выход АЦП изменяет свое состояние почти при каждом отсчете. Сигнал ошибки квантования от входного линейного пилообразного сигнала аппроксимируется сигналом пилообразной формы с максимальным размахом Δ , и его среднеквадратичное значение равно Δ/( √12). Поэтому средняя мощность шума кантования равна:
Отношение среднеквадратичного значения синусоидального сигнала, соответствующего полной шкале, к среднеквадратичному значению шума квантования (выраженное в дБ) равно:
где SNR (signal to noise ratio) – отношение сигнал-шум, N — число разрядов в идеальном АЦП. Это уравнение имеет силу только в том случае, если шум измерен на полной ширине полосы Найквиста от 0 до fД/2.
Таким образом, для АЦП микроконвертора ADUC842, используемого в лабораторном стенде LESO1, справедливо:
Для оценки погрешностей АЦП приведем характеристику АЦП, где указаны погрешности в значениях LSB и в напряжениях.
Таблица 5.1 – Характеристики АЦП ADuc842
| Параметры | Значение в LSB | Значение в мкВ | Примечание | |
| Точность по постоянному току | Разрядность | 12 битный | От внутреннего ИОН Uоп = 2,5 В | |
| Интегральная нелинейность | ±1 макс. ±0,3 сред. |
±610 макс. ±183 сред. |
||
| Дифференциальная нелинейность | ±1 макс. ±0,3 сред. |
±610 макс. ±183 макс. |
||
| Калибровочные ошибки конечных точек шкалы | Ошибка смещения | ±3 макс | ±1830 макс. | |
| Ошибка усиления | ±3 макс. | ±1830 макс. | ||
| Аналоговый вход | Диапазон входных напряжений | 0 ÷ Uоп В. | ||
| Входной ток | ±1 мкА макс. | |||
| Входная емкость | 32 пФ сред. |
Так как интегральная и дифференциальная нелинейности относятся к случайным ошибкам и являются независимыми друг от друга ошибками их необходимо сложить по «закону сложения независимых случайных ошибок»:
где X1,…,Xn – номинальные значения независимых случайных величин, ΔX1,…,ΔXn – ошибки случайных величин, Y — номинальное значение конечной измеряемой величины, ΔY – абсолютная ошибка конечной измеряемой величины.
Случайная ошибка АЦП будет состоять из интегральной и дифференциальной нелинейности, а также из ошибки квантования, которая составляет Δ/2 = 610мкВ/2 = 305мкВ = 0,305·10-3 В. Номинальное значения этих величин есть опорное напряжение АЦП, которое равно 2,5В.
Итак, относительная ошибка измерения АЦП:
Из относительной ошибки измерения АЦП найдем абсолютное значение ошибки измерения:
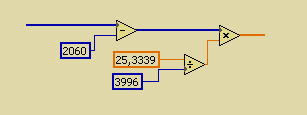
Систематическую ошибку составляют ошибка смещения нуля и ошибка усиления. Так как основную часть ошибки смещения и ошибки усиления вносит тракт передачи сигнала (инструментальный усилитель и масштабирующее звено), поправки вносятся программной калибровкой в LabVIEW.
Рисунок 5.5 – Калибровка в LabVIEW
5.3 Экспериментальные исследования
В задачу каждого измерения входит оценка точности полученного результата. Но в результате измерении мы всегда получаем нужную величину с некоторой погрешностью.Смысл экспериментальных исследований состоит в том, чтобы проверить на опыте теоретические выкладки и дать оценку характеристикам прибора.
Результат экспериментального исследования АЧХ устройства без цифрового фильтра или аналогового фильтра Бесселя записан в таблице 5.2. Экспериментальные данные были сняты с помощью низкочастотного генератора сигналов Г3-112.
Таблица 5.2 – Измеренное АЧХ устройства без цифрового фильтра
 |
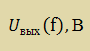 |
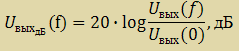 |
| 0 | 5,00 | 0,00 |
| 10 | 5,00 | 0,00 |
| 20 | 4,88 | -0,21 |
| 30 | 4,68 | -0,58 |
| 40 | 4,31 | -1,28 |
| 50 | 3,95 | -2,04 |
| 60 | 3,43 | -3,28 |
| 70 | 2,90 | -4,72 |
| 80 | 2,34 | -6,60 |
| 90 | 1,77 | -8,99 |
| 100 | 1,24 | -12,10 |
| 110 | 0,94 | -14,56 |
| 120 | 0,64 | -17,90 |
| 130 | 0,43 | -21,36 |
| 140 | 0,26 | -25,75 |
| 150 | 0,18 | -29,00 |
| 160 | 0,13 | -31,77 |
Проверим, действие цифрового фильтра на сигнал. Результаты измерения АЧХ после цифрового фильтра приведены в таблице 5.3.
Таблица 5.2 – Измеренное АЧХ устройства без цифрового фильтра
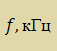 |
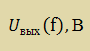 |
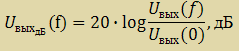 |
| 0 | 5,00 | 0,00 |
| 10 | 5,00 | 0,00 |
| 20 | 5,00 | 0,00 |
| 30 | 5,00 | 0,00 |
| 40 | 5,00 | 0,00 |
| 50 | 5,00 | 0,00 |
| 60 | 4,80 | -0,36 |
| 70 | 4,23 | -1,45 |
| 80 | 3,67 | -2,69 |
| 90 | 2,94 | -4,62 |
| 100 | 2,26 | -6,91 |
| 110 | 1,61 | -9,83 |
| 120 | 0,73 | -16,67 |
| 130 | 0,23 | -26,60 |
| 140 | 0,08 | -35,85 |
| 150 | 0,00 | -60,32 |
| 160 | 0,00 | -71,66 |
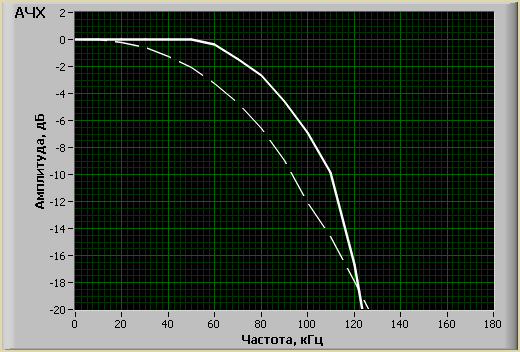
Для сравнения действия цифрового фильтра, приведем графики АЧХ устройства без и с цифровым фильтром. Как видно из рисунка 6.6, цифровой фильтр выравнивает амплитудную неравномерность. Полоса пропускания цифрового осциллографа-приставки на уровне -3 дБ, равна от 0 до 80 кГц.
Рисунок 5.6 – АЧХ устройства без цифрового фильтр (штрих.) и с цифровым фильтром (сплош.)
Нелинейные искажения измерительного тракта можно оценить по первой гармонике. Уровень первой гармоники при номинальном входном напряжении Uвх = 5В на частоте 10 кГц равен -65дБ.
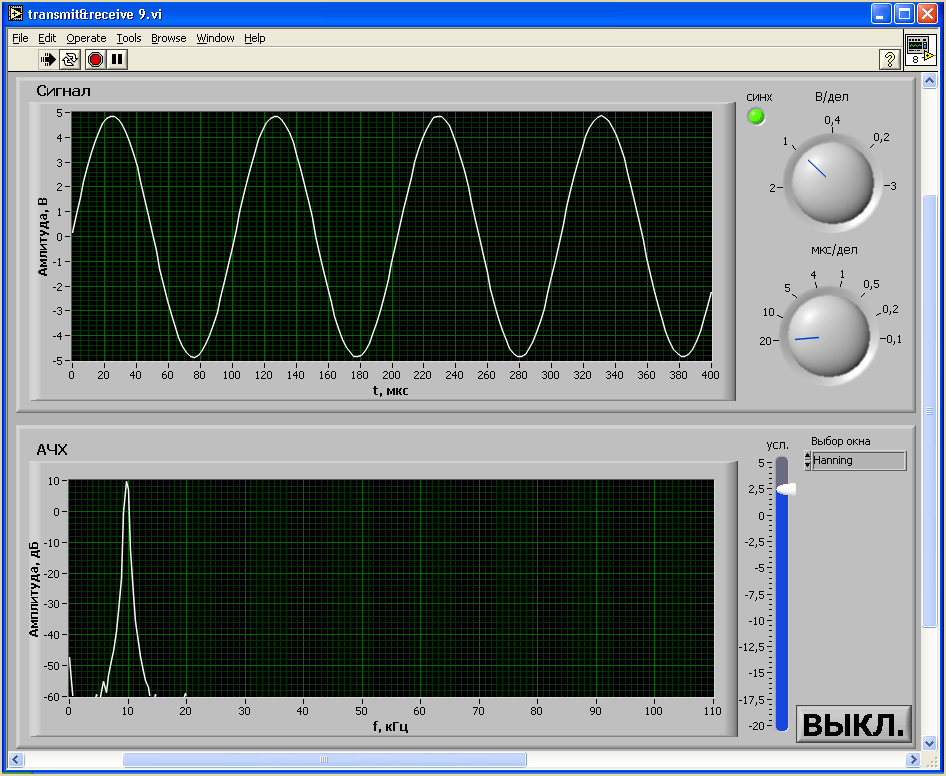
Рисунок 5.7 — Уровень первой гармоники при номинальном входном напряжении 5В
На цифровой осциллограф-приставку подавались тестовые испытательные сигналы трех видов: синусоидального, треугольного и прямоугольного частотой 10 кГц. Результаты измерений приведены на рисунках 5.8, 5.9 и 5.10 соответственно синусоидального, треугольного и прямоугольного сигналов.
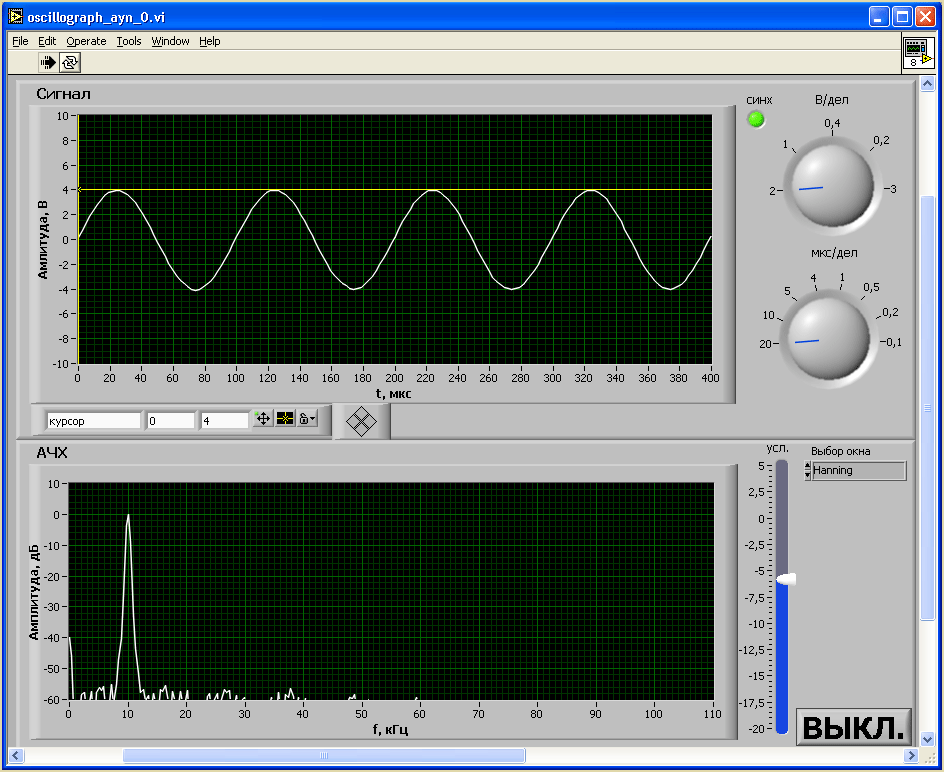
Рисунок 5.8 — Измерение синусоидального сигнала цифровым осциллографом-приставкой
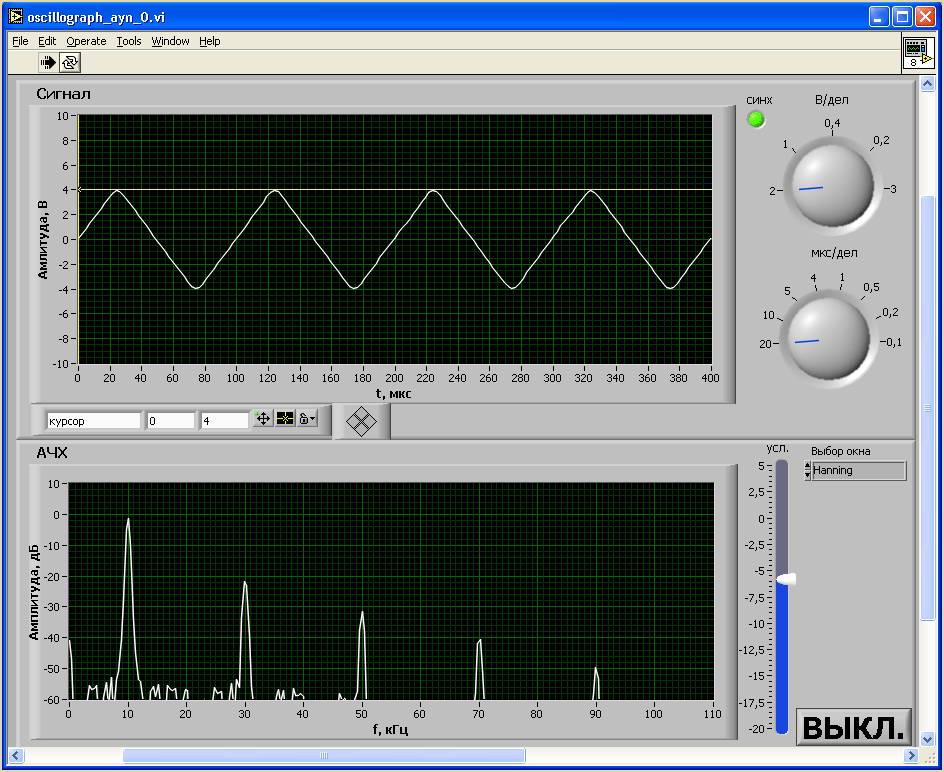
Рисунок 5.9 — Измерение треугольного сигнала цифровым осциллографом-приставкой

Рисунок 5.10 — Измерение прямоугольного сигнала цифровым осциллографом-приставкой
5.4 Выводы
Проанализированы основные источники погрешности измерений, определено из чего состоит ошибка измерения цифровым осциллографом-приставкой. Она состоит в из случайной и систематической ошибок. Случайная ошибка АЦП менее 0,1 %, а систематическая корректируется программной калибровкой в LabVIEW.
На рисунке 5.6 показано, насколько цифровой фильтр корректирует АЧХ аналогового фильтра.
Экспериментальные исследования тестовыми сигналами показывают, что уровень первой гармоники при номинальном входном напряжении Uвх = 5В на частоте 10 кГц равен -65дБ, что очень хорошо.
5.1. Преобразование аналогового сигнала в цифровую форму
5.2. Цифро-аналоговые преобразователи (ЦАП)
5.3. Типовые схемы АЦП
5.4. Интеллектуальные датчики
5.1. Преобразование аналогового сигнала в цифровую форму
В настоящее время в большинстве случаев датчики являются элементами цифровых систем управления, что требует преобразования сигнала датчиков в цифровую форму, при вводе в контроллер и иногда обратного преобразования цифрового управляющего сигнала контроллера в аналоговую форму при выводе на исполнительное устройство. Аналого-цифровое преобразование (АЦП, ADC) содержит 3 фазы: дискретизацию по времени, квантование по уровню, цифровое, двоичное кодирование.
а) При дискретизации по времени из непрерывного сигнала x(t) формируется последовательность отсчетов y(Ti). В случае равномерной дискретизации . Возможность восстановления исходного сигнала по отсчетам определена теоремой Котельникова, по которой между частотой квантования и максимальной частотой спектра сигнала, которую надо учитывать, должно выполняться соотношение.
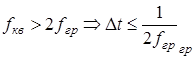
Для упрощения построения АЦП обычно выбирают . Рис. 48.
Рис. 48. Аналого-цифровое преобразование
b) Квантование по уровню состоит в округлении значения отсчета до ближайшего уровня квантования. Весь диапазон значений измеряемой величины от до
разбивается на равные интервалы. Действительные значения воспроизводятся с помощью дискретных, отличающихся на
. Процесс перехода от непрерывных значений в дискретные называется квантованием.
— шаг квантования. Шаг выбирается в пределах допускаемой погрешности измерения. Времени
соответствует значение
, и т.д. Величина
— единицы измерения. Это равномерная шкала квантования, реже используются другие, например, логарифмические или специальные: A, l.. При квантовании возникает задержка нулевого уровня, которую надо учитывать при оценке динамических характеристик системы:
.
c) Отсчеты кодируются в двоичном или двоично-десятичном коде. Для цифрового кодирования необходимо в каждый дискретный момент времени воспроизвести в цифровой форме значения, заменившее непрерывную измеряемую величину. Для этого дискретные значения представляют в виде последовательности цифровых кодов. Например, Х0 – 001, Х1 – 101, Х2 – 111 и т. д.
Преимущества цифровой формы, кроме непосредственной обработки контроллером:
1) большая помехоустойчивость;
2) простота передачи на расстояние;
Аналого-цифровое преобразование приводит к образованию двух видов ошибок: это ошибки метода и приборные ошибки.
Ошибки метода:
1. Задержка нулевого уровня
.
2. Ошибка квантования
. При N-разрядном коде
, где S – диапазон входной величины.
Приборные ошибки АЦП.
1. Нелинейность характеристики; дрейф нуля, дребезг младшего разряда.
2. Динамические ошибки при переходном процессе, конечное время преобразования.
3. Ложные частоты.
5.2. Цифро-аналоговые преобразователи (ЦАП)
ЦАП служат для преобразования информации из цифровой формы в аналоговый сигнал. ЦАП широко применяется в различных устройствах автоматики для связи контроллеров, вырабатывающих сигналы управления в виде цифрового кода, с аналоговыми элементами системы.
Принцип работы ЦАП состоит в суммировании аналоговых сигналов, пропорциональных весам разрядов входного цифрового кода, с коэффициентами, равными нулю или единице в зависимости от значения соответствующего разряда кода.
ЦАП преобразует цифровой двоичный код а0, а1, а2, .. ап-1 в аналоговую величину, обычно напряжение Uвых.. Каждый разряд двоичного кода имеет определенный вес i-го разряда вдвое больше, чем вес (i-1)-го. Работу ЦАП можно описать следующей формулой:
,
где e = — напряжение, соответствующее весу младшего разряда, аi — значение i -го разряда двоичного кода (0 или 1).
Например, числу 1001 соответствует: Uвых=e*(0*1+0*2+1*4+1*8)=12*e.
Точность преобразования: ,и для
.
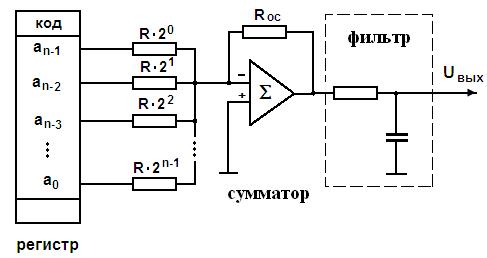
Выбором е можно установить требуемый масштаб аналоговой величины. На рисунке 49 приведена схема цифро-аналогового преобразователя.
Рис. 49. Схема цифро-аналогового преобразователя
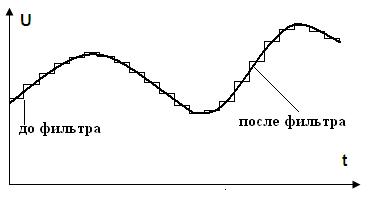
В регистр записывается двоичный код выходного сигнала, на выходе сумматора формируется аналоговый эквивалентный сигнал. Этот сигнал имеет ступенчатую форму (рис. 50) и для его сглаживания нужен фильтр низкой частоты.
Рис. 50. Сигналы на выходе сумматора и фильтра
5.3. Типовые схемы АЦП
Существуют различные типы АЦП. Мы остановимся лишь на тех типах, которые получили в настоящее время наибольшее распространение.
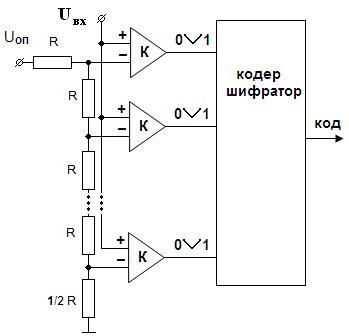
АЦП параллельного типа является самым быстродействующим. У него существенно меньше, чем у других АЦП время преобразования (tпр). Структурная схема АЦП параллельного типа приведена на рис. 51.
Рис. 51. Схема АЦП параллельного типа
Здесь входная аналоговая величина Uвх с выхода схемы ВХ сравнивается с помощью 2n+1 – 1 компараторов с 2(2n-1) эталонными уровнями, образованными делителем из резисторов равного сопротивления. На вход делителя подается стабилизированное опорное напряжение Uоп. При этом срабатывают те (m) младших компараторов, на входе которых уровень сигнала выше эталонного уровня. На выходах этих компараторов образуется единичный код, на выходе остальных (n-m) нулевой код. Код с выхода компараторов затем с помощью специального кодера-дешифратора преобразуется в двоично-кодированный выходной сигнал.
Погрешность АЦПП определяется неточностью и нестабильностью эталонного напряжения, резистивного делителя и погрешностями компараторов. Значительную роль могут играть входные токи компараторов, если делитель недостаточно низкоомный. Основной недостаток требуется набор прецизионных сопротивлений.
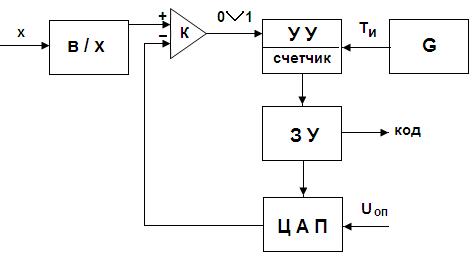
АЦП последовательного приближения является наиболее распространенным. Существует много различных вариантов схемы такого АЦП. Структурная схема АЦППП со счетчиком приведена на рисунке 52. Схема работает следующим образом. Входной аналоговый сигнал Х перед началом преобразования запоминается схемой выборки – хранения (В/Х), что необходимо, так как в процессе преобразования необходимо фиксировать значение аналогового сигнала. Сигнал с выхода схемы выборки – хранения подается на один из входов компаратора, на второй вход которого подается сигнал с выхода ЦАП. Состояние ЦАП определяется кодом, хранящимся в запоминающем устройстве (ЗУ), а этот код соответствует в свою очередь состоянию счетчика, входящего в состав устройства управления (УУ).
В начальный момент времени счетчик обнулен, на выходе ЦАП нулевой сигнал, на выходе компаратора сигнал логической единицы.
Рис. 52. Схема АЦП последовательного приближения
Далее по команде “Пуск” с генератора G на счетчик подаются тактовые счетные импульсы; код на выходе счетчик последовательно увеличивается; соответственно увеличивается напряжение на выходе ЦАП. Как только оно сравнивается с входным аналоговым сигналом, срабатывает компаратор, процесс счета останавливается и на выходе ЗУ формируется двоичный цифровой код, соответствующий входному аналоговому сигналу.
Погрешность АЦП определяется разрядностью АЦП, неточностью ЦАП, зоной нечувствительности и т. д.
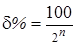
На входе АЦП тоже включают аналоговый фильтр нижних частот, для уменьшения помех, после АЦП. В системах управления обязательно используют цифровой фильтр для усреднения сигнала, устранения влияния помех и субчастот.
5.4. Интеллектуальные датчики
В настоящее время все чаще применяют «интеллектуальные датчики». Интеллектуальный датчик имеет встроенный микропроцессор, выполняющий некоторую обработку сигнала, и поэтому может давать более точные показания благодаря применению числовых вычислений для компенсации нелинейностей чувствительного элемента или температурной зависимости. В круг возможностей некоторых приборов входит измерение нескольких параметров и пересчет их в одно измерение (например, объемный расход, температуру и давление – в массовый расход, т.н. многопараметрические датчики), функции встроенной диагностики, автоматическая калибровка.
Некоторые интеллектуальные приборы (например, семейство приборов Rosemount SMART FAMILY) позволяют посылать в канал передачи аналоговый сигнал, и цифровой. В случае одновременной трансляции обоих видов сигналов, аналоговый используется для трансляции значения измеренного параметра, а цифровой – для функций настройки, калибровки, а также позволяет считывать измеряемый параметр. d = 0,075%. Эти устройства обеспечивают преимущества цифровой связи и, в то же время, сохраняют совместимость и надежность аналоговых средств, которые требуются для существующих систем.
Считывание измеряемого параметра в цифровой форме повышает точность за счет ограничений операций цифро-аналогового и аналого-цифрового преобразований сигнала 4..20 мА. Но цифровой способ измерения вносит задержку в измерения (время, затраченное на последовательную передачу информационной посылки), которая может быть неприемлема для управления быстродействующими контурами.
Цифровой датчик позволяет хранить последовательную информацию о процессе (тэг, описатель позиции измерения, диапазон калибровки, единицы измерения), записи о процедурах его обслуживания и т.п., считываемой по запросу. Многопараметрические приборы содержат базу данных по физическим свойствам измеряемых жидкостей и газов. Для сильно распределенных объектов интеллектуальному датчику нет альтернативы. благодаря встроенному интерфейсу с промышленной локальной сетью.
В класс интеллектуальных цифровых устройств входят и специализированные микросхемы, например контроллеры для работы с термопарами.
Фирма Analog Device выпускает AD596/AD597 – монолитные контроллеры, оптимизированные для использования в условиях любых температур в различных случаях. В них осуществляется компенсация напряжения холодного спая и усиление сигналов с J- и К-термопары таким образом, чтобы получить сигнал, пропорциональный температуре. Схемы могут быть подстроены так, чтобы обеспечить выходное напряжение 10 мВ/°С непосредственно от термопар типа J или К. Каждый из чипов размещен в металлическом корпусе с десятью выводами и настроен на работу при температуре окружающей среды от 25°С до 100°С.
AD596 усиливает сигналы термопары, работающей в температурном диапазоне от 200°С до +760°С, рекомендованном для термопар типа J, в то время как AD597 работает в диапазоне от -200°С до +1250°С (диапазон термопар типа К). Усилители откалиброваны с точностью ±4°С при температуре окружающей среды 60°С и характеризуются температурной стабильностью 0,05°С/°С при изменении температуры окружающей среды в пределах от 25°С до 100°С.
Все вышеописанные усилители не в состоянии компенсировать нелинейность термопары: они способны лишь корректировать и усиливать сигнал с термопарного выхода. АЦП с высокой разрешающей способностью, входящие в семейство AD77xx, могут использоваться для прямой оцифровки сигнала с выхода термопары, без предварительного усиления. Преобразование и линеаризацию осуществляет микроконтроллер. Два мультиплексируемых входа АЦП используются для прямой оцифровки сигнала с термопары и с теплового датчика, находящегося в контакте с ее холодным спаем. Вход PGA (программируемого усилителя) программируется на усиление от 1 до 128, и разрешающая способность АЦП лежит в пределах от 16 до 22 бит в зависимости от того, какая из микросхем выбрана пользователем. Микроконтроллер осуществляет как компенсацию напряжения холодного спая, так и линеаризацию характеристики.

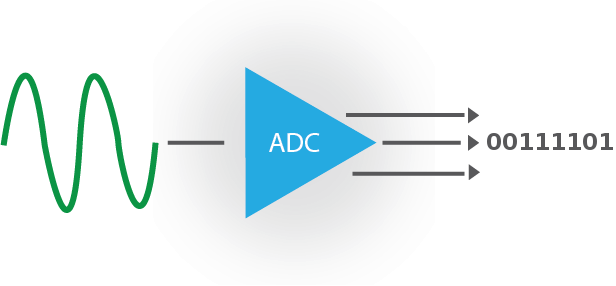
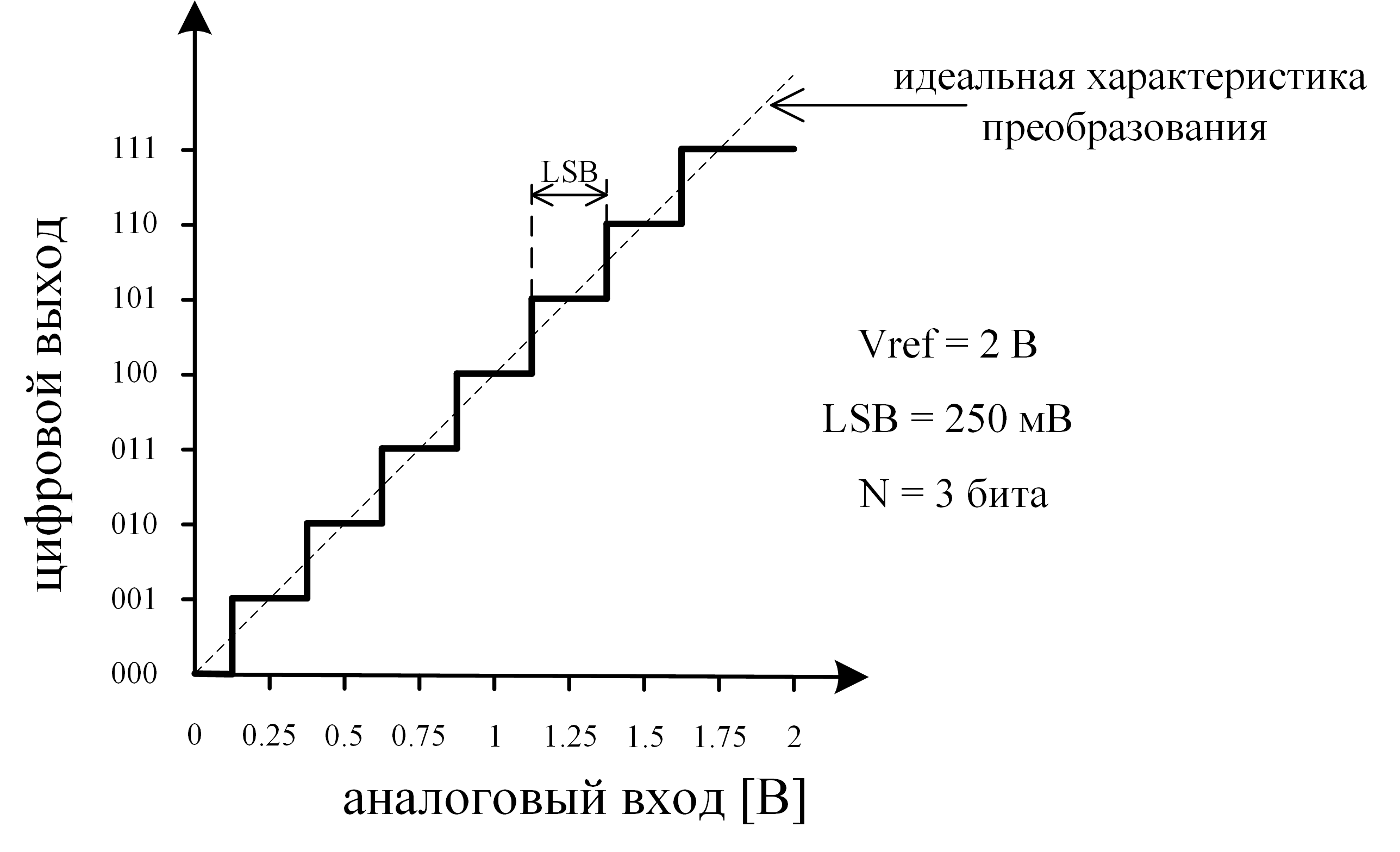
 Рис. 2: Ошибка смещения
Рис. 2: Ошибка смещения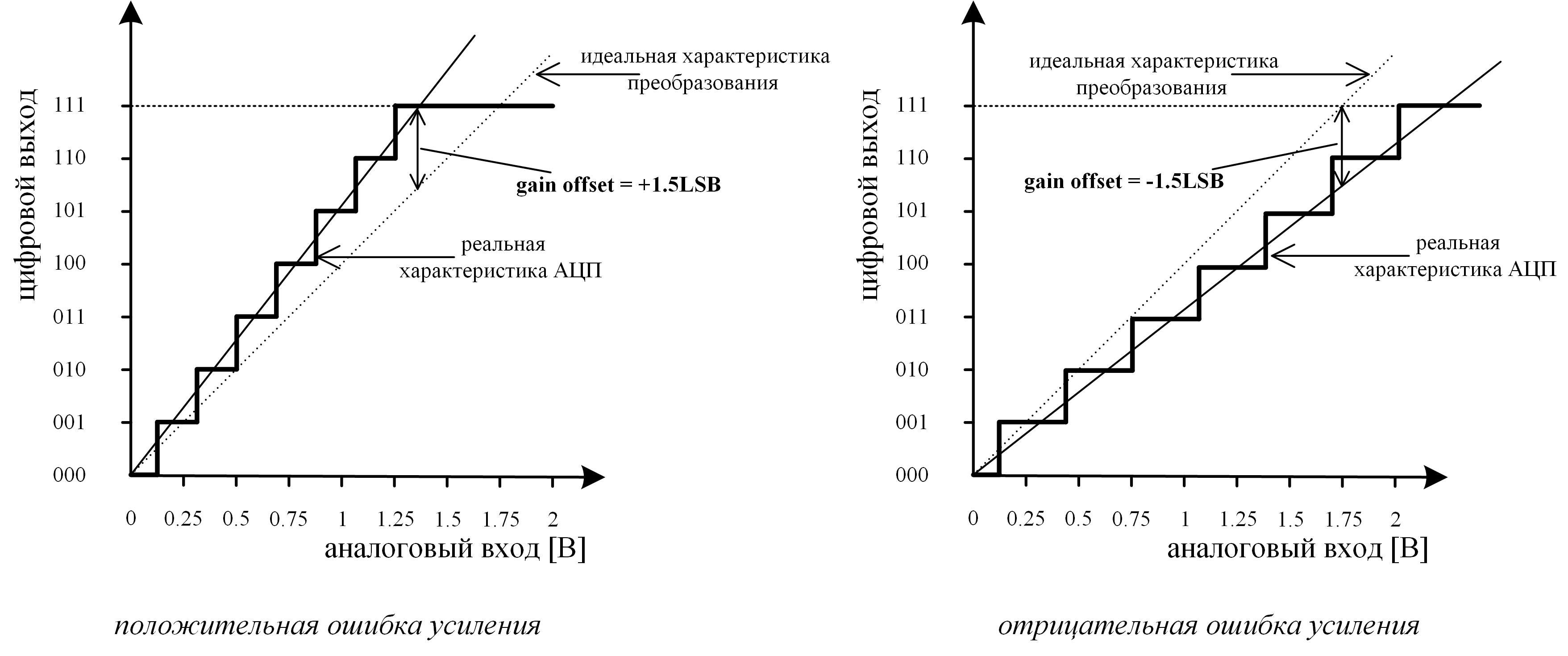 Рис. 3: Ошибка усиления
Рис. 3: Ошибка усиления