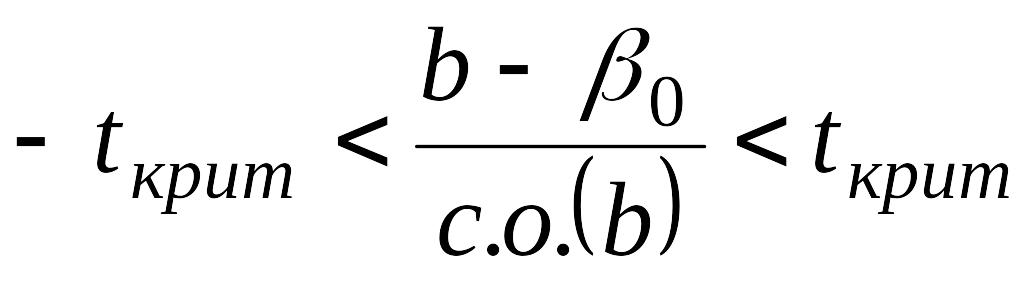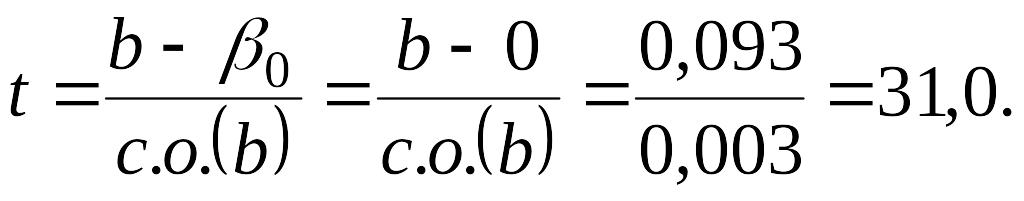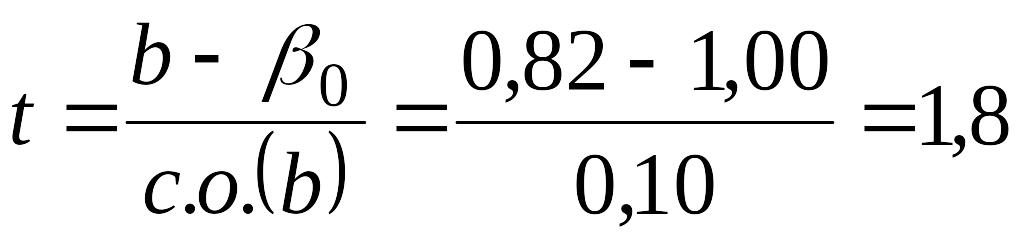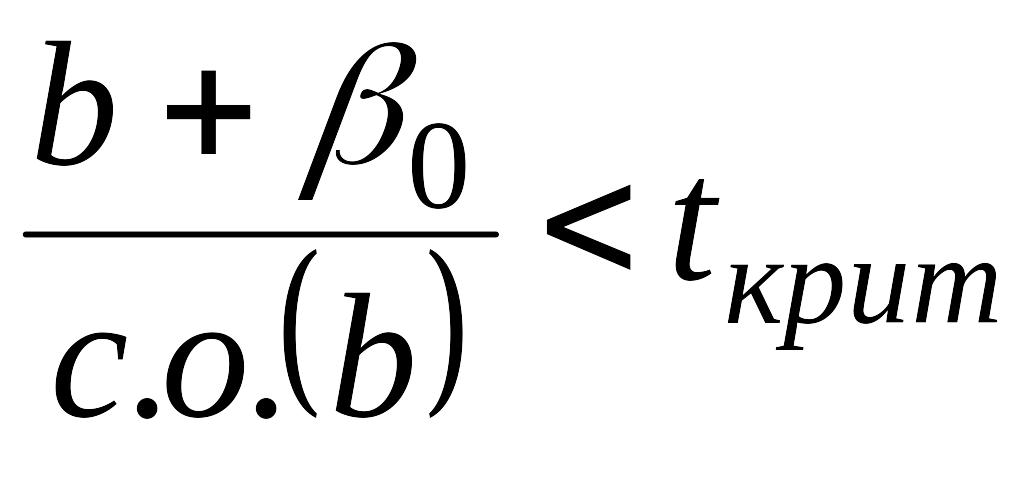Можно задаться
вопросом: почему исследователи обычно
представляют свои результаты при уровнях
значимости в 5 и 1%? Почему недостаточно
ограничиться только одним уровнем?
Причина заключается в том, что обычно
делается попытка найти баланс между
риском допущения ошибок I и II рода.
Ошибка
1 рода —
ситуация, когда оценка параметра не
попала в область принятия нулевой
гипотезы, нулевая гипотеза была
отвергнута, а она была истинной.
Ошибка
II рода —
ситуация, когда не отвергнута ложная
гипотеза.
Ошибки 1 и II
рода в повседневной жизни
Проблема, как
избежать ошибок 1 и II рода, известна
всем. Типичным примером этого является
расследование уголовного преступления.
Если за нулевую гипотезу принять вариант,
что подсудимый невиновен, то ошибка 1
рода происходит, когда суд присяжных
признает его виновным. Ошибка II рода
имеет место в том случае, когда суд
присяжных ошибочно оправдывает виновного
подсудимого.
Вполне очевидно,
что чем ниже критическая вероятность,
тем меньше риск получения ошибок 1 рода.
Если вы используете уровень значимости,
равный 5%, то вы отвергнете истинную
гипотезу в 5% случаев. Если уровень
значимости составляет 1%, вы совершите
ошибку I рода в 1% случаев. Таким образом,
в этом отношении однопроцентный уровень
значимости более надежен. Если вы
отвергли гипотезу на данном уровне, вы
почти наверняка были вправе сделать
это. Именно по этой причине однопроцентный
уровень значимости описывается как
«более высокий» в сравнении с 5%-ным
уровнем.
В то же время если
нулевая гипотеза ложна, то чем выше
уровень значимости, тем шире область
принятия гипотезы, тем выше вероятность
того, что вы не отвергнете ее, и тем выше
риск допущения ошибки II рода. Таким
образом, вы оказываетесь перед дилеммой.
Если вы будете стаивать на очень высоком
уровне значимости, то столкнетесь с
относительно высоким риском допущения
ошибки II рода, когда гипотеза окажется
ложной. Если вы выбираете низкий уровень
значимости, то оказываетесь перед
относительно высоким риском допущения
ошибки I рода, если гипотеза истинна.
Один
из способов сопоставления ущерба от
ошибок разного рода извести функцию
цены ошибки. Цена
ошибки —
численное выражение ущерба от ошибки,
величина «штрафа» за ошибку. Функция
цены — функция,
где аргументом является род ошибки, а
значением функции цена ошибки.
Большинство
людей выбирают достаточно простую форму
обеспечения гарантий и осуществляют
проверку на обоих уровнях значимости,
представляя результаты каждой такой
проверки. На самом деле часто нет
необходимости непосредственно ссылаться
на оба результата. Так как величина
должна быть более «экстремальной»
для гипотезы, отвергаемой при 1%-ном
уровне значимости, но не при 5%-м, и если
вы отклоняете ее при однопроцентном
уровне, то из этого автоматически
следует, что вы отклоните ее, а при уровне
значимости в 5%, и нет необходимости
упоминать об этом. Если же вы не отвергаете
гипотезу при уровне значимости в 5%, то
из этого автоматически следует, что вы
не отвергнете ее и при однопроцентном
уровне значимости, и вновь нет смысла
об этом говорить. Только в одном случае
вы должны представить оба результата:
если гипотеза отвергается на 5%-ном, но
не на 1%-ном уровне значимости.
До
сих пор мы считали, что стандартное
отклонение величины
известно. Однако на практике это допущение
нереально. Это можно показать на примере
стандартной ошибки для величины
,
взятой из уравнения (3.31). Это приводит
к двум изменениям процедуры проверки
гипотез. Во-первых, величина
определяется на основе использования
стандартной ошибки
вместо стандартного отклонения
.
Для испытания нулевой гипотезы
с помощью теста Стьюдента надо составить
t-статистику:
(4.8)
t
-тест (тест Стьюдента)
— проверка гипотезы
о значении коэффициента
с помощью распределения Стьюдента. Чаще
всего проверяют значимость коэффициента
— гипотезу
.
Во-вторых,
критические уровни t определяются
величиной, имеющей так называемое
t-распределение
вместо нормального распределения. Мы
не будем вдаваться в причины этого или
даже описывать t-распределение
математически. Достаточно будет сказать,
что оно родственно нормальному
распределению, а его точная форма зависит
от числа степеней свободы в регрессии,
и оно все лучше аппроксимируется
нормальным распределением по мере
увеличения числа степеней свободы.
Оценивание
каждого параметра в уравнении регрессии
поглощает одну степень свободы в выборке.
(Число степеней
свободы —
натуральное число, характеристика таких
законов распределения, как распределение
Стьюдента, распределение Фишера и
некоторых других.) Отсюда число степеней
свободы для t-статистики равно числу
наблюдений в выборке минус количество
оцениваемых коэффициентов. Для парной
регрессии, при которой оцениваются два
параметра, число степеней свободы равно
.
Критическое
значение теста
при р-процентном уровне значимости —
граничное значение области принятия
гипотезы, проверяемой тестом, ср-процентной
вероятностью совершить ошибку I рода.
При попадании оценки в критическое
значение сохраняется неопределенность
в отношении гипотезы.
Если в тесте
Стьюдента значение t-статистики попало
между критическими значениями
распределения Стьюдента, соответствующими
уровню значимости р%, то мы не отвергаем
нулевую гипотезу. В противном случае
нулевая гипотеза отвергается с
вероятностью допущения ошибки I рода в
р%.
Критическое
значение
,
которое мы обозначим как
,
заменит число 1,96 в уравнении (3.39). Таким
образом, условие того, что оценка
регрессии не должна приводить к отказу
от нулевой гипотезы
,
будет следующим:
.
(4.9)
Рассмотрим
примеры:
В разделе 2.3 функция
расходов на питание оценивалась как
зависимость от личного располагаемого
дохода на основании совокупных ежегодных
данных для США за 25-летний срок (1959-1983
гг.) и уравнение регрессии было представлено
формулой (2.22)
Цифры, указанные
в скобках, являются стандартными
ошибками.
Предположим,
что одна из задач оценивания регрессии
состояла Подтверждении догадки о том,
что уровень расходов на питание зависит
от размера дохода. Соответственно, мы
формулируем нулевую гипотезу о том, что
величина
равняется нулю, и затем пытаемся
опровергнуть ее. Соответствующая
t-статистика, вычисленная по формуле
(4.8), есть оценка коэффициента, деленная
на ее стандартную ошибку:
(4.10)
Так
как в выборку включено 25 наблюдений и
мы оценили два параметра, то число
степеней свободы составляет 23. Критическое
значение для
при 5%-ном уровне значимости с 23 степенями
свободы равняется 2,069. Причем t-статистика
не лежит между значениями 2,069 —2,069.
Следовательно, неравенство (4.9) не
выполняется и мы отвергаем нулевую
гипотезу, сделав вывод о том, что величина
в действительности отличается от нуля
и, следовательно, размер дохода влияет
на уровень расходов на питание.
Если этот критерий
описать словами, то верхний и нижний
2,5%-е «хвосты» t -распределения
начинаются со стандартного отклонения
2,069 вверх и вниз от его математического
ожидания, равного нулю. Коэффициент
регрессии, который по оценкам находится
в пределах 2,069 стандартного отклонения
от гипотетического значения, не приводит
к отказу от последнего. В рассматриваемом
случае расхождение будет эквивалентно
31,0 стандартного отклонения, и мы приходим
к выводу о том, что результат оценивания
регрессии противоречит нулевой гипотезе.
Конечно,
в том, что мы используем уровень значимости
в 5% в качестве основы для проверки
гипотезы, существует 5%-ный риск допущения
ошибки I рода. В этом случае мы могли бы
снизить риск до 1% за счет применения
уровня значимости в 1%. Критическое
значение для
при однопроцентном уровне значимости
с 23 степенями свободы составляет 2,807.
Используя это число в соотношении (4.9),
мы видим, что можно легко отказаться от
нулевой гипотезы также и при этом уровне
значимости.
Процедура
установления взаимосвязи между зависимой
и объясняющей переменными путем
формулирования, а затем отклонения
нулевой гипотезы о том, что
,
используется очень часто.
Соответственно,
большая часть, если не все программы
регрессии, автоматически выводят
t-статистику для этого специального
случая; иными словами, коэффициент
делится на его стандартную ошибку.
Данное отношение часто обозначается
как «t-статистика».
Если,
однако, нулевая гипотеза определяет
некоторое ненулевое значение величины
,
то необходимо использовать более общее
выражение, (3.43), а t-статистика вычисляется
вручную. Например, вновь рассмотрим
модель регрессии между общей инфляцией
и инфляцией, вызванной ростом заработной
платы (3.34), и предположим, что выбранное
уравнение регрессии оказалось следующим
(в скобках указаны стандартные ошибки):
.
(4.11)
Если
теперь исследовать гипотезу о том, что
общая инфляция в долгосрочном периоде
будет равна инфляции, вызванной ростом
заработной платы, то нулевая гипотеза
будет состоять в том, что коэффициент
при
равен 1,0. Соответствующая t-статистика
примет вид
.
Если в выборке
содержится, скажем, 20 наблюдений, то
число степеней свободы составит 18, а
критическое значение для t при 5%-ном
уровне значимости будет 2,101. В этом
случае t-статистика лежит между 2,101 и
-2,101, поэтому мы не отвергаем нулевую
гипотезу. Оценка, равная 0,82, лежит ниже
нашего гипотетического значения 1,00, но
не настолько ниже, чтобы исключить
возможность правильности нулевой
гипотезы.
До
сих пор мы предполагали, что гипотеза
предшествует эмпирическим исследованиям.
Однако это необязательно. Очень часто
гипотеза и эксперимент взаимодействуют,
в этом отношении типичным примером
является регрессия расходов на питание.
Вначале мы оцениваем регрессию, потому
что в соответствии с экономической
теорией ожидаем, что размер дохода
влияет на уровень расходов на питание.
Результат оценивания регрессии подтвердил
это интуитивное ожидание в том смысле,
что мы отвергли нулевую гипотезу
.
Но после этого возникло ощущение
некоторой пустоты, поскольку на основе
I гипотезы нельзя выдвинуть предположения
о том, что значение
равняется некоторому конкретному числу.
Теперь, однако, мы можем двинуться в
противоположном направлении и задаться
вопросом о том, какие гипотезы совместимы
с результатом оценивания регрессии.
Вполне
очевидно, что гипотеза о том, что
=0,093,
будет совместимой, так как гипотеза и
результаты эксперимента совпадают.
Кроме того, совместимыми будут и гипотезы
о том, что
=0,09229
и
=0,09301,
так как разница между гипотезой и
результатом эксперимента будет небольшой.
Вопрос в том, насколько сильно
гипотетическое значение может отличаться
от результата эксперимента, прежде чем
они станут несовместимыми, и мы должны
будем отклонить нулевую гипотезу.
Можно
ответить на этот вопрос, используя
предшествующие Суждения. Из уравнения
(4.9) видно, что коэффициент регрессии
и гипотетическое значение
будут несовместимыми, если выполняются
условия:
или
.
(4.12)
т.е. если
или
.
(4.14)
Отсюда
следует, что гипотетическое значение
является совместимым с результатом
оценивания регрессии, если одновременно
выполнены условия:
или
(4.15)
т. е. если величина
Р удовлетворяет двойному неравенству:
.
(4.16)
Любое
гипотетическое значение
,
которое удовлетворяет соотношению
(4.16), будет автоматически совместимо с
оценкой
,
иными словами, не будет опровергаться
ею. Множество всех этих значений,
определенных как интервал между нижней
и верхней границами неравенства, известно
как доверительный интервал для величины
.
Отметим,
что посредине доверительного интервала
лежит сама величина
.
Границы интервала одинаково отстоят
от
.
Отметим также, что, так как значение
зависит от выбора уровня значимости,
границы будут также зависеть от этого
выбора. Если принимается 5%-ный уровень
значимости, то соответствующим
доверительным интервалом считается
95%-ный интервал. Если выбирается
однопроцентный уровень, то получают
доверительный интервал в 99% и т.д.
Таким
образом, можно определить доверительный
интервал
как интервал с центром в полученной
оценке параметра, который содержит
истинное значение параметра с доверительной
вероятностью.
Проверка корректности А/Б тестов
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
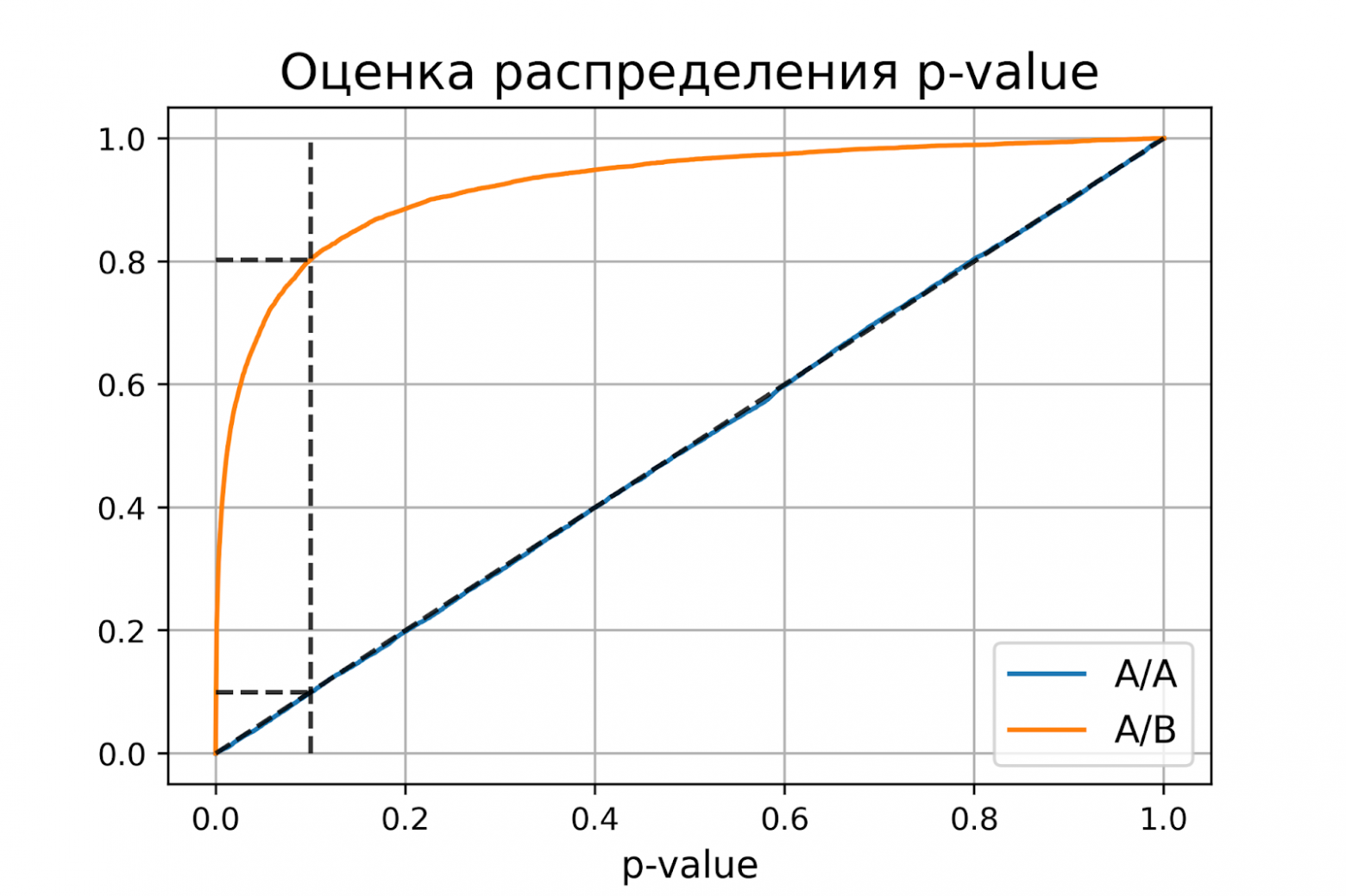
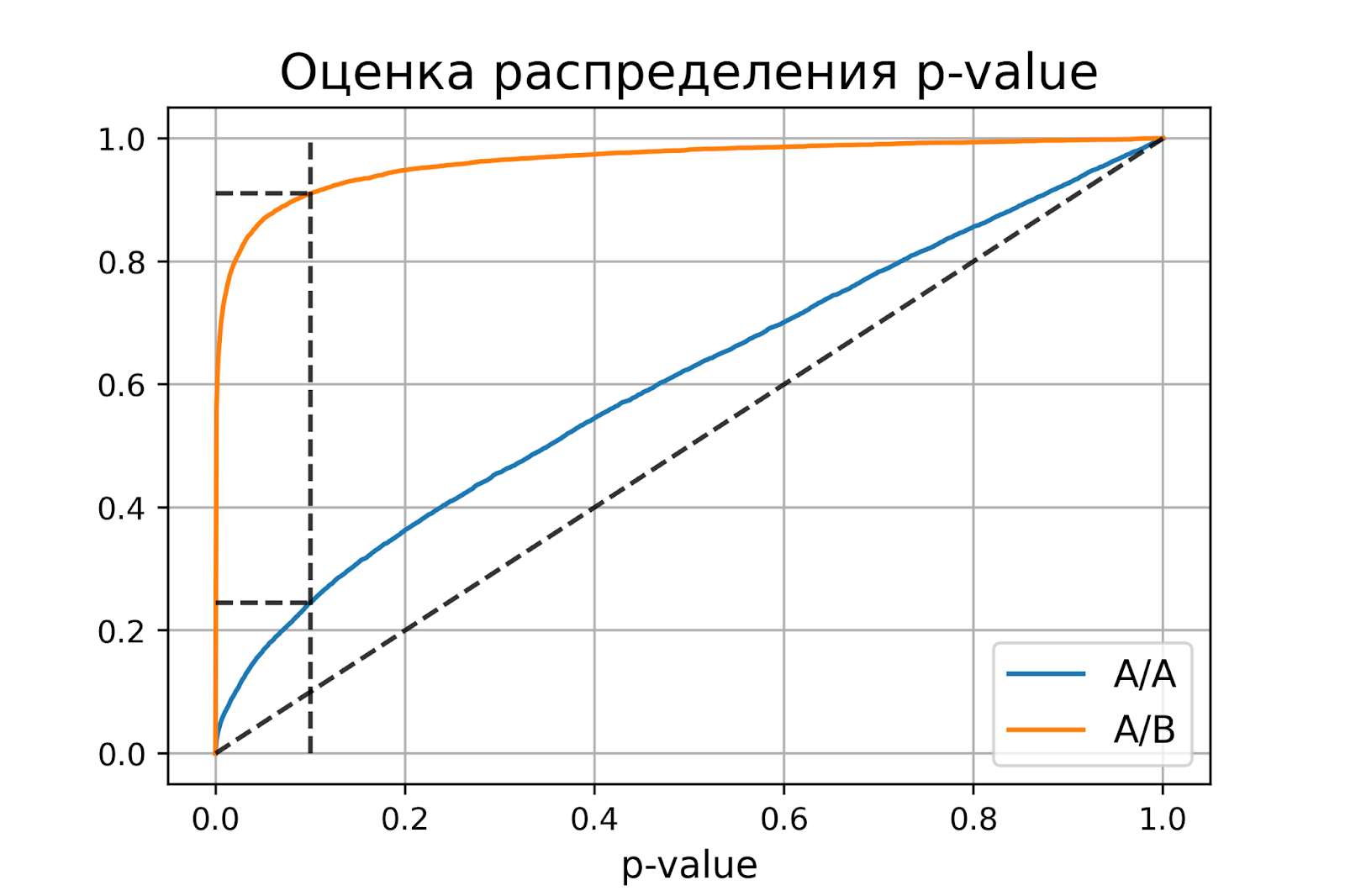
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
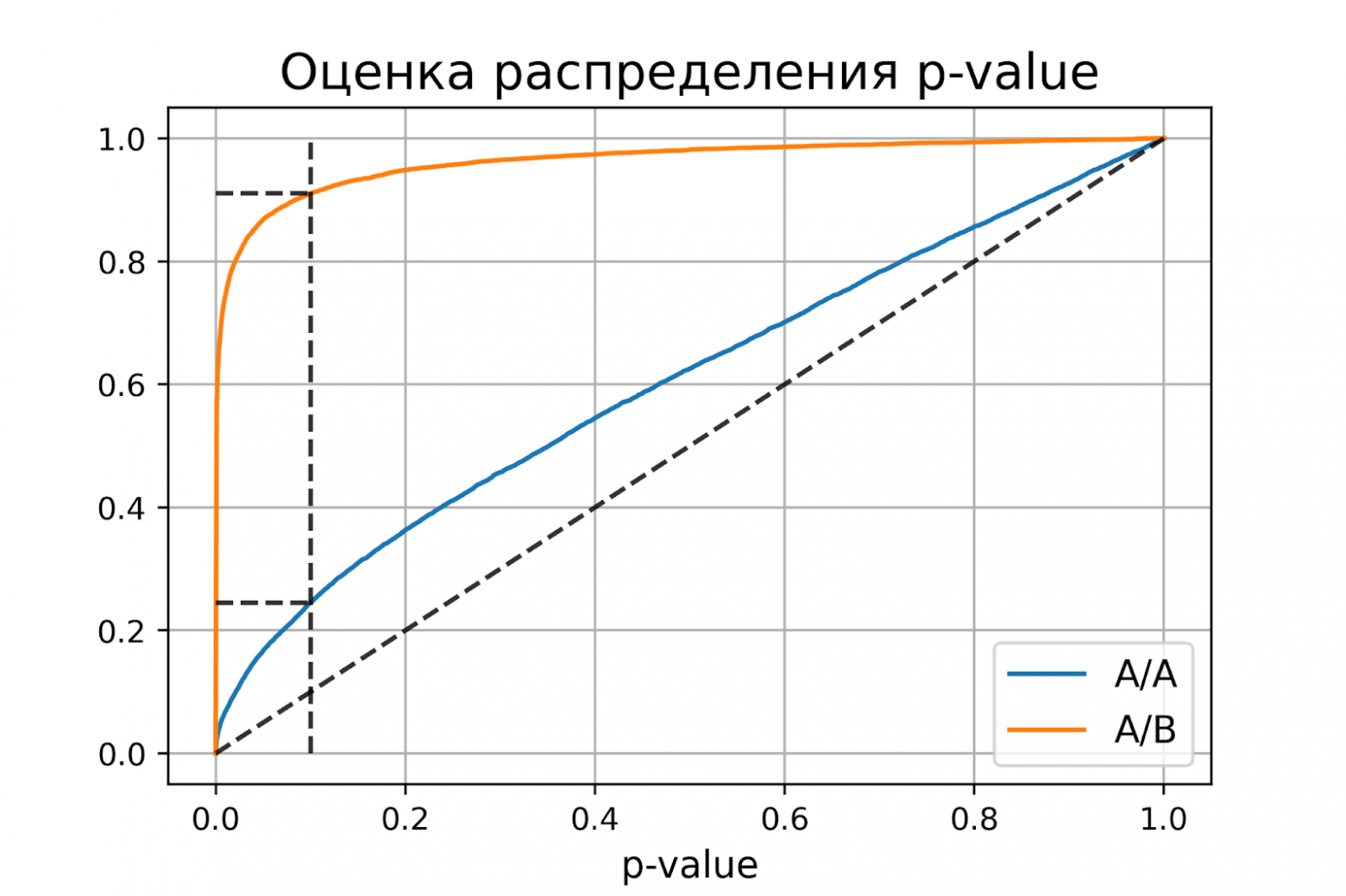
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
5.6. Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Высказывания, имеющие вероятность ошибки р <= 0,05 — называются значимыми.
- Высказывания с вероятностью ошибки р <= 0,01 — очень значимыми,
- А высказывания с вероятностью ошибки р <= 0,001 — максимально значимыми.
В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.
| Вероятность ошибки | Значимость | Обозначение |
| р > 0.05 | Не значимая | ns |
| р <= 0.05 | Значимая | * |
| р <= 0.01 | Очень значимая | ** |
| р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
Определим выражение для вычисления ошибки второго рода и мощности теста, построим в
MS
EXCEL
кривые оперативной характеристики (Operating-characteristic curves).
Тема этой статьи – вычисление
ошибки второго рода
(type II error) при
проверке гипотез
. Основная статья про
проверку гипотез
находится здесь
.
Напомним, что процедура
проверки гипотез
состоит из следующих шагов:
- из исследуемого распределения берется
выборка
; - на основании значений
выборки
вычисляется
тестовая статистика
; - значение
тестовой статистики
сравнивается со значениями, соответствующим заданномууровню значимости (ошибке первого рода)
;
- по результату сравнения делается вывод об отклонении (или не отклонении)
нулевой гипотезы
.
Обычно с
проверкой гипотез
связывают 2 типа ошибок. Если
нулевая гипотеза
отклоняется, когда она верна – это
ошибка первого рода
(обозначается α,
альфа
). Если нулевая гипотеза не отклоняется, когда она неверна, то это
ошибка второго рода
(обозначается β,
бета
).
Ошибка первого рода
часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина
ошибки первого рода
задается перед
проверкой гипотезы
, таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи. После этого, процедура проверки гипотезы составляется таким образом, чтобы вероятность
ошибки второго рода
была как можно меньше.
Ошибка второго рода
β
зависит от размера
выборки
n и
уровня значимости α
, и поэтому контролируется косвенно. Чем больше размер
выборки
, тем меньше
ошибка второго рода
(при прочих равных).
Часто также используют величину
1-β
, которая называется
мощностью статистического критерия
(мощностью теста, мощностью исследования, англ. power of a statistical test).
Мощность статистического критерия
— это вероятность правильно отклонить нулевую гипотезу. Чем ближе эта величина к единице, тем меньше у нас шансов ошибиться при проверке гипотезы (тем лучше критерий различает гипотезы Н
0
и Н
1
).
Ошибку второго рода
вычисляют для каждого вида
проверки гипотез
по-разному. Получим выражение для вычисления
ошибки второго рода
для
проверки двусторонней гипотезы о равенстве среднего значения распределения некоторой величине (стандартное отклонение известно)
.
Для
проверки гипотезы
этого типа используется
тестовая статистика
Z
0
:
которая имеет
стандартное нормальное распределение
.
Чтобы найти
Ошибку второго рода
необходимо предположить, что гипотеза Н
0
: μ=μ
0
не верна, и соответственно истинное
среднее значение распределения
μ=μ
0
+Δ, где Δ>0. В этом случае,
тестовая статистика
Z
0
будет иметь
нормальное распределение
N(Δ√n/σ;1), т.е. будет смещено вправо на Δ√n/σ (см.
файл примера на листе Бета
).
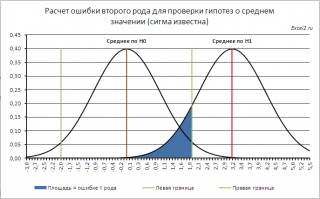
Согласно определения,
ошибка второго рода
равна вероятности, принять нулевую гипотезу, если на самом деле справедлива Н
1
. Эта вероятность соответствует выделенной на рисунке области.
Статистика
Z
0
, в этом случае, примет значение между -Z
α/2
и Z
α/2
(эти значения соответствуют границам
доверительного интервала
). Z
α/2
– это
верхний α/2-квантиль стандартного нормального распределения
.
Определим
ошибку второго рода
в терминах
стандартного нормального распределения
:
Это выражение будет работать и для Δ<0. Как видно из выражения,
ошибка второго рода
является функцией от α, Δ и n. В
файле примера на листе Бета
можно быстро рассчитать β и
мощность теста
в зависимости от этих параметров. Диаграмма, приведенная выше, будет автоматически перестроена.
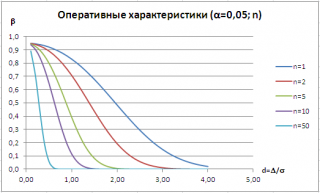
Для заданного значения α часто строят семейство кривых, которые иллюстрируют зависимость
ошибки второго рода
от Δ и n. Такие кривые называются
операционными характеристиками
(Operating-characteristic curves).
Как видно из рисунка, чем дальше истинное значение
среднего
от μ
0
, т.е. чем больше Δ, тем меньше
ошибка второго рода.
Таким образом, для заданных α и n, тест легче определит большие отклонения от
среднего
, чем малые (тест обладает, в данном случае, большей
мощностью
). При росте n
мощность теста
также растет.
Кривые
операционных характеристик
используются для оценки размера
выборки
, достаточного для определения заданной разницы между истинным значением
среднего
μ
от μ
0
с требуемой вероятностью.
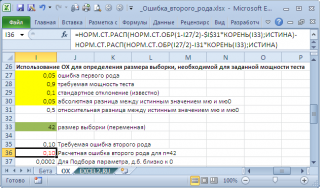
В
файле примера на листе ОХ
создана форма для определения размера
выборки
, достаточного для обеспечения заданной
мощности теста
.
Например, Н
0
: μ
0
=20, истинное значение μ=20,05,
стандартное отклонение
=0,1, α=0,05. Чтобы вероятность правильно отклонить гипотезу H
0
была равна 0,9 (
мощность теста
), размер
выборки
должен быть 42 или более.
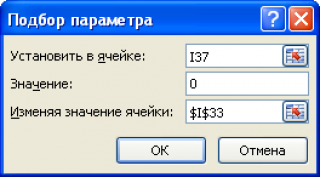
Примечание
:
Для нахождения размера
выборки
потребуется использование инструмента MS EXCEL
Подбор параметра
.
Проверка корректности А/Б тестов
Время на прочтение
8 мин
Количество просмотров 7.7K
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 — alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA — Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
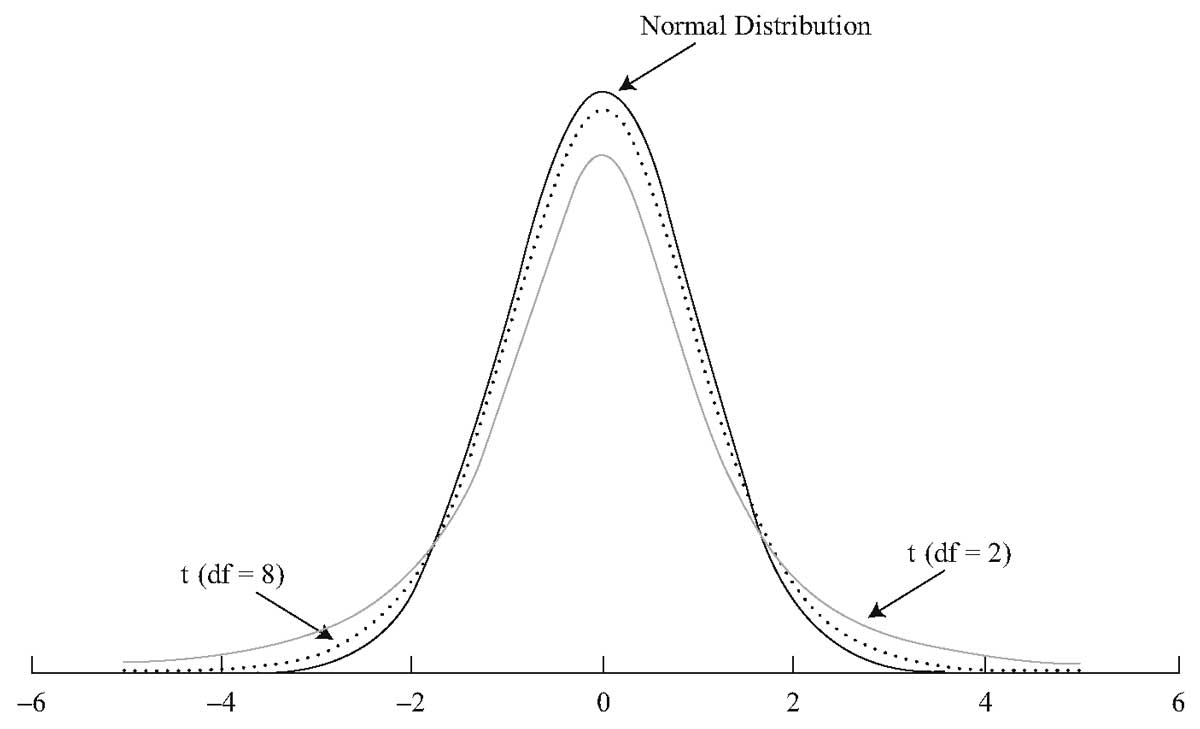
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) — это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.
Значение обобщающего показателя, рассчитанное по выборочной совокупности (выборке), может в той или иной мере отличаться от значения этого показателя в генеральной совокупности.
Ошибка выборки– это возможное расхождение между характеристиками выборочной и генеральной совокупности.
По выборочной совокупности обычно рассчитывают два вида обобщающих показателей.
1) Средняя величина количественного признака (Выборочная средняя ) – это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности. Например, средняя зарплата, средний рост, средний возраст и т. д.
2) Относительная величина альтернативного признака (Выборочная доля W) характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием (отсутствием) изучаемого признака. Например, доля бракованных изделий в партии, удельный вес женщин среди работников предприятия и т. д.
В генеральной совокупности среднюю величину количественного признака называют Генеральной средней (обозначается ), а долю единиц, обладающих изучаемым признаком, называют Генеральной долей (обозначается Р).
Выборочная средняя определяется по формуле средней арифметической.
Выборочная доля W (частость) определяется по формуле

Где M – число единиц, обладающих изучаемым признаком, N – общая численность выборочной совокупности (Объем выборки).
Основная задача выборочного исследования – на основе характеристик выборочной совокупности w и получить достоверные суждения о показателях доли p и средней
в генеральной совокупности.
Возможные расхождения между характеристиками выборочной и генеральной совокупностей измеряются средней ошибкой выборки μ.
В математической статистике доказывается, что При Случайном повторном отборе средние ошибки теоретически рассчитывают по формулам:
· для выборочной средней

Где S2 – генеральная дисперсия;
· для выборочной доли W

Но при проведении выборочных обследований генеральная дисперсия S2 и генеральная доля P, как правило, неизвестны. На практике вместо них используют оценки, полученные по выборочной совокупности.
Таким образом, на практике расчетные формулы для определения средней ошибки выборки При Случайном повторном отборе будут иметь вид:
· для выборочной средней

Где S2 – дисперсия, рассчитанная для выборочной совокупности (Выборочная дисперсия);
· для выборочной доли W

При случайном бесповторном отборе формулы средней ошибки выборки включают дополнительный множитель 
· для выборочной средней

· для выборочной доли W

Значения средней ошибки выборки необходимы для установления диапазонов возможных значений генеральной доли P И генеральной средней , что позволяет указать доверительные интервалы:
· для генеральной средней
; (5.8)
· для генеральной доли P , (5.9)
Где – предельная ошибка выборки для генеральной средней;
– предельная ошибка выборки для генеральной доли.
Коэффициент T – это Коэффициент доверия, зависящий от Доверительной вероятности A.
E Заметим, что генеральная характеристика ( или Р) нам неизвестна, и мы лишь можем утверждать, что с доверительной вероятностью A генеральная характеристика принадлежит доверительному интервалу (т. е. с доверительной вероятностью доверительный интервал покроет
или Р).
В общем случае значения коэффициента доверия T при заданной доверительной вероятности A и известном объеме выборки N можно найти с помощью таблиц распределения Стьюдента (см. приложение).
На практике для выборок достаточно большого объема (N³30) часто применяют следующие приближенные значения коэффициента доверия T без учета объема выборки N.
|
Доверительная вероятность A |
0,90 |
0,95 |
0,954 |
0,990 |
0,9973 |
|
Коэффициент доверия T |
1,645 |
1,9600 |
2,000 |
2,576 |
3,000 |
| < Предыдущая | Следующая > |
|---|