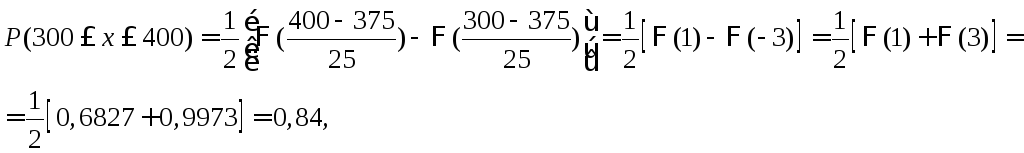Ошибки измерений прибора подчиняются нормальному распределению - Не ошибается лишь тот, кто ничего не делает!

Тема. Законы распределения случайных величин

1. Нормальное распределение

Пример 1.Вес вылавливаемых в пруду
рыб подчиняется нормальному закону с
математическим ожиданием, равным 375 г,
и средним квадратическим отклонением
25 г. Определить вероятность того, что
вес одной пойманной рыбы будет заключен
в пределах от 300 до 400г.

Решение.

Дано: М(Х)=а=375 г.,
г.,
с=300г.,d=400г.

Найдем искомую вероятность.

где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.

Пример 2. Ошибка измерения прибора
подчиняется нормальному распределению.
С вероятностью 0,92 ошибка измерения не
превосходит 4. Найти среднее квадратическое
отклонение ошибки прибора. Систематическая
ошибка отсутствует.

Решение.

Дано:
,

Воспользовавшись второй теоремой о
нормальной случайной величине, найдем
величину
.

Из таблицы Лапласа, зная
, найдемt=1,75.

Тогда
или

Ответ:
.

2. Равномерное распределение

Пример 3. Цена деления шкалы
прибора 0,5 вольт. При измерениях показания
округляются до ближайшего целого
деления. Найти вероятность того, что
при считывании показаний будет сделана
ошибка, не превышающая 0,01 вольт.

Решение.

Дано: Случайная величина Х — истинное
показание прибора имен равномерное
распределение с параметрами а=0 ,в=0,5. Тогда.
Искомая вероятность – это вероятность
показания х либо на,
либо на.

Задания для самостоятельной работы

1) Размер детали подчиняется
нормальному закону распределения со
средней арифметической 15 мм и дисперсией
0,25. Определить ожидаемый процент брака,
если допустимые размеры находятся в
пределах от 14 мм до 17 мм. Найти выражение
интегральной и дифференциальной функции.

2) Изготовленные цехом детали по
размерам диаметра распределяются по
нормальному закону с математическим
ожиданием, равным 4,5 см, и средним
квадратическим отклонением 0,5 см.
Определить вероятность того, что размер
диаметра наудачу взятой детали отклонится
от математического ожидания не более,
чем на 1 см.

3) Математическое ожидание нормально
распределенной случайной величины
равно 15, среднее квадратическое отклонение
равно 5. Определить вероятность того,
что абсолютная величина отклонения
Х-М(Х) будет меньше 10.

4) Ошибка измерения – нормально
распределенная случайная величина с
дисперсией, равной 100. Систематическая
ошибка отсутствует. Найти вероятность
того, что ошибка измерения окажется в
интервале (3;6).

5) Ошибка взвешивания – случайная
нормально распределенная величина с
дисперсией 400. Весы заранее настроены
на обвес 50 г. Найти вероятность того,
что ошибка взвешивания находится в
пределах от 30 до 70 г.

6) Автобус некоторого маршрута идет
с интервалом в десять минут. Пассажир
в какой-то момент подходит к остановке.
Время, в течении которого пассажир
ожидает автобус, представляет случайную
величину, имеющую равномерное
распределение. Определить дифференциальную
функцию распределения этой случайной
величины, ее математическое ожидание
и дисперсию.

7) По данным задачи 6 определить
вероятность того, что пассажир подошедший
к остановке, будет ждать автобус менее
4 минут.

Цена деления шкалы измерительного
прибора равна 0,2. Показания прибора
округляют до ближайшего целого деления.
Найти вероятность того, что при отсчете
будет сделана ошибка:

а) меньшая 0,04;

б) большая 0,05.

9) Минутная стрелка электрических
часов перемещается скачком в конце
каждой минуты. Найти вероятность того,
что в данное мгновение часы покажут
время, которое отличается от истинного
не более чем на 20 сек.

Форма контроля:
Проверка
решений задач и заданий

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Закажите у меня новую работу, просто написав мне в чат!

Ошибки измерений прибора подчиняются нормальному распределению. Прибор имеет систематическую ошибку 1 см и среднюю квадратическую ошибку 2 см. Найти вероятность того, что три ошибки измерений попадут в интервал (0; 3 см). Измерения независимы.

Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна: где 𝑚 − математическое ожидание; 𝜎 − среднее квадратическое отклонение. По условию Вероятность того, что при одном испытании случайная величина 𝑋 попадет в интервал (0; 3), равна: Найдем вероятность события 𝐴 − при трех испытаниях случайная величина 𝑋 три раза попадет в интервал (0; 3). Воспользуемся формулой Бернулли. Для данного случая

Источник

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями

p( X = i) = pi = qi p ,

где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.

Числовые характеристики геометрического распределения:

Дискретная значения 0, 1, … ,

m X = q / p , D X = q / p 2 .

СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:

p(X =i) = p =	n!	piqn−i	(7.2)

i	i!(n −i)!	,

где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:

m X = n p , D X = n q p .

Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, … , ∞ со следующими вероятностями:

p(X =i) = p = ai	e−a	(7.3)
i	i!	,
где a – параметр распределения (a > 0).

Числовые характеристики пуассоновской СВ:
m X = a , D X	= a .

Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:

0, x <

f ( x ) = 1

b − a

0, x >

a ,	0 , x	< a ,
		− a
, a ≤ x ≤ b , F ( x ) =	x	, a	≤	x ≤	b ,
				(7.4)
		a
b.	b	−
1, x	> b .

Числовые характеристики равномерно распределенной СВ:

m X =	a + b	, D X	=	( b − a ) 2	.
2	1 2

Непрерывная СВ T, принимающая только положительные значения, имеет экспоненциальное распределение, если ее плотность вероятности и функция распределения равны

		λ e	− λ t	, t	≥ 0 ,	− e	−λt	, t ≥ 0,
f (t ) =		1		(7.5)
	0 , t < 0 ,	F(t) =	0, t < 0,

где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:

m T = 1 / λ , D T = 1 / λ 2 .

Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности и функция распределения равны

f (x ) =

exp −

(x − m)2

F ( x ) =

0 .5 + Φ

x − m

(7.6)

σ 2π

2σ

где m, σ – параметры распределения ( σ >0),

Φ(x) =

∫e−

dt — функция Лапласа.

2π

Значения функции Лапласа приведены в приложении. При использовании таблицы значений функции Лапласа следует учитывать, что Φ(–x) = –Φ(x),

Φ(0) = 0, Φ(∞) = 0,5.

Числовые характеристики нормальной СВ:

m X = m , D X = σ 2 ,

I [ k / 2 ]

k −2 i

(σ

/ 2)

αk ( x) = k ! ∑

(k − 2i)!i !

i =0

0 , k − нечетное,

( x ) =

2 k / 2

k !

, k − четное.

( k / 2 ) !

Пример 7.1. Время безотказной работы аппаратуры является случайной величиной Х, распределенной по экспоненциальному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени.

Решение. Так как среднее время безотказной работы, т.е. математическое ожидание, равно 100 ч, то параметр λ экспоненциального закона будет равен λ = 1 / m X = 1 / 100 = 0, 01 . Искомая вероятность

p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.

Пример 7.2. Для замера напряжения используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2.

Решение. Из условия задачи следует, что p(-0,2<X<0,2) = 0,8. Так как распределение ошибок нормальное, а математическое ожидание m равно 0 (систематические ошибки отсутствуют), то

р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.

По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда

σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ

7.1. По каналу связи пересылается пакет информации до тех пор, пока он не будет передан без ошибок. Вероятность искажения пакета равна 0,1, найти среднее количество попыток передать пакет.

Ответ: 1,11.

7.2. При работе прибора в случайные моменты времени возникают неисправности. Количество неисправностей, возникающих за определенный промежуток времени, подчиняется закону Пуассона. Среднее число неисправностей за сутки равно двум. Определить вероятность того, что: а) за двое суток не будет ни одной неисправности; б) в течение суток возникнет хотя бы одна неисправность; в) за неделю работы прибора возникнет не более трех неисправностей.

Ответ: а) 0,018; б) 0,865; в) 0,004.

7.3. Шкала рычажных весов имеет цену деления 1 г. При измерении массы отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность того, что абсолютная ошибка определения массы: а) не превысит величины среднего квадратического отклонения возможных ошибок определения массы; б) будет заключена между

значениями σX и2σX .

Ответ: а)	1	; б) 1 −	1	.

3	3

7.4. Среднее время работы электронного модуля равно 700 ч. Определить время безотказной работы модуля с надежностью 0,8.

Ответ: 140 ч.

7.5. Сообщение передается последовательностью амплитудномодулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). На сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.

Ответ: 3,4 σ.

7.6. СВ X – ошибка измерительного прибора – распределена нормально с дисперсией 16 мВ2. Систематическая ошибка прибора отсутствует. Вычислить вероятность того, что в пяти независимых измерениях ошибка: а) превысит по модулю 6 мВ не более трех раз; б) хотя бы один раз окажется в интервале

(0,5; 3,5) мВ.

Ответ: а) 0,999; б) 0,776.

8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

Рассмотрим функцию одного случайного аргумента Y = ϕ(X). Если X – непрерывная случайная величина, то плотность вероятности g(y) величины Y определяется по формуле

k
g( y) = ∑ f (ψ j ( y))	ψ′j ( y)	,	(8.1)

j=1

где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);

k – число обратных функций для данного y.

Весь диапазон значений Y необходимо разбить на интервалы, в которых число k обратных функций постоянно, и определить вид g(y) по формуле (8.1) для каждого интервала.

Если X – дискретная случайная величина, принимающая значения xi, то величина Y будет принимать дискретные значения yi = ϕ(xi) с вероятностями

p(yi) = p(xi).

Числовые характеристики функции Y = ϕ(X) одного случайного аргумента

Xопределяются по формулам:

–начальные моменты

		∑n	ϕ k ( xi ) pi	для ДСВ
	i =1		;	(8.2)
α k ( y ) = M [Y k ] = M [ϕ k ( x)] =	∞
		∫ ϕ k ( x) f ( x)dx для НСВ
– математическое ожидание		−∞

m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ;	(8.3)
– центральные моменты
	n
∑(ϕ( xi ) − m y )k pi	для ДСВ
i=1			;	(8.4)
µk ( y) = M[(Y − mY )k ] =	∞
	∫ (ϕ( x) − my )k f ( x)dx для НСВ
	−∞
– дисперсия
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 .	(8.5)

Пример 8.1. Определить плотность вероятности величины Y = X2, если X – случайная величина, равномерно распределенная на интервале [–1, 2].

Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее

плотность вероятности равна (7.4):	−1≤ x ≤ 2,
1/3,
f (x) =	x < −1, x > 2.
0,

Построим график величины Y = X2 для x в интервале [–1, 2] и в зависимости от числа k обратных функций выделим следующие интервалы для

Y (рис. 8.1):

k = 0,

[–∞, 0[

[0, 1]

k = 2,

]1, 4]

k = 1,

]4, +∞]

k = 0.

Так как на интервалах [–∞, 0[ и ]4, +∞]

обратная функция не существует, то для этих

интервалов g(y) = 0.

В интервале [0, 1] две обратные функции:

ψ1(y) = + y и ψ2(y) = – y .

По формуле (8.1) получим

g( y) = fx (ψ1( y))

ψ1′( y)

+ fx (ψ2( y))

ψ2′ ( y)

= fx ( y )

+ fx

(− y )

В интервале ]1, 4] одна обратная функция

ψ1(y) = +

y , следовательно,

g( y) = fx (ψ1( y))

ψ1′( y)

= fx (

y )

Рис. 8.1

Таким образом, плотность вероятности величины Y равна

y < 0,

0 ≤ y ≤1,

g ( y) =

1 < y ≤ 4,

y > 4.

Пример 8.2 Случайная величина X равномерно распределена от –1 до +1. Определить математическое ожидание и дисперсию величины Y = X2.

Решение. Плотность вероятности СВ X равна

0,5, −1 ≤ x ≤1, f (x) =

0 , x < −1, x >1.

Вычислим математическое ожидание Y по формуле (8.3):

m y = M [X 2 ] = ∫1	x 2 0, 5dx =	1 .
−1		3

Дисперсию Dy рассчитаем по формуле (8.5):

Dy = M[( X 2 )2 ] − mY2 = ∫1	(x2 )2 0,5dx − my2 =	4	.
45
−1

ЗАДАЧИ

8.1. Определить плотность вероятности величины Y = lnX, если X – случайная величина, равномерно распределенная на интервале (1, 3).

		0, 5e	y	, 0	≤ y < ln 3,
Ответ:	g ( y ) =
		0 , y < 0, y > ln 3 .

8.2. Определить плотность вероятности величины Y = |X|, если X – случайная равномерно распределенная величина со следующими характеристиками mx = 1, Dx = 1, и вычислить вероятность того, что р{1 ≤ Y < 2}.


0, y < 0, y > 2, 73,
	1

Ответ: g( y) =		, 0	≤ y < 0, 73,
3

	1		, 0, 73 ≤ y ≤ 2, 73.

2 3

р{1 ≤ Y < 2} = 0,445.

8.3. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y = X – 0,2 .

Ответ: mY = 0,34; DY = 0,0574.

8.4. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.

Ответ: DY = 1/18.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Тема: Задача по теор веру, определить СКО (Прочитано 2222 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Ребята, помогите срочно решить задачу по теор веру…
Итоговая работа на сессии

Ошибка Х измерительного прибора распределена нормально. Систематической ошибки прибор не имеет (mx=0). Каким должно быть среднее квадратическое отклонение Qx ( сигма), чтобы с вероятностью не меньшей 0,9 ошибка измерения не превышала 20 микрометров по модулю?

« Последнее редактирование: 20 Января 2012, 10:36:38 от Asix »

Всегда пожалуйста, только Вы забыли сообщить, какая помощь нужна. Видимо, кусок сообщения, где Вы рассказываете, как решали задачу и что не получается, куда-то потерялся.

К сожалению, я не могу написать ход решения, т к не понимаю, как можно сделать
Поэтому и обращаюсь за помощью к вам.
Знаю только что ответ должен получиться : Qx<12.2(мкм)
натолкните на умные мысли пожалуйста.

Всё просто: изучаете по учебнику, что такое нормальное распределение, как считаются вероятности для него, и задачка сразу решается.

Измерительный прибор работает без систематических ошибок.doc

Зарегистрируйся в два клика и получи неограниченный доступ к материалам, а также
промокод

на новый заказ в Автор24. Это бесплатно.

Условие

Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что mx=0). Известно, что вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08. Пусть случайная величина X- это величина ошибки измерения. Предполагается, что случайная величина X нормально распределена, найти:
а) приближенное значение дисперсии;
б) вероятность того, что ошибка измерения не превысит ε=4;
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6.

Решение

А) Для случайной величины Х имеещей нормальный закон распределения с параметрами mx и σx справедливо:
Px-mx≤ε=Фε σx, где Фt=12π-∞xe- t22dt-функция Лапласа.
По условию задачи вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08
. Тогда вероятность противоположного события (вероятность того, что случайная величина Х не превышает по абсолютной величине 7, равна 1-0,08=0,92. Имеем:
Px-0≤7=Ф7 σx=0,92⇒7 σx≈5⇒ σx≈7 5=1,4.
Тогда искомая дисперсия приближенно равна: Dx=σx2≈1,96.
б) вероятность того, что ошибка измерения не превысит ε=4:
Px-0≤4=Ф4 1,4≈Ф2,857≈0,4979..
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6 найдем по формуле:
Pα≤Х≤β=Фβ-mxσx-Фα-mxσx.
P-4≤Х≤6=Ф61,4-Ф-41,4≈Ф4,286-Ф-2,857=
≈0,499997+0,4979≈0,998.
Ответ

50% решения задач недоступно для прочтения

Закажи персональное решение задач. Эксперты

напишут качественную работу за 30 минут! ⏱️

Макеты страниц

Ошибки измерений и способ наименьших квадратов

9.1.21. Ошибки измерений и нормальный закон распределения.

Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.

Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.

Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.

Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно Ошибки, соответствующие измерениям будут равны

Это чисто случайные ошибки.

Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины

Рассмотрим величины

Величины называются отклонениями. Так как речь здесь идет только о случайных ошибках, то величины х и у могут быть а положительными, и отрицательными, а малые значения будут встречаться чаще, чем большие. Примем допущение, что эти величины, следуют нормальному закону распределения

Положим

как известно, называется мерой точности. При этом примет вид

где относительное число ошибок, равных х.

Вычертим кривые Гаусса при двух различных значениях мерь; точности Легко заметить, что чем больше тем кривые острее, тем круче их склоны. Это означает, что чем больше параметр тем реже встречаются большие ошибки. Поэтому величину и называют мерой точности.

Вероятность того, что ошибка будет заключаться между равна

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с вероятностью 0,8 они не превосходят по абсолютной величине 12 мм. Найти среднюю квадратическую ошибку.

Используем нормальный закон и следующую формулу, таблицу значений функции Лапласа Ф(х):
px-a<δ=2Фδσ;
0.8=2Ф12σ;1.62=12σ;σ=7.407 мм.
Ответ: 7,407 мм.

Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что
Измерить и записать результат измерения активной мощности Р = U·I·cosφ, рассеиваемой на нагрузке Zнагр.;
—
Измеряется мощность трехфазного тока двумя ваттметрами. Какова наибольшая погрешность измерения, если стрелка первого ваттметра
Измеряется напряжение в виде периодической последовательности прямоугольных импульсов с параметрами: длительность импульсов τ, период
Измеряется напряжение переменного тока.
Дано.
Цифровой вольтметр:
— предел измерения Uк = 200 B;
— измеренное
Измеряется размер некоторой детали, затем из генеральной совокупности берется выборка объемом n=8. Зная, что
Измеряется электрическое сопротивление постоянному току (рисунок).
Получено:
UV =(5,00±0,50) мВ; Р=1
IA=(2,60±0,25) мА; Р=1
RV=
Записать результат измерения сопротивления
Измерительный канал включает в себя термометр сопротивления типа 150М и вторичный прибор со шкалой
Измерительный механизм (ИМ) магнитоэлектрической системы расситан на ток и Iии напряжение Uи и имеет
Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=15 мA и напряжение Uи=75 мB
Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=100 мB
Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=75 мB
Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=7,5 мA и напряжение Uи=75 мB
Измерительный прибор (ИП) магнитоэлектрической системы рассчитан на ток IП и напряжение UП и имеет

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями

p( X = i) = pi = qi p ,

где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.

Числовые характеристики геометрического распределения:

Дискретная значения 0, 1, … ,

m X = q / p , D X = q / p 2 .

СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:

p(X =i) = p =	n!	piqn−i	(7.2)

i	i!(n −i)!	,

где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:

m X = n p , D X = n q p .

p(X =i) = p = ai	e−a	(7.3)
i	i!	,
где a – параметр распределения (a > 0).

Числовые характеристики пуассоновской СВ:
m X = a , D X	= a .

0, x <

f ( x ) = 1

b − a

0, x >

a ,	0 , x	< a ,
		− a
, a ≤ x ≤ b , F ( x ) =	x	, a	≤	x ≤	b ,
				(7.4)
		a
b.	b	−
1, x	> b .

Числовые характеристики равномерно распределенной СВ:

m X =	a + b	, D X	=	( b − a ) 2	.
2	1 2

		λ e	− λ t	, t	≥ 0 ,	− e	−λt	, t ≥ 0,
f (t ) =		1		(7.5)
	0 , t < 0 ,	F(t) =	0, t < 0,

где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:

m T = 1 / λ , D T = 1 / λ 2 .

f (x ) =

exp −

(x − m)2

F ( x ) =

0 .5 + Φ

x − m

(7.6)

σ 2π

2σ

где m, σ – параметры распределения ( σ >0),

Φ(x) =

∫e−

dt — функция Лапласа.

2π

Φ(0) = 0, Φ(∞) = 0,5.

Числовые характеристики нормальной СВ:

m X = m , D X = σ 2 ,

I [ k / 2 ]

k −2 i

(σ

/ 2)

αk ( x) = k ! ∑

(k − 2i)!i !

i =0

0 , k − нечетное,

( x ) =

2 k / 2

k !

, k − четное.

( k / 2 ) !

p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.

р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.

По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда

σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ

Ответ: 1,11.

Ответ: а) 0,018; б) 0,865; в) 0,004.

значениями σX и2σX .

Ответ: а)	1	; б) 1 −	1	.

3	3

Ответ: 140 ч.

Ответ: 3,4 σ.

(0,5; 3,5) мВ.

Ответ: а) 0,999; б) 0,776.

8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

k
g( y) = ∑ f (ψ j ( y))	ψ′j ( y)	,	(8.1)

j=1

где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);

k – число обратных функций для данного y.

p(yi) = p(xi).

Числовые характеристики функции Y = ϕ(X) одного случайного аргумента

Xопределяются по формулам:

–начальные моменты

		∑n	ϕ k ( xi ) pi	для ДСВ
	i =1		;	(8.2)
α k ( y ) = M [Y k ] = M [ϕ k ( x)] =	∞
		∫ ϕ k ( x) f ( x)dx для НСВ
– математическое ожидание		−∞

m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ;	(8.3)
– центральные моменты
	n
∑(ϕ( xi ) − m y )k pi	для ДСВ
i=1			;	(8.4)
µk ( y) = M[(Y − mY )k ] =	∞
	∫ (ϕ( x) − my )k f ( x)dx для НСВ
	−∞
– дисперсия
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 .	(8.5)

Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее

плотность вероятности равна (7.4):	−1≤ x ≤ 2,
1/3,
f (x) =	x < −1, x > 2.
0,

Y (рис. 8.1):

k = 0,

[–∞, 0[

[0, 1]

k = 2,

]1, 4]

k = 1,

]4, +∞]

k = 0.

Так как на интервалах [–∞, 0[ и ]4, +∞]

обратная функция не существует, то для этих

интервалов g(y) = 0.

В интервале [0, 1] две обратные функции:

ψ1(y) = + y и ψ2(y) = – y .

По формуле (8.1) получим

g( y) = fx (ψ1( y))

ψ1′( y)

+ fx (ψ2( y))

ψ2′ ( y)

= fx ( y )

+ fx

(− y )

В интервале ]1, 4] одна обратная функция

ψ1(y) = +

y , следовательно,

g( y) = fx (ψ1( y))

ψ1′( y)

= fx (

y )

Рис. 8.1

Таким образом, плотность вероятности величины Y равна

y < 0,

0 ≤ y ≤1,

g ( y) =

1 < y ≤ 4,

y > 4.

Решение. Плотность вероятности СВ X равна

0,5, −1 ≤ x ≤1, f (x) =

0 , x < −1, x >1.

Вычислим математическое ожидание Y по формуле (8.3):

m y = M [X 2 ] = ∫1	x 2 0, 5dx =	1 .
−1		3

Дисперсию Dy рассчитаем по формуле (8.5):

Dy = M[( X 2 )2 ] − mY2 = ∫1	(x2 )2 0,5dx − my2 =	4	.
45
−1

ЗАДАЧИ

		0, 5e	y	, 0	≤ y < ln 3,
Ответ:	g ( y ) =
		0 , y < 0, y > ln 3 .


0, y < 0, y > 2, 73,
	1

Ответ: g( y) =		, 0	≤ y < 0, 73,
3

	1		, 0, 73 ≤ y ≤ 2, 73.

2 3

р{1 ≤ Y < 2} = 0,445.

Ответ: mY = 0,34; DY = 0,0574.

Ответ: DY = 1/18.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Макеты страниц

Ошибки измерений и способ наименьших квадратов

9.1.21. Ошибки измерений и нормальный закон распределения.

Это чисто случайные ошибки.

Рассмотрим величины

Положим

как известно, называется мерой точности. При этом примет вид

где относительное число ошибок, равных х.

Вероятность того, что ошибка будет заключаться между равна

Источник

§ 6. ТЕОРЕМЫ ЛЯПУНОВА И ЛАПЛАСА.

6.2. Основной закон ошибок.

Когда мы производим некоторое измерение, то на его результат влияет большое количество факторов, которые
порождают ошибки измерений. Ошибки измерений в основном можно подразделить на три группы: 1) грубые ошибки; 2) систематические ошибки;
3) случайные ошибки.

Грубые ошибки возникают от невнимательности при чтении показателей прибора, неправильной записи показаний,
неправильном использовании прибора. Эти ошибки могут быть исключены соблюдением правил измерения.

Систематические ошибки искажают обычно результат измерения в определенную сторону. Они происходят, например,
от несовершенства приборов, от личных качеств наблюдателя и могут быть устранены соответствующими поправками.

Случайные ошибки вызываются большим числом отдельных причин, не поддающихся точному учету и действующих в
каждом отдельном случае различным образом. Эти ошибки возникают от незаметных механических причин, из-за изменения параметров
измерительных приборов, зависящих от метеорологических условий, и т. д. Каждая из этих причин в отдельности порождает при измерении ничтожную
ошибку . Складываясь, эти ничтожно малые ошибки порождают суммарную ошибку , которой уже нельзя пренебречь.
Эта суммарная ошибка v есть случайная величина, являющаяся суммой огромного числа незначительных, независимых друг от друга случайных
величин и имеет, согласно следствию из теоремы Ляпунова, нормальное распределение.

Предполагая измерение свободным от грубых и систематических
ошибок, можно считать, что возможный результат измерения есть случайная величина , математическое ожидание
которой равно истинному значению а измеряемой величины: (см. Теорему Ляпунова).
Так как суммарная ошибка подчиняется нормальному закону распределения, то возможный результат
измерения также подчиняется нормальному закону распределения (см. § 4, п. 3).
В этом заключается основной закон ошибок.

Дальше…

Источник

Фрагмент работы:

Ошибки измерений прибора подчиняются нормальному закону распределе…

К.Р. №1.

№1.

В урне тысяча лотерейных билетов с номерами от 1 до 1000. Найти вероятность того, что номер наудачу вынутого билета: а) четный; б) нечетный; в)  1000; г)  1000.

РЕШЕНИЕ:

…

№2.

Три фирмы выполняют один и тот же заказ. Вероятность того, что первая фирма выполнит заказ в срок 0.75, вторая — 0.8, третья — 0.9, по отдельности. Определить вероятность того, что: а) одновременно первая и вторая выполнят заказ, а третья не успеет; 6) все три одновременно не выполнят заказ в срок.

РЕШЕНИЕ:

…

№3.

В клетке 30 попугаев: 20 говорящих и 10 неговорящих. Наудачу выбирают 4 попугая. Какова вероятность того, что среды них трое будут говорящих?

РЕШЕНИЕ:

…

№4.

На экспертизу под скрытыми девизами поступают проекты от трех конкурирующих фирм. Вероятность того, что проект первой фирмы пройдет экспертизу с положительной оценкой равна 0.8, второй — 0.6, третий — 0.9. Для экспертизы выбрали наудачу только один проект. Он ее прошел с хорошей оценкой. Какова вероятность того, что это был проект первой фирмы?

РЕШЕНИЕ:

…

К.Р. №2.

№1.

Производится ряд выстрелов по мишени с вероятностью попадания 0.7 при каждом выстреле; стрельба ведется до первого попадания в мишень, но не свыше 5 выстрелов. Найти закон распределения, математическое ожидание и дисперсию числа произведенных выстрелов. Построить функцию распределения, определить вероятность того, что число выстрелов до первого попадания будет не меньше трех.

РЕШЕНИЕ:

…

№2.

Для непрерывной случайной величины задана плотность распределения

-x+

Требуется построить графики плотности распределения и функции распределения, определив предварительно параметр А. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение. Найти вероятность того, что отклонение случайной величины от математического ожидания будет не более среднеквадратического отклонения.

РЕШЕНИЕ:

…

№3.

Ошибки измерений прибора подчиняются нормальному закону распределения. Прибор имеет систематическую ошибку a и среднеквадратическую ошибку :

a= 5 м =75 м n=3 =0 м =80 м

Какова вероятность того, что n ошибок измерений попадают в интервал (;)?

РЕШЕНИЕ:

…

Список файлов
33531.docx	97 КБ

Информация по контрольной
код работы (ID)	33531
просмотров	1597
страниц	7
таблиц	2
формул	> 36
изображений	3
оформление по ГОСТу	ДА
были доработки	НЕТ
проверено преподавателем Сибстрин	ДА

Источник

Тема. Законы распределения случайных величин

1. Нормальное распределение

2. Равномерное распределение

Задания для самостоятельной работы

8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

<img decoding="async" src="https://www.webmath.ru/forum/Themes/LikeIPBTheme/images/topic/normal_post.gif" alt /> Тема: Задача по теор веру, определить СКО (Прочитано 2222 раз)

Условие

Решение

Ошибки измерений и способ наименьших квадратов

9.1.21. Ошибки измерений и нормальный закон распределения.

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с

8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

Ошибки измерений и способ наименьших квадратов

9.1.21. Ошибки измерений и нормальный закон распределения.

Ошибки измерений прибора подчиняются нормальному закону распределе…

Тема: Задача по теор веру, определить СКО (Прочитано 2222 раз)