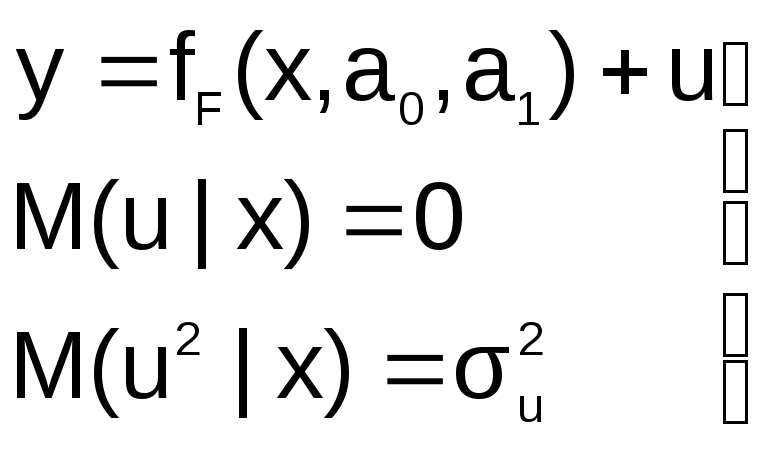Ошибки измерения эконометрика - Не ошибается лишь тот, кто ничего не делает!

Регрессивный анализ
Часть серии по

Модели
Линейная регрессия Простая регрессия Полиномиальная регрессия Общая линейная модель
Обобщенная линейная модель Дискретный выбор Биномиальная регрессия Бинарная регрессия Логистическая регрессия Полиномиальный логит Смешанный логит Пробит Полиномиальный пробит Заказал логит Заказал пробит Пуассон
Многоуровневая модель Фиксированные эффекты Случайные эффекты Линейная модель смешанных эффектов Нелинейная модель смешанных эффектов
Нелинейная регрессия Непараметрический Полупараметрический Крепкий Квантиль Изотонический Основные компоненты Наименьший угол Местный Сегментированный
Ошибки в переменных
Оценка
Наименьших квадратов Линейный Нелинейный
Обычный Взвешенный Обобщенный
Частичное Общий Неотрицательный Регрессия хребта Регулярный
Наименьшие абсолютные отклонения Итеративно переназначенный Байесовский Байесовский многомерный
Фон
Проверка регрессии Средний и прогнозируемый ответ Ошибки и остатки Доброту соответствия Студентизованный остаток Теорема Гаусса – Маркова
Математический портал

В статистика, модели ошибок в переменных или же модели ошибок измерения^[1]^[2]^[3] находятся регрессионные модели это объясняет погрешности измерения в независимые переменные. Напротив, стандартные модели регрессии предполагают, что эти регрессоры были точно измерены или наблюдались без ошибок; как таковые, эти модели учитывают только ошибки в зависимые переменные, или ответы.^{[нужна цитата ]}

Иллюстрация регрессионное разбавление (или смещение затухания) по диапазону оценок регрессии в моделях с ошибками в переменных. Две линии регрессии (красные) ограничивают диапазон возможностей линейной регрессии. Неглубокий наклон получается, когда независимая переменная (или предиктор) находится на абсциссе (ось x). Более крутой наклон получается, когда независимая переменная находится на ординате (ось y). По соглашению с независимой переменной на оси x получается более пологий наклон. Зеленые контрольные линии — это средние значения в пределах произвольных интервалов по каждой оси. Обратите внимание, что более крутые оценки регрессии для зеленого и красного более согласуются с меньшими ошибками в переменной оси Y.

В случае, когда некоторые регрессоры были измерены с ошибками, оценка на основе стандартного предположения приводит к непоследовательный оценки, что означает, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. За простая линейная регрессия эффект является недооценкой коэффициента, известного как смещение затухания. В нелинейные модели направление смещения, вероятно, будет более сложным.^[4]^[5]

Мотивационный пример

Рассмотрим простую модель линейной регрессии вида

$y_ {t} = alpha + eta x_ {t} ^ {*} + varepsilon_t ,, quad t = 1, ldots, T,$

куда $х_ {т} ^ {*}$ обозначает истинный но ненаблюдаемый регрессор. Вместо этого мы наблюдаем это значение с ошибкой:

$x_ {t} = x_ {t} ^ {*} + eta_ {t},$

где ошибка измерения $eta_ {t}$ считается независимым от истинного значения $х_ {т} ^ {*}$ .

Если $г_ {т}$ Просто регрессируют на $x_ {t}$ ‘S (см. простая линейная регрессия ), то оценка коэффициента наклона будет

$hat {eta} = frac {frac {1} {T} sum_ {t = 1} ^ T (x_t- ar {x}) (y_t- ar {y})} {frac {1} {T} sum_ {t = 1} ^ T (x_t- ar {x}) ^ 2} ,,$

который сходится как размер выборки неограниченно увеличивается:

$шляпа {eta} xrightarrow {p} frac {имя оператора {Cov} [, x_t, y_t,]} {имя оператора {Var} [, x_t,]} = frac {eta sigma ^ 2_ {x ^ *}} {sigma_ {x ^ *} ^ 2 + sigma_eta ^ 2} = frac {eta} {1 + sigma_eta ^ 2 / sigma_ {x ^ *} ^ 2} ,.$

Вариации неотрицательны, так что в пределе оценка меньше по величине, чем истинное значение эта , эффект, который статистики называют затухание или же регрессионное разбавление.^[6] Таким образом, «наивная» оценка методом наименьших квадратов непоследовательный в этой обстановке. Однако оценка — это согласованная оценка параметра, необходимого для наилучшего линейного предсказателя данный Икс : в некоторых приложениях это может быть то, что требуется, а не оценка «истинного» коэффициента регрессии, хотя это предполагает, что дисперсия ошибок при наблюдении $х ^ {*}$ остается фиксированным. Это непосредственно следует из приведенного выше результата и того факта, что коэффициент регрессии, относящийся к $г_ {т}$ К фактически наблюдаемым $x_ {t}$ ′ S в простой линейной регрессии определяется выражением

$eta _ {x} = {frac {имя оператора {Cov} [, x_ {t}, y_ {t},]} {имя оператора {Var} [, x_ {t},]}}.$

Именно этот коэффициент, а не эта , что потребовалось бы для построения предиктора на основе наблюдаемых Икс который подвержен шуму.

Можно утверждать, что почти все существующие наборы данных содержат ошибки разной природы и величины, поэтому систематическая ошибка ослабления встречается очень часто (хотя при многомерной регрессии направление систематической ошибки неоднозначно.^[7]). Джерри Хаусман видит в этом железный закон эконометрики: «Величина оценки обычно меньше ожидаемой».^[8]

Технические характеристики

Обычно модели ошибок измерения описываются с помощью скрытые переменные подход. Если переменная ответа и Икс наблюдаемые значения регрессоров, тогда предполагается, что существуют некоторые скрытые переменные $у ^ {*}$ и $х ^ {*}$ которые соответствуют «истинным» моделям функциональные отношения , и такие, что наблюдаемые величины являются их зашумленными наблюдениями:

${displaystyle {egin {case} y ^ {*} = g (x ^ {*} !, w, |, heta), y = y ^ {*} + varepsilon, x = x ^ {*} + eta , конец {case}}}$

куда модель параметр и это те регрессоры, которые считаются безошибочными (например, когда линейная регрессия содержит точку пересечения, регрессор, который соответствует константе, безусловно, не имеет «ошибок измерения»). В зависимости от спецификации эти безошибочные регрессоры могут или не могут рассматриваться отдельно; в последнем случае просто предполагается, что соответствующие элементы в матрице дисперсии эта ноль.

Переменные , Икс , все наблюдаемый, что означает, что статистик обладает набор данных из статистические единицы $влево {y_ {i}, x_ {i}, w_ {i} ight} _ {i = 1, dots, n}$ которые следуют за процесс генерации данных описано выше; скрытые переменные $х ^ {*}$ , $у ^ {*}$ , , и эта однако не наблюдаются.

Эта спецификация не охватывает все существующие модели ошибок в переменных. Например в некоторых из них работают может быть непараметрический или полупараметрический. Другие подходы моделируют отношения между $у ^ {*}$ и $х ^ {*}$ как распределительные, а не функциональные, то есть они предполагают, что $у ^ {*}$ условно на $х ^ {*}$ следует определенному (обычно параметрическому) распределению.

Терминология и предположения

Наблюдаемая переменная можно назвать манифест, индикатор, или же доверенное лицо Переменная.
Незаметная переменная $х ^ {*}$ можно назвать скрытый или же истинный Переменная. Его можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональная модель), либо как случайная величина (соответственно структурная модель).^[9]
Связь между ошибкой измерения и скрытая переменная $х ^ {*}$ можно моделировать разными способами:
- Классические ошибки: ошибки независимый скрытой переменной. Это наиболее распространенное предположение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
- Средняя независимость: $имя оператора {E} [eta | x ^ *], =, 0,$ ошибки равны нулю в среднем для каждого значения скрытого регрессора. Это менее ограничительное предположение, чем классическое,^[10] так как это позволяет наличие гетероскедастичность или другие эффекты в ошибках измерения.
- Ошибки Берксона: ошибки не зависят от наблюдаемый регрессор Икс. Это предположение имеет очень ограниченную применимость. Один из примеров — ошибки округления: например, если у человека возраст* это непрерывная случайная величина, тогда как наблюдаемые возраст усекается до следующего наименьшего целого числа, тогда ошибка усечения приблизительно не зависит от наблюдаемого возраст. Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени. скажи на , то реальное измерение может происходить при другом значении $х ^ {*}$ (например, из-за конечного времени реакции), и такая ошибка измерения обычно не зависит от «наблюдаемого» значения регрессора.
- Ошибки неправильной классификации: специальный случай, используемый для фиктивные регрессоры. Если $х ^ {*}$ является индикатором определенного события или состояния (например, лицо мужского / женского пола, какое-либо лечение было предоставлено / нет и т. д.), то ошибка измерения в таком регрессоре будет соответствовать неправильной классификации, аналогичной ошибки типа I и типа II в статистическом тестировании. В этом случае ошибка может принимать только 3 возможных значения, а его распределение зависит от $х ^ {*}$ моделируется двумя параметрами: $альфа = имя оператора {Pr} [eta = -1 | х ^ * = 1]$ , и $eta = имя оператора {Pr} [eta = 1 | х ^ * = 0]$ . Необходимым условием идентификации является то, что , то есть ошибочная классификация не должна происходить «слишком часто». (Эту идею можно обобщить на дискретные переменные с более чем двумя возможными значениями.)

Линейная модель

Сначала были изучены линейные модели ошибок в переменных, вероятно, потому что линейные модели были так широко распространены и легче нелинейных. В отличие от стандартных наименьших квадратов регрессии (OLS), расширение ошибок в регрессии переменных (EiV) от простого к многомерному случаю непросто.

Простая линейная модель

Простая линейная модель ошибок в переменных уже была представлена в разделе «мотивация»:

${egin {case} y_ {t} = alpha + eta x_ {t} ^ {*} + varepsilon _ {t}, x_ {t} = x_ {t} ^ {*} + eta _ {t}, конец {случаи}}$

где все переменные скаляр. Здесь α и β — интересующие параметры, тогда как σ_ε и σ_η— стандартные отклонения членов погрешности — мешающие параметры. «Настоящий» регрессор Икс* рассматривается как случайная величина (структурный модель), независимо от погрешности измерения η (классический предположение).

Эта модель идентифицируемый в двух случаях: (1) либо скрытый регрессор Икс* является нет нормально распределенный, (2) или Икс* имеет нормальное распределение, но ни один ε_т ни η_т делятся на нормальное распределение.^[11] То есть параметры α, β можно последовательно оценить на основе набора данных $стиль сценария (x_ {t} ,, y_ {t}) _ {{t = 1}} ^ {T}$ без дополнительной информации, при условии, что скрытый регрессор не является гауссовским.

Прежде чем этот результат идентифицируемости был установлен, статистики пытались применить максимальная вероятность метод, предполагая, что все переменные нормальные, а затем пришел к выводу, что модель не идентифицирована. Предлагаемое средство правовой защиты заключалось в предполагать что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся:^[12]

Регрессия Деминга — предполагает, что соотношение δ = σ²_ε/σ²_η известен. Это может быть уместно, например, когда ошибки в у и Икс оба вызваны измерениями, и точность измерительных устройств или процедур известна. Случай, когда δ = 1 также известен как ортогональная регрессия.
Регресс с известными коэффициент надежности λ = σ²_∗/ ( σ²_η + σ²_∗), куда σ²_∗ — дисперсия скрытого регрессора. Такой подход может быть применим, например, когда доступны повторяющиеся измерения одного и того же устройства, или когда коэффициент надежности известен из независимого исследования. В этом случае последовательная оценка наклона равна оценке наименьших квадратов, деленной на λ.
Регрессия с известными σ²_η может возникнуть, когда источник ошибок в Икс’s известно, и их дисперсия может быть рассчитана. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда σ²_η известно, что коэффициент надежности можно вычислить как λ = ( σ²_Икс − σ²_η) / σ²_Икс и сведем проблему к предыдущему случаю.

Более новые методы оценки, которые не предполагают знания некоторых параметров модели, включают:

Метод моментов — GMM оценка на основе соединения третьего (или более высокого) порядка кумулянты наблюдаемых переменных. Коэффициент наклона можно оценить по формуле ^[13]

${hat eta} = {frac {{шляпа {K}} (n_ {1}, n_ {2} +1)} {{hat {K}} (n_ {1} + 1, n_ {2})}} , четверка n_ {1}, n_ {2}> 0,$

куда (п₁,п₂) таковы, что K(п₁+1,п₂) — сустав кумулянт из (Икс,у) — не ноль. В случае, когда третий центральный момент скрытого регрессора Икс* отлична от нуля, формула сводится к

${hat eta} = {frac {{frac {1} {T}} sum _ {{t = 1}} ^ {T} (x_ {t} - {ar x}) (y_ {t} - {ar y }) ^ {2}} {{frac {1} {T}} sum _ {{t = 1}} ^ {T} (x_ {t} - {ar x}) ^ {2} (y_ {t} - {ar y})}}.$
Инструментальные переменные — регрессия, требующая некоторых дополнительных переменных данных z, называется инструменты, были доступны. Эти переменные не должны коррелировать с ошибками в уравнении для зависимой переменной (действительный), и они также должны быть коррелированы (соответствующий) с истинными регрессорами Икс*. Если такие переменные могут быть найдены, то оценка принимает вид
${hat eta} = {frac {{frac {1} {T}} sum _ {{t = 1}} ^ {T} (z_ {t} - {ar z}) (y_ {t} - {ar y })} {{frac {1} {T}} sum _ {{t = 1}} ^ {T} (z_ {t} - {ar z}) (x_ {t} - {ar x})}} .$

Многопараметрическая линейная модель

Многопараметрическая модель выглядит точно так же, как простая линейная модель, только на этот раз β, η_т, Икс_т и Икс*_т находятся k ×1 векторов.

${egin {case} y_ {t} = alpha + eta 'x_ {t} ^ {*} + varepsilon _ {t}, x_ {t} = x_ {t} ^ {*} + eta _ {t}. конец {case}}$

В случае, когда (ε_т,η_т) вместе нормально, параметр β не идентифицируется тогда и только тогда, когда существует неособаяк × к блочная матрица [а А] (куда а это k ×1 вектор) такая, что a′x * распространяется нормально и независимо отA′x *. В случае, когда ε_т, η_t1,…, η_тк взаимно независимы, параметрβ не идентифицируется тогда и только тогда, когда в дополнение к указанным выше условиям некоторые ошибки могут быть записаны как сумма двух независимых переменных, одна из которых является нормальной.^[14]

Некоторые из методов оценивания многомерных линейных моделей:

Всего наименьших квадратов является продолжением Регрессия Деминга к многопараметрической настройке. Когда все k+1 компоненты вектора (ε,η) имеют равные дисперсии и независимы, это эквивалентно запуску ортогональной регрессии у на векторе Икс — то есть регрессия, которая минимизирует сумму квадратов расстояний между точками (у_т,Икс_т) и k-мерная гиперплоскость «наилучшего соответствия».
В метод моментов оценщик ^[15] можно построить на основе моментных условий E [z_т·(у_т − α − β’x_т)] = 0, где (5k+3) -мерный вектор инструментов z_т определяется как

$egin {align} & z_t = left (1 z_ {t1} 'z_ {t2}' z_ {t3} 'z_ {t4}' z_ {t5} 'z_ {t6}' z_ {t7} 'ight)', quad ext {где} & z_ {t1} = x_t circ x_t & z_ {t2} = x_t y_t & z_ {t3} = y_t ^ 2 & z_ {t4} = x_t circ x_t circ x_t - 3 ig (имя оператора {E} [x_tx_t '] circ I_k ig) x_t & z_ {t5} = x_t circ x_t y_t - 2 ig (имя оператора {E} [y_tx_t '] circ I_k ig) x_t - y_t ig (имя оператора {E} [x_tx_t'] circ I_k ig) iota_k & z_ {t6} = x_t y_t ^ 2 - имя оператора {E} [y_t ^ 2] x_t - 2y_ имя оператора {E} [x_ty_t] & z_ {t7} = y_t ^ 3 - 3y_toperatorname {E} [y_t ^ 2] конец {выровнять}$

куда обозначает Произведение Адамара матриц и переменных Икс_т, у_т были предварительно разорваны. Авторы метода предлагают использовать модифицированную оценку IV Фуллера.^[16]

При необходимости этот метод может быть расширен для использования моментов выше третьего порядка, а также для учета переменных, измеренных без ошибок.^[17]
В инструментальные переменные подход требует поиска дополнительных переменных данных z_т который будет служить инструменты для неверно измеренных регрессоров Икс_т. Этот метод является наиболее простым с точки зрения реализации, однако его недостаток в том, что он требует сбора дополнительных данных, что может быть дорогостоящим или даже невозможным. Когда инструменты могут быть найдены, оценщик принимает стандартную форму

${hat eta} = {ig (} X'Z (Z'Z) ^ {{- 1}} Z'X {ig)} ^ {{- 1}} X'Z (Z'Z) ^ {{- 1}} З'ы.$

Нелинейные модели

Общая модель нелинейных ошибок измерения принимает форму

${egin {case} y_ {t} = g (x_ {t} ^ {*}) + varepsilon _ {t}, x_ {t} = x_ {t} ^ {*} + eta _ {t} .end {случаи}}$

Здесь функция грамм может быть параметрическим или непараметрическим. Когда функция грамм параметрический, он будет записан как г (х *, β).

Для общего векторного регрессора Икс* условия для модели идентифицируемость не известны. Однако в случае скалярной Икс* модель идентифицирована, если функция грамм имеет «логарифмическую» форму ^[18]

$g (x ^ {*}) = a + bln {ig (} e ^ {{cx ^ {*}}} + d {ig)}$

и скрытый регрессор Икс* имеет плотность

$f _ {{x ^ {*}}} (x) = {egin {case} Ae ^ {{- Be ^ {{Cx}} + CDx}} (e ^ {{Cx}} + E) ^ {{- F}}, & {ext {if}} d> 0 Ae ^ {{- Bx ^ {2} + Cx}} & {ext {if}} d = 0end {case}}$

где константы A, B, C, D, E, F может зависеть от а, б, в, г.

Несмотря на этот оптимистичный результат, в настоящее время не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако есть несколько методов, которые используют некоторые дополнительные данные: инструментальные переменные или повторные наблюдения.

Методы инструментальных переменных

Метод моделирования моментов Ньюи^[19] для параметрических моделей — требуется дополнительный набор наблюдаемых переменные-предикторы z_т, так что истинный регрессор может быть выражен как

$x_ {t} ^ {*} = pi _ {0} 'z_ {t} + sigma _ {0} zeta _ {t},$

куда π₀ и σ₀ являются (неизвестными) постоянными матрицами, и ζ_т ⊥ z_т. Коэффициент π₀ можно оценить с помощью стандартных наименьших квадратов регресс Икс на z. Распределение ζ_т неизвестен, однако мы можем смоделировать его как принадлежащий к гибкому параметрическому семейству — Серия Эджворта:

$f_ {zeta} (v;, гамма) = phi (v), сумма extstyle _ {{j = 1}} ^ {J}! гамма _ {j} v ^ {j}$

куда ϕ это стандартный нормальный распределение.

Смоделированные моменты могут быть вычислены с помощью выборка по важности алгоритм: сначала мы генерируем несколько случайных величин {v_ts ~ ϕ, s = 1,…,S, т = 1,…,Т} из стандартного нормального распределения, то вычисляем моменты при т-е наблюдение как

$m_ {t} (heta) = A (z_ {t}) {frac {1} {S}} sum _ {{s = 1}} ^ {S} H (x_ {t}, y_ {t}, z_ {t}, v _ {{ts}}; heta) sum _ {{j = 1}} ^ {J}! gamma _ {j} v _ {{ts}} ^ {j},$

куда θ = (β, σ, γ), А это просто некоторая функция инструментальных переменных z, и ЧАС — двухкомпонентный вектор моментов

${начало {выровнено} & H_ {1} (x_ {t}, y_ {t}, z_ {t}, v _ {{ts}}; heta) = y_ {t} -g ({hat pi} 'z_ {t } + sigma v _ {{ts}}, eta), & H_ {2} (x_ {t}, y_ {t}, z_ {t}, v _ {{ts}}; heta) = z_ {t} y_ { t} - ({hat pi} 'z_ {t} + sigma v _ {{ts}}) g ({hat pi}' z_ {t} + sigma v _ {{ts}}, eta) конец {выровнено}}$

С моментными функциями м_т можно применить стандарт GMM метод оценки неизвестного параметра θ.

Повторные наблюдения

В этом подходе два (а может и больше) повторных наблюдения регрессора Икс* доступны. Оба наблюдения содержат собственные ошибки измерения, однако эти ошибки должны быть независимыми:

${egin {case} x _ {{1t}} = x_ {t} ^ {*} + eta _ {{1t}}, x _ {{2t}} = x_ {t} ^ {*} + eta _ {{ 2t}}, конец {case}}$

куда Икс* ⊥ η₁ ⊥ η₂. Переменные η₁, η₂ не обязательно должны быть одинаково распределены (хотя, если они есть, эффективность оценщика может быть немного улучшена). Только с этими двумя наблюдениями можно согласованно оценить функцию плотности Икс* с использованием Котлярского деконволюция техника.^[20]

Метод условной плотности Ли для параметрических моделей.^[21] Уравнение регрессии может быть записано в терминах наблюдаемых переменных как

$имя оператора {E} [, y_ {t} | x_ {t},] = int g (x_ {t} ^ {*}, eta) f _ {{x ^ {*} | x}} (x_ {t} ^ {*} | x_ {t}) dx_ {t} ^ {*},$

где можно было бы вычислить интеграл, если бы мы знали условную функцию плотности ƒ_{х * | х}. Если эта функция может быть известна или оценена, тогда проблема превратится в стандартную нелинейную регрессию, которую можно оценить, например, с помощью NLLS метод.
Предполагая для простоты, что η₁, η₂ одинаково распределены, эта условная плотность может быть вычислена как

${шляпа f} _ {{x ^ {*} | x}} (x ^ {*} | x) = {гидроразрыв {{шляпа f} _ {{x ^ {*}}} (x ^ {*}) } {{hat f} _ {{x}} (x)}} prod _ {{j = 1}} ^ {k} {hat f} _ {{eta _ {{j}}}} {ig (} x _ {{j}} - x _ {{j}} ^ {*} {ig)},$

где с небольшим нарушением обозначений Икс_j обозначает j-й компонент вектора.
Все плотности в этой формуле можно оценить с помощью обращения эмпирического характеристические функции. Особенно,

$egin {align} & hat varphi_ {eta_j} (v) = frac {hatvarphi_ {x_j} (v, 0)} {hatvarphi_ {x ^ * _ j} (v)}, quad ext {где} hatvarphi_ {x_j} (v_1, v_2) = frac {1} {T} sum_ {t = 1} ^ T e ^ {iv_1x_ {1tj} + iv_2x_ {2tj}}, hatvarphi_ {x ^ * _ j} (v) = exp int_0 ^ v frac {partialhatvarphi_ {x_j} (0, v_2) / partial v_1} {hatvarphi_ {x_j} (0, v_2)} dv_2, & hat varphi_x (u) = frac {1} {2T} sum_ {t = 1} ^ T Big (e ^ {iu'x_ {1t}} + e ^ {iu'x_ {2t}} Big), quad hat varphi_ {x ^ *} (u) = frac {hatvarphi_x (u)} {prod_ {j = 1} ^ k hatvarphi_ {eta_j} (u_j)}. конец {выровнять}$

Чтобы инвертировать эти характеристические функции, необходимо применить обратное преобразование Фурье с параметром обрезки C необходимо для обеспечения численной устойчивости. Например:

${hat f} _ {x} (x) = {frac {1} {(2pi) ^ {k}}} int _ {{- C}} ^ {{C}} cdots int _ {{- C}} ^ {C} e ^ {{- iu'x}} {hat varphi} _ {x} (u) du.$
Оценщик Шеннаха для параметрической линейной по параметрам нелинейной модели в переменных.^[22] Это модель вида
${egin {case} y_ {t} = extstyle sum _ {{j = 1}} ^ {k} eta _ {j} g_ {j} (x_ {t} ^ {*}) + sum _ {{j = 1}} ^ {ell} eta _ {{k + j}} w _ {{jt}} + varepsilon _ {t}, x _ {{1t}} = x_ {t} ^ {*} + eta _ {{ 1t}}, x _ {{2t}} = x_ {t} ^ {*} + eta _ {{2t}}, конец {случаи}}$

куда ш_т представляет переменные, измеренные без ошибок. Регрессор Икс* здесь — скаляр (метод можно распространить на случай векторных Икс* также).
Если бы не ошибки измерения, это было бы стандартным линейная модель с оценщиком

$hat {eta} = ig (шляпа {имя оператора {E}} [, xi_txi_t ',] ig) ^ {- 1} шляпа {имя оператора {E}} [, xi_t y_t,],$

куда

$xi _ {t} '= (g_ {1} (x_ {t} ^ {*}), cdots, g_ {k} (x_ {t} ^ {*}), w _ {{1, t}}, cdots , w _ {{l, t}}).$

Оказывается, все ожидаемые значения в этой формуле можно оценить с помощью одного и того же трюка с деконволюцией. В частности, для типичной наблюдаемой ш_т (который может быть 1, ш_1т, …, ш_{ℓ т}, или же у_т) и некоторая функция час (который может представлять любой грамм_j или же грамм_яграмм_j) у нас есть

$имя оператора {E} [, w_ {t} h (x_ {t} ^ {*}),] = {frac {1} {2pi}} int _ {{- infty}} ^ {infty} varphi _ {h} (-u) psi _ {w} (u) du,$

куда φ_час это преобразование Фурье из час(Икс*), но с использованием того же соглашения, что и для характеристические функции,

$varphi _ {h} (u) = int e ^ {{iux}} h (x) dx$ ,

и

$psi_w (u) = имя оператора {E} [, w_te ^ {iux ^ *},] = frac {имя оператора {E} [w_te ^ {iux_ {1t}}]} {имя оператора {E} [e ^ {iux_ {1t}}]} exp int_0 ^ u ifrac {имя оператора {E} [x_ {2t} e ^ {ivx_ {1t}}]} {имя оператора {E} [e ^ {ivx_ {1t}}]} dv$

Полученная оценка непротиворечиво и асимптотически нормально.
Оценщик Шеннаха для непараметрической модели.^[23] Стандарт Оценка Надарая – Ватсона для непараметрической модели принимает вид

$шляпа {g} (x) = гидроразрыв {шляпа {имя оператора {E}} [, y_tK_h (x ^ * _ t - x),]} {шляпа {имя оператора {E}} [, K_h (x ^ * _ t - x) ,]},$

для подходящего выбора ядро K и пропускная способность час. Оба ожидания здесь можно оценить с помощью того же метода, что и в предыдущем методе.

дальнейшее чтение

Догерти, Кристофер (2011). «Стохастические регрессоры и ошибки измерения». Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. С. 300–330. ISBN 978-0-19-956708-9.
Кмента Ян (1986). «Оценка с недостаточными данными». Элементы эконометрики (Второе изд.). Нью-Йорк: Макмиллан. стр.346–391. ISBN 978-0-02-365070-3.
Шеннах, Сюзанна. «Погрешность измерения в нелинейных моделях — обзор». Серия рабочих документов Cemmap. Cemmap. Получено 6 февраля, 2018.

внешняя ссылка

Исторический обзор линейной регрессии с ошибками в обеих переменных, Дж. Гиллард 2006
Лекция по эконометрике (тема: Стохастические регрессоры и ошибка измерения) на YouTube к Марк Тома.

Источник

Пусть переменные (y_{i}) и (x_{i}^{*}) связаны точным соотношением

(y_{i} = beta_{1} + beta_{2}*x_{i}^{*})

Однако вместо точных значений регрессора мы наблюдаем измеренные с ошибкой значения: (x_{i} = x_{i}^{*} + varepsilon_{i}), (text{cov}left( x_{i}^{*},varepsilon_{i} right) = 0).

Мы оцениваем методом наименьших квадратов уравнение

(y_{i} = beta_{1} + beta_{2}*x_{i} + u_{i}.)

Покажем, что и в этом случае МНК-оценка (widehat{beta_{2}}) будет несостоятельной.

Так как (y_{i} = beta_{1} + beta_{2}*left( x_{i} — varepsilon_{i} right) = beta_{1} + beta_{2}*x_{i} — beta_{2}*varepsilon_{i},) то

(u_{i} = — beta_{2}*varepsilon_{i}.)

(widehat{beta_{2}}text{~~}overset{text{~~p~~}}{rightarrow} beta_{2} + frac{text{cov}left( x_{i}, u_{i} right)}{text{var}left( x_{i} right)} = beta_{2} + frac{text{cov}left( x_{i}^{*} + varepsilon_{i}, — beta_{2}*varepsilon_{i} right)}{text{var}left( x_{i} right)} =)

(= beta_{2} — beta_{2}frac{text{cov}left( x_{i}^{*}, varepsilon_{i} right) + covleft( varepsilon_{i}, varepsilon_{i} right)}{text{var}left( x_{i} right)} = beta_{2} — beta_{2}frac{text{var}left( varepsilon_{i} right)}{text{var}left( x_{i} right)} =)

(= beta_{2} — beta_{2}frac{text{var}left( varepsilon_{i} right)}{text{var}left( varepsilon_{i} right) + varleft( x_{i}^{*} right)} = frac{text{var}left( x_{i}^{*} right)}{text{var}left( varepsilon_{i} right) + varleft( x_{i}^{*} right)}*beta_{2})

Величина (left| frac{text{var}left( x_{i}^{*} right)}{text{var}left( varepsilon_{i} right) + text{var}left( x_{i}^{*} right)} right| < 1), поэтому независимо от знака (beta_{2}) эта оценка несостоятельна и смещена к нулю.

Можно привести много примеров ситуаций, когда в эконометрическом исследовании приходится мириться с ошибками измерения. Скажем, если вашим регрессором является уровень безработицы или валовой внутренний продукт, вы неизбежно столкнетесь с этой проблемой, так как статистические службы не могут измерить указанные показатели идеально точно.

Исследования, опирающиеся на индивидуальные данные, также иногда связаны с ошибками измерений. Типичная ситуация тут — использование данных, основанных на опросах. Если регрессором в вашей модели является возраст индивида, информация о котором собрана в ходе опроса (например, в процессе переписи населения), то, скорее всего, в измерениях будут содержаться неточности: демографам хорошо известно, что многие индивиды склонны при ответах на вопросы о возрасте округлять его до чисел, кратных пяти или десяти годам. Похожий эффект возникает и в случае ответов на вопросы о доходе.

Конечно, в условиях ошибок измерений всегда можно посоветовать исследователю найти данные поточнее. Это хороший совет. Однако, к сожалению, на практике последовать ему бывает трудно, поэтому приходится использовать альтернативный путь.

Как мы выясним в главе 8, проблема ошибок измерения также может быть решена при помощи инструментальных переменных.

Иногда, однако, эту проблему просто игнорируют. Мотивация тут такая: если вам интересна не количественная оценка силы влияния переменной x на переменную y, а просто сам факт наличия или отсутствия этого влияния, то, получив статистически значимый коэффициент при регрессоре, вы можете не предпринимать дальнейших корректировок. Действительно, мы точно знаем, что ошибки измерения сдвигают оценку коэффициента к нулю. Поэтому, если коэффициент оказался значимым даже в условиях ошибок измерения, то после их устранения он тем более должен быть значим.

Источник

Теория ошибок.

Ошибки измерения.

Измерение объектов не могут быть
произведены абсолютно точно, и каждое
конкретное измерение даёт лишь
приближённое значение величины явления,
истинное значение которой неизвестно.
Ошибки измерения представляют собой
разность между результатом измерения
величины явления и истинным его значением.
E– ошибка Х – результат
измерения, А – истинное значение (Е=Х-А).

Рассмотрим такие измерения, производимые
одним наблюдателем, одним и тем же
инструментом в одинаковых условиях.
Это так называемое равноточные измерения.
Различают два вида ошибок измерения:

1. Систематические – такие, которые при
данных условиях проведения измерения
имеют определённое значение, например
ошибка измерительного прибора.

2. Случайные ошибки 0 такие, которые
являются результатом взаимодействия
большого числа незначительных в
отдельности факторов и имеют в каждом
отдельном случае различные значения.

Задача статистики предусмотреть
возможность возникновения систематических
ошибок и добиться либо их ликвидации,
либо сведения к минимуму. Случайные
ошибки измерения обладают рядом свойств:
при большом числе измерений – крупные
ошибки встречаются реже мелких, и число
положительных оценок примерно равно
числу отрицательных.

Если ошибки получаются весьма малыми
по сравнению с величиной явления, то
ими или пренебрегают, или учитывают
только наибольшую возможную ошибку,
чтобы обезопасить себя от влияния
случайной неточности.

В теории ошибок изучаются такие ошибки,
которые вялясь с одной стороны ошибками
случайного характера по своему абсолютному
значению настолько велики, что ими
пренебречь нельзя, а с другой стороны
для низ существует закон, позволяющий
установить зависимость между величиной
ошибки и вероятностью её появления.
Закон случайных ошибок Гаусса состоит
в том, что случайные ошибки подчиняются
закону нормального распределения.

Точность одного измерения и средняя
ошибка сводного результата измерения.

Принимая за действительное значение
измеряемой величины при равноточном
измерении среднюю арифметическую из
всех результатов измерений можно
охарактеризовать точность одного
измерения из абсолютных величин значений
ошибок.

Еср.=∑|x-xср.|
/n– точность одного
измерения,X– измерение,
Хср. — измерение

Eср (от хср.) =Eср.
/–
среднее

δ =

А за меру точность соответствие принятой
средней арифметической истинному
значению измеряемой величины Aпринимают среднюю ошибку сводного
результата измерения.

Квадратическая точность измерения и
средняя квадратическая ошибка.

Если в качестве меры точности одного
измерения принять несреднюю арифметическую
из абсолютных средних значений ошибок,
а среднюю квадратическую из ошибок
измерений, так называемую квадратическую
точность измерения (δ), то средняя
квадратическая ошибка найденной средней
арифметической из ошибок вычисления
вычисляется по формуле

δср(хср)=δ/

Между средней квадратической ошибкой
и средней ошибкой и средней ошибкой
сводного результата измерения существует
следующая связь.

δср(хср)/Eср.(хср)=~1,25
(1,250-1,259).

Если находится в этом интервале, То
случайные ошибки подчиняются закону
нормального распределения.

Вероятная ошибка.

За меру точности одного измерения иногда
принимают вероятную ошибку

r(xср.)=2/3δср(хср)

Наиболее вероятные границы сводных
результатов измерения.

В качестве значения измеряемой величины
применяется среднее арифметическое
всех измерений (если они равноточны).
Использование отклонений результатов
измерений от средней из них (X-Xср.),
называемых в теории ошибок кажущимися
ошибками позволяет произвести оценку
точности соответствия средней
арифметической неизвестному истинному
значению измеряемой величины А. Для
этой цели используют утроенную среднюю
квадратическую среднюю квадратическую
ошибку сводного результата измерения.
Найденные границы соблюдаются с большой
вероятностью (99,7)

A=Xср +-
3δср(хср)

Задача: произведено 10 измерений.
Определить:

1) точность одного измерения

2) среднюю ошибку сводного результата
измерения

3) квадратическую точность измерения

4) среднюю квадратическую ошибку

5) связь между средней квадратической
ошибкой и средней ошибкой сводного
результата измерений.

6) вероятную ошибку

7) вероятные границы сводных результатов
измерений.

140, 141, 142, 138,, 143, 139, 141, 142, 144, 145

п/п	Х	Х-Xср	\|x-xср\|	(x-xср)^2
1	138	-3,5	3,5	12,25
2	139	-2,5	2,5	6,25
3	140	-1,5	1,5	2,25
4	141	-0,5	0,5	0,25
5	142	0,5	0,5	0,25
6	143	1,5	1,5	2,25
7	144	2,5	2,5	6,25
8	145	3,5	3,5	12,25
9	142	0,5	0,5	0,25
10	141	-0,5	0,5	0,25
Итого	141,5		17	42,5

Еср=∑|x-xср| / n – точность одного измерения,
X – измерение, Хср — измерение

Eср (хср) = Eср. /
– среднее

δ =

1. Хср.=141,5

Е=

Eср=17/10=1,7

2.Eср(хср)=1,7 / (10)^1/2=0,538

3. δ=
=2,061

4. δср(хср)=δ /= 2,061/= 0,652

5. δср(хср)/Eср.(хср)=~1,25 (1,250-1,259).

0,652/0,537=1,214 (не удовлетворяет) – не
подчиняется закону нормального
распределения

6. r(xср.)=2/3δср(хср)=0,435 – вероятная
ошибка

7. 135,137 < A< 147, 683

Но т.к. 5 пункт не удовлетворяет, то
измерения не верны, и их нужно менять.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Ошибки измерения показателей, принятых в качестве аргументов, должны быть ничтожно малы по сравнению с ошибками измерения зависимой переменной. [c.66]

Теперь, пользуясь независимостью и аддитивностью v, q, м1а, включим ошибку измерения зависимой переменной. [c.79]

До сих пор мы безоговорочно предполагали, что переменные X измерены без ошибок и что единственной допустимой формой ошибок в рассматриваемом соотношении могут быть возмущения и. Последнее было продиктовано стремлением учесть воздействие различных объясняющих переменных, не включенных явно в это соотношение. Можно, конечно, ввести составляющую, которая отражает ошибку измерения зависимой переменной Y, и не нарушить все полученные ранее результаты. Выясним теперь, к чему приведет предположение о наличии ошибки измерения у переменных X. Мы предполагаем, что р есть вектор коэффициентов, полученных для точно измеренных значений переменных X. Что произойдет, если воспользоваться нашей техникой наименьших квадратов в применении к имеющимся в наличии реальным измерениям переменных X и переменной У Ответ на этот вопрос таков оценки, полученные обыкновенным методом наименьших квадратов, будут не только смещенными, но и несостоятельными. Это можно продемонстрировать следующим образом. [c.280]

Ошибки в измерениях зависимой переменной. Предположим, что истинной является модель (8.1), но вектор у измеряется с ошибкой, т. е. наблюдается вектор у — у + и, где и — ошибки, имеющие нулевое математическое ожидание и не зависящие от е и X. Тогда нетрудно понять, что построение МНК-оценок на основании у эквивалентно регрессии [c.214]

Стохастические связи между различными явлениями и их признаками в отличие от функциональных, жестко детерминированных, характеризуются тем, что результативный признак (зависимая переменная) испытывает влияние не только рассматриваемых независимых факторов, но и подвергается влиянию ряда случайных (неконтролируемых) факторов. Причем полный перечень факторов не известен, так же как и точный механизм их воздействия на результативный признак. В этих условиях значения зависимой переменной тоже не могут быть измерены точно. Их можно определить с определенной вероятностью, поскольку они подвержены случайному разбросу и содержат неизбежные ошибки измерения переменных. [c.69]

Возникновение понятия статистической связи обуславливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п. [c.51]

В дальнейшем используются следующие обозначения Xt, xt, Zt, ztr q, v — зависимая и независимая переменные при отсутствии и наличии ошибок измерения, ошибки измерения в этих переменных и 1 ы<2> d2> — остаточные возмущения и белый шум в уравнениях для временных рядов и для временных рядов перекрестных выборок М, s2, л(1>, я(2), 2W, 2(2) — математическое ожидание, выборочная дисперсия, остаточные ковариационные матрицы и ковариационные матрицы коэффициентов в уравнениях для временных рядов и временных рядов перекрестных выборок N(0, s2), гг, Т, п, К, Е, i, ML — обозначение нормального распределения, коэффициент остаточной марковской автокорреляции первого порядка, количество наблюдений временного ряда и выборочного обследования, число независимых переменных, единичная матрица и единичный вектор, обозначение оценки наибольшего правдоподобия. [c.73]

Если рассмотреть зависимость одной из характеристик системы T V(X/), как функцию только одной переменной х/, (рис. 7.2), то при фиксированных значениях xt будем получать различные значения тЦх,). Разброс значений т в данном случае определяется не только ошибками измерения, а главным образом влиянием помех z,. Сложность задачи оптимального управления характеризуется не только сложностью самой зависимости Т У( Ь 2> > )> но и влиянием z,, [c.243]

Изучение зависимостей экономических переменных начнем со случая двух переменных (обозначим их х и у). Этот случай наиболее прост и может быть рассмотрен графически. Предположим, что имеются ряды значений переменных, соответствующие им точки нанесены на график и соединены линией. Если это реальные статистические данные, то мы никогда не получим простую линию — линейную, квадратичную, экспоненциальную и т.д. Всегда будут присутствовать отклонения зависимой переменной, вызванные ошибками измерения, влиянием неучтенных величин или случайных факторов. Но если мы не получили, например, точную прямую линию, это еще не значит, что в основе рассматриваемой зависимости лежит нелинейная функция. Возможно, зависимость переменных линейна, и лишь случайные факторы приводят к некоторым отклонениям от нее. То же самое можно сказать и про любой другой вид функции. Связь переменных, на которую накладываются воздействия случайных факторов, называется статистической связью. Наличие такой связи заключается в том, что изменение одной переменной приводят к изменению математического ожидания другой пе- [c.293]

Понятно, что можно рассматривать общий случай, когда есть ошибки в измерениях независимых и зависимых переменных. Ясно, что, как и в предыдущем случае, применение метода наименьших квадратов будет приводить к смещенным и несостоятельным оценкам. [c.215]

Регрессионная зависимость случайного результирующего показателя г) от неслучайных предсказывающих переменных X (схема В). Природа такой связи может носить двойственный характер а) регистрация результирующего показателя г неизбежно связана с некоторыми случайными ошибками измерения е, в то время как предикторные (объясняющие) переменные X = (х(1) лс(2),. .., х(р ) измеряются без ошибок (или величины этих ошибок пренебрежимо малы по сравнению с со-ответствукмвдми ошибками измерения результирующего показателя) б) значения результирующего показателя г) зависят не только от соответствующих значений X, но и еще от [c.35]

Отрицательные знаки коэффициентов регрессии соответствуют здесь теоретическим представлениям. Коэффициент при переменной GNPзначительно меньше по абсолютной величине, чем коэффициент при RSR, но это не значит, что данная величина воздействует на зависимую переменную слабее. Здесь все определяется единицами измерения, и если ВНП измерять не в миллиардах, а в триллионах долларов, то соответствующий коэффициент регрессии будет равен не 0,017, а 17, при стандартной ошибке 4. [c.336]

В предыдущих разделах предполагалось, что независимые переменные (матрица X) являются неслучайными. Ясно, что такое условие выполнено не всегда, например, во многих ситуациях при измерении независимых переменных могут возникать случайные ошибки. Кроме того, при анализе временных рядов значение исследуемой величины в момент t может зависеть от ее значений в предыдущие моменты времени, т. е. в некоторых уравнениях эти значения выступают в качестве независимых, а в других — в качестве зависимых переменных (модели с лагированными переменными). Поэтому возникает необходимость рассматривать модели со стохастическими регрессорами. [c.149]

На практике редко встречается ситуация, когда матрица М вырождена. Более распространен случай, когда она плохо обусловлена (между переменными Z существуют зависимости близкие к линейным). В этом случае имеет место мультиколлинеарность факторов. Поскольку гипотеза 2 в части отсутствия ошибок измерения, как правило, нарушается, получаемые (при мультиколлинеарности) оценки в значительной степени обусловлены этими ошибками измерения. В таком случае (если связь существует), обычно, факторы по отдельности оказываются незначимыми по t-критерию, а все вместе существенными по F-критерию. Поэтому в регрессию стараются не вводить факторы сильно скоррелированные с остальными. [c.23]

Третьим источником ошибок являются ошибки наблюдения и мерения. Точная линейная зависимость Z = а + (ЗХ переменно X может оказаться скрытой в результате того, что вместо H TI значения Z мы будем наблюдать величину Y = Z + и, где и — о измерения. Тогда мы имеем [c.20]

Источник

Возможные ошибки спецификации модели:

1. Неправильный выбор вида уравнения
регрессии

2. В уравнение регрессии включена лишняя
(незначимая) переменная

3. В уравнении регрессии пропущена
значимая переменная

Неправильный выбор вида функции в
уравнении

Пусть на первом этапе была сделана
спецификация модели в виде:

в
которой функция f_F(x,a₀,a₁)
выбрана не верно. Предположим, что
y_T=f_T(x,a₀,a₁)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:

И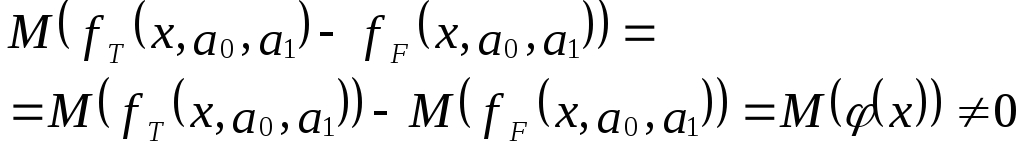з
выражения следует:

Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций f_T
и f_F
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется

Следовательно, в результате оценивания
такой модели параметры а₀ и а₁
будут смещенными

Симптомы наличия ошибки спецификации
первого типа:

1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации

2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений

Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!

В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.

Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.

2. В уравнение регрессии включена
лишняя переменная

П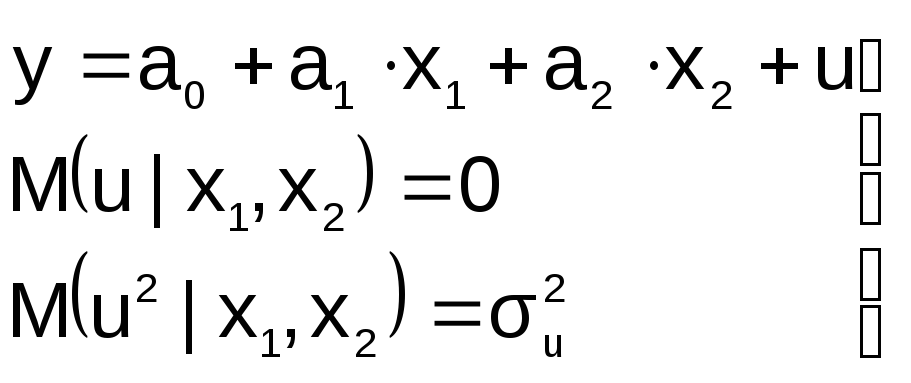усть
на этапе спецификации в модель включена
«лишняя» переменная, например, X₂

«Правильная»
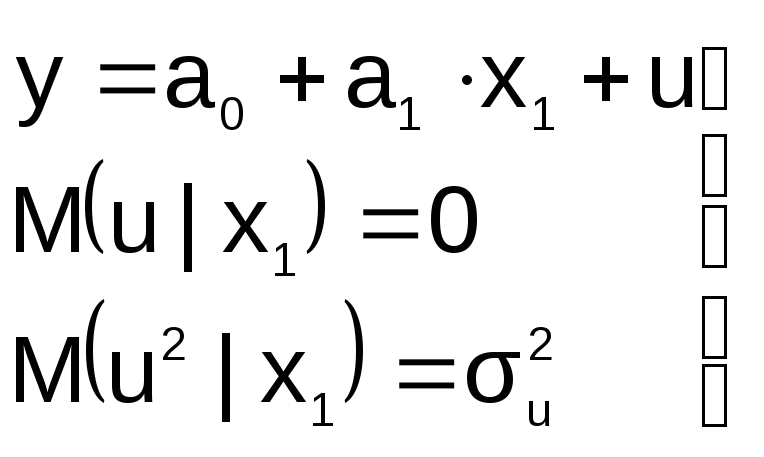
спецификация должна иметь вид:

Последствия:

1.
Оценки параметров а₀, а₁, а₂останутся несмещенными, но потеряют
свою эффективность (точность)

2. Увеличивается ошибка прогноза по
модели

как за счет ошибок оценок коэффициентов
и σ_u,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора

Диагностика:

В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H₀: a_i=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n₂ = n – (k+1)

3.
В модели не достает важной переменной

Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели

Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель

29. Фиктивные переменные и особенности их использования в моделях.

На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.

Примеры.

Моделирование влияния пола специалистов
на уровень зарплаты.

Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)

Модель инфляции с учетом различных
видов регулирования со стороны государства

Возможны два подхода к решению задачи:

— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной

— учесть влияние качественного фактора
в одной модели

Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели

Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N

Предположим:

Зависимость затрат на обучение от
количества учащихся N в
обоих типах школ одинакова

2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам

Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:

Y^o
= a₀ +
a₁N +u

Y^s
= b₀ +
a₁N +
v

Обе
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:

Спецификация такой модели имеет вид:

Y = a₀
+ a₁N
+ δd + u

Тогда при d=0 получим Y^o
= a₀ + a₁N
+ u

при d=1 получим Y^s
= (a₀+δ)
+a₁N +
v

d – фиктивная переменная
сдвига

Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор

Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)

Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные

Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена

Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной

В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора

Например:

Однако, если взять спецификацию модели
в виде:

Y=a₀
+ a₁d₁+a₂d₂+a₃d₃+a₄d₄+a₅N+u

при этом всегда верно тождество
d₁+d₂+d₃+d₄=1

Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.

Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает

Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»

Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;

d=1 – профессиональная
школа

Спецификацию модели следует записать
в виде:

Y = a₀
+ a₁N
+ a₂*d
+ a₃dN
+U

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

анастасия александровна янченко

Эксперт по предмету «Эконометрика»

Задать вопрос автору статьи

Проблема спецификации эконометрической модели

Проблема спецификации эконометрической модели предполагает определение:

конечной цели моделирования;
набора эндогенных и экзогенных переменных;
состава и структуры системы уравнений, набора переменных;
первоначальных ограничений стохастических составляющих.

Спецификация в эконометрике является важнейшим этапом исследования, эффективность решения влияет на успех исследования в целом. В основе спецификации — имеющиеся теории, интуиция и специальные знания.

Проблема идентифицируемости

В эконометрике проблема идентифицируемости сводится к следующему: нас интересует такие эндогенные переменные, которые относятся к случайным величинам.

Уравнение структурной формы является точно идентифицируемым тогда, когда каждый участвующий неизвестный коэффициент однозначно восстанавливается по коэффициентам приведенной формы, не ограничивая значения последних.

Учим создавать игры

Создавай 3D-графику и концепты, придумывай персонажей, учись программировать с нуля

Записаться на курс

Определение 1

Эконометрическую модель можно назвать точно идентифицируемой, если каждое уравнение ее структурной формы является точно идентифицируемым.

Если какой-либо коэффициент не может быть восстановлен, не идентифицируемо и уравнение, и модель. Проблемы идентификации сводятся к «настройкам» модели по реальным статистическим данным.

Проблема верификации

Замечание 1

Проблема верификации применительно к эконометрическим моделям заключается в разрешении вопросов относительно возможностей использования модели.

Иными словами эта проблема сводится к точности имитационных и прогнозных расчетов. Верификация подразумевает статистическую проверку гипотез и анализ параметров точности оценки. Зачастую применяется ретроспективный расчет: исходные данные делятся на части: обучающая выборка и экзаменующая выборка.

«Проблемы эконометрики» 👇

Обучающая выборка позволяет определить значения неизвестных параметров и получить модельные значения для экзаменующей выборки, которые затем подлежат сравнению с реальными значениями.

Недостаточный набор данных

Замечание 2

Проблема недостаточности данных заключается в том, что имеющиеся данные могут быть недостаточны для определения функциональной связи между переменными, или они мало варьируются для выявления отличий влияния одних факторов от влияния других.

Последнюю проблему в эконометрическом моделировании часто называют «мультиколлинеарностью».

В отличие от экспериментальной науки, отдельный исследователь, изучающий экономические процессы обычно не имеет возможности заметно повлиять на них.

Для восполнения недостатка данных, исследователь должен принимать определенные априорные допущения, которые часто могут быть недостаточно обоснованными.

Обычно функциональная форма эконометрической модели неизвестна заранее. В таком случае целесообразно использовать непараметрические методы оценивания. Но применение подобных методов требует достаточно значительного набора данных. На практике поэтому, как правило, предполагается, что зависимость двумя переменных линейна. Это связано с тем, что линейная зависимость подразумевает хороший уровень аппроксимации гладкой зависимости в определенной окрестности. Однако нет никаких гарантий, что истинная зависимость не будет нелинейной в интервале, к которому отнесены данные.

В случае применении методов эконометрики следует понимать, что обычно постулируемые свойства имеют асимптотический характер, или проявляются при стремлении числа наблюдений к бесконечности. Например, если линейная регрессия подразумевает использование в качестве регрессоров лагов (запаздывания) зависимых переменных, то, даже при выполнении стандартных предположений регрессионного анализа, итоговые оценки будут смещенными, но состоятельными.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Шпоры по эконометрике.

№ 1. СПЕЦИФИКАЦИЯ МОДЕЛИ

Простая регрессия представляет собой регрессию между двумя переменными у и х, т.е. модель вида , где у результативный признак; х — признак-фактор.

Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида

Спецификация модели — формулировка вида модели, исходя из соответствующей теории связи между переменными. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. где yj фактическое значение результативного признака;

yxj -теоретическое значение результативного признака.

случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.

Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным у.

К ошибкам спецификации относятся неправильный выбор той или иной математической функции для, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

Ошибки выборки — исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками.

Ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.

Графический метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.

Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у =, то Docm =0. Если имеют место отклонения фактических данных от теоретических (у ) то .

Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 7 раз превышать число рассчитываемых параметров при переменной х.

№ 2 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ.

Линейная регрессия сводится к нахождению уравнения вида или .

Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее параметров а и в.

Оценки параметров линейной регрессии могут быть найдены разными методами.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально а значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.

Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэффициента корреляции.

Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

№ 3. МНК.

МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) минимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Решается система нормальных уравнений

№ 4. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от средне го значения у на две части — «объясненную» и «необъясненную»:

— общая сумма квадратов отклонений

— сумма квадратов отклонения объясненная регрессией — остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степеней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов.

Дисперсия на одну степень свободы D.

F-отношения (F-критерий):

Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.

Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.

Стандартная ошибка коэффициента регрессии

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое

затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr:

Общая дисперсия признака х:

Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации:

№ 5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ

РЕГРЕССИИ

Оценка стат. значимости параметров регрессии проводится с помощью t статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t критерия Стьюдента.

Определяется стат. значимость параметров.

ta ›Tтабл — a стат. значим

tb ›Tтабл — b стат. значим

Находятся границы доверительных интервалов.

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что п

Источник

Мотивационный пример

Технические характеристики

Терминология и предположения

Линейная модель

Простая линейная модель

Многопараметрическая линейная модель

Нелинейные модели

Методы инструментальных переменных

Повторные наблюдения

Рекомендации

дальнейшее чтение

внешняя ссылка

Теория ошибок.

29. Фиктивные переменные и особенности их использования в моделях.

Проблема спецификации эконометрической модели

Проблема идентифицируемости

Проблема верификации

Недостаточный набор данных