Содержание
39. Мерная лента.
Измерение длин линий мерной лентой.
Ошибки измерений расстояний штриховой
стальной лентой 3
41. Оптические
дальномеры. Сущность определения
расстояния 3
42. Теория оптического
нитяного дальномера и его устройство 3
44. Сущность
измерения линий свето- и радиодальномерами,
их использование в геодезии 3
45. Определение
неприступных расстояний 4
46. Основные части
теодолита и их назначение 4
47.Уровни в
геодезических приборах, их назначение
и требования к ним 5
48. Измерение
горизонтальных углов в теодолитном
ходе 5
49. Измерение
вертикальных углов 6
50. Основные
источники ошибок при измерении
горизонтальных углов 6
52. Камеральная
обработка хода тригонометрического
нивелирования 6
54. Построение
государственной плановой сети 6
55. Построение
государственной нивелирной сети 6
56. Методы
нивелирования 7
51. Метод
тригонометрического нивелирования 7
53. Основные виды
геодезических сетей 7
57. Сущность
геометрического нивелирования.
Отклонение визирного луча уровенной
поверхности 61. Геометрические условия,
которым должен удовлетворять нивелир 8
58. Типы нивелиров
59. Основные части уровенного нивелира
и их назначение 8
60. Нивелир с
самоустанавливающейся линией
визирования 9
63. Основные
источники погрешностей геометрического
нивелирования 9
64. Производство
технического нивелирования. Работа на
нивелирной станции 9
66. Сущность
барометрического нивелирования 9
67. Сущность
гидростатического нивелирования 10
68. Сущность
мензульной съемки. Общий порядок
производства съемки 10
69. Построение
съемочной сети для мензульной съемки 10
70. Принадлежности
для мензульной съемки 10
71. Основные части
кипрегеля КА-2 и их назначение 10
72. Основные отличия
кипрегеля КН от кипрегеля КА-2 11
76. Геометрические
условия, которым должен удовлетворять
кипрегель 11
77. Подготовка
планшета 11
78. Съемка ситуации
и рельефа при мензульной съемке 12
79.Сущность
тахеометрической съемки. Приборы.
Тахеометрические ходы 12
80. Глазомерная
съемка 12
81. Общие сведения
об аэрофотосъемке местности. Фотокамера 13
82. Плановый и
перспективный снимки 13
83. Масштаб
горизонтального аэрофотоснимка 13
84. Система координат
снимка и его главная точка 13
85. Основные свойства
моно- и бинокулярного зрения 13
86. Геометрические
свойства аэрофотоснимка 13
87. Измерение высот
по аэрофотоснимкам, понятие об угловом
и продольном параллаксе 14
88. Сущность и этапы
контурно-комбинированной съемки 14
89. Понятие о
стереотопографической съемке. Основные
этапы 14
90. Сущность
фототеодолитной съемки 14
Мерные ленты
обеспечивают точность измерений около
1 / 2 000, т.е. для расстояния в 1 км ошибка
может достигать 50 см. Мерная лента — это
стальная лента шириной от 10 до 20 мм и
толщиной 0.4 — 0.5 мм. Мерные ленты имеют
длину 20, 24 и 50 м. Целые метры отмечены
пластинами с выбитыми на них номерами
метров, полуметры отмечены круглыми
заклепками, дециметры — круглыми
отверстиями диаметром 2 мм.
Фактическая длина
ленты или проволоки обычно отличается
от ее номинальной длины на величину Δl.
Фактическую длину ленты определяют,
сравнивая ее с эталонной мерой. Процесс
сравнения длины мерного прибора с
эталоном называется компарированием,
а установка, на которой производится
компарирование, — компаратором.
Согласно ГОСТ 7502
— 80 допускается отклонение фактической
длины новой ленты 2 мм для 20- и 30-метровых
лент и 3 мм для 50-метровых. Вследствие
износа фактическая длина ленты изменяется,
поэтому компарирование производится
каждый раз перед началом полевых работ.
Длина стальных
рулеток бывает 20, 30, 50, 75 и 100 м. Точность
измерения расстояния стальными рулетками
зависит от методики измерений и колеблется
от 1/2 000 до 1/10 000.
Измерение линий
мерной лентой. Измеряют линии,
последовательно укладывая мерную ленту
в створе линии. Прежде чем измерять
линию, ее нужно подготовить, а именно:
закрепить на местности ее концевые
точки и обозначить створ. Створом линии
называют отвесную плоскость, проходящую
через концевые точки. Для обозначения
створа линию провешивают, т.е. устанавливают
вехи через 50-150 м в зависимости от рельефа.
Измерение линии
выполняют два человека. Они укладывают
ленту в створ и считают число уложений.
В комплект кроме самой ленты входят 6
или 11 шпилек и 2 проволочных кольца
(рис.4.1), на которые надевают шпильки.
Передний мерщик в процессе измерения
линии втыкает шпильки в землю, а задний
собирает их. В конце линии измеряют
остаток с точностью до 1 см.
40. Измерение длины наклонной линии и приведение ее на плоскость горизонта 43. Измерение дальномером наклонных расстояний
Пусть визирная
линия трубы JK при измерении расстояния
АВ имеет угол наклона ν, и по рейке
измерен отрезок l. Если бы рейка была
установлена перпендикулярно визирной
линии трубы, то наклонное расстояние
было бы равно:
D
= l0
* C + c.
Но
l0
= l*Cos ν, поэтому
D = C*l*Cosν +
c. (4.36)
Горизонтальное
проложение линии S определим из Δ JKE :
S
= D*Cosν
или
S=
C*l*Cos2ν
+ c*Cosν. (4.37)

Для удобства
вычислений принимаем второе слагаемое
равным с*Cos2ν ; поскольку с величина
небольшая (около 30 см), то такая замена
не внесет заметной ошибки в вычисления.
Tогда
S
= (C * l + c) * Cos2ν,
или
S = D’*
Cos2ν. (4.38)
Oбычно величину
(C*l + c) назыывают дальномерным расстоянием.
Обозначим разность (D’ — S) через ΔD и
назовем ее поправкой за приведение к
горизонту, тогда
S
= D’ — ΔD,
где
ΔD
= D’ * Sin2
ν. (4.39)
Угол ν измеряют
вертикальным кругом теодолита; причем
при поправка ΔD не учитывается. Точность
измерения расстояний нитяным дальномером
обычно оценивается относительной
ошибкой от 1/100 до 1/300.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
Контроль вычисления приращений координат: d АВ 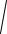
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |
ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
8.1. Измерение длин линий мерными лентами и рулетками
Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.
Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.
Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.
Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.
Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.
Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.
Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:
l = l0 + Dl + a l0 (t— t0). (8.1)
Здесь l — длина ленты при температуре t; l0 — номинальная длина; Dl — поправка к номинальной длине при температуре компарирования t0 ; a — температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.
Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.
|
|
Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане). |
Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D — вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D1, то есть в створ точек C и B. Затем из точки С веху переносят в точку С1 и так далее до тех пор, когда обе вехи окажутся в створе AB.
Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n — число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).
Длину измеряют дважды — в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях — 1/1000). За окончательное значение принимают среднее.
Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.
Поправка за компарирование определяется по формуле
Dk = n Dl ,
где Dl — отличие длины ленты от 20 м и n — число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.
Поправка за температуру определяется по формуле
Dt = aD(t—t0)
где a — термический коэффициент расширения (для стали a = 0,0000125); t и t0 — температура ленты во время измерений и при компарировании. Поправку Dt учитывают, если ½t—t0½>10°.
Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D
d = D cosn , (8.2)
где n — угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где
Dn = d — D = D (cosn — 1) = -2D sin2 . (8.3)
По формуле (8.3) составляют таблицы, облегчающие вычисления.
Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.
Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.
Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.
Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами — глазным 1 и предметным 4.
|
|
|
Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона
Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 — 30¢.
Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.
Точность измерений лентой в разных условиях различна и зависит от многих причин — неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.
Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта di определяют по формуле
di = П — З,
где П и З — передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).
Если линия имеет наклон, необходимо учесть поправку
,
где h — превышение между концами пролёта, измеряемое нивелиром.
Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 — 1:10000.
Подборка по базе: гигиена модуль 1 ответы.docx, Задание №2 Менеджмент с ответами.docx, Задание №1 Менеджмент с ответ.docx, теория ответы июнь .pdf, ору без предмета.odt, Курсовая Материальная ответственность.doc, Вопросы+вар ответа.docx, Виды юридической ответственности.rtf, новый предмет.docx, физика ответы на билеты 2 семестр.docx
1. Предмет геодезии
Геодезия (греч. Jeodaisia, от ge- Земля, и daio – делю, разделяю) – наука о методах определения формы, размеров и гравитационного поля Земли и о методах измерений на земной поверхности, для отображения ее на планах и картах, а также для проведения различных инженерных мероприятий.
По условию производства работ геодезия разделяется на:
-наземную геодезию, где геодезический измерительный процесс выполняется на поверхности Земли;
-аэрогеодезию, предусматривающую преобразование и измерений изображений местности, полученных с воздуха;
-космическую геодезию, где рассматриваются, преобразуются и измеряются изображения Земли и ее частей, полученных из космоса;
-подземную геодезию (маркшейдерию) – включает специальные виды геодезических работ, проводимых под землей;
-подводную геодезию (морская геодезия) – занимается изучением методов и приборов, необходимых для создания планов и карт дна морей и океанов.
Отрасли геодезии:
Высшая геодезия решает задачу определения фигуры и размеров Земли, ее внешнего гравитационного поля, а также вопросы создания высокоточных геодезических опорных сетей.
Картография занимается изучением методов и процессов создания сплошных изображений значительных территорий земной поверхности в виде карт или специальных моделей местности.
Топография изучает вопросы, связанные с изображением сравнительно небольших частей земной поверхности в виде планов, профилей, фотопланов.
Инженерная геодезия занимается применением геодезических методов и техники для изысканий и строительства новых или реконструкции и эксплуатации существующих инженерных сооружений, а также для установки и монтажа сложного оборудования промышленных предприятий и научных сооружений.
2. Проекция Гаусса-Крюгера для составления топокарт
Все современные топографические карты России составлены в проекции Гаусса – Крюгера. Сущность этой проекции заключается в следующем.
1) Земной эллипсоид меридианами разбивается на зоны. Средний меридиан зоны называется осевым. Нумерация зон ведется от Гринвичского меридиана на восток;
2) Каждая зона в отдельности конформно проектируется на плоскость таким образом, чтобы осевой меридиан изображался прямой линией без искажений (т.е. с точным сохранением длин вдоль осевого меридиана). Экватор также изобразится прямой линией. За начало счета координат в каждой зоне принимается пересечение изображений осевого меридиана – оси абсцисс Х и экватора – оси ординат – Y.
3) Искажения длин линий в проекции Гаусса – Крюгера возрастают по мере удаления от осевого меридиана пропорционально квадрату ординаты.
4) Система координат в каждой зоне одинакова. Для установления зоны, к которой относится точка с данными координатами, к значению ординаты слева приписывается номер зоны. Чтобы не иметь отрицательных ординат, точкам осевого меридиана условно приписывается ордината, равная 500 км.
3. Понятие о форме и размерах Земли, уровенная поверхность, эллипсоид Красовского.
Наша Земля близка по форме к сфероиду вращения, но ввиду неравномерностей она не может быть телом строгой математической формы. Различают:
1) действительную (физическую) фигуру Земли, ограниченную реальной физической поверхностью Земли;
2) фигуру Земли, ограниченную основной уровенной поверхностью, называемую геоидом.
Уровенная поверхность – это замкнутая поверхность, которая получается путем продолжения поверхности океанов под материками в спокойном состоянии, и которая в каждой своей точке перпендикулярна к направлению действия силы тяжести. Такая поверхность называют основной уровенной поверхностью или поверхностью геоида.
Уровенная поверхность
Поверхность геоида всюду выпукла. Направления силы тяжести не пересекаются в центре Земли, так как горные породы разной плотности расположены в земле неравномерно. Вследствие этого фигура геоида весьма сложна и зависит от внутреннего строения Земли.
Наиболее близкой к геоиду является математическая поверхность – эллипсоид вращения, называемый земным эллипсоидом.
Параметры: α =
а – большая и в — малая полуоси эллипсоида.
α — сжатие эллипсоида.
Эллипсоид, имеющий наибольшую близость к фигуре Земли в целом, называется общим земным эллипсоидом.
Эллипсоид Красовского имеет параметры: а= 6378245 м, в= 6356863 м, α =

Этот эллипсоид является наиболее подходящим к телу Земли в пределах России, называется референц-эллипсоидом – это эллипсоид, имеющий строго определенные размеры, определенным образом ориентированный в теле Земли и принимаемый для обработки геодезических измерений в данной стране.
Референц-эллипсоида называют поверхностью относимости. Она служит координатной поверхностью, на которой решаются геодезические задачи.
4. Понятие о плане, карте, профиле. Номенклатура топокарт.
План – уменьшенное и подобное изображение на плоскости (на бумаге) горизонтальных проекций небольших участков местности (мах. 20х20км.)учета кривизны Земли.
Карта – уменьшенное и построенное по определенным математическим законам уменьшенное изображение на плоскости значительных частей земной поверхности, размеры которых не позволяют пренебречь кривизной Земли..Карта, с изображением ситуации и рельефа называется топографической.
Топокарты имеют многоцелевое назначение, поэтому на них показывают все элементы местности.
Профили местности представляют собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного или заданного направления.
Масштабы:
—Числовой 1:1000 1 см. планы или карты – 1000 см. на местности 1 см. – 10 м.
—Линейный
—Поперечный
Для удобства пользования картой размер одного листа принят близким к квадрату со стороной 40-50 см. Границами листа карты служат меридианы и параллели, широты и долготы которых выбраны так, чтобы обеспечивался указанный размер листа.
Система обозначения листов карт называется номенклатурой.
Деление карт на отдельные листы меридианами и параллелями называется разграфкой. Для топопланов участков местности площадью менее 20 кв. км применяется квадратная разграфка. В основу разграфки планов положен лист масштаба 1:5000, обозначенный условной арабской цифрой, но не в скобках . В пределах этого листа расположены 4 листа плана масштаба 1:2000 с обозначением листов заглавными буквами русского алфавита ( А,Б,В,Г ). Каждый лист плана масштаба 1:2000 содержит 4 листа плана масштаба 1:1000 с обозначением их римскими цифрами (1, 11, 111, 1V ) или 16 листов плана масштаба 1:500 с обозначением их арабскими цифрами ( 1,2,3,…16 ).
5. Условные знаки на топокартах.
Виды условных знаков масштабные; внемасштабные; пояснительные; специальные.
Под условными знаками карт и планов понимают графические, буквенные и цифровые обозначения, предназначенные для изображения на карте, плане местных предметов и их разновидностей.
Условные знаки подразделяются на масштабные или площадные, внемасштабные, масштабно-линейные, пояснительные и специальные.
Масштабные (рис. 1, 2 ) — условные знаки, выражающие собой площади в масштабе карты или плана. Они состоят из контура в виде точечного пунктира или сплошной линии, площадь которого заполняется пояснительными знаками или раскрашивается соответствующей краской.
Рис.1 Хвойный лес
Рис. 2 Проходимое болото
Внемасштабные условные знаки (рис. 3) – условные знаки, отображающие собой объекты, которые не могут быть в силу их малых размеров выражены в масштабе карты (мельницы колодцы мосты и т.п.). У этих знаков приводятся различные пояснительные характеристики. Например, геодезический пунк, приведенный на рисунке 3, имеет отметку над уровнем моря 216.4 м.

Рис.3 Внемасштабные условные знаки
Масштабно-линейные условные знаки (рисунок 4) – условные знаки, предназначенные для отображения на карте объектов линейного характера (дороги, ручьи, реки, линии электропередач, связи, нефтепроводы и т.п.), у которых выражается в данном масштабе только длина. Кроме того, на картах и планах приводятся, как правило, и характеристики знаков.
Рис. 4 Масштабно-линейные условные знаки
Пояснительные условные знаки — условные знаки, предназначенные для дополнительной характеристики местных предметов. К ним относят полные и сокращённые подписи (например, названия населённых пунктов, характеристика заводов, фабрик и т.п. ), буквенные обозначения ( например, материал покрытия шоссе ), цифровые надписи ( например, отметки горизонталей, отдельных точек местности), графические обозначения ( например, направление течения реки, фигуры хвойных или лиственных деревьев и т.п. ).
Специальные условные знаки — условные знаки, устанавливаемые различными ведомствами для составления специальных карт и планов, на которых изображаются теплотрассы, водопроводы канализация и т.п.
6. Масштаба, определение, виды масштабов.
Отношение длины линии на плане или карте к длине горизонтального проложения соответствующей линии местности называется масштабом карты или плана.
Виды масштаба:
1) Масштаб выраженный дробью, числитель которой — единица, а знаменатель — число, показывающее, во сколько раз уменьшены линии и предметы при изображении их на плане или карте, называется численным масштабом. Например, 1:5000.
2) Линейный масштаб представляет собой линию, разделённую на равные отрезки, называемые основанием масштаба. Основание масштаба соответствует определённому числу метров горизонтального проложения на местности.
Линейный масштаб применяется для измерения длин линии с невысокой точностью.
3) Для более точных измерений применяют поперечный масштаб. Его гравируют на специальных металлических линейках, называемых масштабными. Для построения поперечного масштаба на прямой откладывают основания масштаба, из концов которых восставляют перпендикуляры.
Невооружённый глаз человека способен рассмотреть на чертеже с расстояния 20-25 см точку размером 0.1 мм и более. Поэтому длину горизонтального отрезка на местности, соответствующую отрезку 0.1 мм на плане или карте, называют точностью масштаба карты ( плана ) или
предельной точностью.
7. Рельеф, его основные формы, точки, линии.
Рельеф играет значительную роль в деятельности человека. Его учитывают при проектировании строительства, преобразуют в формы, удобные для эксплуатации сооружений. Правильное освоение и использование территорий невозможно без учёта рельефа. На картах и планах рельеф изображают горизонталями, а также масштабными и внемасштабными условными знаками.
Горизонталь – это кривая замкнутая линия, соединяющая на карте точки с одинаковыми высотами
С помощью горизонталей на картах и планах изображают основные формы рельефа Из всего разнообразия форм рельефа можно выделить следующие:
1. Гора ( холм, сопка ). Основание горы – подошва, наивысшая точка – вершина, вершина остроконечной формы – пик, наклонная часть горы – склон или скат
2. Котловина ( впадина ) – чашеобразное, замкнутое со всех сторон углубление. Самая низкая часть котловины называется дном, а верхний край – бровкой.
3. Хребет – вытянутая в одном направлении возвышенность, постепенно понижающаяся к водоёму, имеющая два ската в противоположных направлениях. Линия пересечения скатов называется водоразделом
4.Лощина – вытянутое в одном направлении понижение с двумя скатами. Линия встречи скатов в нижней части называется водосливом. Верхняя часть лощины называется верховьем, а нижняя – устьем
5. Седловина – понижение между двумя возвышенностями. Седловину образуют два хребта и две лощины. Наиболее низкая точка седловины называется перевалом.Горизонтали, изображающие основные формы рельефа естественного происхождения, наносятся на карту или план коричневым цветом.
8. Простейшие геодезические работы на местности (вешение, измерение линий). Относительная ошибка линейных измерений, назначение.
Вешение линии — установка на измеряемой линии (длина больше 150м) вешек (палка или шест в красную или белую полоску) для обеспечения видимости.
Этапы измерения длины линии:
— предварительный осмотр местности
— вешение линии
— закрепление линии на местности
— измерение
Геометрическое нивелирование:
1. При нивелировании из середины. В точках А и В устанавливают отвесно рейки. На которых нанесены шкалы, а по середине нивелир. Когда осуществляют нивелирование от А к В то рейку в точке А считают задней а В передней. Если взять отсчёты а и в то превышение будет равно h = a — b
2. При нивелировании вперёд нивелир устанавливают в точке А, измеряют высоту прибора I а затем берут отсчёт b. Превышение вычисляется по формуле h = i — b
После определения высоты точек находят: Нв=На+h. Когда высоты точек расположены на значительном расстоянии. В этом случае от точки А до В прокладывают нивелирный ход, состоящий из нескольких станций. Превышение между точками будет равно сумме превышений hав. Высоту точки В находят по формуле Нв=На+ hав
Относительная ошибка – отношение абсолютной ошибки к среднему значению измеренной величины.
1. Относительная средняя погрешность –
2. Относительная средняя квадратическая погрешность –
3. Относительная предельная случайная погрешность-
Назначение – проверка точности теодолитного хода.
9. Основные части и плоскости теодолита 2Т-30. Оси теодолита.
Основными частями теодолита 2Т-30 являются:
1- наводящий винт лимба горизонтального круга;
2- окуляр микроскопа;
3- зеркало;
4- боковая крышка;
5- паз для буссоли;
6- оптический визир (коллиматор, центрир);
7- закрепительный винт трубы;
8- наводящий винт трубы;
9- цилиндрический уровень горизонтального круга;
10- наводящий винт алидады;
11- заглушка винта;
12- подставка теодолита;
13- подъемные винты;
14-основание теодолита (поддон футляра),
15- закрепительный винт лимба горизонтального круга,
16- закрепительный винт алидады горизонтального круга,
17- цилиндрический уровень при зрительной трубе,
18- кремальера,
19- диоптрийное кольц птический визир (коллиматор, центрир);
Основные геометрические условия, которые должны быть соблюдены в теодолите, вытекают из принципиальной схемы измерения горизонтального угла и заключается в следующем:
1.вертикальная ось прибора должна быть отвесной;
2.плоскость лимба должна быть горизонтальна,
3.визирная плоскость должна быть вертикальна.
Основными геометрическими элементами теодолита являются оси.
1. ось вращения прибора VV1;
2. ось вращения зрительной трубы ZZ1;
3. визирная ось зрительной трубы (это ось проходящая через центр окуляра и центр объектива) WW1;
4. ось цилиндрического уровняUU1;
5. сетка нитей, которую видим в окуляре.

10. Поверки теодолита 2Т-30.
Поверка теодолита:
1. ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к вертикальной оси прибора;
2. визирная ось трубы должна быть перпендикулярна к горизонтальной оси теодолита;
3. горизонтальная ось должна быть перпендикулярна к вертикальной оси прибора;
4. одна из нитей сетки должна быть горизонтальна, другая вертикальна.
Перед измерением углов исправленным теодолитом необходимо: привести прибор в рабочее положение, предварительного отцентрировав над вершиной угла.
11. Виды ошибок измерений линий 20 м стальной ленты, меры борьбы с ними.
Точность измерений лентой в разных условиях различна и зависит от многих причин — неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др. Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
При измерении линий могут быть погрешности, которые различаются по свойствам и в зависимости от них разделяются на три группы: грубые, систематические и случайные.
Чтобы уменьшить величину погрешностей, необходимо учитывать следующее:
1. Отклонение концов рулетки от створа измерений всегда уменьшает измеряемую длину. Чем меньше отклоняются концы от створа, тем меньше погрешность измерения. При измерениях для многих целей укладку мерных приборов в створ производят с использованием оптических труб. К такому приему прибегают в тех случаях, когда хотят получить результат с относительной погрешностью менее 1:3000 от измеряемой длины. Отклонения от створа концов 50 и 30 м рулетки более чем на 0,15 м недопустимы.
2. Большую погрешность в измеряемую длину может внести разное натяжение прибора при эталонировании и практической работе. Следует избегать избыточного натяжения, так как тонкое полотно рулеток растягивается, при этом часто не восстанавливая начальную длину. Достаточно точно (до ± 100 Н) можно выдержать натяжение, используя для этого ручные приборы — динамометры типа ПН-2 или пружинные бытовые весы.
3. Недопустимо ослаблять внимание при отсчитывании по концам мерного прибора или его фиксации. Достигнутая точность может быть утрачена при неодновременном снятии отсчетов, подвижке мерного прибора во время фиксации его концов. Поэтому не следует пренебрегать возможностью дважды или даже трижды взять отсчеты по концам мерного прибора и сравнить разности отсчетов по переднему и заднему концам (П-3). Разность отсчетов (для одного пролета измерений) при работе рулетками не должна превышать 2 мм, а при измерении мерными лентами — 1 см.
4. Необходимо следить не только за превышением концов мерного прибора, но и за его изгибом в вертикальной плоскости. Точность определения поправки за наклон зависит от точности определения превышений: чем короче линия, тем точнее надо знать превышение. Как правило, достаточно их знать с погрешностью до 1,0 — 1,5 см на 100 м длины.
5. При введении поправок за отличие температуры, данной в уравнении рулетки (+20 °С), и температуры измерений следует помнить, что измеряют температуру воздуха, а поправку вводят за изменение температуры металлического мерного прибора. Поэтому при прямом солнечном облучении мерного прибора термометр подкладывают под его полотно и держат 3 — 5 мин с тем, чтобы точнее определить температуру мерного полотна. Разность температуры воздуха и мерного прибора измеряют с погрешностью не грубее 5 °С.
6. Существенно исказить результат измерения может плохое закрепление точек, между которыми ведется измерение. Вязкая почва, зыбко забитые кол, штырь или шпилька, изменяющие свое положение от случайных ударов, приводят к появлению недопустимых погрешностей в измеряемой длине.


![inj_geo_1-245.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-245.jpg)
![inj_geo_1-247.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-247.jpg)
![inj_geo_1-248.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-248.jpg)




