From Wikipedia, the free encyclopedia
A faulty generalization is an informal fallacy wherein a conclusion is drawn about all or many instances of a phenomenon on the basis of one or a few instances of that phenomenon. It is similar to a proof by example in mathematics.[1] It is an example of jumping to conclusions.[2] For example, one may generalize about all people or all members of a group, based on what one knows about just one or a few people:
- If one meets a rude person from a given country X, one may suspect that most people in country X are rude.
- If one sees only white swans, one may suspect that all swans are white.
Expressed in more precise philosophical language, a fallacy of defective induction is a conclusion that has been made on the basis of weak premises, or one which is not justified by sufficient or unbiased evidence.[3] Unlike fallacies of relevance, in fallacies of defective induction, the premises are related to the conclusions, yet only weakly buttress the conclusions, hence a faulty generalization is produced. The essence of this inductive fallacy lies on the overestimation of an argument based on insufficiently-large samples under an implied margin or error.[2]
Logic[edit]
A faulty generalization often follows the following format:
- The proportion Q of the sample has attribute A.
- Therefore, the proportion Q of the population has attribute A.
Such a generalization proceeds from a premise about a sample (often unrepresentative or biased), to a conclusion about the population itself.[3]
Faulty generalization is also a mode of thinking that takes the experiences of one person or one group, and incorrectly extends it to another.
Inductive fallacies[edit]
- Hasty generalization is the fallacy of examining just one or very few examples or studying a single case and generalizing that to be representative of the whole class of objects or phenomena.
- The opposite, slothful induction, is the fallacy of denying the logical conclusion of an inductive argument, dismissing an effect as «just a coincidence» when it is very likely not.
- The overwhelming exception is related to the hasty generalization but works from the other end. It is a generalization that is accurate, but tags on a qualification that eliminates enough cases (as exceptions); that what remains is much less impressive than what the original statement might have led one to assume.
- Fallacy of unrepresentative samples is a fallacy where a conclusion is drawn using samples that are unrepresentative or biased.[4]
- Misleading vividness is a kind of hasty generalization that appeals to the senses.
- Statistical special pleading occurs when the interpretation of the relevant statistic is «massaged» by looking for ways to reclassify or requantify data from one portion of results, but not applying the same scrutiny to other categories.[5]
- This can be considered a special case of the fallacy of composition, where the item under discussion is a group, and the fallacy is what can be derived from knowledge of part of the item.
Hasty generalization[edit]
«Over-extension» redirects here. For the error common in language-learning, see Errors in early word use.
Hasty generalization is an informal fallacy of faulty generalization, which involves reaching an inductive generalization based on insufficient evidence[3]—essentially making a rushed conclusion without considering all of the variables or enough evidence. In statistics, it may involve basing broad conclusions regarding a statistical survey from a small sample group that fails to sufficiently represent an entire population.[1][6][7] Its opposite fallacy is called slothful induction, which consists of denying a reasonable conclusion of an inductive argument (e.g. «it was just a coincidence»).
Examples[edit]
Hasty generalization usually follows the pattern:
- X is true for A.
- X is true for B.
- Therefore, X is true for C, D, E, etc.
For example, if a person travels through a town for the first time and sees 10 people, all of them children, they may erroneously conclude that there are no adult residents in the town.
Alternatively, a person might look at a number line, and notice that the number 1 is a square number; 3 is a prime number, 5 is a prime number, and 7 is a prime number; 9 is a square number; 11 is a prime number, and 13 is a prime number. From these observations, the person might claim that all odd numbers are either prime or square, while in reality, 15 is an example that disproves the claim.
Alternative names[edit]
The fallacy is also known as:
- Black Swan fallacy
- Illicit generalization
- Fallacy of insufficient sample
- Generalization from the particular
- Leaping to a conclusion
- Blanket statement
- Hasty induction
- Law of small numbers
- Unrepresentative sample
- Secundum quid
When referring to a generalization made from a single example, the terms «fallacy of the lonely fact»,[8] or the «fallacy of proof by example», might be used.[9]
When evidence is intentionally excluded to bias the result, the fallacy of exclusion—a form of selection bias—is said to be involved.[10]
See also[edit]
- Accident (fallacy) – Informal fallacy
- Association fallacy – Informal inductive fallacy
- Availability bias – Heuristic bias that if something can be recalled, it must be important
- Blind men and an elephant – Parable illustrating ontologic reasoning
- Cherry picking (fallacy) – Fallacy of incomplete evidence
- Cognitive distortion – Exaggerated or irrational thought pattern
- Confirmation bias – Bias confirming existing attitudes
- Converse accident – Informal fallacy
- Generalization (logic) – rule in predicate logic
- Generalization error – Measure of algorithm accuracy
- Hypercorrection – Non-standard language usage from the over-application of a perceived prescriptive rule
- Package-deal fallacy – Logical fallacy
- Pooh-pooh – Fallacy in informal logic
- Problem of induction – Question of whether inductive reasoning leads to definitive knowledge
- Statistical significance – Concept in inferential statistics
- Stereotype – Generalized but fixed and oversimplified image or idea of a particular type of person or thing
- Straw man – Form of argument and informal fallacy
- Syllogism – Type of logical argument that applies deductive reasoning
References[edit]
- ^ a b «Hasty Generalization». logicallyfallacious.com. Retrieved 2019-12-05.
- ^ a b Dowden, Bradley. «Hasty Generalization». Internet Encyclopedia of Philosophy. Retrieved 2019-12-05.
- ^ a b c Nordquist, Richard. «Logical Fallacies: Examples of Hasty Generalizations». ThoughtCo. Retrieved 2019-12-05.
- ^ Dowden, Bradley. «Fallacies — Unrepresentative Sample». Internet Encyclopedia of Philosophy. Retrieved 2019-12-05.
- ^ Fischer, D. H. (1970), Historians’ Fallacies: Toward A Logic of Historical Thought, Harper torchbooks (first ed.), New York: HarperCollins, pp. 110–113, ISBN 978-0-06-131545-9, OCLC 185446787
- ^ «Fallacy: Hasty Generalization (Nizkor Project)». Archived from the original on 2008-12-17. Retrieved 2008-10-01.
- ^ «Fallacy». www.ditext.com. Retrieved 2019-12-05.
- ^ Fischer, David Hackett (1970). Historians’ Fallacies: Toward a Logic of Historical Thought. HarperCollins. pp. 109–110. ISBN 978-0-06-131545-9.
- ^ Marchant, Jamie. «Logical Fallacies». Archived from the original on 2012-06-30. Retrieved 2011-04-26.
- ^ «Unrepresentative Sample». Archived from the original on 2008-04-15. Retrieved 2008-09-01.
Видовые
и родовые понятия тесно связаны между
собой логическими операциями ограничения
и обобщения.
Ограничение
понятия
– это логическая операция перехода от
родового понятия к видовому с помощью
прибавления к его содержанию какого-либо
признака (или нескольких признаков).
Вспомним
об обратном отношении между объёмом и
содержанием понятия: чем больше объём,
тем меньше содержание, и наоборот.
Ограничение понятия, или переход от
родового понятия к видовому – это
уменьшение его объёма, а значит –
увеличение содержания. Вот почему при
добавлении каких-либо признаков к
содержанию понятия автоматически
уменьшается его объём. Например, если
к содержанию понятия «физический
прибор»
(Ф. п.) прибавить признак «измерять
напряжение электрического тока»,
то оно превратится в понятие «вольтметр»
(В), которое будет видовым по отношению
к исходному родовому понятию «физический
прибор»
(рис. 10).
Так
же, если к содержанию понятия «геометрическая
фигура»
(Г. ф.) прибавить признак «иметь
равные стороны и прямые углы»,
то оно превратится в понятие «квадрат»
(К), которое будет видовым по отношению
к исходному родовому понятию «геометрическая
фигура»
(рис. 11).
Обобщение
понятия
– это логическая операция перехода от
видового понятия к родовому с помощью
исключения из его содержания какого-либо
признака (или нескольких признаков).
Содержание понятия, лишённое каких-то
признаков, уменьшается, но при этом
автоматически увеличивается объём
понятия, которое из видового становится
родовым или обобщается. Например, если
от содержания понятия «биология»
(Б) отбросить признак «изучать
различные формы жизни»,
то оно превратится в понятие «наука»
(Н), которое будет родовым по отношению
к исходному видовому понятию «биология»
(рис. 12).
Так
же, если от содержания понятия «атом
водорода»
(А. в.) отбросить признак «иметь
один электрон»,
то оно превратится в понятие «атом
химического элемента»
(А. х. э.), которое будет родовым по
отношению к исходному видовому понятию
«атом
водорода»
(рис. 13).
Ограничения
и обобщения понятий складываются в
логические цепочки, в которых каждое
понятие (за исключением начального и
конечного) является видовым по отношению
к одному соседнему понятию и родовым
по отношению к другому. Например, если
последовательно обобщать понятие
«Солнце»,
то получится следующая цепочка: Солнце
→ звезда
→ небесное
тело→
→ физическое
тело
→ форма
материи.
В этой цепочке понятие «звезда»
является родовым по отношению к понятию
«Солнце»,
но видовым по отношению к понятию
«небесное
тело»;
так же понятие «небесное
тело»
является родовым по отношению к понятию
«звезда»,
но видовым по отношению к понятию
«физическое
тело»
и т. д. Движение по нашей цепочке от
понятия «Солнце» к понятию «форма
материи»
представляет собой серию последовательных
обобщений, а движение в обратном
направлении – серию ограничений. Если
изобразить отношения между понятиями
из указанной цепочки на схеме Эйлера,
то получатся круги, последовательно
располагающиеся один в другом: самый
маленький будет обозначать понятие
«Солнце»,
а самый большой – «форма
материи».
Пределом
цепочки ограничения любого понятия
всегда будет какое-либо единичное
понятие (см. раздел 1.1.), а пределом цепочки
обобщения, как правило, будет какое-либо
широкое, философское понятие, например:
объект
мироздания, форма материи
или форма
бытия.
Наиболее
частые ошибки, которые допускают при
ограничении и обобщении понятий,
заключаются в том, что вместо вида для
какого-то рода называют часть из некого
целого, и вместо рода для какого-то вида
называют целое по отношению к какой-либо
части. Например, в качестве ограничения
понятия «цветок»
предлагают понятие «стебель».
Действительно, стебель – это часть
цветка, но ограничить понятие – значит
подобрать не часть для целого, а вид для
рода. Следовательно, правильным
ограничением понятия «цветок»
будет понятие «ромашка»,
или «тюльпан»,
или «хризантема»
и т. п. В качестве обобщения понятия
«дерево»
нередко предлагают понятие «лес».
Конечно же, лес является неким целым по
отношению к деревьям, из которых он
состоит, но обобщить понятие – значит
подобрать не целое для части, а род для
вида. Следовательно, правильным обобщением
понятия «дерево»
будет понятие «растение»,
или «объект
флоры»,
или «живой
организм»
и т. п.
Итак,
почти любое понятие (за исключением
единичных и широких, философских) можно
как ограничить, так и обобщить. Другими
словами, подобрать для него как видовое
понятие, так и родовое. Например,
ограничением понятия «человек»
(Ч) будет понятие «спортсмен»
(С) или «писатель»,
или «мужчина»,
или «молодой
человек»
и т. п., а его обобщением будет понятие
«живое
существо»
(Ж. с.) (рис. 14).
Операции
обобщения и ограничения понятий следует
отличать от отношений целого к части
(и наоборот). Например, неправильно
обобщать понятие “городская улица”
до понятия “город” или ограничивать
понятие “педагогический институт” до
понятия “факультет педагогического
института”, так как в обоих случаях
речь идет не об отношении рода и вида,
а об отношении части и целого.
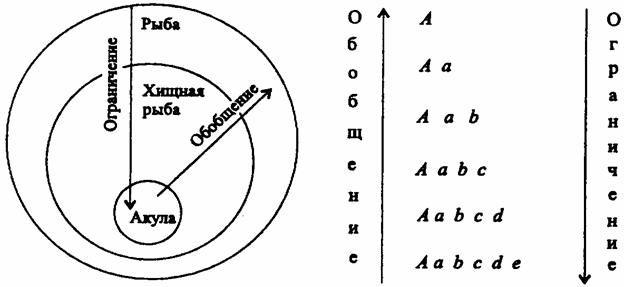
Обобщение
и ограничение понятий схематически
можно изобразить так:
При
обобщении отбрасываются признаки, при
этом содержание уменьшается, а объем
увеличивается. При ограничении, наоборот,
к родовому понятию А
добавляются все новые и новые видовые
признаки (а,
b, с
и т. д.), поэтому объем уменьшается, а
содержание увеличивается.
Произведем
обобщение и ограничение понятий: “волк”
и “река”
Волк
|
Обобщение |
Ограничение |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
|
|
5. |
|
|
б. |
Река
|
Ограничение |
Обобщение |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
4. |
|
5. |
Проверьте
себя:
1.
Что такое ограничение понятия?
2.
Что представляет собой логическая
операция обобщения понятия?
3.
Каким образом ограничения и обобщения
понятий складываются в логические
цепочки? Каковы пределы цепочек
ограничений и обобщений?
4.
Какие ошибки часто допускают при
ограничении и обобщении понятий?
Продемонстрируйте на самостоятельно
подобранных примерах, что целое и часть
нельзя путать с видом и родом.
5.
Всякое ли понятие можно подвергнуть
ограничению или обобщению? Какие понятия
не поддаются этим логическим операциям?
6.
Правильно ли проведены ограничения:
Строение
— комната;
строение
— беседка;
населенный
пункт — столица — центр столицы — центр
современной столицы?
Степная
птица — редкая степная птица — редкая
степная птица высотой около метра
(дрофа).
7.
Правильно ли проведены обобщения:
а)
береза — лиственное дерево — смешанный
лес — лес;
б)
улица — квартал — поселок городского
типа — город — населенный пункт.
в)
верблюд — самое выносливое и неприхотливое
домашнее животное пустыни — выносливое
и неприхотливое домашнее животное
пустыни — домашнее животное пустыни —
домашнее животное — животное.
г)
соболь — ценный пушной зверек — пушной
зверь — зверь.
8.
Подберите пять любых понятий и проделайте
с ними ограничение и обобщение, т. е.
подберите для каждого как видовое, так
и родовое понятие, иллюстрируя эти
операции схемами Эйлера.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщение и ограничение понятий ошибки
Обобщение и ограничение понятий
Обобщение – этологическая операция, состоящая в переходе от понятия с меньшим объёмом, но с большим содержанием, к понятию с большим объёмом, но меньшим содержанием
роза (А) — цветок (Б) — растение (В) — живой организм (Г) — организм (Д) — предмет (Е)

На схеме этот процесс обобщения выглядит следующим образом:
Ограничение – это логическая операция перехода от понятия с большим объёмом, но с меньшим содержанием, к понятию с меньшим объёмом, но большим содержанием
— произведение музыкального искусства (Е) — опера (Д)
— опера русского композитора (Г)
— опера русского композитора XIX века (В)
— опера Мусоргского Модеста Петровича (Б) — опера Мусоргского М. П. «Хованщина» (А)
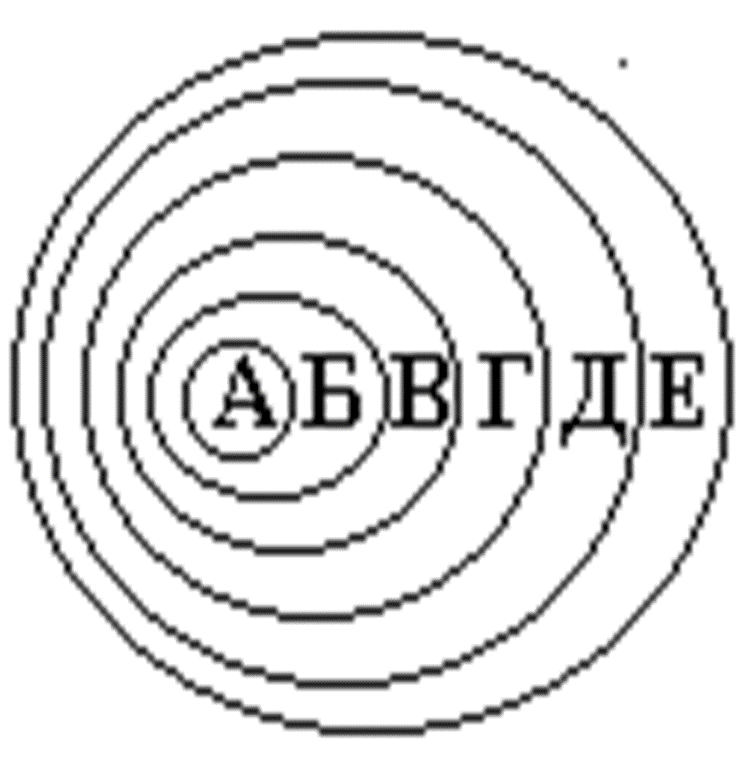
Пределом ограничения является единичное понятие с одним элементом объёма: в нашем случае это понятие А — опера «Хованщина»
Можно обе рассматриваемые нами операции изобразить и такой схемой:
Назначение операций обобщения и ограничения заключается в том, что они придают определённость мышлению, подчиняя его элементарным правилам:
1) обобщение правильно, если мысль осуществляет переход от видового понятия к родовому;
2) ограничение правильно, если мысль осуществляет переход от родового понятия к видовому
ОПЕРАЦИИ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ОСУЩЕСТВЛЯЮТСЯ ТОЛЬКО МЕЖДУ ПОНЯТИЯМИ, КОТОРЫЕ НАХОДЯТСЯ В ОТНОШЕНИЯХ ПОДЧИНЕНИЯ
1) Обобщение и ограничение часто смешивают с мысленным переходом от части к целому и выделением части из целого
2) Ограничение понятий часто происходит с помощью добавления признака: «студент» — «добросовестный студент».
Но имейте в виду, что нередко добавление эпитета не ведёт к ограничению понятия и является излишним:
«девушка» — «молодая девушка» (а кто видел старых девушек?),
«шар» — «круглый шар» (а какие ещё шары бывают?)
Данная ошибка называется плеоназмом (излишеством)
Деление понятий
Для упорядочения знания,поиска закономерных связей и уточнения смысла многих слов человеческим мышлением используется такая интеллектуальная процедура как классификация
Классификация – это распределение предметов какого-либо рода на взаимосвязанные группы (классы) согласно наиболее существенным признакам, присущим предметам данного рода и отличающим их от предметов других родов; при этом каждый класс занимает в получившейся системе своё постоянное, определённое место
В основе любой классификации лежит такая логическая процедура как деление понятий – это логическая операция, раскрывающая объём понятия
1) Делимым называется родовое понятие, в объёме которого выделяются возможные виды
2) Основание деления – признак, в соответствии с которым выделяются члены деления
3) Члены деления – полученные в результате самой операции соподчинённые виды
1) Деление по наличию или отсутствию признака, служащего основанием деления (его называют часто дихотомическим делением)
2) Деление по видоизменению признака, положенного в основание этой операции
3) Смешанное деление, когда используются оба вида деления одновременно
Примеры дихотомического деления:
· государства можно разделить на демократические и недемократические,
· людей – на счастливых и несчастливых,
· школьников – на добросовестных и недобросовестных,
· предпринимателей – на удачливых и неудачливых,
· граждан – на дееспособных и недееспособных
Право может быть оформлено (признак – форма выражения) в виде:
Людей по социально-классовому признаку можно разделить на:
· лиц свободных профессий
Смешанное деление, когда используются оба вида деления одновременно
Пример:
1) политические институты делятся на государственные и негосударственные;
2) среди негосударственных различаются партийные и непартийные;
3) непартийные же включают в себя профессиональные, женские, молодёжные, спортивные, художественные и так далее
Основные правила и ошибки деления:
1) Правило соразмерности
2) Правило исключения
3) Правило одного основания:
4) Правило непрерывности
1)Правило соразмерности – объединение объёмов членов деления должно совпадать с объёмом делимого понятия или объём делимого должен полностью исчерпываться членами деления. (А = В1 + В2 + В3 + . + Вn)
Это означает, что при делении:
a) не должно быть пропущено ни одного предмета из объёма делимого понятия;
b) не должно появиться ни одного лишнего члена деления
Если данное правило не соблюдается, то возможны две основные ошибки:
17. Обобщение и ограничение понятий
17. Обобщение и ограничение понятий
Обобщение понятия – это совершение перехода от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом и меньшим содержанием. При обобщении осуществляется переход от видового понятия к родовому.
Например, обобщая понятие «хвойный лес», мы переходим к понятию «лес». Содержание этого нового понятия уже, зато объем значительно шире. Содержание уменьшилось, потому что мы изъяли (убрав слово «хвойный») ряд характерных видовых признаков, отражающих особенности хвойного леса. Лес – это род по отношению к понятию «хвойный лес», являющемуся видом. Исходное понятие может быть как общим, так и единичным. Например, можно осуществить обобщение понятия «Париж» (единичное понятие) путем перехода к понятию «европейская столица», следующим шагом будет переход к понятию «столица», потом «город», «селение». Таким образом, постепенно исключая характерные признаки, присущие предмету, мы движемся в сторону наибольшего расширения объема понятия, жертвуя содержанием в пользу абстракции.
Цель обобщения – максимальное отстранение от характерных признаков. При этом желательно, чтобы такое отстранение происходило как можно более постепенно, т. е. переход от рода должен происходить к самому близкому виду (с наиболее широким содержанием).
Обобщение понятий не безгранично, и пределом обобщения являются философские категории, например «бытие» и «сознание», «материя» и «идея». Поскольку категории лишены родового понятия, обобщение их невозможно.
Ограничение понятия – это логическая операция, противоположная обобщению. Если обобщение идет по пути постепенного отстранения от признаков предмета, ограничение, напротив, обогащает совокупность признаков понятия. Таким образом, осуществляется переход от общего к частному, от вида к роду, от единичных понятий к общим.
Эта логическая операция характеризуется уменьшением объема за счет расширения содержания.
Операция ограничения не может продолжаться дальше, когда в его процессе достигается единичное понятие. Оно характеризуется максимально полным содержанием и объемом, в котором мыслится лишь один объект.
Таким образом, операции ограничения и обобщения – это процесс конкретизации и абстракции в рамках от единичного понятия до философских категорий. Эти операции учат человека мыслить более правильно, способствуют познанию предметов, явлений, процессов окружающего мира, их взаимосвязей. Благодаря обобщению и ограничению мышление становится более ясным, четким и последовательным. Однако не следует путать обобщение и ограничение с выделением из целого части и рассмотрением этой части отдельно. Например, двигатель автомобиля состоит из деталей (карбюратор, воздушный фильтр, стартер), детали состоят из более мелких, а те в свою очередь из еще более мелких. В этом примере понятие, следующее за предыдущим, не является его видом, а есть лишь его составной частью.
ОБОБЩЕНИЕ И ОГРАНИЧЕНИЕ ПОНЯТИЙ;
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
К логическим операциям над понятиями относятся обобщение, ограничение, определение и деление.
Обобщить понятие– значит, перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием, т.е. от видового понятия к родовому понятию.
Пример:Результатом обобщения понятия «Московский государственный университет» (А) является понятие «государственный университет» (В), а результатом обобщения последнего – понятие «университет» (С).
Обобщение понятий не может быть беспредельным и проводится в рамках той или иной науки. Пределом обобщения являются понятия с наиболее широким объемом – категории, например, «материя», «сознание» и т. п. Категории не имеют рода, поэтому обобщить их нельзя. Ограничить понятие – значит, перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с большим содержанием, т.е. от вида к роду. Например, ограничивая понятие «министерство», можно перейти к понятию «министерство иностранных дел». Пределом ограничения служит единичное понятие, в данном случае понятие «Министерство иностранных дел России».
Логические операции обобщения и ограничения часто применяются в практике мышления: переходя от понятия одного объема к понятию другого объема, мы уточняем предмет нашей мысли, процесс мышления становится определеннее и последовательнее.
Возможные ошибки при осуществлении логических операций – обобщения и ограничения понятий:
1. «Переход от части к целому». Например, параграф – глава учебника.
2. «Переход в другой род». Например, сотовый телефон – телефонный аппарат.
3. «Переход от целого к части». Например, дом – этаж – квартира.
4. «Мнимое ограничение» (плеоназм). Например, шар – круглый шар – самый круглый шар.
Упражнение 16
Проверьте, правильно ли обобщены понятия в следующих примерах:
1. Радость – чувство. 2. Живопись – искусство. 3. Брянск – город в России. 4. Планета – Юпитер. 5. Черта характера – гордость. 6. Большой театр России – Малый театр России. 7. К. Брюллов – выдающийся художник ХIХ века. 8. Спорт – гребля. 9. Юрист – человек. 10. Логика – наука. 11. Староста группы – староста курса. 12. Торговый зал супермаркета – супермаркет. 13. Опубликованная книга – написанная книга. 14. Еженедельная газета – газета выходящая регулярно. 15. Невиновность – непричастность.
Пример:Кинотеатр «Ударник» — кинотеатр. Правильно.
Упражнение 17
Проверьте, правильно ли ограничены понятия в следующих примерах:
1. Степень – кубическая степень. 2. Университет – московский университет. 3. Республика – государство. 4. Генерал российской армии – офицер. 5. Москва – столица России. 6. Староста группы – студент. 7. Организм – живая клетка. 8. Офицер – полковник. 9. Государство – республика. 10. Стихотворение – элегия. 11. Среда – природная среда. 12. Политика – политический режим. 13. Организация – партия. 14. Профсоюз – член профсоюза. 15. Русские – «новые русские».
Пример:Учебник – учебник по политологии. Правильно.
Упражнение 18
1. Море. 2. Книга. 3. Выдающаяся личность. 4. Растение. 5. Смоленский кремль. 6. Элемент. 7. Словарь. 8. Город. 9. Вторая мировая война. 10. Клевета. 11. Государство. 12. Монархия. 13. Съезд. 14. Депутат. 15. Закон.
Пример:Политическое движение – движение за мир.
Упражнение 19
1. Проректор по науке. 2. Журнал «Политические исследования». 3. Сооружение. 4. Газета «Российские ведомости». 5. Спикер Парламента. 6. Высшее учебное заведение. 7. Опера. 8. Редактор. 9. Художественное произведение. 10. Доктор наук. 11. Республика. 12. Римское право. 13. Правовое государство. 14. Справедливость. 15. Специалист в области социальной работы.
Пример:Лето– время года.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
В результате освоения данной темы студент должен:
знать
- – логические операции с понятиями: обобщение, ограничение, определение, деление,
- – способы обобщения и ограничения понятий,
- – виды определения и деления понятий,
- – виды классификаций понятий;
уметь
- – производить логические операции ограничения и обобщения понятий,
- – применять в практической деятельности логические правила определения и деления понятий;
владеть
– навыками практического обобщения и ограничения понятий и логическими операциями – определением и делением понятий.
Обобщение и ограничение понятий
Обобщить понятие – значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но меньшим содержанием, т.е. перейти от видового понятия к родовому понятию за счет уменьшения информативности содержания, т.е. от вида к роду.
К логическим операциям с понятиями относятся обобщение и ограничение, определение и деление.
Поскольку различают логический и фактический объемы, то можно говорить о фактическом и логическом обобщении.
Например, результатом обобщения понятия «Московский государственный университет» (А) является понятие «государственный университет» (В), а результатом обобщения последнего – понятие «университет» (С). Схематически это можно представить следующим образом (рис. 4.1).
Производя обобщение, необходимо следить, чтобы не совершить ошибку «переход в другой род», например, эта ошибка
Рис. 4.1
будет иметь место, если в процессе обобщения будет совершен переход от понятия «студент» к понятию «студенчество» или от понятия «раздел учебника» к понятию «учебник». Во втором случае мы имеем дело с ошибкой «переход от части к целому«.
Что касается предела обобщения, то здесь следует различать вопрос о пределах обобщения отдельно взятого понятия в составе некоторой системы знаний.
Если обобщение производится в рамках той или иной науки, то пределом обобщения являются понятия с наиболее широким объемом – категории, например, «материя», «сознание», «форма общественного сознания». Категории не имеют рода, поэтому обобщить их нельзя.
Если речь идет об обобщении понятия в рамках обыденного сознания, то пределом обобщения любого отдельно взятого понятия может быть понятие «нечто».
Противоположная обобщению операция – ограничение
Ограничить понятие – значит перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с большим содержанием, т.е. от рода к виду.
Например, ограничивая понятие «министерство» (А), можно перейти к понятию «министерство иностранных дел» (В). Пределом ограничения служит единичное понятие, в данном случае понятие «Министерство иностранных дел России» (С).
Это можно представить, как показано на рис. 4.2.
То есть, как это следует из определения операции ограничения и приведенного примера, ограничение происходит за счет увеличения информативности содержания исходного понятия.
Применяя в практике познания операции обобщения и ограничения мы осуществляем последовательность мыслительных действий: в случае обобщения совершаем процесс восхождения от отдельного или особенного к общему; в случае ограничения понятий совершаем обратный процесс – движение от общего к конкретному, к особенному или отдельному.
Используя эти операции в процессе мыслительной и практической деятельности, необходимо учитывать:
- 1) при осуществлении данных операций нужно избегать скачков в обобщениях и ограничениях, т.е. в случае обобщения понятий каждый шаг должен быть переходом от вида к ближайшему роду; в случае ограничения – наоборот: переход от рода к ближайшему виду;
- 2) при осуществлении данных операций нужно учитывать также и тот факт, что обобщение и ограничение одного и того же понятия может идти по разным направлениям;
- 3) обобщение и ограничение базируются на родовидовых отношениях, которые не требуется подменять отношениями «часть – целое»;
- 4) в качестве критерия правильности осуществления операций обобщения и ограничения выступает отношение логического следования, которое можно определить следующим образом: «Если из высказывания или высказывательной формы А логически следует В, то есть А|=В, по обратное неверно, тогда А более информативно, чем В», где |= – отношение логического следования.
Возможны следующие конкретные случаи следования между содержаниями понятий.
1. Из всякой совокупности признаков содержания понятий, соединенных конъюнктивно, следует любой из этих признаков или меньшая их совокупность. Например, из содержания «Московский гуманитарный университет» следует содержание «московский университет» и «гуманитарный университет».
Таким образом, увеличить содержание понятия можно путем добавления новых информационно непустых признаков с помощью конъюнкции.
- 2. Из всякого признака следует сложный признак, образованный с помощью добавления некоторого нового признака с помощью дизъюнкции. Например, из признака «быть веселым» следует признак «быть веселым или находчивым». Следовательно, можно увеличить содержание понятия путем уменьшения членов дизъюнкции, если они есть в содержании понятия.
- 3. В том случае, когда признак содержит квантор общности, то из него следует признак, который получается подстановкой имени любого предмета, находящегося в области действия квантора общности или путем подстановки имен нескольких предметов из этой области. Так, из признака «знающий всех своих преподавателей» логически следует признак «знающий преподавателей логики и психологии».
- 4. Если признак содержит предметную константу, то из него может следовать признак с квантором существования (выражается с помощью слов «некоторые», «часть», «большинство» и т.п.) по предметам этой области. В данном случае увеличение содержания понятия может идти следующими способами:
- а) заменой признака, содержащего общее имя с квантором существования на единичные имена. Например, увеличится содержание понятия (и уменьшится его объем), если мы перейдем от признака «посетивший некоторые европейские столицы» к признаку «посетивший Москву и Париж»;
- б) заменой признака с квантором существования на признак с квантором общности.
Например, увеличится содержание понятия (и уменьшится его объем), если мы перейдем от признака «посетивший некоторые европейские столицы» к признаку «посетивший все европейские столицы»;
в) заменой признака с единичными именами на признак с общим именем и с квантором общности (слова «все», «всякий», «каждый» и т.п.) по предметам соответствующей области. Например, можно увеличить содержание понятия (уменьшив его объем), заменив признак «посетивший европейские столицы Москву и Париж» признаком «посетивший все европейские столицы».
Известный отечественный логик Е. Б. Кузина выделяет следующие способы обобщения и ограничения понятий.
Способы обобщения понятий:
«(1) Отбрасыванием признака, включенного в содержание посредством конъюнкции.
- (2) Добавлением в содержание понятия признака с помощью дизъюнкции.
- (3) Заменой в признаке единичного имени на общее имя с квантором существования.
- (4) Заменой квантора общности в признаке на квантор существования.
- (5) Заменой признака с квантором общности на признак с единичными именами» [1] .
Способы ограничения понятий:
«(1) Прибавление информативно непустого признака конъюнктивно.
- (2) Отбрасывание информативно непустого признака, если он включен в содержание понятия через дизъюнкцию.
- (3) Уточнение признака путем замены в нем общего имени с квантором существования на единичные имена.
- (4) Замена квантора существования в признаке квантором общности.
- (5) Замена признака с единичными именами на признаках с общим именем и квантором общности» [2] .
Возможные ошибки при осуществлении логических операций обобщения и ограничения понятий.
«Переход от части к целому» – заключается в том, что часть не обладает всеми признаками целого. Например, «параграф – глава учебника».
«Переход в другой род». Например, «сотовый телефон – телеграф».
«Переход от целого к части». Например, «дом – этаж квартира».
«Мнимое ограничение» (плеоназм). Например, «шар – круглый шар – самый крупный шар».
Логические операции обобщения и ограничения часто применяются η практике мышления, переходя от понятия одного объема, мы уточняем предмет нашей мысли, процесс мышления становится определеннее и последовательнее.
- [1]Кузина Е. Б. Логика в кратком изложении и упражнениях: учеб. пособие / Е. Б. Кузина. М.: Издательство МГУ, 2000. С. 61.
- [2] Там же. 60.
Обобщение и ограничение понятий
Обобщение – логическая операция, при которой уменьшается количество признаков в содержании понятия.
Ограничение – логическая операция, при которой увеличивается число признаков.
Определение понятий – логическая операция, которая раскрывает содержание понятия.


Правила и ошибки определений:
1. Определение не должно быть слишком широким
2. определение не должно быть узким
3. определение не должно содержать круга
4. определение не должно быть двусмысленным
5. определение не должно быть сложным
6. определение не должно быть непонятным
7. определение не должно быть отрицательным.
Деление понятий – логическая операция, которая раскрывает объем понятия.
Деление может происходить по любому признаку.
1. должно быть по одному основанию
2. должно быть полным
3. должно быть последовательным.
Суждение
— это логическая форма, в которой что-либо утверждается или отрицается.
Выражается в форме предложения, как правило, повествовательного (+ риторические вопросы и восклицания).
В любом суждении есть понятие, о котором идет речь – субъект S. Кроме того, существует предикат P – то, что отличает субъект от других, характеризует его.
Суждения могут быть оценены как истинные или ложные. Нельзя оценить истинность того, что будет в будущем.


1. атрибутивные (признаки некоторого объекта)
2. релятивные (отношения между субъектами)
3. экзистенциональные (существования).
Отношения между субъектом и предикатом в одном суждении:

Основные типы сложных суждений
Умозаключение
— это логическая форма, в которой из нескольких (от одного до N) связанных между собой суждений делается вывод (качественно новое суждение).
1. дедуктивные. Вывод истинный при истинности посылок.
2. индукция. Вывод вероятностный. Важна репрезентативность выборки.
3. традукция – аналогия. Вывод вероятностный. Ход мысли: частн. – частн.; общ. – общ.
Индуктивное умозаключение – при котором из частных случаев делается общий вывод, как правило, вероятностный.
Для того чтобы индуктивное умозаключение было близко к истинному, важно выполнение следующих правил:
1. Рассмотрение как можно больших элементов множества.
2. Рассмотрение только существенных признаков
3. Рассмотрение разнообразных признаков
Ошибки, допускаемые при неполной индукции:
1. подмена условного безусловным
2. «После того» = «В следствии этого»
3. поспешное обощение.
Причинная связь – связь между двумя явлениями, когда одно из них – причина – предшествует и вызывает другое – действие.
Свойства (1 множество) Отношений
Дедукция
Все дедуктивные умозаключения называются силлогизмами. Виды:
1) Простой категорический силлогизм – из двух связанных между собой простых суждений делается вывод – новое суждение.
Взаимное расположение терминов в умозаключении определяет одну из четырех фигур силлогизма. Комбинации суждений в фигурах силлогизма называются Модус.
Дающих истинный ответ – 19.
1. Энтимема – сокращенный силлогизм, в котором пропущена одна из посылок или вывод.
2. Эпихейрема – простой силлогизм, в котором обе посылки энтимемы.
3. Полисиллогизм (прогрессивный и регрессивный)
4. Сорит – полисиллогизм, в котором пропущена посылка следующего силлогизма, являющаяся выводом предыдущего.
2) Условный силлогизм – содержит в одной или двух посылка условие
А) чисто условный
Б) условно-категорический (утверждение или отрицание)
3) Разделительный силлогизм – включает в себя дизъюнкцию (выбор)
А) чисто разделительный
4) Условно-разделительный силлогизм – умозаключение, в котором в первой посылке должно быть условие, во второй — выбор. Лемма.
5. Законы логики
1. ЗАКОНЫ ТОЖДЕСТВА: любая мысль должна быть тождественной самой себе.
Нарушение может привести к:
2. ЗАКОНЫ ПРОТИВОРЕЧИЯ: если одно суждение утверждает, а другое тоже самое отрицает, то эти два суждения не могут быть одновременно истинными.
Два противоречивых суждения одновременно могут быть ложными.
3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО: два суждения, противоречащих друг другу в одном месте, в одно время об одном предмете, не могут быть одновременно истинными или одновременно ложными.
4. ЗАКОН ДОСТАТОЧНОГО ОСНОВАНИЯ: любая мысль, для того, чтобы иметь силу, обязательно должна быть доказана достаточным аргументом.
— это логическое рассуждение, в процессе которого с помощью положений, проверенных практикой подтверждается или отрицается истинность какой-либо мысли.
Тезис – положение, истинность которого необходимо доказать.
Аргументы – положения, истинность которых уже доказана.
Демонстрация – процесс, связывающий между собой тезис и аргументы
Ошибки в доказательстве
1. ошибки тезиса: а) потеря тезиса
б) подмена тезиса
2. ошибки в аргументах: а) довод к человеку
б) ложность основания
в) предвосхищение основания
г) круг в доказательстве
д) аргумент к публике
3. ошибки в демонстрации: а) мнимое следование
б) нарушение правил силлогизма
Задачи на логику
Задача №1
Было взято 10 листов бумаги. Некоторые листы разрезали на 10 частей,
затем некоторые из получившихся кусков вновь разрезали на 10 частей и т.д.
На каком-то этапе подсчитали общее количество получившихся листов бумаги. Оказалось их всего 1386 листов бумаги. Правильно ли подсчитали количество листов?
Ответ: В результате разрезания одного листа общее количество листов увеличивается на 9. Поэтому конечное число листов, за вычетом 10-ти исходных, должно быть кратным 9; следовательно, подсчет выполнен неверно.
Задача №2
3 женщины решили купить чайник, который стоит 30 долларов, и скинулись по 10 долларов. Потом менеджер узнал, что чайник стоит 25 доларов, он получил из кассы 5 долларов и решил отдать их женщинам. Но как поделить 5 на 3. Поэтому он каждой женщине отдал по 1 доллару (всего получается 3), а себе взял 2. Итак, каждая женщина получила обратно по 1 доллару. То есть вместо 10 потратила 9 долларов. Во сколько обошелся чайник женщинам? Правильно, в 9х3 = 27 долларов. К
ним прибавляем 2 доллара, которые менеджер положил себе в карман. Получается 29. Вопрос: где тридцатый доллар?
Ответ: Просто от 27 надо отнять 2 , а не сложить
Задача №3
Было это в одной местности, где только скотоводы, наверное в Казахстане.
Решили как-то два батыра жениться. Да только проблема — хотят на одной и той же. Ну и решили им устроить состязание (было это в те времена когда про Fairy и мытье котлов ничего не знали) — скачки. Но и устроили им конкурс. Собрались — на лучших конях, при параде — Да только условие поставили хитрое — «получит невесту тот, чья лошадь приедет последней». Ну ребята погарцевали час, два — ни с места. Тут подошел к ним отец невесты чего-то сказал (не нарушающее условие конкурса) и ребята полетели к финишу как стрелы.
Ответ: Можно оперировать словом «чья» во фразе «выиграет тот, чья лошадь придет последним». Т.е. «чья» по принадлежности (праву собственности), а не по тому, кто на данную минуту в седле. В этом случае отец сказал всадникам нечто вроде того «Поменяйтесь лошадьми» или «Я поменял лошадей». В итоге каждый заинтересован, чтоб его лошадь (но под седлом соперника) пришла последней, и соответственно будет ехать как можно быстрей на чужой.

Автор: Энтони Уэстон (Anthony Weston), профессор философии, декан философского факультета Элонского университета (США). Материал публикуется в сокращенном переводе с английского.
Логические ошибки — это примеры ложной аргументации. Многие из них настолько навязчивы и настолько часто встречаются, что имеют собственные названия. Чтобы понять логические ошибки, необходимо определить, какие правила они нарушают.
Две основные логические ошибки
1. Одна из наиболее часто встречающихся логических ошибок — наше навязчивое желание делать вывод на основании очень небольшого количества фактов. Например, если у первого встреченного мной араба был вспыльчивый характер, я могу поспешить с выводом, что у всех арабов вспыльчивый характер. Это — логическая ошибка обобщения на основании неполной информации.
Чтобы оградить вас от этой ошибки, примеров должно быть несколько: вы не можете сделать вывод обо всех студентах вашего вуза, судя только по себе и своему соседу по комнате в общежитии.
Примеры эти должны быть репрезентативными: вы не можете сделать вывод обо всех студентах вашего вуза, судя только по вашим друзьям, даже если у вас их много. Также требуется дополнительная информация: если вы делаете вывод выборке из 30 человек, вы также должны сообщить, сколько студентов всего (30? 30 000?)
Аргументация со ссылкой на авторитет требует, чтобы авторитет не делал слишком широкого обобщения: он должен располагать информацией или обладать компетенцией, позволяющей ему делать утверждения, на которые вы ссылаетесь. Кроме того, даже если мы нашли одну возможную причину события, не следует предполагать, что мы тем самым нашли его действительную причину. Другие причины могут оказаться более вероятными.
2. Вторая часто встречающаяся логическая ошибка — неспособность увидеть альтернативы. Из того факта, что события А и Б кажутся связанными, не следует, что А является причиной Б. Ведь Б может являться причиной А; что-то другое может являться причиной как А, так и Б; А может являться причиной Б, и Б являться причиной А; или А и Б могут оказаться вообще не связанными.
Эти альтернативные объяснения могут остаться незамеченными, если вы примете первое пришедшее вам в голову объяснение. Не спешите: как правило, существует намного больше альтернативных объяснений, чем вы думаете.
Мы также часто не замечаем альтернатив, когда принимаем решения. Две-три возможности находятся на поверхности, и мы рассматриваем только их. В своем знаменитом трактате «Экзистенциализм — это гуманизм» философ Жан-Поль Сартр рассказывает об одном своем студенте, который во время оккупации Франции нацистами должен был выбирать между тем, чтобы отправиться в рискованное путешествие в Англию, где он хотел присоединиться к движению «Свободная Франция», и тем, чтобы остаться со своей матерью в Париже, где он мог заботиться о ней.
Сартр рисует такую картину, как если бы этот молодой человек должен был или поставить на карту все ради побега в Англию — и таким образом бросить свою мать, или полностью посвятить себя ей и отказаться от надежды бороться с нацистами. Конечно же, были и другие возможности. Он мог остаться со своей матерью и все-таки помогать «Свободной Франции» в Париже; он мог остаться со своей матерью на год и попытаться обеспечить ее, постепенно подготовив свой отъезд.
Думать ли нам о его матери как о совершенно беспомощной, эгоистичной и жадной женщине? Или она, вероятно, все-таки была патриоткой и, возможно, даже была способна позаботиться о себе сама? Спрашивал ли он ее когда-нибудь, чего хочет она? Поэтому, скорее всего, у этого студента были и другие возможности. Старайтесь расширить список возможностей, которые вы рассматриваете, — и никогда не сужайте его!
Наиболее распространенные логические ошибки
Ad hominem («к человеку»). Атака на личность авторитета, а не на его компетентность.
Ad ignorantiam («к невежеству»). Аргументация, которая доказывает, что утверждение истинно, поскольку не было показано, что оно ложно. Классический пример — слова, сказанные сенатором Джозефом Маккарти, когда его попросили предъявить факты для поддержки выдвинутого им обвинения, что некий человек является коммунистом: «У меня немного информации по этому вопросу, за исключением того общего заявления компетентных органов, что в его досье нет ничего, чтобы исключало его связи с коммунистами».
Ad misericordiam («к жалости»). Апелляция к жалости в качестве довода, со ссылкой на особые отношения: «Я знаю, что я провалил все экзамены, но если я не окончу курс, мне придется повторно проходить его летом. Вы должны дать мне его закончить».
Ad populum («к толпе»). Апелляция к эмоциям толпы; также призыв к человеку согласиться с мнением толпы. Например: «Это все делают!». Ad populum — это хороший пример плохой аргументации со ссылкой на авторитет: не приводится никаких доводов, показывающих, что «все» — это информированный и беспристрастный источник.
Non sequitur («не следует»). Приход к выводу, который не является логическим заключением из имеющихся фактов. Самое общее определение плохой аргументации. Попробуйте выяснить, что именно в данной аргументации кажется не так.
Petitio principii: латинское название предвосхищения основания.
Post hoc, ergo propter hoc («после этого, значит, по причине этого»). Выведение причинности на основании простой последовательности во времени.
Безоговорочное определение: определение понятия словами, которые кажутся простыми, но на самом деле эмоционально окрашены. Безоговорочные определения могут быть эмоционально окрашены и с целью «приукрасить» понятие: например, определяя «консерватора» как «человека, имеющего реальные взгляды на человеческие возможности».
Ложная дилемма: сужение числа рассматриваемых вами возможностей всего до двух, часто резко противоположных и несправедливых к людям, против которых эта дилемма направлена. Например: «Не нравится — убирайтесь!» Вот более тонкий пример из студенческой работы: «Поскольку вселенная не могла быть создана из ничего, она должна была быть создана разумной жизненной силой». Является ли посредничество «разумной жизненной силы» единственной возможностью? Ложная дилемма часто использует эмоционально окрашенный язык; она также, очевидно, не учитывает альтернатив.
Ложное основание: общее определение сомнительного вывода о причине и следствии.
Наведение на ложный след: введение посторонней или второстепенной идеи и тем самым отвлечение внимания от основной идеи. Как правило, «ложный след» — это проблема, о которой люди имеют устойчивые мнения; поэтому-то и предполагается, что противник не заметит, как его внимание было отвлечено. При обсуждении относительной безопасности разных моделей автомобилей, например, проблема выбора между отечественными и импортными автомобилями — это «ложный след».
Огородное пугало. Карикатурное изображение взглядов противника, с тем чтобы его легко можно было опровергнуть.
Отравление колодца. Использование эмоционально окрашенного языка с целью принизить аргументацию, прежде чем даже упомянуть о ней: «Я убежден, что вас не собьют с толку несколько болтунов, которые так и не избавились от предубеждений относительно…» Или более тонко: «Ни один по-настоящему чуткий человек не думает, что…»
Отрицание антецедента: ошибка в дедукции формы
Если М, то Н.
Не- М.
Поэтому не- Н.
В высказывании «если М, то Н» М называется «антецедентом», а Н — «консеквентом». Вторая посылка modus tollens отрицает консеквент. Отрицание антецедента, с другой стороны, приводит к неправильной форме. Истинный вывод не гарантирован, даже если посылки истинны. Например:
Когда на дорогах гололедица, почта опаздывает.
На дорогах нет гололедицы.
Поэтому почта не опоздает.
Хотя почта опоздает, если дороги обледенеют, она может опоздать и по другим причинам. Эта аргументация не учитывает альтернативных объяснений.
Подтверждение консеквента: ошибка в дедукции формы
Если М, то Н.
Н.
Поэтому М.
В высказывании «если М, то Н» М называется «антецедентом», а Н — «консеквентом». Вторая посылка modus ponens подтверждает (доказывает) антецедент (проверьте).
Подтверждение консеквента, с другой стороны, приводит к неправильной форме. Истинный вывод не гарантирован, даже если посылки истинны. Например:
Когда на дорогах гололедица, почта опаздывает.
Почта опаздывает.
Поэтому на дорогах гололедица.
Хотя почта опоздает, если дороги обледенеют, она может опоздать и по другим причинам. Эта аргументация не учитывает альтернативных объяснений.
Предвосхищение основания: неявное использование вывода в качестве посылки.
Бог существует, поскольку об этом говорится в Библии, которая, как мне известно, истинна, потому что ее написал Бог!
Переписав эту аргументацию в форме «причина — следствие», вы получите:
Библия истинна, потому что ее написал Бог.
Библия говорит, что Бог существует.
Поэтому Бог существует.
Чтобы защитить утверждение об истинности Библии, утверждается, что ее написал Бог. Очевидно, однако, что если Бог написал Библию, то Бог существует. Эта аргументация предполагает (предвосхищает) именно то, что она пытается доказать.
Слово-хамелеон: изменение значения слова в процессе аргументации таким образом, что ваш вывод может быть сохранен, однако его смысл радикально изменится. Как правило, такой маневр предпринимают в ответ на контрпример.
А: Всякое обучение — это пытка.
Б: А как насчет обучения логике? Тебе же это нравится!
А: Ну, это и обучением назвать нельзя.
Здесь «обучение» — слово-хамелеон. Ответ А на возражение Б по сути меняет значение слова «обучение» на «обучение, которое есть пытка»: так что первое утверждение А остается истинным, но только ценой того, что оно превращается в тавтологию («Всякое обучение, которое есть пытка, есть пытка»).
Сложный вопрос: представление вопроса или проблемы таким образом, что люди не могут ни согласиться, ни не согласиться с вами, не обязав себя согласиться с каким-то другим утверждением, которое вы собираетесь сделать. Простой пример: «Вы по-прежнему такой же эгоист, каким были?» Ответ «да» или «нет» обязывает вас согласиться с тем, что когда-то вы были эгоистом.
Более тонкий пример: «Вы поступите так, как подсказывает вам ваша совесть, а не ваш кошелек, и пожертвуете на благородное дело?». Ответ «нет», независимо от реальных причин отказа в пожертвовании, вызывает у людей чувство вины. Ответ «да», независимо от реальных причин согласия на пожертвование, делает их благородными.
Научитесь логично мыслить, думать и поступать, изучив курс «Практическая логика и аргументация»:
Обновлено: 29.01.2023
Содержание работы
Содержимое работы — 1 файл
Логика.Коля..docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Кафедра: Теория Государства и права.
Выполнил студент Группы: ЮРз-11-3
Проверил: ст. преподаватель каф. ТГП
Итак, под логическими ошибками мы будем понимать случайные или намеренные искажения фактов, рассуждений, выводов, предпосылок или связей между ними. Важно отметить, что наличие логической ошибки в рассуждении не означает автоматически, что доказываемое утверждение ложно. Оно может оказаться как ложно, так и истинно, так что наличие логической ошибки полностью обессмысливает доказательство, превращая его просто в набор слов.
Логические ошибки — это примеры ложной аргументации. Многие из них настолько навязчивы и настолько часто встречаются, что имеют собственные названия. Чтобы понять логические ошибки, необходимо определить, какие правила, они нарушают. Одна из наиболее часто встречающихся логических ошибок — желание делать вывод на основании очень небольшого количества фактов. Вторая — неспособность увидеть альтернативы.
1. Одна из наиболее часто встречающихся логических ошибок — наше навязчивое желание делать вывод на основании очень небольшого количества фактов. Например, если у первого встреченного мной араба был вспыльчивый характер, я могу поспешить с выводом, что у всех арабов вспыльчивый характер. Это — логическая ошибка обобщения на основании неполной информации.
Чтобы оградить вас от этой ошибки, примеров должно быть несколько: вы не можете сделать вывод обо всех студентах вашего вуза, судя только по себе и своему соседу по комнате в общежитии. Примеры эти должны быть представительными: вы не можете сделать вывод обо всех студентах вашего вуза, судя только по вашим друзьям, даже если у вас их много. Также требуется дополнительная информация: если вы делаете вывод выборке из 30 человек, вы также должны сообщить, сколько студентов всего (30? 30 000?) Аргументация со ссылкой на авторитет требует, чтобы авторитет не делал слишком широкого обобщения: он должен располагать информацией или обладать компетенцией, позволяющей ему делать утверждения, на
которые вы ссылаетесь. Кроме того, даже если мы нашли одну возможную причину события, не следует предполагать, что мы тем самым нашли его действительную причину. Другие причины могут оказаться более вероятными.
2. Вторая часто встречающаяся логическая ошибка — неспособность увидеть альтернативы. Из того факта, что события А и Б кажутся связанными, не следует, что А является причиной Б. Ведь Б может являться причиной А; что-то другое может являться причиной как А, так и Б; А может являться причиной Б, и Б являться причиной А; или А и Б могут оказаться вообще не связанными. Эти альтернативные объяснения могут остаться незамеченными, если вы примете первое, пришедшее вам в голову объяснение. Не спешите: как правило, существует намного больше альтернативных объяснений, чем вы думаете.
Список наиболее распространенных логических ошибок
Petitio principii: латинское название предвосхищения основания.
дилемма часто использует эмоционально окрашенный язык; она также, очевидно, не учитывает альтернатив.
Ложное основание: общее определение сомнительного вывода о причине и следствии.
Огородное пугало. Карикатурное изображение взглядов противника, с тем чтобы его легко можно было опровергнуть.
Отрицание антецедента: ошибка в дедукции формы
Если М, то Н.
Не — М.
Поэтому не — Н.
Когда на дорогах гололедица, почта опаздывает.
На дорогах нет гололедицы.
Поэтому почта не опоздает.
Хотя почта опоздает, если дороги обледенеют, она может опоздать и по другим причинам. Эта аргументация не учитывает альтернативных объяснений.
Подтверждение консеквента: ошибка в дедукции формы
Если М, то Н.
Н.
Поэтому М.
Когда на дорогах гололедица, почта опаздывает.
Почта опаздывает.
Поэтому на дорогах гололедица.
Хотя почта опоздает, если дороги обледенеют, она может опоздать и по
другим причинам. Эта аргументация не учитывает альтернативных объяснений.
Предвосхищение основания: неявное использование вывода в качестве посылки.
Бог существует, поскольку об этом говорится в Библии, которая, как мне известно, истинна, потому что ее написал Бог, как-никак!
Библия истинна, потому что ее написал Бог.
Библия говорит, что Бог существует.
Поэтому Бог существует.
Чтобы защитить утверждение об истинности Библии, утверждается, что ее написал Бог. Очевидно, однако, что если Бог написал Библию, то Бог существует. Эта аргументация предполагает (предвосхищает) именно то, что она пытается доказать.
Слово-хамелеон: изменение значения слова в процессе аргументации таким образом, что ваш вывод может быть сохранен, однако его смысл радикально изменится. Как правило, такой маневр предпринимают в ответ на контрпример.
А: Всякое обучение — это пытка.
Б: А как насчет обучения логике? Тебе же это нравится!
А: Ну, это и обучением назвать нельзя.
Основные логические формы: понятие, суждение, умозаключение и доказательство. Приемы, облегчающие нахождение логических ошибок. Существование объективных связей в мыслях. Ошибки, относящиеся к мыслям. Примеры связи суждений. Навыки правильного мышления.
| Рубрика | Философия |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 02.01.2014 |
| Размер файла | 27,2 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
1. Понятие логической ошибки
2. Ошибки в основных формах мышления
3. Логические ошибки в доказательствах
4. Приемы, облегчающие нахождение логических ошибок
В настоящее время вследствие незнания законов логики людьми допускается очень много логических ошибок, которые как правило ведут к неправильному истолкованию мыслей человека и некорректному пониманию его другим лицом. Таким образом, актуальность темы работы очевидна.
Целью написания реферата является рассмотрение логических ошибок и приемов, облегчающих их нахождение. Для её достижения необходимо решить некоторые задачи. Сначала следует изучить сущность логических ошибок. После этого будет необходимо рассмотреть виды логических ошибок. Далее следует отметить способы их нахождения.
При этом объектом исследования является логика как наука о правильном мышлении, предметом — логические ошибки и способы их устранения.
1. Понятие логической ошибки
В чем же суть логических ошибок?
Если человеку, который смотрит на уходящие вдаль рельсы железной дороги, кажется, что они сходятся на горизонте в одной точке, то он ошибается. Ошибается тот, кому кажется, что падение одного зерна на землю не производит ни малейшего шума, что пушинка не имеет веса и т. д. Можно ли назвать эти ошибки логическими? Нет. Они связаны с обманом зрения, слуха и т. д., это ошибки чувственного восприятия. Логические же ошибки относятся к мыслям. Мыслить можно и о предметах, которых в данный момент не видишь, не слышишь, не осязаешь, то есть чувственно не воспринимаешь. Мы можем думать о том, что Земля вращается вокруг Солнца, хотя непосредственно этого не ощущаем. При этом наши мысли могут соответствовать действительности, то есть быть истинными, и могут противоречить реальному положению, вещей, то есть быть ошибочными, неистинными.
Ошибки, относящиеся к мыслям, также далеко не всегда являются логическими. Ребенок может сказать, что дважды два — три. Студент на экзамене может неправильно назвать дату того или иного события. Тот и другой в этом случае допускают ошибку. Если причина этих ошибок — только плохая память, например, ребенок не помнит таблицу умножения, а студент плохо выучил хронологию и забыл нужную дату, тогда допущенные ими ошибки не могут быть отнесены к логическим.
Конечно, совершенно несомненен тот факт, что мысли связываются между собой в голове человека по-разному, в зависимости от состояния психики, от воли и желаний. Один человек с мыслью о приближающейся зиме связывает приятные мысли о катанье на коньках и на лыжах. У другого та же самая мысль вызывает совсем другие, возможно, менее приятные мысли. Все такого рода связи между мыслями являются субъективными, то есть зависящими от психики каждого отдельного человека. От особенностей психики разных людей будет зависеть и то, установит ли человек связь между мыслью о замерзании озера зимой и мыслями о том, что зимой температура опускается ниже нуля и вода при этой температуре замерзает. Однако независимо от того, думает человек об этом или нет, связывает или не связывает он между собой эти обстоятельства, приятно ему это или неприятно, — из истинности мыслей о том, что вода замерзает при температуре ниже нуля и зимой температура ниже нуля, неизбежно, объективно, совершенно независимо от субъективных вкусов и желаний следует истинность мысли о том, что озеро зимой замерзает.
Для того чтобы различить случаи, когда искажаются отношения непосредственно между вещами, с одной стороны, и отношения между мыслями, с другой, вводятся два разных слова, два особых термина. Когда имеет место искажение отношений реального мира, то говорят о неистинности мысли. Тогда же, когда речь идет об искажении отношений между самими мыслями, говорят о неправильности.
Ошибки, связанные с неистинностью мыслей, т. е. с искажением в мыслях отношений между предметами и явлениями окружающей действительности, называются фактическими. Ошибки же, связанные с неправильностью мысли, то есть с искажением связей между самими мыслями, являются логическими.
2. Ошибки в основных формах мышления
Каким же образом логика может выполнить свою задачу? Как она может установить общие условия правильности всех мыслей? Ведь мыслей существует бесчисленное множество, и они очень разнообразны: мысли о музыке, о дне моря, об электронах, о революции и т. д. Все мысли перечислить невозможно, следовательно, нельзя сформулировать особое правило для каждой отдельной мысли. Правила должны быть общими. И, подобно тому, как существуют различные пространственные отношения между элементами тел, то есть разные геометрические формы, так могут существовать и разные соотношения между мыслями и их элементами, то есть разные логические формы мыслей. Выделяют следующие основные логические формы: понятие, суждение, умозаключение и доказательство.
Те существенные признаки, которые мыслятся в понятии о предмете, образуют содержание понятия. Круг предметов, к которым относится данное понятие, называется объемом понятия.
В понятии группа признаков мыслится настолько слитно, что иногда довольно трудно точно определить, выделить эти признаки. В суждении же дело обстоит иначе. Само определение суждения указывает на то, что здесь отчетливо выделяются три элемента:
1) понятие, обозначающее то, о чем говорится в суждении; это — подлежащее, или субъект, суждения;
2) то, что говорится о субъекте; это — сказуемое, или предикат, суждения;
Таким образом, суждение имеет четкую структуру. Поэтому его можно выразить в общем виде при помощи буквенных обозначений, подобно тому, как это делается в алгебре. Субъект обозначается буквой S (первая буква латинского слова subjectum — подлежащее), предикат — буквой P (латинское praedicatum — сказуемое). Получаются формулы суждения:
S есть P или S не есть P.
Суждения, так же как и понятия, не существуют сами по себе, вне связи с другими суждениями. Они связываются между собой, образуя более сложные мысли, более сложные логические формы. Примеры такой связи суждений у нас уже были выше:
все млекопитающие дышат легкими;
дельфин дышит легкими;
имена собственные пишутся с большой буквы;
Логическая форма, которую образует такого рода связь суждений, называется умозаключением. К умозаключениям относится и то преобразование двух разделительных суждений в одно условное, которое было только что проделано.
От умозаключений необходимо отличать другую логическую форму — доказательство.
В умозаключении мы приходим к выводу из посылок, причем иногда мы совсем не знаем, к какому именно выводу приведут данные посылки, то есть вывод в принципе может быть совершенно неожиданным.
Если в обычном умозаключении определяется то, что следует из данных посылок, то в данном случае определяется то, из чего следует данное утверждение. Такая логическая форма, в которой обосновывается истинность того или другого положения, называется доказательством.
В доказательстве выделяются три части: 1) тезис — то, что нужно доказать; 2) аргументы — то, чем доказывается тезис; 3) рассуждение, которое показывает, как доказывается тезис, каким образом осуществляется переход от посылок к аргументам.
Мы уже раньше видели примеры того, как более сложные формы включают в себя более простые в качестве составных частей: суждение — это соотношение понятий, умозаключение — соотношение суждений. Как понятие является составной частью суждения, суждение — составной частью умозаключения, так умозаключение входит в качестве составной части в доказательство: третья часть доказательства — рассуждение — представляет собой умозаключение.
Мы познакомились с логическими формами мышления. Теперь можно выяснить, какие правила должны соблюдаться в каждой из этих форм мысли для того, чтобы мыслить правильно и избежать логических ошибок в рассуждениях.
Всякая логическая ошибка относится к тому или другому определенному типу мыслей. Мысли же, как мы выяснили, различаются по логической форме. Поэтому, естественно, и ошибки различаются по тому, к какой логической форме они относятся.
Логические ошибки можно разделить на четыре группы, соответствующие четырем логическим формам мыслей:
1) ошибки, относящиеся к понятию;
2) ошибки в суждениях;
3) ошибки в умозаключениях;
4) ошибки в доказательствах.
А) Логические ошибки в понятиях.
Логические ошибки в понятиях могут быть основаны на нарушении закона тождества.
Рассмотрим такой пример. Два охотника увидели во время охоты белку, которая сидела на дереве и смотрела прямо на них. Они решили обойти ее, но по мере того как они продвигались по окружности, белка тоже передвигалась так, что все время была обращена к охотникам одной стороной и смотрела на них, и так продолжалось до тех пор, пока они не вернулись на прежнее место. Спрашивается, обошли охотники белку или нет? Один из них утверждал, что обошли, поскольку они описали вокруг белки замкнутую линию — окружность. Другой возражал, что, если бы они обошли белку, они должны были видеть ее со всех сторон, а они видели ее все время только с одной стороны. Спорили они долго, но так ни к чему и не пришли. Кто же из них прав?
Но необходимо иметь в виду, что иногда подобное противоречие в понятии является только кажущимся. Это противоречие может выполнять известную художественную задачу, позволяет сильнее подчеркнуть определенную мысль.
Б) Логические ошибки в суждениях.
Все уже известные нам общие законы мышления применительно к суждению будут формулироваться следующим образом.
1. Закон тождества: каждое суждение тождественно самому себе.
2. Закон противоречия: суждение не может быть тождественно чему-то, отрицающему это суждение.
3. Закон исключенного третьего: данное суждение или тождественно другому суждению, или отлично от него.
4. Закон достаточного основания: суждение может считаться истинным или правильным только в том случае, если для этого приведены достаточные основания.
5. Как избежать логических ошибок в умозаключениях.
В) Логические ошибки в умозаключениях.
Прежде всего, остановимся на умозаключениях, которые сводятся к преобразованию посылок, то есть на умозаключениях дедуктивных. Простейшие среди них, как мы знаем, — непосредственные умозаключения.
3. Логические ошибки в доказательствах
Внутри одного доказательства могут быть допущены ошибки трех совершенно разных типов в соответствии с тремя частями доказательства: тезисом, аргументами и рассуждением. Среди них только ошибки, относящиеся к третьей части, связаны с нарушением специальных правил умозаключения.
Основное правило, относящееся к тезису, является следствием одного из общих законов мышления — закона тождества: в процессе доказательства нужно доказывать именно тот тезис, который требуется доказать. Нельзя подменять один тезис другим.
Подмена тезиса особенно часто наблюдается при опровержениях, когда обосновывается не истинность, а ложность какого-либо утверждения. В этих случаях очень часто опровергается совсем не то, что нужно опровергнуть.
Теперь посмотрим, каким требованиям должна удовлетворять вторая часть доказательства — аргументы, для того чтобы доказательство было правильным.
Прежде всего, положения, которые приводятся в качестве аргументов, должны быть, безусловно, истинными. Это одно из самых важных правил доказательства. Если умозаключение в принципе может быть правильным даже при наличии фактических ошибок в посылках, то обязательным условием логической правильности доказательства является фактическая истинность посылок.
Но истинность аргументов — это еще не все, что от них требуется для правильности доказательства. Обратимся снова к сочинениям по литературе. Вот как обосновывает тезис своего сочинения студентка техникума:
«Роман „Поднятая целина“ Шолохов посвятил коллективизации сельского хозяйства в деревне. Роман говорит о социальной перестройке казачества, о переходе на новую жизнь. В этом романе Шолохов показал образы коммунистов в дни перехода деревни на новую жизнь, а также крестьянина-середняка, вступившего на путь социалистического строительства.
4. Приемы, облегчающие нахождение логических ошибок
Мы показали, какие правила необходимо знать для того, чтобы избежать логических ошибок. Однако одного знания правил логики недостаточно, как недостаточно знания правил грамматики для того, чтобы грамотно писать. Необходимо вырабатывать логические навыки правильного мышления. Наличие таких навыков позволяет правильно рассуждать, не поддаваясь действию разного рода аффектов, под влиянием которых возникают логические ошибки.
Наконец, можно обнаружить, что в рассуждении есть какая-то ошибка, путем подбора определенного факта из жизни, несовместимого с данным выводом. Если этот вывод сделан из истинных посылок, то наличие такого факта явно будет указывать на наличие ошибки в рассуждении, например:
в правильно решенной задаче результат совпадает с ответом, данным в задачнике;
в этой задаче результат совпадает с ответом, данным в задачнике;
следовательно, эта задача решена правильно.
Если человек может привести хотя бы один такой факт или даже просто быть уверенным в возможности такого факта, когда в задаче, решенной неправильно, ответ совпадает с заданным, то тем самым он докажет, что вывод в данном случае сделан неправильно.
Наконец, ни один из этих приемов не дает возможности точно определять логическую сущность каждой ошибки и свободно ориентироваться в правильности и неправильности самых разнообразных рассуждений, выводов, доказательств и т. д. Действительную, по-настоящему высокую логическую культуру могут дать человеку только приобретенные прочные навыки правильного мышления, основанные на знании общих законов мышления и вытекающих из них логических правил.
В данном реферате мы рассмотрели сущность логических ошибок, описали их основные виды и некоторые приемы, облегчающие их нахождение.
Проверить и доказать истинность таких утверждений можно только логическим путем, с помощью выяснения того, в каких отношениях находятся данные мысли к некоторым другим мыслям, истинность или ложность которых нам уже известна. В этом случае на первый план уже выступает правильность или неправильность рассуждения. От этого будет зависеть истинность или ложность сделанного нами вывода. Если рассуждение построено правильно, если между данными мыслями установлены именно те связи, которые существуют на самом деле, то, будучи уверены в истинности этих мыслей, мы можем быть вполне уверены в истинности того вывода, который получен в результате рассуждения. Но как бы ни были достоверны исходные положения, мы нисколько не можем доверять выводу в том случае, если в рассуждении допущена логическая ошибка.
Подобные документы
Предмет и законы логики. Понятие логической формы. Логические категории и символы. Виды и структура суждений. Распределенность терминов в простом атрибутивном суждении. Понятие и виды умозаключений. Простой категорический силлогизм: правила, фигуры.
контрольная работа [97,0 K], добавлен 08.11.2008
Понятия «мировая экономика», «пеня». Инструменты финансового менеджмента. Примеры экзистенциальных, атрибутивных суждений, суждений с отношением. Законы правильного мышления, примеры нарушения. Определение вида доказательства, содержащегося в рассуждении.
контрольная работа [48,9 K], добавлен 28.05.2015
Суждение как форма мышления. Структура простого категорического суждения в логике. Суждение как логическая форма мышления. Суждение и вопрос. Требование истинности предпосылок при постановке вопроса, логические ошибки. Принципы классификации суждений.
реферат [22,8 K], добавлен 23.09.2010
Проведение анализа дефиниций, операции отрицания суждений об отношениях, дедуктивных выводов из вероятностных и логических умозаключений. Приведение примеров нарушения принципов правильного мышления. Изучение аргументация как способа опровержения теорий.
контрольная работа [216,2 K], добавлен 11.03.2010
Умозаключение — форма мышления, посредством которого из одного или нескольких суждений выводится новое суждение. Виды умозаключений. Логика суждений (высказываний). «Аксиомы» логики суждений. Правила вывода логики суждений. «Условный силлогизм».
ЛОГИЧЕСКИЕ ОШИБКИ
- Описание
- Алфавитный указатель
- Арабская философия
- Индийская философия
- Китайская философия
- Русская философия
- Этика
- Авторы
- Приложения
К числу ошибок типа (1) относится прежде всего ошибка ложного основания, когда в качестве посылки доказательства принимается ложное суждение (эта ошибка называется также основным заблуждением, ее лат. название – error fundamentalis). Поскольку из ложных суждений по законам и правилам логики могут быть выведены в одних случаях ложные, а в других – истинные следствия, постольку наличие в числе посылок ложного суждения оставляет открытым вопрос об истинности доказываемого тезиса. Частным случаем этой ошибки является такое использование (в качестве посылки доказательства) некоторого суждения, требующего для своей истинности определенных ограничительных условий, при котором это суждение рассматривается безотносительно к этим условиям, что приводит к определенной ложности. Другой случай этой же ошибки состоит в том, что вместо некоторой нужной для данного доказательства истинной посылки берется более сильное суждение, являющееся, однако, ложным (суждение А называется более сильным, чем суждение В, если из А в предположении его истинности следует В, но не наоборот).
Учение традиционной логики о логических ошибках охватывает все основные виды логических дефектов в содержательных рассуждениях людей. Средства современной формальной логики позволяют лишь уточнить характеристику многих из них. В связи с развитием математической логики понятие логической ошибки естественно распространяется на случаи ошибок, связанных с построением и использованием рассматриваемых в ней исчислений, в частности, всякая ошибка в применении правил образования или преобразования выражений исчисления может рассматриваться как логическая. Источником ошибок в мышлении являются различные причины психологического, языкового, логико-гносеологического и иного характера. Появлению логических ошибок способствует прежде всего то, что многие логически неправильные рассуждения внешне похожи на правильные. Немаловажную роль играет также и то, что в обычных рассуждениях не все их шаги – суждения и умозаключения, в них входящие, – обычно бывают выраженными в явной форме. Сокращенный характер рассуждений часто маскирует неявно подразумеваемые в нем ложные посылки или неправильные логические приемы. Важным источником логических ошибок является недостаточная логическая культура, сбивчивость мышления, нечеткое понимание того, что дано и что требуется доказать в ходе рассуждения, неясность применяемых в нем понятий и суждений. Сбивчивость мышления бывает тесно связана с логическим несовершенством языковых средств, применяемых при формулировке тех или иных суждений и выводов. Источником логических ошибок может быть также эмоциональная неуравновешенность или возбужденность. Питательной средой для логических ошибок, особенно для ошибки ложного основания, являются те или иные предрассудки и суеверия, предвзятые мнения и ложные теории.
В борьбе с логическими ошибками немаловажное значение имеет использование средств логики. Эти средства дают должный результат в тех областях, где фактический материал позволяет осуществить предписываемое формальной логикой уточнение формы рассуждений, выявление опущенных звеньев доказательств, развернутое словесное выражение выводов, четкое определение понятий. В этих областях применение логики является эффективным средством устранения сбивчивости, непоследовательности и бездоказательности мышления. Дальнейшее развитие средств логики – уже в рамках математической логики – привело к оформлению строгой теории дедуктивного вывода, к логической формализации целых разделов науки, к разработке искусственных (напр., т.н. информационно-логических) языков. Вместе с тем выяснилось, что чем сложнее область исследования, тем сильнее проявляется неизбежная ограниченность формально-логических средств. Средства логики сами по себе, как правило, не гарантируют правильности решения научных и практических вопросов; при всей их необходимости они дают должный эффект лишь в комплексе всей практической и познавательной деятельности человечества.
1. Асмус В.Ф. Учение логики о доказательстве и опровержении. М., 1954, гл. 6;
2. Уемов А.И. Логические ошибки. Как они мешают правильно мыслить. М., 1958.
В первой главе вы узнали о том, откуда могут взяться логические ошибки. Это могут быть самые разнообразные причины: от умысла до несовершенства ума, от художественных приёмов до языковых причин. Вы узнали, что логические ошибки, да и ошибки вообще, не всегда играют плохую роль, так как, например, в искусстве порой уместно заменять истину правдоподобием, а при выступлениях на публике не всегда уместно строго что-то доказывать, достаточно лишь убедительно говорить (честно или нечестно – это уже другой вопрос).
Василий Иванович и Петька маневрируют на танке посреди поля боевых действий, ситуация крайне напряжённая. Василий Иванович коротко спрашивает:
– Петька, приборы!
– Двадцать!
– Что двадцать? – уточняет Василий Иванович.
– А что приборы? – недоумевает Петька.
Однако пагубность логических ошибок в том, что иногда человек всё же делает совершенно неправильные выводы, так как не замечает ошибок или делает их намеренно с корыстными целями. А иногда люди просто не понимают друг друга. Так, например, кажущийся формально верным пример
Все люди смертны. Сократ – человек. Следовательно, Сократ смертен.
Изложение главы ведётся по следующим источникам:
Главным образом все логические ошибки делятся на формальныеи неформальные. Первые связаны с нарушением формальных логических правил. В них нарушена правильность умозаключений, которые в принципе можно выразить математически. Вторые связаны с восприятием самого человека, с тем, как он понимает содержание исходных предпосылок или заключений. Формально говоря, неформальные логические умозаключения могут быть логически и математически безупречными, но всё равно могут содержать ошибки. У формальных ошибок ошибка именно в форме мысли. У неформальных – в содержании мыслей.
Пример формальной ошибки: Если у человека аллергия на бананы, то он не ест бананы. Вася не ест бананы. Значит у него аллергия на бананы.
Здесь классическая ошибка перестановки причины и следствия. Мы говорим Если P, то Q, но из этого не следует Если Q, то P. Как видно, формальная логика приходит на помощь и поясняет ошибку.
Пример неформальной ошибки: Практика – путь к совершенству. У преподавателя очень большая практика. Следовательно, преподаватель совершенен.
Не стоит слишком активно пользоваться подобным разделением ошибок на формальные и неформальные, потому что, как показал выше пример с Сократом, одна и та же ситуация может рассматриваться как с формальных, так и с неформальных позиций. Формальные и неформальные ошибки могут переходить одна в другую в зависимости от угла зрения, а также комбинироваться самыми разными способами.
Однако существует и другая классификация логических ошибок: по характеру заложенного в них приёма. Всё многообразие логических ошибок может быть разбито на относительно небольшое количество однотипных приёмов, с помощью которых из предпосылок получается следствие. Вот такой классификации мы и будем следовать.
Ложное (необоснованное, поспешное) обобщение (Dicto simpliciter, Hasty Generalization)
Есть два основных варианта такой ошибки. В первом некое частное свойство, присущее члену группы, обобщается на всю группу.
Пример: Все чиновники – взяточники. Все мужики — козлы.
Другой пример: (по дороге у автомобиля прокололось колесо)
— Дорогая, я не умею сам менять колёса в автомобиле.
— Да что вы мужики вообще умеете?!
В другом варианте частный случай не принимается во внимание и закон обобщается на него тоже.
Пример: Правду говорить легко и приятно. Вас взяли в плен. Вы должны легко и приятно сказать врагам правду о ваших стратегических планах и о расположении ваших военных частей.
Другой пример: Резать человека ножом — преступление, а хирург делает именно это. Значит, хирург — преступник.
Любой читатель может подумать, будто бы этот вариант логической ошибки настолько прост, что его никто в реальности не совершает. Но, увы, простые примеры вовсе не означают, что ошибка такая же простая. Давайте перейдём к более сложным вариантам ложного обобщения.
Один из таких сложных вариантов проявляется тогда, когда человек по одной частной проекции пытается сделать выводы об объекте в целом.
Читателю также ясно, что по совокупности проекций вполне можно восстановить целое, как это делает, например, мастер резьбы, вырезая предмет по серии проекций и эскизов. Но к чему же я тогда веду?
Иными словами, приписывать различные широкие свойства некоторому объекту, который оказался выше в рейтинге по частным критериям — этот и есть вариант ложного обобщения. И он прямо-таки правит этим миром.
- J. Hietala, “Novel Use of Biomarkers and their Combinations for Detecting Excessive Drinking” (2007).
- K. Fillmore, T. Stockwell, T. Chikritzhs, et al. “Moderate Alcohol Use and Reduced Mortality Risk — Systematic Error in Prospective Studies and New Hypotheses” (2007).
- T. Chikritzhs, K. Fillmore, T. Stockwell, “A healthy dose of scepticism — Four good reasons to think again” (2009).
- R. Harriss et al. “Alcohol consumption and cardiovascular mortality accounting for possible misclassification of intake: 11-year follow-up of the Melbourne Collaborative Cohort Study” (2007).
Кстати, вера в науку — одна из довольно распространённых логических ошибок, о ней, возможно, ещё поговорим.
Безотносительное суждение (Ignoratio elenchi, Missing the Point)
Это также распространённая ошибка, когда приводимый аргумент может быть верным, но он не имеет к обсуждаемому никакого отношение.
Пример 1: (на дебатах)
– Защищает ли закон безработных граждан?
– Закон должен защищать безработных граждан, потому что они такие же граждане, но оказались в сложной ситуации, им нужно помочь найти работу.
Пример 2:
– Я бы хотел купить дом на берегу моря.
– Как ты можешь мечтать о доме на берегу моря, когда в Африке каждый день умирают люди?
Ошибка в том, что хотя ужасающий аргумент не является ошибочным, он не относится к обсуждаемой теме. Кроме того, люди каждый день умирают не только а Африке, и отнюдь не всегда это для кого-то (в том числе для умирающих) является чем-то трагичным.
Пример 3:
– Советую бегать по утрам, это даёт такие-то и такие-топреимущества.
– Давно доказано, что бег плохо влияет на коленные суставы, они разрушаются.
Ошибка в том, что частный тезис, истинный в некоторых случаях (только при неправильном беге или патологиях суставов), выступает в качестве опровержения основного тезиса о пользе бега. Приведу аналогию, доведённую до абсурда: человеку вредно пить воду, потому что если он выпьет её ]]> 14 литров за 3 часа ]]> , в его организме начнутся необратимые процессы, приводящие к смерти. Но согласитесь, этим тезисом я не доказал, что пить воду вредно. Точно также тезис о том, что бег разрушает коленные суставы не опровергает пользу бега, а лишь демонстрирует спортивную безграмотность человека. При правильном беге здоровый человек не испортит ноги. Во всяком случае, мне и двум моим тренерам неизвестны подобные случаи.
Вообще, безотносительное суждение является одним из способов сменить тему разговора. Пример:
– Алкоголь вреден в любых дозах, а люди, его употребляющие, просто не хотят разобраться в ситуации.
– У меня дед Иннокентий 70 лет пил, и ничего, прожил долгую жизнь. Да и вообще, во время войны боевые 50 грамм могли жизнь спасти.
В результате собеседник вместо объяснения своего тезиса о вреде алкоголя будет вынужден тратить время на объяснение типичных мифов про деда Иннокентия и боевые 50 грамм (подобных историй можно накопать добрую сотню). А пока он это делает, время уходит, и желание слушать человека тоже. Поэтому человек, у которого на вооружении есть ряд заранее подготовленных аргументов, не имеющих отношения к теме, может гарантированно заболтать вас ими до такой степени, что вместо темы доклада вы будете говорить всякую ерунду. И не важно, успешно у вас это получится или нет: собеседник добился своего, он не позволил вам сказать то, что вы хотели. Один из вариантов такого поведения характерен для дебатов: нужно заставить человека доказывать, что он не верблюд, просто навешивая на него заведомо нелепые ярлыки и вынуждая тратить время на отрицание очевидного.
Вот так, приписав собеседнику заведомо удобную для себя точку зрения, с лёгкостью опровергаешь её, а потом говоришь, что опроверг его исходный тезис. К сожалению, подобную логику любят как креационисты, так и представители научного метода.
Домашнее задание
Напомню, что задачи не следует обсуждать в комментариях (если только не обнаружили ошибку в формулировке).
Задача 1
Попробуйте перечислить здесь все логические ошибки и более подробно объяснить те, что мы рассмотрели в этой части второй главы.
Задача 2
Задача 3
Перед вами анекдот.
Рассмотрите анекдот с позиции пройденного материала. Какой ошибке он посвящён? Какова культурная ценность его содержания?
Задача 4
Один историк как-то сказал, что древние пирамиды Египта не могли быть построены теми, кто жил в то время, потому что даже сегодня ни один современный метод обработки камня не может столь безупречно ровно резать такие огромные блоки. Он же сказал о невозможности построения некоторых зданий Баальбека, так как даже современная техника не позволяет поднимать камни такого огромного размера.
Есть ли здесь ошибка ложного обобщения? Если да, то в чём? Есть ли здесь другие ошибки из известных вам?
Задача 5
Это задача непростая: в данном ответе нужно не только обнаружить логическую ошибку, но предложить ситуации, в которых от неё нельзя уйти. То есть когда ответить без ошибки невозможно.
Читайте также:
- Реферат день петра и февронии
- Реферат потребность в образовании
- Реферат на тему познание обществознание
- Бюджет времени студентов реферат
- Семья и развитие личности реферат
3.15. Ошибки индукции
Говоря о дедуктивных умозаключениях, как можно было заметить, мы рассматривали ту или иную ошибку вместе с правилом, нарушение которого ее порождает. В данном случае сначала представлены правила неполной индукции, а потом, отдельно, – ее ошибки. Это объясняется тем, что каждая из них не связана непосредственно с каким-то из вышеприведенных правил. Любую индуктивную ошибку можно рассматривать как результат одновременного нарушения всех правил, и в то же время нарушение каждого правила возможно представить как причину, приводящую к любой из ошибок.
Первая ошибка, часто встречающаяся в неполной индукции, называется поспешным обобщением. Скорее всего, каждый из нас, хорошо с ней знаком. Кому не приходилось в жизни слышать такие высказывания как: Все мужчины черствые; Все женщины легкомысленные; Все евреи хитрые и т. д. и т. п.? Эти расхожие стереотипные фразы представляют собой не что иное, как поспешное обобщение в неполной индукции: если некоторые объекты из какой-либо группы обладают неким признаком, то это вовсе не означает, что данным признаком характеризуется вся группа без исключения. Из истинных посылок индуктивного умозаключения может вытекать ложный вывод, если допустить поспешное обобщение. Например:
К. учится плохо.
Н. учится плохо.
С. учится плохо.
К., Н., С. – это ученики 10 «А».
Все ученики 10 «А» учатся плохо.
Неудивительно, что поспешное обобщение лежит в основе многих голословных утверждений, слухов и сплетен.
Вторая ошибка носит длинное и, на первый взгляд, странное название: после этого, значит по причине этого (лат. post hoc, ergo propter hoc). В данном случае речь идет о том, что если одно событие происходит после другого, то это не означает с необходимостью их причинно-следственную связь. Два события могут быть связаны всего лишь временной последовательностью (одно – раньше, другое – позже). Когда мы говорим, что одно событие обязательно является причиной другого, потому что одно из них произошло раньше другого, то допускаем логическую ошибку. Например, в следующем индуктивном умозаключении обобщающий вывод является ложным, несмотря на истинность посылок:
Позавчера двоечнику Н. перебежала дорогу черная кошка, и он получил двойку.
Вчера двоечнику Н. перебежала дорогу черная кошка, и его
родителей вызвали в школу.
Сегодня двоечнику Н. перебежала дорогу черная кошка, и его
исключили из школы.
Во всех несчастьях двоечника Н. виновата черная кошка.
Неудивительно, что ошибка «после этого, значит по причине этого» лежит в основе многих небылиц, суеверий и мистификаций. Обратим внимание на то, что слова «мистика» (лат. mistikos – таинственный) и «мистификация» (лат. mistikos – таинственный + facere – делать) обозначают различные явления: мистика – это что-то действительно таинственное, непостижимое, сверхъестественное, а мистификация – это преднамеренное введение кого-то в заблуждение, путем искусственного создания чего-то таинственного и непостижимого там, где ничего подобного нет.
Третья ошибка, широко распространенная в неполной индукции, называется подмена условного безусловным. Рассмотрим индуктивное умозаключение, в котором из истинных посылок вытекает ложный вывод:
Дома вода кипит при температуре 100 °C.
На улице вода кипит при температуре 100 °C.
В лаборатории вода кипит при температуре 100 °C.
Вода везде кипит при температуре 100 °C.
Мы знаем, что высоко в горах вода кипит при более низкой температуре, что связано с изменением атмосферного давления. (Известный отечественный поруляризатор науки Я. И. Перельман в одной из своих книг отмечает, что если кто-нибудь стал бы кипятить воду на планете Марс, то вода там закипала бы при температуре в 45 градусов по Цельсию, так что кипяток, как то ни удивительно, не всегда и не везде является горячим.) То, что проявляется в одних условиях, может не проявляться в других. В посылках рассмотренного примера присутствует условное (т. е. происходящее в определенных условиях), которое подменяется безусловным (т. е. происходящим во всех условиях одинаково, не зависящим от них) в выводе. Хороший пример подмены условного безусловным содержится в известной нам с детства сказке про вершки и корешки, в которой речь идет о том, как мужик и медведь посадили репу, договорившись поделить урожай следующим образом: мужику – корешки, медведю – вершки. Получив ботву от репы, медведь понял, что мужик его обманул и совершил логическую ошибку подмены условного безусловным: надо всегда брать только корешки, – решил он. На следующий год, когда мужик и медведь делили урожай пшеницы, медведь сам предложил, что он возьмет корешки, а мужик – вершки, и опять остался ни с чем.
Данный текст является ознакомительным фрагментом.
Читайте также
§ 1. Виды индукции
§ 1. Виды индукции
В зависимости от характера исследования различают полную и неполную индукцию.Полная индукция — это умозаключение, в котором общее заключение делается на основе изучения всех предметов или явлений данного класса. В этом случае рассуждение имеет
V. Логика индукции
V. Логика индукции
Создание новой науки, открывшее эпоху в истории философии вообще, было и в логике началом второй эпохи – эпохи индуктивной логики. Не Бэкон, человек дилетантского склада ума и любитель разных планов, а сам творец новой науки создал и «Новый органон».
3.14. Правила индукции
3.14. Правила индукции
Чтобы повысить степень вероятности выводов неполной индукции, следует соблюдать следующие важные правила.1. Необходимо подбирать как можно больше исходных посылок. Для примера рассмотрим следующую ситуацию. Требуется проверить уровень
Проблема индукции
Проблема индукции
С каждым новым философским открытием и с каждым последующим философским обсуждением, кажется, всё более подтверждается утверждение философа С.Д.Брода: индукция есть триумф естествознания и позор философии.(Stegmuller, 1971, 13)В статье, которая открывается
§ 4. МЕТОДЫ НАУЧНОЙ ИНДУКЦИИ
§ 4. МЕТОДЫ НАУЧНОЙ ИНДУКЦИИ
Существует пять методов установления причинных связей: (1) метод сходства, (2) метод различия, (3) соединенный метод сходства и различия, (4) метод сопутствующих изменений, (5) метод остатков.Рассмотрим логическую структуру этих методов.1. Метод
2. Виды индукции
2. Виды индукции
1. О каких видах индукции идет речь в следующих примерах, приведенных слушателями:
«Допустим, что необходимо проверить рабочую дисциплину в отделах правоохранительного органа. Известно, что в его состав входят 10 отделов. Способ проверки — анализ
2. Две юмовские проблемы индукции
2. Две юмовские проблемы индукции
Юма интересовал статус человеческого знания или, как он мог бы сказать, вопрос о том, можно ли наши верования (beliefs) — и какие именно —оправдать достаточными основаниями (reasons)[6]Он поставил две проблемы: логическую (HL) и психологическую (HPs).
4. Мой подход к проблеме индукции
4. Мой подход к проблеме индукции
(1) Я придаю первостепенное значение неявно содержащемуся в трактовке Юма различию между логической и психологической проблемами индукции. Вместе с тем я считаю взгляды Юма на то, что сам я склонен называть «логикой», не вполне
12. Традиционная проблема индукции и несостоятельность всех принципов или правил индукции
12. Традиционная проблема индукции и несостоятельность всех принципов или правил индукции
Теперь я вернусь к тому, что я называю традиционной философской проблемой индукции.Под этим названием я подразумеваю точку зрения человека, который видит вызов, брошенный Юмом
42. Понятие индукции
42. Понятие индукции
Такие понятия, как общее и частное, могут рассматриваться только во взаимосвязи. Ни одно из них не имеет самостоятельности, так как при рассмотрении процессов, явлений и предметов окружающего мира только через призму, скажем, частного картина
43. Правила индукции
43. Правила индукции
Чтобы избегать ошибок, неточностей и неправильностей в своем мышлении, не допускать курьезов, нужно соблюдать требования, которые определяют правильность и объективную обоснованность индуктивного вывода. Ниже подробнее рассмотрены эти
1. Понятие индукции
1. Понятие индукции
Такие понятия, как общее и частное, могут рассматриваться только во взаимосвязи. Ни одно из них не имеет самостоятельности, так как при рассмотрении процессов, явлений и предметов окружающего мира только через призму, скажем, частного картина
2. Правила индукции
2. Правила индукции
Чтобы избегать ошибок, неточностей и неправильностей в своем мышлении, не допускать курьезов, нужно соблюдать требования, которые определяют правильность и объективную обоснованность индуктивного вывода. Ниже подробнее рассмотрены эти
Глава 19. Об индукции
Глава 19. Об индукции
В предыдущей главе мы с Челпановым обсуждали дедукцию, или умозаключение от общего к частному. Например, от общего заключения «все негры белозубы» мы приходили к частному заключению «Пушкин белозуб». А от общего заключения «у всех пьяниц трясутся
Основание индукции
Основание индукции
На чём мы основываемся, когда делаем общие выводы из частных посылок? Например, исследовав несколько школьников, мы делаем вывод: «все школьники тоскуют и страдают на уроках». Правомерно ли наше заключение?Георгий Иванович придерживается на этот счёт
Обобщение и ограничение понятий ошибки
Обобщение и ограничение понятий
Обобщение – этологическая операция, состоящая в переходе от понятия с меньшим объёмом, но с большим содержанием, к понятию с большим объёмом, но меньшим содержанием
роза (А) — цветок (Б) — растение (В) — живой организм (Г) — организм (Д) — предмет (Е)

На схеме этот процесс обобщения выглядит следующим образом:
Ограничение – это логическая операция перехода от понятия с большим объёмом, но с меньшим содержанием, к понятию с меньшим объёмом, но большим содержанием
— произведение музыкального искусства (Е) — опера (Д)
— опера русского композитора (Г)
— опера русского композитора XIX века (В)
— опера Мусоргского Модеста Петровича (Б) — опера Мусоргского М. П. «Хованщина» (А)

Пределом ограничения является единичное понятие с одним элементом объёма: в нашем случае это понятие А — опера «Хованщина»
Можно обе рассматриваемые нами операции изобразить и такой схемой:
Назначение операций обобщения и ограничения заключается в том, что они придают определённость мышлению, подчиняя его элементарным правилам:
1) обобщение правильно, если мысль осуществляет переход от видового понятия к родовому;
2) ограничение правильно, если мысль осуществляет переход от родового понятия к видовому
ОПЕРАЦИИ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ОСУЩЕСТВЛЯЮТСЯ ТОЛЬКО МЕЖДУ ПОНЯТИЯМИ, КОТОРЫЕ НАХОДЯТСЯ В ОТНОШЕНИЯХ ПОДЧИНЕНИЯ
1) Обобщение и ограничение часто смешивают с мысленным переходом от части к целому и выделением части из целого
2) Ограничение понятий часто происходит с помощью добавления признака: «студент» — «добросовестный студент».
Но имейте в виду, что нередко добавление эпитета не ведёт к ограничению понятия и является излишним:
«девушка» — «молодая девушка» (а кто видел старых девушек?),
«шар» — «круглый шар» (а какие ещё шары бывают?)
Данная ошибка называется плеоназмом (излишеством)
Деление понятий
Для упорядочения знания,поиска закономерных связей и уточнения смысла многих слов человеческим мышлением используется такая интеллектуальная процедура как классификация
Классификация – это распределение предметов какого-либо рода на взаимосвязанные группы (классы) согласно наиболее существенным признакам, присущим предметам данного рода и отличающим их от предметов других родов; при этом каждый класс занимает в получившейся системе своё постоянное, определённое место
В основе любой классификации лежит такая логическая процедура как деление понятий – это логическая операция, раскрывающая объём понятия
1) Делимым называется родовое понятие, в объёме которого выделяются возможные виды
2) Основание деления – признак, в соответствии с которым выделяются члены деления
3) Члены деления – полученные в результате самой операции соподчинённые виды
1) Деление по наличию или отсутствию признака, служащего основанием деления (его называют часто дихотомическим делением)
2) Деление по видоизменению признака, положенного в основание этой операции
3) Смешанное деление, когда используются оба вида деления одновременно
Примеры дихотомического деления:
· государства можно разделить на демократические и недемократические,
· людей – на счастливых и несчастливых,
· школьников – на добросовестных и недобросовестных,
· предпринимателей – на удачливых и неудачливых,
· граждан – на дееспособных и недееспособных
Право может быть оформлено (признак – форма выражения) в виде:
Людей по социально-классовому признаку можно разделить на:
· лиц свободных профессий
Смешанное деление, когда используются оба вида деления одновременно
Пример:
1) политические институты делятся на государственные и негосударственные;
2) среди негосударственных различаются партийные и непартийные;
3) непартийные же включают в себя профессиональные, женские, молодёжные, спортивные, художественные и так далее
Основные правила и ошибки деления:
1) Правило соразмерности
2) Правило исключения
3) Правило одного основания:
4) Правило непрерывности
1)Правило соразмерности – объединение объёмов членов деления должно совпадать с объёмом делимого понятия или объём делимого должен полностью исчерпываться членами деления. (А = В1 + В2 + В3 + . + Вn)
Это означает, что при делении:
a) не должно быть пропущено ни одного предмета из объёма делимого понятия;
b) не должно появиться ни одного лишнего члена деления
Если данное правило не соблюдается, то возможны две основные ошибки:
17. Обобщение и ограничение понятий
17. Обобщение и ограничение понятий
Обобщение понятия – это совершение перехода от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом и меньшим содержанием. При обобщении осуществляется переход от видового понятия к родовому.
Например, обобщая понятие «хвойный лес», мы переходим к понятию «лес». Содержание этого нового понятия уже, зато объем значительно шире. Содержание уменьшилось, потому что мы изъяли (убрав слово «хвойный») ряд характерных видовых признаков, отражающих особенности хвойного леса. Лес – это род по отношению к понятию «хвойный лес», являющемуся видом. Исходное понятие может быть как общим, так и единичным. Например, можно осуществить обобщение понятия «Париж» (единичное понятие) путем перехода к понятию «европейская столица», следующим шагом будет переход к понятию «столица», потом «город», «селение». Таким образом, постепенно исключая характерные признаки, присущие предмету, мы движемся в сторону наибольшего расширения объема понятия, жертвуя содержанием в пользу абстракции.
Цель обобщения – максимальное отстранение от характерных признаков. При этом желательно, чтобы такое отстранение происходило как можно более постепенно, т. е. переход от рода должен происходить к самому близкому виду (с наиболее широким содержанием).
Обобщение понятий не безгранично, и пределом обобщения являются философские категории, например «бытие» и «сознание», «материя» и «идея». Поскольку категории лишены родового понятия, обобщение их невозможно.
Ограничение понятия – это логическая операция, противоположная обобщению. Если обобщение идет по пути постепенного отстранения от признаков предмета, ограничение, напротив, обогащает совокупность признаков понятия. Таким образом, осуществляется переход от общего к частному, от вида к роду, от единичных понятий к общим.
Эта логическая операция характеризуется уменьшением объема за счет расширения содержания.
Операция ограничения не может продолжаться дальше, когда в его процессе достигается единичное понятие. Оно характеризуется максимально полным содержанием и объемом, в котором мыслится лишь один объект.
Таким образом, операции ограничения и обобщения – это процесс конкретизации и абстракции в рамках от единичного понятия до философских категорий. Эти операции учат человека мыслить более правильно, способствуют познанию предметов, явлений, процессов окружающего мира, их взаимосвязей. Благодаря обобщению и ограничению мышление становится более ясным, четким и последовательным. Однако не следует путать обобщение и ограничение с выделением из целого части и рассмотрением этой части отдельно. Например, двигатель автомобиля состоит из деталей (карбюратор, воздушный фильтр, стартер), детали состоят из более мелких, а те в свою очередь из еще более мелких. В этом примере понятие, следующее за предыдущим, не является его видом, а есть лишь его составной частью.
ОБОБЩЕНИЕ И ОГРАНИЧЕНИЕ ПОНЯТИЙ;
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
К логическим операциям над понятиями относятся обобщение, ограничение, определение и деление.
Обобщить понятие– значит, перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием, т.е. от видового понятия к родовому понятию.
Пример:Результатом обобщения понятия «Московский государственный университет» (А) является понятие «государственный университет» (В), а результатом обобщения последнего – понятие «университет» (С).
Обобщение понятий не может быть беспредельным и проводится в рамках той или иной науки. Пределом обобщения являются понятия с наиболее широким объемом – категории, например, «материя», «сознание» и т. п. Категории не имеют рода, поэтому обобщить их нельзя. Ограничить понятие – значит, перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с большим содержанием, т.е. от вида к роду. Например, ограничивая понятие «министерство», можно перейти к понятию «министерство иностранных дел». Пределом ограничения служит единичное понятие, в данном случае понятие «Министерство иностранных дел России».
Логические операции обобщения и ограничения часто применяются в практике мышления: переходя от понятия одного объема к понятию другого объема, мы уточняем предмет нашей мысли, процесс мышления становится определеннее и последовательнее.
Возможные ошибки при осуществлении логических операций – обобщения и ограничения понятий:
1. «Переход от части к целому». Например, параграф – глава учебника.
2. «Переход в другой род». Например, сотовый телефон – телефонный аппарат.
3. «Переход от целого к части». Например, дом – этаж – квартира.
4. «Мнимое ограничение» (плеоназм). Например, шар – круглый шар – самый круглый шар.
Упражнение 16
Проверьте, правильно ли обобщены понятия в следующих примерах:
1. Радость – чувство. 2. Живопись – искусство. 3. Брянск – город в России. 4. Планета – Юпитер. 5. Черта характера – гордость. 6. Большой театр России – Малый театр России. 7. К. Брюллов – выдающийся художник ХIХ века. 8. Спорт – гребля. 9. Юрист – человек. 10. Логика – наука. 11. Староста группы – староста курса. 12. Торговый зал супермаркета – супермаркет. 13. Опубликованная книга – написанная книга. 14. Еженедельная газета – газета выходящая регулярно. 15. Невиновность – непричастность.
Пример:Кинотеатр «Ударник» — кинотеатр. Правильно.
Упражнение 17
Проверьте, правильно ли ограничены понятия в следующих примерах:
1. Степень – кубическая степень. 2. Университет – московский университет. 3. Республика – государство. 4. Генерал российской армии – офицер. 5. Москва – столица России. 6. Староста группы – студент. 7. Организм – живая клетка. 8. Офицер – полковник. 9. Государство – республика. 10. Стихотворение – элегия. 11. Среда – природная среда. 12. Политика – политический режим. 13. Организация – партия. 14. Профсоюз – член профсоюза. 15. Русские – «новые русские».
Пример:Учебник – учебник по политологии. Правильно.
Упражнение 18
1. Море. 2. Книга. 3. Выдающаяся личность. 4. Растение. 5. Смоленский кремль. 6. Элемент. 7. Словарь. 8. Город. 9. Вторая мировая война. 10. Клевета. 11. Государство. 12. Монархия. 13. Съезд. 14. Депутат. 15. Закон.
Пример:Политическое движение – движение за мир.
Упражнение 19
1. Проректор по науке. 2. Журнал «Политические исследования». 3. Сооружение. 4. Газета «Российские ведомости». 5. Спикер Парламента. 6. Высшее учебное заведение. 7. Опера. 8. Редактор. 9. Художественное произведение. 10. Доктор наук. 11. Республика. 12. Римское право. 13. Правовое государство. 14. Справедливость. 15. Специалист в области социальной работы.
Пример:Лето– время года.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
В результате освоения данной темы студент должен:
знать
- – логические операции с понятиями: обобщение, ограничение, определение, деление,
- – способы обобщения и ограничения понятий,
- – виды определения и деления понятий,
- – виды классификаций понятий;
уметь
- – производить логические операции ограничения и обобщения понятий,
- – применять в практической деятельности логические правила определения и деления понятий;
владеть
– навыками практического обобщения и ограничения понятий и логическими операциями – определением и делением понятий.
Обобщение и ограничение понятий
Обобщить понятие – значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но меньшим содержанием, т.е. перейти от видового понятия к родовому понятию за счет уменьшения информативности содержания, т.е. от вида к роду.
К логическим операциям с понятиями относятся обобщение и ограничение, определение и деление.
Поскольку различают логический и фактический объемы, то можно говорить о фактическом и логическом обобщении.
Например, результатом обобщения понятия «Московский государственный университет» (А) является понятие «государственный университет» (В), а результатом обобщения последнего – понятие «университет» (С). Схематически это можно представить следующим образом (рис. 4.1).
Производя обобщение, необходимо следить, чтобы не совершить ошибку «переход в другой род», например, эта ошибка
Рис. 4.1
будет иметь место, если в процессе обобщения будет совершен переход от понятия «студент» к понятию «студенчество» или от понятия «раздел учебника» к понятию «учебник». Во втором случае мы имеем дело с ошибкой «переход от части к целому«.
Что касается предела обобщения, то здесь следует различать вопрос о пределах обобщения отдельно взятого понятия в составе некоторой системы знаний.
Если обобщение производится в рамках той или иной науки, то пределом обобщения являются понятия с наиболее широким объемом – категории, например, «материя», «сознание», «форма общественного сознания». Категории не имеют рода, поэтому обобщить их нельзя.
Если речь идет об обобщении понятия в рамках обыденного сознания, то пределом обобщения любого отдельно взятого понятия может быть понятие «нечто».
Противоположная обобщению операция – ограничение
Ограничить понятие – значит перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с большим содержанием, т.е. от рода к виду.
Например, ограничивая понятие «министерство» (А), можно перейти к понятию «министерство иностранных дел» (В). Пределом ограничения служит единичное понятие, в данном случае понятие «Министерство иностранных дел России» (С).
Это можно представить, как показано на рис. 4.2.
То есть, как это следует из определения операции ограничения и приведенного примера, ограничение происходит за счет увеличения информативности содержания исходного понятия.
Применяя в практике познания операции обобщения и ограничения мы осуществляем последовательность мыслительных действий: в случае обобщения совершаем процесс восхождения от отдельного или особенного к общему; в случае ограничения понятий совершаем обратный процесс – движение от общего к конкретному, к особенному или отдельному.
Используя эти операции в процессе мыслительной и практической деятельности, необходимо учитывать:
- 1) при осуществлении данных операций нужно избегать скачков в обобщениях и ограничениях, т.е. в случае обобщения понятий каждый шаг должен быть переходом от вида к ближайшему роду; в случае ограничения – наоборот: переход от рода к ближайшему виду;
- 2) при осуществлении данных операций нужно учитывать также и тот факт, что обобщение и ограничение одного и того же понятия может идти по разным направлениям;
- 3) обобщение и ограничение базируются на родовидовых отношениях, которые не требуется подменять отношениями «часть – целое»;
- 4) в качестве критерия правильности осуществления операций обобщения и ограничения выступает отношение логического следования, которое можно определить следующим образом: «Если из высказывания или высказывательной формы А логически следует В, то есть А|=В, по обратное неверно, тогда А более информативно, чем В», где |= – отношение логического следования.
Возможны следующие конкретные случаи следования между содержаниями понятий.
1. Из всякой совокупности признаков содержания понятий, соединенных конъюнктивно, следует любой из этих признаков или меньшая их совокупность. Например, из содержания «Московский гуманитарный университет» следует содержание «московский университет» и «гуманитарный университет».
Таким образом, увеличить содержание понятия можно путем добавления новых информационно непустых признаков с помощью конъюнкции.
- 2. Из всякого признака следует сложный признак, образованный с помощью добавления некоторого нового признака с помощью дизъюнкции. Например, из признака «быть веселым» следует признак «быть веселым или находчивым». Следовательно, можно увеличить содержание понятия путем уменьшения членов дизъюнкции, если они есть в содержании понятия.
- 3. В том случае, когда признак содержит квантор общности, то из него следует признак, который получается подстановкой имени любого предмета, находящегося в области действия квантора общности или путем подстановки имен нескольких предметов из этой области. Так, из признака «знающий всех своих преподавателей» логически следует признак «знающий преподавателей логики и психологии».
- 4. Если признак содержит предметную константу, то из него может следовать признак с квантором существования (выражается с помощью слов «некоторые», «часть», «большинство» и т.п.) по предметам этой области. В данном случае увеличение содержания понятия может идти следующими способами:
- а) заменой признака, содержащего общее имя с квантором существования на единичные имена. Например, увеличится содержание понятия (и уменьшится его объем), если мы перейдем от признака «посетивший некоторые европейские столицы» к признаку «посетивший Москву и Париж»;
- б) заменой признака с квантором существования на признак с квантором общности.
Например, увеличится содержание понятия (и уменьшится его объем), если мы перейдем от признака «посетивший некоторые европейские столицы» к признаку «посетивший все европейские столицы»;
в) заменой признака с единичными именами на признак с общим именем и с квантором общности (слова «все», «всякий», «каждый» и т.п.) по предметам соответствующей области. Например, можно увеличить содержание понятия (уменьшив его объем), заменив признак «посетивший европейские столицы Москву и Париж» признаком «посетивший все европейские столицы».
Известный отечественный логик Е. Б. Кузина выделяет следующие способы обобщения и ограничения понятий.
Способы обобщения понятий:
«(1) Отбрасыванием признака, включенного в содержание посредством конъюнкции.
- (2) Добавлением в содержание понятия признака с помощью дизъюнкции.
- (3) Заменой в признаке единичного имени на общее имя с квантором существования.
- (4) Заменой квантора общности в признаке на квантор существования.
- (5) Заменой признака с квантором общности на признак с единичными именами» [1] .
Способы ограничения понятий:
«(1) Прибавление информативно непустого признака конъюнктивно.
- (2) Отбрасывание информативно непустого признака, если он включен в содержание понятия через дизъюнкцию.
- (3) Уточнение признака путем замены в нем общего имени с квантором существования на единичные имена.
- (4) Замена квантора существования в признаке квантором общности.
- (5) Замена признака с единичными именами на признаках с общим именем и квантором общности» [2] .
Возможные ошибки при осуществлении логических операций обобщения и ограничения понятий.
«Переход от части к целому» – заключается в том, что часть не обладает всеми признаками целого. Например, «параграф – глава учебника».
«Переход в другой род». Например, «сотовый телефон – телеграф».
«Переход от целого к части». Например, «дом – этаж квартира».
«Мнимое ограничение» (плеоназм). Например, «шар – круглый шар – самый крупный шар».
Логические операции обобщения и ограничения часто применяются η практике мышления, переходя от понятия одного объема, мы уточняем предмет нашей мысли, процесс мышления становится определеннее и последовательнее.
- [1]Кузина Е. Б. Логика в кратком изложении и упражнениях: учеб. пособие / Е. Б. Кузина. М.: Издательство МГУ, 2000. С. 61.
- [2] Там же. 60.
Обобщение и ограничение понятий
Обобщение – логическая операция, при которой уменьшается количество признаков в содержании понятия.
Ограничение – логическая операция, при которой увеличивается число признаков.
Определение понятий – логическая операция, которая раскрывает содержание понятия.


Правила и ошибки определений:
1. Определение не должно быть слишком широким
2. определение не должно быть узким
3. определение не должно содержать круга
4. определение не должно быть двусмысленным
5. определение не должно быть сложным
6. определение не должно быть непонятным
7. определение не должно быть отрицательным.
Деление понятий – логическая операция, которая раскрывает объем понятия.
Деление может происходить по любому признаку.
1. должно быть по одному основанию
2. должно быть полным
3. должно быть последовательным.
Суждение
— это логическая форма, в которой что-либо утверждается или отрицается.
Выражается в форме предложения, как правило, повествовательного (+ риторические вопросы и восклицания).
В любом суждении есть понятие, о котором идет речь – субъект S. Кроме того, существует предикат P – то, что отличает субъект от других, характеризует его.
Суждения могут быть оценены как истинные или ложные. Нельзя оценить истинность того, что будет в будущем.


1. атрибутивные (признаки некоторого объекта)
2. релятивные (отношения между субъектами)
3. экзистенциональные (существования).
Отношения между субъектом и предикатом в одном суждении:

Основные типы сложных суждений
Умозаключение
— это логическая форма, в которой из нескольких (от одного до N) связанных между собой суждений делается вывод (качественно новое суждение).
1. дедуктивные. Вывод истинный при истинности посылок.
2. индукция. Вывод вероятностный. Важна репрезентативность выборки.
3. традукция – аналогия. Вывод вероятностный. Ход мысли: частн. – частн.; общ. – общ.
Индуктивное умозаключение – при котором из частных случаев делается общий вывод, как правило, вероятностный.
Для того чтобы индуктивное умозаключение было близко к истинному, важно выполнение следующих правил:
1. Рассмотрение как можно больших элементов множества.
2. Рассмотрение только существенных признаков
3. Рассмотрение разнообразных признаков
Ошибки, допускаемые при неполной индукции:
1. подмена условного безусловным
2. «После того» = «В следствии этого»
3. поспешное обощение.
Причинная связь – связь между двумя явлениями, когда одно из них – причина – предшествует и вызывает другое – действие.
Свойства (1 множество) Отношений
Дедукция
Все дедуктивные умозаключения называются силлогизмами. Виды:
1) Простой категорический силлогизм – из двух связанных между собой простых суждений делается вывод – новое суждение.
Взаимное расположение терминов в умозаключении определяет одну из четырех фигур силлогизма. Комбинации суждений в фигурах силлогизма называются Модус.
Дающих истинный ответ – 19.
1. Энтимема – сокращенный силлогизм, в котором пропущена одна из посылок или вывод.
2. Эпихейрема – простой силлогизм, в котором обе посылки энтимемы.
3. Полисиллогизм (прогрессивный и регрессивный)
4. Сорит – полисиллогизм, в котором пропущена посылка следующего силлогизма, являющаяся выводом предыдущего.
2) Условный силлогизм – содержит в одной или двух посылка условие
А) чисто условный
Б) условно-категорический (утверждение или отрицание)
3) Разделительный силлогизм – включает в себя дизъюнкцию (выбор)
А) чисто разделительный
4) Условно-разделительный силлогизм – умозаключение, в котором в первой посылке должно быть условие, во второй — выбор. Лемма.
5. Законы логики
1. ЗАКОНЫ ТОЖДЕСТВА: любая мысль должна быть тождественной самой себе.
Нарушение может привести к:
2. ЗАКОНЫ ПРОТИВОРЕЧИЯ: если одно суждение утверждает, а другое тоже самое отрицает, то эти два суждения не могут быть одновременно истинными.
Два противоречивых суждения одновременно могут быть ложными.
3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО: два суждения, противоречащих друг другу в одном месте, в одно время об одном предмете, не могут быть одновременно истинными или одновременно ложными.
4. ЗАКОН ДОСТАТОЧНОГО ОСНОВАНИЯ: любая мысль, для того, чтобы иметь силу, обязательно должна быть доказана достаточным аргументом.
— это логическое рассуждение, в процессе которого с помощью положений, проверенных практикой подтверждается или отрицается истинность какой-либо мысли.
Тезис – положение, истинность которого необходимо доказать.
Аргументы – положения, истинность которых уже доказана.
Демонстрация – процесс, связывающий между собой тезис и аргументы
Ошибки в доказательстве
1. ошибки тезиса: а) потеря тезиса
б) подмена тезиса
2. ошибки в аргументах: а) довод к человеку
б) ложность основания
в) предвосхищение основания
г) круг в доказательстве
д) аргумент к публике
3. ошибки в демонстрации: а) мнимое следование
б) нарушение правил силлогизма
Задачи на логику
Задача №1
Было взято 10 листов бумаги. Некоторые листы разрезали на 10 частей,
затем некоторые из получившихся кусков вновь разрезали на 10 частей и т.д.
На каком-то этапе подсчитали общее количество получившихся листов бумаги. Оказалось их всего 1386 листов бумаги. Правильно ли подсчитали количество листов?
Ответ: В результате разрезания одного листа общее количество листов увеличивается на 9. Поэтому конечное число листов, за вычетом 10-ти исходных, должно быть кратным 9; следовательно, подсчет выполнен неверно.
Задача №2
3 женщины решили купить чайник, который стоит 30 долларов, и скинулись по 10 долларов. Потом менеджер узнал, что чайник стоит 25 доларов, он получил из кассы 5 долларов и решил отдать их женщинам. Но как поделить 5 на 3. Поэтому он каждой женщине отдал по 1 доллару (всего получается 3), а себе взял 2. Итак, каждая женщина получила обратно по 1 доллару. То есть вместо 10 потратила 9 долларов. Во сколько обошелся чайник женщинам? Правильно, в 9х3 = 27 долларов. К
ним прибавляем 2 доллара, которые менеджер положил себе в карман. Получается 29. Вопрос: где тридцатый доллар?
Ответ: Просто от 27 надо отнять 2 , а не сложить
Задача №3
Было это в одной местности, где только скотоводы, наверное в Казахстане.
Решили как-то два батыра жениться. Да только проблема — хотят на одной и той же. Ну и решили им устроить состязание (было это в те времена когда про Fairy и мытье котлов ничего не знали) — скачки. Но и устроили им конкурс. Собрались — на лучших конях, при параде — Да только условие поставили хитрое — «получит невесту тот, чья лошадь приедет последней». Ну ребята погарцевали час, два — ни с места. Тут подошел к ним отец невесты чего-то сказал (не нарушающее условие конкурса) и ребята полетели к финишу как стрелы.
Ответ: Можно оперировать словом «чья» во фразе «выиграет тот, чья лошадь придет последним». Т.е. «чья» по принадлежности (праву собственности), а не по тому, кто на данную минуту в седле. В этом случае отец сказал всадникам нечто вроде того «Поменяйтесь лошадьми» или «Я поменял лошадей». В итоге каждый заинтересован, чтоб его лошадь (но под седлом соперника) пришла последней, и соответственно будет ехать как можно быстрей на чужой.