Метрики в задачах машинного обучения
Время на прочтение
9 мин
Количество просмотров 525K
Привет, Хабр!
В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть работы датасатаниста.
В этой статье мы рассмотрим некоторые критерии качества в задачах классификации, обсудим, что является важным при выборе метрики и что может пойти не так.
Метрики в задачах классификации
Для демонстрации полезных функций sklearn и наглядного представления метрик мы будем использовать датасет по оттоку клиентов телеком-оператора.
Загрузим необходимые библиотеки и посмотрим на данные
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rc, plot
import seaborn as sns
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
df.head(5)Предобработка данных
# Сделаем маппинг бинарных колонок
# и закодируем dummy-кодированием штат (для простоты, лучше не делать так для деревянных моделей)
d = {'Yes' : 1, 'No' : 0}
df['International plan'] = df['International plan'].map(d)
df['Voice mail plan'] = df['Voice mail plan'].map(d)
df['Churn'] = df['Churn'].astype('int64')
le = LabelEncoder()
df['State'] = le.fit_transform(df['State'])
ohe = OneHotEncoder(sparse=False)
encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1))
tmp = pd.DataFrame(encoded_state,
columns=['state ' + str(i) for i in range(encoded_state.shape[1])])
df = pd.concat([df, tmp], axis=1)Accuracy, precision и recall
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| True Positive (TP) | False Positive (FP) | |
| False Negative (FN) | True Negative (TN) |
Здесь — это ответ алгоритма на объекте, а
— истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
Обучение алгоритма и построение матрицы ошибок
X = df.drop('Churn', axis=1)
y = df['Churn']
# Делим выборку на train и test, все метрики будем оценивать на тестовом датасете
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42)
# Обучаем ставшую родной логистическую регрессию
lr = LogisticRegression(random_state=42)
lr.fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
Accuracy
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую accuracy:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Precision, recall и F-мера
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
Precision можно интерпретировать как долю объектов, названных классификатором положительными и при этом действительно являющимися положительными, а recall показывает, какую долю объектов положительного класса из всех объектов положительного класса нашел алгоритм.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Как мы отмечали ранее, ошибки классификации бывают двух видов: False Positive и False Negative. В статистике первый вид ошибок называют ошибкой I-го рода, а второй — ошибкой II-го рода. В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Классическим примером является задача определения оттока клиентов.
Очевидно, что мы не можем находить всех уходящих в отток клиентов и только их. Но, определив стратегию и ресурс для удержания клиентов, мы можем подобрать нужные пороги по precision и recall. Например, можно сосредоточиться на удержании только высокодоходных клиентов или тех, кто уйдет с большей вероятностью, так как мы ограничены в ресурсах колл-центра.
Обычно при оптимизации гиперпараметров алгоритма (например, в случае перебора по сетке GridSearchCV ) используется одна метрика, улучшение которой мы и ожидаем увидеть на тестовой выборке.
Существует несколько различных способов объединить precision и recall в агрегированный критерий качества. F-мера (в общем случае ) — среднее гармоническое precision и recall :
в данном случае определяет вес точности в метрике, и при
это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = 1 иметь
)
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
В sklearn есть удобная функция _metrics.classificationreport, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned'])
print(report)
| class | precision | recall | f1-score | support |
|---|---|---|---|---|
| Non-churned | 0.88 | 0.97 | 0.93 | 941 |
| Churned | 0.60 | 0.25 | 0.35 | 159 |
| avg / total | 0.84 | 0.87 | 0.84 | 1100 |
Здесь необходимо отметить, что в случае задач с несбалансированными классами, которые превалируют в реальной практике, часто приходится прибегать к техникам искусственной модификации датасета для выравнивания соотношения классов. Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
AUC-ROC и AUC-PR
При конвертации вещественного ответа алгоритма (как правило, вероятности принадлежности к классу, отдельно см. SVM) в бинарную метку, мы должны выбрать какой-либо порог, при котором 0 становится 1. Естественным и близким кажется порог, равный 0.5, но он не всегда оказывается оптимальным, например, при вышеупомянутом отсутствии баланса классов.
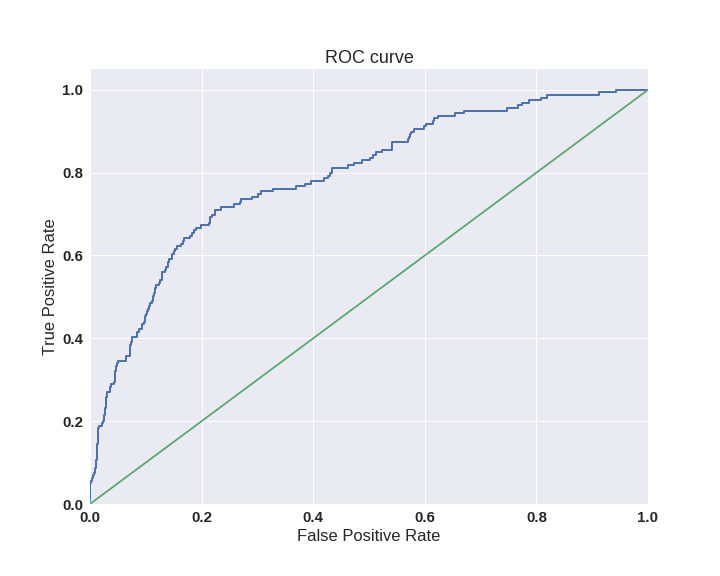
Одним из способов оценить модель в целом, не привязываясь к конкретному порогу, является AUC-ROC (или ROC AUC) — площадь (Area Under Curve) под кривой ошибок (Receiver Operating Characteristic curve ). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR нам уже известна, это полнота, а FPR показывает, какую долю из объектов negative класса алгоритм предсказал неверно. В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
Каждая точка на графике соответствует выбору некоторого порога. Площадь под кривой в данном случае показывает качество алгоритма (больше — лучше), кроме этого, важной является крутизна самой кривой — мы хотим максимизировать TPR, минимизируя FPR, а значит, наша кривая в идеале должна стремиться к точке (0,1).
Код отрисовки ROC-кривой
sns.set(font_scale=1.5)
sns.set_color_codes("muted")
plt.figure(figsize=(10, 8))
fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1)
lw = 2
plt.plot(fpr, tpr, lw=lw, label='ROC curve ')
plt.plot([0, 1], [0, 1])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
Критерий AUC-ROC устойчив к несбалансированным классам (спойлер: увы, не всё так однозначно) и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.
Рассмотрим следующую задачу: нам необходимо выбрать 100 релевантных документов из 1 миллиона документов. Мы намашинлернили два алгоритма:
- Алгоритм 1 возвращает 100 документов, 90 из которых релевантны. Таким образом,
- Алгоритм 2 возвращает 2000 документов, 90 из которых релевантны. Таким образом,
Скорее всего, мы бы выбрали первый алгоритм, который выдает очень мало False Positive на фоне своего конкурента. Но разница в False Positive Rate между этими двумя алгоритмами крайне мала — всего 0.0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
Для того чтобы поправить положение, вернемся к полноте и точности :
- Алгоритм 1
- Алгоритм 2
Здесь уже заметна существенная разница между двумя алгоритмами — 0.855 в точности!
Precision и recall также используют для построения кривой и, аналогично AUC-ROC, находят площадь под ней.
Здесь можно отметить, что на маленьких датасетах площадь под PR-кривой может быть чересчур оптимистична, потому как вычисляется по методу трапеций, но обычно в таких задачах данных достаточно. За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
Logistic Loss
Особняком стоит логистическая функция потерь, определяемая как:
здесь — это ответ алгоритма на
-ом объекте,
— истинная метка класса на
-ом объекте, а
размер выборки.
Подробно про математическую интерпретацию логистической функции потерь уже написано в рамках поста про линейные модели.
Данная метрика нечасто выступает в бизнес-требованиях, но часто — в задачах на kaggle.
Интуитивно можно представить минимизацию logloss как задачу максимизации accuracy путем штрафа за неверные предсказания. Однако необходимо отметить, что logloss крайне сильно штрафует за уверенность классификатора в неверном ответе.
Рассмотрим пример:
def logloss_crutch(y_true, y_pred, eps=1e-15):
return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print('Logloss при неуверенной классификации %f' % logloss_crutch(1, 0.5))
>> Logloss при неуверенной классификации 0.693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585Отметим, как драматически выросла logloss при неверном ответе и уверенной классификации!
Следовательно, ошибка на одном объекте может дать существенное ухудшение общей ошибки на выборке. Такие объекты часто бывают выбросами, которые нужно не забывать фильтровать или рассматривать отдельно.
Всё становится на свои места, если нарисовать график logloss:
Видно, что чем ближе к нулю ответ алгоритма при ground truth = 1, тем выше значение ошибки и круче растёт кривая.
Подытожим:
- В случае многоклассовой классификации нужно внимательно следить за метриками каждого из классов и следовать логике решения задачи, а не оптимизации метрики
- В случае неравных классов нужно подбирать баланс классов для обучения и метрику, которая будет корректно отражать качество классификации
- Выбор метрики нужно делать с фокусом на предметную область, предварительно обрабатывая данные и, возможно, сегментируя (как в случае с делением на богатых и бедных клиентов)
Полезные ссылки
- Курс Евгения Соколова: Семинар по выбору моделей (там есть информация по метрикам задач регрессии)
- Задачки на AUC-ROC от А.Г. Дьяконова
- Дополнительно о других метриках можно почитать на kaggle. К описанию каждой метрики добавлена ссылка на соревнования, где она использовалась
- Презентация Богдана Мельника aka ld86 про обучение на несбалансированных выборках
Благодарности
Спасибо mephistopheies и madrugado за помощь в подготовке статьи.
Kaggle – площадка, объединяющая соревновательную систему по исследованию данных, образовательный ресурс по искусственному интеллекту и машинному обучению, а также соцсеть специалистов в указанных областях.
Перед тем, как начать работать, необходимо зарегистрироваться на сайте. Заходим по ссылке, находим кнопку Register и заполняем поля. Уверен, что вы сами с этим отлично справитесь. После регистрации, подтверждения и логина попадаем на главную страницу ресурса.
Слева в столбце мы видим разделы:
- Home – новостная лента, в которую попадают публикации, которые могут вас заинтересовать. Чем выше активность пользователя на сайте, тем точнее рекомендации.
- Competitions – соревнования в области анализа данных. Здесь же находятся учебные соревнования, которые помечены словом Knowledge.
- Datasets – различные наборы данных, с которыми можно поиграться. Также можно выкладывать собственные датасеты.
- Code – раздел, в котором можно создать Jupyter Notebook или посмотреть чужой.
- Discussions – местный аналог форумов.
- Courses – учебные курсы. Довольно приличный объем и приемлемое качество. Раскрыты основные базовые разделы ML.
Отвлечемся пока от Kaggle и поговорим о машинном обучении, а также о решаемых с его помощью задачах.
Теоретический минимум о Machine Learning
Машинное обучение – набор математических, статистических и вычислительных методов, с помощью которых возможно решить задачу путем поиска закономерностей в представленных данных.
Существует огромное количество методов машинного обучения. Здесь я покажу всего несколько самых базовых, а остальные вы сможете найти самостоятельно, пройдя по рекомендованным ссылкам в конце.
Все методы ML можно разделить на несколько крупных групп:
- Обучение с учителем (от англ. Supervised learning) – алгоритмы из этой группы обучаются с помощью заранее подготовленных данных, которые содержат как наборы входных исследуемых признаков, так и “ответы” на эти наборы. “Ответом” является выходное значение, которое должен выдать алгоритм в результате своей работы, т.е. алгоритм “обучается”. К этой группе, например, можно отнести задачи классификации и регрессии.
- Обучение без учителя (от англ. Unsupervised learning) – группа алгоритмов, в которых система спонтанно обучается на входных данных без вмешательства извне. К этой группе можно отнести задачи кластеризации, понижения размерности.
- Обучение с подкреплением (от англ. Reinforcement learning) – группа алгоритмов, в которых система обучается с помощью взаимодействия со средой, в которой она находится. Подробнее можно ознакомиться хотя бы в вики. В моей статье алгоритмы этой группы не рассматриваются.
Задачи машинного обучения
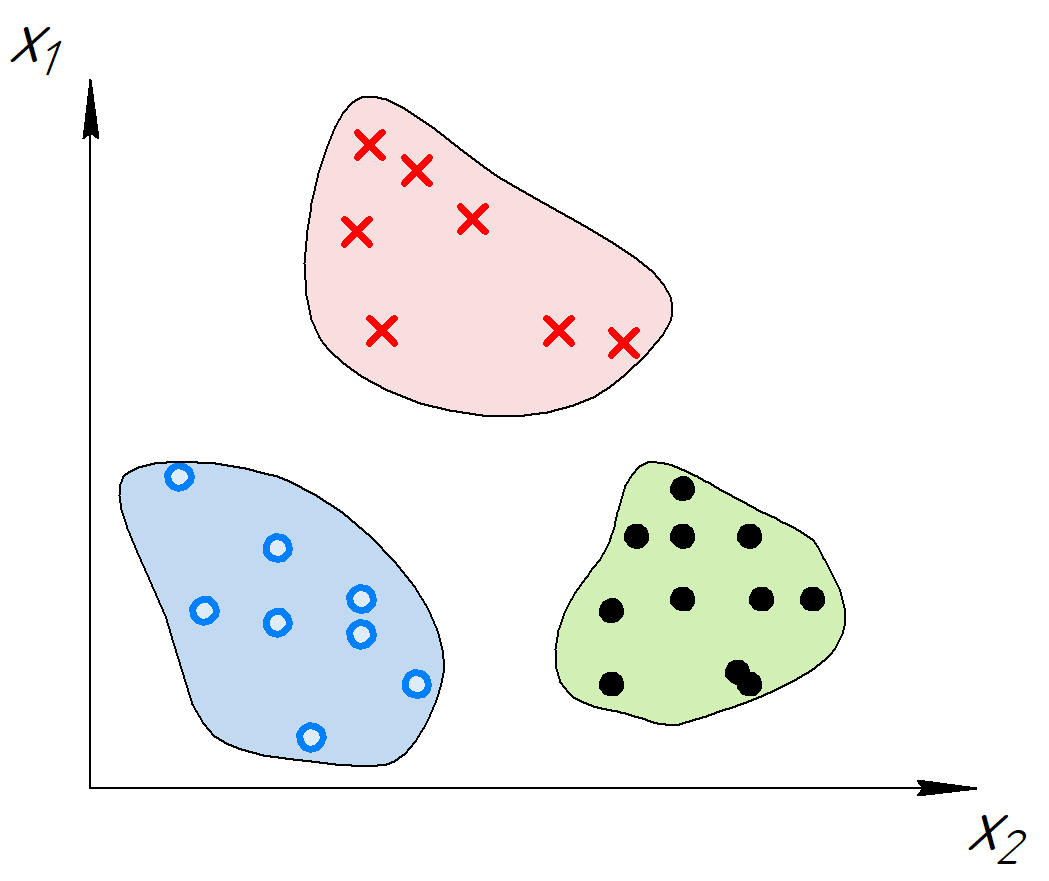
Классификация
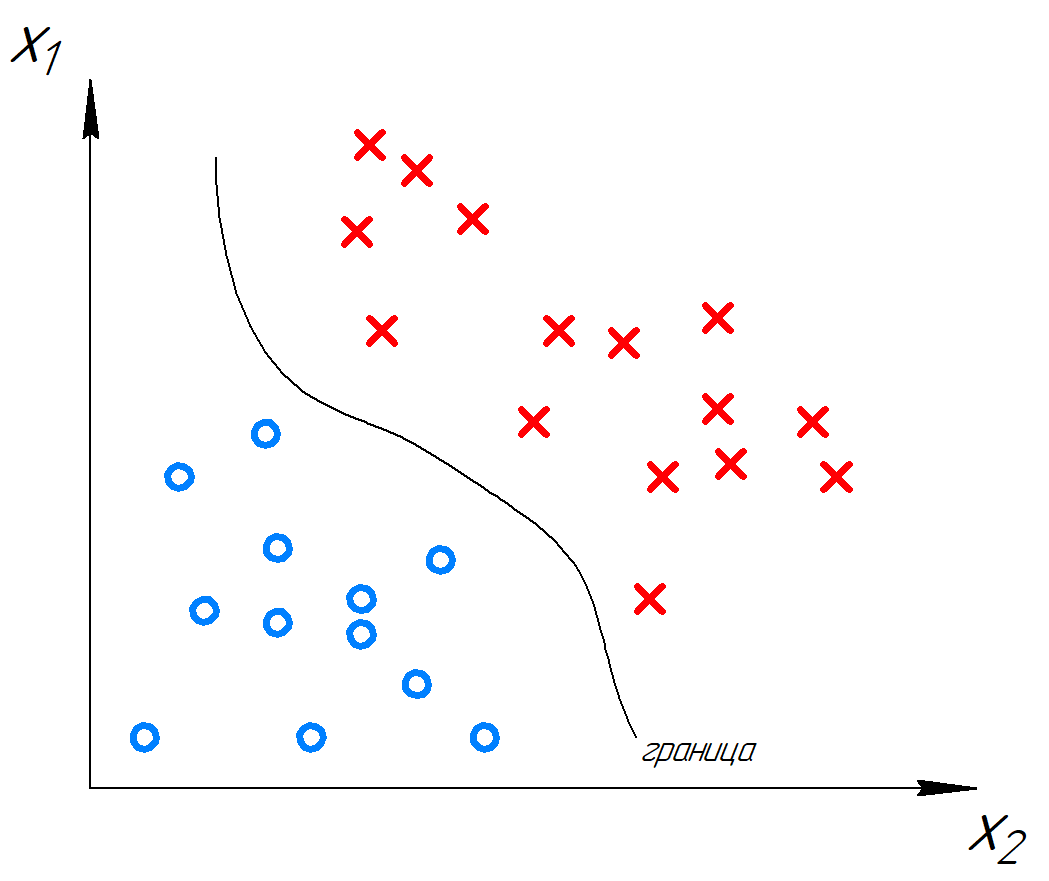
Вероятно, это самая популярная задача машинного обучения. Ее суть состоит в присвоении какому-то набору признаков (т.е. свойств объекта) какому-то классу. Например, стоит задача автоматической модерации токсичных комментариев на сайте. Алгоритм получает на вход текст комментария, а на выходе присваивает ему метку: токсичный или нетоксичный. Это пример бинарной классификации. К этому же типу классификации можно отнести задачу выявления сердечно-сосудистых проблем по анализам человека, определение спама в письмах и т.п. Второй тип классификации – множественная (многоклассовая). В ней классов больше двух. Примером может служить классификация жанра книги.
Для демонстрации посмотрим графической решение задачи бинарной классификации. Алгоритм разделяет пространство признаков на две группы.
Для решения задачи обычно используются следующие алгоритмы: логистическая регрессия, KNN, SVM, деревья решений.
Регрессия
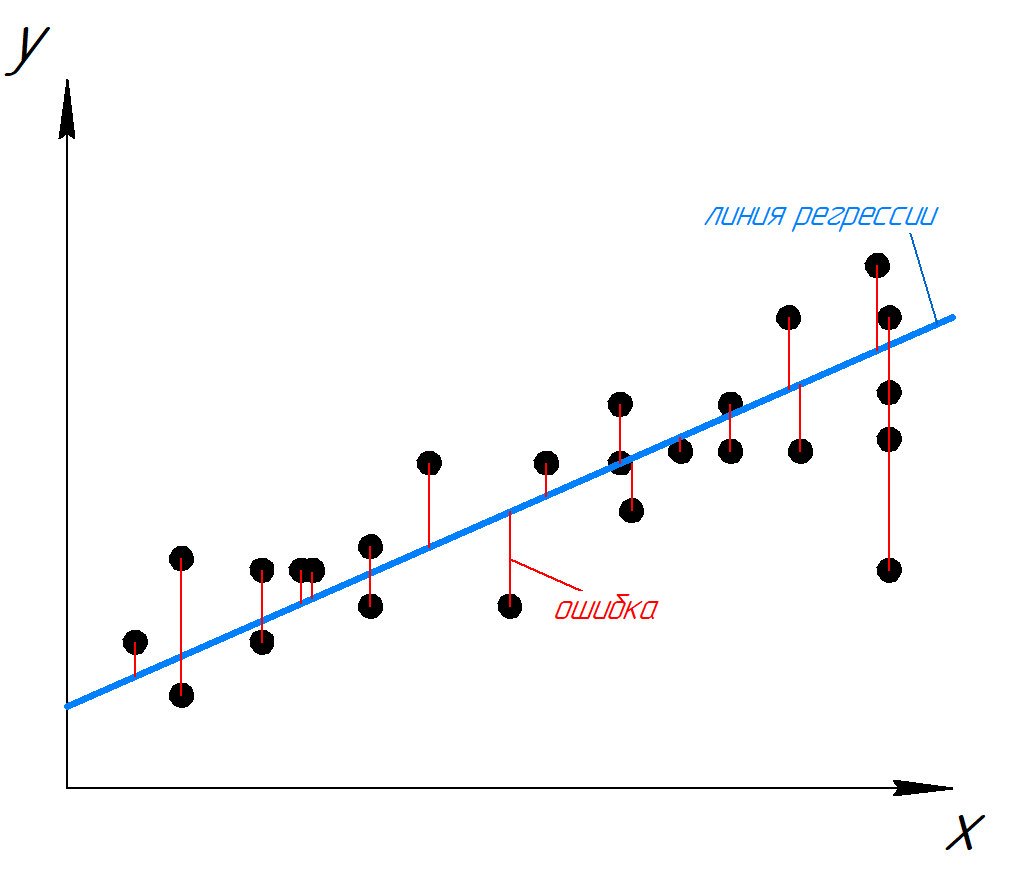
Задача регрессии – предсказание (прогнозирование) целевого признака по входным параметрам. Например, предсказание загруженности дороги в зависимости от времени суток, дня недели, погоды, предсказание цены квартиры от количества комнат, этажа, района. Предсказание времени на путь из пункта А в пункт Б в зависимости от пробок и т.п. Т.е. задача регрессии это задача получения неизвестного числа по известным параметрам.
Посмотрим на рисунок. По ряду известных значений y(x) была предсказана кривая – линия регрессии. Ее можно продлить, чтобы предсказывать значения y для неизвестных x.
Для решения задачи применяются следующие алгоритмы и методы: линейная и полиномиальная регрессии, KNN, деревья решений.
Кластеризация
Задача кластеризации состоит в разделении заданной выборки объектов таким образом, чтобы похожие объекты попали в один кластер, а кластеры сильно бы различались между собой. Кластеризацию применяют для анализа и поиска признаков по которым можно объединить объекты, сжатия данных и поиска новизны (что не входит ни в один кластер).
Возникает логичный вопрос: а чем различаются классификация и кластеризация, ведь они решают похожие задачи? При классификации есть набор предопределенных классов, которым обучается алгоритм на наборе примеров. Далее алгоритм предсказывает, к какому классу принадлежит новый объект. При кластеризации используется алгоритм, который пытается сгруппировать набор объектов и определить, существует ли какая-либо взаимосвязь между объектами, т.е. машина учится сама.
Графическим примером кластеризации может быть следующая иллюстрация.
Для решения задачи применяются следующие алгоритмы и методы: K-Means, DBSCAN.
Метрики качества регрессии
Начнем с регрессии. При оценке качества работают с таблицей, содержащей два столбца (помимо индекса): правильные значения и предсказанные. Для простоты рассмотрим четыре строки, и пусть объектами будет количество килограмм картошки для сети ресторанов. Для простоты расчетов возьмем кратные десяти значения.
| Номер | Значение из выборки (сколько в реальности потребовалось кг картошки) | Предсказанное значение (кг) |
| 1 | 200 | 180 |
| 2 | 150 | 190 |
| 3 | 140 | 120 |
| 4 | 160 | 220 |
При таком количестве данных даже визуально можно оценить качество предсказанных данных. Предсказания под номерами 1 и 3 были достаточно точны, номер 2 показал бОльшую ошибку, а в строке номер 4 ошибка оказалась очень большой.
Для тысяч таких строк визуально оценить качество невозможно, необходимы агрегированные показатели.
Mean Absolute Error (MAE) – средняя абсолютная ошибка
Довольно интуитивный способ – сложить ошибки каждого из предсказаний и разделить на количество предсказаний. Посчитаем для нашей таблицы:
В среднем наш алгоритм ошибается на 35 кг картошки. Где-то в плюс, где-то в минус. Такая метрика называется средней абсолютной ошибкой, mean absolute error или MAE.
где yi – предсказанные значения, а xi – реальные известные значения, ei — ошибка i-го предсказания.
Mean Square Error (MSE) – Средняя квадратичная ошибка
Достаточно часто используется похожая метрика, MSE. Она рассчитывается почти так же, только берется не модуль ошибки ei, а ее квадрат.
Для нашего примера:
Но мы получили не ошибку в килограммах, а “кг в квадрате”. Чтобы вернуться к исходной величине, необходимо извлечь из MSE квадратный корень:
По сравнению с RMSE, метрика MAE более интуитивна, т.к. усредняются сами отклонения, но RMSE удобнее использовать при обучении алгоритмов. Хотя для MAE обучение тоже успешно выполняется.
Еще одна особенность метрики MAE — она более устойчива к выбросам, чем RMSE. Это означает, что если для одного объекта ошибка очень большая (объект-выброс), а для остальных объектов – маленькая, то значение MAE подскочит от этого одного объекта меньше, чем RMSE, т.к. в RMSE ошибки возводятся в квадрат. В нашем примере объектом-выбросом является четвертое предсказание.
Quantile loss
Иногда ошибка в меньшую или большую сторону может иметь разное влияние на бизнес. Например, если мы предскажем на одну тысячу единиц товара меньше, чем реально потребуется, то потеряем прибыль: некоторым клиентам не достанется товара. А если мы предскажем на одну тысячу единиц больше товара, чем реально потребуется, то появятся дополнительные издержки на хранение товара.
Предположим, что товар занимает мало места (т.к. площади хранения в ресторанах велики) и расходы на хранение невелики, тогда лучше ошибиться в большую сторону, чем в меньшую. В этом случае отрицательную и положительную разницу домножают на разные коэффициенты, например, возьмем 0.5 и 1.5.
В нашем примере, коэффициент 1.5 будет применен к предсказаниям 1 и 3 (180 < 200 и 120 < 140), а коэффициент 0.5 к остальным. Тогда значение метрики будет равно:
Данная метрика называется квантильной ошибкой.
Само по себе значение метрик MSE или MAE можно сравнивать со средним значением целевой переменной: например, нам нужно предсказывать десятки, при этом допустимы ошибки порядка единиц. Если хочется получать значения ошибки в процентах («алгоритм в среднем ошибается на столько-то процентов»), можно использовать метрики с нормировками.
К примеру, метрика MAPE (mean average percentage error) усредняет значения ошибок, деленных на значение целевой переменной:
В нашем случае, алгоритм в среднем ошибается на 22.1%.
Важно понимать, что идеальных алгоритмов, как и нулевых значений метрик ошибок, в машинном обучении не бывает: такова суть этой области, что она помогает выполнять приблизительные предсказания. Величину метрик обычно определяет заказчик.
Метрики качества классификации
Accuracy – доля правильных ответов
В задаче классификации самой простой метрикой качества является доля правильных ответов (accuracy). Она показывает, в каком проценте случаев алгоритм правильно указал класс объекта.
Для примера будет рассматривать задачу предсказания токсичности комментариев. Т.е. имеем задачу бинарной классификации, где 0 – комментарий нетоксичен, 1 – комментарий токсичен. Возьмем для простоты пять комментариев и сведем все в таблицу.
| ID комментария | Значение в данных (токсичен ли комментарий в действительности) | Предсказанное значение |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 0 | 0 |
| 4 | 0 | 1 |
| 5 | 0 | 0 |
В нашем примере, алгоритм выдал правильные ответы для комментариев 1,2,3,5, т.е. в 80% случаев. Это и есть значение accuracy.
Accuracy – простая и интерпретируемая метрика, но она не отражает полную картину, в частности, в какую сторону алгоритм ошибается чаще. Кроме того, использовать эту метрику может быть неудобно в ситуации с несбалансированными классами, то есть, когда объектов одного класса много больше, чем объектов другого. К примеру, если в данных 95% объектов из класса 0 и 5% из класса 1, а алгоритм всегда предсказывает, что объект относится к классу 0, то его accuracy будет равно 95%, хотя алгоритм совершенно бесполезный! В таких случаях часто используют другие метрики.
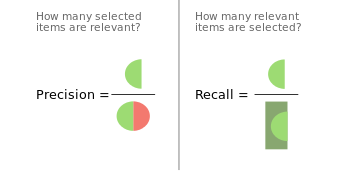
Precision and Recall – Точность и полнота
Чтобы понять, что такое точность и полнота, разберемся сначала с возможными типами ошибок. Для этого отлично подходит картинка из википедии.
В нашем примере, если алгоритм пометит нормальный комментарий как токсичный, то ничего особо страшного не произойдет. Этот коммент будет в дальнейшей проверен модератором. Такая ошибка называется ошибкой первого рода (false positive). Если же комментарий будет распознан как нормальный, но он токсичный, то такая ошибка называется ошибкой второго рода (false negative). На мой взгляд, в нашем примере ошибка второго рода страшнее, чем ошибка первого. Но бывает и наоборот.
Для отслеживания двух видов ошибок используют метрики точность (Precision) и полнота (Recall).
- Точность измеряет, какой процент объектов, для которых алгоритм предсказал класс 1, действительно относится к классу 1. В нашем примере, точность – это отношение количества реально токсичных комментариев к количеству помеченных как токсичные. И эта метрика составляет ⅔ = 66%.
- Полнота измеряет, для какого процента объектов класса 1 алгоритм предсказал класс 1. Для нашего примера полнота составляет 100%. Для простоты понимания, в вики формулы расчеты показаны визуально.
Отслеживать обе метрики сразу может быть неудобно, и может понадобиться скомбинировать их в одной. Для этого используют F-меру – среднее гармоническое точности P и полноты R:
Такой способ усреднения был выбран потому, что F-мера принимает высокие значения, только когда обе метрики принимают высокие значения. Иными словами, если хотя бы одна из двух метрик близка к 0, F-мера тоже будет близка к 0. Это свойство не выполняется, например, для среднего арифметического из точности и полноты.
Ансамблевые методы
В этом разделе поговорим про ансамбли – методы, наиболее часто используемые в машинном обучении при работе с табличными данными. Ансамбли обычно применяют в задачах классификации и регрессии, но они годятся и для других задач, которые сводятся к этим двум. Стоит сказать, что это только вершина айсберга и методов машинного обучения очень много. Их обзор можно найти в этой статье.
Вспомним постановку задач регрессии и классификации. В обеих требуется набор табличных данных: по строкам таблицы заданы объекты (например, клиенты), а по столбцам – признаки, то есть некоторые характеристики объектов (возраст, заработная плата, стаж работы клиента и т. д.). Кроме того, нужна разметка данных: для каждого объекта должно быть известно значение целевой переменной (класс в задаче классификации или число в задаче регрессии). Имея набор размеченных данных, мы обучаем алгоритм, который будет предсказывать значение целевой переменной для новых объектов на стадии внедрения.
Ансамблирование чаще всего используют применительно к решающим деревьям, поэтому начнем блок с разбора этого метода.
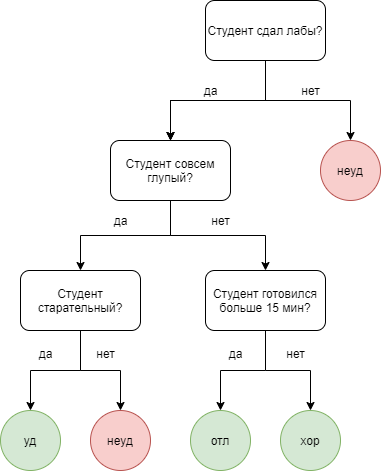
Решающее дерево – это алгоритм, который делает предсказания на основе серии вопросов об объекте.
Например, покажем решающее дерево, которое определяет возможность проставления оценки по какому-то предмету студенту.
Ансамблирование заключается в том, чтобы обучить несколько алгоритмов и усреднять их предсказания.
Например, строится несколько разных решающих деревьев, и берется среднее результатов их работы. Подробно про ансаблирование в машинном обучении можно почитать тут.
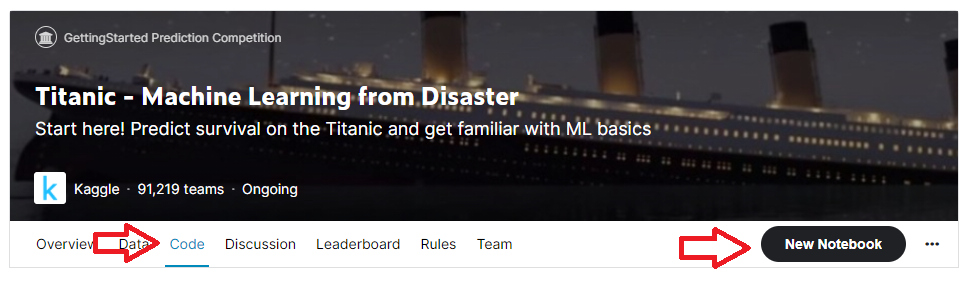
Решаем Titanic на Kaggle
Для начала неплохо было бы ознакомиться с задачей и данными, которые нам предоставляют. Идем на kaggle.com/c/titanic/overview. Изучив описание, узнаем, что нам предстоит решить задачу классификации: по заданным признакам необходимо определить, выживет ли пассажир при крушении Титаника или нет. Предлагаемые данные (раздел Data) состоят из трех файлов .csv: train.csv – обучающая выборка, в которой содержатся метки, выжил ли каждый конкретный пассажир или нет; test.csv – собственно данные для решения, именно в этом файле нам нужно определить выживаемость; gender_submission.csv – пример того, как должен выглядит файл-ответ.
Что нужно делать – понятно. Начинаем смотреть наши данные. Переходим на вкладку Code и нажимаем New notebook.
Таким образом, мы получаем продвинутый jupyter notebook. Чтобы активировать систему, нажмем на значок Play слева от верхней ячейки ноутбука. Система будет запущена и в результате, под ячейкой увидим пути до csv файлов.
Можно приступать. Если вы не знакомы с jupyter notebook и pandas, то рекомендую сначала прочитать данный материал.
Чтение и анализ датасета Titanic
Первым делом, загружаем в датафреймы файлы .csv.
train_data = pd.read_csv('/kaggle/input/titanic/train.csv')
test_data = pd.read_csv('/kaggle/input/titanic/test.csv')
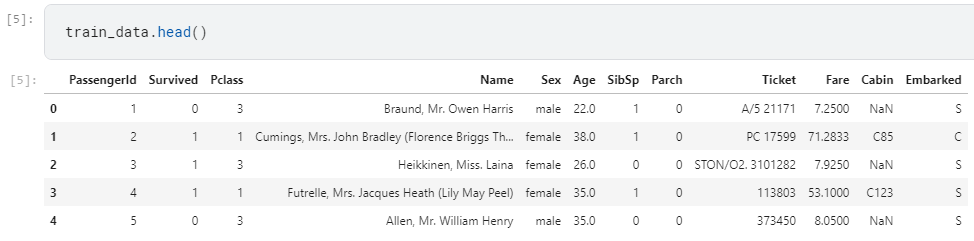
Проверим, что все у нас удачно и взглянем на эти датафреймы. Для примера приведу train_data.
train_data.head()
Первым делом оценим размеры датафрейма. Для этого используем свойство shape.
train_data.shape
В результате получаем (891, 12), т.е. 12 столбцов и 891 строку.
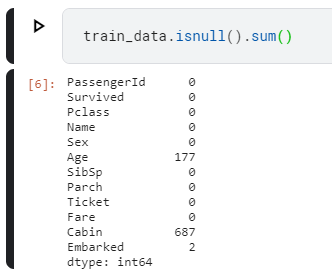
Следующим этапом неплохо было бы оценить количество пустых ячеек в столбцах обучающей выборки. Для этого вызовем:
train_data.isnull().sum()
Получаем, что в столбце Age у нас 177 пропусков, а в Cabin аж 687, что сильно больше половины.
Далее, оценим выживаемость. Для простоты визуализации будем использовать библиотеку seaborn. Для этого подключить ее и matplotlib.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
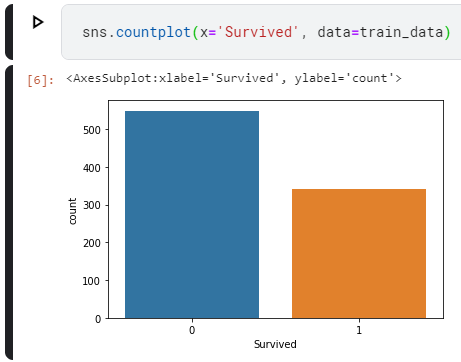
sns.countplot(x='Survived', data=train_data)
Как видим, выжило людей меньше, чем погибло.
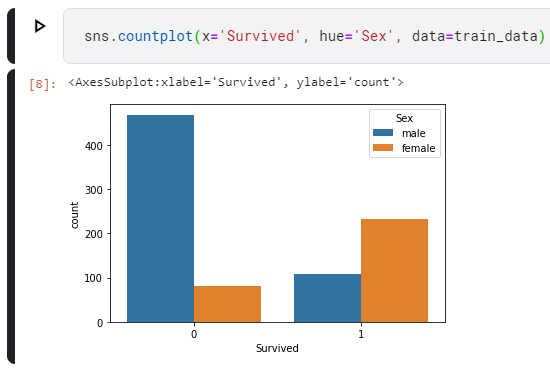
Теперь посмотрим, как с выживаемостью у мужчин и женщин отдельно.
sns.countplot(x='Survived', hue='Sex', data=train_data)
Видим, что мужчин погибло гораздо больше, чем выжило. И большая часть женщин выжила.
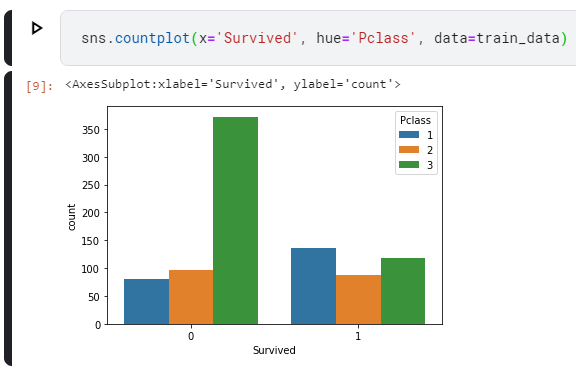
Далее взглянем, как зависела выживаемость от класса каюты.
sns.countplot(x='Survived', hue='Pclass', data=train_data)
Видим всплеск среди погибших пассажиров 3 класса.
Не закапываясь глубоко в датасет, видим явную зависимость выживаемости от пола и класса каюты.
В качестве признаков кроме выбранных пола и класса каюты, возьмем количество родителейдетей и количество братьевсестер на борту. Итоговый список признаков будет выглядеть следующим образом:
features = ['Sex', 'Pclass', 'SibSp', 'Parch']
Информацию о выживших и погибших пассажирах поместим в переменную y:
y = train_data['Survived']
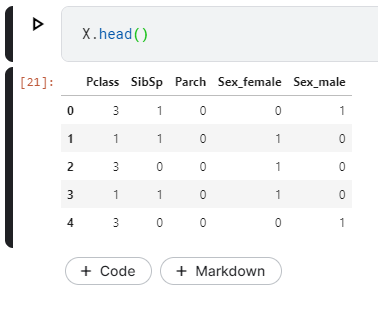
Если вы немного отмотаете назад, то увидите, что в столбце Sex находятся не числа, а строки, когда остальные отобранные нами признаки являются числами. Давайте превратим этот столбец в пару фиктивных переменных. Для этого в Pandas есть специальный метод, который называется get_dummies(). Сделаем эту операцию как для обучающей выборки, так и для тестовой.
X = pd.get_dummies(train_data[features])
X_test = pd.get_dummies(test_data[features])
Обратите внимание, что столбец Sex исчез, а вместо него появилось два столбца Sex_female и Sex_male.
Теперь с помощью ансамбля решающих деревьев обучим нашу модель, сделаем предсказание для тестовой выборки и сохраним результат. Ансамбль решающих деревьев называется Random Forest.
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
model.fit(X, y) # обучаем модель
prediction = model.predict(X_test) # делаем предсказание
output = pd.DataFrame({'PassengerId':test_data.PassengerId, 'Survived':prediction})
output.to_csv('my_submission.csv', index=False) # формируем итоговый датафрейм и сохраняем его в csv файл
Вот и все. Осталось отправить результат в соревнование. Для этого в правом верхнем углу наживаем кнопку Save version. После того, как блокнот сохранится, нажимаем на цифру возле этой кнопки.
Откроется окно Version history. В правом списке, нажимаем на многоточие около только что сохраненной версии и нажимаем Submit to competition.
Появляется окошко, в котором нажимаем submit.
Поздравляю! Вы закончили свое первое соревнование на kaggle. Нажмите на view my submission, чтобы взглянуть на результат.
Чем ближе число к 1, тем лучше. Но 0.775, согласитесь, неплохо для первого раза.
Путями улучшения результата могут быть: введение дополнительных признаков, введение своих новых признаков, выбор другого алгоритма, выбор другим параметров алгоритма RandomForestClassifier. Для начала, попробуйте поиграть с числами в этой строке (называются эти числа гиперпараметрами).
model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=1)
Дополнительные материалы для изучения:
- https://github.com/girafe-ai/ml-mipt/tree/master
- https://machinelearning.ru/
При подготовке были использованы материала из Википедии и Летней школы Сбера.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
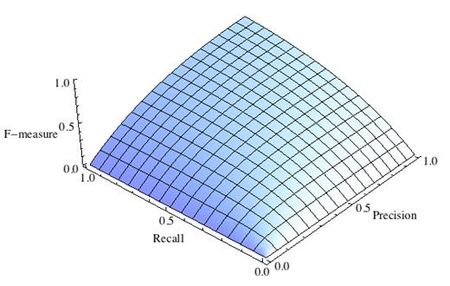
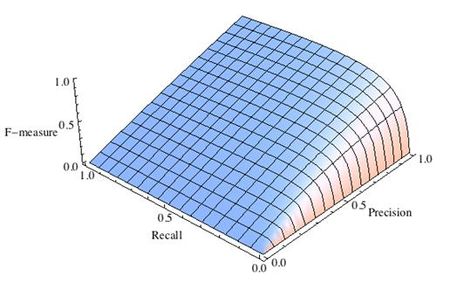
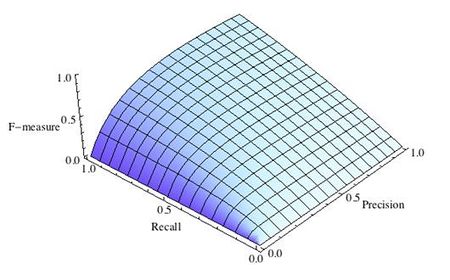
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
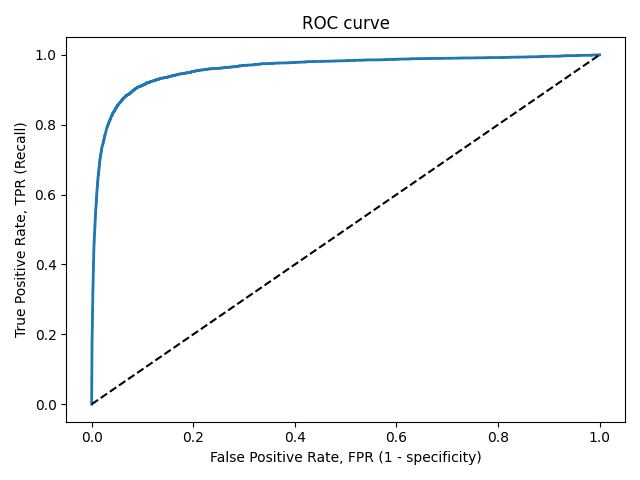
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
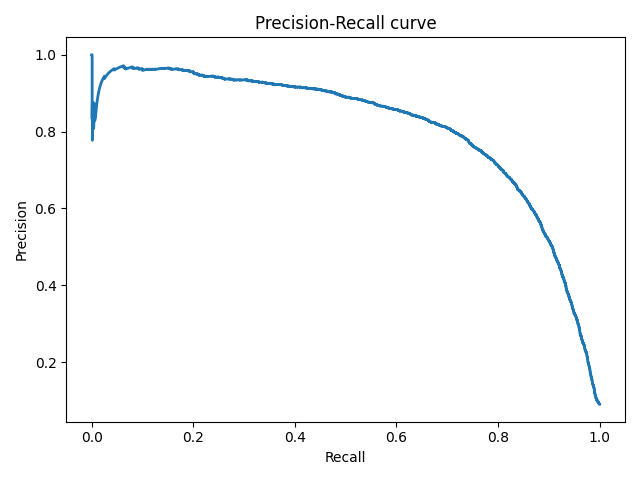
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
8 июля 2021 г.
При проверке гипотез нулевая гипотеза — это гипотеза по умолчанию, которая утверждает, что между переменными нет статистической значимости. Исследователь проверяет нулевую гипотезу, чтобы увидеть, достаточно ли статистической значимости, чтобы опровергнуть ее, и это иногда приводит к ошибке типа 1 или типа 2. Если вы занимаетесь проверкой гипотез как частью своей работы, важно понимать, как ошибки типа 1 и типа 2 могут повлиять на ваши результаты.
В этой статье мы объясним, что такое ошибки типа 1 и типа 2, рассмотрим, как они могут возникнуть, обсудим их важность в исследованиях и приведем примеры, которые помогут вам понять эти концепции.
Ошибки типа 1 и типа 2 относятся к неправильным определениям нулевой гипотезы, но они различаются тем, что исследователь считает верным или ложным в отношении гипотезы. Ошибка 1-го типа, также называемая ложноположительной, возникает, когда исследователь отвергает нулевую гипотезу, которая является истинной, и решает, что существует статистически значимое различие, которого не существует. Ошибка типа 2 является обратной ошибкой типа 1. Также известная как ложный отрицательный результат, она возникает, когда исследователь не отвергает нулевую гипотезу, когда альтернативная гипотеза верна.
Например, в судебном деле нулевая гипотеза будет заключаться в том, что обвиняемый невиновен, пока его вина не будет доказана, а альтернативная гипотеза будет состоять в том, что он виновен. Есть четыре возможных исхода в отношении истинного характера дела:
-
Истинно отрицательный: признан невиновным в суде и невиновен на самом деле.
-
Ложное срабатывание: признан виновным в суде, но на самом деле невиновен.
-
Ложноотрицательный: признан невиновным в суде, но на самом деле виновен.
-
Истинно положительный: признан виновным в суде и фактически виновен
В приведенном выше примере второй и третий результаты являются ошибками типа 1 и типа 2 соответственно. В случае ложного срабатывания присяжные ошибочно отвергают нулевую гипотезу, утверждающую, что подсудимый невиновен. В случае ложноотрицательного результата они ошибочно не отвергают нулевую гипотезу.
Почему возникают ошибки первого рода?
Есть два фактора, которые обычно способствуют возникновению ошибок 1-го рода:
Шанс
Проверка гипотез никогда не бывает стопроцентной, поэтому всегда есть возможность сделать неверные выводы на основе имеющихся данных. Как правило, данные поступают из выборочной совокупности, относительно небольшой выборки лиц, предназначенных для обозначения более широкой демографической группы. Иногда данные, генерируемые выборочными совокупностями, искажают выводы, которые не обязательно отражают интересы всего населения. Это переменная, которую исследователи не могут контролировать, но они могут помочь смягчить ее, выбрав более крупные выборки.
Злоупотребление служебным положением
Иногда ошибки 1-го рода возникают из-за неправильной исследовательской практики. Например, исследователи могут неосознанно исказить результаты теста, завершив его слишком рано. Им может показаться, что у них достаточно данных, хотя стандартная практика рекомендует продолжить тест. В качестве альтернативы они могут сделать вывод, несмотря на то, что им не удалось достичь соответствующего уровня статистической значимости. Исследователи могут избежать выводов типа 1, связанных с злоупотреблением служебным положением, если будут следовать протоколам исследований и обеспечивать надежность своей практики.
Почему возникают ошибки второго рода?
Основным фактором, способствующим возникновению ошибок 2-го рода, является размер выборки. Чем больше размер выборки, тем больше вероятность обнаружения различий в статистическом тесте. Например, если вы хотите проверить, относятся ли студенты колледжа положительно или отрицательно к определенному продукту, группа из трех человек может выразить только два к одному разнообразию или вообще ничего не сказать. Для сравнения, выборка из 1000 человек с большей вероятностью вызовет широкий спектр мнений и, таким образом, более точно отразит большую часть населения.
Какова важность ошибок типа 1 по сравнению с ошибками типа 2?
Ошибки типа 1 и типа 2 являются значительными из-за последствий, которые они имеют в реальных приложениях. Ошибки типа 1 обычно приводят к ненужному использованию ресурсов без какой-либо выгоды. Например, если исследователь-медик совершает ошибку 1-го рода в отношении эффективности нового лечения, он может подтвердить ошибочность исследований и методов, что может привести к созданию лекарства, не приносящего облегчения.
Ошибки 2-го типа важны тем, что могут помешать выделению ресурсов и выполнению необходимых действий. Например, при скрининге пациента на наличие заболевания ложноотрицательный результат может свидетельствовать о том, что пациент здоров, хотя на самом деле он нуждается в медицинском вмешательстве.
Примеры ошибок типа 1 и типа 2
Рассмотрим эти примеры ошибок типа 1 и типа 2, чтобы помочь вам понять, что они из себя представляют:
Пример ошибки 1 рода
Медицинский исследователь проверяет эффективность домашнего средства от головной боли. Нулевая гипотеза состоит в том, что домашнее средство не влияет на головную боль, в то время как альтернативная гипотеза состоит в том, что оно лечит головную боль. Исследователь набирает выборку из 20 пациентов с хроническими головными болями и назначает лекарство половине из них в течение одного месяца. Половина, не получающая лекарство, продолжает страдать от хронических головных болей, в то время как у шести человек из оставшейся половины головные боли прекратились.
На основании вышеизложенного исследователь отвергает нулевую гипотезу. Однако, учитывая небольшое количество тех, кто испытал облегчение, могут возникнуть сомнения относительно того, было ли это лекарство или посторонний фактор, который улучшил состояние шести участников. Если эти шесть участников использовали другие средства от головной боли вместе с тестируемым средством, вполне вероятно, что исследователь совершил ошибку 1-го типа.
Пример ошибки 2 рода
Интернет-магазин хочет знать, могут ли изменения дизайна его веб-сайта помочь увеличить продажи. Нулевая гипотеза состоит в том, что изменения дизайна не влияют на продажи, а альтернативная гипотеза говорит об обратном. Продавец проводит A/B-тестирование, в ходе которого сравниваются две версии сайта, существующая версия и обновленная версия. Три дня мониторят продажи на основе существующей версии. Затем в течение следующих трех дней они представляют новую версию и смотрят, как она повлияет на продажи. По истечении шести дней они не видят значительных изменений в показателях продаж.
Однако возможно, что увеличение периодов наблюдения для каждой версии сайта привело бы к статистически значимой разнице. Если бы розничный продавец отслеживал продажи в течение одного месяца каждый и заметил увеличение продаж во втором месяце, он совершил бы ошибку второго рода, ошибочно приняв нулевую гипотезу.
Этот пост продолжает серию про функции ошибки и функционалы качества в машинном обучении. Сейчас разберёмся с самой простой подтемой — как измерять качество чёткого ответа в задачах бинарной классификации. Уровень для чтения — начальный;)
Предыдущие посты в блоге на эту тему:
- AUC ROC
- Джини
- Логистическая функция ошибки
- Функции ошибок в задачах регрессии
Рассматриваем задачу классификации на два класса (с метками 0 и 1), на рис. 1 показано её графическое представление.
Пусть классификатор выдаёт метку класса. Используем принятые в этом блоге обозначения: yi – метка i-го объекта, ai – ответ на этом объекте нашего алгоритма, m – число объектов в выборке.
Естественным, простым и распространённым функционалом качества является точность (Accuracy или Mean Consequential Error):
т.е. просто доля (процент) объектов, на которых алгоритм выдал правильные ответы. Недостаток такого функционала очевиден: он плох в случае дисбаланса классов, когда представителей одного из класса существенно больше, чем другого. В этом случае, с точки зрения точности, выгодно почти всегда выдавать метку самого популярного класса. Это может не согласовываться с логикой использования решения задачи. Например, в задаче детектирования очень редкой болезни алгоритм, который всех относит к классу «здоровые», на практике не нужен.
Рассмотрим т.н. матрицу несоответствий / ошибок (confusion matrix) – матрицу размера 2×2, ij-я позиция которой равна числу объектов i-го класса, которым алгоритм присвоил метку j-го класса.
На рис. 2 показана такая матрица для решения рис. 1, также показаны названия элементов матрицы. Два класса делятся на положительный (обычно метка 1) и отрицательный (обычно метка 0 или –1). Объекты, которые алгоритм относит к положительному классу, называются положительными (Positive), те из них, которые на самом деле принадлежат к этому классу – истинно положительными (True Positive), остальные – ложно положительными (False Positive). Аналогичная терминология есть для отрицательного (Negative) класса. Дальше используем естественные сокращения:
- TP = True Positive,
- TN = True Negative,
- FP = False Positive,
- FN = False Negative.
Замечание. Иногда матрицу ошибок изображают по-другому: в транспонированном виде (ответы алгоритма соответствуют строкам, а правильные метки – столбцам).
Замечание. Стандартная терминология немного нелогична: естественно называть положительными объектами объекты положительного класса, но здесь – объекты, отнесённые алгоритмом к положительному классу (т.е. это даже не свойство объектов, а алгоритма). Но в контексте употребления терминов «истинно положительный» и «ложно положительный» это уже кажется логичным.
Для точности (Accuracy) справедлива формула:
Ошибки классификатора делятся на две группы: первого и второго рода. В идеале (когда точность равна 100%) матрица несоответствий диагональная, ошибки вызывают отличие от нуля двух недиагональных элементов:
ошибка 1 рода (Type I Error) случается, когда объект ошибочно относится к положительному классу (= FP/m).
ошибка 2 рода (Type II Error) случается, когда объект ошибочно относится к отрицательному классу (= FN/m).
На заглавном рис. поста показаны известные шуточные иллюстрации ошибок 1 и 2 рода: ошибка 1 рода (слева) и ошибка 2 рода (справа). Когда я объясняю студентам, всегда привожу такой пример, который позволяет запомнить отличие ошибок 1 и 2 рода. Пусть студент приходит на экзамен. Если он учил и знает, то принадлежит классу с меткой 1, иначе — имеет метку 0 (вполне логично называть знающего студента «положительным»). Пусть экзаменатор выполняет роль классификатора: ставит зачёт (т.е. метку 1) или отправляет на пересдачу (метку 0). Самое желаемое для студента «не учил, но сдал» соответствует ошибке 1 рода, вторая возможная ошибка «учил, но не сдал» – 2 рода.
Через введённые выше обозначения выражаются следующие функции:
Полнота (Sensitivity, True Positive Rate, Recall, Hit Rate) отражает какой процент объектов положительного класса мы правильно классифицировали:
Здесь и далее показан числитель формулы (тёмно синим) и знаменатель (тёмно и светло синим). Слева это сделано для матрицы несоответствий, справа – для множеств: круглое – объекты положительного класса, квадратное – положительные объекты по мнению классификатора.
Точность (Precision, Positive Predictive Value) отражает какой процент положительных объектов (т.е. тех, что мы считаем положительными) правильно классифицирован:
Точность и полноту можно неформально называть «ортогональными критериями качества». Легко построить алгоритм со 100%-й полнотой: он все объекты относит к классу 1, но при этом точность может быть очень низкой. Нетрудно построить алгоритм с близкой к 100% точностью: он относит к классу 1 только те объекты, в которых уверен, при этом полнота может быть низкая.
Замечание. Отличайте «Accuracy» и «Precision». К сожалению, по-русски их называют одинаково «точность».
F1-мера (F1 score) является средним гармоническим точности и полноты, максимизация этого функционала приводит к одновременной максимизации этих двух «ортогональных критериев»:
Также рассматривают весовое среднее гармоническое точности (P) и полноты (R) – Fβ-меру (Fβ score):
Обратите внимание, что β здесь не вес в среднем гармоническом:
Почему используется среднее гармоническое понятно из рис. 4, на которых показаны линии уровня различных функций усреднения.
Видно, что линии уровня среднего гармонического сильно похожи на «уголки», т.е. на линии функции min, что вынуждает при максимизации функционала сильнее «тянуть вверх» меньшее значение. Если, например, точность очень мала, то увеличение полноты, пусть и в два раза, не сильно меняет значение функционала. Нагляднее это показано на рис. 5: при точности 10% F1-мера не может быть больше 20%.
При использовании Fβ-меры линии уровня «перекашиваются», один из критериев (точность или полнота) становится важнее при оптимизации, см. рис. 6.
Из функционалов качества, которые получаются из матрицы несоответствий, можно также отметить специфичность (Specificity) или TNR – True Negative Rate:
т.е. процент правильно классифицированных объектов негативного класса. Полноту иногда называют чувствительностью (Sensitivity) и используют в паре со специфичностью для оценки качества, также часто их усредняют (об этом поговорим дальше). Оба функционала имеют смысл «процент правильно классифицируемых объектов одного из класса». Можно ввести понятие полноты Rk для k-го класса: это полнота, если считать класс k положительным, тогда
Также запомним False Positive Rate (FPR, fall-out, false alarm rate):
– доля объектов негативного класса, которых мы ошибочно отнесли к положительному (это нужно для понимания функционала AUC ROC).
Коэффициент Мэттьюса (MCC – Matthews correlation coefficient) равен
его рекомендуют применять для несбалансированных выборок. Давайте разберёмся, что означает эта «сложная формула». Рассмотрим среднее геометрическое точности и полноты:
Теперь возьмём среднее геометрическое точности и полноты класса 0 (т.е. считая это класс положительным), перемножив эти средние геометрические, получим
Логично полученное выражение максимизировать, по аналогии можно выписать выражение для минимизации. Если теперь внимательно посмотреть на формулу MCC, то становится понятным, что она означает и почему её значение лежит на отрезке [–1, +1] (оставляем это как задание читателю).
Каппа Коэна (Cohen’s Kappa)
В задачах классификации часто используют функционал качества Каппа Коэна (Cohen’s Kappa). Его идея довольно простая: поскольку использование точности (Accuracy) вызывает сомнение в задачах с сильном дисбалансом классов, надо её значения немного перенормировать. Делается это с помощью статистики chance adjusted index: мы точность нашего решения (Accuracy) пронормируем с помощью точности, которую можно было получить случайно (Accuracychance). Под случайной здесь понимаем точность решения, которое получено из нашего случайной перестановкой ответов.
здесь красным выделена вероятность угадать класс 0, а синим – класс 1. Действительно, класс k угадывается, если алгоритм выдаёт метку k и объект действительно принадлежит этому классу. Предполагаем, что это независимые события (мы же хотим вычислить случайную точность). Вероятность принадлежности к классу k можно оценить по матрице несоответствий как долю объектов класса k. Аналогично, вероятность выдать метку оцениваем как долю таких меток в ответах построенного алгоритма.
Сбалансированная точность (Balanced Accuracy)
В случае дисбаланса классов есть специальный аналог точности – сбалансированная точность:
Для простоты запоминания – это среднее полноты всех классов (мы ещё вернёмся к этому определению), ну или в других терминах: среднее чувствительности (Sensitivity) и специфичности (Specificity). Отметим, что чувствительность и специфичность тоже, неформально говоря, «ортогональные критерии». Легко сделать специфичность 100%-й, отнеся все объекты к классу 0, при этом будет 0%-я чувствительность, и наоборот, если отнести все объекты к классу 1, то будет 0%-я специфичность и 100%-я чувствительность.
Если в бинарной задаче классификации представителей двух классов примерно поровну, то TP + FN ≈ TN + FP ≈ m/2 и сбалансированная точность примерно равна точности обычной (Accuracy).
Все указанные функционалы реализованы в библиотеке scikit-learn:
Сравнение функционалов
Рассмотрим модельную задачу, в которой плотности распределения классов на оценках, порождённых алгоритмом, линейные, см. рис. 7 (алгоритм выдаёт оценки принадлежности к классу 1 из отрезка [0, 1], именно на этом отрезке они линейные). На рис. 7 показана конечная небольшая выборка, которая соответствует изображённым плотностям, мы же будем считать, что выборка бесконечная, поскольку плотности простые и позволяют в явном виде вычислить функционалы качества даже в случае такой бесконечной выборки. Будем считать, что классы равновероятны, т.е. наша бесконечная выборка сбалансирована. Выбранная задача очень удобна для исследования и уже использовалась при анализе функционала AUC ROC.
Заметим, что подобные распределения возникают в задаче, показанной на рис. 8 (объекты лежат внутри квадрата [0, 1]×[0, 1], два класса разделяются диагональю квадрата), если алгоритм в качестве оценки выдаст значения первого признака.
Изобразив плотности немного по-другому, мы в явном виде можем вычислить элементы матрицы несоответствий при конкретном пороге бинаризации, см. рис. 9. Все они пропорциональны площадям выделенных зон (обратите внимание на масштаб осей):
Теперь можно вывести формулы для рассмотренных функционалов качества как функции от порога бинаризации:
Попробуйте вывести эти формулы сами, кроме того, попробуйте определить пороги бинаризации при которых указанные функционалы максимальны (здесь будет один сюрприз).
Возникает естественный вопрос: на практике у нас нет бесконечных выборок, что изменится, если мы вычислим значения функционалов на конечной, объекты которой сгенерированы в соответствии с указанными распределениями? Частично ответ на этот вопрос показан на рис. 10. Как видно, кривые довольно близки к теоретическим при m=300, при увеличении выборки в 10 раз практически совпадают.
Рассмотрим теперь графики наших функционалов качества как функций от порога бинаризации, см. рис. 11. Заметим, что кроме F1-меры все они симметричны относительно порога 0.5, но это вполне логично. Теперь рассмотрим ситуацию неравновероятных классов, т.е. когда выборка несбалансированна. На рис. 12 показаны графики функционалов в случае, когда класс 1 в два раза чаще встречается в выборке, чем класс 0. Обратите внимание, что все графики стали несимметричными, кроме графика сбалансированной точности – эта функция не зависит от пропорций классов!
Вопросы для самопроверки
В конце серия вопросов с подвохом… если Вы хотите кого-нибудь «завалить» по простой теме «оценка качества в задачах бинарной классификации», то непременно задайте их:
- у какого функционала качества самый маленький оптимальный порог бинаризации в общем случае, почему? Для справки: ответ «у F1-меры» в общем случае неверный (можно даже простой пример привести).
- какой функционал качества действительно имеет смысл использовать в задачах с сильным дисбалансом классов (заметим, что стандартные советы: BA, MCC, κ, F1 обладают совершенно разными свойствами)?
- какой «самый неустойчивый» из перечисленных функционалов (его значения на небольших выборках сильнее отличаются от вычисленных на достаточно больших)?
- что изменится в примерах выше, если от линейных плотностей перейти к нормальным? Как это сделать корректно (и в чём некорректность описанной модельной задачи)?
- верно ли, что максимальное значение точности (т.е. значение точности при оптимальном выборе порога) всегда не меньше максимального значения сбалансированной точности?
Что дальше…
По задачам классификации осталось рассказать про все скоринговые функции оценки качества в задачах бинарной классификации, про AUC ROC и LogLoss уже было. А потом — как все рассмотренные функционалы обобщаются на случай многих классов. Соответствующие посты скоро будут.
Традиционное в последнее время видео к материалу поста я залью чуть позже.
На правах рекламы
С сентября чему-то научиться у автора блога можно в этом замечательном проекте: Ozon Masters. Кроме курса по машинному обучению, будет много других с потрясающими преподавателями: Андрей Соболевский, Иван Оселедец, Павел Клеменков, Юрий Дорн, Александр Дайняк.