Ошибки регулирования может быть уменьшена если

1. Виды ошибок регулирования и методы их снижения.

Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.

Показателями качества динамических
режимов определяются из графика
переходного процесса и основными из
них являются (рис.1.42):

—перерегулирование или забросσ,
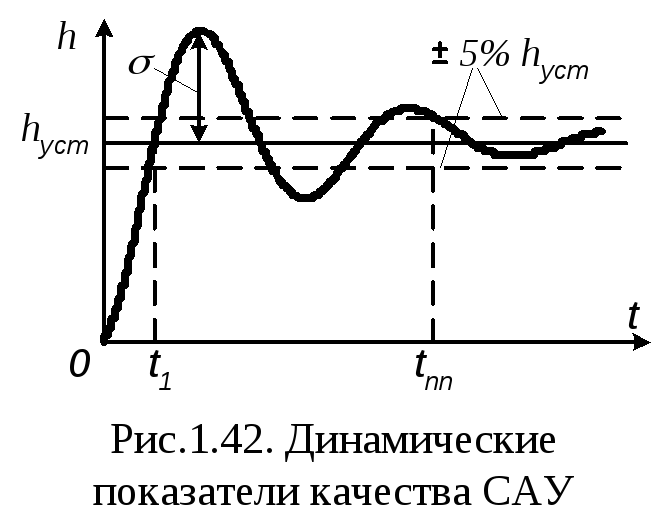
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаh_ycm;

— время первой установки t₁,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияh_ycm;

— время переходного процесса t_ПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаh_ycm.

Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.

Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (ε_СТ) и
скоростные ошибки (ε_СК) и
ошибки (ε_m)
при отработке гармонического входного
сигнала.

Д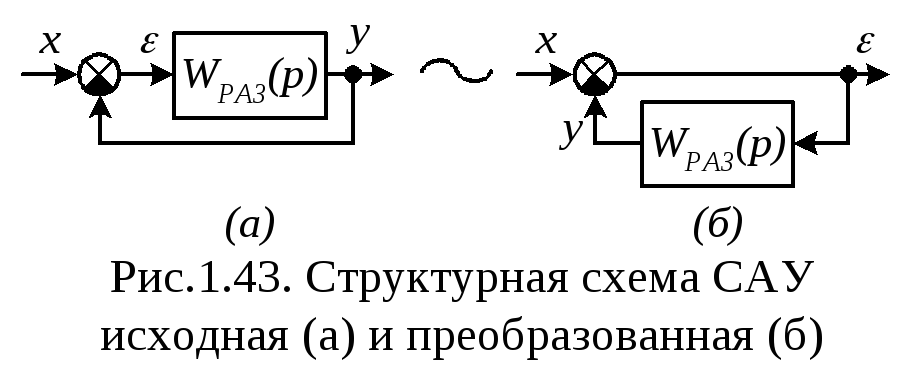ля
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.

Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ W_ε(p)по ошибке и изображенияε(р)ошибки
регулирования:

Расчет ошибки ε_mотработки гармонического входного
сигналаx=X_msinωt
производится по формуле

где
— модуль комплексного числа.

Статическая (ε_СТ) и
скоростная (ε_СК) ошибки
равны установившимся значениям оригиналаи,
или в общем виде, по формуле.
Значениевычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,

(1.54)

Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:

(1.55)

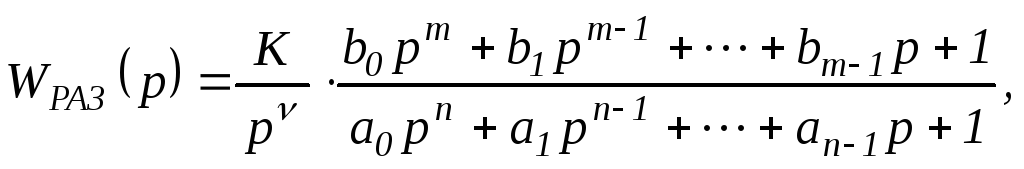
где К– общий коэффициент усиления
разомкнутой САУ:

ν— порядок астатизма САУ, причемνявляется целым неотрицательным
числом.

Для удобства вычислений по формуле
(1.54) подставим в нее выражение W_РАЗ(р)из (1.55) и выполним предельный переход:

(1.56)

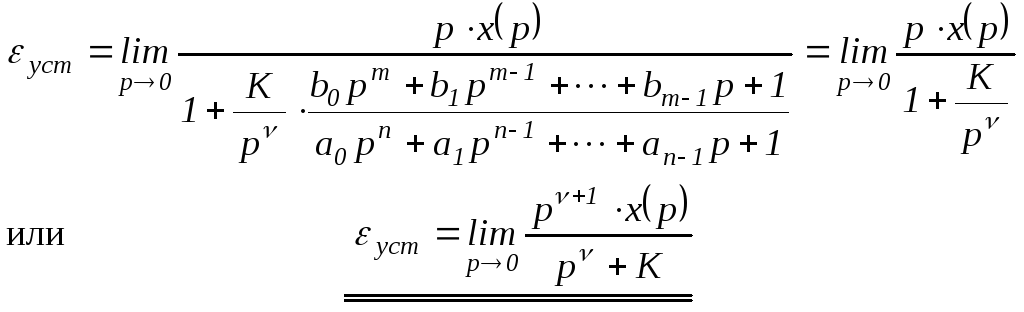
Статическая ошибка регулирования ε_СТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяε_СК— при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (ε_СТ)
и скоростной (ε_СК) ошибок
выполним раздельно.

Расчеты статической ошибки εСт регулирования

Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуε_СТследует вычислять по
формуле

(1.57)

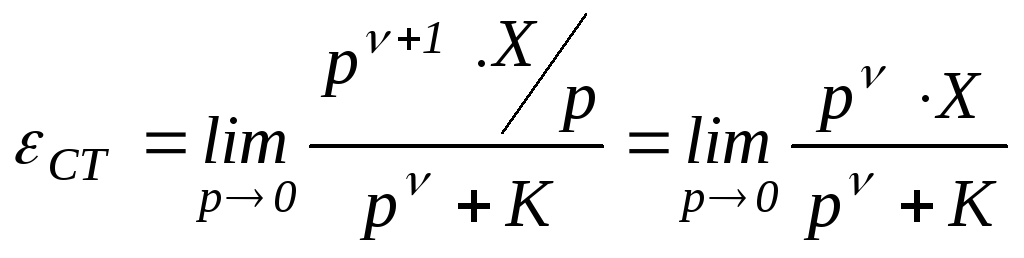
1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаε_СТбудет равна

В статической САУ имеется статическая
ошибка ε_СТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.

2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаε_СТбудет равна

В астатической САУ 1-го порядка статическая
ошибка ε_СТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчеты статической ошибки εСт регулирования

Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуε_СТследует вычислять по
формуле

(1.57)

1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаε_СТбудет равна

В статической САУ имеется статическая
ошибка ε_СТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.

2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаε_СТбудет равна

В астатической САУ 1-го порядка статическая
ошибка ε_СТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.

Расчеты скоростной ошибки εСт регулирования

Входной сигнал x(t)=Vtи изображением его является.
В соответствии с (1.56) скоростную ошибкуε_СКследует вычислять по
формуле

(1.58)

1). Пусть в (1.58) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
скоростная ошибкаε_СКбудет равна

В статической САУ скоростная ошибка
ε_СКбесконечно большая
и, поэтому, такая САУ неработоспособна.

2). Пусть в (1.58) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаε_СКбудет равна

В астатической САУ 1-го порядка имеется
скоростная ошибка ε_СК,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияКразомкнутой САУ, но обратить в
ноль ее нельзя.

3). Пусть в (1.58) значение порядка νастатизма САУ равно 2:ν=2. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаε_СКбудет равна

В астатической САУ 2-го порядка скоростная
ошибка ε_СКравна нулю,
т.е САУ является абсолютно точной.

Выводы по расчетам статической и скоростной ошибок регулирования:

1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления Ки порядка
астатизмаνразомкнутой САУ.

2. При увеличении Кошибки регулирования
только уменьшаются. но не обращаются в
ноль.

3. При увеличении νСАУ становится
абсолютно точной — ошибка регулирования
становится нулевой.

Косвенные
показатели качества САУ и их связь с
прямыми показателями качества.
Использование ЛАЧХ для оценки качества
САУ

Невозможность получения формул для
расчета динамических показателей
качества (рис.1.42), а также требования
задач синтеза САУ, обусловило разработки
комплексных показателей качества.
Косвенные показатели качества, в
большинстве своем, являются частотными,
которые определяются из ЧХ, АЧХ, ФЧХ и
ЛАЧХ. Косвенные показатели качества
должны удовлетворять следующим
требованиям:

1. Косвенные показатели должны просто
вычисляться или определяться из частотных
характеристик разомкнутой САУ.

2. Погрешность определения значений
прямых показателей качества через
значения косвенных показателей качества
должна быть мала.

3. Косвенные показатели должны быть
приспособлены для эффективного решения
задач синтеза САУ.

4.
Косвенные показатели должны давать
возможность просто анализировать
влияние параметров настроек регуляторов
САУ и характеристик любых других звеньев
САУ на прямые показатели качества.

Косвенных показателей качества или их
наборов разработано достаточно много.
Каждый косвенный показатель качества
или их набор вводятся для эффективного
решения конкретных типов задач
автоматического управления и, поэтому,
универсальных косвенных показателей
качества не существует в принципе. По
сути, косвенные показатели упрощают
анализ и синтез САУ, но прямые показатели
качества определяются через косвенные
всегда неточно.

Прежде всего рассмотрим набор косвенных
показателей качества, полученных из
построений Найквиста (см. тему 1.12):
частоту среза ω_СРи запас
по фазеγ. Частота срезаω_СРпросто определяется из ЛАЧХ (рис.1.41).
Запас по фазеγрассчитывается по
выражению ФЧХφ(ω) только при
одном значении частотыω_СР:γ=φ(ω_СР ).

Основой применения косвенных показателей
качества — частоты среза ω_СРи запаса по фазеγ— являются
графические зависимости (рис.14.1) между
косвенными и прямыми показателями
качества — перерегулированиемσ,
временем первой установкиt₁и временем переходного процессаt_ПП.

По оси ординат отложены значения
перерегулирования σ, в процентах
от установившегося значенияh_ycm(рис.1.42). По оси временt₁иt_ППзаписаны
формулы, по которым рассчитываютсяt₁иt_ППв
зависимости от частоты срезаω_СР.
Если из частотных характеристик
определены значения запаса по фазеγи частоты срезаω_СР, то по
графикам можно определить значения
перерегулированияσ, времени первой
установкиt₁и времени переходного процессаt_ПП.
Например, пусть заданы значенияγ=30^оиω_СР=1,5 с^-1.
Тогда, согласно приведенным на рис.1.44
построениям, получим:

σ=19 %,

Найденные значения σ,t₁иt_ППне
являются точными. Этот факт, отражен на
рис.1.44 как «размытость» графиков.

По этим значениям σ,t₁иt_ППможно
построить примерный график переходного
процесса (рис.1.45). Как принято, косвенные
показатели качества выбираются такими,
чтобы найденные с их помощью оценки
прямых показателей качества имели бы
погрешность не более 10 %. Это вполне
приемлемо в инженерной практике.

Графические зависимости между косвенными
γиω_СРи прямымиσ,t₁иt_ППпоказателями качества САУ, приведенные
на рис.1.44, можно описать в виде следующих
зависимостей пропорционального типа

Важная в практике эксплуатации САУ
задача определения влияния типовых
законов регулирования (пропорционального,
интегрального и дифференциального) на
прямые показатели качества чрезвычайно
эффективно решается с помощью введенных
косвенных показателей γиω_СР.

Частотный
метод синтеза следящей САУ (см. тему
1.23) основан на использовании косвенного
показателя качества – показателя
колебательностиМ. Показателем
колебательностиМназывается
величина, численно равная максимуму
нормированной АЧХ (рис.1.46). По значению
показателя колебательностиМможно
оценить величину перерегулированияσ(рис.1.47).

Значение показателя колебательности
Мможет быть найдено графически,
без вычислений АЧХ, при использовании
только годографа частотной характеристикиW_раз(p)и, соответственно, ЛАЧХ разомкнутой
САУ. Именно такие построения положены
в основу расчета среднечастотного
участка желаемой ЛАЧХ при упомянутом
выше частотном синтезе следящей САУ.

Требования

САУ рулевого устройства.

привод должен обеспечивать перекладку
от -35˚ до +30˚ за 28с.

При полном ходе в течение 1 часа привод
должен обеспечить 350 перекладок.

Посты управления должны снабжаться
аксиометрами с точностью до 1º в ДП и
1,5º при α = ± 5º. При больших углах ± 2,5º

Требования к СЭЭС:

А) статические требования:

Ошибка регулирования частоты- менее 5%

Ошибка регулирования напряжения – от
-10 до +6%

Неравномерность распределения нагрузки
параллельно работающих генераторов :
не более 10% от мощности наибольшего
генератора или не более 25% от мощности
наименьшего генератора. Из двух вариантов
или выбирается меньший.

Б) динамические показатели

Заброс/провал частоты – не более 10% в
течение 5сек

Заброс/провал напряжения – не более
20% в течение 1,5сек

Требования ДАУ ГД

1. Регулятор
   частоты должен быть всережимным,
   допустимая регулировка частоты в
   пределах от 40 до 115%

2. Не
   должно быть временной задержки между
   перемещением рукоятки на мостике и
   началом разворота лопастей и частоты
   вращения дизеля

3. Точность
   поддержания частоты не хуже 1,5%

4. Должно
   быть реализовано несколько постов
   управления ГД и ВРШ, а именно с разных
   постов, при наборе и сбросе хода, при
   реверсе, при управлении ВГ, когда он
   включен в судовую сеть

5. Пуск
   реверсивной характеристики ГД должны
   быть соизмеримы с квалифицированным
   ручным управлением

1. Перечислите
   типовые позиционные, интегрирующие и
   дифференцирующие звенья САУ и приведите
   их примеры из судовых систем автоматики.
   Укажите передаточные функции и
   переходные характеристики этих звеньев.

Виды типовых позиционных звеньев:

1. Безинерционное (пропорциональное)
звеноимеет передаточную функцию и
описывается алгебраическим уравнением,
соответственно, вида W(p)=k, y=kx

Примерами безинерционных звеньев служат
рычажная передача (рис.1.10а),
потенциометрический датчик перемещения
(рис.1.10б).

В этих звеньях выходной сигнал уповторяет без задержки по форме входной
сигналх.

Выражение переходного процесса y=kx

2. Апериодическое (инерционное) звено
1-го порядка имеет передаточную функцию
и описывается уравнением вида

где k, Т — коэффициент
передачи и постоянная времени звена.

Примерами этого звена служат интегрирующая
RC—цепь (рис.1.11а),
‘электродвигатель, обмотки которого
разогреваются во время работы (рис.1.11б).

Выполним вывод передаточной функции
для RC—цепи. Используя
закон Ома, получим

Переходный процесс описывается
выражением

где вместо x=1(t),
как должно быть для переходного процесса,
принято фактическое значение сигналаx, благодаря чему
рассчитывается реакция звена на скачок
произвольной величины.

График переходного процесса приведён
на рис.1.11в. Установившееся значение
y_уст, равноеkx, достигается на
бесконечности:t.
Время переходного процессаt_пп,
определяемое по моменту окончательного
вхождения графика в 5% зону допуска оту_уст, составляет3T.
Звено обладаетсамовыравниванием.
Свойство самовыравнивания состоит в
том, что звено самостоятельно без
применения дополнительного регулирования
приходит к постоянному по величине
установившемуся значению.

3.
Инерционное звено 2-го порядкаимеет
передаточную функцию

Особенность звена в том, что его
характеристическое уравнение имеет
действительные корни.

Примерами этого звена служит RLC-цепь
(рис.1.13а) при большом сопротивленииRрезистора,
электропривод, приводящий во вращение
нагрузку с большим моментом инерцииJ(рис.6.4б).

Переходный процесс описывается выражением

где с₁ и с₂
— постоянные интегрирования.

График
переходного процесса (рис.1.14а) имеет
точку перегиба. Время переходного
процессаt_ппможно определить только графически.

4. Колебательное звеноимеет
передаточную функцию

где T— период свободных
(незатухающих) колебаний;

ξ— параметр затухания,
принимающий значения0<ξ<1.

Особенность звена в том, что его
характеристическое уравнение имеет
комплексно сопряженные корни.

Примерами этого звена служит RLC-цепь
(рис.1.13а) при малом сопротивленииRрезистора,
электропривод, приводящий во вращение
нагрузку с малым моментом инерцииJ(рис.1.13б). Переходный процесс описывается
выражением

где
— резонансная частота с учётом затухания
колебаний.

График переходного процесса приведён
на рис.1.14б. Чем меньше значение параметра
ξ, тем медленнее
затухает переходный процесс. Время
переходного процесса можно определить
только графически.

Уменьшение — статическая ошибка

Cтраница 1

Уменьшение статической ошибки осуществляется в результате воздействия астатической части, которая в основном и служит для ликвидации остаточного отклонения. По окончании переходного режима движок реостатного датчика Rn и контактные группы обоих реле приходят в первоначальное среднее положение, соответствующее заданному значению регулируемой величины, а положение рукоятки спаренных сопротивлений Л5 и jR6 ( ручная перестановка) показывает степень открытия регулирующего органа в процентах от полного открытия. Доля участия пропорциональной части в перемещении регулирующего органа зависит от диапазона пропорциональности, а астатической — от величины времени действия астатической части.
 [1]

Уменьшение статической ошибки ( а при бесконечно большом коэффициенте усиления усилителя в статике — сведение ее к нулю) в контуре с объектом в виде интегрирующего звена может быть достигнуто путем использования ПИ-регулятора.
 [2]

Уменьшение статической ошибки регулирования ( ошибки в установившемся режиме) и увеличение быстродействия системы может быть достигнуто последовательным включением в контур системы автоматического регулирования ( в регулятор, осуществляющий основную обратную связь) безынерционного звена с большим коэффициентом усиления.
 [4]

Для уменьшения статической ошибки используют также принцип управления по возмущению в комбинированных САУ. Из множества возмущений выбирается главное, и на основе его измерения воздействуют на объект управления таким образом, чтобы компенсировать естественное влияние данного воздействия на выходную величину системы. Комбинированные системы позволяют значительно снизить статическую ошибку системы без повышения степени ее астатизма.
 [5]

Для уменьшения статической ошибки без нарушения устойчивости необходимо в контур ввести первую производную от входного сигнала.
 [6]

Для уменьшения статической ошибки следует увеличивать коэффициент усиления системы. До известной степени можно считать, что величина коэффициента усиления определяется требованиями к величине статической ошибки.
 [8]

Для уменьшения статической ошибки регулирования иногда рекомендуется установка в приточной камере двух калориферов ( или двух рядов калориферов), соединенных последовательно по воздуху и параллельно по воде. Теплопроизводительность каждого калорифера составляет приблизительно 50 % от общей требуемой. Благодаря этому статическая ошибка выбранного регулятора может быть снижена вдвое, так как регулируется только половина нагрузки. Первый по ходу воздуха калорифер отключается двухпозиционным регулятором, датчик которого установлен на входе наружного воздуха, когда достигается температура, при которой требуется только половина нагрузки — теплопроизводительности. Для определения температуры настройки двухпозиционного регулятора требуется провести дополнительные несложные расчеты.
 [9]

Для уменьшения статической ошибки копирования в следящей системе предусмотрено интегрирующее звено по управляющему воздействию.
 [10]

Пусть теперь для уменьшения статической ошибки в систему вводится воздействие по производной.
 [11]

Например, для уменьшения статической ошибки и улучшения динамических характеристик необходимо увеличивать коэффициент усиления, однако это ухудшает устойчивость системы. Поэтому для усилительной схемы задаются предельные значения / Ста и / тт, при достижении которых возникает отказ.
 [13]

Это всегда полезно для уменьшения статической ошибки, ибо в этом случае при изменении нагрузки остаточное отклонение регулируемого параметра будет меньше. Обычно пропорциональные регуляторы применяются с объектами средней емкости при малых запаздываниях и малых изменениях нагрузки.
 [14]

Есть, однако, способ уменьшения статической ошибки системы вне зависимости от динамических ее свойств.
 [15]

Страницы:  

   1

   2

   3

5.5.1. Качество регулирования

5.5.2. Выбор параметров регулятора

5.5.3. Ручная настройка, основанная на правилах

5.5.4. Методы оптимизации

Перед тем, как рассчитывать параметры регулятора, необходимо сформулировать цель и критерии качества регулирования, а также ограничения на величины и скорости изменения переменных в системе. Традиционно основные качественные показатели формулируются исходя из требований к форме реакции замкнутой системы на ступенчатое изменение уставки. Однако такой критерий очень ограничен. В частности, он ничего не говорит о величине ослабления шумов измерений или влияния внешних возмущений, может дать ошибочное представление о робастности системы.

Поэтому для полного описания или тестирования системы с ПИД-регулятором нужен ряд дополнительных показателей качества, о которых речь пойдет ниже.

В общем случае выбор показателей качества не может быть формализован полностью и должен осуществляться исходя из смысла решаемой задачи.

5.5.1. Качество регулирования

Выбор критерия качества регулирования зависит от цели, для которой используется регулятор. Такой целью может быть:

• поддержание постоянного значения параметра (например, температуры);
• слежение за изменением уставки или программное управление;
• управление демпфером в резервуаре с жидкостью и т.д.

Для той или иной задачи наиболее важными могут быть следующие факторы:

• форма отклика на внешнее возмущение (время установления, перерегулирование, коэффициент затухания и др.);
• форма отклика на шумы измерений;
• форма отклика на сигнал уставки;
• робастность по отношению к разбросу параметров объекта управления;
• требования к экономии энергии в управляемой системе;
• минимум шумов измерений и др.

Для классического ПИД-регулятора параметры, которые являются наилучшими для слежения за уставкой, в общем случае отличаются от параметров, наилучших для ослабления влияния внешних возмущений. Для того, чтобы оба параметра одновременно были оптимальными, необходимо использовать ПИД-регуляторы с двумя степенями свободы (см. раздел «Принцип разомкнутого управления»).

Например, точное слежение за изменением уставки необходимо в системах управления движением, в робототехнике. В системах управления технологическими процессами, где уставка обычно остается длительное время без изменений, требуется максимальное ослабление влияния нагрузки (внешних возмущений). В системах управления резервуарами с жидкостью требуется обеспечение ламинарности потока (минимизация дисперсии выходной переменной регулятора).

Ослабление влияния внешних возмущений

Как было показано в разделе «Запас устойчивости и робастность», обратная связь ослабляет влияние внешних возмущений в раз за исключением тех частот, на которых . Внешние возмущения могут быть приложены к объекту в самых разных его частях, однако, когда конкретное место неизвестно, считают, что возмущение воздействует на вход объекта. В этом случае отклик системы на внешние возмущения определяется передаточной функцией (см. (5.42))

.

(5.109)

Поскольку внешние возмущения обычно лежат в низкочастотной части спектра, где , и, следовательно, , то предыдущее выражение можно упростить:

.

(5.110)

Таким образом, для ослабления влияния внешних возмущений (в частности, влияния нагрузки) можно уменьшить постоянную интегрирований .

Во временной области реакцию на внешние возмущения оценивают по отклику на единичный скачок (см. рис. 5.56).

Ослабление влияния шумов измерений

Передаточная функция от точки приложения шума (рис. 5.35) на выход системы имеет вид (см. (5.42)):

.

(5.111)

Благодаря спаду АЧХ объекта на высоких частотах функция чувствительности стремится к 1 (см. рис. 5.81). Поэтому ослабить влияние шумов измерений с помощью обратной связи невозможно. Однако эти шумы легко устраняются применением фильтров нижних частот, а также правильным экранированием и заземлением [Денисенко, Денисенко].

Робастность к вариации параметров объекта

Замкнутая система остается устойчивой при изменении параметров объекта на величину , если выполняется условие (5.100).

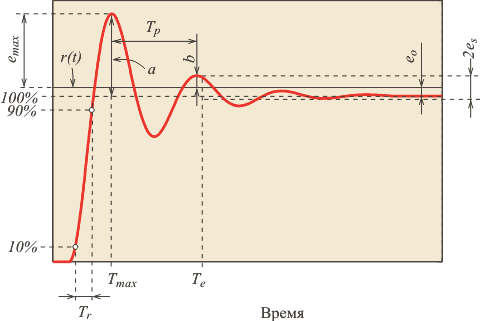
Критерии качества во временной области

Для оценки качества регулирования в замкнутой системе с ПИД-регулятором обычно используют ступенчатое входное воздействие и ряд критериев для описания формы переходного процесса (рис. 5.84):

и момент времени , при котором ошибка достигает этого максимума;

(5.112)

;

(5.113)

;

(5.114)

.

(5.115)

Отметим, что в литературе встречаются и другие определения декремента затухания, в частности, как или как коэффициент в показателе степени экспоненты, описывающей огибающую затухающих колебаний;

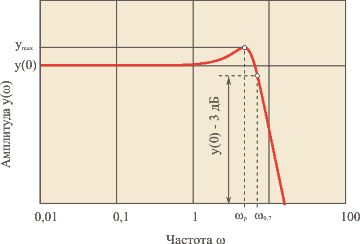
Рис. 5.84. Критерии качества регулирования во временной области	Рис. 5.85. Критерии качества регулирования в частотной области

Для систем управления движением в качестве тестового сигнала чаще используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы обычно имеют ограниченную скорость нарастания выходной величины.

Приведенные выше критерии используются как для оценки качества реакции на изменение уставки, так и на воздействие внешних возмущений и шумов измерений.

Частотные критерии качества

В частотной области обычно используются следующие критерии, получаемые из графика амплитудно-частотной характеристики замкнутой системы (см. рис. 5.85):

, типовыми значениями являются =1,5…1,6;

(5.114)

Частотные критерии у реальных регуляторов не могут быть однозначно связаны с временными критериями из-за нелинейностей (обычно это нелинейности типа ограничений) и алгоритмов устранения эффекта интегрального насыщения. Однако приближенно можно установить следующие зависимости между критериями в частотной и временной области:

5.5.2. Выбор параметров регулятора

В общей теории автоматического управления структура регулятора выбирается исходя из модели объекта управления. При этом более сложным объектам управления соответствуют более сложные регуляторы. В нашем же случае структура регулятора уже задана — мы рассматриваем ПИД-регулятор, причем эта структура очень простая. Поэтому ПИД-регулятор не всегда может дать хорошее качество регулирования, хотя в подавляющем большинстве приложений в промышленности применяются именно ПИД-регуляторы.

Впервые методику расчета параметров ПИД-регуляторы предложили Зиглер и Никольс в 1942 году [Ziegler]. Эта методика очень проста и дает не очень хорошие результаты. Тем не менее, она до сих пор часто используется на практике, хотя с тех пор появилось множество более точных методов.

После расчета параметров регулятора обычно требуется его ручная подстройка для улучшения качества регулирования. Для этого используется ряд правил, хорошо обоснованных теоретически.

Для настройки ПИД-регуляторов можно использовать и общие методы теории автоматического управления, такие, как метод назначения полюсов и алгебраические методы. В литературе опубликовано и множество других методов, которые имеют преимущества в конкретных применениях. Мы приводим ниже только самые распространенные из них.

Все аналитические (формульные) методы настройки регуляторов основаны на аппроксимации динамики объекта моделью первого или второго порядка с задержкой. Причиной этого является невозможность аналитического решения систем уравнений, которое необходимо при использовании моделей более высокого порядка. Поэтому в последние годы, в связи с появлением мощных контроллеров и персональных компьютеров, получили развитие и распространение численные методы оптимизации. Они являются гибким инструментом для оптимальной настройки параметров регулятора для моделей любой сложности и легко учитывают нелинейности объекта управления и требования к робастности.

Настройка параметров регулятора по методу Зиглера и Никольса

Зиглер и Никольс предложили два метода настройки ПИД-регуляторов [Ziegler]. Один из них основан на параметрах отклика объекта на единичный скачок; второй метод основан на частотных характеристиках объекта управления.

Для расчета параметров ПИД-регулятора по первому методу Зиглера-Никольса используются всего два параметра: и (см. рис. 5.29 и пояснения к нему в тексте). Формулы для расчета коэффициентов ПИД-регулятора сведены в табл. 27.

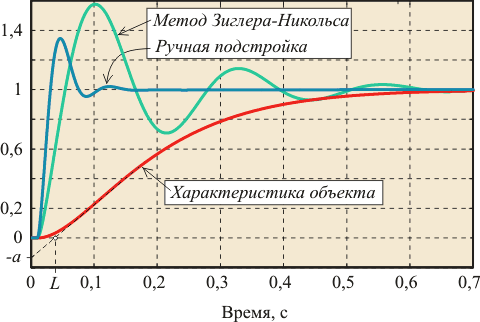
Рис. 5.86. Результат настройки ПИД-регулятора по методу Зиглера-Никольса для объекта второго порядка с задержкой: , .

В качестве примера на рис. 5.86 приведен отклик на единичный скачок системы с объектом второго порядка и ПИД-регулятором, настроенным по табл. 27 и переходная характеристика самого объекта управления. Из характеристики объекта получены значения и . По табл.1 для этих значений и можно найти коэффициенты ПИД регулятора: , , . На рис. 5.86 приведен также отклик на единичный скачок той же системы при параметрах , , , полученных путем ручной подстройки. Как видим, метод Зиглера-Никольса дает параметры, далекие от оптимальных. Это объясняется не только упрощенностью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом исходя из требования к декременту затухания, равному 4, что и дает медленное затухание процесса колебаний.

Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод дает слишком малый запас устойчивости.

Второй метод Зиглера-Никольса (частотный метод) в качестве исходных данных для расчета использует частоту , на которой сдвиг фаз в разомкнутом контуре достигает 180˚, и модуль коэффициента передачи объекта на этой частоте . О методике определении этих параметров см. раздел «Частотная идентификация в режиме релейного регулирования». Зная параметр , сначала находят период собственных колебаний системы , затем по табл.1 определяют параметры регулятора. Точность настройки регулятора и недостатки обоих методов Зиглера-Никольса одинаковы.

Метод CHR

В отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) [Chien] использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20%-ного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса.

CHR метод дает две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (табл. 28), вторая — при наблюдении отклика на внешние возмущения (табл. 29). Какую систему параметров выбирать — зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки, или ослабление внешних воздействий. Если же важно и то, и другое, то необходимо использовать регуляторы с двумя степенями свободы (см. раздел «Принцип разомкнутого управления»).

Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой (5.5).

Табл. 29. Формулы для расчета коэффициентов регулятора по методу CHR, по отклику на внешние возмущения
	Без перерегулирования	С 20%-ным перерегулированием
Регулятор
П		—	—		—	—
ПИ			—			—
ПИД

Примечание. Система обозначений параметров регулятора и формулы соответствует уравнению (5.36).

В методе CHR используются те же исходные параметры и , что и в методе Зиглера-Никольса.

Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.

5.5.3. Ручная настройка, основанная на правилах

Расчет параметров по формулам не может дать оптимальной настройки регулятора, поскольку аналитически полученные результаты основываются на сильно упрощенных моделях объекта. В частности, в них не учитывается всегда присутствующая нелинейность типа «ограничение» для управляющего воздействия (см. раздел «Интегральное насыщение»). Кроме того, модели используют параметры, идентифицированные с некоторой погрешностью. Поэтому после расчета параметров регулятора желательно сделать его подстройку. Подстройку можно выполнить на основе правил, которые используются для ручной настройки. Эти правила получены из опыта, теоретического анализа и численных экспериментов. Они сводятся к следующему [Astrom]:

• увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
• с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
• уменьшение постоянной интегрирования уменьшает запас устойчивости;
• увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.

Перечисленные правила применяются также для регуляторов, использующих методы экспертных систем и нечеткой логики.

Ручную настройку с помощью правил удобно выполнять с применением интерактивного программного обеспечения на компьютере, временно включенном в контур управления. Для оценки реакции системы на изменение уставки, внешние воздействия или шумы измерений подают искусственные воздействия и наблюдают реакцию на них. После выполнения настройки значения коэффициентов регулятора записывают в память ПИД-контроллера, а компьютер удаляют.

Отметим, что применение правил возможно только после предварительной настройки регулятора по формулам. Попытки настроить регулятор без начального приближенного расчета коэффициентов могут быть безуспешными. Сформулированные выше правила справедливы только в окрестности оптимальной настройки регулятора. Вдали от нее эффекты могут быть иными, см. раздел «Классический ПИД-регулятор»

При регулировке тепловых процессов настройка по правилам может занять недопустимо много времени.

5.5.4. Методы оптимизации

Методы оптимизации для нахождения параметров регулятора концептуально очень просты и аналогичны численным методам идентификации параметров объекта (см. раздел «Методы минимизации критериальной функции»). Выбирается критерий минимизации, в качестве которого может быть один из показателей качества или комплексный критерий, составленный из нескольких показателей с разными весовыми коэффициентами. К критерию добавляются ограничения, накладываемые требованиями робастности. Таким путем получается критериальная функция, зависящая от параметров ПИД-регулятора. Далее используются численные методы минимизации критериальной функции с заданными ограничениями, которые и позволяют найти искомые параметры ПИД-регулятора.

Методы, основанные на оптимизации, имеют следующие достоинства:

• позволяют получить оптимальные значения параметров, не требующие дальнейшей подстройки;
• не требуют упрощения модели объекта, модель может быть как угодно сложной;
• позволяют быстро достичь конечного результата (избежать процедуры длительной подстройки параметров).

Однако реализация данного подхода связана с большими проблемами, которые не один десяток лет являются предметов научных исследований. К этим проблемам относится:

• низкая надежность метода (во многих случаях вычислительный процесс может расходиться и искомые коэффициенты не будут найдены);
• низкая скорость поиска минимума для овражных функций и функций с несколькими минимумами.

Тем не менее, методы оптимизации являются мощным средством настройки ПИД-регуляторов с помощью специально разработанных для этого компьютерных программ (см. раздел «Программные средства настройки»).