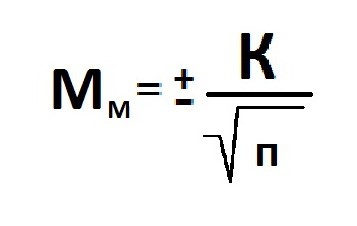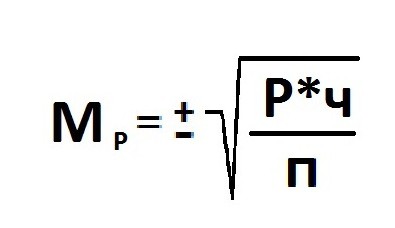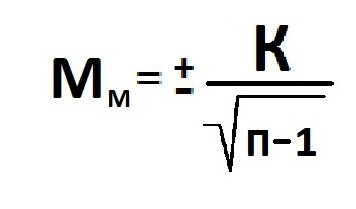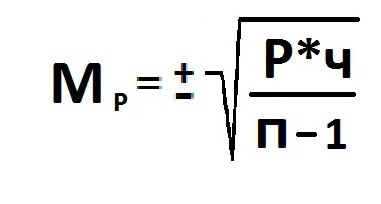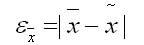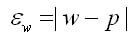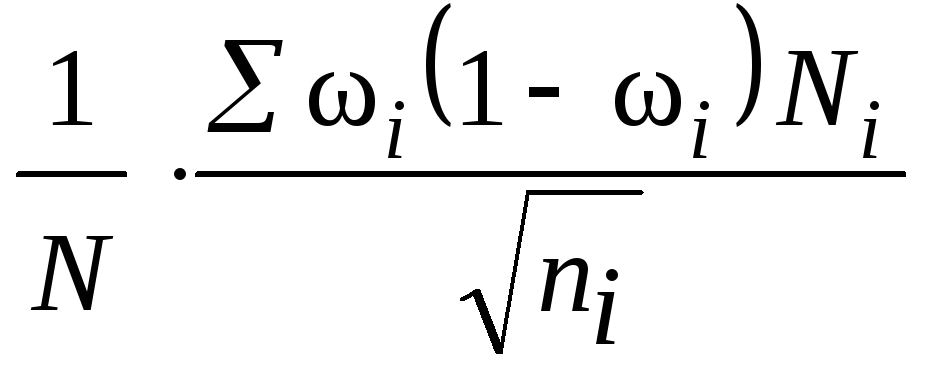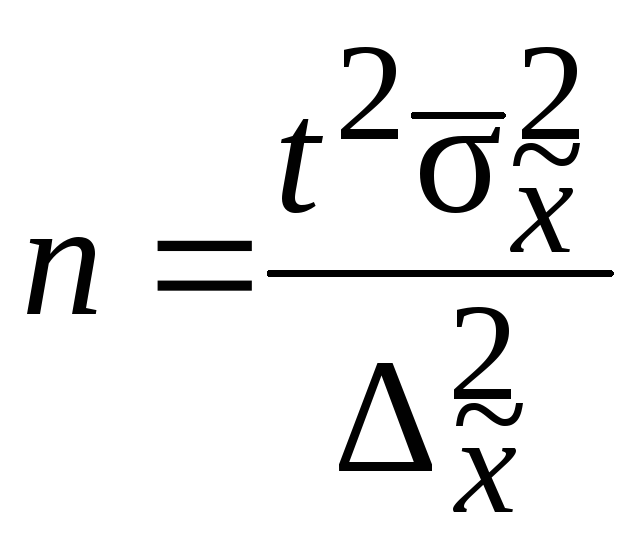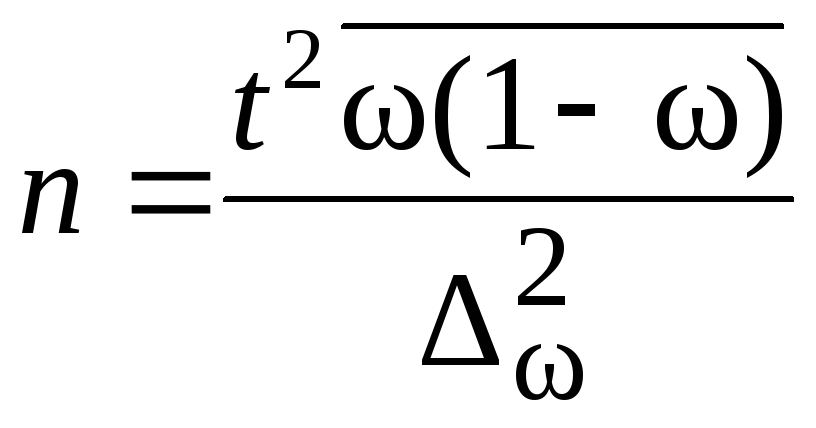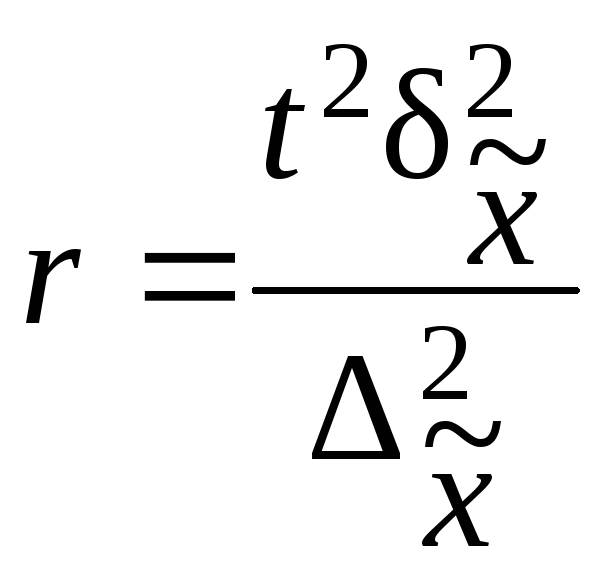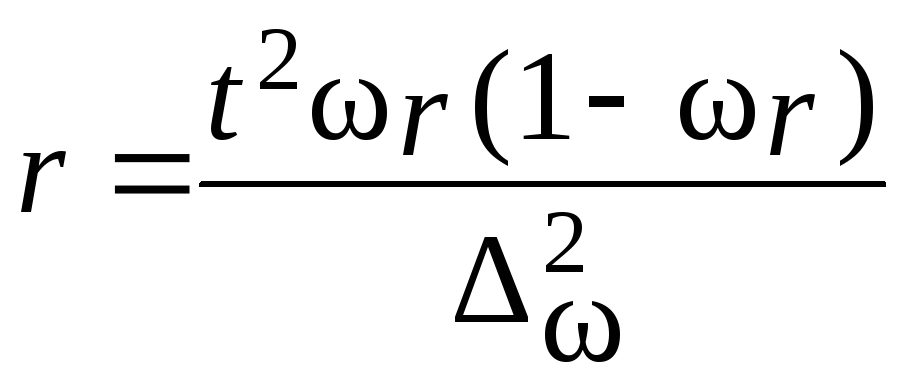В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):

где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):
,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
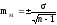

Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
83. Определение доверительных границ средних и относительных величин.
Знание
величины ошибки недостаточно для того,
чтобы быть уверенным в результатах
выборочного исследования, так как
конкретная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
определения точности, с которой
исследователь желает получить результат,
в статистике используется такое понятие,
как вероятность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:
Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безошибочного прогноза 95% равен 2,6;
при вероятности безошибочного
прогноза 99% — 3,0; при вероятности
безошибочного прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы,
в которых с определенной вероятностью
безошибочного прогноза заключено
действительное значение статистической
величины,
характеризующей
всю генеральную совокупность (средней
или относительной).
Для
определения доверительных границ
используются следующие формулы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
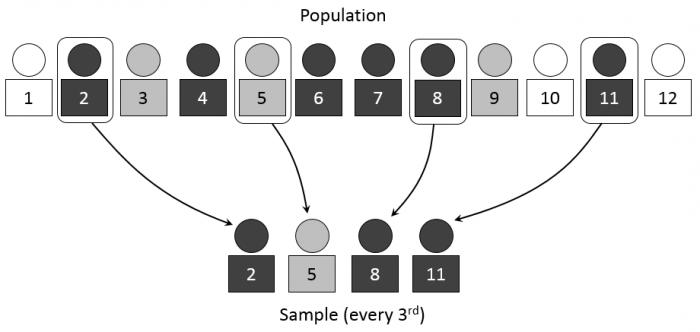
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Ошибки в статистике
Ошибки в статистике (сплошных и выборочных) могут возникнуть ошибки двух видов: репрезентативности и регистрации.
Ошибки репрезентативности характерны только для выборочного наблюдения и возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Они определяются как расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном сплошном наблюдении с одинаковой степенью точности.
Ошибки регистрации могут иметь случайный, систематический и непреднамеренный характер.
Случайные ошибки часто уравновешивают друг друга, так как они не имеют преимущественного направления в сторону преувеличения (преуменьшении) значения изучаемого показателя. Данные ошибки имеют объективный характер и возникают в следствии случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. В результате и структуры этих совокупностей чаще всего не совпадают. Научным обоснованием случайных ошибок являются теория вероятностей и ее предельные теоремы.
Систематические ошибки направлены в одну сторону в результате предумышленного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения.
Ошибка выборки в статистике
Ошибка выборки или ошибка репрезентативности определяется как разница между значением показателя, который был получен по выборке, и генеральным параметром. Она характерна только для выборочных наблюдений. Чем больше значение этой ошибки, тем в большей степени выборочные показатели отличаются от соответствующих им генеральных показателей.
Ошибку выборки часто определяют по формулам:
1. Для среднего количественного признака:
где первое — среднее значение признака в генеральной совокупности или генеральная средняя;
второе — выборочная средняя.
2. Для доли (альтернативного признака):
где w — выборочная доля;
р — генеральная доля, или доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности.
Ошибки выборки возникают вследствие двух причин из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки) и в результате случайного отбора (случайные ошибки). Выборки являются случайными величинами и могут принимать разные значения.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Расхождения
между величиной какого-либо показателя,
найденного посредством статистического
наблюдения, и действительными его
размерами называются ошибками
наблюдения.В зависимости от
причин возникновения различают ошибки
регистрации и ошибки репрезентативности.
Ошибки
регистрациивозникают в результате
неправильного установления фактов или
ошибочной записи в процессе наблюдения
или опроса. Они бывают случайными или
систематическими. Случайные ошибки
регистрации могут быть допущены как
опрашиваемыми в их ответах, так и
регистраторами. Систематические ошибки
могут быть и преднамеренными, и
непреднамеренными. Преднамеренные –
сознательные, тенденциозные искажения
действительного положения дела.
Непреднамеренные вызываются различными
случайными причинами (небрежность,
невнимательность).
Ошибки
репрезентативности(представительности)
возникают в результате неполного
обследования и в случае, если обследуемая
совокупность недостаточно полно
воспроизводит генеральную совокупность.
Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности
– это отклонения, возникающие при
несплошном наблюдении из-за того, что
совокупность отобранных единиц наблюдения
(выборка) неполно воспроизводит всю
совокупность в целом. Систематические
ошибки репрезентативности – это
отклонения, возникающие вследствие
нарушения принципов случайного отбора
единиц. Ошибки репрезентативности
органически присущи выборочному
наблюдению и возникают в силу того, что
выборочная совокупность не полностью
воспроизводит генеральную. Избежать
ошибок репрезентативности нельзя,
однако, пользуясь методами теории
вероятностей, основанными на использовании
предельных теорем закона больших чисел,
эти ошибки можно свести к минимальным
значениям, границы которых устанавливаются
с достаточно большой точностью.
Ошибки
выборки –разность между
характеристиками выборочной и генеральной
совокупности. Для среднего значения
ошибка будет определяться по формуле
(7.1)
где
Величина
называетсяпредельной ошибкойвыборки.
Предельная
ошибка выборки – величина случайная.
Исследованию закономерностей случайных
ошибок выборки посвящены предельные
теоремы закона больших чисел. Наиболее
полно эти закономерности раскрыты в
теоремах П. Л. Чебышева и А. М. Ляпунова.
Теорему П.
Л. Чебышева применительно к
рассматриваемому методу можно
сформулировать следующим образом: при
достаточно большом числе независимых
наблюдений можно с вероятностью, близкой
к единице (т. е. почти с достоверностью),
утверждать, что отклонение выборочной
средней от генеральной будет сколько
угодно малым. В теореме П. Л. Чебышева
доказано, что величина ошибки не должна
превышать.
В свою очередь величина,
выражающая среднее квадратическое
отклонение выборочной средней от
генеральной средней, зависит от
колеблемости признака в генеральной
совокупностии числа отобранных единицn. Эта
зависимость выражается формулой
,
(7.2)
где
зависит также от способа производства
выборки.
Величину
=
называютсредней ошибкой выборки. В
этом выражении– генеральная дисперсия,n– объем
выборочной совокупности.
Рассмотрим, как
влияет на величину средней ошибки число
отбираемых единиц n. Логически
нетрудно убедиться, что при отборе
большого числа единиц расхождения между
средними будут меньше, т. е. существует
обратная связь между средней ошибкой
выборки и числом отобранных единиц. При
этом здесь образуется не просто обратная
математическая зависимость, а такая
зависимость, которая показывает, что
квадрат расхождения между средними
обратно пропорционален числу отобранных
единиц.
Увеличение
колеблемости признака влечет за собой
увеличение среднего квадратического
отклонения, а следовательно, и ошибки.
Если предположить, что все единицы будут
иметь одинаковую величину признака, то
среднее квадратическое отклонение
станет равно нулю и ошибка выборки
также исчезнет. Тогда нет необходимости
применять выборку. Однако следует иметь
в виду, что величина колеблемости
признака в генеральной совокупности
неизвестна, поскольку неизвестны размеры
единиц в ней. Можно рассчитать лишь
колеблемость признака в выборочной
совокупности. Соотношение между
дисперсиями генеральной и выборочной
совокупности выражается формулой
Поскольку
величина
при достаточно большихnблизка к
единице, можно приближенно считать, что
выборочная дисперсия равна генеральной
дисперсии, т. е.
Следовательно,
средняя ошибка выборки показывает,
какие возможны отклонения характеристик
выборочной совокупности от соответствующих
характеристик генеральной совокупности.
Однако о величине этой ошибки можно
судить с определенной вероятностью. На
величину вероятности указывает множитель
Теорема А.
М. Ляпунова. А. М. Ляпунов доказал,
что распределение выборочных средних
(следовательно, и их отклонений от
генеральной средней) при достаточно
большом числе независимых наблюдений
приближенно нормально при условии, что
генеральная совокупность обладает
конечной средней и ограниченной
дисперсией.
Математически
теорему Ляпуноваможно записать
так:

где
,
(7.4)
где – математическая постоянная;
–предельная ошибка выборки,которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.
Значения этого
интеграла для различных значений
коэффициента доверия tвычислены и
приводятся в специальных математических
таблицах. В частности, при:
Поскольку tуказывает на вероятность расхождения,
т. е. на вероятность того, на какую
величину генеральная средняя будет
отличаться от выборочной средней, то
это может быть прочитано так: с вероятностью
0,683 можно утверждать, что разность между
выборочной и генеральной средними не
превышает одной величины средней ошибки
выборки. Другими словами, в 68,3 % случаев
ошибка репрезентативности не выйдет
за пределыС вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает(т. е. в 95 % случаев). С вероятностью
0,997, т. е. довольно близкой к единице,
можно ожидать, что разность между
выборочной и генеральной средней не
превзойдет трехкратной средней ошибки
выборки и т. д.
Логически связь
здесь выглядит довольно ясно: чем больше
пределы, в которых допускается
возможная ошибка, тем с большей
вероятностью судят о ее величине.
Зная выборочную
среднюю величину признака
и предельную ошибку выборки
,
можно определить границы (пределы),
в которых заключена генеральная
средняя
(7.5)
1.
Собственно-случайная выборка–
этот способ ориентирован на выборку
единиц из генеральной совокупности без
всякого расчленения на части или группы.
При этом для соблюдения основного
принципа выборки – равной возможности
всем единицам генеральной совокупности
быть отобранным – используются схема
случайного извлечения единиц путем
жеребьевки (лотереи) или таблицы случайных
чисел. Возможен повторный и бесповторный
отбор единиц
Средняя ошибка
собственно-случайной выборки
представляет собой среднеквадратическое
отклонение возможных значений выборочной
средней от генеральной средней. Средние
ошибки выборки при собственно-случайном
методе отбора представлены в табл. 7.2.
Таблица 7.2
|
Средняя ошибка |
При отборе |
|
|
повторном |
бесповторном |
|
|
Для средней |
|
|
|
Для доли |
|
|
В таблице
использованы следующие обозначения:
– дисперсия выборочной совокупности;
– численность выборки;
– численность генеральной совокупности;
– выборочная доля единиц, обладающих
изучаемым признаком;
– число единиц, обладающих изучаемым
признаком;
– численность выборки.
Для увеличения
точности вместо множителя
следует
брать множитель
,
но при большой численностиNразличие
между этими выражениями практического
значения не имеет.
Предельная
ошибка собственно-случайной выборки
рассчитывается по формуле
,
(7.6)
где t
– коэффициент доверия зависит от
значения вероятности.
Пример.При
обследовании ста образцов изделий,
отобранных из партии в случайном порядке,
20 оказалось нестандартными. С вероятностью
0,954 определите пределы, в которых
находится доля нестандартной продукции
в партии.
Решение.
Вычислим генеральную долю (Р):
.
Доля нестандартной
продукции:

Предельная
ошибка выборочной доли с вероятностью
0,954 рассчитывается по формуле (7.6) с
применением формулы табл. 7.2 для доли:
С вероятностью
0,954 можно утверждать, что доля нестандартной
продукции в партии товара находится в
пределах 12 % ≤ P≤ 28 %.
В практике
проектирования выборочного наблюдения
возникает потребность определения
численности выборки, которая необходима
для обеспечения определенной точности
расчета генеральных средних. Предельная
ошибка выборки и ее вероятность при
этом являются заданными. Из формулы
и формул средних ошибок выборки
устанавливается необходимая численность
выборки. Формулы для определения
численности выборки (n) зависят от
способа отбора. Расчет численности
выборки для собственно-случайной выборки
приведен в табл. 7.3.
Таблица 7.3
|
Предполагаемый |
Формулы |
|
|
для средней |
для доли |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
2.
Механическая выборка– при этом
методе исходят из учета некоторых
особенностей расположения объектов в
генеральной совокупности, их упорядоченности
(по списку, номеру, алфавиту). Механическая
выборка осуществляется путем отбора
отдельных объектов генеральной
совокупности через определенный интервал
(каждый 10-й или 20-й). Интервал рассчитывается
по отношению,
гдеn– численность выборки,N–
численность генеральной совокупности.
Так, если из совокупности в 500 000 единиц
предполагается получить 2 %-ную выборку,
т. е. отобрать 10 000
единиц, то пропорция отбора составитОтбор
единиц осуществляется в соответствии
с установленной пропорцией через равные
интервалы. Если расположение объектов
в генеральной совокупности носит
случайный характер, то механическая
выборка по содержанию аналогична
случайному отбору. При механическом
отборе применяется только бесповторная
выборка [1, 5–10].
Средняя ошибка
и численность выборки при механическом
отборе подсчитывается по формулам
собственно-случайной выборки (см.
табл. 7.2 и 7.3).
3.
Типическая выборка, при котрой
генеральная совокупность делится по
некоторым существенным признакам на
типические группы; отбор единиц
производится из типических групп. При
этом способе отбора генеральная
совокупность расчленяется на однородные
в некотором отношении группы, которые
имеют свои характеристики, и вопрос
сводится к определению объема выборок
из каждой группы. Может бытьравномерная
выборка– при этом способе из каждой
типической группы отбирается одинаковое
число единицТакой подход оправдан лишь при равенстве
численностей исходных типических групп.
При типическом отборе, непропорциональном
объему групп, общее число отбираемых
единиц делится на число типических
групп, полученная величина дает
численность отбора из каждой типической
группы.
Более совершенной
формой отбора является пропорциональная
выборка. Пропорциональной называется
такая схема формирования выборочной
совокупности, когда численность выборок,
взятых из каждой типической группы в
генеральной совокупности, пропорциональна
численностям, дисперсиям (или комбинированно
и численностям, и дисперсиям). Условно
определяем численность выборки в 100
единиц и отбираем единицы из групп:
– пропорционально
численности их генеральной совокупности
(табл. 7.4). В таблице
обозначено:
Ni– численность типической группы;
dj
– доля (Ni/N);
N– численность
генеральной совокупности;
ni– численность выборки из типической
группы вычисляется:
, (7.7)
n – численность выборки из генеральной
совокупности.
Таблица
7.4
-
Группы
Ni
dj
ni
1
300
0,3
30
2
500
0,5
50
3
200
0,2
20
1000
1,0
100
–
пропорционально среднему квадратическому
отклонению(табл. 7.5).
здесь
i– среднее
квадратическое отклонение типических
групп;
ni
– численность выборки из типической
группы вычисляется по формуле
(7.8)
Таблица
7.5
-
Ni
i
ni
300
5
0,25
25
500
7
0,35
35
200
8
0,40
40
1000
20
1,0
100
–
комбинированно (табл. 7.6).
Численность
выборки вычисляется по формуле
. (7.9)
Таблица 7.6
-
i
iNi
300
5
1500
0,23
23
500
7
2100
0,53
53
200
8
1600
0.24
24
1000
20
6600
1,0
100
При проведении
типической выборки непосредственный
отбор из каждой группы проводится
методом случайного отбора.
Средние ошибки
выборки рассчитываются по формулам
табл. 7.7 в зависимости от способа отбора
из типических групп.
Таблица 7.7
|
Способ |
Повторный |
Бесповторный |
||
|
для |
для |
для |
для |
|
|
Непропорциональный |
|
|
|
|
|
Пропорциональный объему групп |
|
|
|
|
|
Пропорциональный |
|
|
|
|
здесь
– средняя из внутригрупповых дисперсий
типических групп;
– доля единиц, обладающих изучаемым
признаком;
– средняя из внутригрупповых дисперсий
для доли;
– среднее квадратическое отклонение
в выборке изi-й типической группы;
– объем выборки из типической группы;
– общий объем выборки;
–
объем типической группы;
– объем генеральной совокупности.
Численность
выборки из каждой типической группы
должна быть пропорциональна среднему
квадратическому отклонению в этой
группе
.Расчет численности
производится по формулам, приведенным
в табл. 7.8.
Таблица 7.8
|
Повторный |
Бесповторный |
|
|
Для определения |
|
|
|
Для определения |
|
|
4. Серийная
выборка– удобена в тех случаях,
когда единицы совокупности объединены
в небольшие группы или серии. При серийной
выборке генеральную совокупность делят
на одинаковые по объему группы – серии.
В выборочную совокупность отбираются
серии. Сущность серийной выборки
заключается в случайном или механическом
отборе серий, внутри которых производится
сплошное обследование единиц. Средняя
ошибка серийной выборки с равновеликими
сериями зависит от величины только
межгрупповой дисперсии. Средние ошибки
сведены в табл. 7.9.
Таблица 7.9
|
Способ |
Формулы |
|
|
для |
для |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
Здесь
R– число серий в генеральной
совокупности;
r – число
отобранных серий;
– межсерийная (межгрупповая) дисперсия
средних;
– межсерийная (межгрупповая) дисперсия
доли.
При серийном
отборе необходимую численность отбираемых
серий определяют так же, как и при
собственно-случайном методе отбора.
Расчет численности
серийной выборки производится по
формулам, приведенным в табл. 7.10.
Таблица 7.10
|
Повторный |
Бесповторный |
|
|
Для |
|
|
|
Для |
|
|
Пример.В
механическом цехе завода в десяти
бригадах работает 100 рабочих. В целях
изучения квалификации рабочих была
произведена 20 %-ная серийная бесповторная
выборка, в которую вошли две бригады.
Получено следующее распределение
обследованных рабочих по разрядам:
|
Рабочие |
Разряды рабочих |
Разряды рабочих |
Рабочие |
Разряды |
Разряды |
|
1 2 3 4 5 |
2 4 5 2 5 |
3 6 1 5 3 |
6 7 8 9 10 |
6 5 8 4 5 |
4 2 1 3 2 |
Необходимо
определить с вероятностью 0,997 пределы,
в которых находится средний разряд
рабочих механического цеха.
Решение.
Определим выборочные средние по
бригадам и общую среднюю как среднюю
взвешенную из групповых средних:
Определим
межсерийную дисперсию по формулам
(5.25):
Рассчитаем
среднюю ошибку выборки по формуле табл.
7.9:
Вычислим
предельную ошибку выборки с вероятностью
0,997:
С вероятностью
0,997 можно утверждать, что средний разряд
рабочих механического цеха находится
в пределах
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Содержание
- Пример об ошибке репрезентативности
- Ошибки статистического наблюдения и основные приёмы их устранения
- Репрезентативность — что это за процесс? Ошибка репрезентативности
- Репрезентативность — что это?
- Другие определения
- Репрезентативная выборка
- Вероятностная выборка
- Вероятностные выборки
- Выборка потребителей
- Размер выборки
- Понятие ошибки репрезентативности
- Виды ошибок
- Преднамеренные и непреднамеренные ошибки репрезентативности
- Валидность, надежность, репрезентативность. Расчет ошибок
- Репрезентативные системы
Пример об ошибке репрезентативности
Лекция 4.1 Выборочный метод
К настоящему времени Вы заработали баллов: 0 из 0 возможных.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
Генеральная совокупность — вся подлежащая изучению совокупность объектов (наблюдений).
Генеральная совокупность носит гипотетический характер. Она представляет собой совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данных условиях. Даже если бы у нас была возможность провести сплошное исследование всей совокупности признака, все равно в нее не попали бы объекты, которое по какой то причине отсутствуют на текущий момент, но должны были существовать при данных условиях.
Та часть объектов, которая отобрана для непосредственного изучения, называется выборочной совокупностьюили выборкой
Сущность выборочного метода
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности выносить суждение о её свойствах в целом
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть репрезентативной(представительной).
Репрезентативная выборка сохраняет и повторяет структуру генеральной совокупности.
Если две выборки взяты из одной генеральной совокупности, то разница в получаемых оценках (например, средних) будет носить случайный характер, как следствие ошибки репрезентативности
Ошибка репрезентативности возникает по причине того, что мы исследуем не всю совокупность, а только её части (выборки). Мы получаем случайную комбинацию элементов из генеральной совокупности.
Для того, чтобы минимизировать различия однородных (взятых из одной генеральной совокупности) выборок необходимо правильным образом их формировать.
Наилучшим способом формирования репрезентативной выборки является случайный отбор элементов из генеральной совокупности без расчленения на части или группы (случайная выборка).
Пример об ошибке репрезентативности
Рассмотрим следующий пример.
Исследователь задался вопросом: «существуют ли различия в эмпатических способностях между психологами и педагогами?». Для того чтобы это прояснить он набрал две группы испытуемых в соответствии с их профессиональной деятельностью и предложил им заполнить опросник на эмпатические способности. Далее, он рассчитал среднее значение в каждой группе.
В группе психологов среднее составило 23,4 балла, а в группе педагогов 21,1. Таким образом, разница в средних между группами составила2,3 балла (23,4 — 21,1 = 2,3).
Если бы представители этих профессий не отличались по изучаемому признаку, тогда разница в средних равнялась бы нулю.
Однако, можно ли считать эту разницу в 2,3 балла достаточной, чтобы судить о реальных различиях между группами? Может сложится так, что психологи и педагоги по эмпатии в реальности не отличаются (выборки однородны), а разница в 2,3 балла, полученная исследователем носит случайный характер, как ошибка репрезентативности.
Таким образом, мы можем сформулировать две гипотезы:
Гипотезы являются альтернативами по отношению к друг другу. Принятие одной из них как верной влечет за собой исключение «истинности» другой.
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА
Статистическая гипотеза – это любое предположение о виде или параметрах неизвестного закона распределения (закона распределения генеральной совокупности)
В статистике принято формулировать пару гипотез. Первая гипотеза называется нулевой, а вторая – альтернативной.
| Нулевая гипотеза Н0 | Альтернативная гипотеза Н1 |
| 1. 1. Является проверяемой 2. Обычно гипотеза об отсутствии явления (например, различий или зависимости) | Является логическим отрицанием нулевой |
| Поскольку нулевая гипотеза является проверяемой, то её можно отвергать и принимать | Альтернативную гипотезу принимают как следствие отрицания нулевой гипотезы |
пример:
· Н0 (нулевая): Женщины не отличаются от мужчин по среднему уровню развития эмпатических способностей (средние значения равны)
· Н1 (альтернативная): Средний уровень эмпатических способностей выше у женщин по сравнению с мужчинами
пример:
· Н0 (нулевая): Линейная корреляция между самооценкой и тревожностью равна 0
· Н1 (альтернативная): Самооценка отрицательно связана с тревожностью (линейная корреляция меньше нуля / чем выше самооценка, тем ниже тревожность и наоборот)
Вопрос:Какая из двух формулировок соответствует нулевой гипотезе Н0?
· А) между психологами и педагогами нет различий по среднему уровню выраженности эмпатии
· Б) между психологами и педагогами есть различия по среднему уровню выраженности эмпатии
Статистический критерий
Правило, по которому нулевая гипотеза отвергается или принимается, называется статистическим критерием.
Статистика – это специально составленная выборочная характеристика (распределение), у которой есть критическое значение такое, что если верна нулевая гипотеза, то вероятность (α) того, что случайная величина превысит это критическое значение, мала (Кремер Н.Ш., 2004).
Критическое значение делит распределение «нулевой гипотезы» на две области: область допустимых значений и область критических значений
Таким образом, критические значения позволяют исследователю либо принять, либо отвергнуть нулевую гипотезу.
В математической статистике можно подбирать критические значение для разных альфа-уровней (уровней значимости). Чаще всего:
1. Критическое значение, которое выделяет критическую область с вероятностью α
Источник
Ошибки статистического наблюдения и основные приёмы их устранения



Всякое статистическое наблюдение должно быть полным и достоверным. Однако по ряду причин степень точности данных может быть различной.
Все ошибки наблюдения подразделяются на два вида:
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи.
Ошибки регистрации могут возникать как при сплошном наблюдении, так и при несплошном и имеют следующие виды:
Случайные ошибки – это ошибки, которые возникают в результате небрежной описки или невнимательного отношения регистратора при заполнении формуляра (ошибки в подсчёте).
Систематические ошибки – это ошибки, которые искажают сведения по каждой отдельной единице наблюдения в одном и том же направлении.
Систематические ошибки делятся на:
Преднамеренные ошибки (сознательные, тенденциозные ошибки), возникающие в результате сознательного искажения статистической информации. К ним относятся: приписки, неправильные сведения об объёме выпущенной продукции, об остатках сырья и материалов и т. д.
Непреднамеренные ошибки – это ошибки, которые возникают в результате случайных причин, т.е. неумышленно (неисправность измерительных приборов, невнимательность регистратора и т.д.).
Ошибки репрезентативности свойственны несплошному наблюдению. Они возникают в результате выборочного наблюдения, когда отобранная часть единиц совокупности недостаточно полно отражает состав всей изучаемой совокупности.
Ошибки репрезентативности (так же, как и ошибки регистрации) могут быть случайными и систематическими.
Случайные ошибки оцениваются с помощью математических методов.
Систематические ошибки – это отклонения, которые возникают в результате случайного отбора единиц изучаемой совокупности. Их размеры не поддаются количественной оценке.
Для выявления и устранения допущенных при регистрации ошибок применяются следующие методы:
а) внешний контроль;
б) логический контроль;
в) счётный контроль.
При внешнем контроле проверяется: правильность оформления документов; наличие всех необходимых записей, которые предусмотрены инструкцией и т.д.
Логический контроль заключается в проверке ответов на вопросы программы наблюдения путём сопоставления полученных данных с другими источниками.
Сущность счётного (арифметического) контроля заключается в счётной проверке всех итоговых показателей, которые содержатся в отчётности или формуляре исследования. Задачей такого контроля является исправление итогов и отдельных числовых показателей.
В ряде случаев, при счётном контроле данных статистического наблюдения применяется метод балансовой увязки показателей (наличие на начало отчётного периода плюс поступления минус расход должно быть равно наличию на конец отчётного периода). Такой метод применяют: при проверках поголовья скота, при учёте поступления и расхода сырья и материалов и т.д.
Указанные методы проверки достоверности статистического наблюдения позволяют сократить до минимального значения допуск ошибок.
Источник
Репрезентативность — что это за процесс? Ошибка репрезентативности
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Источник
О размере выборки и статистической ошибке измерений подробно написано в статье «Выборка. Размер – не главное. Или главное» . В этой статье будет рассмотрено второе требование к выборке, также обеспечивающее качество исследования – репрезентативность.
Согласно теории выборочного метода, неоднократно подтвержденной практикой, опрашивать всех нет необходимости, а можно опросить лишь часть группы, которая может быть в тысячи раз меньше. Эта маленькая часть называется выборкой (или выборочной совокупностью), а большая группа, которую она представляет, называется генеральной совокупностью.
При этом если выборка сформирована правильно, выводы, полученные на основе изучения выборки, могут быть перенесены и на генеральную совокупность. Например, если в выборке женщины значимо чаще, чем мужчины, пользуются дезодорантами, то делается вывод, что и в генеральной совокупности (например, в исследованном городе) присутствует такая закономерность. Процесс переноса выводов с выборки на генеральную совокупность называется генерализацией. А свойство выборки отражать характеристики генеральной совокупности называется репрезентативностью. Для более комфортного запоминания термина на рис.1. приведены иллюстрации, когда выборка отражает свойства генеральной совокупности и когда свойства выборки отличаются от свойств генеральной совокупности.

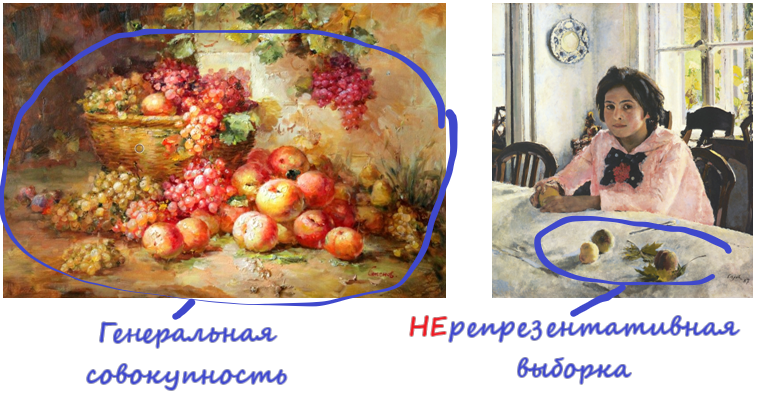
Рис.1. Иллюстративные примеры соответствия (несоответствия) свойств генеральной совокупности и выборки
Не стоит путать понятие репрезентативности с такими понятиями как валидность и релевантность, хотя они тоже относятся к характеристикам качества исследования. В социальных науках валидность понимается довольно широко, но чаще всего – как обоснованность. Понятие валидности относится не к выборке, а к исследовательской методике. Методика или измерение (анкета, блок вопросов, тест) считается валидным, если фиксирует именно то понятие или свойство, которое планируется измерить. Например, если мы захотим оценить уровень лояльности клиента к магазину и выберем для этого лишь показатель частоты посещения магазина, валидность этого подхода будет неполной: возможно, респондент часто заходит в магазин только из-за банкомата, который там установлен. Валидная методика в данном примере должна включать и другие показатели: предпочтение магазина, суммы покупок в этом и других магазинах, готовность переключиться на другие магазины, готовность рекомендовать магазин и др.
При установлении валидности решающую роль играет обоснование и последующая проверка гипотезы релевантности, то есть соответствия измеряемых параметров характеристикам исследуемого объекта. Житейский пример нерелевантности – измерять уровень счастья человека количеством денег у него (хотя, наверное, не все с этим согласятся). Очевидный пример нерелевантности – попытка измерить массу тела по его температуре.
Но вернемся к понятию репрезентативности. В то время как точность измерений зависит от размера выборки, размер выборки не гарантирует ее репрезентативности. Репрезентативность выборки главным образом обеспечивается способом отбора ее участников (респондентов). Примером явного нарушения репрезентативности может послужить шутка о том, что интернет-опрос показал, что 100% людей пользуется интернетом.
Можно выделить несколько вариантов нарушения репрезентативности выборки: когда опрошены не те люди и когда опрошено слишком много (или мало) определенных людей (например, женщин намного больше, чем мужчин). Кроме того, чем меньше размер выборки, тем меньше вероятность того, что она будет репрезентативной. Например, допустим, 1% населения мог бы заинтересоваться новой услугой. Это 1 из 100 людей. Если размер выборки составляет всего 60 человек, то в вашей выборке может отсутствовать человек, который, скорее всего, будет заинтересован в услуге. Ваша выборка менее репрезентативна, потому что она меньше. Ваши результаты будут разными в зависимости от того, содержит ли ваша выборка одного из этих людей или нет. Пример репрезентативной и нерепрезентативной выборки показан на рис.2.
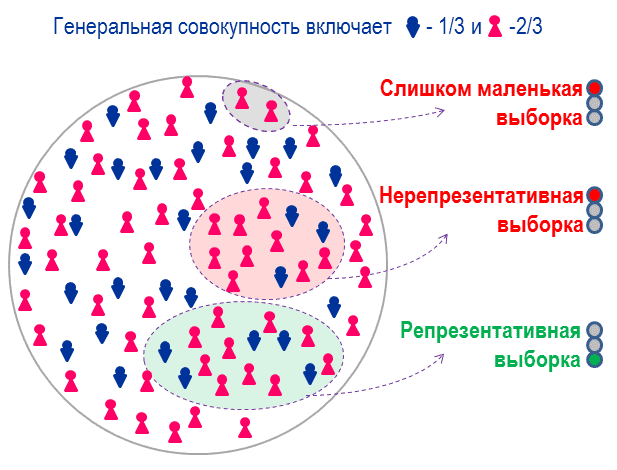
Рис.2. Пример репрезентативной и нерепрезентативной выборки
На рис.3 показана та же по составу генеральная совокупность, но с другим расположением объектов внутри круга.
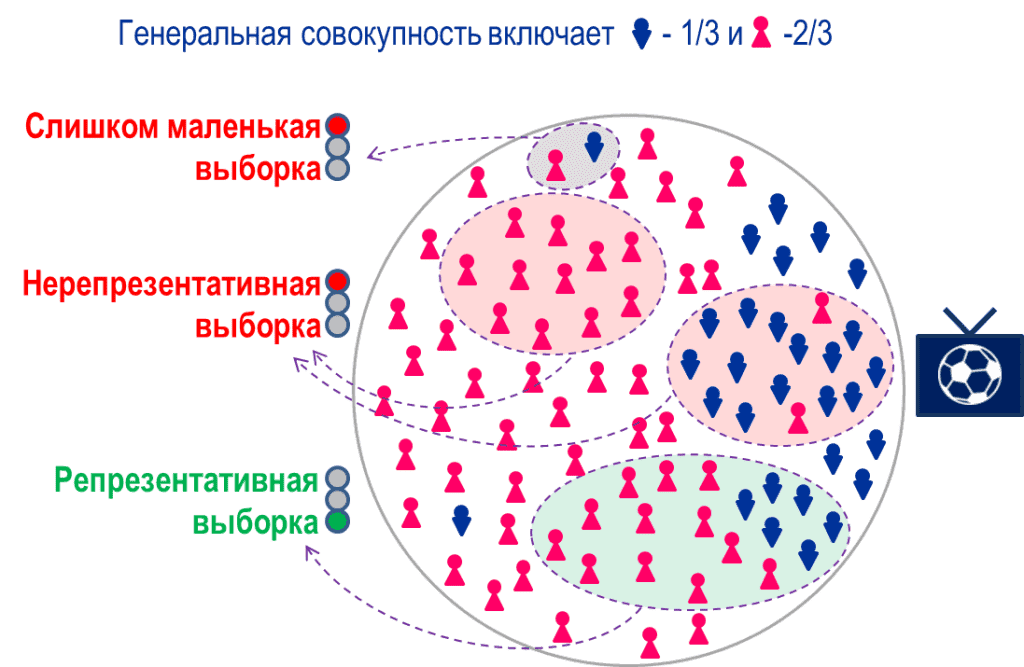
Рис.3. Пример репрезентативной и нерепрезентативной выборки при другом расположении объектов генеральной совокупности
Говоря простым языком, репрезентативная выборка – это такая выборка, в которой представлены все подгруппы, важные для исследования. Помимо этого, характер распределения рассматриваемых параметров в выборке должен быть таким же, как в генеральной совокупности.
Простой случайный отбор респондентов представляется оптимальным способом формирования репрезентативной выборки. Поскольку в этом случае у любого представителя генеральной совокупности одинаковая вероятность попасть в выборку, в нее попадут люди с разными характеристиками пропорционально их долям в генеральной совокупности. В итоге выборка будет представлять собой нечто вроде уменьшенной копии генеральной совокупности.
Случайность отбора респондентов в выборку обеспечивается разными способами. Например, для телефонного опроса жителей города берется база данных всех телефонных номеров, и номера респондентов случайным образом выбираются компьютером (с использованием генератора случайных чисел). При уличном опросе интервьюеров распределяют по случайно выбранным точкам и инструктируют опрашивать каждого N-ного прохожего.
Наглядным примером репрезентативной выборки может служить пицца. Если целая пицца – это генеральная совокупность, которую мы хотим изучить, то кусок пиццы – это выборка. Как правило, достаточно одного куска пиццы, чтобы судить обо всей пицце (при условии, что ингредиенты равномерно распределены по ее поверхности). Таким образом, кусок пиццы пиццы на рис.4 – это репрезентативная выборка из пиццы.

Рис.4. Наглядный пример репрезентативной выборки (пицца)
Важно отметить, что не любой кусок пиццы будет репрезентативной выборкой. Разные способы получения куска пиццы могут принципиально повлиять на качество исследования и выводы, которые будут получены при анализе каждого варианта выборки (рис.4)
(рисунок в сушильной камере, готовится к публикации)
Рис.5. Наглядный пример формирования репрезентативной и нерепрезентативной выборки.
Еще один показательный пример формирования репрезентативной выборки – кастрюля, содержимое которой мы должны узнать (допустим, там скрывается борщ). Мы только один раз можем зачерпнуть из кастрюли ложкой (провести исследование). В нашем примере ложка – это выборка, а содержимое кастрюли – генеральная совокупность.
Если мы зачерпнем сверху, то придем к выводу, что в кастрюле бульон. Если снизу – решим, что в кастрюле мясо. Зачерпнув где-то посередине, мы получим картошку или капусту. В любом из трех случаев выводы будут неверны. Чтобы получить достоверный результат, нам стоит хорошенько перемешать содержимое кастрюли, перед тем как пробовать его. Перемешивание в данном случае – аналог процедуры простого случайного отбора, поскольку оно предоставляет всем ингредиентам примерно равную вероятность попадания в ложку-выборку (или тарелку-выборку).

Рис.6. Борщ как модель, демонстрирующая репрезентативность выборки.
В реальности применить простой случайный отбор респондентов не всегда удается в полной мере. Например, мы можем абсолютно корректно отобрать в выборку нужное количество номеров домашних телефонов случайным образом, но при их прозвоне выяснится, что дозвониться и поговорить удается преимущественно с пенсионерами, а «поймать» дома молодежь и работающих людей получается плохо.
Возвращаясь к примеру с борщом, если у нас вместо кастрюли – огромный ресторанный котел, а в руках все та же обычная ложка, перемешивание будет неэффективным. Чтобы решить задачу, потребуются иные подходы. Например, мы можем теоретически разделить глубину котла на несколько слоев и постараться зачерпнуть содержимое из каждого слоя (из случайного места слоя: не только в центре, но и по краям). Таким образом, наша итоговая выборка будет состоять уже из нескольких выборок и при этом адекватно отражать содержимое всех слоев котла. Подобные альтернативные подходы называются типами выборки, которых придумано достаточно много для того, чтобы максимизировать репрезентативность выборки в сложных условиях реального мира.
Последствия нарушения репрезентативности выборки: некорректные выводы исследования, выброшенный на ветер бюджет исследования, финансовые потери вследствие применения неправильных выводов. Вы можете выбрать валидную исследовательскую методику, рассчитать объем выборки, обеспечивающий приемлемую точность измерений, но, если выборка исследования нерепрезентативна, получить достоверную информацию не удастся.
ПРИМЕРЫ НАРУШЕНИЯ РЕПРЕЗЕНТАТИВНОСТИ ВЫБОРКИ
ПРЕДВЫБОРНЫЙ ОПРОС
Самым известным примером нарушения репрезентативности выборки является история провала американского журнала «Литературный дайджест».
В 1936 году журнал в очередной раз провел почтовый опрос общественного мнения о вероятных результатах грядущих президентских выборов в США. До 1936 года опрос всегда правильно предсказывал победителя. Опрос 1936 года показал, что победителем с большим отрывом станет кандидат от республиканцев, но в итоге победителем оказался представитель демократов.
Таким образом, гигантская выборка (около 2,4 млн. человек) не обеспечила достоверных результатов. В чем же заключалась причина ошибки?
Называются две основные причины провала: смещение при формировании выборки и смещение вследствие отказа респондентов от участия в опросе.
Прежде всего, журнал включил своих подписчиков в список для рассылки анкет и, желая расширить выборку, использовал два других доступных тогда списка граждан: зарегистрированных автовладельцев и пользователей телефонов. Во времена Великой Депрессии представители этих групп отличались от остального населения более высоким доходом, как и подписчики самого журнала. Таким образом, полученная база для рассылки не являлась корректным отражением структуры населения США.
Вторая проблема с опросом заключалась в том, что из 10 миллионов человек, чьи имена были в первоначальном списке рассылки, только 2,4 миллиона ответили на опрос. Вероятно, высокий процент отказов был связан с тем, что опрос проводился по почте. Уже в те времена американцы относились к почтовым рассылкам как к спаму. Таким образом, размер выборки составил примерно одну четверть от того, что первоначально планировалось. Когда доля ответивших низка (как это было в данном случае), считается, что исследование страдает от необъективности ответов.
У этой истории две морали: Большая, но неправильно сформированная выборка гораздо хуже маленькой, но правильно сформированной выборки. При проведении опроса не упускайте из внимания смещение отбора и смещение в результате отказов.
СИСТЕМАТИЧЕСКАЯ ОШИБКА ВЫЖИВШЕГО
Пример из военной практики. Во Вторую мировую войну американские военные столкнулись со следующей проблемой. Не все американские бомбардировщики после задания возвращались на базу. На вернувшихся самолетах оставалось множество пробоин от выстрелов противника, но распределены они были неравномерно: больше всего на фюзеляже и прочих частях, меньше в топливной системе и гораздо меньше — в двигателе. Командованию казалось логичным, что в наиболее поврежденных местах нужно установить больше брони.
Привлеченный к решению задачи математик возразил: данные как раз показывают, что самолет, получивший пробоины в этих местах, еще может вернуться на базу. А самолет, которому попали в бензобак или двигатель, выходит из строя и не возвращается. Поэтому укреплять следует те места, которые у вернувшихся самолетов повреждены меньше всего.
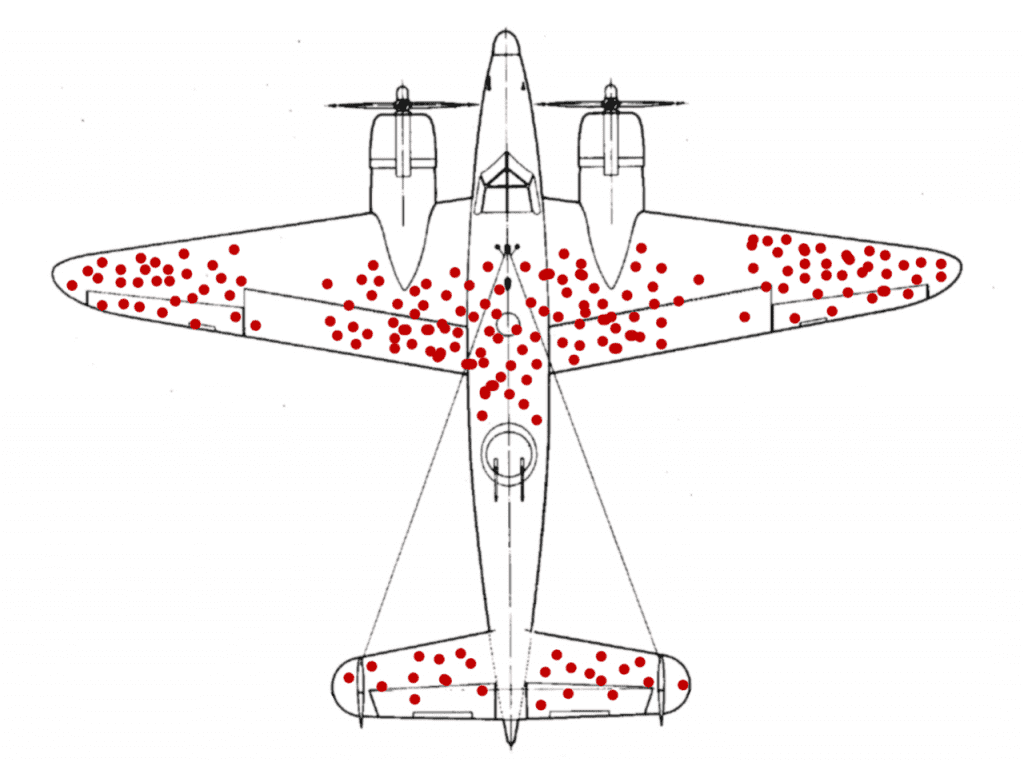
Рис .7. Пробоины на вернувшихся самолётах.
Получившие повреждения в других местах не смогли вернуться на базу
Эта задача служит примером нарушения репрезентативности выборки, когда в нее включены не те респонденты: в данном случае, вернувшиеся самолеты, в то время как не вернувшиеся проигнорированы.
Применительно к маркетинговым исследованиям, эта ситуация подобна следующей. При опросе клиентов бизнеса будет ошибкой опрашивать только текущих клиентов и не опрашивать потерянных клиентов (а какие «пробоины» получили они?).
НЕПРАВИЛЬНЫЕ МЕСТА ОПРОСА
При опросе посетителей ТРЦ важно правильно расставить интервьюеров. Например, если поставить интервьюеров только у главного входа, в выборку не попадут посетители, приехавшие в ТРЦ на автомобиле и попавшие в него через парковку. Как следствие, выводы, полученные на собранных данных, будут корректны только для той части посетителей, которые приходят в ТРЦ пешком, а значит, делают меньше покупок, не покупают габаритные товары, живут ближе к ТРЦ, чем приезжающие на автомобиле.
ОТСУТСТВИЕ КВОТИРОВАНИЯ
Другой пример. Бывает, что в разных районах города сбор анкет идет с разной скоростью: где-то (например, в центре города) большой пешеходный поток и у людей есть время на участие в опросе (отдыхающие, в отпуске, офисные сотрудники на обеде), а на окраинах либо мало людей на улицах, либо все спешат на работу и отказываются участвовать. В результате, если не ограничивать доли районов, в выборке будут преобладать люди из центрального района, которые могут значимо отличаться от остальных людей родом занятий, уровнем дохода и образования, уровнем осведомленности о магазинах и др. Таким образом, собранная выборка уже не будет репрезентативной по отношению к населению всего города.
ОНЛАЙН-ОПРОСЫ (ОНЛАЙН-ПАНЕЛИ)
Несмотря на многие положительные стороны онлайн-опросов, такие как экономичность, оперативность сбора информации, удобство ее обработки и т. д., некоторые их особенности напрямую угрожают репрезентативности исследования:
Во-первых, участники онлайн-опросов – это, как правило, активные пользователи интернета, хорошо в нем разбирающиеся и больше подверженные влиянию интернет-культуры, чем обычные люди.
Во-вторых, люди, у которых есть время и желание регулярно участвовать в онлайн-опросах за небольшое вознаграждение, скорее всего, значительно отличаются от остальных людей как по социально-демографическим, так и по психографическим характеристикам.
В-третьих, профессиональное участие в опросах приводит к так называемой профессиональной деформации, когда ответы респондентов на вопросы новых исследований обусловлены предыдущим опытом, но не жизненным, а опытом участия в других опросах.
Таким образом, в данном случае возникает та ситуация, когда опрашиваются не те люди, хотя по формальным характеристикам они подходят под описание целевой аудитории.
ВЫВОДЫ
Итак, чтобы получить достаточно точные данные об интересующей нас группе людей, необязательно опрашивать их всех, благодаря свойству репрезентативности выборки.
«Чем больше, тем лучше» – неправильный подход к формированию выборки.
Небольшая репрезентативная выборка лучше большой, но нерепрезентативной выборки. Применительно к выборке не стоит пугаться слова «случайная». Это вовсе не значит, что в исследовании будут получены случайные результаты. Напротив, случайный подход к формированию выборки делает ее максимально похожей на генеральную совокупность, а значит, репрезентативной.
При проектировании выборки следует учитывать опасность смещения структуры выборки вследствие особенностей сбора информации и других условий.
Вы можете подписаться на уведомления о новых материалах СканМаркет