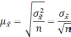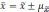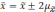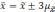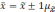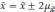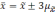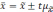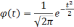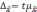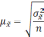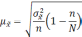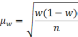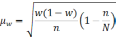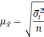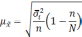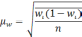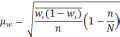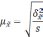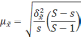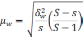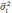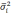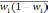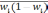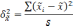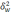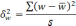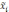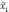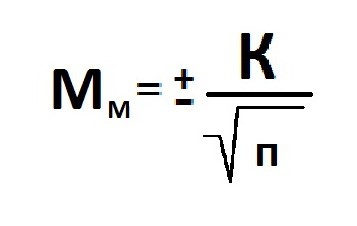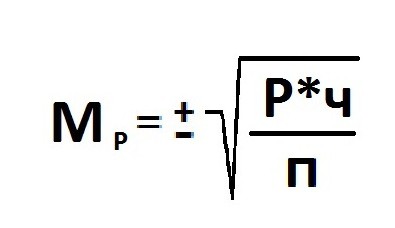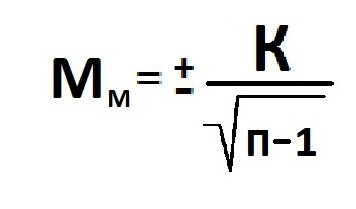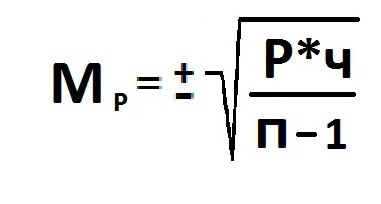Ошибка
репрезентативности
— расхождение между выборочной
характеристикой и характеристикой
генеральной совокупности.
Ошибки
репрезентативности
-
Систематические
— возникают в результате нарушения
научных принципов отбора единиц
совокупности (преднамеренные и
непреднамеренные). -
Случайные
возникают в результате несплошного
характера наблюдения (средняя и
предельная ошибки выбора).
Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.
Средняя
ошибка выборки
— такое расхождение между средними
выборочной и генеральной совокупностями,
которое не превышает ±.
В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:
Формула
для определения величины средней ошибки
выборки для количественного признака:
Формула
для определения величины средней ошибки
выборки для альтернативного признака:
Полученное
значение средней ошибки необходимо для
установления возможного значения 
Которое определяется по формуле:
Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.
В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

вероятность достигает 0,954 (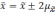
Если утроить значение то вероятность
увеличится до 0,997 (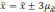
|
Возможное |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:
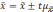
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:
На
практике пользуются готовыми таблицами
этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 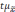
Полученную величину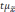
ошибкой выборки.
Предельная
ошибка выборки
—
максимально
возможное расхождение выборочной и
генеральной средних,
т.е.
максимум ошибки при заданной вероятности
ее появления.
Предельная
ошибка выборки для количественного
признака:
Предельная
ошибка выборки для альтернативного
признака:
В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:
|
Способ |
Оцениваемый |
Повторный |
Бесповторный |
|
Собственно случайный механический |
Средняя |
|
|
|
Доля |
|
|
|
|
Типический |
Средняя |
|
|
|
Доля |
|
|
|
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
— средняя из групповых дисперсий;
wi
— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;
— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S
– общее число серий;
s
– число отобранных серий;
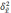
межгрупповая дисперсия средних,
определяемая по формуле:
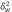
межгрупповая дисперсия доли, определяемая
по формуле:
— средняя
i-й
серии;
—
средняя по всей выборочной совокупности;
w
— доля признака i-й
серии;
— общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
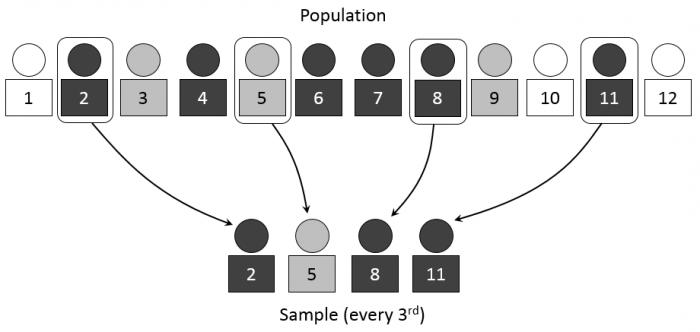
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Ошибка
репрезентативности –
это отклонение значения показателя
обследований совокупности от его
величины по исходной совокупности.
Такие ошибки характерны только для не
сплошного наблюдения. Возникают потому,
что отобранная и обследованная
совокупность недостаточно точно
воспроизводит (репрезентирует) всю
исходную совокупность в целом. Также
бывают случайными и систематическими.
Систематическими
называются ошибки репрезентативности,
которые возникают из-за нарушения
научного принципа отбора единиц в
выборочную совокупность. Они возникают
в тех случаях, когда в результате
неправильной организации отбора в
выборочную совокупность попали
преимущественно наилучшие или наихудшие
в отношении того или иного признака
единицы.
Случайные
ошибки репрезентативности –
это неточности, которые возникают из-за
того, что выборочная совокупность не
совсем правильно воспроизводит структуру
генеральной совокупности.
Ошибки
репрезентативности свойственны только
выборочному наблюдению. Они не могут
быть полностью устранены, но они могут
быть доведены до незначительных размеров.
Так как случайная ошибка выборки
возникает в результате случайных
различий между единицами выборочной и
генеральной совокупности, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
ошибку выборки и предельную ошибку
выборки. Под средней ошибкой выборки
понимают такое расхождение между средней
выборочной и средней генеральной
совокупностями ,
которое не превышает.
Измерения
рассматриваются с двух точек
зрения: количественной,
выражающей числовое значение измеренной
физической величины и качественной,
характеризующей точность измерения.
Результаты измерений не являются точным
значением измеряемой величины, а
несколько отличаются (отклоняются) от
него. Отклонение измеренной величины
ℓ от ее истинного (точного) значения Х
называется истинной
ошибкой
или погрешностью измерения и обозначается
D. Ошибки всегда имеют величину и знак
плюс или минус. Величина ошибки показывает
на сколько измеренное значение отклонилось
от истинного; знак — в какую сторону
произошло отклонение. Ошибки характеризуют
точность измерения, т.е. степень близости
измеренной величины к ее истинному
значению. Чем меньше ошибка, тем точнее
измерение. На результат измерения
оказывают влияние многие факторы и
каждый из них порождает свою часть общей
ошибки. Ошибки, происходящие от отдельных
факторов, называют элементарными. Х
— ℓ = D или ℓ — Х = D (1) Ошибка (погрешность
) результата измерения является
алгебраической суммой элементарных
ошибок: [D] = D1 +
D2 +
D3 +
… + Dn (2)
Квадратные скобки означают знак суммы
( ввел Гаусс). Ошибки различают по двум
признакам: по источнику возникновения
(происхождения) и по характеру действия. По
источнику возникновения ошибки
подразделяют на приборные (инструментальные),
методические, личные и внешние. Приборные или
инструментальные ошибки обусловлены
неточным изготовлением и сборкой
отдельных деталей и узлов приборов,
неточной установкой их во время измерений
и др. причинами. Методические ошибки
возникают из-за несоблюдения методики
измерений. Личные ошибки связаны
с особенностями органов зрения человека
выполняющего измерения (наведение
зрительной трубы на удаленный предмет,
оценку доли наименьшего деления шкалы
«на глаз»каждый человек делает по-
разному). Внешние ошибки возникают
из-за воздействия внешней среды в которой
производятся измерения: температура,
давление и влажность воздуха; неравномерное
нагревание солнцем отдельных частей
приборов; степень освещенности; ветер,
турбулентность воздуха и др. По
характеру действия ошибки разделяют
на систематические и случайные.
Кроме того, результаты измерений могут
содержать грубые
ошибки. Грубыми
считают ошибки, превосходящие по
абсолютной величине некоторый
установленный предел. Они появляются
главным образом в результате промахов
и просчетов из-за невнимательности или
недостаточной квалификации (опытности)
исполнителя. Их выявляют путем повторных
(контрольных) измерений. Измерения,
содержащие грубые ошибки, не берут в
дальнейшую обработку, бракуют и заменяют
новыми. С целью выявления грубых ошибок
все геодезические измерения выполняют
с контролем, не менее двух раз: углы
измеряют при двух положениях теодолита;
длины линий — в прямом и обратном
направлениях; превышения — по двум
сторонам рейки и в прямом и обратном
ходах. Систематическими называют
ошибки, которые по знаку или величине
однообразно повторяются в многократных
измерениях какой-либо величины. Для их
выявления считают число положительных
и отрицательных ошибок и их сумму. При
отсутствии систематической части общей
ошибки число ошибок с разными знаками
примерно одинаковое и суммы их также
примерно равны между собой. Они возникают
из-за приборных, методических, личных
и внешних факторов. Например, несоответствие
фактической длины мерного прибора
указанному на нем. Систематические
ошибки различают по характеру проявления.
Они могут быть: а) переменные, прогрессивного
типа; б) односторонне действующие; в)
периодические; г) постоянные; д) смешанные.
Систематические ошибки прогрессивно
типа в процессе измерений возрастают
или убывают. Такого рода ошибки возникают,
например , при измерении линий стальной
лентой, длина которой больше или меньше
номинальной. Если ряд ошибок с переменными
абсолютными значениями искажен в одном
и том же направлении, то такой ряд ошибок
называется систематическим и
односторонним по знаку. Систематические
ошибки периодического характера
соответственно изменяют знак и величину.
Подобные ошибки возникают, например,
при измерении углов теодолитом, в котором
имеется эксцентриситет алидады. Если
при многократных измерениях ошибки
остаются неизменными как по абсолютному
значению, так и по знаку, то такие ошибки
называютсяпостоянными.
Так при многократном измерении угла
теодолитом имеет место одна и та же
ошибка за центрировку. При измерении
линий больше длины мерной ленты возникает
постоянная ошибка одинаковая на каждом
уложении ленты. Постоянная ошибка
является частным выражением систематической
ошибки.Знание причин возникновения
систематических ошибок позволяет
заранее принять меры по исключению их
из результатов измерений или уменьшению.
Систематические ошибки характерны тем,
что поддаются учету. Они могут быть
исключены или сведены к минимуму путем
тщательной проверки измерительных
приборов, изменением методики измерений,
предупреждением влияния внешних
факторов. Но несмотря на это общая ошибка
всегда содержит остаточную часть
систематической ошибки, хотя она и мала
по сравнению со случайной ошибкой. В
ряду измерений всегда имеется остаточная
часть ошибки. Случайными называют
ошибки, размер и влияние которых на
результат измерения неизвестны, величину
и знак их заранее определить нельзя.
Случайная величина – это переменная
величина, конкретное значение которой
зависит от случая, она может быть, а
может и не быть. Случайными ошибки
называют потому, что в ряду измерений
каждая последующая ошибка по абсолютной
величине может быть больше или меньше
предыдущей, иметь знак плюс или минус
и по предыдущим членам такого ряда
нельзя установить, какой именно будет
следующий за ним член ряда. Тем не менее,
случайные ошибки подчинены статистическим
закономерностям, называемых свойствами.
Чем больше число измерений войдет в ряд
их, тем резче выявится статистическая
закономерность. Знание свойств дает
возможность получить наиболее надежный
результат из ряда (нескольких) измерений,
а также оценить его точность.
33.
По данным распределения начертить
вариационную кривую. Предположим, нами
просчитано число зацепок на левом заднем
крыле у 100 экземпляров рабочих пчел
данного улья. Получены такие цифры: 21,
20, 18, 19, 24, 22 и так далее. Можно подсчитать,
сколько же раз попались пчелы с числом
зацепок 18, сколько с 19 зацепками и т. д.
Сделав это для всех 100 пчел.
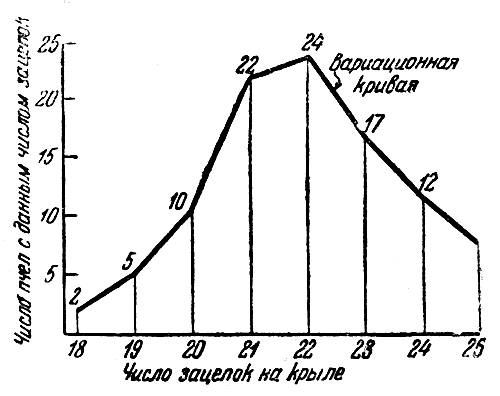
Число
зацепок в крыле-18 19 20 21 22 23 24 25
Число
пчел с данным числом зацепок- 2 5 10 22 24
17 12 8
Число
зацепок в крыле-18 19 20 21 22 23 24 25, а число
пчел с данным числом зацепок- 2 5 10 22 24
17 12 8. Видно, что пчел с 18 зацепками была
две, с 19 — пять и т. д. Вариационный ряд
можно изобразить графически. На
горизонтальной оси помечено число
зацепок, а над соответственным числом
зацепок в виде вертикальной черты
изображено приходящееся сюда число
случаев. Если соединить вершины
вертикальных линий друг с другом, то
получится ломаная линия, которая носит
название вариационной кривой (см. рис.
2).
Рис.
2. Вариационная кривая числа зацепок на
заднем крыле рабочих пчел.
Первой
и основной характеристикой вариационного
ряда является среднее арифметическое.
Чтобы его получить, надо сложить все
100 чисел, характеризующих зацепки крыльев
вышеприведенной семьи пчел — +21 +20 +18 и
т. д., и сумму разделить на 100. Если наш
материал уже классифицирован в
вариационный ряд, для быстроты можно
заменить сложение умножением каждой
цифры, показывающей число случаев, на
стояющую над ней величину. Все эти
произведения надо просуммировать и
разделить на 100.
Среднее
арифметическое условно принято обозначать
буквой М.
В
нашем примере вычисление дает следующее:
М
= (2,18 + 5,19 + 10,20 + 22,21 + 24,22 + 17,23 + 12,24 +
8,25)/100=22,00
Кроме
вопроса о среднем арифметическом ряде,
его типе, ибо свойство М таково, что оно
является центром, вокруг которого налево
и направо распределяется одинаковое
количество отдельных случаев (При
так называемом «нормальном» распределении ),
может возникнуть вопрос, насколько
сильно рассеиваются вокруг типа отдельные
случаи. Раньше для учета этого явления
пользовались указанием размеров самого
мелкого и самого крупного экземпляра
вариационного ряда. В нашем примере
указали бы границы 18—25.
Теперь
же по ряду соображений принято пользоваться
так называемым стандартным отклонением
и коэффициентом изменчивости или
вариации.
Получаются
эти величины так. Возьмем в нашем примере
пчел с 18 зацепками. Каждая отклоняется
от М на 4 зацепки. Квадрат четырех 16. Так
как таких пчел две, то для них имеем
16х2=32.
Хотя
отклонение было с отрицательным знаком,
но вследствие возведения в квадрат
отрицательные знаки уничтожаются. Для
пчел с 19 зацепками имеем 3х3х5 = 45. Суммируя
все таким образом найденные произведения,
деля сумму на число всех случаев — 100,
получаем среднее квадратическое
уклонение, а извлекши из него квадратный
корень, получаем стандартное отклонение
(стандарт по-английски — тип), обозначаемое
греческой буквой σ (сигма). Для нашего
примера имеем:
σ
= ± √ (16,2 + 9,5 + 4,10 + 1,22 + 1,17 + 4,12 + 9,8)/100 = ±
√2,76 = ± 1,661 зацепок.
Сигма
— величина именованная и выражается в
тех же единицах как изучаемый признак.
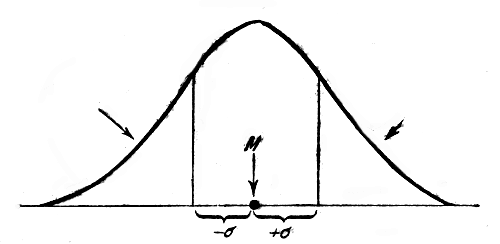
Геометрический смысл сигмы таков. Если
взять много материала (например 1000 пчел)
и по вышеизложенному начертить
вариационную кривую, то она будет весьма
плавно подниматься и перегибаться над
М. Если отложить налево и направо от М
по отсеку, равному сигме, то место
перехода каждой ветви кривой из вогнутой
в выпуклую будет как раз приходиться
над наружными точками сигм (см. рис. 3).
Рис.
3. Схема, поясняющая положение перелома
ветвей нормальной кривой над точками,
лежащими на расстоянии одной сигмы от
среднего арифметического.
Ясно,
что чем больше сигма, тем дальше будут
эти точки находиться от М, тем уплощеннее
будет кривая, тем больше будет рассеянность
отдельных особей вокруг типа.
Для
возможности сравнивать изменчивость
признаков, выражаемых разными единицами
измерений и дающих ряды с различной
величиной М, придумали характеристику
отвлеченную. Ее находят, выражая сигму
ряда в процентах среднего арифметического
данного ряда по формуле
С%
= (σ•100)/М = (1,661•100)/22 = 7,54%.
Это
— коэффициент вариации или коэффициент
изменчивости.
Так
вычисляют средние арифметические и
стандартные отклонения для признаков
счетных (число зацепок, число яйцевых
трубочек и т. д.). Несколько иначе
поступают, когда приходится иметь дело
с признаками, получаемыми путем измерений,
взвешиваний и т. д. При этом признаки
особей пчел или целых семей выражаются
не целыми числами, а числами с дробями
(например 25,1 кг меда с семьи и т. д.). В
этом случае при составлении вариационного
ряда: и вариационной кривой составляют
шкалу классов и разносят по классам
измерения особей или семей. Возьмем в
качестве примера определения, времени
остановки движения 15 особей пчел,
помещенных в атмосферу паров серного
эфира. Цифры в минутах и долях минуты
таковы: 6,25; 8,5; 5,0; 8,0; 6,25; 6,5; 3,5;, 6,5; 4,25; 4,4;
4,8; 7,8; 5,25; 5,75 и 6,7. Сперва надо наметить
пределы вариации: 3,5 до 8,5 минут.
Предположим, что мы хотим создать классы
величиной в 2 минуты. Toгда шкала классов
будет такова: 3—5—7—9. Всего у нас будет
три класса. Для того чтобы на границу
класса не попал ни один случай, припишем
к каждой границе 0,01. Границы будут
обозначаться; 3,01—5,01—7,01—9,01, а весь
вариационный ряд после распределения
показателей всех 15 пчел будет таков:
|
Шкала |
3,01 |
|
Число |
5 |
Вычисление
среднего арифметического и стандартного
отклонения можно вести как для вариационных
рядов счетных признаков (см. выше пример
с зацепками), только надо принимать, что
частоты — число пчел в классе — относятся
как бы к середине класса, например пять
пчел в первом классе падают на 4,01 минуты,
7 —на 6,01.
В
биометрических сочинениях приведенная
нами характеристика типа — среднее
арифметическое — и характеристики
разбросанности отклонений вокруг типа
— стандартное отклонение и коэфициент
вариации, сопровождаются так называемыми
средними и вероятными ошибками. Значение
этих ошибок в биометрии необычайно
велико. Дело в том, что когда мы определяем
среднее число зацепок у ста пчел одной
семьи, нас не интересуют именно эти 100
пчел, а интересует среднее число зацепок
на крыльях всех пчел этой семьи, из
которой в качестве пробной группы взято
100 штук. Оказывается, что о действительной
средней величине нашего признака можно
сделать заключение на основе пробы,
причем характеристики, носящие название
средних и вероятных ошибок, дают нам
возможность сделать это заключение с
такой точностью и уверенностью, с какой
мы это пожелаем. Здесь не место выводить
применяемые формулы; укажем, что формула
для средней ошибки среднего арифметического
такова: m = σ/√N , а для вероятной — РЕ=
6,6745(σ/√N) (m есть сокращенное условное
обозначение средней ошибки, а РЕ —
вероятной), где N — число случаев пробы.
Для
нашего примера с зацепками m = 1,661/√100 =
1,661/10 = 0,17 Теория вероятности отрасль
математики, которая лежит в основе
математической статистики, учит, что
если к среднему арифметическому прибавить
тройную среднюю ошибку: 22,0 + 3х0,17 = 22,51 и
вычесть ее из него 22—3х0,17 = 21,49, то мы
получаем такие пределы: 21,49 — 22,51. В этих
пределах с уверенностью, которую
практически можно считать достоверностью
(998 шансов против 2 в пользу нашего
утверждения), лежит среднее арифметическое
всего материала, из которого мы взяли
пробу и который нас собственно и
интересует. Если пользоваться вероятной
ошибкой, т. е. величиной, равной
приблизительно семи десятым средней
ошибки (множитель 0,6745), то для получения
той же степени достоверности надо брать
не утроенную среднюю ошибку, а вероятную
ошибку, помноженную на 4,5. Наконец, ошибки
имеют большое применение, когда нам
надо сравнить две характеристики двух
пробных групп и сделать заключение о
том, отличаются ли средние тех исходных
групп, из которых мы взяли пробу.
Предположим, у нас промерены пробы пчел
из Москвы и Харькова в отношений длины
их хоботка. Первые дали среднюю длину
в 6,115±0,003 мм, а вторые 6,549±0,003 мм. Насколько
достоверны эти отличия? Находят разницу
6,549 — 6,115 = 0,434 и ее вероятную ошибку по
следующей формуле: РЕ=± PE12+PE22
которая гласит, что вероятная ошибка
разницы средних равна корню квадратному
из суммы квадратов ошибок сравниваемых
средних. Если разница превышает свою
ошибку в 4, 5 или больше раз, мы вправе
говорить о статистической достоверности
различия всех харьковских и московских
пчел. В нашем примере это так и есть, ибо
0,434 в 108 раз больше, чем РЕ = ± √0,0032+0,0032 =
0,004.
Соседние файлы в предмете Ветеринарная генетика
- #
- #
- #
97 вопросов
Выполним любые типы работ
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Ошибки репрезентативности могут возникать при проведении … наблюдения
+Только не сплошного
Как сплошного, так и не сплошного
Только сплошного
Если себестоимость продукции увеличилась на 15%, а количество продукции
снизилось на 7%, то индекс издержек производства составит
123,65%
80,87%
+106,95%
При увеличении всех вариантов значений признака на А единиц средняя
величина…
увеличится на А единиц
В построенной интервальной группировке персонала предприятия по
величине заработной платы, состоящей из 5 групп, с шириной равного
интервала 20 тыс. руб. и максимальным размером зарплаты 130 тыс. руб.,
минимальный размер ежемесячной заработной платы сотрудников равен
30 тыс. руб.
По охвату единиц совокупности различают
+Сплошное и не сплошное наблюдение,
непосредственное наблюдение, документальное наблюдение и опрос
непрерывное, единовременное и периодическое наблюдение
Если средняя величина признака в совокупности составила 100, а
среднеквадратическое отклонение – 28, то коэффициент вариации будет
равен
28%
По направлению связи выделяют …связь
+прямая
+обратная
тесная
криволинейная
При увеличении всех значений признака в 6 раз среднее квадратическое
отклонение
увеличится в 6 раз
Содержание
- Пример об ошибке репрезентативности
- Ошибки статистического наблюдения и основные приёмы их устранения
- Репрезентативность — что это за процесс? Ошибка репрезентативности
- Репрезентативность — что это?
- Другие определения
- Репрезентативная выборка
- Вероятностная выборка
- Вероятностные выборки
- Выборка потребителей
- Размер выборки
- Понятие ошибки репрезентативности
- Виды ошибок
- Преднамеренные и непреднамеренные ошибки репрезентативности
- Валидность, надежность, репрезентативность. Расчет ошибок
- Репрезентативные системы
Пример об ошибке репрезентативности
Лекция 4.1 Выборочный метод
К настоящему времени Вы заработали баллов: 0 из 0 возможных.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
Генеральная совокупность — вся подлежащая изучению совокупность объектов (наблюдений).
Генеральная совокупность носит гипотетический характер. Она представляет собой совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данных условиях. Даже если бы у нас была возможность провести сплошное исследование всей совокупности признака, все равно в нее не попали бы объекты, которое по какой то причине отсутствуют на текущий момент, но должны были существовать при данных условиях.
Та часть объектов, которая отобрана для непосредственного изучения, называется выборочной совокупностьюили выборкой
Сущность выборочного метода
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности выносить суждение о её свойствах в целом
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть репрезентативной(представительной).
Репрезентативная выборка сохраняет и повторяет структуру генеральной совокупности.
Если две выборки взяты из одной генеральной совокупности, то разница в получаемых оценках (например, средних) будет носить случайный характер, как следствие ошибки репрезентативности
Ошибка репрезентативности возникает по причине того, что мы исследуем не всю совокупность, а только её части (выборки). Мы получаем случайную комбинацию элементов из генеральной совокупности.
Для того, чтобы минимизировать различия однородных (взятых из одной генеральной совокупности) выборок необходимо правильным образом их формировать.
Наилучшим способом формирования репрезентативной выборки является случайный отбор элементов из генеральной совокупности без расчленения на части или группы (случайная выборка).
Пример об ошибке репрезентативности
Рассмотрим следующий пример.
Исследователь задался вопросом: «существуют ли различия в эмпатических способностях между психологами и педагогами?». Для того чтобы это прояснить он набрал две группы испытуемых в соответствии с их профессиональной деятельностью и предложил им заполнить опросник на эмпатические способности. Далее, он рассчитал среднее значение в каждой группе.
В группе психологов среднее составило 23,4 балла, а в группе педагогов 21,1. Таким образом, разница в средних между группами составила2,3 балла (23,4 — 21,1 = 2,3).
Если бы представители этих профессий не отличались по изучаемому признаку, тогда разница в средних равнялась бы нулю.
Однако, можно ли считать эту разницу в 2,3 балла достаточной, чтобы судить о реальных различиях между группами? Может сложится так, что психологи и педагоги по эмпатии в реальности не отличаются (выборки однородны), а разница в 2,3 балла, полученная исследователем носит случайный характер, как ошибка репрезентативности.
Таким образом, мы можем сформулировать две гипотезы:
Гипотезы являются альтернативами по отношению к друг другу. Принятие одной из них как верной влечет за собой исключение «истинности» другой.
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА
Статистическая гипотеза – это любое предположение о виде или параметрах неизвестного закона распределения (закона распределения генеральной совокупности)
В статистике принято формулировать пару гипотез. Первая гипотеза называется нулевой, а вторая – альтернативной.
| Нулевая гипотеза Н0 | Альтернативная гипотеза Н1 |
| 1. 1. Является проверяемой 2. Обычно гипотеза об отсутствии явления (например, различий или зависимости) | Является логическим отрицанием нулевой |
| Поскольку нулевая гипотеза является проверяемой, то её можно отвергать и принимать | Альтернативную гипотезу принимают как следствие отрицания нулевой гипотезы |
пример:
· Н0 (нулевая): Женщины не отличаются от мужчин по среднему уровню развития эмпатических способностей (средние значения равны)
· Н1 (альтернативная): Средний уровень эмпатических способностей выше у женщин по сравнению с мужчинами
пример:
· Н0 (нулевая): Линейная корреляция между самооценкой и тревожностью равна 0
· Н1 (альтернативная): Самооценка отрицательно связана с тревожностью (линейная корреляция меньше нуля / чем выше самооценка, тем ниже тревожность и наоборот)
Вопрос:Какая из двух формулировок соответствует нулевой гипотезе Н0?
· А) между психологами и педагогами нет различий по среднему уровню выраженности эмпатии
· Б) между психологами и педагогами есть различия по среднему уровню выраженности эмпатии
Статистический критерий
Правило, по которому нулевая гипотеза отвергается или принимается, называется статистическим критерием.
Статистика – это специально составленная выборочная характеристика (распределение), у которой есть критическое значение такое, что если верна нулевая гипотеза, то вероятность (α) того, что случайная величина превысит это критическое значение, мала (Кремер Н.Ш., 2004).
Критическое значение делит распределение «нулевой гипотезы» на две области: область допустимых значений и область критических значений
Таким образом, критические значения позволяют исследователю либо принять, либо отвергнуть нулевую гипотезу.
В математической статистике можно подбирать критические значение для разных альфа-уровней (уровней значимости). Чаще всего:
1. Критическое значение, которое выделяет критическую область с вероятностью α
Источник
Ошибки статистического наблюдения и основные приёмы их устранения



Всякое статистическое наблюдение должно быть полным и достоверным. Однако по ряду причин степень точности данных может быть различной.
Все ошибки наблюдения подразделяются на два вида:
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи.
Ошибки регистрации могут возникать как при сплошном наблюдении, так и при несплошном и имеют следующие виды:
Случайные ошибки – это ошибки, которые возникают в результате небрежной описки или невнимательного отношения регистратора при заполнении формуляра (ошибки в подсчёте).
Систематические ошибки – это ошибки, которые искажают сведения по каждой отдельной единице наблюдения в одном и том же направлении.
Систематические ошибки делятся на:
Преднамеренные ошибки (сознательные, тенденциозные ошибки), возникающие в результате сознательного искажения статистической информации. К ним относятся: приписки, неправильные сведения об объёме выпущенной продукции, об остатках сырья и материалов и т. д.
Непреднамеренные ошибки – это ошибки, которые возникают в результате случайных причин, т.е. неумышленно (неисправность измерительных приборов, невнимательность регистратора и т.д.).
Ошибки репрезентативности свойственны несплошному наблюдению. Они возникают в результате выборочного наблюдения, когда отобранная часть единиц совокупности недостаточно полно отражает состав всей изучаемой совокупности.
Ошибки репрезентативности (так же, как и ошибки регистрации) могут быть случайными и систематическими.
Случайные ошибки оцениваются с помощью математических методов.
Систематические ошибки – это отклонения, которые возникают в результате случайного отбора единиц изучаемой совокупности. Их размеры не поддаются количественной оценке.
Для выявления и устранения допущенных при регистрации ошибок применяются следующие методы:
а) внешний контроль;
б) логический контроль;
в) счётный контроль.
При внешнем контроле проверяется: правильность оформления документов; наличие всех необходимых записей, которые предусмотрены инструкцией и т.д.
Логический контроль заключается в проверке ответов на вопросы программы наблюдения путём сопоставления полученных данных с другими источниками.
Сущность счётного (арифметического) контроля заключается в счётной проверке всех итоговых показателей, которые содержатся в отчётности или формуляре исследования. Задачей такого контроля является исправление итогов и отдельных числовых показателей.
В ряде случаев, при счётном контроле данных статистического наблюдения применяется метод балансовой увязки показателей (наличие на начало отчётного периода плюс поступления минус расход должно быть равно наличию на конец отчётного периода). Такой метод применяют: при проверках поголовья скота, при учёте поступления и расхода сырья и материалов и т.д.
Указанные методы проверки достоверности статистического наблюдения позволяют сократить до минимального значения допуск ошибок.
Источник
Репрезентативность — что это за процесс? Ошибка репрезентативности
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Источник