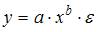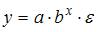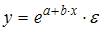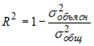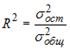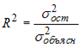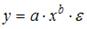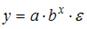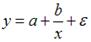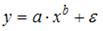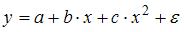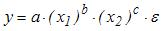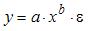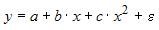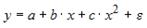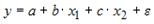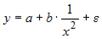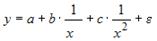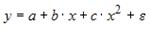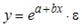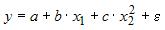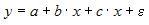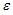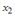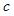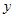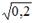к ошибкам спецификации
относятся не неправильный выбор той
или иной математической функции для
,
но и недоучет в уравнении регрессии
какого-то существенного фактора, то
есть использование парной регрессии
вместо множественной.
2. Для регрессионной
модели вида
необходим
минимальный объем наблюдений, содержащий
_____ объектов наблюдения.
«15».
3. Нелинейным по
объясняющим переменным, но линейным по
параметрам уравнением регрессии
является …
4. В модели вида
количество
объясняющих переменных равно …3.
5. При идентификации
модели множественной регрессии
количество
оцениваемых параметров равно …Итого
5 параметров.
1. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,
и
близок
к единице. Это означает, что факторы,
и
…мультиколлинеарны
2. При моделировании
линейного уравнения множественной
регрессии вида
необходимо,
чтобы выполнялось требование отсутствия
взаимосвязи между …
между x1
и x2.
3. Дана матрица
парных коэффициентов корреляции.

являются факторы …
и
коллинеарны.
4. В модели
множественной регрессии
определитель
матрицы парных коэффициентов корреляции
между факторами,
и
близок
к нулю. Это означает, что факторы,
и
…мультиколлинеарность
факторов.
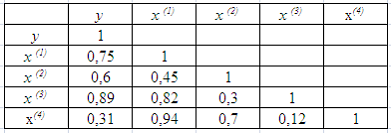
5. Для эконометрической
модели линейного уравнения множественной
регрессии вида
построена
матрица парных коэффициентов линейной
корреляции (y
– зависимая переменная; х(1),
х(2),
х(3),
x(4)–
независимые переменные):
Коллинеарными
(тесно связанными) независимыми
(объясняющими) переменными не
являются
…x(2)
и x(3)
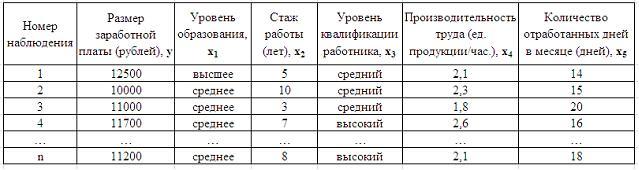
1. Дана таблица
исходных данных для построения
эконометрической регрессионной модели:
переменными не
являются …
стаж работы
производительность
труда
2. При исследовании
зависимости потребления мяса от уровня
дохода и пола потребителя можно
рекомендовать …
использовать
фиктивную переменную – пол потребителя
разделить
совокупность на две: для потребителей
женского пола и для потребителей мужского
пола
3. Изучается
зависимость цены квартиры (у)
от ее жилой площади (х)
и типа дома. В модель включены фиктивные
переменные, отражающие рассматриваемые
типы домов: монолитный, панельный,
кирпичный. Получено уравнение регрессии:
,
где

уравнениями регрессии для кирпичного
и монолитного являются …
для типа дома
кирпичный
для типа дома
монолитный
4. При анализе
промышленных предприятий в трех регионах
(Республика Марий Эл, Республика Чувашия,
Республика Татарстан) были построены
три частных уравнения регрессии:
для
Республики Марий Эл;
для
Республики Чувашия;
для
Республики Татарстан.
Укажите вид
фиктивных переменных и уравнение с
фиктивными переменными, обобщающее три
частных уравнения регрессии.
5. В эконометрике
фиктивной переменной принято считать
…
переменную,
принимающую значения 0 и 1
описывающую
количественным образом качественный
признак
1. Для регрессионной
модели зависимости среднедушевого
денежного дохода населения (руб., у)
от объема валового регионального
продукта (тыс. р., х1)
и уровня безработицы в субъекте (%, х2)
получено уравнение
.
Величина коэффициента регрессии при
переменнойх2
свидетельствует о том, что при изменении
уровня безработицы на 1% среднедушевой
денежный доход ______ рубля при неизменной
величине валового регионального
продукта.
изменится на
(-1,67)
2. В уравнении
линейной множественной регрессии:
,
где– стоимость основных фондов (тыс. руб.);
–
численность занятых (тыс. чел.);y
– объем промышленного производства
(тыс. руб.) параметр при переменной х1,
равный 10,8, означает, что при увеличении
объема основных фондов на _____ объем
промышленного производства _____ при
постоянной численности занятых.
на 1 тыс. руб. …
увеличится на 10,8 тыс. руб.
3. Известно, что
доля остаточной дисперсии зависимой
переменной в ее общей дисперсии равна
0,2. Тогда значение коэффициента
детерминации составляет …0,8
4. Построена
эконометрическая модель для зависимости
прибыли от
реализации единицы продукции (руб., у)
от величины оборотных средств предприятия
(тыс. р., х1):
.
Следовательно, средний размер прибыли
от реализации, не зависящий от объема
оборотных средств предприятия, составляет
_____ рубля. 10,75
5. F-статистика
рассчитывается как отношение ______
дисперсии к ________ дисперсии, рассчитанных
на одну степень свободы.факторной
… остаточной
1. Для эконометрической
модели уравнения регрессии ошибка
модели определяется как ______ между
фактическим значением зависимой
переменной и ее расчетным значением.Разность
2. Величина
называется
…случайной
составляющей
3. В эконометрической
модели уравнения регрессии величина
отклонения фактического значения
зависимой переменной от ее расчетного
значения характеризует …ошибку
модели
4. Известно, что
доля объясненной дисперсии в общей
дисперсии равна 0,2. Тогда значение
коэффициента детерминации составляет
… 0,2
5. При методе
наименьших квадратов параметры уравнения
парной линейной регрессии
определяются
из условия ______ остатков.минимизации
суммы квадратов
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки спецификации эконометрической модели имеют место вследствие …
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 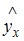
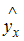
Эконометрика : учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М. : Финансы и статистика, 2005. – С. 45.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 20–30 .
ответ тест i-exam
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 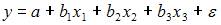
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 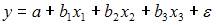
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 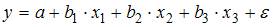






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 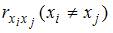

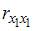
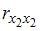
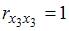
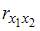
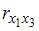
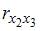
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
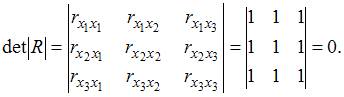
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

V7: Система линейных одновременных уравнений
S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами
-: состоятельности, смещенности и эффективности
+: состоятельности, несмещенности и эффективности
-: состоятельности, смещенности и неэффективности
-: несостоятельности, смещенности и эффективности
S: Для регрессионной модели вида 
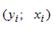
S: Для обнаружения автокорреляции в остатках используется
+: статистика Дарбина – Уотсона
-: критерий Гольдфельда – Квандта
S: Величина 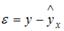
S: Строится эконометрическая модель линейного уравнения множественной регрессии вида
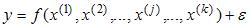

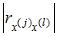
S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение
S: В эконометрической модели линейного уравнения регрессии
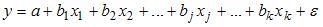
S: Система эконометрических уравнений включает совокупность _________ переменных.
S: Несмещенность оценок параметров регрессии означает, что …
-: дисперсия остатков минимальная
-: точность оценок выборки увеличивается с увеличением объема выборки
+: математическое ожидание остатков равно нулю
-: дисперсия остатков не зависит от величины
S: Дана автокорреляционная функция временного ряда
Верным будет утверждение, что ряд …
-: содержит только тенденцию, и не содержит сезонной компоненты
-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту
+: имеет выраженную сезонную компоненту с лагом 4
-: имеет выраженную сезонную компоненту с лагом 6
S: Если параметр эконометрической модели является статистически значимым, то его значение признается …
+: равным коэффициенту парной корреляции
S: Для регрессионной модели вида 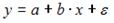
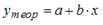

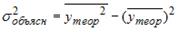

-:
+:
-:
-:
S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 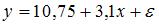
S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
-:
-:
-:
+:
S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …
-: принадлежность тому или иному региону
-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье
+: площадь жилья (м2)
S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
+:
-:
-:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
-:
-:
-:
+:
S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 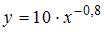
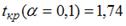
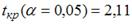
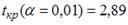
-: при уровне значимости 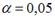
-: при уровне значимости 
-: эластичность спроса по цене составляет –0,8
+: при уровне значимости 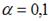
S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.
-: стохастические и вероятностные
-: линейные и парные
-: множественные и парные
+: линейные и нелинейные
S: Дана таблица исходных данных для построения эконометрической регрессионной модели:
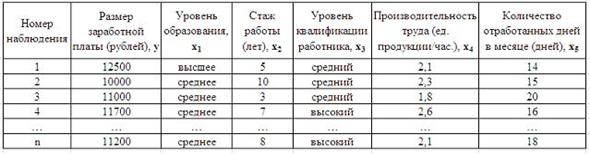
Фиктивными переменными не являются …
-: уровень квалификации работника
S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …
-: коэффициента множественной корреляции
-: показателей существенности параметров модели
+: матрицы парных коэффициентов линейной корреляции
-: системы нормальных уравнений МНК
S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 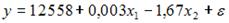
-: увеличится на 1,67
-: изменится на (-1,67)
-: изменится на 0,003
+: уменьшится на (-1,67)
S: В модели вида 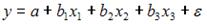
S: В модели множественной регрессии 
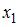
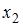
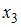
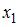
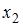
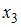
S: В уравнении линейной множественной регрессии: 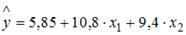
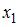
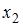
-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.
-: на 1% … увеличится на 10,8%
-: на 1 тыс. руб. … увеличится на 10,8%
+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
S: Переменная х является нелинейной в уравнении
-:
-:
+:
-:
S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является
-:
-:
+:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 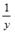
-:
-:
-:
+:
S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 
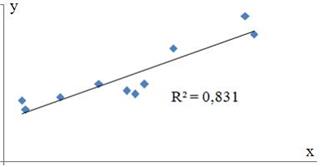
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.
S: Пусть 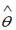




S: Степенной модельюне является регрессионная модель …
-:
+:
-:
-:
S: Нелинейным уравнением множественной регрессии является …
+:
-:
-:
-:
S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
+: бесконечно большого количества
S: В эконометрической модели линейного уравнения регрессии 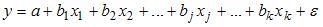
+:
S: Для эконометрической модели линейного уравнения множественной регрессии вида 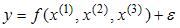
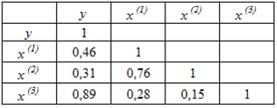
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
S: Регрессионная модель вида 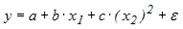
-: переменной
+: переменной
-: параметра
-: переменной
S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет
-:
-:
S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.
-: гомоскедастичными и некоррелированными
+: автокоррелированными и/или гетероскедастичными
S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
S: Автокорреляцией уровней ряда называется корреляционная зависимость между …
-: факторами, формирующими уровень ряда
-: уровнями двух рядов
+: последовательными уровнями ряда
-: компонентами, образующими уровни ряда
S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 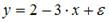
S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 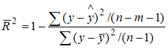
+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
-: n – число параметров при независимых переменных; m – число наблюдений
-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
S: Для эконометрической модели вида 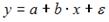


S: Ошибкой спецификации эконометрической модели уравнения регрессии является …
+: использование парной регрессии вместо множественной
-: расчет показателей качества модели
-: учет случайных факторов
-: оценка параметров при помощи МНК
S: В модели множественной регрессии 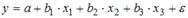
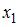
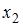
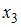
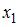
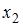
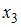
S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
-: между трендовой, сезонной и случайной компонентами
+: первого, второго, третьего и последующих порядков
-: факторов, формирующих уровень ряда
-: между несколькими временными рядами
S: Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …
-: yt = 7; T = 6,5; S = 0; E = 0,5
-: yt = 7; T = -3,5; S = -2; E = -1
+: yt = 7; T = 3,5; S = 2; E = 1
-: yt = 7; T = 3,5; S = -2; E = 1
источники:
http://poisk-ru.ru/s16310t6.html
http://lektsia.com/2×1276.html
Подборка по базе: Действия спасательной группы (пожарного расчета) в ходе проведен, 56 тема Яременко Е.А. Бухгалтерский финансовый баланс как источн, ПСП тема №11.2.doc, Эконометрика и методы моделирования в экономике.docx, Практическая работа №1 Тема_ «Особенности содержания обновленных, АСР тема 3.doc, Практическая работа №1 Тема_ «Особенности содержания обновленных, ПП Тема №3 «Общие принципы общения с пострадавшв =.doc, впп тема 2.docx, Задание Тема 5.docx
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
15
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
4. В модели вида количество объясняющих переменных равно …
3
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
5
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
Мультиколлинеарны
2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
x1 и x2
3. Дана матрица парных коэффициентов корреляции.
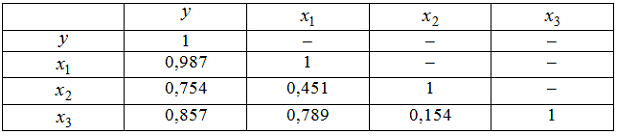
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …
мультиколлинеарны
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4)– независимые переменные):
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
x(2) и x(3)
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
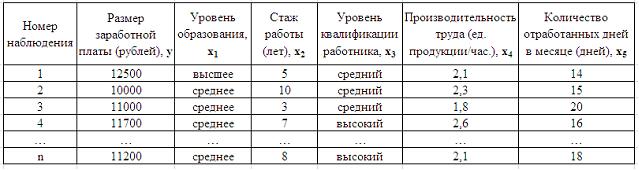
стаж работы
производительность труда
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный
для типа дома монолитный
для типа дома кирпичный
для типа дома монолитный
Решение:
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или
для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.
4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет
5. В эконометрике фиктивной переменной принято считать …
переменную, принимающую значения 0 и 1
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,8
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
10,75
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … остаточной
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
разность
2. Величина называется …
случайной составляющей
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
ошибку модели
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
минимизации суммы квадратов
Тема 6: Предпосылки МНК, методы их проверки
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
тест Уайта
критерий Гольдфельда – Квандта
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
положительной
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
Гетероскедатичность
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
отрицательной
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
несмещенности
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
0
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
обобщенный
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников
.После применения обобщенного метода наименьших квадратов новая модель приняла вид
. Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции
.Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид
. Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
фондоемкости продукции при неизменном уровне трудоемкости продукции
Тема 9: Оценка тесноты связи
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
Регрессии
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
[–1; 0]
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
[0,7; 1]
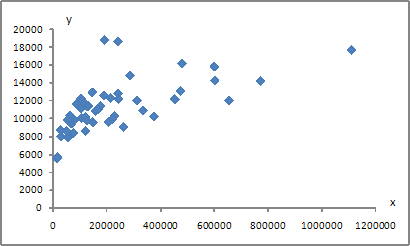
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
полем корреляции
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений,
. Тогда значение коэффициента детерминации равно …
0,8
3. Для регрессионной модели вида , где рассчитаны дисперсии:
;
;
. Тогда величина
характеризует долю …
остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений
, то сумма квадратов отклонений, объясненная регрессией, равна …
90
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Для автокорреляции характерным является соотношение (u u ) __ 0: k i COV
1) ?
2) >
3) ?
4) =
Процесс выбора необходимых переменных для регрессии переменных и отбрасывание лишних переменных называется:
1) прогнозированием
2) подгонкой
3) унификацией переменных
4) моделированием
5) спецификацией переменных
В авторегрессионной схеме первого порядка предполагается, что значение ? в каждом
наблюдении:
1) зависит от его значения в предыдущих наблюдениях
2) зависит от его значения в первом наблюдении
3) зависит от его значения во всех других наблюдениях
4) не зависит от его значения во всех других наблюдениях
5) равны 0
Множественный регрессионный анализ является ________ парного регрессионного анализа:
1) эквивалентностью
2) противоположностью
3) развитием
4) подобием
5) частным случаем
Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна …
0
1
лагу
половине лага
Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии _______ наблюдений:
1) зависит от номера наблюдений
2) зависит от характера
3) зависит от числа
4) одинакова для всех
5) зависит от времени проведения
Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия _____________ переменных:
1) фиктивных
2) циклических
3) сезонных
4) не включенных в уравнение
5) лишних
Сумма квадратов отклонений величины y от своего выборочного значения ? _____ сумма квадратов отклонений:
1) результирующая
2) необъясняющая
3) общая
4) случайная
5) объясняющая
Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y …
сбалансированным
стационарным
автокорреляционным
нестационарным
К зоне неопределенности в тесте Дарбина-Уотсона относится случай, при котором ________ (d1, d2 – нижняя и верхняя границы):
1) DW
2) DW = 0
3) DW > d2
4) DW ? 0
5) d1
Значение статистики DW находится между значениями:
1) 0 и 6
2) 0 и 4
3) -1 и 1
4) -2 и 2
5) -3 и 3
Если предположение о природе гетероскедастичности верно, то дисперсия случайного
члена для первых наблюдений в упорядоченном ряду будет ________ для последних:
1) ниже, чем
2) равно 0
3) больше, чем
4) такая же, как
5) равно 1
Условие гетероскедастичности означает, что вероятность того, что случайный член при-
мет какое-либо конкретное значение ________ наблюдений:
1) зависит от числа
2) зависит от времени проведения
3) зависит от номера
4) одинакова для всех
5) не зависит от времени проведения
Ошибки спецификации эконометрической модели имеют место вследствие …
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостаточного количества данных
В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.
сезонная
циклическая
случайная
трендовая