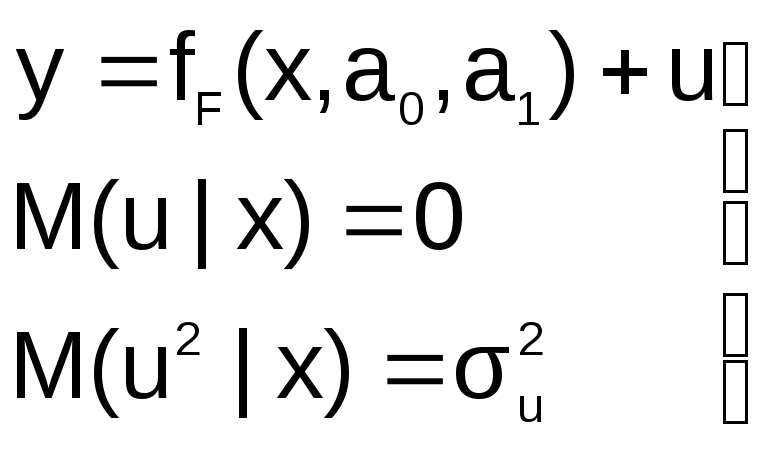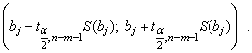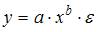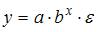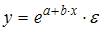Ошибки спецификации модели множественной регрессии

Возможные ошибки спецификации модели:

1. Неправильный выбор вида уравнения
регрессии

2. В уравнение регрессии включена лишняя
(незначимая) переменная

3. В уравнении регрессии пропущена
значимая переменная

1. Неправильный выбор вида функции в
   уравнении

Пусть на первом этапе была сделана
спецификация модели в виде:

в
которой функция f_F(x,a₀,a₁)
выбрана не верно. Предположим, что
y_T=f_T(x,a₀,a₁)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:

И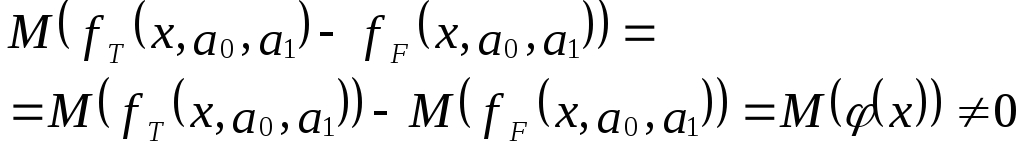з
выражения следует:

Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций f_T
и f_F
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется

Следовательно, в результате оценивания
такой модели параметры а₀ и а₁
будут смещенными

Симптомы наличия ошибки спецификации
первого типа:

1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации

2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений

Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!

В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.

Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.

2. В уравнение регрессии включена
лишняя переменная

П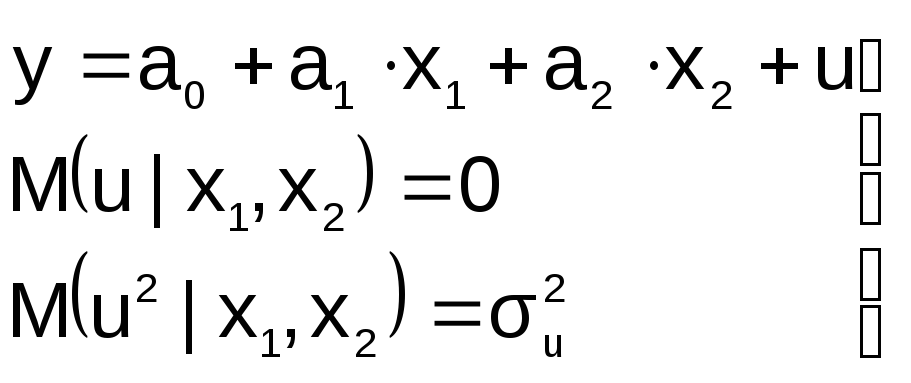усть
на этапе спецификации в модель включена
«лишняя» переменная, например, X₂

«Правильная»
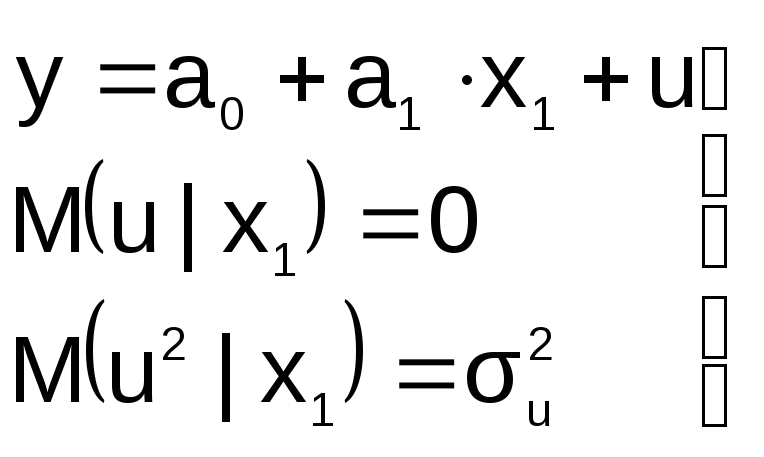
спецификация должна иметь вид:

Последствия:

1.
Оценки параметров а₀, а₁, а₂
останутся несмещенными, но потеряют
свою эффективность (точность)

2. Увеличивается ошибка прогноза по
модели

как за счет ошибок оценок коэффициентов
и σ_u,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора

Диагностика:

В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H₀: a_i=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n₂ = n – (k+1)

3.
В модели не достает важной переменной

Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели

Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель

29. Фиктивные переменные и особенности их использования в моделях.

На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.

Примеры.

Моделирование влияния пола специалистов
на уровень зарплаты.

Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)

Модель инфляции с учетом различных
видов регулирования со стороны государства

Возможны два подхода к решению задачи:

— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной

— учесть влияние качественного фактора
в одной модели

Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели

Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N

Предположим:

1. Зависимость затрат на обучение от
   количества учащихся N в
   обоих типах школ одинакова

2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам

Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:

Y^o
= a₀ +
a₁N +u

Y^s
= b₀ +
a₁N +
v

Обе
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:

Спецификация такой модели имеет вид:

Y = a₀
+ a₁N
+ δd + u

Тогда при d=0 получим Y^o
= a₀ + a₁N
+ u

при d=1 получим Y^s
= (a₀+δ)
+a₁N +
v

d – фиктивная переменная
сдвига

Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор

Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)

Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные

Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена

Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной

В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора

Например:

Однако, если взять спецификацию модели
в виде:

Y=a₀
+ a₁d₁+a₂d₂+a₃d₃+a₄d₄+a₅N+u

при этом всегда верно тождество
d₁+d₂+d₃+d₄=1

Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.

Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает

Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»

Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;

d=1 – профессиональная
школа

Спецификацию модели следует записать
в виде:

Y = a₀
+ a₁N
+ a₂*d
+ a₃dN
+U

50

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Построение и тестирование адекватности эконометрических моделей множественной регрессии: выбор функциональной формы модели

Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования

«Тверской государственный
технический университет»

(ТвГТУ)

Кафедра «Бухгалтерский учет,
анализ и аудит»

Курсовой проект

по дисциплине
«Эконометрика»

Выполнила: студентка 3-го курса

учебной группы РБА 36-11

Антонова Н.В.

г.

Содержание

Введение

Глава I. Аналитическая часть

1.1 Основы построения и тестирования адекватности экономических
моделей множественной регрессии

1.2 Проблема спецификации экономических моделей множественной
регрессии

1.3 Последствия ошибок спецификации экономических моделей
множественной регрессии

Глава II. Проектная часть

2.1 Методическое обеспечение множественной регрессии

2.2 Информационное обеспечение множественной регрессии

2.3 Числовой пример модели множественной регрессии и выводы
множественной регрессии

Заключение

Список использованных источников

Введение

Эконометрика — это самостоятельная научная дисциплина,
объединяющая совокупность теоретических результатов, приемов, методов и
моделей, предназначенных для того, чтобы на базе экономической теории,
экономической статистики и экономических измерений, математико-статистического
инструментария придавать конкретное количественное выражение общим
(качественным) закономерностям, обусловленным экономической теорией.

Целью работы является получение практических навыков
построения эконометрических моделей.

Эконометрический метод складывался в преодолении следующих
трудностей, искажающих результаты применения классических статистических
методов (сущность новых терминов будет раскрыта в дальнейшем):

.        асимметричности связей;

2.       мультиколлинеарности связей;

.        эффекта гетероскедастичности;

.        автокорреляции;

.        ложной корреляции;

.        наличия лагов.

Для описания сущности эконометрической модели удобно разбить
весь процесс моделирования на шесть основных этапов:

-й этап (постановочный) — определение конечных целей
моделирования, набора участвующих в модели факторов и показателей, их роли;

-й этап (априорный) — предмодельный анализ экономической
сущности изучаемого явления, формирование и формализация априорной информации,
в частности, относящейся к природе и генезису исходных статистических данных и
случайных остаточных составляющих;

-й этап (параметризация) — собственно моделирование, т.е.
выбор общего вида модели, в том числе состава и формы входящих в нее связей;

-й этап (информационный) — сбор необходимой статистической
информации, т.е. регистрация значений участвующих в модели факторов и
показателей на различных временных или пространственных тактах функционирования
изучаемого явления;

-й этап (идентификация модели) — статистический анализ модели
и в первую очередь статистическое оценивание неизвестных параметров модели;

-й этап (верификация модели) — сопоставление реальных и
модельных данных, проверка адекватности модели, оценка точности модельных
данных.

Эконометрическое моделирование реальных
социально-экономических процессов и систем обычно преследует два типа конечных
прикладных целей (или одну из них):

) прогноз экономических и социально-экономических
показателей, характеризующих состояние и развитие анализируемой системы;

) имитацию различных возможных сценариев
социально-экономического развития анализируемой системы (многовариантные
сценарные расчеты, ситуационное моделирование).

При постановке задач эконометрического моделирования следует
определить их иерархический уровень и профиль.

Анализируемые задачи могут относиться к макро — (страна,
межстрановой анализ), мезо — (регионы внутри страны) и микро — (предприятия,
фирмы, семьи) уровням и быть направленными на решение вопросов различного
профиля инвестиционной, финансовой или социальной политики, ценообразования,
распределительных отношений и т.п.

Глава I.
Аналитическая часть

1.1 Основы
построения и тестирования адекватности экономических моделей множественной
регрессии

В настоящее время множественная регрессия — один из наиболее
распространенных методов в эконометрике. Основная цель множественной регрессии
— построить модель с большим числом факторов, определив при этом влияние
каждого из них в отдельности, а также совокупное их воздействие на моделируемый
показатель.

Множественная регрессия широко используется в решении проблем
спроса, доходности акций, при изучении функции издержек производства, в
макроэкономических расчетах и целом ряде других вопросов эконометрики. В
настоящее время множественная регрессия — один из наиболее распространенных
методов в эконометрике.

Основная цель множественной регрессии — построить модель с
большим числом факторов, определив при этом влияние каждого из них в
отдельности, а также совокупное их воздействие на моделируемый показатель.

Линейная модель множественной регрессии имеет общий вид:

₁= β₀+ β₁ х_i1+ β₂ х_i2+…+ β_m х_im+ ε

где n — объём выборки, который по крайней мере в 3
раза превосходит количество независимых переменных;

у_i — значение результативной
переменной в наблюдении I;

х_i1, х_i2,., х_im-значения
независимых переменных в наблюдении i;

β₀, β₁, … β_m — параметры уравнения
регрессии, подлежащие оценке;

ε — значение случайной
ошибки модели множественной регрессии в наблюдении I,

При построении модели множественной линейной регрессии учитываются
следующие пять условий:

. величины х_i1, х_i2,., х_im
— неслучайные и независимые переменные;

. математическое ожидание случайной ошибки уравнения
регрессии равно нулю во всех наблюдениях: М (ε) = 0, i= 1,m;

. дисперсия случайной ошибки уравнения регрессии является
постоянной для всех наблюдений: D (ε) =σ² =const;

4. случайные ошибки модели регрессии не коррелируют между
собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): соv
(ε_i,ε_j.) = 0, i≠j;

. случайная ошибка модели регрессии — случайная величина,
подчиняющаяся нормальному закону распределения с нулевым математическим
ожиданием и дисперсией σ².

Функция , описывающая зависимость показателя от параметров,
называется уравнением (функцией) регрессии.

Уравнение регрессии показывает ожидаемое значение зависимой
переменной при определенных значениях зависимых
переменных .

В зависимости от количества включенных в модель факторов Х
модели делятся на однофакторные (парная модель регрессии) и многофакторные
(модель множественной регрессии).

В зависимости от вида функции модели делятся на линейные и нелинейные.

Модель множественной линейной регрессии имеет вид:

y _i = a₀ + a₁x _{i 1} +a₂x _{i 2} +…+ a_k x _{i k} + e_{i  (}1.1)

 — количество
наблюдений.

множественная регрессия экономическая модель

Коэффициент регрессии a_j показывает,
на какую величину в среднем изменится результативный признак , если переменную x_j
увеличить на единицу измерения, т.е. a_j
является нормативным коэффициентом.

Коэффициент  может быть отрицательным. Это означает,
что область существования показателя не включает нулевых значений параметров.
Если же а0>0, то область существования показателя включает нулевые
значения параметров, а сам коэффициент характеризует среднее значение
показателя при отсутствии воздействий параметров.

Анализ уравнения (1.1) и методика определения параметров
становятся более наглядными, а расчетные процедуры существенно упрощаются, если
воспользоваться матричной формой записи:

 (1.2).

Где  — вектор зависимой переменной размерности
п ´ 1,
представляющий собой п наблюдений значений .

 — матрица п наблюдений независимых переменных , размерность матрицы  равна п ´ (k+1). Дополнительный фактор , состоящий из единиц, вводится для
вычисления свободного члена. В качестве исходных данных могут быть временные
ряды или пространственная выборка.

 — количество факторов, включенных в модель.

a — подлежащий
оцениванию вектор неизвестных параметров размерности (k+1) ´ 1;

 — вектор случайных отклонений (возмущений) размерности п ´ 1.  отражает тот факт, что изменение  будет неточно описываться изменением объясняющих переменных , так как существуют и другие факторы,
неучтенные в данной модели.

Таким образом,

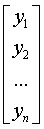
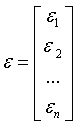
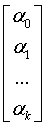
Y = , X = , , a = .

Уравнение (1.2) содержит значения неизвестных параметров a₀,a₁,a₂,…,a_k.

Эти величины оцениваются на основе выборочных наблюдений, поэтому
полученные расчетные показатели не являются истинными, а представляют собой
лишь их статистические оценки.

Модель линейной регрессии, в которой вместо истинных значений
параметров подставлены их оценки (а именно такие регрессии и применяются на
практике), имеет

, (1.3)

где A — вектор оценок параметров; е — вектор
«оцененных» отклонений регрессии, остатки регрессии е = Y — ХА;
-оценка значений Y, равная ХА.

Построение уравнения регрессии осуществляется, как правило, методом
наименьших квадратов (МНК), суть которого состоит в минимизации суммы квадратов
отклонений фактических значений результатного признака от его расчетных
значений, т.е.:

.

Формулу для вычисления параметров регрессионного уравнения по
методу наименьших квадратов приведем без вывода

 (1.4).

Для того чтобы регрессионный анализ, основанный на обычном методе
наименьших квадратов, давал наилучшие из всех возможных результаты, должны выполняться
следующие условия, известные как условия Гаусса — Маркова.

Первое условие. Математическое ожидание случайной составляющей в
любом наблюдении должно быть равно нулю. Иногда случайная составляющая будет положительной, иногда
отрицательной, но она не должна иметь систематического смещения ни в одном из
двух возможных направлений.

Фактически если уравнение регрессии включает постоянный член, то
обычно это условие выполняется автоматически, так как роль константы состоит в
определении любой систематической тенденции , которую не учитывают объясняющие переменные, включенные в
уравнение регрессии.

Второе условие
означает, что дисперсия случайной составляющей должна быть постоянна для всех
наблюдений. Иногда случайная составляющая будет больше, иногда меньше,
однако не должно быть априорной причины для того, чтобы она порождала большую
ошибку в одних наблюдениях, чем в других.

Эта постоянная дисперсия обычно обозначается , или часто в более краткой форме , а условие записывается следующим
образом:

.

Выполнимость данного условия называется гомоскедастичностью
(постоянством дисперсии отклонений). Невыполнимость данной предпосылки
называется гетероскедастичностью, (непостоянством дисперсии отклонений).

Третье условие предполагает отсутствие систематической связи между
значениями случайной составляющей в любых двух наблюдениях. Например, если случайная составляющая
велика и положительна в одном наблюдении, это не должно обусловливать
систематическую тенденцию к тому, что она будет большой и положительной в
следующем наблюдении. Случайные составляющие должны быть независимы друг от
друга.

В силу того, что , данное условие можно записать следующим образом:

Возмущения  не коррелированны (условие независимости
случайных составляющих в различных наблюдениях).

Это условие означает, что отклонения регрессии (а значит, и сама
зависимая переменная) не коррелируют. Условие некоррелируемости ограничительно,
например, в случае временного ряда . Тогда третье условие означает отсутствие автокорреляции ряда . Четвертое условие состоит в том, что
в модели (1.1) возмущение  (или зависимая переменная ) есть величина случайная, а объясняющая переменная  — величина неслучайная.

Если это условие выполнено, то теоретическая ковариация между
независимой переменной и случайным членом равна нулю.

Наряду с условиями Гаусса — Маркова обычно также предполагается
нормальность распределения случайного члена.

Качество модели регрессии связывают с адекватностью модели
наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия)
модели регрессии наблюдаемым данным проводится на основе анализа остатков — .

Анализ остатков позволяет получить представление, насколько хорошо
подобрана сама модель и насколько правильно выбран метод оценки коэффициентов.
Согласно общим предположениям регрессионного анализа, остатки должны вести себя
как независимые (в действительности, почти независимые) одинаково распределенные
случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

проверка качества всего уравнения регрессии;

проверка значимости всего уравнения регрессии;

проверка статистической значимости коэффициентов уравнения
регрессии;

проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь,
используется коэффициент детерминации, который определяется следующим образом:

, (1.5)

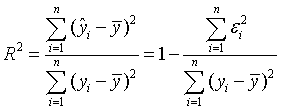
где  — среднее значение зависимой переменной,

 — предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминации показывает долю вариации
результативного признака, находящегося под воздействием изучаемых факторов,
т.е. определяет, какая доля вариации признака Y учтена в модели и
обусловлена влиянием на него факторов.

Чем ближе  к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также
использовать коэффициент множественной корреляции (индекс корреляции) R

= =  (1.6)

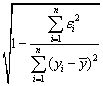
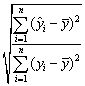
Данный коэффициент является универсальным, так как он отражает
тесноту связи и точность модели, а также может использоваться при любой форме
связи переменных.

Важным моментом является проверка значимости построенного
уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии — это означает установить, соответствует
ли математическая модель, выражающая зависимость между Y и Х, фактическим
данным и достаточно ли включенных в уравнение объясняющих переменных Х для
описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы
узнать, пригодно уравнение регрессии для практического использования (например,
для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий
Фишера. Если расчетное значение с n₁= k и
n₂ = (n — k — 1) степенями свободы, где k — количество
факторов, включенных в модель, больше табличного при заданном уровне
значимости, то модель считается значимой.

 (1.7)

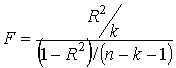
В качестве меры точности применяют несмещенную оценку дисперсии
остаточной компоненты, которая представляет собой отношение суммы квадратов
уровней остаточной компоненты к величине (n — k — 1), где k — количество
факторов, включенных в модель. Квадратный корень из этой величины () называется стандартной ошибкой:

 (1.8)

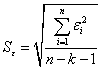
значимость отдельных коэффициентов регрессии проверяется по
t-статистике путем проверки гипотезы о равенстве нулю j-го параметра
уравнения (кроме свободного члена):

, (1.9)

где S_aj — это стандартное (среднеквадратическое)
отклонение коэффициента уравнения регрессии a_j. Величина S_aj
представляет собой квадратный корень из произведения несмещенной оценки
дисперсии и j — го диагонального элемента
матрицы, обратной матрице системы нормальных уравнений.

где  — диагональный элемент матрицы .

Если расчетное значение t-критерия с (n — k — 1) степенями
свободы превосходит его табличное значение при заданном уровне значимости,
коэффициент регрессии считается значимым. В противном случае фактор,
соответствующий этому коэффициенту, следует исключить из модели (при этом ее
качество не ухудшится).

 

1.2 Проблема
спецификации экономических моделей множественной регрессии

Построение уравнения множественной регрессии
<#»704204.files/image050.gif»>

Если же определитель матрицы межфакторной корреляции близок к
единице, то мультколлинеарности нет. Существуют различные подходы преодоления
сильной межфакторной корреляции. Простейший из них — исключение из модели
фактора (или факторов), в наибольшей степени ответственных за
мультиколлинеарность при условии, что качество модели при этом пострадает
несущественно (а именно, теоретический коэффициент детерминации — R2y (x1. xm)
снизится несущественно).

Определение факторов, ответственных за мультиколлинеарность, может
быть основано на анализе матрицы межфакторной корреляции. При этом определяют
пару признаков-факторов, которые сильнее всего связаны между собой (коэффициент
линейной парной корреляции максимален по модулю). Из этой пары в наибольшей
степени ответственным за мультиколлинеарность будет тот признак, который теснее
связан с другими факторами модели (имеет более высокие по модулю значения
коэффициентов парной линейной корреляции <#»704204.files/image051.gif»>понимают числовую последовательность , элементы которой вычисляются по
определенному правилу как функция времени t. Исключив детерминированную
составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может
в одном предельном случае представлять чисто случайные скачки, а в другом —
плавное колебательное движение. В большинстве случаев будет нечто среднее:
некоторая иррегулярность и определенный систематический эффект, обусловленный
зависимостью последовательных членов ряда.

Проблема спецификации экономических моделей множественной
регрессии по существу решается на первых трех этапах моделирования и включает в
себя:

определение конечных целей моделирования (прогноз, имитация
различных сценариев социально-экономического развития анализируемой системы,
управление);

определение списка экзогенных и эндогенных переменных;

определение состава анализируемой системы уравнений и тождеств, их
структуры и соответственно списка предопределенных переменных;

формулировку исходных предпосылок и априорных ограничений
относительно: стохастической природы остатков (в классических вариантах моделей
постулируются их взаимная статистическая независимость или некоррелированность,
нулевые значения их средних величин и, иногда, сохранение постоянными в
процессе наблюдения значений их дисперсий — гомоскедастичностъ);

числовых значений отдельных элементов матриц коэффициентов в
модели;

поведение некоторых эндогенных переменных.

Итак, спецификация модели — это первый и, быть может, важнейший
шаг эконометрического исследования. От того, насколько удачно решена проблема
спецификации и, в частности, насколько реалистичны наши решения и предположения
относительно состава эндогенных, экзогенных и предопределенных переменных,
структуры самой системы уравнений и тождеств, стохастической природы случайных
остатков и конкретных числовых значений части элементов матриц коэффициентов,
решающим образом зависит успех всего эконометрического моделирования.

Спецификация опирается на имеющиеся экономические теории,
специальные знания или на интуитивные представления исследователя об
анализируемой экономической системе. Эти априорные сведения определяют, в
частности, природу матриц коэффициентов.

Например, информация (или предположение) о том, что определенные
переменные непосредственно не участвуют в том или ином уравнении, означает
равенство нулю соответствующих элементов в строках матриц коэффициентов.
Дополнительные сведения о системе могут иметь вид ограничений на комбинации
элементов матриц коэффициентов.

1.3
Последствия ошибок спецификации экономических моделей множественной регрессии

Возможные ошибки спецификации регрессионной модели:

Невключение значимых переменных

Включение незначимых переменных

Невключение значимых переменных

(-) Смещенность оценок коэффициентов регрессии

(-) Смещенность оценки дисперсии ошибок регрессии

(+) Меньшая вариация оценок коэффициентов регрессии

Включение незначимых переменных

(+) Несмещенность оценок коэффициентов регрессии

(+) Несмещенность оценки дисперсии ошибок регрессии

(-) Большая вариация оценок коэффициентов регрессии

Замещающие переменные, причины:

. Необходимость показателя не была учтена при составлении
выборки

. Переменная трудноизмерима (например, уровень образования)

. Сбор данных о переменной x1 требует значительных затрат

При оценивании модели без переменной x1 полученные оценки
будут смешенными.

Последствия использования замещающих переменных:

. Оценки коэффициентов при переменных x2,…, xk становятся
несмещенными

. Стандартные ошибки и t-статистики коэффициентов te ze

. R2 имеет такое же значение, как и при оценивании с
переменной x1

. Коэффициент β1 нельзя оценить
(оценивается только β1δ1), но его стандартная
ошибка и t-статистика позволяет оценить значимость x1

. Получить оценку свободного члена модели невозможно (но она
часто и не особенно важна) последствия справедливы приблизительно

Мультиколлинеарность — это понятие, которое используется для
описания проблемы, когда нестрогая линейная зависимость между объясняющими
переменными приводит к получению ненадежных оценок регрессии. Оценка любой
регрессии будет страдать от нее в определенной степени, если только все
независимые переменные не окажутся абсолютно некоррелированными.

Различные методы, которые могут быть использованы для
смягчения мультиколлинеарности, делятся на две категории: к первой категории
относятся попытки повысить степень выполнения четырех условий, обеспечивающих
надежность оценок регрессии; ко второй категории относится использование
внешней информации, но можно привнести или усилить автокорреляцию, но она может
быть нейтрализована. Кроме того, можно привнести (или усилить) смещение,
вызванное ошибками измерения, если поквартальные данные измерены с меньшей
точностью, чем соответствующие ежегодные данные.

Глава II.
Проектная часть

2.1
Методическое обеспечение множественной регрессии

Суть регрессионного анализа: построение математической модели
и определение ее статистической надежности.

Вид множественной линейной модели регрессионного анализа:

= b₀ + b₁x_i1 +. + b_jx_ij
+. + b_kx_ik + e_i

где e_i — случайные ошибки наблюдения, независимые
между собой, имеют нулевую среднюю и дисперсию s.

Назначение множественной регрессии: анализ связи между
несколькими независимыми переменными и зависимой переменной.

Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии b_j показывает, на какую величину
в среднем изменится результативный признак Y, если переменную X_j
увеличить на единицу измерения, т.е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного
анализа:

= Xb + e

где Y — случайный вектор — столбец размерности (n x 1)
наблюдаемых значений результативного признака (y₁, y₂,.,
y_n);- матрица размерности [n x (k+1)] наблюдаемых значений
аргументов;- вектор — столбец размерности [ (k+1) x 1] неизвестных, подлежащих
оценке параметров (коэффициентов регрессии) модели;- случайный вектор — столбец
размерности (n x 1) ошибок наблюдений (остатков).

На практике рекомендуется, чтобы n превышало k не менее, чем
в три раза.

Задачи регрессионного анализа Основная задача регрессионного
анализа заключается в нахождении по выборке объемом n оценки неизвестных
коэффициентов регрессии b₀, b₁,., b_k. Задачи
регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным
для переменных X_i и Y:

·              получить наилучшие оценки
неизвестных параметров b₀, b₁,., b_k;

·              проверить статистические
гипотезы о параметрах модели;

·              проверить, достаточно ли
хорошо модель согласуется со статистическими данными (адекватность модели
данным наблюдений).

Построение моделей множественной регрессии состоит из
следующих этапов:

.        выбор формы связи (уравнения регрессии);

2.       определение параметров выбранного уравнения;

.        анализ качества уравнения и поверка адекватности
уравнения эмпирическим данным, совершенствование уравнения.

Множественная регрессия:

·              Множественная регрессия с
одной переменной

·              Множественная регрессия с
двумя переменными

·              Множественная регрессия с
тремя переменными

Пример
решения нахождения модели множественной регрессии

Множественная регрессия с двумя переменными

Модель множественной регрессии вида Y = b₀ +b₁X₁
+ b₂X₂;

) Найти неизвестные b₀, b₁,b₂
можно, решим систему трехлинейных уравнений с тремя неизвестными b₀,b₁,b₂:

 

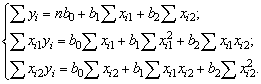
Для решения системы можете воспользоваться решение системы
методом Крамера или использовав формулы

 

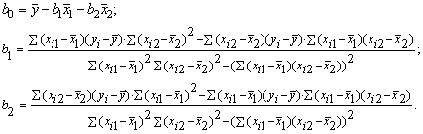
Для этого строим таблицу вида:

Таблица 1.

Y	x1	x2	(y-yср) 2	(x1-x1ср) 2	(x2-x2ср) 2	(y-yср) (x1-x1ср)	(y-yср) (x2-x2ср)	(x1-x1ср) (x2-x2ср)

Выборочные дисперсии эмпирических коэффициентов множественной
регрессии можно определить следующим образом:

 

Здесь z’_jj — j-тый диагональный элемент матрицы Z^-1
= (X^TX) — ¹.

 

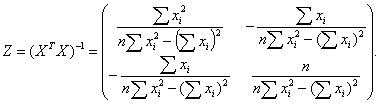
При этом:

 

где m — количество объясняющих переменных модели.

В частности, для уравнения множественной регрессии

= b₀ + b₁X₁ + b₂X₂

с двумя объясняющими переменными используются следующие
формулы:

 

 Или

 

 и

 ,,.

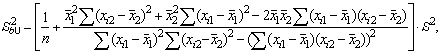
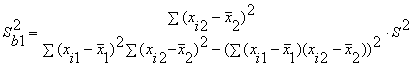
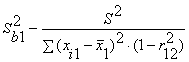
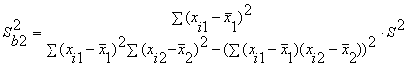
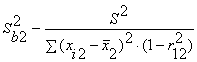
Здесь r₁₂ — выборочный коэффициент корреляции
между объясняющими переменными X₁ и X₂; Sb_j —
стандартная ошибка коэффициента регрессии; S — стандартная ошибка множественной
регрессии (несмещенная оценка).

По аналогии с парной регрессией после определения точечных
оценок b_j коэффициентов βj (j=1,2,…,m)
теоретического уравнения множественной регрессии могут быть рассчитаны
интервальные оценки указанных коэффициентов.

Доверительный интервал, накрывающий с надежностью (1-α) неизвестное значение параметра βj, определяется как

Множественная
регрессия в Excel

Чтобы найти параметры множественной регреcсии средствами
Excel, используется функция ЛИНЕЙН (Y; X; 0;1), где Y — массив для значений Y,
где X — массив для значений X (указывается как единый массив для всех значений
Х_i)

Проверка
статистической значимости коэффициентов уравнения множественной регрессии

Как и в случае множественной регрессии, статистическая
значимость коэффициентов множественной регрессии с m объясняющими переменными
проверяется на основе t-статистики: 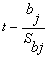 имеющей в данном случае
распределение Стьюдента с числом степеней свободы v = n — m-1. При требуемом
уровне значимости наблюдаемое значение t-статистики сравнивается с критической
точной распределения Стьюдента.

В случае, если , то статистическая
значимость соответствующего коэффициента множественной регрессии
подтверждается. Это означает, что фактор Xj линейно связан с зависимой
переменной Y. Если же установлен факт незначимости коэффициента b_j,
то рекомендуется исключить из уравнения переменную Xj. Это не приведет к
существенной потере качества модели, но сделает ее более конкретной.

Проверка
общего качества уравнения множественной регрессии

Для этой цели, как и в случае множественной регрессии,
используется коэффициент детерминации R²:

 

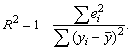
Справедливо соотношение 0<=R2<=1. Чем ближе этот
коэффициент к единице, тем больше уравнение множественной регрессии объясняет
поведение Y. Для множественной регрессии коэффициент детерминации является
неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей
переменной никогда не уменьшает значение R², так как каждая
последующая переменная может лишь дополнить, но никак не сократить информацию,
объясняющую поведение зависимой переменной. Иногда при расчете коэффициента
детерминации для получения несмещенных оценок в числителе и знаменателе
вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е.
вводится так называемый скорректированный (исправленный) коэффициент
детерминации:

 

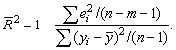
Соотношение может быть представлено вследующем виде:   для m>1. С ростом
значения m скорректированный коэффициент детерминации растет медленнее, чем
обычный. Очевидно, что только при R² = 1.  может принимать
отрицательные значения.

Доказано, что  увеличивается при добавлении новой объясняющей
переменной тогда и только тогда, когда t-статистика для этой переменной по
модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных
осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.

Рекомендуется после проверки общего качества уравнения
регрессии провести анализ его статистической значимости. Для этого используется
F-статистика:

 

Показатели F и R2 равны или не равен нулю одновременно. Если
F=0, то R²=0, следовательно, величина Y линейно не зависит от
X1,X2,…,Xm. Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из
требуемого уровня значимости α и чисел степеней свободы
v1 = m и v2 = n — m — 1, определяется на основе распределения Фишера. Если
F>Fкр, то R² статистически значим.

Проверка
выполнимости предпосылок МНК множественной регрессии. Статистика
Дарбина-Уотсона для множественной регрессии

Статистическая значимость коэффициентов множественной
регрессии и близкое к единице значение коэффициента детерминации R²
не гарантируют высокое качество уравнения множественной регрессии. Поэтому
следующим этапом проверки качества уравнения множественной регрессии является
проверка выполнимости предпосылок МНК. Причины и последствия невыполнимости
этих предпосылок, методы корректировки регрессионных моделей будут рассмотрены
в последующих главах. В данном параграфе рассмотрим популярную в регрессионном
анализе статистику Дарбина-Уотсона.

При статистическом анализе уравнения регрессии на начальном
этапе часто проверяют выполнимость одной предпосылки: условия статистической
независимости отклонений между собой.

При этом проверяется некоррелированность соседних величин e_i,
i=1,2,…n.

Для анализа коррелированности отклонений используют
статистику Дарбина-Уотсона:

 

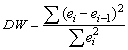
Критические значения d₁ и d₂
определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n и количества объясняющих переменных m.

Автоматический
расчет

Полностью произвести подобный расчет можно автоматически,
используя популярный сервис Множественная регрессия (с оформлением в Word)

Частные
коэффициенты корреляции при множественной регрессии

Частные коэффициенты (или индексы) корреляции, измеряющие
влияние на у фактора х_i при неизменном уровне других факторов
определяются по стандартной формуле линейного коэффициента корреляции, т.е.
последовательно берутся пары yx₁,yx₂,., x₁x₂,
x₁x₃ и так далее и для каждой пары находится коэффициент
корреляции Вычисления в MS Excel. Матрицу парных коэффициентов корреляции
переменных можно рассчитать, используя инструмент анализа данных Корреляция.

Для этого:

) Выполнить команду Сервис / Анализ данных / Корреляция.

) Указать диапазон данных;

Проверка
общего качества уравнения множественной регрессии

Для этой цели, как и в случае множественной регрессии,
используется коэффициент детерминации R2:

Справедливо соотношение 0 < =R2 < = 1. Чем ближе
этот коэффициент к единице, тем больше уравнение множественной регрессии
объясняет поведение Y.

Для множественной регрессии коэффициент детерминации является
неубывающей функцией числа объясняющих переменных.

Добавление новой объясняющей переменной никогда не уменьшает
значение R2, так как каждая последующая переменная может лишь дополнить, но
никак не сократить информацию, объясняющую поведение зависимой переменной.

Иногда при расчете коэффициента детерминации для получения
несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби
делается поправка на число степеней свободы, т.е. вводится так называемый
скорректированный (исправленный) коэффициент детерминации:

Соотношение может быть представлено в следующем виде:

  для m>1.

С ростом значения m скорректированный коэффициент
детерминации растет медленнее, чем обычный. Очевидно, что только при R²
= 1.  может принимать
отрицательные значения.

Доказано, что  увеличивается при добавлении новой объясняющей
переменной тогда и только тогда, когда t-статистика для этой переменной по
модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных
осуществляется до тех пор, пока растет скорректированный коэффициент
детерминации.

Рекомендуется после проверки общего качества уравнения
регрессии провести анализ его статистической значимости. Для этого используется
F-статистика:

Показатели F и R2 равны или не равен нулю одновременно. Если
F=0, то R²=0, следовательно, величина Y линейно не зависит от X₁,X₂,…,X_m.
Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого
уровня значимости α и чисел степеней свободы
v₁ = m и v₂ = n — m — 1, определяется на
основе распределения Фишера. Если F > Fкр, то R2 статистически значим.

 

2.2
Информационное обеспечение множественной регрессии

По данным, представленным в таблице 2, изучается зависимость
объёма валового национального продукта Y (млрд. долл.) от следующих переменных:
Х₁ — потребление, млрд. долл., Х₂ — инвестиции, млрд. долл.

Таблица 2.

	1	2	3	4	5	6	7	8	9	10
Y	8	9,5	11	12	13	14	15	16,5	17	18
Х1	1,65	1,8	2,0	2,1	2,2	2,4	2,65	2,85	3,2	3,55
Х2	14	16	18	20	23	23,5	25	26,5	28,5

.        Для заданного набора данных постройте линейную
модель множественной регрессии. Оцените точность и адекватность построенного
уравнения регрессии.

2.       Дайте экономическую интерпретацию параметров модели.

.        Для полученной модели проверьте выполнение условия
гомоскедастичности остатков, применив тест Голдфельда-Квандта.

.        Проверьте полученную модель на наличие
автокорреляции остатков с помощью теста Дарбина-Уотсона.

.        Проверьте, адекватно ли предположение об
однородности исходных данных в регрессионном смысле. Можно ли объединить две
выборки (по первым 5 и остальным 5 наблюдениям) в одну и рассматривать единую
модель регрессии Y по X?

 

2.3 Числовой
пример модели множественной регрессии и выводы множественной регрессии

1.       Построим линейную модель множественной регрессии с
помощью Microsoft Office Excel. Регрессионный анализ предназначен для исследования
зависимости исследуемой переменной Y от различных факторов и отображение их
взаимосвязи в форме регрессионной модели.

В зависимости от количества включенных в модель факторов Х
модели делятся на:

Однофакторные (парная модель регрессии).

Многофакторные (модель множественной регрессии).

Линейная модель множественной регрессии имеет вид:

=b₀+ b ₁*x₁+ b ₂*x₂+…+
b _n*x_n

Для построения линейной модели множественной
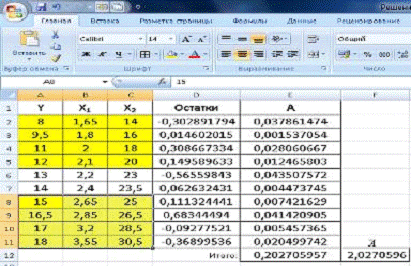
регрессии на листе Microsoft Office Excel (2007) создадим табличку с нашими
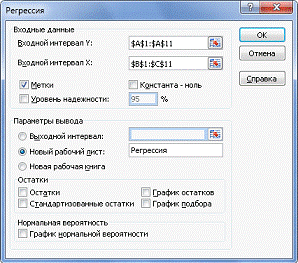
данными (Рис.1) и построим регрессию. Для этого на закладке Данные выберем
строку Анализ данных и в качестве инструмента данных — Регрессия — ок. В
открывшемся окне Регрессии зададим Входной интервал Yи Х (рис.2,3).

Рис. 1. Линейная модель множественной регрессии

Рис. 2. Окно Анализ данных

Рис. 3. Окно Регрессия.

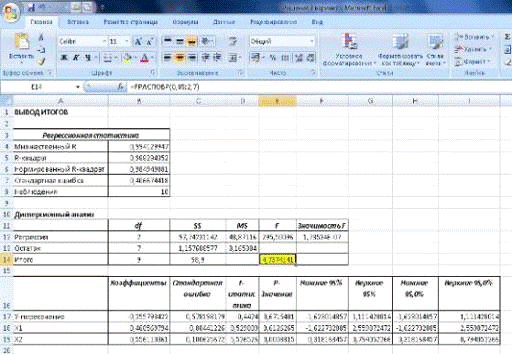
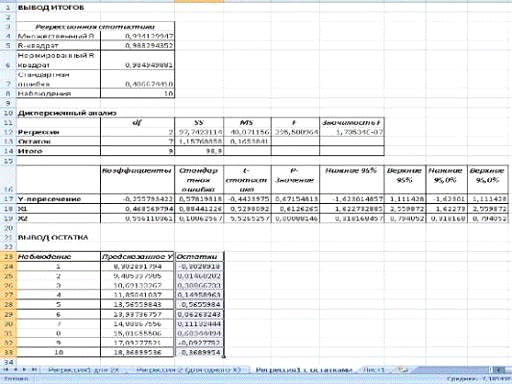
Получим результаты регрессионного анализа на новом листе Регрессия
(Рис. 4)

Рис. 4. Лист Регрессия.

По данным регрессионной статистики мы получили следующие данные:

Множественный R — это √R^2, где R² — коэффициент
детерминации.

R-квадрат —
это R². В нашем примере значение R²=0,9883 свидетельствует
о том, что изменения зависимой переменной Y (объём валового национального
продукта (ВНП)) в основном (на 98,83%) можно объяснить изменениями включенных в
модель объясняющих переменных — Х₁, Х₂ (потребление и
инвестиции). И лишь на 1,17% (100-98,83) объём ВНП зависит от других неучтённых
факторов. Такое значение свидетельствует об адекватности модели.

Нормированный R-квадрат — поправленный (скорректированный по числу степеней свободы)
коэффициент детерминации.

Стандартная ошибка регрессии S=√S², где S²=∑ (е_i²/
(n-m)) — необъясненная дисперсия (мера разброса зависимой переменной вокруг
линии регрессии); n — число наблюдений (в нашем случае 10), m — число
объясняющих переменных (в нашем примере равно 2).

Наблюдения —
число наблюдений n (10).

Рассмотрим таблицу с результатами дисперсионного анализа:

df — число
степеней свободы связано с числом единиц совокупности n и с числом определяемых
по ней констант (m+1).

SS — сумма
квадратов (регрессионная RSS, остаточная ESS и общая TSS соответственно).

MS — сумма
квадратов на одну степень свободы. MS=SS/df.

F —
расчетное значение F-критерия Фишера. Если нет табличного значения, то для
проверки значимости уравнения регрессии в целом можно посмотреть Значимость F.
На уровне значимости α=0,05
уравнение регрессии признается значимым в целом, если Значимость F<0,05, и
незначимым, если Значимость F≥0,05.

Для нашего примера имеем следующие значения:

Таблица 2

	df	SS	MS	F	Значимость F
Регрессия	m=2	RSS=97,74	RSS/df=48,87	(RSS/ESS) * ( (n-m-1) /m) =295,50	1,73534E-07
Остаток	n-m — =7	ESS=1,15	ESS/df=0,165
Итого	n-1=9	TSS= 98,9

В нашем случае расчетное значение F-критерия Фишера
составляет 295,50. Значимость F=1,74E-07, что меньше 0,05. Таким образом,
полученное уравнение в целом значимо.

В последней таблице приведены значения параметров
(коэффициентов) модели, их стандартные ошибки и расчетные значения t-критериев
Стьюдента для оценки значимости отдельных параметров модели.

Таблица 4

	Коэффи-циенты	Стандарт-ная ошибка	t-статистика	Р-значение	Нижние 95%	Верхние 95%
Y	b0=-0,26	mb0=0,58	tb0=-0,44	0,67	-1,62≤ b0≤ 1,11
X1	b1=0,47	mb1=0,88	tb1=0,53	0,61	-1,62≤ b1≤ 2,56
X2	b2=0,56	mb2=0,10	tb2=5,53	0,0008	0,32≤ b2≤ 0,79

Анализ данной таблицы позволяет сделать вывод о том, что на
уровне значимости α=0,05 значимым оказывается
лишь коэффициент при факторе X₂, так как лишь для него Р-значение
меньше 0,05. Таким образом, фактор Х₁ не существенен и его включение
в модель не целесообразно. Поскольку коэффициент регрессии в экономических
исследованиях имеют четкую экономическую интерпретацию, то границы
доверительного интервала для коэффициента регрессии не должны содержать
противоречивых результатов, как например, — 1,62≤ b₁≤
2,56. Такого рода запись указывает, что истинное значение коэффициента
регрессии одновременно содержит положительные и отрицательные величины и даже
ноль, чего не может быть. Это также подтверждает вывод о статистической
незначимости коэффициентов регрессии при факторе Х₁. Таким образом,
целесообразно исключить несущественный фактор Х_1. Но мы оставим этот
фактор, так как у нас всего 2 переменных и в случае его исключения, модель не
будет многофакторной. Поэтому мы будем иметь ввиду, что фактор Х₁ малозначим
и построим уравнение зависимости Y (объёма валового национального продукта) от значимой
объясняющей переменной X₂ (инвестиции) и незначимой Х₁
(потребление).

Оценим точность и адекватность полученной модели.

Согласно проведенной регрессионной статистики мы видим
следующие результаты:

1. Коэффициент множественной корреляции (множественный
R) равен 0,994. Следовательно, связь между факторами весьма тесная (по
шкале Чудока)

2. Значение R²=0,9883 свидетельствует о том,
что вариация зависимой переменной Y (объём валового национального продукта) в
основном (на 98,78%) можно объяснить вариацией включенных в модель объясняющих
переменных Х₂ (инвестиции) и Х₁. Это свидетельствует об
адекватности модели.

3. По результатам дисперсионного анализа мы получили
расчетное значение F-критерия Фишера, которое составляет 295,50. Рассчитаем с
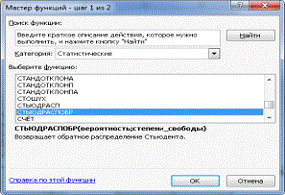
помощью Excel табличное значение Фишера (результат см. рис.7). Для этого в
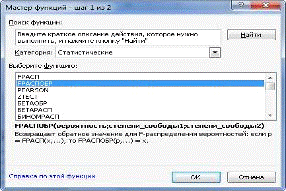
ячейке Е14 (см. рис 4) обратимся к мастеру функций f (x) и выберем категорию:
Статистические функции — функцию FРАСПОБР, как показано на рис.5.

Рис.5. Мастер функции.

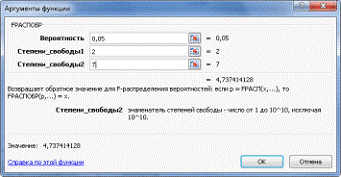
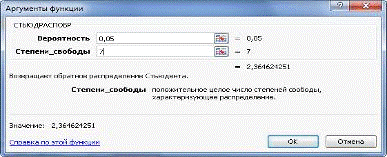
Затем зададим нужные аргументы: Вероятность α=0,05. Степень свободы 1 — количество факторов Х. Степень свободы 2 —
это число степеней свободы: n-m-1=10-2-1=7, где n — число наблюдений (в нашем
случае 10), m — число объясняющих переменных (в нашем примере равно 2) (см.
рис.6).

Рис.6. Аргументы функции (расчет табличного значения Фишера в
Microsoft Office Excel).

Рис.7. Результат расчета табличного значения Фишера с помощью
редактора Microsoft Office Excel.

Сравнивая расчетное значение F-критерия Фишера 295,50
с табличным 4,74 мы видим, что 295,50> 4,74.

Следовательно, в целом, уравнение регрессии значимо.

Значимость F=1,735*10^-7, что меньше 0,05.
Это так же говорит о значимости уравнения.

Далее оценим значимость отдельных параметров построенной
модели.

Границы доверительного интервала для коэффициентов регрессии
не содержат противоречивых результатов:

С надежностью 0,95 (с вероятностью 95%) коэффициент b₁ лежит
в интервале 0,55≤ b₁≤ 0,66.

Сравним полученное значение t-статистики с табличным, которое
рассчитаем с помощью мастера функций (рис.8,9)

Рис.8 Мастер функций.

Рис.9. Аргументы функции.

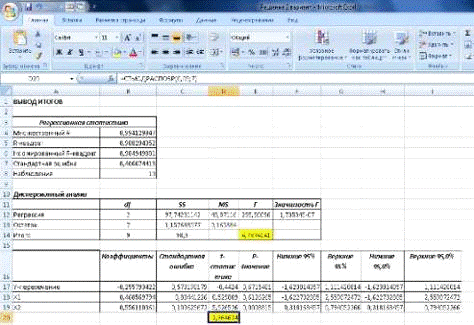
Результат расчета представлен на рис.10 в ячейке D20.

Рис.10. Результаты регрессии с рассчитанными табличными
значениями F и t-статистики.

Сравнивая расчетные значения t-статистики с табличным 2,36 мы
ещё раз убеждаемся, что значение переменной Х₁ не значимое, так как
0,53< 2,36. А значение переменной Х₂ является значимым, так как
оно больше порогового 5,52>2,36.

Таким образом, модель балансовой прибыли предприятия торговли
запишется в следующем виде:

 =-0,26+0,47*Х₁+0,57*X_2.

Теперь построим в Excel заново нашу регрессию с выведением
остатков:

Рис.11. Регрессия с остатками.

Получим:

Рис.12. Регрессия с рассчитанными остатками.

Найдём долю ошибки в Y (по модулю): ошибка аппроксимации
(выравнивания) А=||*100%. Разделим ошибку аппроксимации на
число наблюдений и получим среднюю ошибку аппроксимации:

= ∑||*100%.

Для нахождения А с помощью редактора Microsoft Office Excel
воспользуемся математическими функциями:

Рис.13. Мастер функций.

Зададим аргументы функций (рис.14.)

Рис.14. Аргументы функции.

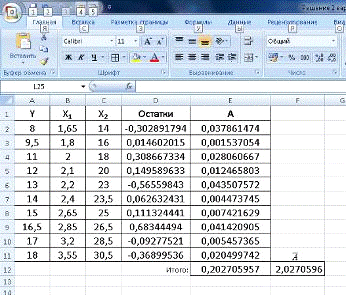
Найдём среднюю ошибку аппроксимации (рис.15)

Рис.15. Расчет ошибки аппроксимации и средней ошибки
аппроксимации.

Мы получили среднюю ошибку аппроксимации равную =2,027. Это говорит о том, что исследуемая
модель является точной (так как <10).

2.       Рассмотрим экономическую интерпретацию параметров
модели.

 =-0,26+0,47*Х₁+0,57*X_2.

Коэффициент b₁=0,47 означает, что при увеличении
потребления на 1 млрд. долл. объём валового национального продукта возрастёт на
0,47 млрд. долл. Коэффициент b₂=0,57 означает, что увеличение
инвестиций на 1 млрд. долл. приведёт к увеличению объёма валового национального
продукта на 0,57 млрд. долл.

3.       Проверим выполнение условия гомоскедастичности
остатков, применив тест Голдфельда-Квандта.

Разобьём модель на 3 части (см. рис.16). Найдём регрессию
1-ой и 3-ей части (результат на рис.17).

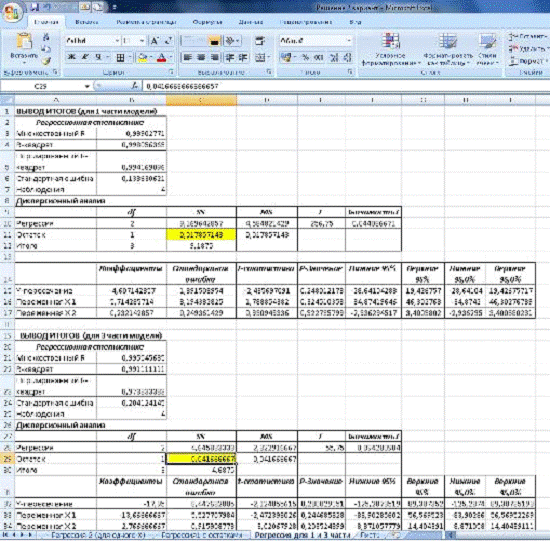
Рис.16. Модель разбили на 3 части.

Рис. 17 Регрессия для 1 и 3 частей модели.

Определим значимость модели по формуле:

На рисунке 17 видно, что для нахождения F необходимо
разделить результат ячейки С11 на результат ячейки С29. Получим:

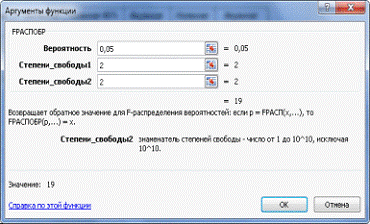
Для того, чтобы узнать табличное значение, воспользуемся
встроенной в EXCEL функцией FРАСПОБР с параметрами α=0,05. В данном случае К₁=К₂=n^| —
m=4-2=2 (см. рис. 18)

Рис. 18. Аргументы функции.

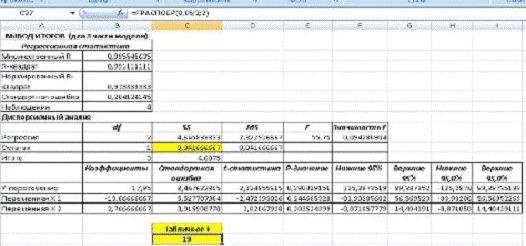
Рис. 19 Расчет табличного F.

Статистика F_расч. =0,429 меньше табличного
значения Фишера F=FРАСПОБР (0,05; 2;

) =19. Следовательно, в данной моделе отсутствует
гетероскедастичность остатков.

4.       Проверим полученную модель на наличие автокорреляции
остатков с помощью теста Дарбина-Уотсона.

Если прослеживается влияние результатов предыдущих наблюдений
на результаты последующих, случайные величины (ошибки) ɛ_i в регрессионной модели не оказываются независимыми. Такие модели
называются моделями с наличием автокорреляции.

Как правило, если автокорреляция присутствует, то наибольшее
влияние на последующее наблюдение оказывает результат предыдущего наблюдения.
Наличие автокорреляции между соседними уровнями ряда можно определить с помощью
теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле:

dw=	∑ (ɛi — ɛi-1) 2
	∑ ɛi 2

Определим его с помощью редактора EXCEL.

Таким образом, мы нашли расчетное значение dw=1,84. Найдём
табличное значение статистики Дарбина-Уотсона для m=2 и n=10. Согласно таблицы
получим d₁= 0,7 и d₂=1,64.

Значение статистики Дарбина-Уотсона распределено в интервале
от 0 до 4. Соответственно, идеальное значение статистики равно 2
(автокорреляция отсутствует). Если расчетное значение:

<dw<d₁, то присутствует положительная
автокорреляция.

-d₁<dw<4,
то присутствует отрицательная автокорреляция.₂<dw<4-d₂,
то автокорреляция отсутствует.₁<dw<d₂ и 4-d₂<dw<4-d₁,
то вопрос о наличии или отсутствии автокорреляции остается открытым (расчетное
значение попадает в зону неопределённости).

Для нахождения
автокорреляции разобьём числовую прямую.

Наше расчетное
значение dw=1,84 попадает в область, где автокорреляции нет.

.        Проверим,
адекватно ли предположение об однородности исходных данных в регрессионном
смысле. Можно ли объединить две выборки (по первым 5 и остальным 5 наблюдениям)
в одну и рассматривать единую модель регрессии Y по X?

Для проверки
предположения об однородности исходных данных в регрессионном смысле применим
тест Чоу.

В соответствии со
схемой теста построим уравнение регрессии по первым n₁=5 наблюдениям
и остальным n₂=5 наблюдениям. Результаты представлены на рис.22.

Результаты
регрессионного и дисперсионного анализа модели, построенной по всем n=n₁
+ n₂=10 наблюдениям.

Рассчитаем
статистику F по формуле:

Fрасч. =	(ESS-ESS1-ESS2) / (2+1)	=	(1,158-0,023-0,070) /3	=15,43
	(ESS1+ESS2) / (10-2*2-2)		(0,023+0,070) /4

Находим табличное значение F_табл. =FРАСПОБР (0,05;
3;

) с помощью редактора EXCEL. Получаем F_табл. =6,59.

Так как F_расч. >F_{табл. (}15,43>6,59),
то можно сделать вывод, что использовать единую модель по всем наблюдениям
нельзя, то есть объединить две выборки (по первым 5 и остальным 5 наблюдениям)
в одну и рассматривать единую модель регрессии Y по X не целесообразно.

Заключение

Итак, многочисленные наблюдения и
исследования показывают, что в окружающем нас мире величины существуют не
изолированно друг от друга, а напротив, они связаны определенным образом.

Не важно рассматриваем мы экономическую
сферу деятельности или какую-либо другую, везде существуют факторы, оказывающие
влияние на объект/итог какого-либо процесса. Для верной интерпретации этого
явления была разработаны методы математической статистики.

Наиболее простым методом, используемым в
экономике для определения зависимости переменных, является модель линейной
регрессии. Также она может случить началом эконометрического анализа. Известно
что на любой экономический показатель, как правило, оказывают влияние несколько
факторов, поэтому чаще всего при построении модели используется множественная
регрессия.

Но построение модели лишь половина дела,
необходимо быть уверенным, что она соответствует реальности. Для проводят
анализ качества модели, состоящий из нескольких этапов.

Одним из способов проверки является
проверка общего качества уравнения регрессии. Для проведения этой проверки
используют коэффициент детерминации. Этот показатель используют как
универсальную меру связи одной случайной величины от другой. После расчета
коэффициента детерминации специалисты смотрят на его величину, она может
варьироваться от нуля до единицы, чем ближе полученная цифра к единице, тем
сильнее влияние факторов на изучаемую величину.

Однако стандартный коэффициент
детерминации имеет сильную зависимость от числа факторов. Чтобы исправить этот
недостаток был веден скорректированный коэффициент детерминации. Эта величина
рассчитывается на основе обычного коэффициента и дает штраф за дополнительно
включенные факторы. Кроме того его можно применять для сравнении моделей с
разным числом факторов или при последовательность включении факторов в модель с
целью выяснения их влияния на зависимую переменную.

По итогам проведенных расчетов мною была
построена модель множественной линейной регрессии и на ее основе рассчитаны
коэффициенты детерминации, общий и скорректированный. Была выявлена обратная
зависимость между количеством малоимущего населения и количеством безработного
населения и среднедушевого дохода. Эта зависимость подтверждает, что чем больше
значение детерминирующего фактора А, тем ниже значения факторов Б и В. Кроме
того, полученные мною результаты доказывают целесообразность использования в
анализе данных такого показателя как скорректированный коэффициент детерминации
чтобы получать оценку тесноты связи, не зависящую от числа факторов.

Список
использованных источников

1.       Айвазян
С.А. Методы эконометрики. Учебник. — М.: Инфра-М, 2010.

2.       Айвазян
С.А., Иванова С.С. Эконометрика. Краткий курс. Учебное пособие. — М.: Маркет
ДС, 2010.

.        Белько
И.В., Криштапович Е.А. Эконометрика. Практикум. Учебное пособие. — М.:
Издательство Гревцова, 2011.

.        Валентинов
В.А. Эконометрика. Практикум. — М.: Дашков, 2009

.        Валентинов
В.А. Эконометрика. Учебник. — М.: Дашков, 2010.

.        И.И.
Елисеева, «Эконометрика», Москва — 2007 г.

.        Молчанов
И.Н., Герасимова И. А, «Компьютерный практикум по начальному курсу
эконометрики (реализация на Eviews)», Ростов-н/Д., — 2001.

.        Мхитарян
В.С. Эконометрика. Учебник. — М.: Проспект, 2010.

.        Сайт
Федеральной служба государственной статистики: www.gks.ru

.        Эконометрика.
Учебник. / Елисеева И.И., Курышева С.В., Нерадовская Ю.В. Под ред. И.И.
Елисеевой. — М.: Проспект, 2010.

4. 
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.

5. 
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).

При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:

1. 
Каковы признаки качественной
модели?

2. 
Какие ошибки спецификации могут
быть?

3. 
Каковы последствия ошибок
спецификации?

4. 
Какие существуют методы
обнаружения и устранения ошибок спецификации?

Рассмотрим основные признаки качественной модели
множественной регрессии:

1. 
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.

2. 
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.

3. 
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.

4. 
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.

5. 
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.

Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.

Различают следующие виды ошибок спецификации:

1. 
Невключение в модель полезной
(значимой) переменной.

2. 
Добавление в модель лишней
(незначимой) переменной

3. 
Выбор неправильной функциональной
формы модели

Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.

При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.

Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.

Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R².

Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.

Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

Тема 1: Спецификация эконометрической модели

1. Ошибки спецификации эконометрической модели имеют место вследствие …

неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора

недостоверности или недостаточности исходной информации

неоднородности данных в исходной статистической совокупности

недостаточного количества данных

Решение:

Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.

2. Для регрессионной модели вида 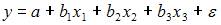необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

Решение:

Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».

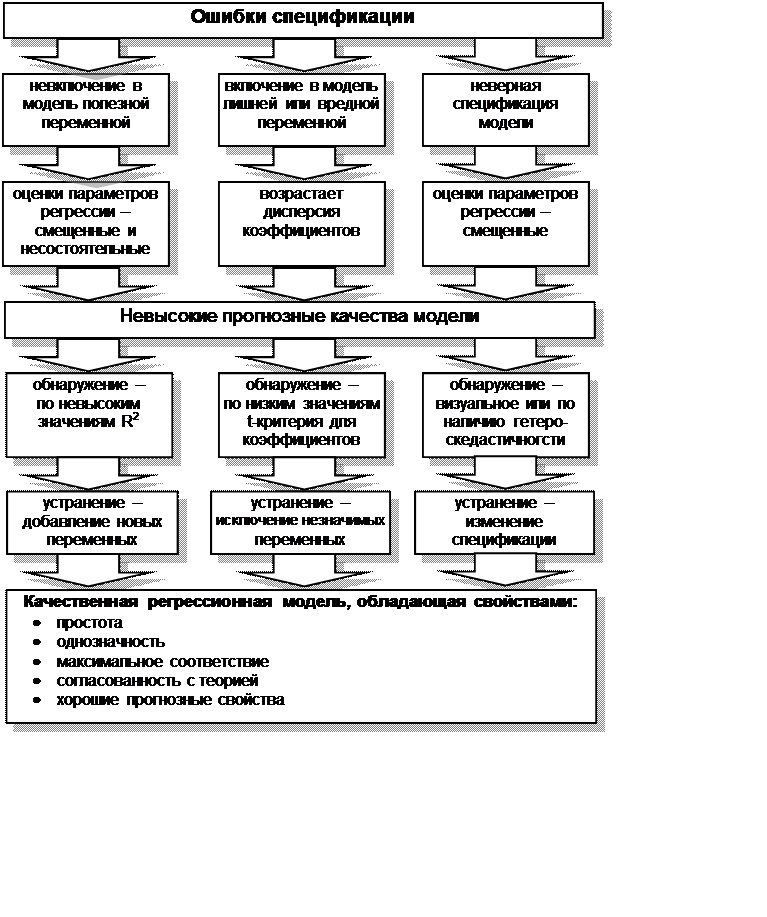
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

Решение:

Из приведенных функций только в функции параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.

4. В модели вида 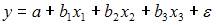количество объясняющих переменных равно …

Решение:

Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; x_j – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, b_j – параметры (a – свободный член уравнения, b_j – коэффициент регрессии); – случайные факторы. Независимые переменные x_j называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии b_j. Поэтому количество объясняющих переменных в модели равно 3.

5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …

Решение:

При оценке модели множественной регрессии рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.

Тема 2: Отбор факторов, включаемых в модель множественной регрессии

1. В модели множественной регрессии 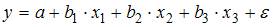определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …

Решение:

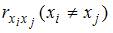
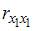
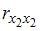
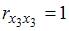
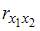
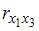
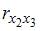
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы были бы равны нулю.
, поскольку = = и = = =0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.

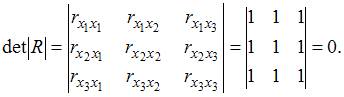
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

Решение:

Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, b_j – параметры (a – свободный член уравнения, b_j – коэффициент регрессии); – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x₁ и x₂.

Ошибка спецификации эконометрической модели уравнения регрессии

Ошибка спецификации

К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. [c.36]

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]

В чем состоят ошибки спецификации модели [c.88]

Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]

Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]

Рис. 5.4. Ошибка спецификации при выборе уравнения тренда

Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]

Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]

Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]

Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]

Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]

Как обнаружить ошибку спецификации [c.190]

Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]

Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]

При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]

Как можно обнаружить ошибки спецификации [c.202]

Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]

Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]

Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]

Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]

Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]

PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]

Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]

Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]

Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]

Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]

Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]

Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]

Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]

Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]

Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]

Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]

В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]

Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]

Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]

Смотреть страницы где упоминается термин Ошибка спецификации

Экономико-математический словарь Изд.5 (2003) — [ c.338 ]

Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие

Название	Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
Дата	02.02.2019
Размер	1.2 Mb.
Формат файла
Имя файла	Baza_po_ekonometrike.doc
Тип	Документы #66133
страница	1 из 4