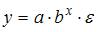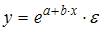Построение
математической модели — это скорее
искусство, чем наука, и, прежде всего,
требует глубоких знаний предметной
области. Социально-экономические системы
имеют чрезвычайно сложную структуру,
со многими явными и неявными взаимосвязями
между элементами системы, подвержены
влиянию многих скрытых факторов,
относятся к классу так называемых
больших систем. Стечением
времени меняются не только их
характеристики, учитываемые в модели
в виде отдельных параметров, но и
структура самих уравнений, которые
описывают процесс. Для их адекватного
описания требуется соответствующий
математический аппарат. Однако, даже
самые сложные математические методы
не в состоянии описать реальную систему
во всех ее деталях, да это и не нужно.
Модель не должна быть слишком сложной.
Излишняя детализация и учет второстепенных
факторов затрудняет
исследование
и не дает существенной информации об
изучаемой системе. Если модель слишком
сложна, то ее трудно использовать и
интерпретировать на практике.
Относительная
простота — важная характеристика
удачно построенной модели.
С другой стороны, слишком упрощенная
модель не будет адекватно описывать
реальную систему. Таким образом, сложность
модели должна соответствовать сложности
изучаемого экономического объекта.
В связи
с этим возникает необходимость
формулировки некоторых разумных
упрощающих гипотез (предположений),
исключения из анализа второстепенных
факторов и т. п., с тем, чтобы была
возможность описать процесс математически.
При этом существенные для
данного
социально-экономического процесса
характерные черты
должны
быть учтены в модели в соответствии с
поставленной целью исследования.
Другой
характерной проблемой, с которой
сталкивается эконометрист, является
то, что часто приходится довольствоваться
неточными
данными,
которые имеются в наличии и быстро
устаревают. Этих данных не всегда
хватает, а провести управляемый
эксперимент с целью получения
дополнительной информации невозможно.
В подобном случае целесообразно сочетание
количественных методов с привлечением
экспертных знаний и суждений.
Таким
образом, при создании эконометрической
модели возникают следующие вопросы.
1.
Какую модель желательно построить —
статическую или динамическую (с
учетом фактора времени), нелинейную или
линеаризованную? Как учесть влияние
внешней среды (возмущений)? (Ответ на
эти вопросы определяет желаемую точность
и сложность модели, выбор адекватного
математического аппарата и т. д.)
2.
Достаточно
ли имеющихся данных, необходимых для
построения адекватной модели,
насколько они достоверны? Существует
ли возможность получения дополнительной
информации, если это необходимо? Следует
ли привлечь экспертную информацию?
3. Как
оценить качество модели, т. е. определить,
насколько адекватно (правильно) она
описывает поведение реального объекта?
В
рамках эконометрического подхода
существует мощный арсенал средств,
который включает многие современные
эффективные
математические методы,
такие, например, как аппарат
нейронных сетей,
и разработанные на их основе компьютерные
технологии, в известной степени помогающие
справиться с этими проблемами. Но
решающая
роль принадлежит специалисту —
эконометристу.
Окончательный успех зависит от его
способности к неформальному анализу
проблемной ситуации, адекватной оценке
возможностей современных эконометрических
методов, от их правильного применения
и интерпретации полученных результатов.
Построив
удачную математическую модель и оценив
ее количественно с использованием
эконометрических методов, экономист-аналитик
получает в распоряжение эффективнейшее
средство анализа и прогноза, а
управляющий-практик — инструмент для
обоснования управленческих решений.
Такие модели широко применяются на
практике.
Практически
величина y
складывается из двух слагаемых:
,
где
— фактическое
значение, результат признака;
— теоретическое
значение результата признака, найденное
из математической модели или уравнения
регрессии;
— СВ, характерное
отклонение реального значения результата
признака от теоретического.
СВ
называется
возмущением. Она включает влияние
неучтённых в модели факторов, случайных
ошибок и особенно измерения. Её присутствие
в модели порождено тремя источниками:
-
спецификацией
модели; -
выборочным
характером исходных данных; -
особенностями
измерения.
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем больше теоретические
значения результативного признака
подходит к фактическим данным y.
К ошибкам спецификации
будут относиться не только неправильный
выбор той или иной математической
функции для
,
но и недоучет в УР какого-либо существенного
фактора (например, использование парной
регрессии вместо множественной).
Наряду с ошибками
спецификации могут иметь место ошибки
выборки (неоднородность данных в исходной
статистической совокупности). Если
совокупность неоднородна, то УР не имеет
практического смысла.
Для получения
хорошего результата обычно исключают
из совокупности единицы с аномальными
значениями исследуемых признаков, то
есть результаты регрессии представляют
собой выборочные характеристики.
Наибольшую опасность
в практическом использовании методов
регрессии представляют ошибки
измерения.
Если ошибки спецификации можно уменьшить,
изменяя форму модели, а ошибки выборки
– увеличивая объём исходных данных, то
ошибки измерения практически сводят
на нет все усилия по количественной
оценке связи между признаками. Особенно
велика роль ошибок измерения при
исследовании на макроуровне.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
04.08.2019218.11 Кб0kv.doc
- #
- #
- #
Содержание
- Types Of Specification Errors
- ECONOMETRIC MODELING
- RELAXING THE ASSUMPTIONS OF THE CLASSICAL MODEL
- 2.2.Спецификация переменных в уравнение регрессии. Ошибки спецификации.
- Тестирование ошибки спецификации уравнения регрессии
- 2.2.6. Учёт некоторых нарушений стандартных предположений о модели
Types Of Specification Errors
Assume that on the basis of the criteria just listed we arrive at a model that we accept as a good model. To be concrete, let this model be
Yi = ft ft Xi ft X ft X3 Uli (13.2.1)
where Y = total cost of production andX = output. Equation (13.2.1) is the familiar textbook example of the cubic total cost function.
But suppose for some reason (say, laziness in plotting the scattergram) a researcher decides to use the following model:
Yi = ai a2 Xi a3 X2 Ui (13.2.2)
Note that we have changed the notation to distinguish this model from the true model.
Since (13.2.1) is assumed true, adopting (13.2.2) would constitute a specification error, the error consisting in omitting a relevant variable (X3). Therefore, the error term u2i in (13.2.2) is in fact
U2i = U1i ft X3 (13.2.3)
We shall see shortly the importance of this relationship.
Now suppose that another researcher uses the following model:
Yi = ft ft Xi A 3 X> ft X3 ft X4 U3i (13.2.4)
If (13.2.1) is the «truth,» (13.2.4) also constitutes a specification error, the error here consisting in including an unnecessary or irrelevant variable
in the sense that the true model assumes ft to be zero. The new error term is in fact
u3i = u1i — ftX4 = u1i since ft = 0 in the true model (Why?)
Now assume that yet another researcher postulates the following model:
ln Yi = Y1 Y2 Xi Y3 Xf Y4 X3 m (13.2.6)
In relation to the true model, (13.2.6) would also constitute a specification bias, the bias here being the use of the wrong functional form: In (13.2.1) Y appears linearly, whereas in (13.2.6) it appears log-linearly.
ECONOMETRIC MODELING
Finally, consider the researcher who uses the following model:
Y* = fa* fa2* X* fa X*2 fa X*3 u* (13.2.7)
where Y* = Y* e* and X* = X* w*, e* and w* being the errors of measurement. What (13.2.7) states is that instead of using the true Y and X* we use their proxies, Y* and X*, which may contain errors of measurement. Therefore, in (13.2.7) we commit the errors of measurement bias. In applied work data are plagued by errors of approximations or errors of incomplete coverage or simply errors of omitting some observations. In the social sciences we often depend on secondary data and usually have no way of knowing the types of errors, if any, made by the primary data-collecting agency.
Another type of specification error relates to the way the stochastic error u* (or ut) enters the regression model. Consider for instance, the following bivariate regression model without the intercept term:
Y = fa XiUi (13.2.8)
where the stochastic error term enters multiplicatively with the property that ln u* satisfies the assumptions of the CLRM, against the following model
Y = a X* U (13.2.9)
where the error term enters additively. Although the variables are the same in the two models, we have denoted the slope coefficient in (13.2.8) by fa and the slope coefficient in (13.2.9) by a. Now if (13.2.8) is the «correct» or «true» model, would the estimated a provide an unbiased estimate of the true fa? That is, will E(a) = fa ? If that is not the case, improper stochastic specification of the error term will constitute another source of specification error.
To sum up, in developing an empirical model, one is likely to commit one or more of the following specification errors:
- Omission of a relevant variable(s)
- Inclusion of an unnecessary variable(s)
- Adopting the wrong functional form
- Errors of measurement
- Incorrect specification of the stochastic error term
Before turning to an examination of these specification errors in some detail, it may be fruitful to distinguish between model specification errors and model mis-specification errors. The first four types of error discussed above are essentially in the nature of model specification errors in that we have in mind a «true» model but somehow we do not estimate the correct model. In model mis-specification errors, we do not know what the true model is to begin with. In this context one may recall the controversy
RELAXING THE ASSUMPTIONS OF THE CLASSICAL MODEL
The monetarists give primacy to money in explaining changes in GDP, whereas the Keynesians emphasize the role of government expenditure to explain changes in GDP. So to speak, there are two competing models.
Источник
2.2.Спецификация переменных в уравнение регрессии. Ошибки спецификации.
Построение математической модели — это скорее искусство, чем наука, и, прежде всего, требует глубоких знаний предметной области. Социально-экономические системы имеют чрезвычайно сложную структуру, со многими явными и неявными взаимосвязями между элементами системы, подвержены влиянию многих скрытых факторов, относятся к классу так называемых больших систем. Стечением времени меняются не только их характеристики, учитываемые в модели в виде отдельных параметров, но и структура самих уравнений, которые описывают процесс. Для их адекватного описания требуется соответствующий математический аппарат. Однако, даже самые сложные математические методы не в состоянии описать реальную систему во всех ее деталях, да это и не нужно. Модель не должна быть слишком сложной. Излишняя детализация и учет второстепенных факторов затрудняет
исследование и не дает существенной информации об изучаемой системе. Если модель слишком сложна, то ее трудно использовать и интерпретировать на практике. Относительная простота — важная характеристика удачно построенной модели. С другой стороны, слишком упрощенная модель не будет адекватно описывать реальную систему. Таким образом, сложность модели должна соответствовать сложности изучаемого экономического объекта.
В связи с этим возникает необходимость формулировки некоторых разумных упрощающих гипотез (предположений), исключения из анализа второстепенных факторов и т. п., с тем, чтобы была возможность описать процесс математически. При этом существенные для данного социально-экономического процесса характерные черты должны быть учтены в модели в соответствии с поставленной целью исследования.
Другой характерной проблемой, с которой сталкивается эконометрист, является то, что часто приходится довольствоваться неточными данными, которые имеются в наличии и быстро устаревают. Этих данных не всегда хватает, а провести управляемый эксперимент с целью получения дополнительной информации невозможно. В подобном случае целесообразно сочетание количественных методов с привлечением экспертных знаний и суждений.
Таким образом, при создании эконометрической модели возникают следующие вопросы.
1. Какую модель желательно построить — статическую или динамическую (с учетом фактора времени), нелинейную или линеаризованную? Как учесть влияние внешней среды (возмущений)? (Ответ на эти вопросы определяет желаемую точность и сложность модели, выбор адекватного математического аппарата и т. д.)
2. Достаточно ли имеющихся данных, необходимых для построения адекватной модели, насколько они достоверны? Существует ли возможность получения дополнительной информации, если это необходимо? Следует ли привлечь экспертную информацию?
3. Как оценить качество модели, т. е. определить, насколько адекватно (правильно) она описывает поведение реального объекта?
В рамках эконометрического подхода существует мощный арсенал средств, который включает многие современные эффективные математические методы, такие, например, как аппарат нейронных сетей, и разработанные на их основе компьютерные технологии, в известной степени помогающие справиться с этими проблемами. Но решающая роль принадлежит специалисту — эконометристу. Окончательный успех зависит от его способности к неформальному анализу проблемной ситуации, адекватной оценке возможностей современных эконометрических методов, от их правильного применения и интерпретации полученных результатов.
Построив удачную математическую модель и оценив ее количественно с использованием эконометрических методов, экономист-аналитик получает в распоряжение эффективнейшее средство анализа и прогноза, а управляющий-практик — инструмент для обоснования управленческих решений. Такие модели широко применяются на практике.
Практически величина y складывается из двух слагаемых:
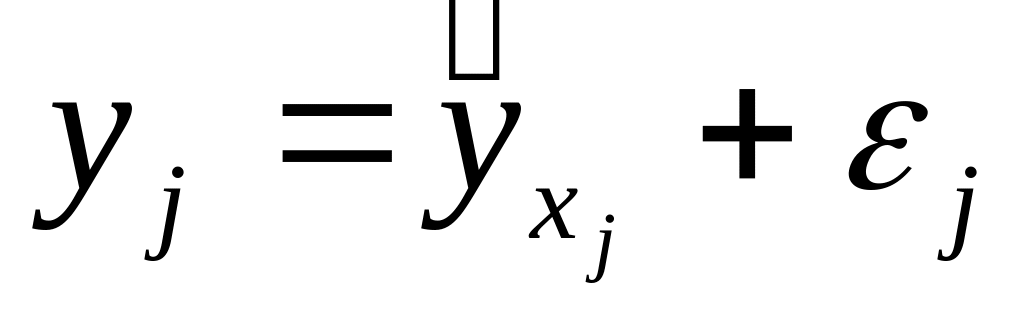
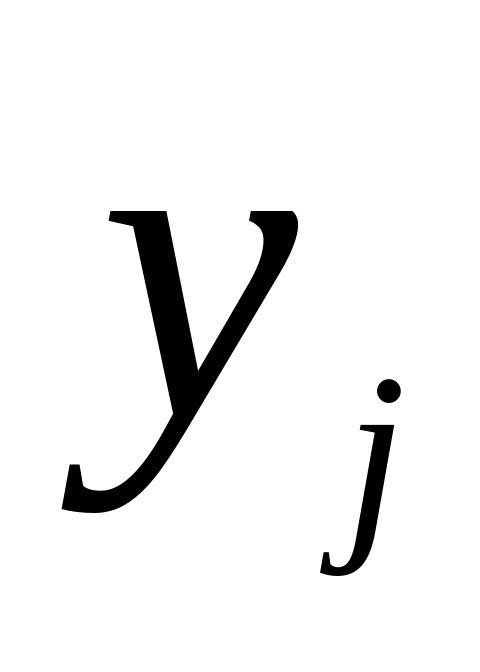
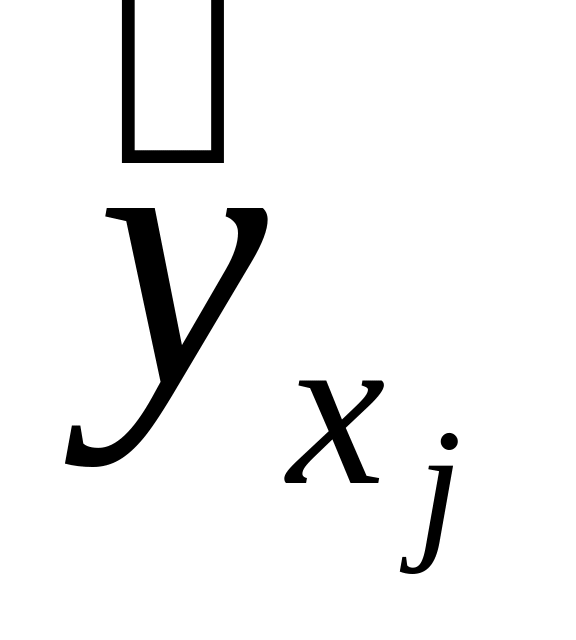
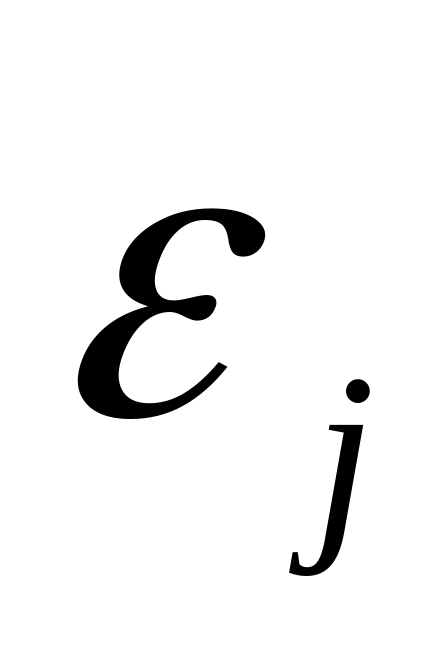
СВ 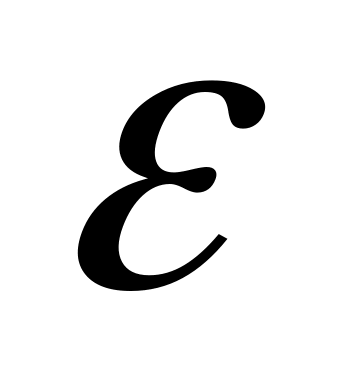
выборочным характером исходных данных;
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем больше теоретические значения результативного признака 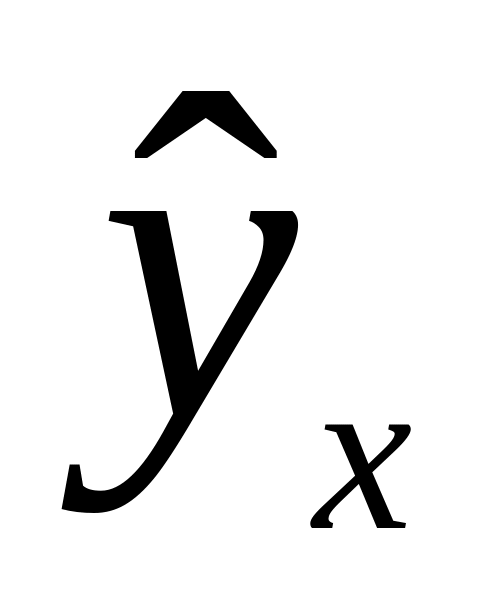
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для , но и недоучет в УР какого-либо существенного фактора (например, использование парной регрессии вместо множественной).
Наряду с ошибками спецификации могут иметь место ошибки выборки (неоднородность данных в исходной статистической совокупности). Если совокупность неоднородна, то УР не имеет практического смысла.
Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков, то есть результаты регрессии представляют собой выборочные характеристики.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели, а ошибки выборки – увеличивая объём исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.
Источник
Тестирование ошибки спецификации уравнения регрессии
Как уже отмечалось, среди предпосылок МНК присутствует предпосылка о нулевом математическом ожидании остатков регрессионной модели и, если при этом остатки и регрессоры независимы, оценки параметров уравнения регрессии будут несмещёнными. Тестирование предположения о том, что в рамках нормальной линейной модели M(
При помощи этого критерия можно выявить:
• наличие пропущенных переменных (т.е. невключение в правую часть уравнения некоторых существенных переменных);
• неправильную функциональную форму представления переменных (например, использование логарифмов переменных вместо их уровней);
• наличие корреляции между объясняющими переменными и остатками уравнения регрессии.
Рассмотрим идею этого теста, реализованного в пакете EViews. В этом тесте сначала оценивается исходная модель и по ней находятся расчётные значения зависимой переменной 
Затем оценивается вспомогательная модель, в которую помимо исходных переменных включаются несколько слагаемых вида 
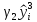

Например, исходная модель имеет вид 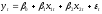

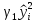


В рамках этой модели проверяется гипотеза
H : 

Эту гипотезу можно тестировать с помощью обычного F-теста. Обычно этот тест применяется при небольших значениях r =1,2,3.
Идея этого теста заключается в том, что добавлением нелинейных членов в уравнение регрессии не удаётся улучшить его качество.
2.2.6. Учёт некоторых нарушений стандартных предположений о модели
Рассмотрим кратко один из вариантов решения проблем, возникающих при наличии автокорреляции и гетероскедастичности в остатках регрессионных уравнений. Как уже отмечалось, в этих случаях МНК-оценки параметров уравнений регрессии будут состоятельными и несмещёнными, но несостоятельными и смещёнными могут оказаться ошибки этих оценок. В связи с этим одним из методов коррекции статистических выводов состоит в использовании обычных МНК-оценок, со скорректированными стандартными ошибками этих оценок, с учётом их автокорреляции и гетероскедастичности .
Рассмотрим эти два случая по отдельности. Предположим, что после оценивания параметров модели каким-либо методом было выяснено, что имеет место гетероскедастичность остатков этой модели при отсутствии какой-либо автокорреляции. Поскольку сами оценки при этом будут несмещёнными, то для верных статистических выводов достаточно будет скорректировать стандартные ошибки этих оценок. Одним из вариантов получения скорректированных на гетероскедастичность стандартных ошибок 
Оценка Уайта строится на основе явного выражения для ковариационной матрицы вектора оценок коэффициентов линейной эконометрической модели, в которой ошибки хотя и имеют нулевые математические ожидания, но не являются одинаково распределёнными, т. е. с разными дисперсиями, но взаимно независимы. Тогда ковариационная матрица остатков примет вид Cov(

Понятно, что это не единственный вариант корректировки последствий гетероскедастичности остатков уравнения регрессии. Иногда достаточно изменить вид зависимости или преобразовать переменные (например, перейти к логарифмам объясняемых переменных вместо их исходных значений).
Пусть теперь имеем более сложный случай, когда остатки не только гетероскедастичны, но и автокоррелированы. Поскольку последствия автокорреляции в остатках аналогичны уже рассмотренным в случае их гетероскедастичности, можно воспользоваться аналогичной процедурой коррекции статистических выводов и при автокоррелированных остатках.
Один из вариантов получения скорректированных на автокоррелированность и гетероскедастичность значений 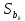
Следует отметить, что автокореляция в остатках может появиться и потому, что при выборе объясняющих переменных была пропущена значимая переменная, и её влияние на зависимую переменную будет отражаться на поведении остатков. Кроме того, автокорреляция в остатках может появиться и при не правильном выборе вида зависимости. Ясно, что в этих случаях простой коррекцией ошибок оценок не обойтись. Необходимо провести более тщательный анализ при определении спецификации уравнения регрессии. Подобные ошибки в спецификации уравнения регрессии вряд ли удастся нейтрализовать описанными методами.
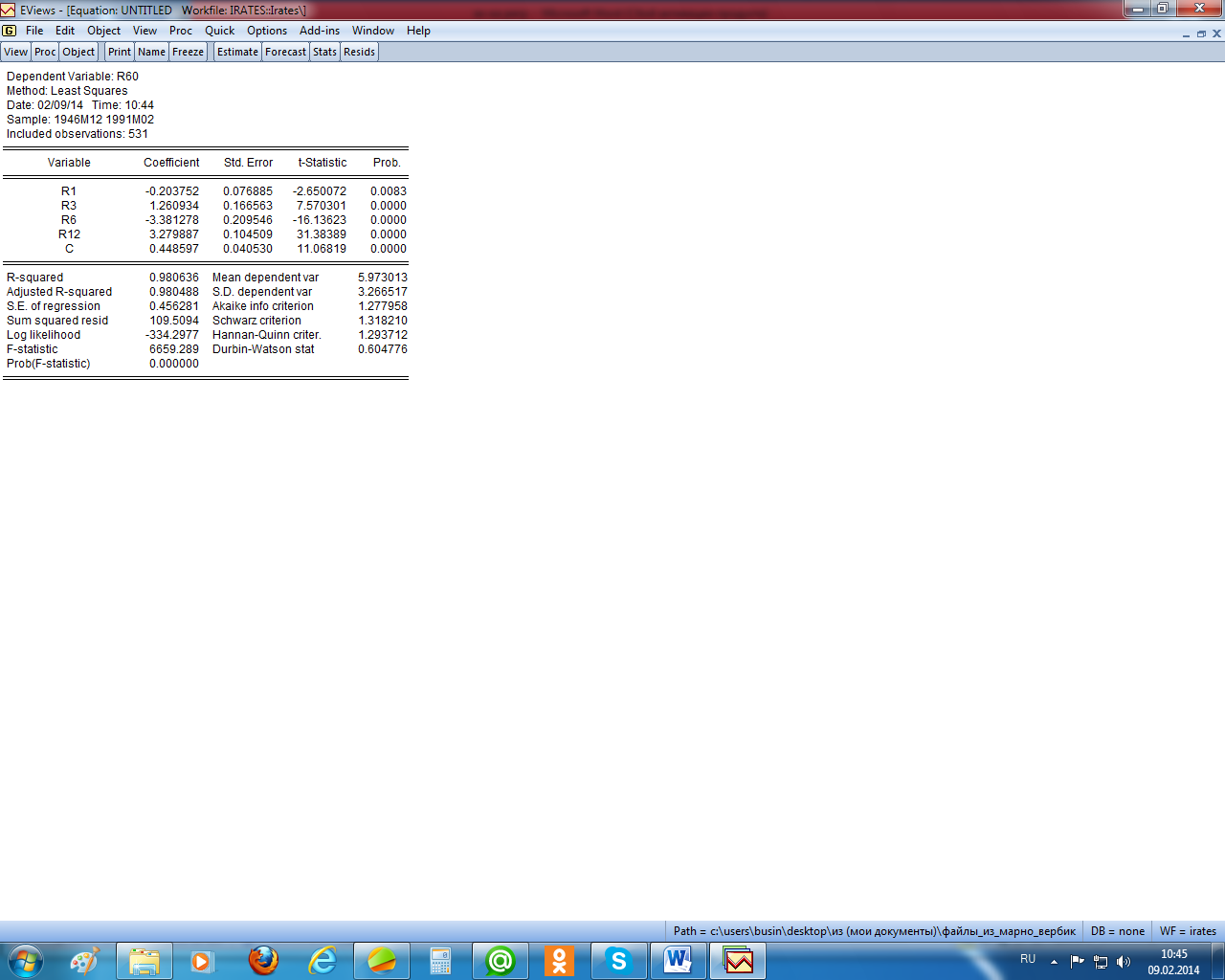
Пример 2. Тестирование предпосылок МНК
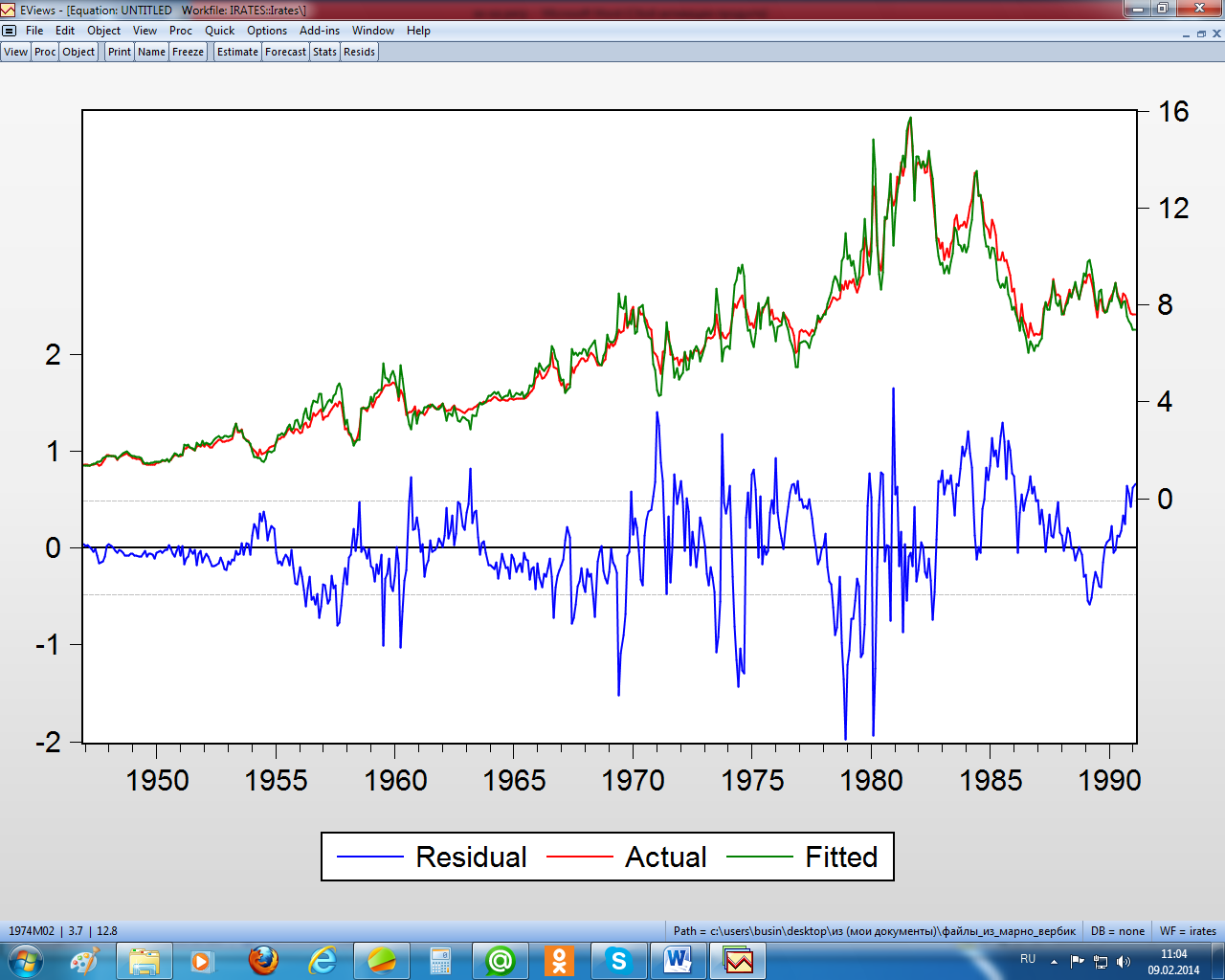
Проиллюстрируем вышеизложенные положения на условном примере, в котором описывается зависимость пятилетних процентных ставок (r60) от одномесячных (r1), квартальных (r3) , полугодовых (r6) и годовых (r12) процентных ставок (данные взяты из М. Вербик, 2008). На рисунке 2.6 приведены графики этих переменных.
Рисунок 2.6 – Графики динамики анализируемых переменных
На рисунке 2.6 видим, что анализируемые переменные изменяются во времени почти параллельно, что может быть причиной их коллинеарности, в чём действительно убеждаемся, просмотрев матрицу парных коэффициентов корреляции (рисунок 2.7). Все коэффициенты корреляции между независимыми переменными оказались больше 0,9. В этом случае «доверять» коэффициентам уравнения не рекомендуется.
Рисунок 2.7. – Матрица парных коэффициентов корреляции
Рисунок 2.8 – «Полное» уравнение регрессии
Рисунок 2.9 – Уравнение регрессии с исключённой переменной
Как известно, мультиколлинеарность искажает смысл коэффициентов регрессии и делает их неустойчивыми. «Полное» уравнение регрессии не позволяет проследить последствия мультиколлинеарноси. Разве что малое значение статистики Дарбина – Уотсона указывает на наличие автокорреляции первого порядка (рисунок 2.8). Но относить этот факт на счёт мультиколлинеарности вряд ли корректно.
Попробуем проверить устойчивость коэффициентов регрессии, удалив из регрессии одну из переменных. Пусть это будет r3 (рисунок 2.9). Как видим, действительно коэффициенты «сокращённого» уравнения существенно отличаются от коэффициентов исходного уравнения. Кроме того, что коэффициенты значимо отличаются от их исходных значений по величине, сменился даже знак коэффициента при переменной r1. При этом точность уравнения регрессии с исключённой переменной значимо не изменилась. Разве что уменьшилось значение статистики Дарбина – Уотсона, что означает, что имеет место существенная автокорреляция первого порядка.
Рисунок 2.10 – Графики остатков, фактических и расчётных значений зависимой переменной
На рисунке 2.10 чётко просматривается наличие автокорреляции и гетероскедастичности остатков. Протестируем эти остатки по всем предпосылкам МНК.
Рисунок 2.11 – Гистограмма остатков регрессии и тест Jarque – Bera
Сначала проверим их на нормальный закон распределения (рисунок 2.11). Тест Jarque – Bera показывает, что гипотезу о нормальном законе следует отклонить, т. к. расчётный уровень значимости (Probability) меньше 0,05. У этого распределения асимметрия отрицательна – более «тяжёлый» левый хвост распределения, а эксцесс значимо больше трёх – более островершинное распределение по сравнению с нормальным. Как уже отмечалось, значимое влияние на свойство оценок этот факт не оказывает.
Рисунок 2.12 – Тест Breusch – Godfrey на автокорреляцию остатков
Протестируем остатки на автокорреляцию на основе теста Breusch – Godfrey (рисунок 2.12). На второй строчке отчёта о тесте Obs*-squared – это nR 2 , расчётный уровень значимости для статистики теста – это Prob. Chi-Square (4). Для тестирования по этому тесту было выбрано 4 лаговых значения для остатков, т. е. тестировалась автокорреляция до 4–го порядка. Prob. Chi-Square(4) = 0,0, что меньше 0,05, значит гипотеза об отсутствии автокорреляции отклоняется.
Просматривая уравнение теста, видим, что имеется автокорреляция первого и четвёртого порядков, т. к. коэффициенты при RESID(–1) и RESID(–4) значимо отличаются от нуля 0 (расчётный уровень значимости для них меньше 0,05).
Автокорреляция первого порядка была видна и на основе статистики
Дарбина – Уотсона, а здесь выяснилось, что ещё имеется автокорреляция более высокого порядка.
Протестируем остатки на гетероскедастичность по тесту Уайта (Heteroskedasticity Test White – рисунок 2.13). В нашем случае nR 2 = 96,46, расчётный уровень значимости меньше 0,05, следовательно, гипотезу о гомоскедастичности остатков отклоняем и по уравнению теста видим, что остатки зависят от произведений переменных r1, r12 и от r6, r12, а также от r12 2 .
Далее, протестируем уравнение регрессии на ошибку спецификации по Ramsey RESET-тесту (рисунок 2.14). Как видим, F-статистика теста равна 7,7 и расчётный уровень значимости (Probability) равен 0,0. Следовательно, гипотеза об отсутствии ошибки спецификации отклоняется. Из уравнения теста видно, что добавление двух нелинейных членов в уравнение регрессии несколько улучшило качество исходного уравнения (хоть и не значимо, но увеличились R 2 и 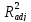
Рисунок 2.13 – Тест White на гетероскедастичность остатков регрессии
Рисунок 2.14 – Ramsey RESET-тест
RESET-тест не указывает на конкретный тип ошибочной классификации. Это дело исследователя. В нашем случае высокий уровень автокоррелированности остатков может указывать на пропуск в уравнении регрессии значимой независимой переменной.
Проиллюстрируем далее коррекцию стандартных ошибок МНК-оценок в случае их гетероскедастичности и автокоррелированности.
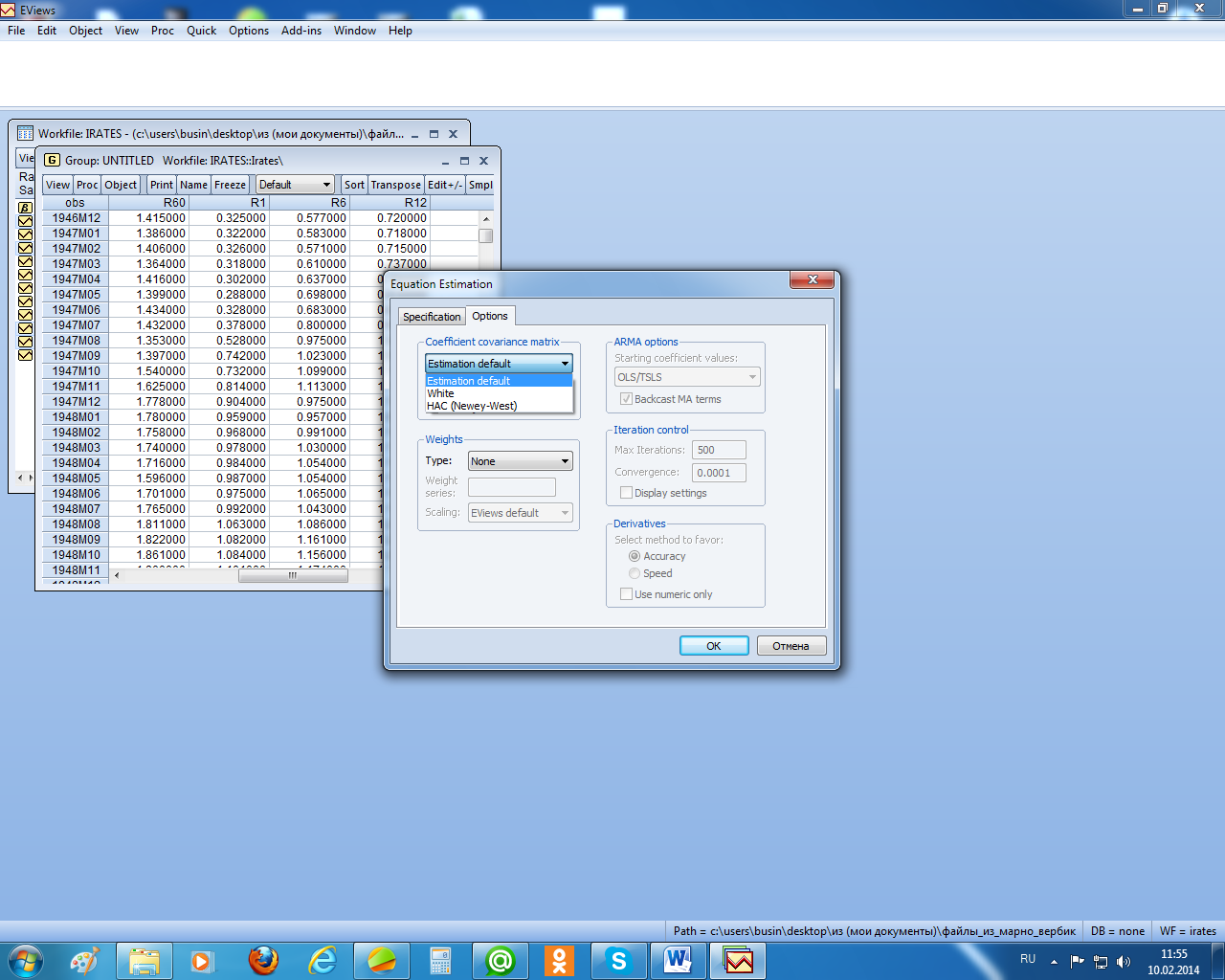
Если оценки гетероскедастичны, но в них отсутствует какая-либо автокорреляция, то, как отмечалось, скорректировать их стандартные ошибки с учётом гетероскедастичности можно, используя стандартные ошибки в форме Уайта. Чтобы реализовать эту процедуру в EViews, надо в окне специализации уравнения регрессии выбрать заставку «Options» и там выбрать в позиции «Coefficient covariance matrix» нужный метод (рисунок 2.15).
После выбора метода «White» получим (рисунок 2.16). Как видим на этом рисунке, стандартные ошибки были пересчитаны и стали больше по сравнению с аналогичными, вычисленными при использовании обычного МНК (рисунок 2.9). Значимость параметров при этом не изменилась.
А теперь проведём корректировку отклонений с помощью метода Ньюи – Веста. Здесь кроме гетероскедастичности предполагается ещё и автокорреляция остатков (см. рисунок 2.17).
Как видим, коррекция в этом случае оказалась более существенной, что привело даже к изменению значимости параметров – коэффициент при r1 оказался незначимым.
Рисунок 2.15 – Выбор процедур коррекции стандартных отклонений
Рисунок 2.16 – Стандартные ошибки в форме Уайта
Рисунок 2.17 – Стандартные ошибки в форме Ньюи – Веста
Источник
Методам простой или парной регрессии и корреляции, возможностям их применения в эконометрике посвящен данный раздел.
Любое эконометрическое исследование начинается со Спецификации модели, т. е. с формулировки вида модели исходя из соответствующей теории связи между переменными.
Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. Например, если зависимость спроса у от цены х будет характеризоваться уравнением , то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:
, (1.1)
Где – фактическое значение результативного признака;
– теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т. е. их уравнения регрессии;
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина ε, или Возмущение, Включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных и особенностями измерения переменных.
При правильно выбранной спецификации модели зависит величина случайных ошибок, поэтому, чем они меньше, тем в большей мере теоретические значения результативного признака подходят к фактическим данным
.
К ошибкам спецификации будет относится не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего работает с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении эконометрических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:
— графическим;
— аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
— экспериментальным.
При изучении зависимости между двумя признаками Графический метод подбора вида уравнения регрессии достаточно нагляден. Он базируется на поле корреляции.
Класс математических функций для описания связи двух переменных достаточно широк. Кроме уже указанных используются и другие типы кривых:
;
;
;
;
;
.
Значительный интерес представляет Аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
При обработке информации на компьютере выбор вида уравнения регрессии обычно проводится экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях.
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии , то фактические значения результативного признака совпадают с теоретическими
, т. е. они полностью обусловлены влиянием фактора х. в этом случае остаточная дисперсия Dост=0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (у-
). Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретацией ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
или
. (1.3)
Построение линейной регрессии сводится к оценке ее параметров – а и b. Классический подход к оцениванию параметров линейной регрессии основан на Методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) минимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной.
Для того чтобы найти минимум функции 1.4, надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю. Обозначим через S, тогда:



Преобразуя формулу 1.5, получим следующую систему нормальных уравнений для оценки параметров а и b:

Решая систему нормальных уравнений 1.6 либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими формулами для а и b:
. (1.7)
Формула 1.7. получена из первого уравнения системы 1.6, если все его члены разделить на n:

Где — ковариация признаков;
— дисперсия признака х.
Поскольку , а
, получим следующую формулу расчета оценки параметра b:

Формула 1.8 получается также при решении системы 1.6 методом определителей, если все элементы расчета разделить на n2.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии b показывает направление связи: при b>0 – связь прямая, а при b<0 – связь обратная.
Формально а – значение у при х=0. Если признак-фактор х не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Попытки интерпретировать экономически параметр а могут привести к абсурду, особенно при a<0. Интерпретировать можно лишь знак при параметре а. Если a>0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Имеются разные модификации формулы линейного коэффициента корреляции, например:


Значение линейного коэффициента корреляции находится в границах . Если коэффициент регрессии b>0, то 0
, и, наоборот, при b<0 —
. Следует отметить, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Чем ближе значение данного коэффициента к 1, тем связь между показателями сильнее, чем ближе к нулю, тем связь слабее.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый Коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

Соответственно величина 1-r2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов. Величина коэффициента детерминации является одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо объясняет исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.
Коэффициенты регрессии – величины именованные, и потому несравнимы для разных признаков. Так, коэффициент регрессии по модели прибыли предприятия от состава выпускаемой продукции несопоставим с коэффициентом регрессии прибыли предприятия от затрат на рекламу.
Сделать коэффициенты регрессии сопоставимыми по разным признакам позволяет определение аналогичного показателя в стандартизованной системе единиц, где в качестве единицы измерения признака используется его среднее квадратическое отклонение (σ). Поскольку коэффициент регрессии b имеет единицы измерения дробные (результат/фактор), то умножив его на среднее квадратическое отклонение фактора х (σх) и разделив на среднее квадратическое отклонение результата (σу), получим показатель, пригодный для сравнения интенсивности изменения результата под влиянием разных факторов. Иными словами, мы вернулись к формуле линейного коэффициента корреляции. Его величина выступает в качестве стандартизованного коэффициента регрессии и характеризует среднее в сигмах (σу) изменение результата с изменением фактора на одну σх.
Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков логически связан не только с коэффициентом регрессии b, но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах. При линейной связи признаков х и у средний коэффициент эластичности в целом по совокупности определяется как и характеризует, на сколько % в среднем изменится у при увеличении фактора x на 1%.
Несмотря на схожесть этих показателей, измерителем тесноты связи выступает линейный коэффициент корреляции (rxy), а коэффициент регрессии (b) и коэффициент эластичности (Э) – показатели силы связи; коэффициент регрессии является абсолютной мерой, ибо имеет единицы измерения, присущие изучаемым признакам у и х, а коэффициент эластичности — относительным показателем силы связи, потому что выражен в процентах.
После того как уравнение линейной регрессии найдено, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b=0, и, следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – «объясненную» и «остаточную» («необъясненную»):

|
Общая сумма квадратов отклонений |
= |
Сумма квадратов отклонений, объясненная регрессией |
+ |
Остаточная сумма квадратов отклонений |
Любая сумма квадратов отклонений связана с числом степеней свободы df, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант.
Так, для общей суммы квадратов необходимо (n-1) независимых отклонений, ибо из совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) число отклонений. Например, имеем ряд значений у: 1,2,3,4,5. Среднее из них равно 3, и тогда n отклонений от среднего составят: -2, -1, 0, 1, 2. Видим, что свободно варьируют только четыре отклонения, а пятое может быть определено, если четыре предыдущие известны.
При расчете объясненной, или факторной, суммы квадратов используются теоретические (расчетные) значения результативного признака
, найденные по линии регрессии:
. Вследствие чего факторная сумма квадратов отклонений имеет число степеней свободы, равное 1.
Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2.
Итак, имеем два равенства:
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим Средний квадрат отклонений или Дисперсию на одну степень свободы D.



Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т. е. критерия F:

Если нулевая гипотеза Н0 справедлива, то факторная и остаточная дисперсия не отличаются друг от друга. Если Н0 несправедлива, то факторная дисперсия превышает остаточную в несколько раз. Кроме расчетных значений F-критерия существуют также и табличные. Табличные значения F-критерия – это максимальная величина отношений дисперсий, которая может быть иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт>Fтабл, Н0 отклоняется. Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым: Fфакт<Fтабл, Н0 не отклоняется.
Величина F-критерия связана с коэффициентом детерминации r2. Факторную сумму квадратов отклонений можно представить как

А остаточную сумму квадратов – как

Тогда значение F-критерия можно выразить следующим образом:

Для измерения точности построенной модели используется Средняя относительная ошибка аппроксимации

Для экономических исследований применяются следующие уровни ошибки аппроксимации: если до 10%, то построенное уравнение регрессии достаточно точно выражает закон изменения исследуемого показателя под действием факторов и приемлемо для целей анализа; в случае построения модели для прогнозирования, допустимое значение
до 4%.
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma.
Стандартная ошибка коэффициента регрессии параметра mb рассчитывается по формуле:

Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при (n-2) степенях свободы. Эта статистика применяется для проверки статистической значимости коэффициента регрессии и для расчета его доверительных интервалов.
Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т. е. определяют фактическое значение t-критерия Стьюдента:

Которое затем сравнивают с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2).
Если фактическое значение t-критерия превышает табличное, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии определяется как .
Стандартная ошибка параметра а определяется по формуле

Процедура оценивания значимости данного параметра не отличается от рассмотренной выше для коэффициента регрессии: вычисляется t-критерий:

Его величина сравнивается с табличным значением при (n-2) степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:

Фактическое значение t-критерия Стьюдента определяется как

Рассмотренную формулу оценки коэффициента корреляции рекомендуется применять при большом числе наблюдений, а также, если r не близко к +1 или -1.
В прогнозных расчетах по уравнению регрессии определяется предсказываемое ур значение как точечный прогноз при хр=хк, т. е. путем подстановки в линейное уравнение регрессии
соответствующего значения х. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки
, т. е.
, и соответственно мы получаем интервальную оценку прогнозного значения у*:
. (1.22)
Для того чтобы понять, как строится формула для определения величин стандартной ошибки , подставим в уравнение линейной регрессии выражение параметра а:
, тогда уравнение регрессии примет вид:
.
Отсюда следует, что стандартная ошибка зависит от ошибки
и ошибки коэффициента регрессии b, т. е.
. (1.23)
Из теории выборки известно, что . Используя в качестве оценки
остаточную дисперсию на одну степень свободы Dост, получим формулу расчета ошибки среднего значения переменной у:

Ошибка коэффициента регрессии определяется формулой 
:

Соответственно имеет выражение:

Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении хк характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при
и возрастает по мере того, как «удаляется» от
в любом направлении.
Графически доверительные интервалы для будут выглядеть как гиперболы, расположенные по обе стороны от линии регрессии, см. рис. 2.
Средняя ошибка прогнозируемого индивидуального значения у составит: 
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. рассмотренная формула средней ошибки индивидуального значения признака может быть использована также для оценки существенности различия предсказываемого значения и некоторого гипотетического значения.
Вопросы для самопроверки
1. В чем состоят ошибки спецификации модели?
2. Поясните смысл коэффициента регрессии, назовите способы его оценивания.
3. Что такое число степеней свободы и как оно определяется для факторной и остаточной сумм квадратов?
4. Какова концепция F-критерия Фишера?
5. Как оценивается значимость параметров уравнения регрессии?
6. Как определяется коэффициент эластичности и что он показывает?
7. В чем смысл средней ошибки аппроксимации и как она определяется?
| < Предыдущая | Следующая > |
|---|
[c.36]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.
[c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис-
[c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
[c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о
[c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4.
[c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных.
[c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных.
[c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным.
[c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры.
[c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации.
[c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь
[c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.
[c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции.
[c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции.
[c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой.
[c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема.
[c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации.
[c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели.
[c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты).
[c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться.
[c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д.
[c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4.
[c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике.
[c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому
[c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика.
[c.422]
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 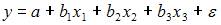
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 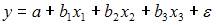
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 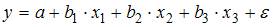






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 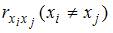

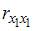
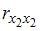
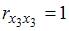
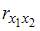
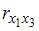
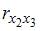
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
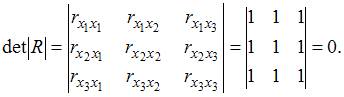
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

Ошибка спецификации эконометрической модели уравнения регрессии
Ошибка спецификации
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. [c.36]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]
Смотреть страницы где упоминается термин Ошибка спецификации
Экономико-математический словарь Изд.5 (2003) — [ c.338 ]
Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
| Название | Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие |
| Дата | 02.02.2019 |
| Размер | 1.2 Mb. |
| Формат файла | |
| Имя файла | Baza_po_ekonometrike.doc |
| Тип | Документы #66133 |
| страница | 1 из 4 |
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
4. В модели вида количество объясняющих переменных равно …
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
3. Дана матрица парных коэффициентов корреляции.
Коллинеарными являются факторы …
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
Фиктивными переменными не являются …
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный
для типа дома монолитный
для типа дома кирпичный
для типа дома монолитный
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.
4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет
5. В эконометрике фиктивной переменной принято считать …
переменную, принимающую значения 0 и 1
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
минимизации суммы квадратов
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
критерий Гольдфельда – Квандта
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников .После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений, . Тогда значение коэффициента детерминации равно …
3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …
остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
http://economy-ru.info/info/15273/
http://topuch.ru/tema-1-specifikaciya-ekonometricheskoj-modeli-oshibki-specifik-v2/index.html
Построение
математической модели — это скорее
искусство, чем наука, и, прежде всего,
требует глубоких знаний предметной
области. Социально-экономические системы
имеют чрезвычайно сложную структуру,
со многими явными и неявными взаимосвязями
между элементами системы, подвержены
влиянию многих скрытых факторов,
относятся к классу так называемых
больших систем. Стечением
времени меняются не только их
характеристики, учитываемые в модели
в виде отдельных параметров, но и
структура самих уравнений, которые
описывают процесс. Для их адекватного
описания требуется соответствующий
математический аппарат. Однако, даже
самые сложные математические методы
не в состоянии описать реальную систему
во всех ее деталях, да это и не нужно.
Модель не должна быть слишком сложной.
Излишняя детализация и учет второстепенных
факторов затрудняет
исследование
и не дает существенной информации об
изучаемой системе. Если модель слишком
сложна, то ее трудно использовать и
интерпретировать на практике.
Относительная
простота — важная характеристика
удачно построенной модели.
С другой стороны, слишком упрощенная
модель не будет адекватно описывать
реальную систему. Таким образом, сложность
модели должна соответствовать сложности
изучаемого экономического объекта.
В связи
с этим возникает необходимость
формулировки некоторых разумных
упрощающих гипотез (предположений),
исключения из анализа второстепенных
факторов и т. п., с тем, чтобы была
возможность описать процесс математически.
При этом существенные для
данного
социально-экономического процесса
характерные черты
должны
быть учтены в модели в соответствии с
поставленной целью исследования.
Другой
характерной проблемой, с которой
сталкивается эконометрист, является
то, что часто приходится довольствоваться
неточными
данными,
которые имеются в наличии и быстро
устаревают. Этих данных не всегда
хватает, а провести управляемый
эксперимент с целью получения
дополнительной информации невозможно.
В подобном случае целесообразно сочетание
количественных методов с привлечением
экспертных знаний и суждений.
Таким
образом, при создании эконометрической
модели возникают следующие вопросы.
1.
Какую модель желательно построить —
статическую или динамическую (с
учетом фактора времени), нелинейную или
линеаризованную? Как учесть влияние
внешней среды (возмущений)? (Ответ на
эти вопросы определяет желаемую точность
и сложность модели, выбор адекватного
математического аппарата и т. д.)
2.
Достаточно
ли имеющихся данных, необходимых для
построения адекватной модели,
насколько они достоверны? Существует
ли возможность получения дополнительной
информации, если это необходимо? Следует
ли привлечь экспертную информацию?
3. Как
оценить качество модели, т. е. определить,
насколько адекватно (правильно) она
описывает поведение реального объекта?
В
рамках эконометрического подхода
существует мощный арсенал средств,
который включает многие современные
эффективные
математические методы,
такие, например, как аппарат
нейронных сетей,
и разработанные на их основе компьютерные
технологии, в известной степени помогающие
справиться с этими проблемами. Но
решающая
роль принадлежит специалисту —
эконометристу.
Окончательный успех зависит от его
способности к неформальному анализу
проблемной ситуации, адекватной оценке
возможностей современных эконометрических
методов, от их правильного применения
и интерпретации полученных результатов.
Построив
удачную математическую модель и оценив
ее количественно с использованием
эконометрических методов, экономист-аналитик
получает в распоряжение эффективнейшее
средство анализа и прогноза, а
управляющий-практик — инструмент для
обоснования управленческих решений.
Такие модели широко применяются на
практике.
Практически
величина y
складывается из двух слагаемых:
,
где
— фактическое
значение, результат признака;
— теоретическое
значение результата признака, найденное
из математической модели или уравнения
регрессии;
— СВ, характерное
отклонение реального значения результата
признака от теоретического.
СВ
называется
возмущением. Она включает влияние
неучтённых в модели факторов, случайных
ошибок и особенно измерения. Её присутствие
в модели порождено тремя источниками:
-
спецификацией
модели; -
выборочным
характером исходных данных; -
особенностями
измерения.
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем больше теоретические
значения результативного признака
подходит к фактическим данным y.
К ошибкам спецификации
будут относиться не только неправильный
выбор той или иной математической
функции для
,
но и недоучет в УР какого-либо существенного
фактора (например, использование парной
регрессии вместо множественной).
Наряду с ошибками
спецификации могут иметь место ошибки
выборки (неоднородность данных в исходной
статистической совокупности). Если
совокупность неоднородна, то УР не имеет
практического смысла.
Для получения
хорошего результата обычно исключают
из совокупности единицы с аномальными
значениями исследуемых признаков, то
есть результаты регрессии представляют
собой выборочные характеристики.
Наибольшую опасность
в практическом использовании методов
регрессии представляют ошибки
измерения.
Если ошибки спецификации можно уменьшить,
изменяя форму модели, а ошибки выборки
– увеличивая объём исходных данных, то
ошибки измерения практически сводят
на нет все усилия по количественной
оценке связи между признаками. Особенно
велика роль ошибок измерения при
исследовании на макроуровне.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
04.08.2019218.11 Кб0kv.doc
- #
- #
- #