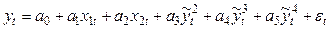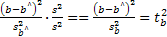RESET-тест
Рамсея — это обобщенный тест на наличие
следующих ошибок спецификации модели
линейной регрессии:
-
наличие
пропущенных переменных. Регрессия
содержит не все объясняющие переменные; -
неверная
функциональная форма. Некоторые или
все переменные должны быть преобразованы
с помощью логарифмической, степенной,
обратной или какой-либо другой функции; -
корреляция
между фактором Х и случайной составляющей
модели, которая может быть вызвана
ошибками измерения факторов, рассмотрением
систем уравнений или другими причинами.
Тест
Рамсея позволяет проверить, стоит ли
начинать поиск дополнительной переменной
для включения в уравнение
1.
Оценивается уравнение регрессии
2.
Вычисляются степени оценок зависимой
переменной
3.
Оценивается уравнение регрессии с этими
степенями
4.
Проводится оценка улучшения по F-критерию
Ошибки
такого рода приводят к смещению среднего
остатков регрессионной модели.
1.
Оценивают зависимость в соответствии
с выбранной моделью по МНК:
2.
Анализируют вид функциональной
зависимости остатков

в модель.
3.
Например, с учетом 2) вычисляют величины
конструируют новую модель:
и
применяют для ее оценивания по МНК.
4)
Сравнивают качество модели по отношению
к модели с помощью F-критерия:
Если

– число
дополнительных переменных, включенных
в модель (M=3),
k
– число
экзогенных переменных в

Недостаток:
он указывает только на наличие ошибочной
спец-ции модели, но не выявляет, сколько
и какого рода переменную нужно добавить
в модель.
Критерий
Амемья (Amemiya):
Решающей
функцией F-критерия служит:
Модель,
для которой значение AF
меньше, является лучше специфицированной.
Этот
критерий минимизирует число экзогенных
переменных.
10. Спецификация эконометрической модели: выбор формы зависимости нелинейной модели
Спецификация
модели
— формулировка вида модели, исходя из
соответствующей теории связи между
переменными. В уравнении регрессии
корреляционная связь признаков
представляется в виде функциональной
связи, выраженной соответствующей
математической функцией.
Принципы спецификаций
-
Модель
появляется в результате перевода на
математический язык (математической
формализации) известных закономерностей
поведения объекта. -
количество
уравнений в модели равно количеству
эндогенных переменных, участвующих в
модели. -
заключается
в необходимости учета влияния времени
на значения переменных. -
необходимость
учета в моделях влияние случайных
возмущений.
Формы
зависимости переменных в эконометрической
модели:
|
Вид |
Модель |
Коэффициент |
Эластичность |
|
Линейная |
|
|
|
|
Двойная |
|
|
|
|
Полулогарифмическая |
|
|
|
|
Полулогарифмическая |
|
|
|
|
Полиноминальная |
|
|
|
|
Обратная |
|
|
|
Приведем
примеры эконометрических моделей, в
которых используют зависимости I – IV.
-
Линейная
модель применяется, например, в
зависимости потребления от национального
дохода:
II.
Двойная логарифмическая модель
применяется при линеаризации
производственной функции Кобба-Дугласа:
.
III.
Отражении зависимости спроса на товар
от располагаемого дохода (кривые Энгела):
IV.
Модель зависимости уровня заработной
платы от стажа и образования занятых:
V.
При оценке взаимосвязи уровня безработицы
(U)
и уровня заработной платы (W)
(кривая Филипса):
Процедура
выбора
наилучшего преобразования
переменной из нелинейной в линейную
модель называется преобразованием
Бокса-Кокса
Идея
метода: переменная
при
а=1 превращается в линейную функцию:
при
а стремящееся к 0 переходит в логарифм:
Тест
Бокса-Кокса:
1шаг.
Выбрать конкретную а {-1;-0,5;0;0,5;1}
2шаг.
Для каждого а оценивают парам. регрессии
3шаг.
Вычисляют остаточную сумму квадратов.
Полученное преобразование будет
наилучшим.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Инструмент поддерживает интерфейс продукта «Форсайт. Аналитическая платформа» версий 9 и ранее.
RESET-тест Рамсея — это обобщенный тест на наличие следующих ошибок спецификации модели линейной регрессии:
-
наличие пропущенных переменных. Регрессия содержит не все объясняющие переменные;
-
неверная функциональная форма. Некоторые или все переменные должны быть преобразованы с помощью логарифмической, степенной, обратной или какой-либо другой функции;
-
корреляция между фактором Х и случайной составляющей модели, которая может быть вызвана ошибками измерения факторов, рассмотрением систем уравнений или другими причинами.
Ошибки такого рода приводят к смещению среднего остатков регрессионной модели.
Параметры теста:
-
Объясняющие переменные. Факторы, которые воздействуют на поведение моделируемой переменной. По умолчанию в списке содержатся все факторы тестируемой модели линейной регрессии. Флажок фактора — признак его участия в тесте. По умолчанию все факторы участвуют в тестировании. Для исключения фактора из теста снимите флажок. Число объясняющих переменных, должно быть не менее одного;
-
Уровень значимости. Значение уровня значимости, при котором гипотеза отвергается;
-
Степень. Количество дополнительных регрессоров, входящих в тестовую регрессию.
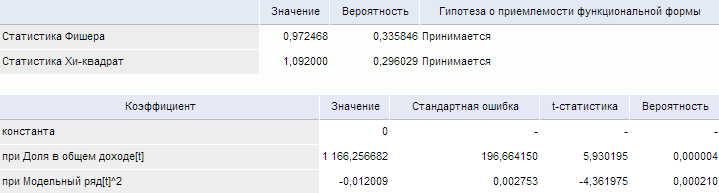
Результаты представлены в виде таблицы, содержащей:
-
статистику Фишера;
-
статистику Хи-квадрат;
Для каждой статистики приведено: значение, вероятность статистики и результат теста: принимается или отвергается гипотеза о приемлемости функциональной формы;
-
коэффициенты. Коэффициенты регрессии, рассчитанные при отмеченных факторах и дополнительных регрессорах.
Пример таблицы результатов:
См. также:
Выполнение диагностических тестов
Слайд 1
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
1
RESET- тест

Расмея неправильной спецификации функциональной формы предназначен для простого указания
на доказательство нелинейности. Чтобы реализовать его, выполняется регрессия и сохраняются
установленные значения зависимой переменной.
Слайд 2
2
Поскольку, по определению, установленные значения являются линейной комбинацией

объясняющих переменных, как показано, Y2 является линейной комбинацией квадратов
Х переменных и их взаимодействий.
^
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
Слайд 3
3
Если в спецификацию регрессии добавляется Y2, то он

должен получать квадратичную и интерактивную нелинейность, и если она
присутствует, то ей не обязательно сильно коррелировать с любой из
Х переменных.
^
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
Добавим в регрессионную спецификацию
Слайд 4
Добавим в регрессионную спецификацию
4
Если показатель

t-статистика значителен, это указывает на то, что может присутствовать
некоторая нелинейность.
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
Слайд 5
5
Сделаем это на примере заработной платы. Вот результат

регрессии EARNINGS на S и EXP с использованием набора
данных EAWE 21. Сохраняем установленные значения как FITTED и генерируем
FITTEDSQ как квадрат.
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
. reg EARNINGS S EXP
—————————————————————————-
Source | SS df MS Number of obs = 500
————+—————————— F( 2, 497) = 35.24
Model | 8735.42401 2 4367.712 Prob > F = 0.0000
Residual | 61593.5422 497 123.930668 R-squared = 0.1242
————+—————————— Adj R-squared = 0.1207
Total | 70328.9662 499 140.939812 Root MSE = 11.132
—————————————————————————-
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
————+—————————————————————-
S | 1.877563 .2237434 8.39 0.000 1.437964 2.317163
EXP | .9833436 .2098457 4.69 0.000 .5710495 1.395638
_cons | -14.66833 4.288375 -3.42 0.001 -23.09391 -6.242752
—————————————————————————-
. predict FITTED
(option xb assumed; fitted values)
. gen FITTEDSQ = FITTED*FITTED
Слайд 6
6
Коэффициент значителен на уровне 5 процентов, что указывает

на то, что добавление квадратичных членов может улучшить спецификацию
модели.
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
. reg EARNINGS S EXP
FITTEDSQ
—————————————————————————-
Source | SS df MS Number of obs = 500
————+—————————— F( 3, 496) = 25.46
Model | 9386.33186 3 3128.77729 Prob > F = 0.0000
Residual | 60942.6344 496 122.868214 R-squared = 0.1335
————+—————————— Adj R-squared = 0.1282
Total | 70328.9662 499 140.939812 Root MSE = 11.085
—————————————————————————-
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
————+—————————————————————-
S | -1.334163 1.413072 -0.94 0.346 -4.110507 1.442181
EXP | -.6441233 .7373115 -0.87 0.383 -2.092762 .8045155
FITTEDSQ | .0460798 .0200203 2.30 0.022 .0067447 .0854148
_cons | 25.09321 17.79509 1.41 0.159 -9.86984 60.05626
—————————————————————————-
Слайд 7
7
Однако мы также увидели, что лучше использовать полулогарифмическую

спецификацию. RESET-тест предназначен для обнаружения нелинейности, но не для
конкретной, наиболее подходящей, нелинейной модели.
RESET-ТЕСТ РАМСЕЯ НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ
ФОРМЫ
. reg EARNINGS S EXP FITTEDSQ
—————————————————————————-
Source | SS df MS Number of obs = 500
————+—————————— F( 3, 496) = 25.46
Model | 9386.33186 3 3128.77729 Prob > F = 0.0000
Residual | 60942.6344 496 122.868214 R-squared = 0.1335
————+—————————— Adj R-squared = 0.1282
Total | 70328.9662 499 140.939812 Root MSE = 11.085
—————————————————————————-
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
————+—————————————————————-
S | -1.334163 1.413072 -0.94 0.346 -4.110507 1.442181
EXP | -.6441233 .7373115 -0.87 0.383 -2.092762 .8045155
FITTEDSQ | .0460798 .0200203 2.30 0.022 .0067447 .0854148
_cons | 25.09321 17.79509 1.41 0.159 -9.86984 60.05626
—————————————————————————-
Слайд 8
8
По итогам проведения теста можно не обнаружить некоторые

типы нелинейности. Однако у него есть достоинства, такие как
легкость в осуществлении и потребление только одной степени свободы.
RESET-ТЕСТ РАМСЕЯ
НЕПРАВИЛЬНОЙ СПЕЦИФИКАЦИИ ФУНКЦИОНАЛЬНОЙ ФОРМЫ
. reg EARNINGS S EXP FITTEDSQ
—————————————————————————-
Source | SS df MS Number of obs = 500
————+—————————— F( 3, 496) = 25.46
Model | 9386.33186 3 3128.77729 Prob > F = 0.0000
Residual | 60942.6344 496 122.868214 R-squared = 0.1335
————+—————————— Adj R-squared = 0.1282
Total | 70328.9662 499 140.939812 Root MSE = 11.085
—————————————————————————-
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
————+—————————————————————-
S | -1.334163 1.413072 -0.94 0.346 -4.110507 1.442181
EXP | -.6441233 .7373115 -0.87 0.383 -2.092762 .8045155
FITTEDSQ | .0460798 .0200203 2.30 0.022 .0067447 .0854148
_cons | 25.09321 17.79509 1.41 0.159 -9.86984 60.05626
—————————————————————————-
Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
Спецификация модели множественной линейной регрессии включает проверку:
1. правильного выбора экзогенных переменных.
2. корректного выбора формы зависимости мду эндо- и экзогенной переменными.
Для решения 1 задачи различают пропущенные и избыточные экзогенные переменные
Пропущенные переменные – существенные факторы, которые не были включены в эконометрическую модель по ошибке. Опасность наличия пропущенных переменных заключается в смещении оценок параметров при включенных переменных. Признак, по которому определяют пропущенную переменную: Знак “+” у произведения оценки параметра при подозреваемой пропущенной переменной и коэффициента корреляции этой переменной с другими переменными, включенными в модель.
Выбранная модель с пропуском переменной 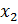

Тогда, применяя МНК для оценки усеченной модели получаем формулу смещения оценки 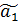
Экзогенную переменную относят к избыточным, если она по ошибке включена в эконометрическую модель. Включение избыточной переменной оказывает влияние на уменьшение точности (увеличение дисперсии) оценок параметров модели, что, в свою очередь, вызывает уменьшение t-статистик и коэффициента детерминации.
Если 

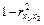

Замещающие переменные – обычно бывает полезно вместо пропущенной переменной, которую трудно измерить, использовать некоторый её заменитель.
4 основных качественных правила спецификации экономической модели:
1. Опираясь на эконометрическую теорию, следует ответить на вопрос: «Является ли переменная существенной в модели зависимости с эндогенной переменной?».
2. Осуществить проверку значимого отличия от нуля t-статистик.
3. Осуществить проверку, насколько значимо изменяется коэффициент детерминации при добавлении некоторой переменной в модель.
4. Существенно ли изменяются оценки других переменных после добавления новой переменной в модель.
Кроме отмеченных правил спецификации модели, наиболее из-вестны два следующих количественных критерия спецификации:
Критерий Рамсея (Ramsey):
RESET-тест Рамсея — это обобщенный тест на наличие следующих ошибок спецификации модели линейной регрессии:
- наличие пропущенных переменных. Регрессия содержит не все объясняющие переменные;
- неверная функциональная форма. Некоторые или все переменные должны быть преобразованы с помощью логарифмической, степенной, обратной или какой-либо другой функции;
- корреляция между фактором Х и случайной составляющей модели, которая может быть вызвана ошибками измерения факторов, рассмотрением систем уравнений или другими причинами.
Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение
1. Оценивается уравнение регрессии
2. Вычисляются степени оценок зависимой переменной
3. Оценивается уравнение регрессии с этими степенями
4. Проводится оценка улучшения по F-критерию
Ошибки такого рода приводят к смещению среднего остатков регрессионной модели.
1. Оценивают зависимость в соответствии с выбранной моделью по МНК:
2. Анализируют вид функциональной зависимости остатков 
3. Например, с учетом 2) вычисляют величины 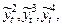
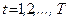
и применяют для ее оценивания по МНК.
4) Сравнивают качество модели по отношению к модели с помощью F-критерия:
Если 

Недостаток: он указывает только на наличие ошибочной спец-ции модели, но не выявляет, сколько и какого рода переменную нужно добавить в модель.
Критерий Амемья (Amemiya):
Решающей функцией F-критерия служит:
Модель, для которой значение AF меньше, является лучше специфицированной.
Этот критерий минимизирует число экзогенных переменных.
F-тест качества спецификации парной линейной регрессионной модели
F-тест — оценивание качества уравнения регрессии — состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fвыч и критического (табличного) Fкрит значений F-критерия Фишера. Fвыч определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы.
Коэффициент детерминации является случайной величиной (так как вычисляется по выборочным данным), и для оценки его статистической
значимости, в соответствии со стандартной процедурой, следовало бы
сравнить его вычисленное значение с табличным (критическим). Однако
таблиц распределения коэффициента детерминации не существует, поэтому для проверки статистической гипотезы о значимости R 2 используется косвенный метод: вычисляется некоторая вспомогательная статистика с известным распределением; проверяется гипотеза ее статистической значимости; устанавливается взаимосвязь между вспомогательной статисткой и коэффициентом детерминации; на основании этой взаимосвязи делается вывод о статистической значимости коэффициента детерминации. Для составления вспомогательной статистики рассмотрим две случайные величины U и V. Статистика U имеет распределение х 2 (хи-квадрат)
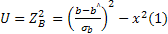
так как случайная величина 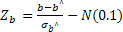
В качестве второй вспомогательной статистики, имеющей распределение х 2 с параметром, равным числу степеней свободы n — 2, используется статистика вида:
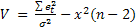
Статистика F, как легко проверить, совпадает с квадратом f-статистики для параметра b:
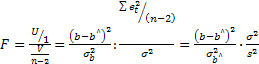
и имеет распределение Фишера с параметрами v1=1,v2=n-2 (n— объем выборки):
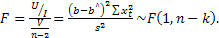
Для проверки гипотезы Н0:b = 0 статистика (3) принимает вид:
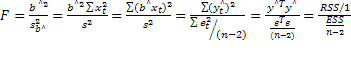
Связь между статистиками F и R 2 для случая парной регрессии
(k=2) имеет вид:
F= 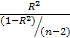
Справедливость (4) проверяется непосредственно:
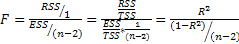
Таким образом, как следует из формулы (5), F = 0 в том случае, если R 2 =0. Поэтому, проверяя значимость F статистики (сравнивая ее вычисленное по выборочным данным значение с табличным), мы можем проверить статистическую значимость коэффициента детерминации. ЕслиFвыч
Дата добавления: 2015-01-10 ; просмотров: 5107 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
F-тест качества спецификации множественной регрессионной модели
Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.
1. Роль степеней свободы (degree of freedom) в статистике
Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:
Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:
А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.
Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.
Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.
Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:
Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.
В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:
где n — число наблюдений, k — число независимых переменных.
2. Анализ дисперсии, F-тест
При выполнении основных предположений линейной регрессии имеет место формула:
где ,
,
В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .
Масштабируем SSE и SSR с учетом их степеней свободы:
Получены хи-квадрат распределения. F-статистика вычисляется по формуле:
Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе в случае линейной регрессионной модели вида (1).
3. Выбор линейной регрессионной модели
Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.
Определим “полную” модель: (10)
Определим “укороченную” модель: (11)
Вычисляем сумму квадратов ошибок для каждой модели:
(12)
(13)
Определяем количество степеней свобод
(14)
Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.
Коэффициент детерминации из формулы (6):
Из формулы (15) выразим SSE(F):
SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:
Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.
Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.
3 Проверка значимости линейной регрессии
Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид . Следовательно. Используя формулу (14.в), получим
Заключение
Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.
Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.
Надеюсь вам было интересно, спасибо за внимание.
При выводе формул очень помогли некоторые главы из курса по статистике STAT 501
http://helpiks.org/2-3401.html
http://habr.com/ru/post/592677/