4.1. Классификация источников ошибок, характерных для спутниковых измерений
При отработке методов высокоточных спутниковых измерений возникает необходимость тщательного исследования влияний всех возможных источников ошибок выполняемых измерений, особенностей их проявления и обоснования методов их учета. В зависимости от характера воздействия отмеченных источников возникающие при этом ошибки подразделяются на две основные группы: систематические погрешности, которые применительно к спутниковым измерениям получили название смещений, и погрешности случайного характера, которые часто отождествляют с понятием «шум».
Для погрешностей первой группы разрабатываются специальные методы их учета. Влияние второй группы удается, в большинстве случаев, минимизировать за счет использования большого массива отдельных измерений. В настоящем разделе основное внимание уделено рассмотрению ошибок систематического характера, обусловливающих появление смещений результатов измерений. При их исследовании и создании методов ослабления их влияния широкое распространение получил метод моделирования, для разработки которого приходится тщательно изучать механизм воздействия таких источников ошибок на результаты измерений с тем, чтобы на основе такого изучения разработать эффективные методы минимизации отмеченного влияния.
Исходя из анализа измерительного процесса, характерного для систем GPS и ГЛОНАСС, все основные источники ошибок можно условно разбить на три основные группы:
1) ошибки, связанные с неточностью знания исходных данных, из которых определяющая роль принадлежит погрешностям знания эфемерид спутников, значения которых должны быть известны на момент измерений;
2) ошибки, обусловленные влиянием внешней среды, среди которых выделяют такие источники, как воздействие атмосферы (ионосферы и тропосферы) на результаты спутниковых измерений, а также отраженных от окружающих объектов радиосигналов (многопутность);
147
3) инструментальные источники ошибок, к которым, как правило, относят неточность знания положения фазового центра антенны приемника, неучтенные временные задержки при прохождении информационных сигналов через аппаратуру, а также погрешности, связанные с работой регистрирующих устройств спутниковых приемников.
Наряду с перечисленными выше группами ошибок приходится учитывать и отдельные факторы, обусловливающие появление ошибок, которые не характерны ни для одной из перечисленных выше групп. В частности, к таким ошибкам могут быть отнесены погрешности, возникающие вследствие неоптимального взаимного расположения наблюдаемых спутников (геометрический фактор). Кроме того, целый ряд ошибок может возникать в процессе перехода от одной координатной системы к другой. Например, от свойственной системе GPS глобальной координатной системы WGS-84 к местной, интересующей потребителя координатной системе.
В следующих подразделах в обобщенном виде проанализированы особенности влияния основных источников ошибок.
4.2. Источники ошибок, связанные с неточным знанием эфемерцд спутников, и методы ослабления их влияния
При нахождении интересующих потребителя координат точек на земной поверхности спутниковыми методами необходимо наряду с измерением расстояний до спутника знать также его эфемериды, которые определяют местоположение спутника на момент выполнения измерений. Как уже отмечалось в подразделе 2.1, неточность знания эфемерид обусловливает соответствующие погрешности определения как абсолютных значений координат определяемых точек, так и их разностей между пунктами наблюдений. Механизм неточного знания эфемерид связан, прежде всего, с наблюдаемыми на практике расхождениями между предсказываемой (невозмущенной) и реальной (подверженной влиянию возмущающих сил) орбитами. К возмущающим силам относят различные факторы как гравитационного, так и негравитационного происхождения. Влияние различных факторов на движение спутников типа GPS и ГЛОНАСС приведено в табл. 4.1 [70, 73].
Первые из них, обусловленные притяжением спутника со стороны Землй, Луны и Солнца, поддаются достаточно эффективному моделированию. В то же время такие возмущающие факторы негравитационного происхождения, как, например, солнечное радиационное давление, плохо поддаются моделированию из-за непредсказуемости отдельных компонент, от которых зависит результирующее воздействие на спутник отмеченного давления.
148
|
Таблица 4.1 |
||
|
Возмущающие |
Максимальное |
Максимальное |
|
факторы |
возмущающее |
возмущение за 1 час, м |
|
Центральное поле |
ускорение, м/с2 |
|
|
5,65-Ю’1 |
||
|
Земли |
— |
|
|
Вторая зональная |
||
|
гармоника |
5,3-Ю-5 |
300 |
|
Гравитация Луны |
5,5-10″6 |
40 |
|
Гравитация Солнца |
310-6 |
20 |
|
Четвертая зональная |
||
|
гармоника |
ю-7 |
0,6 |
|
Солнечная радиация |
ю-7 |
0,6 |
|
Гравитационные |
||
|
аномалии |
ю-8 |
0,06 |
|
Другие факторы |
ю-8 |
0,06 |
Проведенные к настоящему времени исследования по количественной оценке отдельных факторов на эфемериды спутника свидетельствуют о том, что наибольшее воздействие на уклонения реальной орбиты от расчетной оказывает гравитационное поле Земли. В частности, из-за влияния второго гармонического коэффициента С20 такие уклонения для трехчасовых дуг орбит достигают 2 км, а для более протяженных двухсуточных дуг до 14 км. С такими значительными уклонениями нельзя не считаться при любых видах спутниковых измерений.
Суммарное гравитационное влияние масс Луны и Солнца хотя и оказывается существенно меньшим (для трехчасовых дуг уклонения от невозмущенной орбиты оцениваются величинами на уровне от 50 до 150 м), но, тем не менее, при прогнозировании значений эфемерид данное влияние также следует учитывать.
Непосредственно с гравитацией связаны также наблюдаемые на земной поверхности различного рода приливные явления, которые из-за перераспределения масс приводят к изменениям в предрассчитываемом гравитационном поле Земли, а следовательно, и к влияниям на орбитальное движение спутника. Проведенная оценка такого влияния свидетельствует о том, что уклонения спутника от расчетной орбиты из-за воздействия данного фактора даже для двухсуточных дуг лежат в пределах от 0,5 до 2 м, и этим влиянием применительно к рассматриваемым спутникам можно пренебречь.
Переходя к оценке влияния факторов негравитационного происхождения, следует заметить, что наиболее существенное влияние на неточность знания эфемерид спутников, входящих в состав систем
149
GPS и ГЛОНАСС, оказывает солнечное радиационное давление. Как показывают предрасчеты, уклонения спутников от расчетной траектории из-за воздействия прямого солнечного радиационного давления лежат в пределах от 5-6 м (для трехчасовых дуг) до 100-800 м (для двухсуточных дуг). Отмеченные предрасчеты характеризуются невысокой надежностью по следующим причинам:
1)интенсивность солнечного излучения не остается постоянной
стечением времени;
2)модель влияния данного фактора существенно изменяется при переходе спутника в зону тени и полутени;
3)эффективная поверхность спутника плохо поддается предрасчету как из-за сложной конфигурации такой поверхности, так и из-за вариаций положения спутника в пространстве.
Дополнительную неопределенность в предрасчет влияния радиационного давления вносит отраженная от земной поверхности солнечная радиация, зависящая от атмосферных условий и отражающих свойств облучаемых Солнцем участков земной поверхности.
Другим возмущающим фактором негравитационного происхождения является атмосферное торможение. При оценке влияния этого фактора следует иметь в виду, что на характерной для рассматриваемых спутников высоте около 20 тыс.км атмосфера оказывается чрезвычайно разреженной, и ее влиянием при предрасчетах орбит спутников, как правило, пренебрегают.
Обобщая оценку суммарного влияния всех перечисленных выше возмущающих факторов, заметим, что эти данные используются только для первоначального приближенного предвычисления реальных орбит спутников. Что касается получения необходимых для наземных наблюдателей значений эфемерид спутников, то на практике применяют более эффективные экспериментальные методы, базирующиеся на использовании опорных станций, установленных на пунктах с известными координатами и выполняющих непрерывные высокоточные наблюдения спутников в автоматическом режиме. За счет использования таких станций слежения решается обратная задача, состоящая в том, что с помощью одновременных измерений с нескольких (не менее трех) станций производится периодическое последовательное определение эфемерид всех наблюдаемых спутников. После соответствующей обработки на центральной станции вычисляются поправки к ранее определенным значениям эфемерид, которые с помощью передающих загружающих станций систематически (три раза в сутки, а последнее время один раз в сутки) передаются на соответствующие спутники, где вводятся в состав навигационного сообщения. Последнее, как уже отмечалось ранее, сбрасывается со спутника потребителю
150
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
19.02.2021
Глава 4 — Источники ошибок ГНСС
В главе 2 мы представили концепцию источников ошибок ГНСС. Это факторы, которые затрудняют определение точного положения ГНСС приемника. В этой главе мы более подробно рассмотрим источники этих ошибок.
Таблица 13: Источники ошибок ГНСС
Источники ошибок
Спутниковые часы
Атомные часы на спутниках ГНСС очень точны, но они немного дрейфуют. К сожалению, небольшая неточность спутниковых часов приводит к значительной ошибке в определении приемником своего местоположения. Например, ошибка часов в 10(−6) сек приводит к ошибке положения в 3 м.
Часы на спутнике контролируются наземной системой управления ГНСС и сравниваются с еще более точными часами, используемыми в ней. В данных, передаваемых спутником пользователю, содержится оценка смещения бортовых часов. Обычно передаваемая точность составляет ± 2 м, хотя она может варьироваться в зависимости от разных систем ГНСС. Чтобы получить свое более точное местоположение, ГНСС приемник должен компенсировать ошибку часов.
Одним из способов компенсации погрешности часов является загрузка точной информации о часах спутника из систем дифференциальной коррекции (SBAS) или систем точного позиционирования (PPP). В передаваемой информации содержатся поправки за ошибки бортовых часов, которые были рассчитаны системами SBAS или PPP. Более подробные сведения о системах SBAS и PPP представлены в главе 5.
Другой способ компенсации погрешности часов — настроить приемник для работы в режиме дифференциальной коррекции или кинематики реального времени (RTK). В главе 5 также подробно рассматриваются дифференциальные методы ГНСС и RTK.
Ошибки эфемерид
Спутники ГНСС движутся по очень точным, хорошо известным орбитам. Однако, параметры орбиты немного меняются. Также, как и в случае с часами спутника, небольшое изменение орбиты приводит к значительной ошибке в вычисленном положении приемника.
Наземная система управления ГНСС постоянно отслеживает орбиты спутников. Когда орбита спутника изменяется, наземная система управления отправляет поправку на спутники, и эфемериды спутников обновляются. Даже с поправками, внесенными наземной системой управления ГНСС, все еще есть небольшие ошибки в параметрах орбиты, которые могут привести к ошибке местоположения до ± 2.5 м.
Одним из способов компенсации ошибок спутниковых орбит является загрузка точной эфемеридной информации из систем SBAS или PPP, которые будут более подробно рассматриваться в главе 5.
Другой способ компенсации ошибок спутниковой орбиты — использование приемника в режиме дифференциальной коррекции или RTK. Более подробная эта информация также представлена в главе 5.
Ионосферные задержки
Ионосфера — это слой атмосферы на высоте от 80 до 600 км над Землей. Этот слой содержит электрически заряженные частицы, называемые ионами. Эти ионы задерживают прохождение спутниковых сигналов и могут вызвать значительную ошибку определения местоположения спутника (обычно ± 5 м, но эта ошибка может возрастать в периоды высокой ионосферной активности, вызванной влиянием Солнца).
Ионосферная задержка зависит от солнечной активности, времени года, сезона, времени суток и места. В результате очень трудно предсказать, насколько ионосферная задержка повлияет на расчетное местоположение.
Ионосферная задержка также изменяется в зависимости от частоты радиосигнала, проходящего через ионосферу. ГНСС приемники, которые принимают более одной частоты, например L1 и L2, могут использовать это для повышения точности. Сравнивая измерения на L1 с измерениями на L2, приемник может определить величину ионосферной задержки и удалить эту ошибку из рассчитанных координат.
Для приемников, которые могут отслеживать только одну частоту ГНСС, используются модели ионосферы для уменьшения влияния ошибок, вызванных влиянием ионосферы. Из-за различного характера ионосферной задержки модели не так эффективны, как использование нескольких частот для их устранения.
Ионосферные условия очень похожи в пределах отдельной области, поэтому спутниковые сигналы, поступающие на приемники базовой станции и подвижные приемники, имеют очень похожую задержку. Это позволяет компенсировать ионосферную задержку дифференциальными методами ГНСС и RTK.
Тропосферные задержки
Тропосфера — это ближайший к поверхности Земли слой атмосферы.
Рис. 37
Вариации задержки в тропосфере вызываются изменением влажности, температуры и атмосферного давления.
Поскольку тропосферные условия в пределах отдельной зоны очень похожи, то базовая станция и приемники подвижного приемника испытывают очень похожее влияние тропосферы. Это позволяет дифференциальным методам ГНСС и RTK компенсировать тропосферную задержку.
Приемники ГНСС также могут использовать тропосферные модели для оценки количества ошибок, вызванных тропосферной задержкой.
Собственные шумы приемника
Шум приемника добавляет к ошибке положения величины, вызванные аппаратным и программным обеспечением. Приемники ГНСС высшего класса, как правило, имеют меньшие ошибки из-за собственного шума, чем более дешевые приемники.
Влияние многолучевости
Как показано на рис. 38 многолучевое распространение происходит, когда сигнал от спутника ГНСС отражается от объекта, например, стены здания, а затем приходит к антенне приемника. Поскольку отраженный сигнал распространяется дольше, то он поступает в приемник с небольшой задержкой. Этот задержанный сигнал может привести к тому, что приемник вычислит неправильное положение.
Рис. 38
Самый простой способ уменьшить ошибки из-за многолучевого распространения это разместить ГНСС антенну в месте, удаленном от отражающих поверхностей. Когда это невозможно, приемник и антенна ГНСС должны уметь обрабатывать многолучевые сигналы.
Ошибки многолучевого распространения с большой задержкой обычно обрабатываются ГНСС приемником, а ошибки сигнала с короткой задержкой отрабатываются антенной. Благодаря применению дополнительных технологий, высокопроизводительные приемники и ГНСС антенны, как правило, лучше устраняют ошибки многолучевости.
Заключение
В этой главе описаны источники ошибок, которые вызывают погрешности при расчете позиции. В главе 5 мы опишем методы, которые используют приемники ГНСС для уменьшения этих ошибок и получения более точного местоположения.
Материалы взяты с сайта компании NovAtel. Ссылка на первоисточник: https://novatel.com/an-introduction-to-gnss
Параллельно в СССР развивалась глобальная навигационная спутниковая система (Глонасс). Принцип действия и характеристики обеих систем примерно одинаковы. Обе эти системы являются государственными и контролируются военными ведомствами.
Системы GPS и Глонасс составляют основу существующей Глобальной навигационной спутниковой системы (ГНСС), Global Navigation Satellite System (GNSS). ГНСС является спутниковой системой для многоцелевого использования для определения местоположения, времени и скорости по всему миру.
Она включает приемники пользователей, одно или более созвездий спутников, наземные сегменты и инфраструктуру управления. ГНСС постоянно развивается и совершенствуется. В Резолюции ИМО А.860(20) 1997 года разработаны морские требования к будущей ГНСС.
Работа спутниковых навигационных систем основана на использовании среднеорбитальных спутников на круговых орбитах высотой примерно 20000 км. В GPS имеется 24 спутника на шести орбитах по 4 спутника на каждой, а в Глонасс — 24 спутника на четырех орбитах по 6 спутников на орбите.
Принцип измерения координат в GNSS
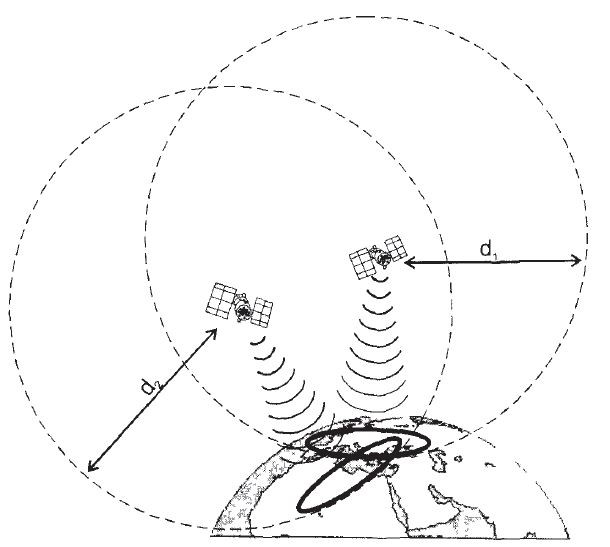
Принцип определения координат основан на измерении задержки распространения радиоволн от спутника до навигационного приемника. Спутник постоянно передает радиосигнал, содержащий точное время и положение спутника в пространстве. Приемник измеряет задержку распространения радиосигнала Δt1, что позволяет вычислить так называемое псевдорасстояние до спутника d1=cΔt1,
где c — скорость света (см. рис. 30.1). Линия пересечения сферы радиусом d1 с центром в точке положения спутника с поверхностью Земли,а это будет окружность, даст совокупность возможных положений приемника.
Если таким же образом измерить задержку радиосигнала At? от второго спутника и построить сферу радиусом d2=cΔt2, то можно получить вторую окружность возможных положений при обсервации второго спутника.
Пересечение этих окружностей даст две точки возможных положений приемника на поверхности Земли. Для устранения неоднозначности требуется обсервация третьего спутника.
В GNSS для передач данных спутниками используются два частотных поддиапазона. L1 и L2. В GPS все спутники передают на одной паре частот fL1=1575,42 МГц и fL2=1227,60 MГu. В Глонасс каждый спутник передает на своей паре частот в диапазонах fL1 = 1502,5625-1615,5 МГц и fL2= 1246,4375-1256,5 МГц.
Для разделения сигналов от разных спутников и использования на спутниках передатчиков сравнительно малой мощности применяются так называемые сложные сигналы в виде псевдослучайных последовательностей (ПСП) с большим периодом повторения. Для таких сигналов информационная «единица» данных представляется некоторой псевдослучайной последовательностью с гораздо большей тактовой частотой, а «ноль» — соответственно ее инверсным значением. В результате ширина спектра сигнала многократно расширяется.
Такой способ позволяет принимать сигнал от спутника при отношении сигнал/шум значительно меньше единицы за счет накопления энергии полезного сигнала в приемнике. Однако, при этом необходимо знание этой псевдослучайной последовательности или кода. Без точного знания кода невозможно осуществить демодуляцию принимаемого сигнала.
В системе GPS есть два кода — короткий (С/А-код) для коммерческого применения и длинный (Р-код) для военных целей. С 1 мая 2000 года американская сторона рассекретила Р-код из-за того, что Российская Глонасс позволяла получить такую же точность. В Глонасс точный код не засекречен и постоянно может быть использован в гражданских целях. Горизонтальная погрешность определения местоположения спутниковых навигационных систем Глонасс и GPS в штатном режиме не превышает 33 метров с вероятностью 95%. В остальных 5% случаев абсолютная погрешность не превышает 100 метров.
В дифференциальном режиме погрешность составляет не более 10 метров с вероятностью 95%. Совместное использование GPS/Глонасс позволяет получить более высокую точность. Известно, что из-за различия в углах наклонения орбит спутников Гтонасс дает лучшие точностные характеристики в высоких шиpoтax, a GPS — в средних широтах.
Европейским Союзом в настоящее время разрабатывается собственная спутниковая навигационная система Галилео, аналогичная системам GPS и Глонасс. Начало эксплуатации системы Галилео планируется с 2008 года. Совместное использование ресурсов всех космических навигационных систем повысить точность и достоверность определения местоположения подвижных объектов любого типа — морских, воздушных, сухопутных.
Источники ошибок в GNSS
Основными факторами, которые определяют точность определения местонахождения, являются следующие.
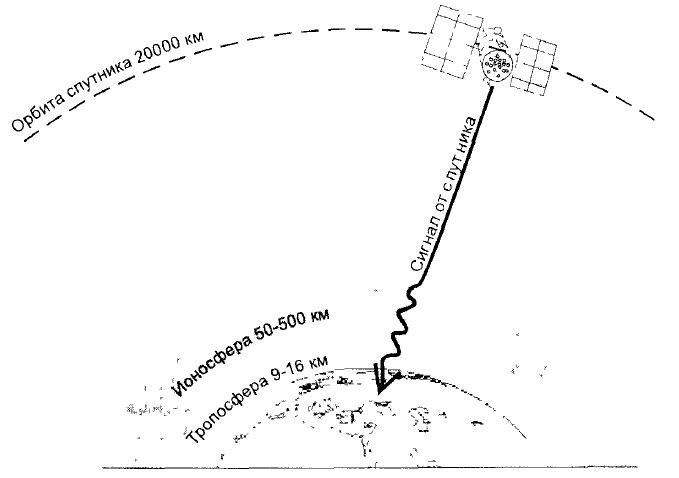
1. Неоднородность ионосферных и тропосферных слоев Земной атмосферы. Точность измерений зависит от постоянства скорости распространения радиоволн. Однако из-за различного рода нсоднородностей в атмосфере скорость может меняться. В результате возникают ошибки в определении расстояний до спутников. Абсолютные ошибки, вызванные влиянием атмосферы составляют порядка 5 метров (для ионосферных ошибок) и 1 метра (для тропосферных ошибок.
2. Многолучевость распространения радиоволн. Приемник GPS принимает не только радиоволны по прямому направлению, но и отраженный от каких-либо объектов — рельефа, самолетов, крупных зданий и т.д. Отраженные сигналы создают дополнительные помехи, влияющие на точность измерения.
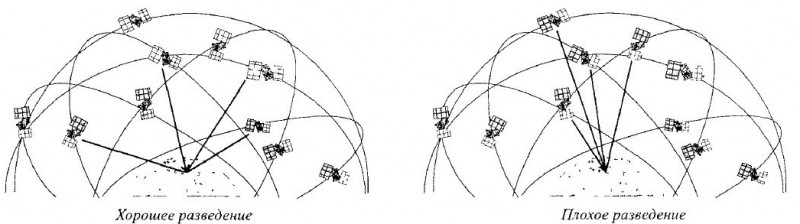
Рис.30.2. Хорошее и плохое разведение спутников при обсервации
3. Ошибки синхронизации. Для точного измерения задержки сигнала от спутника необходима синхронизация приемника. На спутниках имеется атомный эталон частоты, который синхронизирует приемник GPS. Нестабильность атомного эталона обуславливаем ошибку в измерении задержки прохождения cигнала и точность позиционирования порядка 1,5 метров.
4. Эфемеричсские ошибки вызваны неточностью расчета положения спутника в пространстве. Их влияние составляет порядка 2,5 метров при определении положения приемника.
5. Геометрическое разведение спутников. Если спутники, па которые производится обсервация находятся под углами близкими к прямым, то точка пересечения окружностей может быть вычислена с меньшей погрешностью, чем в случае, когда спутники находятся под острыми углами. Хорошее взаимное положение (разведение) (Good dilution) спутников позволяет получить меньшую погрешность, чем плохое разведение (Poor dilution) (рис. 30.2).
6. Солнечная активность. Вспышки па Солнце, которые сопровождаются выбросами гигантских масс солнечного вещества, порождают резкие изменения свойств магнитосферы и ионосферы Земли. Такие вспышки повгоряются с цикличностью примерно 11 лет при относительно спокойном состоянии Солнца между ними. В периоды солнечной активности ошибки возрастают.
Рис.30.3. Источники ошибок в GNSS
7. Избирательная возможность путем засекречивания кодов. Преднамеренно точность измерений может ухудшаться путем засекречивания точного кода. Коммерческий короткий код позволяет получить точность примерно на порядок хуже, чем длинный код для военных применений.
При вычислении координат особое значение приобретает используемая геодезическая координатная система. В различных геодезических системах точки с одними и теми же координатами могут отстоять на сотни мет- ров. GPS для расчета координат использует систему WGS84 (World Geodetic System), а Глонасс — Советскую геоцентрическую систему параметров Земли 1990 года PZ90.
Дифференциальный режим GPS/Глонасс
Спутниковые навигационные системы Глонасс и GPS не позволяют обеспечить в штатном режиме точность, необходимую для безопасной навигации судов на подходах к портам и в узкостях с ограничением свободы маневрирования судов. В этой зоне точность регламентируется Резолюцией ИМО А.815(19) 1995 года по Всемирной радионавигационной системе. Эта точность не должна быть хуже 10 метров с вероятностью 95%.
Другим недостатком спутниковых навигационных систем является неспособность в настоящее время обеспечивать оперативное оповещение потребителей о нарушениях в работе систем или их элементов, которые про- исходят пока довольно часто.
Наиболее рациональным путем устранения указанных недостатков и улучшения точностных характеристик систем Глонасс и GPS, необходимых для расширения их функциональных возможностей, является применение дифференциального режима работы.
Сущность дифференциального режима поясняется следующим образом. Ошибки в спутниковых навигационных системах для измерений, сделанных в данное время и данном месте, носят, главным образом, систематический характер.
Поэтому, если привязаться к какой-либо точке на берегу с точно известным географическим положением и измерить се местоположение с помощью навигационного приемника GPS/Глонасс, то можно получить некоторое значение поправки. Это значение поправки следует далее ввести в полученное измерение местоположения судна.
Различают два метода использования поправок. Первый метод (называемый дифференциалом положений) базируется на вычислении разности расчетного положения и точно известного положения опорной точки. Роль опорной точки выполняет опорная (или контролыю-коррегирующая) станция. Однако в данном методе необходимо при обсервации на судне использовать те же спутники, что и на опорной станции.
Другой метод (дифференциал псевдорасстояний) предполагает получение ошибок вычисления псевдорасстояний для каждого спутника. Достоинством данного метода является независимый от опорной станции выбор «созвездия» на судне благодаря наличию поправок псевдодальностей по всем спутникам.
Данный метод практически используется в дифференциальном режиме. Коррекции псевдорасстояний рассчитываются на береговой опорной станции и передаются в диапазоне средних волн 285-325 кГц для всех заинтересованных пользователей. Интервал передачи поправок составляет не более 5-10 секунд. Поправки вводятся в судовой приемник GPS и учитываются при расчете местоположения судна.
Погрешности определения места увеличиваются с увеличением расстояния от опорной станции и при старении дифференциальных поправок, но не должны превышать 10 метров в рабочей зоне с вероятностью 0,95.
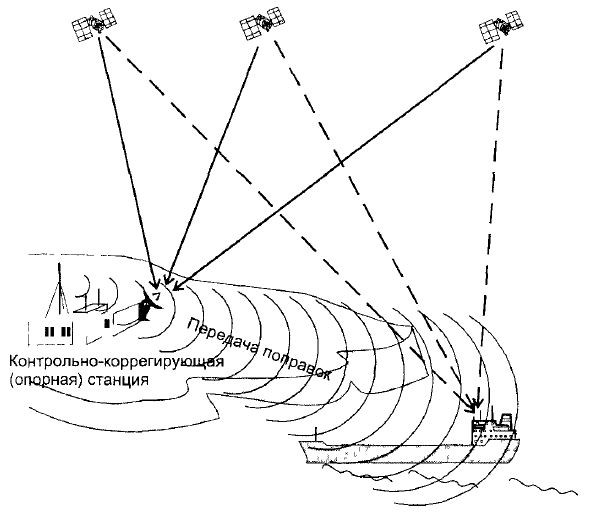
Рис.30.4. Дифференциальный метод измерения координат
В дифференциальном режиме одновременно повышается надежность работы системы за счет оперативного извещения всех пользователей о возможных нарушениях в спутниковой системе.
Принцип действия дифференциальной системы иллюстрируется на рис. 30.4. На береговой станции измеряются координаты с помощью приемника GPS и сравниваются с точно известными координатами положения приемника. На основании этого рассчитываются поправки, которые необходимо ввести в измеренные координаты на судне.
Поправки передаются в диапазоне средних волн. Прием поправок возможен на расстояниях примерно 50 — 250 м. миль от передающей станции. Для передач используется класс излучения G1D при модуляции с минимальным сдвигом (MSK). На судне должен быть установлен приемник дифференциальных поправок и приемник GPS с входом дифференциальных поправок.
Дифференциальный режим является наиболее перспективным для обеспечения плавания в узкостях, каналах и подходах к портам, а также позволяет успешно решить следующие специальные навигационные задачи:
— обеспечение высокоточного судовождения на внутренних водных путях;
— рыбный промысел в прибрежных водах, узкостях и в районах со сложной навигационной обстановкой;
— геодезические и другие научные исследования;
— прокладка кабелей и трубопроводов как в прибрежных водах, так и в открытом море;
— добыча полезных ископаемых и проведение необходимых изыскательских работ и др.
В настоящее время в более чем 20-ти странах эксплуатируются более 200 опорных станций дифференциальной подсистемы GPS/Глонасс.
Список и координаты опорных станций приведены в ALRS, vol 8, Satellite Navigation Systems.
ГНСС Galileo
Глобальная спутниковая навигационная система Galileo — масштабный западноевропейский проект, разрабатываемый Европейским космическим агентством в сотрудничестве с Европейским союзом.
Проект Galileo обеспечит Европу собственной глобальной спутниковой навигационной системой, позволяющей с высокой точностью определять местоположение объекта и гарантирующей глобальное покрытие.
Она будет обеспечивать перспективные потребности авиационного, морского, железнодорожного и автомобильного транспорта Европейского союза, а также других стран. С ее помощью можно будет точно устанавливать местонахождение воздушного или морского судна, регулировать транспортные потоки, проводить спасательные операции.
Европейская система спутниковой навигации Галилео
Создаваемая система Galileo станет третьей в мире по счету глобальной системой космического позиционирования. Сейчас только США (система GPS) и Россия (система Глонасс) обладают подобными космическими сетями, позволяющими определять с помощью системы спутников точное местонахождение объекта на Земле.
Политическое значение этого проекта заключается в том, что Galileo станет конкурентом американской системы GPS и подорвет монополию США в этой области. Вашингтон предпринял перед ЕС ряд шагов, призывая его опереться на американскую систему.
Однако после многих колебаний и согласований страны ЕС на саммите в Барселоне все же решили сделать ставку на Galileo. Пo словам одного из руководителей Европейской комиссии, собственная спутниковая система позволит Европе сохранить свою автономность, суверенитет и технический потенциал.
Какими причинами обусловлено создание новой системы глобального позиционирования? Пользователи спутниковой навигации в Европе сегодня для определения своего положения не имеют альтернативы помимо существующих систем GPS и Глонасс. Но военные операторы обеих указанных систем не гарантируют постоянного и непрерывного предоставления услуг.
В то же время спутниковая навигация уже сегодня стала обычным способом определения местоположения на море, а в ближайшем будущем следует ожидать его столь же широкого распространения на суше и в воздухе. И если завтра сигнал по каким-то причинам будет отключен, то штурманам морских судов придется вернуться к традиционным методам навигации с использованием секстантов и навигационных таблиц.
А еще через несколько лет зависимость от ГНСС станет такова, что последствия исчезновения сигнала могут оказаться еще более серьезными, и затронут уже не только экономическую эффективность использования транспортных средств, но и их безопасность. Поэтому в начале 1990-х годов Европейский Союз посчитал необходимым наличие собственной европейской глобальной спутниковой навигационной системы.
Система Galileo будет предоставлять беспрецедентную для гражданских средств точность позиционирования до 1 м в режиме реального времени, гарантировать доступ к сервису при всех обстоятельствах, за исключением особо экстремальных, и информировать пользователя в течение нескольких секунд об отказе любого спутника. Это делает се незаменимой при решении таких задач, как управление движением поездов или посадкой самолетов, где обеспечение безопасности особенно критично.
Развертывание Galileo позволит странам Евросоюза провести существенные усовершенствования в системах управления движением всех видов транспорта, а также в коммерческих, индустриальных и других стратегических областях.
С технической точки зрения система Galileo представляет собой флотилию из тридцати (27 действующих и 3 резервных) спутников, работающих в том же диапазоне частот, что и американская система GPS. Орбиты спутников — круговые высотой 23616 км и наклонением 56°. Это наклонение чуть выше, чем у спутников системы GPS (55°), но значительно меньше, чем в системе Глонасс (64,8°).
Тем не менее, их сигналы будут обеспечивать надежное покрытие поверхности Земли вплоть до широты 75° (мыс Нордкап — северная конечность Норвегии) и даже в более высоких широтах.
Большое число аппаратов, оптимизация их размещения на орбитах и наличие трех активных резервных спутников, гарантируют, что даже потеря одного из них не будет заметна для пользователя. Еще одно заявленное преимущество системы Galileo — возможность точного определения положения объектов в крупных городах, где здания экранируют сигнал со спутников, находящихся низко над горизонтом. Она достигается за счет того, что число аппаратов, доступных для использования при позиционировании, в два раза больше минимально необходимого.
Для осуществления контроля функционирования спутников и управления навигационной системой на территории Европы предполагается построить два специализированных центра управления GCC (Galileo Control Centre).
Сюда будет стекаться информация, передаваемая двадцатью наземными станциями слежения GSS (Galileo Sensor Station). Центры GCC также будут осуществлять синхронизацию шкал времени на всех спутниках и наземных станциях.
Обмен данными между центром управления и космическим сегментом будет осуществляться с помощью пяти передающих станций, работающих в S-диапазоне, и 10 станций, работающих в С-диапазоне.
Artist’s conception of GPS Block II-F satellite in orbit
The error analysis for the Global Positioning System is important for understanding how GPS works, and for knowing what magnitude of error should be expected. The GPS makes corrections for receiver clock errors and other effects but there are still residual errors which are not corrected. GPS receiver position is computed based on data received from the satellites. Errors depend on geometric dilution of precision and the sources listed in the table below.
Overview[edit]
Sources of User Equivalent Range Errors (UERE)
| Source | Effect (m) |
|---|---|
| Signal arrival C/A | ±3 |
| Signal arrival P(Y) | ±0.3 |
| Ionospheric effects | ±5 |
| Ephemeris errors | ±2.5 |
| Satellite clock errors | ±2 |
| Multipath distortion | ±1 |
| Tropospheric effects | ±0.5 |
 C/A C/A
|
±6.7 |
 P(Y) P(Y)
|
±6.0 |
Geometric Error Diagram Showing Typical Relation of Indicated Receiver Position, Intersection of Sphere Surfaces, and True Receiver Position in Terms of Pseudorange Errors, PDOP, and Numerical Errors
User equivalent range errors (UERE) are shown in the table. There is also a numerical error with an estimated value, 

The term user equivalent range error (UERE) refers to the error of a component in the distance from receiver to a satellite. These UERE errors are given as ± errors thereby implying that they are unbiased or zero mean errors. These UERE errors are therefore used in computing standard deviations. The standard deviation of the error in receiver position,



PDOP is computed as a function of receiver and satellite positions. A detailed description of how to calculate PDOP is given in the section Geometric dilution of precision computation (GDOP).

The standard deviation of the error in estimated receiver position 
The error diagram on the left shows the inter relationship of indicated receiver position, true receiver position, and the intersection of the four sphere surfaces.
Signal arrival time measurement[edit]
The position calculated by a GPS receiver requires the current time, the position of the satellite and the measured delay of the received signal. The position accuracy is primarily dependent on the satellite position and signal delay.
To measure the delay, the receiver compares the bit sequence received from the satellite with an internally generated version. By comparing the rising and trailing edges of the bit transitions, modern electronics can measure signal offset to within about one percent of a bit pulse width, 
This component of position accuracy can be improved by a factor of 10 using the higher-chiprate P(Y) signal. Assuming the same one percent of bit pulse width accuracy, the high-frequency P(Y) signal results in an accuracy of 
Atmospheric effects[edit]
Inconsistencies of atmospheric conditions affect the speed of the GPS signals as they pass through the Earth’s atmosphere, especially the ionosphere. Correcting these errors is a significant challenge to improving GPS position accuracy. These effects are smallest when the satellite is directly overhead and become greater for satellites nearer the horizon since the path through the atmosphere is longer (see airmass). Once the receiver’s approximate location is known, a mathematical model can be used to estimate and compensate for these errors.
Ionospheric delay of a microwave signal depends on its frequency. It arises from ionized atmosphere (see Total electron content). This phenomenon is known as dispersion and can be calculated from measurements of delays for two or more frequency bands, allowing delays at other frequencies to be estimated.[1] Some military and expensive survey-grade civilian receivers calculate atmospheric dispersion from the different delays in the L1 and L2 frequencies, and apply a more precise correction. This can be done in civilian receivers without decrypting the P(Y) signal carried on L2, by tracking the carrier wave instead of the modulated code. To facilitate this on lower cost receivers, a new civilian code signal on L2, called L2C, was added to the Block IIR-M satellites, which was first launched in 2005. It allows a direct comparison of the L1 and L2 signals using the coded signal instead of the carrier wave.
The effects of the ionosphere generally change slowly, and can be averaged over time. Those for any particular geographical area can be easily calculated by comparing the GPS-measured position to a known surveyed location. This correction is also valid for other receivers in the same general location. Several systems send this information over radio or other links to allow L1-only receivers to make ionospheric corrections. The ionospheric data are transmitted via satellite in Satellite Based Augmentation Systems (SBAS) such as Wide Area Augmentation System (WAAS) (available in North America and Hawaii), EGNOS (Europe and Asia), Multi-functional Satellite Augmentation System (MSAS) (Japan), and GPS Aided Geo Augmented Navigation (GAGAN) (India) which transmits it on the GPS frequency using a special pseudo-random noise sequence (PRN), so only one receiver and antenna are required.
Humidity also causes a variable delay, resulting in errors similar to ionospheric delay, but occurring in the troposphere. This effect is more localized than ionospheric effects, changes more quickly and is not frequency dependent. These traits make precise measurement and compensation of humidity errors more difficult than ionospheric effects.[2]
The Atmospheric pressure can also change the signals reception delay, due to the dry gases present at the troposphere (78% N2, 21% O2, 0.9% Ar…). Its effect varies with local temperature and atmospheric pressure in quite a predictable manner using the laws of the ideal gases.[3]
Multipath effects[edit]
GPS signals can also be affected by multipath issues, where the radio signals reflect off surrounding terrain; buildings, canyon walls, hard ground, etc. These delayed signals cause measurement errors that are different for each type of GPS signal due to its dependency on the wavelength.[4]
A variety of techniques, most notably narrow correlator spacing, have been developed to mitigate multipath errors. For long delay multipath, the receiver itself can recognize the wayward signal and discard it. To address shorter delay multipath from the signal reflecting off the ground, specialized antennas (e.g., a choke ring antenna) may be used to reduce the signal power as received by the antenna. Short delay reflections are harder to filter out because they interfere with the true signal, causing effects almost indistinguishable from routine fluctuations in atmospheric delay.
Multipath effects are much less severe in moving vehicles. When the GPS antenna is moving, the false solutions using reflected signals quickly fail to converge and only the direct signals result in stable solutions.
Ephemeris and clock errors[edit]
While the ephemeris data is transmitted every 30 seconds, the information itself may be up to two hours old. Variability in solar radiation pressure[5] has an indirect effect on GPS accuracy due to its effect on ephemeris errors. If a fast time to first fix (TTFF) is needed, it is possible to upload a valid ephemeris to a receiver, and in addition to setting the time, a position fix can be obtained in under ten seconds. It is feasible to put such ephemeris data on the web so it can be loaded into mobile GPS devices.[6] See also Assisted GPS.
The satellites’ atomic clocks experience noise and clock drift errors. The navigation message contains corrections for these errors and estimates of the accuracy of the atomic clock. However, they are based on observations and may not indicate the clock’s current state.
These problems tend to be very small, but may add up to a few meters (tens of feet) of inaccuracy.[7]
For very precise positioning (e.g., in geodesy), these effects can be eliminated by differential GPS: the simultaneous use of two or more receivers at several survey points. In the 1990s when receivers were quite expensive, some methods of quasi-differential GPS were developed, using only one receiver but reoccupation of measuring points. At the TU Vienna the method was named qGPS and post processing software was developed.[citation needed]
Dilution of precision [edit]
Selective availability[edit]
GPS included a (currently disabled) feature called Selective Availability (SA) that adds intentional, time varying errors of up to 100 meters (328 ft) to the publicly available navigation signals. This was intended to deny an enemy the use of civilian GPS receivers for precision weapon guidance.
SA errors are actually pseudorandom, generated by a cryptographic algorithm from a classified seed key available only to authorized users (the U.S. military, its allies and a few other users, mostly government) with a special military GPS receiver. Mere possession of the receiver is insufficient; it still needs the tightly controlled daily key.
Before it was turned off on May 2, 2000, typical SA errors were about 50 m (164 ft) horizontally and about 100 m (328 ft) vertically.[8] Because SA affects every GPS receiver in a given area almost equally, a fixed station with an accurately known position can measure the SA error values and transmit them to the local GPS receivers so they may correct their position fixes. This is called Differential GPS or DGPS. DGPS also corrects for several other important sources of GPS errors, particularly ionospheric delay, so it continues to be widely used even though SA has been turned off. The ineffectiveness of SA in the face of widely available DGPS was a common argument for turning off SA, and this was finally done by order of President Clinton in 2000.[9]
DGPS services are widely available from both commercial and government sources. The latter include WAAS and the U.S. Coast Guard’s network of LF marine navigation beacons. The accuracy of the corrections depends on the distance between the user and the DGPS receiver. As the distance increases, the errors at the two sites will not correlate as well, resulting in less precise differential corrections.
During the 1990–91 Gulf War, the shortage of military GPS units caused many troops and their families to buy readily available civilian units. Selective Availability significantly impeded the U.S. military’s own battlefield use of these GPS, so the military made the decision to turn it off for the duration of the war.
In the 1990s, the FAA started pressuring the military to turn off SA permanently. This would save the FAA millions of dollars every year in maintenance of their own radio navigation systems. The amount of error added was «set to zero»[10] at midnight on May 1, 2000 following an announcement by U.S. President Bill Clinton, allowing users access to the error-free L1 signal. Per the directive, the induced error of SA was changed to add no error to the public signals (C/A code). Clinton’s executive order required SA to be set to zero by 2006; it happened in 2000 once the U.S. military developed a new system that provides the ability to deny GPS (and other navigation services) to hostile forces in a specific area of crisis without affecting the rest of the world or its own military systems.[10]
On 19 September 2007, the United States Department of Defense announced that future GPS III satellites will not be capable of implementing SA,[11] eventually making the policy permanent.[12]
Anti-spoofing[edit]
Another restriction on GPS, antispoofing, remains on. This encrypts the P-code so that it cannot be mimicked by a transmitter sending false information. Few civilian receivers have ever used the P-code, and the accuracy attainable with the public C/A code was much better than originally expected (especially with DGPS), so much so that the antispoof policy has relatively little effect on most civilian users. Turning off antispoof would primarily benefit surveyors and some scientists who need extremely precise positions for experiments such as tracking tectonic plate motion.
Relativity[edit]
Special Relativity (SR) and General Relativity (GR) are two separate and distinct theories under the title of the Theory of Relativity. SR and GR make different (opposite) predictions when it comes to the clocks on-board GPS satellites. Note the opposite signs (plus and minus) below due to the different effects.
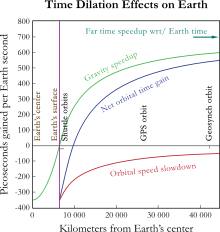
Satellite clocks are slowed by their orbital speed but sped up by their distance out of the Earth’s gravitational well.
A number of sources of error exist due to relativistic effects[13] that would render the system useless if uncorrected. Three relativistic effects are time dilation, gravitational frequency shift, and eccentricity effects. Examples include the relativistic time slowing due to the speed of the satellite of about 1 part in 1010, the gravitational time dilation that makes a satellite run about 5 parts in 1010 faster than an Earth-based clock, and the Sagnac effect due to rotation relative to receivers on Earth. These topics are examined below, one at a time.
Special Relativity (SR)[edit]
SR predicts that clocks slow down as velocity increases. That is the frequency of the atomic clocks moving at GPS orbital speeds will tick more slowly than stationary ground clocks by a factor of 
General Relativity (GR)[edit]
GR has the opposite effect. GR predicts that clocks speed up as they get further away from a massive object (the Earth in this case). The effect of gravitational frequency shift on the GPS due to general relativity is that a clock closer to a massive object will be slower than a clock farther away. Applied to the GPS, the receivers are much closer to Earth than the satellites, causing the GPS clocks in the satellites to be faster by a factor of 5×10−10, or about +45.8 μs/day. This gravitational frequency shift is measurable. During early development it was believed that GPS would not be affected by GR effects, but the Hafele–Keating experiment showed it would be.
Combined SR and GR[edit]
When combining SR and GR, the discrepancy is about +38 microseconds per day. This is a difference of 4.465 parts in 1010.[14] Without correction, errors of roughly 11.4 km/day would accumulate in the position.[15] This initial pseudorange error is corrected in the process of solving the navigation equations. In addition, the elliptical, rather than perfectly circular, satellite orbits cause the time dilation and gravitational frequency shift effects to vary with time. This eccentricity effect causes the clock rate difference between a GPS satellite and a receiver to increase or decrease depending on the altitude of the satellite.
SR and GR combined
| Theory | Value | Notes |
|---|---|---|
| SR (Special Relativity) | -7.2 μs/day | Clocks slowed in Satellites due to Velocity |
| GR (General Relativity) | +45.8 μs/day | Clocks sped up in Satellites due to lower Gravity |
| Total (Combined) | +38.6 μs/day | GR is larger effect than SR |
To compensate for the discrepancy, the frequency standard on board each satellite is given a rate offset prior to launch, making it run slightly slower than the desired frequency on Earth; specifically, at 10.22999999543 MHz instead of 10.23 MHz.[16] Since the atomic clocks on board the GPS satellites are precisely tuned, it makes the system a practical engineering application of the scientific theory of relativity in a real-world environment.[17] Placing atomic clocks on artificial satellites to test Einstein’s general theory was proposed by Friedwardt Winterberg in 1955.[18] The conclusion is that the GPS satellites must compensate for GR, the physics of black holes and extreme gravity.
Calculations[edit]
To calculate the amount of daily time dilation experienced by GPS satellites relative to Earth we need to separately determine the amounts due to special relativity (velocity) and general relativity (gravity) and add them together.
Special Relativity (SR)[edit]
The amount due to velocity will be determined using the Lorentz transformation. This will be:
For small values of v/c, by using binomial expansion this approximates to:
The GPS satellites move at 3874 m/s relative to Earth’s center.[16] We thus determine:
This difference below 1 of 8.349×10−11 represents the fraction by which the satellites’ clocks move slower than Earth’s. It is then multiplied by the number of nanoseconds in a day:
That is the satellites’ clocks lose 7214 nanoseconds a day due to SR effects.
- Note that this speed of 3874 m/s is measured relative to Earth’s center rather than its surface where the GPS receivers (and users) are. This is because Earth’s equipotential makes net time dilation equal across its geodesic surface.[19] That is, the combination of Special and General effects make the net time dilation at the equator equal to that of the poles, which in turn are at rest relative to the center. Hence we use the center as a reference point to represent the entire surface.
General Relativity (GR)[edit]
The amount of dilation due to gravity will be determined using the gravitational time dilation equation:
For small values of M/r, by using binomial expansion this approximates to:
We are again only interested in the fraction below 1, and in the difference between Earth and the satellites. To determine this difference we take:
Earth has a radius of 6,357 km (at the poles) making Rearth = 6,357,000 m and the satellites have an altitude of 20,184 km[16] making their orbit radius Rgps = 26,541,000 m. Substituting these in the above equation, with Mearth = 5.974×1024, G = 6.674×10−11, and c = 2.998×108 (all in SI units), gives:
This represents the fraction by which the satellites’ clocks move faster than Earth’s. It is then multiplied by the number of nanoseconds in a day:
That is the satellites’ clocks gain 45850 nanoseconds a day due to GR effects.
Combined SR and GR[edit]
These effects are added together to give (rounded to 10 ns):
- 45850 – 7210 = 38640 ns
Hence the satellites’ clocks gain approximately 38,640 nanoseconds a day or 38.6 μs per day due to relativity effects in total.
In order to compensate for this gain, a GPS clock’s frequency needs to be slowed by the fraction:
- 5.307×10−10 – 8.349×10−11 = 4.472×10−10
This fraction is subtracted from 1 and multiplied by the pre-adjusted clock frequency of 10.23 MHz:
- (1 – 4.472×10−10) × 10.23 = 10.22999999543
That is we need to slow the clocks down from 10.23 MHz to 10.22999999543 MHz in order to negate both the SR and GR effects of relativity.
Sagnac distortion[edit]
GPS observation processing must also compensate for the Sagnac effect. The GPS time scale is defined in an inertial system but observations are processed in an Earth-centered, Earth-fixed (co-rotating) system, a system in which simultaneity is not uniquely defined. A coordinate transformation is thus applied to convert from the inertial system to the ECEF system. The resulting signal run time correction has opposite algebraic signs for satellites in the Eastern and Western celestial hemispheres. Ignoring this effect will produce an east–west error on the order of hundreds of nanoseconds, or tens of meters in position.[20]
Natural sources of interference[edit]
Since GPS signals at terrestrial receivers tend to be relatively weak, natural radio signals or scattering of the GPS signals can desensitize the receiver, making acquiring and tracking the satellite signals difficult or impossible.
Space weather degrades GPS operation in two ways, direct interference by solar radio burst noise in the same frequency band[21] or by scattering of the GPS radio signal in ionospheric irregularities referred to as scintillation.[22] Both forms of degradation follow the 11 year solar cycle and are a maximum at sunspot maximum although they can occur at any time. Solar radio bursts are associated with solar flares and coronal mass ejections (CMEs)[23] and their impact can affect reception over the half of the Earth facing the sun. Scintillation occurs most frequently at tropical latitudes where it is a night time phenomenon. It occurs less frequently at high latitudes or mid-latitudes where magnetic storms can lead to scintillation.[24] In addition to producing scintillation, magnetic storms can produce strong ionospheric gradients that degrade the accuracy of SBAS systems.[25]
Artificial sources of interference[edit]
In automotive GPS receivers, metallic features in windshields,[26] such as defrosters, or car window tinting films[27] can act as a Faraday cage, degrading reception just inside the car.
Man-made EMI (electromagnetic interference) can also disrupt or jam GPS signals. In one well-documented case it was impossible to receive GPS signals in the entire harbor of Moss Landing, California due to unintentional jamming caused by malfunctioning TV antenna preamplifiers.[28][29] Intentional jamming is also possible. Generally, stronger signals can interfere with GPS receivers when they are within radio range or line of sight. In 2002 a detailed description of how to build a short-range GPS L1 C/A jammer was published in the online magazine Phrack.[30]
The U.S. government reported that such jammers were used occasionally during the War in Afghanistan, and the U.S. military destroyed six GPS jammers during the Iraq War, including one that was destroyed with a GPS-guided bomb, noting the ineffectiveness of the jammers used in that situation.[31] A GPS jammer is relatively easy to detect and locate, making it an attractive target for anti-radiation missiles. The UK Ministry of Defence tested a jamming system in the UK’s West Country on 7 and 8 June 2007.[citation needed]
Some countries allow the use of GPS repeaters to allow the reception of GPS signals indoors and in obscured locations; while in other countries these are prohibited as the retransmitted signals can cause multi-path interference to other GPS receivers that receive data from both GPS satellites and the repeater. In the UK Ofcom now permits the use of GPS/GNSS Repeaters[32] under a ‘light licensing’ regime.
Due to the potential for both natural and man-made noise, numerous techniques continue to be developed to deal with the interference. The first is to not rely on GPS as a sole source. According to John Ruley, «IFR pilots should have a fallback plan in case of a GPS malfunction».[33] Receiver Autonomous Integrity Monitoring (RAIM) is a feature included in some receivers, designed to provide a warning to the user if jamming or another problem is detected. The U.S. military has also deployed since 2004 their Selective Availability / Anti-Spoofing Module (SAASM) in the Defense Advanced GPS Receiver (DAGR).[34] In demonstration videos the DAGR was shown to detect jamming and maintain its lock on the encrypted GPS signals during interference which caused civilian receivers to lose lock.
See also[edit]
- GPS augmentation
Notes[edit]
- ^ The same principle, and the math behind it, can be found in descriptions of pulsar timing by astronomers.
- ^ Navipedia: Troposphere Monitoring
- ^ Navipedia: Tropospheric Delay
- ^ Navipedia: Multipath
- ^ «IPN Progress Report 42-159 (2004)» (PDF).
- ^ SNT080408. «Ephemeris Server Example». Tdc.co.uk. Archived from the original on January 12, 2009. Retrieved 2009-10-13.
- ^ «Unit 1 – Introduction to GPS». Archived from the original on April 29, 2009.
- ^ Grewal (2001), p. 103.
- ^ «President Clinton Orders the Cessation of GPS Selective Availability».
- ^ a b «Statement by the President regarding the United States’ Decision to Stop Degrading Global Positioning System Accuracy». Federal Aviation Administration. May 1, 2000. Archived from the original on 2011-10-21. Retrieved 2013-01-04.
- ^ «DoD Permanently Discontinues Procurement Of Global Positioning System Selective Availability». DefenseLink. September 18, 2007. Archived from the original on February 18, 2008. Retrieved 2008-02-20.
- ^ «Selective Availability». National space-based Positioning, Navigation, and Timing Executive Committee. Archived from the original on January 13, 2008. Retrieved 2008-02-20.
- ^ Webb (2004), p. 32.
- ^ Rizos, Chris. University of New South Wales. GPS Satellite Signals Archived 2010-06-12 at the Wayback Machine. 1999.
- ^ Faraoni, Valerio (2013). Special Relativity (illustrated ed.). Springer Science & Business Media. p. 54. ISBN 978-3-319-01107-3. Extract of page 54
- ^ a b c The Global Positioning System by Robert A. Nelson Via Satellite Archived 2010-07-18 at the Wayback Machine, November 1999
- ^ Pogge, Richard W.; «Real-World Relativity: The GPS Navigation System». Retrieved 25 January 2008.
- ^ «Astronautica Acta II, 25 (1956)». 1956-08-10. Retrieved 2009-10-23.
- ^ S. P. Drake (January 2006). «The equivalence principle as a stepping stone from special to general relativity» (PDF). Am. J. Phys., Vol. 74, No. 1. pp. 22–25.
- ^ Ashby, Neil Relativity and GPS. Physics Today, May 2002.
- ^ Cerruti, A., P. M. Kintner, D. E. Gary, A. J. Mannucci, R. F. Meyer, P. H. Doherty, and A. J. Coster (2008), Effect of intense December 2006 solar radio bursts on GPS receivers, Space Weather, doi:10.1029/2007SW000375, October 19, 2008
- ^ Aarons, Jules; Basu, Santimay (1994). «Ionospheric amplitude and phase fluctuations at the GPS frequencies». Proceedings of ION GPS. 2: 1569–1578.
- ^ S. Mancuso and J. C. Raymond, «Coronal transients and metric type II radio bursts. I. Effects of geometry, 2004, Astronomy and Astrophysics, v.413, p.363-371′
- ^ Ledvina, B. M.; J. J. Makela & P. M. Kintner (2002). «First observations of intense GPS L1 amplitude scintillations at midlatitude». Geophysical Research Letters. 29 (14): 1659. Bibcode:2002GeoRL..29.1659L. doi:10.1029/2002GL014770. S2CID 133701419.
- ^ Tom Diehl, Solar Flares Hit the Earth- WAAS Bends but Does Not Break, SatNav News, volume 23, June 2004.
- ^ «I-PASS Mounting for Vehicles with Special Windshield Features» (PDF). Archived from the original (PDF) on March 26, 2010.
- ^ «3M Automotive Films».. Note that the ‘Color Stable’ films are specifically described as not interfering with satellite signals.
- ^ «The Hunt for RFI». GPS World. 1 January 2003.
- ^ «EMC compliance club «banana skins» column 222″. Compliance-club.com. Retrieved 2009-10-13.
- ^ Low Cost and Portable GPS Jammer. Phrack issue 0x3c (60), article 13. Published December 28, 2002.
- ^ American Forces Press Service. Centcom charts progress. March 25, 2003. Archived December 3, 2009, at the Wayback Machine
- ^ [1] Ofcom Statement on Authorisation regime for GNSS repeaters
- ^ Ruley, John. AVweb. GPS jamming. February 12, 2003.
- ^ US Army DAGR page Archived 2012-08-05 at archive.today
References[edit]
- Grewal, Mohinder S.; Weill, Lawrence Randolph; Andrews, Angus P. (2001). Global positioning systems, inertial navigation, and integration. John Wiley and Sons. ISBN 978-0-471-35032-3.
- Parkinson; Spilker (1996). The global positioning system. American Institute of Aeronautics & Astronomy. ISBN 978-1-56347-106-3.
- Webb, Stephen (2004). Out of this world: colliding universes, branes, strings, and other wild ideas of modern physics. Springer. ISBN 0-387-02930-3. Retrieved 2013-08-16.
External links[edit]
- GPS.gov—General public education website created by the U.S. Government
- GPS SPS Performance Standard—The official Standard Positioning Service specification (2008 version).
- GPS SPS Performance Standard—The official Standard Positioning Service specification (2001 version).
Artist’s conception of GPS Block II-F satellite in orbit
The error analysis for the Global Positioning System is important for understanding how GPS works, and for knowing what magnitude of error should be expected. The GPS makes corrections for receiver clock errors and other effects but there are still residual errors which are not corrected. GPS receiver position is computed based on data received from the satellites. Errors depend on geometric dilution of precision and the sources listed in the table below.
Overview[edit]
Sources of User Equivalent Range Errors (UERE)
| Source | Effect (m) |
|---|---|
| Signal arrival C/A | ±3 |
| Signal arrival P(Y) | ±0.3 |
| Ionospheric effects | ±5 |
| Ephemeris errors | ±2.5 |
| Satellite clock errors | ±2 |
| Multipath distortion | ±1 |
| Tropospheric effects | ±0.5 |
 C/A C/A
|
±6.7 |
 P(Y) P(Y)
|
±6.0 |
Geometric Error Diagram Showing Typical Relation of Indicated Receiver Position, Intersection of Sphere Surfaces, and True Receiver Position in Terms of Pseudorange Errors, PDOP, and Numerical Errors
User equivalent range errors (UERE) are shown in the table. There is also a numerical error with an estimated value, 

The term user equivalent range error (UERE) refers to the error of a component in the distance from receiver to a satellite. These UERE errors are given as ± errors thereby implying that they are unbiased or zero mean errors. These UERE errors are therefore used in computing standard deviations. The standard deviation of the error in receiver position,



PDOP is computed as a function of receiver and satellite positions. A detailed description of how to calculate PDOP is given in the section Geometric dilution of precision computation (GDOP).

The standard deviation of the error in estimated receiver position 
The error diagram on the left shows the inter relationship of indicated receiver position, true receiver position, and the intersection of the four sphere surfaces.
Signal arrival time measurement[edit]
The position calculated by a GPS receiver requires the current time, the position of the satellite and the measured delay of the received signal. The position accuracy is primarily dependent on the satellite position and signal delay.
To measure the delay, the receiver compares the bit sequence received from the satellite with an internally generated version. By comparing the rising and trailing edges of the bit transitions, modern electronics can measure signal offset to within about one percent of a bit pulse width, 
This component of position accuracy can be improved by a factor of 10 using the higher-chiprate P(Y) signal. Assuming the same one percent of bit pulse width accuracy, the high-frequency P(Y) signal results in an accuracy of 
Atmospheric effects[edit]
Inconsistencies of atmospheric conditions affect the speed of the GPS signals as they pass through the Earth’s atmosphere, especially the ionosphere. Correcting these errors is a significant challenge to improving GPS position accuracy. These effects are smallest when the satellite is directly overhead and become greater for satellites nearer the horizon since the path through the atmosphere is longer (see airmass). Once the receiver’s approximate location is known, a mathematical model can be used to estimate and compensate for these errors.
Ionospheric delay of a microwave signal depends on its frequency. It arises from ionized atmosphere (see Total electron content). This phenomenon is known as dispersion and can be calculated from measurements of delays for two or more frequency bands, allowing delays at other frequencies to be estimated.[1] Some military and expensive survey-grade civilian receivers calculate atmospheric dispersion from the different delays in the L1 and L2 frequencies, and apply a more precise correction. This can be done in civilian receivers without decrypting the P(Y) signal carried on L2, by tracking the carrier wave instead of the modulated code. To facilitate this on lower cost receivers, a new civilian code signal on L2, called L2C, was added to the Block IIR-M satellites, which was first launched in 2005. It allows a direct comparison of the L1 and L2 signals using the coded signal instead of the carrier wave.
The effects of the ionosphere generally change slowly, and can be averaged over time. Those for any particular geographical area can be easily calculated by comparing the GPS-measured position to a known surveyed location. This correction is also valid for other receivers in the same general location. Several systems send this information over radio or other links to allow L1-only receivers to make ionospheric corrections. The ionospheric data are transmitted via satellite in Satellite Based Augmentation Systems (SBAS) such as Wide Area Augmentation System (WAAS) (available in North America and Hawaii), EGNOS (Europe and Asia), Multi-functional Satellite Augmentation System (MSAS) (Japan), and GPS Aided Geo Augmented Navigation (GAGAN) (India) which transmits it on the GPS frequency using a special pseudo-random noise sequence (PRN), so only one receiver and antenna are required.
Humidity also causes a variable delay, resulting in errors similar to ionospheric delay, but occurring in the troposphere. This effect is more localized than ionospheric effects, changes more quickly and is not frequency dependent. These traits make precise measurement and compensation of humidity errors more difficult than ionospheric effects.[2]
The Atmospheric pressure can also change the signals reception delay, due to the dry gases present at the troposphere (78% N2, 21% O2, 0.9% Ar…). Its effect varies with local temperature and atmospheric pressure in quite a predictable manner using the laws of the ideal gases.[3]
Multipath effects[edit]
GPS signals can also be affected by multipath issues, where the radio signals reflect off surrounding terrain; buildings, canyon walls, hard ground, etc. These delayed signals cause measurement errors that are different for each type of GPS signal due to its dependency on the wavelength.[4]
A variety of techniques, most notably narrow correlator spacing, have been developed to mitigate multipath errors. For long delay multipath, the receiver itself can recognize the wayward signal and discard it. To address shorter delay multipath from the signal reflecting off the ground, specialized antennas (e.g., a choke ring antenna) may be used to reduce the signal power as received by the antenna. Short delay reflections are harder to filter out because they interfere with the true signal, causing effects almost indistinguishable from routine fluctuations in atmospheric delay.
Multipath effects are much less severe in moving vehicles. When the GPS antenna is moving, the false solutions using reflected signals quickly fail to converge and only the direct signals result in stable solutions.
Ephemeris and clock errors[edit]
While the ephemeris data is transmitted every 30 seconds, the information itself may be up to two hours old. Variability in solar radiation pressure[5] has an indirect effect on GPS accuracy due to its effect on ephemeris errors. If a fast time to first fix (TTFF) is needed, it is possible to upload a valid ephemeris to a receiver, and in addition to setting the time, a position fix can be obtained in under ten seconds. It is feasible to put such ephemeris data on the web so it can be loaded into mobile GPS devices.[6] See also Assisted GPS.
The satellites’ atomic clocks experience noise and clock drift errors. The navigation message contains corrections for these errors and estimates of the accuracy of the atomic clock. However, they are based on observations and may not indicate the clock’s current state.
These problems tend to be very small, but may add up to a few meters (tens of feet) of inaccuracy.[7]
For very precise positioning (e.g., in geodesy), these effects can be eliminated by differential GPS: the simultaneous use of two or more receivers at several survey points. In the 1990s when receivers were quite expensive, some methods of quasi-differential GPS were developed, using only one receiver but reoccupation of measuring points. At the TU Vienna the method was named qGPS and post processing software was developed.[citation needed]
Dilution of precision [edit]
Selective availability[edit]
GPS included a (currently disabled) feature called Selective Availability (SA) that adds intentional, time varying errors of up to 100 meters (328 ft) to the publicly available navigation signals. This was intended to deny an enemy the use of civilian GPS receivers for precision weapon guidance.
SA errors are actually pseudorandom, generated by a cryptographic algorithm from a classified seed key available only to authorized users (the U.S. military, its allies and a few other users, mostly government) with a special military GPS receiver. Mere possession of the receiver is insufficient; it still needs the tightly controlled daily key.
Before it was turned off on May 2, 2000, typical SA errors were about 50 m (164 ft) horizontally and about 100 m (328 ft) vertically.[8] Because SA affects every GPS receiver in a given area almost equally, a fixed station with an accurately known position can measure the SA error values and transmit them to the local GPS receivers so they may correct their position fixes. This is called Differential GPS or DGPS. DGPS also corrects for several other important sources of GPS errors, particularly ionospheric delay, so it continues to be widely used even though SA has been turned off. The ineffectiveness of SA in the face of widely available DGPS was a common argument for turning off SA, and this was finally done by order of President Clinton in 2000.[9]
DGPS services are widely available from both commercial and government sources. The latter include WAAS and the U.S. Coast Guard’s network of LF marine navigation beacons. The accuracy of the corrections depends on the distance between the user and the DGPS receiver. As the distance increases, the errors at the two sites will not correlate as well, resulting in less precise differential corrections.
During the 1990–91 Gulf War, the shortage of military GPS units caused many troops and their families to buy readily available civilian units. Selective Availability significantly impeded the U.S. military’s own battlefield use of these GPS, so the military made the decision to turn it off for the duration of the war.
In the 1990s, the FAA started pressuring the military to turn off SA permanently. This would save the FAA millions of dollars every year in maintenance of their own radio navigation systems. The amount of error added was «set to zero»[10] at midnight on May 1, 2000 following an announcement by U.S. President Bill Clinton, allowing users access to the error-free L1 signal. Per the directive, the induced error of SA was changed to add no error to the public signals (C/A code). Clinton’s executive order required SA to be set to zero by 2006; it happened in 2000 once the U.S. military developed a new system that provides the ability to deny GPS (and other navigation services) to hostile forces in a specific area of crisis without affecting the rest of the world or its own military systems.[10]
On 19 September 2007, the United States Department of Defense announced that future GPS III satellites will not be capable of implementing SA,[11] eventually making the policy permanent.[12]
Anti-spoofing[edit]
Another restriction on GPS, antispoofing, remains on. This encrypts the P-code so that it cannot be mimicked by a transmitter sending false information. Few civilian receivers have ever used the P-code, and the accuracy attainable with the public C/A code was much better than originally expected (especially with DGPS), so much so that the antispoof policy has relatively little effect on most civilian users. Turning off antispoof would primarily benefit surveyors and some scientists who need extremely precise positions for experiments such as tracking tectonic plate motion.
Relativity[edit]
Special Relativity (SR) and General Relativity (GR) are two separate and distinct theories under the title of the Theory of Relativity. SR and GR make different (opposite) predictions when it comes to the clocks on-board GPS satellites. Note the opposite signs (plus and minus) below due to the different effects.
Satellite clocks are slowed by their orbital speed but sped up by their distance out of the Earth’s gravitational well.
A number of sources of error exist due to relativistic effects[13] that would render the system useless if uncorrected. Three relativistic effects are time dilation, gravitational frequency shift, and eccentricity effects. Examples include the relativistic time slowing due to the speed of the satellite of about 1 part in 1010, the gravitational time dilation that makes a satellite run about 5 parts in 1010 faster than an Earth-based clock, and the Sagnac effect due to rotation relative to receivers on Earth. These topics are examined below, one at a time.
Special Relativity (SR)[edit]
SR predicts that clocks slow down as velocity increases. That is the frequency of the atomic clocks moving at GPS orbital speeds will tick more slowly than stationary ground clocks by a factor of 
General Relativity (GR)[edit]
GR has the opposite effect. GR predicts that clocks speed up as they get further away from a massive object (the Earth in this case). The effect of gravitational frequency shift on the GPS due to general relativity is that a clock closer to a massive object will be slower than a clock farther away. Applied to the GPS, the receivers are much closer to Earth than the satellites, causing the GPS clocks in the satellites to be faster by a factor of 5×10−10, or about +45.8 μs/day. This gravitational frequency shift is measurable. During early development it was believed that GPS would not be affected by GR effects, but the Hafele–Keating experiment showed it would be.
Combined SR and GR[edit]
When combining SR and GR, the discrepancy is about +38 microseconds per day. This is a difference of 4.465 parts in 1010.[14] Without correction, errors of roughly 11.4 km/day would accumulate in the position.[15] This initial pseudorange error is corrected in the process of solving the navigation equations. In addition, the elliptical, rather than perfectly circular, satellite orbits cause the time dilation and gravitational frequency shift effects to vary with time. This eccentricity effect causes the clock rate difference between a GPS satellite and a receiver to increase or decrease depending on the altitude of the satellite.
SR and GR combined
| Theory | Value | Notes |
|---|---|---|
| SR (Special Relativity) | -7.2 μs/day | Clocks slowed in Satellites due to Velocity |
| GR (General Relativity) | +45.8 μs/day | Clocks sped up in Satellites due to lower Gravity |
| Total (Combined) | +38.6 μs/day | GR is larger effect than SR |
To compensate for the discrepancy, the frequency standard on board each satellite is given a rate offset prior to launch, making it run slightly slower than the desired frequency on Earth; specifically, at 10.22999999543 MHz instead of 10.23 MHz.[16] Since the atomic clocks on board the GPS satellites are precisely tuned, it makes the system a practical engineering application of the scientific theory of relativity in a real-world environment.[17] Placing atomic clocks on artificial satellites to test Einstein’s general theory was proposed by Friedwardt Winterberg in 1955.[18] The conclusion is that the GPS satellites must compensate for GR, the physics of black holes and extreme gravity.
Calculations[edit]
To calculate the amount of daily time dilation experienced by GPS satellites relative to Earth we need to separately determine the amounts due to special relativity (velocity) and general relativity (gravity) and add them together.
Special Relativity (SR)[edit]
The amount due to velocity will be determined using the Lorentz transformation. This will be:
For small values of v/c, by using binomial expansion this approximates to:
The GPS satellites move at 3874 m/s relative to Earth’s center.[16] We thus determine:
This difference below 1 of 8.349×10−11 represents the fraction by which the satellites’ clocks move slower than Earth’s. It is then multiplied by the number of nanoseconds in a day:
That is the satellites’ clocks lose 7214 nanoseconds a day due to SR effects.
- Note that this speed of 3874 m/s is measured relative to Earth’s center rather than its surface where the GPS receivers (and users) are. This is because Earth’s equipotential makes net time dilation equal across its geodesic surface.[19] That is, the combination of Special and General effects make the net time dilation at the equator equal to that of the poles, which in turn are at rest relative to the center. Hence we use the center as a reference point to represent the entire surface.
General Relativity (GR)[edit]
The amount of dilation due to gravity will be determined using the gravitational time dilation equation:
For small values of M/r, by using binomial expansion this approximates to:
We are again only interested in the fraction below 1, and in the difference between Earth and the satellites. To determine this difference we take:
Earth has a radius of 6,357 km (at the poles) making Rearth = 6,357,000 m and the satellites have an altitude of 20,184 km[16] making their orbit radius Rgps = 26,541,000 m. Substituting these in the above equation, with Mearth = 5.974×1024, G = 6.674×10−11, and c = 2.998×108 (all in SI units), gives:
This represents the fraction by which the satellites’ clocks move faster than Earth’s. It is then multiplied by the number of nanoseconds in a day:
That is the satellites’ clocks gain 45850 nanoseconds a day due to GR effects.
Combined SR and GR[edit]
These effects are added together to give (rounded to 10 ns):
- 45850 – 7210 = 38640 ns
Hence the satellites’ clocks gain approximately 38,640 nanoseconds a day or 38.6 μs per day due to relativity effects in total.
In order to compensate for this gain, a GPS clock’s frequency needs to be slowed by the fraction:
- 5.307×10−10 – 8.349×10−11 = 4.472×10−10
This fraction is subtracted from 1 and multiplied by the pre-adjusted clock frequency of 10.23 MHz:
- (1 – 4.472×10−10) × 10.23 = 10.22999999543
That is we need to slow the clocks down from 10.23 MHz to 10.22999999543 MHz in order to negate both the SR and GR effects of relativity.
Sagnac distortion[edit]
GPS observation processing must also compensate for the Sagnac effect. The GPS time scale is defined in an inertial system but observations are processed in an Earth-centered, Earth-fixed (co-rotating) system, a system in which simultaneity is not uniquely defined. A coordinate transformation is thus applied to convert from the inertial system to the ECEF system. The resulting signal run time correction has opposite algebraic signs for satellites in the Eastern and Western celestial hemispheres. Ignoring this effect will produce an east–west error on the order of hundreds of nanoseconds, or tens of meters in position.[20]
Natural sources of interference[edit]
Since GPS signals at terrestrial receivers tend to be relatively weak, natural radio signals or scattering of the GPS signals can desensitize the receiver, making acquiring and tracking the satellite signals difficult or impossible.
Space weather degrades GPS operation in two ways, direct interference by solar radio burst noise in the same frequency band[21] or by scattering of the GPS radio signal in ionospheric irregularities referred to as scintillation.[22] Both forms of degradation follow the 11 year solar cycle and are a maximum at sunspot maximum although they can occur at any time. Solar radio bursts are associated with solar flares and coronal mass ejections (CMEs)[23] and their impact can affect reception over the half of the Earth facing the sun. Scintillation occurs most frequently at tropical latitudes where it is a night time phenomenon. It occurs less frequently at high latitudes or mid-latitudes where magnetic storms can lead to scintillation.[24] In addition to producing scintillation, magnetic storms can produce strong ionospheric gradients that degrade the accuracy of SBAS systems.[25]
Artificial sources of interference[edit]
In automotive GPS receivers, metallic features in windshields,[26] such as defrosters, or car window tinting films[27] can act as a Faraday cage, degrading reception just inside the car.
Man-made EMI (electromagnetic interference) can also disrupt or jam GPS signals. In one well-documented case it was impossible to receive GPS signals in the entire harbor of Moss Landing, California due to unintentional jamming caused by malfunctioning TV antenna preamplifiers.[28][29] Intentional jamming is also possible. Generally, stronger signals can interfere with GPS receivers when they are within radio range or line of sight. In 2002 a detailed description of how to build a short-range GPS L1 C/A jammer was published in the online magazine Phrack.[30]
The U.S. government reported that such jammers were used occasionally during the War in Afghanistan, and the U.S. military destroyed six GPS jammers during the Iraq War, including one that was destroyed with a GPS-guided bomb, noting the ineffectiveness of the jammers used in that situation.[31] A GPS jammer is relatively easy to detect and locate, making it an attractive target for anti-radiation missiles. The UK Ministry of Defence tested a jamming system in the UK’s West Country on 7 and 8 June 2007.[citation needed]
Some countries allow the use of GPS repeaters to allow the reception of GPS signals indoors and in obscured locations; while in other countries these are prohibited as the retransmitted signals can cause multi-path interference to other GPS receivers that receive data from both GPS satellites and the repeater. In the UK Ofcom now permits the use of GPS/GNSS Repeaters[32] under a ‘light licensing’ regime.
Due to the potential for both natural and man-made noise, numerous techniques continue to be developed to deal with the interference. The first is to not rely on GPS as a sole source. According to John Ruley, «IFR pilots should have a fallback plan in case of a GPS malfunction».[33] Receiver Autonomous Integrity Monitoring (RAIM) is a feature included in some receivers, designed to provide a warning to the user if jamming or another problem is detected. The U.S. military has also deployed since 2004 their Selective Availability / Anti-Spoofing Module (SAASM) in the Defense Advanced GPS Receiver (DAGR).[34] In demonstration videos the DAGR was shown to detect jamming and maintain its lock on the encrypted GPS signals during interference which caused civilian receivers to lose lock.
See also[edit]
- GPS augmentation
Notes[edit]
- ^ The same principle, and the math behind it, can be found in descriptions of pulsar timing by astronomers.
- ^ Navipedia: Troposphere Monitoring
- ^ Navipedia: Tropospheric Delay
- ^ Navipedia: Multipath
- ^ «IPN Progress Report 42-159 (2004)» (PDF).
- ^ SNT080408. «Ephemeris Server Example». Tdc.co.uk. Archived from the original on January 12, 2009. Retrieved 2009-10-13.
- ^ «Unit 1 – Introduction to GPS». Archived from the original on April 29, 2009.
- ^ Grewal (2001), p. 103.
- ^ «President Clinton Orders the Cessation of GPS Selective Availability».
- ^ a b «Statement by the President regarding the United States’ Decision to Stop Degrading Global Positioning System Accuracy». Federal Aviation Administration. May 1, 2000. Archived from the original on 2011-10-21. Retrieved 2013-01-04.
- ^ «DoD Permanently Discontinues Procurement Of Global Positioning System Selective Availability». DefenseLink. September 18, 2007. Archived from the original on February 18, 2008. Retrieved 2008-02-20.
- ^ «Selective Availability». National space-based Positioning, Navigation, and Timing Executive Committee. Archived from the original on January 13, 2008. Retrieved 2008-02-20.
- ^ Webb (2004), p. 32.
- ^ Rizos, Chris. University of New South Wales. GPS Satellite Signals Archived 2010-06-12 at the Wayback Machine. 1999.
- ^ Faraoni, Valerio (2013). Special Relativity (illustrated ed.). Springer Science & Business Media. p. 54. ISBN 978-3-319-01107-3. Extract of page 54
- ^ a b c The Global Positioning System by Robert A. Nelson Via Satellite Archived 2010-07-18 at the Wayback Machine, November 1999
- ^ Pogge, Richard W.; «Real-World Relativity: The GPS Navigation System». Retrieved 25 January 2008.
- ^ «Astronautica Acta II, 25 (1956)». 1956-08-10. Retrieved 2009-10-23.
- ^ S. P. Drake (January 2006). «The equivalence principle as a stepping stone from special to general relativity» (PDF). Am. J. Phys., Vol. 74, No. 1. pp. 22–25.
- ^ Ashby, Neil Relativity and GPS. Physics Today, May 2002.
- ^ Cerruti, A., P. M. Kintner, D. E. Gary, A. J. Mannucci, R. F. Meyer, P. H. Doherty, and A. J. Coster (2008), Effect of intense December 2006 solar radio bursts on GPS receivers, Space Weather, doi:10.1029/2007SW000375, October 19, 2008
- ^ Aarons, Jules; Basu, Santimay (1994). «Ionospheric amplitude and phase fluctuations at the GPS frequencies». Proceedings of ION GPS. 2: 1569–1578.
- ^ S. Mancuso and J. C. Raymond, «Coronal transients and metric type II radio bursts. I. Effects of geometry, 2004, Astronomy and Astrophysics, v.413, p.363-371′
- ^ Ledvina, B. M.; J. J. Makela & P. M. Kintner (2002). «First observations of intense GPS L1 amplitude scintillations at midlatitude». Geophysical Research Letters. 29 (14): 1659. Bibcode:2002GeoRL..29.1659L. doi:10.1029/2002GL014770. S2CID 133701419.
- ^ Tom Diehl, Solar Flares Hit the Earth- WAAS Bends but Does Not Break, SatNav News, volume 23, June 2004.
- ^ «I-PASS Mounting for Vehicles with Special Windshield Features» (PDF). Archived from the original (PDF) on March 26, 2010.
- ^ «3M Automotive Films».. Note that the ‘Color Stable’ films are specifically described as not interfering with satellite signals.
- ^ «The Hunt for RFI». GPS World. 1 January 2003.
- ^ «EMC compliance club «banana skins» column 222″. Compliance-club.com. Retrieved 2009-10-13.
- ^ Low Cost and Portable GPS Jammer. Phrack issue 0x3c (60), article 13. Published December 28, 2002.
- ^ American Forces Press Service. Centcom charts progress. March 25, 2003. Archived December 3, 2009, at the Wayback Machine
- ^ [1] Ofcom Statement on Authorisation regime for GNSS repeaters
- ^ Ruley, John. AVweb. GPS jamming. February 12, 2003.
- ^ US Army DAGR page Archived 2012-08-05 at archive.today
References[edit]
- Grewal, Mohinder S.; Weill, Lawrence Randolph; Andrews, Angus P. (2001). Global positioning systems, inertial navigation, and integration. John Wiley and Sons. ISBN 978-0-471-35032-3.
- Parkinson; Spilker (1996). The global positioning system. American Institute of Aeronautics & Astronomy. ISBN 978-1-56347-106-3.
- Webb, Stephen (2004). Out of this world: colliding universes, branes, strings, and other wild ideas of modern physics. Springer. ISBN 0-387-02930-3. Retrieved 2013-08-16.
External links[edit]
- GPS.gov—General public education website created by the U.S. Government
- GPS SPS Performance Standard—The official Standard Positioning Service specification (2008 version).
- GPS SPS Performance Standard—The official Standard Positioning Service specification (2001 version).
Художественная концепция спутника GPS Block II-F на орбите
В анализ ошибок для спутниковая система навигации важно для понимания того, как работает GPS, и для того, чтобы знать, какой величины ошибок следует ожидать. GPS вносит поправки на ошибки часов приемника и другие эффекты, но остаются остаточные ошибки, которые не исправляются. Положение приемника GPS вычисляется на основе данных, полученных со спутников. Ошибки зависят от геометрического снижения точности и источников, перечисленных в таблице ниже.
Обзор
|
|
В этом разделе фактическая точность оспаривается. Соответствующее обсуждение можно найти на Обсуждение: Анализ ошибок для глобальной системы позиционирования. Пожалуйста, помогите убедиться, что оспариваемые утверждения надежный источник. (Июнь 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
Источники ошибок эквивалентного диапазона пользователя (UERE)
| Источник | Эффект (м) |
|---|---|
| Прибытие сигнала C / A | ±3 |
| Прибытие сигнала P (Y) | ±0.3 |
| Ионосферные эффекты | ±5 |
| Ошибки эфемерид | ±2.5 |
| Ошибки спутниковых часов | ±2 |
| Многолучевое искажение | ±1 |
| Тропосферные эффекты | ±0.5 |
 C / A C / A |
±6.7 |
 P (Y) P (Y) |
±6.0 |
Диаграмма геометрических ошибок, показывающая типичное соотношение отображаемого положения приемника, пересечения поверхностей сфер и истинного положения приемника в терминах ошибок псевдодальности, PDOP и числовых ошибок
Ошибки эквивалентного диапазона пользователя (UERE) показаны в таблице. Также есть числовая ошибка с оценочной стоимостью, 

Термин «ошибка эквивалентного диапазона пользователя» (UERE) относится к ошибке компонента на расстоянии от приемника до спутника. Эти ошибки UERE представлены как ошибки ±, что означает, что они являются несмещенными или нулевыми средними ошибками. Поэтому эти ошибки UERE используются при вычислении стандартных отклонений. Стандартное отклонение ошибки положения приемника,


PDOP вычисляется как функция положения приемника и спутника. Подробное описание того, как рассчитать PDOP, дано в разделе Геометрическое снижение точности вычислений (GDOP).

Стандартное отклонение ошибки в предполагаемом положении приемника 
Диаграмма ошибок слева показывает взаимосвязь указанного положения приемника, истинного положения приемника и пересечения четырех сферических поверхностей.
Измерение времени прихода сигнала
Положение, вычисленное приемником GPS, требует текущего времени, положения спутника и измеренной задержки принятого сигнала. Точность определения местоположения в первую очередь зависит от местоположения спутника и задержки сигнала.
Чтобы измерить задержку, приемник сравнивает битовую последовательность, полученную от спутника, с версией, созданной внутри. Сравнивая нарастающий и задний фронты битовых переходов, современная электроника может измерять смещение сигнала с точностью до одного процента от ширины битового импульса, 
Этот компонент точности позиционирования можно улучшить в 10 раз, используя сигнал P (Y) с более высокой чиповой скоростью. Предполагая тот же один процент точности ширины битового импульса, высокочастотный сигнал P (Y) дает точность 
Атмосферные эффекты
Несоответствие атмосферных условий влияет на скорость сигналов GPS, когда они проходят через Атмосфера Земли, особенно ионосфера. Исправление этих ошибок является серьезной проблемой для повышения точности определения местоположения GPS. Эти эффекты наименьшие, когда спутник находится прямо над головой, и усиливаются для спутников, расположенных ближе к горизонт так как путь через атмосферу длиннее (см. масса воздуха ). Как только приблизительное местоположение приемника известно, можно использовать математическую модель для оценки и компенсации этих ошибок.
Ионосферная задержка СВЧ-сигнала зависит от его частоты. Он возникает из ионизированной атмосферы (см. Общее электронное содержание ). Это явление известно как разброс и может быть рассчитан на основе измерений задержек для двух или более полос частот, что позволяет оценить задержки на других частотах.[1] Некоторые военные и дорогие гражданские приемники исследовательского класса рассчитывают атмосферную дисперсию по различным задержкам на частотах L1 и L2 и применяют более точную поправку. Это можно сделать в гражданских приемниках без расшифровки сигнала P (Y), передаваемого по L2, путем отслеживания несущая волна вместо модулированный код. Чтобы облегчить это на более дешевых приемниках, новый гражданский кодовый сигнал на L2, названный L2C, был добавлен к спутникам Block IIR-M, которые были впервые запущены в 2005 году. Он позволяет прямое сравнение сигналов L1 и L2 с использованием кодированных сигнал вместо несущей.
Воздействие ионосферы обычно изменяется медленно и может быть усреднено по времени. Эти значения для любой конкретной географической области можно легко вычислить, сравнив положение, измеренное с помощью GPS, с известным местом съемки. Эта поправка также действительна для других приемников в том же месте. Некоторые системы отправляют эту информацию по радио или другим каналам, чтобы приемники, работающие только на L1, могли вносить ионосферные поправки. Ионосферные данные передаются через спутник в Спутниковые системы дополнения (SBAS) такие как Система увеличения площади (WAAS) (доступно в Северной Америке и на Гавайях), EGNOS (Европа и Азия), Многофункциональная спутниковая система дополнения (MSAS) (Япония) и GPS-навигация с гео-дополнениями (GAGAN) (Индия), который передает его на частоте GPS с использованием специальной псевдослучайной шумовой последовательности (PRN), поэтому требуются только один приемник и антенна.
Влажность также вызывает переменную задержку, приводящую к ошибкам, аналогичным ионосферной задержке, но возникающим в тропосфера. Этот эффект более локализован, чем ионосферные эффекты, изменяется быстрее и не зависит от частоты. Эти особенности делают точное измерение и компенсацию ошибок влажности более трудными, чем ионосферные эффекты.[2]
В Атмосферное давление может также изменить задержку приема сигналов из-за присутствия в тропосфере сухих газов (78% N2, 21% O2, 0,9% Ar …). Его действие меняется в зависимости от местной температуры и атмосферного давления вполне предсказуемым образом с использованием законов идеальных газов.[3]
Эффекты многолучевого распространения
На сигналы GPS также могут влиять многолучевость проблемы, при которых радиосигналы отражаются от окружающей местности; здания, стены каньона, твердый грунт и т. д. Эти задержанные сигналы вызывают ошибки измерения, которые различны для каждого типа сигнала GPS из-за его зависимости от длины волны.[4]
Для уменьшения ошибок, связанных с многолучевым распространением, были разработаны различные методы, в первую очередь узкий интервал между корреляторами. Для многолучевого распространения с большой задержкой приемник сам может распознать встречный сигнал и отбросить его. Для решения проблемы многолучевого распространения с более короткой задержкой от сигнала, отражающегося от земли, специальные антенны (например, дроссельная заслонка антенны ) может использоваться для уменьшения мощности сигнала, принимаемого антенной. Отражения с короткой задержкой труднее отфильтровать, потому что они мешают истинному сигналу, вызывая эффекты, почти неотличимые от обычных колебаний атмосферной задержки.
Эффекты многолучевого распространения гораздо менее серьезны в движущихся транспортных средствах. Когда антенна GPS движется, ложные решения с использованием отраженных сигналов быстро не сходятся, и только прямые сигналы приводят к стабильным решениям.
Эфемериды и ошибки часов
В то время как эфемериды данные передаются каждые 30 секунд, сама информация может быть старше двух часов. Изменчивость давления солнечной радиации[5] косвенно влияет на точность GPS из-за влияния на ошибки эфемерид. Если пост время сначала исправить (TTFF), можно загрузить действительные эфемериды в приемник, и в дополнение к установке времени, определение местоположения может быть получено менее чем за десять секунд. Такие эфемеридные данные можно разместить в Интернете, чтобы их можно было загрузить в мобильные устройства GPS.[6] Смотрите также Вспомогательный GPS.
Атомные часы спутников испытывают шум и часы дрейф ошибки. В навигационном сообщении содержатся исправления этих ошибок и оценки точности атомных часов. Однако они основаны на наблюдениях и могут не указывать на текущее состояние часов.
Эти проблемы, как правило, очень малы, но могут составлять несколько метров (десятков футов) неточности.[7]
Для очень точного позиционирования (например, в геодезия ) эти эффекты могут быть устранены дифференциальный GPS: одновременное использование двух и более приемников на нескольких точки обследования. В 1990-е годы, когда приемники были довольно дорогими, некоторые методы квазидифференциальный GPS были разработаны, используя только один приемник, но повторное заселение точек измерения. В Венском техническом университете метод получил название qGPS и было разработано программное обеспечение для постобработки.[нужна цитата ]
Геометрическое снижение точности вычислений (GDOP)
Расчет геометрического снижения точности
Понятие геометрического снижения точности было введено в разделе, источники ошибок и анализ. Были предоставлены расчеты, чтобы показать, как использовался PDOP и как он влиял на стандартное отклонение ошибки местоположения приемника.
Когда видимые спутники GPS расположены близко друг к другу в небе (т. Е. С небольшим угловым разделением), значения DOP высокие; когда они далеко друг от друга, значения DOP низкие. По идее, спутники, которые расположены близко друг к другу, не могут предоставить столько информации, как спутники, которые находятся на большом расстоянии друг от друга. Низкие значения DOP представляют лучшую точность позиционирования GPS из-за более широкого углового разнесения между спутниками, используемыми для расчета положения приемника GPS. HDOP, VDOP, PDOP и TDOP — это соответственно по горизонтали, вертикали, позиции (3-D) и временного снижения точности.
Рисунок 3.1 Снижение точности данных Navstar GPS от береговой охраны США дает графическое представление о том, как геометрия влияет на точность.[8]
Теперь мы беремся за задачу, как вычислить снижение точности. В качестве первого шага в вычислении DOP рассмотрим единичный вектор от приемника к спутнику i с компонентами 



куда 



Первые три элемента каждой строки А являются компонентами единичного вектора от приемника до указанного спутника. Элементами в четвертом столбце являются c, где c обозначает скорость света. Сформулируйте матрицу, Q, так как
Это вычисление производится в соответствии с главой 11 Глобальной системы позиционирования Паркинсона и Спилкера, где весовая матрица п, был установлен в единичную матрицу. Элементы Q матрицы обозначены как:[9]
Греческая буква 
в соответствии с «Раздел 1.4.9 ПРИНЦИПОВ РАЗМЕЩЕНИЯ СПУТНИКОВ».
Горизонтальное снижение точности, 

Вывод уравнений для вычисления геометрического снижения точности
Уравнения для вычисления геометрического снижения точности членов были описаны в предыдущем разделе. В этом разделе описывается вывод этих уравнений. Используемый здесь метод аналогичен используемому в «Глобальная система позиционирования (превью) Паркинсона и Спайкера»
Рассмотрим вектор ошибки положения, 







куда 




.
Переставляем обе стороны:
.
После умножения матриц с обеих сторон уравнения (2) на соответствующие матрицы в уравнении (3) получаем
.
Взяв ожидаемое значение с обеих сторон и взяв неслучайные матрицы за пределы оператора ожидания, E, получаем:
Предполагая, что ошибки псевдодальности некоррелированы и имеют одинаковую дисперсию, ковариационная матрица с правой стороны может быть выражена как скаляр, умноженный на единичную матрицу. Таким образом
поскольку
Примечание: 
Замена на 
Из уравнения (7) следует, что отклонения указанного положения приемника и времени равны
и
Остальные условия дисперсии ошибки положения и времени следуют прямо.
Выборочная доступность
В GPS есть (в настоящее время отключена) функция под названием Выборочная доступность (SA), который добавляет к общедоступным навигационным сигналам преднамеренные изменяющиеся во времени погрешности до 100 метров (328 футов). Это было сделано с целью запретить противнику использовать гражданские приемники GPS для наведения высокоточного оружия.
Ошибки SA на самом деле являются псевдослучайными, генерируются криптографическим алгоритмом из классифицированного семя ключ доступный только авторизованным пользователям (военные США, их союзники и некоторые другие пользователи, в основном правительственные) со специальным военным приемником GPS. Простого владения приемником недостаточно; ему по-прежнему нужен строго контролируемый ежедневный ключ.
До отключения 2 мая 2000 года типичные ошибки SA составляли около 50 м (164 фута) по горизонтали и около 100 м (328 футов) по вертикали.[10] Поскольку SA влияет на каждый приемник GPS в данной области почти одинаково, фиксированная станция с точно известным местоположением может измерять значения ошибок SA и передавать их местным приемникам GPS, чтобы они могли исправить свои определения местоположения. Это называется дифференциальным GPS или DGPS. DGPS также исправляет несколько других важных источников ошибок GPS, в частности ионосферную задержку, поэтому он продолжает широко использоваться, даже если SA отключен. Неэффективность SA перед лицом широко доступной DGPS была распространенным аргументом в пользу отключения SA, и в конечном итоге это было сделано по приказу президента. Клинтон в 2000 г.[11]
Услуги DGPS широко доступны как из коммерческих, так и из государственных источников. К последним относятся WAAS и Береговая охрана США сеть LF морские навигационные маяки. Точность поправок зависит от расстояния между пользователем и приемником DGPS. По мере увеличения расстояния ошибки на двух участках также не будут коррелировать, что приведет к менее точным дифференциальным поправкам.
В 1990–91 гг. Война в Персидском заливе из-за нехватки военных устройств GPS многие военнослужащие и их семьи покупали легкодоступные гражданские устройства. Выборочная доступность значительно затруднила использование этих GPS военными США на поле боя, поэтому военные приняли решение отключить его на время войны.
В 1990-е гг. FAA начал оказывать давление на военных, чтобы они отключили СА навсегда. Это позволило бы FAA ежегодно экономить миллионы долларов на обслуживании собственных радионавигация системы. Сумма добавленной ошибки была «установлена на ноль».[12] в полночь 1 мая 2000 г. после заявления президента США Билл Клинтон, позволяя пользователям получать доступ к безошибочному сигналу L1. Согласно директиве, вызванная ошибка SA была изменена, чтобы не добавлять ошибок к общедоступным сигналам (код C / A). Указ Клинтона требовал, чтобы SA была обнулена к 2006 году; это произошло в 2000 году, когда американские военные разработали новую систему, которая дает возможность отказывать в использовании GPS (и другим навигационным службам) враждебным силам в конкретной зоне кризиса, не затрагивая остальной мир или свои собственные военные системы.[12]
19 сентября 2007 г. Министерство обороны США объявил, что будущее GPS III спутники не смогут реализовать SA,[13] в конечном итоге сделав политику постоянной.[14]
Антиспуфинг
Остается еще одно ограничение по GPS — антиспуфинг. Это шифрует P-код так что он не может быть имитирован передатчиком, отправляющим ложную информацию. Немногие гражданские приемники когда-либо использовали P-код, и точность, достигаемая с помощью общедоступного кода C / A, была намного лучше, чем ожидалось изначально (особенно с DGPS ), настолько сильно, что политика защиты от подделки имеет относительно небольшое влияние на большинство гражданских пользователей. Отключение функции защиты от подделки в первую очередь принесет пользу геодезистам и некоторым ученым, которым необходимы чрезвычайно точные положения для таких экспериментов, как отслеживание движения тектонических плит.
Относительность
Спутниковые часы замедляются из-за своей орбитальной скорости, но ускоряются из-за расстояния от гравитационного колодца Земли.
Существует ряд источников ошибок из-за релятивистский последствия[15] это сделало бы систему бесполезной, если бы ее не исправляли. Три релятивистских эффекта — это замедление времени, гравитационный сдвиг частоты и эффекты эксцентриситета. Примеры включают релятивистское время замедление из-за скорости спутника около 1 части из 1010, гравитационное замедление времени, которое заставляет спутник лететь примерно на 5 частей из 1010 Быстрее чем часы на Земле, и Эффект Саньяка из-за вращения относительно приемников на Земле. Эти темы рассматриваются ниже по очереди.
Специальная и общая теория относительности
Согласно теории относительности, из-за их постоянного движения и высоты относительно Земли в центре, невращающиеся приблизительно инерционные система отсчета на часы спутников влияет их скорость. Специальная теория относительности предсказывает, что частота атомных часов, движущихся с орбитальной скоростью GPS, будет идти медленнее, чем стационарные наземные часы, в раз 
Влияние сдвига частоты гравитации на GPS из-за общая теория относительности в том, что часы ближе к массивному объекту будут медленнее, чем часы дальше. Применительно к GPS приемники расположены намного ближе к Земле, чем спутники, в результате чего часы GPS работают быстрее в 5 × 10 раз.−10, или около 45,9 мкс / день. Этот сдвиг частоты гравитации заметен.
При объединении замедления времени и гравитационного сдвига частоты расхождение составляет около 38 микросекунд в сутки, то есть разница в 4,465 частей на 1010.[16] Без исправления в позиции будут накапливаться ошибки примерно 11,4 км / день.[17] Эта начальная ошибка псевдодальности исправляется в процессе решения уравнения навигации. Вдобавок эллиптические, а не идеально круглые орбиты спутников вызывают изменение во времени эффектов замедления времени и гравитационного сдвига частоты. Этот эффект эксцентриситета приводит к тому, что разница в тактовой частоте спутника GPS и приемника увеличивается или уменьшается в зависимости от высоты спутника.
Чтобы компенсировать это несоответствие, стандарту частоты на борту каждого спутника перед запуском дается сдвиг скорости, что делает его немного медленнее, чем желаемая частота на Земле; в частности, на 10,22999999543 МГц вместо 10,23 МГц.[18] Поскольку атомные часы на борту спутников GPS точно настроены, это делает систему практическим инженерным приложением научной теории относительности в реальной среде.[19] Размещение атомных часов на искусственных спутниках для проверки общей теории Эйнштейна было предложено Фридвардт Винтерберг в 1955 г.[20]
Расчет замедления времени
Чтобы рассчитать количество ежедневного замедления времени, которое испытывают спутники GPS относительно Земли, нам необходимо отдельно определить суммы, связанные с специальная теория относительности (скорость) и общая теория относительности (гравитация) и сложите их вместе.
Сумма из-за скорости будет определяться с помощью Преобразование Лоренца. Это будет:
Для малых значений v / c, используя биномиальное разложение это приблизительно:
Спутники GPS движутся на 3874 м / с относительно центра Земли.[18] Таким образом, мы определяем:
Эта разница ниже 1 из 8.349×10−11 представляет собой долю, на которую часы спутников движутся медленнее, чем часы Земли. Затем оно умножается на количество наносекунд в день:
То есть часы спутников теряют 7214 наносекунд в сутки из-за специальная теория относительности последствия.
- Обратите внимание, что эта скорость 3874 м / с измеряется относительно центра Земли, а не ее поверхности, где находятся приемники GPS (и пользователи). Это связано с тем, что эквипотенциал Земли делает чистое замедление времени равным по всей ее геодезической поверхности.[21] То есть комбинация специальных и общих эффектов делает чистое замедление времени на экваторе равным таковому у полюсов, которые, в свою очередь, покоятся относительно центра. Следовательно, мы используем центр как опорную точку для представления всей поверхности.
Степень расширения под действием силы тяжести будет определяться с помощью гравитационное замедление времени уравнение:
Для малых значений Мистер, используя биномиальное разложение это приблизительно:
Нас снова интересует только дробь меньше 1 и разница между Землей и спутниками. Для определения этой разницы берем:
Земля имеет радиус 6,357 км (на полюсах), что рземной шар = 6 357 000 м, а спутники имеют высоту 20 184 км.[18] делая их радиус орбиты рGPS = 26 541 000 м. Подставив их в приведенное выше уравнение, с Mземной шар = 5.974×1024, грамм = 6.674×10−11, и c = 2.998×108 (все в SI ед.), дает:
Это часть, на которую часы спутников движутся быстрее, чем часы Земли. Затем оно умножается на количество наносекунд в день:
То есть часы спутников набирают 45 850 наносекунд в день за счет общая теория относительности последствия. Эти эффекты суммируются, чтобы дать (округлено до 10 нс):
- 45850 — 7210 = 38640 нс
Таким образом, часы спутников набирают примерно 38 640 наносекунд в день или 38,6 мкс в день в целом из-за эффектов относительности.
Чтобы компенсировать это усиление, частота часов GPS должна быть уменьшена на долю:
- 5.307×10−10 – 8.349×10−11 = 4.472×10−10
Эта доля вычитается из 1 и умножается на предварительно настроенную тактовую частоту 10,23 МГц:
- (1 – 4.472×10−10) × 10.23 = 10.22999999543
То есть нам нужно замедлить частоту с 10,23 МГц до 10,22999999543 МГц, чтобы свести на нет эффекты относительности.
Искажение Саньяка
Обработка данных GPS-наблюдений также должна компенсировать Эффект Саньяка. Шкала времени GPS определяется в инерционный системы, но наблюдения обрабатываются в В центре Земли, фиксировано на Земле (совместно вращающаяся) система, система, в которой одновременность не определено однозначно. Таким образом, для преобразования инерциальной системы в систему ECEF применяется преобразование координат. Полученная коррекция времени прохождения сигнала имеет противоположные алгебраические знаки для спутников в Восточном и Западном небесных полушариях. Игнорирование этого эффекта приведет к ошибке восток-запад порядка сотен наносекунд или десятков метров в местоположении.[22]
Естественные источники помех
Поскольку сигналы GPS на наземных приемниках обычно относительно слабые, естественные радиосигналы или рассеяние сигналов GPS могут снижать чувствительность приемник, что затрудняет или делает невозможным получение и отслеживание спутниковых сигналов.
Космическая погода ухудшает работу GPS двумя способами: прямые помехи из-за всплесков солнечного радио в той же полосе частот[23] или путем рассеяния радиосигнала GPS на ионосферных неоднородностях, называемого сцинтилляцией.[24] Обе формы деградации следуют за 11-летием. солнечный цикл и максимальны при максимуме солнечных пятен, хотя они могут произойти в любое время. Солнечные радиовсплески связаны с солнечные вспышки и выбросы корональной массы (CME)[25] и их воздействие может повлиять на прием на половине Земли, обращенной к Солнцу. Сцинтилляция чаще всего возникает в тропических широтах, где это ночное явление. Это происходит реже в высоких или средних широтах, где магнитные бури могут приводить к мерцанию.[26] Помимо мерцаний, магнитные бури могут создавать сильные ионосферные градиенты, снижающие точность систем SBAS.[27]
Искусственные источники помех
В автомобильных GPS-приемниках металлические детали на лобовых стеклах,[28] например, антиобледенители или тонировочные пленки для автомобильных стекол[29] может действовать как Клетка Фарадея, унизительный прием прямо в машине.
Рукотворный EMI (электромагнитные помехи) также могут нарушить или варенье Сигналы GPS. В одном хорошо задокументированном случае невозможно было принимать сигналы GPS во всей гавани Моховая посадка, Калифорния из-за непреднамеренных помех, вызванных неисправностью предварительных усилителей телевизионной антенны.[30][31] Также возможно преднамеренное заклинивание. Как правило, более сильные сигналы могут создавать помехи для приемников GPS, когда они находятся в пределах радиосвязи или в пределах прямой видимости. В 2002 году в онлайн-журнале было опубликовано подробное описание того, как построить глушитель GPS L1 C / A ближнего действия. Phrack.[32]
В правительство США считает, что такие глушилки иногда использовались во время Война в Афганистане, а военные США утверждают, что уничтожили шесть глушителей GPS во время Война в Ираке, в том числе тот, который был уничтожен бомбой с наведением GPS.[33] Глушитель GPS относительно легко обнаружить и найти, что делает его привлекательной целью для противорадиационные ракеты. 7 и 8 июня 2007 года Министерство обороны Великобритании провело испытания системы постановки помех в западной части Великобритании.[нужна цитата ]
В некоторых странах разрешено использование ретрансляторов GPS для приема сигналов GPS в помещении и в недоступных местах; в то время как в других странах это запрещено, поскольку ретранслируемые сигналы могут вызывать многолучевые помехи для других приемников GPS, которые получают данные как от спутников GPS, так и от ретранслятора. В Великобритании Ofcom теперь разрешает использование репитеров GPS / GNSS.[34] в режиме «облегченного лицензирования».
Из-за возможности возникновения как естественного, так и искусственного шума продолжают развиваться многочисленные методы устранения помех. Первое — не полагаться на GPS как на единственный источник. По словам Джона Рули, «IFR у пилотов должен быть запасной план на случай отказа GPS ».[35] Автономный мониторинг целостности приемника (RAIM) — это функция, включенная в некоторые приемники, предназначенная для предупреждения пользователя при обнаружении помех или другой проблемы. Американские военные также развернули с 2004 г. Модуль выборочной доступности / защиты от спуфинга (SAASM) в Усовершенствованный GPS-приемник Defense (ДАГР).[36] В демонстрационных видеороликах было показано, что DAGR обнаруживает помехи и сохраняет свою блокировку на зашифрованных сигналах GPS во время помех, из-за которых гражданские приемники теряют захват.
Смотрите также
- Дополнение GPS
Примечания
- ^ Тот же принцип и лежащая в его основе математика можно найти в описании хронометраж пульсаров астрономами.
- ^ Navipedia: Мониторинг тропосферы
- ^ Navipedia: задержка тропосферы
- ^ Navipedia: Multipath
- ^ Отчет о ходе работы IPN 42-159 (2004)
- ^ SNT080408. «Пример эфемеридного сервера». Tdc.co.uk. Архивировано из оригинал 12 января 2009 г.. Получено 2009-10-13.
- ^ «Блок 1 — Введение в GPS». Архивировано из оригинал 29 апреля 2009 г.
- ^ «Введение в пользовательское оборудование NAVSTAR GPS» (PDF). Центр навигации береговой охраны США. Береговая охрана США. Сентябрь 1996. Получено 5 июля, 2014.
- ^ Паркинсон (1996)
- ^ Grewal (2001), стр. 103.
- ^ «Президент Клинтон приказывает прекратить выборочную доступность GPS».
- ^ а б «Заявление президента относительно решения США прекратить снижение точности глобальной системы позиционирования». Федеральная авиационная администрация. 1 мая 2000 г.. Получено 2013-01-04.
- ^ «DoD навсегда прекращает закупку выборочной доступности глобальной системы позиционирования». DefenseLink. 18 сентября 2007 г. Архивировано с оригинал 18 февраля 2008 г.. Получено 2008-02-20.
- ^ «Выборочная доступность». Национальный космический исполнительный комитет по позиционированию, навигации и хронометражу. Архивировано из оригинал 13 января 2008 г.. Получено 2008-02-20.
- ^ Уэбб (2004), стр. 32.
- ^ Ризос, Крис. Университет Нового Южного Уэльса. Спутниковые сигналы GPS В архиве 2010-06-12 на Wayback Machine. 1999.
- ^ Фараони, Валерио (2013). Специальная теория относительности (иллюстрированный ред.). Springer Science & Business Media. п. 54. ISBN 978-3-319-01107-3. Выдержка страницы 54
- ^ а б c Глобальная система позиционирования Роберта А. Нельсона через спутник, Ноябрь 1999 г.
- ^ Погге, Ричард В .; «Реальная теория относительности: система навигации GPS». Проверено 25 января 2008 года.
- ^ «Astronautica Acta II, 25 (1956)». 1956-08-10. Получено 2009-10-23.
- ^ С. П. Дрейк (январь 2006 г.). «Принцип эквивалентности как ступенька от специальной теории относительности к общей» (PDF). Являюсь. J. Phys., Vol. 74, №1. С. 22–25.
- ^ Эшби, Нил Относительность и GPS. Физика сегодня, Май 2002 г.
- ^ Черрути А., П. М. Кинтнер, Д. Э. Гэри, А. Дж. Маннуччи, Р. Ф. Мейер, П. Х. Доэрти и А. Дж. Костер (2008), Влияние интенсивных солнечных радиовсплесков в декабре 2006 г. на приемники GPS, Космическая погода, Дои:10.1029 / 2007SW000375, 19 октября 2008 г.
- ^ Аарон, Жюль; Басу, Сантимей (1994). «Ионосферные амплитудные и фазовые флуктуации на частотах GPS». Труды ION GPS. 2: 1569–1578.
- ^ С. Манкузо и Дж. К. Раймонд, «Корональные транзиенты и метрические радиовсплески типа II. I. Эффекты геометрии, 2004 г., Астрономия и астрофизика, т. 413, стр. 363-371»
- ^ Ледвина, Б. М .; Дж. Дж. Макела и П. М. Кинтнер (2002). «Первые наблюдения интенсивных мерцаний амплитуды GPS L1 на средних широтах». Письма о геофизических исследованиях. 29 (14): 1659. Bibcode:2002GeoRL..29.1659L. Дои:10.1029 / 2002GL014770.
- ^ Том Диль, Солнечные вспышки поражают Землю — WAAS изгибается, но не ломается, Новости спутниковой навигации, том 23, июнь 2004 г.
- ^ «Крепление I-PASS для автомобилей с особыми функциями лобового стекла» (PDF). Архивировано из оригинал (PDF) 26 марта 2010 г.
- ^ «3М Автомобильные пленки».. Обратите внимание, что пленки со стабильным цветом специально описаны как нет создание помех спутниковым сигналам.
- ^ «Охота на RFI». GPS мир. 1 января 2003 г.
- ^ «Клуб соответствия требованиям EMC» банановые кожуры «колонка 222». Compliance-club.com. Получено 2009-10-13.
- ^ Недорогой портативный глушитель GPS. Phrack выпуск 0x3c (60), статья 13. Опубликовано 28 декабря 2002 г.
- ^ Пресс-служба американских войск. Прогресс Centcom. 25 марта 2003 г. В архиве 3 декабря 2009 г. Wayback Machine
- ^ [1] Заявление Ofcom о режиме авторизации для ретрансляторов GNSS
- ^ Рули, Джон. AVweb. Глушение GPS. 12 февраля 2003 г.
- ^ Страница DAGR армии США В архиве 2012-08-05 в Archive.today
Рекомендации
- Grewal, Mohinder S .; Вайль, Лоуренс Рэндольф; Эндрюс, Ангус П. (2001). Системы глобального позиционирования, инерциальная навигация и интеграция. Джон Уайли и сыновья. ISBN 978-0-47135-032-3.
- Паркинсон; Спилкер (1996). Система глобального позиционирования. Американский институт аэронавтики и астрономии. ISBN 978-1-56347-106-3.
- Уэбб, Стивен (2004). Не из этого мира: сталкивающиеся вселенные, браны, струны и другие дикие идеи современной физики. Springer. ISBN 0-387-02930-3. Получено 2013-08-16.
внешняя ссылка
- GPS.gov —Общий веб-сайт общественного образования, созданный правительством США.
- Стандарт производительности GPS SPS — Официальная спецификация стандартной службы позиционирования (версия 2008 г.).
- Стандарт производительности GPS SPS — Официальная спецификация стандартной службы позиционирования (версия 2001 г.).
Пользователя GPS-навигатора всегда интересует реальная точностьсистемы GPS-навигации и степень доверия к ее показаниям. Насколько можно приближаться к какой-либо навигационной опасности, полагаясь только на приемник GPS-навигатора? К сожалению, однозначного ответа на этот вопрос не существует. Это связано со статистическим характером ошибок GPS-навигации. Рассмотрим их подробнее.
Точность определения координат в GPS-навигации и причины ошибок GPS.
На скорость распространения радиоволн влияют ионосфера и тропосфера, ионосферная и тропосферная рефракция. Это главный, после отключения SA, источник погрешностей. Скорость радиоволн в пустоте постоянна, но при входе сигнала в атмосферу изменяется. Для сигналов от разных спутников задержка времени различна. Задержки распространения радиоволн зависят от состояния атмосферы и высоты спутника над горизонтом. Чем нижеспутник, тем больший путь проходит его сигнал через атмосферу и тем больше искажения. Большинство приемников исключают использование сигналов от спутников с возвышением над горизонтом менее 7,5 градусов.
Кроме того, атмосферные помехи зависят от времени суток. После захода солнца плотность ионосферы и ее влияние на радиосигналы уменьшается, явление, хорошо знакомое радистам-коротковолновикам. Военные и гражданские приемники GPS-навигаторов могут автономно определять атмосферную задержку сигнала, сравнивая задержки на разных частотах. Одночастотные потребительские приемники вносят приблизительную поправку на основании прогноза, передаваемого в составе навигационного сообщения. Качество этой информации в последнее время выросло, что дополнительно повысило точность GPS-навигации.
Режим SA.
Для сохранения преимущества высокой точности для военных GPS-навигаторов с марта 1990 года был введен режим ограничения доступа SA (Selective Availability), искусственно снижающий точность гражданского GPS-навигатора. При задействованном режиме SA в мирное время добавляется ошибка в несколько десятков метров. В особых случаях могут вводиться ошибки в сотни метров. Правительство США отвечает за работоспособность системы GPS перед миллионами пользователей, и можно рассчитывать, что повторное включение SA, и тем более, столь значительное снижение точности не будет введено без достаточно серьезных причин.
Загрубление точности достигается путем хаотического сдвига времени передачи псевдослучайного кода. Ошибки, возникающие от SA, — случайные и равновероятные в каждую сторону. SA влияет также на точность курса и скорости по GPS-навигатору. По этой причине неподвижный приемник часто показывает слегка изменяющиеся скорость и курс. Так что оценить степень воздействия SA можно по периодическим изменениям курса и скорости по GPS.
Погрешности в эфемеридных данных при GPS-навигации.
Прежде всего это погрешности, связанные с отклонением спутника от расчетной орбиты, неточностями часов, задержками сигнала в электронных схемах. Коррекция этих данных производится с Земли периодически, в промежутках между сеансами связи ошибки накапливаются. Ввиду малости эта группа погрешностей не имеет значения для гражданских пользователей.
Крайне редко, но могут иметь место более крупные ошибки из-за внезапных сбоев информации в устройствах памяти спутника. Если такой сбой не выявляется средствами самодиагностики, то до момента обнаружения ошибки наземной службой и передаче команды о неисправности спутник может какое-то время передавать неверную информацию. Происходит так называемое нарушение непрерывности или как часто переводят термин integrity, целостности навигации.
Влияние отраженного сигнала на точность GPS-навигации.
Кроме прямого сигнала от спутника GPS-приемник также может принять сигналы, отраженные от скал, зданий, проходящих судов так называемое характеризующие многолучевое распространение (multypath). Если прямой сигнал закрыт от приемника надстройками или такелажем судна, отраженный сигнал может быть сильнее. Этот сигнал проделывает более длинный путь, и приемник «думает», что находится дальше от спутника, чем на самом деле. Как правило, эти ошибки намного меньше 100 метров, поскольку только близко расположенные предметы способны дать достаточно сильное эхо.
Спутниковая геометрия при GPS-навигации.
Зависит от расположения приемника относительно спутников, по которым определяется позиция. Если приемник поймал четыре спутника и все они находятся на севере — спутниковая геометрия плохая. Результат ошибка до 50-100 метров или даже невозможность определения координат.
Все четыре измерения — из одного и того же направления, и область пересечения линий положений слишком велика. Но если 4 спутника будут расположены равномерно по сторонам горизонта, то точность намного возрастет. Спутниковая геометрия измеряется геометрическим фактором PDOP (Position Dilution Of Precision). Идеальному расположению спутников соответствует PDOP = 1. Большие значения говорят о плохой спутниковой геометрии.
Пригодными для навигации считаются значения PDOP меньше 6,0. В двухмерной навигации применяется HDOP (Horizontal Dilution Of Precision), меньше 4,0. Также используются вертикальный геометрический фактор VDOP, меньше 4,5, и временной TDOP, меньше 2,0. PDOP служит множителем для учета ошибок от других источников. Каждая измеренная приемником псевдодальность имеет свою погрешность, зависящую от атмосферных помех, ошибок в эфемеридах, режима SA, отраженного сигнала и так далее.
Так, если предполагаемые значения суммарных задержек сигнала по этим причинам, URE User Range Error или UERE User Equivalent Range Error, по-русски ЭДП — эквивалентная дальномерная погрешность, в сумме составляют 20 метров и HDOP = 1,5, то ожидаемая ошибка определения места будет равна 20 х 1,5 = 30 метров. Приемники GPS-навигаторов по-разному представляют информацию для оценки точности с использованием PDOP.
Кроме PDOP или HDOP, используется GQ (Geometric Quality) величина, обратная HDOP, или качественная оценка в баллах. Многие современные приемники показывают ЕРЕ (Estimated Position Error — ожидаемую ошибку позиции) непосредственно в единицах дистанции. ЕРЕ учитывает расположение спутников и прогноз погрешности сигналов для каждого спутника в зависимости от SA, состояния атмосферы, ошибок спутниковых часов, передаваемых в составе эфемеридной информации.
Спутниковая геометрия также становится проблемой при использовании приемника GPS-навигатора внутри транспортных средств, в густом лесу, горах, вблизи высоких зданий. Когда сигналы от отдельных спутников блокированы, положение оставшихся спутников определит, насколько точной будет позиция GPS, и их число покажет, может ли позиция вообще быть определена. Хороший приемник GPS-навигатора покажет не только, какие спутники используются, но и их местоположение, азимут и возвышение над горизонтом, так что вы можете определить, затруднен ли прием данного спутника.
По материалам книги Все о GPS-навигаторах.
Найман В.С., Самойлов А.Е., Ильин Н.Р., Шейнис А.И.
25.11.2021
Источники ошибок GNSS
Приемник GNSS обычно выдает местоположение с номинальной погрешностью менее 15 метров с достоверностью 95 %. На результат влияет ряд шибок.
1. Атмосферные эффекты
Слабый спутниковый сигнал, подвергается воздействию во время своего прохождения через ионосферу и тропосферу. Это искажение выступает наибольшим для сигналов со спутников, расположенных вблизи горизонта.

GPS-графики для пришвартованного судна, показывающие разброс около +/- 15 метров для ряда прошлых позиций. (Функция отслеживания отслеживания) Фото A Knutas
Ошибки тропосферы вызваны ближайшим к Земле слоем атмосферы, который простирается примерно на 10 км от поверхности. Именно здесь существует «погода». Азот, кислород и водяной пар − это газы, которые могут искажать сигнал. Ошибки уменьшаются за счет компенсационных расчетов, основанных на математической модели тропосферы.
Прохождение сигнала через ионосферу, которая представляет собой слой от 50 до 1000 км, вносит другие ошибки. В этом случае на сигнал влияет присутствие электрически заряженных частиц, что приводит к ошибке синхронизации. Чтобы ограничить размер этой ошибки, так называемая маска высоты, установленная на 10°− 15°, отфильтровывает сигналы со спутников, расположенных близко к горизонту. Военные приемники могут уменьшить размер этого эффекта, используя несколько частот для измерения и моделирования ионосферы. Гражданские приемники смогут использовать дополнительную частоту L5 и затем смогут использовать несколько частот для измерения.
2. Ошибка синхронизации
Ошибка синхронизации возникает, когда часы спутника и приемника не полностью совпадают. Поскольку спутник оснащен несколькими очень точными атомными часами, эта ошибка в первую очередь вызвана приемником. Большую часть этой ошибки можно устранить, подключившись по крайней мере к четырем различным спутникам.
3. Ошибка эфемериды
Станции мониторинга, расположенные по всему экватору, постоянно регистрируют спутниковые сигналы, чтобы рассчитать их орбиты. Орбитальные данные отправляются пользователям, как часть навигационного сообщения, которое включает параметры орбиты, то есть информацию о местоположении спутников. Ошибка в этом источнике называется ошибками траектории орбиты и вносит 3−5 метров в общую величину погрешности.
4. Ошибка мультилучей
Если спутниковые сигналы отражаются от поверхностей таких, как вода, стены или поверхности на борту или трубы, до достижения приемника, то генерируются так называемые «ошибки мультилучей». Отсечение сигналов со спутников, близких к горизонту до >15°, уменьшит размер ошибок мультилучей.
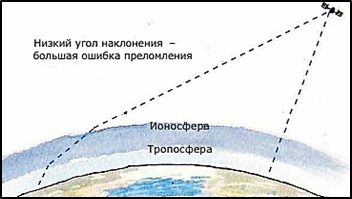
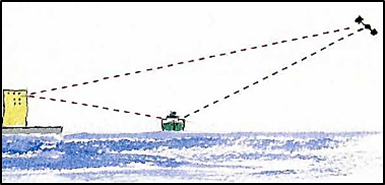
Расположение и доступность спутников
Точность определения положения снижается, когда позиционные линии пересекаются под неблагоприятными углами. Поскольку, спутниковый приемник не отображает никаких линий положения, он показывает, так называемое, значение DOP (размытие точности). Это показатель того, насколько хорошо пересекаются линии координат со спутников.
Хорошее распределение спутников по небу дает низкое значение DOP (1−3), что способствует точному построению карты положения.
Морских навигаторов больше всего интересует HDOP (Горизонтальный DOP). Другие параметры включают: PDOP (Позиционный DOP), который является ошибкой в трехмерном положении и GDOP (Геометрический DOP), который содержит PDOP и ошибку синхронизации.
Фактическая ошибка системы, умноженная на HOOP, генерирует значение позиционной погрешности. HOOP должен быть меньше 4. При загрузке HOOP, изначально велик и уменьшается по мере того, как положение вычисляется с использованием все большего и большего количества спутников. Иногда могут возникать довольно большие неточности, но они, как правило, кратковременны.

Страница в плоттере, на которой показано количество и расположение спутников. В этом случае доступно только пять и три из них находятся рядом друг с другом. Это приводит к неудачному пересечению линий положения. (Az = Азимут)
В этом случае, доступно только несколько спутников и некоторые из них находятся относительно близко друг к другу, тогда HDOP может быть необычно большим. Если ошибка преломления в атмосфере вместе с другими погрешностями составит +/-15 метров, то общее отклонение будет уже 15 х 16 = +/- 240 метров.
Высоты и азимуты на полярной диаграмме, сила сигнала в виде гистограммы
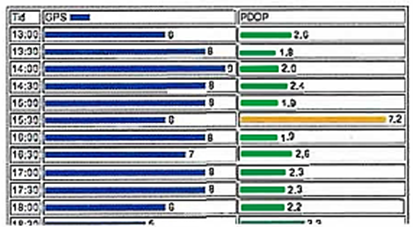
Информация PDOP с официального сайта. Это показывает, что PDOP может сильно и быстро меняться. PDOP − это описание качества трехмерной позиции. Навигатор больше всего интересует HDOP, который несколько меньше, чем PDOP.
6. Отключение GPS
Солнечные вспышки − это более холодные области, которые кажутся темнее на диске Солнца. Они показывают неравномерное распределение магнитного поля звезды. Их периодичность около 11 лет, с последним максимумом в 2012/13 годах. Процессы на Солнце оказывают влияние на ионосферу Земли и, следовательно, влияют на распространение радиоволн.
На солнечной стороне Земли эффекты солнечных пятен заблокировали приемники GPS от приема спутниковых сигналов 5 и 6 декабря 2006 года.
7. Вмешательство
Спутниковые приемники чрезвычайно чувствительны, чтобы собирать очень слабые сигналы со спутников. Один из результатов этого, то, что другие источники электромагнитного излучения могут создавать помехи для подлинных сигналов. Обнаружение и отслеживание спутников в этом случае может быть затруднено или даже невозможно.
Некоторыми естественными источниками помех являются: солнечный ветер, магнитные бури, северное сияние, поля излучения, окружающее Землю и метеорологические условия, что сказывается на работе приемника. Физические объекты между спутником и приемником также могут помешать сигналу. Высокая чувствительность приемников, к сожалению, также делает их чувствительными к этим источникам ошибок.
Относительно слабый источник излучения мощностью всего в несколько тысяч ватт, но работающий на частоте GPS, создаст помехи реальному сигналу на большой территории.
В 2001 году GPS-приемники в гавани Мосс-Лэндинг в заливе Монтерей, ощутили помехи в области диаметром около 1000 метров. После их интенсивного поиска, источник был обнаружен на предусилителе телевизионной антенны на лодке.
8. Помехи и подмена
Доступны портативные передатчики, которые намеренно блокируют, глушат или создают помехи сигналам GNSS (глушение). Этот вид оборудования был испытан во время военных маневров. Хотя технически это сложнее, можно обмануть приемник GNSS, генерируя ложные сигналы (подделка).
9. Ошибки приемника
В зависимости от его качества внутренние помехи в приемнике (ошибки программного обеспечения и синхронизации) могут привести к ошибкам в 2 метра и более.
10. Неадекватные сигналы
GPS-приемнику требуется свободной и прямая видимость со спутников. Высокие здания, густая растительность могут в достаточной степени мешать спутниковым сигналам, так, что местоположение может быть не определяться. Так же, на это сильно влияет направление, на котором расположены препятствия. Физические помехи на юге хуже всего, поскольку спутники GPS проходят на максимальной широте 55°. Это обстоятельство серьезно ограничивает количество спутников в северных широтах.
11. Надежность
Существует ряд факторов, влияющих на точность и надежность, которых можно достичь на борту. Спецификация доступности (Надежности обслуживания) указана на уровне 99,996%.
RAIM (Автономный мониторинг целостности приемника) это функция в некоторых приемниках, которая подает сигнал тревоги, когда надежность системы низкая. Функция проверяет сигналы от различных спутников и распознает, когда один из них выдает неожиданное положение. Если это так, то этот спутник удаляется из расчета. Для обнаружения ошибки функции требуется не менее пяти спутников. Если доступно шесть спутников, то программа может не учитывать плохой сигнал.
Надежность системы на судне зависит от того, как была проведена установка и техническое обслуживание, включая модернизацию!

19.02.2021
Глава 4 — Источники ошибок ГНСС
В главе 2 мы представили концепцию источников ошибок ГНСС. Это факторы, которые затрудняют определение точного положения ГНСС приемника. В этой главе мы более подробно рассмотрим источники этих ошибок.
Таблица 13: Источники ошибок ГНСС
Источники ошибок
Спутниковые часы
Атомные часы на спутниках ГНСС очень точны, но они немного дрейфуют. К сожалению, небольшая неточность спутниковых часов приводит к значительной ошибке в определении приемником своего местоположения. Например, ошибка часов в 10(−6) сек приводит к ошибке положения в 3 м.
Часы на спутнике контролируются наземной системой управления ГНСС и сравниваются с еще более точными часами, используемыми в ней. В данных, передаваемых спутником пользователю, содержится оценка смещения бортовых часов. Обычно передаваемая точность составляет ± 2 м, хотя она может варьироваться в зависимости от разных систем ГНСС. Чтобы получить свое более точное местоположение, ГНСС приемник должен компенсировать ошибку часов.
Одним из способов компенсации погрешности часов является загрузка точной информации о часах спутника из систем дифференциальной коррекции (SBAS) или систем точного позиционирования (PPP). В передаваемой информации содержатся поправки за ошибки бортовых часов, которые были рассчитаны системами SBAS или PPP. Более подробные сведения о системах SBAS и PPP представлены в главе 5.
Другой способ компенсации погрешности часов — настроить приемник для работы в режиме дифференциальной коррекции или кинематики реального времени (RTK). В главе 5 также подробно рассматриваются дифференциальные методы ГНСС и RTK.
Ошибки эфемерид
Спутники ГНСС движутся по очень точным, хорошо известным орбитам. Однако, параметры орбиты немного меняются. Также, как и в случае с часами спутника, небольшое изменение орбиты приводит к значительной ошибке в вычисленном положении приемника.
Наземная система управления ГНСС постоянно отслеживает орбиты спутников. Когда орбита спутника изменяется, наземная система управления отправляет поправку на спутники, и эфемериды спутников обновляются. Даже с поправками, внесенными наземной системой управления ГНСС, все еще есть небольшие ошибки в параметрах орбиты, которые могут привести к ошибке местоположения до ± 2.5 м.
Одним из способов компенсации ошибок спутниковых орбит является загрузка точной эфемеридной информации из систем SBAS или PPP, которые будут более подробно рассматриваться в главе 5.
Другой способ компенсации ошибок спутниковой орбиты — использование приемника в режиме дифференциальной коррекции или RTK. Более подробная эта информация также представлена в главе 5.
Ионосферные задержки
Ионосфера — это слой атмосферы на высоте от 80 до 600 км над Землей. Этот слой содержит электрически заряженные частицы, называемые ионами. Эти ионы задерживают прохождение спутниковых сигналов и могут вызвать значительную ошибку определения местоположения спутника (обычно ± 5 м, но эта ошибка может возрастать в периоды высокой ионосферной активности, вызванной влиянием Солнца).
Ионосферная задержка зависит от солнечной активности, времени года, сезона, времени суток и места. В результате очень трудно предсказать, насколько ионосферная задержка повлияет на расчетное местоположение.
Ионосферная задержка также изменяется в зависимости от частоты радиосигнала, проходящего через ионосферу. ГНСС приемники, которые принимают более одной частоты, например L1 и L2, могут использовать это для повышения точности. Сравнивая измерения на L1 с измерениями на L2, приемник может определить величину ионосферной задержки и удалить эту ошибку из рассчитанных координат.
Для приемников, которые могут отслеживать только одну частоту ГНСС, используются модели ионосферы для уменьшения влияния ошибок, вызванных влиянием ионосферы. Из-за различного характера ионосферной задержки модели не так эффективны, как использование нескольких частот для их устранения.
Ионосферные условия очень похожи в пределах отдельной области, поэтому спутниковые сигналы, поступающие на приемники базовой станции и подвижные приемники, имеют очень похожую задержку. Это позволяет компенсировать ионосферную задержку дифференциальными методами ГНСС и RTK.
Тропосферные задержки
Тропосфера — это ближайший к поверхности Земли слой атмосферы.
Рис. 37
Вариации задержки в тропосфере вызываются изменением влажности, температуры и атмосферного давления.
Поскольку тропосферные условия в пределах отдельной зоны очень похожи, то базовая станция и приемники подвижного приемника испытывают очень похожее влияние тропосферы. Это позволяет дифференциальным методам ГНСС и RTK компенсировать тропосферную задержку.
Приемники ГНСС также могут использовать тропосферные модели для оценки количества ошибок, вызванных тропосферной задержкой.
Собственные шумы приемника
Шум приемника добавляет к ошибке положения величины, вызванные аппаратным и программным обеспечением. Приемники ГНСС высшего класса, как правило, имеют меньшие ошибки из-за собственного шума, чем более дешевые приемники.
Влияние многолучевости
Как показано на рис. 38 многолучевое распространение происходит, когда сигнал от спутника ГНСС отражается от объекта, например, стены здания, а затем приходит к антенне приемника. Поскольку отраженный сигнал распространяется дольше, то он поступает в приемник с небольшой задержкой. Этот задержанный сигнал может привести к тому, что приемник вычислит неправильное положение.
Рис. 38
Самый простой способ уменьшить ошибки из-за многолучевого распространения это разместить ГНСС антенну в месте, удаленном от отражающих поверхностей. Когда это невозможно, приемник и антенна ГНСС должны уметь обрабатывать многолучевые сигналы.
Ошибки многолучевого распространения с большой задержкой обычно обрабатываются ГНСС приемником, а ошибки сигнала с короткой задержкой отрабатываются антенной. Благодаря применению дополнительных технологий, высокопроизводительные приемники и ГНСС антенны, как правило, лучше устраняют ошибки многолучевости.
Заключение
В этой главе описаны источники ошибок, которые вызывают погрешности при расчете позиции. В главе 5 мы опишем методы, которые используют приемники ГНСС для уменьшения этих ошибок и получения более точного местоположения.
Материалы взяты с сайта компании NovAtel. Ссылка на первоисточник: https://novatel.com/an-introduction-to-gnss
4.1. Классификация источников ошибок, характерных для спутниковых измерений
При отработке методов высокоточных спутниковых измерений возникает необходимость тщательного исследования влияний всех возможных источников ошибок выполняемых измерений, особенностей их проявления и обоснования методов их учета. В зависимости от характера воздействия отмеченных источников возникающие при этом ошибки подразделяются на две основные группы: систематические погрешности, которые применительно к спутниковым измерениям получили название смещений, и погрешности случайного характера, которые часто отождествляют с понятием «шум».
Для погрешностей первой группы разрабатываются специальные методы их учета. Влияние второй группы удается, в большинстве случаев, минимизировать за счет использования большого массива отдельных измерений. В настоящем разделе основное внимание уделено рассмотрению ошибок систематического характера, обусловливающих появление смещений результатов измерений. При их исследовании и создании методов ослабления их влияния широкое распространение получил метод моделирования, для разработки которого приходится тщательно изучать механизм воздействия таких источников ошибок на результаты измерений с тем, чтобы на основе такого изучения разработать эффективные методы минимизации отмеченного влияния.
Исходя из анализа измерительного процесса, характерного для систем GPS и ГЛОНАСС, все основные источники ошибок можно условно разбить на три основные группы:
1) ошибки, связанные с неточностью знания исходных данных, из которых определяющая роль принадлежит погрешностям знания эфемерид спутников, значения которых должны быть известны на момент измерений;
2) ошибки, обусловленные влиянием внешней среды, среди которых выделяют такие источники, как воздействие атмосферы (ионосферы и тропосферы) на результаты спутниковых измерений, а также отраженных от окружающих объектов радиосигналов (многопутность);
147
3) инструментальные источники ошибок, к которым, как правило, относят неточность знания положения фазового центра антенны приемника, неучтенные временные задержки при прохождении информационных сигналов через аппаратуру, а также погрешности, связанные с работой регистрирующих устройств спутниковых приемников.
Наряду с перечисленными выше группами ошибок приходится учитывать и отдельные факторы, обусловливающие появление ошибок, которые не характерны ни для одной из перечисленных выше групп. В частности, к таким ошибкам могут быть отнесены погрешности, возникающие вследствие неоптимального взаимного расположения наблюдаемых спутников (геометрический фактор). Кроме того, целый ряд ошибок может возникать в процессе перехода от одной координатной системы к другой. Например, от свойственной системе GPS глобальной координатной системы WGS-84 к местной, интересующей потребителя координатной системе.
В следующих подразделах в обобщенном виде проанализированы особенности влияния основных источников ошибок.
4.2. Источники ошибок, связанные с неточным знанием эфемерцд спутников, и методы ослабления их влияния
При нахождении интересующих потребителя координат точек на земной поверхности спутниковыми методами необходимо наряду с измерением расстояний до спутника знать также его эфемериды, которые определяют местоположение спутника на момент выполнения измерений. Как уже отмечалось в подразделе 2.1, неточность знания эфемерид обусловливает соответствующие погрешности определения как абсолютных значений координат определяемых точек, так и их разностей между пунктами наблюдений. Механизм неточного знания эфемерид связан, прежде всего, с наблюдаемыми на практике расхождениями между предсказываемой (невозмущенной) и реальной (подверженной влиянию возмущающих сил) орбитами. К возмущающим силам относят различные факторы как гравитационного, так и негравитационного происхождения. Влияние различных факторов на движение спутников типа GPS и ГЛОНАСС приведено в табл. 4.1 [70, 73].
Первые из них, обусловленные притяжением спутника со стороны Землй, Луны и Солнца, поддаются достаточно эффективному моделированию. В то же время такие возмущающие факторы негравитационного происхождения, как, например, солнечное радиационное давление, плохо поддаются моделированию из-за непредсказуемости отдельных компонент, от которых зависит результирующее воздействие на спутник отмеченного давления.
148
|
Таблица 4.1 |
||
|
Возмущающие |
Максимальное |
Максимальное |
|
факторы |
возмущающее |
возмущение за 1 час, м |
|
Центральное поле |
ускорение, м/с2 |
|
|
5,65-Ю’1 |
||
|
Земли |
— |
|
|
Вторая зональная |
||
|
гармоника |
5,3-Ю-5 |
300 |
|
Гравитация Луны |
5,5-10″6 |
40 |
|
Гравитация Солнца |
310-6 |
20 |
|
Четвертая зональная |
||
|
гармоника |
ю-7 |
0,6 |
|
Солнечная радиация |
ю-7 |
0,6 |
|
Гравитационные |
||
|
аномалии |
ю-8 |
0,06 |
|
Другие факторы |
ю-8 |
0,06 |
Проведенные к настоящему времени исследования по количественной оценке отдельных факторов на эфемериды спутника свидетельствуют о том, что наибольшее воздействие на уклонения реальной орбиты от расчетной оказывает гравитационное поле Земли. В частности, из-за влияния второго гармонического коэффициента С20 такие уклонения для трехчасовых дуг орбит достигают 2 км, а для более протяженных двухсуточных дуг до 14 км. С такими значительными уклонениями нельзя не считаться при любых видах спутниковых измерений.
Суммарное гравитационное влияние масс Луны и Солнца хотя и оказывается существенно меньшим (для трехчасовых дуг уклонения от невозмущенной орбиты оцениваются величинами на уровне от 50 до 150 м), но, тем не менее, при прогнозировании значений эфемерид данное влияние также следует учитывать.
Непосредственно с гравитацией связаны также наблюдаемые на земной поверхности различного рода приливные явления, которые из-за перераспределения масс приводят к изменениям в предрассчитываемом гравитационном поле Земли, а следовательно, и к влияниям на орбитальное движение спутника. Проведенная оценка такого влияния свидетельствует о том, что уклонения спутника от расчетной орбиты из-за воздействия данного фактора даже для двухсуточных дуг лежат в пределах от 0,5 до 2 м, и этим влиянием применительно к рассматриваемым спутникам можно пренебречь.
Переходя к оценке влияния факторов негравитационного происхождения, следует заметить, что наиболее существенное влияние на неточность знания эфемерид спутников, входящих в состав систем
149
GPS и ГЛОНАСС, оказывает солнечное радиационное давление. Как показывают предрасчеты, уклонения спутников от расчетной траектории из-за воздействия прямого солнечного радиационного давления лежат в пределах от 5-6 м (для трехчасовых дуг) до 100-800 м (для двухсуточных дуг). Отмеченные предрасчеты характеризуются невысокой надежностью по следующим причинам:
1)интенсивность солнечного излучения не остается постоянной
стечением времени;
2)модель влияния данного фактора существенно изменяется при переходе спутника в зону тени и полутени;
3)эффективная поверхность спутника плохо поддается предрасчету как из-за сложной конфигурации такой поверхности, так и из-за вариаций положения спутника в пространстве.
Дополнительную неопределенность в предрасчет влияния радиационного давления вносит отраженная от земной поверхности солнечная радиация, зависящая от атмосферных условий и отражающих свойств облучаемых Солнцем участков земной поверхности.
Другим возмущающим фактором негравитационного происхождения является атмосферное торможение. При оценке влияния этого фактора следует иметь в виду, что на характерной для рассматриваемых спутников высоте около 20 тыс.км атмосфера оказывается чрезвычайно разреженной, и ее влиянием при предрасчетах орбит спутников, как правило, пренебрегают.
Обобщая оценку суммарного влияния всех перечисленных выше возмущающих факторов, заметим, что эти данные используются только для первоначального приближенного предвычисления реальных орбит спутников. Что касается получения необходимых для наземных наблюдателей значений эфемерид спутников, то на практике применяют более эффективные экспериментальные методы, базирующиеся на использовании опорных станций, установленных на пунктах с известными координатами и выполняющих непрерывные высокоточные наблюдения спутников в автоматическом режиме. За счет использования таких станций слежения решается обратная задача, состоящая в том, что с помощью одновременных измерений с нескольких (не менее трех) станций производится периодическое последовательное определение эфемерид всех наблюдаемых спутников. После соответствующей обработки на центральной станции вычисляются поправки к ранее определенным значениям эфемерид, которые с помощью передающих загружающих станций систематически (три раза в сутки, а последнее время один раз в сутки) передаются на соответствующие спутники, где вводятся в состав навигационного сообщения. Последнее, как уже отмечалось ранее, сбрасывается со спутника потребителю
150
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
УДК 621.396; 681.34
ОБ ОЦЕНКАХ СТАТИСТИКИ ОШИБОК ПИЛОТИРОВАНИЯ И ВЕРОЯТНОСТИ СБОЯ СПУТНИКОВОЙ НАВИГАЦИОННОЙ СИСТЕМЫ
В.Л. КУЗНЕЦОВ, Е.С. ГОРЯЧЕНКОВА
Развивается новый подход к задаче совместной обработки данных о положении воздушного судна с помощью спутниковой навигационной системы и системы вторичных обзорных радиолокаторов. Цель задачи — получение оценок для распределений собственных ошибок систем контроля и ошибок пилотирования. Учитывается возможная статистическая зависимость между ошибками пилотирования и ошибками данных спутниковой навигационной системы.
Введение
То обстоятельство, что вещательное автоматическое зависимое наблюдение (АЗН-В) рассматривается в настоящее время как перспективная система наблюдения обслуживания воздушного движения (ОВД), стимулировало дополнительный интерес к исследованию надежности измерений спутниковых навигационных систем (СНС). АЗН-В предполагает, что координаты каждого воздушного судна (ВС), определяемые на борту, передаются диспетчеру для использования в системе ОВД. Можно также предположить, что с введением АЗН-В данные СНС официально будет разрешено использовать при пилотировании ВС. В этом случае потенциально возможные ошибки, сбои в работе СНС как измерительной системы могут сказаться на статистике ошибок пилотирования. В работе [1] контроль целостности информации АЗН-В предложено проводить путем сравнения измерений координат ВС с данными, полученными от независимой системы наблюдения, например, от вторичных обзорных радиолокаторов (ВОРЛ).
В работе [2] был предложен метод фурье-сепарации для оценок распределений собственных ошибок двух независимых систем контроля положения ВС и ошибок пилотирования. Лаконичность предложенного в [1] решения во многом определялась статистической независимостью ошибок пилотирования и систем наблюдения. Однако использование данных СНС для улучшения точности пилотирования делает гипотезу о независимости ошибок неадекватной новой постановке задачи. В этой работе мы предпримем попытку расширения области применения метода фурье-сепарации на случай такой зависимости и получим формулы для оценки вероятности сбоя в работе СНС.
1. Постановка задачи и основные гипотезы модели
Рассмотрим движение ВС по плановой траектории в соответствии с некоторым известным законом Я = Я0 (). Реально при полете ВС откланяется от плановой траектории, имеет ошибки
пилотирования г () = ) — Я0 (V), статистические характеристики которых требуется определить. Будем полагать, что положение ВС в пространстве отслеживается с помощью двух независимых систем наблюдения — СНС и вторичных обзорных радиолокаторов (ВОРЛ), характеризуемых своими ошибками (рис. 1). Поскольку пилот (автопилот) управляет ВС, опираясь на данные СНС, то ошибки пилотирования — г () и ошибки СНС — р() в такой постановке задачи нельзя считать статистически независимыми.
Рис. 1. Плановая (пунктир) и реальная траектории движения ВС с отметками СНС и РЛС -наблюдений
Ошибки СНС можно разделить на 2 класса: «быстрые», существенно изменяющие свою величину от измерения к измерению, и «медленные» — слабо эволюционирующие во времени. В последнем случае будем говорить, что в работе СНС наблюдается сбой. Отметим, что именно медленные ошибки представляют для нашей задачи особый интерес, поскольку они после векторного суммирования с ошибкой пилотирования воспринимаются экипажем как реальное отклонение ВС от плановых параметров полета (рис. 2).
Рис. 2. Отклонение метки СНС от плановой траектории ВС: Г — отклонение ВС от плановой траектории; р — погрешность измерительной системы; Г + р — отклонение метки СНС от плановой траектории
Набирая статистику данных СНС и вычисляя фиксируемые (но не реальные) отклонения ВС от плановой траектории, можно экспериментально получить распределение / (г + р). Однако для определения распределений истинных ошибок пилотирования — w1 (г) и ошибок СНС -w2 (р) этих данных явно недостаточно. Дополнительная информация может быть получена от
ВОРЛ в виде распределения /2 (г + 5), где 5 — ошибки измерений радиолокационной системы. Обрабатывая далее совместно данные АЗН-В и РЛС, можно также экспериментально построить распределение /3(р-5). В работе [2] задача об определении распределений w1 (Г), w2(р) и w3 (5) решалась в предположении, что все ошибки: г, р и 5 — статистически независимы. Здесь мы будем полагать, что ошибки СНС и пилотирования статистически связаны, и существует маленькая, но конечная вероятность того, что в работе СНС наблюдается сбой. Будем
полагать здесь также, что распределение ошибок данных ВОРЛ -w3 (5) известно.
Основные гипотезы модели можно кратко сформулировать в виде следующих положений:
1. Пилот (автопилот) управляет ВС так, чтобы усредненная отметка СНС совпадала с плановой траекторией полета. При этом полагаем, что действия пилота не зависят от того, исправна СНС или она дает сбой.
2. Медленные и быстрые ошибки СНС статистически независимы, поскольку порождены различными физическими механизмами.
3. Ошибки пилотирования также могут быть разделены на две группы: первая порождена медленными ошибками СНС и в соответствии с первой гипотезой однозначно определяется ими, а вторая порождена случайными внешними воздействиями на ВС, такими как сдвиг ветра, турбулентность и т.д.
2. Вывод основных уравнений модели
Рассмотрим сначала представление ошибок СНС. Представим полную текущую ошибку СНС — р в виде суммы быстрой и медленно меняющейся ошибок р = % + Х& Вводя обозначения для распределений этих величин — w21)(|) и w22&1(X), представим их совместное распределение в виде
W2 (|, X ) = /Х1}(|) • 5(Х) + р w21)(|) • w22)(X), (1)
где Р1 — вероятность того, что СНС работает без сбоев; Р2 — вероятность появления сбоев.
Для получения распределения w2 (р) воспользуемся стандартным приемом: перейдем в (1)
к новым переменным й = I + X, V = X и проинтегрируем полученное выражение по V . В результате получаем
(I + X) = \dvwp(й, у)| г=|+х ^^(и) + Р2\dvwf(й — V) • w22)(v) Переходя в (2) к фурье-образам, находим
й=|+X . (2)
w2(K) = w21)(K) р + Р2 w22)(K) ]. (3)
Перейдем теперь к описанию ошибок пилотирования. Совместное распределение отклонений ВС от плановых параметров полета — У и медленных ошибок СНС может быть представлено в виде
(7,X) = р <}(7ЖХ) + P2 w?/. (Y / X) • wf(X). (4)
Условная вероятность w ^ (Y / X) , фигурирующая в последнем слагаемом правой части
(4), отображает статистическую зависимость ошибок пилотирования и медленных ошибок СНС. Для определения этой величины воспользуемся первой гипотезой модели. Заметим, что
сечения распределения w. ^ (Y,X) при X = const подобны с точностью до сдвига, т.е.
w. X (Y + X, X) = w22)( X) F (Y), (5)
где F (Y) — некоторая универсальная функция. С другой стороны,
w?,X (Y + X, X) = wF/X (Y + X / X) • w22)( X). (6)
Из (5) и (6) получаем
w.X (Y + X, X) … .
r,X (2) .— = w.|X(Y + X | X) = F(Y) (7)
w22)(X) .|xV 1 y w. w
Из приведенного соотношения видно, что w.x (Y + X | X) не зависит отX , т.е. X может
быть любым, в частности, можно положить X = 0 . Но w.x (Y + 0 | 0) имеет смысл распределения собственных ошибок пилотирования, порожденных внешними воздействиями на ВС -w1(1)(Y) . С учетом сказанного уравнение (4) можно переписать в виде
w. X (Y, X) = P( w(() (Y) S( X) + p2 wi(1) (Y — X) w22) (X). (8)
Интегрируя (8) по X и проводя преобразование Фурье по Y, находим
wx(k) = w1V)[ P + P2 w^K)]. (9)
Перейдем теперь к соотношениям, в которых фигурируют ошибки ВОРЛ. Поскольку они не зависят от ошибок СНС и не влияют на качество пилотирования, то согласно результатам работы [2] можно записать:
f2(К) = w1(K) w3(K); (10)
f3(K) = w2(K) w3(K).
Несколько сложнее обстоит дело с распределением отклонений меток СНС. Однако здесь мы вновь воспользуемся первой гипотезой, согласно которой пилотирование осуществляется так, как если бы медленные ошибки СНС отсутствовали вовсе. Это соответствует тому, что распределение f1 (r + р) имеет одинаковый вид как при наличии сбоев в работе СНС, так и при их отсутствии. Это позволяет записать для f1 (r + р) следующее соотношение
f1(. + р) = \w?\r + р- z)w™(z)dz. (11)
Или после преобразования Фурье получаем
/1(К) = w;l)(K) w2l)(K)
Тот факт, что фурье-образ функции распределения отклонения меток СНС не зависит от наличия или отсутствия сбоев, видится вполне естественным, поскольку ВС пилотируется так, чтобы метки СНС ложились как можно ближе к плановой траектории полета. Из-за этого может создаться впечатление, что статистика меток СНС не несет в себе информации о наличии сбоев. Однако, как это будет показано далее, /1(К) входит в явном виде в выражение для вероятности работы системы без сбоев.
Выпишем теперь совместно всю систему уравнений, определяющую математическую модель процесса регистрации отклонений ВС от плановой траектории полета
/(К) = w1(1)(K) w21)(K) /2(К) = ^(Л) Щ(К)
/3(К) = ^^ Щ(К) . (13)
W2(К) = w21)(К) [ р + Р2 w22)(К) ] w1 (К) = w1(1)(К)[р + Р2 w22)(К)]
3. Оценка вероятности сбоя в работе СНС
Проанализируем теперь возможность получения на основании системы (13) оценки вероятности сбоя в работе СНС.
Из второго и третьего уравнений системы следует, что
/2(К) = ^^ Ш) W2(К)
Из четвертого и пятого уравнений аналогично получаем
Wl(К) wí1)(К)
W2(К) w21)(К)
Таким образом, распределения w1(1)(к) и w!!1)(к) связаны между собой соотношением
w;l)(К)
/2(К) • w21)(К)
Подставляя (14) в первое уравнение системы (13), находим
wí1)(К)
/1(К) /2 (К)
Заметим, что выражение в правой части (15) совпадает с выражением для w1(К), полученным в работе [2] для случая, когда данные СНС не используются для коррекции пилотирования.
Теперь, используя (14), находим выражение для w!,1)(К) .
С учетом (15) и последнего уравнения системы (13) находим, что
[р + Р2 w(¡2)(к)] = 41 /2(К(Кз(К) /^з(К). (16)
Соотношение (16) представляет собой выражение для фурье-образа функции распределения медленных ошибок СНС — Г (X). Применяя к (16) обратное преобразование Фурье, находим
. -1 F (X) = Г
Л(К)-/3(К) / к
где — оператор обратного преобразования Фурье.
Вероятность отсутствия сбоев в работе СНС — Р1 можно определить как значение функции
распределения Г (X) вблизи нуля, т.е. как интеграл от Г (X) по малой области АО, где
т.е. там, где ошибка СНС меньше допустимого значения. Тогда искомая вероятность появления сбоев будет равна Р2 = 1 — р .
Необходимость введения е — окрестности при вычислении искомых вероятностей связана с тем, что все конкретные вычисления могут быть реализованы лишь численно. Это приведет к
тому, что сингулярная составляющая в распределении Г (X) «размажется», и получаемое значение Г (0) будет давать очень грубые оценки искомых величин.
Заключение
В работе развивается новый подход к задаче об оценке распределения ошибок пилотирования ВС на основании обработки статистических данных, полученных с помощью двух независимых систем наблюдения — спутниковой навигационной системы и вторичных обзорных радиолокаторов. Существенным является то, что в работе предполагается возможная статистическая связь между ошибками пилотирования и ошибками показаний СНС.
Литература
1. Спрысков В.Б., Дупиков В.В. Математические модели оценки вероятности ложной тревоги и риска целостности координатной информации вещательного автоматического зависимого наблюдения // Научный Вестник МГТУ ГА. — 2012. — № 184. — С. 14-22.
2. Кузнецов В.Л. Метод фурье-сепарации в задаче оценки распределений ошибок пилотирования, АЗН-В и РЛС — наблюдений // Научный Вестник МГТУ ГА. — 2012. — № 180. — С. 106-109.
ESTIMATION PILOTING ERRORS STATISTICS AND PROBABILITY OF SATELLITE NAVIGATION SYSTEM FAILURE
Kuznetsov V.L., Goryachenkova E.S.
A new approach to the problem of co-processing of data about the aircraft position with the help of satellite navigation systems and secondary surveillance radar system is been developed. The purpose of the task is to obtain estimates of mistakes distribution for control systems and piloting errors. Possibility of a statistical relationship between piloting errors and mistakes of satellite navigation system is taken into account.
Сведения об авторах
Кузнецов Валерий Леонидович, 1949 г.р., окончил МГУ им. М.В. Ломоносова (1972), профессор, доктор технических наук, заведующий кафедрой прикладной математики МГТУ ГА, автор более 100 научных работ, область научных интересов — методы математического моделирования в задачах распространения излучения в пространственно неоднородных, случайных и периодических средах; задачи УВД и безопасность полетов.
Горяченкова Екатерина Сергеевна, окончила МГТУ ГА (2013), аспирантка МГТУ ГА, область научных интересов — использование спутниковых технологий при ОрВД.
Художественная концепция спутника GPS Block II-F на орбите
В анализ ошибок для спутниковая система навигации важно для понимания того, как работает GPS, и для того, чтобы знать, какой величины ошибок следует ожидать. GPS вносит поправки на ошибки часов приемника и другие эффекты, но остаются остаточные ошибки, которые не исправляются. Положение приемника GPS вычисляется на основе данных, полученных со спутников. Ошибки зависят от геометрического снижения точности и источников, перечисленных в таблице ниже.
Обзор
|
|
В этом разделе фактическая точность оспаривается. Соответствующее обсуждение можно найти на Обсуждение: Анализ ошибок для глобальной системы позиционирования. Пожалуйста, помогите убедиться, что оспариваемые утверждения надежный источник. (Июнь 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Источник | Эффект (м) |
|---|---|
| Прибытие сигнала C / A | ±3 |
| Прибытие сигнала P (Y) | ±0.3 |
| Ионосферные эффекты | ±5 |
| Ошибки эфемерид | ±2.5 |
| Ошибки спутниковых часов | ±2 |
| Многолучевое искажение | ±1 |
| Тропосферные эффекты | ±0.5 |
 C / A C / A |
±6.7 |
 P (Y) P (Y) |
±6.0 |
Диаграмма геометрических ошибок, показывающая типичное соотношение отображаемого положения приемника, пересечения поверхностей сфер и истинного положения приемника в терминах ошибок псевдодальности, PDOP и числовых ошибок
Ошибки эквивалентного диапазона пользователя (UERE) показаны в таблице. Также есть числовая ошибка с оценочной стоимостью, 

Термин «ошибка эквивалентного диапазона пользователя» (UERE) относится к ошибке компонента на расстоянии от приемника до спутника. Эти ошибки UERE представлены как ошибки ±, что означает, что они являются несмещенными или нулевыми средними ошибками. Поэтому эти ошибки UERE используются при вычислении стандартных отклонений. Стандартное отклонение ошибки положения приемника,


PDOP вычисляется как функция положения приемника и спутника. Подробное описание того, как рассчитать PDOP, дано в разделе Геометрическое снижение точности вычислений (GDOP).

Стандартное отклонение ошибки в предполагаемом положении приемника 
Диаграмма ошибок слева показывает взаимосвязь указанного положения приемника, истинного положения приемника и пересечения четырех сферических поверхностей.
Измерение времени прихода сигнала
Положение, вычисленное приемником GPS, требует текущего времени, положения спутника и измеренной задержки принятого сигнала. Точность определения местоположения в первую очередь зависит от местоположения спутника и задержки сигнала.
Чтобы измерить задержку, приемник сравнивает битовую последовательность, полученную от спутника, с версией, созданной внутри. Сравнивая нарастающий и задний фронты битовых переходов, современная электроника может измерять смещение сигнала с точностью до одного процента от ширины битового импульса, 
Этот компонент точности позиционирования можно улучшить в 10 раз, используя сигнал P (Y) с более высокой чиповой скоростью. Предполагая тот же один процент точности ширины битового импульса, высокочастотный сигнал P (Y) дает точность 
Атмосферные эффекты
Несоответствие атмосферных условий влияет на скорость сигналов GPS, когда они проходят через Атмосфера Земли, особенно ионосфера. Исправление этих ошибок является серьезной проблемой для повышения точности определения местоположения GPS. Эти эффекты наименьшие, когда спутник находится прямо над головой, и усиливаются для спутников, расположенных ближе к горизонт так как путь через атмосферу длиннее (см. масса воздуха ). Как только приблизительное местоположение приемника известно, можно использовать математическую модель для оценки и компенсации этих ошибок.
Ионосферная задержка СВЧ-сигнала зависит от его частоты. Он возникает из ионизированной атмосферы (см. Общее электронное содержание ). Это явление известно как разброс и может быть рассчитан на основе измерений задержек для двух или более полос частот, что позволяет оценить задержки на других частотах.[1] Некоторые военные и дорогие гражданские приемники исследовательского класса рассчитывают атмосферную дисперсию по различным задержкам на частотах L1 и L2 и применяют более точную поправку. Это можно сделать в гражданских приемниках без расшифровки сигнала P (Y), передаваемого по L2, путем отслеживания несущая волна вместо модулированный код. Чтобы облегчить это на более дешевых приемниках, новый гражданский кодовый сигнал на L2, названный L2C, был добавлен к спутникам Block IIR-M, которые были впервые запущены в 2005 году. Он позволяет прямое сравнение сигналов L1 и L2 с использованием кодированных сигнал вместо несущей.
Воздействие ионосферы обычно изменяется медленно и может быть усреднено по времени. Эти значения для любой конкретной географической области можно легко вычислить, сравнив положение, измеренное с помощью GPS, с известным местом съемки. Эта поправка также действительна для других приемников в том же месте. Некоторые системы отправляют эту информацию по радио или другим каналам, чтобы приемники, работающие только на L1, могли вносить ионосферные поправки. Ионосферные данные передаются через спутник в Спутниковые системы дополнения (SBAS) такие как Система увеличения площади (WAAS) (доступно в Северной Америке и на Гавайях), EGNOS (Европа и Азия), Многофункциональная спутниковая система дополнения (MSAS) (Япония) и GPS-навигация с гео-дополнениями (GAGAN) (Индия), который передает его на частоте GPS с использованием специальной псевдослучайной шумовой последовательности (PRN), поэтому требуются только один приемник и антенна.
Влажность также вызывает переменную задержку, приводящую к ошибкам, аналогичным ионосферной задержке, но возникающим в тропосфера. Этот эффект более локализован, чем ионосферные эффекты, изменяется быстрее и не зависит от частоты. Эти особенности делают точное измерение и компенсацию ошибок влажности более трудными, чем ионосферные эффекты.[2]
В Атмосферное давление может также изменить задержку приема сигналов из-за присутствия в тропосфере сухих газов (78% N2, 21% O2, 0,9% Ar …). Его действие меняется в зависимости от местной температуры и атмосферного давления вполне предсказуемым образом с использованием законов идеальных газов.[3]
Эффекты многолучевого распространения
На сигналы GPS также могут влиять многолучевость проблемы, при которых радиосигналы отражаются от окружающей местности; здания, стены каньона, твердый грунт и т. д. Эти задержанные сигналы вызывают ошибки измерения, которые различны для каждого типа сигнала GPS из-за его зависимости от длины волны.[4]
Для уменьшения ошибок, связанных с многолучевым распространением, были разработаны различные методы, в первую очередь узкий интервал между корреляторами. Для многолучевого распространения с большой задержкой приемник сам может распознать встречный сигнал и отбросить его. Для решения проблемы многолучевого распространения с более короткой задержкой от сигнала, отражающегося от земли, специальные антенны (например, дроссельная заслонка антенны ) может использоваться для уменьшения мощности сигнала, принимаемого антенной. Отражения с короткой задержкой труднее отфильтровать, потому что они мешают истинному сигналу, вызывая эффекты, почти неотличимые от обычных колебаний атмосферной задержки.
Эффекты многолучевого распространения гораздо менее серьезны в движущихся транспортных средствах. Когда антенна GPS движется, ложные решения с использованием отраженных сигналов быстро не сходятся, и только прямые сигналы приводят к стабильным решениям.
Эфемериды и ошибки часов
В то время как эфемериды данные передаются каждые 30 секунд, сама информация может быть старше двух часов. Изменчивость давления солнечной радиации[5] косвенно влияет на точность GPS из-за влияния на ошибки эфемерид. Если пост время сначала исправить (TTFF), можно загрузить действительные эфемериды в приемник, и в дополнение к установке времени, определение местоположения может быть получено менее чем за десять секунд. Такие эфемеридные данные можно разместить в Интернете, чтобы их можно было загрузить в мобильные устройства GPS.[6] Смотрите также Вспомогательный GPS.
Атомные часы спутников испытывают шум и часы дрейф ошибки. В навигационном сообщении содержатся исправления этих ошибок и оценки точности атомных часов. Однако они основаны на наблюдениях и могут не указывать на текущее состояние часов.
Эти проблемы, как правило, очень малы, но могут составлять несколько метров (десятков футов) неточности.[7]
Для очень точного позиционирования (например, в геодезия ) эти эффекты могут быть устранены дифференциальный GPS: одновременное использование двух и более приемников на нескольких точки обследования. В 1990-е годы, когда приемники были довольно дорогими, некоторые методы квазидифференциальный GPS были разработаны, используя только один приемник, но повторное заселение точек измерения. В Венском техническом университете метод получил название qGPS и было разработано программное обеспечение для постобработки.[нужна цитата ]
Геометрическое снижение точности вычислений (GDOP)
Расчет геометрического снижения точности
Понятие геометрического снижения точности было введено в разделе, источники ошибок и анализ. Были предоставлены расчеты, чтобы показать, как использовался PDOP и как он влиял на стандартное отклонение ошибки местоположения приемника.
Когда видимые спутники GPS расположены близко друг к другу в небе (т. Е. С небольшим угловым разделением), значения DOP высокие; когда они далеко друг от друга, значения DOP низкие. По идее, спутники, которые расположены близко друг к другу, не могут предоставить столько информации, как спутники, которые находятся на большом расстоянии друг от друга. Низкие значения DOP представляют лучшую точность позиционирования GPS из-за более широкого углового разнесения между спутниками, используемыми для расчета положения приемника GPS. HDOP, VDOP, PDOP и TDOP — это соответственно по горизонтали, вертикали, позиции (3-D) и временного снижения точности.
Рисунок 3.1 Снижение точности данных Navstar GPS от береговой охраны США дает графическое представление о том, как геометрия влияет на точность.[8]
Теперь мы беремся за задачу, как вычислить снижение точности. В качестве первого шага в вычислении DOP рассмотрим единичный вектор от приемника к спутнику i с компонентами 



куда 



Первые три элемента каждой строки А являются компонентами единичного вектора от приемника до указанного спутника. Элементами в четвертом столбце являются c, где c обозначает скорость света. Сформулируйте матрицу, Q, так как
Это вычисление производится в соответствии с главой 11 Глобальной системы позиционирования Паркинсона и Спилкера, где весовая матрица п, был установлен в единичную матрицу. Элементы Q матрицы обозначены как:[9]
Греческая буква 
в соответствии с «Раздел 1.4.9 ПРИНЦИПОВ РАЗМЕЩЕНИЯ СПУТНИКОВ».
Горизонтальное снижение точности, 

Вывод уравнений для вычисления геометрического снижения точности
Уравнения для вычисления геометрического снижения точности членов были описаны в предыдущем разделе. В этом разделе описывается вывод этих уравнений. Используемый здесь метод аналогичен используемому в «Глобальная система позиционирования (превью) Паркинсона и Спайкера»
Рассмотрим вектор ошибки положения, 







куда 




.
Переставляем обе стороны:
.
После умножения матриц с обеих сторон уравнения (2) на соответствующие матрицы в уравнении (3) получаем
.
Взяв ожидаемое значение с обеих сторон и взяв неслучайные матрицы за пределы оператора ожидания, E, получаем:
Предполагая, что ошибки псевдодальности некоррелированы и имеют одинаковую дисперсию, ковариационная матрица с правой стороны может быть выражена как скаляр, умноженный на единичную матрицу. Таким образом
поскольку
Примечание: 
Замена на 
Из уравнения (7) следует, что отклонения указанного положения приемника и времени равны
и
Остальные условия дисперсии ошибки положения и времени следуют прямо.
Выборочная доступность
В GPS есть (в настоящее время отключена) функция под названием Выборочная доступность (SA), который добавляет к общедоступным навигационным сигналам преднамеренные изменяющиеся во времени погрешности до 100 метров (328 футов). Это было сделано с целью запретить противнику использовать гражданские приемники GPS для наведения высокоточного оружия.
Ошибки SA на самом деле являются псевдослучайными, генерируются криптографическим алгоритмом из классифицированного семя ключ доступный только авторизованным пользователям (военные США, их союзники и некоторые другие пользователи, в основном правительственные) со специальным военным приемником GPS. Простого владения приемником недостаточно; ему по-прежнему нужен строго контролируемый ежедневный ключ.
До отключения 2 мая 2000 года типичные ошибки SA составляли около 50 м (164 фута) по горизонтали и около 100 м (328 футов) по вертикали.[10] Поскольку SA влияет на каждый приемник GPS в данной области почти одинаково, фиксированная станция с точно известным местоположением может измерять значения ошибок SA и передавать их местным приемникам GPS, чтобы они могли исправить свои определения местоположения. Это называется дифференциальным GPS или DGPS. DGPS также исправляет несколько других важных источников ошибок GPS, в частности ионосферную задержку, поэтому он продолжает широко использоваться, даже если SA отключен. Неэффективность SA перед лицом широко доступной DGPS была распространенным аргументом в пользу отключения SA, и в конечном итоге это было сделано по приказу президента. Клинтон в 2000 г.[11]
Услуги DGPS широко доступны как из коммерческих, так и из государственных источников. К последним относятся WAAS и Береговая охрана США сеть LF морские навигационные маяки. Точность поправок зависит от расстояния между пользователем и приемником DGPS. По мере увеличения расстояния ошибки на двух участках также не будут коррелировать, что приведет к менее точным дифференциальным поправкам.
В 1990–91 гг. Война в Персидском заливе из-за нехватки военных устройств GPS многие военнослужащие и их семьи покупали легкодоступные гражданские устройства. Выборочная доступность значительно затруднила использование этих GPS военными США на поле боя, поэтому военные приняли решение отключить его на время войны.
В 1990-е гг. FAA начал оказывать давление на военных, чтобы они отключили СА навсегда. Это позволило бы FAA ежегодно экономить миллионы долларов на обслуживании собственных радионавигация системы. Сумма добавленной ошибки была «установлена на ноль».[12] в полночь 1 мая 2000 г. после заявления президента США Билл Клинтон, позволяя пользователям получать доступ к безошибочному сигналу L1. Согласно директиве, вызванная ошибка SA была изменена, чтобы не добавлять ошибок к общедоступным сигналам (код C / A). Указ Клинтона требовал, чтобы SA была обнулена к 2006 году; это произошло в 2000 году, когда американские военные разработали новую систему, которая дает возможность отказывать в использовании GPS (и другим навигационным службам) враждебным силам в конкретной зоне кризиса, не затрагивая остальной мир или свои собственные военные системы.[12]
19 сентября 2007 г. Министерство обороны США объявил, что будущее GPS III спутники не смогут реализовать SA,[13] в конечном итоге сделав политику постоянной.[14]
Антиспуфинг
Остается еще одно ограничение по GPS — антиспуфинг. Это шифрует P-код так что он не может быть имитирован передатчиком, отправляющим ложную информацию. Немногие гражданские приемники когда-либо использовали P-код, и точность, достигаемая с помощью общедоступного кода C / A, была намного лучше, чем ожидалось изначально (особенно с DGPS ), настолько сильно, что политика защиты от подделки имеет относительно небольшое влияние на большинство гражданских пользователей. Отключение функции защиты от подделки в первую очередь принесет пользу геодезистам и некоторым ученым, которым необходимы чрезвычайно точные положения для таких экспериментов, как отслеживание движения тектонических плит.
Относительность
Спутниковые часы замедляются из-за своей орбитальной скорости, но ускоряются из-за расстояния от гравитационного колодца Земли.
Существует ряд источников ошибок из-за релятивистский последствия[15] это сделало бы систему бесполезной, если бы ее не исправляли. Три релятивистских эффекта — это замедление времени, гравитационный сдвиг частоты и эффекты эксцентриситета. Примеры включают релятивистское время замедление из-за скорости спутника около 1 части из 1010, гравитационное замедление времени, которое заставляет спутник лететь примерно на 5 частей из 1010 Быстрее чем часы на Земле, и Эффект Саньяка из-за вращения относительно приемников на Земле. Эти темы рассматриваются ниже по очереди.
Специальная и общая теория относительности
Согласно теории относительности, из-за их постоянного движения и высоты относительно Земли в центре, невращающиеся приблизительно инерционные система отсчета на часы спутников влияет их скорость. Специальная теория относительности предсказывает, что частота атомных часов, движущихся с орбитальной скоростью GPS, будет идти медленнее, чем стационарные наземные часы, в раз 
Влияние сдвига частоты гравитации на GPS из-за общая теория относительности в том, что часы ближе к массивному объекту будут медленнее, чем часы дальше. Применительно к GPS приемники расположены намного ближе к Земле, чем спутники, в результате чего часы GPS работают быстрее в 5 × 10 раз.−10, или около 45,9 мкс / день. Этот сдвиг частоты гравитации заметен.
При объединении замедления времени и гравитационного сдвига частоты расхождение составляет около 38 микросекунд в сутки, то есть разница в 4,465 частей на 1010.[16] Без исправления в позиции будут накапливаться ошибки примерно 11,4 км / день.[17] Эта начальная ошибка псевдодальности исправляется в процессе решения уравнения навигации. Вдобавок эллиптические, а не идеально круглые орбиты спутников вызывают изменение во времени эффектов замедления времени и гравитационного сдвига частоты. Этот эффект эксцентриситета приводит к тому, что разница в тактовой частоте спутника GPS и приемника увеличивается или уменьшается в зависимости от высоты спутника.
Чтобы компенсировать это несоответствие, стандарту частоты на борту каждого спутника перед запуском дается сдвиг скорости, что делает его немного медленнее, чем желаемая частота на Земле; в частности, на 10,22999999543 МГц вместо 10,23 МГц.[18] Поскольку атомные часы на борту спутников GPS точно настроены, это делает систему практическим инженерным приложением научной теории относительности в реальной среде.[19] Размещение атомных часов на искусственных спутниках для проверки общей теории Эйнштейна было предложено Фридвардт Винтерберг в 1955 г.[20]
Расчет замедления времени
Чтобы рассчитать количество ежедневного замедления времени, которое испытывают спутники GPS относительно Земли, нам необходимо отдельно определить суммы, связанные с специальная теория относительности (скорость) и общая теория относительности (гравитация) и сложите их вместе.
Сумма из-за скорости будет определяться с помощью Преобразование Лоренца. Это будет:
Для малых значений v / c, используя биномиальное разложение это приблизительно:
Спутники GPS движутся на 3874 м / с относительно центра Земли.[18] Таким образом, мы определяем:
Эта разница ниже 1 из 8.349×10−11 представляет собой долю, на которую часы спутников движутся медленнее, чем часы Земли. Затем оно умножается на количество наносекунд в день:
То есть часы спутников теряют 7214 наносекунд в сутки из-за специальная теория относительности последствия.
- Обратите внимание, что эта скорость 3874 м / с измеряется относительно центра Земли, а не ее поверхности, где находятся приемники GPS (и пользователи). Это связано с тем, что эквипотенциал Земли делает чистое замедление времени равным по всей ее геодезической поверхности.[21] То есть комбинация специальных и общих эффектов делает чистое замедление времени на экваторе равным таковому у полюсов, которые, в свою очередь, покоятся относительно центра. Следовательно, мы используем центр как опорную точку для представления всей поверхности.
Степень расширения под действием силы тяжести будет определяться с помощью гравитационное замедление времени уравнение:
Для малых значений Мистер, используя биномиальное разложение это приблизительно:
Нас снова интересует только дробь меньше 1 и разница между Землей и спутниками. Для определения этой разницы берем:
Земля имеет радиус 6,357 км (на полюсах), что рземной шар = 6 357 000 м, а спутники имеют высоту 20 184 км.[18] делая их радиус орбиты рGPS = 26 541 000 м. Подставив их в приведенное выше уравнение, с Mземной шар = 5.974×1024, грамм = 6.674×10−11, и c = 2.998×108 (все в SI ед.), дает:
Это часть, на которую часы спутников движутся быстрее, чем часы Земли. Затем оно умножается на количество наносекунд в день:
То есть часы спутников набирают 45 850 наносекунд в день за счет общая теория относительности последствия. Эти эффекты суммируются, чтобы дать (округлено до 10 нс):
- 45850 — 7210 = 38640 нс
Таким образом, часы спутников набирают примерно 38 640 наносекунд в день или 38,6 мкс в день в целом из-за эффектов относительности.
Чтобы компенсировать это усиление, частота часов GPS должна быть уменьшена на долю:
- 5.307×10−10 – 8.349×10−11 = 4.472×10−10
Эта доля вычитается из 1 и умножается на предварительно настроенную тактовую частоту 10,23 МГц:
- (1 – 4.472×10−10) × 10.23 = 10.22999999543
То есть нам нужно замедлить частоту с 10,23 МГц до 10,22999999543 МГц, чтобы свести на нет эффекты относительности.
Искажение Саньяка
Обработка данных GPS-наблюдений также должна компенсировать Эффект Саньяка. Шкала времени GPS определяется в инерционный системы, но наблюдения обрабатываются в В центре Земли, фиксировано на Земле (совместно вращающаяся) система, система, в которой одновременность не определено однозначно. Таким образом, для преобразования инерциальной системы в систему ECEF применяется преобразование координат. Полученная коррекция времени прохождения сигнала имеет противоположные алгебраические знаки для спутников в Восточном и Западном небесных полушариях. Игнорирование этого эффекта приведет к ошибке восток-запад порядка сотен наносекунд или десятков метров в местоположении.[22]
Естественные источники помех
Поскольку сигналы GPS на наземных приемниках обычно относительно слабые, естественные радиосигналы или рассеяние сигналов GPS могут снижать чувствительность приемник, что затрудняет или делает невозможным получение и отслеживание спутниковых сигналов.
Космическая погода ухудшает работу GPS двумя способами: прямые помехи из-за всплесков солнечного радио в той же полосе частот[23] или путем рассеяния радиосигнала GPS на ионосферных неоднородностях, называемого сцинтилляцией.[24] Обе формы деградации следуют за 11-летием. солнечный цикл и максимальны при максимуме солнечных пятен, хотя они могут произойти в любое время. Солнечные радиовсплески связаны с солнечные вспышки и выбросы корональной массы (CME)[25] и их воздействие может повлиять на прием на половине Земли, обращенной к Солнцу. Сцинтилляция чаще всего возникает в тропических широтах, где это ночное явление. Это происходит реже в высоких или средних широтах, где магнитные бури могут приводить к мерцанию.[26] Помимо мерцаний, магнитные бури могут создавать сильные ионосферные градиенты, снижающие точность систем SBAS.[27]
Искусственные источники помех
В автомобильных GPS-приемниках металлические детали на лобовых стеклах,[28] например, антиобледенители или тонировочные пленки для автомобильных стекол[29] может действовать как Клетка Фарадея, унизительный прием прямо в машине.
Рукотворный EMI (электромагнитные помехи) также могут нарушить или варенье Сигналы GPS. В одном хорошо задокументированном случае невозможно было принимать сигналы GPS во всей гавани Моховая посадка, Калифорния из-за непреднамеренных помех, вызванных неисправностью предварительных усилителей телевизионной антенны.[30][31] Также возможно преднамеренное заклинивание. Как правило, более сильные сигналы могут создавать помехи для приемников GPS, когда они находятся в пределах радиосвязи или в пределах прямой видимости. В 2002 году в онлайн-журнале было опубликовано подробное описание того, как построить глушитель GPS L1 C / A ближнего действия. Phrack.[32]
В правительство США считает, что такие глушилки иногда использовались во время Война в Афганистане, а военные США утверждают, что уничтожили шесть глушителей GPS во время Война в Ираке, в том числе тот, который был уничтожен бомбой с наведением GPS.[33] Глушитель GPS относительно легко обнаружить и найти, что делает его привлекательной целью для противорадиационные ракеты. 7 и 8 июня 2007 года Министерство обороны Великобритании провело испытания системы постановки помех в западной части Великобритании.[нужна цитата ]
В некоторых странах разрешено использование ретрансляторов GPS для приема сигналов GPS в помещении и в недоступных местах; в то время как в других странах это запрещено, поскольку ретранслируемые сигналы могут вызывать многолучевые помехи для других приемников GPS, которые получают данные как от спутников GPS, так и от ретранслятора. В Великобритании Ofcom теперь разрешает использование репитеров GPS / GNSS.[34] в режиме «облегченного лицензирования».
Из-за возможности возникновения как естественного, так и искусственного шума продолжают развиваться многочисленные методы устранения помех. Первое — не полагаться на GPS как на единственный источник. По словам Джона Рули, «IFR у пилотов должен быть запасной план на случай отказа GPS ».[35] Автономный мониторинг целостности приемника (RAIM) — это функция, включенная в некоторые приемники, предназначенная для предупреждения пользователя при обнаружении помех или другой проблемы. Американские военные также развернули с 2004 г. Модуль выборочной доступности / защиты от спуфинга (SAASM) в Усовершенствованный GPS-приемник Defense (ДАГР).[36] В демонстрационных видеороликах было показано, что DAGR обнаруживает помехи и сохраняет свою блокировку на зашифрованных сигналах GPS во время помех, из-за которых гражданские приемники теряют захват.
Смотрите также
- Дополнение GPS
Примечания
- ^ Тот же принцип и лежащая в его основе математика можно найти в описании хронометраж пульсаров астрономами.
- ^ Navipedia: Мониторинг тропосферы
- ^ Navipedia: задержка тропосферы
- ^ Navipedia: Multipath
- ^ Отчет о ходе работы IPN 42-159 (2004)
- ^ SNT080408. «Пример эфемеридного сервера». Tdc.co.uk. Архивировано из оригинал 12 января 2009 г.. Получено 2009-10-13.
- ^ «Блок 1 — Введение в GPS». Архивировано из оригинал 29 апреля 2009 г.
- ^ «Введение в пользовательское оборудование NAVSTAR GPS» (PDF). Центр навигации береговой охраны США. Береговая охрана США. Сентябрь 1996. Получено 5 июля, 2014.
- ^ Паркинсон (1996)
- ^ Grewal (2001), стр. 103.
- ^ «Президент Клинтон приказывает прекратить выборочную доступность GPS».
- ^ а б «Заявление президента относительно решения США прекратить снижение точности глобальной системы позиционирования». Федеральная авиационная администрация. 1 мая 2000 г.. Получено 2013-01-04.
- ^ «DoD навсегда прекращает закупку выборочной доступности глобальной системы позиционирования». DefenseLink. 18 сентября 2007 г. Архивировано с оригинал 18 февраля 2008 г.. Получено 2008-02-20.
- ^ «Выборочная доступность». Национальный космический исполнительный комитет по позиционированию, навигации и хронометражу. Архивировано из оригинал 13 января 2008 г.. Получено 2008-02-20.
- ^ Уэбб (2004), стр. 32.
- ^ Ризос, Крис. Университет Нового Южного Уэльса. Спутниковые сигналы GPS В архиве 2010-06-12 на Wayback Machine. 1999.
- ^ Фараони, Валерио (2013). Специальная теория относительности (иллюстрированный ред.). Springer Science & Business Media. п. 54. ISBN 978-3-319-01107-3. Выдержка страницы 54
- ^ а б c Глобальная система позиционирования Роберта А. Нельсона через спутник, Ноябрь 1999 г.
- ^ Погге, Ричард В .; «Реальная теория относительности: система навигации GPS». Проверено 25 января 2008 года.
- ^ «Astronautica Acta II, 25 (1956)». 1956-08-10. Получено 2009-10-23.
- ^ С. П. Дрейк (январь 2006 г.). «Принцип эквивалентности как ступенька от специальной теории относительности к общей» (PDF). Являюсь. J. Phys., Vol. 74, №1. С. 22–25.
- ^ Эшби, Нил Относительность и GPS. Физика сегодня, Май 2002 г.
- ^ Черрути А., П. М. Кинтнер, Д. Э. Гэри, А. Дж. Маннуччи, Р. Ф. Мейер, П. Х. Доэрти и А. Дж. Костер (2008), Влияние интенсивных солнечных радиовсплесков в декабре 2006 г. на приемники GPS, Космическая погода, Дои:10.1029 / 2007SW000375, 19 октября 2008 г.
- ^ Аарон, Жюль; Басу, Сантимей (1994). «Ионосферные амплитудные и фазовые флуктуации на частотах GPS». Труды ION GPS. 2: 1569–1578.
- ^ С. Манкузо и Дж. К. Раймонд, «Корональные транзиенты и метрические радиовсплески типа II. I. Эффекты геометрии, 2004 г., Астрономия и астрофизика, т. 413, стр. 363-371»
- ^ Ледвина, Б. М .; Дж. Дж. Макела и П. М. Кинтнер (2002). «Первые наблюдения интенсивных мерцаний амплитуды GPS L1 на средних широтах». Письма о геофизических исследованиях. 29 (14): 1659. Bibcode:2002GeoRL..29.1659L. Дои:10.1029 / 2002GL014770.
- ^ Том Диль, Солнечные вспышки поражают Землю — WAAS изгибается, но не ломается, Новости спутниковой навигации, том 23, июнь 2004 г.
- ^ «Крепление I-PASS для автомобилей с особыми функциями лобового стекла» (PDF). Архивировано из оригинал (PDF) 26 марта 2010 г.
- ^ «3М Автомобильные пленки».. Обратите внимание, что пленки со стабильным цветом специально описаны как нет создание помех спутниковым сигналам.
- ^ «Охота на RFI». GPS мир. 1 января 2003 г.
- ^ «Клуб соответствия требованиям EMC» банановые кожуры «колонка 222». Compliance-club.com. Получено 2009-10-13.
- ^ Недорогой портативный глушитель GPS. Phrack выпуск 0x3c (60), статья 13. Опубликовано 28 декабря 2002 г.
- ^ Пресс-служба американских войск. Прогресс Centcom. 25 марта 2003 г. В архиве 3 декабря 2009 г. Wayback Machine
- ^ [1] Заявление Ofcom о режиме авторизации для ретрансляторов GNSS
- ^ Рули, Джон. AVweb. Глушение GPS. 12 февраля 2003 г.
- ^ Страница DAGR армии США В архиве 2012-08-05 в Archive.today
Рекомендации
- Grewal, Mohinder S .; Вайль, Лоуренс Рэндольф; Эндрюс, Ангус П. (2001). Системы глобального позиционирования, инерциальная навигация и интеграция. Джон Уайли и сыновья. ISBN 978-0-47135-032-3.
- Паркинсон; Спилкер (1996). Система глобального позиционирования. Американский институт аэронавтики и астрономии. ISBN 978-1-56347-106-3.
- Уэбб, Стивен (2004). Не из этого мира: сталкивающиеся вселенные, браны, струны и другие дикие идеи современной физики. Springer. ISBN 0-387-02930-3. Получено 2013-08-16.
внешняя ссылка
- GPS.gov —Общий веб-сайт общественного образования, созданный правительством США.
- Стандарт производительности GPS SPS — Официальная спецификация стандартной службы позиционирования (версия 2008 г.).
- Стандарт производительности GPS SPS — Официальная спецификация стандартной службы позиционирования (версия 2001 г.).