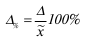Ошибки выборочного наблюдения реферат

Ошибки выборочного наблюдения

Информация, получаемая в результате
любого статистического наблюдения,
имеет расхождение с реальной
действительностью. Такое расхождение
получило название ошибок статистического
наблюдения. При массовом наблюдении
ошибки неизбежны, но возникают они
в результате действия различных причин
(см. гл. 4).

В данной главе рассматривается только
ошибка репрезентативности и причины
ее возникновения. Под ошибкой
репрезентативности (представительства)
понимают расхождение между выборочной
характеристикой и предполагаемой
характеристикой генеральной
совокупности. Причиной образования
этой ошибки является то обстоятельство,
что обследуются не все единицы генеральной
совокупности, а лишь их некоторая часть,
и различия между единицами, попавшими
в выборку, не соответствуют различиям
единиц, не попавших в выборку. Вследствие
этого выборочная совокупность становится
непредставительной по отношению к
генеральной совокупности. Ошибка
репрезентативности может возникнуть
по двум причинам: из-за нарушения научных
принципов отбора —систематическая
ошибка — и в результате случайности
отбора —случайная ошибка. В результате
первой причины выборка легко может
оказаться смещенной, так как при отборе
каждой единицы допускается ошибка,
всегда направленная в одну и ту же
сторону. Эта ошибка получила названиеошибки смещения. Ее размер может
превышать величину случайной ошибки.
Особенность ошибки смещения состоит
в том, что, представляя собой постоянную
часть ошибки репрезентативности, она
увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить (см. ниже), тогда как размер
ошибки смещения непосредственно
практически определить очень сложно,
а иногда — невозможно. Поэтому необходимо
знать причины, вызывающие ошибку смещения
и меры, способствующие её устранению.

Ошибки смещения бывают преднамеренные
и непреднамеренные. Причиной
возникновения преднамеренной ошибки
является тенденциозный подход к
выбору единиц из генеральной совокупности.
Мерой устранения этой ошибки может быть
только исключение тенденциозности.
Выявить эту ошибку можно только путем
проведения повторного отбора с
обязательным соблюдением принципа
случайности.

Непреднамеренные ошибки могут
возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чаще всего создаются условия
для возникновения ошибок смещения на
стадии подготовки выборочного наблюдения.
Недостаточно хорошо продуманные и четко
сформулированные взаимоувязанные
вопросы плана организации и проведения
выборочного обследования могут дать
информацию, не соответствующую цели
исследования или, что еще хуже, вводящую
в заблуждение. Если при сплошном
наблюдении это возможно только при
преднамеренном искажении фактов, то
при выборочном это связано с
непреднамеренными ошибками смещения.
При разработке плана организации и
проведения выборочного наблюдения
особое внимание следует уделятьединице
отбора, т. е. такой единице изучаемой
совокупности, которая является
основанием самого процесса отбора.
Единицей отбора могут служить естественные
единицы изучаемого явления, например
предприятие, рабочий, покупатель, семья
и т. д. В некоторых случаях необходимо
создать искусственные единицы, не
соответствующие естественному делению
изучаемой совокупности. Удачное
установление единицы отбора уменьшает
вероятность получить смещенную выборку.

Сокращению опасности возникновения
ошибок смещения во многом способствует
хорошая основа выборки, т. е. та
генеральная совокупность, из которой
предполагается производить отбор,
например список единиц отбора. Поэтому
при подготовке выборочного наблюдения
необходимо особенно тщательно
ознакомиться с тем, какова основа
выборки, пригодна ли она для производства
отбора, позволит ли она образовать
несмещенную выборку. Если готовой основы
выборки нет, то ее необходимо построить.

Основа выборки должна быть достоверной,
полной и соответствовать цели
исследования, а единицы отбора и их
характеристики должны соответствовать
действительному их состоянию на
момент подготовки выборочного наблюдения.
Если основа выборки не отвечает
перечисленным требованиям, ее
необходимо либо существенно улучшить,
внеся соответствующие изменения,
уточнения, дополнения, либо создать
заново.

На стадиях формирования выборочной
совокупности и производства наблюдения
ошибки смещения особенно опасны, так
как их трудно заметить и исправить. При
формировании выборочной совокупности
ошибку смещения чаще всего дает неточное
соблюдение установленного порядка
отбора, предусматривающего отбор
вполне определенных единиц. Иногда
может показаться, что выборочная
совокупность «не пострадает», если,
например, вместо предусмотренной десятой
единицы по списку взять одиннадцатую
или двенадцатую; в действительности же
такое нарушение установленного порядка
отбора нередко приводит к смещенной
выборке. Ошибки смещения при анализе
данных могут возникнуть из-за неправильных
приемов распространения выборочных
характеристик на генеральную
совокупность (см. 11.4).

Случайная ошибка выборки возникает
в результате случайных различий
между единицами, попавшими в выборку,
и единицами генеральной совокупности,
т. е. она связана со случайным отбором.
Теоретическим обоснованием появления
случайных ошибок выборки является
теория вероятностей и ее предельные
теоремы.

Сущность предельных теорем состоит в
том, что в массовых явлениях совокупное
влияние различных случайных причин на
формирование закономерностей и обобщающих
характеристик будет сколь угодно малой
величиной или практически не зависит
от случая. Так как случайная ошибка
выборки возникает в результате случайных
различий между единицами выборочной
и генеральной совокупностей, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Этот вывод,
опирающийся на доказательства предельных
теорем, позволяет предполагать, что
характеристики выборочного наблюдения
могут достаточно хорошо представлять
характеристики генеральной
совокупности.

Предельные теоремы исходят из закона
нормального распределения, согласно
которому большая часть выборочных
средних сосредоточивается около
генеральной средней
.
Следовательно, закон нормального
распределения теоретически позволяет
установить, в какой мере изменяется
размер случайной ошибки выборки с
изменением вероятности ее появления.
Так как многие массовые явления
подчиняются закону нормального
распределения, то он служит основой при
оценке вероятности тех или иных
результатов выборочного наблюдения.

Предельные теоремы теории вероятностей
позволяют определять размер случайных
ошибок выборки. Различают среднюю
(стандартную) и предельную ошибку
выборки. Под средней (стандартной)
ошибкой выборки понимают расхождение
между средней выборочной и генеральной
совокупностей,не
превышающее.
Предельной ошибкой выборки принято
считать максимально возможное расхождение,
т. е. максимум ошибки при заданной
вероятности ее появления. На основании
теоремы, доказанной П. Л. Чебышевым,
величину стандартной ошибки так
называемого собственно-случайного
отбора при достаточно большом объёме
выборки можно определить по формуле:

где
— стандартная ошибка.

Величина стандартной ошибки прямо
пропорциональна колеблемости признака
в генеральной совокупности и обратно
пропорциональна квадратному корню
объёма выборки. Величина
зависит также от способа и вида отбора.

Академик А.М.Ляпунов, продолжив разработки
П.Л.Чебышева, доказал, что вероятность
появления случайной ошибки выборки при
её достаточно большом объёме подчиняется
закону нормального распределения. Эта
вероятность определяется по формуле:

Значения функции
табулированы
при различных значенияхt.

Предельная ошибка выборки определяется
по формуле

где
-предельная
ошибка,t– заданный
коэффициент доверия.

Так, при t=1 величина
предельной ошибки составит,
гарантированную с вероятностью 0,683. Это
означает, что в 683 выборках из тысячи
подобных максимальная ошибка выборки
(предельная) не превысит.
Приt=2 с вероятностью
0,954 она не выйдет за пределыи
т.д. В практике выборочных наблюдений
массовых общественных явлений максимальный
предел ошибок, как правило, вполне
достаточен в пределах.

Однако приведённые формулы нахождения
ошибок выборки практически непригодны,
т.к. в них σ – это показатель колеблемости
признака в генеральной совокупности,
который неизвестен, как неизвестна и
генеральная средняя. Но в теории
вероятностей доказывается, что

Так как
при
достаточно большомn– величина, близкая к единице, то условно
принимается, что.
На основании этого утверждения в
вышеприведённых формулах вместо
генеральной дисперсии принимают значение
выборочной дисперсии.

Предельная ошибка выборки позволяет
определять предельные значения
характеристик генеральной совокупности
при заданной вероятности и их доверительные
интервалы:

Это означает следующее: с заданной
вероятностью можно утверждать, что
значение генеральной средней ожидается
в пределах от
до.

Наряду с абсолютной величиной предельной
ошибки выборки рассчитывают и относительную
ошибку, определяемую как процентное
отношение предельной ошибки выборки к
соответствующей характеристике
выборочной совокупности:

Если при выборочном наблюдении изучению
подлежит альтернативный признак, то
случайная ошибка выборки для доли
определяется в соответствии с теоремой
Я.Бернулли. так
как вероятность расхождения между
частостью и долей тоже подчиняется
закону нормального распределения, то
стандартная ошибка выборки альтернативного
признака определяется по формуле:

где pq– дисперсия
доли альтернативного признака в
генеральной совокупности.

Так как pqнеизвестно,
то на практике её заменяют дисперсией
выборочной совокупностиw(1-w)
и формула принимает вид:

Соседние файлы в папке 14-05-2013_10-41-11

Источник

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ВЫБОРКИ И ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

1.1 Понятие выборочного наблюдения, основные виды

.2 Определение объема выборки

.3 Ошибки выборочного наблюдения

2. СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

2.1 Выборочное исследование в статистическом анализе

.2 Методика расчета ошибок выборочного наблюдения

.3 Расчет средних ошибок выборочной доли и выборочной средней

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

ПРИЛОЖЕНИЕ

ВВЕДЕНИЕ

В современном мире многие процессы, с одной стороны, являются достаточно сложными и изменчивыми, а, с другой стороны, эти процессы можно выразить с помощью числовых значений.

В экономике, как и в других областях деятельности человека, часто применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Поэтому в статистическом анализе применяется выборочное наблюдение. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п. Поэтому в статистическом анализе применяется выборочное наблюдение.

Из этого следует, что тема выбранной курсовой работы является весьма актуальной.

Целью данной курсовой работы является теоретическое, а также практическое обоснование выбранной темы.

В связи с поставленной целью можно выделить ряд задач:

.Раскрытие понятия выборочного наблюдения, ее категории.

2.Обосновать виды отбора в выборочном наблюдении.

.Дать определение численности выборки.

.Показать практическое применение в статистическом анализе выборочного наблюдения.

Объектом данной курсовой работы является выборочное наблюдение в статистическом исследовании.

Предмет курсовой работы — это выборка и выборочная совокупность.

По результатам написания данной работы будут сделаны определенные теоретические и практические выводы.

1.ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ВЫБОРКИ И ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

1.1Понятие выборочного наблюдения, основные виды

Теория выборочного наблюдения базируется на статистических закономерностях, которые формируются и обнаруживаются в массовых явлениях и процессах. Это свойство закономерностей получило название закона больших чисел. Математической основой закона больших чисел, да и статистической науки в целом, служит теория вероятностей. Последняя представляет собой раздел математики, в котором изучаются случайные явления (события), имеющие устойчивую частность, а, следовательно, и вероятность, что помогает выявлять закономерности при массовом повторении явлений [2].

Основная задача выборочного метода — определение ошибки выборки, ибо, если не известен размер ошибки, данные выборки не могут иметь практического значения.

Под выборочным наблюдением (сокращенно выборка) понимается не сплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергается не всё, а отдельные единицы (обычно до 5-10%, реже до 15-20%), отобранные с соблюдением определенных условий.

Выборочный метод — это наиболее совершенная с научной точки зрения разновидность несплошного статистического наблюдения на основе статистической индукции, при котором характеристики всей статистической (генеральной) совокупностью (N) получаются в результате изучения некоторой ее части (n), отобранной с соблюдением определенных правил (на основе случайного отбора) и поэтому являющейся репрезентативной, т.е. репрезентативной и достоверной.

Самый важный признак выборочного наблюдения как вида сплошного наблюдения — случайный характер выборки, а главная его особенность заключается в том, что при отборе единиц совокупности для обследования обеспечивается равная возможность в отобранную часть любой из единиц.

В зависимости от характеристик выборочных совокупностей выборки могут быть представительными, расслоенными, засоренными и цензурированными.

Представительная выборка — выборка наблюдений из генеральной совокупности, наиболее полно и адекватно представляющая ее свойства.

Расслоенная выборка — выборка, включающая ряд выборочных совокупностей, взятых из соответствующих слоев генеральной совокупности. Широко используется при выборочном обследовании в экономике, демографии и социологии [7].

Засоренная выборка — выборка наблюдений, содержащая «грубые» ошибки. Основная масса элементов засоренной выборки является реализацией случайной величины X, закон распределения которой известен. Такие элементы («типичные») появляются в совокупности с вероятностью . С вероятностью элементы совокупности оказываются реализацией другой случайной величины Y, закон распределения которой в общем случае неизвестен. Такие элементы называются грубыми ошибками. Обычные оценки, например, средняя арифметическая выборочная, на засоренной выборке теряют свои оптимальные свойства (эффективность, несмещенность) с ростом интенсивности засорения.

Цензурированная выборка — выборка, полученная из вариационного ряда наблюдений путем отбрасывания некоторого числа экстремальных наблюдений. Если отбрасывание производится по признаку выхода наблюдений за пределы заданного интервала, то такой прием называется цензурирование первого типа. В этом случае число оставшихся наблюдений является случайной величиной. Если отбрасывается фиксированная доля крайних малых значений и фиксированная доля крайних больших значений, то это называется цензурированием второго типа уровня. При этом, число оставшихся в рассмотрении наблюдений является величиной заранее заданной.

Проведение выборочных исследований статистической информации состоит из следующих этапов:

¾формулировка цели статистического наблюдения;

¾обоснование целесообразности выборочного наблюдения;

¾отграничение генеральной совокупности;

¾установление системы отбора единиц для наблюдения;

¾определение числа единиц, подлежащих отбору;

¾проведение отбора единиц;

¾проведение наблюдения;

¾расчет выборочных характеристик и их ошибок;

¾распространение выборочных данных на генеральную совокупность.

Выборочное исследование осуществляется с минимальными затратами труда и средств и в более короткие сроки, чем сплошное наблюдение, что повышает оперативность статистической информации, уменьшает ошибки регистрации. В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции, сопровождающимся разрушением проверяемого изделия [10].

Выборочный метод дает достаточно точные результаты, поэтому он может применяться для проверки данных сплошного наблюдения. Минимальная численность обследуемых единиц позволяет провести исследование более тщательно и квалифицированно. Например, при переписях населения практикуются выборочные контрольные наблюдения для проверки правильности записей сплошного наблюдения.

В основе теории выборочного наблюдения лежат теоремы законов больших чисел, которые позволяют решить два взаимосвязанных вопроса выборки: рассчитать ее объем при заданной точности исследования и определить ошибку при данном объеме выборки.

При использовании выборочного метода обычно используются два вида обобщающих показателей: относительную величину альтернативного признака и среднюю величину количественного признака.

Относительная величина альтернативного признака характеризует долю (удельный вес) единиц в статистической совокупности, обладающих изучаемым признаком. В генеральной совокупности эта доля единиц называется генеральной долей (p), а в выборочной совокупности — выборочной долей (w).

Средняя величина количественного признака в генеральной совокупности называется генеральной средней (), а в выборочной совокупности — выборочной средней ().

Процесс образования выборки называется отбором, который осуществляется в порядке беспристрастного, случайного отбора единиц из генеральной совокупности.

Основным условием проведения выборочного наблюдения является предупреждение возникновения систематических (тенденциозных) ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.

Существуют различные способы отбора: индивидуальный, групповой (серийный), комбинированный, повторный (возвратный), бесповторный (безвозвратный), одноступенчатый, многоступенчатый, собственно-случайный, механический, типический, двухфазный и многофазный отбор [3].

При индивидуальном отборе в выборку отбираются отдельные единицы совокупности. Отбор повторяется столько раз, сколько необходимо отобрать единиц.

Групповой (серийный) отбор заключается в отборе серий (например, отбор изделий для проверки их целыми партиями). Если обследованию подвергаются все единицы отобранных серий, отбор называется серийным, а если обследуется только часть единиц каждой серии, отбираемых в индивидуальным порядке из серии, то — комбинированным.

Если в процессе отбора отобранная единица не исключается из совокупности, т.е. возвращается в совокупность, и может быть повторно отобранной, то такой отбор называется повторным или возвратным, в противном случае — бесповторным или безвозвратным. Серийный отбор, как правило, безвозвратный.

При одноступенчатом отбираются единицы совокупности (или серии) непосредственно для наблюдения. При многоступенчатом отбираются сначала крупные серии единиц (первая ступень отбора), наблюдению они не подвергаются. Затем из них отбираются серии, меньшие по численности единиц (вторая ступень), наблюдению не подвергаются, и так до тех пор, пока не будут отобраны те единицы совокупности (серии), которые будут подвергнуты наблюдению.

Собственно-случайный отбор состоит в отборе единиц (серий) из всей генеральной совокупности в целом посредством жеребьевки или на основании таблиц случайных чисел.

Жеребьевка состоит в том, что на каждую единицу отбора составляется карточка, которой присуждается порядковый номер. После тщательного перемешивания по очереди извлекаются карточки, пока не будет отобрано требуемое число единиц [8].

Случайными числами называются ряды чисел, являющихся реализациями последовательности взаимно независимых и одинаково распределенных случайных величин. Эти последовательности чисел получаются либо с помощью физических генераторов (подбрасывание кубиков с нанесенными на их сторонами цифрами; вытягиванием из урны карточек с написанными на них цифрами, преобразование случайных сигналов и др. физико-технические процессы), либо с помощью программных генераторов (аналитическим методом с помощью программ для ЭВМ). Числа, являющиеся результатами соответствующей вычислительной процедуры, называются псевдослучайными числами. Последовательность псевдослучайных чисел носит детерминированный характер, но в определенных границах она удовлетворяет свойствам равномерного распределения и свойству случайности.

Механический отбор заключается в том, что составляется список единиц генеральной совокупности и в зависимости от числа отбираемых единиц (серий) устанавливается шаг отбора, т.е. через какой интервал следует брать для наблюдения единицы (серии). Например, в простейшем случае, при 10%-м отборе, отбирается каждая десятая единица по этому списку, т.е. если первой взята единица за №1, то следующими отбираются 11-я, 21-я и т.д. В такой последовательности производится отбор, если единицы совокупности расположены в списке без учета их рангов, т.е. значимости по изучаемым признакам. Начало отбора в этом случае не имеет значения, его можно начать в приведенном примере от любой единицы из первого десятка. При расположении единиц совокупности в ранжированном порядке за начало отбора должна быть принята середина интервала (шага отбора) во избежание систематической ошибки выборки.

При типическом отборе генеральная совокупность разбивается на типические группы единиц по какому-либо признаку (формируются однородные совокупности), а затем из каждой из них производится механический или собственно-случайный отбор. Отбор единиц из типов производится тремя методами: пропорционально численности единиц типических групп, непропорционально численности единиц типических групп и пропорционально колеблемости признака в группах.

В целях экономии средств данные по некоторым интересующим исследователя признакам можно анализировать на основании изучения всех единиц выборочной совокупности, а по другим признакам — на основании части единиц выборочной совокупности, которые представляют подвыборку из единиц первоначальной выборки. Этот метод называется двухфазным отбором. При наличии нескольких подвыборок — метод многофазного отбора.

Многофазный отбор по своей структуре отличается от многоступенчатого отбора, так при многофазном отборе используются на каждой фазе одни и те же отобранные единицы, при многоступенчатом отборе на разных ступенях применяются единицы отбора разных порядков. Многофазным отбором чаще всего пользуются в тех случаях, когда различно число единиц, необходимых для определения отдельных показателей с заданной точностью. Это связано как с различиями в степени колеблемости признаков, так и с разной точностью, требуемой для расчетов. Ошибки при многофазной выборке рассчитываются на каждой фазе отдельно.

Отличие в методах повторного и бесповторного отбора математически отображают с помощью поправочного коэффициента на бесповторность (К):

— численность единиц выборочной совокупности;- численность единиц генеральной совокупности.

В математической статистике разработана методика анализа выборочного наблюдения случайных явлений. Основой такого анализа является предположение о множественности производимых выборочных наблюдений, и, как следствие, построение целого ряда распределения вероятностей различных характеристик полученных выборок. Предполагается осуществление только отдельного выборочного наблюдения.

Результаты выборочного наблюдения должны быть корректно перенесены на генеральную совокупность. При применении выборочного метода всегда происходит погашение особенностей отдельных единиц генеральной совокупности. Именно поэтому предполагается несоответствие параметров генеральной совокупности параметрам выборочной, т.е. наличие больших или меньших ошибок наблюдения. Чтобы исключить такое несоответствие параметры генеральной совокупности обычно представляют не с помощью отдельного значения, а в виде границ интервала, в пределах которого могут происходить колебания параметров.

Применение выборочного исследования предполагает определение параметров совокупности с некоторой степенью точности. Причем, точность зависит от меры репрезентативности выборки относительно генеральной совокупности, т.е. от качества выборочных данных. Чем хуже представлена в выборке генеральная совокупность, тем меньше степень точности выводов. Следовательно, тем дальше должны быть «раздвинуты» пределы интервала, в которых может колебаться параметр генеральной совокупности.

Еще одним определителем степени точности выводов служит их последующее применение. То есть, чем более корректные данные о генеральной совокупности требуется получить, тем дальше «раздвигаются» пределы интервала. Например, если исследование проводится в целях обучения студентов методике выборки, то принимается условная (низкая) степень точности. Тогда как, исследование, необходимое для государственного управления, предполагает высокую степень точности.

Как уже говорилось ранее, основным условием проведения выборочного наблюдения является предупреждение возникновения систематических (тенденциозных) ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы совокупности. Поэтому в следующем разделе речь пойдет об ошибках, возникающих при статистическом исследовании [4].

1.2Определение объема выборки

Определение необходимого объема выборки n основывается на формулах предельных ошибок выборочной доли и выборочной средней. Например, для повторного отбора предельные ошибки равны:

Отсюда объемы выборок для расчета выборочной доли nw и выборочной средней nx следующие:

Аналогичным образом определяются объемы выборок при различных способах отбора выборочной совокупности. Для серийного отбора определяется число отобранных серий.

При серийном или типическом отборе, не пропорциональном объему групп, общее число отбираемых единиц делится на количество групп. Полученная величина является объемом выборки из каждой группы.

При отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется по формуле:

где nj — объем выборки из j -й группы; — общий объем выборки;

Nj — объем j -й группы;

N — объем генеральной совокупности.

При отборе с учетом вариации признака, приводящем к минимальной ошибке выборки, процент выборки из каждой типической группы должен быть пропорционален среднему квадратическому отклонению в этой группе.

Расчет численности выборки производится по формулам:

для средней

, для доли

Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 20-30 и может составлять 5-6. С увеличением численности выборочной совокупности повышается точность выборочных данных, однако приходится иногда ограничиваться малым числом наблюдений. Эта необходимость возникает, например, при проверке качества продукции, связанной с уничтожением проверяемой единицы продукции. В математической статистике доказывается, что при малых выборках характеристики выборочной совокупности можно распространять на генеральную, но расчет средней и предельной ошибок выборки имеет особенности.

Ранее указывалось, что при большом объеме выборочной совокупности (n > 100) коэффициент , на который необходимо умножить выборочную дисперсию, чтобы получить генеральную, не играет большой роли. Но когда выборочная совокупность небольшая, этот коэффициент необходимо принимать во внимание. Средняя ошибка малой выборки () вычисляется по формуле:

где — дисперсия в малой выборке, которая определяется следующим образом:

Предельная ошибка имеет вид:

Значение коэффициента доверия зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Английский ученый Стьюдент доказал, что в случаях малой выборки действует особый закон распределения вероятности.

При большом числе единиц исследуемой совокупности ошибки и неточности могут погашаться, однако, если применяется выборочное наблюдение, тогда ошибки могут существенно повлиять на результаты исследования. В следующем разделе речь пойдет об ошибках выборочного наблюдения [6].

1.3Ошибки выборочного наблюдения

Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая , а во втором — выборочная доля величин, обозначаемая w. В генеральной совокупности соответственно: генеральная средняя и генеральная доля р.

В ходе наблюдения могут возникнуть следующие ошибки:

1.Ошибки регистрации — ошибочные результаты наблюдения, полученные в результате недостаточной квалификации исследователя, неточности измерительных приборов, некорректности подсчетов и т.д.

2.Ошибки могут быть случайными и систематическими:

¾систематические ошибки репрезентативности — ошибки, вызванные нарушением правил выбора единиц совокупности для наблюдения;

¾ошибки репрезентативности (случайные) — ошибки, отражающие несовпадение выводов о части явления с выводами о явлении в целом. Такие ошибки возникают при применении несплошного метода наблюдения, случайные ошибки репрезентативности — ошибки, отражающие неравномерное распределение единиц в совокупности, в связи с чем, выборочная совокупность не корректно характеризует генеральную совокупность.

Разности — и W — р называются ошибкой выборки, которая делится на ошибку регистрации и ошибку репрезентативности.

Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки по формулам:

Средняя ошибка повторной выборки — повторная;

где Дв — выборочная дисперсия.

При определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней. Систематическая ошибка репрезентативности возникает вследствие нарушения правил отбора единиц генеральной совокупности, в частности принципа беспристрастного, непреднамеренного отбора. Систематическая ошибка может привести к полной непригодности результатов наблюдений.

Ошибка выборочной средней представляет собой расхождение (разность) между выборочной средней и генеральной средней , возникающее вследствие несплошного выборочного характера наблюдения. Величина ошибки выборочной средней определяется как предел отклонения от , гарантируемый с заданной вероятностью:

где — гарантийный коэффициент, зависящий от вероятности , с которой гарантируется невыход разности за пределы ; — средняя ошибка выборочной средней.

Практическая часть рассматриваемой курсовой работы будет представлена в следующем разделе [9].

статистический выборочный средний ошибка

2. СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

2.1Выборочное исследование в статистическом анализе

Рассмотрим на практике как проводится статистический анализ выборочного наблюдения.

Случайные числа могут быть выбраны по таблице случайных чисел (ПРИЛОЖЕНИЕ), которая содержит 2000 случайных чисел, объединенных для удобства пользования таблицей в 500 блоков по 4 значения. Например, 5489, 5583, 3156, 0835, 1988, 3912.

Применение комбинаций этих цифр зависит от размера совокупности: если в генеральной совокупности 1000 единиц, то порядковый номер каждой единицы должен состоять из двух цифр от 000 до 999. В этом случае первые 8 номеров единиц выборочной совокупности следующие:

, 955, 833, 156, 083, 519, 883, 912.

При произвольном объеме генеральной совокупности, отличающегося от 100, 1000, 10000 могут использоваться псевдослучайные числа, сформированные на ЭВМ, или из таблицы случайных чисел формируется последовательность случайных величин, распределенных в интервале от 0 до 1. Например, в приведенном выше примере:

,5489; 0,5583; 0,3156; 0,0835; 0,1988; 0,3912 и т.д.

Если генеральная совокупность состоит из 2000 единиц, то в выборочную совокупность должны войти единицы с номерами:

* 0,5489 = 1097,8 или 1099;

* 0,5583 = 1116,6 или 1117;

* 0,3156 = 631,2 или 631;

* 0,0835 = 167,0 или 167;

* 0,1988 = 397,6 или 398;

* 0,3912 = 782,4 или 782.

Процесс формирования случайных чисел и определения номера отбираемой единицы продолжается до тех пор, пока не будет получен заданный объем выборочной совокупности.

Можно предложить другой способ случайного отбора единиц в выборку. Допустим, что выборка состоит из 75 единиц, а генеральная совокупность — из 780. Из таблицы случайных чисел выбираются, например, следующие: 5489, 5583, 3156, 0835, 1988, 3912.

В выборку могут войти только единицы, порядковые номера которых равны трехзначным числам меньше 780. Поэтому, используя только три последние цифры каждого числа, отбирается необходимые 75 номеров: 489, 583, 156 и т.д. Можно использовать и первые три цифры каждого числа, тогда отобранные номера: 548, 558, 315, 83, 198, 391. Можно разбить случайные четырехзначные случайные числа на ряд, состоящий из трехзначных чисел:

, 955, 833, 156, 083, 519, 883, 912

и отобрать из них номера, которые меньше 780, а именно: 548, 156, 83, 519.

Как уже отмечалось в предыдущей главе определение необходимого объема выборки n основывается на формулах предельных ошибок выборочной доли и выборочной средней.

Для серийного отбора определяется число отобранных серий. Формулы расчета приведены в табл.1.

Таблица 1

Методы отбора выборкиОбъем выборки или число серий для определениявыборочной доливыборочной среднейМеханический и собственно-случайный повторный отборМеханический и собственно-случайный бесповторный отборСерийный отбор при повторном отборе равновеликих серийСерийный отбор при бесповторном отборе равновеликих серийТипический отбор при повторном случайном отборе внутри групп, пропорциональном объему группТипический отбор при бесповторном случайном отборе внутри групп, пропорциональном объему групп

где nw, nx — объемы выборок соответственно для определения ошибок выборочной доли и выборочной средней;w, rx — число отобранных серий соответственно для определения ошибок выборочной доли и выборочной средней;

— предельные ошибки соответственно выборочной доли и выборочной средней.

Вариация () признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Для приближенной оценки используются следующие способы:

1.Дисперсия определяется на основе результатов проведения «пробного» обследования (обычно небольшого объема). По данным нескольких пробных обследований выбирается наибольшее значение дисперсии.

2.Дисперсия принимается из предыдущих исследований.

3.По правилу «трех сигм» общий размах вариации Н укладывается в 6 сигм, среднее квадратическое отклонение принимается равным Для большей точности размах делится на 5.

.Если хотя бы приблизительно известна средняя величина изучаемого признака, то .

.При изучении альтернативного признака (изучении доли), если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, принимается максимально возможная величина дисперсии, равная 0,25.

В связи с тем, что генеральная дисперсия оценивается приближенно, рекомендуется рассчитанный объем выборки округлять в большую сторону.

Часто на практике задается не величина абсолютной предельной ошибки , а величина относительной погрешности , выраженная в процентах к средней величине

откуда

В этом случае объем выборки будет:

Если известен коэффициент вариации , то объем выборки будет:

Например, по данным пробного обследования коэффициент вариации составляет 40%. Сколько необходимо отобрать единиц, чтобы с вероятностью 0,954 предельная относительная ошибка выборки не превышала 5%?

При

При отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется по формуле

где nj — объем выборки из j -й группы; — общий объем выборки;

Nj — объем j -й группы;

N — объем генеральной совокупности.

для средней

для доли

Таким образом, планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который входит в план всего статистического анализа выборочного наблюдения и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов.

Далее рассмотрим на практике как определяются в статистическом анализе ошибки выборочного наблюдения.

2.2Методика расчета ошибок выборочного наблюдения

Как говорилось ранее, при определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней. Систематическая ошибка репрезентативности возникает вследствие нарушения правил отбора единиц генеральной совокупности, в частности принципа беспристрастного, непреднамеренного отбора. Систематическая ошибка может привести к полной непригодности результатов наблюдений.

Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным об успеваемости студентов (две 10%-е выборки) (табл. 2).

Таблица 2

Данные по выборкам

ОценкаЧисло студентов, челГенеральная совокупностьПервая выборкаВторая выборка2 3 4 5100 300 520 809 27 54 1012 29 52 7Итого1000100100

Средний балл для генеральной совокупности

по первой выборке

по второй выборке

Доля студентов, получивших оценки «4» и «5»:

по генеральной совокупности

по первой выборке

по второй выборке

Разность между показателями выборочной и генеральной совокупности является случайной ошибкой репрезентативности (ошибкой выборки).

Ошибки репрезентативности:

где — гарантийный коэффициент, зависящий от вероятности ,с которой гарантируется невыход разности за пределы ; — средняя ошибка выборочной средней.

Значения гарантийного коэффициента и соответствующие им вероятности приведены в таблице 3. Обычно вероятность принимается равной 0,9545 или 0,9973, а при этом равно соответственно 2 и 3.

Таблица 3

Значения гарантийного коэффициента

1,00 1,10 1,20 1,30 1,40 1,50 1,60 1,70 1,80 1,90 2,00 2,10 2,20 2,30 2,40 2,50 2,60 2,70 2,80 2,90 3,000,6827 0,7287 0,7699 0,8064 0,8385 0,8664 0,8904 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973

Средняя ошибка определяется как среднее квадратическое отклонение средней величины в генеральной совокупности (средней генеральной)

В математической статистике доказывается, что величина средней квадратической стандартной ошибки простой случайной повторной выборки может быть определена по формуле:

где — дисперсия признака в генеральной совокупности.

Дисперсия суммы независимых величин равна сумме дисперсий слагаемых

Если все величины Xi имеют одинаковую дисперсию, то:

Тогда дисперсия средней будет:

Тогда средняя ошибка при определении средней:

Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:

где — дисперсия признака в выборке.

Если n достаточно велико, то близко к единице и дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.

Тогда средняя ошибка средней в генеральной совокупности может быть как среднее квадратическое отклонение средней величины в выборочной совокупности (средней выборочной)

Средняя ошибка выборочной средней:

Значения средней ошибки выборки определяются по формуле:

где — дисперсия в генеральной совокупности.

Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:

где — дисперсия в выборке.

При повторном отборе средняя ошибка определяется следующим образом:

где — средняя величина дисперсии количественного признака , которая рассчитывается по формуле средней арифметической невзвешенной

или средней арифметической взвешенной:

где fi — статистический вес.

В данном разделе были показаны общие формулы расчета ошибок выборочного наблюдения в статистическом анализе. Однако, в зависимости от способов отбора выборочной совокупности, расчет средней ошибки выборочной средней имеет свои особенности и формулы расчета. Это будет проиллюстрировано в следующем разделе.

2.3Расчет средних ошибок выборочной доли и выборочной средней

Формулы расчета средней ошибки выборочной средней для различных, наиболее часто используемых способов отбора выборочной совокупности приведены в таблице 4.

Таблица 4

Формулы расчета средних ошибок выборочной доли и выборочной средней

Метод отбора выборкиСредняя ошибкавыборочной доливыборочной среднейМеханический или собственно-случайный повторный отборМеханический или собственно-случайный бесповторный отборСерийный отбор при повторном отборе равновеликих серийСерийный отбор при бесповторном отборе равновеликих серийТипический отбор при повторном случайном отборе внутри групп, пропорциональном объему группТипический отбор при бесповторном случайном отборе внутри групп, пропорциональном объему групп

где N — численность генеральной совокупности;

— межсерийная дисперсия выборочной доли;- число отобранных серий;- число серий в генеральной совокупности;

— средняя из групповых дисперсий выборочной доли;

— дисперсия признака x в выборке;

— межсерийная дисперсия выборочных средних;

— средняя из групповых дисперсий выборочной средней.

При бесповторном оборе с каждой отобранной единицей или серией вероятность отбора оставшихся единиц или серий повышается, при этом средняя ошибка выборочной средней уменьшается по сравнению с повторным отбором и имеет следующий вид:

1)для механического или собственно случайного бесповторного отбора:

При достаточно большом объеме совокупности N можно воспользоваться формулой:

2)для серийного бесповторного отбора равновеликих серий:

При достаточно большом числе серий в генеральной совокупности R можно воспользоваться формулой:

3)для типического отбора с бесповторным случайном отборе внутри групп, пропорциональном объему групп:

Межсерийная дисперсия выборочных средних и средняя из выборочных дисперсий типических групп вычисляются следующим образом:

где — среднее значение показателя в j — й серии;

— дисперсия признака x в j — й типической группе;j — число единиц в j -й типической группе.

Средние ошибки выборки при типическом методе отбора, пропорциональном объему групп и колеблемости признака в группе приведены в таблице 5.

Таблица 5

Формулы расчета средних ошибок выборочной средней и выборочной доли при типическом методе отбора

Метод отбора выборкиСредняя ошибкавыборочной доливыборочной среднейповторный случайный отбор внутри групп, непропорциональный объему группбесповторный случайный отбор внутри групп, непропорциональный объему группповторный случайный отбор внутри групп, пропорциональный колеблемости признака в группахбесповторный случайный отбор внутри групп, пропорциональный колеблемости признака в группах

где Nj — число единиц в j -й типической группе;j — число отобранных единиц в j -й типической группе;

— выборочная дисперсия признака x в j — й типической группе (дисперсия признака в выборке из j — й типической группы);

— выборочная дисперсия доли в j — й типической группе

(дисперсия доли в выборке из j — й типической группы);

— среднее квадратическое отклонение признака x в выборке из j — й типической группе.

Средние ошибки выборки при комбинированной выборке с равновеликими сериями приведены в табл.6.

Таблица 6

Формулы расчета средних ошибок выборки при комбинированной выборке с равновеликими сериями

Метод отбора выборкиСредняя ошибкавыборочной доливыборочной среднейповторный отбор серийбесповторный отбор серий

где — общее число единиц в отобранных сериях ();

n — выбранное число единиц, подвергающихся обследованию, из

отобранных серий.

При многоступенчатом отборе на каждой ступени отбора может быть найдена своя средняя ошибка. При отборе, например, крупных групп из генеральной совокупности средняя ошибка выборки — ; при отборе мелких групп из крупных средняя ошибка выборки — ; при отборе отдельных единиц совокупности из мелких групп средняя ошибка выборки — . Если численность групп одинаковая, то средняя ошибка, как для средней, так и для доли, трехступенчатого отбора может быть определена по формуле:

Предельная ошибка выражается следующим образом:

и зависит от вариации изучаемого признака в генеральной совокупности, объема и доли выборки, способа отбора единиц из генеральной совокупности и от величины вероятности, с которой гарантируются результаты выборочного наблюдения.

Средняя величина количественного признака в генеральной совокупности определяется с у четом предельной ошибки выборочной средней

Из всего вышесказанного можно сделать следующие выводы:

1.Определение объема выборки зависит от метода отбора, который может быть механический бесповторный и механический повторный отбор, серийный при повторном и серийный при бесповторном отборе, типический при повторном случайном и типический при бесповторном случайном отборе. В зависимости от принадлежности к тому или иному методу, объем выборки рассчитывается по определенным формулам.

2.Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который входит в план всего статистического анализа выборочного наблюдения и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов.

.Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. Во 2 и 3 разделе были представлены формулы расчета ошибок выборочного наблюдения в статистическом анализе в зависимости от способов отбора выборочной совокупности.

ЗАКЛЮЧЕНИЕ

Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения — по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.

Данная курсовая работа содержит 2 главы, а именно: теоретические аспекты выборочного наблюдения и статистический анализ выборочного наблюдения.

Поставленная во введении цель дипломного проекта достигнута и решены основные задачи.

В результате решения вышеизложенных проблем можно сделать следующие выводы.

Теоретическое обоснование поставленного вопроса выявило понятие выборочного наблюдения, его основные виды, определение объема выборки, ошибки выборочного наблюдения.

Статистический анализ выборочного наблюдения показал следующие основные моменты:

. Определение объема выборки зависит от метода отбора, который может быть механический бесповторный и механический повторный отбор, серийный при повторном и серийный при бесповторном отборе, типический при повторном случайном и типический при бесповторном случайном отборе. В зависимости от принадлежности к тому или иному методу, объем выборки рассчитывается по определенным формулам.

. Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который входит в план всего статистического анализа выборочного наблюдения и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов.

. Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. Во 2 и 3 разделе были представлены формулы расчета ошибок выборочного наблюдения в статистическом анализе в зависимости от способов отбора выборочной совокупности.

И в заключение следует отметить, что практическое применение анализа статистического наблюдения активно используется во многих областях жизнедеятельности людей, например, широко применяется в социальной и экономической статистике, в частности в контроле за коммерческой деятельностью юридических и физических лиц со стороны финансовых организаций. Это подтверждает актуальность выбора данной темы курсовой работы.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.Статистика: учебник: Васильева Э.К., Лялин В.С. Издательство: Юнити Дана, 2012 г. — 398 страниц.

2.Статистика: учебное пособие: Эриашвили Н.Д., Воронин В.Ф., Жильцова Ю.В. Издательство: Юнити-Дана, 2012 г. — 536 страниц.

.Социально-экономическая статистика: учебное пособие: Мухина И.А. Издательство: ФЛИНТА, 2011 г. — 116 страниц.

.Статистика: учебное пособие: Кузнецова Е.И., Гусаров В.М. Издательство: Юнити-Дана, 2011 г. — 479 страниц.

.Общая теория статистики: Учебное пособие: Балдин К.В., Рукосуев А.В. Издательство: Дашков и К, 2010 г. — 312 страниц.

.Общая теория статистики: учебник: Илышев А.М. Издательство: Юнити-Дана, 2008 г. — 535 страниц.

.Статистика предприятий и бизнес-статистика: учебное пособие: Образцова О.И. Издательство: Издательский дом Высшей школы экономики, 2011 г. — 698 страниц.

.Статистика: учебное пособие: Плохотников К.Э., Колков С.В. Издательство: ФЛИНТА, 2012 г. — 286 страниц.

.Методология статистического исследования социально-экономических процессов: под ред. В.Г. Минашкина. Издательство: Юнити-Дана, 2012 г. — 391 страница.

.Статистика. Учебник / Под. Ред. Елисеевой И.И., — М.: Высшее образование, 2009. — 252 страницы.

11.

ПРИЛОЖЕНИЕ

Таблица случайных чисел

5489558331560835198839120938746008694420352209357877566570209555737571247878554475557579255024879477086423491012825026335759355450809074700162493224636891022672630368953371319672312918738004387547264473515634532326237803837421910464069695297068780388325119635001205026368456570304361314281796844705035654325473369536194415143453421050368789024734240865294351422981551447649863861378070534548652456570857801277681610132867993839303203569617691187″095159915245570055647352089162496568;4184217945549083225424352965515412097069291629729885027501448034812232137666023055241341986065656981984201712284270730080146529123545694037753366460958534152358492028265238540279371993433223276875523079781947, 63803425726772851130772201648573745306533645749759698682419129760361933414736938489953481641365208525296453844568162879780004707188096608446188397680881564542190807330142794168430599373120554720421192117588516432463557576656166053895470770269589080592585190127923324527341404517306005170403453275473848622556833358801257616344397276635369120731903352949083426052774998429852043965,402889365148176287131189109089897273321319359321482020232589174004248924000519691636723712277965385547650703167808417543030897321289769004808098962948197219724151283853192192920426957349035916657683683270664100330867165670164220253363458227190451382537050521278255527622333956411881996380634062959795111257612575683733369322740383456323261534103365’11172417317624345240545586728536296657735412811409304697691945691422550775960670301313513886326894692584265314725113573514699545933153039914639404384376332886498327011045497955527528902851215700477085112904606821832325728962796227533077871874188004142537068822149438374098022012174732015016371097104073728542412692742251060743018730769062353477013907658039948425777859197606231418668566871943430705798171822486417034359538756242558258723197491927925991405897691918685996060522499303458958128988256941768565901932604336231973411217958465211080453482047802216738732356434767010622729862

Теги:
Выборочное наблюдение в статистическом исследовании
Курсовая работа (теория)
Экономическая теория

Источник

1.3. Ошибки выборочного отбора
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении формуляров и т.д.

      Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам и т.д.), и случайные,проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.
        Расхождение между значениями изучаемого признака выборочной и генеральных совокупностей является ошибкой репрезентативности (представи-тельности). Она может быть случайной и систематической. Случайная возникает в силу того, что выборочное статистическое наблюдение является несплошным наблюдением, и выборка недостаточно точно воспроизводит (репрезентирует) генеральную совокупность.
        Систематические ошибка репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки — принцип случайности.

При определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней. Систематическая ошибка репрезентативности возникает вследствие нарушения правил отбора единиц генеральной совокупности, в частности принципа беспристрастного, непреднамеренного отбора. Систематическая ошибка может привести к полной непригодности результатов наблюдений.

Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным об успеваемости студентов (две 10%-е выборки):

Оценка	Число студентов, чел
	Генеральная совокупность	Первая выборка	Вторая выборка
2 3 4 5	100 300 520 80	9 27 54 10	12 29 52 7
Итого	1000	100	100

Средний балл для генеральной совокупности

по первой выборке

по второй выборке

Доля студентов, получивших оценки «4» и «5»:

по генеральной совокупности

по первой выборке

по второй выборке

Ошибки репрезентативности:

Как видно из расчетов, выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку.
1.3.1. Ошибка выборочной средней
Ошибка выборочной средней представляет собой расхождение (разность) между выборочной средней и генеральной средней , возникающее вследствие несплошного выборочного характера наблюдения. Величина ошибки выборочной средней определяется как предел отклонения от , гарантируемый с заданной вероятностью:

где – гарантийный коэффициент, зависящий от вероятности , с которой гарантируется невыход разности за пределы ; – средняя ошибка выборочной средней.

Значения гарантийного коэффициента и соответствующие им вероятности приведены в табл.4.1. Обычно вероятность принимается равной 0,9545 или 0,9973, а при этом равно соответственно 2 и 3.

Таблица 4.1

Значения гарантийного коэффициента

1,00

1,10

1,20

1,30

1,40

1,50

1,60

0,6827

0,7287

0,7699

0,8064

0,8385

0,8664

0,8904

1,70

1,80

1,90

2,00

2,10

2,20

2,30

0,9109

0,9281

0,9426

0,9545

0,9643

0,9722

0,9786

2,40

2,50

2,60

2,70

2,80

2,90

3,00

0,9836

0,9876

0,9907

0,9931

0,9949

0,9963

0,9973

Н.В.Смирнов, И.В.Дунин-Барковский. Курс теории вероятностей и математической статистики для технических приложений. — М.: Наука, 1965. 512 с.

Стр.173

В математической статистике доказывается, что величина средней квадратической стандартной ошибки простой случайной повторной выборки может быть определена по формуле

где — дисперсия признака в генеральной совокупности.
Дисперсия суммы независимых величин равна сумме дисперсий слагаемых

Если все величины
X_i
имеют одинаковую дисперсию, то

Тогда дисперсия средней

Тогда средняя ошибка при определении средней

Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:

где – дисперсия признака в выборке.

Тогда средняя ошибка средней в генеральной совокупности может быть как среднее квадратическое отклонение средней величины в выборочной совокупности (средней выборочной)
Средняя ошибка выборочной средней

Значения средней ошибки выборки определяются по формуле

где – дисперсия в генеральной совокупности.

Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:

где – дисперсия в выборке.

Если n достаточно велико, то близко к единице и дисперсию в генеральной совокупности можно заменить на дисперсию в выборке.
При повторном отборе средняя ошибка определяется следующим образом:

где – средняя величина дисперсии количественного признака , которая рассчитывается по формуле средней арифметической невзвешенной

или средней арифметической взвешенной

где f_i – статистический вес.
Формулы расчета средней ошибки выборочной средней для различных, наиболее часто используемых способов отбора выборочной совокупности приведены в табл.4.2.
Таблица 4.2
Формулы расчета средних ошибок выборочной доли

и выборочной средней

Метод отбора выборки	Средняя ошибка
	выборочной доли	выборочной средней
Механический или собственно–случайный повторный отбор
Механический или собственно–случайный бесповторный отбор
Серийный отбор при повторном отборе равновеликих серий
Серийный отбор при бесповторном отборе равновеликих серий
Типический отбор при повторном случайном отборе внутри групп, пропорциональном объему групп
Типический отбор при бесповторном случайном отборе внутри групп, пропорциональном объему групп

где N – численность генеральной совокупности;

– межсерийная дисперсия выборочной доли;

r – число отобранных серий;

R – число серий в генеральной совокупности;

– средняя из групповых дисперсий выборочной доли;

– дисперсия признака x в выборке;

– межсерийная дисперсия выборочных средних;

– средняя из групповых дисперсий выборочной средней.
При бесповторном оборе с каждой отобранной единицей или серией вероятность отбора оставшихся единиц или серий повышается, при этом средняя ошибка выборочной средней уменьшается по сравнению с повторным отбором и имеет следующий вид:

для механического или собственно случайного бесповторного отбора

При достаточно большом объеме совокупности
N можно воспользоваться формулой

для серийного бесповторного отбора равновеликих серий

При достаточно большом числе серий в генеральной совокупности
R можно воспользоваться формулой

для типического отбора с бесповторным случайном отборе внутри групп, пропорциональном объему групп
.
Межсерийная дисперсия выборочных средних и средняя из выборочных дисперсий типических групп вычисляются следующим образом:

где – среднее значение показателя в
j – й серии;

– дисперсия признака x в
j – й типической группе;

       n
_j
   – число единиц в
j –й типической группе.
И.Г.Венецкий, В.И.Венецкая. Основные математико-статистические понятия и формулы в экономическом анализе. — М.: Статистика, 1974. 279 с.
        Средние ошибки выборки при типическом методе отбора, пропорциональном объему групп и колеблемости признака в группе приведены в табл.3
Таблица 3
Формулы расчета средних ошибок выборочной средней

и выборочной доли при типическом методе отбора

Метод отбора выборки	Средняя ошибка
	выборочной доли	выборочной средней
повторный случайный отбор внутри групп, непропорциональный объему групп
бесповторный случайный отбор внутри групп, непропорциональный объему групп
повторный случайный отбор внутри групп, пропорциональный колеблемости признака в группах
бесповторный случайный отбор внутри групп, пропорциональный колеблемости признака в группах

где N
_j – число единиц в
j –й типической группе;

n
_j
– число отобранных единиц в
j –й типической группе;

– выборочная дисперсия признака x в
j – й типической группе

(дисперсия признака в выборке из j – й типической группы);

– выборочная дисперсия доли в
j – й типической группе

(дисперсия доли в выборке из j – й типической группы);

– среднее квадратическое отклонение признака x в выборке из

j – й типической группе;
Средние ошибки выборки при комбинированной выборке с равновеликими сериями приведены в табл.4

Таблица 4
Формулы расчета средних ошибок выборки при комбинированной

выборке с равновеликими сериями

Метод отбора выборки	Средняя ошибка
	выборочной доли	выборочной средней
повтор-ный отбор серий
бесповторный отбор серий

где — общее число единиц в отобранных сериях ( );

n — выбранное число единиц, подвергающихся обследованию, из отобранных

серий.
При многоступенчатом отборе на каждой ступени отбора может быть найдена своя средняя ошибка. При отборе, например, крупных групп из генеральной совокупности средняя ошибка выборки — ; при отборе мелких групп из крупных средняя ошибка выборки — ; при отборе отдельных единиц совокупности из мелких групп средняя ошибка выборки — . Если численность групп одинаковая, то средняя ошибка, как для средней, так и для доли, трехступенчатого отбора может быть определена по формуле

Предельная ошибка выражается следующим образом:

Средняя величина количественного признака в генеральной совокупности определяется с у четом предельной ошибки выборочной средней
Иногда для определения размеров предельной ошибки величина определяется из эмпирической формулы (И.Г.Венецкий, В.И.Венецкая. Основные математико-статистические понятия и формулы в экономическом анализе. — М.: Статистика, 1974. 279 с. — стр.188)

1.3.2. Ошибка выборочной доли
Выборочная доля представляет собой отношение числа единиц, обладающих данным признаком или данным его значением ( m ) к общему числу единиц выборочной совокупности ( n )

(Эту статистическую характеристику не следует путать с долей выборки, являющейся отношением числа единиц выборочной совокупности к числу единиц генеральной совокупности).

Ошибка выборочной доли представляет собой расхождение (разность) между долей в выборочной совокупности ( w ) и долей в генеральной совокупности ( p ), возникающее вследствие несплошного характера наблюдения. Величина ошибки выборочной доли определяется как предел отклонения w от p , гарантируемый с заданной вероятностью:

где – гарантийный коэффициент, зависящий от вероятности , с которой гарантируется невыход разности w –p за пределы ; – средняя ошибка выборочной доли.

Средняя ошибка выборочной доли определяется по формуле

Или, как было доказано выше,

где – дисперсия доли в генеральной совокупности (дисперсия генеральной доли);

– дисперсия доли в выборке (дисперсия выборочной доли).

        Приведенная формула средней ошибки выборочной доли применяется при повторном отборе.
       Для определения дисперсии альтернативного признака допустим, что общее число единиц совокупности равно
n    . Число единиц, обладающих данным признаком —
f , тогда   число единиц, не обладающих данным признаком, равно   n
—
f . Ряд распределения качественного (альтернативного) признака

Значение переменной

Частота повторений

1
0

n-f

Итого

Средняя арифметическая такого ряда равна:

то есть равна относительной частолте (частости) появления данного признака, которую можно обозначить через p , тогда

Таким образом, доля единиц, обладающих данным признаком равна p ; соответственно доля единиц, не обладающих данным признаком, равна q ;
p
+
q
=1. Тогда дисперсия альтернативного признака определяется по формуле

Для показателя доли альтернативного признака в выборке (выборочной доли) дисперсия определяется по формуле

При бесповторном отборе численность генеральной совокупности сокращается, поэтому дисперсия умножается на коэффициент Формулы расчета средних ошибок выборочной доли для различных способов отбора единиц из генеральной совокупности приведены в табл. 4.2; 3 и 4.
Дисперсии в формулах расчета средних ошибок выборочной доли в табл.4.2. рассчитываются следующим образом:

– межсерийная дисперсия выборочной доли

где w
_j – выборочная доля в j
–й серии;

– средняя величина доли во всех сериях;
– средняя из групповых дисперсий

где w_j – выборочная доля в j –й типической группе;

n_j – число единиц в j –й типической группе;

k – число типических групп.
Для случая, когда доля (частость) даже приблизительно неизвестна, можно произвести «грубый» расчет средней ошибки выборки для доли, используя в расчете максимальную величину дисперсии доли, равную 0,25. Тогда для

повторного отбора

бесповторного отбора

Предельное значение ошибки выборочной доли определяется по следующей формуле:

Величина средней ошибки выборочной доли зависит от доли изучаемого признака в генеральной совокупности, числа наблюдений и способа отбора единиц из генеральной совокупности для наблюдения, а величина предельной ошибки зависит еще и от величины вероятности , с которой гарантируются результаты выборочного наблюдения.

Распространение выборочных данных на генеральную совокупность производится с учетом доверительных интервалов. Доля альтернативного признака в генеральной совокупности равна
Пример
Сущность процесса случайного отбора и основные свойства простой повторной выборки можно показать на условном примере.

Генеральная совокупность состоит из трех единиц (
N = 3 ), например

Порядковый номер рабочего	1	2	3	4
Тарифный разряд, x_i	3	4	4	5

Генеральная средняя

разряд;

генеральная дисперсия

доля рабочих в генеральной совокупности, имеющих 4 тарифный разряд

Задача. Определить параметры генеральной совокупности ( средний разряд, дисперсию и долю рабочих с тарифным разрядом, равным 4) по результатам проведения простой случайной повторной выборки объемом 2 единицы (
n = 2 ).

В данном примере с одинаковой степенью вероятности могла бы появиться любая из 16 возможных комбинаций единиц, то есть любая из 16 возможных выборок. Результаты 16 выборок приведены в табл. 1

Таблица 1

Номер выборки	Номера единиц, входящих в выборку	Значения признака по данным выборки	Выборочная средняя	Отклонение выборочной средней от генеральной средней	Выбо- рочная доля
1	1; 1	3; 3	3,0	-1,0	0,0
2	1; 2	3; 4	3,5	-0,5	0,5
3	1; 3	3; 4	3,5	-0,5	0,5
4	1; 4	3; 5	4,0	0,0	0,0
5	2; 1	4; 3	3,5	-0,5	0,5
6	2; 2	4; 4	4,0	0,0	1,0
7	2; 3	4; 4	4,0	0,0	1,0
8	2; 4	4; 5	4,5	+0,5	0,5
9	3; 1	4; 3	3,5	-0,5	0,5
10	3; 2	4; 4	4,0	0,0	1,0
11	3; 3	4; 4	4,0	0,0	1,0
12	3; 4	4; 5	4,5	+0,5	0,5
13	4; 1	5; 3	4,0	0,0	0,0
14	4; 2	5; 4	4,5	+0,5	0,5
15	4; 3	5; 4	4,5	+0,5	0,5
16	4; 4	5; 5	5,0	+1,0	0,0

Возможные варианты значений выборочных средних и отклонения их от генеральной средней представлены в виде ряда распределения (табл.2)

Таблица 2

Выборочные средние разряды рабочих	Число выборок с данной выборочной средней f_j	Отклонение выборочной средней от генеральной средней	Вероятность появления данного значения выборочной средней (или величины отклонения выборочной средней от генеральной)
3,0	1	-1,0	0,0625
3,5	4	-0,5	0,2500
4,0	6	0,0	0,3750
4,5	4	+0,5	0,2500
5,0	1	+1,0	0,0625
Итого	16		1,0000

В распределении величин выборочных средних и их отклонений наблюдаются определенные закономерности.

1. Из возможных результатов случайной повторной выборки наиболее вероятны такие, при которых величина выборочной средней будет близка к величине генеральной средней. Таким образом, чем больше величина случайной ошибки выборки, тем менее вероятно появление такой ошибки.

2. В примере не встречаются ошибки больше единицы по абсолютной величине, т.е. всегда существует предел расхождений между выборочной и генеральной средней.

По данным табл.2, где представлены все возможные варианты выборочных средних и их отклонения от генеральной средней, определяется величина стандартной ошибки выборки

Однако на практике исследователь оперирует данными какой-то одной конкретной выборки, а поэтому указанным способом определить стандартную ошибку средней невозможно.

Среднюю ошибку можно определить по формуле, используя величину дисперсии в генеральной совокупности (в данном примере генеральная дисперсия признака равна 0,5)

Распределение выборочной доли представлено в табл.3

Таблица 3

Выборочная доля	Число выборок с данной выборочной долей f_j	Отклонение выборочной доли от генеральной
0,0	4	-0,5	0,0	1,0
0,5	8	0,0	4,0	0,0
1,0	4	+0,5	4,0	1,0
Итого	16		8,0	2,0

В среднем для всех возможных вариантов выборок величина выборочной доли совпадает с долей признака в генеральной совокупности

Средняя квадратическая ошибка доли в генеральной совокупности

Среднюю квадратическую ошибку доли в генеральной совокупности можно определить, используя долю признака в генерального совокупности ( p = 0,5),

В формулы средних ошибок выборки

;
входят дисперсии признака и доли в генеральной совокупности, величины которых, как правило, при проведении выборочного наблюдения неизвестны. Поэтому для расчета средних ошибок выборки приходится использовать выборочные дисперсии в качестве оценки генеральной совокупности.

Источник

2. Ошибки выборочного наблюдения

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.

Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:

где µ_x– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µ_x зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:

В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.

Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:

Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности ^x и величину предельной ошибки этой средней ^?_x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.

Данный текст является ознакомительным фрагментом.

Ошибки выборочного наблюдения

Читайте также

Наблюдения за объемом

Закономерности и наблюдения

Ошибки в инвестициях – это ошибки инвесторов

8. Способы статистического наблюдения

9. Формы статистического наблюдения

2. Ошибки выборочного наблюдения

19. Наблюдения

6. Организация статистического наблюдения

11. Ошибки статистического наблюдения и контроль материалов наблюдения

34. Определение выборочного наблюдения

Часть 5 Наблюдения

Введение процедуры наблюдения

1. Организация статистического наблюдения

5. Ошибки статистического наблюдения и контроль материалов наблюдения

1. Определение выборочного наблюдения

Общие наблюдения и впечатления