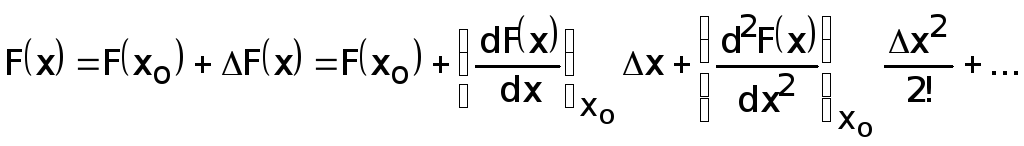Ошибкой регулирования называется

Действительные
значения регулируемой величины в
реальных САР отличаются от предписанных.
Разность между предписанным и
действительным значениями регулируемой
величины называется ошибкой
регулирования.

∆xз(t)
= xз
– x(t)
– ошибка регулирования

хз
– предписанное (заданное) значение
управляемой величины;

x(t)
– ее текущее значение

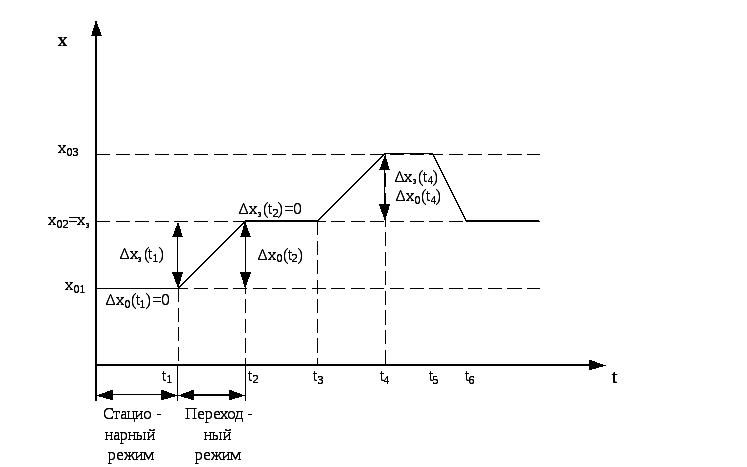
В
процессе функционирования САР может
переходить от одного состояния,
принимаемого за исходное, в другое.
Разность между текущими значениями
регулируемой величины и значением,
соответствующим исходному состоянию,
принято называть отклонением регулируемой
величины

∆x0(t)
= x(t)
– x0(t) (1.3)

где
xo
– значение регулируемой величины в
исходном состоянии.

x0(t)
– исходное значение регулируемой
величины.

Рис.
1.3. Изменение значения регулируемой
величины в процессе регулирования

1.4. Статическое и астатическое регулирование

В
зависимости от того, является или нет
ошибка регулирования функцией возмущающего
воздействия в установившемся режиме,
различают статическое
и астатическое
регулирование.

При
статическом регулировании ошибка
регулирования возрастает с увеличением
значения возмущающего воздействия.
Пример статического регулирования
приведен на рис. 1.4, а).

а)

б)

в)

Рис.
1.4. Пример статического регулятора и
его характеристика (1 – генератор; 2 –
электронный усилитель, 3 – регулировочный
реостат, Uг
– напряжение генератора (регулируемый
параметр);Uзад
– задающее воздействие, которое равно
заданному (предписанному) значению
напряжения генератора; Pг
– активная мощность генератора
(возмущающее воздействие); UИП
– напряжение источника питания; UОВ
– напряжения обмотки возбуждения; ΔU
– входное напряжения электронного
усилителя)

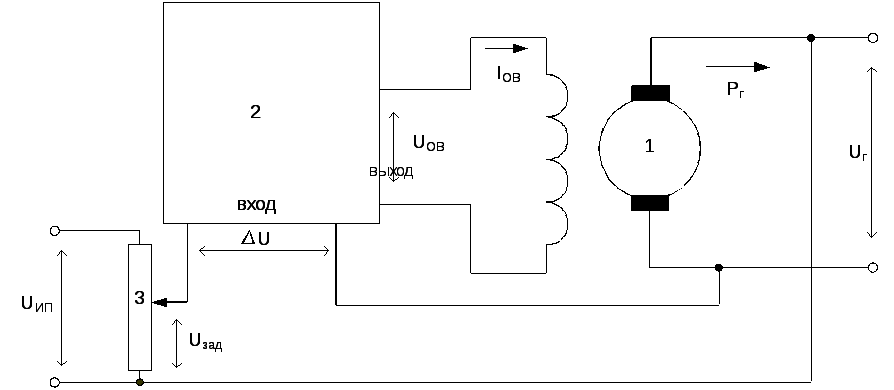
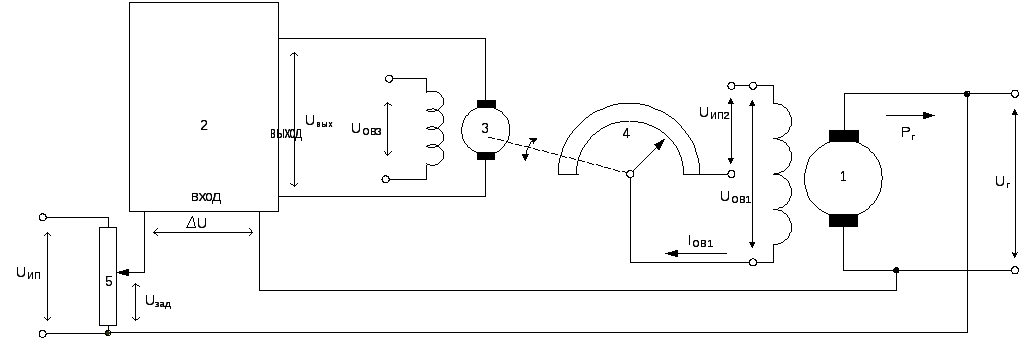
Принцип
действия этого регулятора достаточно
ясно виден из рассмотрения схемы и
особых пояснений не требует. Заметим
лишь, что требуемого возбуждение
генератора 1 осуществляется путем
изменения входного сигнала (ΔU)
электронного усилителя 2. В свою очередь
этот сигнал пропорционален отклонению
регулируемого параметра Uг
от заданного значения Uзад
(ΔU=Uг–Uзад).
Поэтому такое отклонение, т.е. наличие
ΔU,
является неизбежным и должно быть тем
больше, чем больше изменяется величина
внешнего возмущения Pг.
Очевидно, что это отклонение регулируемого
параметра от заданного значения
сохраняется также и в установившемся
режиме.

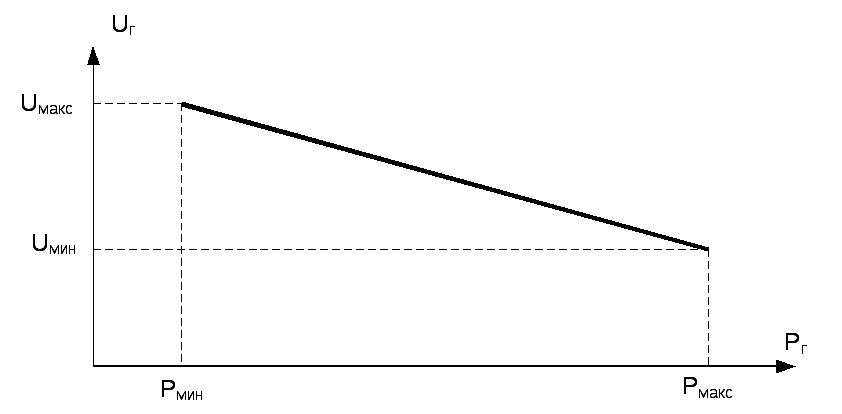
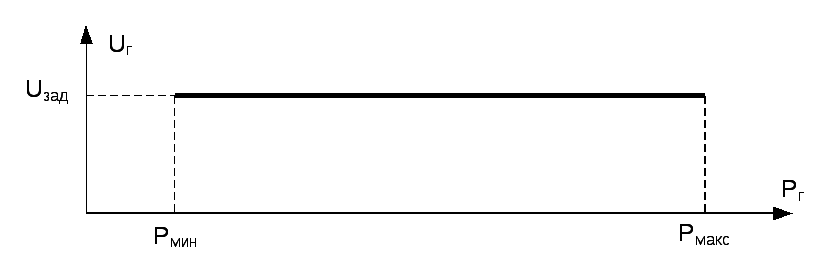
Рабочая
характеристика (зависимость напряжения
генератора от нагрузки – активной
мощности Pг)
статического регулятора приведена на
рис. 1.4, б).

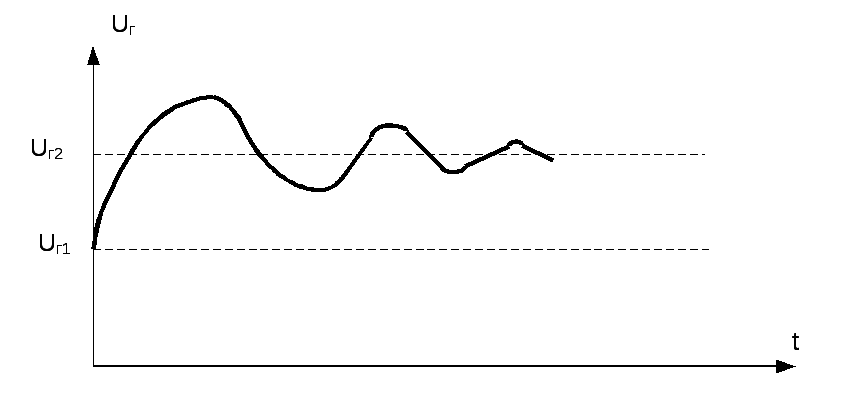
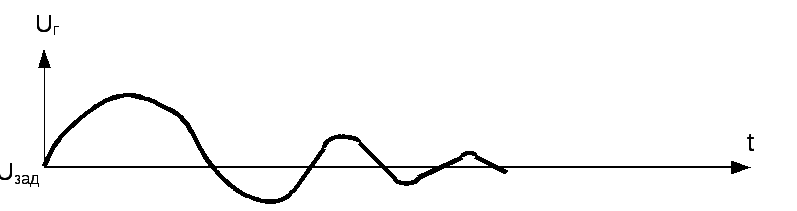
На
рис. 1.4, в)
показан переходный процесс в системе
при уменьшении нагрузки генератора.

Регулированием
с астатической
характеристикой
называется такое регулирование, при
котором в установившемся состоянии
системы отклонение регулируемого
параметра от заданного значения равно
нулю при любой величине внешнего
возмущения. Равновесие системы имеет
место всегда при заданном значении
регулируемого параметра.

Пример
астатического регулирования приведен
на рис. 1.5, а).

а)

б)

в)

Рис.
1.5. Пример астатического регулятора
и его характеристика (1 – генератор;
2 – электронный усилитель; 3 – якорь
двигателя постоянного тока; 4, 5 –
регулировочные реостаты, Uг
– напряжение генератора (регулируемый
параметр); Uзад
– задающее воздействие, которое равно
заданному (предписанному) значению
напряжения генератора; Pг
– активная мощность генератора
(возмущающее воздействие); UИП1,
UИП2
– напряжения источников питания №1
и №2; UОВ1
и UОВ3
– напряжения обмоток возбуждений
генератора и двигателя; ΔU
– входное напряжения электронного
усилителя; Uвых
–напряжение на выходе электронного
усилителя)

Характеристика
астатического регулятора приведена на
рис. 1.5, б),
а кривая переходного процесса – на рис.
1.5, в).

При
увеличении нагрузки на генераторе, т.е.
увеличении активной мощности генератора
Pг,
уменьшается напряжение на его выводах
Uг,
что приводит к появлению отклонения
регулируемого параметра Uг
от заданного значения Uзад
(ΔU=Uг–Uзад).
Параметр Uзад
задается
регулировочным реостатом 5. При этом
появляется напряжение на якоре двигателя
постоянного тока Uвых,
и двигатель начинает перемещать контакт
регулировочного реостата 4 по часовой
стрелке, что приводит к увеличению тока
возбуждения генератора IОВ1,
а значит, и напряжения на его выводах
Uг.
Параметр Uг
будет увеличиваться до тех пор, пока
ошибка регулирования ΔU
не станет равной 0.

Астатические
САР обеспечивают высокую точность
регулирования. Однако по сравнению со
статическими они являются более сложными
и инерционными, т.е. процессы регулирования
в них являются замедленными.

1.5.
Линейные и нелинейные системы. Линеаризация
уравнений

Системы,
процессы в которых могут быть описаны
линейными дифференциальными уравнениями
с постоянными коэффициентами, называются
линейными.
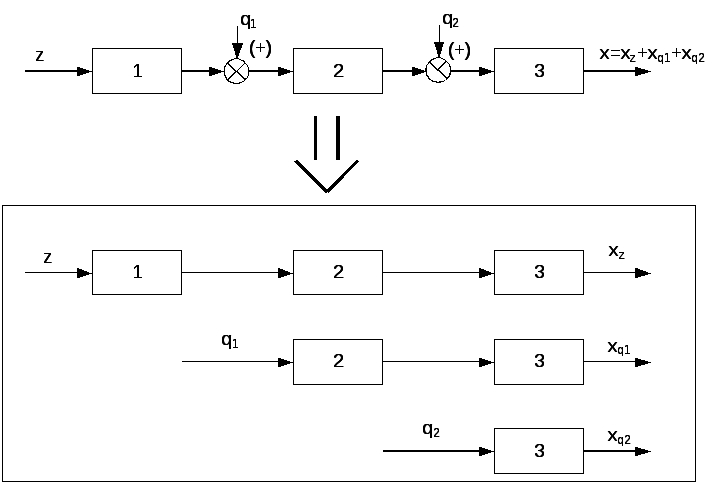
Для линейных систем применим принцип
суперпозиции, позволяющий рассматривать
независимое прохождение воздействий,
что дает существенное упрощение (рис.
1.6).

Рис.
1.6. Принцип суперпозиции

Нелинейной
называется система, для описания
процессов в которой приходится применять
одно или несколько нелинейных уравнений.
К нелинейным относятся уравнения,
коэффициенты которых зависят от значений
переменных величин или их производных,
а также уравнения, содержащие произведения
или степени (выше первой) этих величин.

Строго
говоря, линейных САУ в технике практически
нет или очень мало. Однако большинство
систем при определенных условиях могут
рассматриваться как линейные. Так, если
оценивать поведение системы при малых
отклонениях величин от исходных значений,
то в большинстве случаев имеющей место
нелинейностью можно пренебречь. Такая
возможность имеет математическое
обоснование.

Пусть
имеем некоторую непрерывную функцию
F(x)
(рис. 1.7).

Если
аргумент X
получил приращение ΔX
от исходного значения Xo,
то функция получит приращение ΔF(X).
Новое значение функции F(X)
можно разложить в ряд Тейлора:

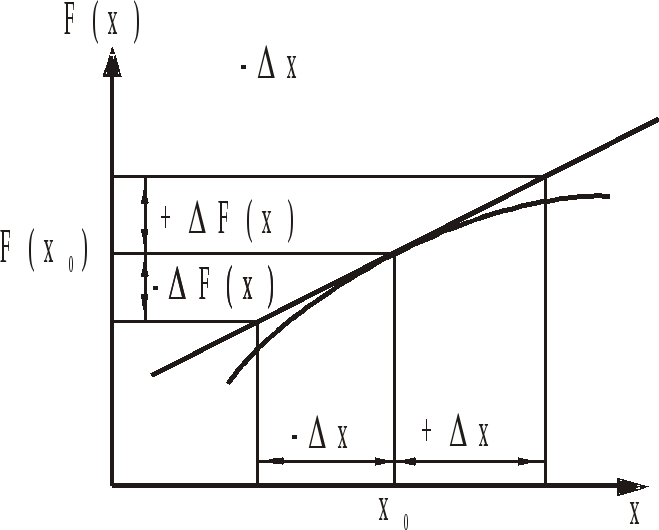
Рис.
1.7. Пример линеаризации нелинейной
функции

При
малых значениях Δx
можно ограничиться только первыми двумя
членами разложения, т.к. остальные имеют
более высокий порядок малости, т.е. можно
считать

,

где
.

Теоретически
это означает, что на интервале ±Δx
(рис. 1.6) кривая F(x)
заменяется прямой линией, являющейся
касательной при x=xo.

Таким
образом, если составлять уравнение
системы не для полных значений величин,
а только для отклонений, то эти уравнения
будут линейными. Такая операция называется
линеаризацией
уравнений.
Следует, однако, отметить, что это
справедливо только для тех случаев,
когда нелинейные функции являются
непрерывными и имеют непрерывные
производные при x=xo.

Пример
линеаризации нелинейного элемента
системы.

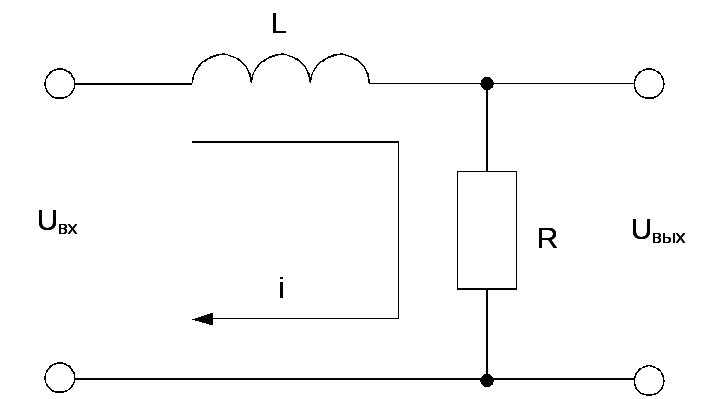
В
качестве типового элемента, уравнение
которого подлежит линеаризации, возьмем
RL-элемент,
часто встречающийся в электрических
системах регулирования и изображенный
на рис. 1.8, а). Пусть входной и выходной
величинами такого элемента являются
напряжения.

а)

б)

Рис.
1.8. Линеаризация нелинейного элемента
системы

Предположим
сначала, что активные сопротивления и
индуктивность не зависят от протекающего
через них тока, т.е. будем считать, что
элемент является линейным.

Тогда
дифференциальное уравнение элемента
в случае, если потокосцепление
катушки
элементазависит от тока линейно, т.е.
если индуктивность L=/i
не зависит от тока и является величиной
постоянной, имеет вид:

Обозначив

и
,
учитывая, что
,
и пользуясь операторной (символической)
формой записи, в которой принято
,
получим:

(1.3)

Предположим
теперь, что в рассматриваемом примере
индуктивность зависит от тока и,
следовательно, элемент является
нелинейным. Тогда уравнение (1.3) для
такого элемента неправомерно, ибо
потокосцепление
зависит от тока нелинейно и, следовательно,
L=/i
есть величина переменная. Для
усатновившегося режима элемента при
входном постоянном напряжении uвх
потокосцепление 0
тоже постоянно во времени и, следовательно,
.
Тогда можно написать:

.

Изменение
входного напряжения повлечет за собой
изменение тока и выходного напряжения.

Текущие
значения uвх
и uвых
и i
можно представить так:

;

;

,

где
Δuвх,
Δuвых
и Δi
– отклонения
соответствующих величин от их
установившихся значений.

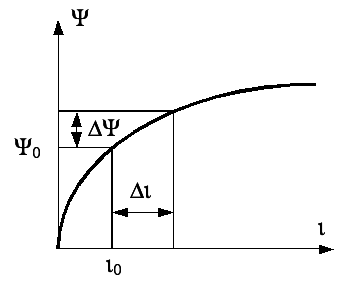
Пусть
потокосцепление является нелинейной
функцией тока, как это показано на рис.
1.8, б).
Эту функцию можно разложить в ряд:

(1.4)

При
достаточно малых отклонения тока можно
ограничиться первыми двумя членами
ряда. Величина

определяется тангенсом угла наклона
касательной к кривой, приведенной на
рис. 1.8,б), в
точке с абсциссой i0.

Обозначив
динамическую индуктивность элемента
для тока i0
через Lд,
т. е.
,
можем написать:

.

Так
как
,
то будем иметь:

.

Исходное
уравнение запишется теперь так:

,

или,
подставляя ранее найденное выражение
для uвых0,
получим:

.

Последнее
выражение является линейным дифференциальным
уравнением с постоянными коэффициентами,
которое можно записать в операторной
форме так:

(1.5)

где

и k=1.

Оно
справедливо только для малых отклонений
входной и выходной величины относительно
начального значения uвх0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Вместо введения

Системы автоматического управления (САУ) предназначены для автоматического изменения одного или нескольких параметров объекта управления с целью установления требуемого режима его работы. САУ обеспечивает поддержание постоянства заданных значений регулируемых параметров или их изменение по заданному закону либо оптимизирует определенные критерии качества управления. Например, к таким системам относятся:

  • системы стабилизации,
  • системы программного управления,
  • следящие системы

Это достаточно широкий класс систем, которые можно найти где угодно. Но какое это отношение имеет к Unity3D и вероятно к играм в частности? В принципе прямое: в любой игре так или иначе использующей симуляцию как элемент геймплея реализуются САУ, к таким играм относятся, например, Kerbal Space Programm, Digital Combat Simulator (бывший Lock On), Strike Suit Zero и т.д. (кто знает еще примеры — пишите в комментариях). В принципе любая игра, моделирующая реальные физические процессы, в том числе и просто кинематику с динамикой движения, может реализовывать те или иные САУ — этот подход проще, естественнее, а у разработчика уже есть есть набор готовых инструментов, предоставленных всякими Вышнеградскими, Ляпуновыми, Калманами, Чебышевами и прочими Коломогоровами, поэтому можно обойтись без изобретения велосипеда, т.к. его уже изобрели, да так, что получилась отдельная наука: Теория автоматического управления. Главное тут не переусердствовать. Одна тут только проблема: рассказывают про ТАУ не везде, не всем, зачастую мало и не очень понятно.

Немножко теории

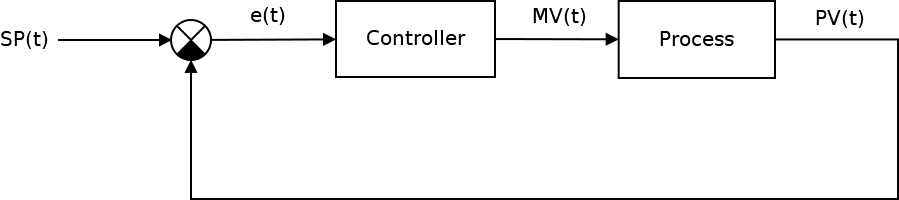
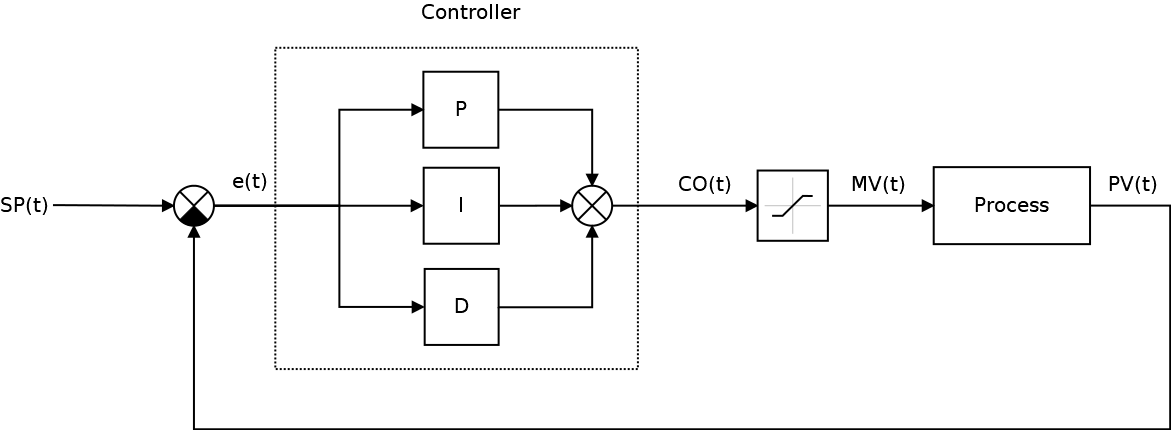
Классическая система автоматического управления представленная на следующем рисунке:

image

Ключевым элементом любой САУ является регулятор представляющий из себя устройство, которое следит за состоянием объекта управления и обеспечивает требуемый закон управления. Процесс управления включает в себя: вычисление ошибки управления или сигнала рассогласования e(t) как разницы между желаемой уставкой (set point или SP) и текущей величиной процесса (process value или PV), после чего регулятор вырабатывает управляющие сигналы (manipulated value или MV).

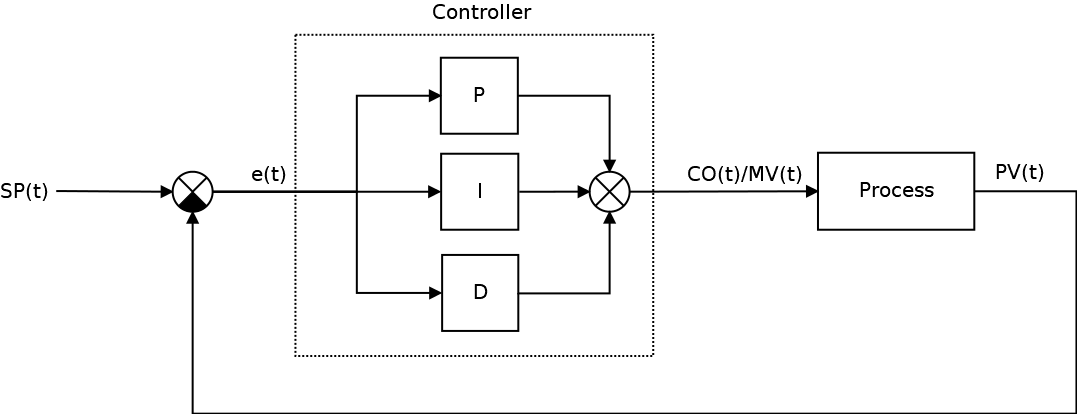
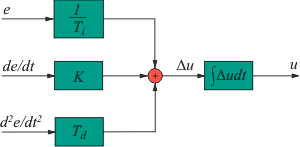
Одной из разновидностью регуляторов является пропорционально-интегрально-дифференцирующий (ПИД) регулятор, который формирует управляющий сигнал, являющийся суммой трёх слагаемых: пропорционального, интегрального и дифференциального.

image

Где, $e(t)$ ошибка рассогласования, а также, $ P = K_p cdot e(t)$ — пропорциональная, $ I = K_i cdot int_0^t e(tau)dtau$ — интегральная, $D = K_d cdot frac{de(t)}{dt}$ — дифференциальная составляющие (термы) закона управления, который в итоговом виде описывается следующими формулами

$ e(t) = SP(t) - PV(t), $

$ MV(t) = underbrace{K_p cdot e(t)}_{P} + underbrace{K_i cdot int_0^t e(tau)dtau}_{I} + underbrace{K_d cdot frac{de(t)}{dt}}_{D}, $

Пропорциональная составляющая P — отвечает за т.н. пропорциональное управление, смысл которого в том, что выходной сигнал регулятора, противодействует отклонению регулируемой величины (ошибки рассогласования или еще это называют невязкой) от заданного значения. Чем больше ошибка рассогласования, тем больше командное отклонение регулятора. Это самый простой и очевидный закон управления. Недостаток пропорционального закона управления заключается в том, что регулятор никогда не стабилизируется в заданном значении, а увеличение коэффициента пропорциональности всегда приводит к автоколебаниям. Именно поэтому в довесок к пропорциональному закону управления приходиться использовать интегральный и дифференциальный.

Интегральная составляющая I накапливает (интегрирует) ошибку регулирования, что позволяет ПИД-регулятору устранять статическую ошибку (установившуюся ошибку, остаточное рассогласование). Или другими словами: интегральное звено всегда вносит некоторое смещение и если система подвержена некоторыми постоянным ошибкам, то оно их компенсирует (за счет своего смещения). А вот если же этих ошибок нет или они пренебрежительно малы, то эффект будет обратным — интегральная составляющая сама будет вносить ошибку смещения. Именно по этой причине её не используют, например, в задачах сверхточного позиционирования. Ключевым недостатком интегрального закона управления является эффект насыщения интегратора (Integrator windup).

Дифференциальная составляющая D пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Примечательно то, что дифференциальная компонента устраняет затухающие колебания. Дифференциальное регулирование особенно эффективно для процессов, которые имеют большие запаздывания. Недостатком дифференциального закона управления является его неустойчивость к воздействую шумов (Differentiation noise).

Таким образом, в зависимости от ситуации могут применятся П-, ПД-, ПИ- и ПИД-регуляторы, но основным законом управления в основном является пропорциональный (хотя в некоторых специфических задачах и могут использоваться исключительно только звенья дифференциаторов и интеграторов).

Казалось бы, вопрос реализации ПИД-регуляторов уже давно избит и здесь на Хабре есть парочка неплохих статей на эту тему в том числе и на Unity3D, также есть неплохая статья PID Without a PhD (перевод) и цикл статей в журнале «Современные технологии автоматизации» в двух частях: первая и вторая. Также к вашим услугам статья на Википедии (наиболее полную читайте в английском варианте). А на форумах коммьюнити Unity3D нет-нет, да и всплывет PID controller как и на gamedev.stackexchange

При вопрос по реализации ПИД-регуляторов несколько глубже чем и кажется. Настолько, что юных самоделкиных, решивших, реализовать такую схему регулирования ждет немало открытий чудных, а тема актуальная. Так что надеюсь сей опус, кому-нибудь да пригодиться, поэтому приступим.

Попытка номер раз

В качестве примера попытаемся реализовать схему регулирования на примере управления поворотом в простенькой космической 2D-аркаде, по шагам, начиная с самого начала (не забыли, что это туториал?).

Почему не 3D? Потому что реализация не измениться, за исключением того, что придется воротить ПИД-регулятор для контроля тангажа, рысканья и крена. Хотя вопрос корректного применения ПИД-регулирования вместе с кватернионами действительно интересный, возможно в будущем его и освящу, но даже в NASA предпочитают углы Эйлера вместо кватернионов, так что обойдемся простенькой моделью на двухмерной плоскости.

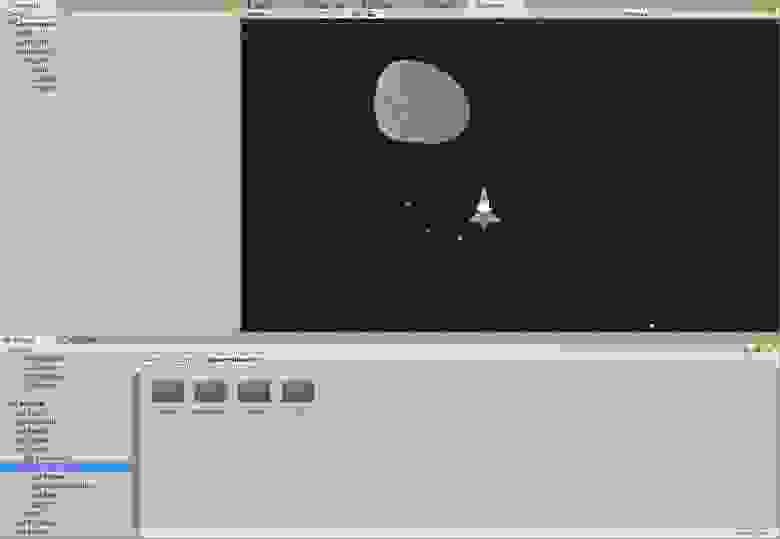
Для начала создадим сам объект игровой объект космического корабля, который будет состоять из собственно самого объекта корабля на верхнем уровне иерархии, прикрепим к нему дочерний объект Engine (чисто спецэффектов ради). Вот как это выглядит у меня:

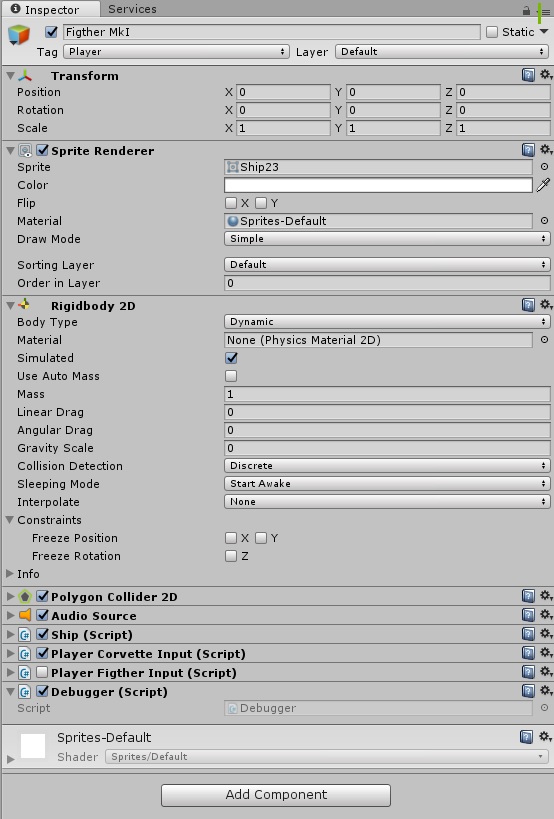
image

А на сам объект космического корабля накидаем в инспекторе всяческих компонент. Забегая вперед, приведу скрин того, как он будет выглядеть в конце:

image
Но это потом, а пока в нем еще нет никаких скриптов, только стандартный джентльменский набор: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (зачем?).

Собственно физика у нас сейчас самое главное и управление будет осуществляться исключительно через неё, в противном случае, применение ПИД-регулятора потеряло бы смысл. Масса нашего космического корабля оставим также в 1 кг, а все коэффициенты трения и гравитации равны нулю — в космосе же.

Т.к. помимо самого космического корабля есть куча других, менее умных космических объектов, то сначала опишем родительский класс BaseBody, который в себе будет содержать ссылки на на наши компоненты, методы инициализации и уничтожения, а также ряд дополнительных полей и методов, например для реализации небесной механики:

BaseBody.cs

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

namespace Assets.Scripts.SpaceShooter.Bodies
{
    [RequireComponent(typeof(SpriteRenderer))]
    [RequireComponent(typeof(AudioSource))]
    [RequireComponent(typeof(Rigidbody2D))]
    [RequireComponent(typeof(Collider2D))]

    public class BaseBody : MonoBehaviour
    {
        readonly float _deafultTimeDelay = 0.05f;

[HideInInspector]
        public static List<BaseBody> _bodies = new List<BaseBody>();

        #region RigidBody

        [HideInInspector]
        public Rigidbody2D _rb2d;

        [HideInInspector]
        public Collider2D[] _c2d;

        #endregion

        #region References

        [HideInInspector]
        public Transform _myTransform;

        [HideInInspector]
        public GameObject _myObject;

        /// <summary>
        /// Объект, который появляется при уничтожении
        /// </summary>
        public GameObject _explodePrefab;

        #endregion

        #region  Audio

        public AudioSource _audioSource;

        /// <summary>
        /// Звуки, которые проигрываются при получении повреждения
        /// </summary>
        public AudioClip[] _hitSounds;

        /// <summary>
        /// Звуки, которые проигрываются при появлении объекта
        /// </summary>
        public AudioClip[] _awakeSounds;

        /// <summary>
        /// Звуки, которые воспроизводятся перед смертью
        /// </summary>
        public AudioClip[] _deadSounds;

        #endregion

        #region External Force Variables
        /// <summary>
        /// Внешние силы воздйствующие на объект
        /// </summary>
        [HideInInspector]
        public Vector2 _ExternalForces = new Vector2();

        /// <summary>
        /// Текущий вектор скорости
        /// </summary>
        [HideInInspector]
        public Vector2 _V = new Vector2();

        /// <summary>
        /// Текущий вектор силы гравитации
        /// </summary>
        [HideInInspector]
        public Vector2 _G = new Vector2();
        #endregion

        public virtual void Awake()
        {
            Init();
        }

        public virtual void Start()
        {

        }

        public virtual void Init()
        {
            _myTransform = this.transform;
            _myObject = gameObject;

            _rb2d = GetComponent<Rigidbody2D>();
            _c2d = GetComponentsInChildren<Collider2D>();
            _audioSource = GetComponent<AudioSource>();

            PlayRandomSound(_awakeSounds);

            BaseBody bb = GetComponent<BaseBody>();
            _bodies.Add(bb);
        }

        /// <summary>
        /// Уничтожение персонажа
        /// </summary>
        public virtual void Destroy()
        {
            _bodies.Remove(this);
            for (int i = 0; i < _c2d.Length; i++)
            {
                _c2d[i].enabled = false;
            }
            float _t = PlayRandomSound(_deadSounds);
            StartCoroutine(WaitAndDestroy(_t));
        }

        /// <summary>
        /// Ждем некоторое время перед уничтожением
        /// </summary>
        /// <param name="waitTime">Время ожидания</param>
        /// <returns></returns>
        public IEnumerator WaitAndDestroy(float waitTime)
        {
            yield return new WaitForSeconds(waitTime);

            if (_explodePrefab)
            {
                Instantiate(_explodePrefab, transform.position, Quaternion.identity);
            }

            Destroy(gameObject, _deafultTimeDelay);
        }

        /// <summary>
        /// Проигрывание случайного звука
        /// </summary>
        /// <param name="audioClip">Массив звуков</param>
        /// <returns>Длительность проигрываемого звука</returns>
        public float PlayRandomSound(AudioClip[] audioClip)
        {
            float _t = 0;
            if (audioClip.Length > 0)
            {
                int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
                AudioClip _audioClip = audioClip[_i];
                _t = _audioClip.length;
                _audioSource.PlayOneShot(_audioClip);
            }
            return _t;
        }

        /// <summary>
        /// Получение урона
        /// </summary>
        /// <param name="damage">Уровень урона</param>
        public virtual void Damage(float damage)
        {
            PlayRandomSound(_hitSounds);
        }

    }
}

Вроде описали все что надо, даже больше чем нужно (в рамках этой статьи). Теперь отнаследуем от него класс корабля Ship, который должен уметь двигаться и поворачивать:

SpaceShip.cs

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

namespace Assets.Scripts.SpaceShooter.Bodies
{
    public class Ship : BaseBody
    {
        public Vector2 _movement = new Vector2();
        public Vector2 _target = new Vector2();
        public float _rotation = 0f;

        public void FixedUpdate()
        {
            float torque = ControlRotate(_rotation);
            Vector2 force = ControlForce(_movement);

            _rb2d.AddTorque(torque);
            _rb2d.AddRelativeForce(force);
        }

        public float ControlRotate(Vector2 rotate)
        {
            float result = 0f;

            return result;
        }

        public Vector2 ControlForce(Vector2 movement)
        {
            Vector2 result = new Vector2();

            return result;

        }
    }
}

Пока в нем нет ничего интересно, на текущий момент это просто класс-заглушка.

Также опишем базовый(абстрактный) класс для всех контроллеров ввода BaseInputController:

BaseInputController.cs

using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;

namespace Assets.Scripts.SpaceShooter.InputController
{
    public enum eSpriteRotation
    {
        Rigth = 0,
        Up = -90,
        Left = -180,
        Down = -270
    }

    public abstract class BaseInputController : MonoBehaviour
    {
        public GameObject _agentObject;
        public Ship _agentBody; // Ссылка на компонент логики корабля
        public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной 
                                                                           // ориентации спрайта "вверх" вместо "вправо"

        public abstract void ControlRotate(float dt);
        public abstract void ControlForce(float dt);

        public virtual void Start()
        {
            _agentObject = gameObject;
            _agentBody = gameObject.GetComponent<Ship>();
        }

        public virtual void FixedUpdate()
        {
            float dt = Time.fixedDeltaTime;
            ControlRotate(dt);
            ControlForce(dt);
        }

        public virtual void Update()
        {
            //TO DO
        }
    }
}

И наконец, класс контроллера игрока PlayerFigtherInput:

PlayerInput.cs

using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;

namespace Assets.Scripts.SpaceShooter.InputController
{
    public class PlayerFigtherInput : BaseInputController
    {
        public override void ControlRotate(float dt)
        {
            // Определяем позицию мыши относительно игрока
            Vector3 worldPos = Input.mousePosition;
            worldPos = Camera.main.ScreenToWorldPoint(worldPos);

            // Сохраняем координаты указателя мыши
            float dx = -this.transform.position.x + worldPos.x;
            float dy = -this.transform.position.y + worldPos.y;

            //Передаем направление
            Vector2 target = new Vector2(dx, dy);
            _agentBody._target = target;

            //Вычисляем поворот в соответствии с нажатием клавиш
            float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
            _agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
        }

        public override void ControlForce(float dt)
        {
            //Передаем movement
            _agentBody._movement = Input.GetAxis("Vertical") * Vector2.up 
                + Input.GetAxis("Horizontal") * Vector2.right;
        }
    }
}

Вроде бы закончили, теперь наконец можно перейти к тому, ради чего все это затевалось, т.е. ПИД-регуляторам (не забыли надеюсь?). Его реализация кажется простой до безобразия:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Assets.Scripts.Regulator
{
    [System.Serializable] // Этот атрибут необходим для того что бы поля регулятора 
                                   // отображались в инспекторе и сериализовывались
    public class SimplePID
    {
        public float Kp, Ki, Kd;

        private float lastError;
        private float P, I, D;

        public SimplePID()
        {
            Kp = 1f;
            Ki = 0;
            Kd = 0.2f;
        }

        public SimplePID(float pFactor, float iFactor, float dFactor)
        {
            this.Kp = pFactor;
            this.Ki = iFactor;
            this.Kd = dFactor;
        }

        public float Update(float error, float dt)
        {
            P = error;
            I += error * dt;
            D = (error - lastError) / dt;
            lastError = error;

            float CO = P * Kp + I * Ki + D * Kd;

            return CO;
        }
    }
}

Значения коэффициентов по умолчанию возьмем с потолка: это будет тривиальный единичный коэффициент пропорционального закона управления Kp = 1, небольшое значение коэффициента для дифференциального закона управления Kd = 0.2, который должен устранить ожидаемые колебания и нулевое значение для Ki, которое выбрано потому, что в нашей программной модели нет никаких статичных ошибок (но вы всегда можете их внести, а потом героически побороться с помощью интегратора).

Теперь вернемся к нашему классу SpaceShip и попробуем заюзать наше творение в качестве регулятора поворота космического корабля в методе ControlRotate:

 public float ControlRotate(Vector2 rotate)
 {
      float MV = 0f;
      float dt = Time.fixedDeltaTime;

      //Вычисляем ошибку
      float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);

      //Получаем корректирующее ускорение
      MV = _angleController.Update(angleError, dt);

      return MV;
 }

ПИД-регулятор будет осуществлять точное угловое позиционировая космического корабля только за счет крутящего момента. Все честно, физика и САУ, почти как в реальной жизни.

И без этих ваших Quaternion.Lerp

 if (!_rb2d.freezeRotation)
     rb2d.freezeRotation = true;

 float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
 float T = dt *  Mathf.Abs( _rotationSpeed / deltaAngle);

 // Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
                _myTransform.rotation,
                Quaternion.Euler(new Vector3(0, 0, targetAngle)),
                T);

 // Изменяем поворот объекта
 _myTransform.rotation = rot;

Получившейся исходный код Ship.cs под спойлером

using UnityEngine;
using Assets.Scripts.Regulator;

namespace Assets.Scripts.SpaceShooter.Bodies
{
    public class Ship : BaseBody
    {
        public GameObject _flame;

        public Vector2 _movement = new Vector2();
        public Vector2 _target = new Vector2();

        public float _targetAngle = 0f;
        public float _angle = 0f;

        [Header("PID")]
        public SimplePID _angleController = new SimplePID();

        public void FixedUpdate()
        {
            float torque = ControlRotate(_targetAngle);
            Vector2 force = ControlForce(_movement);

            _rb2d.AddTorque(torque);
            _rb2d.AddRelativeForce(force);
        }

        public float ControlRotate(float rotate)
        {
            float MV = 0f;
            float dt = Time.fixedDeltaTime;

            _angle = _myTransform.eulerAngles.z;

            //Вычисляем ошибку
            float angleError = Mathf.DeltaAngle(_angle, rotate);

            //Получаем корректирующее ускорение
            MV = _angleController.Update(angleError, dt);

            return MV;
        }

        public Vector2 ControlForce(Vector2 movement)
        {
            Vector2 MV = new Vector2();

            //Кусок кода спецэффекта работающего двигателя ради
            if (movement != Vector2.zero)
            {
                if (_flame != null)
                {
                    _flame.SetActive(true);
                }
            }
            else
            {
                if (_flame != null)
                {
                    _flame.SetActive(false);
                }
            }

            MV = movement;
            return MV;
        }
    }
}

Все? Расходимся по домам?

WTF! Что происходит? Почему корабль поворачивается как-то странно? И почему он так резко отскакивает от других объектов? Неужели этот глупый ПИД-регулятор не работает?

Без паники! Давайте попробуем разобраться что происходит.

В момент получения нового значения SP, происходит резкий (ступенчатый) скачок рассогласования ошибки, которая, как мы помним, вычисляется вот так: $e(t) = SP(t) - PV(t), $ соответственно происходит резкий скачок производной ошибки $frac{de(t)}{dt}$, которую мы вычисляем в этой строчке кода:

D = (error - lastError) / dt;

Можно, конечно, попробовать другие схемы дифференцирования, например, трехточечную, или пятиточечную, или… но все равно это не поможет. Ну вот не любят производные резких скачков — в таких точках функция не является дифференцируемой. Однако поэкспериментировать с разными схемами дифференцирования и интегрирования стоит, но потом и не в этой статье.

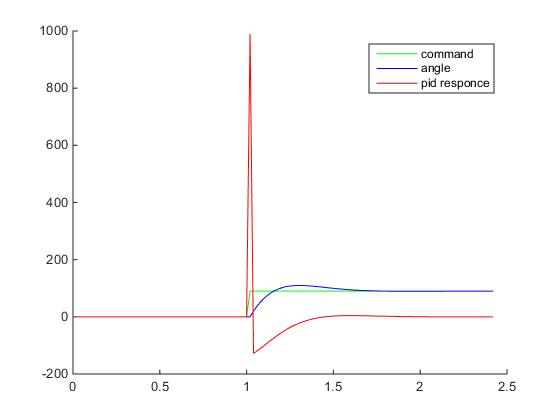
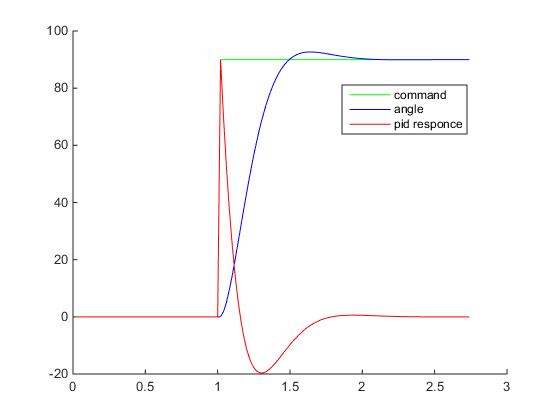
Думаю что настал момент построить графики переходного процесса: ступенчатое воздействие от S(t) = 0 в SP(t) = 90 градусов для тела массой в 1 кг, длинной плеча силы в 1 метр и шагом сетки дифференцирования 0.02 с — прям как в нашем примере на Unity3D (на самом деле не совсем, при построении этих графиков не учитывалось, что момент инерции зависит от геометрии твердого тела, поэтому переходный процесс будет немножко другой, но все же достаточно похожий для демонстрации). Все величены на грифике приведены в абсолютных значениях:
image
Хм, что здесь происходит? Куда улетел отклик ПИД-регулятора?

Поздравляю, мы только что столкнулись с таким явлением как «удар» (kick). Очевидно, что в момент времени, когда процесс еще PV = 0, а уставка уже SP = 90, то при численном дифференцировании получим значение производной порядка 4500, которое умножится на Kd=0.2 и сложится с пропорциональным теромом, так что на выходе мы получим значение углового ускорения 990, а это уже форменное надругательство над физической моделью Unity3D (угловые скорости будут достигать 18000 град/с… я думаю это предельное значение угловой скорости для RigidBody2D).

  • Может стоит подобрать коэффициенты ручками, так чтобы скачок был не таким сильным?
  • Нет! Самое лучше чего мы таким образом сможем добиться — небольшая амплитуда скачка производной, однако сам скачок как был так и останется, при этом можно докрутиться до полной неэффективности дифференциальной составляющей.

Впрочем можете поэкспериментировать.

Попытка номер два. Сатурация

Логично, что привод (в нашем случае виртуальные маневровые двигатели SpaceShip), не может отрабатывать сколько угодно большие значения которые может выдать наш безумный регулятор. Так что первое что мы сделаем — сатурируем выход регулятора:

public float ControlRotate(Vector2 rotate, float thrust)
{
    float CO = 0f;
    float MV = 0f;
    float dt = Time.fixedDeltaTime;

    //Вычисляем ошибку
    float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);

    //Получаем корректирующее ускорение
    CO = _angleController.Update(angleError, dt);

    //Сатурируем
    MV = CO;
    if (MV > thrust) MV = thrust;
    if (MV< -thrust) MV = -thrust;

    return MV;
}

А очередной раз переписанный класс Ship полностью выглядит так

namespace Assets.Scripts.SpaceShooter.Bodies
{
    public class Ship : BaseBody
    {
        public GameObject _flame;

        public Vector2 _movement = new Vector2();
        public Vector2 _target = new Vector2();

        public float _targetAngle = 0f;
        public float _angle = 0f;

        public float _thrust = 1f;

        [Header("PID")]
        public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);

        public void FixedUpdate()
        {
            _torque = ControlRotate(_targetAngle, _thrust);
            _force = ControlForce(_movement);

            _rb2d.AddTorque(_torque);
            _rb2d.AddRelativeForce(_force);
        }

        public float ControlRotate(float targetAngle, float thrust)
        {
            float CO = 0f;
            float MV = 0f;
            float dt = Time.fixedDeltaTime;

            //Вычисляем ошибку
            float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);

            //Получаем корректирующее ускорение
            CO = _angleController.Update(angleError, dt);

            //Сатурируем
            MV = CO;
            if (MV > thrust) MV = thrust;
            if (MV< -thrust) MV = -thrust;

            return MV;
        }

        public Vector2 ControlForce(Vector2 movement)
        {
            Vector2 MV = new Vector2();

            if (movement != Vector2.zero)
            {
                if (_flame != null)
                {
                    _flame.SetActive(true);
                }
            }
            else
            {
                if (_flame != null)
                {
                    _flame.SetActive(false);
                }
            }

            MV = movement * _thrust;

            return MV;
        }

        public void Update()
        {

        }        
    }
}

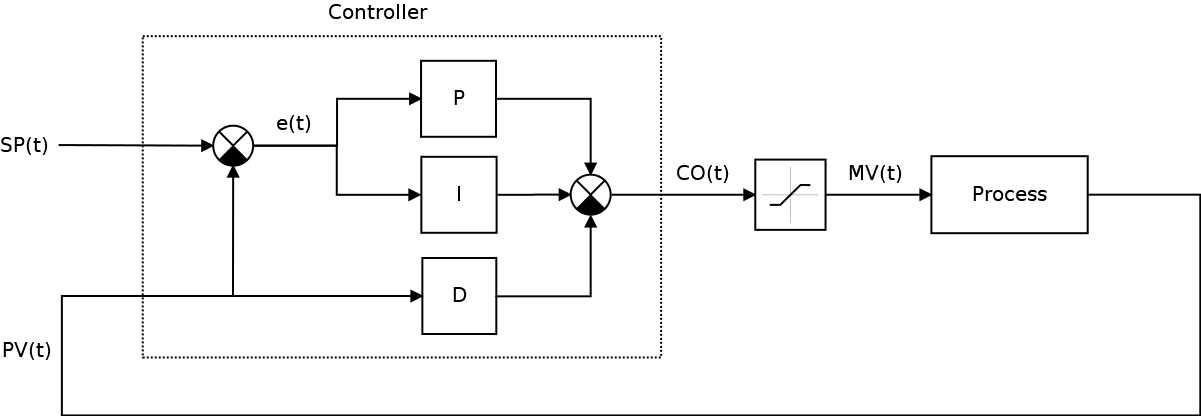
Итоговая схема нашего САУ тогда станет уже вот такой
image

При этом уже становится понятно, что выход контроллера CO(t) немного не одно и тоже, что управляемая величина процесса MV(t).

Собственно с этого места можно уже добавлять новую игровую сущность — привод, через которую и будет осуществляться управление процессом, логика работы которой может быть более сложной, чем просто Mathf.Clamp(), например, можно ввести дискретизацию значений (дабы не перегружать игровую физику величинами идущими шестыми после запятой), мертвую зону (опять таки не имеет смысл перегружать физику сверхмалыми реакциями), ввести задержку в упраление и нелинейность (например, сигмоиду) привода, после чего посмотреть, что из этого получится.

Запустив игру, мы обнаружим, что космический корабль стал наконец управляемым:

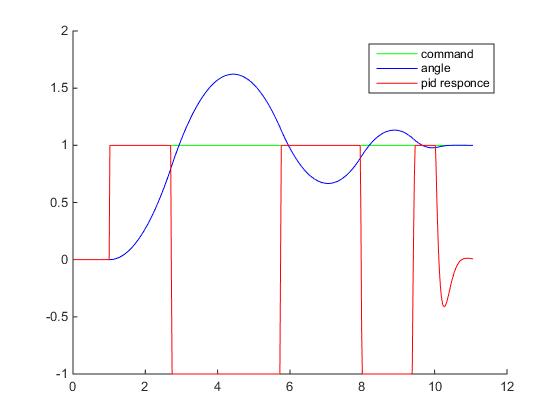
Если построить графики, то можно увидеть, что реакция контроллера стала уже вот такой:
image
Здесь уже используются нормированные величены, углы поделены на значение SP, а выход контроллера отнормирован относительно максимального значения на котором уже происходит сатурация.

Теперь на графике видно наличие ошибки перерегулирования (overshooting) и затухающие колебания. Уменьшая Kp и увеличивая Kd можно добиться уменьшения колебаний, но зато увеличится время реакции контроллера (скорость поворота корабля). И наоборот, увеличивая Kp и уменьшая Kd — можно добиться увеличения скорости реакции контроллера, но появятся паразитные колебания, которые при определенных (критических) значениях, перестанут быть затухающими.

Ниже приведена известна таблица влияния увеличения параметров ПИД-регулятора (как уменьшить шрифт, а то таблица безе переносов не лезет?):

А общий алгоритм ручной настройки ПИД-регулятора следующий:

  1. Подбираем пропорциональный коэффициенты при отключенных дифференциальных и интегральных звеньях до тех пор пока не начнутся автоколебания.
  2. Постепенно увеличивая дифференциальную составляющую избавляемся от автоколебаний
  3. Если наблюдается остаточная ошибка регулирования (смещение), то устраняем её за счет интегральной составляющей.

Каких-то общих значений параметров ПИД-регулятора нет: конкретные значения зависят исключительно от параметров процесса (его передаточной характеристики): ПИД-регулятор отлично работающий с одним объектом управления окажется неработоспособным с другим. Более того, коэффициенты при пропорциональной, интегральной и дифференциальной составляющих еще и взаимозависимы.

В общем не будем о грустном, дальше нас ждет самое интересное…

Попытка номер три. Еще раз производные

Приделав костыль в виде ограничения значений выхода контроллера мы так и не решили самую главную проблему нашего регулятора — дифференциальная составляющая плохо себя чувствует при ступенчатом изменении ошибки на входе регуляторе. На самом деле есть множество других костылей, например, в момент скачкообразного изменения SP «отключать» дифференциальную составляющую или же поставить фильтры нижних частот между SP(t) и операцией $SP(t)-PV(t)$ за счет которого будет происходить плавное нарастание ошибки, а можно совсем развернуться и впендюрить самый настоящий фильтр Калмана для сглаживания входных данных. В общем костылей много, и добавить наблюдателя конечно хотелось бы, но не в этот раз.

Поэтому снова вернемся к производной ошибки рассогласования и внимательно на неё посмотрим:

$ frac{de(t)}{dt} = frac{d(SP(t)-PV(t))}{dt} = frac{dSP(t)}{dt} - frac{dPV(t)}{dt}, $

Ничего не заметили? Если хорошенько присмотреться, то можно обнаружить, что вообще-то SP(t), не меняется во времени (за исключением моментов ступенчатого изменения, когда регулятор получает новую команду), т.е. её производная равна нулю:

$ frac{dSP(t)}{dt} = 0, $

тогда

$ frac{de(t)}{dt} = - frac{dPV(t)}{dt}, $

Иными словами, вместо производной ошибки, которая дифференцируема не везде мы можем использовать производную от процесса, который в мире классической механики как правило непрерывен и дифференцируем везде, а схема нашей САУ уже приобретет следующий вид:
image

$ e(t) = SP(t) - PV(t), $

$ CO(t) = underbrace{K_p cdot e(t)}_{P} + underbrace{K_i cdot int_0^t e(tau)dtau}_{I} - underbrace{K_d cdot frac{dPV(t)}{dt}}_{D}, $

Модифицируем код регулятора:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Assets.Scripts.Regulator
{
    [System.Serializable]
    public class SimplePID
    {
        public float Kp, Ki, Kd;
        private float P, I, D;

        private float lastPV = 0f;   

        public SimplePID()
        {
            Kp = 1f;
            Ki = 0f;
            Kd = 0.2f;
        }

        public SimplePID(float pFactor, float iFactor, float dFactor)
        {
            this.Kp = pFactor;
            this.Ki = iFactor;
            this.Kd = dFactor;
        }

        public float Update(float error, float PV, float dt)
        {
            P = error;
            I += error * dt;
            D = -(PV - lastPV) / dt;

            lastPV = PV;

            float CO = Kp * P + Ki * I + Kd * D;

            return CO;
        }
    }
}

И немного изменим метод ControlRotate:

public float ControlRotate(Vector2 rotate, float thrust)
{
     float CO = 0f;
     float MV = 0f;
     float dt = Time.fixedDeltaTime;

     //Вычисляем ошибку
     float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);

     //Получаем корректирующее ускорение
     CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);

     //Сатурируем
     MV = CO;
     if (CO > thrust) MV = thrust;
     if (CO < -thrust) MV = -thrust;

     return MV;
}

И-и-и-и… если запустить игру, то обнаружиться, что на самом деле ничего ничего не изменилось с последней попытки, что и требовалось доказать. Однако, если убрать сатурацию, то график реакции регулятора будет выглядеть вот так:
image
Скачок CO(t) по прежнему присутствует, однако он уже не такой большой как был в самом начале, а самое главное — он стал предсказуемым, т.к. обеспечивается исключительно пропорциональной составляющей, и ограничен максимально возможной ошибкой рассогласования и пропорциональным коэффициентом ПИД-регулятора (а это уже намекает на то, что Kp имеет смысл выбрать все же меньше единицы, например, 1/90f), но не зависит от шага сетки дифференцирования (т.е. dt). В общем, я настоятельно рекомендую использовать именно производную процесса, а не ошибки.

Думаю теперь никого не удивит, но таким же макаром можно заменить $K_p cdot e(t)$ на $-K_p cdot PV(t)$, однако останавливаться на этом мы не будем, можете сами поэкспериментировать и рассказать в комментариях, что из этого получилось (самому интересно)

Попытка номер четыре. Альтернативные реализации ПИД-регулятор

Помимо описанного выше идеального представления ПИД-регулятора, на практике часто применяется стандартная форма, без коэффициентов Ki и Kd, вместо которых используются временные постоянные.

Такой подход связан с тем, что ряд методик настройки ПИД-регулятора основан на частотных характеристиках ПИД-регулятора и процесса. Собственно вся ТАУ и крутится вокруг частотных характеристик процессов, поэтому для желающих углубиться, и, внезапно, столкнувшихся с альтернативной номенклатурой, приведу пример т.н. стандартной формы ПИД-регулятора:

$ e(t) = SP(t) - PV(t), $

$ CO(t) =CO_{bias} + K_p cdot Bigl(e(t) + frac{1}{T_i} cdot int_0^t e(tau)dtau - T_d cdot frac{dPV(t)}{dt} Bigl), $

где, $T_d= frac{K_d}{K_p}$ — постоянная дифференцирования, влияющая на прогнозирование состояния системы регулятором,
$T_i = frac{K_p}{K_i}$ — постоянная интегрирования, влияющая на интервал усреднения ошибки интегральным звеном.

Основные принципы настройки ПИД-регулятора в стандартной форме аналогичны идеализированному ПИД-регулятору:

  • увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
  • с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
  • уменьшение постоянной интегрирования уменьшает запас устойчивости;
  • увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие

Исходный код стандартной формы, вы можете найти под спойлером

namespace Assets.Scripts.Regulator
{
    [System.Serializable]    
    public class StandartPID
    {
        public float Kp, Ti, Td;
        public float error, CO;
        public float P, I, D;

        private float lastPV = 0f;

        public StandartPID()
        {
            Kp = 0.1f;
            Ti = 10000f;
            Td = 0.5f;
            bias = 0f;
        }

        public StandartPID(float Kp, float Ti, float Td)
        {
            this.Kp = Kp;
            this.Ti = Ti;
            this.Td = Td;
        }

        public float Update(float error, float PV, float dt)
        {
            this.error = error;
            P = error;
            I += (1 / Ti) * error * dt;
            D = -Td * (PV - lastPV) / dt;

            CO = Kp * (P + I + D);
            lastPV = PV;

            return CO;
        }
    }
}

В качестве значений по умолчанию, выбраны Kp = 0.01, Ti = 10000, Td = 0.5 — при таких значениях корабль поворачивается достаточно быстро и обладает некоторым запасом устойчивости.

Помимо такой формы ПИД-регулятора, часто используется т.н. реккурентная форма:

$ CO(t_k)=CO(t_{k-1})+K_pleft[left(1+dfrac{Delta t}{T_i}+dfrac{T_d}{Delta t}right)e(t_k)+left(-1-dfrac{2T_d}{Delta t}right)e(t_{k-1})+dfrac{T_d}{Delta t}e(t_{k-2})right] $

Не будем на ней останавливаться, т.к. она актуальна прежде всего для хардверных программистов, работающих с FPGA и микроконтроллерами, где такая реализация значительно удобнее и эффективнее. В нашем же случае — давайте что-нибудь сваям на Unity3D — это просто еще одна реализация ПИД-контроллера, которая ни чем не лучше других и даже менее понятная, так что еще раз дружно порадуемся как хорошо программировать в уютненьком C#, а не в жутком и страшном VHDL, например.

Вместо заключения. Куда бы еще присобачить ПИД-регулятор

Теперь попробуем немного усложнить управление корабля используя двухконтурное управление: один ПИД-регулятор, уже знакомый нам _angleController, отвечает по прежнему за угловое позиционирование, а вот второй — новый, _angularVelocityController — контролирует скорость поворота:

public float ControlRotate(float targetAngle, float thrust)
{
    float CO = 0f;
    float MV = 0f;
    float dt = Time.fixedDeltaTime;

    _angle = _myTransform.eulerAngles.z;

    //Контроллер угла поворота
    float angleError = Mathf.DeltaAngle(_angle, targetAngle);
    float torqueCorrectionForAngle = 
    _angleController.Update(angleError, _angle, dt);

    //Контроллер стабилизации скорости
    float angularVelocityError = -_rb2d.angularVelocity;
    float torqueCorrectionForAngularVelocity = 
        _angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);

    //Суммарный выход контроллера
    CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;

    //Дискретизируем с шагом 100            
    CO = Mathf.Round(100f * CO) / 100f;

    //Сатурируем
    MV = CO;
    if (CO > thrust) MV = thrust;
    if (CO < -thrust) MV = -thrust;

    return MV;
}

Назначение второго регулятора — гашение избыточных угловых скоростей, за счет изменения крутящего момента — это сродни наличию углового трения, которое мы отключили еще при создании игрового объекта. Такая схема управления [возможно] позволит получить более стабильное поведение корабля, и даже обойтись только пропорциональными коэффициентами управления — второй регулятор будет гасить все колебания, выполняя функцию, аналогичную дифференциальной составляющей первого регулятора.

Помимо этого, добавим новый класс ввода игрока — PlayerInputCorvette, в котором повороты буду осуществляться уже за счет нажатия клавиш «вправо-влево», а целеуказание с помощью мыши мы оставим для чего-нибудь более полезного, например, для управления турелью. Заодно у нас теперь появился такой параметр как _turnRate — отвечающий за скорость/отзывчивость поворота (не понятно только куда его поместить лучше в InputCOntroller или все же Ship). 

public class PlayerCorvetteInput : BaseInputController
{
     public float _turnSpeed = 90f;

     public override void ControlRotate()
     {
         // Находим указатель мыши
         Vector3 worldPos = Input.mousePosition;
         worldPos = Camera.main.ScreenToWorldPoint(worldPos);

         // Сохраняем относительные координаты указателя мыши
         float dx = -this.transform.position.x + worldPos.x;
         float dy = -this.transform.position.y + worldPos.y;

         //Передаем направление указателя мыши
         Vector2 target = new Vector2(dx, dy);
         _agentBody._target = target;

         //Вычисляем поворот в соответствии с нажатием клавиш
         _agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
    }

    public override void ControlForce()
    {            
         //Передаем movement
         _agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
    }
}

Также для наглядности накидаем на коленках скрипт для отображения отладочной информации

namespace Assets.Scripts.SpaceShooter.UI
{
    [RequireComponent(typeof(Ship))]
    [RequireComponent(typeof(BaseInputController))]
    public class Debugger : MonoBehaviour
    {
        Ship _ship;
        BaseInputController _controller;
        List<SimplePID> _pids = new List<SimplePID>();
        List<string> _names = new List<string>();

        Vector2 _orientation = new Vector2();

        // Use this for initialization
        void Start()
        {
            _ship = GetComponent<Ship>();
            _controller = GetComponent<BaseInputController>();

            _pids.Add(_ship._angleController);
            _names.Add("Angle controller");

            _pids.Add(_ship._angularVelocityController);
            _names.Add("Angular velocity controller");

        }

        // Update is called once per frame
        void Update()
        {
            DrawDebug();
        }

        Vector3 GetDiretion(eSpriteRotation spriteRotation)
        {
            switch (_controller._spriteOrientation)
            {
                case eSpriteRotation.Rigth:
                    return transform.right;
                case eSpriteRotation.Up:
                    return transform.up;
                case eSpriteRotation.Left:
                    return -transform.right;
                case eSpriteRotation.Down:
                    return -transform.up;
            }
            return Vector3.zero;
        }

        void DrawDebug()
        {
            //Направление поворота
            Vector3 vectorToTarget = transform.position 
                + 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad), 
                    Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);

            // Текущее направление
            Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);

            //Угловое ускорение
            Vector3 torque = heading - transform.right * _ship._Torque;

            Debug.DrawLine(transform.position, vectorToTarget, Color.white);
            Debug.DrawLine(transform.position, heading, Color.green);
            Debug.DrawLine(heading, torque, Color.red);
        }

        void OnGUI()
        {
            float x0 = 10;
            float y0 = 100;

            float dx = 200;
            float dy = 40;

            float SliderKpMax = 1;
            float SliderKpMin = 0;
            float SliderKiMax = .5f;
            float SliderKiMin = -.5f;
            float SliderKdMax = .5f;
            float SliderKdMin = 0;

            int i = 0;
            foreach (SimplePID pid in _pids)
            {
                y0 += 2 * dy;

                GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");

                pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10), 
                    pid.Kp, 
                    SliderKpMin, 
                    SliderKpMax);
                pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10), 
                    pid.Ki, 
                    SliderKiMin, 
                    SliderKiMax);
                pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10), 
                    pid.Kd, 
                    SliderKdMin, 
                    SliderKdMax);

                GUIStyle style1 = new GUIStyle();
                style1.alignment = TextAnchor.MiddleRight;
                style1.fontStyle = FontStyle.Bold;
                style1.normal.textColor = Color.yellow;
                style1.fontSize = 9;

                GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
                GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
                GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);

                GUIStyle style2 = new GUIStyle();
                style2.alignment = TextAnchor.MiddleLeft;
                style2.fontStyle = FontStyle.Bold;
                style2.normal.textColor = Color.yellow;
                style2.fontSize = 9;

                GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
                GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
                GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);

                GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
            }
        }
    }
}

Класс Ship также претерпел необратимые мутации и теперь должен выглядеть вот так:

namespace Assets.Scripts.SpaceShooter.Bodies
{
    public class Ship : BaseBody
    {
        public GameObject _flame;

        public Vector2 _movement = new Vector2();
        public Vector2 _target = new Vector2();

        public float _targetAngle = 0f;
        public float _angle = 0f;

        public float _thrust = 1f;

        [Header("PID")]
        public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
        public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);

        private float _torque = 0f;
        public float _Torque
        {
            get
            {
                return _torque;
            }
        }

        private Vector2 _force = new Vector2();
        public Vector2 _Force
        {
            get
            {
                return _force;
            }
        }

        public void FixedUpdate()
        {
            _torque = ControlRotate(_targetAngle, _thrust);
            _force = ControlForce(_movement, _thrust);

            _rb2d.AddTorque(_torque);
            _rb2d.AddRelativeForce(_force);
        }

        public float ControlRotate(float targetAngle, float thrust)
        {
            float CO = 0f;
            float MV = 0f;
            float dt = Time.fixedDeltaTime;

            _angle = _myTransform.eulerAngles.z;

            //Контроллер угла поворота
            float angleError = Mathf.DeltaAngle(_angle, targetAngle);
            float torqueCorrectionForAngle = 
                _angleController.Update(angleError, _angle, dt);

            //Контроллер стабилизации скорости
            float angularVelocityError = -_rb2d.angularVelocity;
            float torqueCorrectionForAngularVelocity = 
                _angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);

            //Суммарный выход контроллера
            CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;

            //Дискретизируем с шагом 100            
            CO = Mathf.Round(100f * CO) / 100f;

            //Сатурируем
            MV = CO;
            if (CO > thrust) MV = thrust;
            if (CO < -thrust) MV = -thrust;

            return MV;
        }

        public Vector2 ControlForce(Vector2 movement, float thrust)
        {
            Vector2 MV = new Vector2();

            if (movement != Vector2.zero)
            {
                if (_flame != null)
                {
                    _flame.SetActive(true);
                }
            }
            else
            {
                if (_flame != null)
                {
                    _flame.SetActive(false);
                }
            }

            MV = movement * thrust;

            return MV;
        }

        public void Update()
        {

        }        
    }
}

А вот, собственно заключительное видео того, что должно получиться:

К сожалению получилось охватить не все, что хотелось бы, в частности почти не затронут вопрос настройки ПИД-регулятора и практически не освящена интегральная составляющая — фактически приведен пример только для ПД-регулятора. Собственно изначально планировалось несколько больше примеров (круиз-контроль, вращение турели и компенсация вращательного момента), но статья итак уже разбухла, да и вообще:
image

Немного ссылок

  1. Годная статья на английской вики
  2. PID tutorial
  3. ПИД-регуляторы: вопросы реализации. Часть 1
  4. ПИД-регуляторы: вопросы реализации. Часть 2
  5. PID Without a PhD
  6. PID Without a PhD. Перевод
  7. Derivative Action and PID Control
  8. Control System Lab: PID
  9. ПИД-регулятор своими руками
  10. Корректная реализация разностной схемы ПИД регулятора
  11. Программируем квадрокоптер на Arduino (часть 1)
  12. Виртуальный квадрокоптер на Unity + OpenCV (Часть 1)
  13. Поляков К.Ю. Теория автоматического управления для чайников
  14. PID control system analysis, design, and technology
  15. Aidan O’Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
  16. PID process control, a “Cruise Control” example
  17. https://www.mathworks.com/discovery/pid-control.html
  18. http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
  19. https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m

Еще немного ссылок на другие примеры
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/3-stabilize-quadcopter/
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/KOS/tutorials/pidloops.html

Источник

5.4.1. Погрешность дифференцирования и шум

5.4.2. Интегральное насыщение

5.4.3. Запас устойчивости и робастность

5.4.4. Сокращение нулей и полюсов

5.4.5. Безударное переключение режимов регулирования

5.4.6. Дискретная форма регулятора

Описанный выше ПИД-регулятор и его модификации являются теоретическими идеализациями реальных регуляторов, поэтому для их практического воплощения необходимо учесть особенности, порождаемые реальными условиями применения и технической реализации. К таким особенностям относятся:

  • конечный динамический диапазон изменений физических переменных в системе (например, ограниченная мощность нагревателя, ограниченная пропускная способность клапана);
  • отсутствие (как правило) в системе поддержания температуры холодильника (управляющее воздействие соответствует включению холодильника, а не выключению нагревателя);
  • ограниченная точность измерений, что требует специальных мер для выполнения операций дифференцирования с приемлемой погрешностью;
  • наличие практически во всех системах типовых нелинейностей: насыщение (ограничение динамического диапазона изменения переменных), ограничение скорости нарастания, гистерезис и люфт;
  • технологический разброс и случайные вариации параметров регулятора и объекта;
  • дискретная реализация регулятора;
  • необходимость плавного (безударного) переключение режимов регулирования.

Ниже описываются методы решения перечисленных проблем.

5.4.1. Погрешность дифференцирования и шум

Проблема численного дифференцирования является достаточно старой и общей как в цифровых, так и в аналоговых регуляторах. Суть ее заключается в том, что производная вычисляется обычно как разность двух близких по величине значений функции, поэтому относительная погрешность производной всегда оказывается больше, чем относительная погрешность численного представления дифференцируемой функции.

В частности, если на вход дифференциатора поступает синусоидальный сигнал , то на выходе получим , т.е. с ростом частоты увеличивается амплитуда сигнала на выходе дифференциатора. Иначе говоря, дифференциатор усиливает высокочастотные помехи, короткие выбросы и шум.

Рис. 5.66. Структурная реализация дифференциального члена ПИД-регулятора

Если помехи, усиленные дифференциатором, лежат за границей рабочих частот ПИД-регулятора, то их можно ослабить с помощью фильтра верхних частот. Структурная реализация дифференциатора с фильтром показана на рис. 5.66. Здесь ,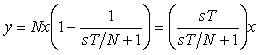

т.е. передаточная функция полученного дифференциатора может быть представлена в виде произведения передаточной функции идеального дифференциатора на передаточную функцию фильтра первого порядка: , где коэффициент задает граничную частоту фильтра и обычно выбирается равным 2…20 [Astrom].

Большее ослабление высокочастотных шумов можно получить с помощью отдельного фильтра, который включается последовательно с ПИД-регулятором. Обычно используют фильтр второго порядка [Astrom] с передаточной функцией .

Постоянную времени фильтра обычно выбирают равной , где =2…20 [Astrom]. Граничную частоту фильтра желательно не выбирать ниже частоты , т.к. это усложняет расчет параметров регулятора и запаса устойчивости.

Кроме шумов дифференцирования на характеристики ПИД-регулятора влияют шумы измерений. Через цепь обратной связи эти шумы поступают на вход системы и затем проявляются как дисперсия управляющей переменной . Высокочастотные шумы вредны тем, что вызывают ускоренный износ трубопроводной арматуры и электродвигателей.

Поскольку объект управления обычно является низкочастотным фильтром, шумы измерений редко проникают по контуру регулирования на выход системы. Однако они увеличивают погрешность измерений и снижают точность регулирования.

В ПИД регуляторах различают шум с низкочастотным спектром, вызванный внешними воздействиями на объект управления, и высокочастотный шум, связанный с электромагнитными наводками, помехами по шинам питания и земли, с дискретизацией измеряемого сигнала и другими причинами [Денисенко, Денисенко]. Низкочастотный шум моделируют как внешние возмущения (), высокочастотный — как шумы измерений ().

5.4.2. Интегральное насыщение

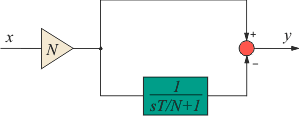
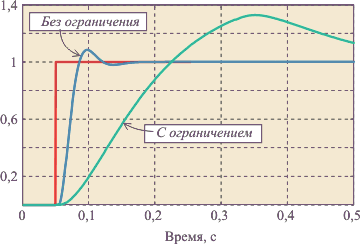
Рис. 5.67. Реакция выходной переменной на скачок входного воздействия для ПИ-регулятора при условии ограничения мощности на входе объекта и без ограничения. Объект — второго порядка, , , . Параметры регулятора: , , .

Рис. 5.68. Сигнал на входе объекта при условии ограничения мощности и без. Объект — второго порядка, , , . Параметры регулятора: , , .

В установившемся режиме работы и при малых возмущениях большинство систем с ПИД-регуляторами являются линейными. Однако процесс выхода на режим практически всегда требует учета нелинейности типа «ограничение». Эта нелинейность связана с естественными ограничениями на мощность, скорость, частоту вращения, угол поворота, площадь поперечного сечения клапана, динамический диапазон, и т. п. Контур регулирования в системе, находящейся в насыщении (когда переменная достигла ограничения), оказывается разомкнутым, поскольку при изменении переменной на входе звена с ограничением его выходная переменная остается без изменений.

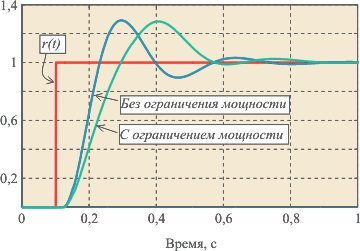
Наиболее типовым проявлением режима ограничения является так называемое «интегральное насыщение», которое возникает в процессе выхода системы на режим в регуляторах с ненулевой постоянной интегрирования . Интегральное насыщение приводит к затягиванию переходного процесса (рис. 5.67 — рис. 5.68). Аналогичный эффект возникает вследствие ограничения пропорционального и интегрального члена ПИД-регулятора (рис. 5.69 — рис. 5.70). Однако часто под интегральным насыщением понимают совокупность эффектов, связанных с нелинейностью типа «ограничение».

Суть проблемы интегрального насыщения состоит в том, что если сигнал на входе объекта управления вошел в зону насыщения (ограничения), а сигнал рассогласования не равен нулю, интегратор продолжает интегрировать т. е. сигнал на его выходе растет, но этот сигнал не участвует в процессе регулирования и не воздействует на объект вследствие эффекта насыщения. Система управления в этом случае становится эквивалентной разомкнутой системе, сигнал на входе которой равен уровню насыщения управляющего сигнала .

Для тепловых систем ограничением снизу обычно является нулевая мощность нагрева, в то время как ПИД-регулятор требует подачи на объект «отрицательной мощности нагрева», т.е. требует охлаждения объекта.

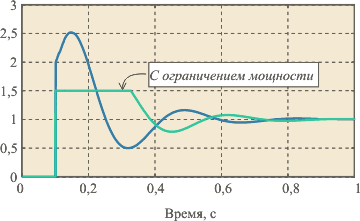
Рис. 5.69. Реакция выходной переменной на скачок входного воздействия для ПИД-регулятора при условии ограничения мощности на входе объекта и без ограничения. Объект — второго порядка, , , . Параметры регулятора: , , .

Рис. 5.70. Сигнал на входе объекта в контуре с ПИД-регулятором при условии ограничения мощности и без. Объект — второго порядка, , , . Параметры регулятора: , , .

Эффект интегрального насыщения известен давно. В аналоговых регуляторах его устранение было достаточно проблематичным, поскольку в них проблема не могла быть решена алгоритмически, а только аппаратными средствами. С появлением микропроцессоров проблему удается решить гораздо эффективнее. Методы устранения интегрального насыщения обычно являются предметом изобретений, относятся к коммерческой тайне фирм-производителей и защищаются патентами. Ниже рассмотрены несколько таких идей, описанных в литературе [Astrom].

Ограничение скорости нарастания входного воздействия

Поскольку максимальное значение входного воздействия на объект управления снижается с уменьшением разности , то для устранения эффекта ограничения можно просто снизить скорость нарастания сигнала уставки , например, с помощью фильтра. Недостатком такого способа является снижение быстродействия системы, а также невозможность устранить интегральное насыщение, вызванное внешними возмущениями, а не сигналом уставки.

Алгоритмический запрет интегрирования

Когда управляющее воздействие на объект достигает насыщения, обратная связь разрывается и интегральная составляющая продолжает расти, даже если при отсутствии насыщения она должна была бы падать. Поэтому один из методов устранения интегрального насыщения состоит в том, что контроллер следит за величиной управляющего воздействия на объект, и как только оно достигает насыщения, контроллер вводит программный запрет интегрирования для интегральной составляющей.

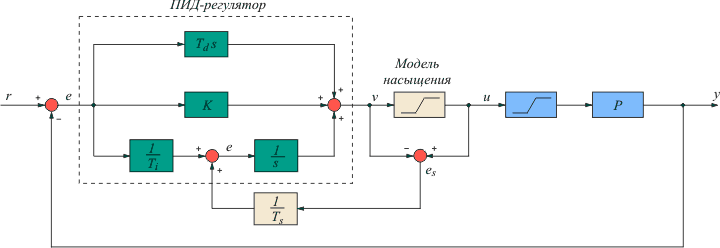
Рис. 5.71. Компенсация эффекта интегрального насыщения с помощью дополнительной обратной связи для передачи сигнала ошибки на вход интегратора

Компенсация насыщения с помощью дополнительной обратной связи

Эффект интегрального насыщения можно ослабить, отслеживая состояние исполнительного устройства, входящего в насыщение, и компенсируя сигнал, подаваемый на вход интегратора [Astrom]. Структура системы с таким компенсатором показана на рис. 5.71.

Принцип ее работы состоит в следующем. В системе вырабатывается сигнал рассогласования между входом и выходом исполнительного устройства . Сигнал на выходе исполнительного устройства либо измеряют, либо вычисляют, используя математическую модель (рис. 5.71). Если , это эквивалентно отсутствию компенсатора и получаем обычный ПИД-регулятор. Если же исполнительное устройство входит в насыщение, то и . При этом сигнал на входе интегратора уменьшается на величину ошибки , что приводит к замедлению роста сигнала на выходе интегратора, уменьшению сигнала рассогласования и величины выброса на переходной характеристике системы (рис. 5.72). Постоянная времени определяет степень компенсации сигнала рассогласования (рис. 5.72).

В некоторых регуляторах вход устройства сравнения выделяют как отдельный вход, называемый «вход слежения», что бывает удобно при построении сложных систем управления и при каскадном соединении нескольких регуляторов.

Условное интегрирование

Этот способ является обобщением алгоритмического запрета интегрирования. После наступления запрета интегральная составляющая остается постоянной, на том же уровне, который она имела в момент появления запрета интегрирования. Обобщение состоит в том, что запрет интегрирования наступает не только при достижении насыщения, но и при некоторых других условиях.

Такими условиями могут быть, например, достижение сигналом ошибки или выходной переменной некоторого заданного значения. При выключении процесса интегрирования нужно следить, в каком состоянии в момент выключения находится интегратор. Если он накапливает ошибку и степень насыщения возрастает, то интегрирование выключают. Если же в момент выключения степень насыщения понижается, то интегратор оставляют включенным [Astrom].

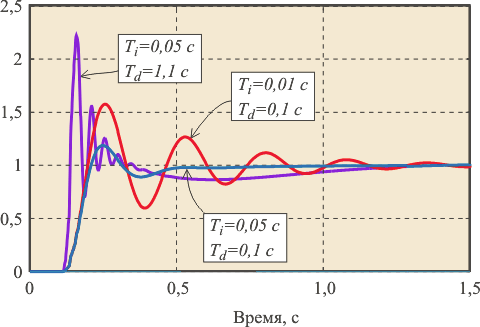
На рис. 5.73 показан пример переходного процесса в системе с отключением интегратора при достижении выходной величины заданного значения (, , ).

Интегратор с ограничением

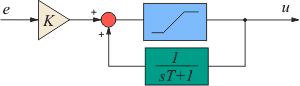
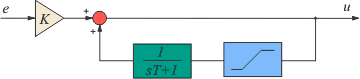
На рис. 5.58 был представлен вариант реализации ПИ-регулятора с помощью интегратора в цепи обратной связи. Если эту схему дополнить ограничителем (рис. 5.74-а), то сигнал на выходе никогда не выйдет за границы, установленные порогами ограничителя, что уменьшает выброс на переходной характеристике системы (рис. 5.75). На рис. 5.74,б представлена модификация такого ограничителя.

Модель эффекта ограничения можно улучшить, если после превышении уровня, при котором наступает ограничение, уменьшить сигнал на выходе модели (рис. 5.76) [Astrom]. Это ускоряет выход системы из режима насыщения.

а)

 б)

Рис. 5.74. Модификации интегратора с ограничением.

5.4.3. Запас устойчивости и робастность

Возможность потери устойчивости является основным недостатком систем с обратной связью. Поэтому обеспечение необходимого запаса устойчивости являются самым важным этапом при разработке и настройке ПИД-регулятора.

Устойчивость системы с ПИД-регулятором — это способность системы возвращаться к слежению за уставкой после прекращения действия внешних воздействий. В контексте данного определения под внешними воздействиями понимаются не только внешние возмущения, действующие на объект, но любые возмущения, действующие на любую часть замкнутой системы, в том числе шумы измерений, временная нестабильность уставки, шумы дискретизации и квантования, шумы и погрешность вычислений. Все эти возмущения вызывают отклонения системы от положения равновесия. Если после прекращения воздействия система возвращается в положение равновесия, то она считается устойчивой. При анализе устойчивости ПИД-регуляторов обычно ограничиваются исследованием реакции системы на ступенчатое изменение уставки , шум измерений и внешние возмущения . Потеря устойчивости проявляется как неограниченное возрастание управляемой переменной объекта, или как ее колебание с нарастающей амплитудой.

Рис. 5.77. Структура разомкнутой системы управления с ПИД-регулятором для анализа устойчивости

В производственных условиях попытки добиться устойчивости системы с ПИД-регулятором опытным путем, без ее идентификации, не всегда приводят к успеху (например, для систем с объектом высокого порядка, для систем с большой транспортной задержкой или для объектов, которые трудно идентифицировать). Это создает впечатление, что устойчивость — мистическое свойство, которым не всегда можно управлять. Однако, если процесс идентифицирован достаточно точно, то мистика исчезает и анализ устойчивости сводится к анализу дифференциального уравнения, описывающего замкнутый контур с обратной связью.

Практически интерес представляет анализ запаса устойчивости, т. е. определение численных значений критериев, которые позволяют указать, как далеко находится система от состояния неустойчивости.

Наиболее полную информацию о запасе устойчивости системы можно получить, решив дифференциальное уравнение, описывающее замкнутую систему при внешних возмущениях. Однако этот процесс слишком трудоемок, поэтому для линейных систем используют упрощенные методы, позволяющие дать оценку запаса устойчивости без решения уравнений [Воронов]. Мы рассмотрим два метода: оценку с помощью годографа комплексной частотной характеристики разомкнутого контура (критерий Найквиста) и с помощью логарифмических АЧХ и ФЧХ (диаграмм Боде).

Устойчивая система может стать неустойчивой при небольших изменениях ее параметров, например, вследствие их технологического разброса. Поэтому ниже мы проанализируем функцию чувствительности системы с ПИД-регулятором, которая позволяет выявить условия, при которых система становится грубой (мало чувствительной к изменению ее параметров).

Система, которая сохраняет заданный запас устойчивости во всем диапазоне изменений параметров вследствие их технологического разброса, старения, условий эксплуатации, во всем диапазоне изменений параметров нагрузки, а также во всем диапазоне действующих на систему возмущений в реальных условиях эксплуатации, называют робастной. Иногда робастность и грубость используют как эквивалентные понятия.

Критерий Найквиста

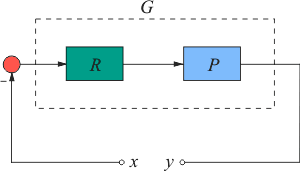
Рассмотрим систему, состоящую из контроллера и объекта управления (рис. 5.77), которая получена путем исключения из классической системы с ПИД-регулятором (рис. 5.34) сигнала уставки . Будем считать, что обратная связь разомкнута, а для ее замыкания достаточно соединить точки и . Предположим теперь, что на вход подан сигнал

.

(5.86)

Тогда, пройдя через регулятор и объект управления, этот сигнал появится на выходе с измененной амплитудой и фазой, в виде

,

(5.87)

где — комплексная частотная характеристика (КЧХ) системы, — аргумент КЧХ, — модуль КЧХ. Таким образом, при прохождении через регулятор и объект амплитуда сигнала изменится пропорционально модулю, а фаза — на величину аргумента КЧХ.

Если теперь замкнуть точки и , то сигнал будет циркулировать по замкнутому контуру, причем будет выполняться условие . Если при этом и , т.е. после прохождения по контуру сигнал попадает на вход регулятора в той же фазе, что и на предыдущем цикле, то после каждого прохождения по контуру амплитуда синусоидального сигнала будет возрастать, пока не достигнет границы диапазона линейности системы, после чего форма колебаний станет отличаться от синусоидальной. В этом случае для анализа устойчивости можно использовать метод гармонической линеаризации, когда рассматривают только первую гармонику искаженного сигнала. В установившемся режиме после наступления ограничения амплитуды колебаний в силу равенства будет выполняться условие

Решив уравнение , можно найти частоту колебаний в замкнутой системе.

Комплексную частотную характеристику графически изображают в виде годографа (диаграммы Найквиста) — графика в координатах и (рис. 5.78). Стрелка на линии годографа указывает направление движения «карандаша» при возрастании частоты. Точка , которая соответствует условию существования незатухающих колебаний в системе, на этом графике имеет координаты и . Поэтому критерий устойчивости Найквиста формулируется следующим образом [Ротач]: контур, устойчивый в разомкнутом состоянии, сохранит устойчивость и после его замыкания, если его КЧХ в разомкнутом состоянии не охватывает точку с координатами [-1, j0]. Более строго, при движении вдоль траектории годографа в направлении увеличения частоты точка [-1, j0] должна оставаться слева [Astrom], чтобы замкнутый контур был устойчив.

На рис. 5.79 показаны реакции замкнутых систем с тремя различными годографами (рис. 5.78) на единичный скачок уставки. Все три системы устойчивы, однако скорость затухания колебаний и форма переходного процесса у них различная. Интуитивно понятно, что система с параметрами наиболее близка к тому, чтобы перейти в состояние незатухающих колебаний при небольшом изменении ее параметров. Поэтому при проектировании ПИД-регулятора важно обеспечить не столько устойчивость, сколько ее запас, необходимый для нормального функционирования системы в реальных условиях.

Запас устойчивости оценивают как степень удаленности КЧХ от критической точки [-1, j0]. Если , то можно найти, во сколько раз осталось увеличить передаточную функцию, чтобы результирующее усиление вывело систему в колебательный режим: , откуда

(5. 89)

Запасом по усилению называется величина, на которую нужно умножить передаточную функцию разомкнутой системы , чтобы ее модуль на частоте сдвига фаз 180˚ стал равен 1.

Если на частоте сдвига фаз 180˚ коэффициент усиления разомкнутого контура равен (рис. 5.78), то дополнительное усиление величиной переведет систему в точку [-1, j0], поскольку .

Аналогично вводится понятие запаса по фазе: это минимальная величина , на которую нужно увеличить фазовый сдвиг в разомкнутой системе , чтобы суммарный фазовый сдвиг достиг 180˚, т.е.

.

(5.90)

Рис. 5.79. Переходная характеристика замкнутой системы, которая имеет годограф, показанный на рис. 5.78

Знак «+» перед стоит потому, что .

Для оценки запаса устойчивости используют также минимальное расстояние от кривой годографа до точки [-1, j0] (рис. 5.78).

На практике считаются приемлемыми значения =2…5, =30˚…60˚, =0,5…0,8 [Astrom].

Для графика на рис. 5.78 эти критерии имеют следующие значения:

  • для случая , =12,1; =15˚; =0,303.
  • для случая , =11,8; =47,6; =0,663.
  • для случая , =1,5; =35,2; =0,251.

Если кривая годографа пересекает действительную ось в нескольких точках, то для оценки запаса устойчивости берут ту из них, которая наиболее близка к точке [-1, j0]. При более сложном годографе может быть использована оценка запаса устойчивости как запас по задержке [Astrom]. Запас по задержке— это минимальная задержка, при добавлении которой в контур он теряет устойчивость. Наиболее часто этот критерий используется для оценки запаса устойчивости систем с предиктором Смита.

Частотный критерий устойчивости

Рис. 5.80. Оценка запаса по фазе и усилению для системы с годографом, показанным на рис. 5.78

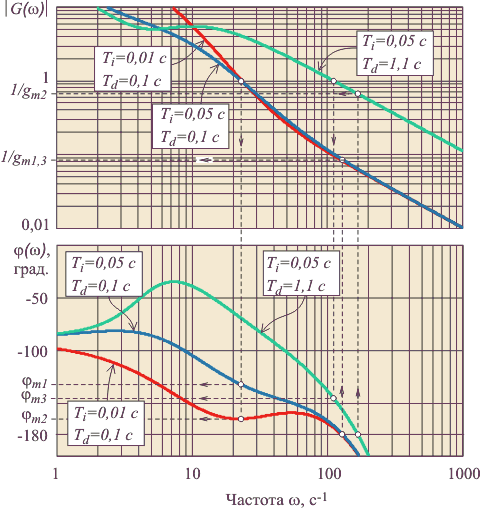
Для графического представления передаточной функции разомкнутой системы и оценки запаса устойчивости могут быть использованы логарифмические АЧХ и ФЧХ (рис. 5.80). Для оценки запаса по фазе сначала с помощью АЧХ находят частоту («частота среза» или «частота единичного усиления«), при которой , затем по ФЧХ находят соответствующий запас по фазе. Для оценки запаса по усилению сначала с помощью ФЧХ находят частоту , на которой фазовый сдвиг равен 180˚, затем по АЧХ находят запас по усилению. На (рис. 5.80) приведены примеры графических построений для оценки запаса по фазе и усилению для системы, годограф которой показан на рис. 5.78.

Если запас по фазе разомкнутого контура равен 0˚ или запас по усилению равен 1, после замыкания контура обратной связи система окажется неустойчивой.

Функции чувствительности

Передаточная функция реального объекта может изменяться в процессе функционирования на величину , например, вследствие изменения нагрузки на валу двигателя, числа яиц в инкубаторе, уровня или состава жидкости в автоклаве, вследствие старения и износа материала, появления люфта, изменения смазки и т.п. Правильно спроектированная система автоматического регулирования должна сохранять свои показатели качества не только в идеальных условиях, но и при наличии перечисленных вредных факторов. Для оценки влияния относительного изменения передаточной функции объекта на передаточную функция замкнутой системы (5.41) найдем дифференциал :

.

(5. 91)

Поделив обе части этого равенства на и подставив в правую часть , получим

.

(5.92)

Из последнего соотношения виден смысл коэффициента — он характеризует степень влияния относительного изменения передаточной функции объекта на относительное изменение передаточной функции замкнутого контура, то есть является коэффициентом чувствительности замкнутого контура к вариации передаточной функции объекта. Поскольку коэффициент является частотозависимым, его называют функцией чувствительности [Astrom].

Как следует из (5.92),

.

(5. 93)

Введем обозначение .

(5.94)

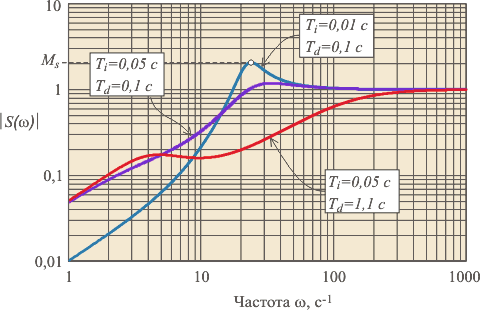
Рис. 5.81. Модули функций чувствительности для систем с годографами, показанными на рис. 5.78

Величина называется комплементарной (дополнительной) функцией чувствительности [Astrom], поскольку .

Заметим, что функция чувствительности входит во все три слагаемые уравнения замкнутой системы с ПИД-регулятором (5.42).

Функция чувствительности позволяет оценить изменение свойств системы после замыкания обратной связи. Поскольку передаточная функция разомкнутой системы равна , а замкнутой , то их отношение . Аналогично, передаточная функция от входа возмущений на выход замкнутой системы равна (см. (5.42)), а разомкнутой — , следовательно, их отношение также равно . Для передаточной функции от входа шума измерений на выход системы можно получить то же отношение .

Таким образом, зная вид функции (см, например, рис. 5.81), можно сказать, как изменится подавление внешних воздействий на систему для разных частот после замыкания цепи обратной связи. Очевидно, шумы, лежащие в диапазоне частот, в котором , после замыкания обратной связи будут усиливаться, а шумы с частотами, на которых , после замыкания обратной связи будут ослаблены.

Наихудший случай (наибольшее усиление внешних воздействий) будет наблюдаться на частоте максимума модуля функции чувствительности (рис. 5.81):

.

(5.95)

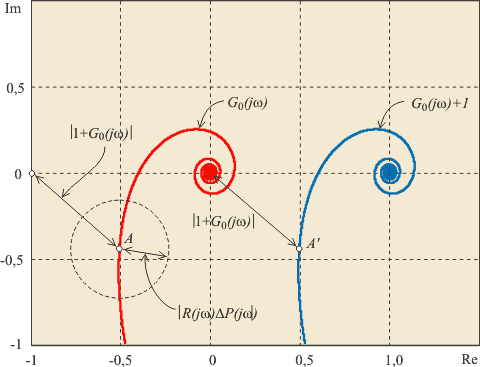
Максимум функции чувствительности можно связать с запасом устойчивости (рис. 5.78). Для этого обратим внимание, что представляет собой расстояние от точки (-1, j0) до текущей точки на годографе функции . Следовательно, минимальное расстояние от точки (-1, j0) до функции равно

.

(5.96)

Сопоставляя (5.95) и (5.96), можно заключить, что .

Если с ростом частоты модуль уменьшается, то, как видно из (рис. 5.78), . Подставляя сюда соотношение , получим оценку запаса по усилению, выраженную через максимум функции чувствительности:

.

(5.97)

Аналогично, но с более грубыми допущениями можно записать оценку запаса по фазе через максимум функции чувствительности [Astrom]:

.

(5.98)

Например, при получим и .

Робастность

Робастность — это способность системы сохранять заданный запас устойчивости при вариациях ее параметров, вызванных изменением нагрузки (например, при изменении загрузки печи меняются ее постоянные времени), технологическим разбросом параметров и их старением, внешними воздействиями, погрешностями вычислений и погрешностью модели объекта. Используя понятие чувствительности, можно сказать, что робастность — это низкая чувствительность запаса устойчивости к вариации параметров объекта.

Если параметры объекта изменяются в небольших пределах, когда можно использовать замену дифференциала конечным приращением, влияние изменений параметров объекта на передаточную функцию замкнутой системы можно оценить с помощью функции чувствительности (5.92). В частности, можно сделать вывод, что на тех частотах, где модуль функции чувствительности мал, будет мало и влияние изменений параметров объекта на передаточную функцию замкнутой системы и, соответственно, на запас устойчивости.

Для оценки влияния больших изменения параметров объекта представим передаточную функцию объекта в виде двух слагаемых

,

(5.99)

где — расчетная передаточная функция, — величина отклонения от , которая должна быть устойчивой передаточной функцией. Тогда петлевое усиление разомкнутой системы можно представить в виде . Поскольку расстояние от точки (-1, j0) до текущей точки на годографе невозмущенной системы (для которой ) равно (см. рис. 5.82), условие устойчивости системы с отклонением петлевого усиления можно представить в виде

,

откуда , или ,

где — дополнительная функция чувствительности (5.94). Окончательно можно записать соотношение

,

(5.100)

Рис. 5.82. Пояснение к выводу соотношения (5.100)

которое должно выполняться, чтобы система сохраняла устойчивость при изменении параметров процесса на величину .

5.4.4. Сокращение нулей и полюсов

Поскольку передаточная функция разомкнутой системы является произведением двух передаточных функций, которые в общем случае имеют и числитель, и знаменатель, то возможно сокращение нулей с полюсами, которые лежат в правой полуплоскости или близки к ней. Поскольку в реальных условиях, когда существует разброс параметров, такое сокращение выполняется неточно, то может возникнуть ситуация, когда теоретический анализ приводит к выводу, что система устойчива, хотя на самом деле при небольшом отклонении параметров процесса от расчетных значений она становится неустойчивой.

Поэтому каждый раз, когда происходит сокращение нулей и полюсов, необходимо проверять устойчивость системы при реальном разбросе параметров объекта.

Вторым эффектом является появление существенного различия между временем установления переходного процесса при воздействии сигнала уставки и внешних возмущений. Поэтому необходимо проверять реакцию синтезированного регулятора для каждого из этих воздействаий.

5.4.5. Безударное переключение режимов регулирования

В ПИД-регуляторах могут существовать режимы, когда их параметры изменяются скачком. Например, когда в работающей системе потребовалось изменить постоянную интегрирования или если после ручного управления системой необходимо перейти на автоматический режим. В описанных случаях могут появиться нежелательные выбросы регулируемой величины, если не принять специальных мер. Поэтому возникает задача плавного («безударного») переключения режимов работы или параметров регулятора.

Основной метод решения проблемы заключается в построении такой структуры регулятора, когда изменение параметра выполнятся до этапа интегрирования. Например, при изменяющемся параметре интегральный член можно записать в двух формах:

или .

В первом случае при скачкообразном изменении интегральный член будет меняться скачком, во втором случае — плавно, поскольку находится под знаком интеграла, значение которого не может изменяться скачком.

Аналогичный метод реализуется в инкрементной форме ПИД-регулятора (см. раздел «Инкрементная форма цифрового ПИД-регулятора») и в последовательной форме ПИД-регулятора, где интегрирование выполняется на заключительной стадии вычисления управляющего воздействия.

5.4.6. Дискретная форма регулятора

Непрерывные переменные удобно использовать для анализа и синтеза ПИД-регуляторов. Для технического воплощения необходимо перейти к дискретной форме уравнений, поскольку основой всех регуляторов является микроконтроллер, контроллер или компьютер, которые оперируют с переменными, полученными из аналоговых сигналов после их дискретизации по времени и квантования по уровню.

Вследствие конечного времени вычисления управляющего воздействия в микроконтроллере и задержки аналого-цифрового преобразования между моментом поступления аналогового сигнала на вход регулятора и появлением управляющего воздействия на его выходе появляется нежелательная задержка, которая увеличивает общую задержку в контуре регулирования и снижает запас устойчивости.

Основным эффектом, который появляется при дискретизации и который часто «открывают заново», является появление алиасных частот в спектре квантованного сигнала в случае, когда частота дискретизации недостаточно высока. Аналогичный эффект возникает при киносъемке вращающегося колеса автомобиля. Частота алиасного сигнала равна разности между частотой помехи и частотой дискретизации. При этом высокочастотный сигнал помехи смещается в низкочастотную область, где накладывается на полезный сигнал и создает большие проблемы, поскольку отфильтровать его на этой стадии невозможно.

Для устранения алиасного эффекта перед входом аналого-цифрового преобразователя необходимо установить аналоговый фильтр, который бы ослаблял помеху по крайне мере на порядок на частоте, равной половине частоты дискретизации. Обычно используют фильтр Баттерворта второго или более высокого порядка. Вторым вариантом решения проблемы является увеличение частоты дискретизации так, чтобы она по крайней мере в 2 раза (согласно теореме Котельникова) была выше максимальной частоты спектра помехи. Это позволяет применить после дискретизации цифровой фильтр нижних частот. При такой частоте дискретизации полученный цифровой сигнал с точки зрения количества информации полностью эквивалентен аналоговому и все свойства аналогового регулятора можно распространить на цифровой.

Переход к конечно-разностным уравнениям

Переход к дискретным переменным в уравнениях аналогового регулятора выполняется путем замены производных и интегралов их дискретными аналогами. Если уравнение записано в операторной форме, то сначала выполняют переход из области изображений в область оригиналов. При этом оператор дифференцирования заменяют производной, оператор интегрирования — интегралом.

Существует множество способов аппроксимации производных и интегралов их дискретными аналогами, которые изложены в курсах численных методов решения дифференциальных уравнений. В ПИД-регуляторах наиболее распространенными являются простейшая аппроксимация производной конечной разностью и интеграла — конечной суммой.

Рассмотрим интегральный член ПИД-регулятора: . Продифференцировав обе части по времени, получим . Заменяя дифференциалы в этом выражении конечными разностями (левыми разностями), получим , где индекс обозначает, что данная величина взята в момент времени (обратим внимание, что здесь и ниже индекс в обозначает не номер временного шага, а интегральный коэффициент ПИД-регулятора). Из последнего выражения получим

.

(5.101)

Таким образом, очередное значение интеграла можно вычислить, зная предыдущее и значение ошибки в предыдущий момент времени. Однако такая формула имеет свойство накапливать ошибку вычислений с течением времени, если отношение недостаточно мало. Более устойчива другая формула интегрирования с правыми разностями, когда значение ошибки берется в тот же момент времени, что и вычисляемый интеграл:

.

(5.102)

Рассмотрим дифференциальный член ПИД-регулятора с фильтром (см. раздел «Погрешность дифференцирования и шум»).

Переходя в этой формуле от изображений к оригиналам, получим . Заменяя дифференциалы конечными приращениями, получим разностное уравнение

.

(5.103)

Для сходимости итерационного процесса (5.103) необходимо, чтобы , т.е.

.

(5.104)

При итерационный процесс (5.103) становится колебательным, что недопустимо для ПИД-регулятора.

Лучшими характеристиками обладает разностное уравнение, полученное при использовании правых разностей:

.

(5.105)

Здесь условие сходимости выполняется для всех и ни при каких значениях параметров не возникает колебаний. Кроме того, последняя формула позволяет «отключить» дифференциальную составляющую в ПИД регуляторе путем назначения , чего нельзя сделать в выражении (5.103), поскольку при этом возникает деление на ноль.

Можно использовать еще более точные формулы численного дифференцирования и интегрирования, известные из курса численных методов решения уравнений.

Величина шага дискретизации выбирается как можно меньше, это улучшает качество регулирования. Для обеспечения хорошего качества регулирования он не должен быть больше чем 1/15…1/6 от времени установления переходной характеристики объекта по уровню 0,95 или 1/4…1/6 от величины транспортной задержки [Изерман]. Однако при увеличении частоты дискретизации более чем в 2 раза по сравнению с верхней частотой спектра возмущающих сигналов (по теореме Котельникова) дальнейшего улучшения качества регулирования не происходит.

Если на входе регулятора нет антиалиасного фильтра, то частоту дискретизации выбирают в 2 раза выше верхней граничной частоты спектра помехи, чтобы использовать цифровую фильтрацию. Необходимо учитывать также, что исполнительное устройство должно успеть отработать за время .

Если контроллер используется не только для регулирования, но и для аварийной сигнализации, то такт дискретизации не может быть меньше, чем допустимая задержка срабатывания сигнала аварии.

При малом такте дискретизации увеличивается погрешность вычисления производной. Для ее снижения можно использовать сглаживание получаемых данных по нескольким собранным точкам перед этапом дифференцирования.

Уравнение цифрового ПИД-регулятора

Основываясь на изложенном выше, уравнение дискретного ПИД-регулятора можно записать в виде

,

(5.106)

где — номер временного такта. Величины и вычисляют по выражениям (5.102) и (5.105). Для начала работы алгоритма выбирают обычно , , , однако могут быть и другие начальные условия, в зависимости от конкретной задачи регулирования.

Отметим, что алгоритм, полученный путем простой замены операторов дифференцирования и интегрирования в выражении (5.36) конечными разностями и конечными суммами

,

(5.107)

(здесь — индекс суммирования отсчетов от начала процесса до текущего i-того временного такта) обладает плохой устойчивостью и низкой точностью, как это было показано выше. Однако с ростом частоты дискретизации различие между приведенными двумя алгоритмами стирается.

Инкрементная форма цифрового ПИД-регулятора

Рис. 5.83. Инкрементная форма ПИД-регулятора

Довольно часто, особенно в нейросетевых и фаззи-регуляторах, используют уравнение ПИД-регулятора в виде зависимости приращения управляющей величины от ошибки регулирования и ее производных (без интегрального члена). Такое представление удобно, когда роль интегратора выполняет внешнее устройство, например, обычный или шаговый двигатель. Угол поворота его оси пропорционален значению управляющего сигнала и времени. В фаззи-регуляторах при формулировке нечетких правил эксперт может сформулировать зависимость управляющей величины от величины производной, но не может — от величины интеграла, поскольку интеграл «запоминает» всю предысторию изменения ошибки, которую человек помнить не может.

Инкрементная форма ПИД-регулятора получается путем дифференцирования уравнения (5.36):

;

Для получения нулевой ошибки регулирования на выходе инкрементного регулятора должен стоять интегратор (рис. 5.83):

Переходя в полученных выражениях к конечным разностям, получим дискретную форму инкрементного ПИД-регулятора:

,

(5.108)

где , .

Более устойчивое и точное разностное уравнение можно получить, подставив в формулу выражения для и из (5.106).

Инкрементная форма регулятора удобна для применения в микроконтроллерах, поскольку в ней основная часть вычислений выполняется с приращениями, для представления которых можно использовать слово с малым количеством двоичных разрядов. Для получения значения управляющей величины можно выполнить накопительное суммирование на финальной стадии вычислений:

.

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookies и персональных данных в соответсвии с политикой. Окей, не возражаю

Источник

Ошибка регулирования

Ошибка регулирования
— имеющая место и обычно накапливающаяся в процессе выполнения регулирующих и управляющих операций ошибка. В кибернетике ошибку регулирования стремятся уменьшить и обычно используют в качестве сигнала для того или иного нового, более совершенного, контура (механизма) внешней обратной связи. В общественных системах ошибка регулирования  обычно является действующим фактором для системы внутренней обратной связи, то есть ведет к накоплению в обществе тех или иных проблем, нарастанию напряженности либо необоснованной безмятежности, хаоса (неразберихи) либо зарегламентированности и обюрокрачивания и т.п.

Теоретические аспекты и основы экологической проблемы: толкователь слов и идеоматических выражений. — Чувашский государственный университет им. И.Н.Ульянова. УНПП «Лаборатория проблем цивилизации».
.
1998.

Смотреть что такое «Ошибка регулирования» в других словарях:

  • ошибка регулирования — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN error …   Справочник технического переводчика

  • ошибка регулирования в процентах — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN percent deviation …   Справочник технического переводчика

  • ошибка регулирования района — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN area control errorACE …   Справочник технического переводчика

  • Астатическая система регулирования —         система автоматического регулирования режимов работы промышленных установок, систем автоматического управления и др., в которой ошибка регулирования стремится к нулю независимо от размера воздействия, если последнее принимает… …   Большая советская энциклопедия

  • Динамическая ошибка —         динамическая погрешность, динамическое отклонение, разность между требуемым и действительным значениями регулируемой величины, возникающая и измеряющаяся в процессе регулирования; см. Регулирование автоматическое …   Большая советская энциклопедия

  • Теория автоматического управления — Содержание 1 История 2 Основные понятия 3 Функциональн …   Википедия

  • Статическая система — Статическая система  это такая система автоматического регулирования, в которой ошибка регулирования стремится к постоянному значению при входном воздействии, стремящемся к некоторому постоянному значению. Иными словами статическая система… …   Википедия

  • полный размах колебаний регулируемой величины от заданного значения — полный размах отклонений регулируемой величины от заданного значения ошибка регулирования — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики… …   Справочник технического переводчика

  • Регулирование автоматическое — (от нем. regulieren регулировать, от лат. regula норма, правило)         поддержание постоянства (стабилизация) некоторой регулируемой величины, характеризующей технический процесс, либо её изменение по заданному закону (программное… …   Большая советская энциклопедия

  • Трунов, Игорь Леонидович — В Википедии есть статьи о других людях с такой фамилией, см. Трунов. Игорь Леонидович Трунов Портрет Род деятельности: Адвокат Дата рождения: 1961 год(1 …   Википедия

Источник

Ошибка — регулирование

Cтраница 1

Ошибка регулирования существует, но она не является ф-цией нагрузки и не наз. При всяком же отклонении х от заданного значения равновесие регулятора нарушается и начинается непрерывное изменение у.
 [2]

Ошибка регулирования определяется величиной шага перемещения цапфы валка при срабатывании реле. Верхнее и нижнее положение подвижного валка, как это было отмечено ранее, ограничивается конечными выключателями.
 [4]

Ошибка регулирования характерна для статических систем. Для астатических систем она равна нулю.
 [5]

Ошибкой регулирования называется разность между требуемым законом изменения регулируемой величины и его действительным законом изменения.
 [6]

Дисперсия ошибки регулирования служит критерием качества АСР при случайных входных сигналах.
 [7]

В результате ошибка регулирования бесконечно быстро сводится к нулю.
 [9]

Для определения ошибки регулирования по возмущающему воздействию структурную схему на рис. 8 — 20 а необходимо преобразовать.
 [10]

Оно пропорционально ошибке регулирования и может быть использовано в качестве сигнала управления схемы регулирования напряжения.
 [12]

Желательно, чтобы ошибка регулирования была бы при этом уровне минимальна. Выражение (7.33) определяет текущее значение ошибки, каким-то образом распределенное по партии деталей, обработанных данной системой, причем распределение ошибки связано с распределением твердости.
 [13]

Статическим системам свойственна ошибка регулирования: они никогда не возвращают регулируемый параметр к заданному значению.
 [14]

Желательно, чтобы ошибка регулирования была бы при этом уровне минимальна. Выражение (7.33) определяет текущее значение ошибки, каким-то образом распределенное по партии деталей, обработанных данной системой, причем распределение ошибки связано с распределением твердости.
 [15]

Страницы:  

   1

   2

   3

   4

   5

Источник

Понравилась статья? Поделить с друзьями:
  • Ошибкой при разрешении конфликтов будет тест
  • Ошибки эпсон т50
  • Ошибкой при разрешении конфликтов будет конфликтология
  • Ошибки эпсон 210
  • Ошибкой при лечении пульпита биологическим методом является тест