Построение
математической модели — это скорее
искусство, чем наука, и, прежде всего,
требует глубоких знаний предметной
области. Социально-экономические системы
имеют чрезвычайно сложную структуру,
со многими явными и неявными взаимосвязями
между элементами системы, подвержены
влиянию многих скрытых факторов,
относятся к классу так называемых
больших систем. Стечением
времени меняются не только их
характеристики, учитываемые в модели
в виде отдельных параметров, но и
структура самих уравнений, которые
описывают процесс. Для их адекватного
описания требуется соответствующий
математический аппарат. Однако, даже
самые сложные математические методы
не в состоянии описать реальную систему
во всех ее деталях, да это и не нужно.
Модель не должна быть слишком сложной.
Излишняя детализация и учет второстепенных
факторов затрудняет
исследование
и не дает существенной информации об
изучаемой системе. Если модель слишком
сложна, то ее трудно использовать и
интерпретировать на практике.
Относительная
простота — важная характеристика
удачно построенной модели.
С другой стороны, слишком упрощенная
модель не будет адекватно описывать
реальную систему. Таким образом, сложность
модели должна соответствовать сложности
изучаемого экономического объекта.
В связи
с этим возникает необходимость
формулировки некоторых разумных
упрощающих гипотез (предположений),
исключения из анализа второстепенных
факторов и т. п., с тем, чтобы была
возможность описать процесс математически.
При этом существенные для
данного
социально-экономического процесса
характерные черты
должны
быть учтены в модели в соответствии с
поставленной целью исследования.
Другой
характерной проблемой, с которой
сталкивается эконометрист, является
то, что часто приходится довольствоваться
неточными
данными,
которые имеются в наличии и быстро
устаревают. Этих данных не всегда
хватает, а провести управляемый
эксперимент с целью получения
дополнительной информации невозможно.
В подобном случае целесообразно сочетание
количественных методов с привлечением
экспертных знаний и суждений.
Таким
образом, при создании эконометрической
модели возникают следующие вопросы.
1.
Какую модель желательно построить —
статическую или динамическую (с
учетом фактора времени), нелинейную или
линеаризованную? Как учесть влияние
внешней среды (возмущений)? (Ответ на
эти вопросы определяет желаемую точность
и сложность модели, выбор адекватного
математического аппарата и т. д.)
2.
Достаточно
ли имеющихся данных, необходимых для
построения адекватной модели,
насколько они достоверны? Существует
ли возможность получения дополнительной
информации, если это необходимо? Следует
ли привлечь экспертную информацию?
3. Как
оценить качество модели, т. е. определить,
насколько адекватно (правильно) она
описывает поведение реального объекта?
В
рамках эконометрического подхода
существует мощный арсенал средств,
который включает многие современные
эффективные
математические методы,
такие, например, как аппарат
нейронных сетей,
и разработанные на их основе компьютерные
технологии, в известной степени помогающие
справиться с этими проблемами. Но
решающая
роль принадлежит специалисту —
эконометристу.
Окончательный успех зависит от его
способности к неформальному анализу
проблемной ситуации, адекватной оценке
возможностей современных эконометрических
методов, от их правильного применения
и интерпретации полученных результатов.
Построив
удачную математическую модель и оценив
ее количественно с использованием
эконометрических методов, экономист-аналитик
получает в распоряжение эффективнейшее
средство анализа и прогноза, а
управляющий-практик — инструмент для
обоснования управленческих решений.
Такие модели широко применяются на
практике.
Практически
величина y
складывается из двух слагаемых:
,
где
— фактическое
значение, результат признака;
— теоретическое
значение результата признака, найденное
из математической модели или уравнения
регрессии;
— СВ, характерное
отклонение реального значения результата
признака от теоретического.
СВ
называется
возмущением. Она включает влияние
неучтённых в модели факторов, случайных
ошибок и особенно измерения. Её присутствие
в модели порождено тремя источниками:
-
спецификацией
модели; -
выборочным
характером исходных данных; -
особенностями
измерения.
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем больше теоретические
значения результативного признака
подходит к фактическим данным y.
К ошибкам спецификации
будут относиться не только неправильный
выбор той или иной математической
функции для
,
но и недоучет в УР какого-либо существенного
фактора (например, использование парной
регрессии вместо множественной).
Наряду с ошибками
спецификации могут иметь место ошибки
выборки (неоднородность данных в исходной
статистической совокупности). Если
совокупность неоднородна, то УР не имеет
практического смысла.
Для получения
хорошего результата обычно исключают
из совокупности единицы с аномальными
значениями исследуемых признаков, то
есть результаты регрессии представляют
собой выборочные характеристики.
Наибольшую опасность
в практическом использовании методов
регрессии представляют ошибки
измерения.
Если ошибки спецификации можно уменьшить,
изменяя форму модели, а ошибки выборки
– увеличивая объём исходных данных, то
ошибки измерения практически сводят
на нет все усилия по количественной
оценке связи между признаками. Особенно
велика роль ошибок измерения при
исследовании на макроуровне.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
04.08.2019218.11 Кб0kv.doc
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
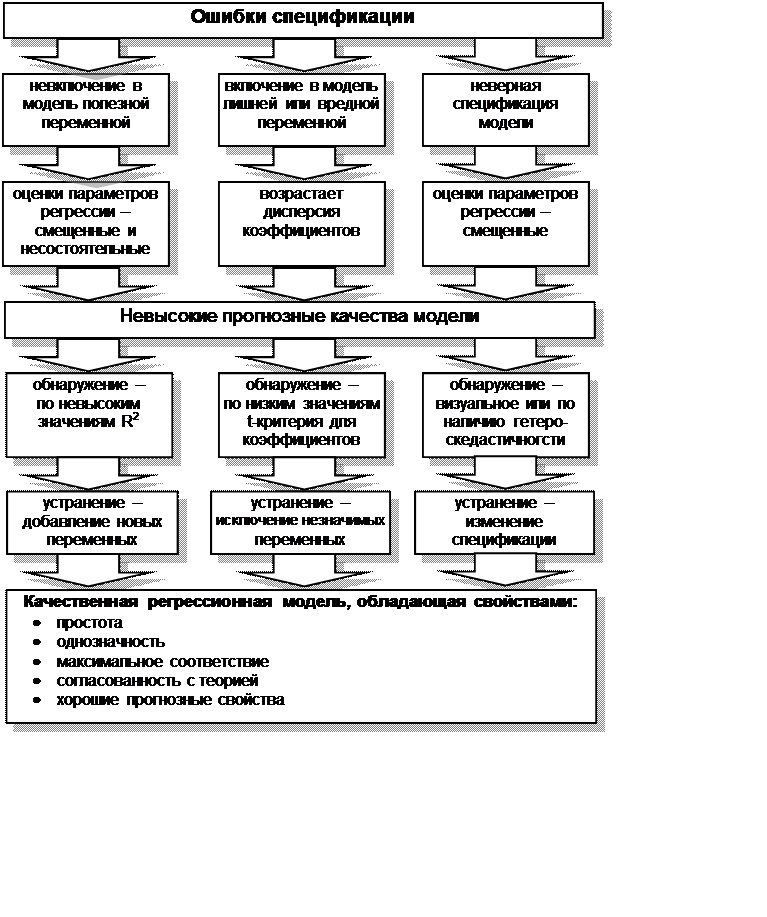
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели

Ошибки спецификации эконометрической модели относятся к различным ошибкам, которые могут быть сделаны при выборе и обработке набора независимых переменных для объяснения зависимой переменной.
Когда модель построена, она должна удовлетворять гипотезе правильной спецификации. Это основано на том факте, что независимые переменные, выбранные для модели, способны объяснить независимую переменную. Следовательно, предполагается, что не существует независимой переменной (x), которая могла бы объяснить независимую переменную (y), и что таким образом были бы выбраны переменные, которые позволяют использовать подход правильной модели.
Ошибки спецификации модели
В спецификации модели имеется ряд ошибок, которые можно сгруппировать в три большие группы:
Группа 1: способ работы указан неверно.
- Пропуск соответствующих переменных: Представим, что мы хотим объяснить доходность акций компании Y. Для этого мы выбираем PER, рыночную капитализацию и балансовую стоимость в качестве независимых переменных. Если свободное плавание коррелирует с любой из переменных, содержащихся в модели, ошибка нашей модели будет коррелирована с переменными, включенными в модель. Это может привести к тому, что параметры, оцениваемые моделью, будут несмещенными и непоследовательными. Таким образом, результаты прогнозов и различных тестов, выполненных на модели, будут недействительными.
- Преобразуемые переменные: Гипотеза регрессионной модели предполагает, что зависимая переменная линейно связана с независимыми переменными. Однако во многих случаях связь между ними не является линейной. Если необходимое преобразование не будет выполнено для независимой переменной, модель не будет иметь правильного соответствия. В качестве примеров преобразования независимых переменных мы можем привести логарифм, квадратный корень или возведение в квадрат среди прочего.
- Плохой сбор выборочных данных: Данные независимых переменных должны быть согласованы со временем, то есть структурных изменений независимых переменных быть не может. Представим, что мы хотим объяснить изменение ВВП в стране X, используя потребление и инвестиции в качестве независимых переменных. Предположим, что в этой стране на государственной земле открыто месторождение нефти, и правительство решает отменить налоги. Это может привести к изменению потребительских привычек страны, которые с этой даты будут сохраняться неопределенно долго. В этом случае мы должны собрать два разных временных ряда и оценить две модели. Одна модель до изменения, другая после. Если бы мы сгруппировали данные в одну выборку и оценили модель, у нас была бы плохо определенная модель, а гипотезы, контрасты и прогнозы были бы неверными.
Группа 2: независимые переменные коррелируют с ошибкой во временном ряду.
- Использование зависимой переменной с запаздыванием в качестве независимой переменной: Использование переменной с запаздыванием означает использование данных тех же переменных, но измеренных за предыдущий период. Предположим, мы используем предыдущую модель ВВП в качестве зависимой переменной. Добавим в модель, помимо потребления и инвестиций, ВВП предыдущего года (GDPт-1). Если ВВП предыдущего года серийно коррелирует с ошибкой, расчетные коэффициенты будут смещены и не будут противоречивыми. Это снова сделает недействительными все проверки гипотез, прогнозы и т. Д.
- Предсказание прошлого: Когда мы измеряем переменную, мы всегда должны брать период перед тем, который мы хотим оценить. Предположим, что наша зависимая переменная — это доходность запаса X, а наша независимая переменная — PER. Предположим далее, что мы берем окончательные данные за февраль. Если мы воспользуемся этим в нашей модели, мы сделаем вывод, что акции с самым высоким PER в конце февраля имели самую высокую доходность в конце февраля. Правильная спецификация модели предполагает использование данных с начала периода для прогнозирования более поздних данных, а не наоборот, как в предыдущем случае. Это называется предсказанием прошлого.
- Измерьте независимую переменную с ошибкой: Предположим, что наша независимая переменная — это доходность акции, а одна из наших независимых переменных — номинальная процентная ставка. Помните, что номинальная процентная ставка — это процентная ставка плюс инфляция. Поскольку инфляционный компонент номинальной процентной ставки не наблюдается в будущем, мы будем измерять переменную с ошибкой. Чтобы правильно измерить процентную ставку, мы должны использовать ожидаемую процентную ставку, которая учитывает ожидаемую инфляцию, а не текущую.