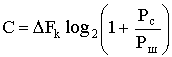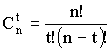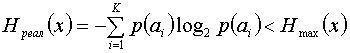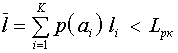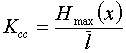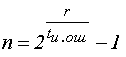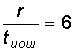Основные принципы кодирования расчет вероятностей ошибок

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 63K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0,\ B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

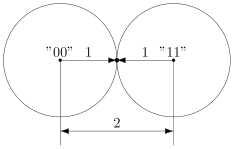
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00,\ B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

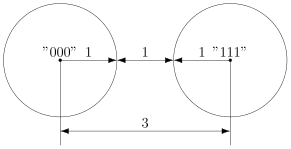
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e,\ x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Основы
передачи дискретных сообщений    

Тема
1. Основные
понятия и определения

назад
| оглавление
|
вперёд

Информация,
сообщения, сигналы

Под
термином “информация”
понимают различные сведения, которые
поступают к получателю. В более строгой
форме определение информации следующее:

Информация
—
это сведения, являющиеся объектом
передачи, распределения, преобразования,
хранения или непосредственного
использования.

В
дальнейшем нас будут интересовать
лишь вопросы, связанные с информацией
как объектом передачи.

Сообщение
является
формой представления информации.

Одно
и то же сведение может быть представлено
в различной форме. Например, сведение
о моменте начала наступления может
быть передано по телефону или телеграфом
или тремя зелеными ракетами. В первом
случае мы имеем дело с информацией,
представленной в непрерывном виде
(непрерывное
сообщение).
Будем считать, что это сообщение
вырабатывается источником непрерывных
сообщений. Во втором и в третьем случае
— с информацией, представленной в
дискретном виде (дискретное
сообщение).
Это сообщение вырабатывается источником
дискретных сообщений.

Основное
отличие дискретного и непрерывного
источников
состоит в следующем. Множество всех
различных сообщений, вырабатываемых
дискретным источником всегда конечно.
Поэтому на конечном отрезке времени
количество символов дискретного
источника так же является конечным.
В то же время число возможных различных
значений звукового давления (или
напряжения в телефонной линии),
измеренное при разговоре, даже на
конечном отрезке времени, будет
бесконечным.

В
нашем курсе мы будем рассматривать
вопросы передачи именно дискретных
сообщений. При этом в случае телефонной
связи под сообщением будем понимать
некоторую последовательность отсчетов
квантованного аналогового сигнала,
передаваемую в канале связи в виде
последовательности кодовых комбинаций.

Информация,
содержащаяся в сообщении, передается
от источника сообщений к получателю
по каналу передачи дискретных сообщений
(ПДС) (рис.1.).

Рис.1.
Тракт передачи дискретных сообщений

Характеристики
источника дискретных сообщений.

Сообщение
поступает от источника дискретных
сообщений, который характеризуется
алфавитом передаваемых сообщений

.

Алфавит
–
есть совокупность всех возможных
(различных) сообщений (знаков) данного
источника.

Объем
алфавита
– число различных символов алфавита
К.

Каждое
сообщение алфавита появляется с
некоторой вероятностью.

Вероятность
выдачи символа (сообщения)

–

.

Количество
информации в сообщении
(символе)
определяется вероятностью его
появления. Чем меньше вероятность
появления того или иного сообщения,
тем большее количество информации мы
извлекаем при его получении. В 1928г.
Хартли предложил определять количество
информации, которое приходится на
одно сообщение

,
выражением


.

Энтропия.
Среднее количество информации Н(А),
которое приходится на одно сообщение,
поступающее от источника без памяти,
получим, применяя операцию усреднения
по всему объему алфавита


,
(1)

Выражение
(1) известно как формула Шеннона для
энтропии источника дискретных
сообщений. Энтропия
—
мера неопределенности в поведении
источника дискретных сообщений.

Энтропия
равна нулю, если с вероятностью единица
источником выдается всегда одно и то
же сообщение (в этом случае неопределенность
в поведении источника сообщений
отсутствует). Энтропия максимальна,
если символы источника появляются
независимо и с одинаковой вероятностью.

Один
бит
— это количество информации, которое
переносит один символ источника
дискретных сообщений в том случае,
когда алфавит источника состоит из
двух равновероятных символов.

Среднее
количество информации, выдаваемое
источником в единицу времени, называют
производительностью
источника


,
[бит/с], (2)

где

—
среднее время, отводимое на передачу
одного символа (сообщения).

Среднее
время может быть определено выражением

.

Основные
характеристики канала ПДС.

Для
каналов передачи дискретных сообщений
вводят аналогичную характеристику —
скорость
передачи информации
по
каналу R. Она определяется количеством
бит, передаваемых в секунду. Максимально
возможное значение скорости передачи
информации по каналу называется
пропускной
способностью канала
и
обозначается С.

Пропускная
способность непрерывного канала с
белым гауссовским шумом определяется
известной формулой Шеннона


.

Как
видно из выражения данная величина
определяется шириной полосы пропускания
и соотношением сигнал-шум.

Сигналы
–
форма
сообщения для передачи по каналу связи

Любая
система связи обеспечивает передачу
именно сигналов,
а не сообщений. Поэтому сообщение,
поступающее от источника, предварительно
должно быть преобразовано в сигнал
определенной природы (электрический,
оптический …),
который является его переносчиком в
данной системе связи.

Виды
сигналов.
Различают четыре вида сигналов:
непрерывный непрерывного времени,
непрерывный дискретного времени,
дискретный непрерывного времени и
дискретный дискретного времени.

Непрерывные
сигналы непрерывного времени
называют
сокращенно непрерывными (аналоговыми)
сигналами. Они могут изменяться в
произвольные моменты, принимая любые
значения из непрерывного множества
возможных значений (рис.2). К таким
сигналам относится и известная всем
синусоида.

Рис.2.
Непрерывный сигнал непрерывного
времени

Рис.3.
Непрерывный сигнал дискретного
времени

Непрерывные
сигналы дискретного времени
могут
принимать произвольные значения, но
изменяться только в определенные,
наперед заданные (дискретные) моменты
t1,
t2,
t3,
… (рис.3).

Дискретные
сигналы непрерывного времени отличаются
тем, что они могут изменяться в
произвольные моменты, но их величины
принимают только разрешенные
(дискретные) значения (рис.4).

Дискретные
сигналы дискретного времени
(сокращенно
дискретные) (рис.5) в дискретные моменты
времени могут принимать только
разрешенные (дискретные) значения.

Рис.4.
Дискретный сигнал непрерывного
времени

Рис.5.
Дискретный сигнал дискретного
времени

Сигналы,
формируемые на выходе преобразователя
дискретного сообщения в сигнал, как
правило, являются по информационному
параметру дискретными, то есть
описываются функцией дискретного
времени и конечным множеством возможных
значений.

В технике
передачи данных такие сигналы называют
цифровыми
сигналами данных (ЦСД).

Рассмотрим
далее основные
определения, относящиеся к ЦСД.

Представляющий
(информационный)
параметр сигнала данных — параметр
сигнала данных, изменение которого
отображает изменение сообщения.

На рис.6.
изображен ЦСД, представляющим параметром
которого является амплитуда, а множество
возможных значений представляющего
параметра равно двум (U=U1
и U=0).

Рис.6.
Цифровой сигнал данных

Элемент
ЦСД — часть
цифрового сигнала данных, отличающаяся
от остальных частей значением одного
из своих представляющих параметров.

Значащая
позиция
— фиксируемое значение состояния
представляющего параметра сигнала.

Значащим
моментом (ЗМ)
— момент, в который происходит смена
значащей позиции сигнала.

Значащим
интервалом времени
— интервал времени между двумя соседними
значащими моментами сигнала.

Единичный
интервал
—
минимальный интервал времени, которому
равны значащие интервалы времени
сигнала, (интервалы а-б, б-в и другие
на рис.6).

Единичный
элемент (е.э.)
— элемент
сигнала, имеющий длительность, равную
единичному интервалу времени.

Различают
изохронные и анизохронные сигналы
данных.

Изохронные
сигналы это сигналы для которых любой
значащий интервал времени равен
единичному интервалу или их целому
числу.

Анизохронными
называются
сигналы, элементы которых могут иметь
любую длительность, но не менее чем

.
Кроме того, анизохронные сигналы могут
отстоять друг от друга на произвольном
расстоянии.

вопросы
по теме:

  1. Дайте
    определение понятиям “Информация”
    и “сообщение”.

  2. Перечислите
    основные характеристики источника
    дискретных сообщений.

  3. Чем
    определяется количество информации
    с дискретном сообщении.

  4. Что такое
    энтропия источника и как она
    определяется.

  5. Как
    определить производительность
    дискретного источника.

  6. Дайте
    определение основным параметрам
    цифровых сигналов данных.

  7. Какие
    сигналы называются изохронными и
    анизохронными.

Тема
2. Структура
системы передачи дискретных сообщений

назад
| оглавление
|
вперёд

Структурная
схема системы ПДС изображена на рис.1
Источник и получатель сообщений вместе
с преобразователем сообщения в сигнал
в состав системы ПДС не входят.

Рисунок
1. Структурная схема системы передачи
дискретных сообщений

Кодер
источника.
Сообщение, поступающее от источника
сообщений, в ряде случаев содержит
избыточность. Это обусловлено тем,
что символы

,
входящие в сообщение, могут быть
статистически связаны. Это позволяет
часть сообщения не передавать,
восстанавливая его на приеме по
известной статистической связи.

Избыточность
приводит к тому, что за заданный
промежуток времени будет передано
меньше сообщений, и, следовательно,
менее эффективно будет использоваться
канал передачи дискретных сообщений.
Задачу устранения избыточности на
передаче в СПДС выполняет кодер
источника.

Кодер
канала.
С целью повышения верности передачи
используется избыточное кодирование,
позволяющее на приеме обнаруживать
или даже исправлять ошибки.

В
процессе кодирования осуществляется
преобразование исходной кодовой
комбинации в другую кодовую комбинацию
с избыточностью. На приемном конце
декодер канала осуществляет обратное
преобразование (декодирование), в
результате которого получаем комбинацию
исходного кода. Часто кодер
и декодер канала называют
устройствами защиты от ошибок (УЗО).

Устройство
преобразования сигнала.
С целью согласования кодера канала и
декодера канала с непрерывным каналом
связи используются на передаче и
приеме устройства преобразования
сигналов (УПС). В частном случае это
модулятор и демодулятор.

Каналы.

Непрерывный
канал.
Это канал связи предназначенный для
передачи непрерывных (аналоговых)
сигналов. Например, абонентская
телефонная линия, канал ТЧ.

Дискретный
канал.
Совместно с каналом связи УПС образуют
дискретный канал, то есть канал,
предназначенный для передачи только
дискретных сигналов (цифровых сигналов
данных).

Различают
синхронные
и асинхронные дискретные каналы.

В
синхронных
дискретных
каналах ввод каждого единичного
элемента производится в строго
определенные моменты времени и они
предназначены для передачи только
изохронных сигналов.

По
асинхронному
каналу
можно передавать любые сигналы —
изохронные, анизохронные.

Расширенный
канал.
Дискретный канал в совокупности с
кодером и декодером канала (УЗО)
называется расширенным дискретным
каналом (РДК).

В
технике передачи данных РДК называют
каналом
передачи данных.

Полунепрерывный
канал (дискретный канал непрерывного
времени).

В
системе ПДС иногда выделяют дискретный
канал непрерывного времени.

Для
определения выхода данного канала
необходимо более детально рассмотреть
УПС приема. Он состоит из демодулятора,
порогового устройства и регенератора.
Выход ПУ одновременно является и
выходом дискретного канала непрерывного
времени.

Если
на выходе дискретного канала имеем
сигнал, являющийся дискретной функцией
дискретного времени, то на выходе
полунепрерывного канала сигнал
является дискретной функцией
непрерывного времени. (Он же канал
постоянного тока).

Контрольные
вопросы по теме:

1.
Нарисуйте структурную схему системы
передачи дискретных сообщений.

2.
Поясните назначение и основные функции
каждого блока структурной схемы.

3.
Перечислите какие каналы выделяются
в составе общей структурной

Тема
3. Каналы,
выделяемые в системе ПДС

назад
| оглавление
|
вперёд

3.1
НЕПРЕРЫВНЫЙ КАНАЛ СВЯЗИ (НКС)

На входе
и выходе НКС – непрерывный сигнал,
непрерывного времени.

НКС
– это канал ТЧ, стандартный широкополосный
канал (60-108 кГц), физическая линия (кабель,
волокно, воздушная линия и т. п.).

НКС может
описывается :

—
импульсной характеристикой или

—
комплексной частотной характеристикой,
которые связаны через преобразование
Фурье

где

;

Вместо ФЧХ
обычно измеряется групповое время
прохождения (ГВП), которое является
производной от ФЧХ.


Одной из
основных характеристик непрерывного
канала является его пропускная способность


.

Модель
НКС.

Канал может
быть представлен цепью с соответствующей
импульсной характеристикой и источниками
помех.

В канале
всегда присутствуют аддитивные гаусовские
помехи. Кроме гаусовских в канале
действуют помехи:

  • гармонические
    (сосредаточенные по частоте ),

  • импульсные
    (сосредаточенные по времени),

  • мультипликативные,

  • перерывы
    связи (17,4 дБ).

К искажениям
формы сигнала, также приводят:

  • сдвиг
    частотных составляющих по частоте,

  • фазовые
    скачки,

  • фазовое
    дрожание.

Упрощенная
модель канала представлена на следующем
рисунке

3.2
ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ

(полунепрерывный
канал или КПТ)

Пусть на
вход КПТ поступает последовательность
прямоугольных импульсов длительностью

.

Если на
выходе канала, все значащие моменты
(ЗМ) задержаны относительно исходных
на одинаковое время (определяемое
конечностью времени распространения
сигнала в канале), то считают, что ЗМ
совпадают с идеальными, а ЗИ с идеальными
значащими интервалами сигналов,
передаваемых на вход.

Под действием
различных дестабилизирующих факторов:

  • не
    идеальность характеристик НКС;

  • действие
    помех,

элементы
сигнала могут искажаться по длительности,
т. е. появляются краевые
искажения и дробления.

Индивидуальные
КИ
– смещения ЗМ относительно идеального
значащего момента D tки;

Относительные
КИ
– это индивидуальные, отнесенное к
длительности единичного элемента.



смещение
вправо считают положительным, смещение
влево – отрицательным

  • краевые
    искажения, возникающие под действием
    помех носят случайный характер и
    описываются соответствующим законам
    распределения (например, Гаусовским).

Преобладания
– элементы одного знака удлиняются, а
другого укорачиваются.


Дробления
– это искажения, при которых один элемент
длительностью

преобразуется
в несколько более коротких (дробится).

Дробления
характеризуются частостью их появления
и плотностью распределения длительности
дроблений.

3.3
МЕТОДЫ РЕГИСТРАЦИИ СИГНАЛОВ

Сигнал,
поступающий с выхода КПТ, должен быть
отождествлен с “1” или “0”. Процесс
определения и запоминания значащей
позиции сигнала данных – называется
регистрацией.

Наиболее
распространены для регистрации методы
стробирования и интегрирования.

Метод
стробирования
– значащая позиция принимаемого элемента
определяются на основании анализа знака
импульса в середине единичного интервала.

Если
индивидуальное КИ не превышает

,
то элемент регистрируются правильно.

Говорят
идеальная исправляющая способность
50%.

Исправляющая
способность
– это величина, на которую допускаются
смещения ЗМ, не вызывающее неправильный
прием элемента.

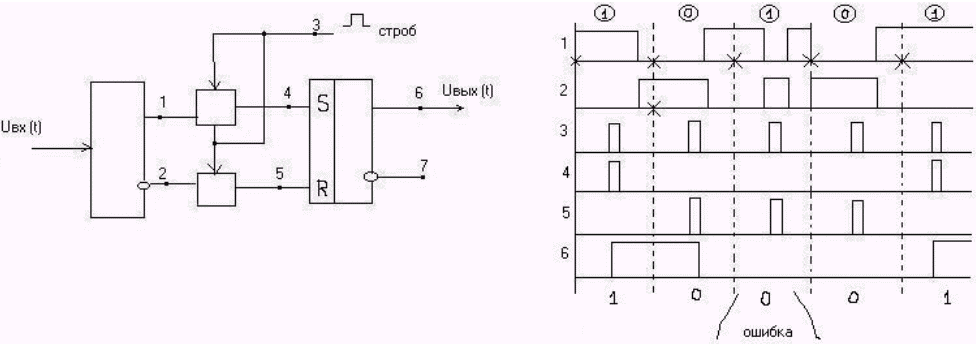
Простейшая
схема регистрации методом стробирования.

Схема
состоит из входного устройства, двух
ключей и RS-триггера. Входное устройство
имеет два выхода на один транслируется
входной сигнал без изменений, а на другой
с инверсией (точки 1 и 2). Стробирующие
импульсы открывают ключи на время своего
существования. Через ключи высокий
потенциал поступает на один из входов
тригера и переводит его в соответствующее
состояние. Последовательность 4 –
устанавливает триггер в “1”, а 5 –
сбрасывает триггер в “0”.

Интегральный
метод регистрации

Решение о
виде принятого элемента выносится на
основании анализа напряжения на всем
единичном интервале.

В идеальном
случае (если единичный. элемент не
искажен), то Uвых=
1

решением
о “1” принимается при

;

решением
о “0” принимается при

.

В цифровом
виде интегральный метод может быть
реализован на основе многократного
стробирования.

Структурная
схема интегрального метода.

На ключ
поступают стробирущие импульсы.
Управление ключом производится сигналом
с выхода порогового устройства. Импульсы
прошедшие ключ подсчитываются счетчиком.
По приходу тактового импульса решающее
устройство считывает показание счетчика,
сравнивает его с пороговым значением
и принимает решение о значащей позиции
на текущем интервале.

Алгоритм
принятия решения:

Пусть за
время неискаженной токовой посылки
появляется N тактовых импульсов, тогда:

если
показание счетчика

–
решение “1”

если меньше, то “0”

Временные
диаграммы работы данной схемы приведены
на следующем рисунке

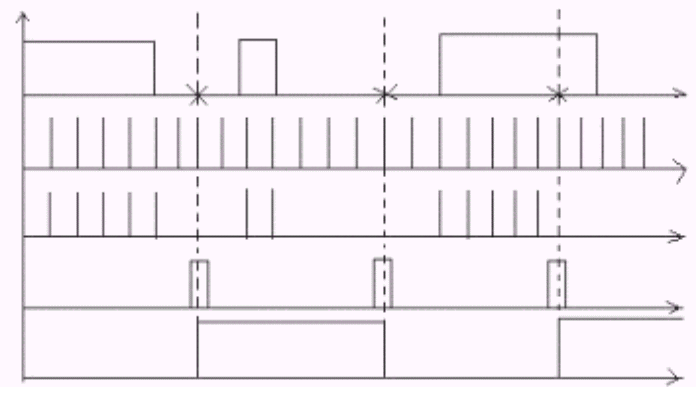
Сравнение
методов регистрации.

1. Вероятность
ошибки при действии КИ у метода
стробирования меньше

[стробирование
лучше].

2. При
дроблениях лучше интегральный метод

.

3.4
ДИСКРЕТНЫЙ КАНАЛ

ДК включает
НКС + УПС приема и передачи.

Алфавит
ДК состоит из двух сообщений “1” и “0”.

Основными
характеристиками ДК являются:

  1. Скорость
    передачи информации R [бит/с].

  2. Скорость
    модуляции B [Бод].

  3. Верность
    передачи информации характеризуется
    коэффициентом ошибок по единичным
    элементам.

–
экспериментально
измеряемая величина kош
является оценкой для вероятности ошибки
–

.

Статистика
ошибок в ДК.

Случайный
процесс возникновения ошибок описывается:

  1. Заданием
    входного А
    и выходного

    алфавитов.

  2. Совокупностью
    переходных вероятностей

    ,

где А
– произвольный символ (последовательность
входного алфавита);

—
произвольный символ (последовательность
выходного алфавита).

Говорят

—
вероятность приема символа

при
условии передачи А.

Для расчета
переходных вероятностей

,
любых последовательностей конечной
длины существуют математические модели
ошибок в дискретном канале.

Дискретный
симметричный канал без памяти.

Это канал,
для которого в любой момент времени
вероятность появления символа на выходе
зависит только от символа на входе.

вероятность
ошибки


.

Вероятности
правильного приема

Если эти
вероятности заданы, то легко получить
вероятность любой последовательности
на выходе, зная последовательность на
входе

.

Положим,
что приемником принята последовательность
длиной n- элементов.

Вероятность
безошибочного приема

Вероятность
что ошибка только в 1ом
элементе

Такая же
вероятность будет и для ошибки во втором
разряде.

ЗНАЧИТ!
Для получения вероятности того, что
среди n принятых элементов содержится
одна ошибка (на любом месте), нужно
просуммировать вероятности всех
возможных комбинаций с ошибкой в одном
разряде. Таких комбинаций будет n.

Для
определения вероятности t ошибок в
n-элементной комбинации, в любом сочетании,
нужно определить вероятность одного,
заданного сочетания ошибок веса t

Затем,
умножить данную вероятность на количество
всех возможных сочетаний ошибок данного
веса.


.

Тогда
окончательно:

3.5
РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ

(Включает
ДК+ Кодер + Декодер канала.)

Алфавит
канала состоит из 2n
сообщений,
где n
– число элементов в кодовой комбинаций

Характеризуется:

Коэффициентом
ошибок по кодовым комбинациям

Эффективной
скоростью передачи информации
– эффективная скорость учитывает, что
не все элементы несут информацию и не
все комбинации поступающие на вход
выдаются получателю.

Так как
РДК=КПД=ДК+УЗО, то основная задача
решается на уровне РДК повышения верности
передачи.

Методы
повышения верности:

  1. Меры
    эксплуатационного и профилактического
    характера

  • повышения
    стабильности работы генераторного
    оборудования

  • резервирование
    электропитания

  • выявление
    и замена отказавшего оборудования

  • повышение
    квалификации обслуживающего персонала

  1. Мероприятия
    по увеличению помехоустойчивости
    передачи единичных элементов

  • увеличение
    отношения сигнал – помеха (увеличение
    амплитуды, длительности…)

  • применение
    более помехоустойчивых методов модуляции

  • совершенствование
    методов обработки

  • выбор
    оптимальных сигналов

однако
это не всегда возможно!

  1. Введение
    избыточности в передаваемую
    последовательность т.е. помехоустойчивое
    кодирование

Оценка требуемой исправляющей способности кода для обеспечения заданной верности приема блока

Положим
что вероятность ошибки двоичного
элемента в

.

Сообщения
источника требуется передавать блоками
по n-двоичных символов.

Требуется
обеспечить вероятность неправильного
приема блока не более некоторой заданной
величины
.

Рассмотрим
все возможные ситуации при приеме
последовательности из n – элементов.

  1. вероятность
    правильного приема блока

    ;

  2. вероятность
    ошибки кратности t

Совокупность
всех возможных исходов будет составлять
полную группу событий. Поэтому можно
записать:

при этом:

—
это вероятность того, что в блоке будет
хотя бы одна ошибка. Другими словами –
это есть

–
если не предпринято никаких мер защиты.

Если

,
то необходимо обеспечить исправления
ошибок некоторой кратности в блоке.

Оценим,
ошибки какой кратности нужно исправить.

Найдем
вероятность неправильного приема при
исправлении однократной ошибки. Она
будет равна:


.

Вновь
проводим сравним Рн.п(1)
и
А, если требования не выполнилось, то
убираем 2х,
3х
и
т.д. кратной ошибки.

Последняя
кратность ошибки, вычитание вероятности
которой привело к выполнению условия
и будет требуемой исправляющей
способностью кода.

При этом
из всех n-элементов блока, часть (r)
необходимо будет отдать на проверочные
элементы, что естественно внесет
избыточность в передаваемое сообщение
и понизит скорость передачи

Контрольные
вопросы по теме:

  1. Что такое
    непрерывный канал связи (НКС).

  2. Назовите
    основные характеристики НКС.

  3. Нарисуйте
    модель НКС и поясните смысл входящих
    в неё элементов

  4. Что является
    входом и выходом дискретного канала
    непрерывного времени (ДКНВ).

  5. Что такое
    краевые искажения и чем они характеризуются.

  6. Что такое
    преобладания и дробления.

  7. Каково
    назначение методов регистрации.

  8. Что такое
    исправляющая способность приемника

  9. В чем
    состоит основная идея регистрации
    методом стробирования

  10. Нарисуйте
    структурную схему устройства, реализующего
    регистрацию методом стробирования и
    поясните принцип её работы.

  11. В чем
    состоит основная идея интегрального
    метода регистрации.

  12. Нарисуйте
    структурную схему устройства, реализующего
    регистрацию интегральным методом и
    поясните принцип работы.

  13. Сравните
    методы регистрации.

  14. Какие
    элементы общей структурной схемы входят
    в дискретный канал.

  15. Перечислите
    основные характеристики дискретного
    канала.

  16. Поясните
    модель дискретного симметричного
    канала без памяти.

  17. Как
    определить вероятность ошибки кратности
    t в комбинации длиной n элементов.

  18. Изобразите
    структурную схему расширенного
    дискретного канала.

  19. Назовите
    основные характеристики расширенного
    дискретного канала.

  20. Перечислите
    методы повышения верности передачи.

  21. Какова
    основная идея выбора исправляющей
    способности кода для обеспечения
    заданной верности передачи.

Тема
4. Эффективное
(статическое) кодирование

назад
| оглавление
|
вперёд

Эффективное
кодирование – это процедуры направленные
на устранение избыточности.

Основная
задача эффективного кодирования –
обеспечить, в среднем, минимальное
число двоичных элементов на передачу
сообщения источника. В этом случае,
при заданной скорости модуляции
обеспечивается передача максимального
числа сообщений, а значит максимальная
скорости передачи информации.

Пусть
имеется источник дискретных сообщений,
алфавит которого

.

При
кодировании сообщений данного источника
двоичным, равномерным кодом, потребуется

двоичных
элементов на кодирование каждого
сообщения.

Если
вероятности

появления
всех сообщений источника равны, то
энтропия источника (или среднее
количество информации в одном сообщении)
максимальна и равна

.

В
данном случае каждое сообщение
источника имеет информационную емкость

бит,
и очевидно, что для его кодирования
(перевозки) требуется двоичная
комбинация не менее

элементов.
Каждый двоичный элемент, в этом случае,
будет переносить 1 бит информации.

Если
при том же объеме алфавита сообщения
не равновероятны, то, как известно,
энтропия источника будет меньше


.

Если
и в этом случае использовать для
перевозки сообщения

-разрядные
кодовые комбинации, то на каждый
двоичный элемент кодовой комбинации
будет приходиться меньше чем 1 бит.

Появляется
избыточность, которая может быть
определена по следующей формуле


.

Среднее
количество информации, приходящееся
на один двоичный элемент комбинации
при кодировании равномерным кодом


.

Пример

Для
кодирования 32 букв русского алфавита,
при условии равновероятности, нужна
5 разрядная кодовая комбинация. При
учете ВСЕХ статистических связей
реальная энтропия составляет около
1,5 бит на букву. Нетрудно показать, что
избыточность в данном случае составит


,

Если
средняя загрузка единичного элемента
так мала, встает вопрос, нельзя ли
уменьшить среднее количество элементов
необходимых для переноса одного
сообщения и как наиболее эффективно
это сделать?

Для
решения этой задачи используются
неравномерные коды.

При
этом, для передачи сообщения, содержащего
большее количество информации, выбирают
более длинную кодовую комбинацию, а
для передачи сообщения с малым объемом
информации используют короткие кодовые
комбинации.

Учитывая,
что объем информации, содержащейся в
сообщении, определяется вероятностью
появления


,
можно перефразировать данное
высказывание.

Для
сообщения, имеющего высокую вероятность
появления, выбирается более короткая
комбинация и наоборот, редко встречающееся
сообщение кодируется длинной
комбинацией.

Т.о.
на одно сообщение будет затрачено в
среднем меньшее единичных элементов

,
чем при равномерном.

Если
скорость телеграфирования постоянна,
то на передачу одного сообщения будет
затрачено в среднем меньше времени

А
значит, при той же скорости телеграфирования
будет передаваться большее число
сообщений в единицу времени, чем при
равномерном кодировании, т.е.
обеспечивается большая скорость
передачи информации.

Каково
же в среднем минимальное количество
единичных элементов требуется для
передачи сообщений данного источника?

Ответ
на этот вопрос дал Шеннон.

Шеннон
показал, что

1.
Нельзя закодировать сообщение двоичным
кодом так, что бы средняя длина кодового
слова

была
численно меньше величины энтропии
источника сообщений

.

,
где

.

2.
Существует способ кодирования, при
котором средняя длина кодового слова
немногим отличается от энтропии
источника

Остается
выбрать подходящий способ кодирования.

Эффективность
применения оптимальных неравномерных
кодов может быть оценена:

  1. Коэффициентом
    статистического сжатия, который
    характеризует уменьшение числа
    двоичных элементов на сообщение, при
    применении методов эффективного
    кодирования в сравнении с равномерным


    .
    Учитывая, что

    ,
    можно записать

    .
    Ксс лежит в пределах от 1 — при равномерном
    коде до

    ,
    при наилучшем способе кодирования.

  2. Коэффициент
    относительной эффективности


—
позволяет сравнить эффективность
применения различных методов
эффективного кодирования.

В
неравномерных кодах возникает проблема
разделения кодовых комбинаций. Решение
данной проблемы обеспечивается
применением префиксных кодов.

Префиксным
называют код, для которого никакое
более короткое слово не является
началом другого более длинного слова
кода. Префиксные коды всегда однозначно
декодируемы.

Веедем
понятие кодового дерева для множества
кодовых слов.

Наглядное
графическое изображение множества
кодовых слов можно получить, установив
соответствие между сообщениями и
концевыми узлами двоичного дерева.
Пример двоичного кодового дерева
изображен на рисунке. 1.

Рисунок
1.
Пример двоичного кодового дерева

Две
ветви, идущие от корня дерева к узлам
первого порядка, соответствуют выбору
между “0” и “1” в качестве первого
символа кодового слова: левая ветвь
соответствует “0”, а правая – “1”.
Две ветви, идущие из узлов первого
порядка, соответствуют второму символу
кодовых слов, левая означает “0”, а
правая – “1” и т. д. Ясно, что
последовательность символов каждого
кодового слова определяет необходимые
правила продвижения от корня дерева
до концевого узла, соответствующего
рассматриваемому сообщению.

Формально
кодовые слова могут быть приписаны
также промежуточным узлам. Например,
промежуточному узлу второго порядка
на рис.1 можно приписать кодовое слово
11, которое соответствует первым двум
символам кодовых слов, соответствующих
концевым узлам, порождаемых этим
узлом. Однако кодовые слова,
соответствующие промежуточным узлам,
не могут быть использованы для
представления сообщений, так как в
этом случае нарушается требование
префиксности кода.

Требование,
чтобы только концевые узлы сопоставлялись
сообщениям, эквивалентно условию,
чтобы ни одно из кодовых слов не совпало
с началом (префиксом) более длинного
кодового слова.

Любой
код, кодовые слова которого соответствуют
различным концевым вершинам некоторого
двоичного кодового дерева, является
префиксным, т. е. однозначно декодируемым.

Метод
Хаффмена

Одним
из часто используемых методов
эффективного кодирования является
так называемый код Хаффмена.

Пусть
сообщения входного алфавита

имеют
соответственно вероятности их появления

.

Тогда
алгоритм кодирования Хаффмена состоит
в следующем:

1.
Сообщения располагаются в столбец в
порядке убывания вероятности их
появления.

2.
Два самых маловероятных сообщения
объединяем в одно сообщение

,
которое
имеет вероятность, равную сумме
вероятностей сообщений

,
т.
е.

.
В результате получим сообщения

,
вероятности
которых

.

3.
Повторяем шаги 1 и 2 до тех пор, пока не
получим единственное сообщение,
вероятность которого равна 1.

4.
Проводя линии, объединяющие сообщения
и образующие последовательные
подмножества, получаем дерево, в
котором отдельные сообщения являются
концевыми узлами. Соответствующие им
кодовые слова можно определить,
приписывая правым ветвям объединения
символ “1”, а левым — “0”. Впрочем,
понятия “правые” и “левые” ветви в
данном случае относительны.

На
основании полученной таблицы можно
построить кодовое дерево

Так
как в процессе кодирования сообщениям
сопоставляются только концевые узлы,
полученный код является префиксным
и всегда однозначно декодируем.

При
равномерных кодах одиночная ошибка
в кодовой комбинации приводит к
неправильному декодированию только
этой комбинации. Одним из серьёзных
недостатков префиксных кодов является
появление трека ошибок, т.е. одиночная
ошибка в кодовой комбинации, при
определенных обстоятельствах, способна
привести к неправильному декодированию
не только данной, но и нескольких
последующих кодовых комбинаций.

Пример
на однозначность декодирования и трек
ошибок

Пусть
передавалась следующая последовательность

1
0
0
1
1
1 0
0
0 1

a
b c d

При
возникновении ошибки в первом двоичном
элементе, получим

0
0 0 1
1
1 0
0
0 1

g
c d

Т.О.
ошибка в одном разряде комбинации
первого символа привела к неправильному
декодированию двух символов. (Трек
ошибок).

Контрольные
вопросы по теме:

  1. Назначение
    и цели эффективного кодирования.

  2. Поясните
    за счет чего, обеспечивается достижение
    сжатия при эффективном кодировании.

  3. Чем
    определяется минимальная средняя
    длина кодовой комбинация при применении
    эффективном кодировании.

  4. Какие
    проблемы возникают при разделении
    неравномерных кодовых комбинаций.

  5. Что
    такое префиксные коды.

  6. В чем
    заключается алгоритм Хаффмана.

  7. Что
    такое трек ошибок, и каковы причины
    его возникновения.

Тема
5. Защита
от ошибок в системах связи

назад
| оглавление
|
вперёд

От
СПДС обычно требуется не только
передавать сообщения с заданной
скоростью передачи информации, но и
обеспечивать при этом требуемую
достоверность.

Получив
сообщение, пользователь должен быть
с высокой степенью уверен, что
отправлялось именно это сообщение.

Помехи,
действующие в канале, как известно,
приводят к возникновению ошибок.
Исходная вероятность ошибки в каналах
связи обычно не позволяет достичь
высокой степени достоверности без
применения дополнительных мероприятий.
К таким мероприятиям, обеспечивающим
защиту от ошибок, относят применения
корректирующих кодов.

В
общей структурной схеме СПДС задачу
защиты от ошибок выполняет кодер и
декодер канала, который иногда называют
УЗО.

5.1
Понятие о корректирующих кодах

Пусть
имеется источник сообщений с объемом
алфавита К.

Поставим
в соответствие каждому сообщению n —
элементную двоичную последовательность.
Всего последовательностей из n —
элементов может быть

.

Если

,
то все последовательности (или кодовые
комбинации) будут использоваться для
кодирования сообщений, т.е. будут
разрешенными.

Полученный
таким образом код называется простым,
он не способен обнаруживать и исправлять
ошибки.

Для
того, что бы код мог обнаруживать и
исправлять ошибки необходимо выполнение
условия

,
при этом неиспользуемые для передачи
комбинации (N0-K)
называют запрещенными.

Появление
ошибки в кодовой комбинации будет
обнаружено, если передаваемая
разрешенная комбинация перейдет в
одну из запрещенных.

Расстояние
Хемминга
– характеризует степень различия
кодовых комбинаций и определяется
числом несовпадающих в них разрядов.

Перебрав
все возможные пары разрешенных
комбинаций рассматриваемого кода
можно найти минимальное расстояние
Хемминга d0.

Минимальное
расстояние d0
— называется кодовым
расстоянием

Кодовое
расстояние определяет способность
кода обнаруживать и исправлять ошибки.

У
простого кода d0=1
– он не обнаруживает и не исправляет
ошибки. Так как любая ошибка переводит
одну разрешенную комбинацию в другую.

В
общем случае справедливы следующие
соотношения


–
для
обнаруживающей способности


–
для
исправляющей способности

Линейные
коды.

Двоичный
блочный код является линейным если
сумма по модулю 2 двух кодовых слов
является также кодовым словом.

Линейные
коды также называют групповыми.

Введем
понятия группы.

Множество
элементов с определенной на нем
групповой операцией называется
группой, если выполняется следующие
условия:

1.
Замкнутость gi
g
j=
gk

G
в результате операции с двумя элементами
группы получается третий, так же
принадлежащий этой группе.

2.
Ассоциативность (сочетательность)
(gi
gj)

gk
= gi

(gj

gk)

3.
Наличие нейтрального элемента gj

e
= gj

4.
Наличие обратного элемента. gi

(gi)-1=
e

Если
выполняется условие gi

gj
=
gj

gi,
то группа называется коммутативной.

Множество
кодовых комбинаций n-элементного кода
является замкнутой группой с заданной
групповой операцией сложение по модулю
2.

Поэтому
используя свойство замкнутости
относительно операции

2,
множество всех элементов можно задать
не перечислением всех элементов, а
производящей матрицей.

Все
остальные элементы, кроме 0, могут быть
получены путем сложения по модулю 2
строк производящей матрицы в различных
сочетаниях.

В
общем случае строки производящей
матрицы могут быть любыми линейно
независимыми, но проще и удобнее брать
в качестве производящей матрицы –
единичную.

5.2
ЦИКЛИЧЕСКИЕ КОДЫ

Широкое
распространение на практике получил
класс линейных кодов, которые называются
циклическими. Данное название происходит
от основного свойства этих кодов:

если
некоторая кодовая комбинация принадлежит
циклическому коду, то комбинация
полученная циклической перестановкой
исходной комбинации (циклическим
сдвигом), также принадлежит данному
коду.

.

Вторым
свойством всех разрешенных комбинаций
циклических кодов является их делимость
без остатка на некоторый выбранный
полином, называемый производящим.

Синдромом
ошибки в этих кодах является наличие
остатка от деления принятой кодовой
комбинации на производящий полином.

Эти
свойства используются при построении
кодов, кодирующих и декодирующих
устройств, а также при обнаружении и
исправлении ошибок.

Представление
кодовой комбинации в виде многочлена.

Описание
циклических кодов и их построение
удобно проводить с помощью многочленов
(или полиномов).

В
теории циклических кодов кодовые
комбинации обычно представляются в
виде полинома. Так, n-элементную кодовую
комбинацию можно описать полиномом
(n-1) степени, в виде


.

где

={0,1},
причем

=
0 соответствуют нулевым элементам
комбинации, а

=
1 — ненулевым.

Запишем
полиномы для конкретных 4-элементных
комбинаций

Действия
над многочленами.

При
формировании комбинаций циклического
кода часто используют операции сложения
многочленов и деления одного многочлена
на другой. Так,


,

поскольку

.

Следует
отметить, что действия над коэффициентами
полинома (сложение и умножение)
производятся по модулю 2.

Рассмотрим
операцию деления на следующем примере:

Деление
выполняется, как обычно, только
вычитание заменяется суммированием
по модулю два.

Отметим,
что запись кодовой комбинации в виде
многочлена, не всегда определяет длину
кодовой комбинации. Например, при n =
5, многочлену

соответствует
кодовая комбинация 00011.

Алгоритм
получения разрешенной кодовой
комбинации циклического кода из
комбинации простого кода

Пусть
задан полином

,
определяющий корректирующую способность
кода и число проверочных разрядов r,
а также исходная комбинация простого
k-элементного кода в виде многочлена

.

Требуется
определить разрешенную кодовую
комбинацию циклического кода (n, k).

  1. Умножаем
    многочлен исходной кодовой комбинации
    на

  1. Определяем
    проверочные разряды, дополняющие
    исходную информационную комбинацию
    до разрешенной, как остаток от деления
    полученного в предыдущем пункте
    произведения на образующий полином

  1. Окончательно
    разрешенная кодовая комбинация
    циклического кода определится так

Для
обнаружения ошибок в принятой кодовой
комбинации достаточно поделить ее на
производящий полином. Если принятая
комбинация — разрешенная, то остаток
от деления будет нулевым. Ненулевой
остаток свидетельствует о том, что
принятая комбинация содержит ошибки.
По виду остатка (синдрома) можно в
некоторых случаях также сделать вывод
о характере ошибки, ее местоположении
и исправить ошибку.

Формирование
базиса (производящей матрицы)
циклического кода

Формирование
базиса циклического кода возможно
как минимум двумя путями.

Вариант
первый.

  1. Составить
    единичную матрицу для простого
    исходного кода.

  2. Определить
    для каждой кодовой комбинации исходного
    кода группу проверочных элементов и
    дописать их в соответствующие строки
    матрицы.

Полученная
матрица и будет базисом циклического
кода. Причем, в данном случае, разрешенные
комбинации заведомо разделимы (т.е.
информационные и проверочные элементы
однозначно определены).

Вариант
второй.

  1. Дописать
    слева от КК, соответствующей образующему
    полиному циклического кода нули так,
    чтобы длина разрешенной кодовой
    комбинации равнялась n.

  2. Получить
    остальные разрешенные кодовые КК
    базиса, используя циклический сдвиг
    исходной. (В базисе должно быть k –
    строк)

В данном
случае код будет неразделимым.

Получив
базис ЦК, можно получить все разрешенные
комбинации, проводя сложение по модулю
2 кодовых комбинаций базиса в различных
сочетаниях и плюс НУЛЕВАЯ.

Циклические
коды достаточно просты в реализации,
обладают высокой корректирующей
способностью (способностью исправлять
и обнаруживать ошибки) и поэтому
рекомендованы МСЭ-Т для применения в
аппаратуре ПД. Согласно рекомендации
V.41 в системах ПД с ОС рекомендуется
применять код с производящим полиномом

Построение
кодера циклического кода

Рассмотрим
код (9,5) образованный полиномом


.

Разрешенная
комбинация циклического кода

образуется
из комбинации простого (исходного)
кода путем умножения ее на

и
прибавления остатка R(x) от деления

на
образующий полином
.

  1. Умножение
    полинома на одночлен

эквивалентно
добавлению к двоичной последовательности
соответствующей G(x) , r — нулей справа.

Пусть

тогда

Для
реализации операции добавления нулей
используется r-разрядный регистр
задержки.

  1. Рассмотрим
    более подробно операцию деления:

Как
видим из примера, процедура деления
одного двоичного числа на другое
сводится к последовательному сложению
по mod2
делителя [10011] с соответствующими
членами делимого [10101], затем с двоичным
числом, полученным в результате первого
сложения, далее с результатом второго
сложения и т.д., пока число членов
результирующего двоичного числа не
станет меньше числа членов делителя.

Это
двоичное число и будет остатком

.

Построение
формирователя остатка циклического
кода

Структура
устройства осуществляющего деление
на полином полностью определяется
видом этого полинома. Существуют
правила позволяющие провести построение
однозначно.

Сформулируем
правила построения ФПГ.

  1. Число
    ячеек памяти равно степени образующего
    полинома r.

  2. Число
    сумматоров на единицу меньше веса
    кодирующей комбинации образующего
    полинома.

  3. Место
    установки сумматоров определяется
    видом образующего полинома.

Сумматоры
ставят после каждой ячейки памяти,
(начиная с нулевой) для которой
существует НЕнулевой член полинома.
Не ставят после ячейки для которой в
полиноме нет соответствующего члена
и после ячейки старшего разряда.

4.
В цепь обратной связи необходимо
поставить ключ, обеспечивающий
правильный ввод исходных элементов
и вывод результатов деления.

Структурная
схема кодера циклического кода (9,5)

Полная
структурная схема кодера приведена
на следующем рисунке. Она содержит
регистр задержки и рассмотренный выше
формирователь проверочной группы.

Рассмотрим
работу этой схемы

1.
На первом этапе К1–
замкнут К2
–
разомкнут. Идет одновременное заполнение
регистров задержки и сдвига информ.
элементами (старший вперед!) и через
4 такта старший разряд в ячейке №4

2.
Во время пятого такта К2
–
замыкается а К1
– размыкается с этого момента в ФПГ
формируется остаток. Одновременно из
РЗ на выход выталкивается задержание
информационные разряды.

За
5 тактов (с 5 по 9 включительно) в линию
уйдут все 5-информационных элемента.
К этому времени в ФПГ сформируется
остаток

3.
К2
– размыкается, К1
– замыкается и в след за информационными
в линию уйдут элементы проверочной
группы.

4.
Одновременно идет заполнение регистров
новой комбинацией.

Второй
вариант построения кодера ЦК.

Рассмотренный
выше кодер очень наглядно отражает
процесс деления двоичных чисел. Однако
можно построить кодер содержащий
меньшее число элементов т.е. более
экономичный.

Устройство
деления на производящий полином

можно
реализовать в следующем виде:

За
пять тактов в ячейках будет сформирован
такой же остаток от деления, что и в
рассмотренном выше Формирователе
проверочной группы. (ФПГ).

За
эти же 5 тактов информационные разряды,
выданные сразу на модулятор.

Далее
в след за информационными уходят
проверочные из ячеек устройств деления.

Но
важно отключить обратную связь на
момент вывода проверенных элементов,
иначе они исказятся.

Окончательно
структурная схема экономичного кодера
выглядит так.

—
На первом такте Кл.1 и Кл.3 замкнуты,
информационные элементы проходят на
выход кодера и одновременно формируются
проверочные элементы.

—
После того, как в линию уйдет пятый
информационный элемент, в устройстве
деления сформируются проверочные;

—
на шестом такте ключи 1 и 3 размыкаются
(разрываются обратная связь), а ключ
2 замыкается и в линию уходят проверочные
разряды.

Ячейки
при этом заполняются нулями и схема
возвращается в исходное состояние.

Определение
ошибочного разряда в ЦК.

Пусть
А(х)-многочлен соответствующий
переданной кодовой комбинации.

Н(х)-
многочлен соответствующей принятой
кодовой комбинацией.

Тогда
сложение данных многочленов по модулю
два даст многочлен ошибки.

E(x)=A(x)

H(x)

При
однократной ошибке Е(х) будет содержать
только один единственный член
соответствующий ошибочному разряду.

Остаток
– полученный от деления принятого
многочлена H(x) на производящей Pr(x)
равен остатку полученному при делении
соответствующего многочлена ошибок
E(x) на Pr(x)

При
этом ошибке в каждом разряде будет
соответствовать свой остаток R(x) (он
же синдром), а значит, получив синдром
можно однозначно определить место
ошибочного разряда.

Алгоритм
определения ошибки.

Пусть
имеем n-элементные комбинации (n = k + r)
тогда:

1.
Получаем остаток от деления Е(х)
соответствующего ошибке в старшем
разряде [1000000000], на образующей поленом
Pr(x)

2.
Делим полученный полином Н(х) на Pr(x)
и получаем текущий остаток R(x).

3.
Сравниваем R0(x)
и R(x).

—
Если они равны, то ошибка произошла в
старшем разряде.

—
Если «нет», то увеличиваем степень
принятого полинома на Х и снова проводим
деления

в)
Опять сравниваем полученный остаток
с R0(x)

—
Если они равны, то ошибки во втором
разряде.

—
Если нет, то умножаем Н(х)х2
и повторяем эти операции до тех пор,
пока R(X) не будет равен R0(x).

Ошибка
будет в разряде соответствующем числу
на которое повышена степень Н(х) плюс
один.

Например:

то
номер ошибочного разряда 3+1=4

Пример
декодирования комбинации ЦК.

Положим,
получена комбинация H(х)=111011010

Проанализируем
её в соответствии с вышеприведенным
алгоритмом.

Реализуя
алгоритм определения ошибок, определим
остаток от деления вектора соответствующего
ошибке в старшем разряде Х8
на производяший полином P(x)=X4+X+1

X8
X2+X+1

X8+X5+X4
x4+x+1

X5+X4

X5+X2+X

X4+X2+X

X4+X+1

X2+1=R0(X)=0101

Разделим
принятую комбинацию на образующий
полином

Полученный
на 9-м такте остаток, как видим, не равен
R0(X).
Значит необходимо умножить принятую
комбинацию на Х и повторить деление.
Однако результаты деления с 5 по 9 такты
включительно будут такими же, значит
необходимо продолжить деление после
девятого такта до тех пор, пока в
остатке не будет R0(Х).
В нашем случае это произойдет на 10
такте, при повышении степени на 1.
Значит ошибки во втором разряде.

Декодер
циклического кода с исправлением
ошибки

Если
ошибка в первом разряде, то остаток
R0(X)=10101
появления после девятого такта в
ячейках ФПГ.

Если
во втором по старшинству то после
10го;

в третьем по старшинству то после
11го;

в
четвертом по старшинству то после
12го

в пятом по старшинству то после
13го

в шестом по старшинству то после
14го

в седьмом по старшинству то после
15го

в восьмом по старшинству то после
16го

в девятом по старшинству то после
17го.

На
10 такте старший разряд покидает регистр
задержки и проходит через сумматор
по модулю 2.

Если
и этому моменту остаток в ФПГ=R0(X),
то логическая 1 с выхода дешифратора
поступит на второй вход сумматора и
старший разряд инвертируется.

В
нашем случае инвертируется второй
разряд на 11 такте.

5.3
Выбор образующего полинома

Рассмотрим
вопрос выбора образующего полинома,
который определяет корректирующие
свойства циклического кода. В теории
циклических кодов показано, что
образующий полином представляет собой
произведение так называемых минимальных
многочленов mi(x),
являющихся простыми сомножителями
(то есть делящимся без остатка лишь
на себя и на 1) бинома xn+
1:

P(x)=m1(x)*
m3(x)…mj(x),
(*)

где
j
= d0
– 2
=(
2tu.ош+1)
– 2 = 2 tи.ош
– 1.

Существуют
специальные таблицы минимальных
многочленов, одна из которых приведена
ниже. Кроме образующего полинома
необходимо найти и количество
проверочных разрядов r.
Оно определяется из следующего свойства
циклических кодов:

для
любых значений l
и
tи.ош
существует циклический код длины n
=2l
– 1, исправляющий все ошибки кратности
tи.ош
и менее, и содержащий не более

проверочных
элементов.

Так
как

,
то

откуда

.
(**)

Очевидно,
что для уменьшения времени передачи
кодовых комбинаций, r
следует выбирать как можно меньше.
Пусть, например, длина кодовых комбинаций
n
=
7, кратность исправляемых ошибок tи.ош
=1. Из (**) получим r
= 1
.
log2
( 7+1 )=3.

После
определения количества проверочных
разрядов r,
вычисления образующего полинома
удобно осуществить, пользуясь таблицей
минимальных многочленов, представленной
в следующем виде:

Таблица минимальных многочленов

J=2tи.ош
-1

Вид
минимальных многочленов для

1

2

3

4

5

6

7

1

x2+x+1

x3+x+1

x4+x+1

x5+x+1

x6+x+1

x7+x+1

3

—

—

x4+x3+

+x2+x+1

x5+x4+

+x3+x2+1

x6+x4+

+x2+x+1

x7+x3+

+x2+x+1

5

—

—

—

x5+x4+

+x2+x+1

x6+x5+

+x2+x+1

x7+x4+

+x3+x2+1

7

—

—

—

—

x6+x3+1

X7+x6+x5+

+x4+x2+x+1

Определяя
образующий полином, нужно из столбца
для соответствующего соотношения

выписать
все многочлены, начиная с верхней
строки до нижней с номером j=2tи.ош–1
включительно. После этого следует
перемножить выбранные минимальные
многочлены в соответствии с (*). В
частности, если r=3,
tи.ош=1,
j=2*1-1=1,
образующий полином будет представлять
собой единственный минимальный
многочлен P(x)=
m1(x)
= x3+x+1
(первая строка, второй столбец таблицы
). Соответственно образующее число
равно 1011.

Контрольные
вопросы по теме:

  1. Что такое
    разрешенные и запрещенные кодовые
    комбинации.

  2. Что
    называется расстоянием Хемминга.

  3. Дайте
    понятие кодового расстояния и как
    его определить.

  4. Как
    связано кодовое расстояние с
    исправляющей и обнаруживающей
    способностью кода.

  5. Какой
    код называется линейным.

  6. Какое
    множество называется группой.

  7. Назовите
    основные свойства циклических кодов.

  8. Запишите
    полином

    в
    двоичном виде.

  9. Запишите
    полином, соответствующий двоичной
    записи 100111.

  10. Получите
    остаток от деления полинома

    на

    .

  11. Как
    получают разрешенные комбинации при
    циклическом кодировании.

  12. Нарисуйте
    кодер для циклического кода, порождаемого
    полиномом

    .
    Поясните принцип работы кодера.

  13. По какому
    признаку обнаруживают ошибку в
    принятой кодовой комбинации.

  14. Каков
    алгоритм определения ошибочного
    разряда в комбинации циклического
    кода.

  15. Нарисуйте
    структурную схему декодера,
    обеспечивающего обнаружение ошибок
    для кода (7,4) при производящем полиноме

    .
    Поясните принцип его работы.

  16. Нарисуйте
    структурную схему декодера,
    обеспечивающего исправление однократной
    ошибки для кода (7,4) при производящем
    полиноме

    .
    Поясните принцип его работы.

  17. Как
    выбирается образующий (производящий)
    полином?

Тема
6. Устройства
преобразования сигнала

назад
| оглавление
|
вперёд

УПС —
обеспечивают согласование параметров
сигналов источника с параметрами канала
связи.

Согласование
может производиться по:

– полосе
частот;

– уровню;

– скорости.

Согласование
спектра может производиться двумя
путями:

  • Перекодированием.

  • С
    использованием несущей (модуляции).

Известно,
что спектр последовательности
прямоугольных импульсов имеет вид (sin
x)/x с максимумом на нулевой частоте.
Основная энергия сигналов в этом случае
сосредоточена в полосе частот

Канал
связи, из-за наличия развязывающих
трансформаторов, не пропускает постоянную
составляющую. Из-за этого однополярные
сигналы будут испытывать значительные
искажение.

6.1
ПЕРЕКОДИРОВАНИЕ

При
перекодировании исходные сигналы
заменяются сигналами другой структуры
спектральные характеристики которых
лучше согласуются с параметрами заданного
канала связи.

Помимо
основной задачи – согласования спектров
при перекодировании стараются подобрать
такой код, который обеспечивал бы:

  • наименьшую
    ширину спектра при одинаковой скорости
    передачи;

  • синхронизацию
    между передатчиком и приёмником;

  • низкую
    стоимость реализации;

  • возможность
    обнаруживать ошибки.

Простейшим
решением является биполярный код (None
return zero NRZ)

Преимущество:
малая полоса пропускания; простая
реализация; нет избыточности.

Недостатки:
потеря
синхронизации при длинных сериях
элементов одного знака.

Обычно при
перекодировании в сигнал вводится
избыточность.

Различают
два способа введения избыточности.

1. Увеличение
в процессе перекодирвания основания
кода (увеличение числа значащих позиций
было две значащих позиции, а стало 3).

Например,
код с чередованием полярности (КЧП он
же AMI)

0 заменяется
на 0, а 1 на ± 1 — чередуется

Достоинства:

  • Данный
    код позволяет избавиться от постоянной
    составляющей;

  • Так как
    чередование обязательно, то такой код
    может обнаружить ошибку.

Недостатки

  • Избыточность
    кода 0,37;

  • Основной
    недостаток – потеря тактовой частоты
    при передаче длинной серии нулей.

2. При втором
подходе каждый элемент на единичном
интервале заменяется двумя разнополярными
импульсами

1

01

0

10

Очевидно,
что избыточность такого кода 0,5 (то есть
больше чем у КЧП)

+ Так как
сигнал изменяется по крайней мере один
раз на единичном интервале, то такой
код обладает хорошими самосинхронизирующими
свойствами.

+ Отсутствие
постоянной составляющей

+ Если
перепада на единичном интервале нет,
то ошибка

Рассмотренный
код называют МАНЧЕСТЕРСКИМ

Он находит
широкое применение в технологиях
локальных сетей, а именно в Ethernet и Token
ring.

Следует
обратить внимание на спектр кода.

При
чередовании 1 и 0 основная гармоника
спектра становиться в два раза ниже (по
частоте) в сравнении с ситуацией, когда
идут элементы одного знака.

(Применительно
к Ethernet со скоростью 10 Мбит /с, частота
несущей 5 или 10 МГц.)

Для вхождения
в синхронизм перед каждым пакетом
передается преамбула, составляющая из
7 байт чередования 10101010 и восьмого
10101011.

Оба подхода
позволяют устранить постоянную
составляющую, чем и достигается
согласование.

Потенциальный
код 2B1Q

В сетях
ISDN и системах xDSL широкое применение
находит код 2B1Q.

Для передачи
используется 4 значащих позиции, при
этом один импульс несёт 2 бита информации

Очевидно,
что для данного кода скорость передачи
информации в два раза выше скорости
модуляции R=2B, или можно сказать при
заданной R требуется меньшая полоса
частот канала.

  • Но, для
    четкого различения 4–х уровней на фоне
    помех требуется большая мощность
    передатчика

  • При передачи
    одинаковых пар бит сигнал превращается
    в постоянную составляющую. Что требует
    дополнительных мер.

Применение
логического кодирования для улучшения
свойств потенциальных кодов.

Потенциальные
коды КЧП, Биполярный Код, 2B1Q-имеют более
узкую полосу частот, что является их
преимуществом, но страдают появлением
постоянной составляющей и потерей
синхронизации при передаче длинных
серий одинаковых элементов или групп.

Для борьбы
с этим явлением применяют логическое
кодирование (ЛК).

ЛК –
заменяет длинные последовательности
элементов, приводящих к постоянному
потенциалу другими последовательностями
устраняющими данный недостаток.

Для
логического кодирования характерны 2
метода:

  • избыточные
    коды;

  • скремблирование.

Избыточные
коды основаны на разбиении исходной
последовательности на порции (символы)
и замене исходной порции, новой имеющей
большее количество бит.

Так как
символы содержат избыточные биты, то
общее количество кодовых комбинаций в
них больше, чем в исходных.

Например,
код 4В/5В. Каждые четыре элемента исходной
последовательности заменяются пятью
элементами выходного кода. Выходные
элементы выбираются таким образом,
чтобы избежать длинных серий “опасных”
элементов приводящих к появлению
постоянки или потере синхронизации.
Остальные комбинации выходного кода
считаются запрещёнными, что позволяет
обнаружить ошибки.

Достоинства:

устранение
постоянной составляющей

улучшение
синхронизирующих свойств

обнаружение
ошибок.

Используются

4В/5В
используется в FDDI и Fast Ethernet.

8B/6T
– Fast Ethernet.

8В/10В
– Gigabit Ethernet

Скремблирование
– обратимое преобразование структуры
цифрового потока без изменения скорости
передачи с целью получения свойств
случайной последовательности.

6.2
Методы преобразования спектра с
использованием несущей

Модулированные
сигнала.

Чаще всего
в качестве несущей используют гармоническое
колебание:

Воздействуя
на соответствующий параметр амплитуду,
частоту или фазу, получаем соответственно
амплитудную, частотную или фазовую
модуляцию

Рассмотрим
данные виды модуляции с точки зрения
их применимости в технике передачи
данных.

Амплитудная
модуляция

Рассмотрим
связь ширины спектра и скорости модуляции.

Известно,
что если на вход идеального фильтра (с
прямоугольной АЧХ и линейной ФЧХ) подать
ступенчатую функцию, то на выходе будет
присутствовать переходной процесс,
длительность которого обратно
пропорциональна граничной частоте ФНЧ.

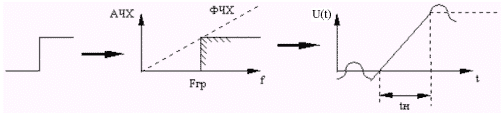
Длительность
импульса передаваемого через такую
систему не может быть менее чем время
нарастания.

Значит,
минимальная длительность сигнала равна

.

Учитывая,
что

получим
для ФНЧ

.

Так как АМ
сигнал в общем случае содержит и верхнюю
и нижнюю боковые полосы частот, то ширина
спектра АМ сигнала в 2 раза больше
исходного — модулирующего.

Если
задана полоса пропускания канала

,
то необходимо выбирать

так,
что бы

.

Оценим
предельный случай

,
тогда

.

Значит
предельная скорость передачи по каналу
при АМ

.

АМ — модулятор
в простейшем случае:

Частотная
модуляция

При передаче
двоичных сигналов в канал посылаются
две частоты f1 (для обозначения 1) и f2 (для
0). Причём по рекомбинациям МСЭ — Т f2 >
f1.

Спектр
сигнала в этом случае выглядит так

Можно
записать

,

Проведем
оценку предельной скорости модуляции
при ЧМ

Пусть
задана полоса канала

При
максимальном использовании полосы
канала

.

Определим
ширину полосы канала постоянного тока

или

Учитывая
что

.

Так как

получим

Таким
образом, при заданном значении

максимальная
скорость модуляции при ЧМ меньше, чем
при АМ, но помехоустойчивость при
частотной модуляции выше, поэтому она
находит ограниченно применение в
системах передачи дискретных сообщений.

Рекомендация
V.21.

R=B=300 [Бод]
[Бит/с]. КТЧ делится на две полосы .

нижняя
полоса для вызывающего модема 1 — 980 Гц,
0 — 1180 Гц

верхняя
полоса (отвечающий ) 1 — 1650 Гц, 0 — 1850 Гц

Протокол
V.21 — является ’’ аварийным ’’

Рекомендация
V.23 R=B=600 или 1200

КТЧ делится
на основной и обратный канал.

основной
при 1200 бит/с fср=1700,

при 600 бит/с
fср=1500,

Обратный
R=75 бит/с для передачи сигналов подтверждения
качества приёма.

Простейший
модулятор

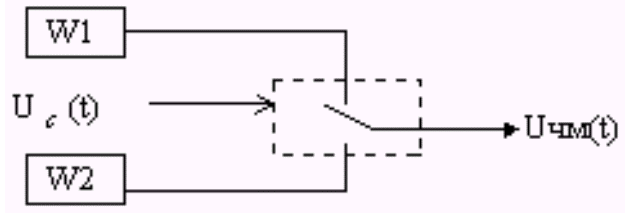
Фазовая
модуляция.

В данном
случае амплитуда и частоты постоянны,
изменяется фаза в соответствии с
модулирующим сигналом.

Если
модулирующий сигнал двоичный “1” или
“0”, то значение фазы модулирующего
сигнала тоже две. Это значение отсчитывается
от фазы несущей.

Обычно,
при передачи “1” модулятор формирует
синусоидальный сигнал, фаза которого
совпадает с фазой несущей. При

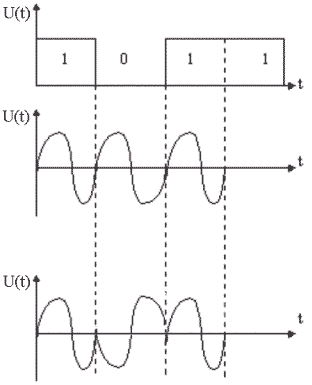
Спектр
ФМ — сигнала.

Из диаграммы
видно, что ФМ состоит, как бы, из двух АМ
сигналов несущие которых имеют одинаковую
частоту, а фазы сдвинуты на 180°

Поэтому
спектр ФМ сигнала будет таким же, как у
АМ по ширине, а несущая подавляется
из-за противофазности. Но все составляющие
увеличатся в 2 раза. Так как амплитуды
составляющих больше, то у ФМ выше
помехоустойчивость.

Для ФМ
можно записать

.

Структурные
схемы ФМ – сигнала

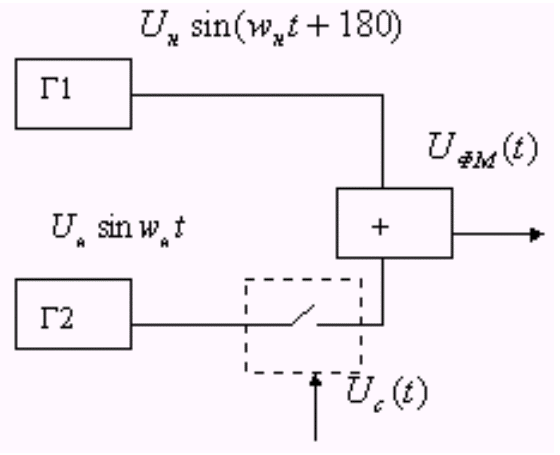
Дискретный
канал с ФМ

На приемной
стороне при демодуляции принятый сигнал
сравнивается с опорным сигналом, при
этом если фазы совпадают, то была 1, нет
– 0.

Если фаза
опорного сигнала изменится на 180° , то
1 будет воспринята как 0, а 0

1.
Такой эффект называется “ОБРАТНОЙ
РАБОТОЙ”.

“Обратная
работа” — это основной недостаток
абсолютной фазовой модуляции, именно
по этой причине фазовая модуляция не
нашла широкого применения в технике
ПДС.

Относительная
фазовая модуляция.

Исключение
явление “обратной работы” обеспечивается
относительной фазовой модуляции ОФМ.

При ОФМ
отсчет фазы передаваемого сигнала
производится не относительно несущей,
а относительно предыдущего элемента.

При модуляции
единицы, фаза элементов такая же, как у
предыдущего, при нуле меняется на
противоположную.

Следует
отметить, что фаза первого элемента
неопределенна, так как для него нет
предыдущего. Прием начинается со второго
элемента.

Для получения
ОФМ используют те же модуляторы, что
для АФМ, но перед подачей на модулятор
исходную последовательность перекодируют.

Правила
перекодирования:

Если в
исходной последовательности 0, то
соответствующий элемент выходной
последовательности изменяется на
противоположный относительно предыдущего.
Если “1”, то текущий элемент такой же,
как предыдущий.

Прием
ОФМ сигналов.

Прием ОФМ
сигналов возможен двумя способами.

1. способом
сравнения фаз (некогерентный прием);

Полосовой
фильтр отсекает помехи вне полосы
сигнала. Элемент памяти задерживает
сигнал на один единичный интервал. ФД
— сравнивает сигнал с предыдущим —
задержанным. Если фазы совпадают, то
принята “1”, если нет то “0”.

2. способом
сравнения полярностей (когерентный).

В данном
случае схема устройства выделения
опорного сигнала формирует его из
рабочей последовательности. Далее идет
сравнение фазы каждого единичного
элемента с фазой опорного, как у АФМ.
Полученная в результате последовательность
поступает в ПКУ, где перекодируется, и
на выходе получаем исходную
последовательность, так как информация
заложена в изменении фазы относительно
предыдущего. “Обратной работы” не
будет. Однако при ошибке в одном элементе
вылетают два, этот и последующий, который
с ним сравнивается.

Правила
перекодирования ПКУ приема:
Если во входной последовательности
изменилась значащая позиция, то в
выходной последовательности – 0, если
нет – 1.

Сравнение
способов приема:

В “сравнении
фаз” при принятии решения используют
два зашумленного сигнала.

В “сравнении
полярностей” один зашумленный и один
“чистый” — опорный.

Поэтому “полярный”
достовернее.

Следует
заметить, что один ошибочный элемент
до ПКУ вызывает две ошибки после ПКУ.

ОФМ
используется в модемах разработанных
по рекомендации V.26 на скорости 1200 бит
/ сек.

Многопозиционная
фазовая модуляция.

Как было
показано ранее, скорость модуляции в
канале определяется шириной спектра
канала:

Канал ТЧ
имеет спектр 0,3 — 3,4 к Гц. D Fтч =3,1 к Гц.

Таким
образом, максимальная скорость модуляции,
которую теоретически можно достичь в
кТЧ 6,2 Бод (передача одной боковой) 3,1
кБод (при передаче двух боковых).

Реально
же в модемах используются скорости
модуляции обычно 1200 и 2400 Бод.

Если для
передачи использовать двухпозиционный
сигнал, то скорость передачи информации
будет такой же низкой R=B=2400 Бит/сек.

Такие
скорости сегодня не устраивают
потребителя.

Выходом в
данном случае является использование
сигналов переносящих более чем 1 бит
информации (то есть многопозиционных
сигналов).

Многопозиционный
сигнал имеет более чем две значащих
позиции

Число
значащих позиций

информационная
емкость элемента

2

1 бит

4

2 бит

8

3 бит

Применение
данного принципа к относительно фазовой
модуляции называется многопозиционной
ОФМ.

Рассмотрим
простейший случай Двукратная ОФМ.

двукратная
или четырехпозиционная.

При
ДОФМ два соседних сигнала могут отличаться
по фазе на одно из четырех возможных
значений.

Дибит

00

01

11

10

45

135

225

315

Первоначально
исходная последовательность разбивается
на дибиты (по 2 элемента), а затем каждый
дибит кодируется на единичном интервале
в соответствии с модуляционным кодом.

В данном
случае обеспечивается R=2B.

Диаграмма
ДОФМ на сигнальной плоскости выглядит
так.

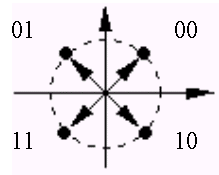
Протокол
V. 22.

B = 600 Бод.
В режиме ОФМ — 600 бит/с. В режиме ДОФМ —
1200 бит/с.

Еще более
повысить скорость R можно используя:

трехкратную
(восьмипозиционную) или

четырехкратную
(шестнадцати позиционную ) модуляции.

Однако при
увеличении числа разрешенных сдвигов
фаз резко уменьшается помехоустойчивость
ОФМ.

Уменьшается
расстояние между разрешенными сигналами
в пространстве. Вследствие этого, ОФМ
кратностью более трех не используется.

Для большего
увеличения скорости передачи используют
амплитудно-фазовую или так называемую
квадратурную — амплитудную модуляцию
КАМ.

В КАМ
изменяется не только фаза, но и амплитуда.
На рисунке показана диаграмма КАМ –
16.

Использование
КАМ — 16 позволяет при скорости модуляции
2400 Бод,

получать
скорость передачи информации 2400 ´ 4 =
9600 бит/с.

Такая
модуляция используется в протоколе

V. 32, R до
9600 в.p.s.

Квадратурная
модуляция имеет большую помехоустойчивость
в сравнении с многократной ОФМ. Но при
увеличении числа позиций свыше 16 и ее
помехоустойчивость оказывается
недостаточно для качественной передачи.

Поэтому
во всех современных высокоскоростных
протоколах КАМ используется, в совокупности
с помехоустойчивым кодированием.

В качестве
ПУ кодирования используется один из
видов сверточных кодов — решетчатый
код. Такое совместное кодирование
получило название “Треллис — модуляции”
(ТСМ).

При
применении Треллис — модуляции число
сигнальных точек увеличивается вдвое
за счет добавления к информационным
битам одного избыточного, образованного
путем сверточного кодирования.

Треллис —
модуляция используется уже в протоколе
V. 32, как альтернатива КАМ — 16. В этом
случае к 4 информационным добавлениям
1 проверочный разряд. Получается 32 точки
из которых выбирается 16 разрешенных.
Треллис – модуляция обеспечивает
большую помехоустойчивость.

Треллис —
модуляции используется в более поздних
протоколах

V.
32 bis — 14.4 b p.s.

V.34 bis — 28.8 b p.s.

Контрольные
вопросы по теме:

  1. Перечислите,
    по каким параметрам проводится
    согласование параметров сигналов с
    характеристиками канала.

  2. Для чего
    необходимо согласование спектра.

  3. Какими
    методами проводят согласование спектра
    сигнала.

  4. Что такое
    перекодирование.

  5. Перечислите
    достоинства и недостатки применения
    биполярного кода.

  6. Перечислите
    достоинства и недостатки применения
    кода с чередованием полярностей.

  7. Перечислите
    достоинства и недостатки применения
    манчестерского кода.

  8. Какой код
    называется 2B1Q.

  9. Что такое
    логическое кодирование и для чего его
    применяют.

  10. Поясните
    смысл преобразования 4B/5B и его цель.

  11. Какова
    максимальная скорость телеграфирования
    в канале с заданной полосой частот и
    аналоговой модуляцией.

  12. Какова
    максимальная скорость телеграфирования
    в канале с заданной полосой частот и
    частотной модуляцией.

  13. Какова
    максимальная скорость телеграфирования
    в канале с заданной полосой частот и
    фазовой модуляцией.

  14. Что такое
    ОФМ и в чем ее преимущества.

  15. Какими
    способами осуществляется прием ОФМ, в
    чем суть этих способов.

  16. Что такое
    многократная ОФМ.

  17. Какая
    модуляция называется квадратурной
    амплитудной.

Тема
7. Синхронизация
в ситемах ПДС

назад
| оглавление
|
вперёд

Синхронизация
–
это процедура установления и поддержания
определенных временных соотношений
между двумя и более процессами.

Различают
поэлементную, групповую и цикловую
синхронизацию.

При
поэлементной
синхронизации устанавливаются и
поддерживаются требуемые фазовые
соотношения между значащими моментами
переданных и принятых единичных элементов
цифровых сигналов данных. Поэлементная
синхронизация позволяет на приеме
правильно отделить один единичный
элемент от другого и обеспечить наилучшие
условия для его регистрации.

Групповая
синхронизация
– обеспечивает правильное разделение
принятой последовательности на кодовые
комбинации.

Цикловая
синхронизация
– обеспечивает правильное разделение
циклов временного объединения.

Источник
фигня
 
  Обноружение ошибок  
 
  Исправление ошибок  
 
  Коррекция ошибок  
 
  Назад  
 

Методы обнаружения ошибок

В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.

Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество
комбинаций можно разбить на два подмножества:
подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.

Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).

Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.

Метричное представление n,k-кодов

В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.

Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:

К основным характеристикам корректирующих кодов относятся:

 

— число разрешенных и запрещенных кодовых комбинаций;
— избыточность кода;
— минимальное кодовое расстояние;
— число обнаруживаемых или исправляемых ошибок;
— корректирующие возможности кодов.

Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением

Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:

Очевидно, что число запрещенных комбинаций:

а с учетом отношение будет

где m – число избыточных (проверочных) разрядов в блочном коде.

Избыточностью корректирующего кода называют величину

откуда следует:

Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет

поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.

Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.

При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.

Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.

Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.

Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:

Здесь под операцией ⊕ понимается сложение «по модулю 2».

Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.

Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.

В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..

Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.

Число обнаруживаемых или исправляемых ошибок

При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.

Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.

В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать

Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu

В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:

Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.

Корректирующие возможности кодов

Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.

Коды Хэмминга

Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.

Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).

В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.

Таким образом, правило формирования проверочного символа сводится к следующему:

где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.

Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:

— ошибок нет,

— однократная ошибка

Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.

Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.

Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой

т.е. (7,4), (15,11) (31,26) …

При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.

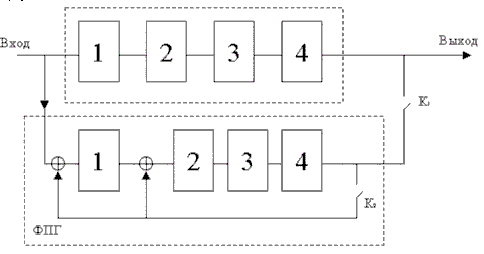
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.

В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.

Таблица 1 Кодовые слова (7,4)-кода Хэмминга

k=4

m=4

i1 i2 i3 i4

r1 r2 r3

0 0 0 0

0 0 0

0 0 0 1

0 1 1

0 0 1 0

1 1 0

0 0 1 1

1 0 1

0 1 0 0

1 1 1

0 1 0 1

1 0 0

0 1 1 0

0 0 1

0 1 1 1

0 1 0

1 0 0 0

1 0 1

1 0 0 1

1 0 0

1 0 1 0

0 1 1

1 0 1 1

0 0 0

1 1 0 0

0 1 0

1 1 0 1

0 0 1

1 1 1 0

1 0 0

1 1 1 1

1 1 1

На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга

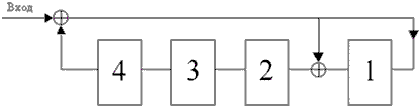
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.

В декодере в режиме исправления ошибок строится последовательность:

Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).

Число возможных синдромов определяется выражением:

При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 8) .
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.

Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга

Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.

Таблица 2 Синдромы (7, 4)-кода Хемминга

Синдром

001

010

011

100

101

110

111

Конфигурация ошибок

0000001

0000010

0000100

0001000

0010000

0100000

1000000

Ошибка в символе

m1

m2

i4

m1

i1

i3

i2

Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.

Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.

Циклические коды

Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.

Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.

Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:

(x7)=(x-1)(x3+x2)(x3+x-1)

Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.

Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.

Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).

Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.

Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.

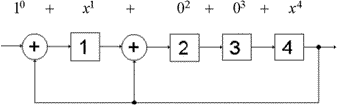
Способы построения циклических кодов по заданному полиному.

1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.

Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:

001110101001111010011011101010011101110100

Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.

Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.

2) Умножение исходных двоичных кодовых комбинаций на задающий полином.

Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.

3) Деление на задающий полином.

Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).

Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.

Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.

Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.

Следует сделать ряд указаний относительно процедуры деления:

1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.

2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.

3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.

Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.

Логический код 4В/5В

Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.

Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.

Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.

Для служебных сигналов отведены девять символов, семь символов — исключены.

Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.

Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.

Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.

Схема кодирования 4В/5В представлена в таблице.

Двоичный код 4В

Результирующий код 5В

0 0 0 0

1 1 1 1 0

0 0 0 1

0 1 0 0 1

0 0 1 0

1 0 1 0 0

0 0 1 1

1 0 1 0 1

0 1 0 0

0 1 0 1 0

0 1 0 1

0 1 0 1 1

0 1 1 0

0 1 1 1 0

0 1 1 1

0 1 1 1 1

1 0 0 0

1 0 0 1 0

1 0 0 1

1 0 0 1 1

1 0 1 0

1 0 1 1 0

1 0 1 1

1 0 1 1 1

1 1 0 0

1 1 0 1 0

1 1 0 1

1 1 0 1 1

1 1 1 0

1 1 1 0 0

1 1 1 1

1 1 1 0 1

Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.

Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.

Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.

Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.

Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.

В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.

Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.

Скрэмблирование

Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.

Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .

При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.

Избыточные биты при этом по линии не передаются.

Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.

Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.

Например, скрэмблер может реализовывать следующее соотношение:

где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).

Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.

Скрэмблер, определенный выше даст следующий результирующий код:

B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.

После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.

Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.

Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.

На практике для этих целей обычно применяется комбинация двух методов:

а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,

б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.

Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.

Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3

На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).

Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.

Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.

Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.

Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.

Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:

Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.

Линейные блочные коды

При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4

Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.

Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений

Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.

С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.

Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.

Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:

Y=S+E

Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.

Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.

Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:

P(Ei)=Pq(1-P)n-q

которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.

Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.

Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.

Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:

P(Y/Si)=P(Ei)=Pqi(1-P)n-qi

где qi – вес вектора Ei=Y+Si

Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):

S‘=Y+EHB

Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.

В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.

Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:

Y→EHB→S‘=Y+EHB

Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.

Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).

Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите эти материалы по теме:

  • Яндекс еда ошибка привязки карты
  • Основные ошибки электромонтажа
  • Основные ошибки эксель
  • Основные ошибки чтения
  • Основные ошибки футбола

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии