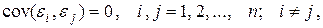Существует
несколько подходов к тестированию
регрессионных остатков на автокорреляцию.
Во многих статистических пакетах решение
задач по построению регрессии дополняется
графическим представлением результатов
моделирования. В том числе предоставляется
возможность визуализации поведения
отклонений
во времени. Как правило, строятся либо
последовательно-временные графики,
либо графики зависимости
от
.
В первом случае
по оси абсцисс откладывается либо время,
в которое было получено статистическое
наблюдение, либо номер наблюдения, а по
оси ординат – отклонение
,
величина которого становится известной
после построения уравнения регрессии.
Рис.
4.1. Зависимость остатков от времени
Анализ графиков,
представленных на рис. 4.1, показывает,
что в случае а)
и б)
изменение остатков
подчиняется некоторой закономерности
и можно предположить, что они
автокоррелированы. Случай в)
свидетельствует об отсутствии какой-либо
зависимости, и предположение о возможной
автокоррелированности
несостоятельно.
Во втором случае
по оси абсцисс откладывается
,
а по оси ординат –
.
Тогда, если график будет иметь вид,
представленный на рис. 4.2, то есть все
основания считать, что остатки
автокоррелированы. Причем, так как
большинство точек на этом графике
расположены в первой и третьей четвертях
декартовой системы координат, то можно
с уверенностью говорить о положительной
зависимости в среднем между соседними
отклонениями.
К сожалению, графики
остатков не всегда выглядят так
убедительно, как на приведенных рисунках.
Поэтому, кроме графических, применяются
и аналитические методы тестирования
на автокорреляцию остатков.
Рис. 4.2. Авторегрессионная
зависимость остатков
Метод рядов. Этот
метод состоит в следующем. После
построения уравнения регрессии
последовательно определяются знаки
отклонений
,
например,
(+ + + +) (- — — — — — —
-) (+ + + + +) ( — — -) (+ + + +) (-),
т.е. 4 «+», 8 «-», 5
«+», 3 «-», 4 «+», 1 «-» получено при построении
модели по выборке из 25 наблюдений.
Будем называть
рядом непрерывную
последовательность одинаковых знаков.
Количество знаков в ряду принято называть
длиной ряда.
Интуитивно понятно,
что если есть ряды, то, скорее всего,
между остатками есть зависимость.
Причем, если рядов слишком мало по
сравнению с количеством наблюдений, то
вполне вероятна положительная
автокорреляция, если же рядов слишком
много, то вероятна отрицательная
автокорреляция. Для более обоснованного
вывода предлагается следующая процедура.
Введем обозначения:
–
объем выборки;
–
общее количество
знаков «+» при
наблюдениях
(количество положительных отклонений
);
–
общее количество
знаков « – » при
наблюдениях
(количество отрицательных отклонений
);
–
количество рядов.
При достаточно
большом количестве наблюдений (>10,
>10)
и отсутствии автокорреляции доказано,
что случайная величина
имеет
асимптотически нормальное распределение
с
;

(4.111)
Тогда, если окажется,
что
удовлетворяет
неравенству
,
(4.112)
то гипотеза об
отсутствии автокорреляции не отклоняется
(–
-квантиль
стандартного нормального распределения).
В противном случае – в остатках
наблюдается автокорреляция.
Критерий Дарбина
– Уотсона. Этот
критерий по сравнению с другими
используется гораздо чаще. В его основу
положена простая идея, в соответствии
с которой, если корреляция случайной
составляющей регрессии
не равна 0, то она должна присутствовать
и в остатках регрессии
,
получающихся в результате обычного
МНК. В тесте Дарбина – Уотсона для оценки
автокорреляции используется статистика

(4.113)
Подробности
применения этого критерия были рассмотрены
в предыдущей главе. Корректное
использование статистики возможно при
выполнении следующих условий:
-
модель, для которой
возникает необходимость применения
этого критерия, должна содержать
свободный член; -
предполагается,
что случайная составляющая модели
определяется в соответствии с
авторегрессионной схемой первого
порядка; -
наблюдения,
используемые для построения модели,
имеют одинаковую периодичность, т.е. в
них нет пропусков; -
критерий нельзя
применять, если в регрессионной модели
в число объясняющих переменных входит
зависимая переменная с лагом в один
период. Такое ограничение связано с
тем, что распределение статистики
зависит
не только от числа наблюдений, но и от
значений самих регрессоров. А это
означает, что тест перестает выполнять
роль критерия в том смысле, что нельзя
указать критическую область, которая
позволяла бы принимать решение об
отсутствии автокорреляции в тех случаях,
когда в эту область попадают наблюдаемые
значения статистики
.
Критерий на
основе h-статистики
Дарбина. Этот
критерий разработан для обнаружения
автокоррелированности остатков в
моделях, содержащих авторегрессионные
члены. Тестирование осуществляется с
помощью h—статистики
Дарбина, которая вычисляется по формуле
,
(4.114)
где
– оценка коэффициента авторегрессии;
– число наблюдений;
–
выборочная дисперсия
коэффициента при лаговой переменной
уравнения регрессии
.
(4.115)
При большом объеме
выборке и справедливости нулевой
гипотезы
статистика h
имеет стандартизованное нормальное
распределение ().
Это позволяет по заданному уровню
значимости определить критическую
точку
из условия
и сравнить h-статистику
с
.
Если
,
то нулевая гипотеза об отсутствии
автокорреляции отклоняется.
Значение
рассчитывается
с помощью статистики Дарбина – Уотсона
по формуле
,
(4.116)
а
представляет собой квадрат стандартной
ошибки
оценки
.
Таким образом,
статистика
h
легко вычисляется на основе данных
оцененной регрессии (4.115). Единственная
проблема, которая может возникнуть
связана с тем, что вполне возможен
случай, когда
.
Тест серий (Бреуша
– Голдфри). Идея
этого теста основана на проверки
значимости коэффициента авторегрессионной
модели
,
(4.117)
где
– остатки регрессии, коэффициенты
которой получены с помощью обычного
МНК.
Схема практической
реализации этого теста довольно проста,
и поэтому не вызывает затруднений.
Преимущество теста серий перед тестом
Дарбина – Уотсона в том, что он не
содержит зону неопределенности. Кроме
того, с помощью критерия Бреуша – Голдфри
можно выявлять автокорреляцию не только
между соседними, но и между отдаленными
наблюдениями, т.е. проверять значимость
коэффициентов в авторегрессионных
моделях первого, второго и более высоких
порядков
.
(4.118)
Тест серий
предусмотрен большинством современных
компьютерных пакетов и осуществляется
специальной командой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
15.04.2015134.66 Кб1835.doc
- #
Постановка задачи
Критерий Дарбина-Уотсона (Durbin–Watson statistic) — один из самых распространенных критериев для проверки автокорреляции.
Данный критерий входит в стандартный инструментарий python:
-
присутствует в таблице выдачи результатов регрессионного анализа модуля линейной регрессии Linear Regression;
-
может быть рассчитан с помощью функции statsmodels.stats.stattools.durbin_watson.
К сожалению, стандартные инструменты python не позволяют получить табличные значения статистики критерия Дарбина-Уотсона, нам предлагается воспользоваться методом грубой оценки: считается, что при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. Durbin–Watson statistic). Однако, для качественного статистического анализа такой подход неприемлем.
Представляет интерес реализовать в полной мере критерий Дарбина-Уотсона средствами python, добавив этот важный критерий в инструментарий специалиста DataScience.
В данном обзоре мы коснемся только собственно критерия Дарбина-Уотсона и его применения для выявления автокорреляции. Особенности построения регрессионных моделей и прогнозирования в условиях автокорреляции (двухшаговый метод наименьших квадратов и пр.) мы рассматривать не будем.
Применение пользовательских функций
Как и в предыдущем обзоре, здесь будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub.
Вот перечень данных функций:
-
graph_plot_sns_np — функция строит линейный график средствами seaborn;
-
graph_regression_plot_sns — функция строит график регрессионной модели и график остатков средствами seaborn;
-
regression_error_metrics — функция возвращает ошибки аппроксимации регрессионной модели;
-
graph_hist_boxplot_probplot_sns — функция позволяет визуализировать исходные данные для одной переменной путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика средствами seaborn; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);
-
norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов.
-
Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;
-
graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.
В процессе данного обзора мы создаем пользовательскую функцию Durbin_Watson_test, которая проверяет гипотезу о наличии автокорреляции (она тоже включена в пользовательский модуль my_module__stat.py).
Основы теории
Информацию о критерии Дарбина-Уотсона можно почерпнуть в [1, с.659], [2, с.117], [3, с.239], [4, с.188], а также:
-
Durbin–Watson statistic
-
Критерий Дарбина — Уотсона
Итак, предположим, мы рассматриваем регрессионную модель:
или в матричном виде:
Критерий Дарбина-Уотсона применяется в ситуации, когда регрессионные остатки связаны автокорреляционной зависимостью 1-го порядка [2, с.111]:
где — некоторое число (
), а случайные величины
удовлетворяют требованиям, предъявляемым к регрессионным остаткам классической модели (т.е. равенство нулю среднего значения, постоянство дисперсии и некоррелированность между собой):
Проверяется нулевая гипотеза об отсутствии автокорреляции:
Альтернативной гипотезой может быть:
-
существование отрицательной автокорреляции (левосторонняя критическая область):
-
существование положительной автокорреляции (правосторонняя критическая область):
-
существование автокорреляции вообще (двусторонняя критическая область):
Расчетное значение статистики критерия Дарбина-Уотсона имеет вид:
где — остатки (невязки) регрессионной модели.
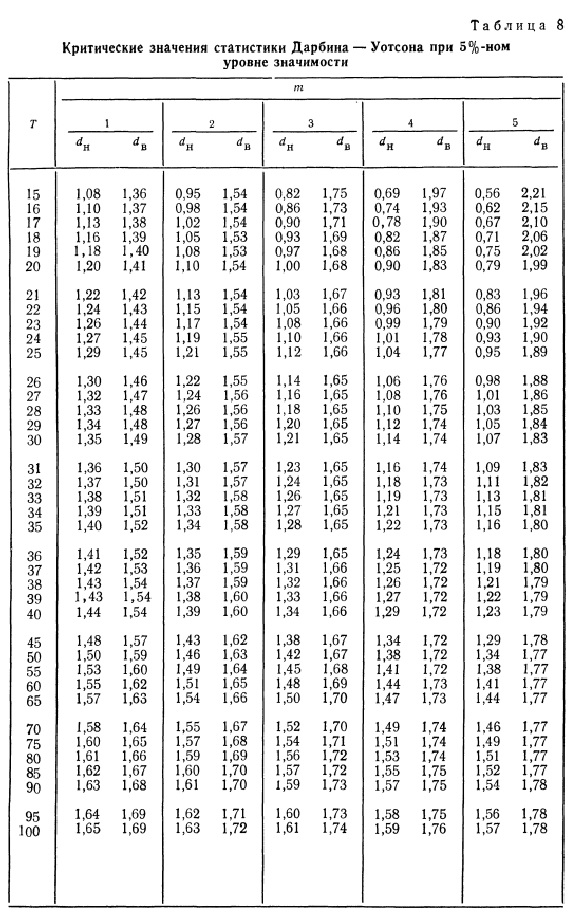
По таблицам (см. [1, с.659], [2, с.402], [3, с.291]) в зависимости от уровня значимости (5%, 2.5%, 1%), числа параметров регрессионной модели
(кроме свободного члена
) (от 1 до 5) и объема выборки
(от 15 до 100) определяются критические значения статистики Дарбина-Уотсона: нижний
и верхний
предел.
Правила принятия гипотез по критерию Дарбина-Уотсона выглядят довольно своеобразно — критические значения образуют пять областей различных статистических решений (причем критические границы принятия и непринятия
не совпадают):
|
Значение |
Принимается гипотеза |
Вывод |
|---|---|---|
|
|
отвергается |
есть положительная автокорреляция |
|
|
неопределенность |
|
|
|
принимается |
автокорреляция отсутствует |
|
|
неопределенность |
|
|
|
отвергается |
есть отрицательная автокорреляция |
Есть очень удачная мнемоническая схема, приведенная в [3, с.240]:
Особенности критерия Дарбина-Уотсона:
-
Критические значения критерия табулированы для объема выборки от 15 до 100, аппроксимаций мне обнаружить не удалось. При меньших значениях критерий применять нельзя, при больших — очевидно, приходиться пользоваться грубым оценочным правилом: при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. https://en.wikipedia.org/wiki/Durbin–Watson_statistic).
-
Критерий позволяет выявить только автокорреляцию 1-го порядка. Отклонение нулевой гипотезы не означает, что автокорреляции нет вообще — возможно наличие автокорреляции более высоких порядков.
-
Критерий построен в предположении, что регрессоры
и ошибки
не коррелированы, поэтому его нельзя применять, в частности, для моделей авторегрессии [4, с.191].
-
Критерий не подходит для моделей без свободного члена
.
-
Критерий имеет зону неопределенности, когда нет оснований ни принимать, ни отвергать нулевую гипотезу.
-
Между статистикой критерия и коэффициентом автокорреляции существует приближенное соотношение:
Существуют и другие критерии для проверки автокорреляции (тест Бройша-Годфри, Льюнга-Бокса и пр.).
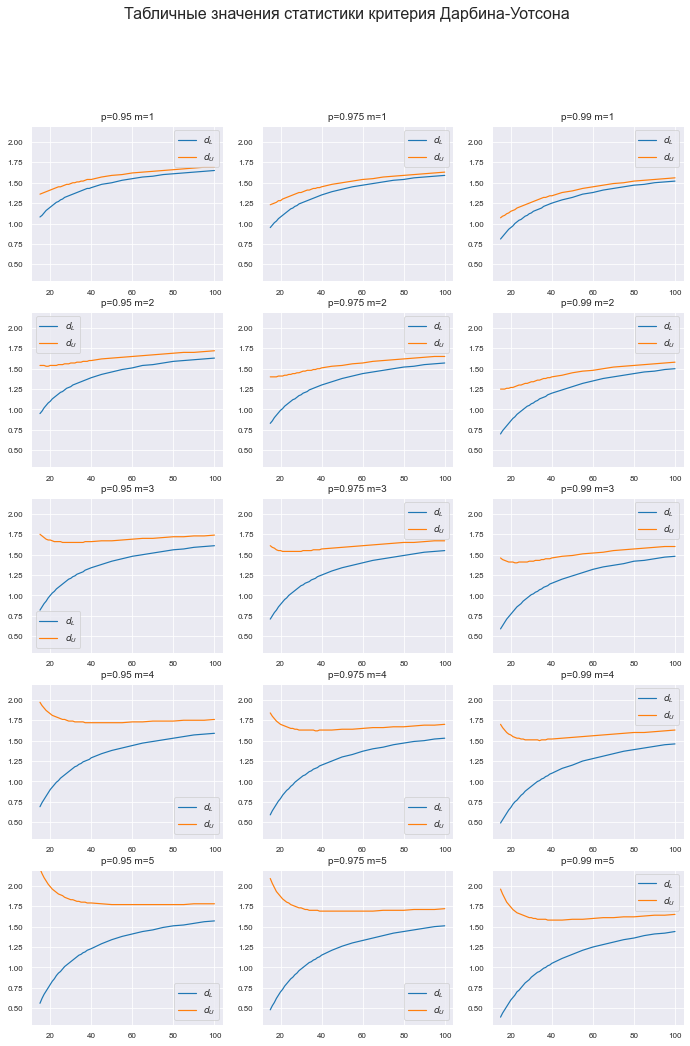
Как было указано выше, большой проблемой является отсутствие табличных значений статистики критерия Дарбина-Уостона в стандартном инструментарии python. Для реализации возможностей данного критерия в полном объеме нам потребуется оцифровка весьма объемных таблиц критических значений.
Оцифровка табличных значений статистики критерия Дарбина — Уотсона
Я решил добавить в обзор этот раздел, хотя, строго говоря, можно было обойтись и без него, а сразу воспользоваться оцифрованными таблицами статистики критерия Дарбина-Уотсона.
Однако, если мы хотим выполнять качественный статистический анализ, неизбежно придется работать с большим количеством статистических критериев и далеко не все из них реализованы в python. Критерий Дарбина-Уотсона — это только один из многих. Количество критериев, рассматриваемых в литературе по прикладной статистике в последние годы постоянно увеличивается. Специалисту придется реализовывать многие критерии самостоятельно и одна из проблем, с которой придется столкнуться — это таблицы критических значений. Далеко не все табличные значения имеют аппроксимации, а значит придется каким-то образом оцифровывать эти таблицы. Небольшие таблицы можно сохранить в файлах вручную, а вот такой подход с объемными таблицами (как в нашем случае) — это слишком непроизводительно и нерационально.
В общем, на мой взгляд, представляет интерес разобрать пример оцифровки статистических таблиц на примере нашего критерия Дарбина-Уотсона — это позволит специалистам сэкономить человеко-часы работы и облегчить совершенствование инструментов статистического анализа.
Замечу сразу, что я не являюсь глубоким специалистом в области анализа и обработки изображений и текстов на python — это не совсем мой профиль. Профессионалы в этой области, возможно, раскритикуют то, как решается поставленная задача и предложат более удачное решение. Если будет так — то заранее спасибо. Я же эту задачу старался решить наиболее простым и рациональным способом, доступным для широкого круга специалистов. На всякий случай могу процитировать Давоса Сиворта из «Игры престолов»: «Простите за то, что увидите».
Алгоритм действий:
Для оцифровки я использовал таблицы, приведенные в [3, с.290-292].
-
Сканируем таблицы, сохраняем в виде jpg-файлов (Durbin_Watson_test_1.jpg, Durbin_Watson_test_2.jpg, Durbin_Watson_test_3.jpg) в папке text_processing, расположенной внутри папки с рабочим .ipynb-файлом:
-
Распознаем текст (я воспользовался онлайн-сервисом https://convertio.co/), полученные текстовые файлы Durbin-Watson-test-1.ocr.txt, Durbin-Watson-test-2.ocr.txt, Durbin-Watson-test-3.ocr.txt также помещаем в папке text_processing.
-
Откроем файлы, запишем содержимое файлов в переменные, каждая из которых соответствует одной странице:
with open('text_processingDurbin-Watson-test-1.ocr.txt') as f1:
Durbin_Watson_test_1 = f1.readlines()
display(Durbin_Watson_test_1, type(Durbin_Watson_test_1), len(Durbin_Watson_test_1))С остальными файлами — действуем аналогично:
with open('text_processingDurbin-Watson-test-2.ocr.txt') as f2:
Durbin_Watson_test_2 = f2.readlines()
display(Durbin_Watson_test_2, type(Durbin_Watson_test_2), len(Durbin_Watson_test_2))
with open('text_processingDurbin-Watson-test-3.ocr.txt') as f3:
Durbin_Watson_test_3 = f3.readlines()
display(Durbin_Watson_test_3, type(Durbin_Watson_test_3), len(Durbin_Watson_test_3))Видим, что переменные представляют собой списки, элементами которых является строки.
Для облегчения дальнейшей обработки данных создадим список, элементами которого являются переменные-страницы:
Durbin_Watson_test = [Durbin_Watson_test_1, Durbin_Watson_test_2, Durbin_Watson_test_3]Далее я не стал публиковать здесь скриншоты с обработкой страниц — из-за экономии места. В ipyng-файле, который доступен в моем репозитории, весь процесс обработки представлен достаточно подробно.
-
Исключаем все строки, которые начинаются не с цифр; при этом воспользуемся алгоритмом перезаписи списка:
# создаем новый список
Durbin_Watson_test_new = list()
# удаляем строки
for page in Durbin_Watson_test:
page_temp = list() # временная страница
for line in page:
if line[0].isdigit():
page_temp.append(line) # перезаписываем список
Durbin_Watson_test_new.append(page_temp)-
Исключаем из текста управляющие символы (t, n) — с помощью регулярных выражений (regex) (модуль re):
# задаем шаблон для удаления символов
pattern = r'[t+n+]'
# выполняем обработку
Durbin_Watson_test_new = [
[re.sub(pattern, ' ', elem) for elem in page]
for page in Durbin_Watson_test_new]-
Удаляем все символы, кроме цифр, точек, запятых и пробелов:
# задаем шаблон для удаления символов
pattern = r'[^0-9,. ]'
# выполняем обработку
Durbin_Watson_test_new = [
[re.sub(pattern, '', elem) for elem in page]
for page in Durbin_Watson_test_new]-
Заменяем запятые на точки:
# задаем шаблон для удаления символов
pattern = r'[,]'
# выполняем обработку
Durbin_Watson_test_new = [
[re.sub(pattern, '.', elem) for elem in page]
for page in Durbin_Watson_test_new]-
Разделяем строки:
# задаем шаблон
pattern = r'[ ]+'
# выполняем обработку
Durbin_Watson_test_new = [[re.split(pattern, elem) for elem in page]
for page in Durbin_Watson_test_new]-
Сохраняем данные в DataFrame — для этого создадим список Durbin_Watson_list_df, элементами которого являются отдельные DataFrame, каждый из которых соответствует отдельной странице:
# создаем новый список
Durbin_Watson_list_df = list()
for page in Durbin_Watson_test_new:
Durbin_Watson_list_df.append(pd.DataFrame(page))-
Исправляем вручную отдельные аномалии, возникшие при распознавании отсканированных данных — к сожалению, работы вручную совсем избежать не удается.
-
Корректируем DataFrame, соответствующий 1-й странице:
# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[0]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[4],] = [19, 1.18, 1.40, 1.08, 1.53, 0.97, 1.68, 0.86, 1.85, 0.75, 2.02]
temp_df.loc[[8],[3]] = 1.17
temp_df.loc[[10],[3]] = 1.21
temp_df.loc[[17],[9]] = 1.11
temp_df.loc[[21],[4]] = 1.59
temp_df.loc[[25],[5]] = 1.34
temp_df.loc[[31],[10]] = 1.77
# записываем изменения
Durbin_Watson_list_df[0] = temp_df-
Корректируем DataFrame, соответствующий 2-й странице:
# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[1]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[2],[8]] = 1.77
temp_df.loc[[10],[9]] = 0.86
temp_df.loc[[10],[10]] = 1.77
temp_df.loc[[14],[9]] = 0.96
temp_df.loc[[17],[10]] = 1.71
temp_df.loc[[34],[10]] = 1.71
# записываем изменения
Durbin_Watson_list_df[1] = temp_df-
Корректируем DataFrame, соответствующий 3-й странице:
# создаем временный DataFrame
temp_df = Durbin_Watson_list_df[2]
# удаляем последние столбцы
temp_df = temp_df.drop(columns=[11, 12])
# корректируем вручную отдельные ошибки
temp_df.loc[[2],[9]] = 0.48
temp_df.loc[[13],] = [28, 1.10, 1.24, 1.04, 1.32, 0.97, 1.41, 0.90, 1.51, 0.83, 1.62]
temp_df.loc[[20],[3]] = 1.14
temp_df.iloc[21:26, 7] = [1.04, 1.06, 1.07, 1.09, 1.10]
temp_df.loc[[26],[9]] = 1.11
temp_df.loc[[35],] = [90, 1.50, 1.54, 1.47, 1.56, 1.45, 1.59, 1.43, 1.61, 1.41, 1.64]
# записываем изменения
Durbin_Watson_list_df[2] = temp_dfОбращаем внимание, что откорректированные вручную значения являются числовыми, а все остальные значения — еще имеют строковый тип.
11. Преобразуем значения из строкового в числовой тип:
for elem_df in Durbin_Watson_list_df:
for col in elem_df.columns:
elem_df[col] = pd.to_numeric(elem_df[col], errors='ignore')-
Корректируем структуру DataFrame:
-
меняем индекс — индексом теперь будет объем выборки n
-
каждый DataFrame снабжаем мультииндексом по столбцам (подробнее см. [7, с.169])
# меняем индекс
Durbin_Watson_list_df = [
elem_df.set_index([0])
for elem_df in Durbin_Watson_list_df]
# добавляем мультииндекс по столбцам
multi_index_list = ['p=0.95', 'p=0.975', 'p=0.99'] # список, содержащий значения для верхней строки мульииндекса
for i, elem_df in enumerate(Durbin_Watson_list_df):
elem_df.index.name = 'n'
elem_df.columns = pd.MultiIndex.from_product(
[[multi_index_list[i]],
['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],
['dL','dU']])-
Объединяем отдельные DataFrame в один:
Durbin_Watson_test_df = Durbin_Watson_list_df[0].copy()
for i, elem_df in enumerate(Durbin_Watson_list_df):
if i > 0:
Durbin_Watson_test_df = Durbin_Watson_test_df.join(elem_df)
display(Durbin_Watson_test_df) Durbin_Watson_test_df.info()Итак, мы сформировали DataFrame с оцифрованными данными таблиц критических значений статистики Дарбина-Уотсона. Получить доступ к данным теперь очень просто — например, нам требуется вывести табличные значения статистики критерия при объеме выборки , доверительной вероятности
и числе параметров регрессионной модели
:
n = 40
p = 0.95
m=2
Durbin_Watson_test_df.loc[[n], (f'p={p}', f'm={m}')]-
Построим график табличных значений.
График получился весьма объемным — 3х5 элементов — однако он необходим: на графике можно увидеть те ошибки (пики и впадины), которые мы могли пропустить при ручной обработке ранее (некорректно отсканированные и распознанные цифры), тогда придется вернуться к этапу 10.
# меняем настройки Mathplotlib
plt.rcParams['axes.titlesize'] = 10 # шрифт заголовка
plt.rcParams['legend.fontsize'] = 9 # шрифт легенды
plt.rcParams['xtick.labelsize'] = 8 # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = 8
fig = plt.figure(figsize=(297/INCH, 420/INCH))
ax_1_1 = plt.subplot(5,3,1)
ax_2_1 = plt.subplot(5,3,2)
ax_3_1 = plt.subplot(5,3,3)
ax_1_2 = plt.subplot(5,3,4)
ax_2_2 = plt.subplot(5,3,5)
ax_3_2 = plt.subplot(5,3,6)
ax_1_3 = plt.subplot(5,3,7)
ax_2_3 = plt.subplot(5,3,8)
ax_3_3 = plt.subplot(5,3,9)
ax_1_4 = plt.subplot(5,3,10)
ax_2_4 = plt.subplot(5,3,11)
ax_3_4 = plt.subplot(5,3,12)
ax_1_5 = plt.subplot(5,3,13)
ax_2_5 = plt.subplot(5,3,14)
ax_3_5 = plt.subplot(5,3,15)
fig.suptitle('Табличные значения статистики критерия Дарбина-Уотсона', fontsize = 16)
(Ymin, Ymax) = (0.3, 2.2)
x = Durbin_Watson_test_df.index
title_fontsize = 10
name_1_1 = ['p=0.95', 'm=1']
ax_1_1.set_title(name_1_1[0] + ' ' + name_1_1[1])
ax_1_1.plot(x, Durbin_Watson_test_df[tuple(name_1_1 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_1_1 + ['dU'])])
name_1_2 = ['p=0.95', 'm=2']
ax_1_2.set_title(name_1_2[0] + ' ' + name_1_2[1])
ax_1_2.plot(x, Durbin_Watson_test_df[tuple(name_1_2 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_1_2 + ['dU'])])
name_1_3 = ['p=0.95', 'm=3']
ax_1_3.set_title(name_1_3[0] + ' ' + name_1_3[1])
ax_1_3.plot(x, Durbin_Watson_test_df[tuple(name_1_3 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_1_3 + ['dU'])])
name_1_4 = ['p=0.95', 'm=4']
ax_1_4.set_title(name_1_4[0] + ' ' + name_1_4[1])
ax_1_4.plot(x, Durbin_Watson_test_df[tuple(name_1_4 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_1_4 + ['dU'])])
name_1_5 = ['p=0.95', 'm=5']
ax_1_5.set_title(name_1_5[0] + ' ' + name_1_5[1])
ax_1_5.plot(x, Durbin_Watson_test_df[tuple(name_1_5 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_1_5 + ['dU'])])
name_2_1 = ['p=0.975', 'm=1']
ax_2_1.set_title(name_2_1[0] + ' ' + name_2_1[1])
ax_2_1.plot(x, Durbin_Watson_test_df[tuple(name_2_1 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_2_1 + ['dU'])])
name_2_2 = ['p=0.975', 'm=2']
ax_2_2.set_title(name_2_2[0] + ' ' + name_2_2[1])
ax_2_2.plot(x, Durbin_Watson_test_df[tuple(name_2_2 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_2_2 + ['dU'])])
name_2_3 = ['p=0.975', 'm=3']
ax_2_3.set_title(name_2_3[0] + ' ' + name_2_3[1])
ax_2_3.plot(x, Durbin_Watson_test_df[tuple(name_2_3 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_2_3 + ['dU'])])
name_2_4 = ['p=0.975', 'm=4']
ax_2_4.set_title(name_2_4[0] + ' ' + name_2_4[1])
ax_2_4.plot(x, Durbin_Watson_test_df[tuple(name_2_4 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_2_4 + ['dU'])])
name_2_5 = ['p=0.975', 'm=5']
ax_2_5.set_title(name_2_5[0] + ' ' + name_2_5[1])
ax_2_5.plot(x, Durbin_Watson_test_df[tuple(name_2_5 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_2_5 + ['dU'])])
name_3_1 = ['p=0.99', 'm=1']
ax_3_1.set_title(name_3_1[0] + ' ' + name_3_1[1])
ax_3_1.plot(x, Durbin_Watson_test_df[tuple(name_3_1 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_3_1 + ['dU'])])
name_3_2 = ['p=0.99', 'm=2']
ax_3_2.set_title(name_3_2[0] + ' ' + name_3_2[1])
ax_3_2.plot(x, Durbin_Watson_test_df[tuple(name_3_2 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_3_2 + ['dU'])])
name_3_3 = ['p=0.99', 'm=3']
ax_3_3.set_title(name_3_3[0] + ' ' + name_3_3[1])
ax_3_3.plot(x, Durbin_Watson_test_df[tuple(name_3_3 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_3_3 + ['dU'])])
name_3_4 = ['p=0.99', 'm=4']
ax_3_4.set_title(name_3_4[0] + ' ' + name_3_4[1])
ax_3_4.plot(x, Durbin_Watson_test_df[tuple(name_3_4 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_3_4 + ['dU'])])
name_3_5 = ['p=0.99', 'm=5']
ax_3_5.set_title(name_3_5[0] + ' ' + name_3_5[1])
ax_3_5.plot(x, Durbin_Watson_test_df[tuple(name_3_5 + ['dL'])],
x, Durbin_Watson_test_df[tuple(name_3_5 + ['dU'])])
ax_1_1.set_ylim(Ymin, Ymax)
ax_2_1.set_ylim(Ymin, Ymax)
ax_3_1.set_ylim(Ymin, Ymax)
ax_1_2.set_ylim(Ymin, Ymax)
ax_2_2.set_ylim(Ymin, Ymax)
ax_3_2.set_ylim(Ymin, Ymax)
ax_1_3.set_ylim(Ymin, Ymax)
ax_2_3.set_ylim(Ymin, Ymax)
ax_3_3.set_ylim(Ymin, Ymax)
ax_1_4.set_ylim(Ymin, Ymax)
ax_2_4.set_ylim(Ymin, Ymax)
ax_3_4.set_ylim(Ymin, Ymax)
ax_1_5.set_ylim(Ymin, Ymax)
ax_2_5.set_ylim(Ymin, Ymax)
ax_3_5.set_ylim(Ymin, Ymax)
legend = (r'$d_L$', r'$d_U$')
ax_1_1.legend(legend)
ax_2_1.legend(legend)
ax_3_1.legend(legend)
ax_1_2.legend(legend)
ax_2_2.legend(legend)
ax_3_2.legend(legend)
ax_1_3.legend(legend)
ax_2_3.legend(legend)
ax_3_3.legend(legend)
ax_1_4.legend(legend)
ax_2_4.legend(legend)
ax_3_4.legend(legend)
ax_1_5.legend(legend)
ax_2_5.legend(legend)
ax_3_5.legend(legend)
plt.show()
# возвращаем настройки Mathplotlib
plt.rcParams['axes.titlesize'] = f_size + 10 # шрифт заголовка
plt.rcParams['legend.fontsize'] = f_size + 6 # шрифт легенды
plt.rcParams['xtick.labelsize'] = f_size + 4 # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4-
Сохраняем полученный DataFrame в csv-файл, помещаем его в папку table, расположенную внутри папки с рабочим .ipynb-файлом (в которой папку table у нас хранятся файлы с данными из статистических таблиц):
Durbin_Watson_test_df.to_csv(
path_or_buf='tableDurbin_Watson_test_table.csv',
mode='w+',
sep=';',
index_label='n')Табличные значения статистики критерия Дарбина-Уотсона у нас теперь имеются, можем приступать к созданию пользовательской функции.
Создание пользовательской функции для реализации критерия Дарбина — Уотсона
Рассчитать статистику критерия Дарбина-Уотсона мы можем с помощью функции statsmodels.stats.stattools.durbin_watson.
Создадим пользовательскую функцию Durbin_Watson_test для проверки гипотезы об автокорреляции:
def Durbin_Watson_test(
data,
m = None,
p_level: float=0.95):
a_level = 1 - p_level
data = np.array(data)
n = len(data)
# расчетное значение статистики критерия
DW_calc = sms.stattools.durbin_watson(data)
# табличное значение статистики критерия
if (n >= 15) and (n <= 100):
# восстанавливаем структуру DataFrame из csv-файла
DW_table_df = pd.read_csv(
filepath_or_buffer='table/Durbin_Watson_test_table.csv',
sep=';',
#index_col='n'
)
DW_table_df = DW_table_df.rename(columns={'Unnamed: 0': 'n'})
DW_table_df = DW_table_df.drop([0, 1, 2])
for col in DW_table_df.columns:
DW_table_df[col] = pd.to_numeric(DW_table_df[col], errors='ignore')
DW_table_df = DW_table_df.set_index('n')
DW_table_df.columns = pd.MultiIndex.from_product(
[['p=0.95', 'p=0.975', 'p=0.99'],
['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],
['dL','dU']])
# интерполяция табличных значений
key = [f'p={p_level}', f'm={m}']
f_lin_L = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dL'])])
f_lin_U = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dU'])])
DW_table_L = float(f_lin_L(n))
DW_table_U = float(f_lin_U(n))
# проверка гипотезы
Durbin_Watson_scale = {
1: DW_table_L,
2: DW_table_U,
3: 4 - DW_table_U,
4: 4 - DW_table_L,
5: 4}
Durbin_Watson_comparison = {
1: ['0 ≤ DW_calc < DW_table_L', 'H1: r > 0'],
2: ['DW_table_L ≤ DW_calc ≤ DW_table_U', 'uncertainty'],
3: ['DW_table_U < DW_calc < 4 - DW_table_U', 'H0: r = 0'],
4: ['4 - DW_table_U ≤ DW_calc ≤ 4 - DW_table_L', 'uncertainty'],
5: ['4 - DW_table_L < DW_calc ≤ 4', 'H1: r < 0']}
r_scale = list(Durbin_Watson_scale.values())
for i, elem in enumerate(r_scale):
if DW_calc <= elem:
key_scale = list(Durbin_Watson_scale.keys())[i]
comparison = Durbin_Watson_comparison[key_scale][0]
conclusion = Durbin_Watson_comparison[key_scale][1]
break
elif n < 15:
comparison = '-'
conclusion = 'count less than 15'
else:
comparison = '-'
conclusion = 'count more than 100'
# формируем результат
result = pd.DataFrame({
'n': (n),
'm': (m),
'p_level': (p_level),
'a_level': (a_level),
'DW_calc': (DW_calc),
'ρ': (1 - DW_calc/2),
'DW_table_L': (DW_table_L if (n >= 15) and (n <= 100) else '-'),
'DW_table_U': (DW_table_U if (n >= 15) and (n <= 100) else '-'),
'comparison of calculated and critical values': (comparison),
'conclusion': (conclusion)
},
index=['Durbin-Watson_test'])
return resultПротестируем созданную функцию — будем моделировать временные ряды с различными свойствами и выполнять проверку автокорреляции:
y_func = lambda x, b0, b1: b0 + b1*x
N = 30 # число наблюдений
(mu, sigma) = (0, 25) # параметры моделируемой случайной компоненты (среднее и станд.отклонение)-
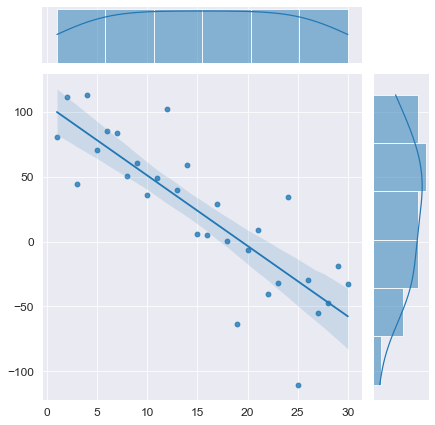
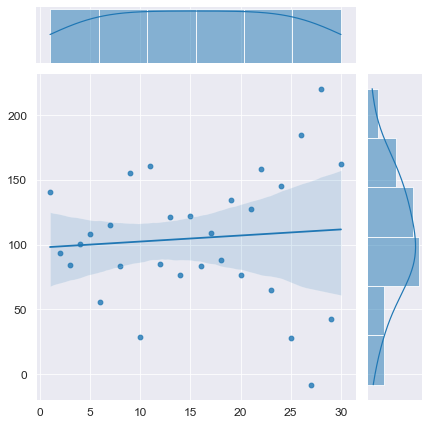
Смоделируем временной ряд с трендом, без автокорреляции остатков:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 5) # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, -5) # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))-
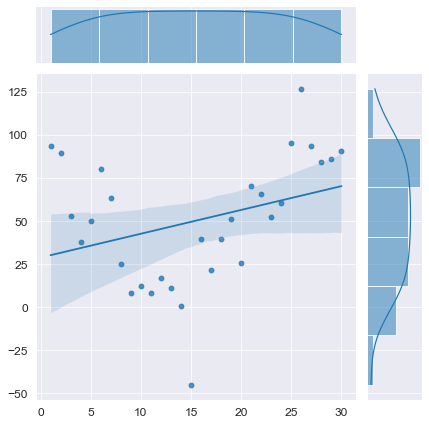
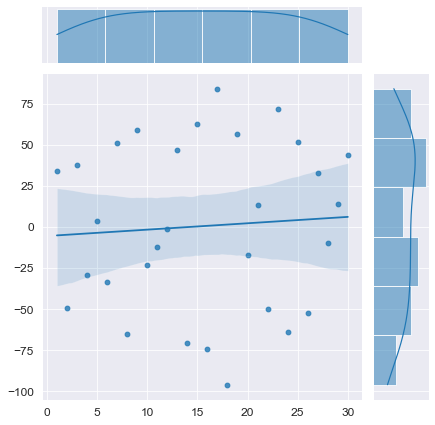
Смоделируем временной ряд без тренда:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 0) # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (0, 0) # параметры моделируемого временного ряда
Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))-
Смоделируем временной ряд с трендом, с положительной автокорреляцией:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 5) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))-
Смоделируем временной ряд с трендом, с отрицательной автокорреляцией:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 5) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))-
Смоделируем временной ряд без тренда, с положительной автокорреляцией:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 0) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (0, 0) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = 0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))-
Смоделируем временной ряд без тренда, с отрицательной автокорреляцией:
# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (100, 0) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))# моделирование
T_model = np.linspace(1, N, N) # независимая переменная - номер наблюдения
(b0, b1) = (0, 0) # параметры моделируемого временного ряда
E = np.array([np.random.normal(mu, sigma, 1)])
r = -0.9
for i in range(1, N):
elem = r*E[i-1] + np.random.normal(mu, sigma, 1)
E = np.append(E, elem)
Y_model = np.array(y_func(T_model, b0, b1)) + E
# визуализация
axes = sns.jointplot(
x=T_model, y=Y_model,
kind='reg')
plt.show()
# проверка автокорреляции
display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))Конечно, данный вычислительный эксперимент не может претендовать на всеобъемлемость, однако определенный любопытный предварительный вывод можно сделать: при наличии любого тренда (даже если этот тренда представляет собой равенство постоянной величине ) критерий Дарбина-Уотсона выдает нам наличие положительной автокорреляции (даже если в модели автокорреляция не заложена нет или она отрицательная). Такой вывод нужно исследовать более глубоко, но это не входит в цель данного обзора. Специалист должен помнить об особенностях критерия Дарбина-Уотсона.
Теперь мы можем перейти к практическим примерам.
Пример 1: проверка автокорреляции модели временного ряда
Формирование исходных данных
В качестве исходных данных рассмотрим динамику показателей индексов пересчета сметной стоимости проектно-изыскательских работ в РФ. Эти показатели ежеквартально публикует Министерство строительства и ЖКХ РФ, а все проектные и изыскательские организации используют эти показатели при составлении смет на свои работы.
В данном случае мы имеем набор показателей в виде временного ряда, для которого будем строить регрессионную модель долговременной тенденции (тренда), и остатки этой регрессионной модели будем исследовать на автокорреляцию.
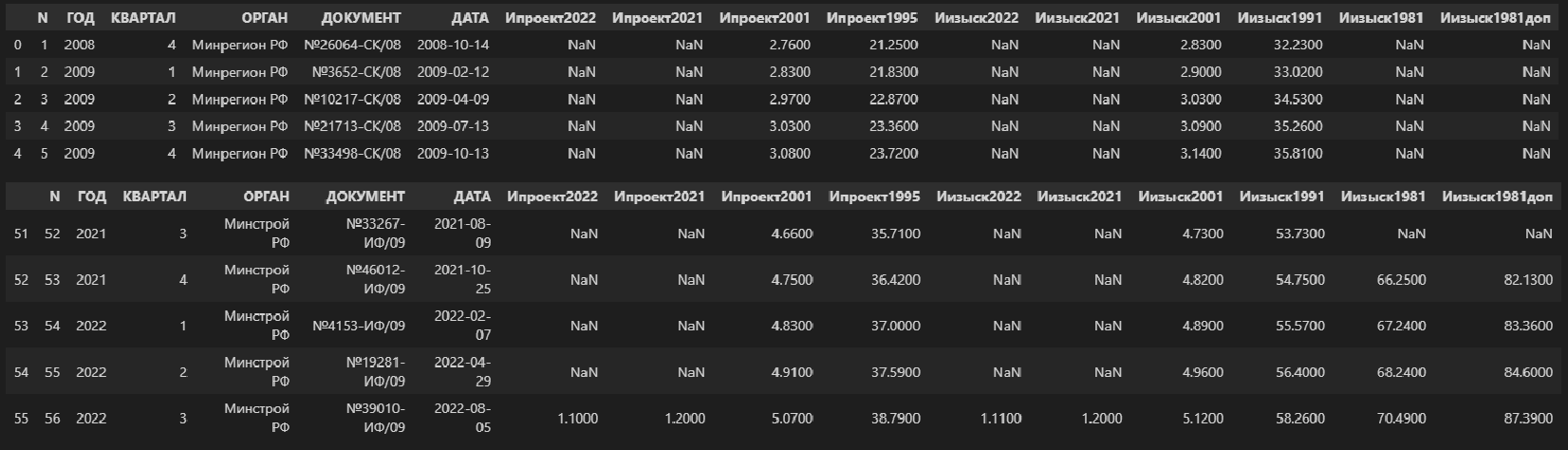
Исходные данные содержаться в файле Ежеквартальные индексы ПИР.xlsx, который помещен в папку data.
Прочитаем xlsx-файл:
data_df = pd.read_excel('data/Ежеквартальные индексы ПИР.xlsx', sheet_name='БД')
#display(data_df)
display(data_df.head(), data_df.tail())
data_df.info()Не будем подробно останавливаться на содержимом файла и его первичной обработке — это выходит за пределы данного обзора. Специалисты, причастные к сфере строительства и проектирования, поймут, а для остальных специалистов эти цифры можно воспринимать по аналогии с индексами инфляции Росстата и Минэкономразвития.
Прочитаем из этого файла интересующие нас данные — индексы изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г.:
Ind_design_2001 = np.array(data_df['Ипроект2001'])
print(Ind_design_2001, 'n', type(Ind_design_2001), len(Ind_design_2001))Сохраним также вспомогательные (технические) переменные, необходимые при анализе временных рядов — дату (Date) и номер наблюдения (T):
# Дата показателя
Date = np.array(data_df['ДАТА'])
# Номер наблюдения
T = np.array(data_df['N'])Для удобства дальнейшей работы сформируем сформируем отдельный DataFrame:
dataset_df = pd.DataFrame({
'T': T,
'Date': Date,
'Ind_design_2001': Ind_design_2001})
display(dataset_df.head(), dataset_df.tail())Визуализация
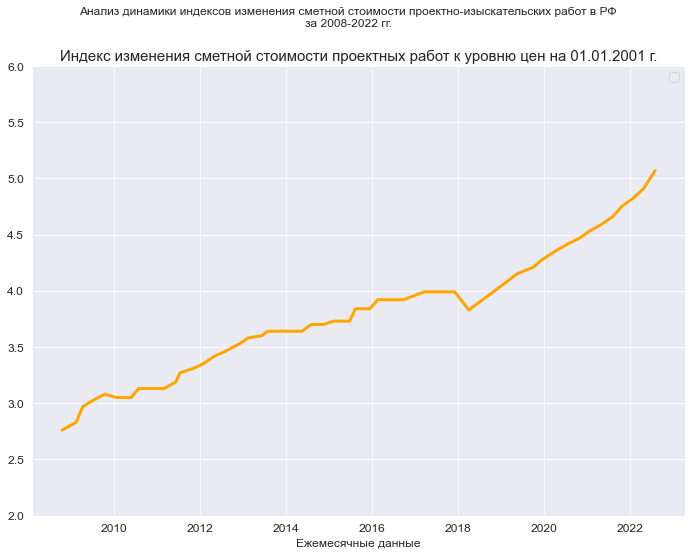
Настройка заголовков:
# Общий заголовок проекта
Task_Project = "Анализ динамики индексов изменения сметной стоимости проектно-изыскательских работ в РФ"
# Заголовок, фиксирующий момент времени
AsOfTheDate = "за 2008-2022 гг."
# Заголовок раздела проекта
Task_Theme = ""
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_T_month = "Ежемесячные данные"
Variable_Name_Ind_design_2001 = "Индекс изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г."
# Границы значений переменных (при построении графиков):
(X_min_graph, X_max_graph) = (0.0, max(T))
(Y_min_graph, Y_max_graph) = (2.0, 6.0)graph_plot_sns_np(
Date, Ind_design_2001,
Ymin_in=Y_min_graph, Ymax_in=Y_max_graph,
color='orange',
title_figure=Title_String, title_figure_fontsize=12,
title_axes=Variable_Name_Ind_design_2001, title_axes_fontsize=15,
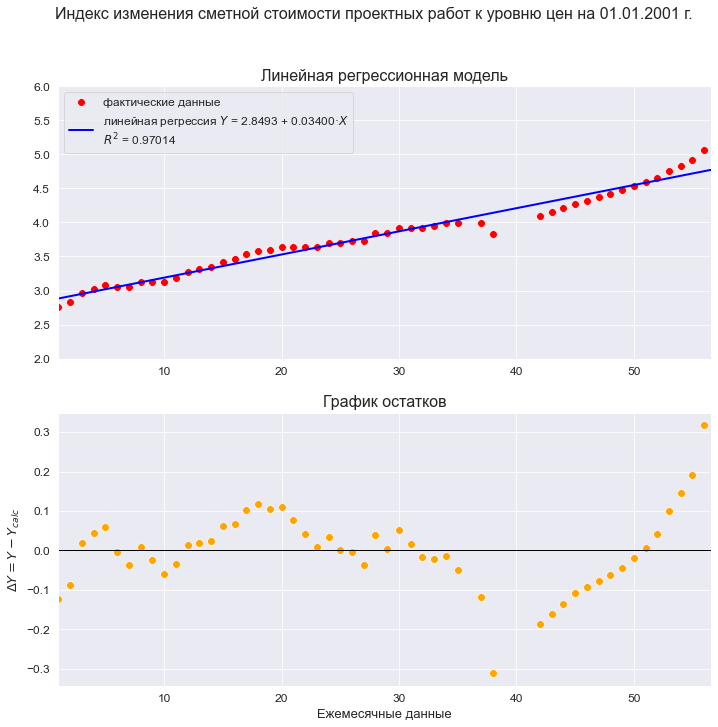
x_label=Variable_Name_T_month, label_fontsize=12)Построение и анализ регрессионной модели
Построим линейную регрессионную модель и проведем ее экспресс-анализ:
model_linear_ols_1 = smf.ols(formula='Ind_design_2001 ~ T', data=dataset_df)
result_linear_ols_1 = model_linear_ols_1.fit()
print(result_linear_ols_1.summary2())Формализация модели:
# Функция линейной регрессионной модели (SLRM - simple linear regression model)
SLRM_func = lambda x, b0, b1: b0 + b1*x
# параметры модели
b0 = result_linear_ols_1.params['Intercept']
b1 = result_linear_ols_1.params['T']
# уравнение модели
regr_model_linear_ols_1_func = lambda x: SLRM_func(x, b0, b1)График модели:
R2 = round(result_linear_ols_1.rsquared, DecPlace)
legend_equation = f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} + {b1:.5f}{chr(183)}' + r'$X$' if b1 > 0 else
f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} - {abs(b1):.5f}{chr(183)}' + r'$X$'
# Пользовательская функция
graph_regression_plot_sns(
T, Ind_design_2001,
regression_model=regr_model_linear_ols_1_func,
#Xmin=X_min_graph, Xmax=X_max_graph,
Ymin=Y_min_graph, Ymax=Y_max_graph,
display_residuals=True,
title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,
title_axes = 'Линейная регрессионная модель',
x_label=Variable_Name_T_month,
#y_label=Variable_Name_Ind_design_2001,
label_legend_regr_model = legend_equation + 'n' + r'$R^2$' + f' = {R2}',
s=60)Ошибки аппроксимации модели:
(model_error_metrics, result) = regression_error_metrics(model_linear_ols_1, model_name='linear_ols')
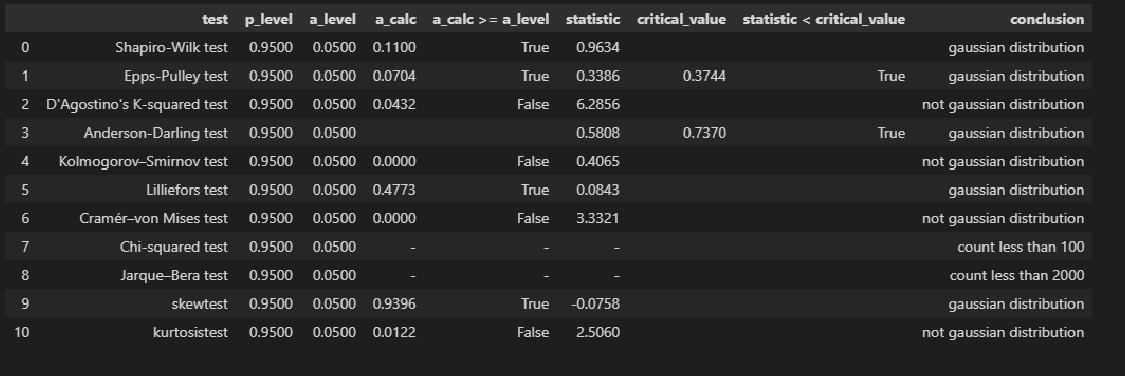
display(result)Проверка нормальности распределения остатков:
res_Y_1 = np.array(result_linear_ols_1.resid)
# Пользовательская функция
graph_hist_boxplot_probplot_sns(
data=res_Y_1,
data_min=-0.25, data_max=0.25,
graph_inclusion='hbp',
data_label=r'$ΔY = Y - Y_{calc}$',
#title_figure=Task_Project,
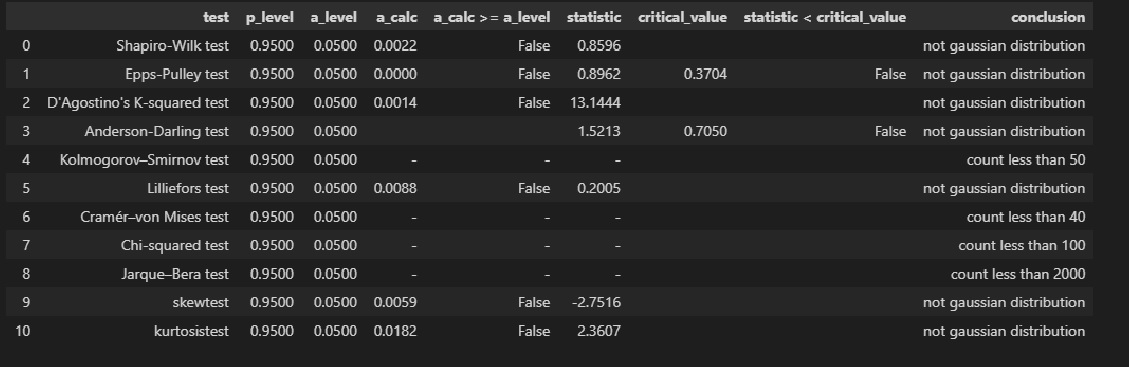
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16) norm_distr_check(res_Y_1)Проверка гетероскедастичности:
Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')
heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)Проверка автокорреляции:
sms.stattools.durbin_watson(res_Y_1)Как видим, результат совпадает со значением статистики критерия в таблице выдачи регрессионного анализа.
display(Durbin_Watson_test(res_Y_1, m=1, p_level=0.95))Выводы по результатам анализа модели:
Итак, мы провели статистический анализ регрессионной модели и установили:
-
Регрессионная модель хорошо аппроксимирует фактические данные.
-
Остатки модели имеют нормальное распределение (хотя результаты тестов противоречивы).
-
Коэффициент детерминации значим; модель объясняет 97% вариации независимой переменной.
-
Коэффициенты регрессии значимы.
-
Обнаружена гетероскедастичность.
-
Тест критерия Дарбина-Уотсона свидетельствует о наличии значимой положительной автокорреляции остатков.
Резюме — несмотря на вроде бы формально хорошие качественные показатели, нам следует признать эту модель некачественной и отвергнуть по следующим негативным причинам:
-
На графике модели хорошо заметна точка излома, которая говорит о смене тенденции (существуют специальные статистические тесты для проверки гипотез о смене тенденции, например, тест Чоу, но мы в данном обзоре рассматривать их не будем).
-
График остатков показывает нам крайне неприглядную картину: на начальном этапе тенденции явно прослеживаются колебания, а после точки излома тенденция вообще кардинально меняется.
-
Противоречивость тестов проверки нормальности распределения остатков.
-
Наличие гетероскедастичности.
-
Наличие автокорреляции. Явление автокорреляции может возникать в случае смены тенденции [5, с.118].
Тот факт, что распределение остатков признается нормальным по результатам таких тестов как Шапиро-Уилка, Эппса-Палли, Андерсона-Дарлинга может иметь разные причины, например, мы можем иметь дело со смесью двух распределений. Этот вопрос требует отдельного тщательного исследования.
Применение построенной модели приведет к ошибке, так как модель хорошо аппроксимирует существующие данные, но из-за смены тенденции неспособна дать качественный прогноз. Проиллюстрировать это можно, построив доверительный интервалы прогноза (формально мы можем это сделать, так как распределение остатков признано нормальным):
graph_regression_pair_predict_plot_sns(
model_fit=result_linear_ols_1,
regression_model_in=regr_model_linear_ols_1_func,
Xmin=X_min_graph, Xmax=X_max_graph+12, Nx=25,
Ymin_graph=2.0, Ymax_graph=Y_max_graph,
title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,
title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
#x_label=Variable_Name_X,
#y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=50,
result_output=False)Нет, такой прогноз нам не нужен.
Пример 2: проверка автокорреляция регрессионной модели
Формирование исходных данных
Рассмотрим пример множественной линейной регрессионной модели, приведенный в источнике [6, с.192].
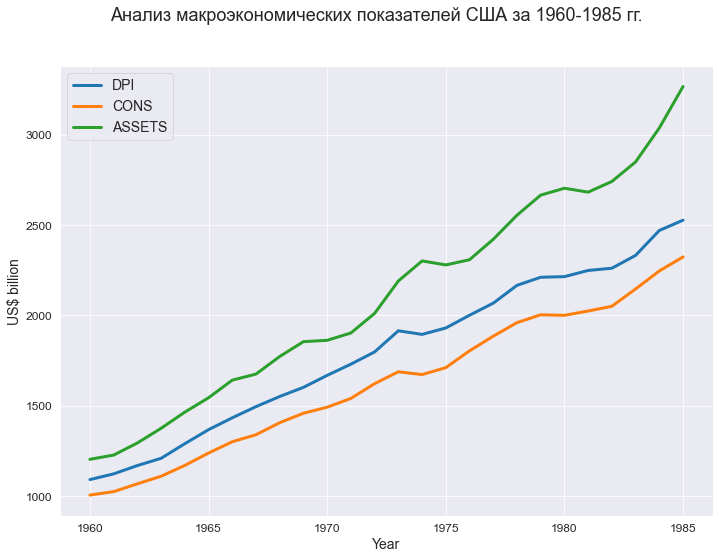
В качестве исходных данных рассматриваются ряд макроэкономических показателей США за 1960-1985 гг. (в сопоставимых ценах 1982 г., млрд.долл):
-
DPI — годовой совокупный располагаемый личный доход;
-
CONS — годовые совокупные потребительские расходы;
-
ASSETS — финансовые активы населения на начало календарного года.
Предполагается, что между переменной CONS и регрессорами DPI, ASSETS имеется линейная регрессионная связь.
Исходные данные содержаться в файле Macroeconomic_indicators_USA_1960_1985.csv, который помещен в папку data.
Прочитаем csv-файл:
data_df = pd.read_csv(filepath_or_buffer='data/Macroeconomic_indicators_USA_1960_1985.csv', sep=';')
display(data_df)
#display(data_df.head(), data_df.tail())
data_df.info()Визуализация
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.'
fig.suptitle(title_figure, fontsize = 18)
sns.lineplot(
x = data_df['YEAR'], y = data_df['DPI'],
linewidth=3,
legend=True,
label='DPI',
ax=axes)
sns.lineplot(
x = data_df['YEAR'], y = data_df['CONS'],
linewidth=3,
legend=True,
label='CONS',
ax=axes)
sns.lineplot(
x = data_df['YEAR'], y = data_df['ASSETS'],
linewidth=3,
legend=True,
label='ASSETS',
ax=axes)
axes.set_xlabel('Year')
axes.set_ylabel('US$ billion')
plt.show()Построение и анализ регрессионной модели
Построим линейную регрессионную модель и проведем ее экспресс-анализ:
y = data_df['CONS']
X = data_df[['DPI', 'ASSETS']]
X = sm.add_constant(X)
model_linear_ols_2 = sm.OLS(y, X)
result_linear_ols_2 = model_linear_ols_2.fit()
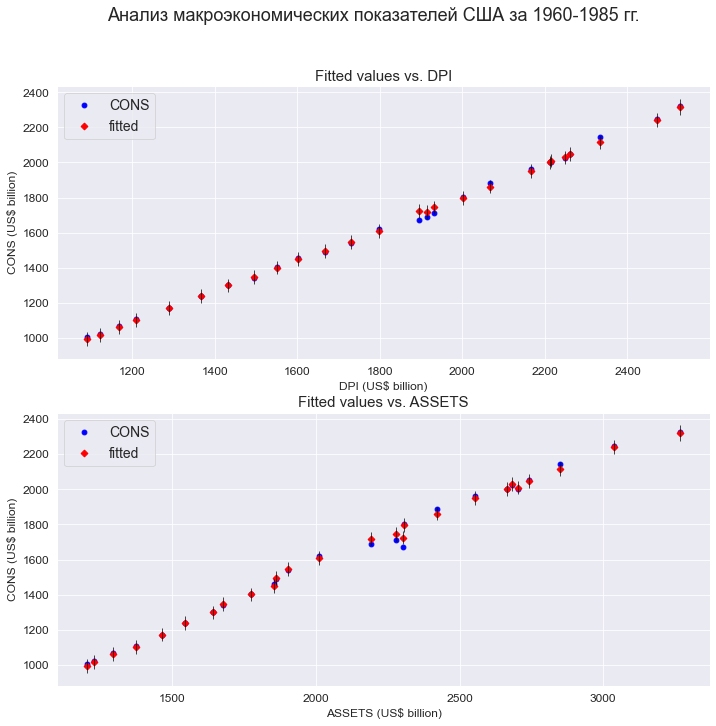
print(result_linear_ols_2.summary2())График модели:
fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.'
fig.suptitle(title_figure, fontsize = 18)
fig = sm.graphics.plot_fit(
result_linear_ols_2, 'DPI',
vlines=True, # это параметр отвечает за отображение доверительных интервалов для Y
ax=ax1)
ax1.set_ylabel('CONS (US$ billion)', fontsize = 12)
ax1.set_xlabel('DPI (US$ billion)', fontsize = 12)
ax1.set_title('Fitted values vs. DPI', fontsize = 15)
fig = sm.graphics.plot_fit(
result_linear_ols_2, 'ASSETS',
vlines=True, # это параметр отвечает за отображение доверительных интервалов для Y
ax=ax2)
ax2.set_ylabel('CONS (US$ billion)', fontsize = 12)
ax2.set_xlabel('ASSETS (US$ billion)', fontsize = 12)
ax2.set_title('Fitted values vs. ASSETS', fontsize = 15)
plt.show()Ошибки аппроксимации модели:
(model_error_metrics, result) = regrpy
ession_error_metrics(model_linear_ols_2, model_name='linear_ols')
display(result)Проверка нормальности распределения остатков:
res_Y_2 = np.array(result_linear_ols_2.resid)
# Пользовательская функция
graph_hist_boxplot_probplot_sns(
data=res_Y_2,
data_min=-60, data_max=60,
graph_inclusion='hbp',
data_label=r'$ΔY = Y - Y_{calc}$',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16)
norm_distr_check(res_Y_2)Прроверка гетероскедастичности:
Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')
heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)Проверка автокорреляции:
display(Durbin_Watson_test(res_Y_2, m=1, p_level=0.95))Выводы по результатам анализа модели:
Как видим, в целом результаты расчетов совпадают с результатами из первоисточника [6], в части выявления автокорреляции аналогично.
Информация к размышлению.
Анализ показывает, что модель хорошо аппроксимирует фактические данные, но имеет место отклонение от нормального закона распределения остатков, противоречивые выводы о гетероскедастичности и наличие автокорреляции, то есть модель некачественная.
Также мы видим, что динамика макроэкономических показателей свидетельствует о наличии трендов, однако, если в модель добавить еще один фактор — год или номер наблюдения — то, этот фактор окажется незначимым.
В дальнейшем автор при анализе остатков модели [6, с.198] выявляет структурный сдвиг (обусловленный мировым топливно-энергетическим кризисом в 1973 г.) и вводит в модель фиктивные переменные, учитывающие этот структурный сдвиг
Итоги
Итак, подведем итоги:
-
мы рассмотрели способы реализации в полной мере критерия Дарбина-Уотсона средствами python, создали пользовательскую функцию, уменьшающую размер кода;
-
разобрали пример оцифровки таблицы критических значений статистического критерия для реализации пользовательской функции.
Исходный код находится в моем репозитории на GitHub.
Надеюсь, данный обзор поможет специалистам DataScience в работе.
Литература
-
Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
-
Айвазян С.А. Прикладная статистика. Основы эконометрики: В 2 т. — Т.2: Основы эконометрики. — 2-е изд., испр. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.
-
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.
-
Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.
-
Тихомиров Н.П., дорохина Е.Ю. Эконометрика. — М.: Экзамен, 2003. — 512 с.
-
Носко В.П. Эконометрика. Кн.1. Ч.1, 2. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.
-
Вандер Плас Дж. Python для сложных задач: наука о данных и машинное обучение. — СПб: Питер, 2018. — 576 с.
Содержание
- Автокорреляция
- Тестирование автокорреляции
- Автокорреляционная функция
- См. также
- Полезное
- Смотреть что такое «Автокорреляция» в других словарях:
- Автокорреляция
- Что такое автокорреляция?
- Ключевые выводы
- Понимание автокорреляции
- Тестирование на автокорреляцию
- Автокорреляция в техническом анализе
- Пример автокорреляции
- АВТОКОРРЕЛЯЦИЯ
- Смотреть что такое «АВТОКОРРЕЛЯЦИЯ» в других словарях:
- Сущность и последствия автокорреляции
- Автокорреляция
- Полезное
- Смотреть что такое «Автокорреляция» в других словарях:
Автокорреляция
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Данное понятие широко используется в эконометрике. Наличие автокорреляции случайных ошибок регрессионной модели приводит к ухудшению качества МНК-оценок параметров регрессии, а также к завышению тестовых статистик, по которым проверяется качество модели (то есть создается искусственное улучшение качества модели относительно её действительного уровня точности). Поэтому тестирование автокорреляции случайных ошибок является необходимой процедурой построения регрессионной модели.
Коэффициенты автокорреляции также имеют самостоятельное важное значение для моделей временных рядов ARMA.
Тестирование автокорреляции
Чаще всего тестируется наличие в случайных ошибках авторегрессионного процесса первого порядка. Для тестирования нулевой гипотезы, о равенстве коэффициента автокорреляции нулю чаще всего применяют критерий Дарбина-Уотсона. При наличии лаговой зависимой переменной в модели данный критерий неприменим, можно использовать асимптотический h-тест Дарбина. Оба эти теста предназначены для проверки автокорреляции случайных ошибок первого порядка. Для тестирования автокорреляции случайных ошибок большего порядка можно использовать более универсальный асимптотический LM-тест Бройша-Годфри. В данном тесте случайные ошибки не обязательно должны быть нормально распределены. Тест применим также и в авторегрессионных моделях (в отличие от критерия Дарбина-Уотсона).
Для тестирования совместной гипотезы о равенстве нулю всех коэффициентов автокорреляции до некоторого порядка можно использовать Q-тест Бокса — Пирса или Q-тест Льюнга-Бокса
Автокорреляционная функция
Автокорреляционная функция показывает зависимость автокорреляции от величины сдвига во времени. При этом предполагается стационарность временного ряда, означающая в том числе независимость автокорреляций от момента времени. Анализ автокорреляционной функции (вместе с частной автокорреляционной функцией) позволяет проводить идентификацию порядка ARMA-моделей.
См. также
Полезное
Смотреть что такое «Автокорреляция» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — [autocorrelation, serial correlation] — корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией … Экономико-математический словарь
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
АВТОКОРРЕЛЯЦИЯ — случайного процесса корреляция значений Термин употребляют (наряду с термином корреляционная функция ) в основном при изучении стационарных случайных процессов, для к рых А. зависит лишь от h(но Не от t). А. В. Прохоров … Математическая энциклопедия
Источник
Автокорреляция
Опубликовано 06.06.2021 · Обновлено 06.06.2021
Что такое автокорреляция?
Автокорреляция – это математическое представление степени сходства между заданным временным рядом и запаздывающей версией самого себя в последовательных временных интервалах. Это концептуально похоже на корреляцию между двумя разными временными рядами, но автокорреляция использует один и тот же временной ряд дважды: один раз в исходной форме и один раз с запаздыванием на один или несколько периодов времени.
Например, если сегодня дождь, данные говорят о том, что завтра будет дождь с большей вероятностью, чем если сегодня будет ясно. Когда дело доходит до инвестирования, акция может иметь сильную положительную автокорреляцию доходности, что говорит о том, что если она «растет» сегодня, то с большей вероятностью она вырастет и завтра.
Естественно, автокорреляция может быть полезным инструментом для трейдеров; особенно для технических аналитиков.
Ключевые выводы
Понимание автокорреляции
Автокорреляцию также можно называть корреляцией с задержкой или последовательной корреляцией, поскольку она измеряет взаимосвязь между текущим значением переменной и ее прошлыми значениями.
В качестве очень простого примера взгляните на пять процентных значений в таблице ниже. Мы сравниваем их с столбцом справа, который содержит тот же набор значений, только что перемещенный на одну строку вверх.
Автокорреляция +1 представляет собой идеальную положительную корреляцию (увеличение, наблюдаемое в одном временном ряду, приводит к пропорциональному увеличению в другом временном ряду).
Автокорреляция измеряет линейные отношения. Даже если автокорреляция мала, все равно может существовать нелинейная взаимосвязь между временным рядом и самой лаговой версией.
Тестирование на автокорреляцию
Наиболее распространенным методом тестовой автокорреляции является тест Дарбина-Ватсона. Не вдаваясь в технические подробности, можно сказать, что Durbin-Watson – это статистика, которая обнаруживает автокорреляцию на основе регрессионного анализа.
Метод Дарбина-Ватсона всегда дает диапазон значений теста от 0 до 4. Значения, близкие к 0, указывают на большую степень положительной корреляции, значения, близкие к 4, указывают на большую степень отрицательной автокорреляции, а значения, близкие к среднему, предполагают меньшую автокорреляцию.
Итак, почему автокорреляция важна на финансовых рынках? Простой. Автокорреляция может применяться для тщательного анализа исторических движений цен, которые инвесторы затем могут использовать для прогнозирования будущих движений цен. В частности, автокорреляция может использоваться, чтобы определить, имеет ли смысл стратегия импульсной торговли.
Автокорреляция в техническом анализе
Автокорреляция может быть полезна для технического анализа, потому что технический анализ больше всего касается тенденций и взаимосвязей между ценами на ценные бумаги с использованием методов построения графиков. Это контрастирует с фундаментальным анализом, который вместо этого фокусируется на финансовом состоянии или управлении компанией.
Технические аналитики могут использовать автокорреляцию, чтобы выяснить, насколько прошлые цены на ценные бумаги влияют на их будущую цену.
Автокорреляция может помочь определить, действует ли фактор импульса для данной акции. Если, например, акция с высокой положительной автокорреляцией демонстрирует значительный рост в течение двух дней подряд, было бы разумно ожидать, что она вырастет и в следующие два дня.
Пример автокорреляции
Предположим, Эмма хочет определить, обнаруживает ли доходность акций в ее портфеле автокорреляцию; то есть доходность акций связана с доходностью предыдущих торговых сессий.
Если доходность демонстрирует автокорреляцию, Эмма могла бы охарактеризовать ее как импульсную акцию, потому что прошлые доходности, похоже, влияют на будущую доходность. Эмма выполняет регрессию с доходностью предыдущей торговой сессии в качестве независимой переменной и текущей доходностью в качестве зависимой переменной. Она обнаружила, что доходность за день до этого имеет положительную автокорреляцию 0,8.
Поскольку 0,8 близко к +1, прошлые прибыли кажутся очень хорошим положительным предиктором будущей доходности для этой конкретной акции.
Следовательно, Эмма может скорректировать свой портфель, чтобы воспользоваться преимуществами автокорреляции или импульса, продолжая удерживать свою позицию или накапливая больше акций.
Источник
АВТОКОРРЕЛЯЦИЯ
случайного процесса 
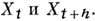
Смотреть что такое «АВТОКОРРЕЛЯЦИЯ» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — Автокорреляция статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса со сдвигом по времени. Данное понятие широко используется в эконометрике. Наличие… … Википедия
Автокорреляция — [autocorrelation, serial correlation] — корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией … Экономико-математический словарь
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
Источник
Сущность и последствия автокорреляции



Автокорреляция – это корреляционная зависимость между текущими значениями некоторой переменной и значениями этой же переменной, сдвинутыми на несколько периодов времени назад. Автокорреляция случайной составляющей e модели – это корреляционная зависимость текущих 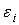
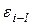
Автокорреляция случайных возмущений модели нарушает одну из предпосылок регрессионного анализа: условие
Автокорреляция может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результирующей переменной. Во-вторых, в ряде случаев причину автокорреляции следует искать в формулировке модели. Модель может не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается на возмущениях, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени t: автокорреляция обычно встречается при анализе временных рядов.
Постоянная направленность воздействия не включенных в модель переменных является наиболее частой причиной так называемой положительной автокорреляции.
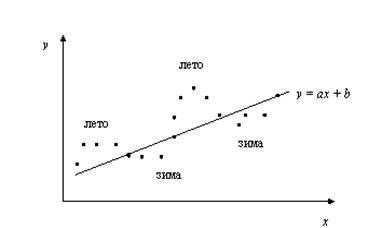
Иллюстрацией положительной автокорреляции может служить следующий пример.
Пример 5.2. Пусть исследуется спрос Y на прохладительные напитки в зависимости от дохода X по ежемесячным и сезонным наблюдениям. Зависимость, отражающая увеличение спроса с ростом дохода, может быть представлена линейной функцией регрессии y = ax + b, изображенной вместе с результатами наблюдений на рис. 5.2.
Рис. 5.2. Положительная автокорреляция
На величину спроса Y оказывают влияние не только доход X (учтенный фактор), но и другие факторы, которые не учтены в модели. Одним из таких факторов является время года.
Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результирующую переменную. Так спрос на прохладительные напитки всегда выше линии регрессии летом (т.е. для летних наблюдений e > 0) и ниже зимой (т.е. для зимних наблюдений e
Рис. 5.3. Отрицательная автокорреляция
Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяют следующие.
1. МНК-оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.
Вследствие вышесказанного все выводы, получаемые на основе соответствующих t— и F— статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при проверке качества оценок (параметров модели и самой модели в целом), могут быть ошибочными и приводить к неверным заключениям по построенной модели.
Источник
Автокорреляция
А. затрудняет применение ряда классических методов анализа временных рядов. В моделях регрессии, описывающих зависимости между случайными значениями взаимосвязанных величин, она снижает эффективность применения метода наименьших квадратов. Поэтому выработаны и применяются специальные статистические приемы для ее выявления (напр. критерий Дарбина — Уотсона) и ее элиминирования (напр., преобразование временного ряда в ряд значений разностей между его соседними членами), а также для модификации самого метода наименьших квадратов.
Полезное
Смотреть что такое «Автокорреляция» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — Автокорреляция статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса со сдвигом по времени. Данное понятие широко используется в эконометрике. Наличие… … Википедия
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
АВТОКОРРЕЛЯЦИЯ — случайного процесса корреляция значений Термин употребляют (наряду с термином корреляционная функция ) в основном при изучении стационарных случайных процессов, для к рых А. зависит лишь от h(но Не от t). А. В. Прохоров … Математическая энциклопедия
Источник
Слайд 1Тестирование автокорреляции
Лекция 6
Тест Дарвина –Уотсона

Слайд 2Цели лекции
Природа проблемы автокорреляции остатков
Последствия автокорреляции
Средства обнаружения автокорреляции
Средства для решения
проблемы автокорреляции.

Слайд 3Понятие автокорреляции
Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы
Гаусса-Маркова:
Cov(ui,uj)≠0 при i≠j.
Автокорреляция (последовательная корреляция) – это корреляция между
наблюдаемыми показателями во времени (временные ряды) или в пространстве (перекрестные данные).
Причина – неправильный выбор спецификации модели.
Последствия автокорреляции
— оценки коэффициентов теряют эффективность;
— стандартные ошибки коэффициентов занижены.

Слайд 5Причины чистой автокорреляции
1. Инерция факторов
Трансформация, изменение многих экономических факторов обладает
инерционностью.
2. Эффект паутины
Многие экономические факторы реагируют на изменение экономических условий
с запаздыванием (временным лагом)
3. Сглаживание данных.
Усреднение данных по некоторому продолжительному интервалу времени.

Слайд 6Автокорреляция первого порядка
случайный член рассматриваемого уравнения регрессии,
коэффициент автокорреляции первого порядка,
случайный член, не подверженный автокорреляции

Слайд 7Сезонная автокорреляция
случайный член рассматриваемого уравнения регрессии,
коэффициент
сезонной автокорреляции,
случайный член, не подверженный автокорреляции

Слайд 8Автокорреляция второго порядка
случайный член рассматриваемого уравнения регрессии,
1, 2
коэффициенты автокорреляции,
случайный член, не подверженный автокорреляции

Слайд 9
Авторегрессия 1-го порядка : AR(1)
Авторкорреляция скользящих средних 3-го порядка: MA(5)
Авторегрессия
5-го порядка : AR(5)
6
Примеры более сложных авторегрессионных корреляций

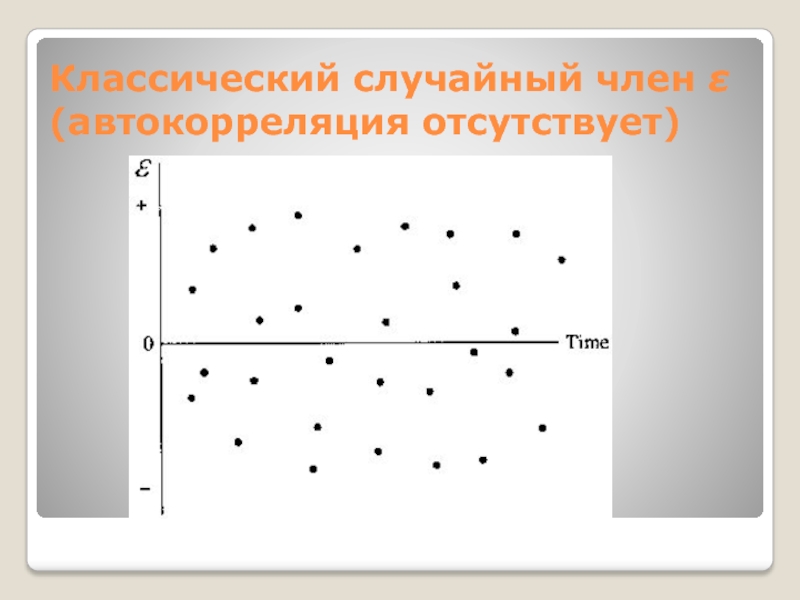
Слайд 10Классический случайный член (автокорреляция отсутствует)
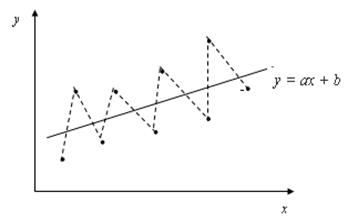
Слайд 11Положительная автокорреляция
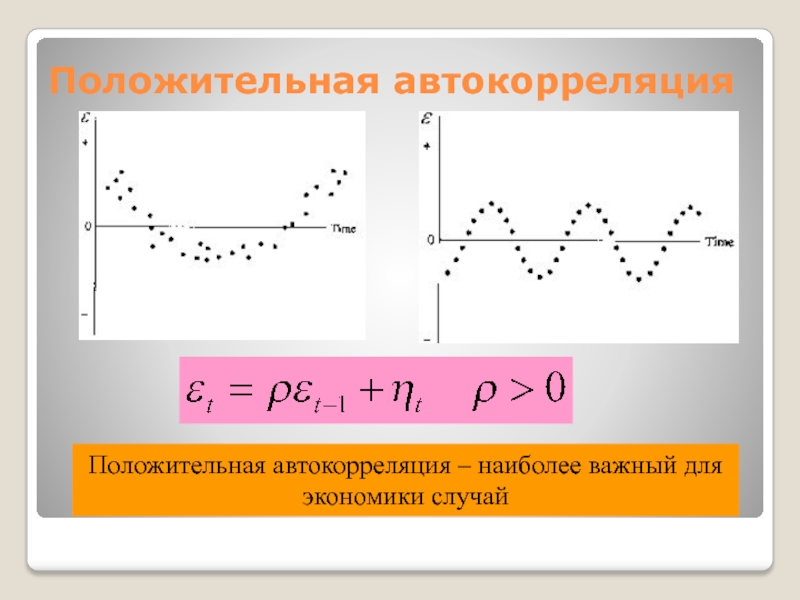
Положительная автокорреляция – наиболее важный для экономики случай
Слайд 13ПОЛОЖИТЕЛЬНАЯ АВТОКОРРЕЛЯЦИЯ
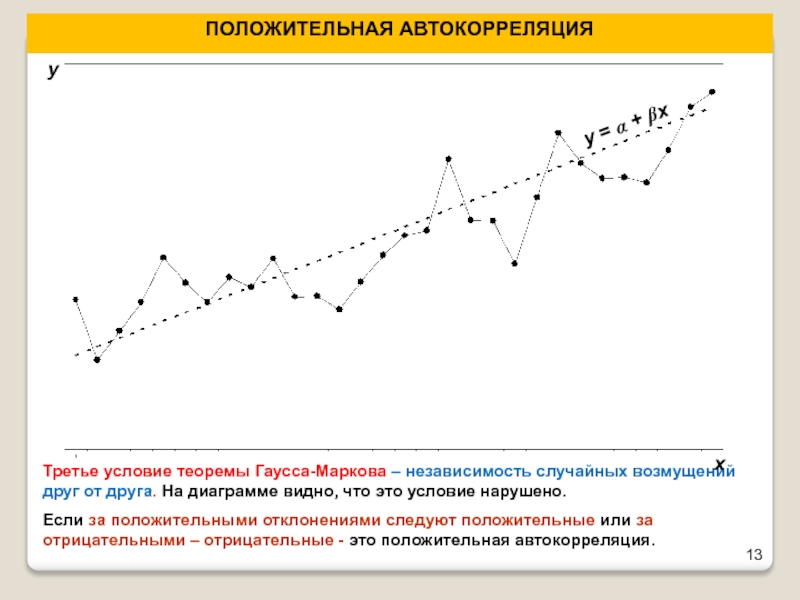
Третье условие теоремы Гаусса-Маркова – независимость случайных возмущений друг
от друга. На диаграмме видно, что это условие нарушено.
Если за
положительными отклонениями следуют положительные или за отрицательными – отрицательные — это положительная автокорреляция.
y
x
y = a + bx
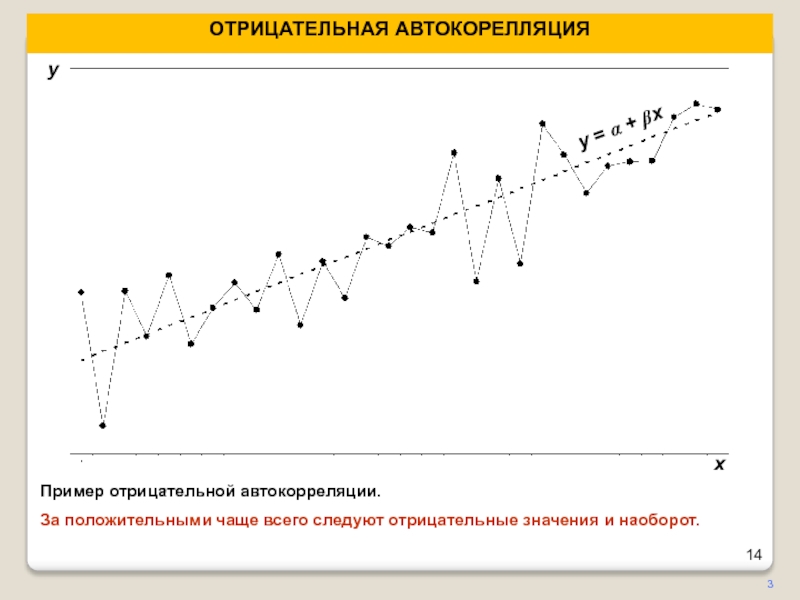
Слайд 14ОТРИЦАТЕЛЬНАЯ АВТОКОРЕЛЛЯЦИЯ
3
Пример отрицательной автокорреляции.
За положительными чаще всего следуют отрицательные
значения и наоборот.
y
y = a + bx
x
Слайд 15Пример влияния автокорреляции на случайную выборку
Рассмотрим пример с выборкой из
50 независимых нормально распределенных с нулевым средним значений i.
et –
распределена по стандартному нормальному закону с 0 средним и дисперсией 1, r (ρ) меняется.
С целью ознакомления с влиянием автокорреляции будем вводить в нее положительную, а затем отрицательную автокорреляцию.

Слайд 16Пример влияния автокорреляции на случайную выборку
ρ = 0, т.е. автокорреляция
отсутствует. Процесс — нормальная случайная величина
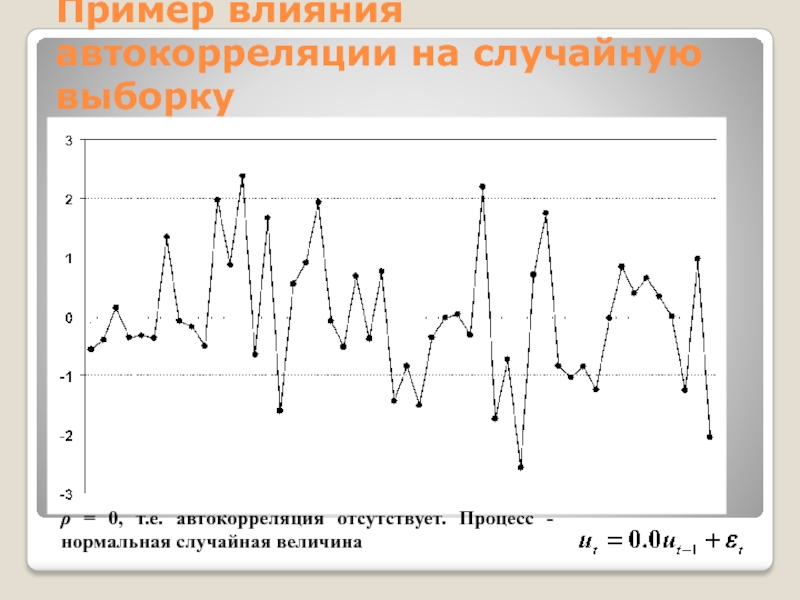
Слайд 17Пример влияния автокорреляции на случайную выборку
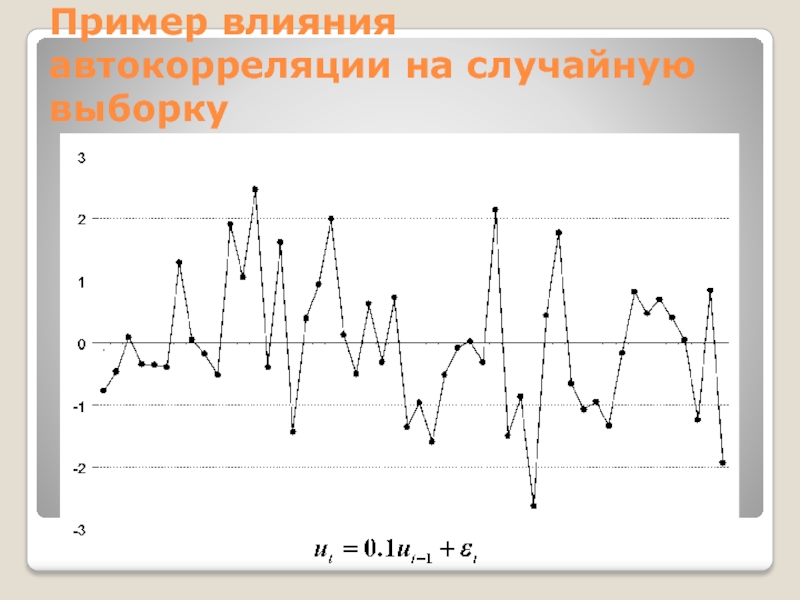
Слайд 18Пример влияния автокорреляции на случайную выборку
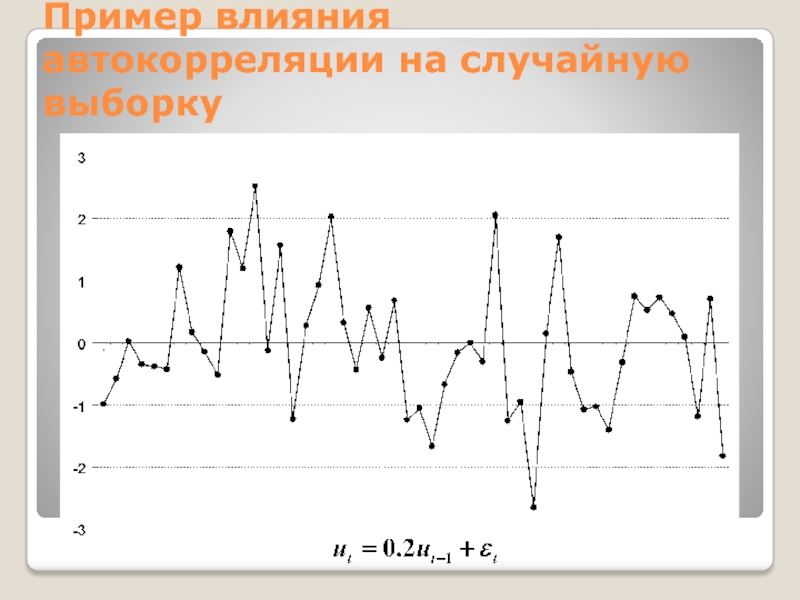
Слайд 19Пример влияния автокорреляции на случайную выборку
начинает проявляться небольшая положительная автокорреляция
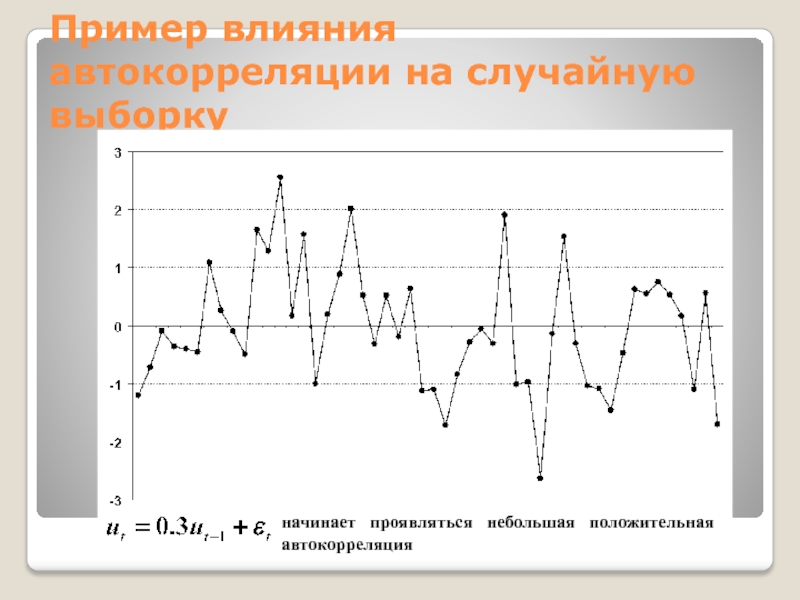
Слайд 20Пример влияния автокорреляции на случайную выборку
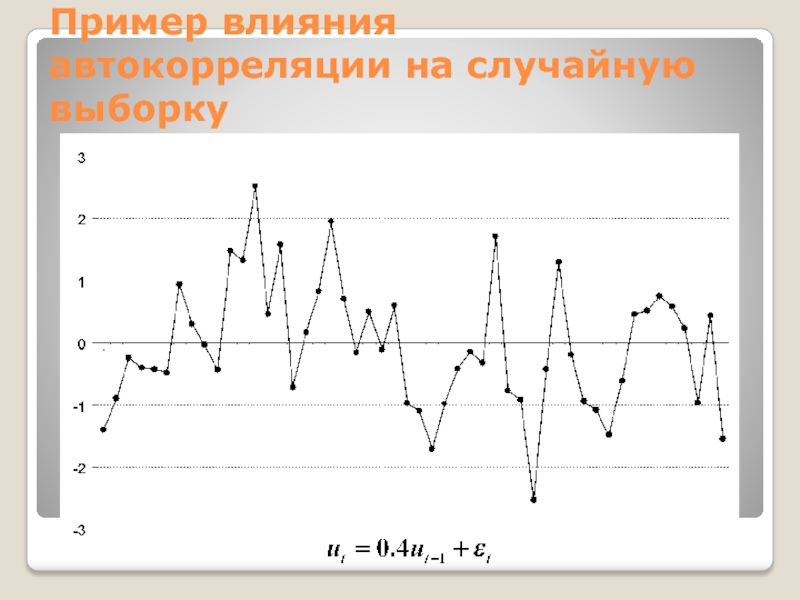
Слайд 21Пример влияния автокорреляции на случайную выборку
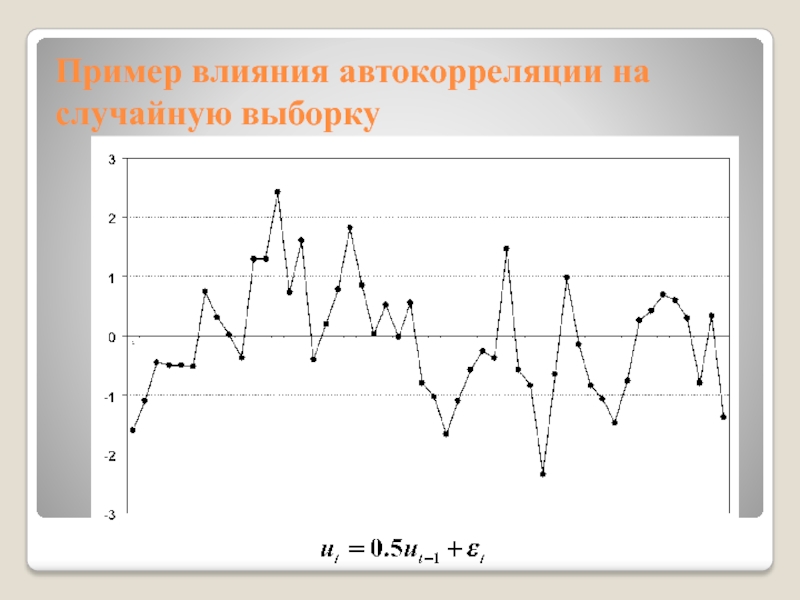
Слайд 22Пример влияния автокорреляции на случайную выборку
С ρ = 0.6 u
подвержена положительной автокорреляции. Положительные значения чаще следуют за положительными, а
отрицательные за отрицательными.
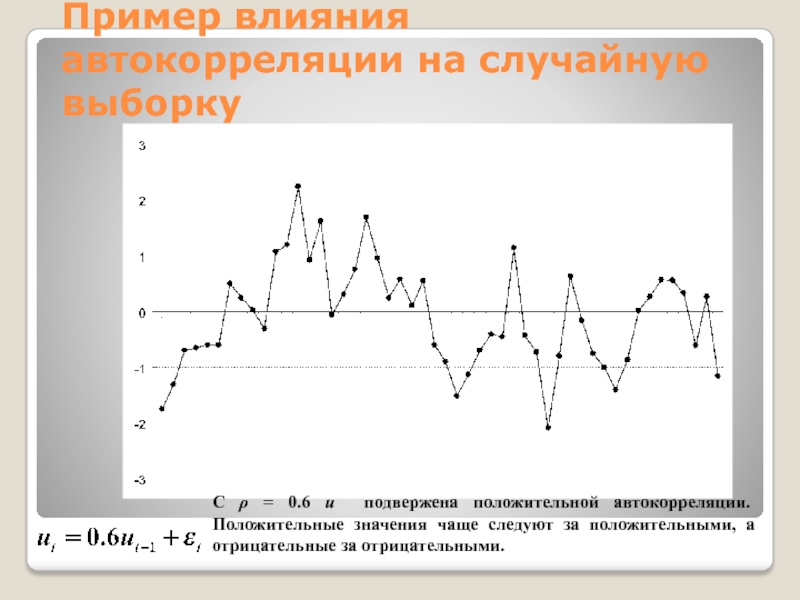
Слайд 23Пример влияния автокорреляции на случайную выборку
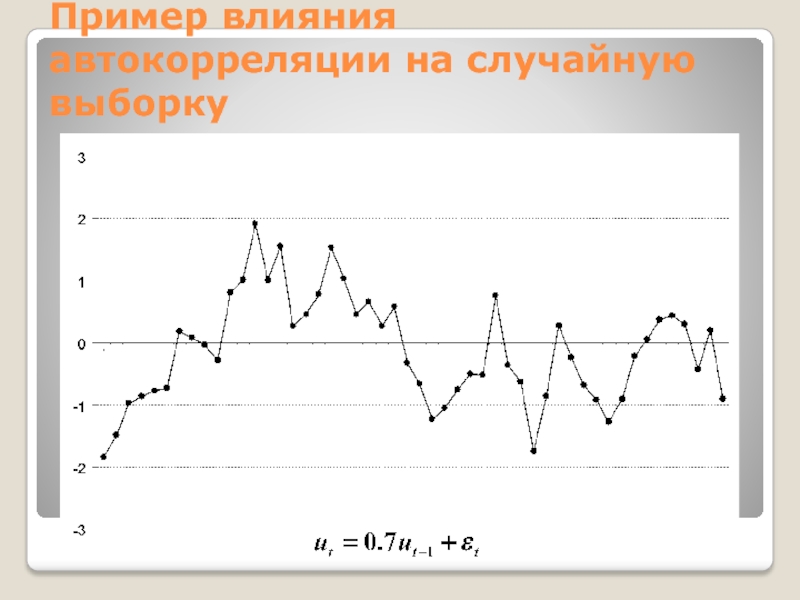
Слайд 24Пример влияния автокорреляции на случайную выборку
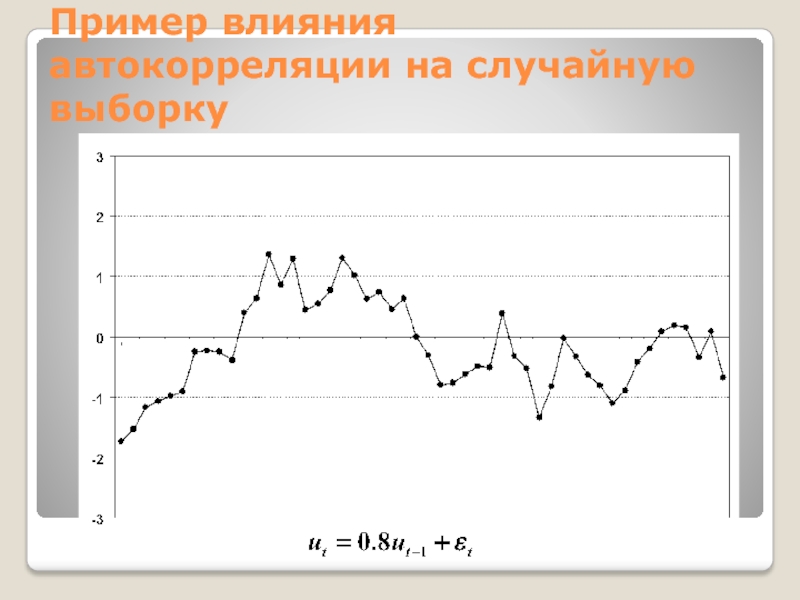
Слайд 25Пример влияния автокорреляции на случайную выборку
С ρ = 0.9 последовательность
значений с одним знаком становится длинной, а тенденция возврата к
0 слабо
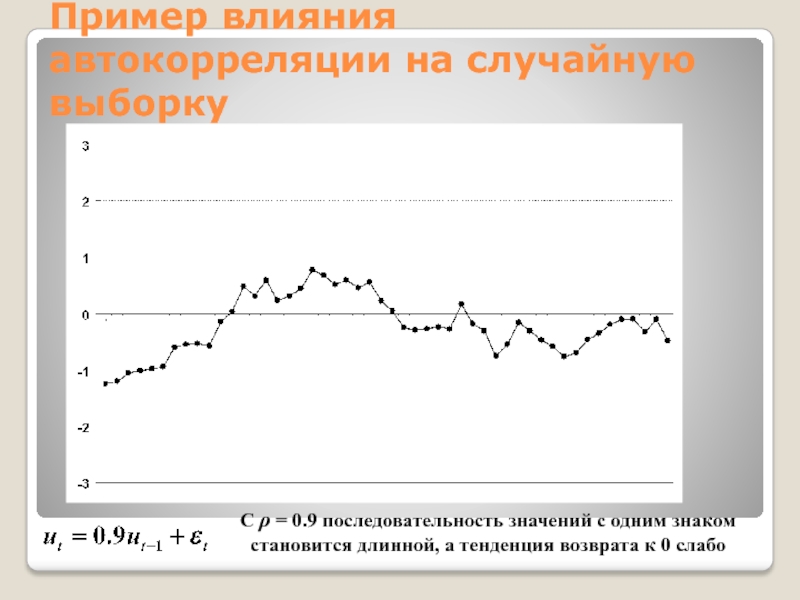
Слайд 26Пример влияния автокорреляции на случайную выборку
При больших значениях ρ процесс
становится нестационарным, приближаясь к случайному блужданию
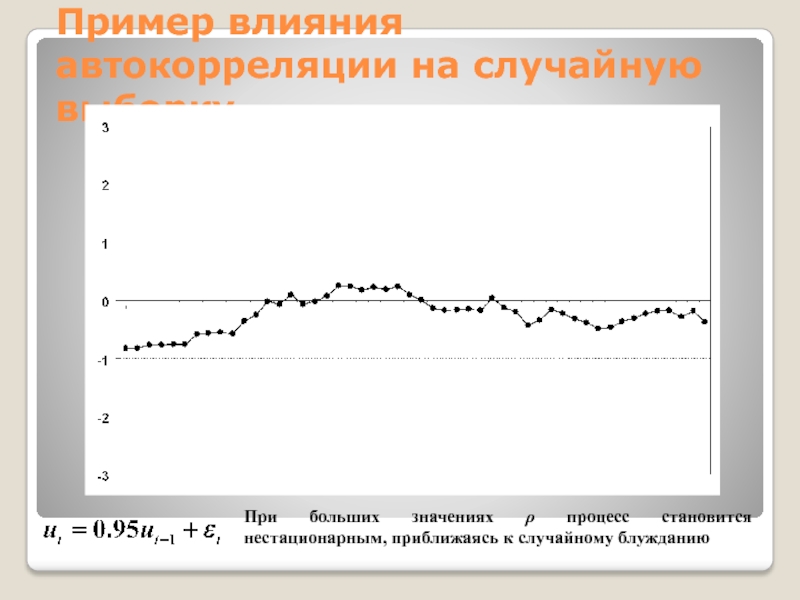
Слайд 27Пример влияния автокорреляции на случайную выборку
Примеры отрицательной автокорреляции для тех
же значений et
Слайд 28Пример влияния автокорреляции на случайную выборку
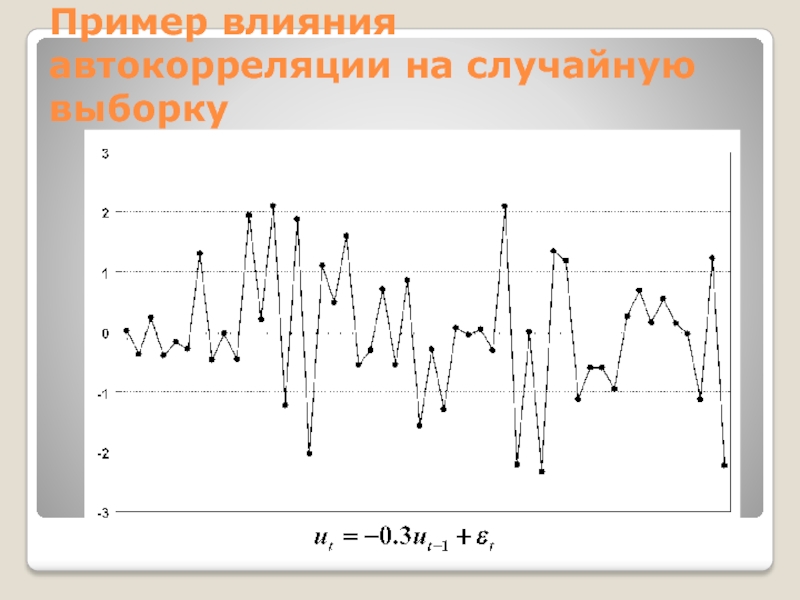
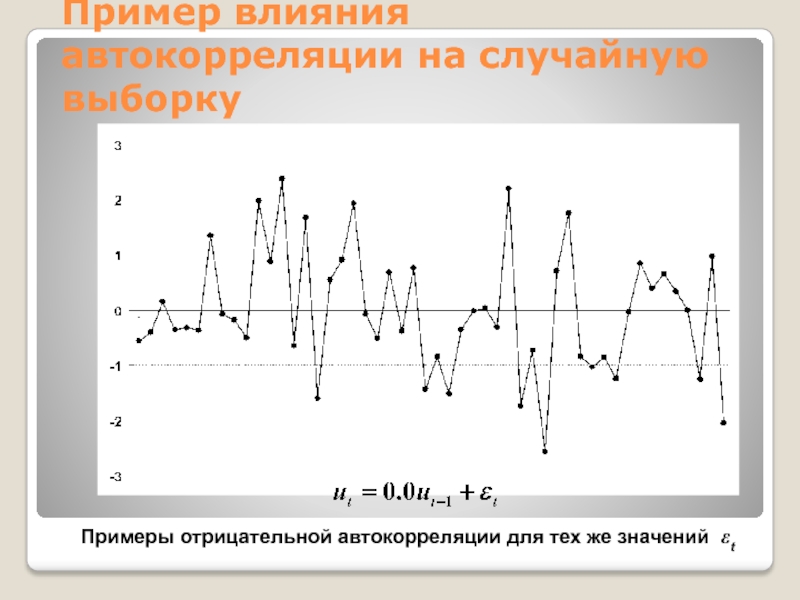
Слайд 29Пример влияния автокорреляции на случайную выборку
С ρ = 0.6 можно
видеть что положительные значения имеют тенденцию следовать за отрицательными и
наоборот. Отрицательная автокорреляция становится очевидно
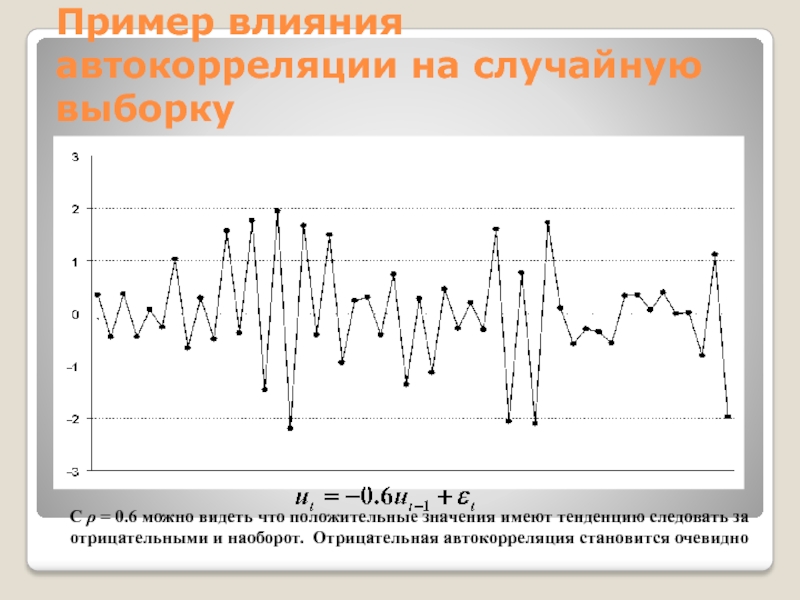
Слайд 30Пример влияния автокорреляции на случайную выборку
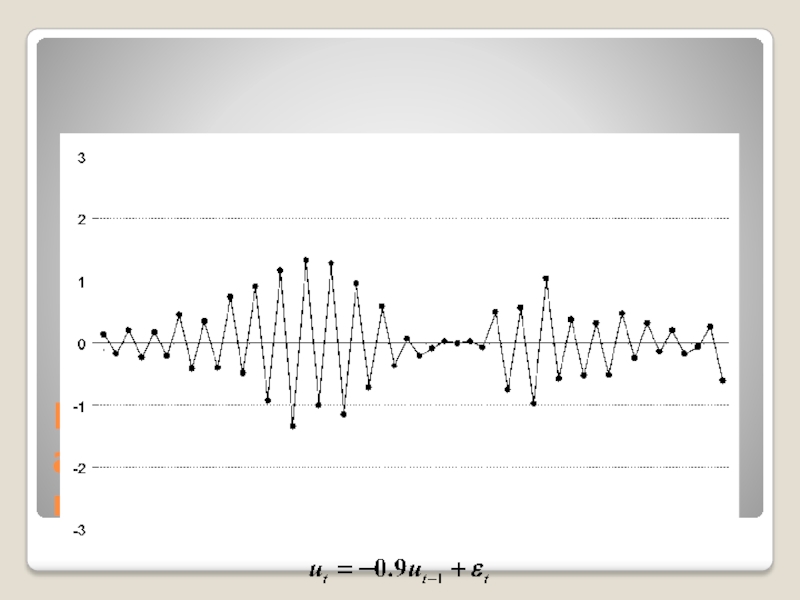
Слайд 31
АВТОКОРЕЛЛЯЦИЯ
На графике видно, что случайные возмущения подвержены положительной
автокорреляции. Сравнивая с примерами имитационного моделирования можно предполагать, что коэффициент
корреляции r не ниже 0.6.
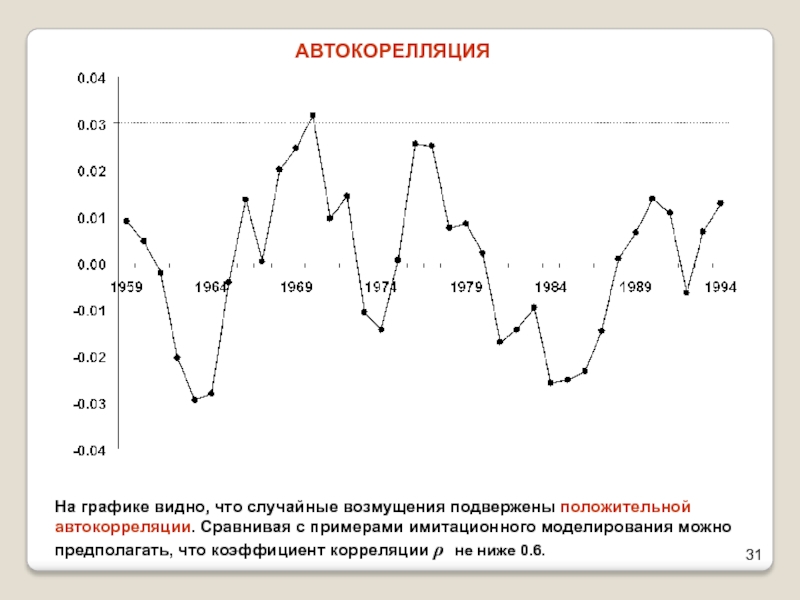
Слайд 32
============================================================
Dependent Variable: LGHOUS
Method: Least Squares
Sample: 1959 2003
Included observations: 45
============================================================
Variable Coefficient Std. Error t-Statistic Prob.
============================================================
C 0.005625 0.167903 0.033501 0.9734
LGDPI 1.031918 0.006649 155.1976 0.0000
LGPRHOUS -0.483421 0.041780 -11.57056 0.0000
============================================================
R-squared 0.998583 Mean dependent var 6.359334
Adjusted R-squared 0.998515 S.D. dependent var 0.437527
S.E. of regression 0.016859 Akaike info criter-5.263574
Sum squared resid 0.011937 Schwarz criterion -5.143130
Log likelihood 121.4304 F-statistic 14797.05
Durbin-Watson stat 0.633113 Prob(F-statistic) 0.000000
============================================================
АВТОКОРРЕЛЯЦИЯ
ПРИМЕР
Зависимость расходов на жилье от располагаемого дохода и индекса цен на жилье
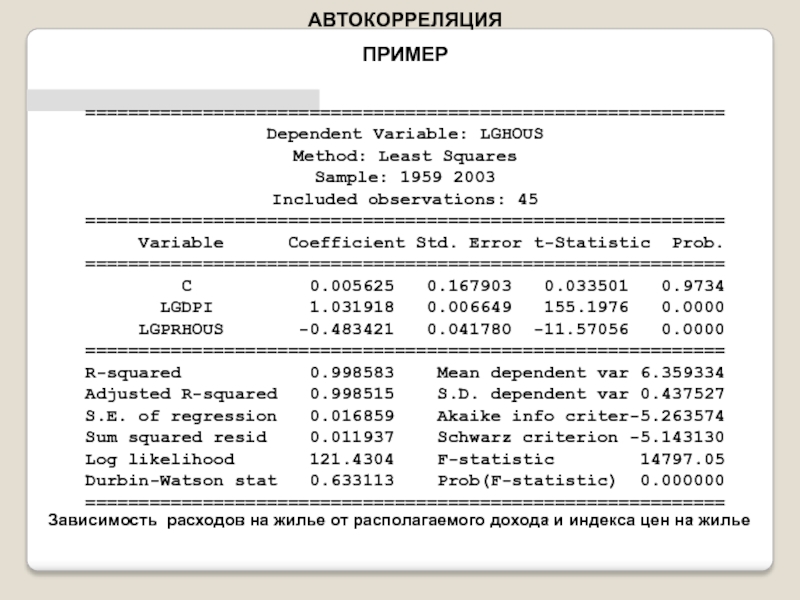
Слайд 33
График остатков соответствует коэффициенту автокорреляции, равному примерно 0,75.
АВТОКОРРЕЛЯЦИЯ
ПРИМЕР
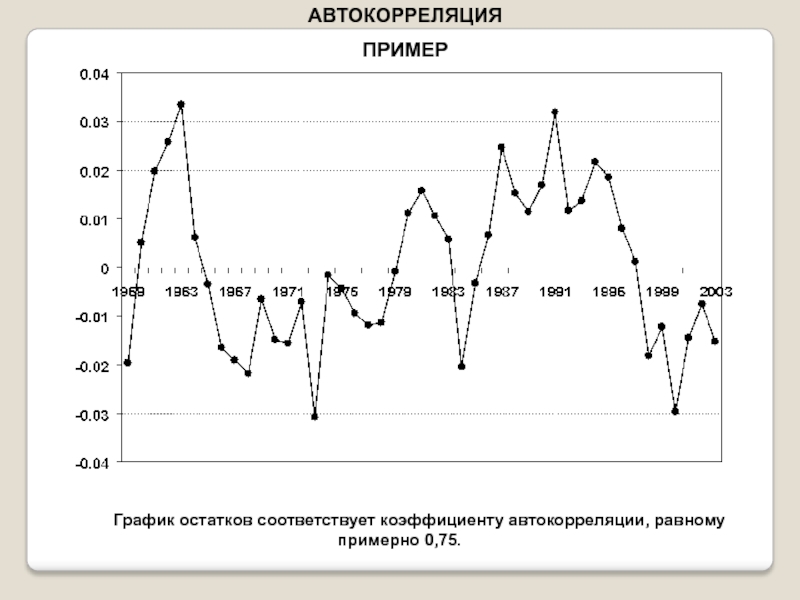
Слайд 34Ложная автокорреляция
(автокорреляция, вызванная ошибочной спецификацией)
X2 сама является автокоррелированной переменной,
а значение мало по сравнению с величиной

Слайд 35Пример. Автокорреляция, вызванная отсутствием значимой переменной

Слайд 36Пример. Автокорреляция, вызванная отсутствием значимой переменной
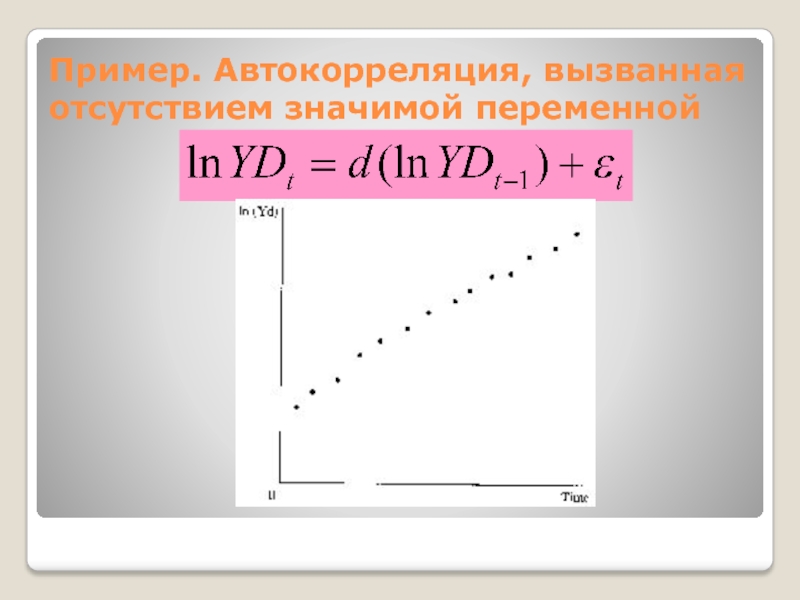
Слайд 37Ложная автокорреляция как результат неправильного выбора функциональной формы
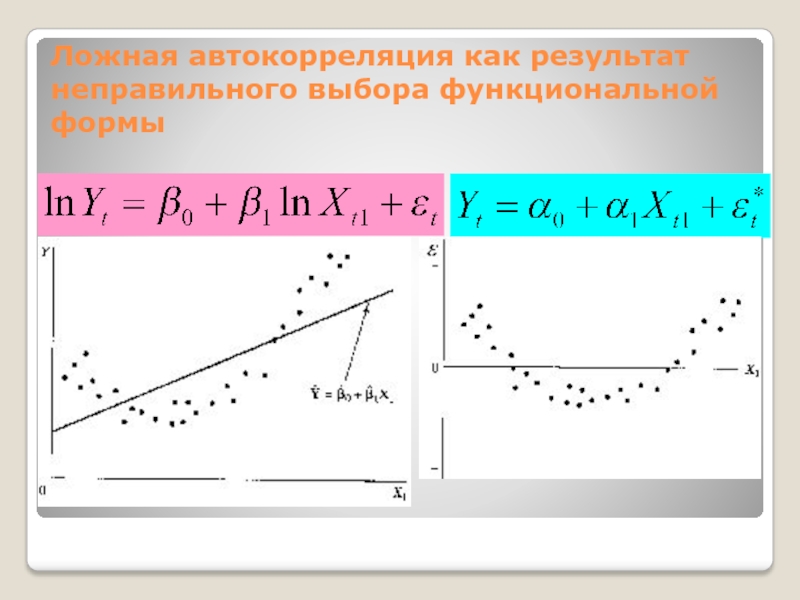
Слайд 38Последствия автокорреляции
1. Истинная автокорреляция не приводит к смещению оценок регрессии,
но оценки перестают быть эффективными.
2. Автокорреляция (особенно положительная) часто
приводит к уменьшению стандартных ошибок коэффициентов, что влечет за собой увеличение t-статистик.
3. Оценка дисперсии остатков Se2 является смещенной оценкой истинного значения e2 , во многих случаях занижая его.
4. В силу вышесказанного выводы по оценке качества коэффициентов и модели в целом, возможно, будут неверными. Это приводит к ухудшению прогнозных качеств модели.

Слайд 39Обнаружение автокорреляции
1. Графический метод.
2. Метод рядов.
3. Специальные тесты.

Слайд 40Динамика реальных расходов на жилье
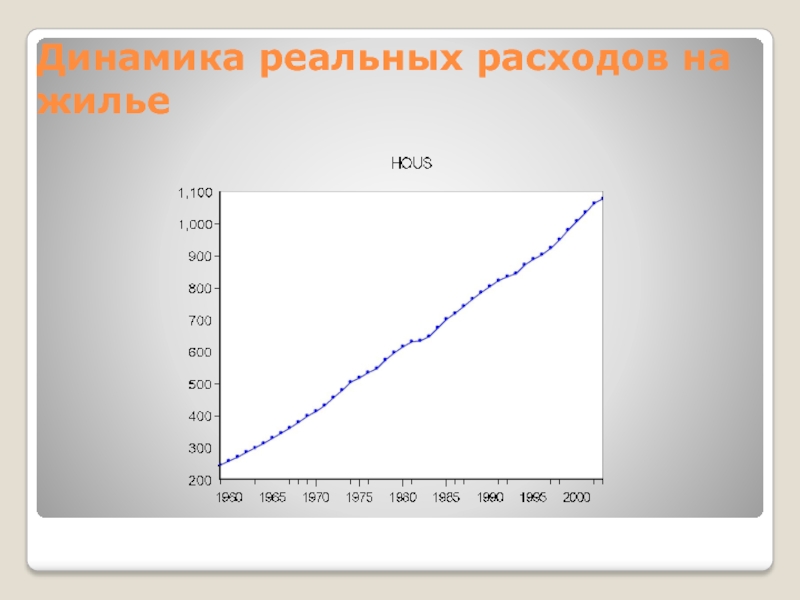
Слайд 414
Присутствует положительная автокорреляция.
Расходы на жилье в зависимости от доходов и
реальных цен
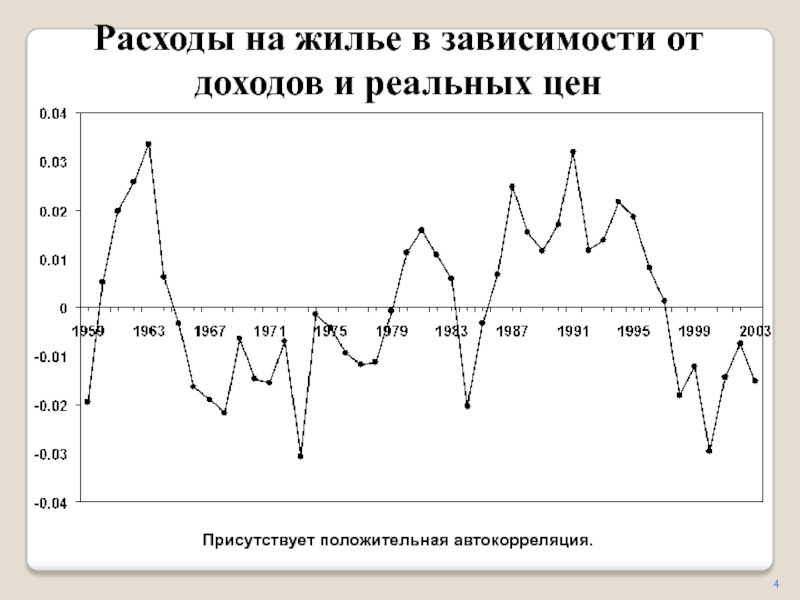
Слайд 42Тест Дарбина-Уотсона
Критерий Дарбина-Уотсона предназначен для обнаружения автокорреляции первого порядка и
основан на анализе остатков уравнения регрессии.
Ограничения:
1. Тест не предназначен для
обнаружения других видов
автокорреляции (более чем первого) и не обнаруживает ее.
2. В модели должен присутствовать свободный член.
3. Данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях).
4. Тест не применим к авторегрессионным моделям, содержащих в качестве объясняющей переменной зависимую переменную с единичным лагом:

Слайд 43Тест Дарбина-Уотсона
1. Предпосылки теста
Случайные возмущения распределены по нормальному закону.
Имеет место
авторегрессия первого порядка:
М(εt)=0; σ2(εt)=Const

Слайд 44Тест Дарбина-Уотсона
Стандартный тест на автокорреляцию типа AR(1) основан на d
статистике Дарбина-Уотсона. Сравнивается среднеквадратичная разность соседних значений с дисперсией остатков.

Слайд 45Тест Дарбина-Уотсона
3. Свойства статистики DW.
где: r (ρ) — коэффициент корреляции
между случайными возмущениями.
Из этого выражения следует:
Для больших выборок DW =
2 — 2ρ
DW изменятся в пределах (0 – 4).
При этом если ρ → + 1, DW близко к 0 — положительная корреляция;
если ρ → 0, DW близко к 2 – корреляция отсутствует;
если ρ → — 1, DW близко к 4 — отрицательная корреляция.

Слайд 46Тест Дарбина-Уотсона
Для статистики DW невозможно найти его критическое значение, т.к.
оно зависит не только от Рдов и степеней свободы k
и n-1, но и от абсолютных значений регрессоров.
Можно определить границы интервала DL и Du, внутри которого находится критическое значение DWкр:
DL ≤ DWкр ≤ Du
Значения Du и DL находятся по таблицам.

Слайд 47Тест Дарбина-Уотсона
Нет автокорреляции
Положительная автокорреляция
Отрицательная автокорреляция
Интервалы (DL, Du) и (4-DL, 4-Du) зоны неопределенности
Нулевая гипотеза
H0: r = 0 (нет автокорреляции). Если DW лежит в доверительном интервале 2 ± dcr то гипотеза не отвергается с заданной вероятностью.
10
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit

Слайд 48
Нет автокорреляции
Положительная автокорреляция
Отрицательная автокорреляция
ТЕСТ ДАРБИНА-УОТСОНА ДЛЯ AR(1) АВТОКОРРЕЛЯЦИИ
Если DW меньше
dL, то то нулевая гипотеза отвергается.
Автокорреляция положительная.
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit

Слайд 50
Нет автокорреляции
Положительная автокорреляция
Отрицательная автокорреляция
ТЕСТ ДАРБИНА-УОТСОНА ДЛЯ AR(1) АВТОКОРРЕЛЯЦИИ
Если DW больше
dU, то нулевая гипотеза (H0) не отвергается, но необходимо проверить
модель на отрицательную автокорреляцию.
Если DW лежит в интервале [dL , dU], то тест не дает определенной оценки.
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit

Слайд 51
При DW=1,42, большим 1,35 и меньшим 1,59,
тест
не дает определенной оценки. DW=1,86
Если 1.59 < DW < 2.41, нулевая гипотеза
не отвергается и можно утверждать, что
автокорреляция остатков отсутствует
ТЕСТ ДАРБИНА-УОТСОНА ДЛЯ AR(1) АВТОКОРРЕЛЯЦИИ
На рисунке приведены значения dL и dU для модели с 2-мя объясняющими переменными (k=2), построенной по 35 (n=35) наблюдениям при 5% пороге значимости. При DW=0,63, как в данном примере, 0,63 < 1,35, то нулевая гипотеза отвергается с 95% вероятностью.
Автокорреляция остатков положительна.
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit
1.35
1.59
2.41
2.65
DW=0,63
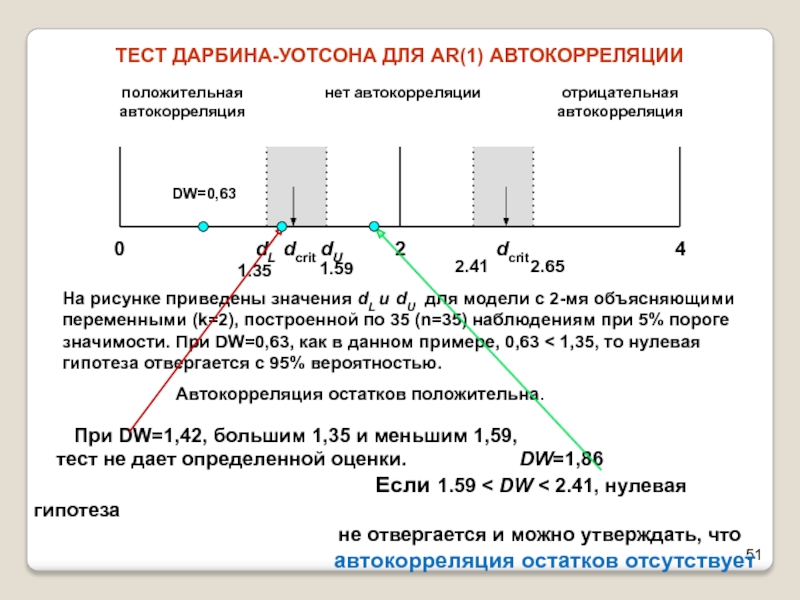
Слайд 52
Если 2.41 < DW
< 2.65, тест не дает однозначной оценки.
Если 2.65 < DW < 4, нулевая гипотеза отвергается и можно утверждать, что имеется отрицательная автокорреляция остатков
Интервалы оценки гипотез при 1% пороге значимости проводятся аналогично.
ТЕСТ ДАРБИНА-УОТСОНА ДЛЯ AR(1) АВТОКОРРЕЛЯЦИИ
2
4
0
dL
dU
dcrit
положительная автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit
1.35
1.59
2.41
2.65
DW=2,51
DW=2,79

Слайд 53Тестирование автокорреляции
Государственные расходы на образование в различных странах
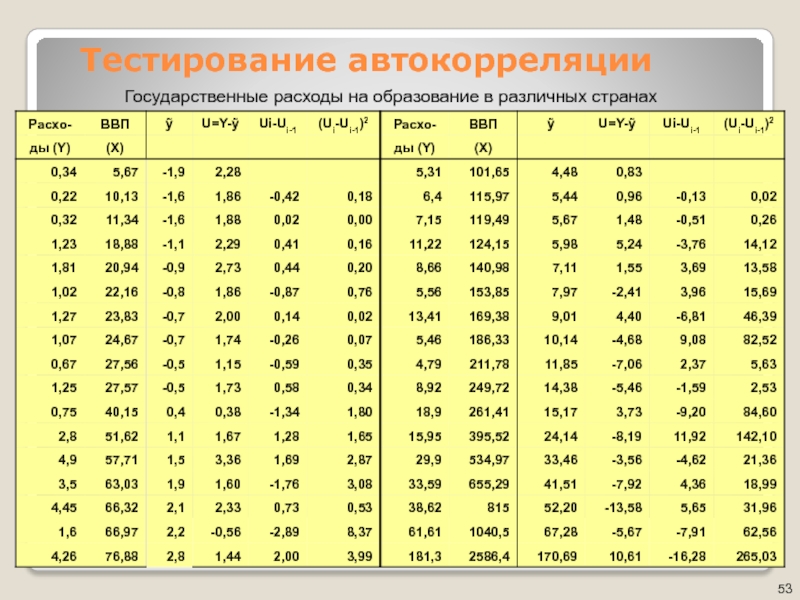
Слайд 54Тестирование автокорреляции
Модель: Y= — 2.32 + 0.669X +U
(0.9) (0.002)
RSS=Σui2=710.34
Σ(ui-ui-1)2 = 832.4
DW = 832.4 /
710.3=1.17
Для n= 30 k=1
Границы интервала
dL=1.35; du=1.49
DW< dL
Вывод: модель автокоррелирована

Слайд 55Метод исправления автокорреляции
Рассматривается случай авторегрессии первого порядка:
Yt=a0+a1x1t+a2x2t+Ut
Ut =ρUt-1+εt
При
этом:
M(εt)=0 σ2(εt ) = σ2t |ρ|
σ2(Ut ) = ρ2 σ2(Ut-1 ) + σ2t + 2Cov(ρ,Ut-1)
Cov(ρ,Ut-1)=0 , т.к. ρ = Const
Следовательно
σ2(Ut ) = ρ2 σ2(Ut-1 ) + σ2t (1)

Слайд 56Метод исправления автокорреляции
Множитель (1-ρ2) обеспечивает стационарность σ2(Ut), т.е. постоянство σ2(Ut)
(2)
σ2(Ut ) = ρ2 σ2(Ut-1 ) + σ2t
Т.к. U0 отсутствует, полагаем, что σ2(U1) =σ2(U0)
Тогда из (1) следует:
Выражение (2) – начальное условие для σ2(U0)
Из выражения (1) с учетом (2) вытекает:
(1)

Слайд 57Для произвольного наблюдения t в силу рекурентности (1) имеем:
(3)
Вывод: введение
корректирующего множителя (1-ρ2) обеспечивает постоянство σ2(u) во всех наблюдениях и,
следовательно, отсутствие автокорреляции между случайными возмущениями.

Слайд 58Метод устранения автокорреляции
Рассмотрим два последовательных уравнения наблюдения
(4)
(5)
Умножим уравнение (5) на
ρ и вычтем из (4)
Учитывая, что Ut — ρUt-1= εt
и делая замену переменных
получим систему уравнений, в которых дисперсия случайных возмущений постоянна.
(6)

Слайд 59Метод устранения автокорреляции
Параметры уравнения (6) можно оценить с помощью МНК.
Если значение ρ известно, то решение окончено.
Замечание. Уравнение (6) имеет
смысл при t = 2, т.к. при t=1 оно не может быть получено.
Для включения первого уравнения наблюдений в систему (6) его умножают на (1-ρ)½.
Этот множитель (поправка Прайса-Уинстона) обеспечивает уменьшение влияния первого уравнения на все остальные при ρ близких к единице.
Тогда окончательно система уравнений наблюдений принимает вид:

Слайд 60УСТРАНЕНИЕ AR(1) АВТОКОРРЕЛЯЦИИ
Автокорреляция AR(1) может быть устранена в лаговых моделях.
Для этого нужно множить уравнение для yt-1 на ρ и
вычесть из yt. Случайный член et, (инновация) не является автокоррелированным. Проблема автокорреляции устранена.
Есть только одна проблема: нелинейность лаговой модели относительно xt-2. В силу этого обычный МНК не применим из за конфликта параметров (0,5*0,8 ≠ 0,6).
Проблема может быть решена численными методами подбора параметров.

Слайд 61УСТРАНЕНИЕ AR(1) АВТОКОРРЕЛЯЦИИ
Аналогично устраняется влияние автокорреляции в множественной регрессионной модели.
Вновь получаем нелинейную лаговую модель свободную от автокорреляции.

Слайд 624
Метод решения состоит в оценке и последовательном уточнении коэффициента корреляции
ρ. Модель может быть преобразована к (*) свободной от автокорреляции
модели. Если автокорреляция AR(1) типа, то CORR(et, et-1) ≈ CORR(ut, ut-1). Используя это ρ, можно вычислить коэффициенты α’ и β для модели (*) и вновь провести оценку ρ.
ИТЕРАТИВНАЯ ПРОЦЕДУРА КОКРАНА — ОРКАТТА

Слайд 63
1. Построить регрессию yt от xt используя МНК
2. Вычислить et = yt
— a — bxt и найти с помощью регрессии et
от et-1 оценку r.
3. Вычислить yt и xt и найти регрессию yt от xt по которой определить оценки для a и b. Повторить с шага 2 до выполнения сходимости.
Сходимость алгоритма достигается когда оценка коэффициента корреляции будет изменяться на величину меньшую заданной точности.
ИТЕРАТИВНАЯ ПРОЦЕДУРА КОКРАНА — ОРКАТТА
~
~
~
~

Слайд 64Устранение автокорреляции первого порядка (при известном коэффициенте автокорреляции)
Пусть имеем:
(
известно)
Процедура устранения автокорреляции остатков:
Отсюда:
Проблема потери первого наблюдения преодолевается с помощью
поправки Прайса-Винстена:

Слайд 65Устранение автокорреляции первого порядка. Обобщения
Рассмотренное авторегрессионное преобразование может быть обобщено
на:
1) Произвольное число объясняющих переменных
2) Преобразования более высоких порядков AR(2),
AR(3) и т.д.:
Однако на практике значения коэффициента автокорреляции обычно неизвестны и его необходимо оценить. Существует несколько методов оценивания.

Слайд 66Способы оценивания коэффициента автокорреляции
1. На основе статистики Дарбина-Уотсона.
2.
Процедура Кохрейна-Оркатта.
3. Процедура Хилдрета-Лу.
4. Процедура Дарбина
5. Метод первых разностей.

Слайд 67Определение коэффициента на основе статистики Дарбина-Уотсона
Этот метод дает удовлетворительные
результаты при большом числе наблюдений.

Слайд 68Итеративная процедура Кохрейна-Оркатта (на примере парной регрессии)
1. Определение уравнения регрессии
и вектора остатков:
2. В качестве приближенного значения берется
его МНК-оценка:
3. Для найденного * оцениваются коэффициенты 0 1:
4. Подставляем в (*) и вычисляем
Возвращаемся к этапу 2.
Критерий остановки: разность между текущей и предыдущей оценками * стала меньше заданной точности.

Слайд 69Итеративная процедура Хилдрета-Лу
(поиск по сетке)
1. Определение уравнения регрессии и
вектора остатков:
2. Оцениваем регрессию
для каждого возможного значения [1,1] с некоторым
достаточно
малым шагом, например 0,001; 0,01 и т.д.
3. Величина *, обеспечивающая минимум стандартной ошибки регрессии принимается в качестве оценки автокорреляции остатков.

Слайд 70Итеративные процедуры оценивания коэффициента . Выводы
1. Сходимость процедур достаточно хорошая.
2.
Метод Кохрейна-Оркатта может «попасть» в локальный, а не глобальный минимум.
3.
Время работы процедуры Хилдрета-Лу значительно сокращается при наличии априорной информации об области возможных значений .

Слайд 71Процедура Дарбина
(на примере парной регрессии)
Пусть имеет место автокорреляция остатков:

Слайд 72Процедура Дарбина представляет собой традиционный МНК с нелинейными ограничениями типа
равенств:
Способы решения:
1. Решать задачу нелинейного программирования.
2. Двухшаговый МНК Дарбина (полученный
коэффициент автокорреляции используется в поправке Прайса-Винстена).
3. Итеративная процедура расчета.
Процедура Дарбина
(на примере парной регрессии)

Слайд 73Процедура Дарбина
Ограничения на коэффициенты записываются в явном виде
============================================================
Dependent Variable: LGHOUS
Method: Least Squares Sample(adjusted): 1960 2003
LGHOUS=C(1)*(1-C(2))+C(2)*LGHOUS(-1)+C(3)*LGDPI-C(2)*C(3)
*LGDPI(-1)+C(4)*LGPRHOUS-C(2)*C(4)*LGPRHOUS(-1)
============================================================
Coefficient Std. Error t-Statistic Prob.
============================================================
C(1) 0.154815 0.354989 0.436111 0.6651
C(2) 0.719102 0.115689 6.215836 0.0000
C(3) 1.011295 0.021830 46.32641 0.0000
C(4) -0.478070 0.091594 -5.219436 0.0000
============================================================
R-squared 0.999205 Mean dependent var 6.379059
Adjusted R-squared 0.999145 S.D. dependent var 0.421861
S.E. of regression 0.012333 Akaike info criter-5.866567
Sum squared resid 0.006084 Schwarz criterion -5.704368
Log likelihood 133.0645 Durbin-Watson stat 1.901081
============================================================
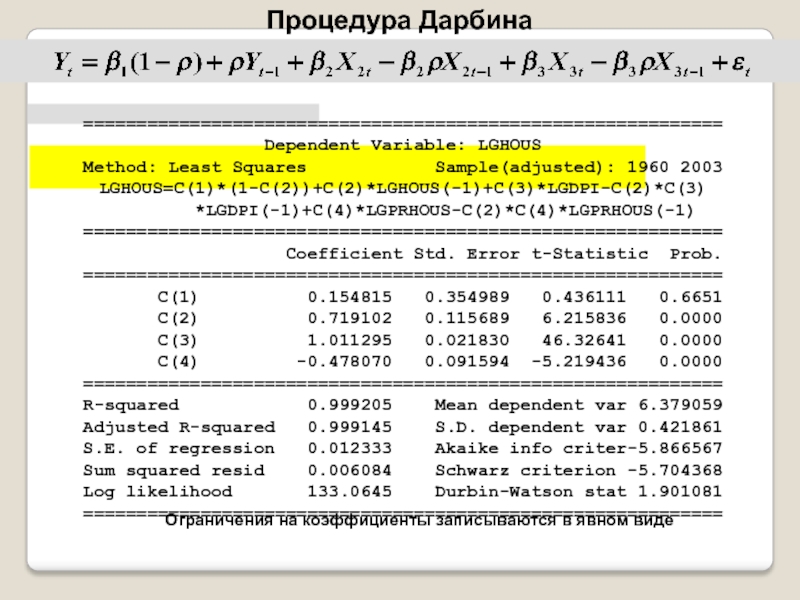
Слайд 74
============================================================
Dependent Variable: LGHOUS
Method:
Least Squares Sample(adjusted): 1960 2003
Included observations: 44 after adjusting endpoints
Convergence achieved after 21 iterations
============================================================
Variable Coefficient Std. Error t-Statistic Prob.
============================================================
C 0.154815 0.354989 0.436111 0.6651
LGDPI 1.011295 0.021830 46.32642 0.0000
LGPRHOUS -0.478070 0.091594 -5.219437 0.0000
AR(1) 0.719102 0.115689 6.215836 0.0000
============================================================
R-squared 0.999205 Mean dependent var 6.379059
Adjusted R-squared 0.999145 S.D. dependent var 0.421861
S.E. of regression 0.012333 Akaike info criter-5.866567
Sum squared resid 0.006084 Schwarz criterion -5.704368
Log likelihood 133.0645 F-statistic 16757.24
Durbin-Watson stat 1.901081 Prob(F-statistic) 0.000000
============================================================
Либо в список регрессоров включается авторегриссионный член 1 порядка AR(1)
Процедура Дарбина
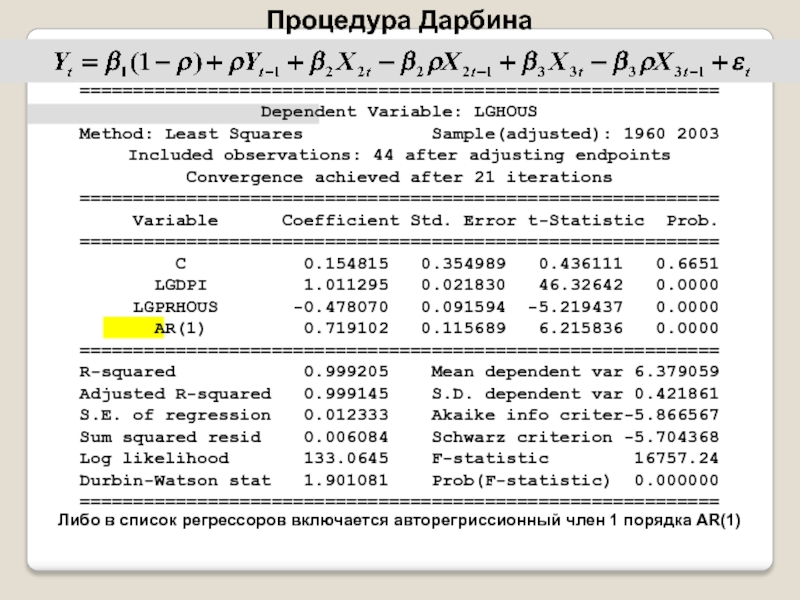
Слайд 75
=============================================================
Dependent Variable: LGHOUS
LGHOUS=C(1)*(1-C(2))+C(2)*LGHOUS(-1)+C(3)*LGDPI-C(2)*C(3)
*LGDPI(-1)+C(4)*LGPRHOUS-C(2)*C(4)*LGPRHOUS(-1)
============================================================
Coefficient Std. Error t-Statistic Prob.
============================================================
C(1) 0.154815 0.354989 0.436111 0.6651
C(2) 0.719102 0.115689 6.215836 0.0000
C(3) 1.011295 0.021830 46.32641 0.0000
C(4) -0.478070 0.091594 -5.219436 0.0000
============================================================
============================================================
Variable Coefficient Std. Error t-Statistic Prob.
============================================================
C 0.154815 0.354989 0.436111 0.6651
LGDPI 1.011295 0.021830 46.32642 0.0000
LGPRHOUS -0.478070 0.091594 -5.219437 0.0000
AR(1) 0.719102 0.115689 6.215836 0.0000
============================================================
Процедура Дарбина
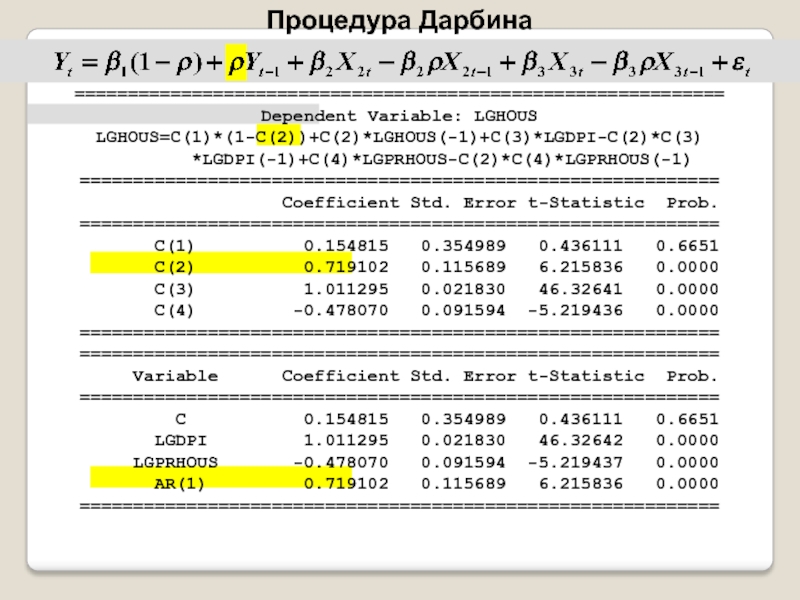
Слайд 76Итеративная процедура метода Дарбина
1. Считается регрессия и находятся остатки.
2. По
остаткам находят оценку коэффициента автокорреляции остатков.
3. Оценка коэффициента автокорреляции
используется для
пересчета данных и цикл
повторяется.
Процесс останавливается, как только
обеспечивается достаточная точность (результаты перестают существенно улучшаться).

Слайд 77Обобщенный метод наименьших квадратов. Замечания
1. Значимый коэффициент DW может указывать
просто на ошибочную спецификацию.
2. Последствия автокорреляции остатков иногда бывают незначительными.
3.
Качество оценок может снизиться из-за уменьшения числа степеней свободы (нужно оценивать дополнительный параметр).
4. Значительно возрастает трудоемкость расчетов.
Не следует применять обобщенный МНК автоматически

17 авг. 2022 г.
читать 1 мин
Одно из ключевых допущений линейной регрессии состоит в том, что между остатками нет корреляции, т. е. остатки независимы.
Один из способов определить, выполняется ли это предположение, — выполнить тест Дарбина-Ватсона , который используется для обнаружения наличия автокорреляции в остатках регрессии. В этом тесте используются следующие гипотезы:
H 0 (нулевая гипотеза): между остатками нет корреляции.
H A (альтернативная гипотеза): остатки автокоррелированы.
В этом руководстве объясняется, как выполнить тест Дарбина-Ватсона в R.
Пример: тест Дарбина-Ватсона в R
Чтобы выполнить тест Дарбина-Ватсона, нам сначала нужно подобрать модель линейной регрессии. Мы будем использовать встроенный набор данных R mtcars и подгоним регрессионную модель, используя mpg в качестве переменной-предиктора и disp и wt в качестве независимых переменных.
#load mtcars dataset
data(mtcars)
#view first six rows of dataset
head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
#fit regression model
model <- lm(mpg ~ disp+wt, data=mtcars)
Затем мы можем выполнить тест Дарбина-Ватсона, используя функцию durbinWatsonTest() из пакета car :
#load car package
library(car)
#perform Durbin-Watson test
durbinWatsonTest(model)
Loading required package: carData
lag Autocorrelation D-W Statistic p-value
1 0.341622 1.276569 0.034
Alternative hypothesis: rho != 0
Из вывода мы видим, что статистика теста равна 1,276569 , а соответствующее значение p равно 0,034.Поскольку это p-значение меньше 0,05, мы можем отклонить нулевую гипотезу и сделать вывод, что остатки в этой регрессионной модели автокоррелированы.
Что делать, если обнаружена автокорреляция
Если вы отвергаете нулевую гипотезу и заключаете, что в остатках присутствует автокорреляция, то у вас есть несколько различных вариантов исправления этой проблемы, если вы считаете ее достаточно серьезной:
- Для положительной последовательной корреляции рассмотрите возможность добавления в модель лагов зависимой и/или независимой переменной.
- Для отрицательной последовательной корреляции убедитесь, что ни одна из ваших переменных не является сверхдифференциальной .
- Для сезонной корреляции рассмотрите возможность добавления в модель сезонных фиктивных переменных.