Q=………..min
соответствует
методу наименьших квадратов
Автокорреляция
— это
корреляционная зависимость уровней
ряда от предыдущих значений.
Автокорреляция
имеется когда
каждое следующее значение остатков
Аддитивная модель
временного ряда имеет вид: Y=T+S+E
Атрибутивная
переменная может употребляться, когда:
независимая переменная качественна;
В каких пределах
изменяется коэффициент детерминанта:
от 0 до 1.
В каком случае
модель считается адекватной Fрасч>Fтабл
В каком случае
рекомендуется применять для моделирования
показателей с увелич. ростом параболу
если
относительная величина…неограниченно
В результате
автокорреляции имеем неэффективные
оценки параметров
В хорошо подобранной
модели остатки должны иметь
нормальный закон
В эконометрическом
анализе Xj
рассматриваются
как случайные величины
Величина
доверительного интервала позволяет
установить предположение о том, что:
интервал содержит оценку параметра
неизвестного.
Величина
рассчитанная по формуле r=…является
оценкой
парного коэф. Корреляции
Внутренне
нелинейная регрессия
— это истинно нелинейная регрессия,
которая не может быть приведена к
линейной регрессии преобразованием
переменных и введением новых переменных.
Временной ряд
— это последовательность значений
признака (результативного переменного),
принимаемых в течение последовательных
моментов времени или периодов.
Выберете
авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt
Выберете модель
с лагами Уt=
a+b0x1…….(самая
длинная формула)
Выборочное
значение Rxy
не > 1, |R|
< 1
Выборочный
коэффициент корреляции r
по абсолютной
величине не превосходит единицы
Гетероскедастичность
— нарушение постоянства дисперсии для
всех наблюдений.
Гетероскедастичность
присутствует когда:
дисперсия случайных остатков не постоянна
Гетероскидастичность
– это когда
дисперсия остатков различна
Гипотеза об
отсутствии автокорреляции остатков
доказана,
если Dтабл2…
Гомоскедастичность
— постоянство
дисперсии для всех наблюдений, или
одинаковость дисперсии каждого отклонения
(остатка) для всех значений факторных
переменных.
Гомоскидастичность
– это когда дисперсия остатков постоянна
и одинакова для всех … наблюдений.
Дисперсия
— показатель вариации.
Для определения
параметров неиденцифицированной модели
применяется.:
не один из сущ. методов применить нельзя
Для определения
параметров сверх иденцифицированной
модели примен.:
применяется. 2-х шаговый МНК
Для определения
параметров структурную форму модели
необходимо преобразовать в
приведенную форму модели
Для определения
параметров точно идентифицируемой
модели:
применяется косвенный МНК;
Для оценки …
изменения y
от x
вводится:
коэффициент эластичности:
Для парной
регрессии ơ²b
равно
….(xi-x¯)²)
Для проверки
значимости отдельных параметров
регрессии используется:
t-тест.
Для регрессии
y=a+bx
из n
наблюдений интервал доверия (1-а)% для
коэф. b
составит
b±t…….·ơb
Для регрессии из
n
наблюдений и m
независимых переменных существует
такая связь между R²
и F..=[(n-m-1)/m](
R²/(1-
R²)]
Доверительная
вероятность
– это вероятность того, что истинное
значение результативного показателя
попадёт в расчётный прогнозный интервал.
Допустим что для
описания одного экономического процесса
пригодны 2 модели. Обе адекватны по f
критерию фишера. какой предоставить
преимущество, у той у кот.: большее
значения F
критерия
Допустим, что
зависимость расходов от дохода описывается
функцией y=a+bx
среднее значение у=2…равняется
9
Если Rxy
положителен, то
с ростом x
увеличивается y.
Если в уравнении
регрессии имеется несущественная
переменная, то она обнаруживает себя
по низкому значению T
статистки
Если качественный
фактор имеет 3 градации, то необходимое
число фиктивных переменных
2
Если коэффициент
корреляции положителен, то в линейной
модели с
ростом х увеличивается у
Если мы заинтересованы
в использовании атрибутивных переменных
для отображения эффекта разных месяцев
мы должны использовать
11 атрибутивных методов
Если регрессионная
модель имеет показательную зависимость,
то метод МНК
применим после приведения к линейному
виду.
Зависимость между
коэффициентом множественной детерминации
(D)
и корреляции (R)
описывается следующим методом R=√D
Значимость
уравнения регрессии
— действительное наличие исследуемой
зависимости, а не просто случайное
совпадение факторов, имитирующее
зависимость, которая фактически не
существует.
Значимость
уравнения регрессии в целом оценивают:
-F-критерий
Фишера
Значимость частных
и парных коэф.
корреляции
поверен. с помощью:
-t-критерия
Стьюдента
Интеркорреляция
и связанная с ней мультиколлинеарность
— это приближающаяся к полной линейной
зависимости тесная связь между факторами.
Какая статистическая
характеристика выражается формулой
R²=…коэффициент
детерминации
Какая статистическая
хар-ка выражена формулой:
rxy=Ca(x;y)
разделить на корень Var(x)*Var(y):
коэффициент. корреляции
Какая функция
используется при моделировании моделей
с постоянным ростом степенная
Какие точки
исключаются из временного ряда процедурой
сглаживания и
в начале, и в конце.
Какое из уравнений
регрессии является степенным
y=a˳aͯ¹a
Классический
метод к оцениванию параметров регрессии
основан на: —
метод наименьших квадратов (МНК)
Количество
степеней свободы для t
статистики при проверки значимости
параметров регрессии из 35 наблюдений
и 3 независимых переменных 31;
Количество
степеней свободы знаменателя F-статистики
в регрессии из 50 наблюдений и 4 независимых
переменных: 45
Компоненты вектора
Ei
имеют
нормальный закон
Корреляция
— стохастическая зависимость, являющаяся
обобщением строго детерминированной
функциональной зависимости посредством
включения вероятностной (случайной)
компоненты.
Коэффициент
автокорреляции:
характеризует тесноту линейной связи
текущего и предстоящего уровней ряда
Коэффициент
детерминации
— показатель тесноты стохастической
связи в общем случае нелинейной регрессии
Коэффициент
детерминации
– это величина, которая характеризует
связь между зависимыми и независимыми
переменными.
Коэффициент
детерминации — это
квадрат множественного коэффициента
корреляции
Коэффициент
детерминации — это: величина,
которая характеризует связь между
независимой и зависимой (зависящей)
переменными;
Коэффициент
детерминации R
показывает
долю вариаций зависимой переменной y,
объяснимую влиянием факторов, включаемых
в модель.
Коэффициент
детерминации изменяется в пределах:
— от 0 до 1
Коэффициент
доверия —
это коэффициент, который связывает
линейной зависимостью предельную и
среднюю ошибки, выясняет смысл предельной
ошибки, характеризующей точность оценки,
и является аргументом распределения
(чаще всего, интеграла вероятностей).
Именно эта вероятность и есть степень
надежности оценки.
Коэффициент
доверия (нормированное отклонение)
— результат деления отклонения от
среднего на стандартное отклонение,
содержательно характеризует степень
надежности (уверенности) полученной
оценки.
Коэффициент
корелляции Rxy
используется
для определения полноты связи X
и Y.
Коэффициент
корелляции меняется в пределах : от -1
до 1
Коэффициент
корелляции равный 0 означает, что:
—отсутствует
линейная связь.
Коэффициент
корелляции равный 1 означает,
что: -существует функциональная
зависимость.
Коэффициент
корреляции используется для:
определения тесноты связи между
случайными величинами X и Y;
Коэффициент
корреляции рассчитывается для
измерения степени линейной взаимосвязи
между двумя случайными переменными.
Коэффициент
линейной корреляции
— показатель тесноты стохастической
связи между фактором и результатом в
случае линейной регрессии.
Коэффициент
регрессии —
коэффициент при факторной переменной
в модели линейной регрессии.
Коэффициент
регрессии b
показывает:
на сколько единиц увеличивается y,
если x
увеличивается на 1.
Коэффициент
регрессии изменяется в пределах:
применяется любое значение ; от 0 до 1;
от -1 до 1;
Коэффициент
эластичности измеряется в:
неизмеримая величина.
Критерий
Дарвина-Чотсона применяется для:
— отбора факторов в модель; или —
определения автокорреляции в остатках
Критерий Стьюдента
— проверка значимости отдельных
коэффициентов регрессии и значимости
коэффициента корреляции.
Критерий Фишера
показывает
статистическую значимость модели в
целом на основе совокупной достоверности
всех ее коэффициентов;
Лаговые переменные
: — это переменные, относящиеся к предыдущим
моментам времени; или -это значения
зависим. перемен. за предшествующий
период времени.
Лаговые переменные
это значение
зависимых переменных за предшествующий
период времени
Модель в целом
статистически значима, если
Fрасч
> Fтабл.
Модель
идентифицирована, если: —
число параметров структурной модели
равно числу параметров приведён. формы
модели.
Модель
неидентифицирована, если: —
число приведён. коэф.
больше
числа структурных коэф.
Модель
сверхидентифицирована, если:
число приведён. коэф. меньше числа
структурных коэф
Мультиколлениарность
возникает, когда:
ошибочное включение в уравнение 2х или
более линейно зависимых переменных;
2. две или более объясняющие переменные,
в нормальной ситуации слабо коррелированные,
становятся в конкретных условиях
выборки сильно коррелированными; .
в модель включается переменная,
сильно коррелирующая с зависимой
переменной.
Мультипликативная
модель временного ряда имеет вид: —
Y=T*S*E
Мультипликативная
модель временного ряда строится, если:
амплитуда
сезонных колебаний возрастает или
уменьшается
На основе
поквартальных данных…значения 7-1
квартал, 9-2квартал и 11-3квартал …-5
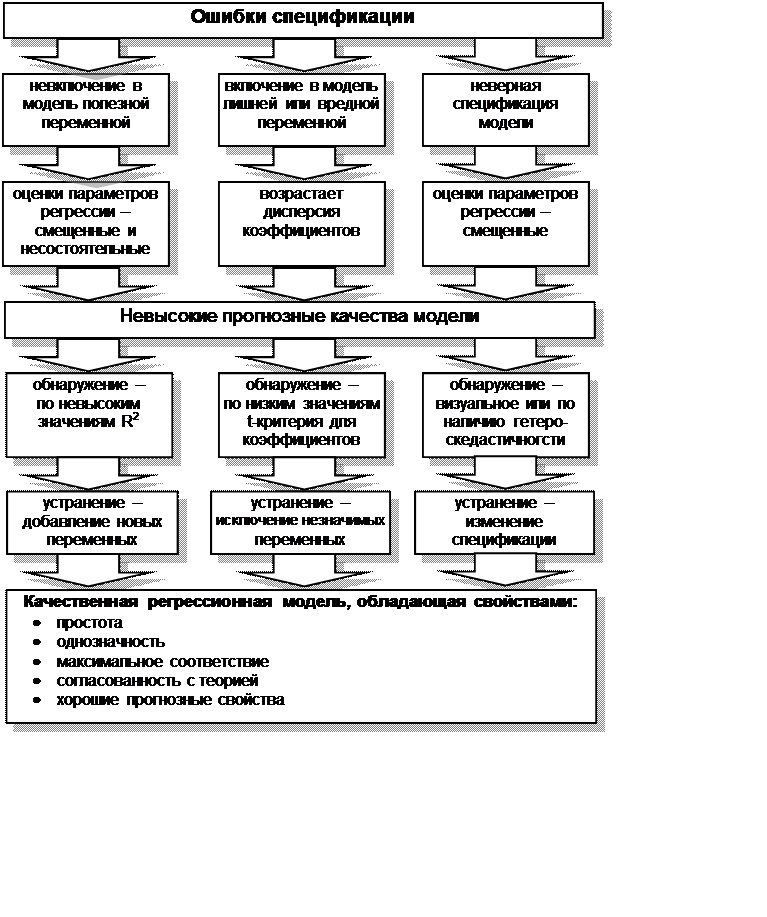
Неправильный
выбор функциональной формы или объясняющих
переменных называется ошибками
спецификации
Несмещённость
оценки параметра регрессии, полученной
по МНК, означает: —
что она характеризуется наименьшей
дисперсией.
Одной из проблем
которая может возникнуть в многофакторной
регрессии и никогда не бывает в парной
регрессии, является
корреляция между независимыми переменными
От чего зависит
количество точек, исключаемых из
временного ряда в результате сглаживания:
от применяемого метода сглаживания.
Отметьте основные
виды ошибок спецификации:
отбрасывание значимой переменной;
добавление незначимой переменной;
Оценки коэффициентов
парной регрессии является несмещённым,
если:
математические ожидания остатков =0.
Оценки параметров
парной линейной регрессии находятся
по формуле b=
Cov(x;y)/Var(x);a=y¯
bx¯
Оценки параметров
регрессии являются несмещенными, если
Математическое
ожидание остатков равно 0
Оценки параметров
регрессии являются состоятельными,
если:
-увеличивается точность оценки при n,
т. е. при увеличении n
вероятность оценки от истинного значения
параметра стремится к 0.
Оценки парной
регрессии явл. эффективными, если:
оценка обладают наименьшей дисперсией
по сравнению с другими оценками
При наличии
гетероскедастичности следует применять:
— обобщённый МНК
При проверке
значимости одновременно всех параметров
используется:
-F-тест.
При проверке
значимости одновременно всех параметров
регрессии используется:
F-тест.
Применим ли метод
наименьших квадратов для расчетов
параметров показательной зависимости
применим после ее приведения
Применим ли метод
наименьших квадратов(МНК) для расчёта
параметров нелинейных моделей?
применим после её специального приведения
к линейному виду
С помощью какого
критерия оценивается значимость
коэффициента регрессии T
стьюдента
С увеличением
числа объясняющих переменных
скоррестированный коэффициент
детерминации:
— увеличивается.
Связь между
индексом множественной детерминации
R²
и
скорректированным индексом множественной
детерминации Ȓ²
есть
Скорректиров.
коэф.
детерминации:
— больше обычного коэф. детерминации
Стандартизованный
коэффициент уравнения регрессии Ƀk
показывает на
сколько % изменится результирующий
показатель у при изменении хi
на 1%при неизмененном среднем уровне
других факторов
Стандартный
коэффициент уравнения регрессии:
показывает на сколько 1 изменится y
при изменении фактора xk
на 1 при сохранении др.
Суть коэф.
детерминации r2xy
состоит
в следующем: — характеризует
долю дисперсии результативного признака
y
объясняем. регресс., в общей дисперсии
результативного признака.
Табличное значение
критерия Стьюдента зависит
от уровня
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда.(от принятого уровня значимости и
от числа степеней свободы ( n — m -1))
Табличные значения
Фишера (F)
зависят от
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда (от доверительной вероятности p
и числа степеней свободы дисперсий f1
и f2)..
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, идентифицируемо если
D+1=H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, НЕидентифицируемо если
D+1<H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, сверхидентифицируемо если
D+1>H
Уравнение
идентифицировано, если: —
D+1=H
Уравнение
неидентифицировано, если: —
D+1<H
Уравнение
сверхидентифицировано, если: —
D+1>H
Фиктивные
переменные — это:
атрибутивные признаки (например, как
профессия, пол, образование), которым
придали цифровые метки;
Формула t=
rxy….используется
для проверки
существенности коэффициента корреляции
Частный F-критерий:
— оценивает
значимость уравнения регрессии в целом
Число степеней
свободы для факторной суммы квадратов
в линейной модели множественной регрессии
равно: m;
Что показывает
коэффициент наклона —
на сколько единиц изменится у, если х
изменился на единицу,
Что показывает
коэффициент. абсолютного роста
на сколько единиц изменится у, если х
изменился на единицу
Экзогенная
переменная
– это независимая переменная или
фактор-Х.
Экзогенные
переменные
— это переменные, которые определяются
вне системы и являются независимыми
Экзогенные
переменные –
это
предопределенные переменные, влияющие
на зависимые переменные (Эндогенные
переменные), но не зависящие от них,
обозначаются через х
Эластичность
измеряется
единица измерения фактора…показателя
Эластичность
показывает
на сколько % изменится редуктивный
показатель y
при изменении на 1% фактора xk.
Эндогенные
переменные — это:
зависимые переменные, число которых
равно числу уравнений в системе и которые
обозначаются через у
Определения
T-отношение
(t-критерий)
— отношение оценки коэффициента,
полученной с помощью МНК, к величине
стандартной ошибки оцениваемой величины.
Аддитивная модель
временного ряда –
это модель, в которой временной ряд
представлен как сумма перечисленных
компонент.
Критерий Фишера
— способ статистической проверки
значимости уравнения регрессии, при
котором расчетное (фактическое) значение
F-отношения сравнивается с его критическим
(теоретическим) значением.
Линейная регрессия
— это связь (регрессия), которая
представлена уравнением прямой линии
и выражает простейшую линейную
зависимость.
Метод инструментальных
переменных
— это разновидность МНК. Используется
для оценки параметров моделей, описываемых
несколькими уравнениями. Главное
свойство — частичная замена непригодной
объясняющей переменной на такую
переменную, которая некоррелированна
со случайным членом. Эта замещающая
переменная называется инструментальной
и приводит к получению состоятельных
оценок параметров.
Метод наименьших
квадратов (МНК)
— способ приближенного нахождения
(оценивания) неизвестных коэффициентов
(параметров) регрессии. Этот метод
основан на требовании минимизации суммы
квадратов отклонений значений результата,
рассчитанных по уравнению регрессии,
и истинных (наблюденных) значений
результата.
Множественная
линейная регрессия
— это множественная регрессия,
представляющая линейную связь по каждому
фактору.
Множественная
регрессия —
регрессия с двумя и более факторными
переменными.
Модель
идентифицируемая
— модель, в которой все структурные
коэффициенты однозначно определяются
по коэффициентам приведенной формы
модели.
Модель рекурсивных
уравнений —
модель, которая содержит зависимые
переменные (результативные) одних
уравнений в роли фактора, оказываясь в
правой части других уравнений.
Мультипликативная
модель –
модель, в которой временной ряд представлен
как произведение перечисленных компонент.
Несмещенная
оценка —
оценка, среднее которой равно самой
оцениваемой величине.
Нулевая гипотеза
— предположение о том, что результат
не зависит от фактора (коэффициент
регрессии равен нулю).
Обобщенный метод
наименьших квадратов (ОМНК)
— метод, который не требует постоянства
дисперсии (гомоскедастичности) остатков,
но предполагает пропорциональность
остатков общему множителю (дисперсии).
Таким образом, это взвешенный МНК.
Объясненная
дисперсия —
показатель вариации результата,
обусловленной регрессией.
Объясняемая
(результативная) переменная
— переменная, которая статистически
зависит от факторной переменной, или
объясняющей (регрессора).
Остаточная
дисперсия —
необъясненная дисперсия, которая
показывает вариацию результата под
влиянием всех прочих факторов, неучтенных
регрессией.
Предопределенные
переменные
— это экзогенные переменные системы и
лаговые эндогенные переменные системы.
Приведенная форма
системы —
форма, которая, в отличие от структурной,
уже содержит одни только линейно
зависящие от экзогенных переменных
эндогенные переменные. Внешне ничем не
отличается от системы независимых
уравнений.
Расчетное значение
F-отношения
— значение, которое получают делением
объясненной дисперсии на 1 степень
свободы на остаточную дисперсию на 1
степень свободы.
Регрессия
(зависимость)
— это усредненная (сглаженная), т.е.
свободная от случайных мелкомасштабных
колебаний (флуктуаций), квазидетерминированная
связь между объясняемой переменной
(переменными) и объясняющей переменной
(переменными). Эта связь выражается
формулами, которые характеризуют
функциональную зависимость и не содержат
явно стохастических (случайных)
переменных, которые свое влияние теперь
оказывают как результирующее воздействие,
принимающее вид чисто функциональной
зависимости.
Регрессор
(объясняющая переменная, факторная
переменная)
— это независимая переменная, статистически
связанная с результирующей переменной.
Характер этой связи и влияние изменения
(вариации) регрессора на результат
исследуются в эконометрике.
Система
взаимосвязанных уравнений
— это система одновременных или
взаимозависимых уравнений. В ней одни
и те же переменные выступают одновременно
как зависимые в одних уравнениях и в то
же время независимые в других. Это
структурная форма системы уравнений.
К ней неприменим МНК.
Система внешне
не связанных между собой уравнений
— система, которая характеризуется
наличием одних только корреляций между
остатками (ошибками) в разных уравнениях
системы.
Случайный остаток
(отклонение)
— это чисто случайный процесс в виде
мелкомасштабных колебаний, не содержащий
уже детерминированной компоненты,
которая имеется в регрессии.
Состоятельные
оценки —
оценки, которые позволяют эффективно
применять доверительные интервалы,
когда вероятность получения оценки на
заданном расстоянии от истинного
значения параметра становится близка
к 1, а точность самих оценок увеличивается
с ростом объема выборки.
Спецификация
модели —
определение существенных факторов и
выявление мультиколлинеарности.
Стандартная
ошибка —
среднеквадратичное (стандартное)
отклонение. Оно связано со средней
ошибкой и коэффициентом доверия.
Степени свободы
— это величины, характеризующие число
независимых параметров и необходимые
для нахождения по таблицам распределений
их критических значений.
Тренд
— основная тенденция развития, плавная
устойчивая закономерность изменения
уровней ряда.
Уровень значимости
— величина, показывающая, какова
вероятность ошибочного вывода при
проверке статистической гипотезы по
статистическому критерию.
Фиктивные
переменные
— это переменные, которые отражают
сезонные компоненты ряда для какого-либо
одного периода.
Эконометрическая
модель — это
уравнение или система уравнений, особым
образом представляющие зависимость
(зависимости) между результатом и
факторами. В основе эконометрической
модели лежит разбиение сложной и
малопонятной зависимости между
результатом и факторами на сумму двух
следующих компонентов: регрессию
(регрессионная компонента) и случайный
(флуктуационный) остаток. Другой класс
эконометрических моделей образует
временные ряды.
Эффективность
оценки — это
свойство оценки обладать наименьшей
дисперсией из всех возможных.
Q=………..min
соответствует
методу наименьших квадратов
Автокорреляция
— это
корреляционная зависимость уровней
ряда от предыдущих значений.
Автокорреляция
имеется когда
каждое следующее значение остатков
Аддитивная модель
временного ряда имеет вид: Y=T+S+E
Атрибутивная
переменная может употребляться, когда:
независимая переменная качественна;
В каких пределах
изменяется коэффициент детерминанта:
от 0 до 1.
В каком случае
модель считается адекватной Fрасч>Fтабл
В каком случае
рекомендуется применять для моделирования
показателей с увелич. ростом параболу
если
относительная величина…неограниченно
В результате
автокорреляции имеем неэффективные
оценки параметров
В хорошо подобранной
модели остатки должны иметь
нормальный закон
В эконометрическом
анализе Xj
рассматриваются
как случайные величины
Величина
доверительного интервала позволяет
установить предположение о том, что:
интервал содержит оценку параметра
неизвестного.
Величина
рассчитанная по формуле r=…является
оценкой
парного коэф. Корреляции
Внутренне
нелинейная регрессия
— это истинно нелинейная регрессия,
которая не может быть приведена к
линейной регрессии преобразованием
переменных и введением новых переменных.
Временной ряд
— это последовательность значений
признака (результативного переменного),
принимаемых в течение последовательных
моментов времени или периодов.
Выберете
авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt
Выберете модель
с лагами Уt=
a+b0x1…….(самая
длинная формула)
Выборочное
значение Rxy
не > 1, |R|
< 1
Выборочный
коэффициент корреляции r
по абсолютной
величине не превосходит единицы
Гетероскедастичность
— нарушение постоянства дисперсии для
всех наблюдений.
Гетероскедастичность
присутствует когда:
дисперсия случайных остатков не постоянна
Гетероскидастичность
– это когда
дисперсия остатков различна
Гипотеза об
отсутствии автокорреляции остатков
доказана,
если Dтабл2…
Гомоскедастичность
— постоянство
дисперсии для всех наблюдений, или
одинаковость дисперсии каждого отклонения
(остатка) для всех значений факторных
переменных.
Гомоскидастичность
– это когда дисперсия остатков постоянна
и одинакова для всех … наблюдений.
Дисперсия
— показатель вариации.
Для определения
параметров неиденцифицированной модели
применяется.:
не один из сущ. методов применить нельзя
Для определения
параметров сверх иденцифицированной
модели примен.:
применяется. 2-х шаговый МНК
Для определения
параметров структурную форму модели
необходимо преобразовать в
приведенную форму модели
Для определения
параметров точно идентифицируемой
модели:
применяется косвенный МНК;
Для оценки …
изменения y
от x
вводится:
коэффициент эластичности:
Для парной
регрессии ơ²b
равно
….(xi-x¯)²)
Для проверки
значимости отдельных параметров
регрессии используется:
t-тест.
Для регрессии
y=a+bx
из n
наблюдений интервал доверия (1-а)% для
коэф. b
составит
b±t…….·ơb
Для регрессии из
n
наблюдений и m
независимых переменных существует
такая связь между R²
и F..=[(n-m-1)/m](
R²/(1-
R²)]
Доверительная
вероятность
– это вероятность того, что истинное
значение результативного показателя
попадёт в расчётный прогнозный интервал.
Допустим что для
описания одного экономического процесса
пригодны 2 модели. Обе адекватны по f
критерию фишера. какой предоставить
преимущество, у той у кот.: большее
значения F
критерия
Допустим, что
зависимость расходов от дохода описывается
функцией y=a+bx
среднее значение у=2…равняется
9
Если Rxy
положителен, то
с ростом x
увеличивается y.
Если в уравнении
регрессии имеется несущественная
переменная, то она обнаруживает себя
по низкому значению T
статистки
Если качественный
фактор имеет 3 градации, то необходимое
число фиктивных переменных
2
Если коэффициент
корреляции положителен, то в линейной
модели с
ростом х увеличивается у
Если мы заинтересованы
в использовании атрибутивных переменных
для отображения эффекта разных месяцев
мы должны использовать
11 атрибутивных методов
Если регрессионная
модель имеет показательную зависимость,
то метод МНК
применим после приведения к линейному
виду.
Зависимость между
коэффициентом множественной детерминации
(D)
и корреляции (R)
описывается следующим методом R=√D
Значимость
уравнения регрессии
— действительное наличие исследуемой
зависимости, а не просто случайное
совпадение факторов, имитирующее
зависимость, которая фактически не
существует.
Значимость
уравнения регрессии в целом оценивают:
-F-критерий
Фишера
Значимость частных
и парных коэф.
корреляции
поверен. с помощью:
-t-критерия
Стьюдента
Интеркорреляция
и связанная с ней мультиколлинеарность
— это приближающаяся к полной линейной
зависимости тесная связь между факторами.
Какая статистическая
характеристика выражается формулой
R²=…коэффициент
детерминации
Какая статистическая
хар-ка выражена формулой:
rxy=Ca(x;y)
разделить на корень Var(x)*Var(y):
коэффициент. корреляции
Какая функция
используется при моделировании моделей
с постоянным ростом степенная
Какие точки
исключаются из временного ряда процедурой
сглаживания и
в начале, и в конце.
Какое из уравнений
регрессии является степенным
y=a˳aͯ¹a
Классический
метод к оцениванию параметров регрессии
основан на: —
метод наименьших квадратов (МНК)
Количество
степеней свободы для t
статистики при проверки значимости
параметров регрессии из 35 наблюдений
и 3 независимых переменных 31;
Количество
степеней свободы знаменателя F-статистики
в регрессии из 50 наблюдений и 4 независимых
переменных: 45
Компоненты вектора
Ei
имеют
нормальный закон
Корреляция
— стохастическая зависимость, являющаяся
обобщением строго детерминированной
функциональной зависимости посредством
включения вероятностной (случайной)
компоненты.
Коэффициент
автокорреляции:
характеризует тесноту линейной связи
текущего и предстоящего уровней ряда
Коэффициент
детерминации
— показатель тесноты стохастической
связи в общем случае нелинейной регрессии
Коэффициент
детерминации
– это величина, которая характеризует
связь между зависимыми и независимыми
переменными.
Коэффициент
детерминации — это
квадрат множественного коэффициента
корреляции
Коэффициент
детерминации — это: величина,
которая характеризует связь между
независимой и зависимой (зависящей)
переменными;
Коэффициент
детерминации R
показывает
долю вариаций зависимой переменной y,
объяснимую влиянием факторов, включаемых
в модель.
Коэффициент
детерминации изменяется в пределах:
— от 0 до 1
Коэффициент
доверия —
это коэффициент, который связывает
линейной зависимостью предельную и
среднюю ошибки, выясняет смысл предельной
ошибки, характеризующей точность оценки,
и является аргументом распределения
(чаще всего, интеграла вероятностей).
Именно эта вероятность и есть степень
надежности оценки.
Коэффициент
доверия (нормированное отклонение)
— результат деления отклонения от
среднего на стандартное отклонение,
содержательно характеризует степень
надежности (уверенности) полученной
оценки.
Коэффициент
корелляции Rxy
используется
для определения полноты связи X
и Y.
Коэффициент
корелляции меняется в пределах : от -1
до 1
Коэффициент
корелляции равный 0 означает, что:
—отсутствует
линейная связь.
Коэффициент
корелляции равный 1 означает,
что: -существует функциональная
зависимость.
Коэффициент
корреляции используется для:
определения тесноты связи между
случайными величинами X и Y;
Коэффициент
корреляции рассчитывается для
измерения степени линейной взаимосвязи
между двумя случайными переменными.
Коэффициент
линейной корреляции
— показатель тесноты стохастической
связи между фактором и результатом в
случае линейной регрессии.
Коэффициент
регрессии —
коэффициент при факторной переменной
в модели линейной регрессии.
Коэффициент
регрессии b
показывает:
на сколько единиц увеличивается y,
если x
увеличивается на 1.
Коэффициент
регрессии изменяется в пределах:
применяется любое значение ; от 0 до 1;
от -1 до 1;
Коэффициент
эластичности измеряется в:
неизмеримая величина.
Критерий
Дарвина-Чотсона применяется для:
— отбора факторов в модель; или —
определения автокорреляции в остатках
Критерий Стьюдента
— проверка значимости отдельных
коэффициентов регрессии и значимости
коэффициента корреляции.
Критерий Фишера
показывает
статистическую значимость модели в
целом на основе совокупной достоверности
всех ее коэффициентов;
Лаговые переменные
: — это переменные, относящиеся к предыдущим
моментам времени; или -это значения
зависим. перемен. за предшествующий
период времени.
Лаговые переменные
это значение
зависимых переменных за предшествующий
период времени
Модель в целом
статистически значима, если
Fрасч
> Fтабл.
Модель
идентифицирована, если: —
число параметров структурной модели
равно числу параметров приведён. формы
модели.
Модель
неидентифицирована, если: —
число приведён. коэф.
больше
числа структурных коэф.
Модель
сверхидентифицирована, если:
число приведён. коэф. меньше числа
структурных коэф
Мультиколлениарность
возникает, когда:
ошибочное включение в уравнение 2х или
более линейно зависимых переменных;
2. две или более объясняющие переменные,
в нормальной ситуации слабо коррелированные,
становятся в конкретных условиях
выборки сильно коррелированными; .
в модель включается переменная,
сильно коррелирующая с зависимой
переменной.
Мультипликативная
модель временного ряда имеет вид: —
Y=T*S*E
Мультипликативная
модель временного ряда строится, если:
амплитуда
сезонных колебаний возрастает или
уменьшается
На основе
поквартальных данных…значения 7-1
квартал, 9-2квартал и 11-3квартал …-5
Неправильный
выбор функциональной формы или объясняющих
переменных называется ошибками
спецификации
Несмещённость
оценки параметра регрессии, полученной
по МНК, означает: —
что она характеризуется наименьшей
дисперсией.
Одной из проблем
которая может возникнуть в многофакторной
регрессии и никогда не бывает в парной
регрессии, является
корреляция между независимыми переменными
От чего зависит
количество точек, исключаемых из
временного ряда в результате сглаживания:
от применяемого метода сглаживания.
Отметьте основные
виды ошибок спецификации:
отбрасывание значимой переменной;
добавление незначимой переменной;
Оценки коэффициентов
парной регрессии является несмещённым,
если:
математические ожидания остатков =0.
Оценки параметров
парной линейной регрессии находятся
по формуле b=
Cov(x;y)/Var(x);a=y¯
bx¯
Оценки параметров
регрессии являются несмещенными, если
Математическое
ожидание остатков равно 0
Оценки параметров
регрессии являются состоятельными,
если:
-увеличивается точность оценки при n,
т. е. при увеличении n
вероятность оценки от истинного значения
параметра стремится к 0.
Оценки парной
регрессии явл. эффективными, если:
оценка обладают наименьшей дисперсией
по сравнению с другими оценками
При наличии
гетероскедастичности следует применять:
— обобщённый МНК
При проверке
значимости одновременно всех параметров
используется:
-F-тест.
При проверке
значимости одновременно всех параметров
регрессии используется:
F-тест.
Применим ли метод
наименьших квадратов для расчетов
параметров показательной зависимости
применим после ее приведения
Применим ли метод
наименьших квадратов(МНК) для расчёта
параметров нелинейных моделей?
применим после её специального приведения
к линейному виду
С помощью какого
критерия оценивается значимость
коэффициента регрессии T
стьюдента
С увеличением
числа объясняющих переменных
скоррестированный коэффициент
детерминации:
— увеличивается.
Связь между
индексом множественной детерминации
R²
и
скорректированным индексом множественной
детерминации Ȓ²
есть
Скорректиров.
коэф.
детерминации:
— больше обычного коэф. детерминации
Стандартизованный
коэффициент уравнения регрессии Ƀk
показывает на
сколько % изменится результирующий
показатель у при изменении хi
на 1%при неизмененном среднем уровне
других факторов
Стандартный
коэффициент уравнения регрессии:
показывает на сколько 1 изменится y
при изменении фактора xk
на 1 при сохранении др.
Суть коэф.
детерминации r2xy
состоит
в следующем: — характеризует
долю дисперсии результативного признака
y
объясняем. регресс., в общей дисперсии
результативного признака.
Табличное значение
критерия Стьюдента зависит
от уровня
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда.(от принятого уровня значимости и
от числа степеней свободы ( n — m -1))
Табличные значения
Фишера (F)
зависят от
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда (от доверительной вероятности p
и числа степеней свободы дисперсий f1
и f2)..
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, идентифицируемо если
D+1=H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, НЕидентифицируемо если
D+1<H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, сверхидентифицируемо если
D+1>H
Уравнение
идентифицировано, если: —
D+1=H
Уравнение
неидентифицировано, если: —
D+1<H
Уравнение
сверхидентифицировано, если: —
D+1>H
Фиктивные
переменные — это:
атрибутивные признаки (например, как
профессия, пол, образование), которым
придали цифровые метки;
Формула t=
rxy….используется
для проверки
существенности коэффициента корреляции
Частный F-критерий:
— оценивает
значимость уравнения регрессии в целом
Число степеней
свободы для факторной суммы квадратов
в линейной модели множественной регрессии
равно: m;
Что показывает
коэффициент наклона —
на сколько единиц изменится у, если х
изменился на единицу,
Что показывает
коэффициент. абсолютного роста
на сколько единиц изменится у, если х
изменился на единицу
Экзогенная
переменная
– это независимая переменная или
фактор-Х.
Экзогенные
переменные
— это переменные, которые определяются
вне системы и являются независимыми
Экзогенные
переменные –
это
предопределенные переменные, влияющие
на зависимые переменные (Эндогенные
переменные), но не зависящие от них,
обозначаются через х
Эластичность
измеряется
единица измерения фактора…показателя
Эластичность
показывает
на сколько % изменится редуктивный
показатель y
при изменении на 1% фактора xk.
Эндогенные
переменные — это:
зависимые переменные, число которых
равно числу уравнений в системе и которые
обозначаются через у
Определения
T-отношение
(t-критерий)
— отношение оценки коэффициента,
полученной с помощью МНК, к величине
стандартной ошибки оцениваемой величины.
Аддитивная модель
временного ряда –
это модель, в которой временной ряд
представлен как сумма перечисленных
компонент.
Критерий Фишера
— способ статистической проверки
значимости уравнения регрессии, при
котором расчетное (фактическое) значение
F-отношения сравнивается с его критическим
(теоретическим) значением.
Линейная регрессия
— это связь (регрессия), которая
представлена уравнением прямой линии
и выражает простейшую линейную
зависимость.
Метод инструментальных
переменных
— это разновидность МНК. Используется
для оценки параметров моделей, описываемых
несколькими уравнениями. Главное
свойство — частичная замена непригодной
объясняющей переменной на такую
переменную, которая некоррелированна
со случайным членом. Эта замещающая
переменная называется инструментальной
и приводит к получению состоятельных
оценок параметров.
Метод наименьших
квадратов (МНК)
— способ приближенного нахождения
(оценивания) неизвестных коэффициентов
(параметров) регрессии. Этот метод
основан на требовании минимизации суммы
квадратов отклонений значений результата,
рассчитанных по уравнению регрессии,
и истинных (наблюденных) значений
результата.
Множественная
линейная регрессия
— это множественная регрессия,
представляющая линейную связь по каждому
фактору.
Множественная
регрессия —
регрессия с двумя и более факторными
переменными.
Модель
идентифицируемая
— модель, в которой все структурные
коэффициенты однозначно определяются
по коэффициентам приведенной формы
модели.
Модель рекурсивных
уравнений —
модель, которая содержит зависимые
переменные (результативные) одних
уравнений в роли фактора, оказываясь в
правой части других уравнений.
Мультипликативная
модель –
модель, в которой временной ряд представлен
как произведение перечисленных компонент.
Несмещенная
оценка —
оценка, среднее которой равно самой
оцениваемой величине.
Нулевая гипотеза
— предположение о том, что результат
не зависит от фактора (коэффициент
регрессии равен нулю).
Обобщенный метод
наименьших квадратов (ОМНК)
— метод, который не требует постоянства
дисперсии (гомоскедастичности) остатков,
но предполагает пропорциональность
остатков общему множителю (дисперсии).
Таким образом, это взвешенный МНК.
Объясненная
дисперсия —
показатель вариации результата,
обусловленной регрессией.
Объясняемая
(результативная) переменная
— переменная, которая статистически
зависит от факторной переменной, или
объясняющей (регрессора).
Остаточная
дисперсия —
необъясненная дисперсия, которая
показывает вариацию результата под
влиянием всех прочих факторов, неучтенных
регрессией.
Предопределенные
переменные
— это экзогенные переменные системы и
лаговые эндогенные переменные системы.
Приведенная форма
системы —
форма, которая, в отличие от структурной,
уже содержит одни только линейно
зависящие от экзогенных переменных
эндогенные переменные. Внешне ничем не
отличается от системы независимых
уравнений.
Расчетное значение
F-отношения
— значение, которое получают делением
объясненной дисперсии на 1 степень
свободы на остаточную дисперсию на 1
степень свободы.
Регрессия
(зависимость)
— это усредненная (сглаженная), т.е.
свободная от случайных мелкомасштабных
колебаний (флуктуаций), квазидетерминированная
связь между объясняемой переменной
(переменными) и объясняющей переменной
(переменными). Эта связь выражается
формулами, которые характеризуют
функциональную зависимость и не содержат
явно стохастических (случайных)
переменных, которые свое влияние теперь
оказывают как результирующее воздействие,
принимающее вид чисто функциональной
зависимости.
Регрессор
(объясняющая переменная, факторная
переменная)
— это независимая переменная, статистически
связанная с результирующей переменной.
Характер этой связи и влияние изменения
(вариации) регрессора на результат
исследуются в эконометрике.
Система
взаимосвязанных уравнений
— это система одновременных или
взаимозависимых уравнений. В ней одни
и те же переменные выступают одновременно
как зависимые в одних уравнениях и в то
же время независимые в других. Это
структурная форма системы уравнений.
К ней неприменим МНК.
Система внешне
не связанных между собой уравнений
— система, которая характеризуется
наличием одних только корреляций между
остатками (ошибками) в разных уравнениях
системы.
Случайный остаток
(отклонение)
— это чисто случайный процесс в виде
мелкомасштабных колебаний, не содержащий
уже детерминированной компоненты,
которая имеется в регрессии.
Состоятельные
оценки —
оценки, которые позволяют эффективно
применять доверительные интервалы,
когда вероятность получения оценки на
заданном расстоянии от истинного
значения параметра становится близка
к 1, а точность самих оценок увеличивается
с ростом объема выборки.
Спецификация
модели —
определение существенных факторов и
выявление мультиколлинеарности.
Стандартная
ошибка —
среднеквадратичное (стандартное)
отклонение. Оно связано со средней
ошибкой и коэффициентом доверия.
Степени свободы
— это величины, характеризующие число
независимых параметров и необходимые
для нахождения по таблицам распределений
их критических значений.
Тренд
— основная тенденция развития, плавная
устойчивая закономерность изменения
уровней ряда.
Уровень значимости
— величина, показывающая, какова
вероятность ошибочного вывода при
проверке статистической гипотезы по
статистическому критерию.
Фиктивные
переменные
— это переменные, которые отражают
сезонные компоненты ряда для какого-либо
одного периода.
Эконометрическая
модель — это
уравнение или система уравнений, особым
образом представляющие зависимость
(зависимости) между результатом и
факторами. В основе эконометрической
модели лежит разбиение сложной и
малопонятной зависимости между
результатом и факторами на сумму двух
следующих компонентов: регрессию
(регрессионная компонента) и случайный
(флуктуационный) остаток. Другой класс
эконометрических моделей образует
временные ряды.
Эффективность
оценки — это
свойство оценки обладать наименьшей
дисперсией из всех возможных.
Тесты по дисциплине
ТЕСТ №1
1. Коэффициент корреляции, равный нулю, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) ситуация не определена.
2. Коэффициент корреляции, равный 1, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) функциональная зависимость;
г) ситуация не определенна.
В регрессионном анализе обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
Y = <р(Xj,…,xk), являющимся функцией от аргументов xj, и с постоянной, от аргументов дисперсией о2 :
а) не зависящей;
б) зависящей.
Статистика Дарбина Уотсона (DW) вычисляется по формуле:
a)
n
Z (et et_i)2
t=2
DW
n
Z et2
б)
n
Z (et et-i)2
t=2
DW
n
Zyt2
t=1
c)
n
DW
Z (yt yt-1)2
t=2
n
Zyt2
В модели lnY = во + (3X+ є коэффициент в имеет смысл:
а) абсолютного прироста;
б) темпа роста;
в) темпа прироста.
При анализе эластичности спроса по цене целесообразно использовать следующую модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Использование обычного Евклидова расстояния оправдано в следующих случаях (выберите необходимые варианты):
а) наблюдения берутся из генеральной совокупности, имеющей многомерное
нормальное распределение с ковариационной матрицей вида а Ек, т.е. компоненты Х взаимно независимы и имеют одну и ту же дисперсию, где Ек единичная матрица;
б) наблюдения берутся из генеральной совокупности, имеющей биномиальное
распределение;
в) компоненты вектора наблюдений Х неоднородны по физическому смыслу и
при классификации используются с определенным весом;
г) компоненты вектора наблюдений Х однородны по физическому смыслу и
одинаково важны для классификации;
д) признаковое пространство совпадает с геометрическим пространством;
е) совпадение признакового пространства с геометрическим пространством необязательно.
Академиком А.Н.Колмогоровым было предложено:
а) «обобщенное расстояние» между классами;
б) расстояние, измеряемое по принципу «ближайшего соседа»;
в) расстояние, измеряемое по принципу «дальнего соседа»;
г) расстояние, измеряемое по «центрам тяжести» групп;
д) расстояние, измеряемое по принципу «средней связи».
Производственная функция Кобба Дугласа с учетом технического прогресса имеет вид:
а) Qt = Aхeet хК? хLet;
б) Q = A х К а х Le х eє;
в) Q = A х K а х L1~a х ee = A х (f)a х L х ee.
10. Оценки неизвестных параметров A, а и в в производственной функции Кобба
Дугласа можно найти с помощью:
а) метода наименьших квадратов;
б) принципа «ближнего соседа»;
а) дисконтированием множителей.
ТЕСТ №2
1. Двумерная корреляционная модель определяется параметрами (вставьте
необходимое слово):
а) тремя;
б) пятью;
в) семью.
2. Коэффициент регрессии определяется по формуле: а) /? = р—=— коэффициент регрессии y на x;
б) M [ ^. ^ ] = р,;
Ox Oy
12/3,4…, k
1
3. Если вектор ошибок имеет постоянную дисперсию, то это явление называется:
а) гомоскедастичностью;
б) гетероскедастичностью;
в) ситуация не определена.
4. С увеличением объема выборки:
а) увеличивается точность оценок;
б) уменьшается ошибка регрессии;
в) расширяются интервальные оценки;
г) уменьшается коэффициент детерминации.
При анализе издержек Y от объемы выпуска X целесообразно использовать следующую модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Модель Y = в0 + Pln X+ є используется, когда необходимо исследовать влияние:
а) процентного изменения независимой переменной на абсолютное изменение
зависимой переменной;
б) процентного изменения независимой переменной на процентное изменение
зависимой переменной;
в) абсолютное изменения независимой переменной на абсолютное изменение
зависимой переменной.
Наиболее употребительными расстояниями и мерами близости между классами объектов являются (выберите необходимый вариант):
а) расстояние, измеряемое по принципу «ближайшего соседа»;
б) расстояние, измеряемого по принципу «дальнего соседа»;
в) расстояние, измеряемое по принципу «родственной связи»;
г) расстояние, измеряемое по «центрам тяжести» групп;
д) расстояние, измеряемое по принципу «незначимой связи»;
е) расстояние, измеряемое по принципу «средней связи»;
ж) расстояние, измеряемое по принципу «значимой связи».
Расстояние, измеряемое по принципу «ближайшего соседа» находится по формуле:
а) Ре (Хг, Xj ) =
У(xu xji) ;
б) pmm (Si, Sm ) = тin р(xi, xj);
в) pmax (Sl, Sm ) = 111ax p(^ , x} );
д) pl,(m,g) = p(S1, S(m,q)) = ap1m + + Wmq + 6(p1m pq X
е) Рср (S, Sm) = — P( x, x]).
9. Параметры а и в в производственной функции Кобба Дугласа называют:
а) коэффициентами эластичности;
б) коэффициентами корреляции;
в) коэффициентами автокорреляции.
10. Коэффициенты эластичности показывают, на какую величину в среднем изменится Q, если а или в увеличить соответственно:
а) на один процент;
б) на единицу своего измерения.
ТЕСТ №3
1. Коэффициент регрессии показывает:
а) на сколько единиц своего измерения увеличится (в>0) или уменьшится (в<0)
в среднем y(My/x), если x увеличить на единицу своего измерения;
б) долю дисперсии одной случайной величины, обусловленную вариацией другой;
в) на сколько % увеличится (в>0) или уменьшится (в<0) в среднем y(My/x), если x увеличится на 1 %.
Коэффициент регрессии изменяется в пределах от:
а) -1 до 1;
б) 0 до 1;
min
Po.Pi—.Pk
в) принимает любое значение.
Квадратичная форма
Q=(Y XP) ) (Y Xf) = __(y; у,)
і=і
соответствует :
а) методу максимального правдоподобия;
б) методу наименьших квадратов;
в) методу «дальнего соседа»;
г) методу «средней связи»;
д) двухшаговому методу наименьших квадратов.
4. На главной диагонали ковариационной матрицы в выражении S(b) = S (XTX)-1 находятся:
а) дисперсии коэффициентов регрессии;
б) средние значения коэффициентов регрессии;
в) коэффициенты корреляции;
г) квадраты коэффициентов корреляции.
5. При анализе производственной функции целесообразно использовать следующую
модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Модели lnY = fP + PPX+ є Y = /Зо + ffln X+ є называются:
а) линейными;
б) полулогарифмическими;
в) логарифмическими.
Расстояние, измеряемое по принципу «дальнего соседа «, находится по формуле:
а) Ре (Хг, xj ) =
1=1
б) pmin (S1, Sm ) = ПІІП s p(X, , Xj );
в) pmax (S1 > Sm ) = ЇПЗЗС s p(x, , Xj );
Д) Pl,(»,,) = P(S1, S(m,q)) = aPlm + PP1q + Wmq + p q );
5. Расстояние, измеряемое по «центрам тяжести » групп, находится по формуле:
|
а) P£ (X,, Xj ) = ^ |
1=1 |
|
В) Pmax(S1, Sm ) = |
|
|
Д) P ,(m,q) = P(S1, S(m,q)) = af>tm + Pftq + YPmq + 6(P1m Pq ); |
|
|
Є) Pop (S1, Sm ) = |
9. Если a + в = 1, то уровень эффективности:
а) не зависит от масштабов производства;
б) зависит от масштабов производства.
10. Если a + в < 1, то средние издержки, рассчитанные на единицу продукции:
а) растут по мере расширения масштабов производства;
б) убывают по мере расширения масштабов производства.
ТЕСТ №4
В двумерной модели для вывода о независимости признаков х и y в генеральной совокупности достаточно проверить значимость:
а) только коэффициента корреляции;
б) коэффициента корреляции и регрессии;
в) коэффициента корреляции, детерминации и регрессии.
Значимость частных и парных коэффициентов корреляции проверяется с помощью:
а) нормального закона распределения;
б) t-критерия Стъюдента;
в) F-критерия;
г) таблицы Фишера Иейтса.
В регрессионном анализе Xj рассматриваются как:
а) неслучайные величины;
б) случайные величины;
в) любые величины.
Для оценки вектора в наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор b, который минимизирует:
а) сумму отклонений наблюдаемых значений у; от модельных значений y;
б) сумму квадратов отклонения наблюдаемых значений у; от модельных значений yt.
Если в модели Y = во + в ln X+ є положить Y = GNP (валовой национальный продукт), а X=M (денежная масса), то из формулы:
GNP = во + вІпМ + є, следует, что если увеличить предложение денег М на ,
тоВНПвырастет на 0,01 в:
а) 1%;
б) 1 измерения.
Для получения качественных оценок уравнений регрессии необходимо выполнение следующих предпосылок МНК (выберите необходимые пункты):
а) отклонения є должны быть нормально распределенными случайными величинами с нулевым математическим ожиданием и постоянной дисперсией;
б) отклонения Єї не должны коррелировать друг с другом;
в) отклонения є должны иметь показательный закон распределения.
Расстояние, измеряемое по принципу «средней связи», находится по формуле:
а) Ре (xi, xj ) =
1=1
б) pmm(S1 > Sm ) = mІП р(^ , x} );
в) pmax (S 1 > Sm ) = max s p(^ , x} );
д) pl,(m,g) = p(S1 > S(m,q)) = ap1m + Pftq + Wmq + 6(p1m plg X
е) pср.(S1, Sm ) = IZ p( xi , xj ).
11 nm xi«Slxj<=Sm
Кластерный анализ позволяет проводить:
а) группировку объектов;
б) группировку признаков;
в) группировку объектов и группировку признаков.
Если а + в> 1, то средние издержки, рассчитанные на единицу продукции:
а) растут по мере расширения масштабов производства;
б) убывают по мере расширения масштабов производства.
10. Исходя из априорных соображений значения а и в должны удовлетворять условиям:
а) 0<а<1 и 0< в<1;
б) -1<а<1 и -1< в<1;
в) -1<а<1 и 0< в<1.
ТЕСТ №5
Коэффициент корреляции считается значимым с вероятностью ошибки а если:
а) 1;набл по модулю будет больше, чем 1кр,
б) не имеет значения;
в) 1;набл по модулю будет меньше, чем 1;кр.
Матрица R парных коэффициентов корреляции является (выберите необходимые пункты):
а) обратной;
б) транспонированной;
в) симметричной;
г) положительно определенной.
3. В каких пределах изменяется множественный коэффициент корреляции:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) от 0 до 10.
4. В каких пределах изменяется коэффициент детерминации:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) от 0 до 10.
5. В хорошо подобранной модели остатки должны (выберите необходимые пункты):
а) иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией;
б) не коррелировать друг с другом;
в) иметь экспоненциальный закон распределения;
г) хаотично разбросаны;
д) форма и вид распределения не важен.
6. Неправильный выбор функциональной формы или объясняющих переменных называется:
а) ошибками спецификации;
б) ошибками прогноза;
в) гетероскедастичностью.
7. С какой целью производят нормирование признаков:
а) с целью устранения влияния различных единиц измерения;
б) с целью уменьшить признаковое пространство;
в) с целью упрощения расчетов.
8. Хемминговорасстояние вычисляется по формуле:
а) Ре (Хг, xj ) =
б) рВе (Хг, Xe )
1=1
1=1
9. Коэффициент а интерпретируется как:
а) эластичность по труду;
б) эластичность по капиталу;
в) эластичность замещения.
10. Для определения параметров и вида производственной функции пользуются
следующими видами данных:
а) динамическими рядами;
б) данными одновременных наблюдений (пространственной информацией);
в) динамическими рядами и пространственной информацией.
ТЕСТ №6
1. С помощью данной формулыr12/34 k =—. 12 можно определить:
а) множественный коэффициент корреляции (£-2)-го порядка между факторами
X1 и X2;
б) частный коэффициент корреляции (&-2)-го порядка между факторами X1 и X2;
в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.
2. С помощью данной формулы r 1/2 3 k =r 1 =
R
1 можно определить:
R11
а) множественный коэффициент корреляции (£-2)-го порядка между факторами
X1 и X2;
б) частный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2;
в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.
Коэффициент детерминации это:
а) квадрат парного коэффициента корреляции;
б) квадрат частного коэффициента корреляции;
в) квадрат множественного коэффициента корреляции.
Метод максимального правдоподобия лучше работает на…, где он, как правило, дает оценки с минимальной дисперсией:
а) больших выборках;
б) малых выборках;
в) любых выборках.
Модель вида Y = AKaLe носит название:
а) функции Энгеля;
б) функции Кобба Дугласа;
в) лог-линейной модели;
г) степенной модели.
Модель вида Yt = Y0(1+r/ носит название:
а) функции Энгеля;
б) функции Кобба Дугласа;
в) лог-линейной модели;
г) степенной модели.
В задаче классификации данное расстояние применяется в тех случаях, когда каждой компоненте xi вектора наблюдений Xудается приписать некоторый «вес «, пропорционально степени важности признака.
а) Хеммингово расстояние;
б) «взвешенное» Евклидово пространство;
в) обычное Евклидово расстояние.
Иерархические (древообразные) процедуры являются наиболее распространенными (в смысле реализации на ЭВМ) алгоритмами кластерного анализа, они бывают … типов:
а) 2;
б) 3;
в) 5;
г) любых.
Если производство, эффективность которого не зависит от масштабов и описывается производственной функцией Кобба Дугласа, то с ростом параметра а параметр в:
а) растет;
б) уменьшается;
в) остается неизменным;
г) растет или уменьшается.
10. Если производство, эффективность которого растет по мере его укрупнения, описывается производственной функцией Кобба Дугласа, то параметры модели удовлетворяют соотношению:
а) a+f<1;
б) a+f=1;
в) a+f=0;
г) a+f>1.
ТЕСТ №7
Уравнение My / X My = f3yX (X Mx) :
а) прямая регрессии y на x;
б) прямая регрессии X на y.
Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой:
а) коэффициент детерминации;
б) парный коэффициент корреляции;
в) частный коэффициент корреляции;
г) множественный коэффициент корреляции.
3. Оценки максимального правдоподобия и метода наименьших квадратов:
а) могут не совпадать;
б) совпадают;
в) никогда не совпадают.
В матричной форме регрессионная модель имеет вид: Y = Xf + є,
где Y:
а) матрица, размерности [n x (k+1)];
б) случайный вектор-столбец размерности (n x 1).
Какой смысл у коэффициентов регрессии в логарифмических регрессионных моделях:
а) показывают процентное изменение Y для данного процентного изменения X;
б) показывают абсолютное изменение Y для данного процентного изменения X;
в) показывают процентное изменение Y для данного абсолютного изменения X.
Изменяются ли свойства случайного отклонения при преобразовании уравнения регрессии:
а) да;
б) нет;
в) случайное отклонение не зависит от вида уравнения регрессии
В … процедурах начальным является разбиение, состоящее из n одноэлементных
классов, а конечным из одного класса; в наоборот (вставьте необходимые буквы):
а) агломеративных, дивизимных;
б) дивизимных, агломеративных;
в) дисконтированных, агломеративных.
Большинство программ, реализующих алгоритм иерархической классификации, предусматривает графическое представление результатов классификации в виде:
а) дендрограммы;
б) длок-схемы;
в) графиков показателей.
В задачах многомерной классификации объектов а, в, 8 и у являются:
а) числовыми коэффициентами;
б) коэффициентами эластичности.
10. В производственной функции Кобба-Дугласа параметр в соответствует коэффициенту:
а) корреляции;
б) вариации;
в) эластичности;
г) детерминации.
ТЕСТ №8
Величина, рассчитанная по формуле r = ——Х-У-, является оценкой:
sxsy
а) коэффициента детерминации;
б) парного коэффициента корреляции;
в) частного коэффициента корреляции;
г) множественного коэффициента корреляции.
Выборочный коэффициент корреляции r по абсолютной величине:
а) не превосходит единицы;
б) не превосходит нуля;
в) принимает любые значения.
В матричной форме регрессионная модель имеет вид: Y = Хв + є,
где X:
а) матрица, размерности [n x (k+1)];
б) случайный вектор-столбец размерности (n x 1).
В матричной форме регрессионная модель имеет вид: Y = Хв+ є,
где є :
а) матрица, размерности [n x (k+1)] ошибок наблюдений (остатков);
б) случайный вектор-столбец размерности (n x 1) ошибок наблюдений (остатков).
5. Отметьте основные виды ошибок спецификации:
а) отбрасывание значимой переменной;
б) добавление незначимой переменной;
в) низкое значение коэффициента детерминации;
г) выбор неправильной формы модели.
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена:
а) да;
б) нет;
в) ситуация не определена.
В задачах многомерной классификации объектов при а=в=-8=1/2и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
В задачах многомерной классификации объектов при а=в=8=1/2 и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
Получены две производственные функции Кобба Дугласа, имеющие равные значения параметров а и в, но различающиеся по параметру А. В каком случае первое производство более эффективно, чем второе:
а) Аі<А2;
б) Аі>А2;
в) Аі=А2;
г) Аі^А2.
10. В матричном виде структурная формы системы одновременных эконометрических уравнений имеет следующий вид: Byt + Txt = et:
а) да, это так;
б) нет;
в) данное уравнение не является структурной формой системы одновременных
эконометрических уравнений.
ТЕСТ №9
1. Есть ли необходимость при определении с надежностью у доверительного интервала для значимого парного или частного коэффициентов корреляции использовать Z-преобразование Фишера и предварительно устанавливать интервальную оценку для Z:
а) нет;
б) да;
в) ситуация не определена.
2. Для проверки значимости какого коэффициента
1 2
Fнабл = k 1
n ■
«(1 )
рассчитывают :
а) коэффициента детерминации;
б) парного коэффициента корреляции;
в) частного коэффициента корреляции;
г) множественного коэффициента корреляции.
Компоненты вектора є i :
а) независимы между собой;
б) зависимы между собой;
в) имеют нормальный закон распределения с нулевым математическим ожиданием (Мє i =0) и неизвестной дисперсией а2 (De i = а2).
На практике при построении регрессионных моделей рекомендуется, чтобы n превышало k не менее, чем:
а) в два раза;
б) в три раза;
в) не имеет значения.
Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению:
а) t-статистики;
б) F-статистики;
в) коэффициента детерминации.
Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения є i, а именно, к их математическому ожиданию Мєі и дисперсии Dei:
а) Мє=1; в) МЄі=0;
Dei=a2; Dei=a2;
б) Мєі=0; г) Мєі=1;
Dei=1; Dei=0
В задачах многомерной классификации объектов при а=в=8=1/2 и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
8. В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа «ближайшего соседа’»:
а) 2; в) 6;
б) 5; г) 7.
9. Если M є t1 є t2 = 0 при t1 ф 12 и t1,12 = 1,2,…, n, то случайные ошибки регрессии:
а) зависимы между собой;
б) независимы между собой;
с) ситуация не определена.
10. Если дисперсия ошибки постоянна Мє2 = а2 = а1 и не зависит от t и Xt,
то это свидетельствует о:
а) гомоскедастичности остатков;
б) гетероскедастичности остатков.
ТЕСТ №10
1. Известно, что при фиксированном значении X3 между величинами X1 и X2 существует положительная связь. Какое значение может принять частный коэффициент корреляции р12/3?
а) -0,8;
б) 0;
в) 0,4;
г) 1,3.
По результатам n=20 наблюдений получен частный коэффициент корреляции r12/3=0,8. Определите, чему при уровне значимости a=0,05 равна разность между наблюдаемым (r12/3) и критическим (гкр) значениями коэффициентов корреляции:
а) -0,513;
б) 0, 357;
в) 0, 700;
г) 0,133.
На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше , то
считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включать только один из показателей Xj или Xe. Вставьте недостающее значение.
а) 0,3;
б) 0,5;
в) 0,6;5;
г) 0,8;
д) 0,9;
е) другое значение.
4. Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез
H0: в=0, где j=1,2,…k, используют:
а) нормальный закон распределения;
б) t-критерий;
в) распределение Фишера.
5. Двойная логарифмическая модель является линейной относительно ее переменных:
а) утверждение истинно;
б) утверждение ложно;
в) утверждение не определено.
Коэффициенты двойной логарифмической модели определяют эластичность зависимой переменной по соответствующим определяющим переменным:
а) утверждение истинно;
б) утверждение ложно;
в) утверждение не определено.
В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа » дальнего соседа»:
а) 2; в) 6;
б) 5; г) 7.
В условиях гетероскедастичности случаных остатков оценки коэффициентов, полученные по методу наименьших квадратов, будут:
а) несмещенными; в) эффективными; д) надежными;
б) смещенными; г) неэффективными; е) ненадежными.
Условием гетероскедастичности является:
а) независимость значений = <J2t от t и xt;
б) зависимость значений Мє2 = a2t от t и xt;
в) ситуация не определена.
10. Систему yt = B~lTxt + B~1є( одновременных уравнений называют рекурсивной,
если выполняются следующие условия (выберите необходимые условия):
а) Матрица значений эндогенных переменных является нижней треугольной
матрицей, т. е. в ij = 0 при j>i и (3 ц = 1;
б) случайные ошибки независимы между собой, т. е. aii > 0, аij = 0 при j ,
где i,j=1,2,…,G;
в) каждое ограничение на структурные коэффициенты относится к отдельному
уравнению.
Q=………..min
соответствует
методу наименьших квадратов
Автокорреляция
— это
корреляционная зависимость уровней
ряда от предыдущих значений.
Автокорреляция
имеется когда
каждое следующее значение остатков
Аддитивная модель
временного ряда имеет вид: Y=T+S+E
Атрибутивная
переменная может употребляться, когда:
независимая переменная качественна;
В каких пределах
изменяется коэффициент детерминанта:
от 0 до 1.
В каком случае
модель считается адекватной Fрасч>Fтабл
В каком случае
рекомендуется применять для моделирования
показателей с увелич. ростом параболу
если
относительная величина…неограниченно
В результате
автокорреляции имеем неэффективные
оценки параметров
В хорошо подобранной
модели остатки должны иметь
нормальный закон
В эконометрическом
анализе Xj
рассматриваются
как случайные величины
Величина
доверительного интервала позволяет
установить предположение о том, что:
интервал содержит оценку параметра
неизвестного.
Величина
рассчитанная по формуле r=…является
оценкой
парного коэф. Корреляции
Внутренне
нелинейная регрессия
— это истинно нелинейная регрессия,
которая не может быть приведена к
линейной регрессии преобразованием
переменных и введением новых переменных.
Временной ряд
— это последовательность значений
признака (результативного переменного),
принимаемых в течение последовательных
моментов времени или периодов.
Выберете
авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt
Выберете модель
с лагами Уt=
a+b0x1…….(самая
длинная формула)
Выборочное
значение Rxy
не > 1, |R|
< 1
Выборочный
коэффициент корреляции r
по абсолютной
величине не превосходит единицы
Гетероскедастичность
— нарушение постоянства дисперсии для
всех наблюдений.
Гетероскедастичность
присутствует когда:
дисперсия случайных остатков не постоянна
Гетероскидастичность
– это когда
дисперсия остатков различна
Гипотеза об
отсутствии автокорреляции остатков
доказана,
если Dтабл2…
Гомоскедастичность
— постоянство
дисперсии для всех наблюдений, или
одинаковость дисперсии каждого отклонения
(остатка) для всех значений факторных
переменных.
Гомоскидастичность
– это когда дисперсия остатков постоянна
и одинакова для всех … наблюдений.
Дисперсия
— показатель вариации.
Для определения
параметров неиденцифицированной модели
применяется.:
не один из сущ. методов применить нельзя
Для определения
параметров сверх иденцифицированной
модели примен.:
применяется. 2-х шаговый МНК
Для определения
параметров структурную форму модели
необходимо преобразовать в
приведенную форму модели
Для определения
параметров точно идентифицируемой
модели:
применяется косвенный МНК;
Для оценки …
изменения y
от x
вводится:
коэффициент эластичности:
Для парной
регрессии ơ²b
равно
….(xi-x¯)²)
Для проверки
значимости отдельных параметров
регрессии используется:
t-тест.
Для регрессии
y=a+bx
из n
наблюдений интервал доверия (1-а)% для
коэф. b
составит
b±t…….·ơb
Для регрессии из
n
наблюдений и m
независимых переменных существует
такая связь между R²
и F..=[(n-m-1)/m](
R²/(1-
R²)]
Доверительная
вероятность
– это вероятность того, что истинное
значение результативного показателя
попадёт в расчётный прогнозный интервал.
Допустим что для
описания одного экономического процесса
пригодны 2 модели. Обе адекватны по f
критерию фишера. какой предоставить
преимущество, у той у кот.: большее
значения F
критерия
Допустим, что
зависимость расходов от дохода описывается
функцией y=a+bx
среднее значение у=2…равняется
9
Если Rxy
положителен, то
с ростом x
увеличивается y.
Если в уравнении
регрессии имеется несущественная
переменная, то она обнаруживает себя
по низкому значению T
статистки
Если качественный
фактор имеет 3 градации, то необходимое
число фиктивных переменных
2
Если коэффициент
корреляции положителен, то в линейной
модели с
ростом х увеличивается у
Если мы заинтересованы
в использовании атрибутивных переменных
для отображения эффекта разных месяцев
мы должны использовать
11 атрибутивных методов
Если регрессионная
модель имеет показательную зависимость,
то метод МНК
применим после приведения к линейному
виду.
Зависимость между
коэффициентом множественной детерминации
(D)
и корреляции (R)
описывается следующим методом R=√D
Значимость
уравнения регрессии
— действительное наличие исследуемой
зависимости, а не просто случайное
совпадение факторов, имитирующее
зависимость, которая фактически не
существует.
Значимость
уравнения регрессии в целом оценивают:
-F-критерий
Фишера
Значимость частных
и парных коэф.
корреляции
поверен. с помощью:
-t-критерия
Стьюдента
Интеркорреляция
и связанная с ней мультиколлинеарность
— это приближающаяся к полной линейной
зависимости тесная связь между факторами.
Какая статистическая
характеристика выражается формулой
R²=…коэффициент
детерминации
Какая статистическая
хар-ка выражена формулой:
rxy=Ca(x;y)
разделить на корень Var(x)*Var(y):
коэффициент. корреляции
Какая функция
используется при моделировании моделей
с постоянным ростом степенная
Какие точки
исключаются из временного ряда процедурой
сглаживания и
в начале, и в конце.
Какое из уравнений
регрессии является степенным
y=a˳aͯ¹a
Классический
метод к оцениванию параметров регрессии
основан на: —
метод наименьших квадратов (МНК)
Количество
степеней свободы для t
статистики при проверки значимости
параметров регрессии из 35 наблюдений
и 3 независимых переменных 31;
Количество
степеней свободы знаменателя F-статистики
в регрессии из 50 наблюдений и 4 независимых
переменных: 45
Компоненты вектора
Ei
имеют
нормальный закон
Корреляция
— стохастическая зависимость, являющаяся
обобщением строго детерминированной
функциональной зависимости посредством
включения вероятностной (случайной)
компоненты.
Коэффициент
автокорреляции:
характеризует тесноту линейной связи
текущего и предстоящего уровней ряда
Коэффициент
детерминации
— показатель тесноты стохастической
связи в общем случае нелинейной регрессии
Коэффициент
детерминации
– это величина, которая характеризует
связь между зависимыми и независимыми
переменными.
Коэффициент
детерминации — это
квадрат множественного коэффициента
корреляции
Коэффициент
детерминации — это: величина,
которая характеризует связь между
независимой и зависимой (зависящей)
переменными;
Коэффициент
детерминации R
показывает
долю вариаций зависимой переменной y,
объяснимую влиянием факторов, включаемых
в модель.
Коэффициент
детерминации изменяется в пределах:
— от 0 до 1
Коэффициент
доверия —
это коэффициент, который связывает
линейной зависимостью предельную и
среднюю ошибки, выясняет смысл предельной
ошибки, характеризующей точность оценки,
и является аргументом распределения
(чаще всего, интеграла вероятностей).
Именно эта вероятность и есть степень
надежности оценки.
Коэффициент
доверия (нормированное отклонение)
— результат деления отклонения от
среднего на стандартное отклонение,
содержательно характеризует степень
надежности (уверенности) полученной
оценки.
Коэффициент
корелляции Rxy
используется
для определения полноты связи X
и Y.
Коэффициент
корелляции меняется в пределах : от -1
до 1
Коэффициент
корелляции равный 0 означает, что:
—отсутствует
линейная связь.
Коэффициент
корелляции равный 1 означает,
что: -существует функциональная
зависимость.
Коэффициент
корреляции используется для:
определения тесноты связи между
случайными величинами X и Y;
Коэффициент
корреляции рассчитывается для
измерения степени линейной взаимосвязи
между двумя случайными переменными.
Коэффициент
линейной корреляции
— показатель тесноты стохастической
связи между фактором и результатом в
случае линейной регрессии.
Коэффициент
регрессии —
коэффициент при факторной переменной
в модели линейной регрессии.
Коэффициент
регрессии b
показывает:
на сколько единиц увеличивается y,
если x
увеличивается на 1.
Коэффициент
регрессии изменяется в пределах:
применяется любое значение ; от 0 до 1;
от -1 до 1;
Коэффициент
эластичности измеряется в:
неизмеримая величина.
Критерий
Дарвина-Чотсона применяется для:
— отбора факторов в модель; или —
определения автокорреляции в остатках
Критерий Стьюдента
— проверка значимости отдельных
коэффициентов регрессии и значимости
коэффициента корреляции.
Критерий Фишера
показывает
статистическую значимость модели в
целом на основе совокупной достоверности
всех ее коэффициентов;
Лаговые переменные
: — это переменные, относящиеся к предыдущим
моментам времени; или -это значения
зависим. перемен. за предшествующий
период времени.
Лаговые переменные
это значение
зависимых переменных за предшествующий
период времени
Модель в целом
статистически значима, если
Fрасч
> Fтабл.
Модель
идентифицирована, если: —
число параметров структурной модели
равно числу параметров приведён. формы
модели.
Модель
неидентифицирована, если: —
число приведён. коэф.
больше
числа структурных коэф.
Модель
сверхидентифицирована, если:
число приведён. коэф. меньше числа
структурных коэф
Мультиколлениарность
возникает, когда:
ошибочное включение в уравнение 2х или
более линейно зависимых переменных;
2. две или более объясняющие переменные,
в нормальной ситуации слабо коррелированные,
становятся в конкретных условиях
выборки сильно коррелированными; .
в модель включается переменная,
сильно коррелирующая с зависимой
переменной.
Мультипликативная
модель временного ряда имеет вид: —
Y=T*S*E
Мультипликативная
модель временного ряда строится, если:
амплитуда
сезонных колебаний возрастает или
уменьшается
На основе
поквартальных данных…значения 7-1
квартал, 9-2квартал и 11-3квартал …-5
Неправильный
выбор функциональной формы или объясняющих
переменных называется ошибками
спецификации
Несмещённость
оценки параметра регрессии, полученной
по МНК, означает: —
что она характеризуется наименьшей
дисперсией.
Одной из проблем
которая может возникнуть в многофакторной
регрессии и никогда не бывает в парной
регрессии, является
корреляция между независимыми переменными
От чего зависит
количество точек, исключаемых из
временного ряда в результате сглаживания:
от применяемого метода сглаживания.
Отметьте основные
виды ошибок спецификации:
отбрасывание значимой переменной;
добавление незначимой переменной;
Оценки коэффициентов
парной регрессии является несмещённым,
если:
математические ожидания остатков =0.
Оценки параметров
парной линейной регрессии находятся
по формуле b=
Cov(x;y)/Var(x);a=y¯
bx¯
Оценки параметров
регрессии являются несмещенными, если
Математическое
ожидание остатков равно 0
Оценки параметров
регрессии являются состоятельными,
если:
-увеличивается точность оценки при n,
т. е. при увеличении n
вероятность оценки от истинного значения
параметра стремится к 0.
Оценки парной
регрессии явл. эффективными, если:
оценка обладают наименьшей дисперсией
по сравнению с другими оценками
При наличии
гетероскедастичности следует применять:
— обобщённый МНК
При проверке
значимости одновременно всех параметров
используется:
-F-тест.
При проверке
значимости одновременно всех параметров
регрессии используется:
F-тест.
Применим ли метод
наименьших квадратов для расчетов
параметров показательной зависимости
применим после ее приведения
Применим ли метод
наименьших квадратов(МНК) для расчёта
параметров нелинейных моделей?
применим после её специального приведения
к линейному виду
С помощью какого
критерия оценивается значимость
коэффициента регрессии T
стьюдента
С увеличением
числа объясняющих переменных
скоррестированный коэффициент
детерминации:
— увеличивается.
Связь между
индексом множественной детерминации
R²
и
скорректированным индексом множественной
детерминации Ȓ²
есть
Скорректиров.
коэф.
детерминации:
— больше обычного коэф. детерминации
Стандартизованный
коэффициент уравнения регрессии Ƀk
показывает на
сколько % изменится результирующий
показатель у при изменении хi
на 1%при неизмененном среднем уровне
других факторов
Стандартный
коэффициент уравнения регрессии:
показывает на сколько 1 изменится y
при изменении фактора xk
на 1 при сохранении др.
Суть коэф.
детерминации r2xy
состоит
в следующем: — характеризует
долю дисперсии результативного признака
y
объясняем. регресс., в общей дисперсии
результативного признака.
Табличное значение
критерия Стьюдента зависит
от уровня
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда.(от принятого уровня значимости и
от числа степеней свободы ( n — m -1))
Табличные значения
Фишера (F)
зависят от
доверительной вероятности и от числа
включённых факторов и от длины исходного
ряда (от доверительной вероятности p
и числа степеней свободы дисперсий f1
и f2)..
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, идентифицируемо если
D+1=H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, НЕидентифицируемо если
D+1<H
Уравнение в
котором H
число эндогенных переменных, D
число отсутствующих экзогенных
переменных, сверхидентифицируемо если
D+1>H
Уравнение
идентифицировано, если: —
D+1=H
Уравнение
неидентифицировано, если: —
D+1<H
Уравнение
сверхидентифицировано, если: —
D+1>H
Фиктивные
переменные — это:
атрибутивные признаки (например, как
профессия, пол, образование), которым
придали цифровые метки;
Формула t=
rxy….используется
для проверки
существенности коэффициента корреляции
Частный F-критерий:
— оценивает
значимость уравнения регрессии в целом
Число степеней
свободы для факторной суммы квадратов
в линейной модели множественной регрессии
равно: m;
Что показывает
коэффициент наклона —
на сколько единиц изменится у, если х
изменился на единицу,
Что показывает
коэффициент. абсолютного роста
на сколько единиц изменится у, если х
изменился на единицу
Экзогенная
переменная
– это независимая переменная или
фактор-Х.
Экзогенные
переменные
— это переменные, которые определяются
вне системы и являются независимыми
Экзогенные
переменные –
это
предопределенные переменные, влияющие
на зависимые переменные (Эндогенные
переменные), но не зависящие от них,
обозначаются через х
Эластичность
измеряется
единица измерения фактора…показателя
Эластичность
показывает
на сколько % изменится редуктивный
показатель y
при изменении на 1% фактора xk.
Эндогенные
переменные — это:
зависимые переменные, число которых
равно числу уравнений в системе и которые
обозначаются через у
Определения
T-отношение
(t-критерий)
— отношение оценки коэффициента,
полученной с помощью МНК, к величине
стандартной ошибки оцениваемой величины.
Аддитивная модель
временного ряда –
это модель, в которой временной ряд
представлен как сумма перечисленных
компонент.
Критерий Фишера
— способ статистической проверки
значимости уравнения регрессии, при
котором расчетное (фактическое) значение
F-отношения сравнивается с его критическим
(теоретическим) значением.
Линейная регрессия
— это связь (регрессия), которая
представлена уравнением прямой линии
и выражает простейшую линейную
зависимость.
Метод инструментальных
переменных
— это разновидность МНК. Используется
для оценки параметров моделей, описываемых
несколькими уравнениями. Главное
свойство — частичная замена непригодной
объясняющей переменной на такую
переменную, которая некоррелированна
со случайным членом. Эта замещающая
переменная называется инструментальной
и приводит к получению состоятельных
оценок параметров.
Метод наименьших
квадратов (МНК)
— способ приближенного нахождения
(оценивания) неизвестных коэффициентов
(параметров) регрессии. Этот метод
основан на требовании минимизации суммы
квадратов отклонений значений результата,
рассчитанных по уравнению регрессии,
и истинных (наблюденных) значений
результата.
Множественная
линейная регрессия
— это множественная регрессия,
представляющая линейную связь по каждому
фактору.
Множественная
регрессия —
регрессия с двумя и более факторными
переменными.
Модель
идентифицируемая
— модель, в которой все структурные
коэффициенты однозначно определяются
по коэффициентам приведенной формы
модели.
Модель рекурсивных
уравнений —
модель, которая содержит зависимые
переменные (результативные) одних
уравнений в роли фактора, оказываясь в
правой части других уравнений.
Мультипликативная
модель –
модель, в которой временной ряд представлен
как произведение перечисленных компонент.
Несмещенная
оценка —
оценка, среднее которой равно самой
оцениваемой величине.
Нулевая гипотеза
— предположение о том, что результат
не зависит от фактора (коэффициент
регрессии равен нулю).
Обобщенный метод
наименьших квадратов (ОМНК)
— метод, который не требует постоянства
дисперсии (гомоскедастичности) остатков,
но предполагает пропорциональность
остатков общему множителю (дисперсии).
Таким образом, это взвешенный МНК.
Объясненная
дисперсия —
показатель вариации результата,
обусловленной регрессией.
Объясняемая
(результативная) переменная
— переменная, которая статистически
зависит от факторной переменной, или
объясняющей (регрессора).
Остаточная
дисперсия —
необъясненная дисперсия, которая
показывает вариацию результата под
влиянием всех прочих факторов, неучтенных
регрессией.
Предопределенные
переменные
— это экзогенные переменные системы и
лаговые эндогенные переменные системы.
Приведенная форма
системы —
форма, которая, в отличие от структурной,
уже содержит одни только линейно
зависящие от экзогенных переменных
эндогенные переменные. Внешне ничем не
отличается от системы независимых
уравнений.
Расчетное значение
F-отношения
— значение, которое получают делением
объясненной дисперсии на 1 степень
свободы на остаточную дисперсию на 1
степень свободы.
Регрессия
(зависимость)
— это усредненная (сглаженная), т.е.
свободная от случайных мелкомасштабных
колебаний (флуктуаций), квазидетерминированная
связь между объясняемой переменной
(переменными) и объясняющей переменной
(переменными). Эта связь выражается
формулами, которые характеризуют
функциональную зависимость и не содержат
явно стохастических (случайных)
переменных, которые свое влияние теперь
оказывают как результирующее воздействие,
принимающее вид чисто функциональной
зависимости.
Регрессор
(объясняющая переменная, факторная
переменная)
— это независимая переменная, статистически
связанная с результирующей переменной.
Характер этой связи и влияние изменения
(вариации) регрессора на результат
исследуются в эконометрике.
Система
взаимосвязанных уравнений
— это система одновременных или
взаимозависимых уравнений. В ней одни
и те же переменные выступают одновременно
как зависимые в одних уравнениях и в то
же время независимые в других. Это
структурная форма системы уравнений.
К ней неприменим МНК.
Система внешне
не связанных между собой уравнений
— система, которая характеризуется
наличием одних только корреляций между
остатками (ошибками) в разных уравнениях
системы.
Случайный остаток
(отклонение)
— это чисто случайный процесс в виде
мелкомасштабных колебаний, не содержащий
уже детерминированной компоненты,
которая имеется в регрессии.
Состоятельные
оценки —
оценки, которые позволяют эффективно
применять доверительные интервалы,
когда вероятность получения оценки на
заданном расстоянии от истинного
значения параметра становится близка
к 1, а точность самих оценок увеличивается
с ростом объема выборки.
Спецификация
модели —
определение существенных факторов и
выявление мультиколлинеарности.
Стандартная
ошибка —
среднеквадратичное (стандартное)
отклонение. Оно связано со средней
ошибкой и коэффициентом доверия.
Степени свободы
— это величины, характеризующие число
независимых параметров и необходимые
для нахождения по таблицам распределений
их критических значений.
Тренд
— основная тенденция развития, плавная
устойчивая закономерность изменения
уровней ряда.
Уровень значимости
— величина, показывающая, какова
вероятность ошибочного вывода при
проверке статистической гипотезы по
статистическому критерию.
Фиктивные
переменные
— это переменные, которые отражают
сезонные компоненты ряда для какого-либо
одного периода.
Эконометрическая
модель — это
уравнение или система уравнений, особым
образом представляющие зависимость
(зависимости) между результатом и
факторами. В основе эконометрической
модели лежит разбиение сложной и
малопонятной зависимости между
результатом и факторами на сумму двух
следующих компонентов: регрессию
(регрессионная компонента) и случайный
(флуктуационный) остаток. Другой класс
эконометрических моделей образует
временные ряды.
Эффективность
оценки — это
свойство оценки обладать наименьшей
дисперсией из всех возможных.
Тесты по дисциплине
ТЕСТ №1
1. Коэффициент корреляции, равный нулю, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) ситуация не определена.
2. Коэффициент корреляции, равный 1, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) функциональная зависимость;
г) ситуация не определенна.
В регрессионном анализе обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
Y = <р(Xj,…,xk), являющимся функцией от аргументов xj, и с постоянной, от аргументов дисперсией о2 :
а) не зависящей;
б) зависящей.
Статистика Дарбина Уотсона (DW) вычисляется по формуле:
a)
n
Z (et et_i)2
t=2
DW
n
Z et2
б)
n
Z (et et-i)2
t=2
DW
n
Zyt2
t=1
c)
n
DW
Z (yt yt-1)2
t=2
n
Zyt2
В модели lnY = во + (3X+ є коэффициент в имеет смысл:
а) абсолютного прироста;
б) темпа роста;
в) темпа прироста.
При анализе эластичности спроса по цене целесообразно использовать следующую модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Использование обычного Евклидова расстояния оправдано в следующих случаях (выберите необходимые варианты):
а) наблюдения берутся из генеральной совокупности, имеющей многомерное
нормальное распределение с ковариационной матрицей вида а Ек, т.е. компоненты Х взаимно независимы и имеют одну и ту же дисперсию, где Ек единичная матрица;
б) наблюдения берутся из генеральной совокупности, имеющей биномиальное
распределение;
в) компоненты вектора наблюдений Х неоднородны по физическому смыслу и
при классификации используются с определенным весом;
г) компоненты вектора наблюдений Х однородны по физическому смыслу и
одинаково важны для классификации;
д) признаковое пространство совпадает с геометрическим пространством;
е) совпадение признакового пространства с геометрическим пространством необязательно.
Академиком А.Н.Колмогоровым было предложено:
а) «обобщенное расстояние» между классами;
б) расстояние, измеряемое по принципу «ближайшего соседа»;
в) расстояние, измеряемое по принципу «дальнего соседа»;
г) расстояние, измеряемое по «центрам тяжести» групп;
д) расстояние, измеряемое по принципу «средней связи».
Производственная функция Кобба Дугласа с учетом технического прогресса имеет вид:
а) Qt = Aхeet хК? хLet;
б) Q = A х К а х Le х eє;
в) Q = A х K а х L1~a х ee = A х (f)a х L х ee.
10. Оценки неизвестных параметров A, а и в в производственной функции Кобба
Дугласа можно найти с помощью:
а) метода наименьших квадратов;
б) принципа «ближнего соседа»;
а) дисконтированием множителей.
ТЕСТ №2
1. Двумерная корреляционная модель определяется параметрами (вставьте
необходимое слово):
а) тремя;
б) пятью;
в) семью.
2. Коэффициент регрессии определяется по формуле: а) /? = р—=— коэффициент регрессии y на x;
б) M [ ^. ^ ] = р,;
Ox Oy
12/3,4…, k
1
3. Если вектор ошибок имеет постоянную дисперсию, то это явление называется:
а) гомоскедастичностью;
б) гетероскедастичностью;
в) ситуация не определена.
4. С увеличением объема выборки:
а) увеличивается точность оценок;
б) уменьшается ошибка регрессии;
в) расширяются интервальные оценки;
г) уменьшается коэффициент детерминации.
При анализе издержек Y от объемы выпуска X целесообразно использовать следующую модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Модель Y = в0 + Pln X+ є используется, когда необходимо исследовать влияние:
а) процентного изменения независимой переменной на абсолютное изменение
зависимой переменной;
б) процентного изменения независимой переменной на процентное изменение
зависимой переменной;
в) абсолютное изменения независимой переменной на абсолютное изменение
зависимой переменной.
Наиболее употребительными расстояниями и мерами близости между классами объектов являются (выберите необходимый вариант):
а) расстояние, измеряемое по принципу «ближайшего соседа»;
б) расстояние, измеряемого по принципу «дальнего соседа»;
в) расстояние, измеряемое по принципу «родственной связи»;
г) расстояние, измеряемое по «центрам тяжести» групп;
д) расстояние, измеряемое по принципу «незначимой связи»;
е) расстояние, измеряемое по принципу «средней связи»;
ж) расстояние, измеряемое по принципу «значимой связи».
Расстояние, измеряемое по принципу «ближайшего соседа» находится по формуле:
а) Ре (Хг, Xj ) =
У(xu xji) ;
б) pmm (Si, Sm ) = тin р(xi, xj);
в) pmax (Sl, Sm ) = 111ax p(^ , x} );
д) pl,(m,g) = p(S1, S(m,q)) = ap1m + + Wmq + 6(p1m pq X
е) Рср (S, Sm) = — P( x, x]).
9. Параметры а и в в производственной функции Кобба Дугласа называют:
а) коэффициентами эластичности;
б) коэффициентами корреляции;
в) коэффициентами автокорреляции.
10. Коэффициенты эластичности показывают, на какую величину в среднем изменится Q, если а или в увеличить соответственно:
а) на один процент;
б) на единицу своего измерения.
ТЕСТ №3
1. Коэффициент регрессии показывает:
а) на сколько единиц своего измерения увеличится (в>0) или уменьшится (в<0)
в среднем y(My/x), если x увеличить на единицу своего измерения;
б) долю дисперсии одной случайной величины, обусловленную вариацией другой;
в) на сколько % увеличится (в>0) или уменьшится (в<0) в среднем y(My/x), если x увеличится на 1 %.
Коэффициент регрессии изменяется в пределах от:
а) -1 до 1;
б) 0 до 1;
min
Po.Pi—.Pk
в) принимает любое значение.
Квадратичная форма
Q=(Y XP) ) (Y Xf) = __(y; у,)
і=і
соответствует :
а) методу максимального правдоподобия;
б) методу наименьших квадратов;
в) методу «дальнего соседа»;
г) методу «средней связи»;
д) двухшаговому методу наименьших квадратов.
4. На главной диагонали ковариационной матрицы в выражении S(b) = S (XTX)-1 находятся:
а) дисперсии коэффициентов регрессии;
б) средние значения коэффициентов регрессии;
в) коэффициенты корреляции;
г) квадраты коэффициентов корреляции.
5. При анализе производственной функции целесообразно использовать следующую
модель:
а) линейную;
б) полиномиальную;
в) логарифмическую;
г) степенную;
д) экспоненциальную.
Модели lnY = fP + PPX+ є Y = /Зо + ffln X+ є называются:
а) линейными;
б) полулогарифмическими;
в) логарифмическими.
Расстояние, измеряемое по принципу «дальнего соседа «, находится по формуле:
а) Ре (Хг, xj ) =
1=1
б) pmin (S1, Sm ) = ПІІП s p(X, , Xj );
в) pmax (S1 > Sm ) = ЇПЗЗС s p(x, , Xj );
Д) Pl,(»,,) = P(S1, S(m,q)) = aPlm + PP1q + Wmq + p q );
5. Расстояние, измеряемое по «центрам тяжести » групп, находится по формуле:
|
а) P£ (X,, Xj ) = ^ |
1=1 |
|
В) Pmax(S1, Sm ) = |
|
|
Д) P ,(m,q) = P(S1, S(m,q)) = af>tm + Pftq + YPmq + 6(P1m Pq ); |
|
|
Є) Pop (S1, Sm ) = |
9. Если a + в = 1, то уровень эффективности:
а) не зависит от масштабов производства;
б) зависит от масштабов производства.
10. Если a + в < 1, то средние издержки, рассчитанные на единицу продукции:
а) растут по мере расширения масштабов производства;
б) убывают по мере расширения масштабов производства.
ТЕСТ №4
В двумерной модели для вывода о независимости признаков х и y в генеральной совокупности достаточно проверить значимость:
а) только коэффициента корреляции;
б) коэффициента корреляции и регрессии;
в) коэффициента корреляции, детерминации и регрессии.
Значимость частных и парных коэффициентов корреляции проверяется с помощью:
а) нормального закона распределения;
б) t-критерия Стъюдента;
в) F-критерия;
г) таблицы Фишера Иейтса.
В регрессионном анализе Xj рассматриваются как:
а) неслучайные величины;
б) случайные величины;
в) любые величины.
Для оценки вектора в наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор b, который минимизирует:
а) сумму отклонений наблюдаемых значений у; от модельных значений y;
б) сумму квадратов отклонения наблюдаемых значений у; от модельных значений yt.
Если в модели Y = во + в ln X+ є положить Y = GNP (валовой национальный продукт), а X=M (денежная масса), то из формулы:
GNP = во + вІпМ + є, следует, что если увеличить предложение денег М на ,
тоВНПвырастет на 0,01 в:
а) 1%;
б) 1 измерения.
Для получения качественных оценок уравнений регрессии необходимо выполнение следующих предпосылок МНК (выберите необходимые пункты):
а) отклонения є должны быть нормально распределенными случайными величинами с нулевым математическим ожиданием и постоянной дисперсией;
б) отклонения Єї не должны коррелировать друг с другом;
в) отклонения є должны иметь показательный закон распределения.
Расстояние, измеряемое по принципу «средней связи», находится по формуле:
а) Ре (xi, xj ) =
1=1
б) pmm(S1 > Sm ) = mІП р(^ , x} );
в) pmax (S 1 > Sm ) = max s p(^ , x} );
д) pl,(m,g) = p(S1 > S(m,q)) = ap1m + Pftq + Wmq + 6(p1m plg X
е) pср.(S1, Sm ) = IZ p( xi , xj ).
11 nm xi«Slxj<=Sm
Кластерный анализ позволяет проводить:
а) группировку объектов;
б) группировку признаков;
в) группировку объектов и группировку признаков.
Если а + в> 1, то средние издержки, рассчитанные на единицу продукции:
а) растут по мере расширения масштабов производства;
б) убывают по мере расширения масштабов производства.
10. Исходя из априорных соображений значения а и в должны удовлетворять условиям:
а) 0<а<1 и 0< в<1;
б) -1<а<1 и -1< в<1;
в) -1<а<1 и 0< в<1.
ТЕСТ №5
Коэффициент корреляции считается значимым с вероятностью ошибки а если:
а) 1;набл по модулю будет больше, чем 1кр,
б) не имеет значения;
в) 1;набл по модулю будет меньше, чем 1;кр.
Матрица R парных коэффициентов корреляции является (выберите необходимые пункты):
а) обратной;
б) транспонированной;
в) симметричной;
г) положительно определенной.
3. В каких пределах изменяется множественный коэффициент корреляции:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) от 0 до 10.
4. В каких пределах изменяется коэффициент детерминации:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) от 0 до 10.
5. В хорошо подобранной модели остатки должны (выберите необходимые пункты):
а) иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией;
б) не коррелировать друг с другом;
в) иметь экспоненциальный закон распределения;
г) хаотично разбросаны;
д) форма и вид распределения не важен.
6. Неправильный выбор функциональной формы или объясняющих переменных называется:
а) ошибками спецификации;
б) ошибками прогноза;
в) гетероскедастичностью.
7. С какой целью производят нормирование признаков:
а) с целью устранения влияния различных единиц измерения;
б) с целью уменьшить признаковое пространство;
в) с целью упрощения расчетов.
8. Хемминговорасстояние вычисляется по формуле:
а) Ре (Хг, xj ) =
б) рВе (Хг, Xe )
1=1
1=1
9. Коэффициент а интерпретируется как:
а) эластичность по труду;
б) эластичность по капиталу;
в) эластичность замещения.
10. Для определения параметров и вида производственной функции пользуются
следующими видами данных:
а) динамическими рядами;
б) данными одновременных наблюдений (пространственной информацией);
в) динамическими рядами и пространственной информацией.
ТЕСТ №6
1. С помощью данной формулыr12/34 k =—. 12 можно определить:
а) множественный коэффициент корреляции (£-2)-го порядка между факторами
X1 и X2;
б) частный коэффициент корреляции (&-2)-го порядка между факторами X1 и X2;
в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.
2. С помощью данной формулы r 1/2 3 k =r 1 =
R
1 можно определить:
R11
а) множественный коэффициент корреляции (£-2)-го порядка между факторами
X1 и X2;
б) частный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2;
в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.
Коэффициент детерминации это:
а) квадрат парного коэффициента корреляции;
б) квадрат частного коэффициента корреляции;
в) квадрат множественного коэффициента корреляции.
Метод максимального правдоподобия лучше работает на…, где он, как правило, дает оценки с минимальной дисперсией:
а) больших выборках;
б) малых выборках;
в) любых выборках.
Модель вида Y = AKaLe носит название:
а) функции Энгеля;
б) функции Кобба Дугласа;
в) лог-линейной модели;
г) степенной модели.
Модель вида Yt = Y0(1+r/ носит название:
а) функции Энгеля;
б) функции Кобба Дугласа;
в) лог-линейной модели;
г) степенной модели.
В задаче классификации данное расстояние применяется в тех случаях, когда каждой компоненте xi вектора наблюдений Xудается приписать некоторый «вес «, пропорционально степени важности признака.
а) Хеммингово расстояние;
б) «взвешенное» Евклидово пространство;
в) обычное Евклидово расстояние.
Иерархические (древообразные) процедуры являются наиболее распространенными (в смысле реализации на ЭВМ) алгоритмами кластерного анализа, они бывают … типов:
а) 2;
б) 3;
в) 5;
г) любых.
Если производство, эффективность которого не зависит от масштабов и описывается производственной функцией Кобба Дугласа, то с ростом параметра а параметр в:
а) растет;
б) уменьшается;
в) остается неизменным;
г) растет или уменьшается.
10. Если производство, эффективность которого растет по мере его укрупнения, описывается производственной функцией Кобба Дугласа, то параметры модели удовлетворяют соотношению:
а) a+f<1;
б) a+f=1;
в) a+f=0;
г) a+f>1.
ТЕСТ №7
Уравнение My / X My = f3yX (X Mx) :
а) прямая регрессии y на x;
б) прямая регрессии X на y.
Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой:
а) коэффициент детерминации;
б) парный коэффициент корреляции;
в) частный коэффициент корреляции;
г) множественный коэффициент корреляции.
3. Оценки максимального правдоподобия и метода наименьших квадратов:
а) могут не совпадать;
б) совпадают;
в) никогда не совпадают.
В матричной форме регрессионная модель имеет вид: Y = Xf + є,
где Y:
а) матрица, размерности [n x (k+1)];
б) случайный вектор-столбец размерности (n x 1).
Какой смысл у коэффициентов регрессии в логарифмических регрессионных моделях:
а) показывают процентное изменение Y для данного процентного изменения X;
б) показывают абсолютное изменение Y для данного процентного изменения X;
в) показывают процентное изменение Y для данного абсолютного изменения X.
Изменяются ли свойства случайного отклонения при преобразовании уравнения регрессии:
а) да;
б) нет;
в) случайное отклонение не зависит от вида уравнения регрессии
В … процедурах начальным является разбиение, состоящее из n одноэлементных
классов, а конечным из одного класса; в наоборот (вставьте необходимые буквы):
а) агломеративных, дивизимных;
б) дивизимных, агломеративных;
в) дисконтированных, агломеративных.
Большинство программ, реализующих алгоритм иерархической классификации, предусматривает графическое представление результатов классификации в виде:
а) дендрограммы;
б) длок-схемы;
в) графиков показателей.
В задачах многомерной классификации объектов а, в, 8 и у являются:
а) числовыми коэффициентами;
б) коэффициентами эластичности.
10. В производственной функции Кобба-Дугласа параметр в соответствует коэффициенту:
а) корреляции;
б) вариации;
в) эластичности;
г) детерминации.
ТЕСТ №8
Величина, рассчитанная по формуле r = ——Х-У-, является оценкой:
sxsy
а) коэффициента детерминации;
б) парного коэффициента корреляции;
в) частного коэффициента корреляции;
г) множественного коэффициента корреляции.
Выборочный коэффициент корреляции r по абсолютной величине:
а) не превосходит единицы;
б) не превосходит нуля;
в) принимает любые значения.
В матричной форме регрессионная модель имеет вид: Y = Хв + є,
где X:
а) матрица, размерности [n x (k+1)];
б) случайный вектор-столбец размерности (n x 1).
В матричной форме регрессионная модель имеет вид: Y = Хв+ є,
где є :
а) матрица, размерности [n x (k+1)] ошибок наблюдений (остатков);
б) случайный вектор-столбец размерности (n x 1) ошибок наблюдений (остатков).
5. Отметьте основные виды ошибок спецификации:
а) отбрасывание значимой переменной;
б) добавление незначимой переменной;
в) низкое значение коэффициента детерминации;
г) выбор неправильной формы модели.
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена:
а) да;
б) нет;
в) ситуация не определена.
В задачах многомерной классификации объектов при а=в=-8=1/2и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
В задачах многомерной классификации объектов при а=в=8=1/2 и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
Получены две производственные функции Кобба Дугласа, имеющие равные значения параметров а и в, но различающиеся по параметру А. В каком случае первое производство более эффективно, чем второе:
а) Аі<А2;
б) Аі>А2;
в) Аі=А2;
г) Аі^А2.
10. В матричном виде структурная формы системы одновременных эконометрических уравнений имеет следующий вид: Byt + Txt = et:
а) да, это так;
б) нет;
в) данное уравнение не является структурной формой системы одновременных
эконометрических уравнений.
ТЕСТ №9
1. Есть ли необходимость при определении с надежностью у доверительного интервала для значимого парного или частного коэффициентов корреляции использовать Z-преобразование Фишера и предварительно устанавливать интервальную оценку для Z:
а) нет;
б) да;
в) ситуация не определена.
2. Для проверки значимости какого коэффициента
1 2
Fнабл = k 1
n ■
«(1 )
рассчитывают :
а) коэффициента детерминации;
б) парного коэффициента корреляции;
в) частного коэффициента корреляции;
г) множественного коэффициента корреляции.
Компоненты вектора є i :
а) независимы между собой;
б) зависимы между собой;
в) имеют нормальный закон распределения с нулевым математическим ожиданием (Мє i =0) и неизвестной дисперсией а2 (De i = а2).
На практике при построении регрессионных моделей рекомендуется, чтобы n превышало k не менее, чем:
а) в два раза;
б) в три раза;
в) не имеет значения.
Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению:
а) t-статистики;
б) F-статистики;
в) коэффициента детерминации.
Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения є i, а именно, к их математическому ожиданию Мєі и дисперсии Dei:
а) Мє=1; в) МЄі=0;
Dei=a2; Dei=a2;
б) Мєі=0; г) Мєі=1;
Dei=1; Dei=0
В задачах многомерной классификации объектов при а=в=8=1/2 и у=0 расстояние между классами определяется по принципу:
а) «дальнего соседа»;
б) «средней связи»;
в) «ближайшего соседа».
8. В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа «ближайшего соседа'»:
а) 2; в) 6;
б) 5; г) 7.
9. Если M є t1 є t2 = 0 при t1 ф 12 и t1,12 = 1,2,…, n, то случайные ошибки регрессии:
а) зависимы между собой;
б) независимы между собой;
с) ситуация не определена.
10. Если дисперсия ошибки постоянна Мє2 = а2 = а1 и не зависит от t и Xt,
то это свидетельствует о:
а) гомоскедастичности остатков;
б) гетероскедастичности остатков.
ТЕСТ №10
1. Известно, что при фиксированном значении X3 между величинами X1 и X2 существует положительная связь. Какое значение может принять частный коэффициент корреляции р12/3?
а) -0,8;
б) 0;
в) 0,4;
г) 1,3.
По результатам n=20 наблюдений получен частный коэффициент корреляции r12/3=0,8. Определите, чему при уровне значимости a=0,05 равна разность между наблюдаемым (r12/3) и критическим (гкр) значениями коэффициентов корреляции:
а) -0,513;
б) 0, 357;
в) 0, 700;
г) 0,133.
На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше , то
считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включать только один из показателей Xj или Xe. Вставьте недостающее значение.
а) 0,3;
б) 0,5;
в) 0,6;5;
г) 0,8;
д) 0,9;
е) другое значение.
4. Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез
H0: в=0, где j=1,2,…k, используют:
а) нормальный закон распределения;
б) t-критерий;
в) распределение Фишера.
5. Двойная логарифмическая модель является линейной относительно ее переменных:
а) утверждение истинно;
б) утверждение ложно;
в) утверждение не определено.
Коэффициенты двойной логарифмической модели определяют эластичность зависимой переменной по соответствующим определяющим переменным:
а) утверждение истинно;
б) утверждение ложно;
в) утверждение не определено.
В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа » дальнего соседа»:
а) 2; в) 6;
б) 5; г) 7.
В условиях гетероскедастичности случаных остатков оценки коэффициентов, полученные по методу наименьших квадратов, будут:
а) несмещенными; в) эффективными; д) надежными;
б) смещенными; г) неэффективными; е) ненадежными.
Условием гетероскедастичности является:
а) независимость значений = <J2t от t и xt;
б) зависимость значений Мє2 = a2t от t и xt;
в) ситуация не определена.
10. Систему yt = B~lTxt + B~1є( одновременных уравнений называют рекурсивной,
если выполняются следующие условия (выберите необходимые условия):
а) Матрица значений эндогенных переменных является нижней треугольной
матрицей, т. е. в ij = 0 при j>i и (3 ц = 1;
б) случайные ошибки независимы между собой, т. е. aii > 0, аij = 0 при j ,
где i,j=1,2,…,G;
в) каждое ограничение на структурные коэффициенты относится к отдельному
уравнению.
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели