
Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
Контроль вычисления приращений координат: d АВ 
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |
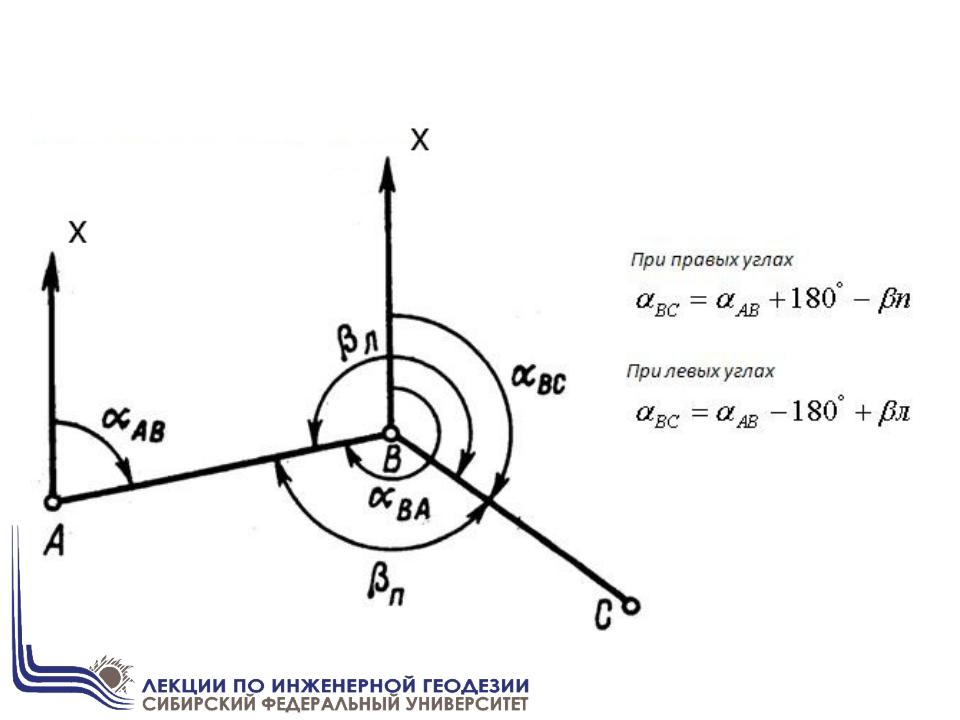
ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
8.1. Измерение длин линий мерными лентами и рулетками
Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.
Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.
Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.
Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.
Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.
Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.
Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:
l = l0 + Dl + a l0 (t— t0). (8.1)
Здесь l — длина ленты при температуре t; l0 — номинальная длина; Dl — поправка к номинальной длине при температуре компарирования t0 ; a — температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.
Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.
|
|
Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане). |
Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D — вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D1, то есть в створ точек C и B. Затем из точки С веху переносят в точку С1 и так далее до тех пор, когда обе вехи окажутся в створе AB.
Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n — число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).
Длину измеряют дважды — в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях — 1/1000). За окончательное значение принимают среднее.
Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.
Поправка за компарирование определяется по формуле
Dk = n Dl ,
где Dl — отличие длины ленты от 20 м и n — число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.
Поправка за температуру определяется по формуле
Dt = aD(t—t0)
где a — термический коэффициент расширения (для стали a = 0,0000125); t и t0 — температура ленты во время измерений и при компарировании. Поправку Dt учитывают, если ½t—t0½>10°.
Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D
d = D cosn , (8.2)
где n — угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где
Dn = d — D = D (cosn — 1) = -2D sin2 . (8.3)
По формуле (8.3) составляют таблицы, облегчающие вычисления.
Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.
Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.
Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.
Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами — глазным 1 и предметным 4.
|
|
|
Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона
Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 — 30¢.
Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.
Точность измерений лентой в разных условиях различна и зависит от многих причин — неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.
Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта di определяют по формуле
di = П — З,
где П и З — передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).
Если линия имеет наклон, необходимо учесть поправку
,
где h — превышение между концами пролёта, измеряемое нивелиром.
Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 — 1:10000.
Ошибки
при измерении лентой возникают из-за:
-
неравномерного
натяжения ленты; -
непостоянства
температуры воздуха; -
неточного
фиксирования концов каждой ленты; -
ошибок
от искривления или прогиба ленты; -
уклонения
ленты от створа; -
ошибок
при взятии отсчетов
Для
контроля лентой измеряют два раза в
прямом и обратном направлении.
Если
при благоприятных условиях погрешность
(разность между измерениями) не превышает
1:3 000, а при неблагоприятных 1:1 000, то за
длину линии принимают среднее
арифметическое значение из двух измерений
Поправку
за температуру, если она отличается от
температуры при которой выполнялось
компарирование рабочей ленты.
Линии
основной полигонометрии измеряются
инварными проволоками на весу по штативам
или кольям с постоянным натяжением в
10 кг
при помощи блочных станков и грузов,
подвешиваемых на концах проволок.
Остатки линий измеряются компарированной
рулеткой. Для тоннелей небольшой
протяженности допускается производить
измерение линий стальными компарированными
рулетками на весу с постоянным натяжением.
Измерение
линий проволоками или стальными рулетками
производится в прямом и обратном
направлениях. До начала работ и по
окончании их проволоки должны быть
прокомпарированы на стационарном
компараторе. В период полевых работ при
измерении линий проволоки компарируются
на полевом компараторе не реже одного
раза в декаду. При отсутствии полевого
компаратора проволоки сравниваются с
двумя нормальными проволоками (не
участвующими в работе). Длина проволоки
в результате компарирования должна
быть определена со средней квадратической
ошибкой не более ± 0,15 мм.
Пример
обработки результатов компарирования
рабочей проволоки на полевом компараторе
с контрольным измерением его длины
двумя нормальными проволоками приведен
в приложении 2-1.
Стальные
рулетки, применяемые при измерении
линий, компарируются не реже одного
раза в два месяца. Установка целиков
штативов или кольев в створе измеряемой
линии производится с помощью теодолита.
Температура
воздуха при работе с инварными проволоками
измеряется через 2 пролета, а при
пользовании стальной рулеткой — на
каждом пролете и отсчитывается до 1°.
Термометр должен находиться в одинаковых
условиях с мерным прибором. На пролете
производится три пары отсчетов. Наибольшие
расхождения разностей отсчетов (П-З) по
шкалам проволоки не должны превышать
0,5 мм.
Запись результатов измерений линий
производится в журнале линейных измерений
по форме, приведенной в приложении 2-2.
Расхождение в длине пролета, измеренного
в прямом и обратном направлениях, после
введения поправок за температуру не
должно превышать 0,5 мм.
Относительная
ошибка измерения линии, полученная по
результатам расхождения прямого и
обратного ходов, не должна превышать 1
: 70000. При длинах линий менее 200 м
расхождение в результатах измерения
прямого и обратного ходов не должно
превышать 3 мм.
Примечание.
При измерении линий в обратном направлении
лотаппараты необходимо поворачивать
на 180°.
Для
определения поправок за наклон мерного
прибора производится нивелирование
целиков штативов или кольев по двусторонним
рейкам — при одном горизонте, по
односторонним рейкам — при двух горизонтах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Относительная ошибка измерения расстояний мерной лентой или рулеткой?
Раздел
Технические дисциплины
Каждая работа проверяется на плагиат, на момент публикации
уникальность составляет не менее 40% по системе проверки eTXT.
Screenshot 2020-06-30 at 17.47.51
26.4 Кбайт
50 ₽
Относительная ошибка измерения расстояний мерной лентой или рулеткой?
a. 1:2000
b. 1:200
c. 1:300
d. 1:5000
Отчет по практике Практика
31
0 покупок
Тест Тест
45
+1
0 покупок
Тест Тест
40
+1
0 покупок
Тест Тест
59
+1
0 покупок
Тест Тест
16
+1
0 покупок
1.
ЛЕКЦИЯ №6
Измерение длин линий на местности.
1. Обозначение точек и вершин линий на
местности.
2. Виды измерений расстояний. Мера
длины, принятая в России.
3. Измерение расстояний мерными лентами
и рулетками.
4. Дальномеры геодезические.
2.
1. Обозначение точек и вершин линий на
местности.
Точки на местности закрепляются в
зависимости от необходимого срока
сохранности:
— деревянными кольями на 1 – 2 сезона
— деревянными столбами на 3-5 лет,
— металлическими трубами или
железобетонными центрами на длительные
сроки.
Линии для измерения расстояний обозначаются :
— вешками ( вехами) из дерева, пластмассы, металла
диаметром 3-4 см, длиной 2 м;
— заменками из стволов молодых деревьев.
3.
Створ – отвесная плоскость, проведенная через
две точки.
Вешение – установка вех или заменок по створу с
целью обозначения створа на местности
К
С
А1
А1
Д
В1
С
С2
С1
Д
Д2
Д1
В1
4.
2. Виды измерений расстояний. Мера длины,
принятая в России.
В зависимости от применяемых приборов
можно рассматривать следующие виды измерений
длин.
Непосредственное измерение при этом
необходимо учитывать линейное расширение этих
материалов при изменении температуры,
коэффициент линейного расширения t
6
1 , для инвара
для стали
12 10 град
t
64%Fe 36%Ni
t 0,5 10 град
6
1
Относительная ошибка определения длин этими
приборами из стали 1:1000 – 1:25000, из инвара –
до 1 : 1000000.
5.
Дальномерное определение (дальномеры).
Относительная ошибка оптическими дальномерами 1:200
– 1:2000; электронными дальномерами– до 1:400000 и
выше.
Косвенное определение применяют, когда
измерение расстояний лентой (через болото, через реку
летом и т.д.) невозможно — на местности строят некоторые
геометрические фигуры, в которых искомая длина
В
получается из вычислений с
β
река
d
φ
С
b1
β=180º-(α+φ)
α
А
использованием других элементов
данной
фигуры,
измеренных на местности и
расположенных в удобном для
измерений месте.
b2
D
d=b sinφ/sinβ
6.
Для измерения длин линий в России принята
метрическая система мер:
1
1метр
10000000
четверти меридиана.
С 1963 года 1 метр = 1650763,73 длин волн криптона
86 в вакууме (ошибка равна 0,001 микрона).
Компарирование мерного прибора- определение
длины мерного прибора сравнением его с
длинами, определенными точнее (эталонными).
При этом определяется систематическая ошибка за
компарирование к: насколько данный прибор длиннее
или короче его номинального значения в определенных
условиях (в России приборы компарируют при
температуре +20ºС ).
7.
3. Измерение расстояний мерными лентами и
рулетками
Мерные рулетки и ленты – простейшие
приборы для измерения расстояний, изготовленные
из полосовой стали, пластмассы или плотной ткани
шириной от 5 до 30 мм и толщиной 0,2 – 1,0 мм, с
обозначенными делениями от 1 до 100 мм. Длина
таких приборов от 1 до 100 метров. Высокоточные
мерные приборы изготавливаются из инвара
(мерные проволоки и рулетки).
Измерение расстояний рулетками ведется 20-м
отрезками, отсчет расстояний производится «на
глаз» с точностью 1 см, в комплект входят 6 мерных
шпилек для откладывании стометровых отрезков .
Нецелая лента в измеряемом расстоянии называется
«остаток» и оценивается по делениям ленты.
8.
Измеряемое расстояние ln вычислится как
n m 100 м n 20 м r
где m – число передач шпилек (число стометровых
пикетов),
n – число шпилек у заднего мерщика (число лент по
20 м.),
r – остаток (нецелая лента).
На местности чаще всего имеем наклонные
расстояния,
которые
необходимо
приводить
к
горизонтальным. Для этого измерения ведут либо
«уступами» — измерением горизонтальных отрезков, либо
измеряют наклонные расстояния и приводят их к
горизонту, определяя угол их наклона (теодолитом).
9.
При измерении расстояний мерной лентой Л3-20
(мерными рулетками) возникают следующие
ошибки.
1.Грубые ошибки
2.Систематические ошибки
— из- за компарирования ( l
k
— из-за температуры
kn
— поправка в длину
из n лент)
lt t lизм ерен tизм t ком п
t – коэффициент линейного расширения материала.
— из-за «ориентирования» (отклонение ленты от створа).
— из-за «провиса» и «прогиба» ленты из-за неровностей
местности.
3.Случайные ошибки: ф – из-за фиксации (из-за
отклонения шпилек от вертикального положения), р – из-за
неравномерности натяжения ленты (нормальное усилие
натяжения равно 100 Н).
10.
4. Дальномеры геодезические
Измерение расстояний дальномерами относятся к виду
непосредственных линейных измерений.
Виды дальномеров: оптические, механические, физические.
Нитяной дальномер в зрительной трубе.
δ
f
d’
d K n C
n
Когда C=0 , тогда
d K n
Отсчет по
нитяному
дальномеру — n;
постоянная
дальномера – С,
К — коэффициент
дальномера
d
При делениях рейки 1см и К=100 каждый сантиметр
дальномерного отсчета соответствует 100см – 1м
расстояния до рейки.
11.
Механические дальномеры основаны на
использовании трения скольжения и заранее известном
размере внешнего обода мерного колеса. Мерным
колесом может быть отдельное колесо со счетчиком
оборотов (и долей оборотов) и мерное колесо со
счетчиком, перемещающееся по натянутой проволоке
(длиномер).
Относительная ошибка определения длин
колеблется от 1:100 до 1:10000.
Физические методы определения расстояний
основаны на известной скорости распространения
электромагнитных волн ( радио и света)
V=(299792,5 0,4)км сек.
Приборы называются радио- и светодальномерами. В
настоящее время в большинстве светодальномеров для
формирования луча используют лазеры.


![inj_geo_1-245.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-245.jpg)
![inj_geo_1-247.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-247.jpg)
![inj_geo_1-248.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-248.jpg)

