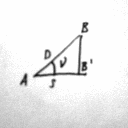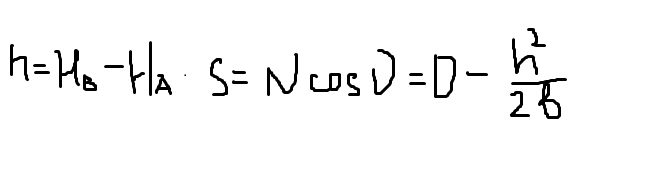Вследствие
неодинакового преломления в атмосфере
верхнего и нижнего лучей возникают
значительные ошибки определения
расстояния, особенно в жаркие Дни. В
такие дни можно измерять линии небольшой
протяженности (100—150 м) и использовать
при отсчетах верхнюю часть рейки. Кроме
того, причинами ошибок служат
неодновременность снятия отсчетов по
дальномерным нитям, отклонения рейки
от вертикального положения и др.
Относительная погрешность определения
расстояния нитяным дальномером при
благоприятных условиях составляет
1:300—1:400 при длине до 200—250 м, а при
неблагоприятных условиях может достигать
1:100.

10. Вычисление длины горизонтального проложения линии, измеренной светодальномером.
Необходимо
знать крутизну ската; следует измерить
ν
ВВ’=h(превышение
над точкой А).
относительная
ошибка
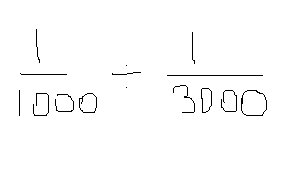
11. Точность измерения расстояний светодальномером.
Характеристики
точности измерения расстояний является
средняя квадратическая ошибка =. Для
получения величины в формуле воспользуемся
формулой оценки точности функции общего
вида. . Для вычисления ср. кв. ошибки
величины D1 применяем ту же самую формулу
оценки точности функции общего вида в
отношении выражения общего вида; будем
считать аргументами все величины, тогда
.

mv-
ошибка скорости распространения волны;
mN
– ср. кв. ошибка счета целого числа
полных периодов колебаний, зависит от
фазы колебаний;
mΔN
— ср. кв. ошибка фазового дальномера.
В
паспортных данных точность представлена
в виде уравнения регрессии m=a(мм)+b*D*10^-6.
12. Измерение превышений. Способы нивелирования.
На
местности закреплены точки А и В.
Уровенная поверхность — начальная (1).
У.п. т.А (2) и т.В (3). Построены отвесные
линии. Расстояние от начальной уровенной
поверхности до т.А – высота точки А, а
расстояние по отвесной линии от начальной
у.п. до т.В – есть высота т.В. Расстояние
между у.п. точек – есть превышение (h).
Численное значение высоты – отметка.
Измерять превышение необходимо с целью
получения отметок точек земной
поверхности. Знание отметок (и высот)
позволяет решить следующие практические
задачи: построить рельеф местности;
прикладные задачи строительства; задачи
трассирования (построение профилей
трасс); научные задачи представления
фигуры Земли. На территории России за
начало счета высот при построении
нивелирных сетей принимается Балтийская
система высот, ведет от нуля Кронштадского
футштока.
Существуют
следующие способы определения превышений
(нивелирования): 1) геометрическое
нивелирование; принцип: визирный луч
(ось) проходит параллельно у.п., визирная
ось горизонтальна в момент измерения
превышений, точность данного способа
определения отметок это мм и десятые
доли; 2) тригонометрическое нив.; наклонный
визирный луч (ось), точность сантиметровая;
3) барометрическое нив.; принцип зависимости
атмосферного давления от высоты точки
местности, точность дм; 4) гидростатическое
нив.; высота столба жидкости в сообщающихся
сосудах, точность мм; 5) автоматическое
нив.; способ основан на определении
превышений путем установки прибора на
движущийся предмет, точность мм, см. В
настоящее время используются первые
2.
13.
Сущность
и виды геометрического нивелирования.
Метод
определения высот точек местности и
превышений между ними называется
нивелированием. Различают геометрическое,
тригонометрическое, барометрическое,
механическое и гидростатическое
нивелирование. Геометрическое
нивелирование-это нивелирование
горизонтальным лучом визирования.
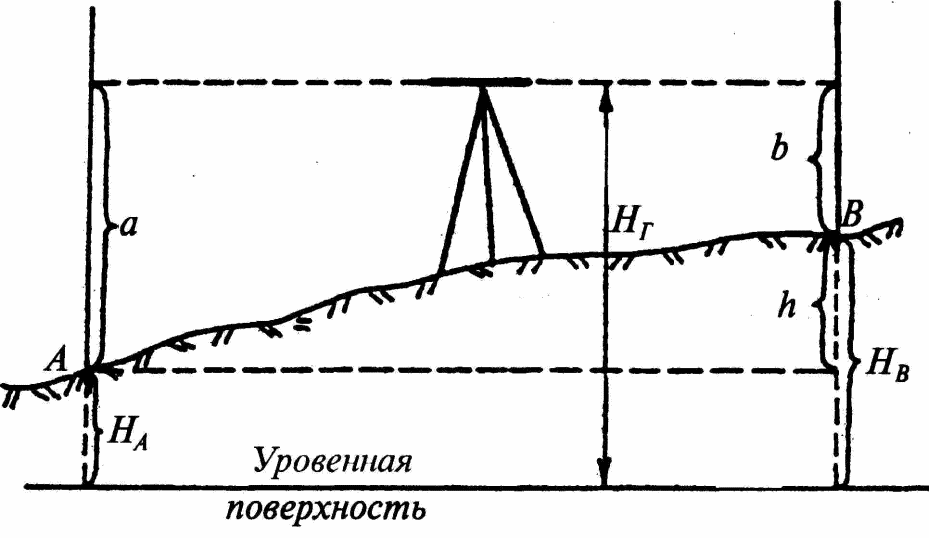
Сущность геометрического нивелирования
сводится к определению превышения точки
B над точкой А. (Нивелирование выполняется
на небольших участках земной поверхности,
поэтому у.п. можно принять за плоскость)
(рис) горизонтальным лучом визирования,
используя нивелир и рейки. Нивелир —
геодезический прибор, у которого в
момент отсчета по рейке визирная ось
устанавливается в горизонтальное
положение. Пусть при наведении зрительной
трубы на рейку, установленную в точке
А, получим отсчет по рейку a,
а
при визировании на рейку в точку В –
отсчет b;
тогда искомое превышение h=a-b.
Если
условно принять точку А задней, а точку
В передней, то превышение равно взгляд
назад минус взгляд вперед.
Если высота точки А над уровенной
поверхностью известна и равна HA,
то высоту точки B легко определить по
формуле: HB=HA+h.
То есть высота последующей точки хода
равна высоте предыдущей плюс превышение.
Высота горизонта прибора Hr=HA+a
или
Hr=HB+b.
Т.е. высота горизонта прибора равна
высоте точки плюс отсчет по рейке,
установленной в этой точке. Различают
следующие способы геометрического
нивелирования: нивелирование «из
середины», нивелирование «вперед» и
сложное (последовательное) нивелирование.
Основным
способом геометрического нивелирования
является нивелирование «из середины»
(см.
рис.73), когда превышение определяют по
формуле h=a-b.
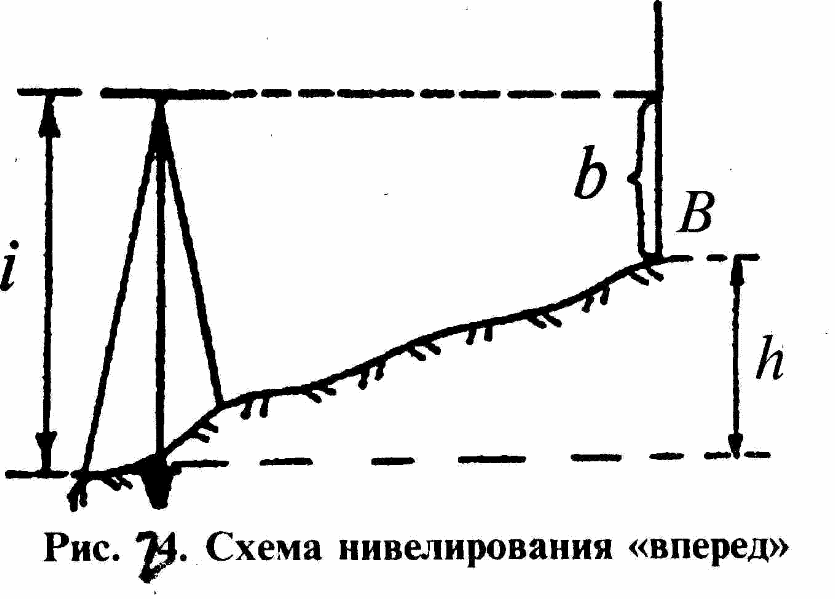
В
способе нивелирования «вперед» (рис
74) превышение определяется по формуле
h=i-b. Способ нивелирования «вперед»
применяется реже, чем способ нивелирования
«из середины» (в основном при выносе
высот точек в натуру). При нивелировании
«вперед» трудно измерять высоту прибора
с необходимой точностью и темпы работ
значительно снижаются. Кроме того, при
нивелировании «вперед» (как будет
доказано далее) необходимо учитывать
влияние кривизны Земли и вертикальной
рефракции (влияние искривления визирного
луча в вертикальной плоскости из-за
неодинаковой плотности слоев атмосферы).
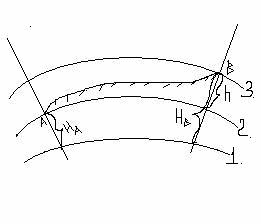
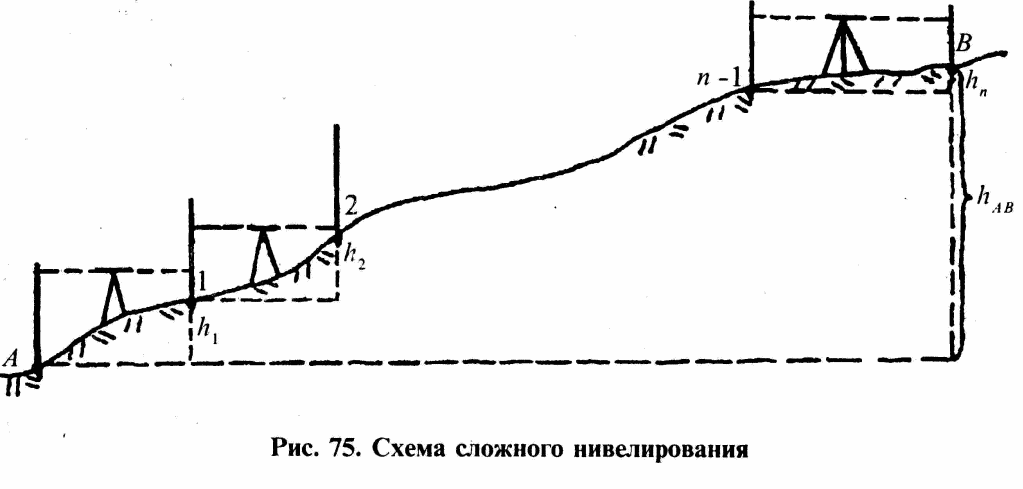
Когда
требуется определить разность высот
hAB
между удаленными друг от друга точками
А и В, применяют последовательное
(сложное) нивелирование (рис. 75).
Точки
установки реек 1,2….n-1, общие для двух
смежных станций прибора, называются
связующими точками. В этих точках рейка
сначала является передней, затем –
задней.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
02.05.201512.77 Mб26Glava_9.doc
- #
- #
- #
- #
- #
- #
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
какую информацию можно извлечь из относительной ошибки? например линейная погрешность или что то в этом роде. пожалуйста привидите пример.
#1
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.139
- Симпатии:
- 635
- Адрес:
-
Химки
1/2000 = 1 м на 2 км
То есть, линейная погрешность в 1 м на 2 км хода дает 1/2000.#2
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
это я знаю, а еще что нибудь из нее нельзя извлечь?
#3
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.139
- Симпатии:
- 635
- Адрес:
-
Химки
Попробуйте, может, получится;)
#4
-
Форумчанин
а вы что хотите извлечь то, вы расскажите причину столь странного интереса…
#5
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
нам преподаватель говорит, что относительная ошибка дает много информации, но не рассказывает, мол мы сами все знаем. а я кроме линейной погрешности ничего незнаю
#6
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
ну, скажем, на первый взгляд: в теодолитном ходе если угловая невязка в допуске а относительная ошибка слишком большая, то это логично говорит о том что у вас есть ошибка в длинах линий, если же вы проверили все длины линий и поняли что они все верны, а относительная ошибка хода по-прежнему вас не устраивает, то у вас ошибка как минимум в двух углах поворота, причем эти ошибки взаимно исключают друг друга.. (а преподаватели, к слову, пользуются относительной ошибкой часто для того что бы определить подгонялись ли углы в ходе или нет.. )
Случай с ошибкой в исходных данных тоже может быть выявлен таким образом..
#7
-
Форумчанин
Самую полезную для студента информацию несет не относительная ошибка, а абсолютные ошибки приращений координат. В случае, если в небольшом ходе Вы где-то пролетели с измерением длин линий лентой (на метр, двадцать метров, остаток до другого края ленты), ним легко узнать дир. угол линии, в которой сидит промах. Как — не скажу, сами догадайтесь.
И тогда в поисках ошибки не придется перемерять весь полигон.
#8
-
Форумчанин
Для теодолитного хода относительная ошибка вычисляется по формуле =√ΣΔX²+ ΣΔY²/P<1/2000, где ΣΔX, ΣΔY — суммы приращений координат, Р — периметр полигона, т.е. относительная ошибка позволяет определить еще и ошибку в вычислениях превышений.
Относительная ошибка как правило характеризует точность линейных измерений. Например, относительная ошибка нитяного дальномера составляет 1/300, ошибка измерения рулеткой 1/2000, значит линия в 50 м в первом случае будет определена с точностью ±17 см, а во втором ±2,5см#9
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
не понял.. а это то откуда?
#10
-
Форумчанин
- Регистрация:
- 30 ноя 2007
- Сообщения:
- 2.702
- Симпатии:
- 2.444
- Адрес:
-
Сибирь
А если промахнулись в двух линиях?
#11
-
Форумчанин
Извините приращений координат
#12
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
спасибо за участие в этом вопросе.
#13
-
Форумчанин
Тогда уже не узнать
Если трасса, и углы близки к 180 градусам, то тоже.
Но в теодолито-рулеточную эпоху этим методом пользовались частенько. Помогало.
#14
Поделиться этой страницей
Нитяной дальномер представляет собой один из видов оптического дальномера.
Состоит из зрительной трубы, в поле зрения которой размещена сетка нитей, состоящая из трех горизонтальных нитей, две из которых симметричны относительно средней, называемые даль-номерными, и схемы определения расстояния при помощи меры или базы. База является переносной рейкой с делениями. Прибор наводится на рейку, т. е. визируется, расстояние до базы пропорционально числу делений, которые видимы между нитями. Подразделяются на дальномеры с постоянной базой, за основу берется параллактический угол, и дальномеры с постоянным углом, где за основной измеряемый элемент берется длина базы. Для измерения наклонного расстояния нитяным дальномером используется база, в которой фигурирует коэффициент и постоянная дальнометра. После измерения наклонных расстояний рассматривается их разность, которая соответствует значениям постоянной дальномера. Относительная погрешность, показывающая точность определения расстояний нитяным дальномером, соответствует 1/300.
Нитяной лазерный дальномер с постоянным углом есть не что иное, как зрительная труба с наличием двух параллельных нитей в поле зрения. В качестве базы берется переносная рейка с равноотстоящими делениями, расстояние до базы соответствует пропорциональному числу делений рейки, наблюдаемых в зрительную трубу между нитями. Нитяным лазерным дальномером оснащается большое количество геодезических инструментов, например теодолиты и нивелиры, относительная погрешность нитяного дальномера такого типа находится в пределах 0,3—1%.