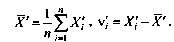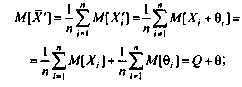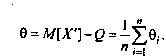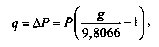Относительная величина систематической ошибки

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.

В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.

1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.

Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.

К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.

2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.

3.   Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.

4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.

По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.

Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.

Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.

Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и

удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.

Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.

Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.

В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.

Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х₂ и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,

Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,

Если систематические погрешности постоянны, т.е. 0_/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:

q = -Oi.

Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.

Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.

Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

где Р — измеряемое давление.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:

•   определения поправок;

•   зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;

•   связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).

Перечисленные погрешности малы, и поправки на них не вводятся.

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

 (1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

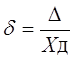
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

• первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
• вторые — старением элементов средства измерения.

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

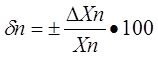
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

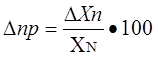
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.

Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Погрешности средств измерений подразделяются также на статические и динамические.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Статистическая обработка результатов химического эксперимента (ОФС.1.1.0013.15)

Государственная фармакопея 13 издание (ГФ XIII)

ОБЩАЯ ФАРМАКОПЕЙНАЯ СТАТЬЯ

Взамен ст. ГФ XI, вып.1

Требования данной общей фармакопейной статьи распространяются на методы, используемые при статистической обработке результатов химического эксперимента.

Обозначения:

А — измеряемая величина;

a — свободный член линейной зависимости;

b — угловой коэффициент линейной зависимости;

F — критерий Фишера;

f — число степеней свободы;

i — порядковый номер варианты;

L — фактор, используемый при оценке сходимости результатов параллельных определений;

т, п — объемы выборки;

P, P̅ — доверительная вероятность соответственно при дву- и односторонней постановке задачи;

Q 1, Qn — контрольные критерии идентификации грубых ошибок;

R — размах варьирования;

r — коэффициент корреляции;

s — стандартное отклонение;

s² — дисперсия;

s _o̅ — стандартное отклонение среднего результата;

s _o̅ ,% — относительное стандартное отклонение среднего результата (коэффициент вариации);

s lg — логарифмическое стандартное отклонение;

s 2lg — логарифмическая дисперсия;

S_lgo̅g — логарифмическое стандартное отклонение среднего геометрического результата;

S²₀ , S²_b , S²_a — общая дисперсия и дисперсия коэффициентов линейной зависимости;

t — критерий Стьюдента;

U — коэффициент для расчета границ среднего результата гарантии качества анализируемого продукта;

х, у — текущие координаты в уравнении линейной зависимости;

Хi, Yi — вычисленные, исходя из уравнения линейной зависимости, значения переменных х и у;

x, у — средние выборки (координаты центра линейной зависимости);

Xi, yi — i-тая варианта (i-тая пара экспериментальных значений х и у);

x ± Δx — граничные значения доверительного интервала среднего результата;

Xi ± Δх — граничные значения доверительного интервала результата отдельного определения;

d, А — разность некоторых величин;

α — уровень значимости, степень надежности;

Δх- полуширина доверительного интервала величины;

δ — относительная величина систематической ошибки;

ε, ε̅ — относительные ошибки соответственно результата отдельного

определения и среднего результата;

μ — истинное значение измеряемой величины;

Σ — знак суммирования (сумма);

X² — критерий хи-квадрат.

Примечание. Термины доверительная вероятность P и уровень значимости (степень надежности) α взаимозаменяемы, поскольку их сумма равна либо 1, либо 100 %.

Метрологические характеристики методов и результатов, получаемых при статистической обработке данных эксперимента, позволяют проводить оценку и сравнение, как методик аналитического эксперимента, так и исследуемых при таком эксперименте объектов, и на этой основе решать ряд прикладных задач.

1. Основные статистические характеристики однородной выборки и их вычисление

Проверка однородности выборки. Исключение выпадающих значений вариант. Термином «выборка» обозначают совокупность статистически эквивалентных найденных в эксперименте величин (вариант). В качестве такой совокупности можно, например, рассматривать ряд результатов, полученных при параллельных определениях содержания какого-либо вещества в однородной по составу пробе.

Допустим, что отдельные значения вариант выборки объема п обозначены через x_i (1 ≤ i ≤ n) и расположены в порядке возрастания:

Х₁; х₂; … x_i; …х_n-1; х_n. (1.1)

Результаты, полученные при статистической обработке выборки, будут достоверны лишь в том случае, если эта выборка однородна, т. е. если варианты, входящие в нее, не отягощены грубыми ошибками, допущенными при измерении или расчете. Такие варианты должны быть исключены из выборки перед окончательным вычислением ее статистических характеристик. Для выборки небольшого объема (n < 10) идентификация вариант, отягощенных грубыми ошибками, может быть выполнена, исходя из величины размаха варьирования R, см. уравнения (1.12), (1.13). Для идентификации таких вариант в выборке большого объема (n ≥ 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности, см. выражение (1.14).

В большинстве случаев среднее выборки х̅ является наилучшей оценкой истинного значения измеряемой величины μ, если его вычисляют как среднее арифметическое всех вариант:

  (1.2)

При этом разброс вариант х_i вокруг среднего х̅ характеризуется величиной стандартного отклонения s. В количественном химическом анализе величина s часто рассматривается как оценка случайной ошибки, свойственной данному методу анализа. Квадрат этой величины s² называют дисперсией. Величина дисперсии может рассматриваться как мера воспроизводимости результатов, представленных в данной выборке. Вычисление величин (оценок) s и s² проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений d_i и число степеней свободы (число независимых вариант) f:

Стандартное отклонение среднего результата S_0̅  рассчитывают по уравнению:

Отношение S_0̅  к x , выраженное в процентах, называют относительным стандартным отклонением среднего результата или коэффициентом вариации S_0̅ %.

Примечание 1.1. При наличии ряда из g выборок с порядковыми номерами k (1 ≤ k ≤ g) расчет дисперсии s целесообразно проводить по формуле:

При этом число степеней свободы равно:

где x_k — среднее k-той выборки;

n_k — число вариант в k-той выборке;

x_ik — i-тая варианта к-той выборки;

s²_k — дисперсия к-той выборки;

d_ik — отклонение i-той варианты к-той выборки.

Необходимым условием применения уравнений (1.8) и (1.9) является отсутствие статистически достоверной разницы между отдельными значениями S²_k. В простейшем случае сравнение крайних значений S²_k проводят, исходя из величины критерия F, которую вычисляют по уравнению (3.4) и интерпретируют, как указано в разделе 3.

Примечание 1.2. Если при измерениях получают логарифмы искомых вариант, среднее выборки вычисляют как среднее геометрическое, используя логарифм вариант:

Откуда

Значения s², s и S^—_x в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через S²_lg , S_lg и S_lgo̅

Пример 1.1. При определении содержания стрептоцида в образце линимента были получены следующие данные:

Как было указано выше, значения x̅, s², s и s_x̅ могут быть признаны достоверными, если ни одна из вариант выборки не отягощена грубой ошибкой, т. е. если выборка однородна.

Проверка однородности выборок малого объема (n < 10) осуществляется без предварительного вычисления статистических характеристик, с этой целью после представления выборки в виде (1.1) для крайних вариант x₁ и x_n рассчитывают значения контрольного критерия Q, исходя из величины размаха варьирования R:

Выборка признается неоднородной, если хотя бы одно из вычисленных значений Q превышает табличное значение Q (P, n), найденное для доверительной вероятности P̅ (см. табл. I приложения). Варианты х1 или xn, для которых соответствующее значение Q > Q (P, n), отбрасываются и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.12) и (1.13) с целью проверки ее однородности. Полученная в конечном счете однородная выборка используется для вычисления x̅, s², s и s_x̅.

Примечание 1.3.

При |x₁ – x₂| < |x₂ – x₃| и x_n – x_n-1 < |x_n-1 – x_n-2| уравнения (1.13 а) и (1.13 б) принимают соответственно вид:

Пример 1.2. При проведении девяти (n = 9) определений содержания общего азота в плазме крови крыс были получены следующие данные (в порядке возрастания):

По уравнениям (1.12) и (1.13 а) находим:

По табл. I приложения находим:

Q(9; 95%) = 0,46 < Q₁ = 0,51;

Q(9; 99%) = 0,55 < Q₁ = 0,51;

Следовательно, гипотеза о том, что значение x₁ = 0,62 должно быть исключено из рассматриваемой совокупности результатов измерений как отягощенное грубой ошибкой, может быть принята с доверительной вероятностью 95 %, но должна быть отвергнута, если выбранное значение доверительной вероятности равно 99 %.

Для выборок большого объема (n ≥ 10) проверку однородности проводят после предварительного вычисления статистических характеристик x̅, s², s и s_x̅. При этом выборка признается однородной, если для всех вариант выполняется условие:

| d_i | ≤ 3s. (1.14)

Если выборка признана неоднородной, то варианты, для которых | di | > 3s, отбрасываются как отягощенные грубыми ошибками с доверительной вероятностью Р > 99,0 %. В этом случае для полученной выборки сокращенного объема повторяют цикл вычислений статистических характеристик по уравнениям (1.2), (1.5), (1.6), (1.9) и снова проводят проверку однородности. Вычисление статистических характеристик считают законченным, когда выборка сокращенного объема оказывается однородной.

Примечание 1.4. При решении вопроса об однородности конкретной выборки небольшого объема также можно воспользоваться выражением (1.14), если известна оценка величины s, ранее найденная для данного метода измерения (расчета) вариант.

2. Доверительные интервалы и оценка их величины

Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины А, имеющей истинное значение μ, то среднее этой выборки x следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала x̅ ± ∆x̅, для которой с заданной доверительной вероятностью Р выполняется условие:

(x̅ — ∆x̅) ≤ μ ≤ (x̅ — ∆x̅) (2.1)

Следует отметить, что данный доверительный интервал не характеризует погрешность определения величины μ, поскольку найденная величина x̅ может быть в действительности очень близка к истинному значению μ. Полученный доверительный интервал характеризует степень неопределенности истинного значения μ величины А по результатам последовательных измерений выборки конечного объема п. Поэтому правильно говорить о «неопределенности результатов анализа» (которая характеризуется доверительным интервалом) вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется.

Расчет граничных значений доверительного интервала проводят по критерию Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально:

Здесь t (P, f) — табличное значение критерия Стьюдента (см. табл. II приложения).

Если при измерении одним и тем же методом двух близких значений А были получены две случайные однородные выборки с объемами п и m, то при m < п для выборки объема m справедливо выражение:

где индекс указывает принадлежность величин к выборке объема m или n.

Выражение (2.3) позволяет оценить величину доверительного интервала среднего x̅_(m), найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего x̅_(m) для выборки относительно малого объема m может быть сужен благодаря использованию известных величин, S_(n) и t (P, f_(n)) найденных ранее для выборки большего объема n (в дальнейшем индекс n будет опущен).

Примечание 2.1. Если n ≤ 15, а ((m + n) / n) > 1,5 , величины s и f целесообразно вычислять, как указано в примечании 1.1.

Подставляя n = 1 в выражение (2.2), или m = 1 в выражение (2.3), получаем:

x_i ± ∆x = x_i ± t (P, f) _* s (2.4)

Этот интервал является доверительным интервалом результата единичного определения. Для него с доверительной вероятностью Р выполняются взаимосвязанные условия:

x_i — ∆x ≤ μ ≤ x_i + ∆x (2.5)

μ — ∆x ≤ x_i ≤ μ + ∆x (2.6)

Значения ∆x̅ и ∆x из выражений (2.2) и (2.4) используют при вычислении относительных погрешностей отдельной варианты (ε) и среднего результата ( ε̅ ), выражая эти величины в %:

Пример 2.1. В результате определения содержания хинона в стандартном образце хингидрона были получены следующие данные (n = 10):

Расчеты по формулам (1.2), (1.4), (1.5), (1.6), (1.9) дали следующие результаты:

Доверительные интервалы результата отдельного определения и среднего результата при Р = 90 % получаем согласно (2.4) и (2.2):

Тогда относительные погрешности ε и ε‾ согласно (2.7) и (2.8), равны:

Обозначая истинное содержание хинона в хингидроне через μ, можно считать, что с 90 % доверительной вероятностью справедливы неравенства:

Примечание 2.2. Вычисление доверительных интервалов для случая, описанного в примечании 1.2, проводят, исходя из логарифмов вариант. Тогда выражения (2.2) и (2.4) принимают вид:

Потенцирование выражений (2.9) и (2.10) приводит к несимметричным доверительным интервалам для значений х и x_i.

При этом для нижних и верхних границ доверительных интервалов и x имеем:

3. Метрологическая характеристика метода анализа. Сравнение двух методов анализа по воспроизводимости.

С целью получения метрологической характеристики метода проводят совместную статистическую обработку одной или нескольких выборок, полученных при анализе образцов с известным содержанием определяемого компонента μ. Результаты статистической обработки представляют в виде табл. 1.

*- Графа 10 заполняется в том случае, если реализуется неравенство (3.2).

Примечание 3.1. При проведении совместной статистической обработки нескольких выборок, полученных при анализе образцов с разным содержанием определяемого компонента μ, данные в графах 1, 2, 3, 4, 9 и 10 табл. 1 приводят отдельно для каждой выборки. При этом в графах 2, 4, 5, 7, 8 в последней строке под чертой приводят обобщенные значения f, s², s, t, ∆x, вычисленные с учетом примечания 1.1.

Если для выборки объема m величина |μ – x̅| > 0, следует решить вопрос о наличии или отсутствии систематической ошибки. Для этого вычисляют критерий Стьюдента t:

Если, например, при Р = 95 % и f = m — 1, реализуется неравенство

t > t (P, f) (3.2)

то полученные данным методом результаты отягощены систематической ошибкой, относительная величина которой δ вычисляется по формуле:

Следует помнить, что если величина А определена как среднее x̅ некоей выборки, полученной эталонным методом, критерий Стьюдента t может рассчитываться по уравнению (4.5).

При сравнении воспроизводимости двух методов анализа с оценками дисперсий s²₁ и s²₂ (s²₁ > s²₂) вычисляют критерий Фишера F:

F = s²₁ / s²₂ (3.4)

Критерий F характеризует при s²₁ > s²₂ достоверность различия между s²₁ и s²₂. Вычисленное значение F сравнивают с табличным значением F (P, f₁, f₂) найденным при P = 99 % (см. табл. III приложения).

Если для вычисленного значения F выполняется неравенство:

F > F (P, f₁, f₂) (3.5)

различие дисперсий s²₁ и s²₂ признается статистически значимым с вероятностью Р, что позволяет сделать заключение о более высокой воспроизводимости второго метода. Если выполняется неравенство:

F ≤ F (P, f₁, f₂) (3.5a)

различие значений s²₁ и s²₂ не может быть признано значимым и заключение о различии воспроизводимости методов сделать нельзя ввиду недостаточного объема информации.

Примечание 3.2. Для случая, описанного в примечании 1.2, в табл. 1 вместо величин μ, x̅, s² и s приводят величины lgμ, lg x̅ _g, s²_lg и s_lg. При этом в графу 8, согласно примечанию 2.2, вносят величину ∆lg x, а в графу 9 — максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (3.1) и F — по уравнению (3.4).

Для сравнения двух методов анализа результаты статистической обработки сводят в табл.2.

Таблица 2 — Данные для сравнительной метрологической оценки двух методов анализа

Метрологическое сравнение методов анализа желательно проводить при μ₁ = μ₂, f₁ > 10 и f₂ > 10. Если точные значения μ1 и μ2 неизвестны, величины δ и tвыч не определяют.

Пример 3.1. Пусть для двух выборок аналитических данных (1 и 2), характеризующих, например, различные методы анализа, получены метрологические характеристики, приведенные в графах 1 — 10 табл. 3

Для заполнения графы 11 вычислим значения tвыч(1) и tвыч(2):

Поскольку t_выч(1) = 1,28 < t₁ (95 %, 20) = 2,09, гипотеза |μ₁ – x̅₂| ≠ 0 может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки. Напротив, поскольку t_выч(2) = 72,36 » t2 (95 %, 15) = 2,13, гипотезу |μ₂ – x̅₂| ≠ 0 приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2.

В графу 14 вносим вычисленное значение δ2:

Заполним графы 12 и 13:

Следовательно, при Р = 99 % гипотезу о различии дисперсий s²₁ и s²₂ следует признать статистически достоверной.

Выводы:

1. результаты, полученные первым методом, являются правильными, т. е. они не отягощены систематической ошибкой;
2. результаты, полученные вторым методом, отягощены систематической ошибкой;
3. по воспроизводимости второй метод существенно превосходит первый метод.

4. Метрологическая характеристика среднего результата. Сравнение средних результатов двух выборок.

Если с помощью данного метода анализа (измерения) следует определить значение некоторой величины А, то для полученной экспериментально однородной выборки объема m рассчитывают значения величин, необходимые для заполнения табл. 4. Так поступают в том случае, если применяемый метод анализа (измерения) не был ранее аттестован метрологически. Если же этот метод уже имеет метрологическую аттестацию, графы 2, 4, 5, 7, 8 и 9 табл. 4 заполняются на основании данных табл. 1, полученных при его аттестации. При заполнении табл. 4 следует при необходимости учитывать примечания 2.1 и 3.1.

Таблица 4 — Метрологические характеристики среднего результата

Таким образом, на основании выражения (2.1) для измеряемой величины А в предположении отсутствия систематической ошибки с вероятностью Р выполняется условие:

x — ∆x ≤ A ≤ x + ∆x , (4.1)

то есть величина А при отсутствии систематической ошибки лежит в пределах:

A = x ± ∆x . (4.2)

Примечание 4.1. В случае, предусмотренном в примечании 1.2, в графе 9 табл. 4 приводят величину ∆lg x̅, а каждую из граф 3, 10 и 11 разбивают на две (а, б). В графе 3а приводят значение x̅_g, в графе 3б – значение lg x̅ _g, в графах 10а и 10б — соответственно значения нижней и верхней границ доверительного интервала для xg (см. уравнения (2.11), (2.12)). Наконец, в графе 11 приводят максимальное по абсолютной величине значение ε̅ (см. уравнение (2.12 а)).

Если в результате измерений одной и той же величины А получены две выборки объема n 1 и n2, причем x1 ≠ x2, может возникнуть необходимость проверки статистической достоверности гипотезы:

x̅1 = x̅2, (4.3)

то есть значимости величины разности ( x̅1 — x̅2)

Такая проверка необходима, если величина А определялась двумя разными методами с целью их сравнения или если величина А определялась одним и тем же методом для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы (4.3) следует установить, существует ли статистически значимое различие между дисперсиями s²₁ и s²₂ . Эта проверка проводится так, как указано в разделе 3 (см. выражения (3.4), (3.5), (3.5 а)).

Рассмотрим три случая.

1. Различие дисперсий s²₁ и s²₂ статистически недостоверно (справедливо неравенство (3.5 а)). В этом случае средневзвешенное значение s₂ вычисляют по уравнению (1.7), а дисперсию s²_p разности |x̅₁ – x̅₂| — по уравнению:

Далее вычисляют критерий Стьюдента:

Если при выбранном значении Р (например, при Р = 95 %):

t > t (P, f), (4.6)

то результат проверки положителен — значение (xi — x2) является значимым и
гипотезу xi = x2 отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.

2. Различие значений s²₁ и s²₂ статистически достоверно (справедливо неравенство (3.5)). Если s²₁ > s²₂, дисперсию s²₁ разности (x̅₁ – x̅₂) находят по уравнению (4.7), а число степеней свободы по f ’ по уравнению (4.8):

Следовательно, в данном случае:

Вычисленное по уравнению (4.9) значение t сравнивают с табличным значением t (Р, f ‘ ), как это описано выше для случая 1.

Рассмотрение проблемы упрощается, когда n₁ ≈ n₂ и s²₁ >> s²₂. Тогда в отсутствие систематической ошибки среднее x̅₂ выборки объема n₂ принимают за достаточно точную оценку величины А, т. е. принимают x2 = μ. Справедливость гипотезы x₁ = μ, эквивалентной гипотезе (4.3), проверяют с помощью выражений (3.1), (3.2), принимая f1 = n 1 — 1. Гипотеза (4.3) отклоняется как статистически недостоверная, если выполнятся неравенство (3.2).

3. Известно точное значение величины А. Если A = μ, проверяют две гипотезы:

x̅₁ = μ (4.3 a) и x̅₂ = μ (4.3 б).

Проверку выполняют так, как описано в разделе 3 с помощью выражений (3.1) и (3.2) отдельно для каждой из гипотез. Если гипотезы (4.3 а) и (4.3 б) статистически достоверны, то следует признать достоверной и гипотезу (4.3). В противном случае гипотеза (4.3) должна быть отброшена.

Примечание 4.2. В случае, предусмотренном примечанием 1.2, при сравнении средних используют величины lgx̅_g , s²_lg и s_lg.

Когда разность (x 1 — x 2) оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних :

Пример 4.1. При определении содержания основного вещества в двух образцах препарата, изготовленных по разной технологии, получены метрологические характеристики средних результатов, приведенные в табл. 5.

Таблица 5 -Полученные данные метрологических характеристик средних результатов

Требуется решить, является ли первый образец по данному показателю лучшим в сравнении со вторым образцом. Поскольку

то согласно неравенству (3.5 а) статистически достоверное различие величин s²₁ и s²₂ отсутствует. Следовательно, гипотеза x̅₁ = x̅₂ (4.3) проверяется с помощью уравнений (1.7), (1.8), (4.4) и (4.5).

Следовательно, с доверительной вероятностью Р = 95 % гипотеза x̅₁ ≠ x̅₂ может быть принята. Однако с доверительной вероятностью Р = 99 % принять эту гипотезу нельзя из-за недостатка информации.

Если гипотеза x̅₁ ≠ x̅₂ принята, то определяют доверительный интервал разности генеральных средних (уравнение (4.10)):

5. Интерпретация результатов анализа

Оценка сходимости результатов параллельных определений. При рядовых исследованиях аналитик обычно проводит 2 — 3, реже 4 параллельных определения. Варианты полученной при этом упорядоченной выборки объема m, как правило, довольно значительно отличаются друг от друга. Если метод анализа метрологически аттестован, то максимальная разность результатов двух параллельных определений должна удовлетворять неравенству:

|x₁ — x_n| < L(P, m)_*s, (5.1)

где L (P, m) — фактор, вычисленный по Пирсону при Р = 95 %.

Если неравенство (5.1) не выполняется, необходимо провести дополнительное определение и снова проверить, удовлетворяет ли величина |x₁ — x_n| неравенству (5.1).

Если для результатов 4 параллельных определений неравенство (5.1) не выполняется, одна из вариант (х₁ или xn) должна быть отброшена и заменена новой. При невозможности добиться выполнения неравенства (5.1) следует считать, что конкретные условия анализа привели к снижению воспроизводимости метода и принятая оценка величины s применительно к данному случаю является заниженной. В этом случае поступают, как указано в разделе 1.

Определение необходимого числа параллельных определений. Если необходимо получить средний результат x̅ с относительной погрешностью ε̅ ≤ φ, причем метод анализа метрологически аттестован, необходимое число параллельных определений m находят учетом с уравнений (2.3) и (2.4):

Гарантия качества продукции. Предположим, что качество продукции регламентируется предельными значениями amin и amax величины А, которую определяют на основании результатов анализа. Примем, что вероятность соответствия качества продукта условию:

a_min < A < a_max, (5.3)

должна составлять P̅ %.

Пусть величину А находят экспериментально, как среднее выборки объема т, а метод ее определения метрологически аттестован. Тогда условие (5.3) будет выполняться с вероятностью P̅, если значение x̅ = A будет лежать в пределах:

Значения коэффициента U для вероятности P̅ = 95 % и P̅ = 99 % соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины А на практике следует ограничить значениями:

Наоборот, если заданы значения A_min и A_max, значения a_min и a_max, входящие в неравенство (5.3), могут быть найдены путем решения уравнений (5.6) и (5.7). Наконец, если заданы пары значений A min, amin и A max, amax, то уравнения (5.6) и (5.7) могут быть решены относительно т. Это может быть использовано для оценки необходимого числа параллельных определений величины А.

Примечание 5.1. В уравнениях (5.5), (5.6) и (5.7) величина коэффициента U(P) должна быть заменена величиной t (P, f), если значение f, определенное по уравнениям (1.4) или (1.8), меньше 15.

Примечание 5.2. Для случая, предусмотренного примечанием 1.2, описанные в разделе 5 вычисления проводят с использованием величин и т. п.

Пример 5.1. Рассмотрим данные табл. 3, относящиеся к выборке 1, как метрологическую характеристику используемого метода анализа.

a) Пусть amin = 98 %, amax = 100,50 %. Тогда для испытуемого образца продукта средний результат анализа A̅ при проведении трех параллельных определений (m = 3) должен находиться в пределах:

б) Реальный средний результат анализа образца испытуемого продукта А = 99 % (при т = 3). Тогда определение пределов amin и amax, гарантированно характеризующих качество данного образца с заданной доверительной вероятностью P, проводим, исходя из уравнения (5.6) или (5.7), полагая

Полученные оценки amin и amax близки к границам доверительного интервала
что соответствует примечанию 5.1.

6. Расчет и статистическая оценка параметров линейной зависимости (линейной регрессии)

При использовании ряда химических и физико-химических методов количественного анализа непосредственному измерению подвергается некоторая величина у, которая рассматривается как линейная функция искомой концентрации (количества) х определяемого вещества или элемента. Иными словами, в основе таких методов анализа лежит экспериментально подтвержденная линейная зависимость:

y = bx + a, (6.1)

где у — измеряемая величина;

х — концентрация (количество) определяемого вещества или элемента;

b — угловой коэффициент линейной зависимости;

а — свободный член линейной зависимости.

(Здесь b и а рассматриваются как коэффициенты (параметры) линейной регрессии y на x).

Для использования зависимости (6.1) в аналитических целях, т. е. для определения конкретной величины х по измеренному значению у, необходимо заранее найти числовые значения констант b и а, иными словами провести калибровку. Если константы зависимости (6.1) рассматриваются с учетом их физического смысла, то, при необходимости, их значения могут оцениваться с учетом доверительных интервалов.

Если калибровка проведена и значения констант а и b определены, величину X_i находят по измеренному значению y_i:

При калибровке величину х рассматривают как аргумент, а величину у — как функцию.

Наличие линейной зависимости между х и у целесообразно подтверждать расчетным путем. Для этого по экспериментальным данным, полученным при калибровке, оценивают достоверность линейной связи между х и у с использованием корреляционного анализа и лишь затем рассчитывают значения констант а и b зависимости (6.1) и их доверительные интервалы. В первом приближении судить о достоверности линейной связи между переменными х и у можно по эмпирической величине коэффициента корреляции r, который вычисляют по уравнению:

исходя из экспериментальных данных, представленных в табл. 6. Чем ближе значение |r| к единице, тем менее наблюдаемая линейная зависимость между переменными х и у может рассматриваться как случайная. В аналитической химии в большинстве случаев используют линейные зависимости, отвечающие условию |r| > 0,98, и только при анализе следовых количеств рассматривают линейные зависимости, для которых |r| > 0,90. При столь близких к 1 значениях величины |r| формальное подтверждение наличия линейной связи между переменными x и у проводить не следует.

Коэффициенты а и b и метрологические характеристики зависимости (6.1) рассчитывают с использованием регрессионного анализа, т. е. методом наименьших квадратов по экспериментально измеренным значениям переменной у для заданных значений аргумента х. Пусть в результате эксперимента найдены представленные в табл. 6 пары значений аргумента х и функции у.

Таблица 6. Значения аргумента х и функции у.

Если полученные значения коэффициентов а и b использовать для вычисления значений у по заданным в табл. 6 значениям аргумента х согласно зависимости (6.1), то вычисленные значения у обозначают через Y 1, Y2, … , Yi, … Yn. Разброс значений Yi относительно значений yi характеризуется величиной дисперсии s²₀, которую вычисляют по уравнению:

В свою очередь, дисперсии констант b и а находят по уравнениям:

Стандартные отклонения s_b и s_a и величины ∆b и ∆a, необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям:

Уравнению (6.1) с константами а и b обязательно удовлетворяет точка с координатами x и у, называемая центром калибровочного графика:

Наименьшие отклонения значений y_i от значений Y_i наблюдаются в окрестностях центра графика. Стандартные отклонения sy и sx величин Y и X, рассчитанных соответственно по уравнениям (6.1) и (6.2), исходя соответственно из известных значений х и у, определяются с учетом удаления последних от центра графика:

где y̅_j — среднее значение для n_j— вариант y, по которым вычислено искомое значение X.

При x = x̅ и y̅_j = y̅ выражения (6.16) и (6.17) принимают вид:

С учетом значений sy и sx могут быть найдены значения величин ∆Y и ∆X:

∆Y = s_y*t(P, f); (6.18)

∆X = s_x*t(P, f). (6.19)

Значения sx и ∆X, найденные при n_j = 1, являются характеристиками воспроизводимости аналитического метода, если х — концентрация (количество), а у есть функция х.

Обычно результаты статистической обработки по методу наименьших квадратов сводят в таблицу (табл. 7).

Таблица 7. Результаты статистической обработки экспериментальных данных, полученных при изучении линейной зависимости у = bx + a

Примечание 6.1. Если целью экспериментальной работы являлось определение констант b и a, графы 11, 12 и 13 табл. 7 не заполняются.

Примечание 6.2. Если y = b lg x + a, вычисления, описанные в разделе 6, выполняют с учетом примечаний 1.2 и 2.2.

Примечание 6.3. Сравнение дисперсий s²₀, полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 3 (см. выражения (3.4), (3.5) и (3.5 а)).

7. Расчет неопределенности функции нескольких случайных переменных

Описанные в разделах 1 — 6 настоящей общей фармакопейной статьи расчеты доверительных интервалов результатов методик анализа применимы лишь в том случае, если измеряемая величина (концентрация, содержание и т.д.) является функцией только одной случайной переменной. Такая ситуация обычно возникает при использовании прямых методов анализа (титрование, определение сульфатной золы, тяжелых металлов и т.д.). Однако большинство методик количественного определения в фармакопейном анализе являются косвенными, то есть используют стандартные образцы. Следовательно, измеряемая величина является функцией, как минимум, двух случайных переменных — аналитических сигналов (оптическая плотность, высота или площадь пика и т.д.) испытуемого и стандартного образцов. Кроме того, нередко возникает проблема прогнозирования неопределенности аналитической методики, состоящей из нескольких стадий (взвешивание, разбавление, конечная аналитическая операция), каждая из которых является по отношению к другой случайной величиной.

Таким образом, возникает общая проблема оценки неопределенности косвенно измеряемой величины, зависящей от нескольких измеряемых величин, в частности, как рассчитывать неопределенность всей аналитической методики, если известны неопределенности отдельных ее составляющих (стадий)?

Если измеряемая на опыте величина у является функцией п независимых случайных величин x_i, то есть:

y = f(x₁, x₂, … x_n), (7.1)

и число степеней свободы величин xi одинаково или достаточно велико (> 30, чтобы можно было применять статистику Гаусса, а не Стьюдента), то диспер­сия величины у связана с дисперсиями величин xi соотношением (правило рас­пространения неопределенностей):

Однако на практике степени свободы величин xt обычно невелики и не равны друг другу. Кроме того, обычно интерес представляют не сами дисперсии (стандартные отклонения), а доверительные интервалы, рассчитать которые, используя уравнение (7.2), при небольших и неодинаковых степенях свободы невозможно. Поэтому для расчета неопределенности величины у (∆у) предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча-Сатертуэйта.

7.1. Линейная модель

Если случайные переменные xi статистически независимы, то доверительный интервал функции ∆у связан с доверительными интервалами переменных ∆xi соотношением (доверительные интервалы берутся для одной и той же вероятности):

Данное выражение является обобщением соотношения (7.2).

В фармакопейном анализе измеряемая величина у представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разбавлений, оптических плотностей или площадей пиков и т.д.), т.е. (К — некая константа):

В этом случае соотношение (7.2) принимает вид:

где использованы относительные доверительные интервалы.

Соотношение (7.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин x_i. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины.

При проведении фармакопейного анализа в суммарной неопределенности (∆_As,r) анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки (∆_SP,r), неопределенность конечной аналитической операции (∆_FAO,r) и неопределенность аттестации стандартного образца (∆_RS,r). Величина (∆_RS,r) обычно столь мала, что ею можно пренебречь. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс «smp»), и для раствора сравнения (индекс «st»), выражение (7.5) можно представить в виде:

При этом каждое из слагаемых рассчитывается из входящих в него ком­понентов по формуле (7.5).

Если число степеней свободы величин xi одинаково или достаточно велико (> 30), выражение (7.5) дает:

Это же соотношение получается при тех же условиях и из выражения (7.2).

7.2. Подход Уэлча-Сатертуэйта

В этом подходе дисперсию величины у (s²_y) рассчитывают по соотношению (7.2), не обращая внимания на различие в степенях свободы (v_i) величин x_i. Для полученной дисперсии s²_y рассчитывают некое «эффективное» число степеней свободы veff (которое обычно является дробным), на основе которого затем по таблицам для заданной вероятности находят интерполяцией значения критерия Стьюдента. На основе его далее рассчитывают обычным путем доверительный интервал величины y (∆_у):

В фармакопейном анализе для определяемой величины у обычно выполняется уравнение (7.4). В этом случае в подходе Уэлча-Сатертуэйта соотношение (7.2) переходит в выражение (7.7), и соотношение (7.8) принимает более простой вид:

Здесь величина s_y,r⁴ рассчитывается из соотношения (7.7).

Подход Уэлча-Сатертуэйта обычно дает более узкие доверительные ин­тервалы, чем линейная модель. Однако он гораздо сложнее в применении и не позволяет выделить так просто неопределенности разных этапов (с последующими рекомендациями по их минимизации), как линейная модель в форме выражения (7.6).

При прогнозе неопределенности анализа используются генеральные величины (с бесконечным числом степеней свободы). В этом случае подход Уэлча-Сатертуэйта совпадает с линейной моделью.

ПРИЛОЖЕНИЯ

Таблица I. Критические значения контрольного критерия Q (Р, n)

Таблица II. Критические значения критерия Стьюдента

t = 1,958788 + 2,429953/f + 2,189891/f ² + 4,630189/f ³ + 1,398179/f ⁹ при P = 95%;

t = 2,5638 + 5,49059/f + 2,72654/f ² + 31,2446/f ³ + 21,6745/f ⁹ при P = 99%.

Таблица III. Критические значения критерия Фишера

F для P = 95 % напечатаны жирным шрифтом, а F для P = 99 % — обычным.

Содержание

• Как рассчитать систематическую ошибку?
• Постоянство и соразмерность
• Систематическая ошибка в химии
• Систематическая ошибка в физический
• Примеры eсистематическая ошибка
• Ссылки

В систематическая ошибка Это одна из составляющих ошибок эксперимента или наблюдений (ошибок измерения), которая влияет на точность результатов. Это также известно как детерминированная ошибка, поскольку в большинстве случаев ее можно обнаружить и устранить, не повторяя эксперименты.

Важной характеристикой систематической ошибки является постоянство ее относительной величины; то есть он не зависит от размера выборки или толщины данных. Например, предполагая, что его относительное значение составляет 0,2%, если измерения повторяются в тех же условиях, ошибка всегда будет оставаться 0,2%, пока не будет исправлена.

Как правило, систематическая ошибка возникает из-за неправильного обращения с приборами или из-за технической неисправности аналитика или ученого. Его легко обнаружить, если сравнить экспериментальные значения со стандартным или сертифицированным значением.

Примеры экспериментальной ошибки этого типа возникают, когда аналитические весы, термометры и спектрофотометры не откалиброваны; или в случаях, когда не выполняется хорошее чтение правил, верньеров, градуированных цилиндров или бюреток.

Как рассчитать систематическую ошибку?

Систематическая ошибка влияет на точность, в результате чего экспериментальные значения могут быть выше или ниже фактических результатов. Под реальным результатом или значением понимается результат, который был исчерпывающе проверен многими аналитиками и лабораториями и зарекомендовал себя в качестве эталона сравнения.

Таким образом, сравнивая экспериментальное значение с реальным, получается разница. Чем больше эта разница, тем больше абсолютное значение систематической ошибки.

Например, предположим, что в аквариуме насчитывается 105 рыб, но известно заранее или из других источников, что истинное число составляет 108. Таким образом, систематическая ошибка составляет 3 (108-105). Мы сталкиваемся с систематической ошибкой, если, повторяя подсчет рыб, мы снова и снова получаем 105 рыб.

Однако более важным, чем вычисление абсолютного значения этой ошибки, является определение ее относительного значения:

Относительная погрешность = (108-105) ÷ 108

= 0,0277

Если выражать в процентах, то получается 2,77%. То есть ошибка подсчета имеет вес 2,77% от истинного количества рыбы. Если в аквариуме теперь есть 1000 рыб, и он будет считать их с той же систематической ошибкой, то будет на 28 рыб меньше, чем ожидалось, а не на 3, как это происходит с меньшим аквариумом.

Постоянство и соразмерность

Систематическая ошибка обычно постоянная, аддитивная и пропорциональная. В приведенном выше примере ошибка 2,77% останется постоянной до тех пор, пока измерения будут повторяться в одних и тех же условиях, независимо от размера аквариума (уже соприкасающегося с аквариумом).

Также обратите внимание на пропорциональность систематической ошибки: чем больше размер выборки или толщина данных (или объем аквариума и количество рыб в нем), тем больше систематическая ошибка. Если в аквариуме теперь 3500 рыб, ошибка будет 97 рыб (3500 x 0,0277); абсолютная погрешность увеличивается, но ее относительное значение неизменно, постоянно.

Если число удвоить, на этот раз с 7000 рыб, то ошибка будет 194 рыбы. Таким образом, систематическая ошибка постоянна и пропорциональна.

Это не означает, что необходимо повторить подсчет рыбы: достаточно знать, что определенное количество соответствует 97,23% от общего количества рыбы (100–2,77%). Отсюда истинное количество рыбы можно рассчитать, умножив на коэффициент 100 / 97,23.

Например, если было подсчитано 5200 рыб, то фактическое количество было бы 5 348 рыб (5200 x 100 / 97,23).

Систематическая ошибка в химии

В химии систематические ошибки обычно возникают из-за неправильного взвешивания из-за некалиброванных весов или из-за неправильного считывания объемов стеклянных материалов. Хотя они могут показаться не такими, как это, они влияют на точность результатов, потому что чем их больше, тем больше их негативных эффектов.

Например, если весы плохо откалиброваны, и при определенном анализе необходимо провести несколько взвешиваний, то окончательный результат будет все дальше и дальше от ожидаемого; это будет более неточно. То же самое происходит, если анализ постоянно измеряет объемы бюреткой, показания которой неверны.

Помимо весов и стеклянных материалов, химики также могут ошибаться в обращении с термометрами и pH-метрами, в скорости перемешивания, во времени, необходимом для протекания реакции, в калибровке весов. спектрофотометры, если предполагается высокая чистота образца или реагента и т. д.

Другие систематические ошибки в химии могут быть связаны с изменением порядка добавления реагентов, нагревом реакционной смеси до температуры выше, чем рекомендованная методом, или неправильной перекристаллизацией продукта синтеза.

Систематическая ошибка в физический

В физических лабораториях систематические ошибки носят еще более технический характер: любое оборудование или инструмент без надлежащей калибровки, неправильное поданное напряжение, неправильное расположение зеркал или деталей в эксперименте, добавление слишком большого момента к объекту, который должен упасть. из-за эффекта гравитации, среди других экспериментов.

Обратите внимание на то, что есть систематические ошибки, которые происходят из инструментального несовершенства, а другие, скорее, операционного типа, являются результатом ошибки со стороны аналитика, ученого или отдельного человека, который выполняет какое-либо действие.

Примеры eсистематическая ошибка

Ниже будут упомянуты другие примеры систематических ошибок, которые не обязательно должны происходить в лаборатории или в научной сфере:

— Поместите булочки в нижнюю часть духовки, поджаривая их больше, чем хотелось бы.

-Плохая осанка при сидении

-Закройте горшок для мокко только из-за недостатка прочности

-Не очищайте пароварки кофемашин сразу после текстурирования или нагрева молока.

-Используйте чашки разных размеров, когда вы следуете или хотите повторить определенный рецепт

-Хотите дозировать солнечную радиацию в тенистые дни

— Выполняйте подтягивания на перекладине, подняв плечи к ушам.

-Играйте несколько песен на гитаре без предварительной настройки струн

-Жарить оладьи с недостаточным количеством масла в казане

-Проведите последующее объемное титрование без повторной стандартизации раствора титранта

Ссылки

1. Дэй Р. и Андервуд А. (1986). Количественная аналитическая химия. (Пятое изд.). ПИРСОН Прентис Холл.
2. Хельменстин, Энн Мари, доктор философии (11 февраля 2020 г.). Случайная ошибка vs. Систематическая ошибка. Получено с: thinkco.com
3. Bodner Research Web. (н.д.). Ошибки. Получено с: chemed.chem.purdue.edu
4. Elsevier B.V. (2020). Систематическая ошибка. ScienceDirect. Получено с: sciencedirect.com
5. Сепульведа, Э. (2016). Систематические ошибки. Получено из Physics Online: fisicaenlinea.com
6. Мария Ирма Гарсиа Ордас. (н.д.). Проблемы с ошибкой измерения. Автономный университет штата Идальго. Получено с: uaeh.edu.mx
7. Википедия. (2020). Ошибка наблюдения. Получено с: en.wikipedia.org
8. Джон Спейси. (2018, 18 июля). 7 видов систематической ошибки. Получено с: simplicable.com