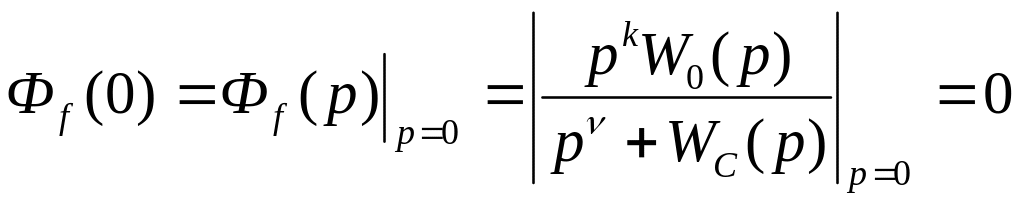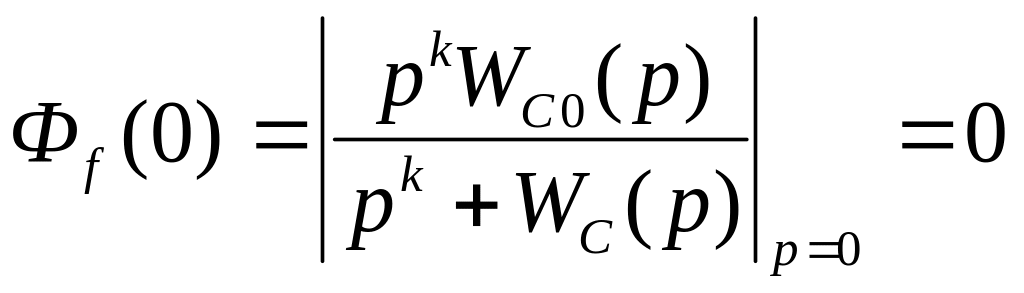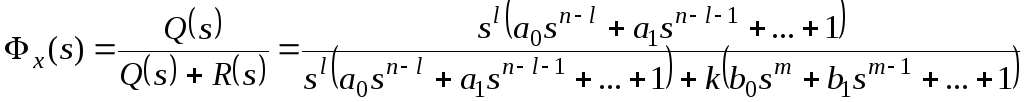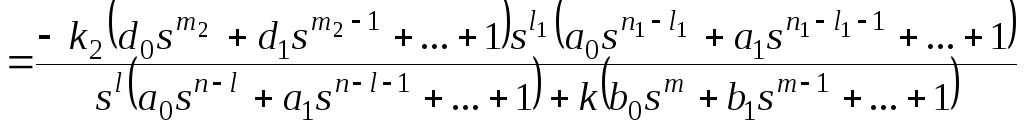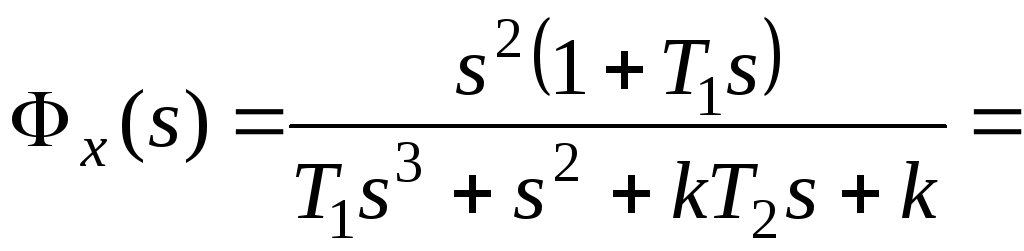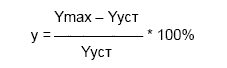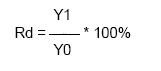Относительное значение установившейся ошибки регулирования называется - Не ошибается лишь тот, кто ничего не делает!

Статические
и астатические системы.

В САР могут быть
звенья, у которых нет установившихся
соотношений между входными и выходными
величинами. Такие звенья не имеют
статической характеристики и называются
астатическими(интегрирующее звено).
При этом следует отметить, что в
астатических звеньях в установившихся
режимах существуют однозначные
зависимости производных выходной
величины от различных постоянных
значений входной величины. Как было
показано ПФ-я остаточной системы может
быть представлена в виде:

(1)

—
порядок астатизма,

— ПФ статической части системы(без
интегрирующих звеньев). При

(система является статической), иногда
говорят, что она обладает астатизмом
«0»- го порядка. Рассмотрим САР, состоящую
из ОР с ПФ

и регулятора с ПФ

(рис. 16)

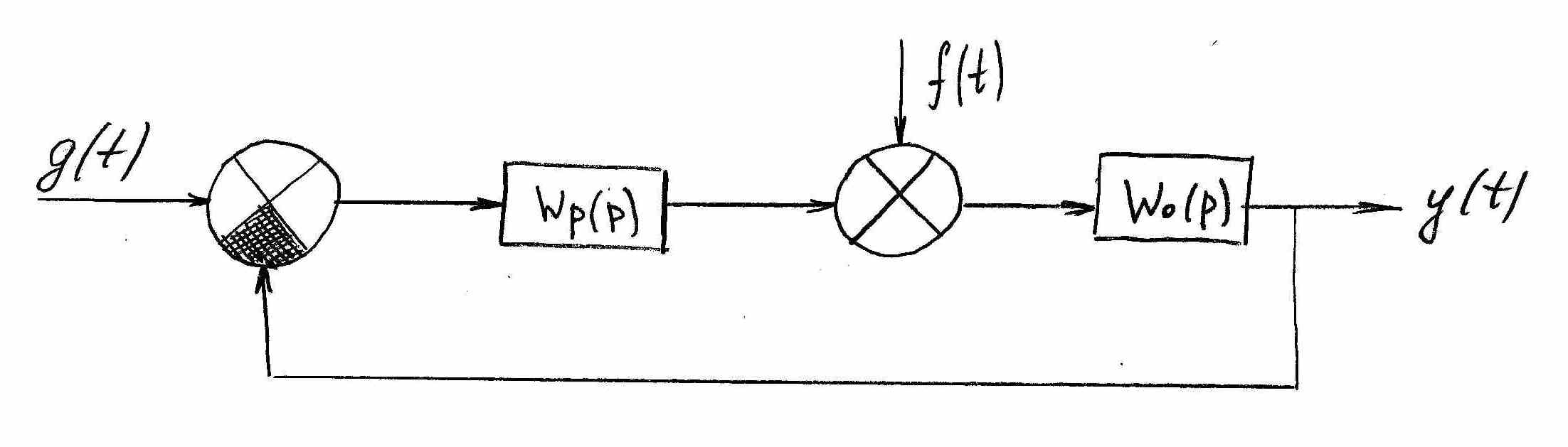
Рисунок 16

;
(*)

ОР и регуляторы,
которые могут быть представлены в виде
астатического звена или соединения,
называются астатическими, иные они
называются статическими. Иногда
астатические объекты называются
объектами без самовыравнивания,
статические – с самовыравниванием.
Физически
эти названия объясняются тем, что в
астатических объектах при поступлении
на их входы постоянного по величине
воздействия значение регулируемой(выходной)
величины теоретически возрастает до
бесконечности (интегрирующего звена

).
В статических
объектах при аналогичном условии
выходная величина увеличивается только
до некоторого постоянного значения,
т.е. происходит стабилизация(самовыравнивание)
выходной величины на новом уровне,
который осуществляется самим объектом
даже при отсутствии регулятора
(апериодическое звено 1-го порядка). Так
как САР имеет различные структурные
схемы относительно задающего и возмущающих
воздействий, то с точки зрения статизма
и астатизма их необходимо оценивать
относительно этих воздействий раздельно.

В установившихся
режимах оценка качества регулирования
проводится по величине установившейся
ошибки (*).Чем меньше ошибка, тем выше
качество системы при влиянии на систему
задающего и возмущающего воздействий:

,
(2)

где

и

.

В соответствии с
(1) ПФ объекта и регулятора:

где e,k
– порядки астатизма объекта и регулятора;

— ПФ статической части объекта и
регулятора. Тогда
ПФ замкнутой системы по ошибке:

где

—
порядок астатизма системы;

_.

_{ПФ замкнутой

системы по возмущению:}

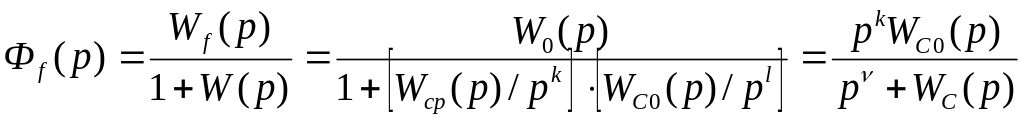
_{Определение

установившихся ошибок при различных

воздействий:}

_{А) оба воздействия

являются ступенчатыми функциями.}

,

,
;

,
,
;

Установившаяся
ошибка возникающая при этих воздействиях
называют статической ошибкой, то есть

В этом случае согласно
формуле (2):

;

Следовательно,
установившаяся ошибка вызвана тем или
иным воздействием зависит не только от
величины этого воздействия, но и от
начального значения соотношений ПФ, то
есть при

.

Если

,
то

и система является астатической по
каналу возмущающего воздействия. Если

,
то

система является астатической по каналу
возмущающего воздействия. Если

или

,
то система является статической по
соответствующему каналу.

Рассмотрим
следующие 4 случая:

Регулятор
астатический (
)
, объект астатический (
)
,

,
тогда

;

,
то есть система является статической
по обоим каналам.

Регулятор
астатический(

)
,объект статический (

),

,тогда

;

Система по обоим
каналам является астатической.

Регулятор
статический (
),
объект астатический (

),

,
тогда

;

,
где

,

— коэффициенты передачи объекта и
регулятора.

Таким образом,
система является астатической по каналу
задающего воздействия и статической
по каналу возмущающего воздействия.

Объект
и регулятор статические (
),
тогда

;

Составляющая
ошибки

практически всегда может быть сведена
к 0 за счет использования неединичной
ОС. Она равна
нулю в системе автоматической стабилизации,
у которой

.

Относительное
значение установившейся ошибки называется
коэффициентом статизма системы по
соответствующему каналу.

— коэффициент
статизма системы по задающему воздействию;

— коэффициент
статизма системы по возмущающему
воздействию.

Таким
образом система с единичной ОС является
статической по обоим каналам.

Полученные результаты представляются
в виде таблицы.

№	Регулятор	Объект
1	А	А	А	А
2	А	С	А	А
3	С	А	А	С
4	С	С	С	С

Выводы:

Если
регулятор астатический, то независимо
от ОР система по обоим каналам
астатическая.
Если
регулятор статический, то независимо
от ОР система статическая по каналу
возмущающего воздействия. Астатизм по
каналу задающего воздействия определяется
астатизмом объекта.

Б) Задающее воздействие
имеет вид линейной функции

,
где

—
скорость изменения задающего воздействия

Преобразуя по
Лапласу, имеем:

,

,
тогда

Такой режим применяется
в следящих системах. Очевидно,
что составляющая

имеет смысл только для системы с
астатизмом 1-го порядка, то есть

.

В
этом случае она называется скоростной
ошибкой или ошибкой по скорости ,т.к
пропорциональна скорости изменения
задающего воздействия.

,где К=

— коэф-т передачи разомкнутой системы
назв. добротностью системы по скорости.

Ошибка
по скорости свидетельствует о том, что
в установившемся режиме выходная
величина будет изменяться со скоростью
равной скорости изменения задающего
воздействия, но с некоторым отставанием
во времени.

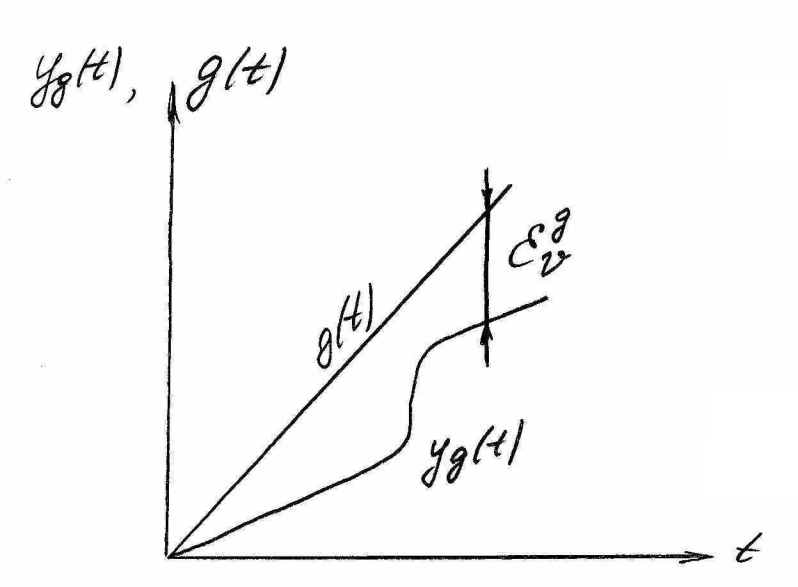
Чем
больше добротность системы по скорости
,тем меньше будет отставать система при
отростке входного воздействия. ,тем
выше качество системы .В статической
системе ,при астатизме

=0
.

Вторая
составляющая ошибки

представляет собой статическую ошибку
,т.к f(t)=
=const

Т.о
в этом типовом режиме

В)
Задающее воздействие имеет вид
квадратичной функции:

,
где

а
=const – ускорение изменения
задающего воздействия F(t)=

1(t)
. Преобразуя по Лапласу
.

Этот
режим имеет смысл только для следящих
систем и систем программного регулирования,
обладающих астатизмом

>1.В этом случае

Это
составляющая имеет смысл с =1 в этом
случае оте назв. ошибкой по ускорению
.

К=

— добротность по ускорению,

Чем
выше

,тем лучше качество САР.В этом типовом
режиме установившееся ошибка
.

С
помощью теоремы о конечном значении
легко показать ,что в системе с =2
статическая скоростная ошибка от
задающего воздействия=0.

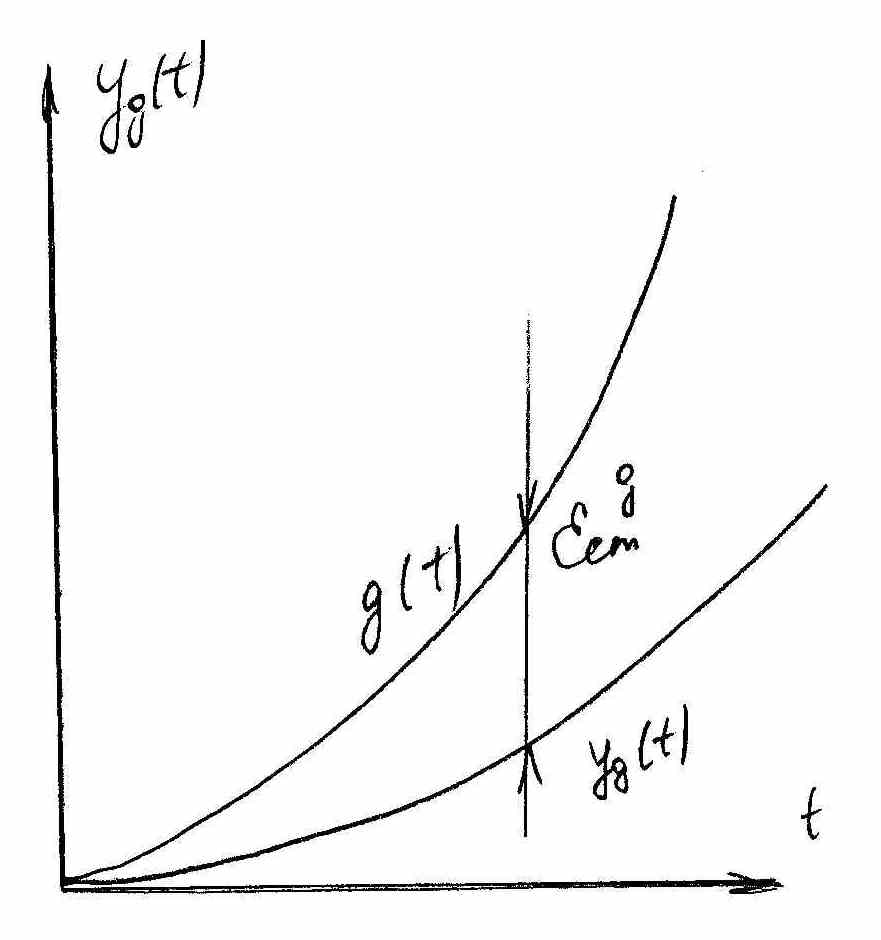
Г)
Задающее воздействие имеет вид
синусоидальной функции.

G(t)=Gmax*
sinwgt

Возмущающее
воздействие изменятся в этом режиме
,либо оставаться постоянным. Рассмотрим
ошибку только от задающего воздействия
,тогда её изображение

(3)

Очевидно
,что в установившемся режиме ошибка
будет также изменятся по синусоидальному
закону с той же частотой

Eуст(t)=Emax
sinn(wgt+ф)

В
этом режиме точность системы обычно
оценивается по амплитуде ошибки, которая
может быть найдена из (3) путем подстановки

P=jwg

Обычно
Gmax

Emax
поэтому модуль знаменателя больше 1 , а
следовательно с большей точностью
можно принять , что

, где

A(wg)-АЧХ
разомкнутой системы.

Из
этого уравнения следует требования и
АЧХ разомкнутой системы ,при достигается
требуемая точность регулирования.

или 20lgA(wg)=L(wg)

20lgGmax/Emax

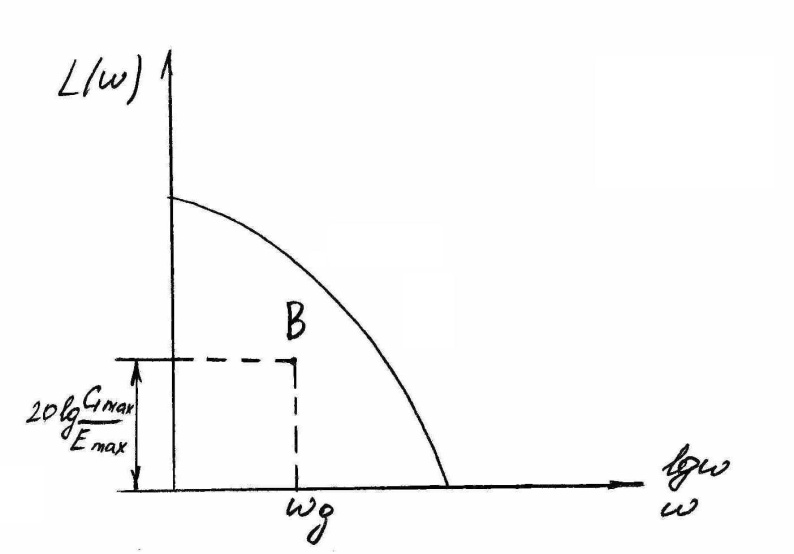
Последнее
выражение ограничивает местоположение.
ЛАХ около точки .Требования по точности.

Д)
Задающее воздействие имеет вид
произвольной функции .Если g(t)
имеет произвольную , то достаточно
плавную форму изменения, то для оценки
точности системы в установившемся
режиме существенное значение имеет
лишь конечное число n-производных

Установившееся
ошибка при задающем воздействии g(t)
может быть определена с помощью интеграла
свертки. Eуст(t)=

,где

-весовая функция ошибки. Преобразуем
это выражение .Для этого разложим функцию
g(t-r)
на интервале от 0 до в ряд Тейлора

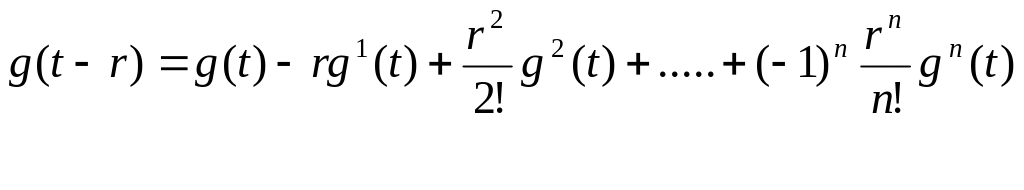
Подставляя
это выражение в формулу свертки будем
иметь

Eуст(t)=

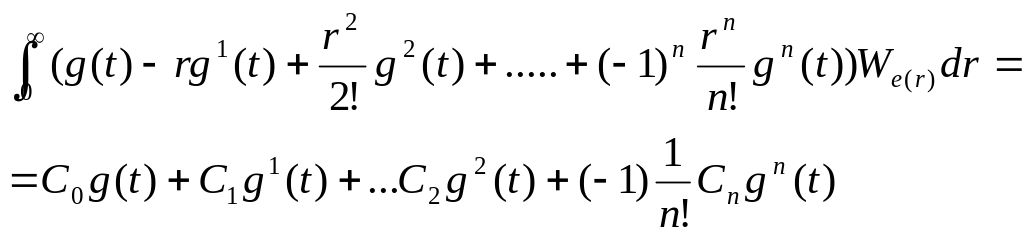
,где

Коэффициенты
определяющие величину ошибки назв.
коэффициентами ошибок. Эти коэф-ты
могут быть найден только с помощью
выражения (3) и с помощью ПФ-и ошибки.

(6)

Из
операционного исчисления известно ,
что условие P=0 соот-т времени t= ,т.е
установившемуся значению функции
времени .Полагая в уравнение (6) р=0 находим
коэффициент ошибки .

Продифференцировав
уравнение (6) по переменной р n-раз и
положив р=0 получим следующие коэффициенты
ошибок.

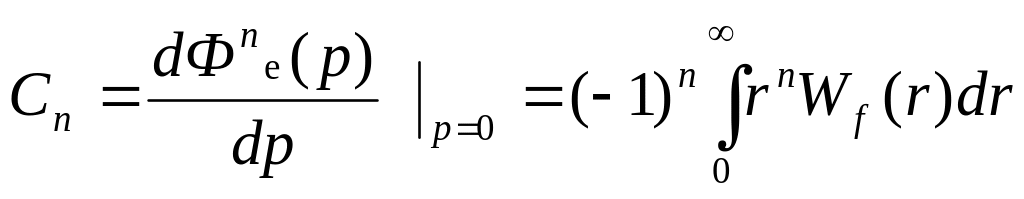
Преобразуя
уравнение (4) при нулевых начальных
условиях получим ,изображение ошибки.

Выражение
(7) представляет собой разложение функции
в ряд Макларена.

Учитывая,
что ПФ ошибки представляет собой
дробно-рациональную функцию

,то
коэф-ты ошибок можно определить путем
деления числителя N(р) на полином
знаменателя D( р) и сравнения получающегося
ряда с выражением (7).

Выше
было показано, что ПФ ошибки может быть
представлена в виде

.Тогда
для статических систем(

=0) ПФ ошибки

коэф-т ошибки .Т.о коэф-т определяет
астатизм системы ,а следовательно
статическую ошибку
.

выше систем с астатизмом 1-го порядка

Т.о
коэф-т хар-т ошибку системы по скорости.

Для
астатических систем 2-го порядка

,откуда

-характеризует
ошибку по ускорению.

Т.о
повышение порядка астатизма соответствует
повышению точности САР.

Сравним
точности статической и астатической
систем.Пусть на вход систем поступает
сигнал

, тогда установившееся ошибка будет
определятся :для статической систем
.

Для
астатической системы 1-го порядка

Для
системы с астатизмом 2-го порядка

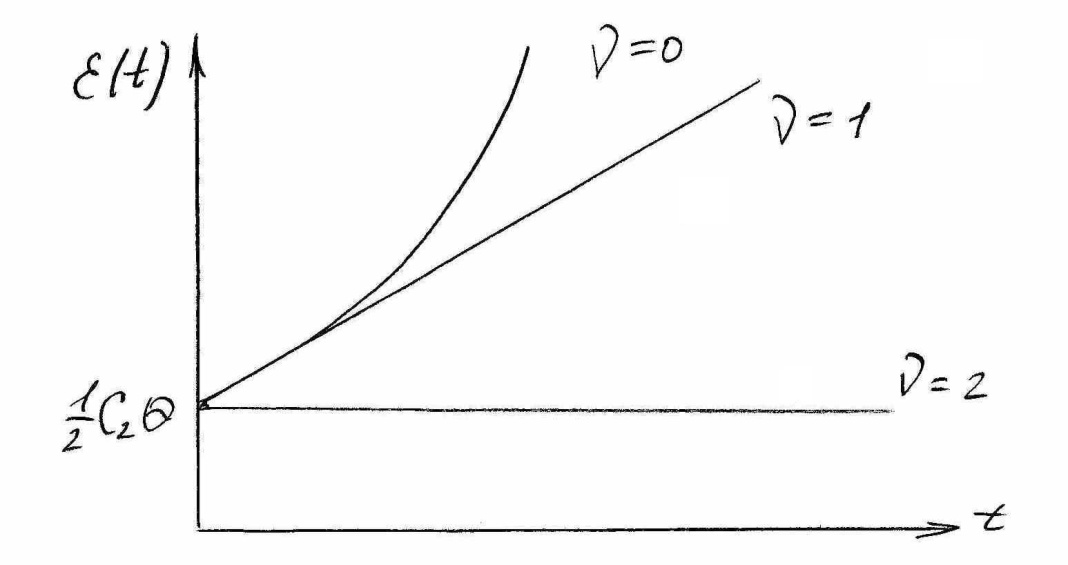
Рисунок 19

Как
видно из рисунка 19 положительную
точность имеет САР с астатизмом 2-го
порядка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок

Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.

Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:

и так далее.

При наличии
нескольких воздействий на линейную
систему для определения x_уст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:

где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.

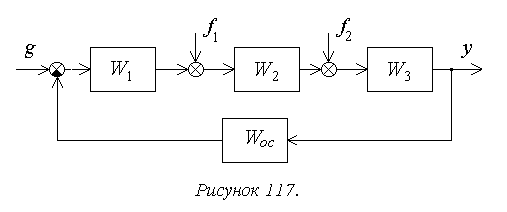
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).

В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.

Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке

при известном изображении задающего
воздействия G(s):

где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117

где

— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.

Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:

В результате:

Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения

при известном изображении возмущающего
воздействия F(s):

где _f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,

;

W_f(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).

Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.

Для f₁:

Для f₂:

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):

где k=k₁k₂k₃
– коэффициент передачи разомкнутой
системы.

Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.

При

получим:

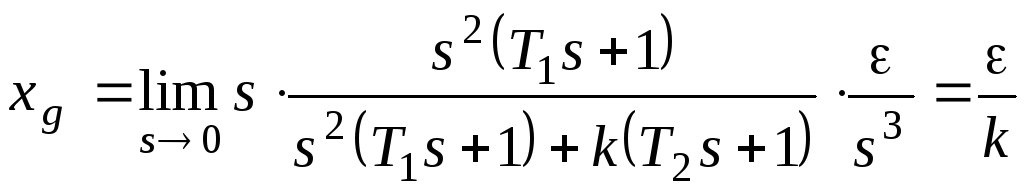
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.

Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.

Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.

Рассмотрим
установившуюся ошибку от возмущения
f₁:

где

– коэффициент передачи разомкнутой
системы по возмущению f₁.

При

получим:

При

получим тот же результат.

Отметим, что по
возмущению f₁
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.

Рассмотрим
установившуюся ошибку от возмущения
f₂:

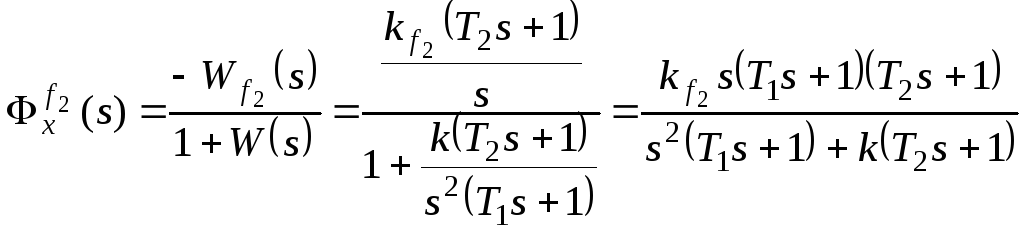
где

– коэффициент передачи разомкнутой
системы по возмущению f₂.

При

получим:

По возмущению f₂
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.

Подведем некоторые
итоги:

1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.

2. Постоянные
времени звеньев системы не влияют на
ее точность.

3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.

Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.

Рассмотрим
структуру, показанную на рисунке 119.

В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

где l0.

Тогда получим:

и для общего вида
задающего воздействия
,
которому соответствует изображение
,

Результат нахождения
этого предела зависит от соотношения
показателей степени:

— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;

— при l=v
получаем константу;

— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.

Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.

Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.

Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.

Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:

где l₁+l₂=l,
k₁k₂=k,
m₁+m₂=m,
n₁+n₂=n,
причем

и
.

Тогда получим:

и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

Все вышеприведенные
выводы можно повторить для показателя
степени l₁.

Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.

Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.

Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные

,
,
…,
,
…

В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять

,
n>m.

Для задачи оценки
установившейся ошибки при

с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.

Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:

где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.

С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:

Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует

или
.

Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:

Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.

Найдем коэффициенты
разложения передаточной функции по
ошибке

в степенной ряд.

Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c₀
и c₁
здесь получаем тождественно равными
нулю.

Далее получим:

В результате
получаем
,
,
,

и так далее.

Найдем производные
задающего воздействия:

,
,
.

Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:

В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.

Соседние файлы в папке Конспект ТАУ

СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Установившаяся ошибка

Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.

+ ~ я»

-R(s) —— *~С>——- *

-Y(s)

G(s)

H(s)

Рис. 4.18. Разомкнутая система управления

Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна

ад=ад — ад=[і — стт. (4.48)

В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна

Для вычисления установившейся ошибки используется теорема о конечном значении:

lim e(t)= lims£(s). (4.50)

_ 1 —КО А—>0

Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:

е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).

■v-»0 s -‘->0

В замкнутой системе при H(s) = 1 имеем:

Случай неединичной обратной связи рассматривается в разд. 5.8.

4.5. Установившаяся ошибка

Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.

Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.

Рис. 4.20

Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом

Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию

G(s) = —. (4.53)

TS+ 1

Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна

е0(со) = 1 — 6X0) = 1 — К (4.54)

при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:

Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна

ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).

.v->0 s

Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,

ес(со) = 1 J! Le_L. (4.55)

1+ К 1+ К

В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.

Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит

Ае0(со) 0,1

(4.56)

IKOI 1

т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно

Аес (оо ) = ——(4.57) 91 101

а относительное приращение составит

Аес (оо)

= 0,0011, (4.58)

IKOI

или 0,11%. Как говорится, результат в комментариях не нуждается.

Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …

Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …

Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества состоит из нескольких групп:

прямые — определяемые непосредственно по переходной характеристике процесса,
корневые — определяемые по корням характеристического полинома,
частотные — по частотным характеристикам,
интегральные — получаемые путем интегрирования функций.

Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:

Установившееся значение выходной величины Yуст,
Степень затухания ?,
Время достижения первого максимума tmax,
Время регулирования tp,
Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
Перерегулирование у,
Динамический коэффициент регулирования Rd,
Показатель колебательности М.

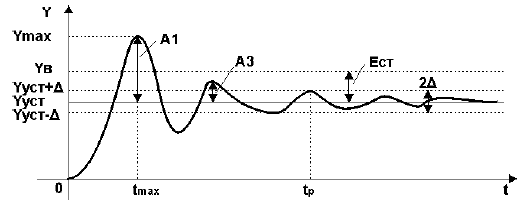
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Рисунок 1 — Определение показателей качества по переходной характеристике

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.

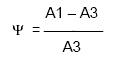
Степень затухания ?

Степень затухания ? определяется по формуле:

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.

Ошибка регулирования Ест

Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.

Перерегулирование у

Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:

где значения величин Ymax и Yуст определяются согласно рис.1.

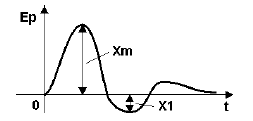
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:

где значения величин Xm и X1 определяются согласно рис. 2.

Рисунок 2 — График переходного процесса при отработке возмущения

Динамический коэффициент регулирования Rd

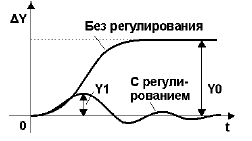
Динамический коэффициент регулирования Rd определяется из формулы:

где значения величин Y1 и Y0 определяются согласно рис. 3.

Рисунок 3 — К понятию динамического коэффициента регулирования

Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.

Показатель колебательности М

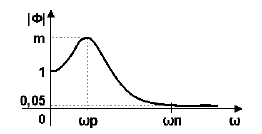
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.

Рисунок 4 — График модуля частотной передаточной функции замкнутой системы

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

Демьян Бондарь

Эксперт по предмету «Автоматизация технологических процессов»

преподавательский стаж — 5 лет

Задать вопрос автору статьи

Качество систем управления в переходном режиме

Определение 1

Качество системы управления – это комплексная оценка работы системы управления в зависимости от ее назначения.

Самыми распространенными показателями качества системы в переходном процессе являются:

Интегральные критерии.
Статическая ошибка регулирования.
Степень колебательности.
Динамическая ошибка регулирования.
Время регулирования.
Степень устойчивости.

Статическая ошибка регулирования представляет собой разность между установившемся значением регулируемого параметра и его заданным значением. Динамическая ошибка регулирования равняется наибольшему отклонению регулируемой величины от ее установившегося значения. Время регулирования определяется, как время, за которое разность между текущим значением регулируемого параметра и его заданным значением становится меньше допустимого отклонения. Степень устойчивости автоматической системы управления характеризует запас устойчивости в плоскости корней характеристического уравнения и равняется расстоянию до оси ближайшего корня. Данный критерий характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса.

Тренируй мозг с удовольствием

Развивай память, внимание и мышление c помощью онлайн-тренажеров

Выбрать программу

Степень колебательности равняется минимальному модулю отношения действительной и мнимой частей корня, то есть:

Рисунок 1.

Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча (как показано на рисунке ниже) таким образом, чтобы одна пара корней находилась на данных лучах, а остальные лежали слева от них, то тангенс угла, который заключен между лучами и мнимой осью, равный отношению действительной и мнимой частей корней, лежащих на лучах АОВ, является степенью колебательности системы.

Рисунок 2. График. Автор24 — интернет-биржа студенческих работ

«Качество систем управления в установившемся и переходном режимах» 👇

Степень затухания является количественной оценкой интенсивности затухания колебательного процесса:

Рисунок 3.

Между степенью затухания и степенью колебательности существует однозначная зависимость:

Рисунок 4.

Степень затухания может изменяться в пределах от 0,1 до 1, а степень колебательности от 0 до бесконечности. В отличии от прямых показателей интегральные критерии дают обобщенную оценку качества системы, они делятся на:

линейный интегральный критерий,
модульные интегральные критерии,
квадратичный интегральный критерий,
обобщенные интегральные критерии.

Качество системы управления в установившемся режиме

Определение 2

Установившийся режим – это режим, параметры которого не изменяются во времени или меняются в соответствии с периодическим законом.

Рассмотрим схему одноконтурной системы, которая представлена на рисунке ниже.

Рисунок 5. Схема одноконтурной системы. Автор24 — интернет-биржа студенческих работ

Рассматриваемая схема может быть упрощена следующим образом.

Рисунок 6. Упрощенная схема. Автор24 — интернет-биржа студенческих работ

Для того, чтобы согласовать сигналы u3(t) и uoc(t) надо подобрать одинаковые передаточные функции Wбз(р) и Wби(р), поэтому должно выполняться следующее равенство:

$Wбз(р) = Wби(р)$

С учетом представленного выше равенства схему рассматриваемой системы можно представить в следующем виде.

Рисунок 7. Схема системы. Автор24 — интернет-биржа студенческих работ

В этом случае ошибка регулирования входит в формулу для определения сигнала рассогласования:

$ΔU(р) = Δ(р) WБИ(р)$

Ошибка δ(t) зависит от величины параметров, задающего и возмущающего воздействия, таким образом ее значение может быть выражено как сумма ошибок данных воздействий:

$δ(t) =δy(t) + δf(t)$

Передаточные функции выражаются следующим образом:

Рисунок 8.

Рисунок 9.

Передаточная функция разомкнутого контура выражается следующим образом

$Wрк (р) =WБИ(р) WБУ (р) WОУ(р)$

Исходя из представленных выше выражений величина изображения ошибки определяется следующим образом:

Рисунок 10.

Существую типовые законы оценки установившегося режима, установленные условиями:

Возмущающее и задающее воздействия не изменяются во времени и постоянны, то есть — yз(t), f (t) = const.
Изменения в системе происходят с постоянной скоростью, то есть — yз (t) = a t и f (t) = const.
Изменения в системе происходят с постоянным ускорением, то есть — y(t) = b t2/2и f (t) = const.
Изменения в системе происходят по гармоническому закону, то есть — yз (t) = y0 sin(ω t) и f (t) = const.

Определение 3

Статическая ошибка – это значение ошибки регулирования при постоянной величине входного воздействия.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Установившаяся ошибка

Cтраница 1

Установившаяся ошибка в данной системе при ступенчатом входном сигнале равна нулю, ( а) Изобразите графически частотные характеристики данной системы и обратите внимание на наличие двух всплесков на амплитудной характеристике, ( б) Предскажите вид переходной характеристики системы с учетом того, что она имеет 4 полюса и не может быть аппроксимирована моделью второго порядка, предполагающей наличие доминирующих полюсов, ( в) Получите график переходной характеристики.
[1]

Установившаяся ошибка характеризует точность регулирования в установившемся режиме.
[3]

Установившаяся ошибка при этом оказывается равной нулю, и система действует подобно линейной системе с однократным астатизмом в контуре ошибки. Фактически регулятор получается двухконтурным, причем пропускание низких частот регулируется параметрическим управляющим контуром, а высоких — релейным контуром.
[5]

Установившаяся ошибка ( в силу рабочего движения) при таком законе управления, очевидно, равна нулю.
[6]

Установившаяся ошибка по положению уменьшается при увеличении статического коэффициента усиления разомкнутой цепи.
[7]

Установившаяся ошибка по положению ликвидируется введением интегратора2 в разомкнутую цепь.
[8]

Установившаяся ошибка при постоянных внешних воздействиях называется статической.
[9]

Установившаяся ошибка характеризует точность регулирования в установившемся режиме.
[10]

Установившаяся ошибка при постоянных внешних воздействиях называется статической. Поэтому статические и астатические системы можно определить следующим образом: система называется статической, если статическая ошибка отлична от нуля, и астатической, если она равна нулю.
[11]

Установившаяся ошибка является ошибкой, которая остается после окончания переходного процесса.
[12]

Установившаяся ошибка равняется сумме статической, ошибки, вызванной действием Мот и скоростной ошибки, обусловленной заданной скоростью изменения входного сигнала.
[13]

Установившаяся ошибка является ошибкой, которая остается после окончания переходного процесса.
[14]

Страницы:

Источник

Байланысты:
Тесты по теории линейных систем автоматического регулирования-1
1 модуль — на 4

128. В теории оптимальных систем регулирования применяют оценки качества

А) интегральные

В) корневые

С) частотные

D) прямые

Е) любые

129. Какой закон линейного регулирования не используется в САР?

А) Д

В) И

С) П

D) ПИ

Е) ПД

130. Какой из перечисленных регуляторов имеет остаточную неравномерность (статизм)?

А) П

В) И

С) ПИД

D) ПИ

Е) любой из перечисленных

131. Какой из перечисленных регуляторов работает с предварением?

А) ПД

В) И

С) Д

D) ПИ

Е) П

132. Установившаяся ошибка по заданию возрастает

А) при уменьшении общего коэффициента усиления системы

В) при уменьшении входного воздействия r(t)

С) при уменьшении коэффициента передачи по каналу ошибки

D) при уменьшении разности между y(t) и r(t)

Е) при уменьшении коэффициента статизма

133. АФЧХ звена чистого запаздывания представляет собой

А) круг

В) эллипс

С) точку

D) многоугольник

Е) прямую линию

134. Частота среза – это частота

A) пересечения ЛАЧХ оси абсцисс

B) пересечения ЛФЧХ линии минус 180 градусов

C) левой границы полосы пропускания

D) правой границы полосы пропускания

E) перелома асимптотической ЛАЧХ

135. Порядок астатизма при построении низкочастотной асимптоты ЛАЧХ это

A) разность числа нулевых корней знаменателя и числителя передаточной функции

B) число корней знаменателя передаточной функции

C) число нулевых корней знаменателя передаточной функции

D) число нулевых корней числителя передаточной функции

E) разность числа нулевых корней числителя и знаменателя передаточной функции

136. Комбинированное управление осуществляется по

А) отклонению регулируемой величины от задания и возмущению

В) возмущению

С) отклонению регулируемой величины от задания

D) заданию без контроля регулируемой величины

Е) возмущению и заданию без контроля регулируемой величины

137. Частотой сопряжения называется частота

А) соответствующая перелому асимптотической ЛАЧХ

В) соответствующая началу координат при построении ЛАЧХ

С) на которой усиление или ослабление системы отсутствует

D) соответствующая началу низкочастотной асимптоты

Е) соответствующая концу низкочастотной асимптоты

138. Общий наклон ЛАЧХ в конце равен

A) (n – m)(-20 дБ/дек)

В) (n + m)(-20 дБ/дек)

С) (n + m)(20 дБ/дек)

D) (n – m)(20 дБ/дек)

Е)  20 дБ/дек

139. Точке пересечения комплексных ветвей корневого годографа с действительной осью соответствуют

А) кратные корни

В) правые корни

С) левые корни

D) нули системы

Е) полюса системы

140. Относительное значение установившейся ошибки регулирования называется

А) статизмом

В) запасом по амплитуде

С) запасом по фазе

D) степенью устойчивости

Е) перерегулированием

141. Общим дифференциальным уравнением с постоянными коэффициентами не описываются во времени

A) импульсные системы

B) стационарные системы

C) одномерные системы

D) сосредоточенные системы

E) линейные системы

142. Главная обратная связь используется в системах

А) с управлением по отклонению

В) детерминированных

С) безрефлексных

D) циклических

Е) с управлением по возмущению

143. Преимущество преобразования Лапласа состоит в том, что оно

A) заменяет операцию дифференцирования алгебраическим умножением

B) заменяет графическое сложение алгебраическим умножением

C) заменяет алгебраическое умножение графическим сложением

D) заменяет алгебраическое сложение графическим умножением

E) заменяет операцию интегрирования алгебраическим сложением

144. По формуле вычисляется

A) правильного ответа нет

B) конечное значение изображения

C) конечное значение оригинала

D) начальное значение изображения

E) начальное значение оригинала

145. Замкнуть аналитически систему единичной отрицательной обратной связью можно

А) добавив к знаменателю передаточной функции ее числитель

В) разделив знаменатель передаточной функции на ее числитель

С) вычтя из знаменателя передаточной функции ее числитель

D) сложив числитель и знаменатель передаточной функции

Е) перемножив числитель и знаменатель передаточной функции

146. Начало координат ЛАЧХ соответствует значению

А)

В)

D) по всем осям начало координат выбирается произвольно

Е)

147. При каком условии звено не является апериодическим звеном второго порядка?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

D) правильный ответ отсутствует

Е)

148. При каком условии звено является колебательным звеном?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

Е) показатель затухания

149. При каком условии звено является консервативным звеном?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

D) показатель затухания

Е)

150. Функция g(t) равна

А) производной от h(t)

В) интегралу от h(t)

С) свободной составляющей переходного процесса

D) вынужденной составляющей переходного процесса

Е) оригиналу частотной передаточной функции

151. Если дифференциальное уравнение системы равно , то начальное значение при t=0_ соответствует изображению по Лапласу

А)

В)

С)

Е)

152. Если , а , то АЧХ и ФЧХ системы равны соответственно

А) 5, -180

В) 1, 90

Достарыңызбен бөлісу:

Источник

Подборка по базе: Соболев Дифференциальные уравнения Теория и практика.pdf, курсова экономическая теория.docx, марекиинк и проекты теория.docx, «деректер базасыны_ теориясы» п_нінен о_у-_дістемелік кешен «5В0, Практическая комплексный экономический анализ.docx, КОНТРА КГТУ ТЕОРИЯ УПРАВЛЕНИЯ ЭТИКА 2017.docx, Экономическая теория Перегримов С.С..docx, Силовое комплексное упражнение.docx, МР Комплекс.docx, псих общен комплекс.pdf

74. Что является оригиналом передаточной функции?

A) импульсная функция

B) переходная функция

C) реакция на начальные условия

D) частотная функция

E) кривая разгона

75. Как называется реакция на гармоническое воздействие в установившемся режиме?

A) частотная функция

B) переходная функция

C) передаточная функция

D) кривая разгона

E) импульсная функция

76. Отношение преобразований Лапласа выходной и входной величин системы при нулевых начальных условиях называется

A) передаточной функцией

B) переходной функцией

C) системной функцией

D) импульсной функцией

E) весовой функцией

77. Изображение по Лапласу 1/s² соответствует типовому воздействию

A) t

C) sin(t)

D) 1(t)

78. Изображение по Лапласу 1 соответствует типовому воздействию

B) 1(t)

C) sin(t)

D) t

79. Звено с комплексным коэффициентом передачи называется

А) астатическим

В) пропорциональным

С) инерционным

D) колебательным

Е) консервативным

80. Если показатель затухания колебательного звена уменьшается, его АФЧХ

А) увеличивается

В) не изменяется

С) уменьшается

D) переходит в другой квадрант

Е) правильный ответ отсутствует

81. АФЧХ интегрирующего, дифференцирующего, консервативного, форсирующего, безинерционного звеньев – это прямая линия

А) да, да, да, да, нет

В) нет, нет, нет, нет, да

С) да, да, да, нет, нет

D) да, нет, да, нет, да

Е) нет, да, нет, да, нет

82. Переходная функция представляет собой импульс

А) у дифференцирующего звена

В) у интегрирующего звена

С) у безинерционного звена

D) у запаздывающего звена

Е) у консервативного звена

83. По формуле вычисляется

A) конечное значение оригинала

B) конечное значение изображения

C) начальное значение оригинала

D) начальное значение изображения

E) правильного ответа нет

84. Запаздывание оригинала во времени на соответствует

А) правильный ответ отсутствует

В) делению оригинала на функцию

C) делению оригинала на функцию

D) умножению оригинала на функцию

Е) умножению оригинала на функцию

85. Какие частоты не используются при построении АФЧХ?

А) частоты сопряжения

В) частоты пересечения с осями

С) частоты разрыва

D) нулевая частота

Е) частота, равная бесконечности

86. Если у инерционного звена уменьшить постоянную времени Т до нуля, звено преобразуется в

А) пропорциональное

В) интегрирующее

С) дифференцирующее

D) апериодическое первого порядка

Е) консервативное

87. Если у инерционного звена увеличивать постоянную времени Т до бесконечности, звено преобразуется в

А) интегрирующее

В) пропорциональное

С) дифференцирующее

D) апериодическое первого порядка

Е) консервативное

88. Звено не является колебательным, если

А) правильного ответа нет

В) выполняется условие

С) выполняется условие при

D) выполняется условие

Е) имеет комплексные сопряженные корни характеристического уравнения

89. Если АФЧХ звена проходит только по действительной оси и терпит разрыв, то это звено

А) консервативное

В) интегрирующее

С) дифференцирующее

D) апериодическое второго порядка

Е) колебательное

90. Если ЛАЧХ и ЛФЧХ звена представляют собой горизонтальные прямые, то это звено

А) пропорциональное

В) интегрирующее

С) дифференцирующее

D) апериодическое первого порядка

Е) консервативное

91. Звено, ЛАЧХ которого представляет собой одиночную асимптоту с наклоном +20 дБ/дек

А) дифференцирующее

В) интегрирующее

С) пропорциональное

D) апериодическое первого порядка

Е) консервативное

92. Звено, ЛАЧХ которого представляет собой одиночную асимптоту с наклоном -20 дБ/дек

А) интегрирующее

В) пропорциональное

С) дифференцирующее

D) апериодическое первого порядка

Е) консервативное

93. Какое утверждение не соответствует требованиям к типовому динамическому звену

А) типовое звено должно иметь положительный коэффициент усиления

В) типовое звено должно характеризоваться одной независимой переменной

С) типовое звено не должно изменять характеристик при подключении других звеньев

D) типовое звено должно описываться дифференциальным уравнением не выше второго порядка

Е) типовое звено должно быть однонаправленным

94. Минимально-фазовым называется звено

А) все нули и полюса которого левые

В) все нули которого левые

С) все полюса которого левые

D) у которого все корни характеристического уравнения имеют отрицательную действительную часть

Е) у которого при левых полюсах имеются правые нули

95. Система устойчива, если

A) все корни знаменателя передаточной функции лежат слева от мнимой оси

B) все корни числителя передаточной функции лежат слева от мнимой оси

C) все корни числителя передаточной функции лежат справа от мнимой оси

D) все корни знаменателя передаточной функции лежат справа от мнимой оси

E) ни один корень передаточной функции не лежит на мнимой оси

96. Система устойчива, если

A) свободная составляющая переходного процесса сходится

B) свободная составляющая переходного процесса расходится

C) вынужденная составляющая переходного процесса сходится

D) совокупный переходный процесс является сходящимся

E) свободная составляющая всегда равна нулю

97. Система находится на периодической границе устойчивости, если в первом столбце таблицы Рауса

А) не последний элемент равен нулю при остальных положительных

В) отсутствует нулевой элемент

С) последний элемент равен нулю при остальных положительных

D) отсутствует отрицательный элемент

Е) хотя бы один элемент равен нулю

98. Система устойчива, если

A) при свободном движении система возвращается в исходное состояние равновесия

B) при свободном движении ее переходный процесс не имеет колебательной составляющей

C) при свободном движении система не возвращается к исходному состоянию равновесия

D) при свободном движении система стремится к новому состоянию равновесия

E) при свободном движении ее переходный процесс имеет колебательный характер

99. Условие положительности всех коэффициентов характеристического уравнения является необходимым и достаточным для устойчивости систем

A) не выше второго порядка

B) первого порядка

C) второго порядка

D) выше второго порядка

Е) нулевого порядка

100. По критерию Гурвица система находится на апериодической границе устойчивости, если

A) правильный ответ отсутствует

B) при остальных отрицательных минорах

С) отсутствуют отрицательные миноры

D) все миноры положительны

Е) при остальных положительных минорах

101. По свойству устойчивости система будет нейтральной, если

А) она имеет нулевой полюс при остальных левых

В) все ее полюса левые

С) она имеет нулевой полюс при остальных правых

D) она не имеет нулевых полюсов

Е) все ее полюса правые

102. Система находится на апериодической границе устойчивости, если в первом столбце таблицы Рауса

А) последний элемент равен нулю при остальных положительных

В) отсутствует нулевой элемент

С) отсутствует отрицательный элемент

D) не последний элемент равен нулю при остальных положительных

Е) хотя бы один элемент равен нулю

103. Критическим (предельным) называется значение параметра, при котором система

А) находится на границе устойчивости

В) становится замкнутой

С) имеет перерегулирование более 30 %

D) имеет запас устойчивости менее 30 %

Е) находится вне области-претендента на устойчивость

104. При каждом переходе границы D-области навстречу штриховке

А) один полюс системы становится правым

В) один нуль системы становится левым

С) один нуль системы становится правым

D) один полюс системы становится левым

Е) один корень системы становится нулевым

105. При изменении частоты от нуля до бесконечности кривая Михайлова устойчивой системы n-го порядка проходит

А) последовательно против часовой стрелки n квадрантов комплексной плоскости

В) против часовой стрелки n квадрантов комплексной плоскости

С) последовательно по часовой стрелке n квадрантов комплексной плоскости

D) по часовой стрелке n квадрантов комплексной плоскости

Е) через начало координат

106. Система n-го порядка находится на периодической границе устойчивости, если при изменении частоты  от нуля до бесконечности кривая Михайлова проходит

А) через начало координат

В) против часовой стрелки n квадрантов комплексной плоскости

С) последовательно по часовой стрелке n квадрантов

D) последовательно против часовой стрелки n квадрантов

Е) по часовой стрелке n квадрантов комплексной плоскости

107. Система n-го порядка находится на апериодической границе устойчивости по критерию Михайлова, если графики четной и нечетной функций

А) начинаются в одной точке

В) пересекаются при одинаковой частоте

С) пересекают ось частот поочередно

D) не пересекают ось частот

Е) имеют n пересечений с осью частот

108. Система находится на периодической границе устойчивости по критерию Михайлова, если графики четной и нечетной функций

А) пересекаются при одинаковой частоте

В) начинаются в одной точке

С) пересекают ось частот поочередно

D) не пересекают ось частот

Е) имеют n пересечений с осью частот

109. Система устойчива по критерию Михайлова, если графики четной и нечетной функций

А) пересекают ось частот поочередно

В) пересекаются при одинаковой частоте

С) начинаются в одной точке

D) не пересекают ось частот

Е) имеют n пересечений оси частот

110. Если корни четной и нечетной функций перемежаются при изменении частоты от нуля до бесконечности, то по критерию Михайлова система

А) устойчива

В) неустойчива

С) находится на периодической границе устойчивости

D) находится на апериодической границе устойчивости

Е) устойчива в замкнутом состоянии

111. Для анализа устойчивости замкнутой системы по критерию Найквиста строят на комплексной плоскости при изменении частоты от 0 до годограф

А) комплексного коэффициента передачи разомкнутой системы

В) передаточной функции разомкнутой системы

С) знаменателя передаточной функции разомкнутой системы

D) комплексного коэффициента передачи системы

Е) правильная формулировка отсутствует

112. АФЧХ называется характеристикой II-го рода, если

А) имеет более одного пересечения отрезка действительной оси [-1, ]

В) проходит два квадранта комплексной плоскости

С) имеет погрешность второго порядка

D) строится для систем второго порядка

E) имеет более одного пересечения отрезка действительной оси [-1, 0]

113. Если годограф комплексного коэффициента передачи не охватывает точку на комплексной плоскости с координатами [-1, j0], система

А) устойчива в замкнутом состоянии

В) устойчива

С) неустойчива

D) устойчива в разомкнутом состоянии

Е) находится на границе устойчивости

114. Если АФЧХ разомкнутой системы начинается в точке на комплексной плоскости с координатами [-1, j0], замкнутая система

А) находится на апериодической границе устойчивости

В) устойчива

С) находится на периодической границе устойчивости

D) указанный случай невозможен

Е) неустойчива

115. Если АФЧХ разомкнутой системы проходит через точку на комплексной плоскости с координатами [-1, j0], замкнутая система

А) находится на периодической границе устойчивости

В) устойчива

С) неустойчива

D) указанный случай невозможен

Е) находится на апериодической границе устойчивости

116. Разница между значением минус 180 и значением ЛФЧХ на частоте среза называется

А) запасом устойчивости

В) фазовой характеристикой

С) степенью устойчивости

D) перерегулированием

Е) колебательностью N

117. Запас устойчивости системы по амплитуде определяется

А) на частоте пересечения ЛФЧХ и линии минус 180

В) на частоте сопряжения

С) на частоте среза

D) на частоте

Е) на частоте

118. При анализе устойчивости по обратной АФЧХ разомкнутой системы замкнутая система будет устойчива, если

А) обратная АФЧХ охватывает точку с координатами (-1, j0)

В) при штриховке справа от кривой точка (-1, j0) не попадает в заштрихованную область

С) обратная АФЧХ не охватывает точку с координатами (-1, j0)

D) обратная АФЧХ проходит через точку с координатами (-1, j0)

Е) обратная АФЧХ не проходит через точку (-1, j0)

119. Качество системы в установившемся режиме определяется

А) величиной отклонения от заданного значения

В) длительностью отклонения от заданного значения

С) устойчивостью системы

D) колебательностью системы

Е) начальным значением ошибки регулирования

120. Для исследования качества систем регулирования не используют воздействие типа

А) единичный импульс

В) скачок ускорения

С) скачок скорости

D) скачок положения

Е) гармонические колебания

121. По максимальному относительному забросу переходной характеристики за линию установившегося значения определяют

А) перерегулирование

В) время установления

С) колебательность

D) время регулирования

Е) установившуюся ошибку

122. Согласно частотным оценкам качества перерегулирование системы не превышает 18 %, если

А)

Е) ВЧХ везде положительна

123. При корневых оценках качества с ошибкой 5 % время регулирования близко к

А)

Е)

124. Колебательный процесс регулирования при ступенчатом образцовом процессе целесообразно оценивать с помощью

А) интегральной квадратичной оценки

В) интегральной линейной оценки

С) улучшенной интегральной квадратичной оценки

D) прямого интегрального преобразования Лапласа

Е) обратного интегрального преобразования Лапласа

125. Доминирующим называется корень (пара корней)

А) лежащий слева от мнимой оси и ближайший к ней

В) лежащий справа от мнимой оси и ближайший к ней

С) имеющий наибольшее абсолютное значение действительной части

D) имеющий наименьшее абсолютное значение действительной части

Е) лежащий на мнимой оси

126. Степень устойчивости системы характеризует

А) время регулирования

В) запас устойчивости по фазе

С) перерегулирование

D) запас устойчивости по амплитуде

Е) запаздывание

127. В корневом методе оценки качества степень колебательности позволяет найти

А) перерегулирование

В) запас устойчивости по фазе

С) запас устойчивости по амплитуде

D) время регулирования

Е) запаздывание

128. В теории оптимальных систем регулирования применяют оценки качества

А) интегральные

В) корневые

С) частотные

D) прямые

Е) любые

129. Какой закон линейного регулирования не используется в САР?

А) Д

В) И

С) П

D) ПИ

Е) ПД

130. Какой из перечисленных регуляторов имеет остаточную неравномерность (статизм)?

А) П

В) И

С) ПИД

D) ПИ

Е) любой из перечисленных

131. Какой из перечисленных регуляторов работает с предварением?

А) ПД

В) И

С) Д

D) ПИ

Е) П

132. Установившаяся ошибка по заданию возрастает

А) при уменьшении общего коэффициента усиления системы

В) при уменьшении входного воздействия r(t)

С) при уменьшении коэффициента передачи по каналу ошибки

D) при уменьшении разности между y(t) и r(t)

Е) при уменьшении коэффициента статизма

133. АФЧХ звена чистого запаздывания представляет собой

А) круг

В) эллипс

С) точку

D) многоугольник

Е) прямую линию

134. Частота среза – это частота

A) пересечения ЛАЧХ оси абсцисс

B) пересечения ЛФЧХ линии минус 180 градусов

C) левой границы полосы пропускания

D) правой границы полосы пропускания

E) перелома асимптотической ЛАЧХ

135. Порядок астатизма при построении низкочастотной асимптоты ЛАЧХ это

A) разность числа нулевых корней знаменателя и числителя передаточной функции

B) число корней знаменателя передаточной функции

C) число нулевых корней знаменателя передаточной функции

D) число нулевых корней числителя передаточной функции

E) разность числа нулевых корней числителя и знаменателя передаточной функции

136. Комбинированное управление осуществляется по

А) отклонению регулируемой величины от задания и возмущению

В) возмущению

С) отклонению регулируемой величины от задания

D) заданию без контроля регулируемой величины

Е) возмущению и заданию без контроля регулируемой величины

137. Частотой сопряжения называется частота

А) соответствующая перелому асимптотической ЛАЧХ

В) соответствующая началу координат при построении ЛАЧХ

С) на которой усиление или ослабление системы отсутствует

D) соответствующая началу низкочастотной асимптоты

Е) соответствующая концу низкочастотной асимптоты

138. Общий наклон ЛАЧХ в конце равен

A) (n – m)(-20 дБ/дек)

В) (n + m)(-20 дБ/дек)

С) (n + m)(20 дБ/дек)

D) (n – m)(20 дБ/дек)

Е)  20 дБ/дек

139. Точке пересечения комплексных ветвей корневого годографа с действительной осью соответствуют

А) кратные корни

В) правые корни

С) левые корни

D) нули системы

Е) полюса системы

140. Относительное значение установившейся ошибки регулирования называется

А) статизмом

В) запасом по амплитуде

С) запасом по фазе

D) степенью устойчивости

Е) перерегулированием

141. Общим дифференциальным уравнением с постоянными коэффициентами не описываются во времени

A) импульсные системы

B) стационарные системы

C) одномерные системы

D) сосредоточенные системы

E) линейные системы

142. Главная обратная связь используется в системах

А) с управлением по отклонению

В) детерминированных

С) безрефлексных

D) циклических

Е) с управлением по возмущению

143. Преимущество преобразования Лапласа состоит в том, что оно

A) заменяет операцию дифференцирования алгебраическим умножением

B) заменяет графическое сложение алгебраическим умножением

C) заменяет алгебраическое умножение графическим сложением

D) заменяет алгебраическое сложение графическим умножением

E) заменяет операцию интегрирования алгебраическим сложением

144. По формуле вычисляется

A) правильного ответа нет

B) конечное значение изображения

C) конечное значение оригинала

D) начальное значение изображения

E) начальное значение оригинала

145. Замкнуть аналитически систему единичной отрицательной обратной связью можно

А) добавив к знаменателю передаточной функции ее числитель

В) разделив знаменатель передаточной функции на ее числитель

С) вычтя из знаменателя передаточной функции ее числитель

D) сложив числитель и знаменатель передаточной функции

Е) перемножив числитель и знаменатель передаточной функции

146. Начало координат ЛАЧХ соответствует значению

А)

В)

D) по всем осям начало координат выбирается произвольно

Е)

147. При каком условии звено не является апериодическим звеном второго порядка?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

D) правильный ответ отсутствует

Е)

148. При каком условии звено является колебательным звеном?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

Е) показатель затухания

149. При каком условии звено является консервативным звеном?

А) показатель затухания

B) показатель затухания

С) оба корня квадратного уравнения действительны

D) показатель затухания

Е)

150. Функция g(t) равна

А) производной от h(t)

В) интегралу от h(t)

С) свободной составляющей переходного процесса

D) вынужденной составляющей переходного процесса

Е) оригиналу частотной передаточной функции

А)

В)

С)

Е)

152. Если , а , то АЧХ и ФЧХ системы равны соответственно

А) 5, -180

В) 1, 90

С) 5, -90

D) 0, 0

Е) -5, -180

153. Если входной и выходной гармонические сигналы линейной системы равны соответственно x(t)=sin(t+90) и y(t)=2sin(t-90), то значения АЧХ и ФЧХ равны

А) 2, -180

В) 2, 180

С) 1, 90

D) 0,5, -180

Е) 0,5, -90

154. Если передаточная функция фильтра равна , то точки начала и конца АФЧХ имеют действительные координаты соответственно

А) 3 и 0,33

В) 0,33 и 3

С) 1 и 2

D) 2 и 3

Е) 0,66 и 1,5

155. Если по измерениям на выходе регулирования системы , то система является

А) статической

В) астатической

С) нейтральной

D) критической

Е) оптимальной

156. Коэффициент при постоянной составляющей оригинала реакции равен

А) 0,5

В) 2

С) бесконечности

D) 0,25

Е) 1

157. По каким параметрам строится низкочастотная асимптота ЛАЧХ?

A) по значениям добротности и степени астатизма

B) по корням числителя передаточной функции

C) по корням знаменателя передаточной функции

D) по величине коэффициента затухания

E) по нулям и полюсам передаточной функции

158. Если все коэффициенты характеристического уравнения системы положительны, то система

A) ещё не может быть оценена по устойчивости

B) неустойчива

C) находится на апериодической границе устойчивости

D) находится на периодической границе устойчивости

E) устойчива

159. Построение в пространстве изменяемых параметров областей с разным числом правых корней характеристического уравнения соответствует

А) методу D-разбиения

В) методу смещенного уравнения

С) методу корневого годографа

D) математическому признаку устойчивости системы

Е) разложению на простые дроби

160. Граница области D-разбиения является

А) отображением нахождения хотя бы одного полюса на мнимой оси плоскости корней

В) отображением мнимой оси плоскости корней

С) указателем направления движения к области-претенденту

D) линией обхода при нанесении штриховки

Е) отображением критического значения параметра (коэффициента)

161. Значения параметра, соответствующие устойчивости системы, по методу D-разбиения выбираются

А) в любой точке на отрезке действительной оси внутри области-претендента

В) в любой точке области-претендента на устойчивость

С) в точке пересечения границы области-претендента с действительной осью

D) в точке пересечения границ нескольких D-областей

Е) на границе области-претендента на устойчивость

162. Частотную характеристику при изменении частоты  от минус бесконечности до нуля используют

А) в методе D-разбиения

В) при построении АЧХ

С) при построении ЛЧХ

D) при построении кривой Михайлова

Е) при построении АФЧХ

163. По правилу штриховки АФЧХ в критерии Найквиста система будет устойчивой в замкнутом состоянии, если

А) точка с координатами (-1, j0) не попадает в заштрихованную область

В) точка с координатами (-1, j0) попадает в заштрихованную область

С) точка с координатами (-1, j0) совпадает с кривой АФЧХ

D) кривая АФЧХ начинается в точке с координатами (-1, j0)

Е) положение заштрихованной области относительно точки (-1, j0) безразлично

164. Если в момент изменения знака главной обратной связи с минуса на плюс общий коэффициент усиления замкнутой системы больше единицы, система

А) неустойчива

В) устойчива

С) находится на периодической границе устойчивости

D) находится на апериодической границе устойчивости

Е) отсутствует правильная формулировка

165. Дугой бесконечного радиуса дополняется для анализа по критерию Найквиста годограф

А) нейтральной в разомкнутом состоянии системы

В) неустойчивой в разомкнутом состоянии системы

С) устойчивой в разомкнутом состоянии системы

D) нейтральной в замкнутом состоянии системы

Е) любой системы

166. Если система замкнута, то для анализа её устойчивости в этом состоянии по критерию Найквиста перед построением АФЧХ систему нужно

А) разомкнуть

В) замкнуть

С) оставить в нынешнем состоянии

D) найти число правых корней характеристического уравнения

Е) найти число левых корней характеристического уравнения

167. По критерию Михайлова число правых корней характеристического уравнения системы равно

А) числу неправильных пересечений кривой Михайлова с осями координат

В) числу пересечений кривой Михайлова с действительной осью

С) числу пересечений кривой Михайлова с мнимой осью

D) числу пересечений кривой Михайлова с осями координат

Е) правильная формулировка отсутствует

168. Величина, показывающая, насколько коэффициент усиления системы при меньше единицы, называется

А) запасом устойчивости

В) частотой среза

С) степенью устойчивости

D) перерегулированием

Е) колебательностью

169. Запас устойчивости по фазе системы после замыкания составит (в процентах)

А) 100

В) 50

С) 0

D) не рассчитывается

Е) правильный ответ отсутствует

170. От чего не зависит характер переходного процесса системы?

А) от величины зоны Δ

В) от места приложения входного воздействия

С) от собственных свойств системы

D) от степени устойчивости системы

Е) от вида входного воздействия

171. Система регулирования называется статической, если

А) коэффициент позиционной ошибки не равен нулю

В) статическая ошибка равна нулю

С) коэффициент ошибки по положению равен нулю

D) коэффициент позиционной ошибки равен нулю

Е) установившаяся ошибка равна нулю

172. По отклонению переходной характеристики выхода системы от 1 в установившемся режиме определяют

А) установившуюся ошибку

В) время установления

С) колебательность

D) перерегулирование

Е) время регулирования

173. При частотных оценках качества время регулирования не превышает

А)

Е)

174. Степень достижения апериодического процесса регулирования целесообразно оценивать с помощью

А) улучшенной интегральной квадратичной оценки

В) интегральной квадратичной оценки

С) интегральной линейной оценки

D) прямого интегрального преобразования Лапласа

Е) обратного интегрального преобразования Лапласа

175. Для нейтральной системы время регулирования равно

А) бесконечности

В) нулю

С)

Е)

176. Сближение полюсов на комплексной плоскости

А) увеличивает размах переходного процесса

В) уменьшает размах переходного процесса

С) не изменяет размах переходного процесса

D) исключает из переходного процесса соответствующую составляющую

Е) уменьшает длительность переходного процесса

177. Совпадение полюса и нуля на комплексной плоскости

А) исключает из переходного процесса соответствующую составляющую

В) увеличивает размах переходного процесса

С) не изменяет размах переходного процесса

D) уменьшает размах переходного процесса

Е) увеличивает длительность переходного процесса

178. Метод коэффициентов ошибок применяется для оценки качества регулирования

А) при полиномиальном входном воздействии

В) при импульсном входном воздействии

С) при ступенчатом входном воздействии

D) при гармоническом входном воздействии

Е) при оптимальном управлении

179. По формуле вычисляется

А) коэффициент ошибки по скорости

В) коэффициент статической ошибки

С) коэффициент позиционной ошибки

D) коэффициент ошибки по ускорению

Е) коэффициент ошибки по положению

180. Для системы время равно

А) не определяется

В) 30

С) 10

D) бесконечности

Е) 0

181. Для системы колебательность N равна

А) 0

В) 1

С) 2

D) 4

Е) 10

182. По каким параметрам строятся средне- и высокочастотные части ЛАЧХ?

A) по нулям и полюсам передаточной функции

B) по корням числителя передаточной функции

C) по значениям добротности и степени астатизма

D) по величине коэффициента затухания

E) по корням знаменателя передаточной функции

183. Наклон ЛАЧХ в начале равен (r – число нулевых корней знаменателя, l – числителя)

A) (r — l)(-20 дБ/дек)

В) (n – m)(-20 дБ/дек)

С) (n + m)(-20 дБ/дек)

D) (r + l)(20 дБ/дек)

Е)  20 дБ/дек

184. Частотой среза называется частота

А) на которой усиление или ослабление системы отсутствует

В) соответствующая началу координат при построении ЛАЧХ

С) соответствующая перелому асимптотической ЛАЧХ

D) соответствующая началу низкочастотной асимптоты

Е) соответствующая концу низкочастотной асимптоты

185. Отклонение действительной ЛАЧХ от асимптотической на частоте резонанса

А) обратно пропорционально показателю затухания

В) пропорционально показателю затухания

С) не связано с показателем затухания

D) пропорционально мнимой части комплексных корней

Е) обратно пропорционально мнимой части комплексных корней

186. Сколько ветвей корневого годографа закончатся в нулях системы?

А) m

B) n

C) n-m

D) m-n

E) m+n

187. Сколько траекторий корневого годографа системы уйдут в бесконечность?

А) n-m

B) n

C) m

D) m-n

E) m+n

188. Сколько траекторий корневого годографа начнутся в нулях разомкнутой системы?

А) правильный ответ отсутствует

B) n

C) n-m

D) m-n

E) m

189. Запас устойчивости по амплитуде системы после замыкания составит (в процентах)

А) 100

В) 50

С) 0

D) не рассчитывается

Е) правильный ответ отсутствует

190. Нечувствительность системы к изменению внутренних или внешних параметров это

А) инвариантность

В) статизм

С) неравномерность

D) самовыравнивание

Е) устойчивость

191. Для коррекции характеристик САР не применяют

А) запаздывающие устройства

В) параллельные устройства

С) инвариантные устройства

D) неединичную обратную связь

Е) последовательные устройства

192. Не ухудшает устойчивость и качество переходного процесса системы коррекция

А) по внешнему воздействию

В) с помощью местных обратных связей

С) с помощью неединичной обратной связи

D) с помощью последовательных фильтров

Е) правильный ответ отсутствует

193. Каким должен быть общий коэффициент усиления системы, чтобы относительное значение ошибки регулирования относительно задания не превышало 10 %?

А) 9

В) бесконечность

С) 10

D) 5

Е) ноль

194. Если задающее воздействие равно t, то для исключения ошибки по скорости от задания необходимо

А) ввести в систему два интегратора

В) ввести в систему интегрирующее звено

С) ввести в систему дифференцирующее звено

D) ввести в систему инерционное звено

Е) ввести в систему два инерционных звена

195. Величина статической ошибки пропорциональна (укажите неверный ответ)

А) величине коэффициента усиления системы

В) величине коэффициента статизма

С) величине входного воздействия

D) величине коэффициента передачи по каналу ошибки

Е) величине статизма системы

196. Если увеличивать коэффициент усиления разомкнутой системы, то величина статической ошибки астатической системы будет

А) равна нулю

В) уменьшаться

С) увеличиваться

D) останется отрицательной

Е) останется положительной

197. Чему равен младший коэффициент знаменателя передаточной функции замкнутой системы, если разомкнутая система описана нулем 10 и полюсом –10 с точностью до k = 5

А) -40

В) -50

С) 40

D) 50

Е) 10

198. Чему равен старший коэффициент знаменателя передаточной функции замкнутой системы, если разомкнутая система описана нулем 10 и полюсами –10, –1, –0,1 с точностью до k =2

A) 1

B) 0

C) 10

D) 40

E) 50

199. Чему равна частота среза ЛАЧХ системы , рад/с

A) отсутствует

B) бесконечности

C) 0,5

D) 2

E) 0

200. Чему равна частота сопряжения ЛАЧХ системы , рад/с

A) 2

B) бесконечности

C) 0,5

D) 0

E) отсутствует
Контрольная работа

Цель контрольной работы – закрепить теоретический материал и освоить методику анализа САУ.

В рамках контрольной работы не ставится задача проектирования CAУ для конкретного технологического процесса, так как подобные задачи решаются в последующих курсах специальности. В выполняемой контрольной работе математическое описание и структура системы заданы. Требуется, используя методы теории управления, обеспечить необходимые статические и динамические показатели качества регулирования системы путем введения в нее корректирующих звеньев.

Контрольная работа включает в себя расчет линейной системы автоматического регулирования.

Контрольная работа представляется в виде расчетно-пояснительной записки, содержащей вариант задания, расчетные формулы и соотношения, список использованной литературы, на которую должны быть сделаны ссылки в тексте, расчеты и необходимые пояснения к ним, выводы на основании полученных результатов.

После проверки контрольной работы преподавателем, необходимо устранить замечания (если это требуется) и защитить её. Во время защиты следует обосновать принятые решения и полученные результаты, объяснить формулы, характеристики и графики, знать теоретические разделы курса, использованные в работе.

Номер варианта задания равен сумме трех последних цифр учебного шифра зачетной книжки, согласно таблиц 1-2.

Источник