Что такое p-value?
P-значение (англ. P-value) — величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-значения является альтернативой классической процедуре проверки через критическое значение распределения.
Обычно P-значение равно вероятности того, что случайная величина с данным распределением (распределением тестовой статистики при нулевой гипотезе) примет значение, не меньшее, чем фактическое значение тестовой статистики. Википедия.
Иначе говоря, p-значение – это наименьшее значение уровня значимости (т.е. вероятности отказа от справедливой гипотезы), для которого вычисленная проверочная статистика ведет к отказу от нулевой гипотезы. Обычно p-значение сравнивают с общепринятыми стандартными уровнями значимости 0,005 или 0,01.
Например, если вычисленное по выборке значение проверочной статистики соответствует p = 0,005, это указывает на вероятность справедливости гипотезы 0,5%. Таким образом, чем p-значение меньше, тем лучше, поскольку при этом увеличивается «сила» отклонения нулевой гипотезы и увеличивается ожидаемая значимость результата.
Интересное объяснение этого есть на Хабре.
Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value).
О чём говорит p-value?
Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры). В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.
Примеры про p-value
Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верное утверждение:
1.Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
2. Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
3. Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
4. Вероятность случайно получить такие различия равняется 0.04.
5. Все утверждения неверны.
Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value.
Давайте разберём все ответы по порядку:
Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.
Это уже более интересное утверждение. Всё дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».
А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.
Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или ещё более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!
Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.
Как найти p-value?
Источник.
1. Определите ожидаемые в вашем эксперименте результаты
Обычно когда ученые проводят эксперимент, у них уже есть идея того, какие результаты считать «нормальными» или «типичными». Это может быть основано на экспериментальных результатах прошлых опытов, на достоверных наборах данных, на данных из научной литературы, либо ученый может основываться на каких-либо других источниках. Для вашего эксперимента определите ожидаемые результаты, и выразите их в виде чисел.
Пример: Например, более ранние исследования показали, что в вашей стране красные машины чаще получают штрафы за превышение скорости, чем синие машины. Например, средние результаты показывают предпочтение 2:1 красных машин перед синими. Мы хотим определить, относится ли полиция точно так же предвзято к цвету машин в вашем городе. Для этого мы будем анализировать штрафы, выданные за превышение скорости. Если мы возьмем случайный набор из 150 штрафов за превышение скорости, выданных либо красным, либо синим автомобилям, мы ожидаем, что 100 штрафов будет выписано красным автомобилям, а 50 синим, если полиция в нашем городе так же предвзято относится к цвету машин, как это наблюдается по всей стране.
2. Определите наблюдаемые результаты вашего эксперимента
Теперь, когда вы опредили ожидаемые результаты, необходимо провести эксперимент, и найти действительные (или «наблюдаемые») значения. Вам снова необходимо представить эти результаты в виде чисел. Если мы создаем экспериментальные условия, и наблюдаемые результаты отличаются от ожидаемых, то у нас есть две возможности – либо это произошло случайно, либо это вызвано именно нашим экспериментом. Цель нахождения p-значения как раз и состоит в том, чтобы определить, отличаются ли наблюдаемые результаты от ожидаемых настолько, чтобы можно было не отвергать «нулевую гипотезу» – гипотезу о том, что между экспериментальными переменными и наблюдаемыми результатами нет никакой связи.
Пример: Например, в нашем городе мы случайно выбрали 150 штрафов за превышение скорости, которые были выданы либо красным, либо синим автомобилям. Мы определили, что 90 штрафов были выписаны красным автомобилям, и 60 синим. Это отличается от ожидаемых результатов, которые равны 100 и 50, соответственно. Действительно ли наш эксперимент (в данном случае, изменение источника данных с национального на городской) привел к данному изменению в результатах, или наша городская полиция относится предвзято точно так же, как и в среднем по стране, а мы видим просто случайное отклонение? P-значение поможет нам это определить.
3. Определите число степеней свободы вашего эксперимента
Число степеней свободы — это степень изменяемости вашего эксперимента, которая определяется числом категорий, которые вы исследуете. Уравнение для числа степеней свободы – Число степеней свободы = n-1, где «n» это число категорий или переменных, которые вы анализируете в своем эксперименте.
Пример: В нашем эксперименте две категории результатов: одна категория для красных машин, и одна для синих машин. Поэтому в нашем эксперименте у нас 2-1 = 1 степень свободы. Если бы мы сравнивали красные, синие и зеленые машины, у нас было бы 2 степени свободы, и так далее.
4. Сравните ожидаемые и наблюдаемые результаты с помощью критерия хи-квадрат
Хи-квадрат (пишется «x2») это числовое значение, которое измеряет разницу между ожидаемыми и наблюдаемыми значениями эксперимента. Уравнение для хи-квадрата следующее x2 = Σ((o-e)2/e), где «o» это наблюдаемое значение, а «e» это ожидаемое значение. Суммируйте результаты данного уравнения для всех возможных результатов (смотри ниже).
Заметьте, что данное уравнение включает оператор суммирования Σ (сигма). Другими словами, вам необходимо подсчитать ((|o-e|-.05)2/e) для каждого возможного результата, и сложить полученные числа, чтобы получить значение критерия хи-квадрат. В нашем примере у нас два возможных результата – либо машина, получившая штраф красная, либо синяя. Поэтому мы должны посчитать ((o-e)2/e) дважды – один раз для красных машин, и один раз для синих машин.
Пример: Давайте подставим наши ожидаемые и наблюдаемые значения в уравнение x2 = Σ((o-e)2/e). Помните, что из-за оператора суммирования нам необходимо посчитать ((o-e)2/e) дважды – один раз для красных автомобилей, и один раз для синих автомобилей. Мы выполним эту работу следующим образом:
x2 = ((90-100)2/100) + (60-50)2/50)
x2 = ((-10)2/100) + (10)2/50)
x2 = (100/100) + (100/50) = 1 + 2 = 3.
5. Выберите уровень значимости
Теперь, когда мы знаем число степеней свободы нашего эксперимента, и узнали значение критерия хи-квадрат, нам нужно сделать еще одну вещь перед тем, как мы найдем наше p-значение. Нам нужно определить уровень значимости. Говоря простым языком, уровень значимости показывает, насколько мы уверены в наших результатах. Низкое значение для значимости соответствует низкой вероятности того, что экспериментальные результаты получились случайно, и наоборот. Уровни значимости записываются в виде десятичных дробей (таких как 0.01), что соответствует вероятности того, что экспериментальные результаты мы получили случайно (в данном случае вероятность этого 1%).
По соглашению, ученые обычно устанавливают уровень значимости своих экспериментов равным 0.05, или 5%.[2] Это означает, что экспериментальные результаты, которые соответствуют такому критерию значимости, только с вероятностью 5% могли получиться чисто случайно. Другими словами, существует 95% вероятность, что результаты были вызваны тем, как ученый манипулировал экспериментальными переменными, а не случайно. Для большинства экспериментов 95% уверенности наличия связи между двумя переменными достаточно, чтобы считать, что они «действительно» связаны друг с другом.
Пример: для нашего примера с красными и синими машинами, давайте последуем соглашению между учеными, и установим уровень значимости в 0.05.
6. Используйте таблицу с данными распределения хи-квадрат, чтобы найти ваше p-значение
Ученые и статисты используют большие таблицы для вычисления p-значения своих экспериментов. Данные таблицы обычно имеют вертикальную ось слева, соответствующую числу степеней свободы, и горизонтальную ось сверху, соответствующую p-значению. Используйте данные таблицы, чтобы сначала найти число ваших степеней свободы, затем посмотрите на ваш ряд слева направо, пока не найдете первое значение, большее вашего значения хи-квадрат. Посмотрите на соответствующее p-значение вверху вашего столбца. Ваше p-значение находится между этим числом и следующим за ним (тем, которое находится левее вашего).
Таблицы с распределением хи-квадрат можно получить из множества источников (вот по этой ссылке можно найти одну из них).
Пример: Наше значение критерия хи-квадрат было равно 3. Так как мы знаем, что в нашем эксперименте всего 1 степень свободы, выберем самую первую строку. Идем слева направо по данной строке, пока не встретим значение, большее 3, нашего значения критерия хи-квадрат. Первое, которое мы находим это 3.84. Смотрим вверх нашего столбца, и видим, что соответствующее p-значение равно 0.05. Это означает, что наше p-значение между 0.05 и 0.1 (следующее p-значение в таблице по возрастанию).
7. Решите, отклонить или оставить вашу нулевую гипотезу
Так как вы определили приблизительное p-значение для вашего эксперимента, вам необходимо решить, отклонять ли нулевую гипотезу вашего эксперимента или нет (напоминаем, это гипотеза о том, что экспериментальные переменные, которыми вы манипулировали не повлияли на наблюдаемые вами результаты). Если ваше p-значение меньше, чем ваш уровень значимости – поздравляем, вы доказали, что очень вероятна связь между переменными, которыми вы манипулировали и результатами, которые вы наблюдали. Если ваше p-значение выше, чем ваш уровень значимости, вы не можете с уверенностью сказать, были ли наблюдаемые вами результаты результатом чистой случайности или манипуляцией вашими переменными.
Пример: Наше p-значение находится между 0,05 и 0,1. Это явно не меньше, чем 0,05, поэтому, к сожалению, мы не можем отклонить нашу нулевую гипотезу. Это означает, что мы не достигли минимум 95% вероятности того, чтобы сказать, что полиция в нашем городе выдает штрафы красным и синим автомобилям с такой вероятностью, которая достаточно сильно отличается от средней по стране.
Другими словами, существует 5-10% шанс, что наблюдаемые нами результаты – это не последствия смены места (анализа города, а не всей страны), а просто случайность. Так как мы потребовали точности меньше чем 5%, мы не можем сказать что мы уверены в том, что полиция нашего города менее предвзято относится к красным автомобилям – существует небольшая (но статистически значимая) вероятность, что это не так.
Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.
Что такое P-значение
P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.
Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.
Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.
Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.
Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном
- Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
- Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
- Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.
Статистическая значимость
Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.
Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.
Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.
Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.
Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.
Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.
Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.
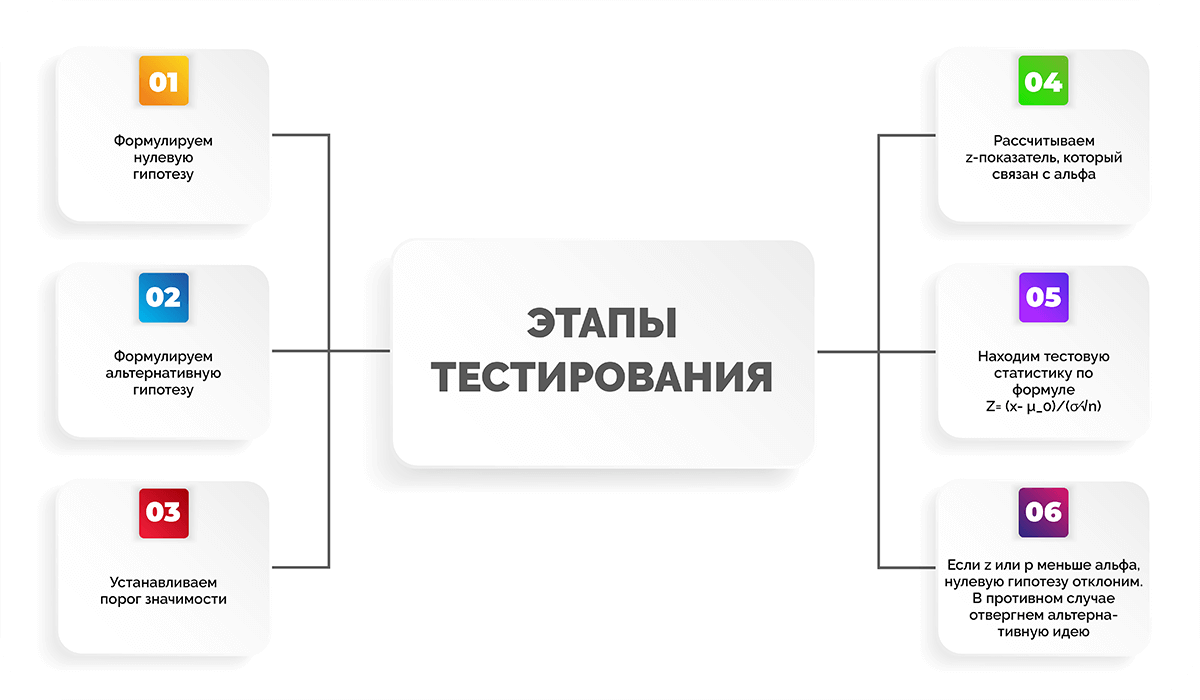
Все тестирование можно разделить на несколько этапов:
- Формулируем нулевую гипотезу.
- Формулируем альтернативную гипотезу.
- Устанавливаем порог значимости.
- Рассчитываем z-показатель, который связан с альфа.
- Находим тестовую статистику по формуле
.
- Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.
Порог вероятности
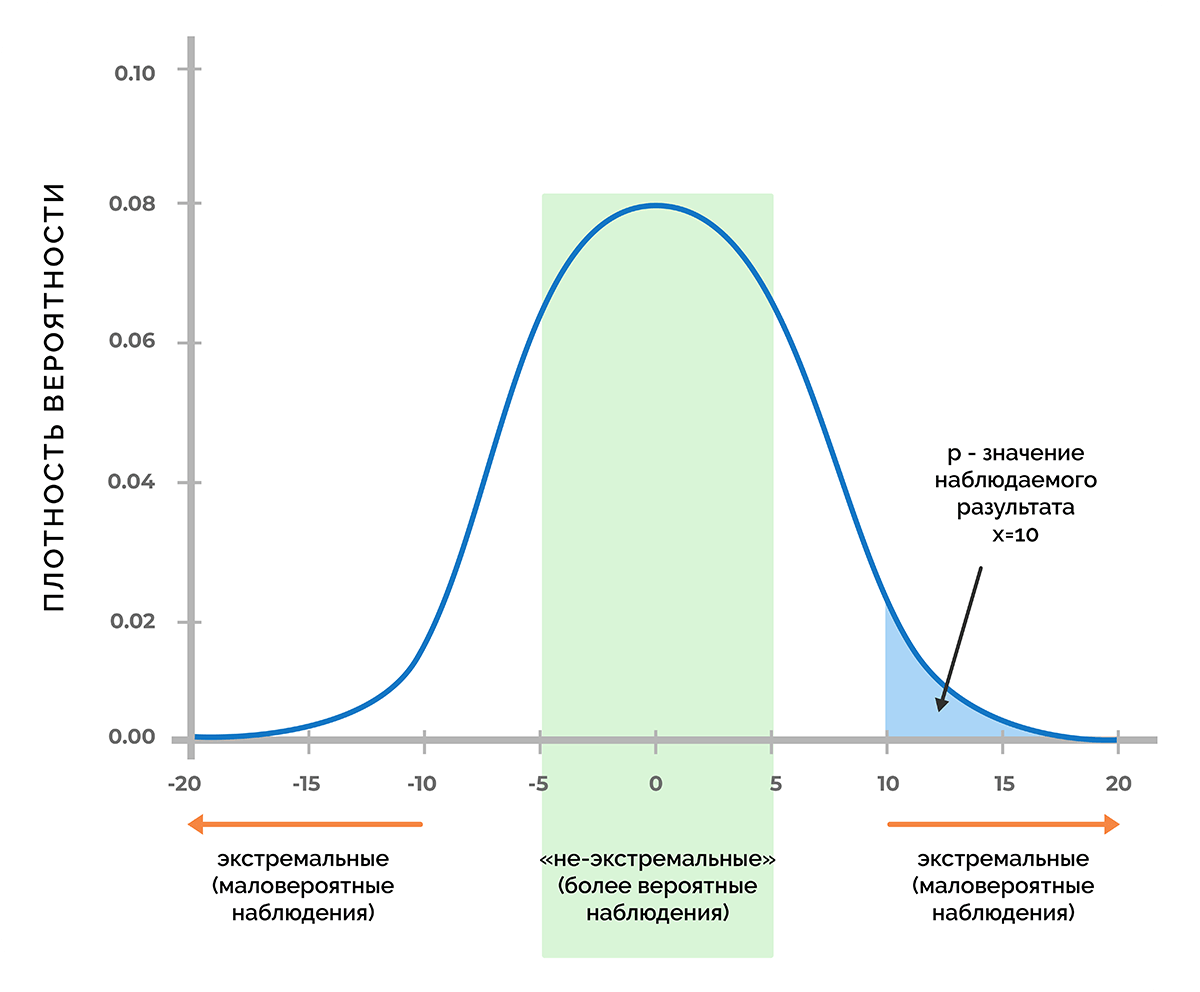
В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.
Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.
Доверительные уровни
Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.
Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.
|
Доверительный уровень |
Стандартное отклонение (z-оценка) |
Вероятность (p-уровень) |
|
90% |
< -1,65 или > +1,65 |
< 0,10 |
|
95% |
< -1,96 или > +1,96 |
< 0,05 |
|
99% |
< -2,58 или > +2,58 |
< 0,01 |
Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.
Проверка статистических гипотез
Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).
Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.
Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии
Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.
В статистике применяется рандомизация и нормализация нулевой гипотезы.
Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.
Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.
Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.
Подход p-value к проверке гипотез
Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.
Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.
Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.
Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».
Как рассчитать P-value
Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.
Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.
Как рассчитать p-значение, используя тестовую статистику
Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.
Левосторонний эксперимент:
P-value = cdf (x)
Правосторонний эксперимент:
P-value = 1 – cdf (x)
Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}
Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.
Пошаговый алгоритм расчета p-значения
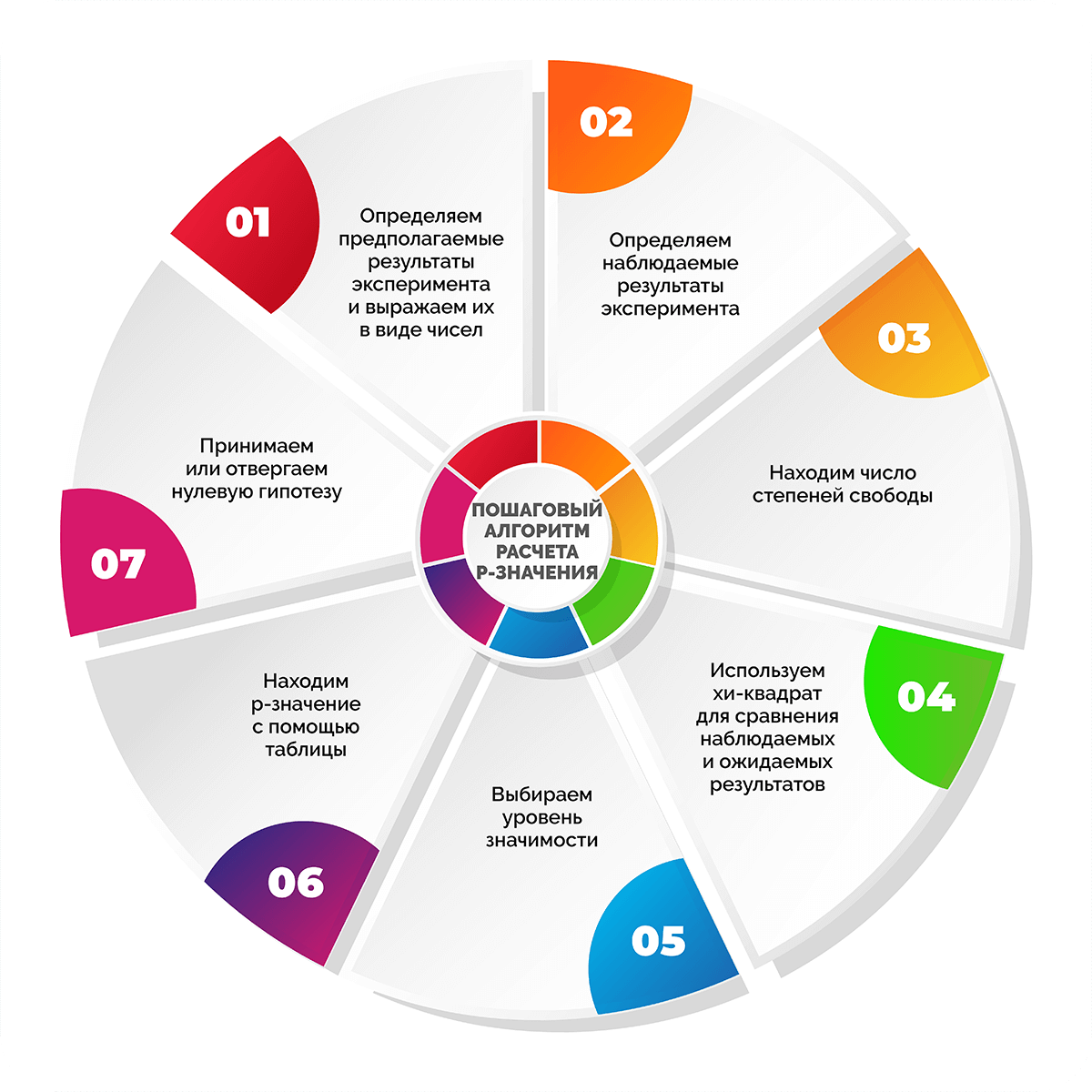
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.
Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.
Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.
Шаг 3. Находим число степеней свободы
Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.
Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.
В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.
Число степеней свободы = 2 – 1 = 1.
Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.
Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов
Хи-квадрат (х2) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.
где:
о – наблюдаемое значение;
е – ожидаемое значение.
Подставляем наши цифры в уравнение и учитываем, что 
х2 = ((220 – 200)2/200) + ((80 – 100)2/100) = ((20)2/200)) + ((-20)2/100) = (400/200) + (400/100) = 2 + 4 = 6.
Шаг 5. Выбираем уровень значимости
Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.
Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.
В нашем случае примем статистическую значимость, равную 0,05.
Шаг 6. Находим p-значение с помощью таблицы
Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.
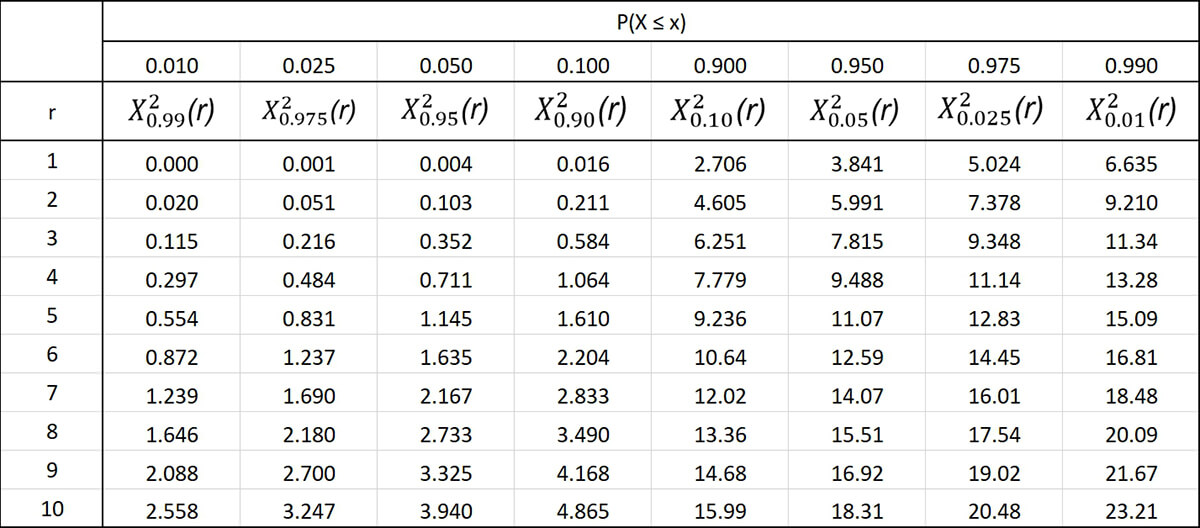
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.
Шаг 7. Принимаем или отвергаем нулевую гипотезу
Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.
В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.
Как интерпретировать P-значение
P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.
P-значение – это…
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
Что нужно помнить о P-значениях
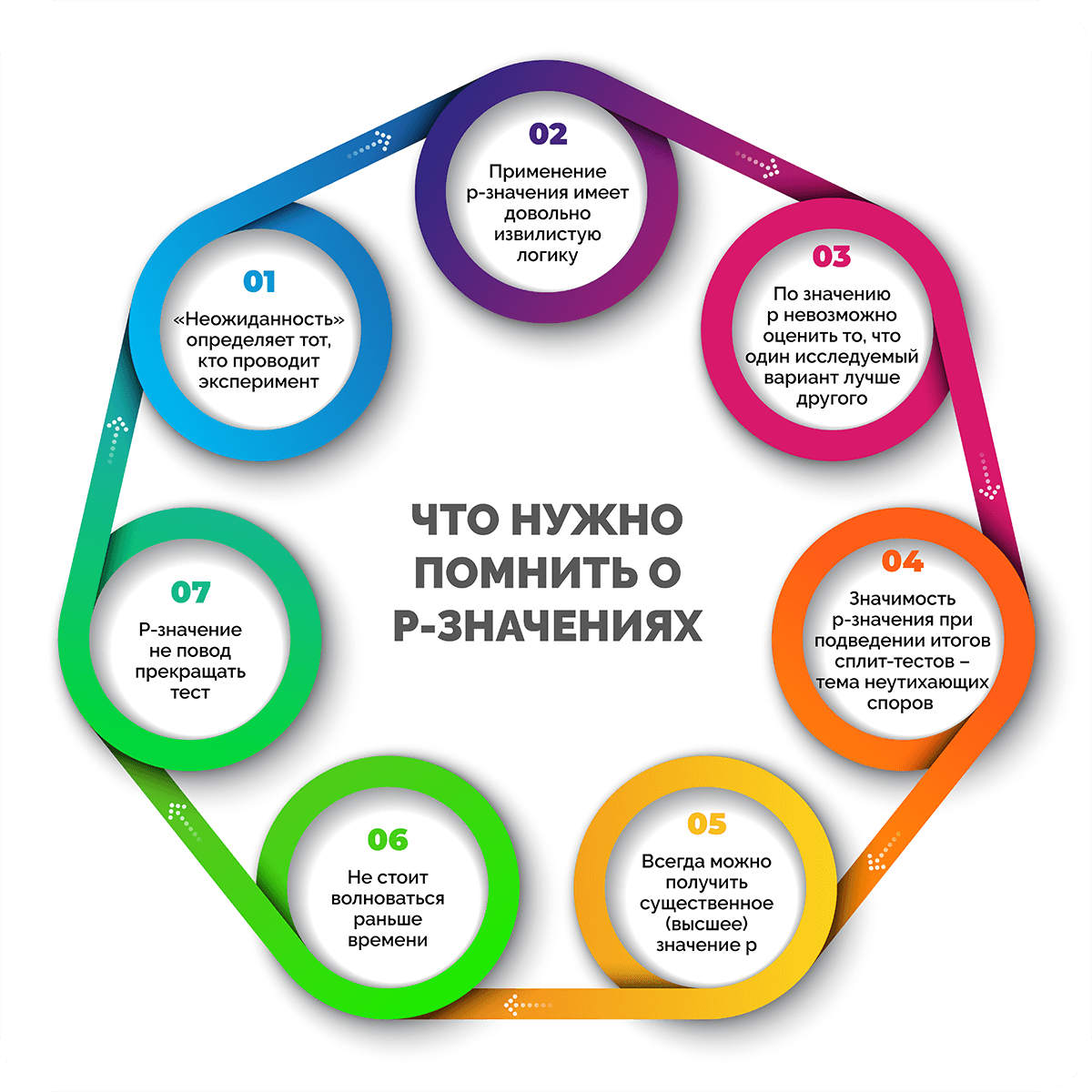
- «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
- Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
- По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
- Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
- Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
- Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
- P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.
Примеры интерпретации P-значений
На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.
По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.
Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.
Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.
Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.
Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.
Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.
Часто задаваемые вопросы
P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.
Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.
Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.
Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:
- При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
- Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.
Заключение
Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Предыдущий пост см. здесь.
Проверка статистических гипотез
Для статистиков и исследователей данных проверка статистической гипотезы представляет собой формальную процедуру. Стандартный подход к проверке статистической гипотезы подразумевает определение области исследования, принятие решения в отношении того, какие переменные необходимы для измерения предмета изучения, и затем выдвижение двух конкурирующих гипотез. Во избежание рассмотрения только тех данных, которые подтверждают наши субъективные оценки, исследователи четко констатируют свою гипотезу заранее. Затем, основываясь на данных, они применяют выборочные статистики с целью подтвердить либо отклонить эту гипотезу.
Проверка статистической гипотезы подразумевает использование тестовой статистики, т.е. выборочной величины, как функции от результатов наблюдений. Тестовая статистика (test statistic) — это вычисленная из выборочных данных величина, которая используется для оценивания прочности данных, подтверждающих нулевую статистическую гипотезу и служит для выявления меры расхождения между эмпирическими и гипотетическими значениями. Конкретные методы проверки называются тестами, например, z-тест, t-тест (соответственно z-тест Фишера, t-тест Студента) и т.д. в зависимости от применяемых в них тестовых статистик.
Примечание. В отечественной статистической науке используется «туманный» термин «статистика критерия». Туманный потому здесь мы снова наблюдаем мягкую подмену: вместо теста возникает критерий. Если уж на то пошло, то критерий — это принцип или правило. Например, выполняя z-тест, t-тест и т.д., мы соответственно используем z-статистику, t-статистику и т.д. в правиле отклонения гипотезы. Это хорошо резюмируется следующей ниже таблицей:
|
Тестирование гипотезы |
Тестовая статистика |
Правило отклонения гипотезы |
|
z-тесты |
z-статистика |
Если тестовая статистика ≥ z или ≤ -z, то отклонить нулевую гипотезу H0. |
|
t-тесты |
t-статистика |
Если тестовая статистика ≥ t или ≤ -t, то отклонить нулевую гипотезу H0. |
|
Анализ дисперсии (ANOVA) |
F-статистика |
Если тестовая статистика ≥ F, то отклонить нулевую гипотезу H0. |
|
Тесты хи-квадрат |
Статистика хи-квадрат |
Если тестовая статистика ≥ χ, то отклонить нулевую гипотезу H0. |
Для того, чтобы помочь сохранить поток посетителей веб-сайта, дизайнеры приступают к работе над вариантом веб-сайта с использованием всех новейших методов по поддержанию внимания аудитории. Мы хотели бы удостовериться, что наши усилия не напрасны, и поэтому стараемся увеличить время пребывания посетителей на обновленном веб-сайте.
Отсюда главный вопрос нашего исследования состоит в том, «приводит ли обновленный вид веб-сайта к увеличению времени пребывания на нем посетителей»? Мы принимаем решение проверить его относительно среднего значения времени пребывания. Теперь, мы должны изложить две наши гипотезы. По традиции считается, что изучаемые данные не содержат того, что исследователь ищет. Таким образом, консервативное мнение заключается в том, что данные не покажут ничего необычного. Все это называется нулевой гипотезой и обычно обозначается как H0.
При тестировании статистической гипотезы исходят из того, что нулевая гипотеза является истинной до тех пор, пока вес представленных данных, подтверждающих обратное, не сделает ее неправдоподобной. Этот подход к поиску доказательств «в обратную сторону» частично вытекает из простого психологического факта, что, когда люди пускаются на поиски чего-либо, они, как правило, это находят.
Затем исследователь формулирует альтернативную гипотезу, обозначаемую как H1. Она может попросту заключаться в том, что популяционное среднее отличается от базового уровня. Или же, что популяционное среднее больше или меньше базового уровня, либо больше или меньше на некоторую указанную величину. Мы хотели бы проверить, не увеличивает ли обновленный дизайн веб-сайта время пребывания, и поэтому нашей нулевой и альтернативной гипотезами будут следующие:
-
H0: Время пребывания для обновленного веб-сайта не отличается от времени пребывания для существующего веб-сайта
-
H1: Время пребывания для обновленного веб-сайта больше по сравнению с временем пребывания для существующего веб-сайта
Наше консервативное допущение состоит в том, что обновленный веб-сайт никак не влияет на время пребывания посетителей на веб-сайте. Нулевая гипотеза не обязательно должна быть «нулевой» (т.е. эффект отсутствует), но в данном случае, у нас нет никакого разумного оправдания, чтобы считать иначе. Если выборочные данные не поддержат нулевую гипотезу (т.е. если данные расходятся с ее допущением на слишком большую величину, чтобы носить случайный характер), то мы отклоним нулевую гипотезу и предложим альтернативную в качестве наилучшего альтернативного объяснения.
Указав нулевую и альтернативную гипотезы, мы должны установить уровень значимости, на котором мы ищем эффект.
Статистическая значимость
Проверка статистической значимости изначально разрабатывалась независимо от проверки статистических гипотез, однако сегодня оба подхода очень часто используются во взаимодействии друг с другом. Задача проверки статистической значимости состоит в том, чтобы установить порог, за пределами которого мы решаем, что наблюдаемые данные больше не поддерживают нулевую гипотезу.
Следовательно, существует два риска:
-
Мы можем принять расхождение как значимое, когда на самом деле оно возникло случайным образом
-
Мы можем приписать расхождение случайности, когда на самом деле оно показывает истинное расхождение с популяцией
Эти две возможности обозначаются соответственно, как ошибки 1-го и 2-го рода:
|
H0 ложная |
H0 истинная |
|
|
Отклонить H0 |
Истинноотрицательный исход |
Ошибка 1-го рода (ложноположительный исход) |
|
Принять H0 |
Ошибка 2-го рода (ложноотрицательный исход) |
Истинноположительный исход |
Чем больше мы уменьшаем риск совершения ошибок 1-го рода, тем больше мы увеличиваем риск совершения ошибок 2-го рода. Другими словами, с чем большей уверенностью мы хотим не заявлять о наличии расхождения, когда его нет, тем большее расхождение между выборками нам потребуется, чтобы заявить о статистической значимости. Эта ситуация увеличивает вероятность того, что мы проигнорируем подлинное расхождение, когда мы с ним столкнемся.
В статистической науке обычно используются два порога значимости. Это уровни в 5% и 1%. Расхождение в 5% обычно называют значимым, а расхождение в 1% — крайне значимым. В формулах этот порог часто обозначается греческой буквой α (альфа) и называется уровнем значимости. Поскольку, отсутствие эффекта по результатам эксперимента может рассматриваться как неуспех (эксперимента либо обновленного веб-сайта, как в нашем случае), то может возникнуть желание корректировать уровень значимости до тех пор, пока эффект не будет найден. По этой причине классический подход к проверке статистической значимости требует, чтобы мы устанавливали уровень значимости до того, как обратимся к нашим данным. Часто выбирается уровень в 5%, и поэтому мы на нем и остановимся.
Проверка обновленного дизайна веб-сайта
Веб-команда в AcmeContent была поглощена работой, конструируя обновленный веб-сайт, который будет стимулировать посетителей оставаться на нем в течение более длительного времени. Она употребила все новейшие методы и, в результате мы вполне уверены, что веб-сайт покажет заметное улучшение показателя времени пребывания.
Вместо того, чтобы запустить его для всех пользователей сразу, в AcmeContent хотели бы сначала проверить веб-сайт на небольшой выборке посетителей. Мы познакомили веб-команду с понятием искаженности выборки, и в результате там решили в течение одного дня перенаправлять случайные 5% трафика на обновленный веб-сайт. Результат с дневным трафиком был нам предоставлен одним текстовым файлом. Каждая строка показывает время пребывания посетителей. При этом, если посетитель пользовался исходным дизайном, ему присваивалось значение «0», и если он пользовался обновленным (и надеемся, улучшенным) дизайном, то ему присваивалось значение «1».
Выполнение z-теста
Ранее при тестировании с интервалами уверенности мы располагали лишь одним популяционным средним, с которым и выполнялось сравнение.
При тестировании нулевой гипотезы с помощью z-теста мы имеем возможность сравнивать две выборки. Посетители, которые видели обновленный веб-сайт, отбирались случайно, и данные для обеих групп были собраны в тот же день, чтобы исключить другие факторы с временной зависимостью.
Поскольку в нашем распоряжении имеется две выборки, то и стандартных ошибок у нас тоже две. Z-тест выполняется относительно объединенной стандартной ошибки, т.е. квадратного корня суммы дисперсий (вариансов), деленных на размеры выборок. Она будет такой же, что и результат, который мы получим, если взять стандартную ошибку обеих выборок вместе:
Здесь σ2a — это дисперсия выборки a, σ2b — дисперсия выборки b и соответственно na и nb — размеры выборок a и b. На Python объединенная стандартная ошибка вычисляется следующим образом:
def pooled_standard_error(a, b, unbias=False):
'''Объединенная стандартная ошибка'''
std1 = a.std(ddof=0) if unbias==False else a.std()
std2 = b.std(ddof=0) if unbias==False else b.std()
x = std1 ** 2 / a.count()
y = std2 ** 2 / b.count()
return sp.sqrt(x + y)С целью выявления того, является ли видимое нами расхождение неожиданно большим, можно взять наблюдавшиеся расхождения между средними значениями на объединенной стандартной ошибке. Эту статистическую величину принято обозначать переменной z:
Используя функции pooled_standard_error, которая вычисляет объединенную стандартную ошибку, z-статистику можно получить следующим образом:
def z_stat(a, b, unbias=False):
return (a.mean() - b.mean()) / pooled_standard_error(a, b, unbias)Соотношение z объясняет, насколько средние значения отличаются относительно величины, которую мы ожидаем при заданной стандартной ошибке. Следовательно, z-статистика сообщает нам о том, на какое количество стандартных ошибок расходятся средние значения. Поскольку стандартная ошибка имеет нормальное распределение вероятностей, мы можем связать это расхождение с вероятностью, отыскав z-статистику в нормальной ИФР:
def z_test(a, b):
return stats.norm.cdf([ z_stat(a, b) ])В следующем ниже примере z-тест используется для сравнения результативность двух веб-сайтов. Это делается путем группировки строк по номеру веб-сайта, в результате чего возвращается коллекция, в которой конкретному веб-сайту соответствует набор строк. Мы вызываем groupby('site')['dwell-time'] для конвертирования набора строк в набор значений времени пребывания. Затем вызываем функцию get_group с номером группы, соответствующей номеру веб-сайта:
def ex_2_14():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе z-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
print('a n: ', a.count())
print('b n: ', b.count())
print('z-статистика:', z_stat(a, b))
print('p-значение: ', z_test(a, b))a n: 284
b n: 16
z-статистика: -1.6467438180091214
p-значение: [0.04980536]Установление уровня значимости в размере 5% во многом аналогично установлению интервала уверенности шириной 95%. В сущности, мы надеемся убедиться, что наблюдавшееся расхождение попадает за пределы 95%-го интервала уверенности. Если это так, то мы можем утверждать, что нашли результат с 5%-ым уровнем значимости.
P-значение — это вероятность совершения ошибки 1-го рода в результате неправильного отклонения нулевой гипотезы, которая в действительности является истинной. Чем меньше p-значение, тем больше определенность в том, что нулевая гипотеза является ложной, и что мы нашли подлинный эффект.
Этот пример возвращает значение 0.0498, или 4.98%. Поскольку оно немногим меньше нашего 5% порога значимости, мы можем утверждать, что нашли нечто значимое.
Приведем еще раз нулевую и альтернативную гипотезы:
-
H0: Время пребывания на обновленном веб-сайте не отличается от времени пребывания на существующем веб-сайте
-
H1: Время пребывания на обновленном веб-сайте превышает время пребывания на существующем веб-сайте.
Наша альтернативная гипотеза состоит в том, что время пребывания на обновленном веб-сайте больше.
Мы готовы заявить о статистической значимости, и что время пребывания на обновленном веб-сайте больше по сравнению с существующим веб-сайтом, но тут есть одна трудность — чем меньше размер выборки, тем больше неопределенность в том, что выборочное стандартное отклонение совпадет с популяционным. Как показано в результатах предыдущего примера, наша выборка из обновленного веб-сайта содержит всего 16 посетителей. Столь малые выборки делают невалидным допущение о том, что стандартная ошибка нормально распределена.
К счастью, существует тест и связанное с ним распределение, которое моделирует увеличенную неопределенность стандартных ошибок для выборок меньших размеров.
t-распределение Студента
Популяризатором t-распределения был химик, работавший на пивоварню Гиннес в Ирландии, Уилльям Госсетт, который включил его в свой анализ темного пива Стаут.
В 1908 Уильям Госсет опубликовал статью об этой проверке в журнале Биометрика, но при этом по распоряжению своего работодателя, который рассматривал использованную Госсеттом статистику как коммерческую тайну, был вынужден использовать псевдоним. Госсет выбрал псевдоним «Студент».
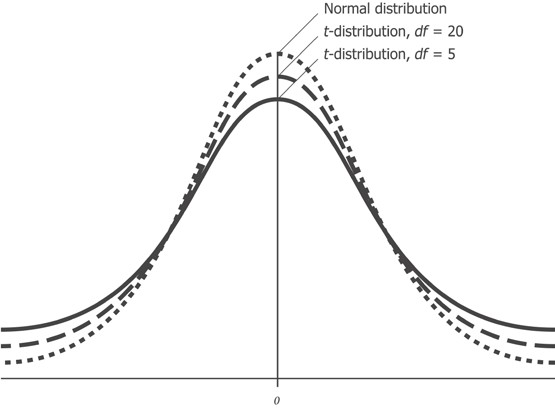
В то время как нормальное распределение полностью описывается двумя параметрами — средним значением и стандартным отклонением, t-распределение описывается лишь одним параметром, так называемыми степенями свободы. Чем больше степеней свободы, тем больше t-распределение похоже на нормальное распределение с нулевым средним и стандартным отклонением, равным 1. По мере уменьшения степеней свободы, это распределение становится более широким с более толстыми чем у нормального распределения, хвостами.
Приведенный выше рисунок показывает, как t-распределение изменяется относительно нормального распределения при наличии разных степеней свободы. Более толстые хвосты для выборок меньших размеров соответствуют увеличенной возможности наблюдать более крупные отклонения от среднего значения.
Степени свободы
Степени свободы, часто обозначаемые сокращенно df от англ. degrees of freedom, тесно связаны с размером выборки. Это полезная статистика и интуитивно понятное свойство числового ряда, которое можно легко продемонстрировать на примере.
Если бы вам сказали, что среднее, состоящее из двух значений, равно 10 и что одно из значений равно 8, то Вам бы не потребовалась никакая дополнительная информация для того, чтобы суметь заключить, что другое значение равно 12. Другими словами, для размера выборки, равного двум, и заданного среднего значения одно из значений ограничивается, если другое известно.
Если напротив вам говорят, что среднее, состоящее из трех значений, равно 10, и первое значение тоже равно 10, то Вы были бы не в состоянии вывести оставшиеся два значения. Поскольку число множеств из трех чисел, начинающихся с 10, и чье среднее равно 10, является бесконечным, то прежде чем вы сможете вывести значение третьего, второе тоже должно быть указано.
Для любого множества из трех чисел ограничение простое: вы можете свободно выбрать первые два числа, но заключительное число ограничено. Степени свободы могут таким образом быть обобщены следующим образом: количество степеней свободы любой отдельной выборки на единицу меньше размера выборки.
При сопоставлении двух выборок степени свободы на две единицы меньше суммы размеров этих выборок, что равно сумме их индивидуальных степеней свободы.
t-статистика
При использовании t-распределения мы обращаемся к t-статистике. Как и z-статистика, эта величина количественно выражает степень маловероятности отдельно взятого наблюдавшегося отклонения. Для двухвыборочного t-теста соответствующая t-статистика вычисляется следующим образом:
Здесь Sa̅b̅ — это объединенная стандартная ошибка. Объединенная стандартная ошибка вычисляется таким же образом, как и раньше:
Однако это уравнение допускает наличие информации о популяционных параметрах σa и σb, которые можно аппроксимировать только на основе крупных выборок. t-тест предназначен для малых выборок и не требует от нас принимать допущения о поплуляционной дисперсии (вариансе).
Как следствие, объединенная стандартная ошибка для t-теста записывается как квадратный корень суммы стандартных ошибок:
На практике оба приведенных выше уравнения для объединенной стандартной ошибки дают идентичные результаты при заданных одинаковых входных последовательностях. Разница в математической записи всего лишь служит для иллюстрации того, что в условиях t-теста мы на входе зависим только от выборочных статистик. Объединенная стандартная ошибка может быть вычислена следующим образом:
def pooled_standard_error_t(a, b):
'''Объединенная стандартная ошибка для t-теста'''
return sp.sqrt(standard_error(a) ** 2 +
standard_error(b) ** 2)Хотя в математическом плане t-статистика и z-статистика представлены по-разному, на практике процедура вычисления обоих идентичная:
t_stat = z_stat
def ex_2_15():
'''Вычисление t-статистики
двух вариантов дизайна веб-сайта'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_stat(a, b)-1.6467438180091214Различие между двумя выборочными показателями является не алгоритмическим, а концептуальным — z-статистика применима только тогда, когда выборки подчинены нормальному распределению.
t-тест
Разница в характере работы t-теста вытекает из распределения вероятностей, из которого вычисляется наше p-значение. Вычислив t-статистику, мы должны отыскать ее значение в t-распределении, параметризованном степенями свободы наших данных:
def t_test(a, b):
df = len(a) + len(b) - 2
return stats.t.sf([ abs(t_stat(a, b)) ], df)Значение степени свободы обеих выборок на две единицы меньше их размеров, и для наших выборок составляет 298.
Напомним, что мы выполняем проверку статистической гипотезы. Поэтому выдвинем нашу нулевую и альтернативную гипотезы:
-
H0: Эта выборка взята из популяции с предоставленным средним значением
-
H1: Эта выборка взята из популяции со средним значением большего размера
Выполним следующий ниже пример:
def ex_2_16():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе t-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test(a, b)array([ 0.05033241])Этот пример вернет p-значение, составляющее более 0.05. Поскольку оно больше α, равного 5%, который мы установили для проверки нулевой гипотезы, то мы не можем ее отклонить. Наша проверка с использованием t-теста значимого расхождения между средними значениями не обнаружила. Следовательно, наш едва значимый результат z-теста отчасти объясняется наличием слишком малой выборки.
Двухсторонние тесты
В нашей альтернативной гипотезе было принято неявное допущение, что обновленный веб-сайт будет работать лучше существующего. В процедуре проверки нулевой статистической гипотезы предпринимаются особые усилия для обеспечения того, чтобы при поиске статистической значимости мы не делали никаких скрытых допущений.
Проверки, при выполнении которых мы ищем только значимое количественное увеличение или уменьшение, называются односторонними и обычно не приветствуются, кроме случая, когда изменение в противоположном направлении было бы невозможным. Название термина «односторонний» обусловлено тем, что односторонняя проверка размещает всю α в одном хвосте распределения. Не делая проверок в другом направлении, проверка имеет больше мощности отклонить нулевую гипотезу в отдельно взятом направлении и, в сущности, понижает порог, по которому мы судим о результате как значимом.
Статистическая мощность — это вероятность правильного принятия альтернативной гипотезы. Она может рассматриваться как способность проверки обнаруживать эффект там, где имеется искомый эффект.
Хотя более высокая статистическая мощность выглядит желательной, она получается за счет наличия большей вероятности совершить ошибку 1-го рода. Правильнее было бы допустить возможность того, что обновленный веб-сайт может в действительности оказаться хуже существующего. Этот подход распределяет нашу α одинаково по обоим хвостам распределения и обеспечивает значимый результат, не искаженный под воздействием априорного допущения об улучшении работы обновленного веб-сайта.
В действительности в модуле stats библиотеки scipy уже предусмотрены функции для выполнения двухвыборочных t-проверок. Это функция stats.ttest_ind. В качестве первого аргумента мы предоставляем выборку данных и в качестве второго — выборку для сопоставления. Если именованный аргумент equal_var равен True, то выполняется стандартная независимая проверка двух выборок, которая предполагает равные популяционные дисперсии, в противном случае выполняется проверка Уэлша (обратите внимание на служебную функцию t_test_verbose, (которую можно найти среди примеров исходного кода в репо):
def ex_2_17():
'''Двухсторонний t-тест'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test_verbose(a, sample2=b, fn=stats.ttest_ind) #t-тест Уэлша{'p-значение': 0.12756432502462475,
'степени свободы ': 17.761382349686098,
'интервал уверенности': (76.00263198799597, 99.89877646270826),
'n1 ': 284,
'n2 ': 16,
'среднее x ': 87.95070422535211,
'среднее y ': 122.0,
'дисперсия x ': 10463.941024237296,
'дисперсия y ': 6669.866666666667,
't-статистика': -1.5985205593851322}По результатам t-теста служебная функция t_test_verbose возвращает много информации и в том числе p-значение. P-значение примерно в 2 раза больше того, которое мы вычислили для односторонней проверки. На деле, единственная причина, почему оно не совсем в два раза больше, состоит в том, что в модуле stats имплементирован легкий вариант t-теста, именуемый t-тестом Уэлша, который немного более робастен, когда две выборки имеют разные стандартные отклонения. Поскольку мы знаем, что для экспоненциальных распределений среднее значение и дисперсия тесно связаны, то этот тест немного более строг в применении и даже возвращает более низкую значимость.
Одновыборочный t-тест
Независимые выборки в рамках t-тестов являются наиболее распространенным видом статистического анализа, который обеспечивает очень гибкий и обобщенный способ установления, что две выборки представляют одинаковую либо разную популяцию. Однако в случаях, когда популяционное среднее уже известно, существует еще более простая проверка, представленная функцией библиотеки sciзy stats.ttest_1samp.
Мы передаем выборку и популяционное среднее относительно которого выполняется проверка. Так, если мы просто хотим узнать, не отличается ли обновленный веб-сайт значимо от существующего популяционного среднего времени пребывания, равного 90 сек., то подобную проверку можно выполнить следующим образом:
def ex_2_18():
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
return t_test_verbose(b, mean=90, fn=stats.ttest_1samp) {'p-значение ': 0.13789520958229415,
'степени свободы df ': 15.0,
'интервал уверенности': (78.4815276659039, 165.5184723340961),
'n1 ': 16,
'среднее x ': 122.0,
'дисперсия x ': 6669.866666666667,
't-статистика ': 1.5672973291495713}Служебная функция t_test_verbose не только возвращает p-значение для выполненной проверки, но и интервал уверенности для популяционного среднего. Интервал имеет широкий диапазон между 78.5 и 165.5 сек., и, разумеется, перекрывается 90 сек. нашего теста. Как раз он и объясняет, почему мы не смогли отклонить нулевую гипотезу.
Многократные выборки
В целях развития интуитивного понимания относительно того, каким образом t-тест способен подтвердить и вычислить эти статистики из столь малых данных, мы можем применить подход, который связан с многократными выборками, от англ. resampling. Извлечение многократных выборок основывается на допущении о том, что каждая выборка является лишь одной из бесконечного числа возможных выборок из популяции. Мы можем лучше понять природу того, какими могли бы быть эти другие выборки, и, следовательно, добиться лучшего понимания опорной популяции, путем извлечения большого числа новых выборок из нашей существующей выборки.
На самом деле существует несколько методов взятия многократных выборок, и мы обсудим один из самых простых — бутстрапирование. При бустрапировании мы генерируем новую выборку, неоднократно извлекая из исходной выборки случайное значение с возвратом до тех пор, пока не сгенерируем выборку, имеющую тот же размер, что и оригинал. Поскольку выбранные значения возвращаются назад после каждого случайного отбора, то в новой выборке то же самое исходное значение может появляться многократно. Это как если бы мы неоднократно вынимали случайную карту из колоды игральных карт и каждый раз возвращали вынутую карту назад в колоду. В результате время от времени мы будем иметь карту, которую мы уже вынимали.
Бутстраповская выборка, или бутстрап, — синтетический набор данных, полученный в результате генерирования повторных выборок (с возвратом) из исследуемой выборки, используемой в качестве «суррогатной популяции», в целях аппроксимации выборочного распределения статистики (такой как, среднее, медиана и др.).
В библиотеке pandas при помощи функции sample можно легко извлекать бутстраповские выборки и генерировать большое число многократных выборок. Эта функция принимает ряд опциональных аргументов, в т.ч. n (число элементов, которые нужно вернуть из числового ряда), axis (ось, из которой извлекать выборку) и replace (выборка с возвратом или без), по умолчанию равный False. После этой функции можно задать метод агрегирования, вычисляющий сводную статистику в отношении бутстраповских выборок:
def ex_2_19():
'''Построение графика синтетических времен пребывания
путем извлечения бутстраповских выборок'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
xs = [b.sample(len(b), replace=True).mean() for _ in range(1000)]
pd.Series(xs).hist(bins=20)
plt.xlabel('Бутстрапированные средние значения времени пребывания, сек.')
plt.ylabel('Частота')
plt.show()Приведенный выше пример наглядно показывает результаты на гистограмме:
Гистограмма демонстрирует то, как средние значения изменялись вместе с многократными выборками, взятыми из времени пребывания на обновленном веб-сайте. Хотя на входе имелась лишь одна выборка, состоящая из 16 посетителей, бутстрапированные выборки очень четко просимулировали стандартную ошибку изначальной выборки и позволили визуализировать интервал уверенности (между 78 и 165 сек.), вычисленный ранее в результате одновыборочного t-теста.
Благодаря бутстрапированию мы просимулировали взятие многократных выборок, при том, что у нас на входе имелась всего одна выборка. Этот метод обычно применяется для оценивания параметров, которые мы не способны или не знаем, как вычислить аналитически.
Проверка многочисленных вариантов дизайна
Было разочарованием обнаружить отсутствие статистической значимости на фоне увеличенного времени пребывания пользователей на обновленном веб-сайте. Хотя хорошо, что мы обнаружили это на малой выборке пользователей, прежде чем выкладывать его на всеобщее обозрение.
Не позволяя себя обескуражить, веб-команда AcmeContent берется за сверхурочную работу и создает комплект альтернативных вариантов дизайна веб-сайта. Беря лучшие элементы из других проектов, они разрабатывают 19 вариантов для проверки. Вместе с нашим изначальным веб-сайтом, который будет действовать в качестве контрольного, всего имеется 20 разных вариантов дизайна веб-сайта, куда посетители будут перенаправляться.
Вычисление выборочных средних
Веб-команда разворачивает 19 вариантов дизайна обновленного веб-сайта наряду с изначальным. Как отмечалось ранее, каждый вариант дизайна получает случайные 5% посетителей, и при этом наше испытание проводится в течение 24 часов.
На следующий день мы получаем файл, показывающий значения времени пребывания посетителей на каждом варианте веб-сайта. Все они были промаркированы числами, при этом число 0 соответствовало веб-сайту с исходным дизайном, а числа от 1 до 19 представляли другие варианты дизайна:
def ex_2_20():
df = load_data('multiple-sites.tsv')
return df.groupby('site').aggregate(sp.mean)Этот пример сгенерирует следующую ниже таблицу:
|
site |
dwell-time |
|
0 |
79.851064 |
|
1 |
106.000000 |
|
2 |
88.229167 |
|
3 |
97.479167 |
|
4 |
94.333333 |
|
5 |
102.333333 |
|
6 |
144.192982 |
|
7 |
123.367347 |
|
8 |
94.346939 |
|
9 |
89.820000 |
|
10 |
129.952381 |
|
11 |
96.982143 |
|
12 |
80.950820 |
|
13 |
90.737705 |
|
14 |
74.764706 |
|
15 |
119.347826 |
|
16 |
86.744186 |
|
17 |
77.891304 |
|
18 |
94.814815 |
|
19 |
89.280702 |
Мы хотели бы проверить каждый вариант дизайна веб-сайта, чтобы увидеть, не генерирует ли какой-либо из них статистически значимый результат. Для этого можно сравнить варианты дизайна веб-сайта друг с другом следующим образом, причем нам потребуется вспомогательный модуль Python itertools, который содержит набор функций, создающих итераторы для эффективной циклической обработки:
import itertools
def ex_2_21():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
по принципу "каждый с каждым"'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
pairs = [list(x) # найти сочетания из n по k
for x in itertools.combinations(range(len(groups)), 2)]
for pair in pairs:
gr, gr2 = groups.get_group( pair[0] ), groups.get_group( pair[1] )
site_a, site_b = pair[0], pair[1]
a, b = gr['dwell-time'], gr2['dwell-time']
p_val = stats.ttest_ind(a, b, equal_var = False).pvalue
if p_val < alpha:
print('Варианты веб-сайта %i и %i значимо различаются: %f'
% (site_a, site_b, p_val))Однако это было бы неправильно. Мы скорее всего увидим статистическое расхождение между вариантами дизайна, показавшими себя в особенности хорошо по сравнению с вариантами, показавшими себя в особенности плохо, даже если эти расхождения носили случайный характер. Если вы выполните приведенный выше пример, то увидите, что многие варианты дизайна веб-сайта статистически друг от друга отличаются.
С другой стороны, мы можем сравнить каждый вариант дизайна веб-сайта с нашим текущим изначальным значением — средним значением времени пребывания, равным 90 сек., измеренным на данный момент для существующего веб-сайта:
def ex_2_22():
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group( site_a )['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается: %f'
% (site_a, p_val))В результате этой проверки будут идентифицированы два варианта дизайна веб-сайта, которые существенно отличаются:
Вариант 6 веб-сайта значимо отличается: 0.005534
Вариант 10 веб-сайта 10 значимо отличается: 0.006881Малые p-значения (меньше 1%) указывают на то, что существует статистически очень значимые расхождения. Этот результат представляется весьма многообещающим, однако тут есть одна проблема. Мы выполнили t-тест по 20 выборкам данных с уровнем значимости α, равным 0.05. Уровень значимости α определяется, как вероятность неправильного отказа от нулевой гипотезы. На самом деле после 20-кратного выполнения t-теста становится вероятным, что мы неправильно отклоним нулевую гипотезу по крайней мере для одного варианта веб-сайта из 20.
Сравнивая таким одновременным образом многочисленные страницы, мы делаем результаты t-теста невалидными. Существует целый ряд альтернативных технических приемов решения проблемы выполнения многократных сравнений в статистических тестах. Эти методы будут рассмотрены в следующем разделе.
Поправка Бонферрони
Для проведения многократных проверок используется подход, который объясняет увеличенную вероятность обнаружить значимый эффект в силу многократных испытаний. Поправка Бонферрони — это очень простая корректировка, которая обеспечивает, чтобы мы вряд ли совершили ошибки 1-го рода. Она выполняется путем настройки значения уровня значимости для тестов.
Настройка очень простая — поправка Бонферрони попросту делит требуемое значение α на число тестов. Например, если для теста имелось k вариантов дизайна веб-сайта, и α эксперимента равно 0.05, то поправка Бонферрони выражается следующим образом:
Она представляет собой безопасный способ смягчить увеличение вероятности совершения ошибки 1-го рода при многократной проверке. Следующий пример идентичен примеру ex-2-22, за исключением того, что значение α разделено на число групп:
def ex_2_23():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
против исходного (0) с поправкой Бонферрони'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05 / len(groups)
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group(site_a)['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается от исходного: %f'
% (site_a, p_val))Если вы выполните приведенный выше пример, то увидите, что при использовании поправки Бонферрони ни один из веб-сайтов больше не считается статистически значимым.
Метод проверки статистической значимости связан с поддержанием равновесия — чем меньше шансы совершения ошибки 1-го рода, тем больше риск совершения ошибки 2-го рода. Поправка Бонферрони очень консервативна, и весьма возможно, что из-за излишней осторожности мы пропускаем подлинное расхождение.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В заключительном посте, посте №4, этой серии постов мы проведем исследование альтернативного подхода к проверке статистической значимости, который позволяет устанавливать равновесие между совершением ошибок 1-го и 2-го рода, давая нам возможность проверить все 20 вариантов веб-сайта одновременно.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Проверка корректности А/Б тестов
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
5.6. Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Высказывания, имеющие вероятность ошибки р <= 0,05 — называются значимыми.
- Высказывания с вероятностью ошибки р <= 0,01 — очень значимыми,
- А высказывания с вероятностью ошибки р <= 0,001 — максимально значимыми.
В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.
| Вероятность ошибки | Значимость | Обозначение |
| р > 0.05 | Не значимая | ns |
| р <= 0.05 | Значимая | * |
| р <= 0.01 | Очень значимая | ** |
| р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
Статистические гипотезы
Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная гипотезы. Ошибки первого и второго рода. Статистический критерий, наблюдаемое значение критерия. Критическая область. Область принятия нулевой гипотезы; критическая точка. Общая методика построения право-, лево- и двухсторонней критических областей
Понятие и определение статистической гипотезы
Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике, экономике для выяснения того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка , то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина с вероятностью принимает значение из интервала , в этом случае распределение случайной величины может быть любым из класса непрерывных распределений.
Часто распределение величины известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Проверяемая гипотеза называется нулевой и обозначается . Наряду с гипотезой рассматривают одну из альтернативных (конкурирующих) гипотез . Например, если проверяется гипотеза о равенстве параметра некоторому заданному значению , то есть , то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: где — заданное значение, . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием . Так как решение принимается на основе выборки наблюдений случайной величины , необходимо выбрать подходящую статистику, называемую в этом случае статистикой критерия . При проверке простой параметрической гипотезы в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра .
Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, — достоверными; Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность , называемая уровнем значимости. Пусть — множество значений статистики , а — такое подмножество, что при условии истинности гипотезы вероятность попадания статистики критерия в равна , то есть .
Обозначим выборочное значение статистики , вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу , если ; принять гипотезу , если . Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество всех значений статистики критерия , при которых принимается решение отклонить гипотезу , называется критической областью; область называется областью принятия гипотезы .
Уровень значимости определяет размер критической области . Положение критической области на множестве значений статистики зависит от формулировки альтернативной гипотезы . Например, если проверяется гипотеза , а альтернативная гипотеза формулируется как , то критическая область размещается на правом (левом) «хвосте» распределения статистики , т. е. имеет вид неравенства , где — значения статистики , которые принимаются с вероятностями соответственно и при условии, что верна гипотеза . В этом случае критерий называется односторонним (соответственно правосторонним и левосторонним). Если альтернативная гипотеза формулируется как , то критическая область размещается на обоих «хвостах» распределения , то есть определяется совокупностью неравенств и в этом случае критерий называется двухсторонним.
Расположение критической области для различных альтернативных гипотез показано на рис. 30, где — плотность распределения статистики критерия при условии, что верна гипотеза , — область принятия гипотезы, .
Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:
1) сформулировать проверяемую и альтернативную гипотезы;
2) назначить уровень значимости ;
3) выбрать статистику критерия для проверки гипотезы ;
4) определить выборочное распределение статистики при условии, что верна гипотеза ;
5) в зависимости от формулировки альтернативной гипотезы определить критическую область одним из неравенств или совокупностью неравенств и ;
6) получить выборку наблюдений и вычислить выборочные значения статистики критерия;
7) принять статистическое решение: если , то отклонить гипотезу как не согласующуюся с результатами наблюдений; если , то принять гипотезу , т. е. считать, что гипотеза не противоречит результатам наблюдений.
Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
Пример 3. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним и дисперсией л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
Решение. Проверим гипотезу о среднем нормально распределенной генеральной совокупности. Проверку проведем по этапам:
1) проверяемая гипотеза ; альтернативная гипотеза ;
2) уровень значимости ;
3) в качестве статистики критерия используем статистику математического ожидания — выборочное среднее;
4) так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией . При условии, что верна гипотеза , математическое ожидание этого распределения равно 10. Нормированная статистика имеет нормальное распределение;
5) альтернативная гипотеза предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством . По прил. 5 находим ;
б) выборочное значение нормированной статистики критерия
7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза отклоняется: следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу критической области для исходной статистики критерия можно получить из соотношения , откуда , т. е. критическая область для статистики определяется неравенством .
Ошибки первого и второго рода
Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза , отклоняется в соответствии с критерием. Если, тем не менее, гипотеза верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы if о, называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза , т. е. равна уровню значимости
Ошибка второго рода происходит тогда, когда гипотеза принимается, но в действительности верна гипотеза . Вероятность ошибки второго рода вычисляется по формуле
Пример 4. В условиях примера 3 предположим, что наряду с гипотезой л рассматривается альтернативная гипотеза л. В качестве статистики критерия снова возьмем выборочное среднее . Предположим, что критическая область задана неравенством л. Найти вероятности ошибок первого и второго рода для критерия с такой критической областью.
Решение. Найдем вероятность ошибки первого рода. Статистика критерия при условии, что верна гипотеза л, имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной . Используя прил. 5, по формуле (11.1) находим
Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива. При условии, что верна гипотеза л, статистика имеет нормальное распределение с математическим ожиданием, равным 9, и дисперсией, равной . Вероятность ошибки второго рода найдем по формуле (11.2):
Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход топлива 10 л.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
5.6. Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Высказывания, имеющие вероятность ошибки р <= 0,05 — называются значимыми.
- Высказывания с вероятностью ошибки р <= 0,01 — очень значимыми,
- А высказывания с вероятностью ошибки р <= 0,001 — максимально значимыми.
В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.
| Вероятность ошибки | Значимость | Обозначение |
| р > 0.05 | Не значимая | ns |
| р <= 0.05 | Значимая | * |
| р <= 0.01 | Очень значимая | ** |
| р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.



 .
.