При
анализе значений, полученных в ходе
измерений, необходимо дифференцировать
такие понятия, как: истинные значения
физических величин и результаты
измерений.
Истинные
значения физических величин
— это значения, идеально отражающие
свойства данного объекта как в
количественном, так и в качественном
отношении.
Результаты
измерений
представляют собой приближенные оценки
значений физической величины, определенных
путем измерения. Степень приближения
зависит от многих факторов: метода
измерения, технических средств, с помощью
которых проводятся измерения, восприятия
наблюдателя, осуществляющего измерения.
Погрешность
измерения
— количественная характеристика
качества измерения, определяемая
разностью между истинным значением
измеряемой величины и результатами
измерения.
Если
истинное значение измеряемой величины
неизвестно, для получения приближенных
сведений используют действительное
значение.
Действительным
значением
физической величины называют значение,
найденное экспериментально и настолько
приближающееся к истинному значению,
что при необходимости может быть
использовано вместо него.
Погрешность
меры
характеризует отличие номинального
значения меры от истинного значения
воспроизводимой ею величины.
Погрешность
средства измерений
— погрешность, вызванная отклонением
влияющих величин от нормального значения
или их выходом за пределы областей
нормальных значений. Чтобы результат
измерения был максимально приближен к
истинному значению измеряемой величины,
необходимо четко определить вопросы,
связанные с выбором метода измерения,
средства измерения, исполнителя. При
неправильном выборе появляются
методические, инструментальные или
субъективные погрешности измерений.
Главными
причинами
возникновения погрешностей
являются:
—
несовершенство методов измерений;
—
несовершенство технических средств,
используемых для измерения физических
величин;
—
несовершенство органов чувств наблюдателя;
—
влияние индивидуальных особенностей
наблюдателя на восприятие результатов
измерения;
—
влияние условий проведения измерений.
Погрешность
измерения в связи с этим имеет следующую
структуру:
∆и
— инструментальная погрешность
(вследствие несовершенства СИ);
∆м
— методическая погрешность (вследствие
несовершенства метода измерения);
∆отс
— погрешность отсчета (из-за неправильной
оценки шкалы);
∆ст
— статическая погрешность;
∆дин
— динамическая погрешность;
∆0
— основная погрешность;
∆д
— дополнительная погрешность;
∆вз
— погрешность взаимодействия (обмен
мощностью между источником сигнала и
СИ).
Инструментальные
погрешности измерений
— это погрешности применяемых средств
измерений.
Методическая
погрешность
— погрешность за счет либо неточного
описания модели физического процесса,
на основе которых строятся средства
измерений, либо неправильного процесса
эксплуатации.
Погрешность
прибора
— это отличие показаний прибора от
истинного или действительного значения
измеряемой величины.
Приведенная
погрешность прибора
— отношение (в процентах) абсолютной
погрешности прибора к нормирующему
значению: у = 100 / Хнорм; это понятие
используется для сравнительной оценки
точности измерительных устройств. В
соответствии с ГОСТ 8 401—80 Хнорм
принимается равным:
—
арифметической сумме модулей пределов
измерений (если нулевая отметка находится
внутри диапазона измерений);
—
установленному номинальному значению
для СИ с установленным номинальным
значением измеряемой величины;
—
большему из пределов измерений и большему
из модулей пределов измерений для СИ с
равномерной или степенной шкалой (если
нулевая отметка находится на краю или
вне диапазона измерений);
—
всей длине шкалы для приборов с существенно
неравномерной шкалой, при этом абсолютные
погрешности также выражают в единицах
длины;
—
установленному стандартами для
соответствующих видов системы единиц
(СИ) в остальных случаях.
Классификация
погрешностей СИ.
Признаки
классификации:
1.
По способу выражения
— абсолютные, относительные;
Абсолютная
погрешность
измерительного прибора — разность
между показанием прибора и действительным
значением измеряемой величины.
Абсолютная
погрешность, взятая с обратным знаком,
называется поправкой
измерительного прибора.
Относительная
погрешность
измерительного прибора — отношение
абсолютной погрешности прибора к
действительному значению величины,
выраженное в процентах.
Пределы
допускаемой абсолютной погрешности
определяются
по
формуле:
∆=
±α или ∆= ± (α + вх), где х — значение
измеряемой величины; α, в — положительные
числа, не зависящие от х.
Пределы
допускаемой приведенной основной
погрешности определяют по формуле:
γ
= 100 ∆/ Хн = ±р %,
где
Хн — нормирующее значение, выраженное
в тех же единицах, что и х; р — отвлеченное
положительное число, выбираемое из
стандартизованного ряда значений.
Значение
относительной погрешности зависит от
значения измеряемой величины, и
максимальная точность измерений
обеспечивается, если показание прибора
находится во второй половине диапазона
измерений.
Диапазоном
измерения
называется область значений измеряемой
величины, для которой нормированы
допустимые погрешности прибора.
Допускаемой
погрешностью
считается погрешность прибора, при
которой он может быть признан годным и
допущен к применению.
Пределы
допускаемых дополнительных погрешностей
устанавливают в виде дольного значения
предела допускаемой основной погрешности.
Пределы
допускаемой основной погрешности,
которые выражают в форме приведенной
или относительной погрешности,
обозначаются числами, равными этим
пределам в процентах. Для того чтобы
отличить от приведенной относительную
погрешность — класс точности, его
обозначение обводят кружком. Если
погрешность нормирована в процентах
от длины шкалы, то под обозначением
класса ставится знак точности.
Суммарная
погрешность
измерения складывается под влиянием
большого количества факторов из
систематической и случайной составляющих.
2.
По характеру проявления
— систематические, случайные;
Систематической
погрешностью
измерения называют составляющие
суммарной погрешности, определяемые
действием постоянных или закономерно
изменяющихся факторов в процессе
измерительного эксперимента, например
плавных изменений влияющих величин или
погрешностей применяемых при измерениях
образцовых мер. Отличительная ее
особенность заключается в том, что она
остается постоянной или закономерно
изменяется при повторных измерениях
одной и той же величины. До тех пор пока
систематические погрешности больше
случайных, последние можно исключить
из результатов измерений соответствующей
постановкой опыта.
Случайной
погрешностью
измерения называют составляющую
суммарной погрешности измерения,
определяемую действием нерегулярно
проявляющихся факторов, неожиданно
исчезающих или появляющихся с
интенсивностью, которую трудно предвидеть,
например перекосы элементов приборов,
нерегулярные изменения моментов трения
в опорах, флуктуации влияющих величин,
изменения внимания операторов и др. Ее
отличительная особенность состоит в
том, что она случайно изменяется при
повторных измерениях одной и той же
величины.
Интенсивность
проявления большинства случайных
факторов удается свести к общему уровню,
поэтому они примерно одинаково влияют
на формирование случайной погрешности.
Но некоторые из них, например падение
напряжения в сети электропитания, могут
проявиться неожиданно сильно, в результате
чего погрешность выйдет за границы
допустимых значений. Такого рода
случайные погрешности называют грубыми
погрешностями.
Субъективная
погрешность
— погрешность, связанная с квалификацией
оператора и его психологическим
состоянием, а также с несовершенством
зрительной системы человека. Промахи
— это погрешности, связанные с человеческим
фактором, например вызванные неправильным
обращением наблюдателя со средствами
измерений, неверным отсчетом показаний
или ошибками при регистрации результатов.
Такие погрешности нельзя скорректировать.
В
процессе измерения физической величины
систематические и случайные погрешности
проявляются одновременно.
Результаты,
максимально приближенные к истинным
значениям физической величины, получают,
осуществляя многократные наблюдения
за измеряемой величиной и проводя
последующую математическую обработку
опытных данных. Поэтому наиболее важно
изучение погрешности как функции
времени.
В
общем случае погрешность является
случайной функцией времени, но в отличие
от классических функций математического
анализа нельзя сказать, какое значение
она примет в момент времени, можно
указать лишь вероятность появления ее
значений в том или ином интервале.
Сечением
случайной функции
называется погрешность измерений,
соответствующая каждому моменту времени.
В каждом сечении можно найти среднее
значение погрешности, относительно
которого группируются погрешности
различных форм.
Систематические
погрешности можно тем или иным способом
исключить из результатов наблюдений и
рассматривать только случайные
погрешности, средние значения которых
равны нулю в каждом сечении, предположив,
что случайные погрешности в различных
сечениях не зависят друг от друга. Тогда
случайную погрешность можно рассматривать
как случайную величину, а ее значения
при каждом из многократных наблюдений
одной и той же физической величины —
как результаты независимых наблюдений
над ней. Поэтому, как правило, для оценки
случайной погрешности пользуются
статистическими методами.
-
По
отношению к условиям применения
— основные, определяемые в нормальных
условиях
применения, и дополнительные, возникающие
вследствие отклонения какой-либо из
влияющих величин (температуры,
относительной влажности, напряжения
сети переменного тока и т.п.) от ее
нормального значения. Если прибор
работает в нормальных условиях, то
дополнительная погрешность равна нулю
и присутствует только основная
погрешность. Статической
называют погрешность,
возникающую при измерении постоянной
во времени величины.
Динамической
погрешностью
называют разность между погрешностью
в динамическом режиме, т.е. погрешностью
при измерении переменной во времени
величины, и статической погрешностью,
которая соответствует значению измеряемой
величины в данный момент времени.
Аддитивная
погрешность
— погрешность, которая искажает результат
за счет арифметического суммирования
и не зависит от абсолютного значения
измеряемой величины. Абсолютные
аддитивные погрешности не зависят от
чувствительности измерительного прибора
и постоянны для всего диапазона измерений.
От значений абсолютной аддитивной
погрешности зависит наименьшее значение
величины, которое может быть определено
измерительным прибором.
Мультипликативная
погрешность
— погрешность, которая изменяется с
изменением значений измеряемых величин,
например при изменении чувствительности
средства измерения.
Мультипликативные
погрешности пропорциональны значению
измеряемой величины и чувствительности
прибора. Источники мультипликативной
погрешности — действие влияющих величин
на параметры элементов и узлов средств
измерений.
Качество
измерительных приборов.
Качество
— это степень соответствия изделия
своему назначению. Соответственно о
качестве измерительного прибора следует
судить по тому, насколько полно исполняется
и реализуется цель измерения — получение
информации об объекте измерения,
необходимой для его управления.
Представление о цели измерения связывает
задачи измерения и задачи создания
методов и СИ с использованием результатов
измерений для управления реальными
объектами, следовательно, эффективность
управления объектами во многом
определяется качественными показателями
СИ.
Обобщающими
показателями качества СИ можно считать:
предел допускаемой погрешности,
долговечность, допуск на долговечность,
значения ограничений.
Метрологические
характеристики
являются основными характеристиками
свойств СИ, оказывающими определяющее
влияние на их обобщенные показатели
качества.
Метрологические
характеристики разделяются на шесть
групп (в соответствии с ГОСТ 8.009—84):
—
динамические характеристики (полные,
частные);
—
характеристики влияния на инструментальную
составляющую погрешности измерений
(входной импеданс, выходной импеданс);
—
характеристики погрешностей СИ
(систематическая и случайная составляющие,
вариация выходного сигнала, погрешности
СИ, функция распределения погрешностей);
—
характеристики для определения
результатов измерения (функция
преобразования, значения меры, цена
деления шкалы, кодовые характеристики);
—
характеристики чувствительности СИ к
влияющим величинам (функция влияния,
изменение МХ при изменении влияющих
величин);
—
неинформативные параметры выходных
сигналов.
Метрологическая
надежность
— свойство средства измерений сохранять
его метрологическую исправность в
течение заданного интервала времени,
т.е. сохранять соответствие нормируемых
метрологических характеристик
установленным нормам.
Понятие
метрологической надежности неразрывно
связано с понятием метрологического
отказа средства измерения.
Метрологическим
отказом
средства измерения называют выход
показаний измерений за установленные
метрологическими характеристиками
нормы.
Существуют
следующие виды
отказа:
—
внезапный отказ, в результате которого
средство измерений полностью теряет
работоспособность;
—
постоянный отказ, в результате которого
с течением времени метрологические
характеристики выходят за допустимые
пределы.
Главными
показателями
метрологической надежности СИ
являются:
—
безотказность — наработка на отказ;
—
ремонтопригодность — среднее время
восстановления средства измерения;
—
долговечность (средний срок службы, или
средний ресурс) — календарная
продолжительность эксплуатации СИ и
его наработка от ее начала до наступления
такого предельного состояния, при
котором эксплуатация СИ должна быть
прекращена.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Общие вопросы измерений
Терминология
Знание метрологической терминологии, параметров измеряемых сигналов и принятой в нашей стране системы единиц измерения физических величин помогает успешно выполнять измерения и изучать литературу, посвященную измерениям физических величин и измерительным приборам.
Основные метрологические термины:
| Метрология | — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. |
| Измерение | — нахождение значения физической величины опытным путем с помощью специальных технических средств. |
| Прямое измерение | — измерение, при котором искомое значение величины находят непосредственно из опытных данных. Например: измерение напряжения при помощи вольтметра. |
| Косвенное измерение | — измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Например: измерение электрической мощности постоянного тока при помощи вольт- и амперметра (P=U I). |
| Истинное значение физической величины | — значение физической величины, которое идеальным образом отражает в качественном и количественном отношениях соответствующее свойство данного объекта. Истинное значение практически недостижимо. |
| Действительное значение физической величины | — значение, полученное экспериментальным путем и настолько приближающееся к истинному значению, что для данной цели может быть использовано вместо него. |
| Средство измерений | — техническое средство, используемое при измерениях и имеющее нормированные метрологические характеристики. Метрологическими называют характеристики, которые оказывают влияние на результат и погрешность измерения (например, рабочий диапазон частот, климатические условия и др.). |
| Погрешность измерения | — отклонение результата измерения от истинного значения измеряемой величины. |
| Погрешность измерительного прибора | — разность между показанием прибора и истинным значением измеряемой величины |
| Точность измерений | — качество измерения, отражающее близость его результатов к истинному значению измеряемой величины. Высокая точность измерений соответствует малым погрешностям. |
| Результат измерения | — значение величины, найденное путем ее измерения. Измерение может быть однократным, и тогда показание средства измерений является результатом измерения, и многократным — в этом случае результат измерения находят путем статистической обработки результатов каждого наблюдения. |
| Показание средства измерений | — это значение измеряемой величины, определяемое по отсчетному устройству средства измерений и выраженное в принятых единицах этой величины. Для нахождения показания прибора Хпр. необходимо величину отсчета N умножить на цену деления шкалы k: Хп.=kN. Цена деления шкалы соответствует интервалу между двумя соседними отметками шкалы, выраженному в значениях измеряемой величины. |
| Принцип измерения | — совокупность физических явлений, на которых основано данное измерение. |
| Метод измерения | — совокупность приемов использования принципов и средств измерений. |
Классификация средств измерений
В силу большого разнообразия средств измерения существует довольно широкий набор их классификационных признаков. Рассмотрим основные.
По функциональному назначению все средства измерения делятся на:
Мера — средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор — средство измерений, предназначенное для выработки сигнала измерительной информации (т.е. сигнала, содержащего количественную информацию об измеряемой физической величине) в форме, доступной для непосредственного восприятия наблюдателем.
Измерительный преобразователь — средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, обработки и хранения, но не обеспечивающей непосредственное восприятия наблюдателем. Наиболее многочисленной группой средств измерений являются измерительные приборы и преобразователи, которые обобщенно называют измерительными устройствами.
Вспомогательное средство измерения — средство измерения величин, влияющих на метрологические характеристики другого средства измерения при его применении.
Измерительная установка — совокупность функционально объединенных средств измерений, предназначенная для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем, и расположенная в одном месте.
Измерительная система — совокупность средств измерений, соединенных между собой каналом общего пользования (КОП) и предназначенная для выработки сигналов измерительной информации в форме, удобной для автоматической обработки. Создание информационно-измерительных систем (ИИС) связано с новым этапом развития измерительной техники — построение автоматизированных ИИС на базе радиоизмерительных приборов общего применения.
По принципу измерений различают электроизмерительные и радиоизмерительные приборы.
Электроизмерительные приборы применяются для измерений на постоянном токе и в области низких частот (20 — 2500 Гц) токов, напряжений, электрических мощностей, частоты, фазовых сдвигов, сопротивлений, емкостей и других величин, характеризующих режим работы электрических цепей и параметры их элементов. Обозначение таких приборов состоит из буквы русского алфавита, характеризующей тип измерительного механизма, и числа, определяющего вид и тип прибора: Д — электродинамические; И — индукционные; М — магнитоэлектрические; Н — самопишущие; Р — меры, измерительные преобразователи, приборы для измерения параметров элементов электрических цепей; С — электростатические; Т — термоэлектрические; Ф — электронные, фотоэлектронные, цифровые; Ц — выпрямительные и комбинированные; Э — электромагнитные. Например: С197 — киловольтметр электростатический. К обозначению могут добавляться буквы М (модернизированный), К (контактный) и др., отмечающие конструктивные особенности или модификации приборов.
Радиоизмерительные приборы применяются для измерения разнообразных электрических и радиотехнических величин как на постоянном токе, так и в широком диапазоне частот, а также для наблюдения и исследования формы радиосигналов и характеристик радиоэлектронных устройств, генерации испытательных сигналов и питания измерительных устройств. Система обозначений данных приборов соответствует ГОСТ 15094-86 и состоит из: буквы русского алфавита, определяющей характер измерений и вид измеряемых величин (таблица 1); цифры (от 1 до 9), обозначающей тип измерительного прибора, и через дефис n-значного числа (n=1, 2, 3), указывающего порядковый номер модели. Например: В7-65 — вольтметр (подгруппа В) универсальный (тип В7) модели номер 65. В обозначении приборов, подвергшихся модернизации, после номера модели добавляется русская буква в алфавитном порядке (например, В7-65А); для обозначения приборов с одинаковыми электрическими характеристиками, различающимися лишь конструктивным исполнением, используется дополнительная цифра, которая пишется через дробь после номера модели (например, В7-65/1). Многофункциональные приборы могут иметь в обозначении типа дополнительную букву «К» (например, СК6-13).
| Подгруппа | Наименование подгруппы |
| А | Приборы для измерения силы тока |
| Б | Источники питания для измерений и измерительных приборов |
| В | Приборы для измерения напряжения |
| Г | Генераторы измерительные |
| Д | Аттенюаторы и приборы для измерения ослаблений |
| Е | Приборы для измерения параметров компонентов и цепей с сосредоточенными постоянными |
| И | Приборы для импульсных измерений |
| К | Комплексные измерительные установки |
| Л | Приборы общего применения для измерения параметров электронных ламп и полупроводниковых приборов |
| М | Приборы для измерения мощности |
| Н | Меры и калибраторы |
| П | Приборы для измерения напряженности поля и радиопомех |
| Р | Приборы для измерения параметров элементов и трактов с распределенными постоянными |
| С | Приборы для наблюдения, измерения и исследования формы сигнала и спектра |
| У | Усилители измерительные |
| Ф | Приборы для измерения фазового сдвига и группового времени запаздывания |
| Х | Приборы для наблюдения и исследования характеристик радиоустройств |
| Ц | Анализаторы логических устройств |
| Ч | Приборы для измерения частоты и времени |
| Ш | Приборы для измерения электрических и магнитных свойств материалов |
| Э | Измерительные устройства коаксиальных и волноводных трактов |
| Я | Блоки радиоизмерительных приборов |
По методу измерений измерительные устройства бывают прямого действия, реализующие метод непосредственной оценки, и устройства использующие метод сравнения.
Простейшим является метод непосредственной оценки, в котором значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора.
Наиболее точным является метод сравнения измеряемой величины с однородной независимой известной величиной. По способу осуществления метод сравнения может быть нулевым, дифференциальным, методом замещения, методом совпадения. При нулевом методе (иначе методе компенсации) результирующий эффект воздействия обеих величин на измерительный прибор доводят до нуля. При дифференциальном методе на измерительный прибор воздействует разность измеряемой и известной величин. При методе замещения измеряемую величину замещают (заменяют) однородной с ней величиной известного размера, который равен размеру замещенной величины, что определяется по сохранению режима в измеряемой цепи. При методе совпадения равенство значений измеряемой и известной величин фиксируется по совпадению отметок шкал, сигналов или другим признакам.
По точности измерений измерительные средства можно разделить на: эталоны, образцовые и рабочие средства измерений.
Эталон единицы — это средство измерений, обеспечивающее воспроизводство и (или) хранение единицы физической величины с целью передачи ее размера образцовым и рабочим средствам измерений.
Образцовое средство измерений — мера или измерительное устройство, служащие для поверки по ним других средств измерений и утвержденные в качестве образцовых.
Рабочее средство измерений — средство применяемое для измерений, не связанных с передачей размера единицы.
По способу обработки сигнала измерительной информации приборы делятся на аналоговые и цифровые.
В аналоговых приборах показания являются непрерывной функцией размера измеряемой величины, т.е. могут, как и измеряемая величина, принимать бесконечное множество значений.
В цифровых приборах непрерывная измеряемая величина дискретизируется по времени, квантуется по уровню, кодируется и в виде цифрового кода отображается на цифровом отсчетом устройстве. В результате показания цифрового прибора могут принимать лишь конечное число значений.
Цифровые средства измерения обеспечивают, как правило, большую точность и быстродействие. Однако не всегда цифровое устройство лучше аналогового. При большом числе одновременно измеряемых величин (контроль сложного объекта) или при динамическом изменении входной величины показания аналоговых приборов воспринимаются легче, обеспечивая оперативность анализа контролируемого процесса. Поэтому для повышения информативности отсчетные устройства современных цифровых приборов могут дополняться, так называемыми, линейными шкалами — определенным образом расположенными сегментами на цифровом индикаторе.
По способу отображения результата измерения аналоговые и цифровые приборы принято разделять на показывающие, допускающие только отсчитывание показаний, и регистрирующие, в которых предусмотрена возможность автоматической и (или) ручной регистрации показаний.
По способу применения и по конструкции измерительные устройства делятся на: щитовые, переносные (портативные) и стационарные.
Объекты исследований и измерений
Объекты исследований характеризуются различными значениями физических величин, неразрывно связанных с объектом.
Объектами электрорадиоизмерений являются значения физических величин, параметры и характеристики сигналов электрорадиоцепей, компонентов и режимов этих цепей. Например, объект исследования — резистор, объекты измерений — сопротивление резистора постоянному току и мощность рассеивания резистора.
Параметры измеряемых сигналов
Мгновенное значение сигнала (x(t)) — значение сигнала в заданный момент времени (рис. 1).
Рис. 1
Максимальное значение сигнала (Xmax) — наибольшее мгновенное значение сигнала на протяжении заданного интервала времени (Ту). Для сигналов синусоидальной формы термин «максимальное значение» часто заменяют термином «амплитуда» (амплитудное значение, Xm).
Минимальное значение сигнала (Xmin) — наименьшее мгновенное значение сигнала на протяжении заданного интервала времени (Ту).
Постоянная составляющая сигнала (Х0) — среднее значение сигнала:
, где Ту — время усреднения.
Для синусоидальных сигналов с периодом Т постоянная составляющая равна:
Средневыпрямленное значение сигнала (Хс.в.) — среднее значение модуля (абсолютной величины) сигнала. Для синусоидальных сигналов:
Для однополярных сигналов:
Среднеквадратическое (действующее, эффективное) значение сигнала Хс.к. — корень квадратный из среднего значения квадрата мгновенных значений сигнала.
Для синусоидальных сигналов:
Для измерения с.к. значения сигналов несинусоидальной формы используют один из следующих режимов:
1. Аналогично режиму измерения синусоидальных сигналов при условии, что Т=Ту. В этом случае необходимо учитывать следующее: чем больше форма сигнала отличается от синусоидальной, тем выше погрешность измерения (до 30%-50%). В зарубежной литературе данный режим принято обозначать RMS;
2. С учетом наличия гармонических составляющих (режим True RMS):
, где Хс.к.n — с.к. значение n-ой гармоники;
3. С учетом наличия постоянной составляющей (режим Total RMS):
, где Х0 — постоянная составляющая.
Переменная составляющая сигнала (х~(t)) — разность между мгновенным значением сигнала и его постоянной составляющей:
х~(t)=х(t) — Х0.
Пиковое отклонение «вверх» (Хв.в.) — наибольшее мгновенное значение переменной составляющей сигнала на протяжении заданного интервала времени.
Пиковое отклонение «вниз» (Хв.н.) — наименьшее мгновенное значение переменной составляющей сигнала на протяжении заданного интервала времени, взятое по модулю.
Размах сигнала (Хр.) — разность между максимальным и минимальным значениями сигнала на протяжении заданного интервала времени:
Хр.=Хmax — Xmin=Хв.в. + Хв.н.
Связь между рассмотренными параметрами устанавливается через коэффициент амплитуды (Peak Factor)
, коэффициент формы (Form Factor)
и коэффициент усреднения
Для каждой формы физически реализуемого сигнала все три коэффициента определены (таблица 2), потому измерения одного из значений сигнала достаточно для вычисления и других его параметров.
Таблица 2.
| Форма сигнала | ka | kф | kу |
| Синусоидальная | 1,41 | 1,11 | 1,57 |
| Треугольная | 1,73 | 1,16 | 2 |
| Прямоугольная со скважностью Q | |||
| Меандр | 1 | 1 | 1 |
| Постоянный ток | 1 | 1 | 1 |
Единицы измеряемых физических величин
В нашей стране подлежат обязательному применению единицы Международной системы единиц (СИ), содержащей основные, дополнительные и производные единицы, а также десятичные кратные и дольные от них.
Единицы СИ некоторых электрических величин приведены в таблице 3. В таблице 4 приведены множители и приставки для образования десятичных кратных и дольных единиц.
Таблица 3.
| Электрическая величина | Единица измерений | |||
| наименование | обозначение | наименова-ние | русское обоз-ние |
международное обоз-ние |
| Сила тока | I | ампер | А | A |
| Напряжение, ЭДС | U, E | вольт | В | V |
| Мощность активная | P | ватт | Вт | W |
| Сопротивление | R | ом | Ом | Ω |
| Емкость | C | фарада | Ф | F |
| Индуктивность, взаимная индуктивность |
L, M | генри | Гн | H |
| Частота | f | герц | Гц | Hz |
| Длина волны | λ | метр | м | m |
| Фазовый сдвиг | φ | радиан | рад | rad |
Таблица 4.
| Множитель | Приставка | Множитель | Приставка | ||||
| наименование | обозначение | наименование | обозначение | ||||
| русское | международное | русское | международное | ||||
| 10-18 | атто | а | a | 101 | дека | да | da |
| 10-15 | фемто | ф | f | 102 | гекто | г | h |
| 10-12 | пико | п | p | 103 | кило | к | k |
| 10-9 | нано | н | n | 106 | мега | М | M |
| 10-6 | микро | мк | μ | 109 | гига | Г | G |
| 10-3 | мили | м | m | 1012 | тера | Т | T |
| 10-2 | санти | с | c | 1015 | пета | П | P |
| 10-1 | деци | д | d | 1018 | экса | Э | E |
При проведении абсолютных измерений, основанных на прямых измерениях одной или нескольких основных величин, значение измеряемой величины определяется в единицах СИ. Результат относительных измерений, выполняемых путем отношения одноименных величин, выражается во внесистемных единицах (например, вольт-ампер) или является безразмерным значением (например, значение коэффициента мощности). В радиотехнической практике результат относительных измерений обычно выражается в децибелах, а при измерениях в технике связи дополнительно используется еще одна внесистемная единица — непер.
Децибел (дб) — относительная единица, основанная на десятичном логарифме отношения двух величин одинаковой размерности (мощность, напряжение, ток):
Nдб=10 lg(P2/P1),
Nдб=20 lg(U2/U1)=20 lg(I2/I1).
Непер (неп.) — относительная единица, основанная на натуральном логарифме отношения двух величин одинаковой размерности:
Nнеп.=ln(U2/U1).
Соотношение между относительными единицами определяется следующим образом:
1 дб=0.115 неп.,
1 неп.=8.686 дб.
Погрешности измерений и измерительных приборов
Отклонение результата измерения от истинного значения измеряемой величины является погрешностью измерения.
Абсолютная погрешность измерения (Δизм.) — разность между действительным и истинным значениями измеряемой величины: Δизм.=Хд. — Хи.
Относительная погрешность измерения (δизм.) — отношение абсолютной погрешности измерения к истинному значению измеряемой величины, выраженное в %:
Для проведения любого измерения необходимо правильно выбрать метод измерения, средство измерения и исполнителя (оператора), чтобы полученный результат был максимально приближен к истинному значению измеряемой величины. В противном случае появляются методические, инструментальные или субъективные погрешности измерений.
Инструментальные погрешности измерений зависят от погрешностей применяемых средств измерений.
Абсолютная погрешность измерительного прибора (Δпр.) — разность между показанием прибора и действительным значением измеряемой величины: Δпр.=Хпр. — Хд.
Относительная погрешность измерительного прибора (δпр.) — отношение абсолютной погрешности прибора к действительному (или измеренному, Хпр.) значению величины, выраженное в %:
Значение относительной погрешности зависит от значения измеряемой величины — при постоянной пр. она возрастает с уменьшением Хпр.. Поэтому максимальная точность измерений обеспечивается, когда показание прибора находится во второй половине диапазона измерений. Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые погрешности прибора. Допускаемой погрешностью считается погрешность прибора, при которой он может быть признан годным и допущен к применению.
Для сравнительной оценки точности измерительных устройств пользуются понятием приведенной погрешности прибора (γпр.), под которой понимают выраженное в % отношение абсолютной погрешности прибора к нормирующему значению шкалы:
В качестве XN чаще всего используют конечное значение диапазона измерений.
Погрешность, свойственная измерительному прибору при его эксплуатации в нормальных условиях, называется основной погрешностью. Для большинства средств измерений нормальными условиями эксплуатации считаются следующие: температура окружающей среды 20±5°С, относительная влажность 65±15%, напряжение питания 220 В±10% с частотой 50±1 Гц. При отклонении условий эксплуатации от нормальных (при рабочих условиях) появляются дополнительные погрешности.
Погрешности некоторых измерительных приборов зависят от текущего значения измеряемой величины Хпр., поэтому погрешности таких приборов представляют двучленными выражениями, в которых первое слагаемое не зависит от Хпр. (аддитивная погрешность), а второе зависит (мультипликативная погрешность):
|
|
|
|
|
|
Проявление погрешностей измерений и средств измерений может носить систематический и (или) случайный характер.
Систематическая погрешность — это составляющая погрешности, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одного и того же значения физической величины.
Случайная погрешность — составляющая погрешности, изменяющаяся случайным образом при повторных измерениях одного и того же значения физической величины. Для исключения из результата измерения случайной погрешности проводят многократные измерения и их статистическую обработку.
Общие рекомендации по подбору средств измерений
Средство измерений в зависимости от его назначения и области применения должно удовлетворять определенным требованиям, из которых наиболее общими являются следующие:
- Диапазон измерений должен охватывать все практически необходимые значения измеряемой величины;
- Основная и дополнительная погрешности должны соответствовать решаемым при измерениях задачам;
- Приборы, предназначенные для измерения режима электрических цепей и параметров радиосигналов, не должны существенно влиять на работу исследуемых устройств. Для этого используется последовательная или параллельная схема подключения, либо режим согласованной нагрузки;
- Прибор должен надежно работать при заданных условиях эксплуатации, что достигается применением современной элементной базы и высокотехнологичным монтажом. Использование передовой SMТ-технологии значительно повышает коэффициент надежности современного измерительного оборудования;
- Управление прибором должно быть максимально простым и удобным для пользователя;
- В эпоху глобальной компьютеризации желательно иметь прибор с возможностью подключения к компьютеру (например, через RS-232);
- Прибор должен удовлетворять требованиям техники безопасности при измерениях;
- Если средство измерения предполагается использовать в сфере деятельности метрологического контроля, то оно в обязательном порядке должно иметь сертификат об утверждении типа средств измерений Госстандарта России.
Актуальность последнего пункта для импортных средств измерения диктуется временем: отечественная радиоэлектронная промышленность переживает существенный спад, поэтому для насыщения российского рынка высококачественным измерительным оборудованием необходимо, в первую очередь, обеспечить его метрологический контроль. Задача по внесению средств измерений в Госреестр требует больших финансовых и временных затрат, при этом орган сертификации подтверждает заявленные производителем метрологические характеристики и проверяет их соответствие российским стандартам. В связи с этим далеко не все поставщики импортного оборудования обеспечивают сертификацию предлагаемых средств измерений.
Автор:
Котельник О.В.
Дата публикации:
01.03.2000
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
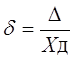
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
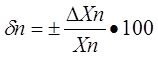
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
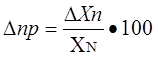
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
Измеряемые величины не могут быть определены абсолютно достоверно. Измерительные инструменты и системы всегда имеют некоторое допустимое отклонение и помехи, которые выражаются степенью неточности. К тому же, необходимо учитывать и особенности конкретных приборов.
В отношении неточности измерений часто используются следующие термины:
- Погрешность — ошибка между истинным и измеренным значением
- Точность — случайный разброс измеренных значений вокруг их среднего
- Разрешение — наименьшая различаемая величина измеренного значения
Часто эти термины путаются. Поэтому здесь я хотел бы подробно рассмотреть вышеуказанные понятия.
Неточность измерения
Неточности измерения могут быть разделены на систематические и случайные измерительные ошибки. Систематические ошибки вызваны отклонениями при усилении и настройкой «нуля» измерительного оборудования. Случайные ошибки вызваны шумом и индуцированными напряжениями и/или токами.
Погрешность и точность
Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением. Точность относится к случайному разбросу измеряемых величин.
Когда мы проводим некоторое число измерений до момента стабилизации напряжения или же какого-то другого параметра, то в измеренных значениях будет наблюдаться некоторая вариация. Это вызвано тепловым шумом в измерительной цепи измерительного оборудования и измерительной установки. Ниже, на левом графике показаны эти изменения.
Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.
Гистограмма
Измеренные значения могут быть изображены в виде гистограммы, как показано справа на рисунке. Гистограмма показывает, как часто наблюдается измеренное значение. Самая высокая точка на гистограмме, это чаще всего наблюдаемое измеренное значение, в случае симметричного распределения равно среднему значению (изображено синей линии на обоих графиках). Черная линия представляет истинное значение параметра. Разница между средним измеренной величины и истинным значением и является погрешностью. Ширина гистограммы показывает разброс отдельных измерений. Этот разброс измерений называется точностью.
Используйте правильные термины
Погрешность и точность, таким образом, имеют различные значения. Поэтому вполне возможно, что измерение является очень точным, но имеющим погрешность. Или наоборот, с малой погрешностью, но не точное. В общем, измерение считается достоверным, если оно точное, и с малой погрешностью.
Погрешность
Погрешность является индикатором корректности измерения. Из-за того, что в одном измерении точность оказывает влияние на погрешность, то учитывается среднее серии измерений.
Погрешность измерительного прибора обычно задается двумя значениями: погрешностью показания и погрешностью по всей шкале. Эти две характеристики вместе определяют общую погрешность измерения. Эти значения погрешности измерения указываются в процентах или в ppm (parts per million, частей на миллион) относительно действуюшего национального стандарта. 1% соответствует 10000 ppm.
Погрешность приводится для указанных температурных диапазонов и для определенного периода времени после калибровки. Обратите внимание, что в разных диапазонах, возможны, и различные погрешности.
Погрешность показаний
Указание процентного отклонения без дополнительной спецификации также относится к показанию. Допустимые отклонения делителей напряжения, точность усиления и абсолютные отклонения при считывании и оцифровке являются причинами этой погрешности.
Неточность показаний в 5% для значения 70 В
Вольтметр, который показывает 70.00 В и имеет спецификацию «± 5% от показаний», будет обладать погрешностью в ±3.5 В (5% от 70 В). Фактическое напряжение будет лежать между 66.5 и 73.5 вольтами.
Погрешность по всей шкале
Этот тип погрешности обусловлен ошибками смещения и ошибками линейности усилителей. Для приборов, которые оцифровывают сигналы, присутствует нелинейность преобразования и погрешности АЦП. Эта характеристика относится ко всему используемому диапазону измерений.
Вольтметр может иметь характеристику «3% шкалы». Если во время измерения выбран диапазон 100 В (равный полной шкале), то погрешность составляет 3% от 100 В = 3 В независимо от измеренного напряжения. Если показание в этом диапазоне 70 В, то реальное напряжение лежит между 67 и 73 вольтами.
Погрешность 3% шкалы в диапазоне 100 В
Из приведенного выше рисунка ясно, что этот тип допустимых отклонений не зависит от показаний. При показании 0 В реальное напряжение лежит между -3 и 3 вольтами.
Погрешность шкалы в цифрах
Часто для цифровых мультиметров приводится погрешность шкалы в разрядах вместо процентного значения.
У цифрового мультиметра с 3½ разрядным дисплеем (диапазон от -1999 до 1999), в спецификации может быть указано «+ 2 цифры». Это означает, что погрешность показания 2 единицы. Например: если выбирается диапазон 20 вольт (± 19.99), то погрешность шкалы составляет ±0.02 В. На дисплее отображается значение 10.00, а фактическое значение будет между 9.98 и 10.02 вольтами.
Вычисление погрешности измерения
Спецификации допустимых отклонений показания и шкалы вместе определяют полную погрешность измерения прибора. Ниже при расчете используются те же значения, что и в приведенных выше примерах:
Точность: ±5% показания (3% шкалы)
Диапазон: 100 В
Показание: 70 В
Полная погрешность измерения вычисляется следующим образом:
В этом случае, полная погрешность ±6.5В. Истинное значение лежит между 63.5 и 76.5 вольтами. На рисунке ниже это показано графически.
Полная неточность для неточностей показания 5% и 3% шкалы для диапазона 100 В и показания 70 В
Процентная погрешность — это отношение погрешности к показанию. Для нашего случая:
Цифры
Цифровые мультиметры могут иметь спецификацию «± 2.0% показания, + 4 цифры». Это означает, что 4 цифры должны быть добавлены к 2% погрешности показания. В качестве примера снова рассмотрим 3½ разрядный цифровой индикатор. Он показывает 5.00 В для выбранного диапазона 20 В. 2% показания будет означать погрешность в 0,1 В. Добавьте к этому численную погрешность (= 0,04 В). Общая погрешность, следовательно, 0,14 В. Истинное значение должно быть в диапазоне между 4.86 и 5,14 вольтами.
Суммарная погрешность
Зачастую в расчет принимается только погрешность измерительного прибора. Но также, дополнительно следует принимать во внимание погрешности измерительных инструментов, в том случае, если они используются. Вот несколько примеров:
Увеличение погрешности при использовании пробника 1:10
Если в процессе измерений используется щуп 1:10, то необходимо учитывать не только измерительную погрешность прибора. На погрешность также влияет входной импеданс используемого прибора и сопротивление щупа, которые вместе составляют делитель напряжения.
Подключенный к осциллографу щуп 1:1
На рисунке выше схематически показан осциллограф с подключенным к нему пробником 1:1. Если мы рассмотрим этот пробник как идеальный (нет сопротивления соединения), то приложенное напряжение передается прямо на вход осциллографа. Погрешность измерения теперь определяется только допустимыми отклонениями аттенюатора, усилителя и цепями, принимающими участие в дальнейшей обработке сигнала и задается производителем прибора. (На погрешность также влияет сопротивление соединения, которое формирует внутреннее сопротивление . Оно включается в заданные допустимые отклонения).
На рисунке ниже показан тот же самый осциллограф, но теперь ко входу подключен щуп 1:10. Этот пробник имеет внутреннее сопротивление соединения и вместе со входным сопротивлением осциллографа
образует делитель напряжения. Допустимое отклонение резисторов в делителе напряжения является причиной его собственной погрешности.
Пробник 1:10, подключенный к осциллографу, вносит дополнительную погрешность
Допустимое отклонение входного сопротивления осциллографа может быть найдено в его спецификации. Допустимое отклонение сопротивления соединения щупа не всегда дано. Тем не менее, погрешность системы заявляется производителем определенного осциллографического пробника для конкретного типа осциллографа. Если щуп используется с другим типом осциллографа, нежели рекомендуемый, то измерительная погрешность становится неопределенной. Этого нужно всегда стараться избегать.
Предположим, что осциллограф имеет допустимое отклонение 1.5% и используется щуп 1:10 с погрешностью в системе 2.5%. Эти две характеристики можно перемножить для получения полной погрешности показания прибора:
Здесь — полная погрешность измерительной системы,
— погрешность показания прибора,
— погрешность щупа, подключенного к осциллографу, подходящего типа.
Измерения с шунтирующим резистором
Часто при измерениях токов используют внешний шунтирующий резистор. Шунт имеет некоторое допустимое отклонение, которое влияет на измерение.
Увеличение погрешности при использовании шунтирующего резистора
Заданное допустимое отклонение шунтирующего резистора влияет на погрешность показания. Для нахождения полной погрешности, допустимое отклонение шунта и погрешность показаний измерительного прибора перемножаются:
В этом примере, полная погрешность показания равна 3.53%.
Сопротивление шунта зависит от температуры. Значение сопротивления определяется для данной температуры. Температурную зависимость часто выражают в .
Для примера вычислим значение сопротивления для температуры окружающей среды . Шунт имеет характеристики:
Ом
(соответственно
и
) и температурную зависимость
.
Ток, протекающий через шунт является причиной рассеяния энергии на шунте, что приводит к росту температуры и, следовательно, к изменению значения сопротивления. Изменение значения сопротивления при протекании тока зависит от нескольких факторов. Для проведения очень точного измерения, необходимо откалибровать шунт на дрейф сопротивления и условия окружающей среды при которых проводятся измерения.
Точность
Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.
Распределение Гаусса
Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:
Здесь — среднее значение,
показывает дисперсию и соответствует RMS-значению шумового сигнала. Функция дает кривую распределения вероятностей, как показано на рисунке ниже, где среднее значение
и эффективная амплитуда шума
.
Распределение вероятностей с и
В таблице указаны шансы получения значений в заданных пределах.
| Граница | Шанс |
| 0.5·σ | 38.3 % |
| 0.674·σ | 50.0 % |
| 1·σ | 68.3 % |
| 2·σ | 95.4 % |
| 3·σ | 99.7 % |
Как видно, вероятность того, что измеренное значение лежит в диапазоне ± равна
.
Повышение точности
Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.
Разрешение
Разрешением, или, как еще говорят, разрешающей способностью измерительной системы является наименьшая различимая измеряемая величина. Определение разрешения прибора не относится к точности измерения.
Цифровые измерительные системы
Цифровая система преобразует аналоговый сигнал в цифровой эквивалент посредством аналого-цифрового преобразователя. Разница между двумя значениями, то есть разрешение, всегда равно одному биту. Или, в случае с цифровым мультиметром, это одна цифра.
Возможно также выразить разрешение через другие единицы, а не биты. В качестве примера рассмотрим цифровой осциллограф, имеющий 8-битный АЦП. Чувствительность по вертикали установлена в 100 мВ/дел и число делений равно 8, полный диапазон, таким образом, равен 800 мВ. 8 бит представляются 28=256 различными значениями. Разрешение в вольтах тогда равно 800 мВ / 256 = 3125 мВ.
Аналоговые измерительные системы
В случае аналогового прибора, где измеряемая величина отображается механическим способом, как в стрелочном приборе, сложно получить точное число для разрешения. Во-первых, разрешение ограничено механическим гистерезисом, причиной которого является трение механизма стрелки. С другой стороны, разрешение определяется наблюдателем, делающем свою субъективную оценку.
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как объяснить погрешность?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Как вычислить погрешность?
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Различают абсолютную (∆ X) и относительную (δ) погрешности измерений. Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Что такое погрешность в математике?
Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения. Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного.
Это отклонение принято называть ошибкой измерения, Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов, На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,
Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность,
Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %. Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как « неопределённость измерения ».
В то же время иногда, особенно в физике, термин «погрешность измерения» ( англ. measurement error ) используется как синоним термина «неопределённость измерения» ( англ. measurement uncertainty ),
Что такое погрешность измерения своими словами?
Определения погрешности и неопределенности измерений. — Погрешность измерения – это отклонение измеренного значения величины от ее «истинного» значения. По своей природе или характеру проявления погрешность может быть «случайной» и «систематической». Метод выражения погрешности измерений – а ± Δа, где а – измеренная величина, Δа – суммарная абсолютная погрешность, определяемая методикой выполнения измерений.
Для чего нужна погрешность?
Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного.
- Это отклонение принято называть ошибкой измерения.
- В ряде источников, например, в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный).
- Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов,
На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,
- Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений.
- Это полученное значение не является точным, а лишь наиболее вероятным.
- Поэтому в измерениях необходимо указывать, какова их точность,
- Для этого вместе с полученным результатом указывается погрешность измерений.
Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка). В 2004 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов.
Что такое погрешность и виды?
Абсолютная погрешность меры — это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины. Относительная погрешность — это число, отражающее степень точности измерения.
В чем измеряется погрешность?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти погрешность измерений формула?
Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).
Чему равна абсолютная погрешность?
При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения.
Что происходит с погрешностью при делении?
| Главная страница УЧЕБНЫЕ МАТЕРИАЛЫ ПРОГРАММА КУРСА КОНСПЕКТЫ ЛЕКЦИЙ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ВОПРОСЫ К ЗАЧЁТУ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА | Кафедра физхимии ЮФУ (РГУ) ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – Щербаков И.Н. Пусть X – некоторая величина, истинное значение которой известно или неизвестно и равно x*, Число x, которое можно принять за значение величины X, мы будем называть ее приближенным значением или просто приближенным числом. Число x называют приближенным значением по недостатку, если оно меньше истинного значения ( x < x* ), и по избытку, если оно больше ( x > x* ). Например, число 3,14 является приближенным значением числа π по недостатку, а 2,72 – приближенным значением числа е (основание натурального логарифма) по избытку. Абсолютная погрешность приближенного числа есть абсолютная величина разности между истинным значением величины и данным ее приближенным значением. Δx = | x * – x | Поскольку истинное значение величины обычно остается неизвестным, неизвестной остается также и абсолютная погрешность. Вместо нее приходится рассматривать оценку абсолютной погрешности, так называемою предельную абсолютную погрешность, которая означает число, не меньшее абсолютной погрешности (далее, в том случае, если это не принципиально, будем под абсолютной погрешностью понимать именно предельную абсолютную погрешность). Абсолютная погрешность приближенного числа не в полной мере характеризует его точность. Действительно, погрешность в 0,1 г слишком велика при взвешивании реактивов для проведения микро-синтеза, допустима при взвешивании 100 г колбасы, и не может быть замечена при измерении массы, например, железнодорожного вагона. Более информативным показателем точности приближенного числа является его относительная погрешность, Относительной погрешностью δx приближенного значения величины X называют абсолютную величину отношения его абсолютной погрешности к истинному значению этой величины. Часто эту относительную погрешность выражают в процентах. C учетом положительности абсолютной погрешности можно записать: δx = Δx / | x* | Ввиду того, что фактически вместо абсолютной погрешности приходится рассматривать предельную, относительную погрешность также заменяют предельной относительной погрешностью, которая означает число, не меньшее относительной погрешности. Более того, при отыскании предельной относительной погрешности приходится заменять неизвестное истинное значение величины x* приближенным – x, Последняя замена обычно не отражается на величине относительной погрешности ввиду близости этих значений и малости абсолютной погрешности. δx = Δx / | x | Например, для приближенного значения π = 3,14 предельная абсолютная погрешность составляет 0,0016, а относительная – 0,00051 или 0,051%. Выражение относительной погрешности в процентах иногда называют процентной погрешностью.
Как найти абсолютную погрешность 8 класс?Погрешность и точность приближения. Найдем значение функции у = х 2 при х=1,5 и при х=2,1. Можно найти значение функции двумя способами: по формуле и с помощью графика. С помощью графика приближенные значения функции равны: при х = 1,5 у ≈ 2,3; при х = 2,1 у ≈ 4,4. Что такое основная приведенная погрешность?Приведенная погрешность (средства измерений) – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерения к нормирующему значению величины. Чем отличается погрешность от точности?Погрешность и точность — Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением.
Ниже, на левом графике показаны эти изменения. Почему возникают погрешности измерений?Они возникают из-за конечной точности приборов, ошибок определения, влияния многих случайных факторов, неправильно выбранного способа измерений (систематических ошибок). Что такое абсолютная погрешность примеры?Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. В чем измеряется погрешность?Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений). Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности. Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий. Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. Что представляет собой приведенная погрешность?Приведенная погрешность (средства измерений) – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерения к нормирующему значению величины. В чем польза относительной погрешности?4.2 Средняя оценка: 4.2 Всего получено оценок: 1947. Обновлено 11 Января, 2021 4.2 Средняя оценка: 4.2 Всего получено оценок: 1947. Обновлено 11 Января, 2021 Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Опыт работы учителем математики — более 33 лет. Что такое погрешность средств измерений?Погрешность средства измерений — это разность между показаниями СИ и истинным (действительным) значением измеряемой величины. Adblock |

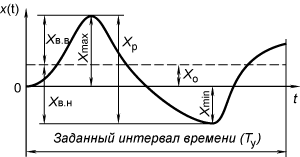
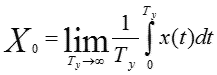
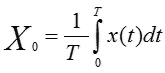
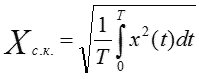
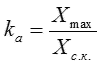
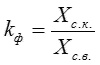
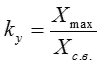
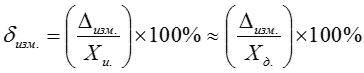
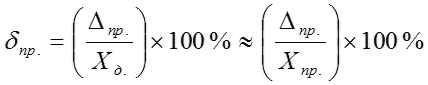
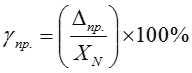
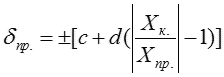
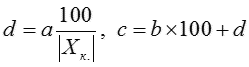

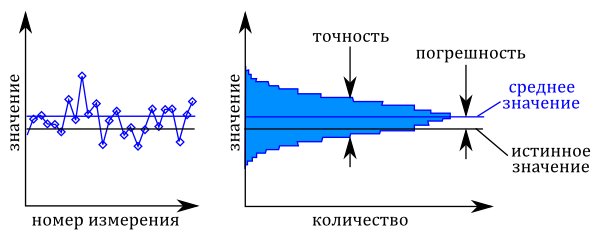
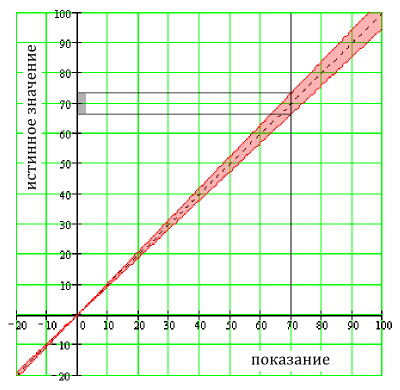
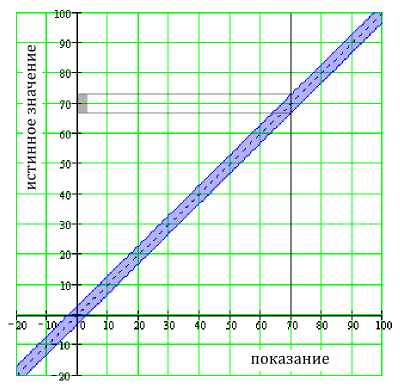
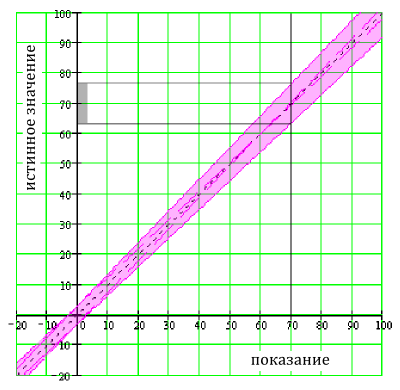
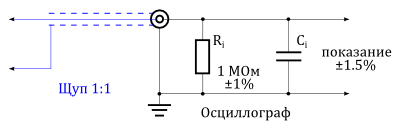
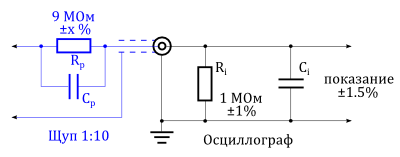
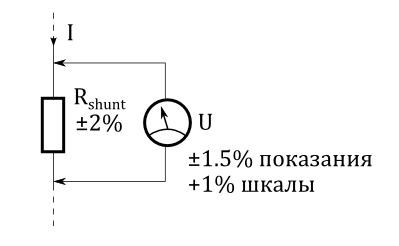
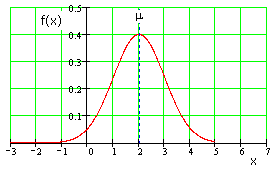

 Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.
Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.