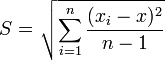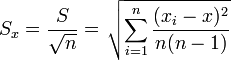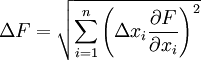Погрешностью ошибкой измерения называют

7

2.02.1 Погрешности измерений и их квалификация

1. Взаимосвязь
точности и погрешности измерения.

2. Классификация
погрешностей измерения.

3. Источники
погрешностей.

4. Основные
составляющие погрешности.

5. Случайные,
систематические и динамические
погрешности.

6. Правила суммирования
погрешностей.

7. Особенности
формирования погрешностей при косвенных,
совместных и совокупных измерениях.

8. Округление
результатов измерения.

1. Взаимосвязь точности и погрешности измерения

Точность
измерения,
является качественной характеристикой,
что выражает собой близость результата
этого измерения к действительному
(истинному) значению. Погрешность в
свою очередь, является обратным понятием
точности, и является некой характеристикой,
которая демонстрирует существующие
отклонения показаний от имеющегося
идеального значения.

Зная класс точности прибора
приведенной погрешности γ и предельное
значение измеряемой величины Х_макс,
можно определить абсолютную
и относительную δ инструментальную
погрешность измерения:   

 ;
   

Чем ближе значение измеряемой
величины к пределу измерения, тем меньше
относительная инструментальная
погрешность.

2. Классификация погрешностей измерения По форме представления

Абсолютной
погрешностью
измерений называют разность между
измеренным и действительным значениями
измеряемой величины:

.

Относительная
погрешность —
погрешность измерения, выраженная
отношением абсолютной погрешности
измерения к действительному или
измеренному значению измеряемой величины

Приведённая
погрешность —
погрешность, выраженная отношением
абсолютной погрешности средства
измерений к условно принятому значению
величины, постоянному во всем диапазоне
измерений или в части диапазона.

где —
нормирующее значение, которое зависит
от типа шкалы измерительного прибора
и определяется по его градуировке:

• если
  шкала прибора односторонняя, то есть
  нижний предел измерений равен нулю,
  то  определяется
  равным верхнему пределу измерений;

• если
  шкала прибора двухсторонняя, то
  нормирующее значение равно ширине
  диапазона измерений прибора.

По причине возникновения

• Инструментальные
  / приборные погрешности —
  погрешности, которые определяются
  погрешностями применяемых средств
  измерений и
  вызываются несовершенством принципа
  действия, неточностью градуировки шкалы,
  ненаглядностью прибора.

• Методические
  погрешности —
  погрешности, обусловленные несовершенством
  метода, а также упрощениями, положенными
  в основу методики.

• Субъективные /
  операторные / личные погрешности —
  погрешности, обусловленные степенью
  внимательности, сосредоточенности,
  подготовленности и другими качествами
  оператора.

Инструментальную
погрешность
подразделяют на основную
погрешность и дополнительную
погрешности.

Основной
погрешностью
называют погрешность, имеющую место в
случае применения средства измерений
в нормальных условиях эксплуатации.

Дополнительной
погрешностью
называют погрешность средств измерений,
которая возникает в условиях, отличающихся
от нормальных, но входящих в допустимую
рабочую область условий эксплуатации.

Соседние файлы в папке Точность измерений

• #
• #
• #
• #
• #
• #

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

• Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

• Средняя квадратическая погрешность:

• Средняя квадратическая погрешность среднего арифметического:

Классификация погрешностей

По форме представления

• Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины X_meas. При этом равенство:

ΔX = | X_true − X_meas | ,

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

• Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

• Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

,

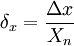
где X_n — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность — безразмерная величина (может измеряться в процентах).

По причине возникновения

• Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
• Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
• Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.

По характеру проявления

• Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
• Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
• Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
• Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).

По способу измерения

• Погрешность прямых измерений
• Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F(x₁,x₂…x_n), где x_i — непосредственно измеряемые независимые величины, имеющие погрешность Δx_i, тогда:

См. также

• Измерение физических величин
• Класс точности
• Метрология
• Система автоматизированного сбора данных со счетчиков по радиоканалу
• Методы электроаналитической химии

Литература

• Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.

• Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.

Погрешность средств измерения и результатов измерения. 

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности. 

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

• Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
  Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
• Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. 

Систематическая и случайная погрешности. 

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

• отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
• неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
• упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
• погрешность градуировки или небольшой сдвиг шкалы;
• неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
• неравномерный износ направляющих устройств для базирования измеряемых деталей;
• износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
• усталостные измерения упругих свойств деталей, а также их естественное старение;
• неисправности средства измерений.

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки. 

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности. 

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0…100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30…100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50…+50, Xn=100).

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

• Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
• Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность 
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность 
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Полученное из опыта значение измеряемой величины может
отличаться от ее действительного (истинного) значения.

Погрешность измерения – отклонение результата измерения от истинного (действительного) значения измеряемой
величины.

Это может быть обусловлено конструктивными недостатками прибора, несовершенством технологии его
изготовления, а также влиянием различных внешних факторов.

Таким образом, погрешности классифицируют:

1. По источнику возникновения (метод, инструмент, субъект)

   -Методические (зависят от метода измерения и способа включения приборов в электрическую цепь)

   -Инструментальные (зависят от средства измерения)

   -Субъективные (зависят от измерителя)

2. По условиям проведения измерений (температура, давление, влажность)

   -Основные (измерения проводятся в нормальных условиях — при нормальной температуре, давлении,
   влажности)

   -Дополнительные (условия отличны от нормальных)

3. По характеру проявления (систематические, случайные, промахи)

   Систематические – погрешности, остающиеся постоянными или закономерно изменяющимися при повторных
   измерениях тем же способом и средствами. Т.е. они заранее известны и их легко исключить.

   Случайные – погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же
   величины.  Обычно выявляются в результате многократных измерений (не менее 10).

   Промах – грубая ошибка, обусловленная неправильным отсчетом или расчетом, небрежностью измеряющего,
   поломки прибора, неправильно собранной схемы, невнимательности и т.д. Такие данные необходимо исключать.

4. По временному поведению измеряемой величины (статическая, динамическая)

   Статическая – когда измеряемая величина не меняется за время измерения

   Динамическая – когда прибор не успевает реагировать на изменения измеряемой величины.

5. По способу выражения измеряемой величины

   • абсолютная;

   • относительная;

   • приведенная.

     Абсолютной погрешностью
     DХ называется разность между измеренным и действительным значениями.

      – измеренное значение;

     – действительное значение измеряемой величины.

     Выражается
     DХ в единицах измеряемой величины.

     Относительная погрешность
      – отношение абсолютной погрешности к действительному значению измеряемой величины.

     Выражается в процентах или относительных единицах. Относительная погрешность характеризует
     точность измерений.

     Приведенная погрешность
     g_пр – отношение абсолютной погрешности к номинальному (нормированному) значению – верхнему пределу диапазона
     или поддиапазона измерения прибора.

     Пределом измерения прибора называется наибольшая величина, на которую рассчитан данный
     прибор.

     Прибор может иметь несколько пределов измерений (например, вольтметр).

     Чем меньшую погрешность дает прибор, тем он точнее.

   • Выражается в процентах.

     Максимальная приведенная погрешность определяет класс точности прибора.

   • Электроизмерительные приборы изготавливаются нескольких классов точности

Эти числа определяют максимальную погрешность прибора при полном отклонении указателя (стрелки).

Определяют также среднеквадратическую погрешность результата измерения по формуле:

Выражается  в единицах измеряемой величины.

За действительное значение измеряемой величины принимается обычно среднее арифметическое из ряда
измерений.

Хд = Х_СР =  (Х₁ + Х₂ +
Х₃ + … + Хn)/n,

где Х₁, Х₂,… , Хn – результаты измерений

       n – количество измерений