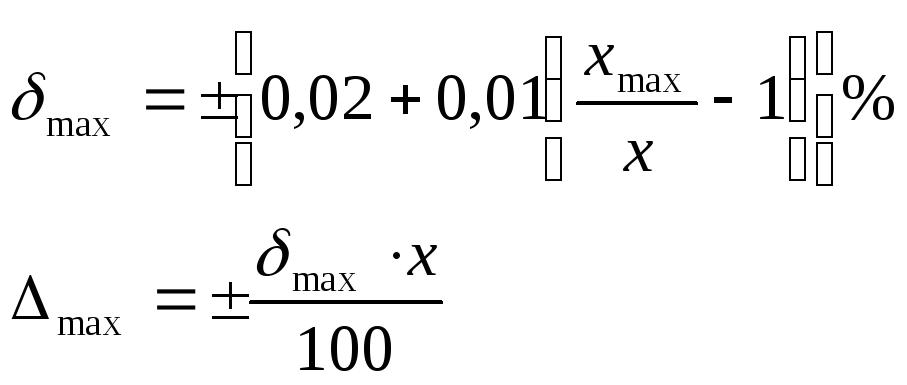Полная абсолютная и относительная ошибки

Источники
погрешностей (инструментальные и
методические погрешности, влияние
помех, субъективные ошибки). Номинальная
и реальная функция преобразования,
абсолютная и относительная погрешность
средства измерений, основная и
дополнительная погрешности. Пределы
допускаемых погрешностей, классы
точности средств измерений. Выявление
и уменьшение систематических погрешностей.
Оценка случайных погрешностей.
Доверительный интервал и доверительная
вероятность. Оценка погрешностей
косвенных измерений. Обработка результатов
измерений. [1:
с.23…35,40,41,53,54,56…61; 2:
с.22…53; 3:
с.48…91; 4:
с.21,22,35…52,63…71, 72…77,85…93].

II.1. Основные сведения и методические указания.

Одним из
основополагающих понятий Метрологии
является понятие погрешности измерений.

Погрешностью
измерения
называют отклонение измеренного

значения физической
величины от её истинного значения.

Погрешность
измерений, в общем случае, может быть
вызвана следующими причинами:

1. Несовершенством
   принципа действия и недостаточным
   качеством элементов используемого
   средства измерения.

2. Несовершенством
   метода измерений и влиянием используемого
   средства измерения на саму измеряемую
   величину, зависящим от способа
   использования данного средства
   измерения.

3. Субъективными
   ошибками экспериментатора.

Так как истинное
значение измеряемой величины никогда
неизвестно (в противном случае отпадает
необходимость в проведении измерений),
то численное значение погрешности
измерений может быть найдено только
приближенно. Наиболее близким к истинному
значению измеряемой величины является
значение, которое может быть получено
при использовании эталонных средств
измерений (средств измерений наивысшей
точности). Это значение условились
называть действительным
значением измеряемой величины.
Действительное значение также является
неточным, однако, из-за малой погрешности
эталонных средств измерений, погрешностью
определения действительного значения
пренебрегают.

Классификация
погрешностей

1. По форме представления
   различают понятия абсолютной погрешности
   измерений и относительной погрешности
   измерений.

Абсолютной
погрешностью
измерений называют разность между

измеренным и
действительным значениями измеряемой

величины:

,

где ∆ — абсолютная
погрешность,

–измеренное
значение,

–действительное
значение измеряемой величины.

Абсолютная
погрешность имеет размерность измеряемой
величины. Знак абсолютной погрешности
будет положительным, если измеренное
значение больше действительного, и
отрицательным в противном случае.

Относительной
погрешностью
называют отношение абсолютной

погрешности к
действительному значению измеряемой
величины:

где δ – относительная
погрешность.

Чаще всего
относительную погрешность определяют
приближенно в процентах от измеренного
значения:

Относительная
погрешность показывает, какую часть (в
%) от измеренного значения составляет
абсолютная погрешность. Относительная
погрешность позволяет нагляднее, чем
абсолютная погрешность, судить о точности
измеренного значения.

1. По источникам
   происхождения погрешности подразделяют
   на следующие виды:

— инструментальные
погрешности;

— методические
погрешности;

— субъективные
погрешности, допущенные экспериментатором
.

Инструментальными
называются погрешности, которые
принадлежат данному типу средств
измерения, могут быть определены при
их испытаниях и занесены в паспорт
средства измерения в виде пределов
допускаемых погрешностей.

Инструментальная
погрешность возникает из-за несовершенства
принципа действия и недостаточно
высокого качества элементов, применяемых
в конструкции средства измерений. По
этой причине реальная передаточная
характеристика каждого экземпляра
средства измерений в большей или меньшей
степени отличается от номинальной
(расчетной) передаточной характеристики.
Отличие реальной характеристики средства
измерений от номинальной (рис.1) определяет
величину инструментальной погрешности
средства измерений.

Рис.1. Иллюстрация
к определению понятия инструментальной

погрешности.

Здесь: 1 – номинальная
характеристика средства измерений;

2 – реальная
характеристика средства измерений.

Как видно из рис.1,
при изменении измеряемой величины,
инструментальная погрешность может
иметь различные значения (как положительные,
так и отрицательные).

При создании
средств измерений какой-либо физической
величины, к сожалению, не удается
полностью избавиться от реакции этого
средства измерений на изменение других
(не измеряемых) величин. Наряду с
чувствительностью средства измерения
к измеряемой величине, оно всегда
реагирует (хотя и существенно в меньшей
степени) на изменение условий эксплуатации.
По этой причине инструментальную
погрешность подразделяют на основную
погрешность и дополнительную
погрешности.

Основной
погрешностью
называют погрешность, имеющую место

в случае применения
средства измерений в нормальных условиях

эксплуатации.

Номенклатура
влияющих на средство измерений величин
и диапазоны их изменений определяются
разработчиками в качестве нормальных
условий для каждого типа средств
измерений. Нормальные условия эксплуатации
всегда указываются в техническом
паспорте средства измерений. Если
эксперимент выполняется в условиях,
отличных от нормальных для данного
средства измерений, его реальная
характеристика искажается сильнее, чем
в нормальных условиях. Погрешности,
которые при этом возникают, называют
дополнительными.

Дополнительной
погрешностью
называют погрешность средств

измерений, которая
возникает в условиях, отличающихся от

нормальных, но
входящих в допустимую рабочую область
условий

эксплуатации.

Рабочие условия
эксплуатации, так же как и нормальные,
в обязательном порядке приводятся в
техническом паспорте средств измерений.

Инструментальная
погрешность средств измерений
определенного типа не должна превышать
некоторого заданного значения – так
называемой предельно допустимой основной
погрешности средств измерений данного
типа. Фактическая основная погрешность
каждого конкретного экземпляра этого
типа является при этом случайной
величиной и может принимать различные
значения, иногда даже равные нулю, но в
любом случае инструментальная погрешность
не должна превышать заданного предельного
значения. Если это условие не выполняется,
средство измерений должно быть изъято
из обращения.

Методическими
называются погрешности, которые возникают
из-за неудачного выбора экспериментатором
средства измерения для решения
поставленной задачи. Они не могут быть
приписаны средству измерения и приведены
в его паспорте.

Методические
погрешности измерения зависят как от
характеристик применяемого средства
измерений, так и во многом от параметров
самого объекта измерения. Неудачно
выбранные средства измерений могут
исказить состояние объекта измерений.
При этом методическая составляющая
погрешности может оказаться существенно
больше инструментальной.

Субъективными
погрешностями
называют погрешности,

допускаемые
самим экспериментатором при проведении

измерений.

Этот тип погрешностей
связан обычно с невнимательностью
экспериментатора: применение прибора
без устранения смещения нуля, неправильное
определение цены деления шкалы, неточный
отсчет доли деления, ошибки в подключении
и т.п.

1. По характеру
   проявления погрешности измерений
   подразделяют на:

— систематические
погрешности;

— случайные
погрешности;

— промахи (грубые
ошибки).

Систематической
называют погрешность, которая при
повторных измерениях одной и той же
величины остается постоянной, или
изменяется закономерно.

Систематические
погрешности обусловлены как несовершенством
метода измерений и влиянием средства
измерений на измеряемый объект, так и
отклонением реальной передаточной
характеристики применяемого средства
измерений от номинальной характеристики.

Постоянные
систематические погрешности средств
измерений могут быть выявлены и численно
определены в результате сличения их
показаний с показаниями эталонных
средств измерений. Такие систематические
погрешности могут быть уменьшены
регулировкой приборов или введением
соответствующих поправок. Следует
заметить, что полностью исключить
систематические погрешности средств
измерений не удается, так как их реальные
передаточные характеристики изменяются
при изменении условий эксплуатации.
Кроме этого всегда имеют место так
называемые прогрессирующие погрешности
(возрастающие или убывающие), вызванные
старением элементов входящих в состав
средств измерений. Прогрессирующие
погрешности могут быть скорректированы
регулировкой или введением поправок
лишь на некоторое время.

Таким образом,
даже после регулировки или введения
поправок, всегда имеет место так
называемая неисключенная систематическая
погрешность результата измерений.

Случайной
называют погрешность, которая при
повторных измерениях одной и той же
величины принимает различные значения.

Случайные погрешности
обусловлены хаотичным характером
изменений физических величин (помех),
влияющих на передаточную характеристику
средства измерений, суммированием помех
с измеряемой величиной, а также наличием
собственных шумов средства измерений.
При создании средств измерений
предусматриваются специальные меры
защиты от помех: экранирование входных
цепей, использование фильтров, применение
стабилизированных источников питающего
напряжения и т.д. Это позволяет уменьшить
величину случайных погрешностей при
проведении измерений. Как правило, при
повторных измерениях одной и той же
величины результаты измерений либо
совпадают, либо отличаются на одну, две
единицы младшего разряда. В такой
ситуации случайной погрешностью
пренебрегают и оценивают только величину
неисключенной систематической
погрешности.

Наиболее сильно
случайные погрешности проявляются при
измерении малых значений физических
величин. Для повышения точности в таких
случаях производятся многократные
измерения с последующей статистической
обработкой результатов методами теории
вероятности и математической статистики.

Промахами
называют грубые погрешности, существенно
превышающие ожидаемые погрешности при
данных условиях проведения измерений.

Промахи большей
частью возникают из-за субъективных
ошибок экспериментатора или из-за сбоев
в работе средства измерений при резких
изменениях условий эксплуатации (броски
или провалы сетевого напряжения, грозовые
разряды и т.п.) Обычно промахи легко
выявляются при повторных измерениях и
исключаются из рассмотрения.

Оценка погрешностей
косвенных измерений.

При косвенных
измерениях результат измерений
определяется по функциоральной
зависимости от результатов прямых
измерений. Поэтому погрешность косвенных
измерений определяется как полный
дифференциал этой функции от величин,
измеряемых с помощью прямых измерений.

;

Где:
—
предельные абсолютные погрешности
результатов прямых

измерений;

—
предельная абсолютная погрешность
результата косвенного

измерения;

—
соответствующие предельные относительные
погрешности.

—
функциональная связь между искомой
измеряемой величиной и

величинами,
подвергающимися прямым измерениям.

Статистическая
обработка результатов измерений

Из-за влияния на
средство измерений помех различного
происхождения (изменение температуры
окружающей среды, электромагнитных
полей, вибраций, изменения частоты и
амплитуды сетевого напряжения, изменения
атмосферного давления, влажности и
т.д.), а также из-за наличия собственных
шумов элементов, входящих в состав
измерительных приборов, результаты
повторных измерений одной и той же
физической величины (особенно ее малых
значений) будут в большей или меньшей
степени отличаться друг от друга. В этом
случае результат измерений является
случайной величиной, которая характеризуется
наиболее вероятным значением и разбросом
(рассеянием) результатов повторных
измерений вблизи наиболее вероятного
значения. Если при повторных измерениях
одной и той же величины результаты
измерений не отличаются друг от друга,
то это означает, что разрешающая
способность отсчетного устройства не
позволяет обнаружить это явление. В
этом случае случайная составляющая
погрешности измерений является
несущественной и ею можно пренебречь.
При этом неисключенную систематическую
погрешность результата измерений
оценивают по величине пределов допускаемых
погрешностей применяемых средств
измерений. Если же при повторных
измерениях одной и той же величины
наблюдается разброс показаний, то это
означает, что наряду с большей или
меньшей неисключенной систематической
погрешностью, имеет место и случайная
погрешность, принимающая при повторных
измерениях различные значения.

Для определения
наиболее вероятного значения измеряемой
величины при наличии случайных
погрешностей и для оценки погрешности,
с которой определено это наиболее
вероятное значение, применяется
статистическая обработка результатов
измерений. Статистическая обработка
результатов серии измерений при
проведении экспериментов позволяет
решить следующие задачи.

1. Более точно
   определить результат измерения путем
   усреднения отдельных наблюдений.

2. Оценить область
   неопределенности уточненного результата
   измерений.

Основной смысл
усреднения результатов измерений
заключается в том, что найденная
усредненная оценка имеет меньшую
случайную погрешность, чем отдельные
результаты, по которым эта усредненная
оценка определяется. Следовательно
усреднение не устраняет полностью
случайного характера усредненного
результата, а лишь уменьшает ширину
полосы его неопределенности.

Таким образом, при
статистической обработке, прежде всего,
определяют наиболее вероятное значение
измеряемой величины путем вычисления
среднего арифметического всех отсчетов:

где: x_i
– результат i
– го измерения;

n
– число проведенных измерений в данной
серии измерений.

После этого
оценивают отклонение результатов
отдельных измерений x_i
от этой оценки среднего значения
;.

Затем находят
оценку среднеквадратического отклонения
наблюдений, характеризующую степень
рассеяния результатов отдельных
наблюдений вблизи,
по формуле:

.

Точность оценки
наиболее вероятного значения измеряемой
величины
зависит от числа наблюдений.
Нетрудно убедиться в том, что результаты
нескольких оценокпо одному и тому же числуотдельных измерений будут отличаться.
Таким образом, сама оценкатакже является случайной величиной. В
связи с этим вычисляется оценка
среднеквадратического отклонения
результата измерения,
которую обозначают.
Эта оценка характеризует степень
разброса значенийпо отношению к истинному значению
результата, т.е. характеризует точность
результата, полученного усреднением
результата многократных измерений.
Следовательно, поможет быть оценена систематическая
составляющая результата серии измерений.
Для различныхона определяется по формуле:

Следовательно,
точность результата многократных
измерений увеличивается с ростом числа
последних.

Однако в большинстве
практических случаев нам важно определить
не просто степень рассеивания значения
погрешности при проведении серии
измерений (т.е. величину
),
а оценить вероятность возникновения
погрешности измерения, не превышающую
допустимую, т.е. не выходящую за пределы
некоторого заданного интервала разброса
получаемых погрешностей.

Доверительным
интервалом
называют
интервал, который с заданной вероятностью,
называемой
доверительной вероятностью
накрывает истинное значение измеряемой
величины.

При определении
доверительных интервалов необходимо,
прежде всего, учитывать, что закон
распределения погрешностей, получаемых
при проведении многократных измерений,
при числе измерений в серии меньше 30,
описывается не нормальным законом
распределения, а так называемым законом
распределения Стьюдента. И, в этих
случаях, величину доверительного
интервала обычно оценивают по формуле:

,

где
— так называемый коэффициент Стьюдента.

В табл.4.1 приведены
значения коэффициентов Стьюдента
в зависимости от заданной доверительной
вероятности и числа проведенных
наблюдений.
При выполнении измерений обычно задаются
доверительной вероятностью 0,95 или 0,99.

Таблица 4.1

Значения
коэффициентов Стьюдента
.

n
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
2	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
3	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
4	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
5	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
6	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
7	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
8	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
9	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
10	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
16	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
25	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

При изучении
материалов данного раздела следует
хорошо уяснить, что погрешности
результатов измерений и погрешности
средств измерений – не идентичные
понятия. Погрешность средства измерения
это его свойство, характеристика, для
описания которого используют ряд правил,
закрепленных в стандартах и нормативных
документах. Это та доля погрешности
измерения, которая определяется только
самим средством измерения. Погрешность
же измерений (результата измерений) –
это число, которое характеризует границы
неопределенности значения измеряемой
величины. В нее, кроме погрешности
средства измерений, могут входить
составляющие погрешности, порожденные
применяемым методом измерения
(методические погрешности), действием
влияющих (неизмеряемых) величин,
погрешность отсчета и др.

Нормирование
погрешностей средств измерения.

Точность СИ
определяется предельно-допустимыми
погрешностями, которые могут быть
получены при его использовании.

Нормированием
погрешностей средств измерений называют

процедуру
назначения допустимых границ основной
и

дополнительных
погрешностей, а также выбор формы
указания

этих границ
в нормативно-технической документации.

Пределы допускаемой
основной и дополнительных погрешностей
определяются разработчиками для каждого
типа средств измерений на стадии
подготовки производства. В зависимости
от назначения средства измерений и
характера изменения погрешности в
пределах диапазона измерений нормируется
для средств измерений различного типа
либо предельно-допустимое значение
основной абсолютной погрешности, либо
предельно-допустимое значение основной
приведенной погрешности, либо
предельно-допустимое значение основной
относительной погрешности.

Для каждого типа
средств измерений характер изменения
погрешности в пределах диапазона
измерений зависит от принципа действия
этого средства измерений и может быть
самым разнообразным. Однако, как показала
практика, среди этого многообразия
часто удается выделить три типовых
случая, предопределяющих выбор формы
представления пределов допускаемой
погрешности. Типовые варианты отклонения
реальных передаточных характеристик
средств измерений от номинальной
характеристики и соответствующие им
графики изменения предельных значений
абсолютной и относительной погрешностей
в зависимости от измеряемой величины
приведены на рис 2.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной (1-й график на рис.2а),
абсолютная погрешность, возникающая
при этом, (1-й график на рис.2б), не зависит
от измеряемой величины.

Составляющую
погрешности средства измерений, не
зависящую от измеряемой величины,
называют аддитивной
погрешностью.

Если угол наклона
реальной передаточной характеристики
средства измерений отличается от
номинального (2-й график на рис. 2а), то
абсолютная погрешность будет линейно
зависеть от измеряемой величины (2-й
график на рис. 2б).

Составляющую
погрешности средства измерений, линейно
зависящую от измеряемой величины,
называют мультипликативной
погрешностью.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной и угол ее наклона отличается
от номинального (3-й график на рис. 2а),
то в этом случае имеет место как
аддитивная, так и мультипликативная
погрешность.

Аддитивная
погрешность возникает из-за неточной
установки нулевого значения перед
началом измерений, ухода нуля в процессе
измерений, из-за наличия трений в опорах
измерительного механизма, из-за наличия
термо-эдс в контактных соединениях и
т.д.

Мультипликативная
погрешность возникает при изменении
коэффициентов усиления или ослабления
входных сигналов (например, при изменении
температуры окружающей среды, или
вследствие старения элементов), из-за
изменения значений, воспроизводимых
мерами, встроенными в измерительные
приборы, из-за изменений жесткости
пружин, создающих противодействующий
момент в электромеханических приборах
и т.д.

Ширина полосы
неопределенности значений абсолютной
(рис.2б) и относительной (рис.2в) погрешностей
характеризует разброс и изменение в
процессе эксплуатации индивидуальных
характеристик множества находящихся
в обращении средств измерений определенного
типа.

А) Нормирование
пределов допускаемой основной погрешности
для

средств
измерений с преобладающей аддитивной
погрешностью.

Для средств
измерений с преобладающей аддитивной
погрешностью (1-й график на рис.2) удобно
нормировать одним числом предельно-допустимое
значение абсолютной погрешности (∆_max=
±а). В этом случае фактическая абсолютная
погрешность ∆ каждого экземпляра
средства измерений данного типа на
различных участках шкалы может иметь
различные значения, но не должна превышать
предельно-допустимой величины (∆ ≤
±а). В многопредельных измерительных
приборах с преобладающей аддитивной
погрешностью для каждого предела
измерений пришлось бы указывать свое
значение предельно допустимой абсолютной
погрешности. К сожалению, как видно из
1-го графика на рис.2в, нормировать одним
числом предел допускаемой относительной
погрешности в различных точках шкалы
не представляется возможным. По этой
причине для средств измерений с
преобладающей аддитивной погрешностью
часто нормируют одним числом значение
так называемой основной приведенной
относительной
погрешности

,

где X_N
– нормирующее значение.

Таким способом,
например, нормируются погрешности
большинства электромеханических и
электронных приборов со стрелочными
индикаторами. В качестве нормирующего
значения X_N
обычно используется предел измерений
(X_N
= X_max),
удвоенное значение предела измерений
(если нулевая отметка находится в
середине шкалы), или длина шкалы (для
приборов с неравномерной шкалой). Если
X_N
= X_max,
то значение приведенной погрешности γ
равно пределу допускаемой относительной
погрешности средства измерений в точке,
соответствующей пределу измерений. По
заданному значению предела допускаемой
основной приведенной погрешности легко
определить предел допускаемой основной
абсолютной погрешности для каждого
предела измерений многопредельного
прибора:.

После этого для
любой отметки шкалы X
может быть произведена оценка
предельно-допустимой основной
относительной погрешности:

.

Б) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с преобладающей мультипликативной

погрешностью.

Как видно из рис.2
(2-й график), для средств измерений с
преобладающей мультипликативной
погрешностью, одним числом удобно
нормировать предел допускаемой основной
относительной погрешности (рис.2в) δ_max=
± b∙100%.
В этом случае, фактическая относительная
погрешность каждого экземпляра средства
измерений данного типа на различных
участках шкалы может иметь различные
значения, но не должна превышать предельно
допустимой величины (δ ≤ ± b∙100%).
По заданному значению предельно
допустимой относительной погрешности
δ_max
для любой точки шкалы может быть
произведена оценка предельно-допустимой
абсолютной погрешности:

.

К числу средств
измерений с преобладающей мультипликативной
погрешностью относится большинство
многозначных мер, счетчики электрической
энергии, счетчики воды, расходомеры и
др. Следует отметить, что для реальных
средств измерений с преобладающей
мультипликативной погрешностью не
удается полностью устранить аддитивную
погрешность. По этой причине в технической
документации всегда указывается
наименьшее значение измеряемой величины,
для которого предел допускаемой основной
относительной погрешности ещё не
превышает заданного значения δ_max.
Ниже этого наименьшего значения
измеряемой величины погрешность
измерений не нормируется и является
неопределенной.

В) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с соизмеримой аддитивной и мультипликативной

погрешностью.

Если аддитивная
и мультипликативная составляющая
погрешности средства измерений соизмеримы
(3-й график на рис.2), то задание
предельно-допустимой погрешности одним
числом не представляется возможным. В
этом случае либо нормируется предел
допускаемой абсолютной основной
погрешности (указываются предельно-допустимые
значения a
и b),
либо (чаще всего) нормируется предел
допускаемой относительной основной
погрешности. В последнем случае численные
значения предельно-допустимых
относительных погрешностей в различных
точках шкалы оцениваются по формуле:

,

где X_max
– предел измерений;

X
— измеренное значение;

d
=

— значение приведенной к пределу измерений

аддитивной
составляющей основной погрешности;

с =
— значение результирующей относительной

основной
погрешности в точке, соответствующей
пределу

измерений.

Рассмотренным
выше способом (указанием численных
значений c
и d)
нормируются, в частности, предельно-допустимые
значения относительной основной
погрешности цифровых измерительных
приборов. В этом случае относительные
погрешности каждого экземпляра средств
измерений определенного типа не должны
превышать установленных для этого типа
средств измерений значений
предельно-допустимой погрешности:

.

При этом абсолютная
основная погрешность определяется по
формуле

.

Г)
Нормирование дополнительных погрешностей.

Наиболее часто
пределы допускаемых дополнительных
погрешностей указывают в технической
документации либо одним значением для
всей рабочей области величины, влияющей
на точность средства измерений (иногда
несколькими значениями для поддиапазонов
рабочей области влияющей величины),
либо отношением предела допускаемой
дополнительной погрешности к интервалу
значений влияющей величины. Пределы
допускаемых дополнительных погрешностей
указываются на каждой , влияющей на
точность средства измерений величине.
При этом, как правило, значения
дополнительных погрешностей устанавливают
в виде дольного или кратного значения
предела допускаемой основной погрешности.
Например, в документации может быть
указано, что при температуре окружающей
среды за пределами нормальной области
температур, предел допускаемой
дополнительной погрешности, возникающей
по этой причине, не должен превышать
0,2% на 10^о С.

Классы
точности средств измерений.

Исторически по
точности средства измерений подразделяют
на классы. Иногда их называют классами
точности, иногда классами допуска,
иногда просто классами.

Класс точности
средства измерений
– это его характеристика, отражающая
точностные возможности средств измерений
данного типа.

Допускается
буквенное или числовое обозначение
классов точности. Средствам измерений,
предназначенным для измерения двух и
более физических величин, допускается
присваивать различные классы точности
для каждой измеряемой величины. Средствам
измерений с двумя или более переключаемыми
диапазонами измерений также допускается
присваивать два или более класса
точности.

Если нормируется
предел допускаемой абсолютной основной
погрешности, или в различных поддиапазонах
измерений установлены разные значения
пределов допускаемой относительной
основной погрешности, то , как правило,
применяется буквенное обозначение
классов. Так, например платиновые
термометры сопротивления изготовляют
с классом допуска А
или классом
допуска В.
При этом для
класса А
установлен
предел допускаемой абсолютной основной
погрешности
,
а для классаВ
—
,
где– температура измеряемой среды.

Если для средств
измерений того или иного типа нормируется
одно значение предельно-допустимой
приведенной основной погрешности, или
одно значение предельно-допустимой
относительной основной погрешности,
или указываются значения c
и d,
то для обозначения классов точности
используются десятичные числа. В
соответствии с ГОСТом 8.401-80 для обозначения
классов точности допускается применение
следующих чисел:

1∙10ⁿ;
1,5∙10ⁿ;
2∙10ⁿ;
2,5∙10ⁿ;
4∙10ⁿ;
5∙10ⁿ;
6∙10ⁿ,
где n
= 0, -1, -2, и т.д.

Для средств
измерений с преобладающей аддитивной
погрешностью численное значение класса
точности выбирается из указанного ряда
равным предельно-допустимому значению
приведенной основной погрешности,
выраженной в процентах. Для средств
измерений с преобладающей мультипликативной
погрешностью численное значение класса
точности соответствует пределу
допускаемой относительной основной
погрешности также выраженной в процентах.
Для средств измерений с соизмеримыми
аддитивными и мультипликативными
погрешностями числа с
и d
также
выбираются из указанного выше ряда. При
этом класс точности средства измерений
обозначается двумя числами, разделенными
косой чертой, например, 0,05/0,02. В этом
случае с
= 0,05%; d
= 0,02%. Примеры
обозначений классов точности в
документации и на средствах измерений,
а также расчетные формулы для оценки
пределов допускаемой основной погрешности
приведены в Таблице 1.

Правила округления
и записи результата измерений.

Нормирование
пределов допускаемых погрешностей
средств измерений производится указанием
значения погрешностей с одной или двумя
значащими цифрами. По этой причине при
расчете значений погрешностей измерений
также должны быть оставлены только
первые одна или две значащие цифры. Для
округления используются следующие
правила:

1. Погрешность
   результата измерения указывается двумя
   значащими цифрами, если первая из них
   не более 2, и одной цифрой, если первая
   из них 3 и более.

2. Показание прибора
   округляется до того же десятичного
   разряда, которым заканчивается
   округленное значение абсолютной
   погрешности.

3. Округление
   производится в окончательном ответе,
   промежуточные вычисления выполняют с
   одной – двумя избыточными цифрами.

Пример 1:

— показание прибора
— 5,361 В;

— вычисленное
значение абсолютной погрешности — ±
0,264 В;

— округленное
значение абсолютной погрешности — ±
0,26 В;

— результат измерения
— (5,36 ± 0,26) В.

Таблица
1

Примеры обозначения
классов точности средств измерений и
расчетные

формулы для оценки
пределов допускаемой основной погрешности.

Форма представления нормируемой основной погрешности	Примеры обозначения класса точности	Расчетные формулы для оценки пределов допускаемой основной погрешности	Примечания
В документации	На средствах измерений
Нормируется предел допускаемой абсолютной основной погрешности	Варианты: — класс B; — класс допуска В; — класс точностиВ.	В	или или	Значения a иb приводятся в документации на средство измерений.
Нормируется предел допускаемой приведенной основной погрешности	Варианты: — класс точности 1,5 2,5 — не обозначается.	1,5	гдепредел измерений.	Для приборов с равномерной шкалой и нулевой отметкой в начале шкалы
Варианты: — класс точности 2,5; — не обозначается		— предел допускаемой абсолютной погрешности в мм. — длина всей шкалы.	Для приборов с неравномерной шкалой. Длина шкалы указывается в документации.
Нормируется предел допускаемой относительной основной погрешности	Класс точности 0,5.	0,5		Для средств измерений с преобладающей мультипликативной погрешностью.
Варианты: — класс точности 0,02/0,01; -не обозначается.	0,02/0,01		Для средств измерений с соизмеримыми аддитивной и мультипликативной погрешностью

Пример 2:

— показание прибора
– 35,67 мА;

— вычисленное
значение абсолютной погрешности — ±
0,541 мА;

— округленное
значение абсолютной погрешности — ± 0,5
мА;

— результат измерений
– (35,7 ± 0,5) мА.

Пример 3:

— вычисленное
значение относительной погрешности –
± 1,268 %;

— округленное
значение относительной погрешности –
± 1,3 %.

Пример 4:

— вычисленное
значение относительной погрешности —
± 0,367 %;

— округленное
значение относительной погрешности —
± 0,4 %.

II.2.
Вопросы для самопроверки

1. Чем вызываются
   погрешности измерений?

2. Перечислите
   разновидности погрешностей, возникающих
   в процессе измерений?

3. Какая разница
   между абсолютной, относительной и
   приведенной погрешностями измерения
   и в чем смысл их введения?

4. Чем отличается
   основная погрешность измерения от
   дополнительной?

5. Чем отличается
   методическая погрешность измерения
   от инструментальной?

6. Чем отличается
   систематическая погрешность измерения
   от случайной?

7. Что понимается
   под аддитивной и мультипликативной
   оставляющими погрешности?

8. В каких случаях
   целесообразно использовать статистическую
   обработку результатов измерений?

9. Какие статистические
   характеристики обработки наиболее
   часто используются на практике?

10. Как оценивается
    неисключенная систематическая
    погрешность при статистической обработке
    результатов измерений?

11. Что характеризует
величина среднеквадратического
отклонения ?

12. В чем заключается
суть понятий «доверительной вероятности»
и «доверительного интервала», используемых
при статистической обработке результатов
измерений?

13. В чем заключается
разность понятий «погрешность измерения»
и

«погрешность
средства измерения»?

2.6. Обработка результатов измерений

Обработка прямых измерений. Для характеристики большинства приборов часто используют понятие приведенной погрешности, равной абсолютной погрешности в процентах диапазона шкалы измерений. По приведенной погрешности приборы разделяются на классы точности. Класс точности указан на панели прибора.

Наибольшая инструментальная погрешность измеряется по формуле:

,               (2.1)

где К – класс точности, А – наибольшее значение шкалы прибора.

Инструментальную погрешность невозможно уменьшить статистической обработкой отсчетов.

При наличии случайных погрешностей наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. В этом случае действительное значение находят как наиболее вероятное из серии отсчетов, а погрешность характеризуют шириной интервала, который с заданной вероятностью показывает истинное значение [44].

Наилучшей оценкой истинного значения величины Х является выборочное среднее значение

,                    (2.2)

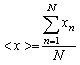
где   – отсчет величины Х,  – число отсчетов.

Для оценки разброса отсчетов при измерении используется выборочное среднее квадратическое отклонение отсчетов

.           (2.3)

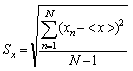
Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

.                          (2.4)

Доверительным интервалом называется интервал , который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.

Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность , с которой доверительный интервал включает истинное значение измеряемой величины.

Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Случайная составляющая погрешности многократных измерений

,                (2.5)

где  – безразмерный коэффициент доверия (коэффициент Стьюдента).

Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.

Полная абсолютная погрешность  прямых измерений равна квадратической сумме ее составляющих: инструментальной –  и случайной –

 .        (2.6)

Полная относительная погрешность  прямых измерений равна отношению полной абсолютной погрешности к выборочному среднему значению

.            (2.7)

Обработка косвенных измерений [44]. Расчет погрешностей косвенных измерений осуществляется по алгоритму, использующему сложение абсолютных величин погрешностей.

Пусть  – функциональная зависимость между измеряемой величиной  и величинами , значения которых найдены прямыми измерениями. Действительное значение  определяется как:

.       (2.8)

Вычисляем относительные погрешности аргументов. Затем определяем абсолютную и относительную погрешности функции

                        (2.9)

и по формулам:

—          для относительной погрешности

;                 (2.10)

—          для абсолютной погрешности

.                           (2.11)

Оценка токсического действия тестируемой пробы воды. Оценка токсического действия тестируемой пробы воды делается на основании достоверности различий между показателями прироста численности клеток водорослей в контроле и в опыте. При этом вычисляют [14]:

– средние арифметические величины прироста численности клеток – X_i и X (в контроле и опыте);

– среднее квадратичное отклонение  по формуле (2.3);

– ошибку среднего арифметического (X):

– Td – критерий достоверности различий двух величин:

;                       (2.12)

,              (2.13)

где x_k и x_о – сравниваемые средние величины (в контроле и опыте),

Sk² и So² – квадраты ошибок средних в контроле и опыте.

Td рассчитывают для каждой тестируемой пробы и сравнивают с табличной величиной Tst – стандартным значением критерия Стьюдента. В нашем случае для его определения принимаем уровень значимости р = 0,05 (95%) и степень свободы = (n1 + n2 – 2), т. е. (3 + 3 – 2) = 4. Tst при степени свободы 4 равно 2,78.

Если Td ≥ Tst, то различие между контролем и опытом достоверно – тестируемая вода загрязнена.

Если Td < Tst, то различие между контролем и опытом не достоверно – тестируемая вода не загрязнена.

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

1. Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
2. Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась  погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому  значению.

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

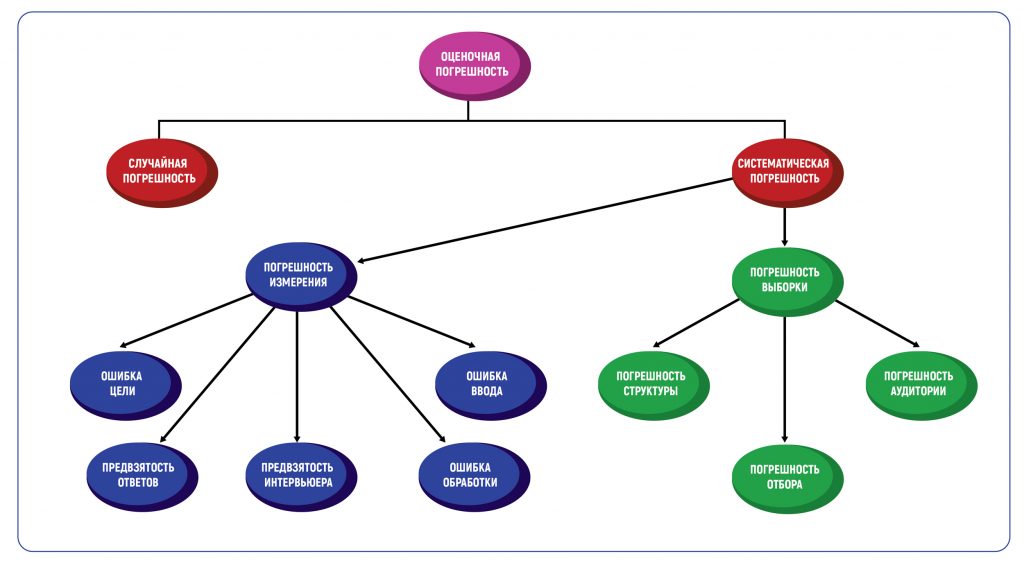
Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения. 

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

• Знайте свою аудиторию.
  Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
• Разделите аудиторию на группы.
  Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
• Увеличьте размер выборки.
  Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть  или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

• Предварительно протестируйте.
  Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
• Проводите выборку случайным образом.
  Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
• Тренируйте команду интервьюеров и наблюдателей.
  Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
• Всегда выполняйте проверку сделанных записей.
  Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок  не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.