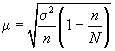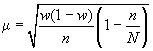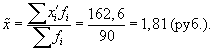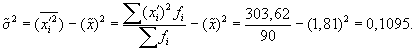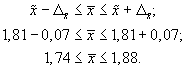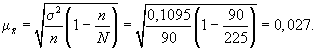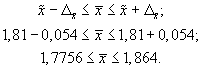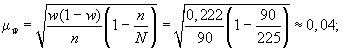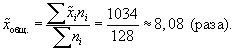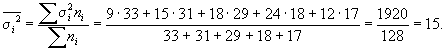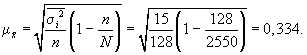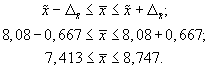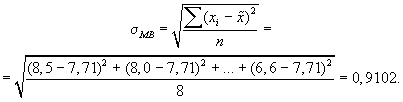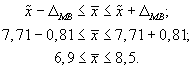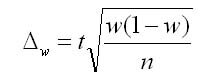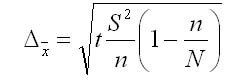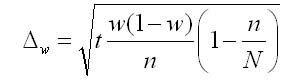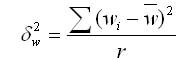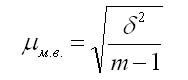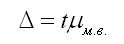В
конкретной выборке действительная
ошибка может быть больше средней, меньше
средней или равна средней. Каждое из
этих расхождений имеет определенную
вероятность.
Предельная
ошибка выборки
– это максимальное различие между
выборочной и генеральной характеристикой,
гарантируемое с определенной вероятностью.
где
t – нормированное
отклонение, зависящее от вероятности,
определяемое как аргумент интегральной
функции Лапласа
Ф(t).
Определение предельной ошибки выборки
основано на теореме Чебышева –Ляпунова.
Теорема
Чебышева-Ляпунова:
С
вероятностью сколь угодно близкой к
единице можно утверждать, что при
достаточно большом объеме выборки и
ограниченной дисперсии выборочная
характеристика будет очень мало
отличаться от генеральной характеристики.
З
начение
этой функций находиться в таблице,
поэтому, зная вероятность P
=Ф(t),
можно определить аргумент
t.
Наиболее часто используемые значения
приведем в таблице:
|
Р(t) |
0,683 |
0,95 |
0,954 |
0,99 |
0,997 |
|
t |
1 |
1,96 |
2 |
2,58 |
3 |
Чем
больше вероятность, с которой гарантируются
результаты, тем больше будет предельная
ошибка и менее надежные результаты
выборки. Поэтому
в экономических исследованиях используется
Р=0,95 и Р=0,954.
6. Распределение результатов выборки на генеральную совокупность
Конечным
итогом выборочного обследования
является оценка неизвестных генеральных
характеристик на основе данных выборки.
По
этой оценке строится доверительный
интервал для генеральной средней
и
генеральной доли.
Ошибка
выборки зависит не только от вероятности,
но и от того, как было организовано
выборочное обследование.
Выделим
основные
этапы
выборочного обследования:
-
определение
объекта исследования; -
постановка
цели и задач; -
определение
процедуры отбора, проведение отбора
единиц в выборку; -
подготовка
кадров и инструментария; -
сбор
данных; -
определение
выборочных характеристик, ошибок
выборки; -
оценка
доверительных интервалов; -
о
ценка
возможностей распространения результатов
на генеральную совокупность. Для этого
определяют относительные ошибки
выборки:
Если
эти ошибки не превышают заранее заданной
величины, то результаты можно распространить
на генеральную совокупность, если
превышает, то изменить процедуру отбора
или методы ремонта выборки.
9.
Распространение результатов. Для этого
применяются следующие способы:
1.
Прямой пересчет, т.е.
границы доверительного интервала
умножаются на объем генеральной
совокупности.
2.
Способ поправочных коэффициентов –
используется в тех случаях, когда
корректируются данные сплошного
обследования. По выборке рассчитывается
поправочный коэффициент, и данные
сплошного обследования исправляются
на этот коэффициент.
7. Определение необходимой численности выборки.
При
проведении выборочного обследования
возникает вопрос, сколько нужно отобрать
единиц в выборку, чтобы результаты
обследования удовлетворяли заранее
заданным величинам, т.е. предельная
ошибка не превышала определенного
значения. Для определения необходимой
численности выборки применяются формулы,
которые выводятся из предельной ошибки.
Возьмем
собственно-случайный повторный отбор:
______
∆x
= t∙μx
= t∙√Sx2
/ n
=> n
=
t2·
Sx2
∆x2
Для
бесповторного отбора:
___________
∆x
= t·√Sx
/ n·(1-n/N) =>
t2·N·Sx2
n
=
____________
∆x2·N
+ t2·
Sx2
Для
других способов отбора формулы необходимой
численности выборки аналогичны,
изменяется только дисперсия.
Значения
дисперсии при определении необходимой
численности выборки достаточно часто
бывает неизвестно. В этом случае ее
определяют:
-
из
предыдущего обследования на данную
тему; -
рассчитывают
приближенно Sx2≈(R/6)2
по пробному обследованию малого
количества единиц; -
неизвестную
дисперсию для доли берут равной 0,25.
Области
применения выборочного метода
обследования.
В
настоящее время выборочный метод сбора
данных является одним из наиболее часто
используемых. Выборочное наблюдение
используется для:
-
статистического
оценивания и проверки различных гипотез; -
при
контроле технологических процессов и
показателей качества продукции; -
при
различных отраслевых обследованиях; -
при
решении задач в сфере предпринимательства. -
Пример:
Имеются данные выборочного
собственно-случайного бесповторного
обследования 30% работников коммерческого
банка об их стаже работы.
Результаты
обследования представлены в таблице.
|
Стаж |
До |
3-5 |
5-7 |
7-9 |
Свыше |
Итого |
|
Число |
10 |
48 |
28 |
10 |
4 |
100 |
С
вероятностью 0,997 определить возможные
пределы среднего стажа работы по всем
работникам банка, а также возможные
пределы для доли работников банка,
имеющих стаж работы менее 5 лет.
Решение:
1
Для
расчетов построим расчетную таблицу
|
Стаж, |
Число fi |
Середина xi |
xi*fi |
_ (xi |
_ (xi |
_ (xi |
|
До |
10 |
2 |
20 |
— |
9 |
90 |
|
3-5 |
48 |
4 |
192 |
— |
1 |
48 |
|
5-7 |
28 |
6 |
168 |
1 |
1 |
28 |
|
7-9 |
10 |
8 |
80 |
3 |
9 |
90 |
|
Свыше |
4 |
10 |
40 |
5 |
25 |
100 |
|
Итого |
100 |
— |
500 |
— |
— |
356 |
С
редний
стаж работников равен
Д
исперсия
равна
Среднеквадратическое
отклонение равно
= 2
=
3,56
= 1,887 лет.
Определим
ошибки выборки. Так как вероятность Р=
0,997, то коэффициент доверия t
= 3.
Рассчитаем выборочную долю для признака
– стаж работы менее 5 лет. Так как данный
стаж работы имеют 1 и 2 группы работников
в выборке, то w
= m/n = (10+48)/100 = 0.58.
Дисперсия выборочной доли 2w
= w*(1 – w) = 0,58*0,42 =0,2434.
Определим
предельную ошибку выборки для среднего
О
пределим
предельную ошибку выборки для доли
Построим
доверительный интервал для среднего.
П
остроим
доверительный интервал для выборочной
доли
В
ывод
2. С
вероятностью 0,997 можно утверждать, что
средний стаж работы всех работников
банка находится в пределах от 4,526 до
5,474 лет, а доля всех работников банка,
имеющих стаж работы менее 5 лет, находится
в пределах от 45,6% до 70,4%.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10.02.201516.87 Mб251321388933_cifrovaya_obrabotka_izobrageniy.djvu
2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка
выборки
показывает, насколько отклоняется в
среднем параметр выборочной
совокупности
от соответствующего параметра генеральной.
Если рассчитать среднюю из ошибок всех
возможных выборок определенного вида
заданного объема (n),
извлеченных из одной и той же генеральной
совокупности,
то получим их обобщающую характеристику
среднюю
ошибку выборки
().
В
теории выборочного наблюдения
выведены формулы для определения ,
которые индивидуальны для разных
способов отбора (повторного и
бесповторного), типов используемых
выборок и видов оцениваемых статистических
показателей.
Например, если
применяется повторная собственно
случайная выборка, то
определяется как:
при
оценивании среднего значения признака;
если
признак альтернативный, и оценивается
доля.
При бесповторном
собственно случайном отборе в формулы
вносится поправка
для
среднего значения признака;
для
доли.
Вероятность
получения именно такой величины ошибки
всегда равна 0,683. На практике же
предпочитают получать данные с большей
вероятностью, но это приводит к возрастанию
величины ошибки выборки.
Предельная
ошибка выборки ()
равна t-кратному
числу средних ошибок выборки (в теории
выборки принято коэффициент t
называть
коэффициентом доверия):
t
.
Если ошибку выборки
увеличить в два раза (t
2), то получим гораздо большую вероятность
того, что она не превысит определенного
предела (в нашем случае
двойной средней ошибки)
0,954. Если взять t
3, то доверительная вероятность составит
0,997
практически достоверность.
Уровень предельной
ошибки выборки зависит от следующих
факторов:
степени вариации
единиц генеральной совокупности;
объема выборки;
выбранных схем
отбора (бесповторный отбор дает меньшую
величину ошибки);
уровня
доверительной вероятности.
Если объем выборки
больше 30, то значение t
определяется по таблице нормального
распределения, если меньше
по таблице распределения Стьюдента
(Приложение
1).
Приведем некоторые
значения коэффициента доверия из таблицы
нормального распределения.
Доверительный
интервал для среднего значения признака
и для доли в генеральной
совокупности
устанавливается следующим образом:
Итак, определение
границ генеральной средней и доли
состоит из следующих этапов:
нахождение в
выборке среднего значения признака
(или доли);
определение
в соответствии с выбранной схемой отбора
и вида выборки;
задание
доверительной вероятности Р
и определение коэффициента доверия t
по
соответствующей таблице;
вычисление
предельной ошибки выборки ;
построение
доверительного интервала для средней
(или доли).
Ошибки выборки
при различных видах отбора
1. Собственно
случайная и механическая выборка.
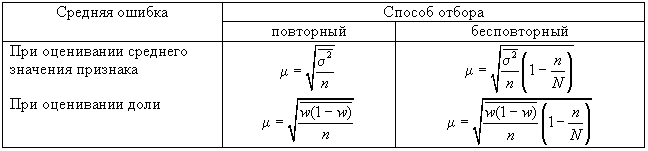
Средняя
ошибка собственно случайной и механической
выборки находятся по формулам,
представленным в табл. 11.1.
Таблица 1
Формулы для
расчета средней ошибки
собственно
случайной и механической выборки ()
где
2
дисперсия
признака в выборочной совокупности.
Пример 2. Для
изучения уровня фондоотдачи было
проведено выборочное обследование 90
предприятий из 225 методом случайной
повторной выборки, в результате которого
получены данные, представленные в
таблице.
В рассматриваемом
примере имеем 40%-ную выборку (90 : 225
0,4, или 40%). Определим ее предельную ошибку
и границы для среднего значения признака
в генеральной совокупности по шагам
алгоритма:
1. По результатам
выборочного обследования рассчитаем
среднее значение и дисперсию в выборочной
совокупности:
Выборочная средняя
Выборочная
дисперсия изучаемого признака
2. Определяем
среднюю ошибку повторной случайной
выборки
3. Зададим
вероятность, на уровне которой будем
говорить о величине предельной ошибки
выборки. Чаще всего она принимается
равной 0,999; 0,997; 0,954.
Для наших данных
определим предельную ошибку выборки,
например, с вероятностью 0,954. По таблице
значений вероятности функции нормального
распределения (см. выдержку из нее,
приведенную в Приложении 1) находим
величину коэффициента доверия t,
соответствующего вероятности 0,954. При
вероятности 0,954 коэффициент t
равен 2.
4. Предельная
ошибка выборки с вероятностью 0,954 равна
5. Найдем доверительные
границы для среднего значения уровня
фондоотдачи в генеральной совокупности
Таким образом, в
954 случаях из 1000 среднее значение
фондоотдачи будет не выше 1,88 руб. и не
ниже 1,74 руб.
Выше была
использована повторная схема случайного
отбора. Посмотрим, изменятся ли результаты
обследования, если предположить, что
отбор осуществлялся по схеме бесповторного
отбора. В этом случае расчет средней
ошибки проводится по формуле
Тогда при вероятности
равной 0,954 величина предельной ошибки
выборки составит:
Доверительные
границы для среднего значения признака
при бесповторном случайном отборе будут
иметь следующие значения:
Сравнив результаты
двух схем отбора, можно сделать вывод
о том, что применение бесповторной
случайной выборки дает более точные
результаты по сравнению с применением
повторного отбора при одной и той же
доверительной вероятности. При этом,
чем больше объем выборки, тем существеннее
сужаются границы значений средней при
переходе от одной схемы отбора к другой.
По данным примера
определим, в каких границах находится
доля предприятий с уровнем фондоотдачи,
не превышающим значения 2,0 руб., в
генеральной совокупности:
1) рассчитаем
выборочную долю.
Количество
предприятий в выборке с уровнем
фондоотдачи, не превышающим значения
2,0 руб., составляет 60 единиц. Тогда
m
60, n
90, w
m/n
60 : 90
0,667;
2) рассчитаем
дисперсию доли в выборочной совокупности
w2
w(1
w)
0,667(1
0,667)
0,222;
3) средняя ошибка
выборки при использовании повторной
схемы отбора составит
Если предположить,
что была использована бесповторная
схема отбора, то средняя ошибка выборки
с учетом поправки на конечность
совокупности составит
4) зададим
доверительную вероятность и определим
предельную ошибку выборки.
При значении
вероятности Р
0,997 по таблице нормального распределения
получаем значение для коэффициента
доверия t
3 (см. выдержку из нее, приведенную в
Приложении 1):
5) установим границы
для генеральной доли с вероятностью
0,997:
Таким образом, с
вероятностью 0,997 можно утверждать, что
в генеральной совокупности доля
предприятий с уровнем фондоотдачи, не
превышающим значения 2,0 руб., не меньше,
чем 54,7%, и не больше 78,7%.
2. Типическая
выборка. При
типической выборке генеральная
совокупность объектов разбита на k
групп, тогда
N1
N2
…
Ni
…
Nk
N.
Объем извлекаемых
из каждой типической группы единиц
зависит от принятого способа отбора;
их общее количество образует необходимый
объем выборки
n1
n2
…
ni
…
nk
n.
Существуют
следующие два способа организации
отбора внутри типической группы:
пропорциональной объему типических
групп и пропорциональной степени
колеблемости значений признака у единиц
наблюдения в группах. Рассмотрим первый
из них, как наиболее часто используемый.
Отбор, пропорциональный
объему типических групп, предполагает,
что в каждой из них будет отобрано
следующее число единиц совокупности:
где ni
количество извлекаемых единиц для
выборки из i-й
типической группы;
n
общий объем выборки;
Ni
количество единиц генеральной
совокупности, составивших i-ю
типическую группу;
N
общее количество единиц генеральной
совокупности.
Отбор единиц
внутри групп происходит в виде случайной
или механической выборки.
Формулы для
оценивания средней ошибки выборки для
среднего и доли представлены в табл.
11.2.
Таблица 2
Формулы для
расчета средней ошибки выборки ()
при использовании типического отбора,
пропорционального объему типических
групп
Здесь
средняя из групповых дисперсий типических
групп.
Пример 3. В
одном из московских вузов проведено
выборочное обследование студентов с
целью определения показателя средней
посещаемости вузовской библиотеки
одним студентом за семестр. Для этого
была использована 5%-ная бесповторная
типическая выборка, типические группы
которой соответствуют номеру курса.
При отборе, пропорциональном объему
типических групп, получены следующие
данные:
Число студентов,
которое необходимо обследовать на
каждом курсе, рассчитаем следующим
образом:
общий объем
выборочной совокупности:
количество
единиц, отобранных из каждой типической
группы:
аналогично для
других групп:
п2
31 (чел.);
п3
29 (чел.);
п4
18 (чел.);
п5
17 (чел.).
Проведем необходимые
расчеты.
1. Выборочная
средняя, исходя из значений средних
типических групп, составит:
2. Средняя из
внутригрупповых дисперсий
3. Средняя ошибка
выборки:
С вероятностью
0,954 находим предельную ошибку выборки:
4. Доверительные
границы для среднего значения признака
в генеральной совокупности:
Таким образом, с
вероятностью 0,954 можно утверждать, что
один студент за семестр посещает
вузовскую библиотеку в среднем от семи
до девяти раз.
3.
Малая выборка. В
связи с небольшим объемом выборочной
совокупности
те формулы для определения ошибок
выборки,
которые использовались нами ранее при
«больших» выборках, становятся
неподходящими и требуют корректировки.
Среднюю ошибку
малой выборки
определяют по формуле
Предельная
ошибка малой выборки:
Распределение
значений выборочных средних всегда
имеет нормальный закон распределения
(или приближается к нему) при п
100, независимо от характера распределения
генеральной
совокупности.
Однако в случае малых выборок действует
иной закон распределения
распределение Стьюдента.
В этом случае коэффициент доверия
находится по таблице t-распределения
Стьюдента в зависимости от величины
доверительной вероятности Р
и объема выборки п.
В Приложении
1
приводится фрагмент таблицы t-распределения
Стьюдента, представленной в виде
зависимости доверительной вероятности
от объема выборки и коэффициента доверия
t.
Пример 4.
Предположим,
что выборочное обследование восьми
студентов академии показало, что на
подготовку к контрольной работе по
статистике они затратили следующее
количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4;
6,6.
Оценим выборочные
средние затраты времени и построим
доверительный интервал для среднего
значения признака в генеральной
совокупности, приняв доверительную
вероятность равной 0,95.
1. Среднее значение
признака в выборке равно
2. Значение среднего
квадратического отклонения составляет
3. Средняя ошибка
выборки:
4. Значение
коэффициента доверия t
2,365 для п
8 и Р
0,95 (Приложение 1).
5. Предельная
ошибка выборки:
6. Доверительный
интервал для среднего значения признака
в генеральной совокупности:
То есть с вероятностью
0,95 можно утверждать, что затраты времени
студента на подготовку к контрольной
работе находятся в пределах от 6,9 до 8,5
ч.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки (
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
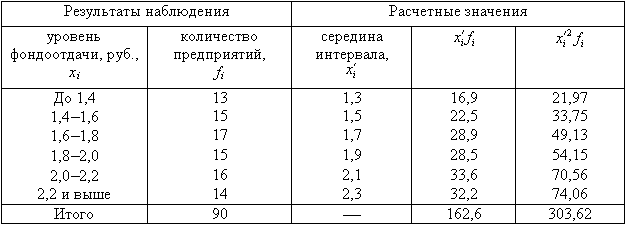
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки (

Здесь 
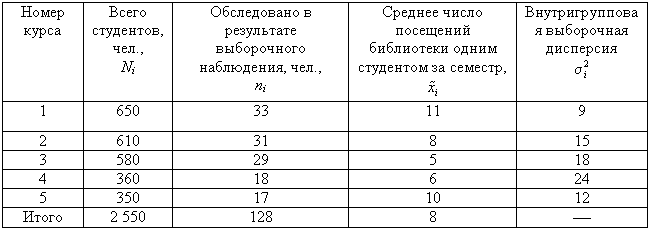
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Предельная ошибка выборки
Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.
1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:
где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;
мю х — средняя ошибка выборки.
2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:
3. Предельная ошибка выборки для средней при бесповторном отборе:
4. Предельная ошибка выборки для доли при бесповторном отборе:
Предельная относительная ошибка выборки
Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:
Малая выборка
Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.
Средняя и предельная ошибки для малой выборки
В малой выборке средняя ошибка рассчитывается по формуле:
Предельная ошибка малой выборки рассчитывается по формуле:
где t — отношение Стьюдента
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Ответы на тесты по теме Статистика
Для более эффективного поиска следует вводить 2-3 ключевых слова из вопроса !!!
Предельная ошибка выборки 1 %. Среднее квадратическое отклонение – 5 %. Определить численность выборки при вероятности 0,954
100 единиц
предельная ошибка выборки рассчитывается путем умножения средней ошибки выборки на:
коэффициент доверия
Стандартная ошибка оценивания при прогнозировании ВВП России по линейному тренду составила 150 млрд. дол. Принятый аналитиком уровень вероятности – 0,954. Чему равна предельная ошибка прогноза:
300
Отобрано 100 проб. Средняя влажность в выборочной совокупности 15 %. Среднее квадратическое отклонение 10 %. Предельная ошибка выборки 1,5 %. Определить вероятность:
0.866
При увеличении уровня доверительной вероятности (например, от 0,683 до 0,990) предельная ошибка выборки __
будет возрастать
Подсчитайте необходимую численность выборки при определении среднего размера вклада населения в отделениях коммерческих банков города, чтобы с вероятностью 0,954 предельная ошибка выборки не превысила 50 руб. Ориентировочная дисперсия вкладов равна 200000
320
![Тест по статистике с правильными ответами [08.03.16]](https://studrb.ru/files/works_screen/2/91/9.png)
Тема: Тест по статистике с правильными ответами
Раздел: Бесплатные рефераты по статистике
Тип: Тест | Размер: 22.65K | Скачано: 238 | Добавлен 08.03.16 в 23:17 | Рейтинг: +1 | Еще Тесты
На странице представлена часть вопросов и ответов на тесты, остальные смотрите в файле.
___________________________________________________________________
Вопрос: Абсолютные величины – это:
Ответ: всегда именованные числа, т.е. имеют единицы измерения
___________________________________________________________________
Вопрос: Абсолютными величинами в статистике называют:
Ответ: суммарные обобщающие показатели, характеризующие размеры (уровни, объемы) общественных явлений в конкретных условиях места и времени
___________________________________________________________________
Вопрос: Базисные темпы роста – это:
Ответ: отношение каждого последующего уровня ряда динамики к одному и тому же уровню, принятому за базу сравнения
___________________________________________________________________
Вопрос: В первом квартале товарооборот магазина составил 300 млн. руб., во втором квартале товарооборот 400 млн.руб., при плане 360 млн.руб. Определите относительную величину планового задания:
Ответ: 120%
___________________________________________________________________
Вопрос: Вариационные ряды бывают следующих видов:
Ответ: интервальные и дискретные
___________________________________________________________________
Вопрос: Вариацию, обусловленную фактором, положенным в основание группировки, принято считать:
Ответ: межгрупповой или систематической вариацией
___________________________________________________________________
Вопрос: Вариация — это:
Ответ: изменяемость величины признака у отдельных единиц совокупности
___________________________________________________________________
Вопрос: Вариация признака в совокупности — это:
Ответ: изменение значения признака при переходе от одной единицы совокупности к другой
___________________________________________________________________
Вопрос: Варьирующие признаки – это признаки:
Ответ: принимающие различное количественное или качественное выражение у разных единиц совокупности
___________________________________________________________________
Вопрос: Ведомственная статистика – это:
Ответ: централизованная система сбора и обработки статистических сведений, осуществляемых соответствующими министерствами и ведомствами
___________________________________________________________________
Вопрос: Величина ошибки выборки зависит от:
Ответ: объема выборки по численности
___________________________________________________________________
Вопрос: Величина теоретического корреляционного отношения, равная 1,587, свидетельствует:
Ответ: об ошибках в вычислениях
___________________________________________________________________
Вопрос: Величина, служащая для целей соизмерения индексируемых величин, называется:
Ответ: весом индекса
___________________________________________________________________
Вопрос: Виды статистических таблиц:
Ответ: простые, групповые и комбинационные
___________________________________________________________________
Вопрос: Выберите метод, используемый для количественной оценки силы воздействия одних факторов на другие:
Ответ: корреляционный анализ
___________________________________________________________________
Вопрос: Выберите метод, используемый для построения аналитической модели воздействия одних факторов на другие:
Ответ: регрессионный анализ
___________________________________________________________________
Вопрос: Выберите методы, используемые для выявления наличия, характера и направления связи в статистике:
Ответ: метод сравнения параллельных рядов
Ответ: метод аналитической группировки
Ответ: графический метод
___________________________________________________________________
Вопрос: Выберите правильное определение единицы наблюдения:
Ответ: первичный элемент объекта статистического наблюдения, который является носителем признаков, подлежащих регистрации
___________________________________________________________________
Вопрос: Выберите правильные высказывания:
Ответ: коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу
Ответ: коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного на 1%
___________________________________________________________________
Вопрос: Выбор вида средней зависит от:
Ответ: характера исходных данных
___________________________________________________________________
Вопрос: Вычисленные параметры по выборочной совокупности:
Ответ: характеризуют саму выборку
Ответ: точно характеризуют генеральную совокупность
___________________________________________________________________
Вопрос: Генеральной совокупностью в выборочном наблюдении называется:
Ответ: совокупность, из которой производится выбор части для изучения
___________________________________________________________________
Вопрос: Гистограмма является графиком ряда:
Ответ: интервального
___________________________________________________________________
Вопрос: Государственная статистика – это:
Ответ: централизованная система сбора и обработки статистической информации, руководство которыми осуществляет Федеральная служба государственной статистики
___________________________________________________________________
Вопрос: График – это:
Ответ: совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели
___________________________________________________________________
Вопрос: Группировки в соответствии с решаемыми задачами делятся на:
Ответ: типологические, структурные и аналитические
___________________________________________________________________
Вопрос: Действие закона больших чисел помогает выявить статистическую закономерность?
Ответ: да
___________________________________________________________________
Вопрос: Дискретный вариационный ряд графически изображается с помощью:
Ответ: полигона
Ответ: кумуляты
Ответ: огивы
___________________________________________________________________
Вопрос: Для анализа общественных явлений достаточна характеристика с использованием величин:
Ответ: необходимо комплексное применение абсолютных и относительных величин
___________________________________________________________________
Вопрос: Для вычисления общего индекса физического объема произведенной продукции в качестве весов могут быть использованы:
Ответ: цены на выпущенную продукцию
Ответ: трудоемкость
Ответ: себестоимость
___________________________________________________________________
Вопрос: Для преобразования натуральных единиц измерения в условно-натуральные и наоборот необходимо воспользоваться коэффициентами:
Ответ: перевода (пересчета)
___________________________________________________________________
Вопрос: Для преобразования условно-натуральных величин в натуральные первые необходимо:
Ответ: разделить на соответствующий коэффициент перевода
___________________________________________________________________
Вопрос: Единица статистического наблюдения — это:
Ответ: первичная единица, от которой должны быть получены необходимые статистические сведения
___________________________________________________________________
Вопрос: Единицей статистической совокупности является:
Ответ: первичный элемент объекта статистического наблюдения, являющийся носителем признака, подлежащего регистрации
___________________________________________________________________
Вопрос: Если веса осредняемого признака выражены в процентах, чему будет равен знаменатель при расчете средней арифметической?
Ответ: 100
___________________________________________________________________
Вопрос: Если все веса увеличить в 2 раза, то средняя величина:
Ответ: не изменится
___________________________________________________________________
Вопрос: Если все веса увеличить на постоянную величину «а», то средняя величина:
Ответ: изменится
___________________________________________________________________
Вопрос: Если данные о заработной плате рабочих представлены интервальным рядом распределения, то за основу расчета среднего заработка следует принимать:
Ответ: середину интервалов
Ответ: средние значения заработной платы в интервале
___________________________________________________________________
Вопрос: Если две группировки несопоставимы из-за различного числа групп, то они могут быть приведены к сопоставимому виду с помощью группировки:
Ответ: вторичной
___________________________________________________________________
Вопрос: Если индекс производительности труда переменного состава меньше индекса производительности труда постоянного состава, то влияние структурных сдвигов:
Ответ: отрицательное
___________________________________________________________________
Вопрос: Если индексируемой величиной индексов являются показатели, характеризующие уровень явления в расчете на единицу совокупности (цена единицы продукции, себестоимость единицы продукции и др.), то они считаются:
Ответ: качественными
___________________________________________________________________
Вопрос: Если признак имеет непрерывный характер, то строится ряд:
Ответ: интервальный вариационный
___________________________________________________________________
Вопрос: Если сведения о заработной плате рабочих по двум цехам представлены уровнями заработков и фондами заработной платы, то средний уровень зарплаты следует определять по формуле:
Ответ: средней гармонической взвешенной
___________________________________________________________________
Вопрос: Если уменьшить все значения признака на одну и ту же величину А, то дисперсия от этого:
Ответ: не изменится
___________________________________________________________________
Вопрос: Имеются следующие данные о продажах картофеля на рынках (см. таблицу). Укажите формулу, по которой следует определить среднюю цену на картофель по трем рынкам:
Ответ: средней гармонической взвешенной
___________________________________________________________________
Вопрос: Индекс производительности труда переменного состава показывает:
Ответ: изменение средней производительности
___________________________________________________________________
Вопрос: Индекс цен Пааше показывает:
Ответ: среднее изменение цен на товарную массу, приобретенную населением в отчетном периоде
___________________________________________________________________
Вопрос: Индекс, отражающий влияние изменения структуры совокупности на изменение среднего значения признака, является индексом:
Ответ: структурных сдвигов
___________________________________________________________________
Вопрос: Индекс, рассчитанный как средняя величина из индивидуальных индексов, — это индекс:
Ответ: средний
___________________________________________________________________
Вопрос: Индекс, характеризующий влияние изменения групповых средних на общее по совокупности среднее значение признака, называется индексом:
Ответ: постоянного ( фиксированного) состава
___________________________________________________________________
Вопрос: Индекс, характеризующий соотношение средних уровней изучаемого явления за разные периоды времени, называется индексом:
Ответ: переменного состава
___________________________________________________________________
Вопрос: Индексы, характеризующие изменение всевозможных количеств (все индексы физического объема: товарооборота, ВВП и др.), являются:
Ответ: количественными (объемными)
___________________________________________________________________
Вопрос: Индивидуальные индексы характеризуют результат сравнения за два периода:
Ответ: отдельных элементов совокупности
___________________________________________________________________
Вопрос: Интерполяцией в рядах динамики называется:
Ответ: нахождение недостающих уровней ряда динамики в пределах временного ряда
___________________________________________________________________
Вопрос: К какому виду абсолютных величин относится показатель «Собственные средства коммерческого банка»?
Ответ: индивидуальные абсолютные величины
___________________________________________________________________
Вопрос: К какому виду относительных величин относится показатель «уровень ВВП РФ на душу населения»?
Ответ: интенсивности и уровня экономического развития
___________________________________________________________________
Вопрос: К какому виду относительных величин следует отнести показатель: “Плотность населения на 1 кв. км. в области в 2000 году составила 75 человек”?
Ответ: интенсивность развития
___________________________________________________________________
Вопрос: Каждый базисный абсолютный прирост равен:
Ответ: сумме последовательных цепных абсолютных приростов
___________________________________________________________________
Вопрос: Каждый цепной темп роста равен:
Ответ: частному от деления последующего базисного темпа роста на предыдущий
___________________________________________________________________
Вопрос: Как называется в статистической таблице объект изучения?
Ответ: подлежащее
___________________________________________________________________
Вопрос: Как называется в статистической таблице перечень числовых показателей, характеризующих объект?
Ответ: сказуемое
___________________________________________________________________
Вопрос: Как определяется интервал для группировки с равными интервалами:
Ответ: отношением размаха вариации к числу образуемых групп
___________________________________________________________________
Вопрос: Как оценивается доверительный интервал коэффициента регрессии:
Ответ: определяется стандартная ошибка коэффициента и применяется t-критерий Стьюдента
___________________________________________________________________
Вопрос: Как оценивается значимость (неслучайность) показателя тесноты корреляционной связи, рассчитанного по выборочным данным:
Ответ: определяется средняя ошибка показателя и применяется t-критерий Стьюдента
___________________________________________________________________
Вопрос: Какие единицы измерения имеют абсолютные величины?
Ответ: натуральные, условно-натуральные, трудовые и стоимостные
___________________________________________________________________
Вопрос: Какие из приведенных чисел могу быть значениями эмпирического корреляционного отношения:
Ответ: 0,4
Ответ: 1,0
Ответ: 0,7
___________________________________________________________________
Вопрос: Какие из приведенных чисел могут быть значениями линейного коэффициента корреляции:
Ответ: 0,4
Ответ: -1
Ответ: 0
Ответ: 1
Ответ: -0,7
___________________________________________________________________
Вопрос: Какие показатели используют при приведении различных рядов динамики к одному основанию?
Ответ: базисные темпы роста
___________________________________________________________________
Вопрос: Какие показатели по своей величине существуют в пределах от минус до плюс единицы:
Ответ: линейный коэффициент корреляции
___________________________________________________________________
Вопрос: Каковы условия применимости метода корреляционно-регрессионного анализа:
Ответ: однородность изучаемой совокупности
Ответ: нормальный характер распределения факторного и результативного признаков
Ответ: независимость факторных признаков
___________________________________________________________________
Вопрос: Какое выражение является не совсем корректным при пояснении значения эмпирического коэффициента детерминации, равного 64,9% :
Ответ: результативный признак на 64,9% зависит от факторного признака
___________________________________________________________________
Вопрос: Какой метод используется в регрессионном анализе для нахождения числовых значений параметров уравнения регрессии:
Ответ: метод наименьших квадратов
___________________________________________________________________
Вопрос: Какой способ отбора осуществляется только как бесповторный?
Ответ: механический
___________________________________________________________________
Вопрос: Какую форму линии регрессии (форму связи) целесообразно выбрать для отображения зависимости между среднегодовой стоимостью основных производственных фондов и объемом выпускаемой за год продукции:
Ответ: прямую
___________________________________________________________________
Вопрос: Классификация – это:
Ответ: особый вид группировки, представляющий собой устойчивую, фундаментальную группировку по атрибутивному признаку, содержащую подробную номенклатуру групп и подгрупп
___________________________________________________________________
Вопрос: Количественный признак принимает всего 2 значения: 10 и 20. Часть первого из них равна 30%. Найдите среднюю величину:
Ответ: 17
___________________________________________________________________
Вопрос: Корреляционная связь является:
Ответ: стохастической
Ответ: статистической
___________________________________________________________________
Вопрос: Коэффициент вариации характеризует:
Ответ: степень вариации признака
Ответ: типичность средней
___________________________________________________________________
Вопрос: Коэффициент опережения (отставания) в сравниваемых рядах динамики рассчитывается отношением:
Ответ: базисных темпов роста
Ответ: средних темпов роста
___________________________________________________________________
Вопрос: Коэффициент регрессии при однофакторной модели (параметр al) показывает:
Ответ: на сколько единиц изменяется функция при изменении аргумента на одну единицу
___________________________________________________________________
Вопрос: Коэффициент эластичности показывает:
Ответ: на сколько процентов изменяется функция с изменением аргумента на один процент
___________________________________________________________________
Вопрос: Кто из ученых ввел в научный обиход термин «статистика»?
Ответ: Готфрид Ахенваль
___________________________________________________________________
Вопрос: Максимальное и минимальное значения признаков в совокупности равны соответственно 28 и 4. Определите величину интервала группировки, если выделяется 6 групп.
Ответ: 4
___________________________________________________________________
Вопрос: Наилучшей характеристикой для сравнения вариации различных совокупностей служит:
Ответ: коэффициент вариации
___________________________________________________________________
Вопрос: Накопленные частоты используются при построении:
Ответ: кумуляты
___________________________________________________________________
Вопрос: Необходимость проверки на значимость коэффициентов уравнения регрессии и показателей тесноты связи обусловлена:
Ответ: ограниченностью выборки фактических значений факторного и результативного признаков
___________________________________________________________________
Вопрос: Необходимые условия расчета средней величины – это:
Ответ: однородность единиц статистической совокупности; наличие у них общих свойств, формирующих типический размер признака; достаточно большой объем данных
___________________________________________________________________
Вопрос: Несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом называется:
Ответ: выборочным
___________________________________________________________________
Вопрос: Обобщающий статистический показатель представляет собой:
Ответ: измеренную величину признака, свойственную всей массе единиц совокупности, но возможно и не свойственную при этом отдельным ее единицам
___________________________________________________________________
Вопрос: Общая дисперсия признака равна:
Ответ: сумме дисперсии групповых средних (межгрупповой) и средней из внутригрупповых дисперсии
___________________________________________________________________
Вопрос: Общие индексы необходимы для характеристики:
Ответ: всех элементов сложной совокупности
Ответ: части элементов сложной совокупности
___________________________________________________________________
Вопрос: Объект статистического наблюдения – это:
Ответ: совокупность общественных явлений и процессов, которые подлежат наблюдению
___________________________________________________________________
Вопрос: Объекты изучения статистики — это:
Ответ: множество единиц (объектов, явлений), объединенных единой закономерностью и варьирующих в пределах общего качества
Ответ: статистическая совокупность
___________________________________________________________________
Вопрос: Объем совокупности – это:
Ответ: общее число единиц совокупности
___________________________________________________________________
Вопрос: Операция по образованию новых групп на основе ранее построенной группировки называется группировкой:
Ответ: вторичной
___________________________________________________________________
Вопрос: Определение статистической сводки:
Ответ: научно-организованная обработка материалов статистического наблюдения, состоящая в их проверке, систематизации, обработке и подсчете итогов
___________________________________________________________________
Вопрос: Определите структуру предприятий на территории районного центра, если крупных предприятий – 1 , средних – 7 и малых – 2.
Ответ: 10%, 70% и 20%
___________________________________________________________________
Вопрос: Основные организационные вопросы статистического наблюдения – это определение:
Ответ: организации, осуществляющей наблюдение, определение срока или времени проведения наблюдения, места наблюдения, проведение подготовительных мероприятий, инструктирование кадров, разъяснительная работа о задачах и целях статистического наблюдения
___________________________________________________________________
Вопрос: Основными элементами ряда динамики являются:
Ответ: уровни ряда и показатели времени
___________________________________________________________________
Вопрос: Остаточные величины регрессионной модели — это:
Ответ: отклонения теоретических значений результативного признака от его фактических значений
___________________________________________________________________
Вопрос: Отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор, является:
Ответ: бесповторным
___________________________________________________________________
Вопрос: Отметьте правильный вывод о характере, направлении и тесноте связи между стоимостью основных фондов и среднесуточной переработкой сырья по следующим данным:
Ответ: связь прямая, корреляционная, достаточно тесная
___________________________________________________________________
Вопрос: Отметьте правильный вывод о характере, направлении и тесноте связи между уровнем издержек обращения и уровнем рентабельности по 40 фирмам.
Ответ: связь обратная, корреляционная, тесная
___________________________________________________________________
Вопрос: Относительная величина координации определяется:
Ответ: отношением между собой двух частей одной совокупности
___________________________________________________________________
Вопрос: Относительная величина выполнения плана есть отношение уровней:
Ответ: достигнутого в отчетном периоде к запланированному
___________________________________________________________________
Вопрос: Относительная величина выполнения плана равна:
Ответ: отношению относительной величины динамики к относительной величине планового задания
___________________________________________________________________
Вопрос: Относительная величина динамики определяется:
Ответ: отношением однородных величин, характеризующих явление за разные периоды времени или даты
___________________________________________________________________
Вопрос: Относительная величина интенсивности развития определяется отношением:
Ответ: двух разноименных показателей, характеризующих определенную связь между собой
___________________________________________________________________
Вопрос: Относительная величина, используемая для сравнения сложных совокупностей и отдельных их единиц во времени, в пространстве или по сравнению с эталоном называется:
Ответ: индексом
___________________________________________________________________
Вопрос: Относительный показатель, призванный служить инструментом пересчета стоимостных показателей из текущих цен в постоянные называется:
Ответ: индексом — дефлятором
___________________________________________________________________
Вопрос: Относительными величинами в статистике называют:
Ответ: обобщающие показатели, выражающие соотношения абсолютных, средних или ранее полученных относительных показателей
___________________________________________________________________
Вопрос: Отношение одноименных абсолютных величин, соответствующих одному и тому же периоду или моменту времени, относящихся к различным совокупностям, называются относительными величинами:
Ответ: сравнения
___________________________________________________________________
Вопрос: Отношение текущего показателя к предшествующему или базисному показателю представляет собой относительную величину:
Ответ: планового задания
___________________________________________________________________
Вопрос: Отношения одной части изучаемой совокупности к другой ее части называют относительной величиной:
Ответ: координации
___________________________________________________________________
Вопрос: Отрицательная величина эмпирического корреляционного отношения свидетельствует:
Ответ: о неверности предыдущих выводов и расчетов
___________________________________________________________________
Вопрос: Ошибка выборки представляет собой возможные пределы отклонений характеристик выборочной совокупности от характеристик генеральной совокупности:
Ответ: да
___________________________________________________________________
Вопрос: Ошибка выборки при механическом отборе уменьшится:
Ответ: если увеличить численность выборочной совокупности
___________________________________________________________________
Вопрос: Первичный элемент объекта, являющийся носителем признаков, подлежащих регистрации, называется:
Ответ: единицей наблюдения
___________________________________________________________________
Вопрос: Перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения, называется:
Ответ: программой наблюдения
___________________________________________________________________
Вопрос: По данным ряда распределения средний уровень должен быть найден по формуле:
Ответ: средней арифметической взвешенной
___________________________________________________________________
Вопрос: По малому предприятию имеются данные за год об остатках задолженности по кредиту на начало каждого месяца. Представленный ряд является:
Ответ: моментным
___________________________________________________________________
Вопрос: По форме внешнего выражения признаки делятся на:
Ответ: атрибутивные
Ответ: количественные
___________________________________________________________________
Вопрос: По характеру различают связи:
Ответ: функциональные и стохастические
___________________________________________________________________
Вопрос: Показатели изменения уровней ряда динамики, исчисленные с переменной базой сравнения (сравниваются последующие уровни с предыдущими), называются:
Ответ: цепными
___________________________________________________________________
Вопрос: Показатели изменения уровней ряда динамики, исчисленные с постоянной базой сравнения (все уровни ряда динамики сравниваются с одним и тем же уровнем), называются:
Ответ: базисными
___________________________________________________________________
Вопрос: Показатели, которые получаются суммированием значений (размеров, объемов) варьирующего признака всех единиц совокупности, называются:
Ответ: объемом варьирующего признака
___________________________________________________________________
Вопрос: Показатель «стоимость продукции на 1000 руб. основных производственных фондов (фондоотдачи) » относится к какому виду относительных величин:
Ответ: интенсивности
___________________________________________________________________
Вопрос: Полигон — это график ряда:
Ответ: дискретного
___________________________________________________________________
Вопрос: Предельная ошибка выборки для количественно варьирующего и альтернативного признаков определяется произведением коэффициента доверия (кратности средней ошибки) на среднюю ошибку выборки:
Ответ: для всех видов выборки
___________________________________________________________________
Вопрос: Предметом изучения статистики являются:
Ответ: размеры и количественные соотношения качественно определенных массовых общественных явлений, закономерности их связи и развития в конкретных условиях места и времени
___________________________________________________________________
Вопрос: Предприятие выпускает фотоаппараты нескольких типов, средняя цена фотоаппарата выросла за год на 100%. Индекс цены фиксированного состава равен 1,25. Величина индекса структурных сдвигов составит:
Ответ: 1,6
___________________________________________________________________
Вопрос: Предприятие выпускает фотоаппараты нескольких типов, средняя цена фотоаппарата выросла за год на 100%. Индекс цены фиксированного состава равен 1,25. Укажите как изменилась структура продукции:
Ответ: выросла доля продажи фотоаппаратов с высокими ценами
___________________________________________________________________
Вопрос: Предприятие выпускает фотоаппараты нескольких типов, средняя цена фотоаппарата выросла за год на 100%. Индекс цены фиксированного состава равен 1,25. Укажите, с помощью какого показателя можно охарактеризовать изменение структуры производства:
Ответ: индекса структурных сдвигов
___________________________________________________________________
Вопрос: При механической выборке отбор единиц из генеральной совокупности осуществляется посредством:
Ответ: отбора единиц из равных групп, на которые разделена генеральная совокупность
___________________________________________________________________
Вопрос: При серийной выборке отбор единиц в выборку из генеральной совокупности осуществляется посредством:
Ответ: отбора не отдельных единиц, а серий (равновеликих групп), из которых состоит генеральная совокупность
___________________________________________________________________
Вопрос: При собственно-случайной выборке отбор единиц в выборку из генеральной совокупности осуществляется посредством:
Ответ: жеребьевки или лотереи
___________________________________________________________________
Вопрос: При типической выборке отбор единиц в выборку из генеральной совокупности осуществляется посредством:
Ответ: отбора единиц из качественно однородных групп, на которые разделена генеральная совокупность
___________________________________________________________________
Вопрос: Признак совокупности принимает два значения: 10 и 20. Частость первого из них 30%, второго 70%. Выберите верное значение коэффициента вариации, при условии, что среднее арифметическое значение равно 17, а среднее квадратическое отклонение 4,1:
Ответ: 24,1%
___________________________________________________________________
Вопрос: Признак, изменение которого изучается индексным методом, называется:
Ответ: индексируемой величиной
___________________________________________________________________
Вопрос: Произведение относительных величин выполнения плана и планового задания равно относительной величине:
Ответ: динамики
___________________________________________________________________
Вопрос: Производительность труда рабочих первой бригады выросла на 8%, второй — на 16%. В отчетном периоде численность рабочих первой бригады в 2 раза меньше, чем второй. Укажите средний прирост производительности труда рабочих двух бригад вместе.
Ответ: 13,3%
___________________________________________________________________
Вопрос: Промилле десятичной дробью составляет:
Ответ: 0,001
___________________________________________________________________
Вопрос: Простая средняя арифметическая из цепных абсолютных приростов является:
Ответ: средним абсолютным приростом
___________________________________________________________________
Вопрос: Расположите в правильной последовательности следующие 3 обстоятельства с точки зрения их важности при выборе формы корреляционной взаимосвязи:
Ответ: предварительный теоретический анализ внутренних связей явлений
Ответ: фактически сложившиеся закономерности в связном изменении явлений
Ответ: объем изучаемой совокупности (численность ее единиц)
___________________________________________________________________
Вопрос: Распределение работников по образованию — это распределение по признаку:
Ответ: атрибутивному
___________________________________________________________________
Вопрос: Ряд динамики – это:
Ответ: ряд статистических данных, характеризующих изменение общественных явлений во времени
___________________________________________________________________
Вопрос: Ряд динамики показывает:
Ответ: изменение общественного явления во времени
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
+1
08.03.16 в 23:17
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Тесты на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Тесты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Тест, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Отзывы о работе:
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Бесплатный тест по статистике
- Тесты по статистике по темам
- Ответы на LAN-Testing по статистике
- Коллекция тестов по статистике с ответами
- Тесты по статистике
- Ответы на тест по статистике онлайн
- Ответы на тестовые вопросы по статистике
- Тест по алфавиту по статистике
- Ответы на лан-тестинг по статистике
- Ответы на тест по статистике по алфавиту