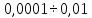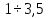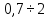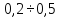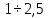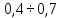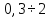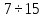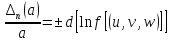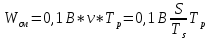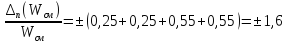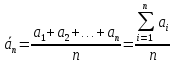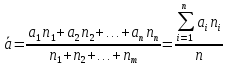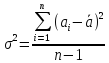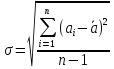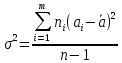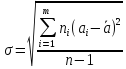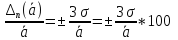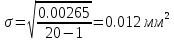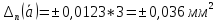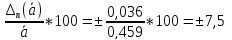Предельные ошибки при различных способах измерения
|
Способ |
Ошибка |
|
|
1 |
Стальная |
|
|
2 |
Угломеры |
|
|
3 |
Тахометры |
|
|
4 |
Весы Технические Аналоговые |
|
|
5 |
Динамометры Гидравлические Электрические |
|
|
6 |
Ртутные |
|
|
7 |
Секундомеры |
|
|
8 |
Ртутные |
|
|
9 |
Твердомеры |
|
Ошибки опытов
Под
опытом подразумевается совокупность
разовых измерений различных величин в
одних и тех же условиях. Способы измерения
можно разбить на два вида:
—
измерить прямые, когда данную величину
измеряют непосредственно
—
измерения косвенные, когда искомая
величина является функцией измеряемых
величин.
Можно
по-разному ставить опыт и выбирать
способы измерений, так как измерения
косвенные зависят от ряда прямых, то
при прочих равных условиях, выгодней
тот способ, при котором будет меньше
прямых измерений, а значит меньше и
сумма ошибок. Предельную относительную
ошибку опыта определяют на основании
следующих правил:
-
Ошибка
суммы заложена между наибольшей и
наименьшей из относительных ошибок
слагаемых, практически берут или
наибольшую относительную ошибку или
среднюю арифметическую. -
Ошибка
произведения или частного от деления
равна сумме относительных ошибок
сомножителей или соответственно
делимого и частного -
Ошибка
n-ой степени какого-то основания (значения
величины) в n раз больше относительной
ошибки основания.
Во
всех случаях установление точности
опыта, точности вычисления результата
должна определяться точностью измерений.
Если рассматривать ошибку измерения
как частное значение переменной величины,
предельную относительную ошибку опыта
можно вычислить по формуле:
А
– является функцией переменных, то есть
предельная относительная ошибка а равна
дифференциалу её натурального логарифма,
причем следует брать сумму абсолютных
значений всех членов такого выражения.
Данное уравнение дает возможность
решить обратную задачу: определить
необходимую точность измерений различными
способами, если задана общая точность
опыта, но проще поступить таким образом:
установить требование заранее к
метрологическим показателям приборов
(цена или интервал деления, пределы
измерения, порог чувствительности,
измерительное усилие, погрешность и
вариация показаний). Вычислить предельную
ошибку и по ней подобрать недостающую
аппаратуру и заменив приборы дающие
слишком большую предельную погрешность.
Используя эту формулу можно найти
измерения, при которых предельная
относительная ошибка функции будет
наименьшей. Условием определенного
решения является наличие минимума
функции. Рассмотрим порядок вычисления
предельной ошибки опыта. Установим
предельную относительную ошибку
вычисления производительности агрегата.
В
– ширина агрегата
v— скорость агрегата
Тр– время работы агрегата
Учитывая
подобранную в этом примере аппаратуру
и средние данные таблицы, получим
предельную ошибку.
Из
изложенного можно сделать вывод: для
того, чтобы правильно подобрать аппаратуру
необходимо провести сравнительную
оценку точности различных способов
измерения, в данном случае полезно
заранее задаться точностью опыта.
Точность измерений должна быть
целесообразной, указав на три основные
обоснования:
-
Заключается
в практическом использовании результатов
(при технологическом процессе заточки
лезвия нельзя добиться его затупленности
меньше 10 микрон, тогда не следует
измерять износ с точностью до десятых
долей микрона). -
В
некоторых случаях нецелесообразно
измерять с ошибкой меньше некоторых
колебаний значений измеряемой величины. -
Экономическая
сторона. Чем точнее измерительная
аппаратура, тем она сложнее и дороже,
тем больше затраты не её ремонт и
калибровку. Может оказаться, что при
таком количестве измерений и той же
надежности, что и при большем количестве
измерений, прибором дающем несколько
большую ошибку, стоимость измерений
дорогим прибором будет выше.
При
определении величины случайных ошибок,
кроме предельной, вычисляют статистическую
ошибку многократных измерений, её
устанавливают после измерений при
помощи методов математической статистики
и теории ошибок. Если, например, диаметр
вала, вязкость масла измерять по одному
разу, случайные ошибки могут исказить
результат, поэтому лучше измерять
какую-либо практически постоянную
величину несколько раз и брать среднюю
арифметическую этих измерений. Среднее
арифметическое измерение является
наиболее вероятным значением измеряемой
величины при данном количестве соединений.
В
теории ошибок доказывается, чем больше
проведено измерений какой-либо величины,
тем меньше суммарная ошибка средней и
при бесконечном числе измерений,
случайная ошибка средней бесконечно
мала.
Лекция
5 – 19.10.11
Чем
больше значений случайных ошибок и
разброс, рассеяние отсчетов, тем больше
число раз необходимо измерять одну и
ту же величину чтобы достигнуть заданной
точности и надежности измерений.
Рассеяние результатов измерений
указывает на большую или меньшую их
изменчивость т оценивается средним
квадратом отклонений наблюдаемых
значений аiот их средних h’ и
квадратным корнем из среднего квадрата.
Среднее
арифметическое
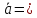
измерений аi, anделение на
количество измерений.
Если
все измерения сгруппированы в m классов
с разными количествами измерений в
каждом классе, то следует вычислять
взвешенную среднюю арифметическую:
а1,
а2, аm– среднее по классу
Отношение
любого отдельного результата измерений
от средней арифметической можно
представить как разность аiи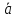
аi– результат любого измерения.
Дисперсией
случайной величиныназывается среднее
значение величины от её среднего
значения.
Корень
квадратный из дисперсии называется
средним квадратическим отклонением
или стандартом.
При
разделении всех измерений на n классов
с массовыми средними дисперсия будет
равна:
Стандарт:
Стандарт
имеет значение величины, для которой
он вычислен. Дисперсия и стандарт это
меры рассеяния или изменчивости. Чем
больше дисперсия или стандарт, тем
больше рассеяны значения измерений.
Таким образом при измерении неизменной
величины СКО (стандарт) является мерой
точности среднего арифметического
значения неоднократно измеренной
величины. Если же неоднократно измеримая
величина переменна, то вычисленное по
её измерениям значение стандарта
показывает не только меру точности как
случайную ошибку измерений, но и меру
изменчивости переменной.
Абсолютное
значение стандарта зависит и от
совершенства измерительных приборов.
Если одну и ту же величину измерять при
помощи приборов различной точности
абсолютное значение стандарта будет
меньше при измерении более точным
прибором. Например, если dотвизмерить сначала нутромером со шкалой
в мм, а затем индикатором со шкалой в
микронах значение стандарта при последних
измерениях будет меньше.
Это
обстоятельство имеет важное значение
при выборе числа опытов.
Для
большинства технических измерений
можно считать, что наибольшей ошибкой
средней арифметической многократных
измерений является абсолютная величина
равная трем стандартная или относительная
величина.
Эта
ошибка называется наибольшей возможной
статической в отличие от придельной
ошибки.
В
качестве примера приведем результаты
проверки на точность показаний
пневматического калибратора, которым
измеряли относительную не плотность в
одном из цилиндров дизельного двигателя.
Было
проведено 20 измерений, при которых
двигатель работая на оборотах близким
к номинальным, по 2-3мин. И получен ряд
значений неплотности.
0,465 0,450 0,425
Отсюда
наибольшая возможная статистическая
ошибка:
Если
предельную ошибку устанавливают до
измерений, а наибольшую статистическую
вычисляют по результатам неоднократных
измерений. Наибольшая статистическая
ошибка при измерении неизменной величина
будет меньше предельной, так как
отклонения отдельных измерений от
средней неоднозначны как это принято
для предельной ошибки. Иногда из значения
измеряемой величины отсчитывают с
большей точностью, чем это предположено
для предельной ошибки.
Точность
разовых измерений оценивают только по
предельной ошибке. При неоднократных
измерениях до их начала следует
пользоваться предельной ошибкой (для
прибора аппаратуры и представления о
возможностях измерений). А после измерений
оценивать их точность по наибольшей
возможной статистической ошибке.
Лекция
6 – 21.10.11
Измерения,
дающие дисп или одинаковой величины,
называют равноточными. Равноточность
измерений серий и опытов облегчает
обработку результатов измерений и
уменьшает суммарные ошибки исследования.
Практически
добиться равноточности измерений можно
только в тех случаях, когда измерение
будет проводить опытный человек одним
и тем же прибором в одинаковых условиях.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешность средств измерения и результатов измерения.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.
Статическая и динамическая погрешности.
- Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. - Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Систематическая и случайная погрешности.
Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.
Причинами возникновения систематических составляющих погрешности измерения являются:
- отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
- неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
- упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
- погрешность градуировки или небольшой сдвиг шкалы;
- неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
- неравномерный износ направляющих устройств для базирования измеряемых деталей;
- износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
- усталостные измерения упругих свойств деталей, а также их естественное старение;
- неисправности средства измерений.
Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.
Погрешности адекватности и градуировки.
Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.
Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.
Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.
Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.
Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0…100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30…100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50…+50, Xn=100).
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
Аддитивные и мультипликативные погрешности.
- Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
- Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.
Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:
– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
- Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
- Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Как вычислить погрешность измерений?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
В чем измеряется погрешность?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
- Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
- Инструментальные и методические погрешности.
- Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
- Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти абсолютную погрешность измерительного прибора?
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Что такое погрешность метода измерений?
По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.
Что такое погрешность измерительного прибора?
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как определить погрешность деления?
Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.
Как рассчитывается приведенная погрешность?
Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.
- Общие требования» и им подобных.
- Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
- Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.
Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
- Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
- Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
- Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).
По характеру проявления:
- систематические (могут быть исключены из результатов);
- случайные;
- грубые или промахи (как правило не включаются в результаты измерений).
В зависимости от эксплуатации приборов:
- основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
- дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.
| Наимено вание погреш ности | Формула | Форма выражения, записи | Обозначение класса точности | |||||||||||||||
| В докумен тации | На сред стве изме рений | |||||||||||||||||
| Абсолют ная | Δ = X д — X изм | Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г | Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов. | М 1 | ||||||||||||||
| Относи тельная | δ = (Δ ⁄ X д ) · 100 | δ = ±0,5 Пример: Измеренное значение изб.
Как вычислить абсолютную погрешность формула?Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ). Чему равна абсолютная погрешность?При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения. Для чего нужна погрешность измерений?Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным. Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации. Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины. Как найти абсолютную погрешность пример?Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. Как определить цену деления и погрешность?Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков. Что такое максимальная погрешность измерений?Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи. Как рассчитывается приведенная погрешность?Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п. Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
По характеру проявления:
В зависимости от эксплуатации приборов:
|
Главная страница » Метрология » Метрологические термины и определения » Погрешности измерений
Погрешности измерений
9.1. Погрешность результата измерения;
погрешность измерения
de Fehler einer Messung
en error of a measurement
fr erreur de mesure
Отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечания
1. Истинное значение величины неизвестно, его применяют только в теоретических исследованиях.
2. На практике используют действительное значение величины
,в результате чего погрешность измерения
определяют по формуле:
(9.1)
где
— измеренное значение величины.
3. Синонимом термина погрешность измерения является термин ошибка измерения, применять который не рекомендуется как менее удачный.
9.2. Систематическая погрешность измерения;
систематическая погрешность
de systematischer Anteil des Fehlers
en systematic error
fr erreur systematique
Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
Примечание. В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодические и погрешности, изменяющиеся по сложному закону.
Постоянные погрешности — погрешности, которые длительное время сохраняют свое значение, например в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности — непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности — погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
9.3. Инструментальная погрешность измерения;
инструментальная погрешность
de Messmittelfehler
en instrumental error
fr erreur instrumentale
Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
9.4. Погрешность метода измерений;
погрешность метода
de Fehler aus dem Messverfahren
en error of method
fr erreur de methode
Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания
1. Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью.
2. Иногда погрешность метода может проявляться как случайная.
9.5. Погрешность (измерения) из-за изменений условий измерения
Составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
9.6. Субъективная погрешность измерения;
субъективная погрешность
Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания
1. Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений.
2. Иногда субъективную погрешность называют личной погрешностью или личной разностью.
9.7. Неисключенная систематическая погрешность;
НСП
Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Примечания
1. Иногда этот вид погрешности называют неисключенный (ые) остаток (остатки) систематической погрешности.
2. Неисключенная систематическая погрешность характеризуется ее границами.
Границы неисключенной систематической погрешности
при числе слагаемых
вычисляют по формуле:
,
где
— граница i-ой составляющей неисключенной систематической погрешности.
3. При числе неисключенных систематических погрешностей
вычисления проводят по формуле:
(9.3)
где K — коэффициент зависимости отдельных неисключенных
систематических погрешностей от выбранной доверительной
вероятности Р при их равномерном распределении (при P = 0,99 K =
1,4). Здесь ТЕТА рассматривается как доверительная квазислучайная
погрешность.
9.8. Случайная погрешность измерения;
случайная погрешность
de zufalliger Anteil des Fehlers
en random error
fr erreur aleatoire
Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
9.9. Абсолютная погрешность измерения;
абсолютная погрешность
de absoluter Messfehler
en absolute error of a measurement
fr erreur absolue de mesure
Погрешность измерения, выраженная в единицах измеряемой величины.
9.10. Абсолютное значение погрешности
en absolute value of an error
fr valeur absolue d’une erreur
Значение погрешности без учета ее знака (модуль погрешности).
Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.
9.11. Относительная погрешность измерения;
относительная погрешность
de relativer Fehler (einer Messung)
en relative error
fr erreur relative
Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Примечание. Относительную погрешность в долях или процентах находят из отношений:
или
(9.4)
где:
— абсолютная погрешность измерений;
— действительное или измеренное значение величины.
9.12. Рассеяние результатов в ряду измерений;
рассеяние результатов;
рассеяние
de Streuung
en dispersion
fr dispersion
Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания
1. Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
2. Оценками рассеяния результатов в ряду измерений могут быть:
— размах,
— среднее квадратическое отклонение (экспериментальное среднее квадратическое отклонение),
— доверительные границы погрешности (доверительная граница).
(в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
9.13. Размах результатов измерений;
размах
Оценка
рассеяния результатов единичных измерений физической n величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле:
(9.5)
где
и
— наибольшее и наименьшее значения физической величины в данном ряду измерений.
Примечание. Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
9.14. Среднее квадратическое отклонение результатов единичных измерений в ряду измерений;
среднее квадратическое отклонение измерений;
среднее квадратическое отклонение;
СКО
en experimental (sample) standard deviation
fr ecart-type experimental
Характеристика S рассеяния результатов измерений в ряду равноточных измерений одной и той же физической величины, вычисляемая по формуле:
(9.6)
где:
— результат i-го единичного измерения;
— среднее арифметическое значение n единичных результатов измерений величины.
Примечание — СКО S является оценкой стандартного отклонения сигма — параметра распределения результатов измерений и одновременно оценкой стандартного отклонения распределения случайной погрешности этих результатов.
(п. 9.14 в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
9.15. Среднее квадратическое отклонение среднего арифметического значения результатов измерений;
среднее квадратическое отклонение среднего арифметического;
СКО среднего арифметического
en experimental (sample) standard deviation
of the average
fr ecart-type experimental de la moyenne
Характеристика
рассеяния среднего арифметического значения результатов равноточных измерений одной и той же величины, вычисляемая по формуле:
(9.7)
где: S — средняя квадратическая погрешность результатов измерений, вычисляемое по формуле (9.6); n — число измерений в ряду.
9.16. Доверительные границы погрешности результата измерений;
доверительные границы погрешности;
доверительные границы
Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
Примечания
1. Доверительные границы в случае нормального распределения вычисляются как
,
где,
– СКО соответственно единичного и среднего арифметического результатов измерений; t — коэффициент, зависящий от доверительной вероятности Р и числа измерений n.
(в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
2. При симметричных границах термин может применяться в единственном числе — доверительная граница.
3. Исключено. — Изменение N 2, введенное Приказом Росстандарта от 04.08.2010 N 203-ст.
9.17. Поправка
de Korrektion
en correction
fr correction
Значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.
9.18. Поправочный множитель
de Korrektionsfaktor
en correction factor
fr coefficient de correction
Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание. Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.
9.19. Точность результата измерений;
точность измерений
de Messgenauigkeit
en accuracy of measurement
fr exactitude de mesure
Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность.
9.20. Неопределенность измерений;
неопределенность
de Messunsicherheit
en uncertainty of measurement
fr incertitude de mesure
Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.
Примечания.
1. Определение взято из VIM-93 [1].
2. К определению в [1] приведены примечания, из которых следует, что:
а) параметром может быть стандартное отклонение (или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень;
б) неопределенность состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются на данных эксперимента или другой информации.
9.21. Погрешность метода поверки
Погрешность применяемого метода передачи размера единицы при поверке.
9.22. Погрешность градуировки средства измерений;
погрешность градуировки
Погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
9.23. Погрешность воспроизведения единицы физической величины;
погрешность воспроизведения
Погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание. Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год.
9.24. Погрешность передачи размера единицы физической величины;
погрешность передачи размера единицы
Погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание. В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений.
9.25. Статическая погрешность измерений;
статическая погрешность
Погрешность результата измерений, свойственная условиям статического измерения.
9.26. Динамическая погрешность измерений;
динамическая погрешность
Погрешность результата измерений, свойственная условиям динамического измерения.
9.27. Промах
Погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание. Иногда вместо термина промах применяют термин грубая погрешность измерений.
9.28. Предельная погрешность измерения в ряду измерений;
предельная погрешность
Максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.
Примечание. Во многих случаях погрешность
принимают за предельную, то есть
. При необходимости за предельную погрешность может быть принято и другое значение погрешности (где S — см. термин 9.14).
9.29. Погрешность результата однократного измерения;
погрешность измерения
Погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример. При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет +/- 0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна +/- 0,01 мм в данных условиях измерений.
9.30. Суммарное среднее квадратическое отклонение среднего арифметического значения результатов измерений;
суммарное среднее квадратическое отклонение среднего арифметического;
суммарное СКО среднего арифметического
Характеристика
рассеяния среднего арифметического результатов измерений, обусловленная влиянием случайных и неисключенных систематических погрешностей и вычисляемая по формуле:
,
(9.8)
где:
вычисляется по формуле (9.7);
— СКО неисключенных систематических погрешностей при равномерном распределении каждой из них. (п. 9.30 в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
Добавить комментарий
Главная страница » Метрология » Метрологические термины и определения » Погрешности измерений
Опыт
проведения измерений показывает, что
при многократных измерениях одной и
той же неизменной физической величины
при постоянных условиях погрешность
измерений можно представить в виде двух
слагаемых, которые по разному проявляются
от измерения к измерению. Существуют
факторы, постоянно или закономерно
изменяющиеся в процессе проведения
измерений и влияющие на результат
измерений и его погрешность. Погрешности,
вызываемые такими факторами, называются
систематическими..
3.1. Систематические погрешности
Систематическая
погрешность
– составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины.
В
зависимости от характера изменения
систематические погрешности подразделяются
на постоянные,
прогрессирующие, периодические,
изменяющиеся по сложному закону.
Близость
к нулю систематической погрешности
отражает правильность
измерений.
Систематические
погрешности обычно оцениваются
либо путем теоретического анализа
условий измерения,
основываясь на известных свойствах
средств измерений, либо использованием
более точных
средств
измерений.
На
возникновение погрешностей влияют
также факторы, нерегулярно появляющиеся
и неожиданно исчезающие. Причем
интенсивность их также не остается
постоянной. Результаты измерения в
таких условиях имеют различия, которые
индивидуально непредсказуемы, а присущие
им закономерности проявляются лишь на
значительном числе результатов.
Погрешности, появляющиеся в результате
действия таких факторов, называются
случайными
погрешностями.
3.2.Случайные погрешности
Случайная
погрешность
– составляющая погрешности измерения,
изменяющаяся случайным образом (по
знаку и значению) при повторных измерениях
одной и той же величины., проведенных с
одинаковой тщательностью.
Малость
случайных погрешностей говорит о хорошей
сходимости
измерений,
т.е. о близости друг к другу результатов
измерений, выполненных повторно одними
и теми же средствами, одним и тем же
методом, в одинаковых условиях и с
одинаковой тщательностью.
Обнаруживаются
случайные погрешности путем повторных
измерений
одной и той же величины в одних и тех же
условиях. Они не могут быть исключены
опытным путем, но могут быть оценены
при обработке результатов наблюдений.
Деление
погрешностей измерений на случайные и
систематические очень важно, т.к. эти
составляющие проявляются по разному и
их определение требует разных подходов.
Факторы,
вызывающие погрешности, как правило,
можно свести к общему уровню, когда
влияние их на формирование погрешности
является более или менее одинаковым.
Однако некоторые факторы могут проявляться
неожиданно сильно, например, резкое
падение напряжения в сети. В таком случае
могут возникать погрешности, существенно
превышающие погрешности, оправданные
условиями измерений, свойствами средств
измерений и метода измерений, квалификацией
оператора. Такие погрешности называются
грубыми,
или промахами.
3.3.
Грубые погрешности.
Грубая
погрешность (промах)
– погрешность, которая для данных
условий резко отличается от остальных
значений погрешности.
Грубые
погрешности необходимо всегда исключать
из рассмотрения, если известно, что они
являются результатом очевидных промахов
при проведении измерений.
Если
же причины появления резко выделяющихся
наблюдений установить нельзя, то для
решения вопроса об их исключении
используют статистические методы.
4.
Принципы
оценивания погрешностей
Как
уже отмечалось, результат измерения
никогда не может быть абсолютно точным,
т.к. нам неизвестно истинное значение
измеряемой величины. В результате
измерения всегда присутствует какая-то
неопределенность. Неопределенность
результата измерений обычно характеризуется
указанием границ
его погрешности.
Если границы
погрешности находят как отвечающие
некоторой вероятности,
то их называют доверительными
границами
погрешности
результата измерений или доверительной
погрешностью.
Доверительные
границы погрешности
результата измерений – наибольшие и
наименьшие значения погрешности
измерений, ограничивающие интервал,
внутри которого с заданной вероятностью
находится искомое (истинное) значение
погрешности результата измерения. Более
подробно построение доверительных
интервалов будет рассмотрено ниже при
изучении случайных погрешностей
Если
границы погрешности оцениваются так,
что погрешность, выходящую за эти
границы, встретить нельзя, то ее называют
предельной
погрешностью измерения.
Предельная
погрешность – максимальная
погрешность измерения (плюс, минус),
допускаемая для данной измерительной
задачи.
Причиной
описания случайных погрешностей
границами, в которых они могут находиться
с определенной вероятностью, является
вероятностный
характер
появления тех или иных значений
погрешности. То есть, мы можем указать
не значение погрешности, которое может
быть определено в процессе измерений,
а только тот диапазон значений, в котором
она может находиться.
Для целей решаемой
измерительной задачи погрешности
описываются с помощью определенной
модели
(деление их на систематические, случайные,
методические, инструментальные, личные
и др.). На этой модели для количественного
описания погрешности результата
измерения вводится понятия характеристик
погрешностей.
Так, например, одной из характеристик
случайной погрешности обычно является
среднее
квадратическое отклонение (СКО).
Для интервальной оценки используются,
как было отмечено выше, доверительные
границы,
в которых погрешность находится с
заданной доверительной вероятностью
(в том числе с вероятностью, равной
единице, для предельной погрешности).
Используются и другие характеристики
погрешности, некоторые из которых будут
рассмотрены ниже.
В каждой
измерительной задаче характеристики
погрешности оцениваются на основе
экспериментальных данных и априорной
информации о решаемой задаче. Погрешность
результата измерений обычно складывается
из нескольких составляющих,
обусловленных различными причинами,
поэтому возникает необходимость
суммирования
характеристик
составляющих погрешности с целью
вычисления общей характеристики
погрешности результата измерения.
Наибольшее
распространение получила процедура
раздельного
суммирования характеристик
систематической составляющей погрешности
и случайной составляющей погрешности.
Затем на основании характеристик
суммарной систематической и случайной
составляющих погрешности вычисляются
характеристики погрешности результата
измерения (обычно это границы с
доверительной вероятностью 0,95 или
0,99). При этом следует отметить, что
систематическая погрешность как правило
оценивается по своим составляющим, в
то время как при рассмотрении случайной
погрешности ее составляющие чаще всего
не выделяются. Это обусловлено тем, что
случайная погрешность определяется
сразу вся по результатам многократных
измерений.
Так как истинное
значение измеряемой величины нам
неизвестно, то при обработке результатов
наблюдений одной из основных задач
является нахождение оценок
характеристик
погрешности. Именно оценок, т.к. полученные
значения характеристик погрешностей
являются тем или иным приближением к
их истинным значениям.
В соответствии
с требованиями измерительной задачи
с точки зрения точности и цели измерений
можно выделить несколько способов
оценивания погрешностей:
-
точное
оценивание погрешностей (с учетом
метрологических свойств конкретного
средства измерений и анализа метода
измерений); -
приближенное
оценивание погрешностей (с учетом лишь
нормативных и типовых характеристик
СИ); -
предварительное
оценивание погрешностей (по типовым
методикам выполнения измерений, на
основании которых заранее оценивается
возможная погрешность результата
измерений).
Для
того, чтобы результаты измерений имели
объективный характер и имели смысл, они
должны быть воспроизводимы
и
сравнимы
с результатами аналогичных измерений,
полученных другими авторами. Мерой же
допускаемой
невоспроизводимости
полученного результата измерений и
служит оцененная погрешность измерения.
Одним
из основных принципов оценивания
погрешности является правило их
оценивания
сверху,
т.е. погрешность измерения лучше
преувеличить, чем приуменьшить. Это
может привести лишь к снижению качества
измерений, но не к их полному обесценению,
как в случае приуменьшения погрешности.
На практике это сводится к тому, что при
оценивании погрешностей используют
такие вероятности, которые позволяют
считать измерения вполне достоверными.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная страница » Метрология » Метрологические термины и определения » Погрешности измерений
Погрешности измерений
9.1. Погрешность результата измерения;
погрешность измерения
de Fehler einer Messung
en error of a measurement
fr erreur de mesure
Отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечания
1. Истинное значение величины неизвестно, его применяют только в теоретических исследованиях.
2. На практике используют действительное значение величины
,в результате чего погрешность измерения
определяют по формуле:
(9.1)
где
— измеренное значение величины.
3. Синонимом термина погрешность измерения является термин ошибка измерения, применять который не рекомендуется как менее удачный.
9.2. Систематическая погрешность измерения;
систематическая погрешность
de systematischer Anteil des Fehlers
en systematic error
fr erreur systematique
Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
Примечание. В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодические и погрешности, изменяющиеся по сложному закону.
Постоянные погрешности — погрешности, которые длительное время сохраняют свое значение, например в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности — непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности — погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
9.3. Инструментальная погрешность измерения;
инструментальная погрешность
de Messmittelfehler
en instrumental error
fr erreur instrumentale
Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
9.4. Погрешность метода измерений;
погрешность метода
de Fehler aus dem Messverfahren
en error of method
fr erreur de methode
Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания
1. Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью.
2. Иногда погрешность метода может проявляться как случайная.
9.5. Погрешность (измерения) из-за изменений условий измерения
Составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
9.6. Субъективная погрешность измерения;
субъективная погрешность
Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания
1. Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений.
2. Иногда субъективную погрешность называют личной погрешностью или личной разностью.
9.7. Неисключенная систематическая погрешность;
НСП
Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Примечания
1. Иногда этот вид погрешности называют неисключенный (ые) остаток (остатки) систематической погрешности.
2. Неисключенная систематическая погрешность характеризуется ее границами.
Границы неисключенной систематической погрешности
при числе слагаемых
вычисляют по формуле:
,
где
— граница i-ой составляющей неисключенной систематической погрешности.
3. При числе неисключенных систематических погрешностей
вычисления проводят по формуле:
(9.3)
где K — коэффициент зависимости отдельных неисключенных
систематических погрешностей от выбранной доверительной
вероятности Р при их равномерном распределении (при P = 0,99 K =
1,4). Здесь ТЕТА рассматривается как доверительная квазислучайная
погрешность.
9.8. Случайная погрешность измерения;
случайная погрешность
de zufalliger Anteil des Fehlers
en random error
fr erreur aleatoire
Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
9.9. Абсолютная погрешность измерения;
абсолютная погрешность
de absoluter Messfehler
en absolute error of a measurement
fr erreur absolue de mesure
Погрешность измерения, выраженная в единицах измеряемой величины.
9.10. Абсолютное значение погрешности
en absolute value of an error
fr valeur absolue d’une erreur
Значение погрешности без учета ее знака (модуль погрешности).
Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.
9.11. Относительная погрешность измерения;
относительная погрешность
de relativer Fehler (einer Messung)
en relative error
fr erreur relative
Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Примечание. Относительную погрешность в долях или процентах находят из отношений:
или
(9.4)
где:
— абсолютная погрешность измерений;
— действительное или измеренное значение величины.
9.12. Рассеяние результатов в ряду измерений;
рассеяние результатов;
рассеяние
de Streuung
en dispersion
fr dispersion
Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания
1. Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
2. Оценками рассеяния результатов в ряду измерений могут быть:
— размах,
— среднее квадратическое отклонение (экспериментальное среднее квадратическое отклонение),
— доверительные границы погрешности (доверительная граница).
(в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
9.13. Размах результатов измерений;
размах
Оценка
рассеяния результатов единичных измерений физической n величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле:
(9.5)
где
и
— наибольшее и наименьшее значения физической величины в данном ряду измерений.
Примечание. Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
9.14. Среднее квадратическое отклонение результатов единичных измерений в ряду измерений;
среднее квадратическое отклонение измерений;
среднее квадратическое отклонение;
СКО
en experimental (sample) standard deviation
fr ecart-type experimental
Характеристика S рассеяния результатов измерений в ряду равноточных измерений одной и той же физической величины, вычисляемая по формуле:
(9.6)
где:
— результат i-го единичного измерения;
— среднее арифметическое значение n единичных результатов измерений величины.
Примечание — СКО S является оценкой стандартного отклонения сигма — параметра распределения результатов измерений и одновременно оценкой стандартного отклонения распределения случайной погрешности этих результатов.
(п. 9.14 в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
9.15. Среднее квадратическое отклонение среднего арифметического значения результатов измерений;
среднее квадратическое отклонение среднего арифметического;
СКО среднего арифметического
en experimental (sample) standard deviation
of the average
fr ecart-type experimental de la moyenne
Характеристика
рассеяния среднего арифметического значения результатов равноточных измерений одной и той же величины, вычисляемая по формуле:
(9.7)
где: S — средняя квадратическая погрешность результатов измерений, вычисляемое по формуле (9.6); n — число измерений в ряду.
9.16. Доверительные границы погрешности результата измерений;
доверительные границы погрешности;
доверительные границы
Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
Примечания
1. Доверительные границы в случае нормального распределения вычисляются как
,
где,
– СКО соответственно единичного и среднего арифметического результатов измерений; t — коэффициент, зависящий от доверительной вероятности Р и числа измерений n.
(в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
2. При симметричных границах термин может применяться в единственном числе — доверительная граница.
3. Исключено. — Изменение N 2, введенное Приказом Росстандарта от 04.08.2010 N 203-ст.
9.17. Поправка
de Korrektion
en correction
fr correction
Значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.
9.18. Поправочный множитель
de Korrektionsfaktor
en correction factor
fr coefficient de correction
Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание. Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.
9.19. Точность результата измерений;
точность измерений
de Messgenauigkeit
en accuracy of measurement
fr exactitude de mesure
Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность.
9.20. Неопределенность измерений;
неопределенность
de Messunsicherheit
en uncertainty of measurement
fr incertitude de mesure
Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.
Примечания.
1. Определение взято из VIM-93 [1].
2. К определению в [1] приведены примечания, из которых следует, что:
а) параметром может быть стандартное отклонение (или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень;
б) неопределенность состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются на данных эксперимента или другой информации.
9.21. Погрешность метода поверки
Погрешность применяемого метода передачи размера единицы при поверке.
9.22. Погрешность градуировки средства измерений;
погрешность градуировки
Погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
9.23. Погрешность воспроизведения единицы физической величины;
погрешность воспроизведения
Погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание. Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год.
9.24. Погрешность передачи размера единицы физической величины;
погрешность передачи размера единицы
Погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание. В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений.
9.25. Статическая погрешность измерений;
статическая погрешность
Погрешность результата измерений, свойственная условиям статического измерения.
9.26. Динамическая погрешность измерений;
динамическая погрешность
Погрешность результата измерений, свойственная условиям динамического измерения.
9.27. Промах
Погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание. Иногда вместо термина промах применяют термин грубая погрешность измерений.
9.28. Предельная погрешность измерения в ряду измерений;
предельная погрешность
Максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.
Примечание. Во многих случаях погрешность
принимают за предельную, то есть
. При необходимости за предельную погрешность может быть принято и другое значение погрешности (где S — см. термин 9.14).
9.29. Погрешность результата однократного измерения;
погрешность измерения
Погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример. При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет +/- 0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна +/- 0,01 мм в данных условиях измерений.
9.30. Суммарное среднее квадратическое отклонение среднего арифметического значения результатов измерений;
суммарное среднее квадратическое отклонение среднего арифметического;
суммарное СКО среднего арифметического
Характеристика
рассеяния среднего арифметического результатов измерений, обусловленная влиянием случайных и неисключенных систематических погрешностей и вычисляемая по формуле:
,
(9.8)
где:
вычисляется по формуле (9.7);
— СКО неисключенных систематических погрешностей при равномерном распределении каждой из них. (п. 9.30 в ред. Изменения N 2, введенного Приказом Росстандарта от 04.08.2010 N 203-ст)
Добавить комментарий
Главная страница » Метрология » Метрологические термины и определения » Погрешности измерений