Предельная ошибка выборки эксель

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.

Расчет ошибки средней арифметической

Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.

В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.

Способ 1: расчет с помощью комбинации функций

Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.

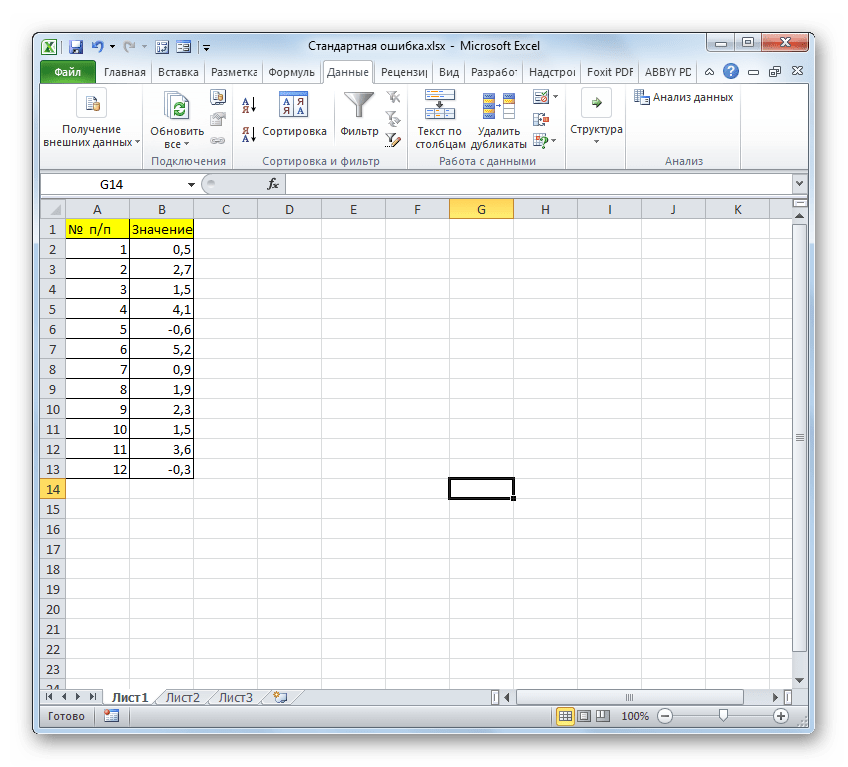
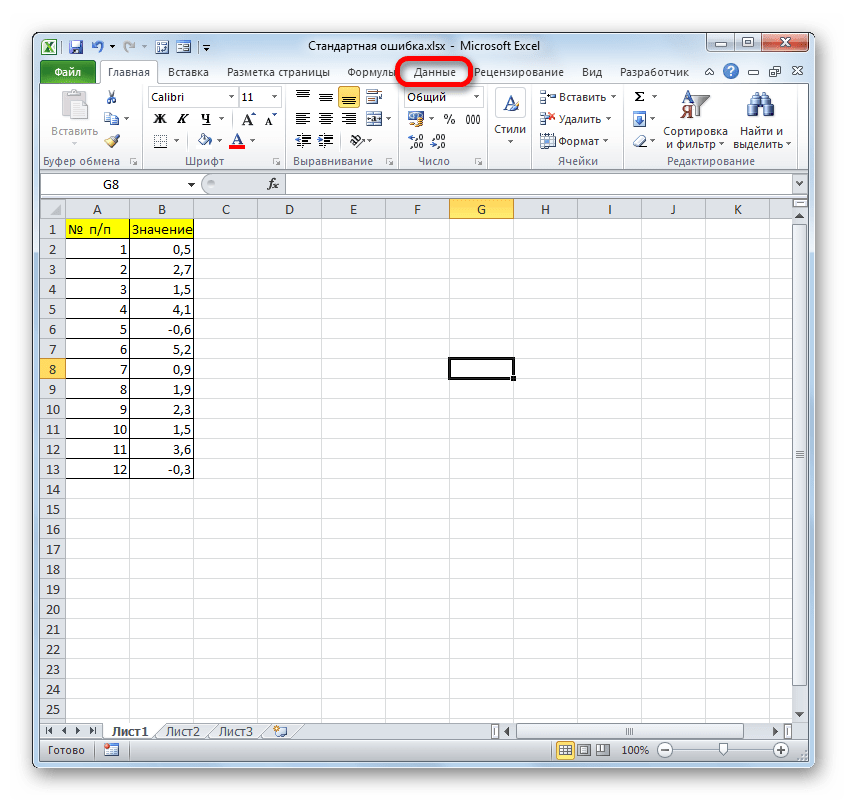
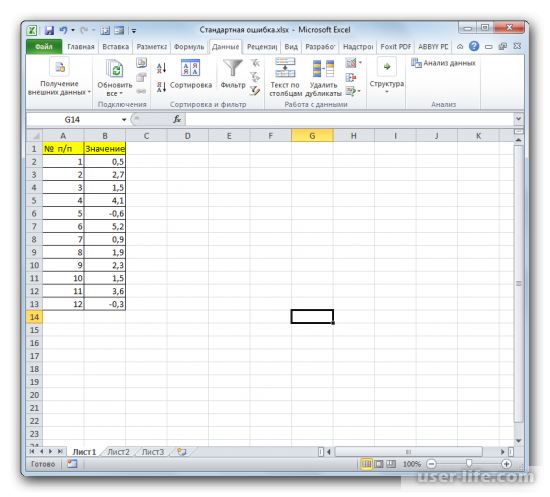
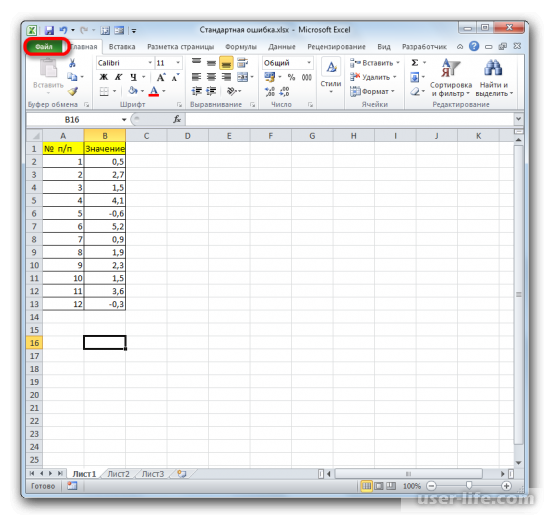
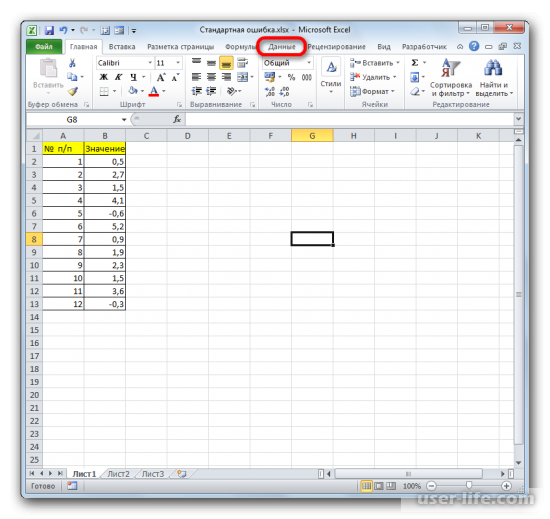
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.

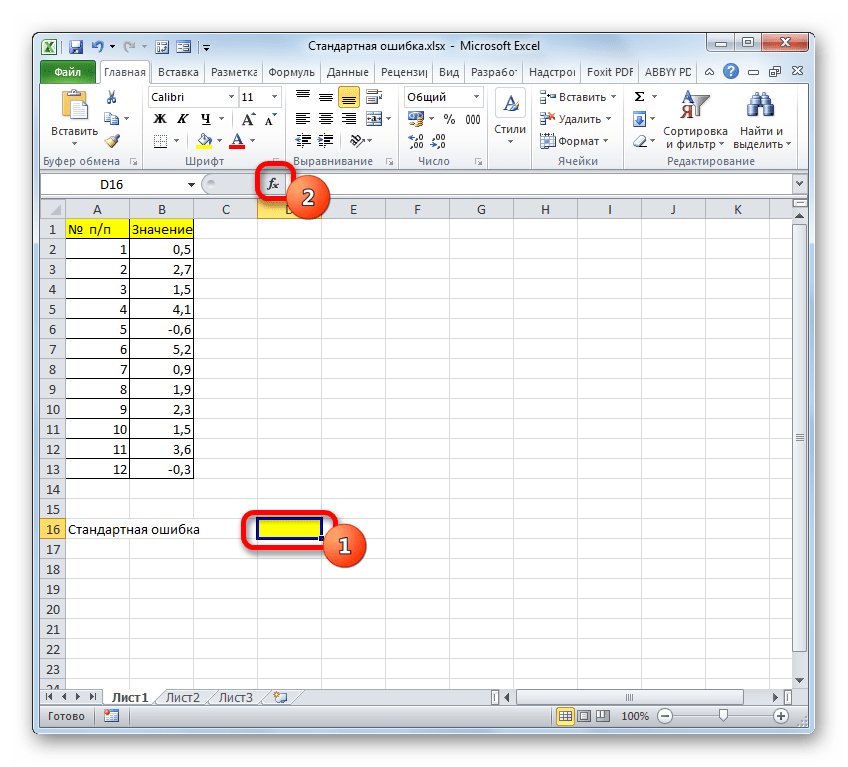
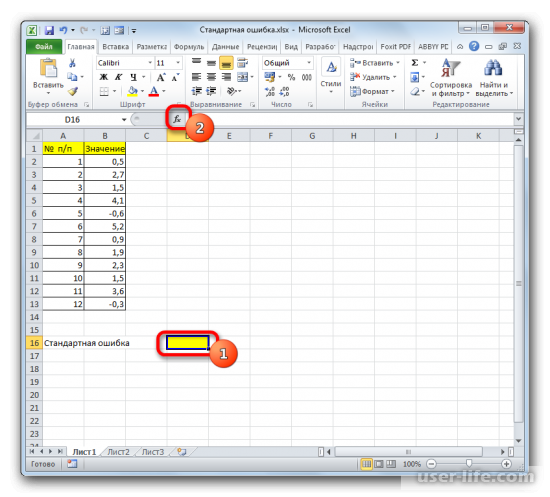
1. Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».

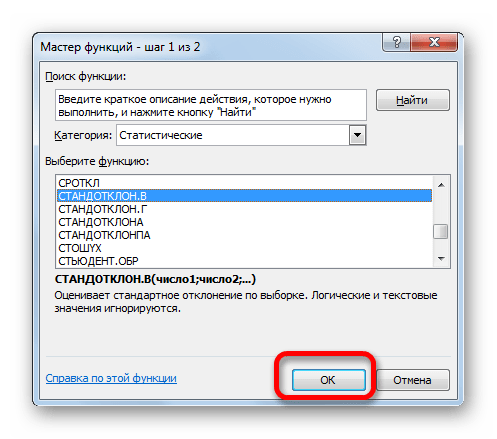
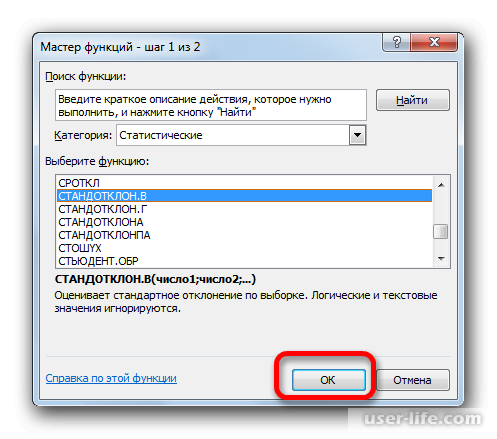
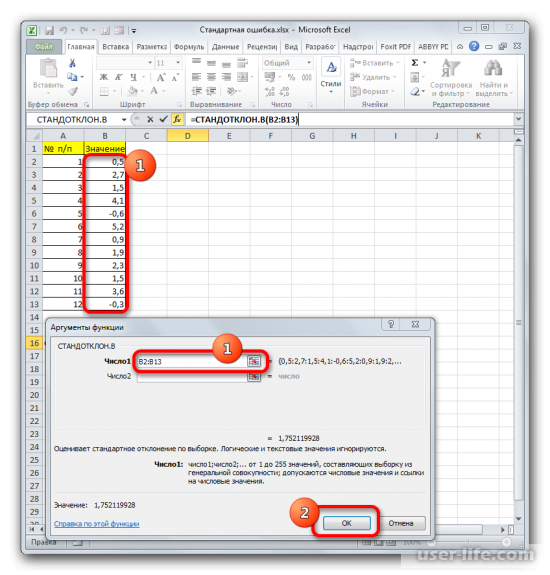
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».

Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:

«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.

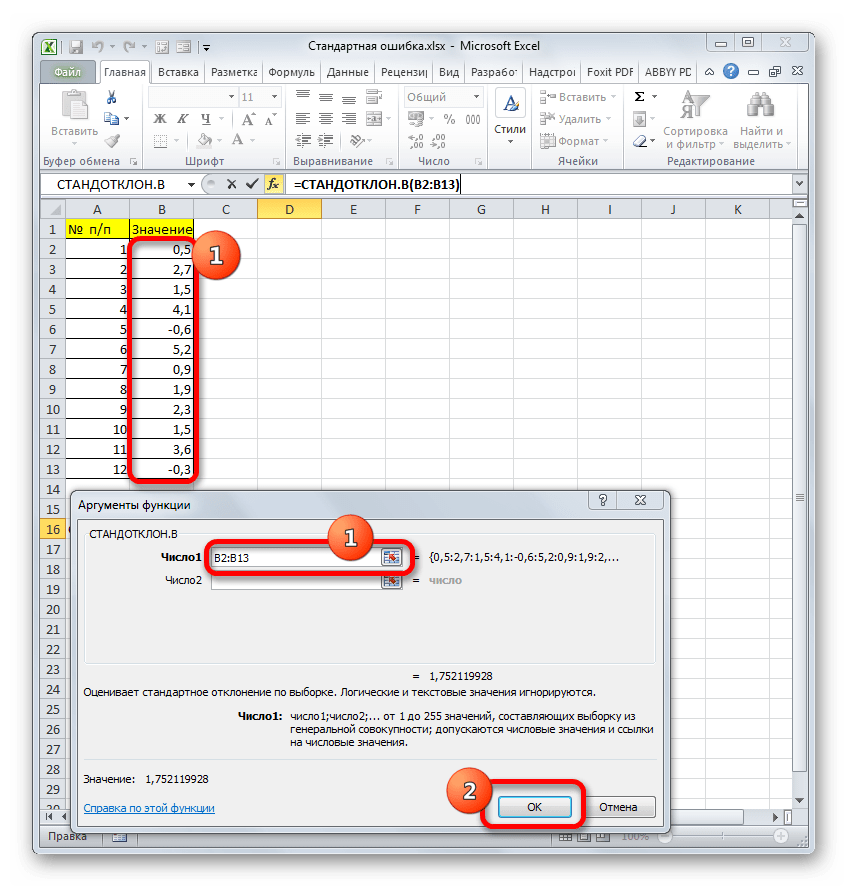
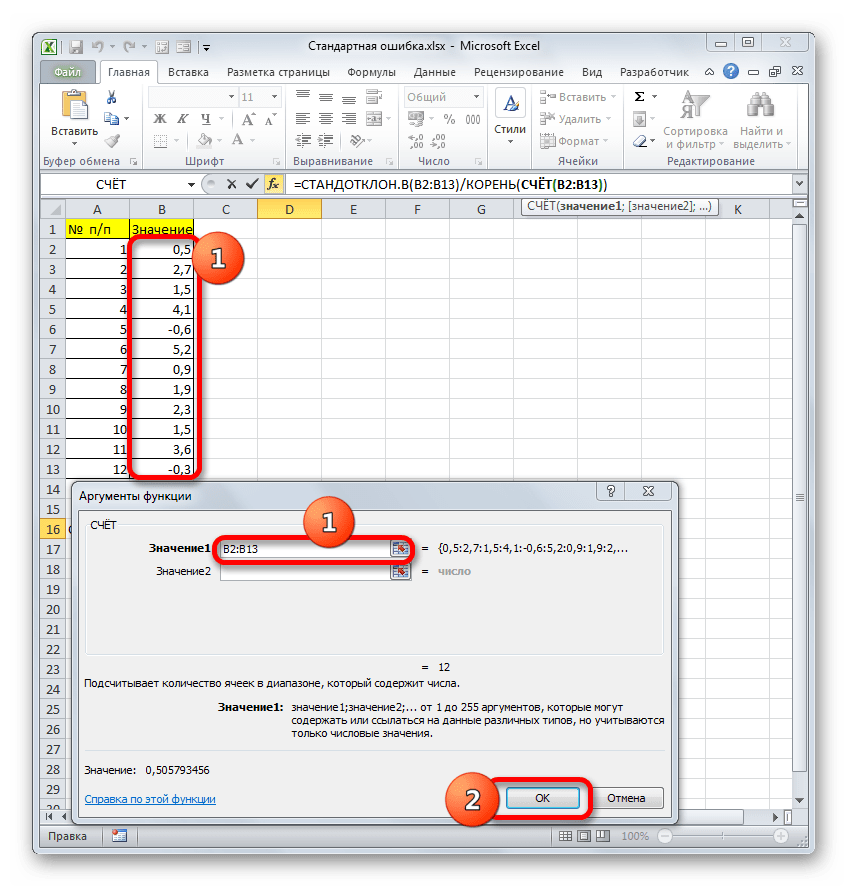
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».

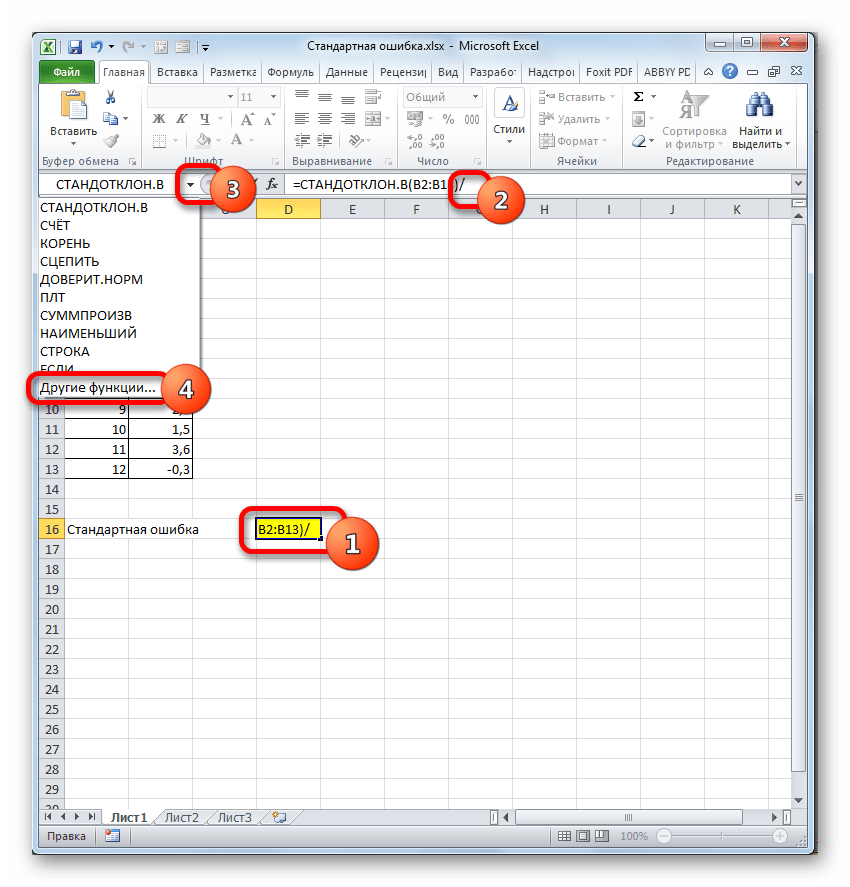
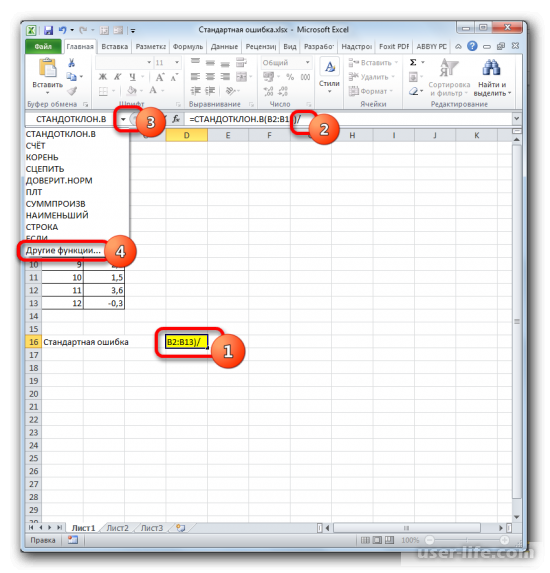
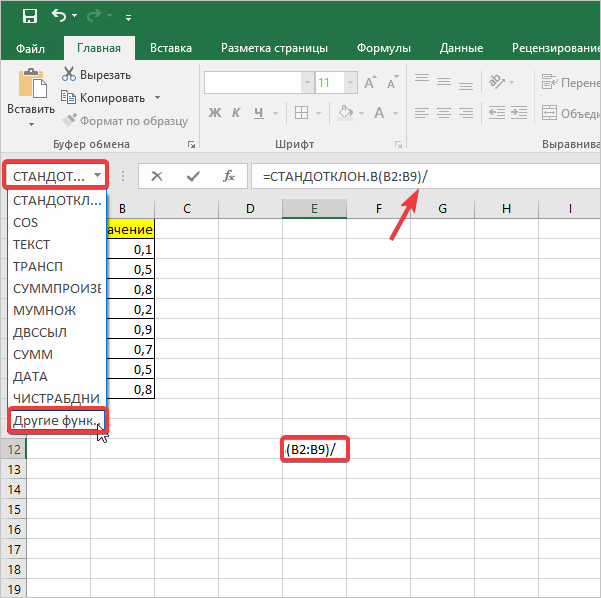
В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».

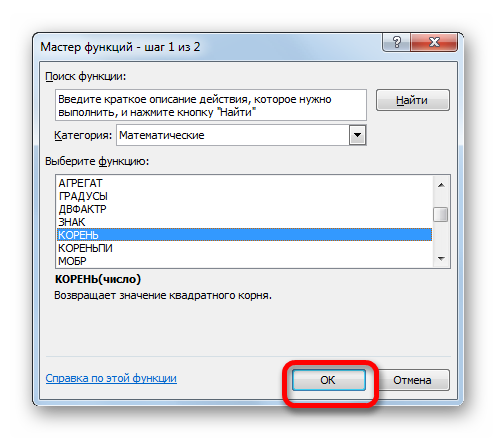
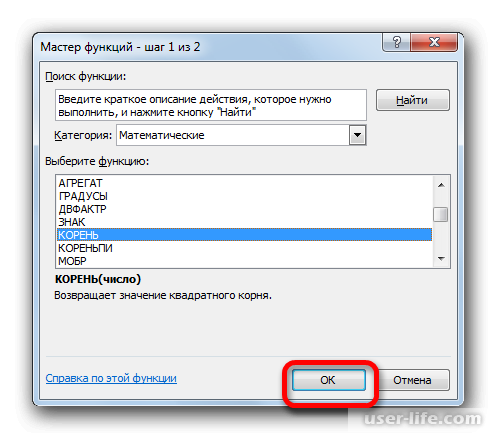
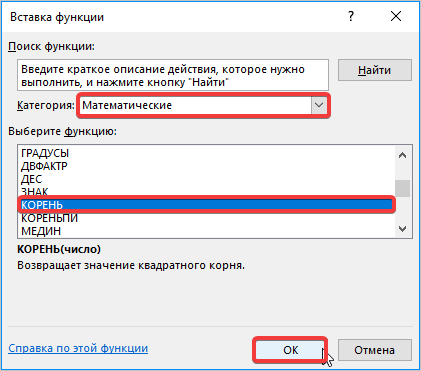
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».

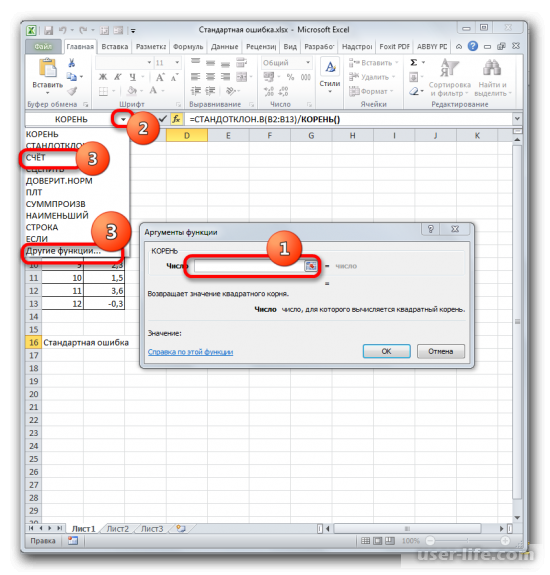
Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:

Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.

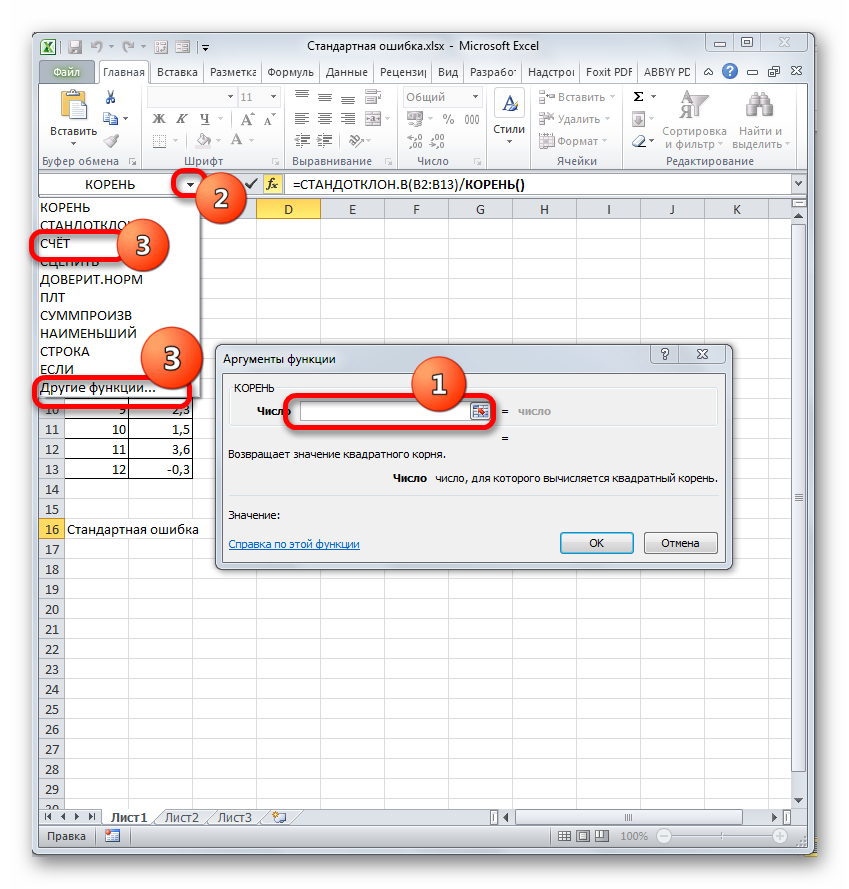
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».

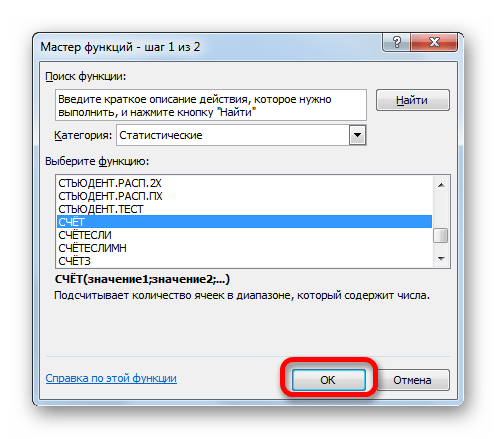
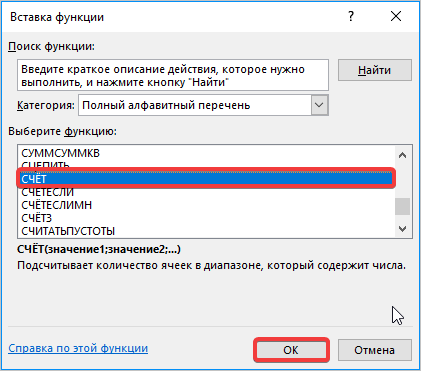
В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».

Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:

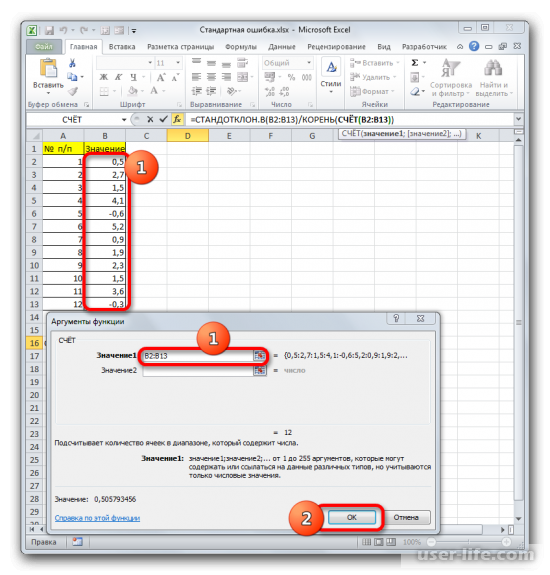
В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».

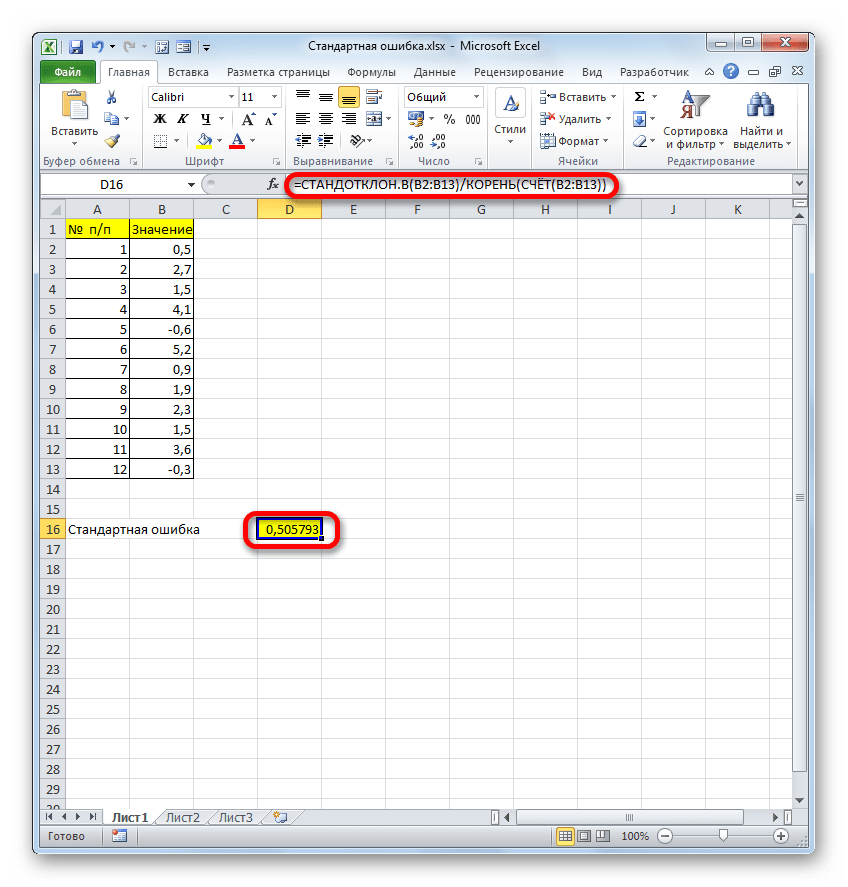
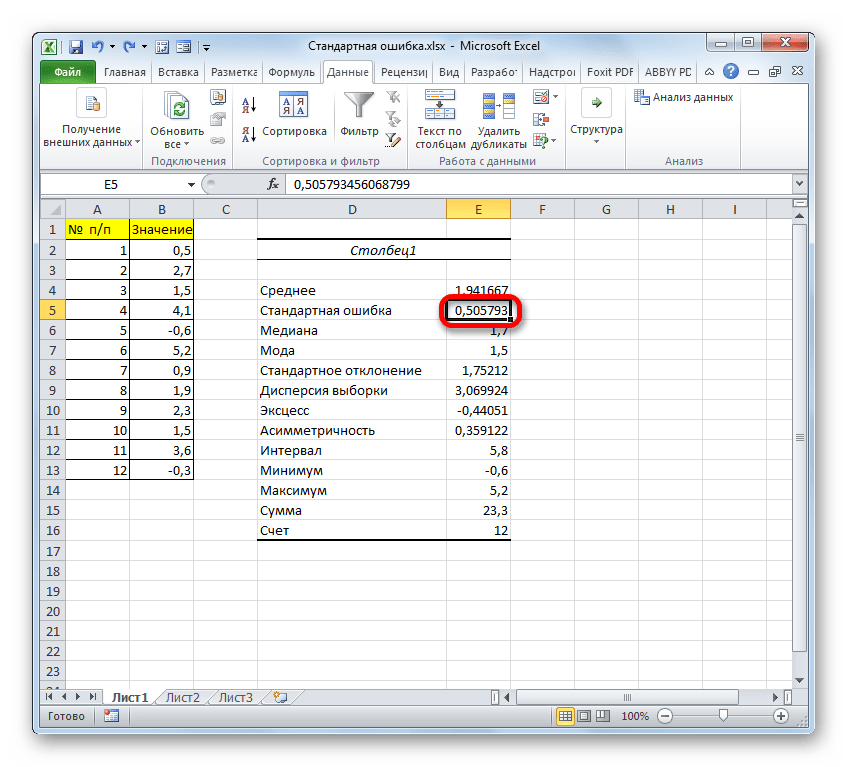
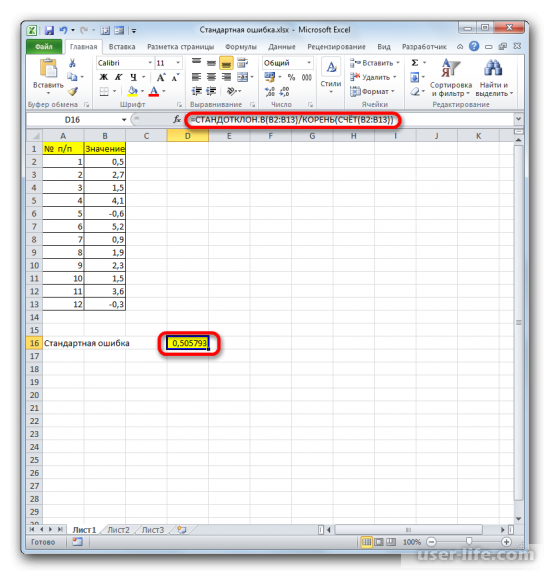
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:

Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.

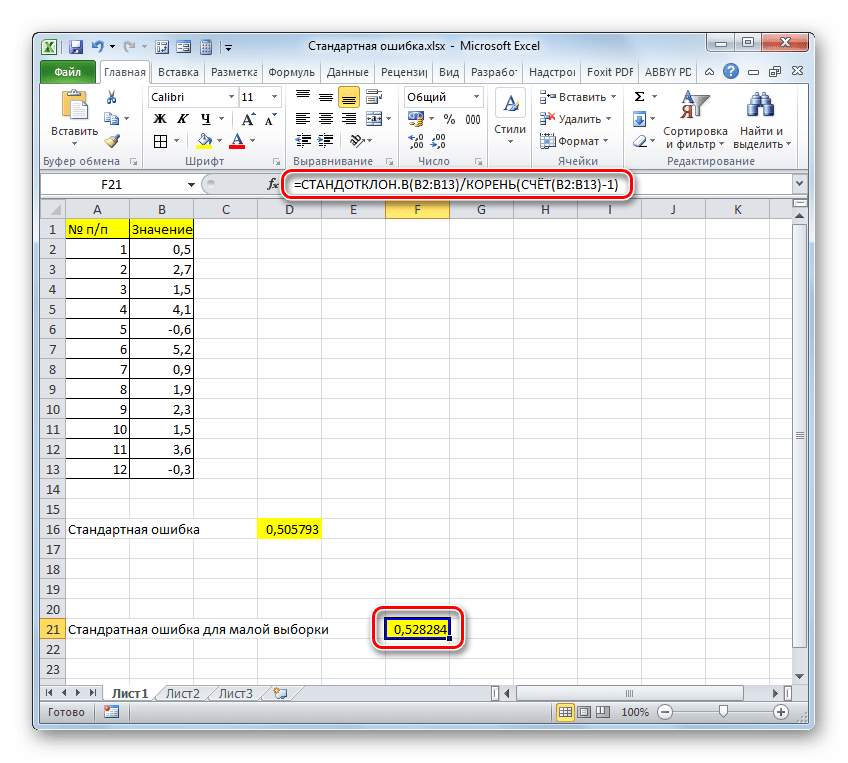
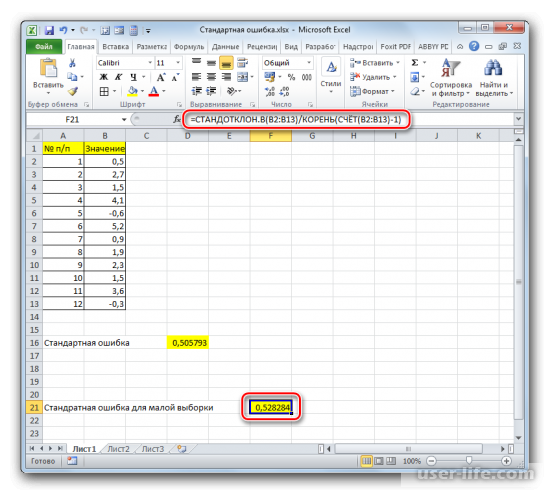
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:

Способ 2: применение инструмента «Описательная статистика»

Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.

Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.

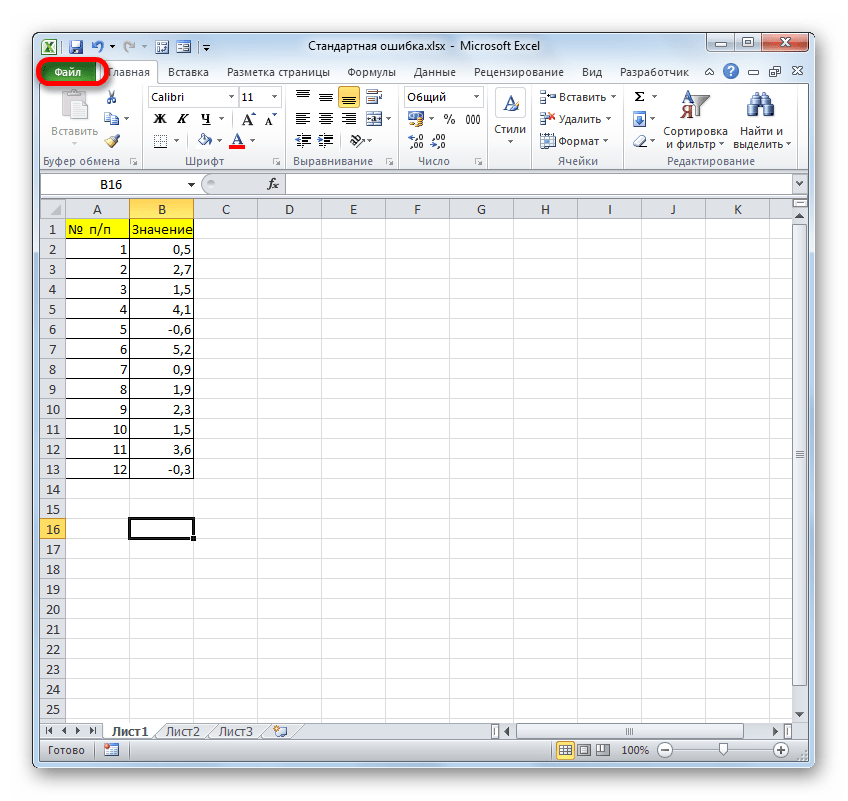
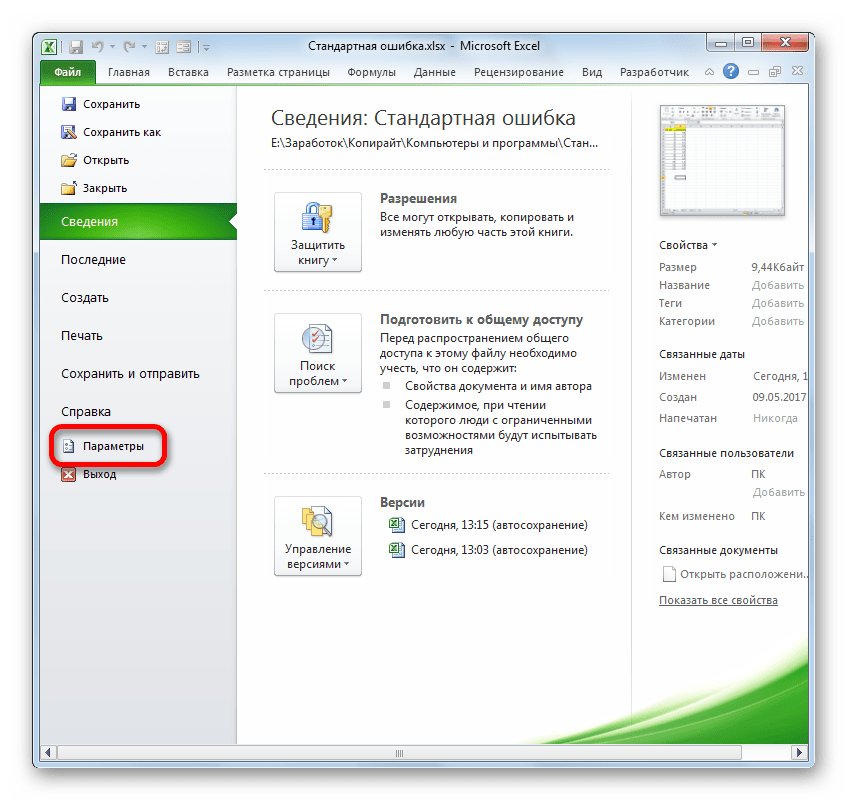
После того, как открыт документ с выборкой, переходим во вкладку «Файл».

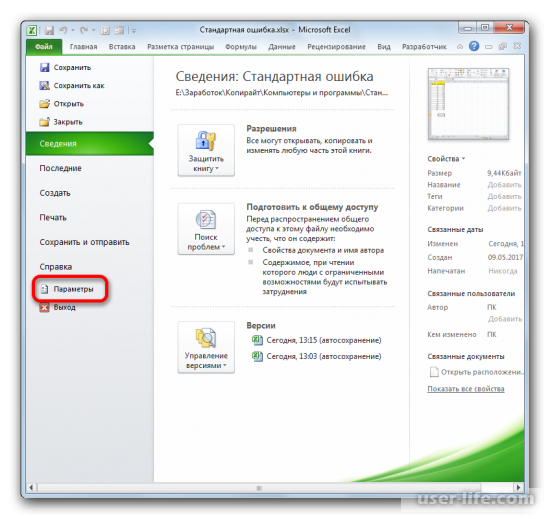
Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».

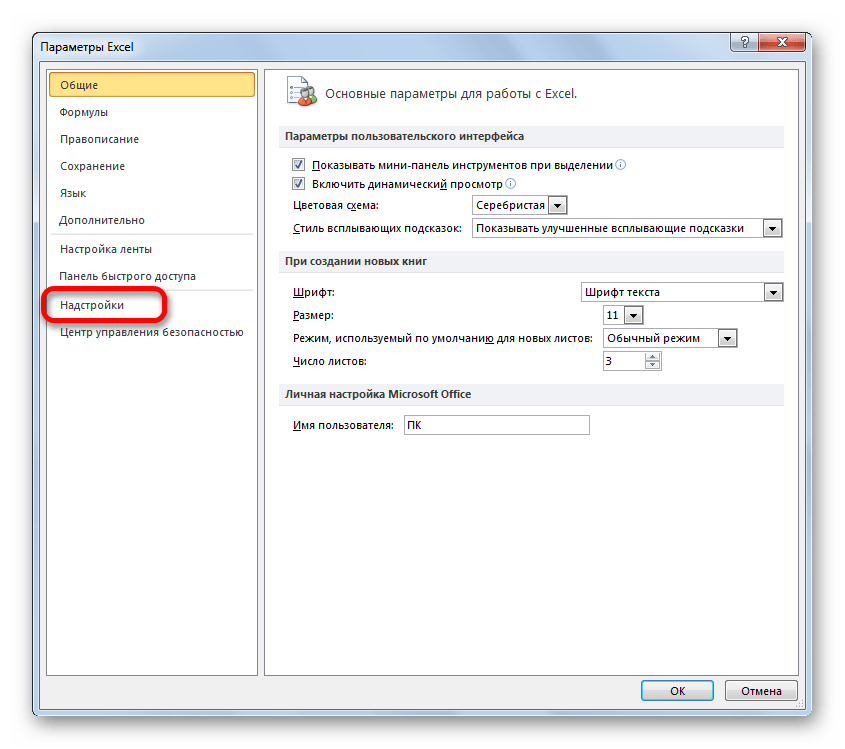
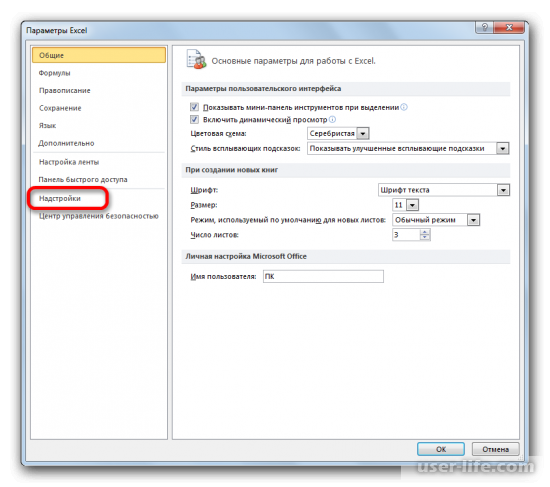
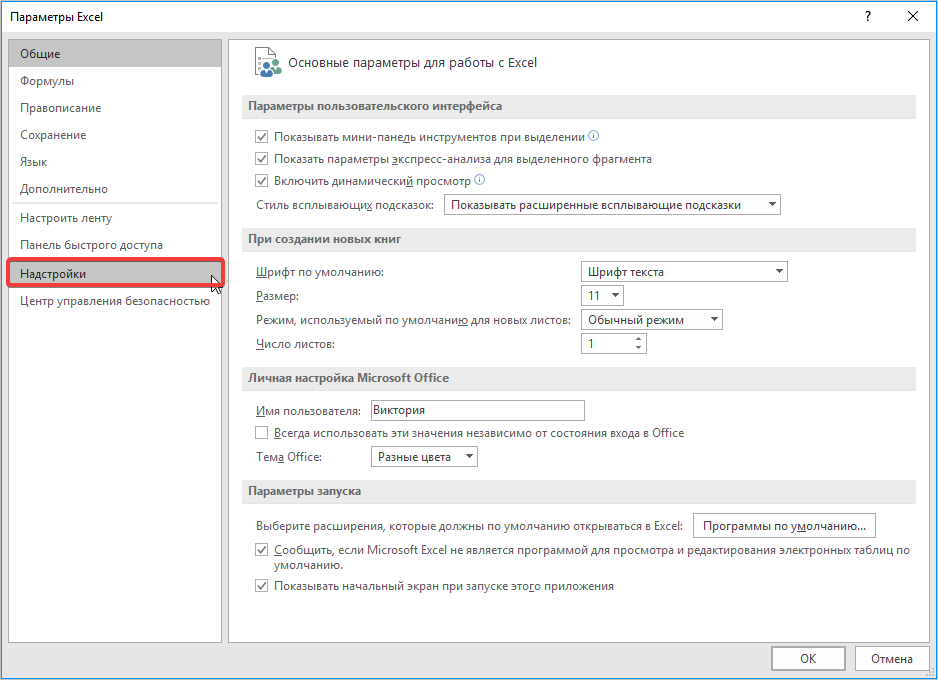
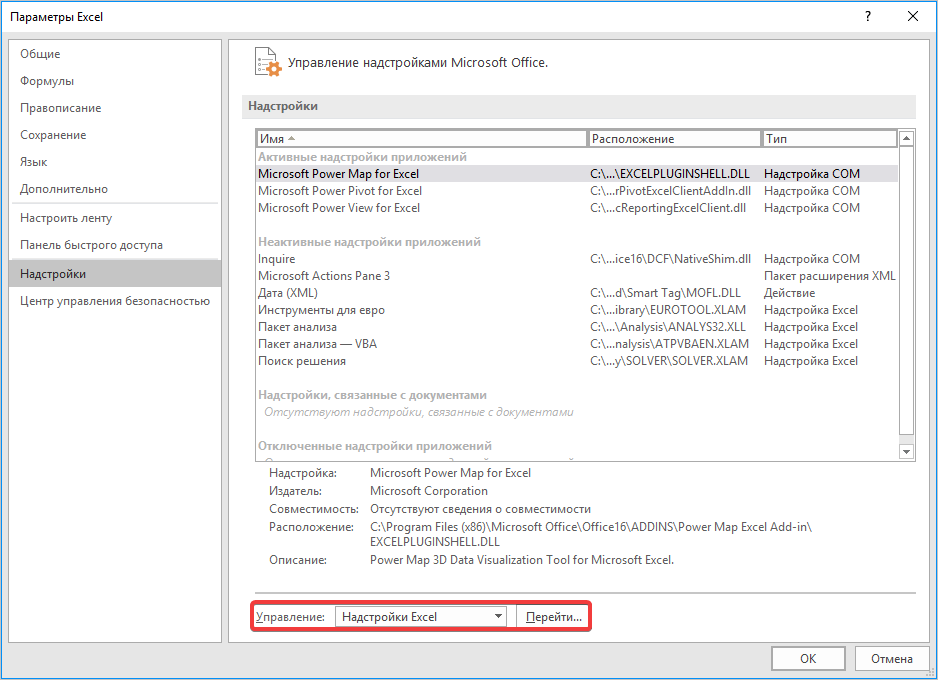
Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».

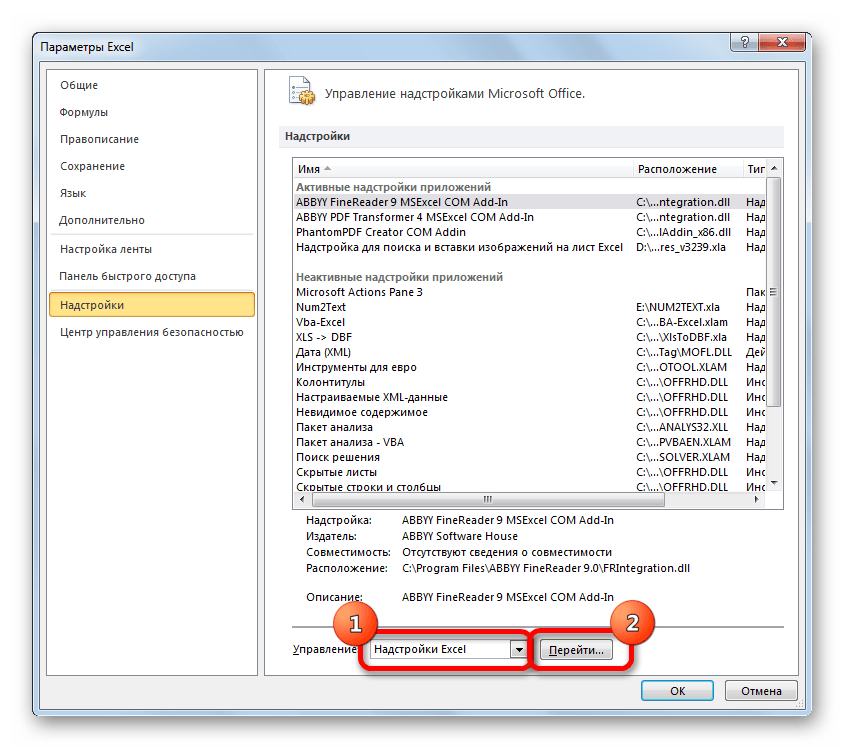
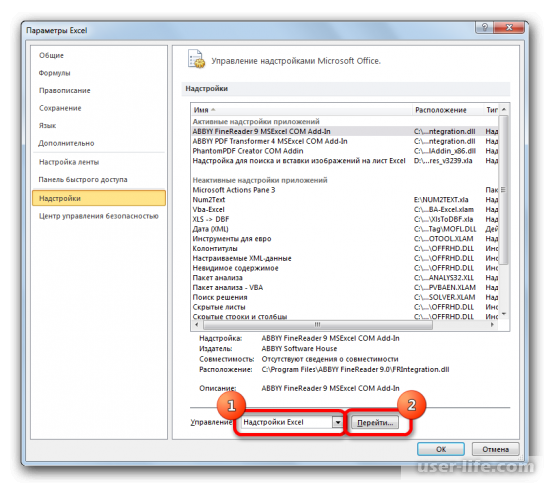
В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.

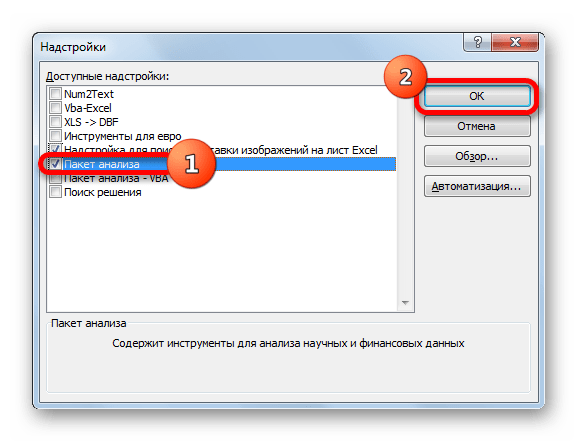
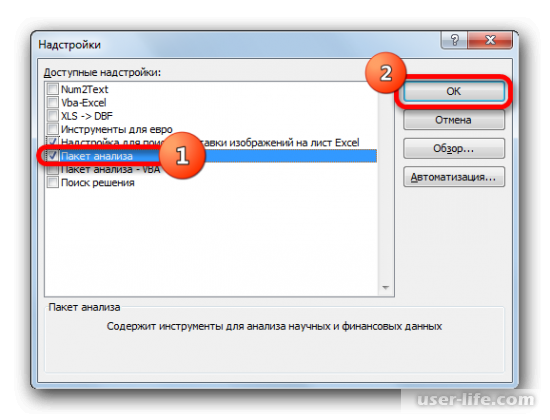
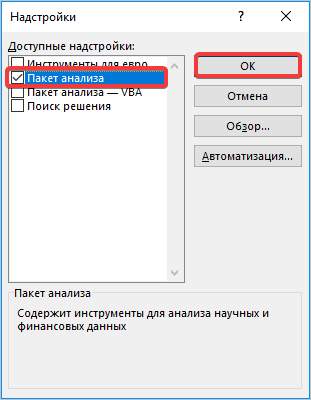
Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.

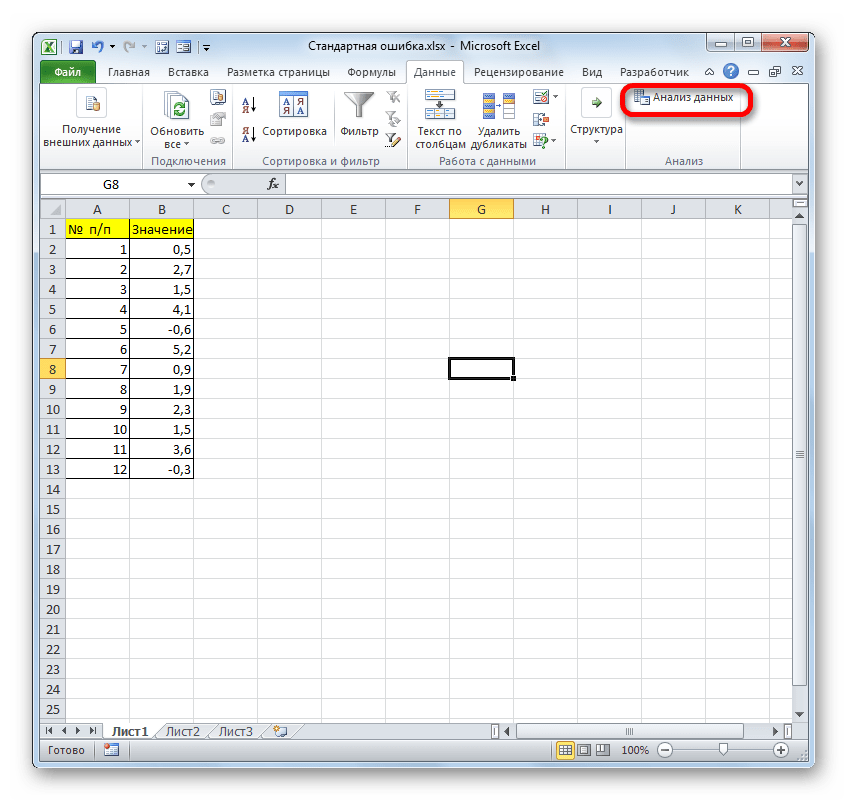
После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».

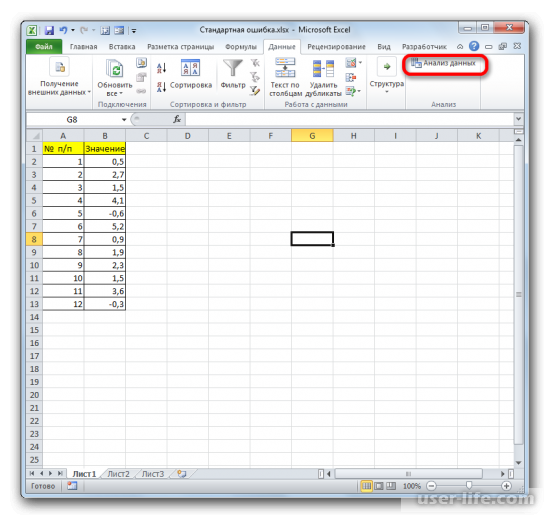
После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.

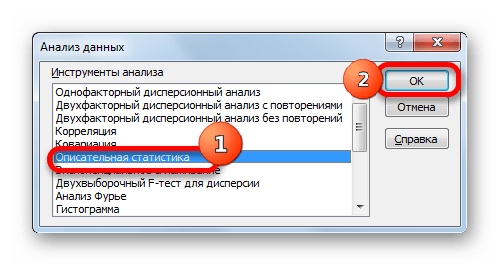
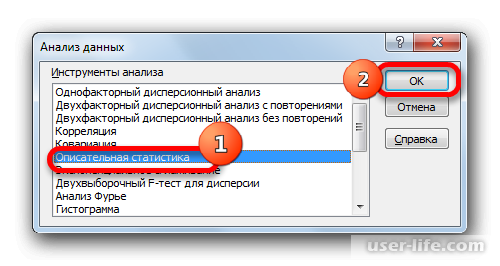
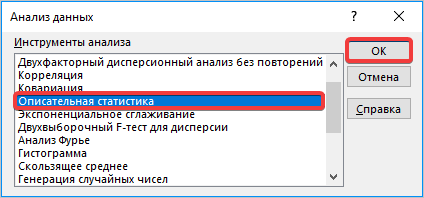
Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.

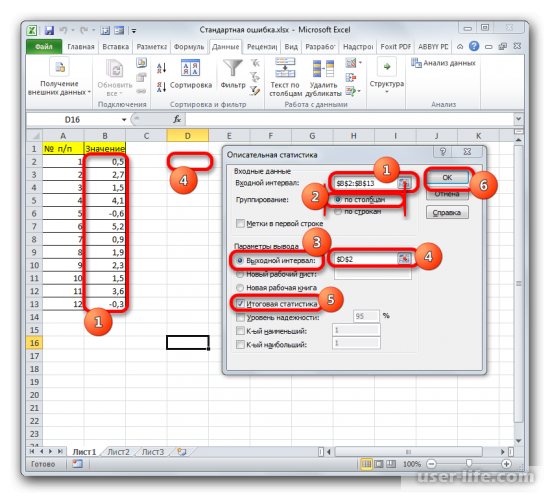
Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».

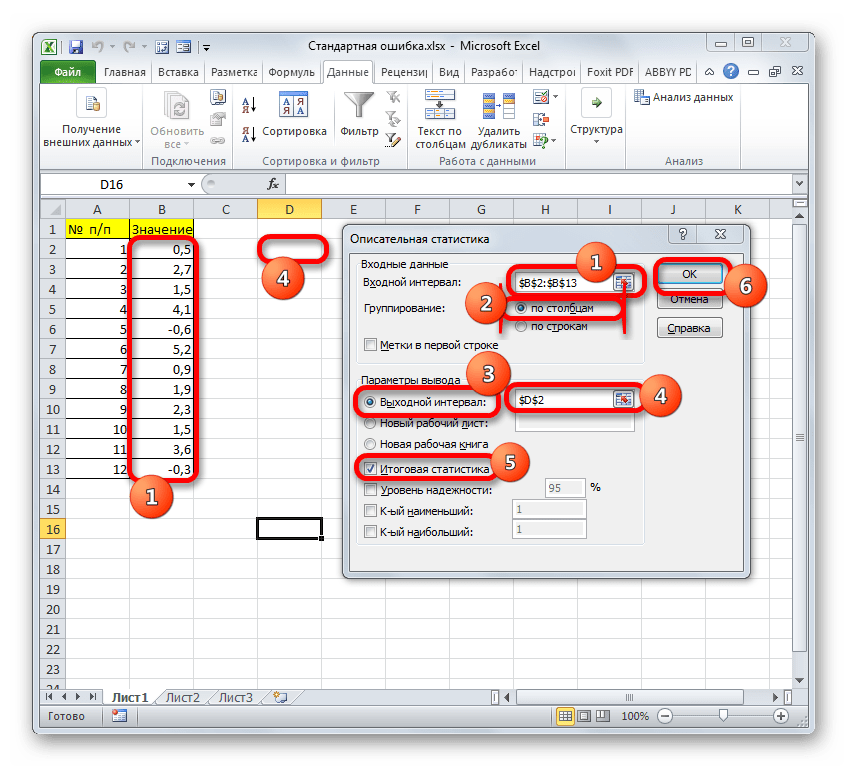
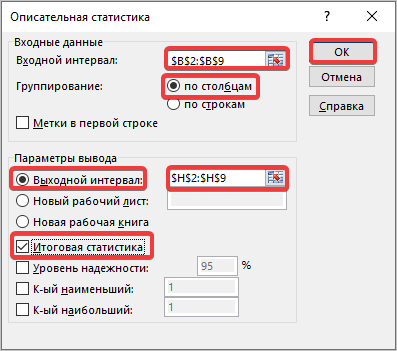
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.

В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.

Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.

Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:

• На новый лист;
• В новую книгу (другой файл);
• В указанный диапазон текущего листа.

Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.

Далее следует блок настроек определяющий, какие именно данные нужно вводить:

• Итоговая статистика;
• К-ый наибольший;
• К-ый наименьший;
• Уровень надежности.

Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.

После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.

После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.

Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Расчет с помощью комбинаций функций

На примере рассмотрим составленный алгоритм действий по расчету ошибки средней арифметической с использованием комбинаций функций. Для того чтобы выполнить задачу, нужно использовать операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ. Выборка будет использоваться из 12 чисел, которые представлены в таблице.

Выделите ячейку, в которой отобразится итоговое значение стандартной ошибки. Кликаете на иконку «Вставить функцию».

Появится Мастер функций, в котором нужно произвести перемещение в блок «Статистические». Появится список наименований, выбираете «СТАНДОТКЛОН.В».

Запустится окно аргументов выбранного оператора, предназначенного для оценивания стандартного отклонения при выборке. У него такой синтаксис — =СТАНДОТКЛОН.В(число1;число2;…). Устанавливаете курсор в полу «Число1». Далее, зажав левую кнопку мыши, выделяете курсором весь диапазон выборки, чтобы координаты этого массива отобразились там же в поле окна. Кликаете на ОК.

В ячейке появится проделанный результат, но это еще не то, что мы хотим получить в итоге. Теперь нужно стандартное отклонение разделить на квадратный корень от числа элементов выборки. Выделяете ячейку с нужной функцией и устанавливаете курсор мышки в строку формул. Дописываете выражение, которое там уже существует, знаком деления (/). Далее нажимаете на пиктограмму перевернутого вниз углом треугольника (находится слева от строки формул). Должен открыться список недавно использованных функций. Находите оператора «КОРЕНЬ» и нажимаете на него. Если его нет в списке, то кликайте на «Другие функции…».

Должен снова запуститься Мастер функций, в котором нужно перейти в категорию «Математические». Выделяете там «КОРЕНЬ» и кликаете ОК.

Далее должно открыться окно аргументов функции КОРЕНЬ. Его синтаксис простой — =КОРЕНЬ(число). Устанавливаете курсор в поле «Число» и нажимаете на уже знакомый треугольник, чтобы показался список последних использованных функций. Находите «СЧЕТ» и нажимаете на него. Если в списке его нет, тогда нажимаете на «Другие функции…».

Появится раскрывшееся окно Мастера функций, в котором нужно переместиться в группу «Статистические». В ней выделяете «СЧЕТ» и кликаете ОК.

Должно запуститься окно аргументов функции СЧЕТ. Синтаксис функции будет таким — =СЧЁТ(значение1;значение2;…). Ставите курсор в строку «Значение1» и зажимаете левую кнопку мыши, чтобы выделить весь диапазон выборки. Когда координаты отобразятся, жмите ОК.

Когда будет выполнено последнее действие, то не только произведется расчет количества ячеек, которые заполнены числами, но и вычисляется ошибка средней арифметической. Величина будет выведена в ячейку с размещенной сложной формулой, вид которой таков — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)).

Если выборка до 30 единиц, тогда лучше применять немного другую формулу — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1).

Применение инструмента «Описательная статистика»

Когда будет открыт документ с выборкой, нужно перейти во вкладку «Файл».

В левом вертикальном меню заходите в раздел «Параметры».

Должно запуститься окно параметров Excel, в левой части которого нужно перейти в «Надстройки».

В самом низу окна находите «Управление» в выставляете в нем параметр «Надстройки Excel». Кликаете на «Перейти…» справа от него.

В окне надстроек появится список скриптов, которые доступны и нужно отметить галочкой «Пакет анализа», а затем нажать ОК.

Теперь на странице должна появиться новая группа инструментов «Анализ». Для перехода к ней кликаете на вкладку «Данные».

Кликаете на «Анализ данных» в блоке инструментов «Анализ» в самом конце.

Запустится окно выбора инструмента анализа, в котором необходимо выделить «Описательная статистика» и нажать справа на ОК.

Далее запустится окно настроек инструмента комплексного статистического анализа «Описательная статистика». Здесь нужно установить все так, в зависимости от того, что именно вы хотите получить в итоге.

После всех совершенных манипуляций, инструмент «Описательная статистика» должен отобразить результаты обработки выборки на текущем листе. Разноплановых статистических показателей будет немало, но среди них находится и тот, который нам нужен – «Стандартная ошибка».

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ 2 – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Стандартная ошибка появляется при прогнозировании каких-либо данных или арифметических вычислениях, поэтому важно научиться находить этот параметр. В этой публикации разбираем, как найти и исправить стандартную ошибку путем использования инструментов Excel.

Расчет средней арифметической ошибки

В Microsoft Excel цельность и однородность выборки определяется при помощи стандартной ошибки. Стандартная ошибка — это квадратный корень из дисперсии. В приложении предусмотрено два варианта поиска стандартной ошибки: при помощи пакетного анализа и расширенных функций программы.
Чтобы найти значение средней арифметической, необходимо выполнить деление суммарной величины выборки на ее количество в электронной книге.

Расчет стандартной ошибки при помощи встроенных функций

Для того, чтобы правильно вычислять, необходимо изучить пошаговую инструкцию. В этом способе подбор результатов будет осуществляться с помощью комбинированных манипуляций.

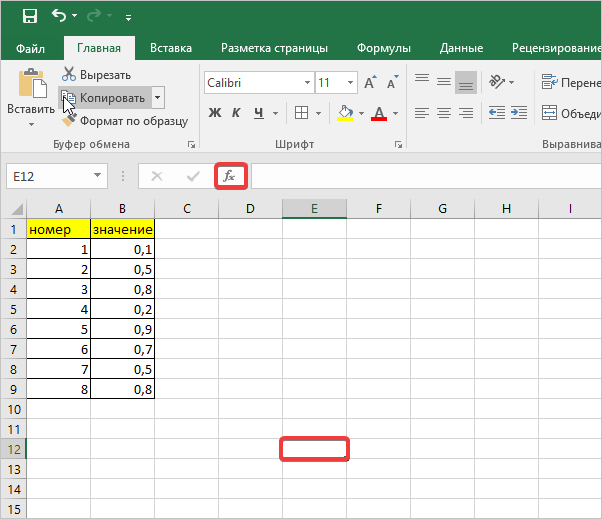
1. Для расчетов будем использовать таблицу с выборкой чисел. Кликаем на любой пустой ячейке на листе, где будет отображаться результат. Затем нажимаем кнопку «Вставить функцию.

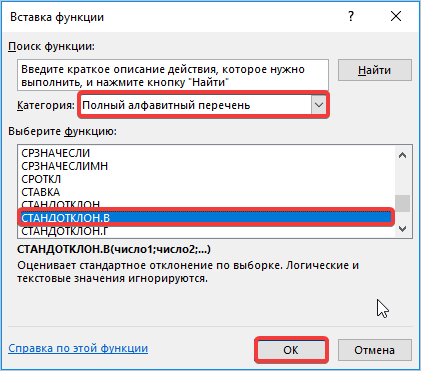
1. Далее перед вами открывается диалоговое окно, в котором необходимо использовать «СТАНДОТКЛ.В», для этого в поле «Категория» необходимо выбрать «Полный алфавитный перечень». Затем нажмите кнопку «ОК».

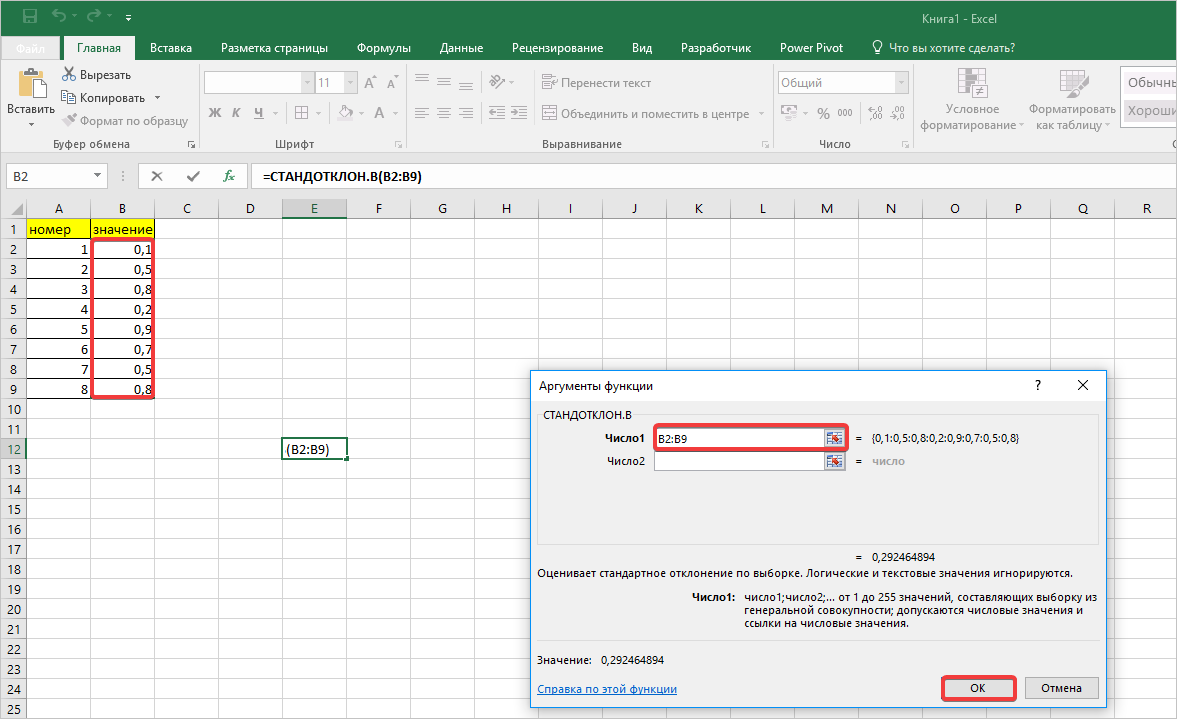
1. В окне «Аргументы функции» кликаем в первом поле «Число 1», затем выполняем выделение мышью диапазона ячеек со значениями таблицы и нажимаем кнопку «ОК».

1. Далее активируем ячейку с нашими значениями, переходим в строку формулы и ставим после значений наклонную линию. Переходим в поле наименования, кликаем на указывающий вниз флажок, где из списка выбираем «Другие функции».

1. Снова активируется окно с перечнем функций, в котором необходимо выбрать категорию «Математические», затем функцию «Корень». Далее нажмите кнопку «ОК».

1. Далее открывается окно, в котором необходимо заполнить поле с числом. Для этого переходим в поле «Имя», где спускаемся к пункту «Счет». Если его нет, ищите в дополнительных функциях.

После выполнения этих шагов, стандартная ошибка высчитывается автоматически, пользователю остается только сверить их и проверить значение на некорректное отображение.

Важно!

Для малых и стандартных выборок необходимо использовать разные формулы. В первом случае (если находится до 30 значений), ее необходимо видоизменить.

Решение задачи с помощью опции «Описательная статистика»

Благодаря опции «Описательная статистика» удается выполнить вычисление по различным критериям. По этим правилам удается найти среднюю арифметическую ошибку. Для использования данного метода предварительно нужно запустить «Пакет анализа».

1. Переходим во вкладку «Файл», где перемещаемся в пункт «Параметры». Далее нажимаем на запись «Надстройки».

1. Открывается окошко, в нем в графе «Управление» должно быть прописано «Надстройки Excel», затем рядом нажимаем кнопку «Параметры».

1. В появившемся окне находим «Пакет анализа» и нажимаем кнопку «ОК».

1. Далее выбираем любую свободную ячейку, переходим во вкладку «Данные» и нажимаем «Анализ данных» в блоке «Анализ».

1. Происходит запуск вспомогательного окошка, в котором необходимо выбрать из всех инструментов «Описательную статистику» и нажать кнопку «ОК».

1. Открывается новый мастер значений. Здесь нужно вводить данные предельно внимательно. В поле «Входной интервал» вносим адрес диапазона ячеек с выборкой. Затем указываем параметр «Группирование» «По столбцам». Затем выбираем место для «выходного интервала», его должно быть столько же, сколько и «входного». Ставим галочку напротив «Итоговая статистика» и нажимаем кнопку «ОК».

В результате вычислений вы получаете небольшую таблицу, в которой указаны все данные с определенной стандартной ошибкой.

При
большом объёме выборки её анализ требует
большого объёма вычислений, поэтому
естественно проводить его за компьютером.
Имеется большое число программных
средств, как специально предназначенных
для статистического анализа, так и
содержащихся в универсальных
программах в качестве подпрограмм и
опций. Достаточно возможностей для
этого предоставляет, в частности,
доступная всем программаExcel.
Команды для
проведения статистического анализа
можно найти в меню «СервисАнализ
данных» и в меню «ФункцииСтатистические»
и «ФункцииРабота
с базами данных».

Таблица
1.

Рассмотрим
работу в этой среде на следующем примере.
В лабораторном практикуме группа из 25
студентов определяла концентрацию
некоторого вещества в выданном им
растворе. Каждый из них сделал по 4
параллельных определения. Их результаты,
округлённые до 0,5 г/л я занёс в таблицу
Excel
(табл.1).У
меня образовался массив, содержащий 4
столбца B,C,D
и E,
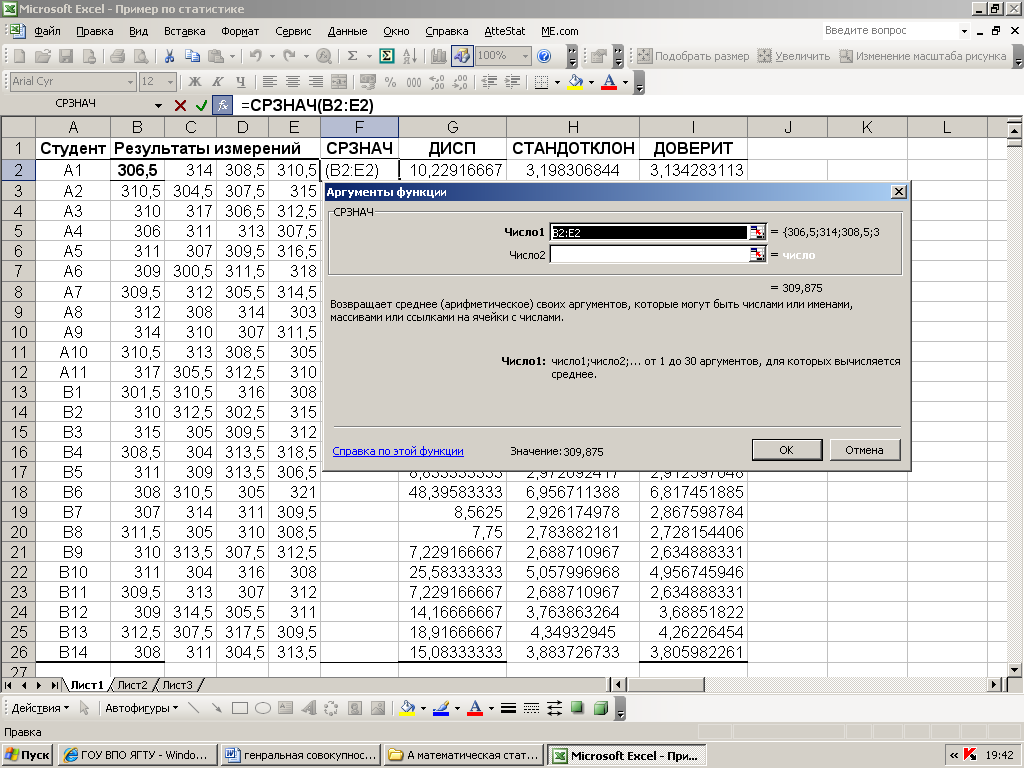
и 25 строк с №2 до №26. Далее я хочу найти
минимальное число из этого массива –
нижнюю границу выборки. Я щёлкаю по
пустой ячейке, в которой хочу найти
ответ, затем навожу курсор на «»,
и нажимаю левую клавишу мыши. Открывается
окно выбора функций – «Мастер функций».
В разделе «Категории» я открываю
«статистические» и нахожу тамМИН.

После
щелчка мышью по этому названию и “OK”
открывается диалоговое окно «Аргументы
функции» с пометкой МИН.
В окошко,
помеченное «Число 1», можно ввести сами
числа, что, конечно, неудобно. Вместо
этого я щёлкаю мышью по крайней левой
верхней клетке массива, затем нажимаю
“Shift”
и одновременно щёлкаю по крайней правой
нижней клетке. При этом в вышеуказанном
окошке появляются границы массива в
виде “$B$2:$E$26.
Ответ «300,5» появляется сразу, а при
щелчке «OK»
— в заготовленной клетке. Точно так же
я могу применить эту функцию к любой
прямоугольной части этого массива,
вызвав саму функцию МИН
(теперь её
позывной можно найти в категории
«Последние») и отметив, как описано
выше, щелчками мыши, клетки в начале и
конце выбранной части массива. Впрочем,
выделять массив можно и движением мыши,
если сначала навести курсор на начало
массива, нажать левую клавишу мыши, и,
не снимая нажатия, провести курсор до
конечной точки массива.

Конечно,
такое подробное описание вызовет улыбку
у продвинутого пользователя, но, возможно,
среди читателей есть и такие, которые
впервые в жизни откроют документ Excel.

Для
краткого описания действий при
использовании других функций будем
использовать следующие обозначения:

ЩАа
– щелчок по клетке начала диапазона,

ЪЩЯя
— щелчок по клетке конца диапазона с
одновременным нажатием Shift,

ЩСс
– щелчок по свободной ячейке, в которой
будет указан результат.

,
серв., дигр., адат, стат. – щелчки по
значкам
,
«сервис», «диаграмма», «анализ данных»,
«статистические» соответственно.
Напомним, что если какая-либо функция
используется повторно, то быстрее найти
её не через «статистические», а через
«последние».

Итак,
считаем, что в таблицу Excel
внесены
данные выборки в виде строки, столбца,
или двумерного массива. Цели и действия
представлены в таблице 2.

Таблица
2.

Что требуется найти	Действия
Объём выборки	ЩСс,, стат.,СЧЕТ, ЩАа, ЪЩЯя,
Нижнюю границу	ЩСс,, стат.,МИН, ЩАа, ЪЩЯя,
Верхнюю границу	ЩСс,, стат.,МАКС, ЩАа, ЪЩЯя,
Среднее арифметическое	ЩСс,, стат.,СРЗНАЧ, ЩАа, ЪЩЯя,
Моду	ЩСс,, стат.,МОДА, ЩАа, ЪЩЯя,
Медиану	ЩСс,, стат.,МЕДИАНА, ЩАа, ЪЩЯя,
Нижний квартиль	ЩСс,, стат.,КВАРТИЛЬ, ЩАа, ЪЩЯя, затем щёлкнуть по окну «значение» и ввести число «1»,
Верхний квартиль	ЩСс,, стат.,КВАРТИЛЬ, ЩАа, ЪЩЯя, затем щёлкнуть по окну «значение» и ввести число «3»,
Выборочную дисперсию	ЩСс,, стат.,ДИСП, ЩАа, ЪЩЯя,
	ЩСс,, стат.,СТАНДОТКЛОН, ЩАа, ЪЩЯя,
Доверительный интервал для среднего	ЩСс,, стат.,ДОВЕРИТ, ЩАа, ЪЩЯя,
Асимметрию	ЩСс,, стат.,СКОС, ЩАа, ЪЩЯя,
Эксцесс	ЩСс,, стат.,ЭКСЦЕСС, ЩАа, ЪЩЯя,

В
таблице 1 в столбцах F—I
вы видите результаты выполнения
соответствующих функций для каждой из
25 строк массива. При этом нет необходимости
вводить формулу функции в каждую строку
отдельно – достаточно ввести её в первую
строку, а в окошко аргументов ввести
координаты начала и конца этой строки:

После
нажатия «»
в ячейке, в которую введена данная
формула, появляется соответствующий
результат:

Если
теперь навести курсор на чёрный квадратик
в нижнем правом углу этой ячейки, и при
нажатой левой клавише мыши провести
его вдоль столбца до последней строки
массива данных, то после отпускания
клавиши весь столбец заполнится
результатами, полученными для всех
остальных строк по той же формуле.

Для
группировки данных и получения
интервального ряда можно использовать
функцию ЧАСТОТА.
Для её
применения
сначала
формируем столбец интервалов. Для нашего
примера, в котором объём выборки
,,
удобно выборку разбить на 7 равных
интервалов шириной 3 . При этом в ячейки
для массива интервалов вводим только
значения верхних границ интервалов.
Так, в ячейкуя внёс число 303 для интервала,
в— число 306 для интервала,
…, в— 321 для интервала.
Затем я выделяю свободную ячейку,
и щёлкаю по.
Появляется мастер функций, в котором я
нахожуЧАСТОТА
и раскрываю
шаблон для ввода аргументов. После
ввода вышеописанным способом границ
массива данных щёлкаем по окну массив
интервалов и
выделяем для ввода ячейки
.
Обратите внимание, что выделена одна
дополнительная ячейка, как этого требует
синтаксис функции.

После
нажатия
в ячейкепоявляется число вариант со значением,.
Для вывода остальных значенийнадо выделить ячейки,
после чего нажать клавишу,
а затем.
В результате в столбцеи появятся все компоненты вектора
частот.

ЧАСТОТА
303	4
306	12
309	23
312	31
315	21
318	7
321	2

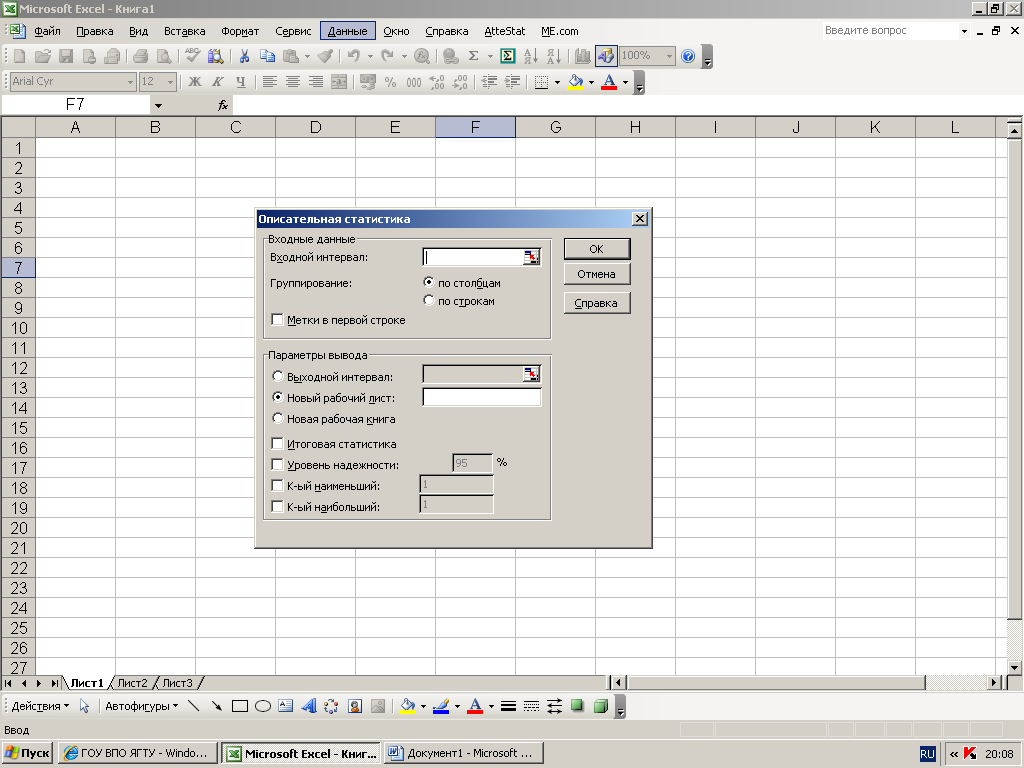
Рассмотрим
теперь, какие возможности для первичной
обработки выборки имеются в меню
«сервис
анализ данных». Раскроем диалоговое
окно«описательная
статистика».

Первая
строка «Входной
интервал»
нам уже знакома: данные в неё можно
внести действиями ЩАа, ЪЩЯя, или
движениями мыши с нажатой правой кнопкой,
или непосредственно введя в окошко
номера левой верхней и правой нижней
ячеек массива, разделённые двоеточием
Аа:Яя. Далее предлагается выбрать
группировку – «По
строкам»
или «По
столбцам».
Дело в том, что эта «описательная
статистика»
может обрабатывать одновременно большое
количество выборок, каждая из которых
может быть введена либо в виде строки,
либо в виде столбца. Поэтому, если мы
выделим массив, содержащий 25 строк и 4
столбца, то программа не
будет рассматривать его как одну выборку,
содержащую 100 вариант. Если мы пометим
окошко «По
столбцам», то
программа будет обрабатывать массив
как 4 выборки по 25 вариант в каждой.
Соответственно, при флажке «По
строкам» мы
получим обработку 25 выборок по 4 варианта.
Далее следует окошко
«Метки в первой строке/столбце». Если
его не помечать, то результаты обработки
каждой из выборок будут помечены
надписями «Строка (Столбец) 1», «Строка
(Столбец) 2», «Строка (Столбец)3»… .Если
же мы хотим , чтобы результаты были
обозначены иначе, (например, фамилиями
студентов), то мы при вводе указаний
массива данных в строку Входной
диапазон должны
захватить и стоящий перед ним столбец
(строку) меток (фамилий или номеров
опытов в данном примере). На этом ввод
данных завершается.

Куда
выводить результаты:

Строка1
Среднее	309,875
Стандартная ошибка	1,599153422
Медиана	309,5
Мода	#Н/Д
Стандартное отклонение	3,198306844
Дисперсия выборки	10,22916667
Эксцесс	-0,02453947
Асимметричность	0,598903954
Интервал	7,5
Минимум	306,5
Максимум	314
Сумма	1239,5
Счет	4

Параметры
вывода. Обычно при открытии
диалогового окна активизировано окошко
Новый рабочий лист.
Это означает, что результаты будут
выведены на новом листе, номер которого
при желании можно задать, так же как и
номер новой книги в окошке Новая
рабочая книга. Если же
надо поместить результаты на исходном
листе, то надо активизировать окошко
Выходной интервал,
после чего щёлкнуть по свободной ячейке,
которая будет левой верхней ячейкой
выходного массива.

Что
выводить.

При
установке флажка
«Итоговая статистика» для
каждой выборки будет выведена таблица
такого вида:

В
этой таблице под стандартным отклонением
понимается величина выборочного
стандарта
,
под стандартной ошибкой – выборочный
стандарт среднего,
интервал – разность между максимальным
и минимальным значениями выборки, сумма
– сумма всех значений выборки, счёт –
объём выборки. Остальные термины
пояснения не требуют.

Если
активизировать окошко «Уровень
надёжности»,
то выводится строка со значением
полуширины симметричного доверительного
интервала, соответствующим указанной
в этом окошке доверительной вероятности
и равным произведению
на соответствующий квантиль распределения
Стьюдента:

Уровень надежности(95,0%)

5,089219898

Активизация
окошек К-ый
наименьший и
К-ый наибольший позволяет
выводить к-ое в порядке возрастания и
(или) к-ое в порядке убывания значения
в выборке, соответствующие указанным
номерам. Значениям к=1 соответствуют
минимальное и максимальное значения
вариант.

Обратимся
теперь к графическому изображению
данных. Для этого в меню Анализ
данных есть
функция Гистограмма,
в диалоговом окне которой в окошко
Входной
интервал вводим
одним из описанных ранее способов номера
ячеек начала и конца массива данных.
Затем в окошко Интервал
карманов вводим
таким же образом номера массива, в
котором указаны верхние границы
интервалов, на которые мы решили разбить
выборку (см. выше описание функции
Частота).
Флажок Метки
надо устанавливать только в том случае,
если в массив данных включён и столбец
меток. Как и в вышеописанных функциях
ставим флажок Новый
лист или
Новая книга (с
указанием номера или без), или Выходной
интервал. В
последнем случае в активизированное
окошко вводим номер левой верхней ячейки
диапазона вывода результата. Игнорируя
надпись Парето,
помечаем
Интегральный процент и
Вывод графика.
выводит нам
во-первых,
таблицу, два первых столбца, как и после
исполнения функции Частота
представляют
интервальный вариационный ряд, а третий
столбец – аналог интегральной функции
распределения, показывает долю вариант
в выборки, имеющих значение меньшее или
равное указанного в первом столбце.
Кроме этого, появляется и графическое
изображение – гистограмма и график
интегрального процента. Можно редактировать
это изображение, но здесь мы не будем
рассматривать все многочисленные
возможности этого.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #